Fault Coverage-Based Test Case Prioritization and Selection Using African Buffalo Optimization

1  Introduction

Software is an inevitable part of our day-to-day lives. In the software development process, software testing is an important part that needs to be handled effectively. Regular testing and maintenance are needed for effective bug-free working and to keep it updated with the new version. This process needs regular maintenance (re-testing) to defeat its obsoleteness. The re-testing is known as Regression testing [1]. It minimizes the cost and effort required during various testing scenarios like test case selection (reducing the size of the original test suite) and test case prioritization (ordering the test cases for execution) [2]. Regression test selection was first proposed in 1977 [3] for the maintenance of the software. In state-of-the-art, various regression test selection techniques are used which include: Data-flow based approach [4], Control Flow Graph-walking approach using incremental programming [5], Path Analysis approach [6], Dynamic slicing [7], Test-tube system [8], Firewall technique [9], and many more. Evolutionary techniques are also utilized in solving regression test selection [10,11]. The detail of the test case selection procedure is determined by how a specific technique defines, seeks, and identifies modifications in the program. Further, test case prioritization techniques like Coverage-based, Cost-aware, and Time Aware are categorized based on prioritization criteria. Coverage-based prioritization focuses on maximum code coverage as early as possible [1]. Cost-aware prioritization was proposed by Elbaum et al. [12]. Walcott et al. [13] proposed the concept of time-aware prioritization and the idea was further adopted in [12]. Time-aware prioritization aims to yield a prioritized subset of test cases that are executed within a specified time budget. In addition, fault proneness estimation [14–16] improves the efficiency of test case prioritization methods. State-of-the-art prioritization work mostly uses structural coverage. Although there are prioritization techniques that are based on non-structural criteria as well [1,17,18]. The concept of lexicographic ordering [18,19] is shown to enhance the performance of the test suite prioritization technique. Recently many evolutionary approaches [19,20] are developed for test case selection or prioritization. A genetic algorithm, an evolutionary approach, is successfully applied for multi-objective regression testing of safety-critical systems [21–24]. Recent reviews [25] comprehensively survey the application of Machine Learning approaches for test case selection and prioritization. Various combinatorial optimization approaches inspired by nature are also interesting areas of research. In this paper, the proposed methodology focuses on performing regression testing within given time constraints and killing the maximum faults.

In this paper, the proposed methodology is tested for test suite prioritization and selection. The proposed approach is inspired by the real-life behavior of African or Cape buffalos that move in herds in search of food and safe locations. African Buffalo Optimization is a nature-inspired approach proposed by Odili et al. [24]. Its swarm intelligence technique is applied to various optimization problems including the traveling salesman problem [25], job scheduling problem [26], flow shop scheduling problem [27], scheduling in the ZigBee network [28], and more. The proposed work is an extension of [29] which puts forwards a detailed application and analysis of the African Buffalo Optimization (ABO) method to solve regression test prioritization and selection. The results of applying ABO to Non-Deterministic Polynomial-Time-Hard problems show encouraging results along with its ease of applicability due to the use of simple operators. For a detailed explanation of the proposed algorithm, its working is explained with an example in Section 3.

Outline: The rest of the paper is organized as follows: Section 2 discusses a brief description of the general ABO approach and features of African buffalos used in optimization. Section 3 discusses the application of ABO in regression test prioritization and selection. It also gives a formal description of the proposed approach with the algorithm, its complexity, and an explanation with the help of an example. Section 4 concludes, with a discussion of the proposed approach and its results on the test data, along with future work.

2  Background, Related Works, and Motivation Behind Proposed Work

In this section, the area of test case prioritization, the problem definition of test case prioritization, and a brief overview of recent available literature in the area are discussed. A comprehensive view of concept definitions is given as follows:

Fault: Fault arises in software due to errors or mistakes while its development. It is detected when the actual results fail to match the expected results.

Test Case: A Test case refers to a document corresponding to a test scenario, aiming for verification of a specific requirement. It comprises test data, pre-conditions, the expected results, and the post-conditions.

Fault Matrix: Fault Matrix is constructed by mapping all the faults detected by each test case. The fault matrix is constructed by considering an ideal condition that the system is aware of the fault detection information.

Average percentage fault detection rate: Average Percentage Fault Detection rate (APFD) is a metric used for quantification of the rate of fault detection. Measurement is used to quantify the rate of fault detection [30]. It quantifies the rate at which the prioritized test cases can detect the faults [31]. The larger the value of APFD, the better the quality of the test suite. APFD value is calculated using Eq. (1):

APFD=1−TF1+ TF2+…+TFnn × m+12× n(1)

where ‘T’ denotes the test suite comprising of ‘n’ test cases and F denotes the set of faults revealed by T. ‘TF1’ denotes the 1st test case picked up from the ordered test suite that can detect the ith fault.

Multi-objective Test case selection and Prioritization (TCS&P) Problem: This problem deals with the selection and prioritization of test cases from a test suite, to fulfill the desired objectives. The objective is the detection of maximum faults so that the overall execution time of test cases is minimized. This helps in reducing overall testing effort, thus minimizing the overall cost incurred in software testing. State-of-the-art in TCS&P has gained increased attention in the past decade [32]. The rising software demand calls for the existing software to be modified and re-checked for its proper functioning. This leads to an emerging need for effective and efficient ways to do regression testing of the modified software. A recent tertiary study on TCS&P [33] indicates that the use of evolutionary and search-based techniques is rising since the year 2015. Amongst these techniques, the Genetic Algorithm (GA) is the most popular technique applied by various researchers in the area [34,35]. Particle Swarm Optimization (PSO) [36] and Ant Colony Optimization (ACO) are also popular techniques. Moreover, other techniques include NSGA-II [37], Bacteriological Algorithm [38], Bee Colony Optimization, and Hill Climbing [34]. Search-based techniques are increasingly adopted to solve such optimization [39–41]. There are many search-based techniques, that are successfully applied in the area of TCS&P. However, there are newer and more efficient search-based approaches available in the literature which is easier to use and give efficient results on other optimization problems. Time-bound TCS&P is an NP-Complete problem. It is solved using many approximation optimization algorithms, however since any approximation algorithm does not guarantee an optimal solution, thus search for new and better algorithms remains an open area [42–48]. ABO is a search-based optimization approach proposed in 2015. It is a randomized approximation approach that is applied to various NP-complete problems [49–55]. Other nature-inspired algorithms are applied to regression testing. One such algorithm is ACO. It is a well-known and highly applied nature-inspired technique and is chosen for comparison with the ABO approach. An APFD-based comparison between ACO and ABO approaches is detailed in Section 3.5. The mapping (or assumptions) of the problem of prioritizing the test suite using the ABO approach is seen in [29]. The major contributions of this paper are as follows:

•   The novel use of ABO in the area of TCS&P.

•   A detailed step-by-step demonstration of ABO on an example.

•   Proof of convergence using complexity analysis for the ABO algorithm.

•   An empirical comparative analysis of ABO with other well-known Ant Colony Optimization (ACO) technique.

3  ABO Applied to Regression Test Selection/Prioritization

Selection along with prioritization for the test cases is a multi-objective problem [56,57]. The target objectives are fault-coverage, branch coverage, node coverage, minimizing the execution time, history-based, and many more [58–64]. The proposed work focuses on selecting as well as prioritizing test cases in a test suite. Objectives achieved are Maximum Fault Coverage along with the Least Running Time for the resultant test cases in the suite. The problem of prioritization along with the selection of test cases is mapped to the problem of searching for an appropriate gazing area by the African buffalos. The aim is to get an optimized test suite. Fig. 2 depicts a block diagram of the technique used. The inputs to the system are test suite details, fault matrix, and the execution time details of the test cases in the original test suite. The input from the user is the total number of iterations that serves as the stopping condition of the system other than the primary objective of minimum execution time and maximum fault coverage. The system then produces four outputs: a) Buffalo Path from each iteration b) Best Path Details, c) Values of wk and mk for each kth buffalo, and d) ABO selected and prioritized resultant test suite.

3.1 African Buffalo Optimization (ABO)

Many nature-inspired techniques are applied to solve various optimization problems such as the intelligent migration behavior of the African buffalos, ABO [21] developed in the year 2015. African Buffalos mainly found in African forests and savannahs, migrate from one place to another in a herd to find huge green pastures to state their hunger and a location safe from any kind of danger. They organize their movement by mainly two kinds of sounds: ‘waa’ and ‘maa’. The alarming sound ‘waa’ indicates that the current place is unsafe or lacks enough food to satiate their appetite and thus needs further exploration. The sound ‘maa’ indicates that the area is appropriate for gazing and is safe [65–70]. The sound with higher intensity lets the herd decide about their movement from the current place. From this process, there are three inspiring features: “Enormous Memory” (of memorizing their movement paths), “Collaborative Alliance” and “Democratic Intelligence”. These enable African buffalos to give a stable solution to their problem. As shown in Fig. 1, “Enormous Memory” refers to the capacity of the African buffalos to memorize their movement paths spanning over a thousand miles. The phrase “Collaborative Alliance” refers to the ability to decide the movement based on the majority of the sound ‘waa’ or ‘maa’, and “Democratic Intelligence” refers to democratic behavior in case of conflict. The majority sound heard lets the herd decide whether to stay or move forward. To understand and apply the ABO approach to regression test selection/prioritization, the approach needs to be understood quantitatively and qualitatively. The locomotion of buffalos in a herd for finding an appropriate gazing area is mapped to combinatorial optimization problems [57]. The movement of the herd is calculated from the sound parameters that buffalos create. The ‘maa’ is the sound for staying and exploiting the current location and the ‘waa’ sound is for exploring new locations. This provides an appropriate blend of exploration and exploitation needed in a meta-heuristic. A fitness function is thereby calculated for the probable movement of the buffalos based on these sounds and some prefixed parameters used for learning. The equation proposed in [57] is given by Eq. (2):

wk+1=mk+C1(bgmax−wk)+C2(bpmax,k−mk)(2)

where, wk and mk represent the sounds ‘waa’ and ‘maa’, for kth buffalo, where k is a constant lying between 1 and N. The constants C1 and C2 are two learning parameters. bpmax,bgmax are path, that is the individual best of a buffalo and the universal best for the complete herd respectively.

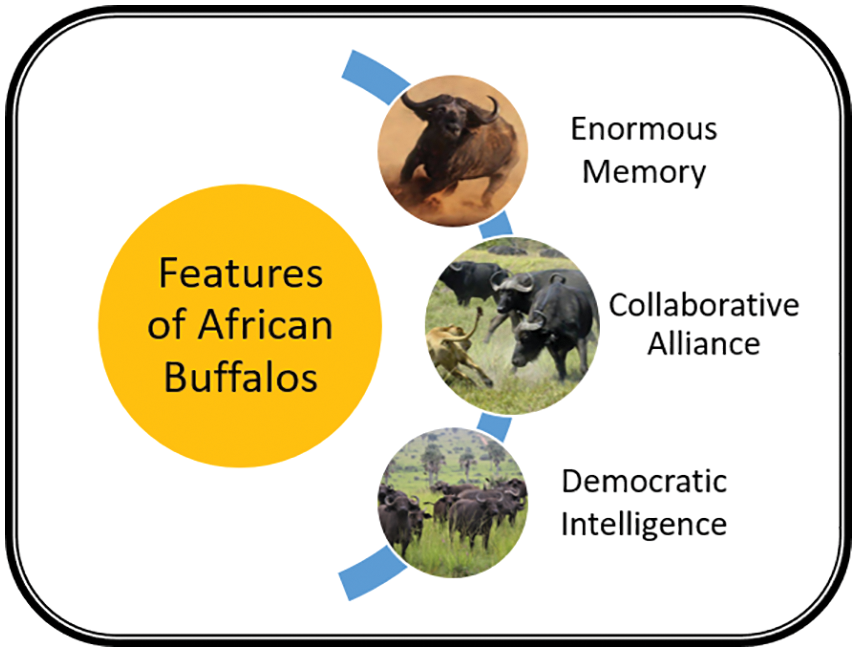
Figure 1: Features of African buffalos

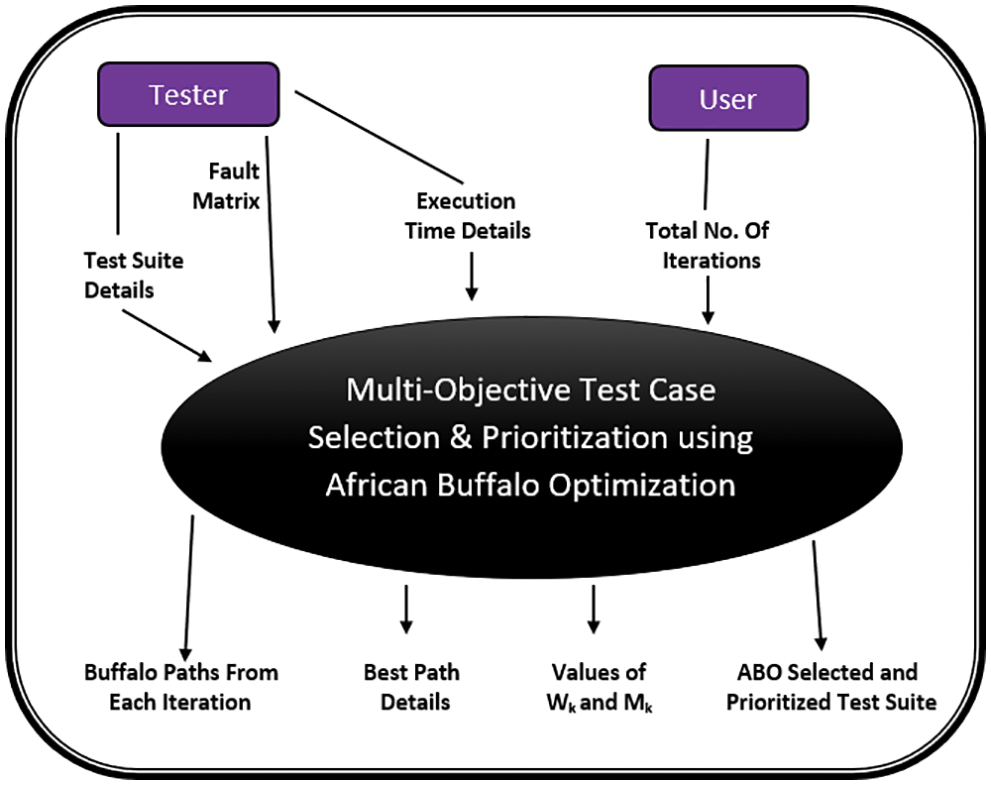
Figure 2: Block diagram of multi-objective test case selection & prioritization using ABO

The location of every buffalo is computed using Eq. (3):

wk+1=(Wk+mk)±0.5(3)

The buffalo movements are pursued and in case of no improvement, all the variables are reset.

3.2 Proposed ABO-TCS&P Algorithm

As described in Sub-Section 3.1, test suite details, fault matrix and execution time details are the basic inputs for the proposed technique [71–76]. A Block Diagram of Multi-Objective Test Case Selection & Prioritization using ABO is given in Fig. 2. Initially ‘N’ buffalos are generated for a test suite of size ‘N’. Initially, each kth buffalo is placed at the kth test case to enhance the exploration which can be achieved. Each buffalo randomly starts moving to construct a path that is considered safe (if all the faults are covered). To achieve this, the ‘maa’ sound or the m values calculated are increased with the number of faults covered (until all of them are covered). Similarly, the ‘waa’ sound or the Wk values are mapped to the time of execution of test cases that belong to the buffalo’s path. A flowchart of the proposed approach is presented in Fig. 3. The step-by-step formal description of the proposed algorithm is presented in Fig. 4.

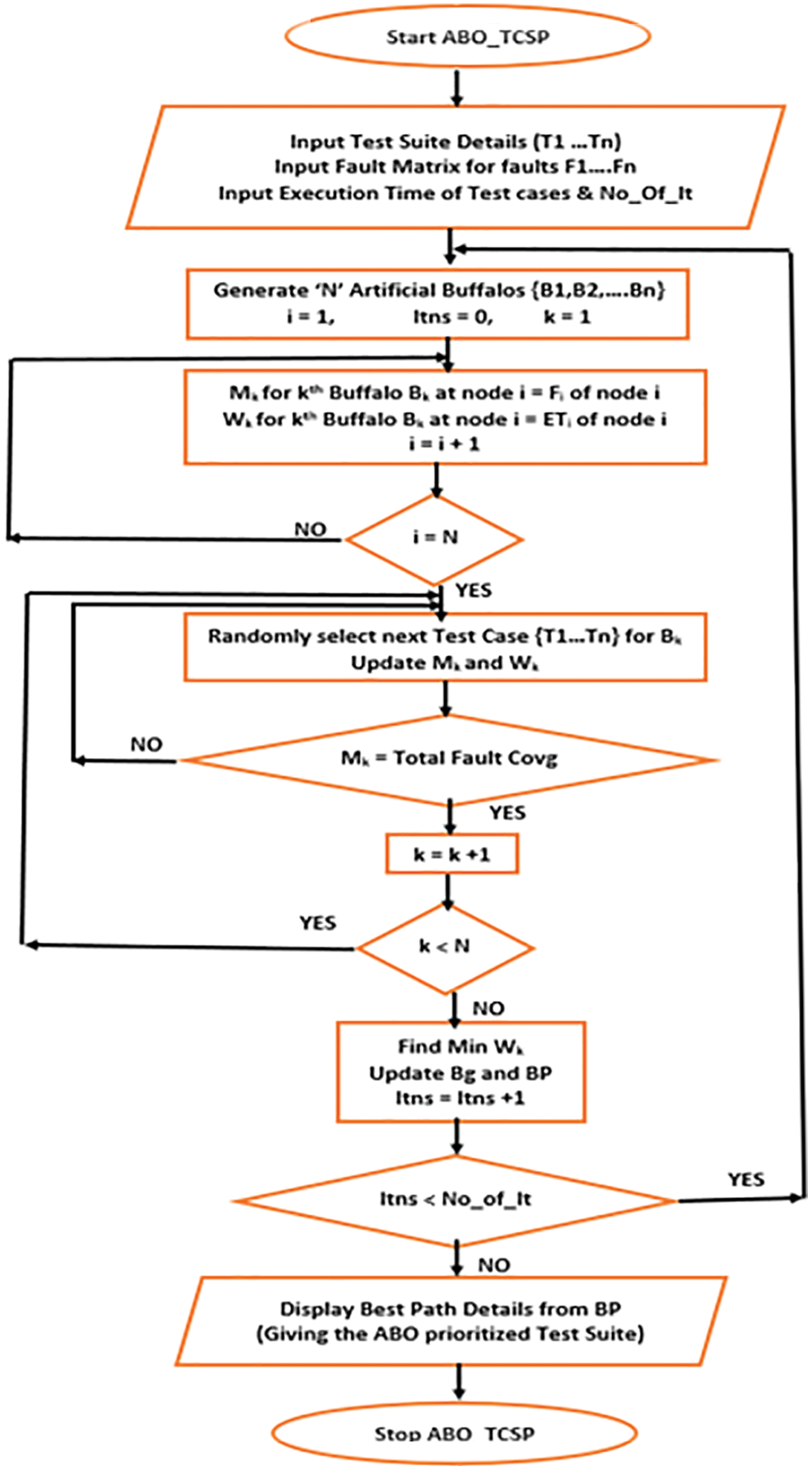
Figure 3: Flowchart of proposed ABO_TCSP

Figure 4: Proposed ABO_TCSP algorithm

Initially, the buffalos explore the search space by following a path and covering various test cases spread over the space. As they cover a test case on their path, the faults associated with the test case are considered as “killed” on that path. A buffalo’s safe place is when all the faults are killed. After each iteration, the paths covered by all the buffalos are compared based on the total execution time (sum of run time for all the test cases covered on the path). Once, all the buffalos have constructed the paths, the buffalo with the best path or the least total execution time of the selected test suite is used to update the values of Bg (global best path) and Bp (personal best path of a buffalo). This marks the end of one iteration. The same process is repeated for the ‘Stopping Criteria (SC)’ number of iterations, as desired by the user. SC represents a pre-set or user-entered number of iterations for which the steps of the algorithm are repeated. In other words, the process of buffalos looking for a safe place repeats till SC iterations, with new information added in every iteration. The same process is iterated SC times and the final solution is the path with minimum run time (that may have been found in any iteration). The best path after the final iteration yields the desired prioritized and selected test suite using ABO_TCS&P.

To effectively analyze the regression testing in terms of cost, the complexity of an algorithm is computed. The overall complexity of the proposed ABO_TCS&P is computed by summing the distinct complexities of all the consecutive steps of the algorithm. The total complexity of the Initialization step, say I1, is calculated by adding the individual complexities of all the consecutive statements from Fig. 5:

I1=1+1+N+N+1

I1=3+3∗N

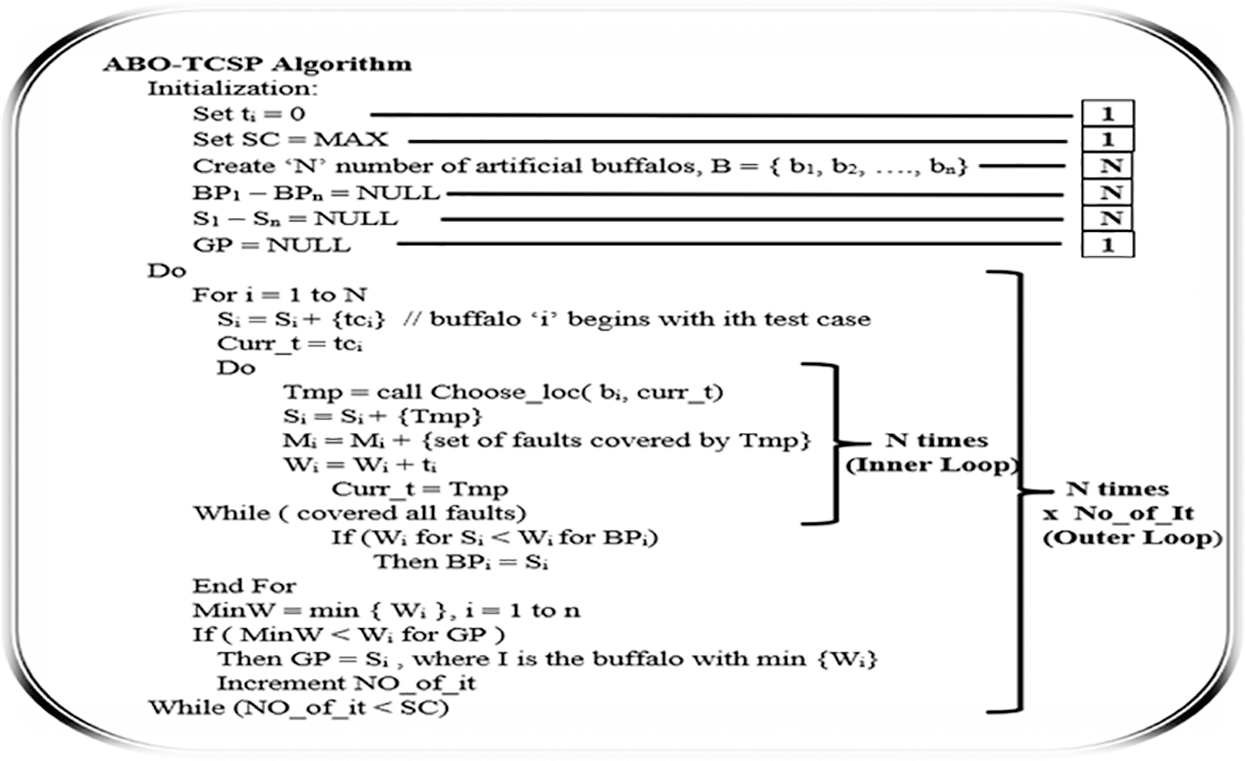
Figure 5: Complexity description for ABO_TCSP algorithm

The complexity of the next sequence of steps constituting loops say I2, can be stepwise calculated from the individual statement complexities (Fig. 5) as shown below:

Complexity of Inner Loop=N∗(1+1+1+1+1)=5∗N

Complexity of For Loop=N∗(1+1+(Complexity of inner loop)+1+1)=N∗(4+5∗N)=4N+5N∗N

The complexity of Outer Loop=No.ofIt(Complexity of for loop+N+1+1+1)

O1=No.ofIt∗(4N+5N∗N+N+3)

Thus, the Total Complexity of the proposed algorithm can be calculated as:

S = Complexity of Initialization Step + Complexity of the Outer Loop

S=I1+O1

S=3+3∗N+No_of_It∗(4∗N+5∗N∗N+N+3)

(Taking No. of_It = ‘C’ to be some positive constant)

S=3+3∗N+C∗(4∗N+5∗N∗N+N+3)

S=3+3∗C+(3+5∗C)∗(N)+5∗C∗N∗N

S<+C1∗C∗N∗N where(C is also a positive constant,thus C2=C1∗C,be another+ve constant)

S≤C2∗N∗N

Thus, the complexity of ABO_TCS&P is upper bounded by N2, or in terms of Big-O notation, it is O (N2) or O(│T│)2. This is an excellent complexity for an approximation ABO_TCS&P as compared to the NP-complete problem of time-constrained regression test selection and prioritization problem.

3.3 Explanation with Example

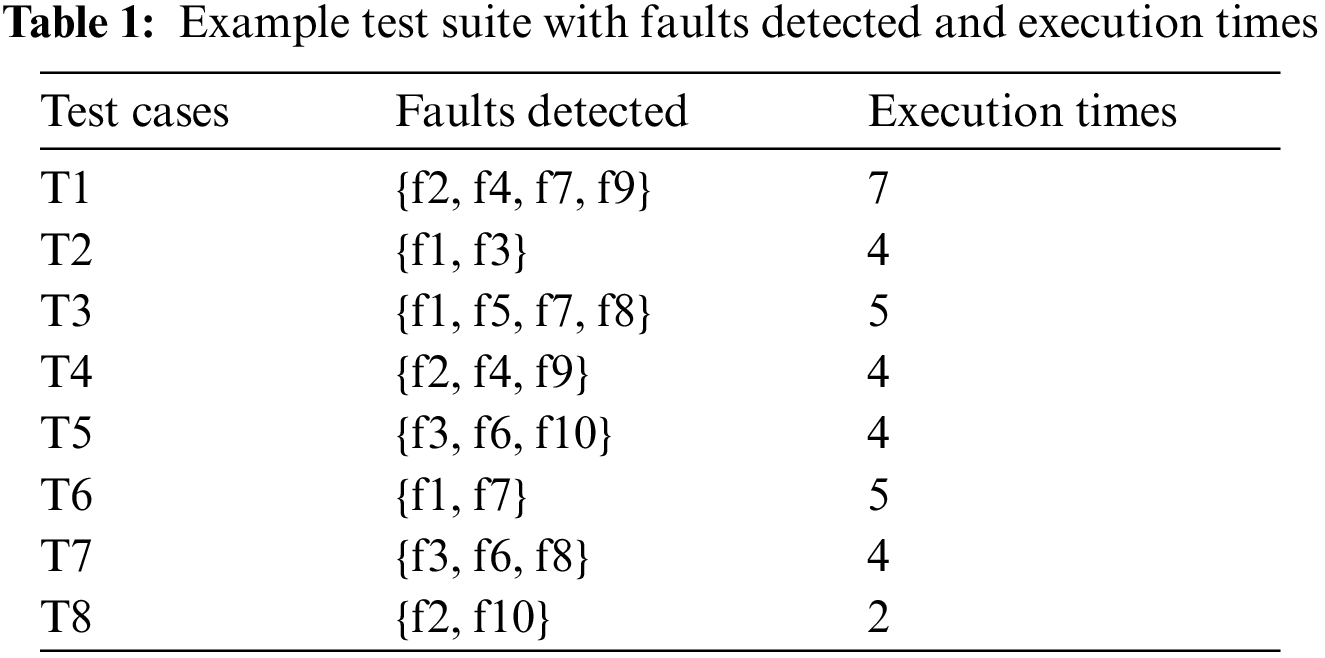
Every buffalo forms a path by finding different test cases to reveal faults until each of the faults is uncovered or the termination criteria are reached [77–81]. The buffalo leading to a path having minimum execution time eventually leads to the global best path, if it is found better [82–90]. The overall best path found at end of all the iterations gives the optimized test suite. Table 1 presents the sample test suite taken for demonstration. The test suite consists of 8 test cases along with 10 mutants. The faults killed by each test case are recorded in Table 1. Furthermore, the execution time (ms) of each test case is also recorded in Table 1.

Ex: Assume the proposed approach is executed for five iterations, i.e., SC = 5. Formerly, the buffalos are assumed to drift toward their respective ith test cases. The buffalo B1, starts from T1 killing faults {f2, f4, f7, f9} in 7 s. Hence, the M and W sounds are updated as per ABO_TCS&P to yield M1 = {f2, f4, f7, f9}, W1 = {7}. Moving as per the algorithm, the subsequent location is selected randomly by B1 is T5, following which, M and W are updated with M1 = {f1, f2, f4, f5, f7, f8, f9}, W1 = {12}. The same process is repeated until the exploitation parameter M touches its highest (which in our case is killing all the faults).

The path followed by B1 is presented in Fig. 6. As can be seen from Fig. 6, the path followed by buffalo B1 is {T1, T5, T8, T6, T7}. The aforementioned steps are repeated for all N buffalos. The paths constructed by buffalos B2-B8 are represented graphically in Figs. 7–13. In Fig. 7, Buffalo B2 begins with the test case T2 and covers T3 to T5 to T7 to T4 for constructing a path. Buffalo B2 stops at T4 as all the faults have now been killed by the test cases on the route. Now it makes, ‘waaaa’ and ‘maaaa’ sounds as per the total execution time of the path. The total run time for buffalo B2 is 21 s. As with buffalo B2, buffalo B3 begins with the test case T3. In Fig. 8, buffalo B3 then moves to the test case T8 to T7 to T1. Buffalo B3 stops at T1 as all the faults are now killed by the 4 test cases on its route. The total run time for buffalo B3 is 18 s, which is lesser than buffalos B1 and B2. Also, only 4 test cases were sufficient to kill all the faults. Thus, this path reduces the size of the test suite by almost 60%. Fig. 9 depicts the path for buffalo B4, beginning with the test case T4. B4 moves from T4 to T6 and checks whether all faults are killed. Then it moves to T1, T5, and finally, T3 which now kills all the faults. The total run time for buffalo B4 is 25 s and the 5 test cases are included. It is an approximate 80% reduction in total run time and 50% in the size of the test suite. As the exploration of paths continues with various buffalos, B5 finds a path with only 2 test cases T5 and T2. The run time being 18 s is the best path found in all the buffalos. The same can be seen in Fig. 10. Buffalo B6 explores yet another possible path from the solution space (Fig. 11). Beginning with test case T6, it covers T3, T5, T1, and T4 before killing all the faults to stop. On the path, it takes a total run time of 25 s and includes 5 test cases. Fig. 12 depicts another wonderful exploration of a new path by 7th buffalo B7. It covers only 4 test cases (T7, T5, T1, T3) before completing the path taking 20 s. This is a very promising exploration by the proposed ABO_TCS&P. At the end of the first iteration, the final buffalo B8 can initially explore yet another new path depicted in Fig. 13. On the path, it visits T8, T5, T3, T4, and T7 in a total of 19 s only. It is very encouraging to note that all the ‘n’ buffalos explore these paths in parallel, taking O (n) time only. Fig. 14 contrasts all the paths found by buffalos at the end of the 1st Iteration of the ABO_TCSP algorithm. It is inferred that beginning with separate test cases, all different paths are explored by the buffalos. After 5 iterations, the best path found is revealed from the details stored in BP. This path is the collection of the final prioritized and selected test suite from the proposed ABO_TCS&P algorithm.

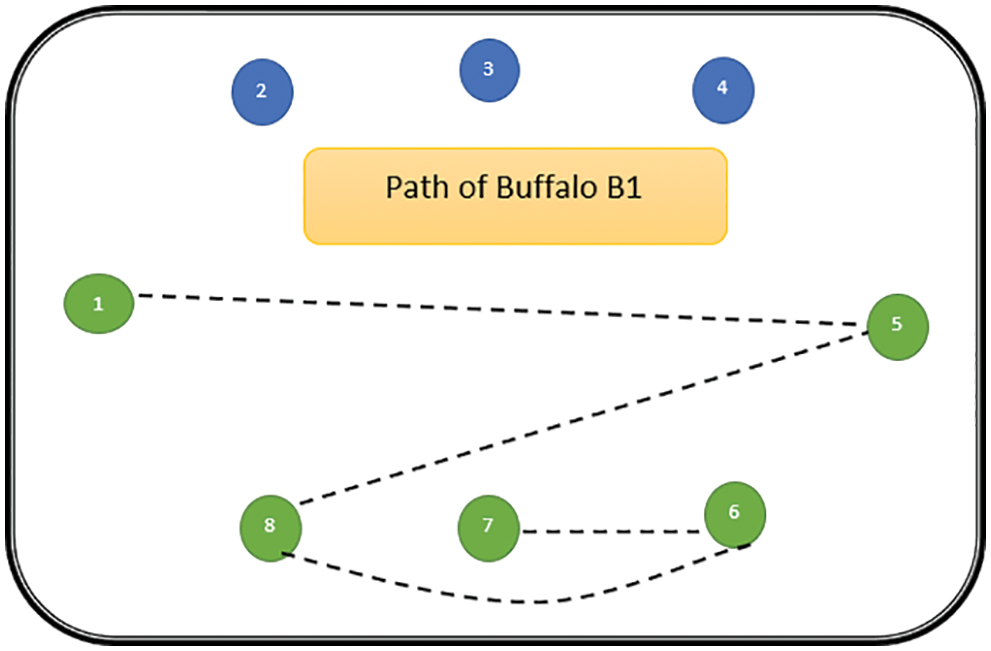
Figure 6: Path of buffalo B1

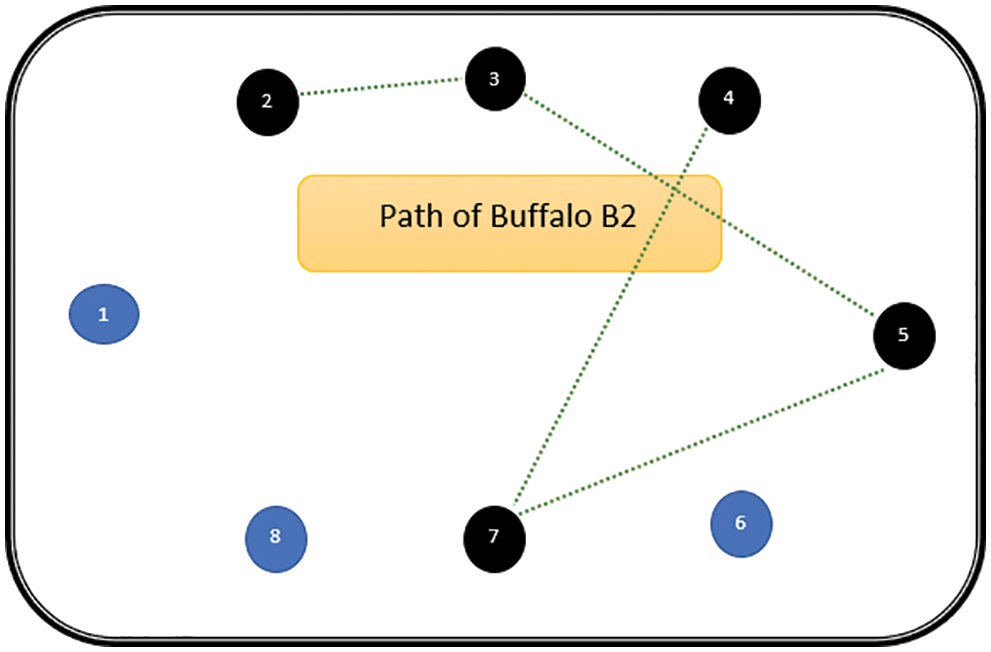
Figure 7: Path of buffalo B2

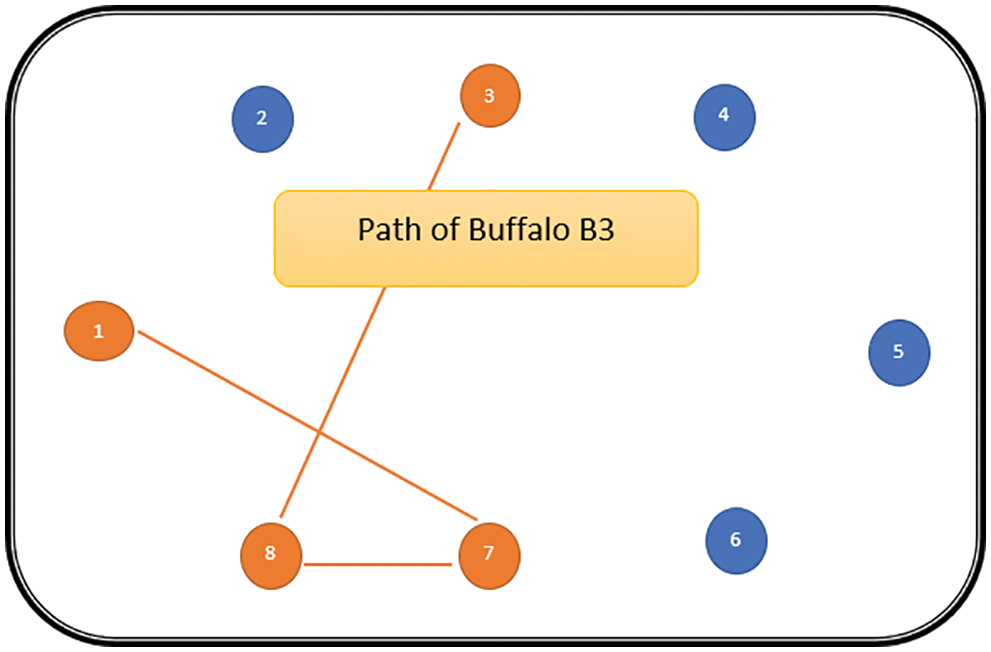
Figure 8: Path of buffalo B3

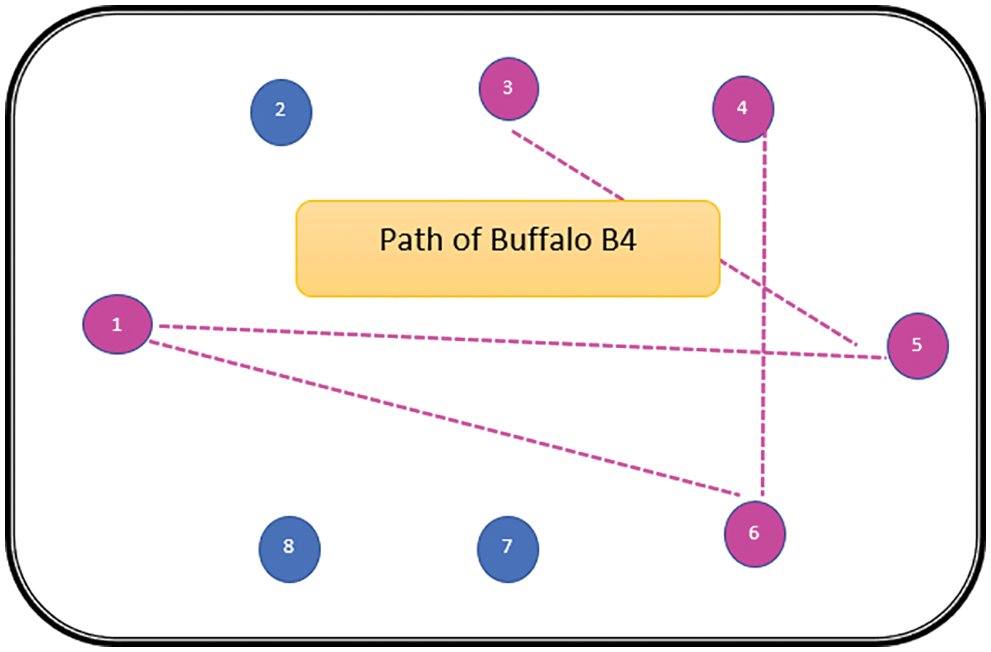
Figure 9: Path of buffalo B4

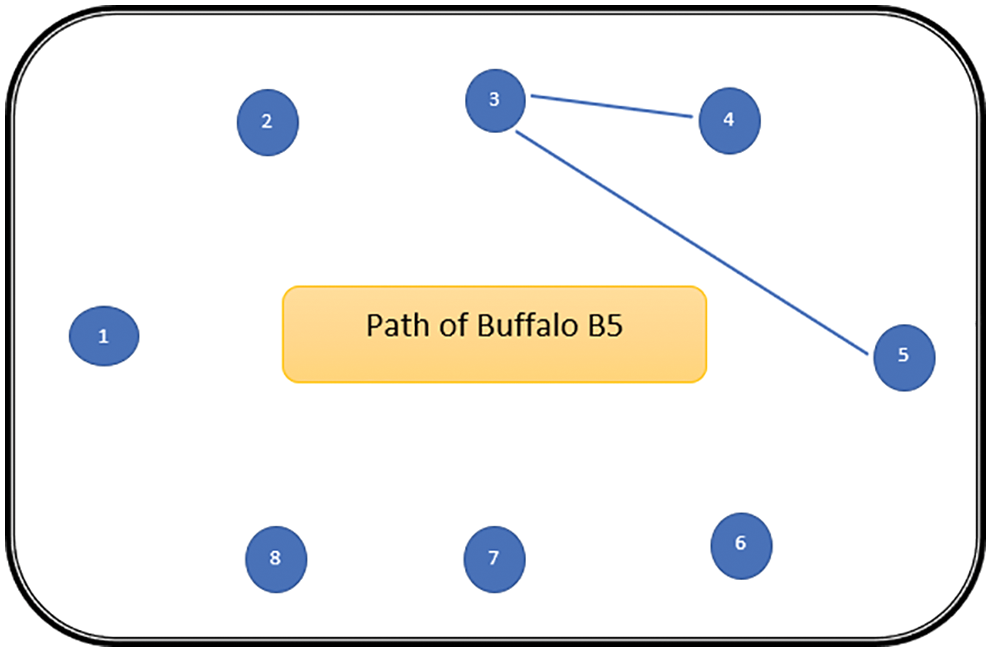
Figure 10: Path of buffalo B5

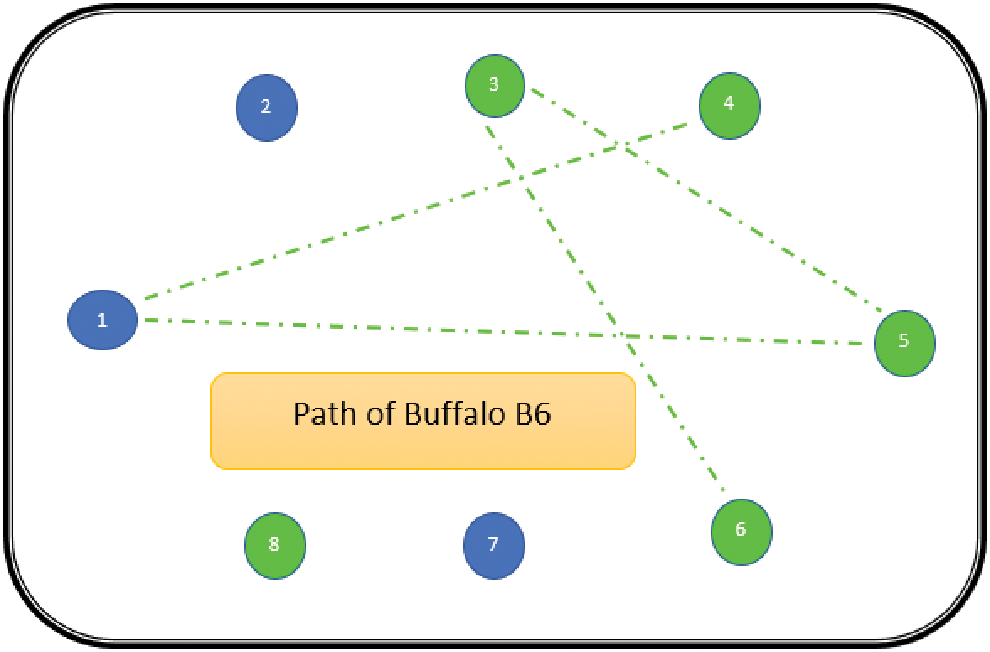
Figure 11: Path of buffalo B6

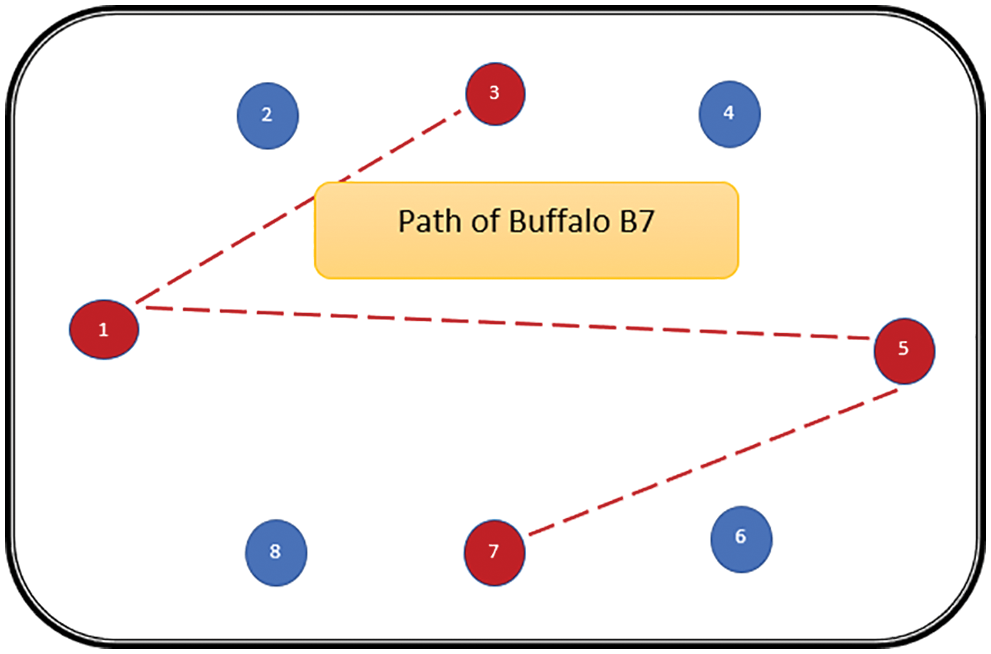
Figure 12: Path of buffalo B7

Figure 13: Path of buffalo B8

Figure 14: Paths of all Buffalos at the end of 1st iteration

3.4 Results of Sample Run

In each iteration, the path having the least value of W is chosen as the best path. Thereafter, GP and BP are updated. Table 2 summarizes the results of the sample run using ABO_TCSP.

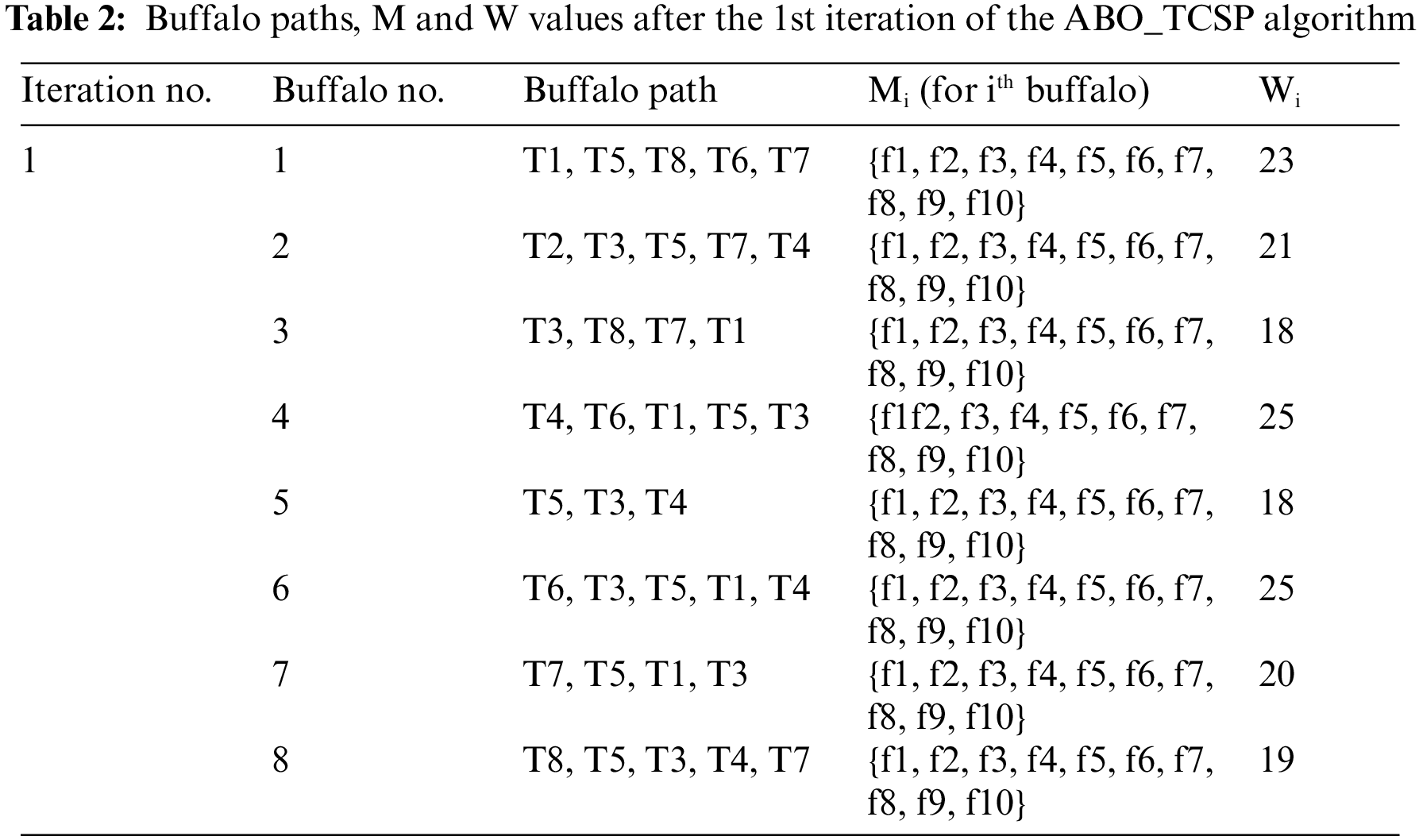
As evident from Table 2, there are two possible options for GP (the paths having the value of MinW = 18). The paths followed by all buffalos during the 1st iteration are taken as their personal best BGs. This process continues iteratively, and thereby, the GP is chosen as the final test suite. Here, the test suite {T4, T5, T3} having execution time = 18 s. The original test suite execution time was 35 s. To better analyze the result obtained, the drop in the amount of time and size (number of test cases) required to run the selected and prioritized test suite is calculated using Eqs. (4) and (5):

TD=(Run time of initial test suite−Run time of ABO test Suite)Run Time of initial test suite∗100%(4)

SD=(Size of initial test suite−Size of ABO test Suite)Size of initial test suite∗100%(5)

TD, the Percentage Time Drop using Eq. (4) was calculated to be 48.57%, i.e., almost half time could be saved in the regression testing for this example using ABO. SD, the Percentage Size Drop was computed using Eq. (5) to be 62.5%. This is a huge drop in the size of the test suite. For the given example, only 3 test cases need to be run as against 8 (in the initial test suite) to kill all the faults.

3.5 Comparison with ACO Technique

To further validate the proposed ABO_TCS&P, a comparison of the same example is made for the majorly explored nature-inspired Ant Colony Optimization (ACO) technique [36]. On applying, ACO on the example from Table 1, the resultant test suite found is {T3, T5, T4} and from ABO (Section 3.3) is {T4, T5, T3}. As observed, both ABO and ACO techniques select the same test cases. The TD, percentage time drop for the resultant test suite is the same for both ACO and ABO (48.57%). The Percentage Size Drop, SD, is the same (62.5%) achieved using both approaches. The same is shown in Fig. 15. Hence, ABO yields similar results in comparison to the well-established ACO technique. Although, it is observed that the order of the test cases is different for ABO and ACO, i.e., the prioritization achieved is slightly varying using both approaches. Hence, further analysis is necessary. Thus, an APFD (Average Percentage of Faults Detected) [2] is used. APFD is a metric that detects how early a test suite can kill the faults. The formula used is given in Eq. (6):

APFD=1−(Pf1+Pf2+⋯+Pf10)No.of Test Cases∗No of faults+1/(2∗No. of TestCases)(6)

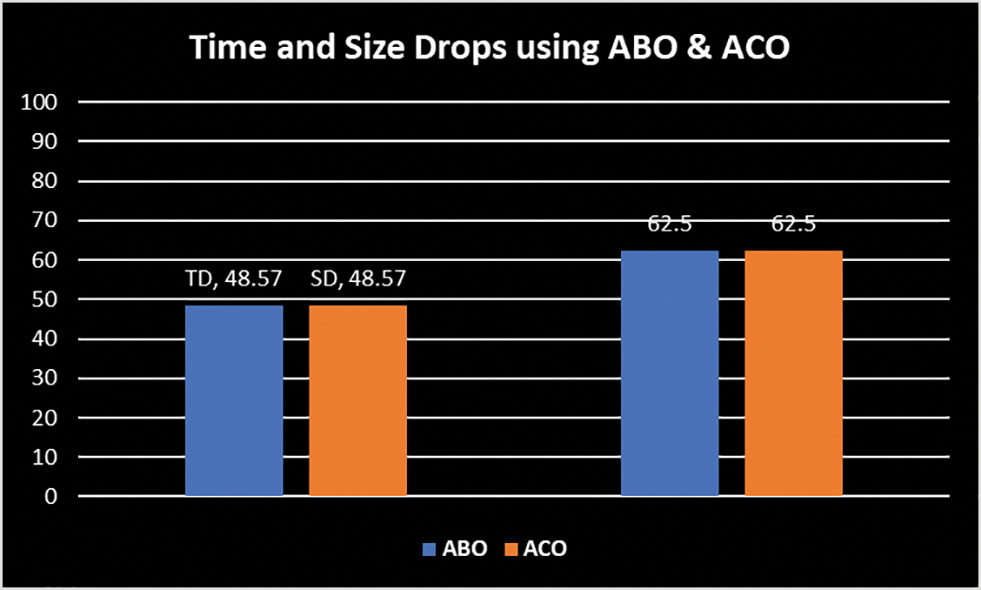
Figure 15: Time and size drop using ABO V/s ACO Approaches

Pf1, Pf2…Pf10 represents the position of faults killed in the prioritized test suite. Eq. (6) is used to calculate the APFD for the test suite prioritized using ABO (T4, T5, T3) to be 80%, while for the test suite prioritized via ACO (T3, T5, T4) to be 82.5%. The same is shown in Fig. 16. ACO prioritizes the test suite slightly better than ABO. The results are still very close and near-optimal using the ABO technique.

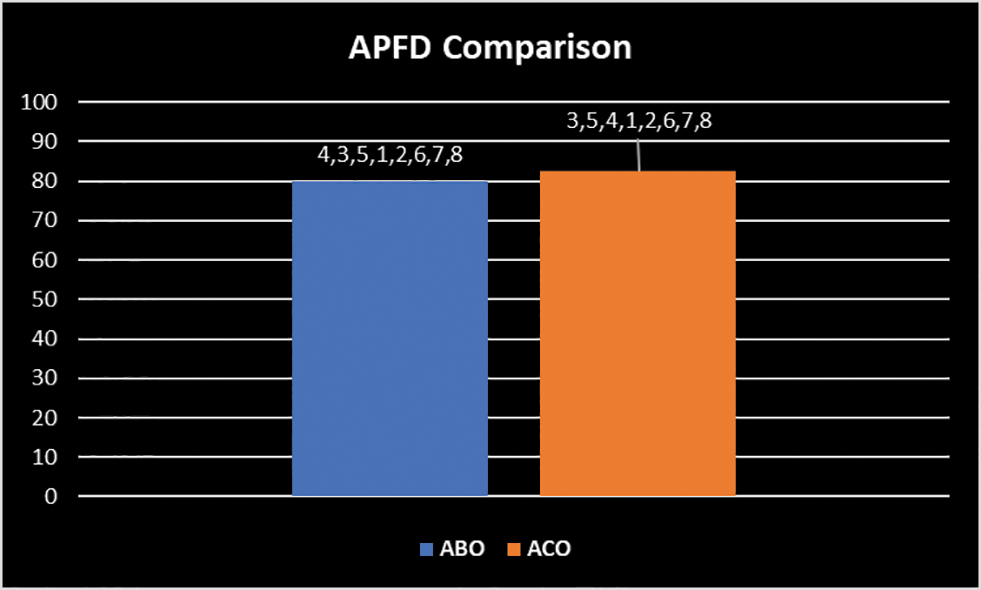
Figure 16: APFD comparison

4  Threats to Validity

Threats to the validity of ABO_TCS&P are of two types: internal or external. Internal threat occurs when the digital buffalos may not be working in the same manner as the real buffalos that always tend to find the right answer to their problem. To resolve this, the proposed approach is mapped using the ABO algorithm [43] which is already developed and tested for other optimization problems [42,43]. External threats to validity are the presence of better possible nature-inspired algorithms than ABO. For this, a comparison with the well-established ACO approach is made and the results obtained are encouraging (Figs. 15 and 16).

5  Conclusion and Future Work

In this paper, ABO_TCS&P is proposed for optimizing test case selection and prioritization using ABO. ABO is a buffalo-inspired optimization method that follows a very unique and intelligent swarm behavior to locate an appropriate gazing area. The approach is mapped to TCS&P, where the artificial buffalos correspond to the test cases and the path (the result of the buffalo’s search) is marked as the selected/prioritized test suite. In the proposed algorithm, time-bound TCS&P being NP-complete opens up opportunities for trying new approximation algorithms. The complexity of the algorithm is polynomial showing encouraging results as a proposed approximation algorithm. ABO is compared with ACO in terms of time and size drop for the initial test suite. The results so obtained, from Sub-sections 3.4 and 3.5, hence advocate the use of the ABO approach in the area of software test selection/prioritization. In the future, the approach can be tested on larger industrial programs in varied programming language platforms and can be compared with the existing nature-inspired approaches to establish its usability in the area.

Acknowledgement: The author would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (22UQU4281755DSR02).

Data Availability Statement: The study did not report any data.

Funding Statement: This research is funded by the Deanship of Scientific Research at Umm Al-Qura University, Grant Code: 22UQU4281755DSR02.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  G. Rothermel and M. J. Harrold, “A safe, efficient algorithm for regression test selection,” in 1993 IEEE Conf. on Software Maintenance, Montreal, Quebec, Canada, pp. 358–367, 1993. [Google Scholar]

 2.  G. Rothermel, R. H. Untch, C. Chu and Harrold, M. J., “Test case prioritization: An empirical study,“ in Proc. IEEE Int. Conf. on Software Maintenance-1999 (ICSM’99). ‘Software Maintenance for Business Change’(Cat. No. 99CB36360), Oxford, UK, pp. 179–188, 1999. [Google Scholar]

 3.  K. Fischer, “A test case selection method for the validation of software maintenance modifications,” in Proc. of the Int. Computer Software and Applications Conf., New York, IEEE Computer Press: Silver Spring, MD, pp. 421–426, 1977. [Google Scholar]

 4.  R. Gupta, M. Harrold and M. Soffa, “An approach to regression testing using slicing,” in Proc. of the Int. Conf. on Software Maintenance (ICSM 1992), Orlando, FL, USA, IEEE Computer Press: Silver Spring, MD, pp. 299–308, 1992. [Google Scholar]

 5.  S. Bates and S. Horwitz, “Incremental program testing using program dependence graphs,” in 20th ACM SIGPLAN-SIGACT Symp. on Principles of Programming Languages, New York, ACM Press, pp. 384–396, 1993. [Google Scholar]

 6.  P. Benedusi, A. Cmitile and U. D. Carlini, “Post-maintenance testing based on path change analysis,” in Int. Conf. on Software Maintenance (ICSM 1988), Scottsdale, AZ, USA, IEEE Computer Press: Silver Spring, MD, pp. 352–361, 1988. [Google Scholar]

 7.  H. Agrawal, J. Horgan, E. Krauser and S. London, “Incremental regression testing,” in Proc. of the Int. Conf. on Software Maintenance (ICSM 1993), Montreal, Quebec, Canada, IEEE Computer Society: Silver Spring, MD, pp. 348–357, 1993. [Google Scholar]

 8.  Y. Chen, D. Rosenblum and K. Vo, “Test tube: A system for selective regression testing,” in 16th Int. Conf. on Software Engineering (ICSE 1994), New York, ACM Press, pp. 211–220, 1994. [Google Scholar]

 9.  M. Skoglund and P. Runeson, “A case study of the class firewall regression test selection technique on a large scale distributed software system,” in Int. Symp. on Empirical Software Engineering, Noosa Heads, Australia, pp. 74–83, 2005. [Google Scholar]

10. B. Suri and S. Singhal, “Development and validation of an improved test selection and prioritization algorithm based on ACO,” International Journal of Reliability, Quality and Safety Engineering, vol. 21, no. 6, pp. 1450032 (13 pages2014. [Google Scholar]

11. G. Rothermel, R. H. Untch, C. Chu and M. J. Harrold, “Test case prioritization: An empirical study,” in Proc. of the Int. Conf. on Software Maintenance, Oxford, England, UK, pp. 179–188, August 1999. [Google Scholar]

12. S. Elbaum, A. Malishevsky and G. Rothermel, “Incorporating varying test costs and fault severities into test case prioritization,” in Int. Conf. on Software Engineering (ICSE 2001), New York, ACM Press, pp. 329–338, 2001. [Google Scholar]

13. K. Walcott, M. Soffa, G. Kapfhammer and R. Roos, “TimeAware test suite prioritization,” in ISSTA ‘06 Proc. of the 2006 Int. Symp. on Software Testing and Analysis, Portland, Maine, USA, pp. 1–12, 2006. [Google Scholar]

14. M. Mahdieh, S. H. Mirian-Hosseinabadi, K. Etemadi, A. Nosrati and S. Jalali, “Incorporating fault-proneness estimations into coverage-based test case prioritization methods,” Information and Software Technology, vol. 121, pp. 106269, 2020. [Google Scholar]

15. M. Mahdieh, S. H. Mirian-Hosseinabadi and M. Mahdieh, “Test case prioritization using test case diversification and fault-proneness estimations,” arXiv preprint arXiv:2106.10524, 2021. [Google Scholar]

16. S. Sampath, R. Bryce, G. Viswanath, V. Kandimalla and A. Koru, “Prioritizing user-session-based test cases for web applications testing,” in 1st Int. Conf. on Software Testing Verification and Validation (ICST 2008), Lillehammer, Norway, IEEE Computer Society: Silver Spring, MD, pp. 141–150, 2008. [Google Scholar]

17. S. Eghbali and L. Tahvildari, “Test case prioritization using lexicographical ordering,” IEEE Transactions on Software Engineering, vol. 42, no. 12, pp. 1178–1195, 2016. [Google Scholar]

18. J. Chi, Y. Qu, Q. Zheng, Z. Yang, W. Jin et al., “Relation-based test case prioritization for regression testing,” Journal of Systems and Software, vol. 163, pp. 110539, 2020. [Google Scholar]

19. N. Jatana and B. Suri, “An improved crow search algorithm for test data generation using search-based mutation testing,” Neural Processing Letters, vol. 52, no. 1, pp. 767–784, 2020. [Google Scholar]

20. N. Jatana and B. Suri, “Particle swarm and genetic algorithm applied to mutation testing for test data generation: A comparative evaluation,” Journal of King Saud University-Computer and Information Sciences, vol. 32, no. 4, pp. 514–521, 2020. [Google Scholar]

21. V. Garousi, R. Özkan and A. Betin-Can, “Multi-objective regression test selection in practice: An empirical study in the defense software industry,” Information and Software Technology, vol. 103, pp. 40–54, 2018. [Google Scholar]

22. R. Pan, M. Bagherzadeh, T. A. Ghaleb and L. Briand, “Test case selection and prioritization using machine learning: A systematic literature review,” arXiv preprint arXiv:2106.13891, 2021. [Google Scholar]

23. A. Subahi, “Cognification of program synthesis—A systematic feature-oriented analysis and future direction,” Computers, vol. 9, no. 27, 2020. [Google Scholar]

24. J. B. Odili, M. N. M. Kahar and S. Anwar, “African buffalo optimization: A swarm-intelligence technique,” in IEEE Int. Symp. on Robotics and Intelligent Sensors (IRIS 2015), Langkawi, Malaysia, pp. 443–448, 2015. [Google Scholar]

25. J. B. Odili and M. N. Mohmad Kahar, “Solving the traveling salesman’s problem using the African buffalo optimization,” Computational Intelligence and Neuroscience, vol. 1, no. 1, pp. 12, 2016. [Google Scholar]

26. T. Jiang, H. Zhu and G. Deng, “Improved African buffalo optimization algorithm for the green flexible job shop scheduling problem considering energy consumption,” Journal of Intelligent & Fuzzy Systems, vol. 38, no. 4, pp. 4573–4589, 2020. [Google Scholar]

27. M. Krisnawati, A. A. Sibarani, A. Mustikasari and D. Aulia, “Makespan, African buffalo optimization for solving flow shop scheduling problem to minimize,” IOP Conference Series: Materials Science and Engineering, vol. 982, no. 1, pp. 012061, 2020. [Google Scholar]

28. N. S. Jebaraj and D. H. Keshavan, “Hybrid genetic algorithm and african buffalo optimization (HGAABO) based scheduling in ZigBee network,” International Journal of Applied Engineering Research, vol. 13, no. 5, pp. 2197–2206, 2018. [Google Scholar]

29. S. Singhal and B. Suri, “Multi-objective test case selection and prioritization using African buffalo optimization,” Journal of Information and Optimization Sciences, vol. 41, no. 7, pp. 1705–1713, 2020. [Google Scholar]

30. G. Rothermel, R. H. Untch, C. Chu and M. J. Harrold, “Test case prioritization: An empirical study,” in Proc. IEEE Int. Conf. on Software Maintenance-1999 (ICSM’99), Oxford, UK, pp. 179–189, 1999. [Google Scholar]

31. G. Rothermel, R. H. Untch, C. Chu and M. J. Harrold, “Prioritizing test cases for regression testing, ” IEEE Transactions on Software Engineering, vol. 27, no. 10, pp. 929–948, 2001. [Google Scholar]

32. C. Catal, “On the application of genetic algorithms for test case prioritization: A systematic literature review,” in Proc. of the 2nd Int. Workshop on Evidential Assessment of Software Technologies, Lund, Sweden, pp. 9–14, 2012. [Google Scholar]

33. S. Singhal, N. Jatana, B. Suri, S. Misra and L. Fernandez-Sanz, “Systematic literature review on test case selection and prioritization: A tertiary study,” Applied Sciences, vol. 11, no. 24, pp. 12121, 2021. [Google Scholar]

34. Z. Li, M. Harman and R. M. Hierons, “Search algorithms for regression test case prioritization,” IEEE Transactions on Software Engineering, vol. 33, no. 4, pp. 225–237, 2007. [Google Scholar]

35. A. Bajaj and O. Sangwan, “A systematic literature review of test case prioritization using genetic algorithms,” IEEE Access, vol. 7, pp. 126355–126375, 2019. [Google Scholar]

36. L. S. De Souza, R. B. Prudêncio, F. D. A. Barros and E. H. D. S. Aranha, “Search-based constrained test case selection using execution effort,” Expert Systems with Applications, vol. 40, no. 12, pp. 4887–4896, 2013. [Google Scholar]

37. S. Yoo and M. Harman, “Pareto efficient multi-objective test case selection,” in 2007 Int. Symp. on Software Testing and Analysis, London, U.K, pp. 1450–150, 2007. [Google Scholar]

38. B. Baudry, F. Fleurey, J. -M. Jézéquel and Y. L. Traon, “Automatic test cases optimization: A bacteriological algorithm,” IEEE Software, vol. 22, no. 2, pp. 76–82, 2005a. [Google Scholar]

39. K. Sheoran and O. P. Sangwan, “Component-based quality prediction via component reliability using optimal fuzzy classifier and evolutionary algorithm,” In: M. Hoda, N. Chauhan, S. Quadri and P. Srivastava, (Eds.Software Engineering. Advances in Intelligent Systems and Computing, vol. 731, pp. 449–456, Singapore: Springer, 2019. [Google Scholar]

40. N. Jatana, B. Suri and S. Rani, “Systematic literature review on search-based mutation testing,” E-Informatica Software Engineering Journal, vol. 11, no. 1, pp. 59–76, 2017. [Google Scholar]

41. P. Kaur and A. Gosain, “FF-SMOTE: A metaheuristic approach to combat class imbalance in binary classification,” Applied Artificial Intelligence, vol. 33, no. 5, pp. 420–439, 2019. [Google Scholar]

42. K. Sheoran, P. Tomar and R. Mishra, “A novel quality prediction model for component-based software system using ACO–NM optimized extreme learning machine,” Cognitive Neurodynamics, vol. 14, no. 4, pp. 509–522, 2020. [Google Scholar]

43. P. Tomar, R. Mishra and K. Sheoran, “Prediction of quality using ANN based on teaching-learning optimization in component-based software systems,” Software: Practice and Experience, vol. 48, no. 4, pp. 896–910, 2018. [Google Scholar]

44. A. Hashmi, N. Goel, S. Goel and D. Gupta, “ “Firefly algorithm for unconstrained optimization,” IOSR Journal of Computer Engineering (IOSR-JCE), vol. 11, no. 1, pp. 75–78, 2013. [Google Scholar]

45. M. N. Malik, H. H. Khan, A. G. Chofreh, F. A. Goni, J. J. Klemeš et al., “Investigating students’ sustainability awareness and the curriculum of technology education in Pakistan,” Sustainability, vol. 11, no. 9, pp. 2651, 2019. [Google Scholar]

46. X. Wang, J. Liu and X. Liu, “Ship feature recognition methods for deep learning in complex marine environments,” Complex & Intelligent Systems, 2022. (Preprint). [Google Scholar]

47. S. Bera, S. K. Das and A. Karati, “Intelligent routing in wireless sensor network based on African buffalo optimization,” In: D. De, A. Mukherjee, S. Kumar Das and N. Dey, (Eds.Nature Inspired Computing for Wireless Sensor Networks. Springer Tracts in Nature-Inspired Computing, pp. 119–142, Singapore: Springer, 2020. [Google Scholar]

48. A. R. Panhalkar and D. D. Doye, “Optimization of decision trees using modified African buffalo algorithm,” Journal of King Saud University-Computer and Information Sciences, 2021. (Preprint). [Google Scholar]

49. B. Sharma, A. Hashmi, C. Gupta, O. Khalaf, G. Abdulsahib et al., “Hybrid sparrow clustered (HSC) algorithm for top-N recommendation system,” Symmetry, vol. 14, no. 793, 2022. [Google Scholar]

50. D. Anuradha, N. Subramani, O. Khalaf, Y. Alotaibi, S. Alghamdi et al., “Chaotic search-and-rescue-optimization-based multi-hop data transmission protocol for underwater wireless sensor networks,” Sensors, vol. 22, no. 2867, pp. 1–20, 2022. [Google Scholar]

51. A. Sundas, S. Badotra, Y. Alotaibi, S. Alghamdi and O. I. Khalaf, “Modified bat algorithm for optimal vm’s in cloud computing,” Computers, Materials & Continua, vol. 72, no. 2, pp. 2877–2894, 2022. [Google Scholar]

52. T. Puri, M. Soni, G. Dhiman, O. I. Khalaf, M. Alazzam et al., “Detection of emotion of speech for RAVDESS audio using hybrid convolution neural network,” Journal of Healthcare Engineering, 2022. (Preprint). [Google Scholar]

53. J. Jayapradha, M. Prakash, Y. Alotaibi, O. I. Khalaf and S. A. Alghamdi, “Heap bucketization anonymity-An efficient privacy-preserving data publishing model for multiple sensitive attributes,” IEEE Access, vol. 10, pp. 28773–28791, 2022. [Google Scholar]

54. S. Sennan, K. Gopalan, Y. Alotaibi, D. Pandey and S. Alghamdi, “EACR-LEACH: Energy-aware cluster-based routing protocol for WSN based IoT,” Computers, Materials & Continua, vol. 72, no. 2, pp. 2159–2174, 2022. [Google Scholar]

55. S. R. Akhila, Y. Alotaibi, O. I. Khalaf and S. Alghamdi,“Authentication and resource allocation strategies during handoff for 5G IoVs using deep learning,” Energies, vol. 15, no. 6, pp. 2006, 2022. [Google Scholar]

56. U. Janniekode, R. Somineni, O. Khalaf, M. Itani, J. Chinna Babu et al., “A symmetric novel 8T3R non-volatile SRAM cell for embedded applications,” Symmetry, vol. 14, pp. 768, 2022. [Google Scholar]

57. J. B. Odili, M. N. M. Kahar and S. Anwar, “African buffalo optimization: A swarm-intelligence technique,” in IEEE Int. Symp. on Robotics and Intelligent Sensors (IRIS 2015), Langkawi, Malaysia, vol. 76, pp. 443–438, 2015. [Google Scholar]

58. N. Subramani, P. Mohan, Y. Alotaibi, S. Alghamdi and O. I. Khalaf, “An efficient metaheuristic-based clustering with routing protocol for underwater wireless sensor networks, ” Sensors, vol. 22, pp. 415, 2022. [Google Scholar]

59. S. Rajendran, O. I. Khalaf, Y. Alotaibi and S. Alghamdi, “MapReduce-Based big data classification model using feature subset selection and hyperparameter tuned deep belief network,” Scientific Reports, vol. 11, no. 1, pp. 1–10, 2021. [Google Scholar]

60. R. Rout, P. Parida, Y. Alotaibi, S. Alghamdi and O. I. Khalaf, “Skin lesion extraction using multiscale morphological local variance reconstruction based watershed transform and fast fuzzy c-means clustering,” Symmetry, vol. 13, no. 11, pp. 2085, 2021. [Google Scholar]

61. S. Bharany, S. Sharma, S. Badotra, O. I. Khalaf, Y. Alotaibi et al., “Energy-efficient clustering scheme for flying ad-hoc networks using an optimized LEACH protocol,” Energies, vol. 14, no. 19, pp. 6016, 2021. [Google Scholar]

62. A. Alsufyani, Y. Alotaibi, A. O. Almagrabi, S. A. Alghamdi and N. Alsufyani, “Optimized intelligent data management framework for a cyber-physical system for computational applications,” Complex & Intelligent Systems, vol. 2021, pp. 1–13, 2021. [Google Scholar]

63. N. Jha, D. Prashar, O. I. Khalaf, Y. Alotaibi, A. Alsufyani et al., “Blockchain based crop insurance: A decentralized insurance system for modernization of Indian farmers,” Sustainability, vol. 13, no. 16, pp. 8921, 2021. [Google Scholar]

64. Y. Alotaibi, “A new meta-heuristics data clustering algorithm based on tabu search and adaptive search memory,” Symmetry, vol. 14, no. 3, pp. 623, 2022. [Google Scholar]

65. S. S. Rawat, S. Alghamdi, G. Kumar, Y. Alotaibi, O. I. Khalaf et al., “Infrared small target detection based on partial sum minimization and total variation,” Mathematics, vol. 10, pp. 671, 2022. [Google Scholar]

66. P. Mohan, N. Subramani, Y. Alotaibi, S. Alghamdi, O. I. Khalaf et al., “Improved metaheuristics-based clustering with multihop routing protocol for underwater wireless sensor networks,” Sensors, vol. 22, no. 4, pp. 1618, 2022. [Google Scholar]

67. Y. Alotaibi, “A new database intrusion detection approach based on hybrid meta-heuristics,” CMC-Computers, Materials & Continua, vol. 66, no. 2, pp. 1879–1895, 2021. [Google Scholar]

68. Y. Alotaibi, M. N. Malik, H. H. Khan, A. Batool, S. ul Islam et al., “Suggestion mining from opinionated text of big social media data,” CMC-Computers Materials & Continua, vol. 68, pp. 3323–3338, 2021. [Google Scholar]

69. Y. Alotaibi, “Automated business process modelling for analyzing sustainable system requirements engineering,” in 2020 6th Int. Conf. on Information Management (ICIM), London, UK, IEEE, pp. 157–161, 2020. [Google Scholar]

70. Y. Alotaibi and A. F. Subahi, “New goal-oriented requirements extraction framework for e-health services: A case study of diagnostic testing during the COVID-19 outbreak,” Business Process Management Journal, vol. 28, no. 1, pp. 273–292, 2021. [Google Scholar]

71. H. H. Khan, M. N. Malik, R. Zafar, F. A. Goni, A. G. Chofreh et al., “Challenges for sustainable smart city development: A conceptual framework,” Sustainable Development, vol. 28, no. 5, pp. 1507–1518, 2020. [Google Scholar]

72. G. Suryanarayana, K. Chandran, O. I. Khalaf, Y. Alotaibi, A. Alsufyani et al., “Accurate magnetic resonance image super-resolution using deep networks and Gaussian filtering in the stationary wavelet domain,” IEEE Access, vol. 9, pp. 71406–71417, 2021. [Google Scholar]

73. G. Li, F. Liu, A. Sharma, O. I. Khalaf, Y. Alotaibi et al., “Research on the natural language recognition method based on cluster analysis using neural network, ” Mathematical Problems in Engineering, vol. 2021, pp. 13, 2021. [Google Scholar]

74. U. Srilakshmi, N. Veeraiah, Y. Alotaibi, S. A. Alghamdi, O. I. Khalaf et al., “An improved hybrid secure multipath routing protocol for MANET,” IEEE Access, vol. 9, pp. 163043–163053, 2021. [Google Scholar]

75. N. Veeraiah, O. I. Khalaf, C. V. P. R. Prasad, Y. Alotaibi, A. Alsufyani et al., “Trust aware secure energy efficient hybrid protocol for manet,” IEEE Access, vol. 9, pp. 120996–121005, 2021. [Google Scholar]

76. Y. Alotaibi, “A new secured E-government efficiency model for sustainable services provision,” Journal of Information Security and Cybercrimes Research, vol. 3, no. 1, pp. 75–96, 2020. [Google Scholar]

77. V. Ramasamy, Y. Alotaibi, O. I. Khalaf, P. Samui and J. Jayabalan, “Prediction of groundwater table for Chennai region using soft computing techniques,” Arabian Journal of Geosciences, vol. 15, no. 9, pp. 1–19, 2022. [Google Scholar]

78. P. Kollapudi, S. Alghamdi, N. Veeraiah, Y. Alotaibi, S. Thotakura et al., “A new method for scene classification from the remote sensing images,” CMC-Computers, Materials & Continua, vol. 72, no. 1, pp. 1339–1355, 2022. [Google Scholar]

79. U. Srilakshmi, S. Alghamdi, V. V. Ankalu, N. Veeraiah and Y. Alotaibi, “A secure optimization routing algorithm for mobile ad hoc networks,” IEEE Access, vol. 10, pp. 14260–14269, 2022. [Google Scholar]

80. S. Palanisamy, B. Thangaraju, O. I. Khalaf, Y. Alotaibi and S. Alghamdi, “Design and synthesis of multi-mode bandpass filter for wireless applications,” Electronics, vol. 10, pp. 2853, 2021. [Google Scholar]

81. S. Sennan, D. Pandey, Y. Alotaibi and S. Alghamdi, “A novel convolutional neural networks based spinach classification and recognition system,” Computers, Materials & Continua, vol. 73, no. 1, pp. 343–361, 2022. [Google Scholar]

82. A. R. Khaparde, F. Alassery, A. Kumar, Y. Alotaibi, O. I. Khalaf et al., “Differential evolution algorithm with hierarchical fair competition model,” Intelligent Automation & Soft Computing, vol. 33, no. 2, pp. 1045–1062, 2022. [Google Scholar]

83. H. S. Gill, O. I. Khalaf, Y. Alotaibi, S. Alghamdi and F. Alassery, “Fruit image classification using deep learning,” Computers, Materials & Continua, vol. 71, no. 3, pp. 5135–5150, 2022. [Google Scholar]

84. H. S. Gill, O. I. Khalaf, Y. Alotaibi, S. Alghamdi and F. Alassery, “Multi-model CNN-RNN-LSTM based fruit recognition and classification,” Intelligent Automation & Soft Computing, vol. 33, no. 1, pp. 637–650, 2022. [Google Scholar]

85. H. H. Khan, M. N. Malik, Y. Alotaibi, A. Alsufyani and S. Alghamdi, “Crowdsourced requirements engineering challenges and solutions: A software industry perspective,” Computer Systems Science and Engineering, vol. 39, no. 2, pp. 221–236, 2021. [Google Scholar]

86. R. Meenakshi, R. Ponnusamy, S. Alghamdi, O. I. Khalaf and Y. Alotaibi, “Development of mobile app to support the mobility of visually impaired people,” Computers, Materials & Continua, vol. 73, no. 2, pp. 3473–3495, 2022. [Google Scholar]

87. P. Tomar, G. Kumar, L. P. Verma, V. K. Sharma, D. Kanellopoulos et al., “CMT-SCTP and MPTCP multipath transport protocols: A comprehensive review,” Electronics, vol. 11, no. 15, pp. 2384, 2022. [Google Scholar]

88. S. S. Rawat, S. Singh, Y. Alotaibi, S. Alghamdi and G. Kumar, “Infrared target-background separation based on weighted nuclear norm minimization and robust principal component analysis,” Mathematics, vol. 10, no. 16, pp. 2829, 2022. [Google Scholar]

89. K. Lakshmanna, N. Subramani, Y. Alotaibi, S. Alghamdi, O. I. Khalaf et al., “Improved metaheuristic-driven energy-aware cluster-based routing scheme for IoT-assisted wireless sensor networks,” Sustainability, vol. 14, no. 13, pp. 7712, 2022. [Google Scholar]

90. Y. Alotaibi and F. Liu, “A novel secure business process modeling approach and its impact on business performance,” Information Sciences, vol. 277, pp. 375–395, 2014. [Google Scholar]