An Automatic Threshold Selection Using ALO for Healthcare Duplicate Record Detection with Reciprocal Neuro-Fuzzy Inference System

1  Introduction

Data linkage and deduplication can be exploited for enhancing the data quality and integrity, which is useful in reusing the available data sources for further analysis and to decrease the expenses and toil involved with the data acquisition. Data deduplication is a specific data compression approach that eliminates similar copies of repeated data. During the deduplication process, distinct sets of data, or byte patterns, are found and saved during the analysis process. During the analysis, the comparison between the other chunks and the saved copy is performed and if there is a similarity, the repetitive set is substituted with a smaller reference, which is a pointer to the saved chunk [1]. Deduplication itself is a primary task that integrates data from different sources. The reuse of data from different data custodians yields an adequate number of patients who ensure the inclusion conditions of a specific analysis. The important problem faced in this task is developing a function, which can help in resolution in the case of a pair of records referring to the same element despite different inconsistencies in data.

The last few years have seen data quality emerging as a significant problem, owing to its considerable effect on the quality achieved with the decisions made. Data cleansing phases are crucial for ensuring the quality of data. Data cleaning or data cleansing aims to remove uncertainties present in the data to be processed. Anomalies in data can be Intra-column anomalies which include heterogeneities, data standardizations, and null values; inter-column anomalies which include functional and conditional dependencies and abnormalities found in inter-lines (rows) which are duplicate records [2]. Record duplications in databases are the most common causes of poor quality of data [3] and hence their detections need to be handled. The procedures for detecting duplicate records comprise finding records, having the reference to the same practical component, through which different quality of data issues can be solved. Different techniques have been introduced to handle the task of duplicate record detection.

Rule-based schemes, distance or active learning-based techniques, and supervised or semi-supervised and unsupervised learning mechanisms are all examples of these approaches [4]. But, string matching is not capable of capturing semantic similarity. However, there are a few specific unresolved problems they all have—what is the way to ideally choose the segment matching algorithm and respectively carry out the weighting and combining of the parts during the record matching, which is very hard to decide. In this technical work, the RANFIS-based technique is introduced for the detection of duplicate record detection having optimal threshold selection employing Ant Lion Optimizer (ALO). In this manner, improving the effectiveness and accuracy of the detection process is made possible.

The research work’s other sections are structured as given. In Section 2, the relevant articles and the concepts of RANFIS-based detection are explained and Section 3 describes the working process. In Section 4, the experimental analysis of the proposed technique with a standard data set is discussed. At last, Section 5 provides the conclusion.

2  Related Work

In a few applications such as data warehousing, data mining or information integration data needs cleaning in the form of a preprocessing step so that the quality of data and the application performance is ensured. One important task in data cleaning is identifying duplicate records. The available detection techniques apply to a variety of data models and record types. These studies still have a few drawbacks that have to be resolved. Lu et al. [5] introduced a genetic neural network-based technique for the detection of duplicate records. Before using NNs (neural networks) in detection processes, topologies and weight vectors of networks are optimized with the help of GAs (genetic algorithms) on specific data sets.

Leitao et al. [6] suggested XML Dup (Extensible Markup Language), a new approach for detecting duplicate XMLs where the scheme used BNs (Bayesian networks) to determine a similarity between two XML elements, taking into consideration not just the information that the entities hold, but also the structuring of that information. Lin et al. [7] studied a new technique to identify near-duplicates out of a huge set of documents. The near-copies of input documents can be determined by retrieving and pre-processing phrases in the documents, computing weights of words separately, and selecting strongly weighted terms as sentence features. SVMs (support vector machines) learned to discriminate training pattern sets and determine near copies of input documents based on similarity degrees.

Liu et al. [8] suggested a technique that depends on a modified Radial Basis Function (RBF) neural network for improving the accuracy and recall rate during duplicated records detection. At first, the clustering of the key fields of records is performed by applying DBSCANs (Density-Based Spatial Clustering of Applications with Noises) and at the end, SCMs (Subtractive Clustering Methods) and PSOs (Particle Swarm Optimizations) are considered for optimizing the parameters of RBF neural network such that the monitoring model of duplicated records is constructed. De Carvalho et al. [9] introduced a genetic programming scheme for recording the deduplication, which integrated various parts of proofs obtained data for deduplication functions and which had the capability of finding if two entries in a repository were copies or not. Ektefa et al. [10] recommended a threshold-based technique that considered string/semantic measures to compare similarities between record pairs. The experimental validation of this technique is carried out on a practical dataset, known as Restaurant and its usefulness is measured in terms of different standard evaluation metrics.

Karapiperis et al. [11] suggested LSHDB, the first parallel and distributed engine for record linkages and similarity searches. The scheme’s Locality-Sensitive Hashing, a known approach for identifying similarity in high-dimensional objects was the primary similarity search engine and was hidden behind abstraction layers of LSHDB. Wilson [12] put forward an outline of the probabilistic record linkage, demonstrating the means of casting it in machine learning terms, and later it is found that it holds similarities with a naïve Bayes classifier. Next, it studies the means of utilizing highly sophisticated features compared to simple field comparisons and also demonstrates the way the probabilistic record linkage formulas can be changed to deal with this. A variety of systems, which depend on persistent data to provide superior quality services, like digital libraries and e-commerce brokers, may suffer due to the presence of replicas, quasi replicas, or near-copy entries in their database. Due to this, a considerable amount has been invested from both private and government organizations to develop techniques that can help eliminate duplicates from its data archives. The repetitive data present in the data archive results in issues such as excessive usage of memory, increased execution time, etc. Therefore, to get over the problems, methods such as deduplication algorithms are helpful to discover and pull out the repetitive data found in a database.

3  Proposed Methodology

The proposed approach includes a technique that depends on RANFIS for the deduplication process. A bunch of data that few similarity metrics generate are considered in the form of the input for the proposed system. Two processes exist that represent the proposed deduplication approach, which includes the training stage and the testing stage. The proposed technique is validated with two diverse datasets to assess the efficiency. In the proposed technique, the input forms the model parameters and the output constitutes the value associated with the replicas and the non-duplicates. Therefore, the RANFIS performs the weight value processing based on the input features considered. Then the weightage values and threshold values are computed employing ALO for the RANFIS developed for the proposed deduplication approach. Next, it is revealed by the results of experiments that the proposed deduplication approach yields improved accuracy compared to contemporary techniques. Fig. 1 shows the overall architecture of the proposed technique.

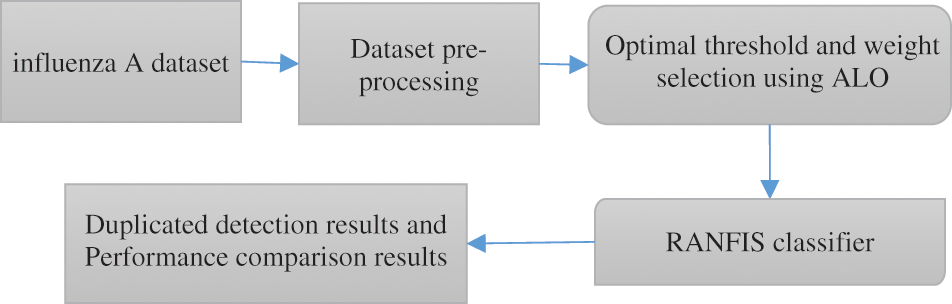
Figure 1: General framework diagram of the proposed methodology

3.1 Dataset Preparation

The experiment is about providing answers to a query on the number of persons affected with influenza A from January 2015 to April 2019. Every laboratory locally requested the IDs of the individuals who tested positive for influenza A during this period, and a synthetic dataset having 5329 records was generated [13,14]. The dataset for analysis was gathered from https://www.kaggle.com/competitions/flu-forecasting.

3.2 Preprocessing and Separation

In data Pre-processing or Data cleaning, the data is cleansed by applying processes like replacing the missing values, smoothing the noisy data, or mitigating the non-uniformities found in the data. Moreover, it is also helpful in eliminating irrelevant data. Popular as a preliminary data mining process, the data pre-processing modifies the data into a form, whose processing can be extremely simple and effective for the user. Once the pre-processing is finished, the data isolation has to be carried out. The blocking algorithms designate every record to a predefined set of identical records and next all the pairs of records are compared within these groups. Every block within the block comparison matrix indicates the comparisons made between all records present in one block and every other record in another block, the equidistant blocking, all the blocks are sized the same. Data extracts are shared across data custodians as VDs (virtual datasets). Consider the query “select the records of patients tested for influenza A viruses in January 2016” that is being run across three data custodians D = {D1, D2, D3}. Fig. 2 depicts results from VDs for data custodians query.

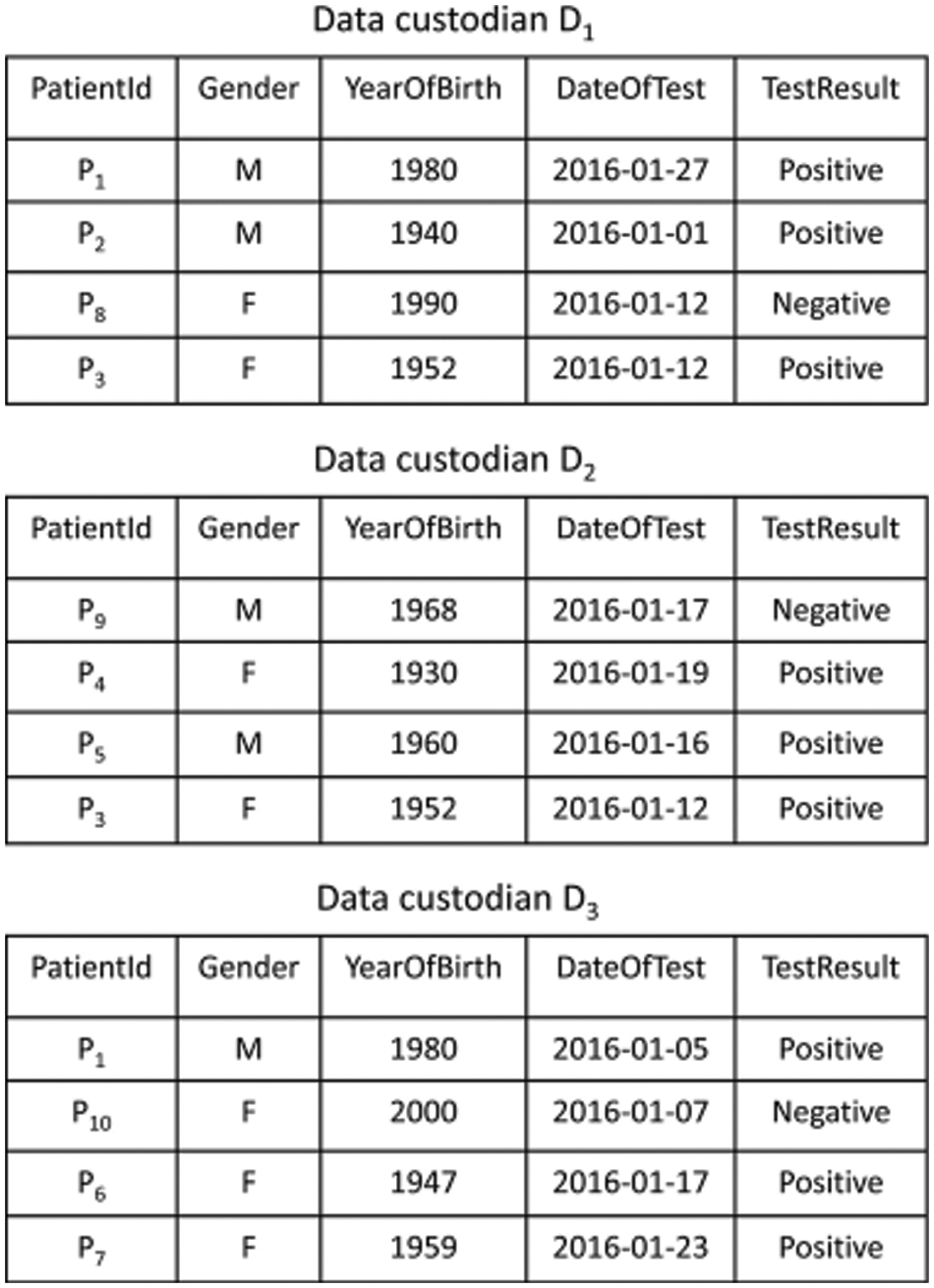
Figure 2: Synthetic dataset of influenza a test results spread across three data custodians

A VD might have duplicated entries from multiple data custodians, which provide coverage for the same or identical places [15–17]. Two types of duplicate records exist, known as accurate and estimated. In case, the comparison between the records is performed with precise comparison functions and all the feature values considered for evaluation depict the same, then the records are properly duplicated. On the other hand, approximate duplicate records are compared by employing comparison functions to aid in the approximate matching and have diverse values for single or multiple variables.

3.3 Duplicate Data Detection Using Ranfis

In this work, a RANFIS model is developed for the detection of duplicate records where before networks were used for duplicate record identifications, ALOs optimize topological formats and weight vectors for certain data sets. The training and application phases are a part of the process wherein in the training phase, specific counts of equally distributed records from data sets are selected for training sets and subsequently corresponding segment similarity measurements are executed and similarity measures of recorded pairs are manually labeled. At last, the characteristic vector that consists of the record similarities is utilized in the form of the input for training the neural network employing the genetic algorithm.

The similarity vectors of record pairs are initially computed in application phases and by computing similarities between segments. Then, using trained RANFIS, record similarities are assessed, and detection procedures are carried out based on the right threshold selections utilizing ALOs. The Dice coefficient, Damerau–Levenshtein distance, Tversky index, and Cosine similarity were used as similarity functions. The RANFIS input value is calculated using the above-shown similarity distance metrics. The documents that need to be examined for data repetition are processed using the similarity measure, with each measure yielding model parameters. These parameters constitute the fundamental processing entities of the RANFIS.

Dice coefficient: It is a similarity measure that is of the same kind as the Sorensen similarity index, known as the Sørensen-Dice coefficient. The range of the function lies between zero and one, similar to Jaccard. Contrary to Jaccard, the respective difference function dist=1−(2|A∩B|)|A|+|B| is not an exact distance metric since it does not have the property of triangle inequality. The similarity function for the dice’s coefficient SFDC can be expressed using the formulae given below,

SFDC=(2|A∩B|)|A|+|B|(1)

where A and B refer to the documents considered for the comparison.

Damerau–Levenshtein distances: Damerau–Levenshtein distances are defined in information theory and computer science as “distances” between two strings, i.e., finite series of symbols, determined by counting minimum operations required to transform one string into another, where operations are insertions, deletions, or substitutions of characters, or transpositions of two consecutive characters. Even though there is no clarity on whether the term Damerau–Levenshtein distances, are referred to as edit distances permitting several edit operations, including transpositions. There are no clarity on the usage of Damerau–Levenshtein distances on non-adjacent transpositions. Damerau–Levenshtein distances provide a portion of this model’s parameters that are processed, RANFIS.

Tversky Indices: They are defined as asymmetric similarity measures, which provide comparisons between versions and prototypes. Tversky indices can be used to observe generalizations of Dice’s coefficients and Tanimoto’s coefficients. For sets A and B of keywords utilized in retrieving information, the Tversky index refers to a number in the range 0 to 1. The similarity function for Tversky index SFTI can be expressed by the formula, SFTC can be expressed as,

SFTI=A∩B|A∩B|+α|A−B|+β|B−A|(2)

where α and β refers to the parameters belonging to the Tversky index. The similarity measure also yields a bunch of model parameters.

Cosine similarities: The following are the cosine similarity between the name fields of two records, “Record 1” and “Record 2”: First, the dimension of both strings is determined by computing the union of two string elements in record 1 and “record 2” as (word1, word2, … word N), and then the frequency of occurrence vectors of the two elements are determined, i.e., “record 1” = (vector value1>, vector value2>, …>) and “record 2” = (vector value1>, vectorvalue2>, …>). Finally, the magnitude and the dot product of each string are determined.

RANFIS: The RANFIS model combines the adaptable fuzzy inputs and a modular neural network for the quick and accurate approximation of complex functions. Fuzzy inference systems are also useful since they provide the combination of the characteristic behavior of rules represented as Membership Functions (MF) which includes the specific subclass of the fuzzy axon with the capability of neural networks. These types of networks are efficient in solving problems compared to NNs while modeling the underlying function A fuzzy axon (fa), which employs membership functions on the inputs, is the basic element of RANFIS. The output of a fuzzy axon may be calculated using the following formula:

fa=min∀i(MF(xi,wij))(3)

where i = input index, j = output index, xi = input i,wij = weights (MF parameters) with respect to the jth MF of input i. This system may be thought of as a three-layer feed-forward neural network with particular functions. The first layer denotes the input variables, the middle (hidden) layer denotes the fuzzy rules, and the third layer denotes the output variables. Fig. 3 shows the RANFIS model utilized in this work.

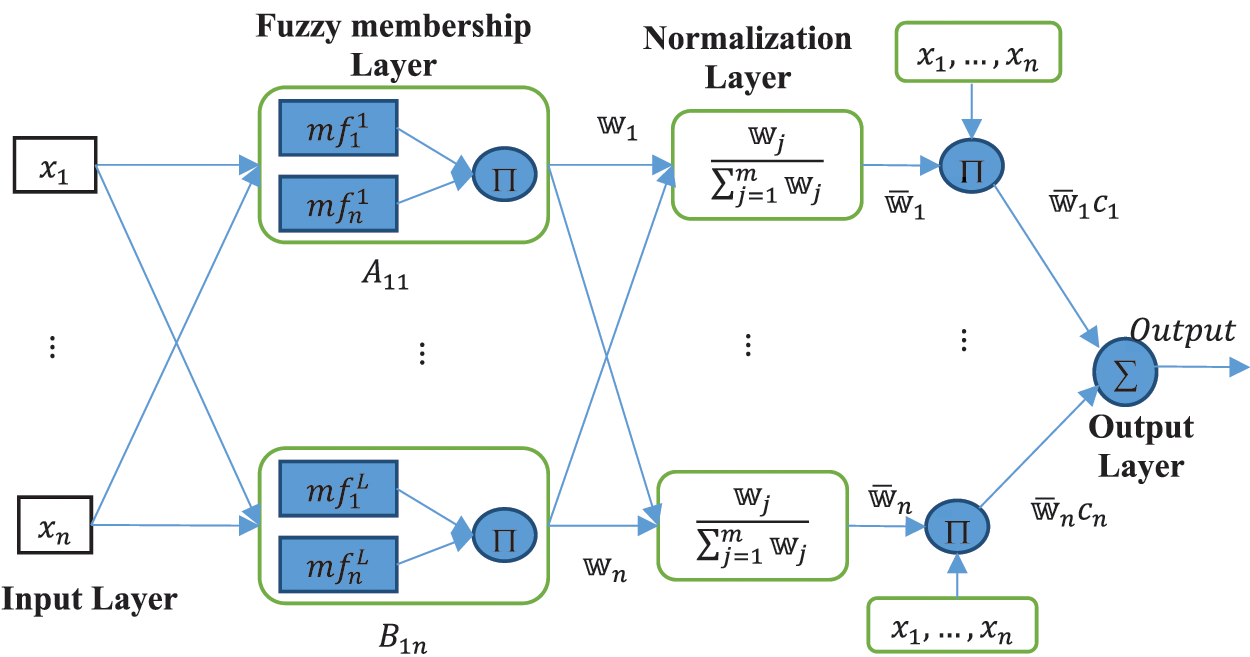
Figure 3: A prototype RANFIS network

Take a RANFIS architecture having n inputs and one output. To initialize the model, a general rule set that has n inputs and mIF-THEN rules is given

Rule 1:Ifx1isA11andx2isA12...andxnisA1n

then u1=p11x1+p12x2+⋅⋅⋅+p1nxn+q1(4)

Rule 1:If x1 is A21 and x2 is A22 . . . and xn is A2n

then u2=p21x1+p22x2+⋅⋅⋅+p2nxn+q2(5)

Rule m:If x1 is Am1 and x2 is Am2 . . . and xn is Amn

then u2=pm1x1+pm2x2+⋅⋅⋅+m2nxn+qm(6)

Layers in RANFIS architecture can be either adaptive or constant and their functions are:

Layer 1 as Premise Parameters: Each node present in this layer is a complex-valued membership function (M ij) having a node function:

O1,ij=|uAij(xi)|⌞uAij(xi)(7)

where (1≤i≤n,1≤j≤m)

Every node in layer 1 constitutes the membership grade of a fuzzy set (Aij) and indicates the degree of belonging of a particular input to one of the fuzzy sets.

Layer 2 as Fuzzy membership layer: Each node present in this layer gives the multiplied value of all the inward signals. This layer gets input as the product of all the output pairs obtained from the first layer:

O2,j=uAi1(x1)∗uAi2(x2)∗,…,∗uAin(xn)↦wj(8)

where (1≤i≤n,1≤j≤m)

Layer 3 as Normalization of firing strength: Each node present in this layer computes the rational of input signals:

O3,j=w¯j=wj∑j=1mwj(9)

where (1≤j≤m)

Layer 4 as Consequence Parameters (cp): Each node in this layer multiplies the Normalization of firing strength results obtained from the third layer and the output of the neural network:

O4,j=wjuj=wj(cpj1x1+cpj2x2+…+cpjnxn+qj)(10)

where (1≤j≤m)

Layer 5 as Overall Output: Here the node yields the output obtained from the RANFIS network:

O5,j=∑wjuj(11)

where (1≤j≤m)

The bell fuzzy axon utilized in this work comprises a kind of fuzzy axon using a bell-like curve in the form of its membership function. Every MF uses three parameters saved in the weight vector of the bell fuzzy axon (Eq. (12))

MF(x,w)=11+|x−wnw0|∗2w1(12)

where (1≤j≤m)

where x = input and w eight of the bell fuzzy axon. Because its MF may be modified bybackpropagation throughout the network training phase to make convergence effective, fuzzy axons are beneficial. A modular network, which utilizes functional rules on the inputs, is the second key component of RANFIS. Concerning the number of MFs, the number of modular networks is the same as the number of network outputs and processing components in each network. The Tsukamoto model and the Sugeno (TSK) model are two fuzzy structures that are commonly used in general. Finally, the MF outputs are applied to the modular network outputs through a combiner. Later, the combined outputs are canceled by a final output layer, and error backpropagation to the MF and modular network is detected.

Fig. 4 above illustrates the processing diagram of the RANFIS based deduplicate detection scheme. Take a document set D which consists of a bunch of replicated and non-duplicate documents. The bunch of documents can be denoted as, D=[d1,d2,…,dn],d=1,2,3. The document set is processed by applying the similarity measures. The similarity measures utilized in the proposed work include DCs (Dice coefficients), DL (Damerau-Levenshtein), TIs (Tversky Indices), and CSs (cosine similarities) (CS). The model parameters are constructed after the input documents from document set D have been processed by the similarity measures. For document set D, each of the similarity metrics gives model parameters individually. Because model parameters are the most significant part of the proposed neural network technique, three similarity metrics are used to compute them. As a result, determining the model parameter must be accurate and correct. The model parameters generated, MP is listed in the following table.

MPSFDC=[mp1,mp2,…,mpn]

MPSFDL=[mp1,mp2,…,mpn](13)

MPSFTI=[mp1,mp2,…,mpn]

MPSFCS=[mp1,mp2,…,mpn]

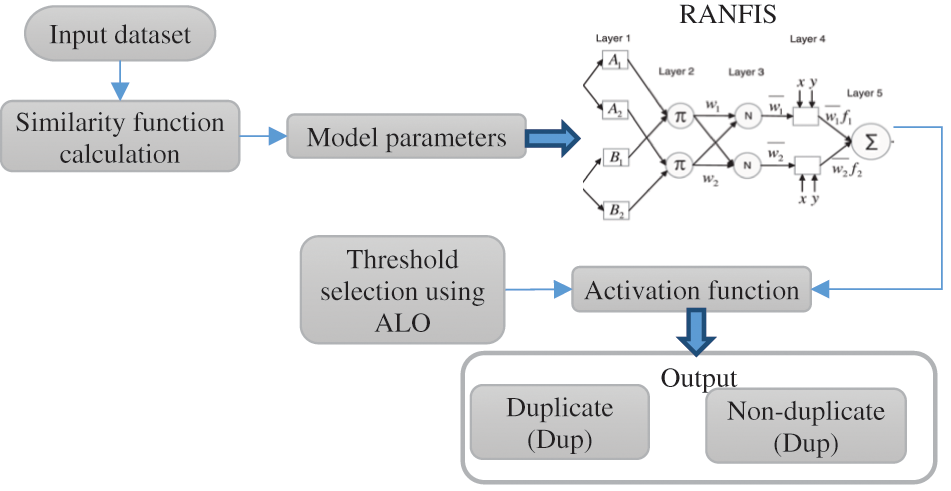
Figure 4: The processing diagram of the RANFIS-based duplicate detection

The above-listed parameters indicate the bunch of model parameters produced based on the similarity measures studied earlier. The suggested mechanism’s next step is to sort and combine the three sets of model parameters for the deduplication process using RANFIS. The RANFIS is provided with two sets of data, one containing the ordered model parameters and the other containing the weightage values. A parameter specified for the RANFIS determines the weightage value.

MPsort=[mp1,mp2,…,mpn](14)

where MPsort refers to the ordered model parameters values and the set W indicates the set having the weightage parameters of the RANFIS. The FOj stands the output attained after the weightage and the model parameters are computed. So, the output for each one of the model parameters is obtained from the set MP sort. The general equation for computing FOj is formulated by,

FOj=∑j=1nwj⋅mpj(15)

where, FOj refers to the output after all of the weightage value wj and mpj the model parameters are processed. The RANFIS developed for the proposed deduplication approach will yield two output values NonDup and Dup. The value FONonDup is unique for the non-duplicate documents and FODup is unique for duplicate documents. The activation function behaves to be a squashing function, operating such that the output of a neuron in a neural network ranges between specific values such as 0 and 1. A threshold is defined to shift the FOj value to any value within the range [0, 1]. A threshold Function exists which uses a value of 0 when the summed input is below a particular threshold value (FOj), and the value is 1 when the summed input is more than or the same as the threshold value. As per the ultimate  FOj values, the deduplication is executed. ALO picks the optimum threshold value.

ALO for optimal threshold and weight selection: This section states that the variable weights and threshold, has an effect on the RANFIS output and the objective of any optimizer is to find values for these variables so that the maximum classification rate and the least error rate is achieved by them. The RANFIS performance is enhanced by applying the Ant Lion Optimizer. RANFIS is an approach that does not permit the local minima and local maxima to get an optimal solution. The ALO [18] algorithm helps compute the RANFIS algorithm’s input. Using the data set provided, the ALO optimizer performs the tuning of the proposed algorithm RANFIS system. This renders the weight and threshold for learning using the model. The application of ALO helps adjust the local minima and local maxima from occurring. The RANFIS approach is an efficient optimization approach. Fig. 5 illustrates the RANFIS through ALO.

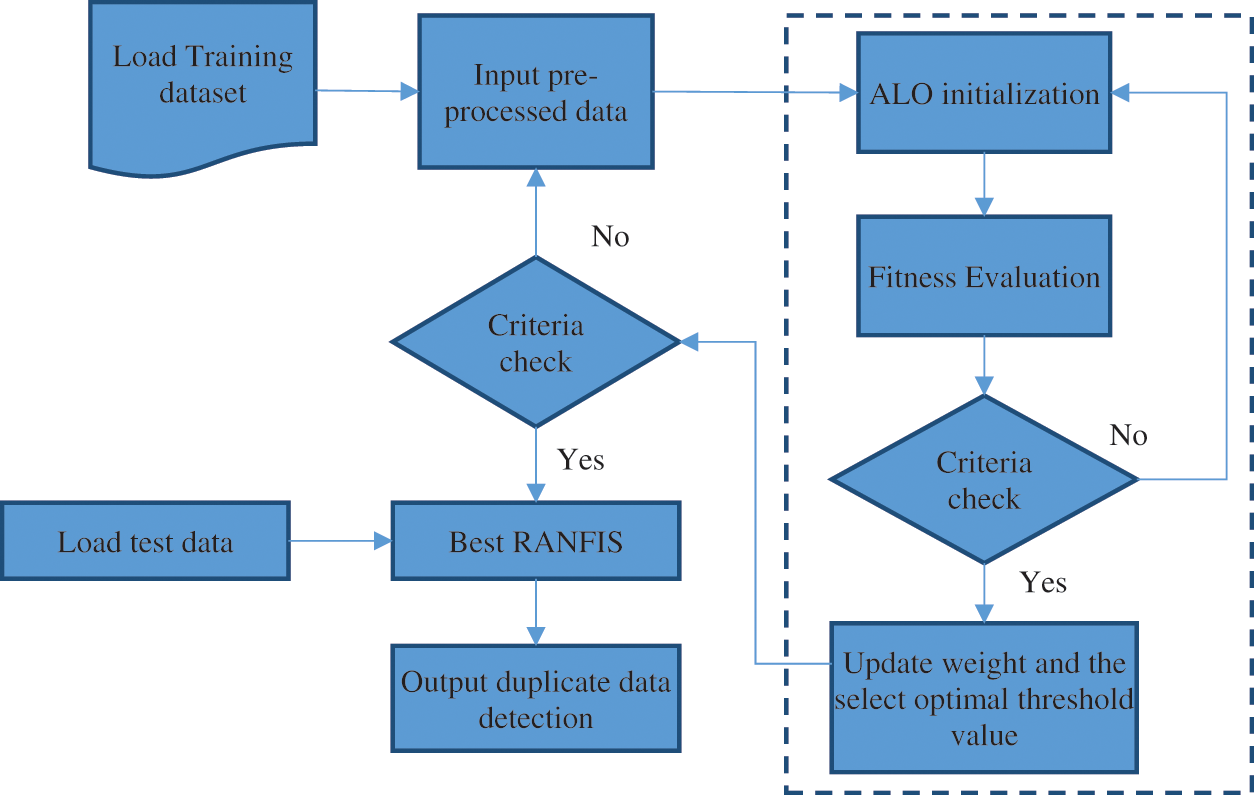
Figure 5: Proposed RANFIS with ALO method

Data quality classification at the early stage is an important step since the classification of the replicated data during the early phases, the ambiguity associated with the duplication, and advancement due to the dynamic characteristics of the data, necessitates a reliable model for the accurate prediction of the redundancy in data. In this work, RANFIS is utilized for classification with the weaker domain detection among the primary 4 domains.

•   Initialize the positions of input variables of the features chosen from the dataset in random.

•   Compute the cumulative sum of the maximum number of iterations, where iteration indicates the steps moved in a random walk. The location of the value of every input is taken in a single matrix. The respective objective values are put in another matrix. Another matrix is generated to save the position and fitness value in the form of accuracy.

•   Random Walk: Update the position of the input value through random weight assignment.

•   Building Traps: Generate two vectors, one having a minimum of all the variables belonging to one input source and the other having a maximum of all the variables belonging to the same input. This provides the best input weight for the required output value.

•   Entrapment of Ants in Traps: Fill in the position of all input variables with the respective fit of the other input variables, when its fit gets better.

•   Catching Preys: At the end, update weight and position.

•   Rebuilding Traps: Verify the stop condition, if it is met, retrieve the optimal solution, else go back to update the position of c.

Once the inference is over, the generation of automatic rules is performed to find data duplication. Elitism (remembering the ideal solution obtained) forms the primary attribute of a nature-influenced algorithm, which helps retain the ideal solution achieved during any step of the optimization process. In this work, the ideal output attained during every iteration is stored and regarded as an Elite. As the Elite is considered the fittest output, it will have an influence on the movements of the weight of every other variable during the iteration.

4  Experimental Results and Discussion

This section studies the performance analysis carried out on the proposed deduplication approach when the proposed mechanism RANFIS is used on the dataset by changing the number of records from 2000 to 10000. Each one of the experiments is conducted by applying the ideal threshold values applied to ALO. The efficiency of record linkages of the proposed similarity technique is assessed by metrics like precision, Recalls, Accuracy, and F-measures, and the proposed approach is compared with the contemporary techniques including BNs, SVMs, and modified RBFs (Radial Basis Functions).

4.1 Precision Comparison Results

Precision indicates the original positive score divided by the positive score that the classification model/algorithm predicts. Precision can be computed using the following expression:

Precision=TPTP+FP∗100(16)

Fig. 6 shows the precision comparison results between the proposed RANFIS classifier and contemporary models (BN, RBF, and SVM) for the particular volume of data in a specified database. When the amount of data is increased, the precision is also increased. RANFIS yields a precision of 94%, whereas BN, RBF, and SVM attain 83.00%, 85.00%, and 87.00% correspondingly for 10000 no. of records. This is because the RANFIS helps in reducing the computation time of the obtained factors making it the simplest fine-tuning of RANFIS and thereby the precision rate is increased.

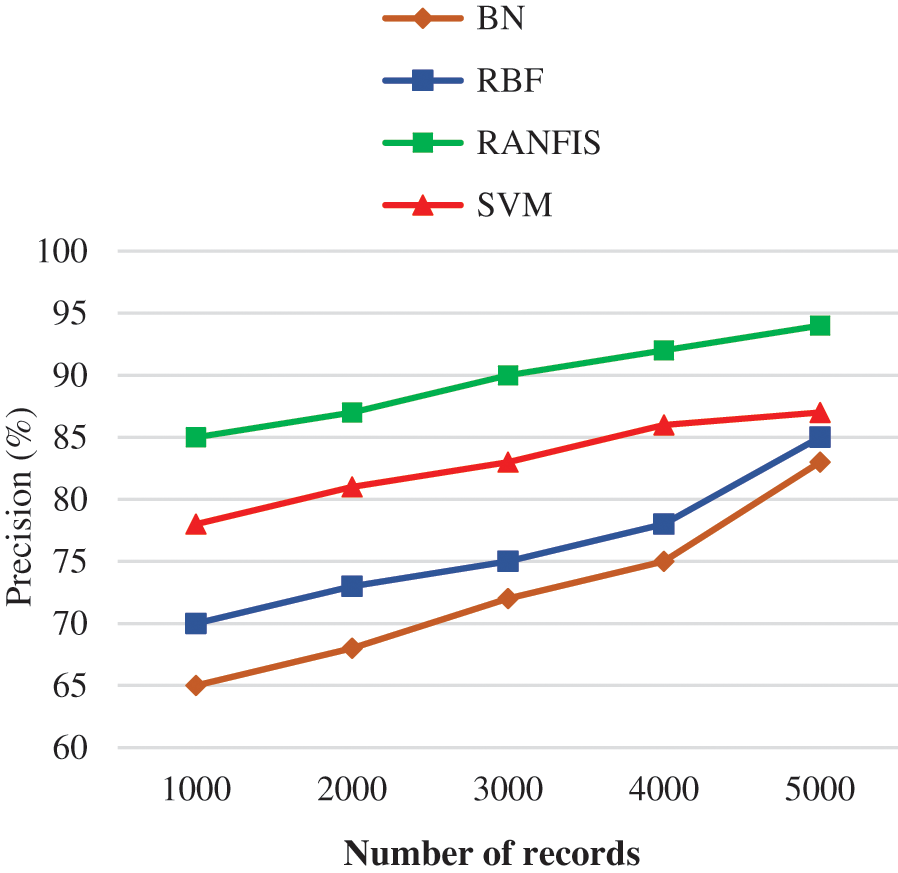
Figure 6: Precision performance comparison results

4.2 Recall Comparison Results

The recall is defined as the proportion between the currently classified heart patients to the overall number of patients suffering from heart disease. It implies that the prediction of the model is positive and the individual is suffering from heart disease. The expression for computing recall is as follows:

recall=TPTP+FN∗100.(17)

Fig. 7 illustrates the recall comparison between the proposed RANFIS classifier, and the contemporary models such as BN, RBF, and SVM for the volume of data in the specified database. The RANFIS helps in improving the accuracy and yields are call value of 96%, while the other techniques like BN, RBF, and SVM yield 86.00%, 88.00%, and 92.00% correspondingly for 10000 records. This way, the proposed algorithm is much better than the contemporary algorithms in terms of improved validation results for duplicate records detection. The proposed RANFIS model had no dependency on the sudden feature modifications and hence it is capable of achieving improved recall value. It can be observed from the recall precision-based analysis that the proposed deduplication approach yields a substantial rise in the value of accuracy at multiple threshold values.

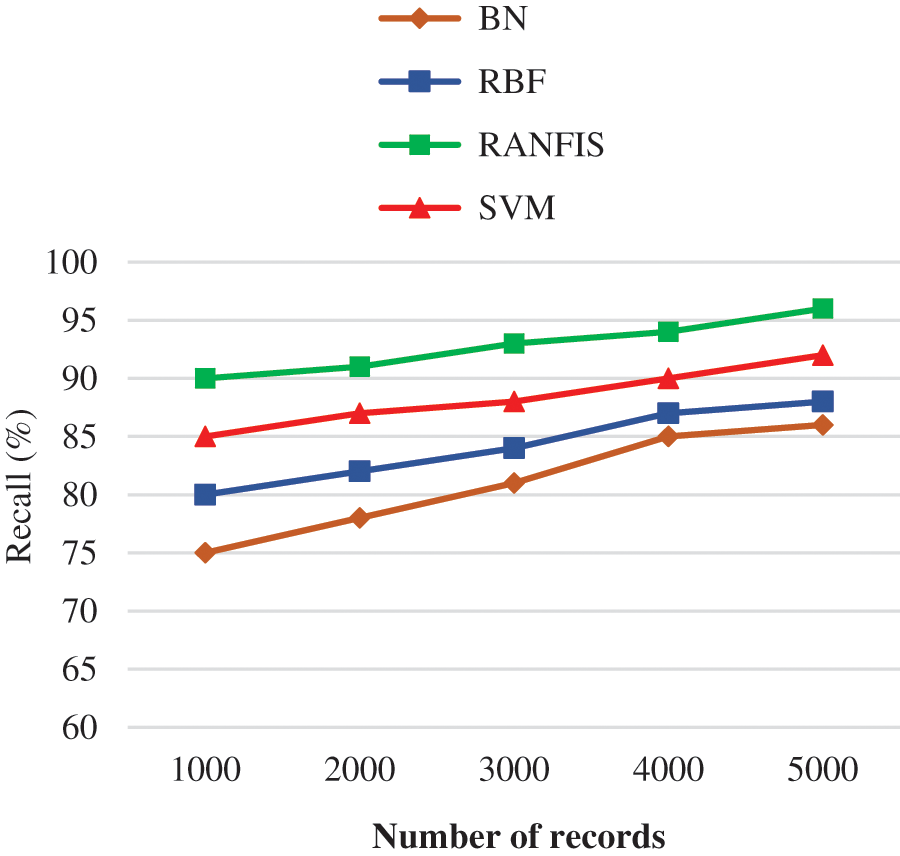
Figure 7: Recall performance comparison results

4.3 F1-Sore Comparison Results

F1-score indicates the weighted measure of both recall precision and sensitivity. The value spans between 0 and 1. In case its value is one, the classification algorithm is commendable and in case the value is 0 then it implies the classification algorithm performs poorly.

F1score=2∗Precision∗RecallPrecision+Recall(18)

Fig. 8 demonstrates the F1-sore comparison between the proposed and contemporary models for a particular volume of data in specific databases. If the data volume is increased, then there is an increase inF1-sore also.

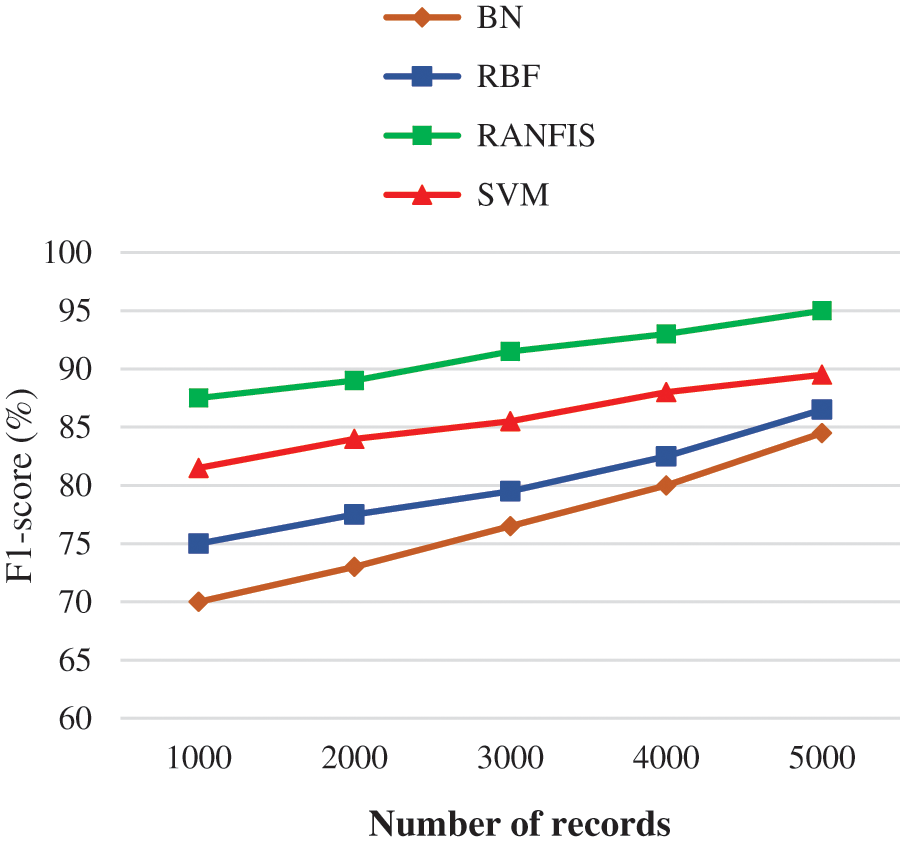
Figure 8: F1-score performance of comparison results

For e.g., the RANFIS yields an F1-sore of 95% when every other model like BN, RBF, and SVM provides just 84.50%, 86.50%, and 89.50% correspondingly for 10000 records.

This is because the ALO helps in the optimization of the threshold value and weight of RANFIS efficiently yielding better convergence speed and therefore its validation results are reasonable with an improved F1-sore rate.

4.4 Accuracy Comparison Results

The accuracy of the classification model reveals how the model performs on the whole and it can be derived using the expression as follows:

Accuracy=TP+TNTP+TN+FP+FN∗100.(19)

Fig. 9 illustrates the accuracy comparison between the proposed RANFIS classifier, and available models (BN, RBF, and SVM) for a certain data volume in the database provided. The RANFIS improves the accuracy with the processing time being reduced. The RANFIS classifier achieves an accuracy of 94.6% for 546744 records, while with other techniques including BN, RBF, and SVM, the accuracy value of 87.00%, 89.00%, and 91.00% is obtained. In this proposed study, there is no need for a large number of extracted features during reduction. Therefore, the proposed algorithm is much better than the contemporary algorithms in terms of improved good validation results during the duplicate data detection.

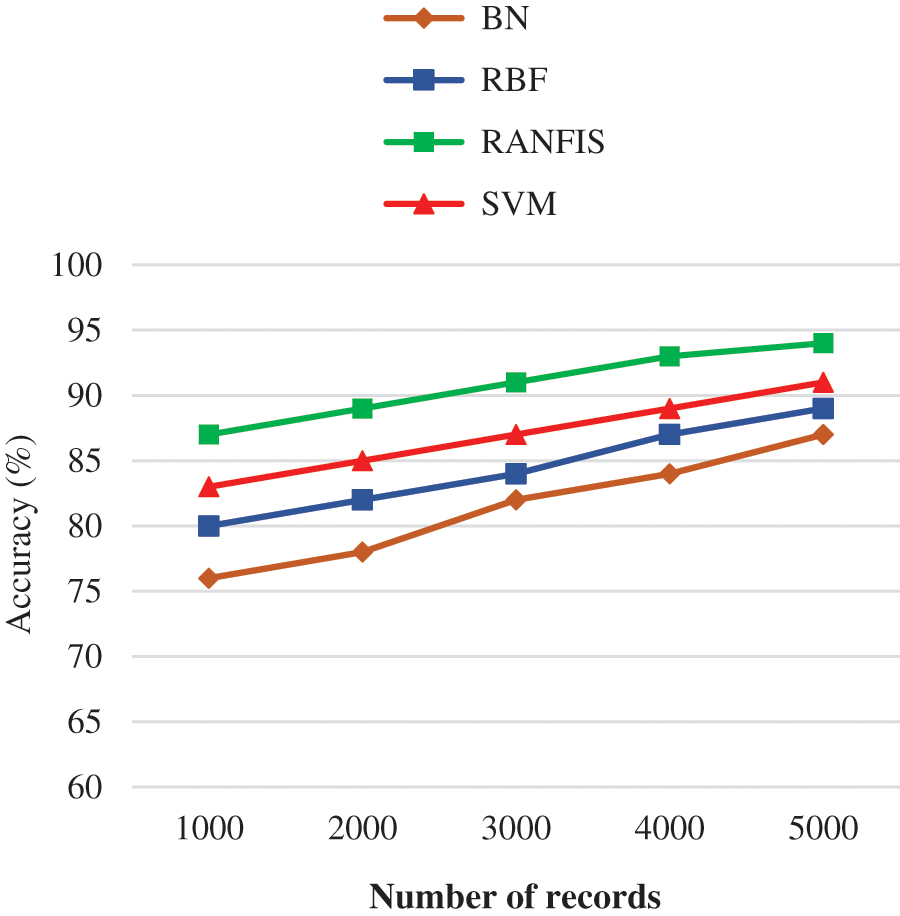
Figure 9: Accuracy performance comparison results

5  Conclusion and Future Work

Deduplication has remained one of the developing approaches for data redundancy and duplication. In duplications, information retrieval systems have several challenges. This research implements a deduplication method based on artificial neural networks. To compute deduplication between datasets, the method generates several similar values. The suggested deduplication method starts with a training phase to calculate the weight parameter for the RANFIS, followed by a testing step to find repeated or replicated data. The proposed deduplication method is used in three datasets for its performance evaluation in terms of the deduplication process. The optimization of the neural network is performed through ALO for its topology, parameters, and distribution of initial weights before its application in the form of a detector to find the replicas. It is proven from the performance analysis that the performance achieved with the proposed approach is much better in identifying the deduplication. The performance analysis depends on two diverse metrics, accuracy and time, and the maximum accuracy achieved for the proposed deduplication technique is about 95% better than existing techniques. A comparison analysis has been carried out between the proposed deduplication technique and the available deduplication methods. Currently, the conventional duplicate record detection techniques make use of discrete features to construct the classification models which are not capable of expressing the semantic information in a better manner, and improvement is needed in the classification accuracy. The proposed system will be useful in improving the efficiency, usefulness, and quality of care that healthcare systems provide. The performance of the deep learning model is excellent in feature extraction and classification. Hence, a duplicate record detection model which relies on deep learning can be proposed in future works.

Acknowledgement: We thank anonymous reviewers for their helpful suggestions.

Funding Statement: This research project was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R234), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors state that they possess no competing for interests to disclose in this work.

References

 1.  F. Naumann and M. Herschel, “An introduction to duplicate detection,” Synthesis Lectures on Data Management, vol. 2, no. 1, pp. 1–87, 2010. [Google Scholar]

 2.  X. Wen, J. Hong, F. Dan and H. Yu, “Similarity and locality-based indexing for high-performance data deduplication,” IEEE Trans. on Computers, vol. 64, no. 4, pp. 1162–1176, 2015. [Google Scholar]

 3.  W. Fan, “Data quality: From theory to practice,” AcmSigmod Record, vol. 44, no. 3, pp. 7–18, 2015. [Google Scholar]

 4.  P. Christen, “A survey of indexing techniques for scalable record linkage and deduplication,” IEEE Transactions on Knowledge and Data Engineering, vol. 24, no. 9, pp. 1537–1555, 2011. [Google Scholar]

 5.  H. Lu, X. Chen, X. Lan and F. Zheng, “Duplicate data detection using GNN,” in IEEE Int. Conf. on Cloud Computing and Big Data Analysis (ICCCBDA), Chengdu, pp. 167–170, 2016. [Google Scholar]

 6.  L. Leitao, P. Calado and M. Herschel, “Efficient and effective duplicate detection in hierarchical data,” IEEE Transactions on Knowledge and Data Engineering, vol. 25, no. 5, pp. 1028–1041, 2012. [Google Scholar]

 7.  Y. S. Lin, T. Y. Liao and S. J. Lee, “Detecting near-duplicate documents using sentence-level features and supervised learning,” Expert Systems with Applications, vol. 40, no. 5, pp. 1467–1476, 2013. [Google Scholar]

 8.  X. Liu, X. Cai, B. Li and M. Chen, “Duplicated record detection based on improved RBF neural network,” in IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conf. (IAEAC), Chongqing, China, pp. 2034–2037, 2017. [Google Scholar]

 9.  M. G. De Carvalho, A. H. Laender, M. A. Gonçalves and A. S. Da Silva, “A genetic programming approach to record deduplication,” IEEE Transactions on Knowledge and Data Engineering, vol. 24, no. 3, pp. 399–412, 2010. [Google Scholar]

10. M. Ektefa, M. A. Jabar, F. Sidi, S. Memar, H. Ibrahim et al., “A Threshold-based similarity measure for duplicate detection,” in IEEE Conf. on Open Systems, Langkawi, Malaysia, pp. 37–41, 2011. [Google Scholar]

11. D. Karapiperis, A. Gkoulalas-Divanis and V. S. Verykios, “LSHDB: A parallel and distributed engine for record linkage and similarity search,” in IEEE 16th Int. Conf. on Data Mining Workshops (ICDMW), Barcelona, Spain, pp. 1–4, 2016. [Google Scholar]

12. D. R. Wilson, “Beyond probabilistic record linkage: Using neural networks and complex features to improve genealogical record linkage,” in The Int. Joint Conf. on Neural Networks, San Jose, CA, USA, pp. 9–14, 2011. [Google Scholar]

13. K. Y. Yigzaw, A. Michalas and J. G. Bellika, “Secure and scalable deduplication of horizontally partitioned health data for privacy-preserving distributed statistical computation,” BMC Medical Informatics and Decision Making, vol. 17, no. 1, pp. 1–19, 2017. [Google Scholar]

14. K. El Emam, J. Hu, J. Mercer, L. Peyton, M. Kantarcioglu et al., “A secure protocol for protecting the identity of providers when disclosing data for disease surveillance,” Journal of the American Medical Informatics Association, vol. 18, no. 3, pp. 212–217, 2011. [Google Scholar]

15. J. T. Finnell, J. M. Overhage and S. Grannis, “All health care is not local: An evaluation of the distribution of emergency department care delivered in indiana,” in AMIA Annual Symp. Proc., MD, Rockville, pp. 409–416, 2011. [Google Scholar]

16. J. Gichoya, R. E. Gamache, D. J. Vreeman, B. E. Dixon and J. T. Finnell, “Grannis an evaluation of the rates of repeat notifiable disease reporting and patient crossover using a health information exchange-based automated electronic laboratory reporting system,” in AMIA Annual Symp. Proc., MD, Rockville, pp. 1229–1236, 2011. [Google Scholar]

17. G. M. Weber, “Federated queries of clinical data repositories: The sum of the parts does not equal the whole,” Journal of the American Medical Informatics Association, vol. 20, no. 1, pp. 155–161, 2013. [Google Scholar]

18. L. Abualigah, M. Shehab, M. Alshinwan, S. Mirjalili and E. M. A. Laziz, “Ant lion optimizer: A comprehensive survey of its variants and applications,” Archives of Computational Methods in Engineering, vol. 28, no. 3, pp. 1397–1416, 2021. [Google Scholar]