Optimization Techniques in University Timetabling Problem: Constraints, Methodologies, Benchmarks, and Open Issues

1  Introduction

University timetabling belongs to a class of problems called NP (non-deterministic polynomial)-COP (combinatorial optimization problem). This class has distinctively recognized features such as:

•   A method to solve this kind of problem in a specific reasonable time is yet to be found.

•   The computational time required to achieve a viable solution grows exponentially with the problem size.

•   It is commonly done by hand; a human can repeat the work routine, and it is time-consuming.

•   The main objective concentrates on fulfilling all the stated hard and soft constraints, which increases the complexity.

•   The exact solution is only achievable for modest cases of optimization problems. The majority of cases adopt approximation algorithms, which do not guarantee the optimal solution but are hopefully able to obtain “good enough” solutions.

The above features help clarify why university timetabling is a very complicated task, since it aims to obtain the ideal feasible timetable among various institutions, and each institute has specific rules, conditions, and structure. Moreover, these institutions continue to grow rapidly every year as the number of registered students increases, as more students mean more teachers, subjects, buildings, and hard manual work. Furthermore, the reached solution may be unsatisfactory in some respects. For these reasons, university timetabling problems require automating the gained solutions to help accelerate the search process for the optimal timetable. Over the years, several algorithms have been presented to solve university timetabling problems. Many publications argue about completely automating university timetabling. However, the human touch is still required to guide and reinforce the search process. Moreover, preferences in the candidate solutions need to be considered that are unable to be made and expressed through automated systems. So, in general, it is a tailor-made process [1].

Even though there are several algorithms for solving university timetabling, this study focuses on optimization algorithms, particularly because they overcome some common classes of problems. Meta-heuristic algorithms are categorized as population-based approaches and are widely applied in solving university timetabling problems due to their approved strength factors. Recently, some articles on timetabling problems were published, which studied systematic mapping for meta-heuristic for university timetabling problems [2] and a survey for optimization methods in school timetabling [3]. Another study introduced a survey focusing on trends and opportunities in university course timetabling [4]. Most recent studies have focused on one category of timetabling problems, such as school, course, and examination timetabling. In this study, university timetabling problems are discussed in detail, considering both course and examination timetabling problems.

This paper aims to comprehensively review optimization approaches for solving university timetabling problems. The classification of current and recent studies is investigated and discussed for both university course timetabling and university examination timetabling problems. In addition, the adopted meta-heuristic optimization algorithms are demonstrated in solving this kind of problem. The constraints related to university timetabling that need to be considered to obtain a good solution are explained, while different methodologies used in previous studies are explored. In addition, methods to analyze and measure the performance of the solution by demonstrating the commonly used benchmark datasets are also elaborated. Moreover, the study provides some robust university timetabling solutions, trends, and future directions.

This study is structured as follows: Section 2 provides context for the problem’s nature, classifications, and constraints. In Section 3, the university timetabling methodologies and approaches are presented. Section 4 addresses the common techniques for analyzing optimization algorithms. Section 5 describes the benchmarking standard. After that, Sections 6 and 7 show the discussion, future direction, and open issues, respectively. Finally, Section 8 concludes the paper.

2  Background

The term “scheduling” is considered a comprehensive term covering various types of problems such as timetabling, sequencing, and rostering. A brief description of these problems is explained below:

Scheduling is the allocation, subject to constraints, of resources to objects being placed in space-time in such a way as to minimize the total cost of some set of the resources used.

Timetabling is the allocation, subject to constraints, of given resources to objects being placed in space-time in such a way as to satisfy as many as possible of a set of desirable objectives.

Sequencing is the construction, subject to constraints, of an order in which activities are to be carried out or objects are to be placed in some representation of a solution.

Rostering is the placing, subject to constraints, of resources into slots in a pattern. One may seek to minimize some objectives or simply to obtain a feasible allocation. Often, the resources will rotate through a roster [5]. Based on that, the issue of timetabling can be described as shown in Fig. 1.

Figure 1: University timetabling is part of the scheduling problem

The timetabling approach covers several types of real problems, such as companies (employees and staff), schools, universities, the military, hospitals (nurses and doctors), transportation (flight, train), and sports. The focus of this paper is particularly on university timetabling and its obstructions and challenges. University timetabling is a difficult optimization problem that is faced every year. Finding the optimal timetable becomes hard and time-consuming due to:

•   There is an increasing number of educational institutions, each with their own ideas about how and when their courses or exams should be completed or performed.

•   The massive number of subjects presented by these institutions.

•   The growing numbers of students, however, mean that these days they can combine subjects from various tracks, possibly even in diverse faculties.

•   There are several hard constraints to be fulfilled.

2.1 University Timetabling

University timetabling problems can be classified as combinatorial optimization problems (COP). The overall goal of this type of problem is to select the best solution from a set of possible solutions. For example, timetabling is intended to assign a timeslot for each event [6]. In certain cases, the problem of timetabling consists of locating any timetable that meets all the stated constraints, in which case the problem is formulated as a search problem. In other cases, what is needed is a timetable that meets all the hard constraints and minimizes or maximizes a declared objective function that embeds the soft constraints; in these instances, the problem is formulated as an optimization problem [1]. The challenge of optimization is to find the best values according to a stated objective function while respecting a set of constraints. In addition, the complexity of the problem comes from the nature of the variables, which are either discrete or continuous [7]. University timetabling is a broad concept with many subfields. However, the following clarification focuses on the two most common essential educational timetabling fields: examination and course timetabling.

2.1.1 Examination Timetabling

Examination timetabling can be formally defined as “the assigning of examinations to a limited number of available time periods in such a way that there are no conflicts or clashes” [8]. Examination timetabling is a substantial educational timetabling concept. In most examination timetabling, the common objective is to avoid clashing and conflicting, where a student must not take two exams at the same time and make sure that there will be only one exam assigned to a room at any time slot. Also, the room capacity is taken into consideration, as the room must be large enough to contain all the students as well as avoid time overlap in the same room [9]. University examination timetabling can be classified into capacitated and un-capacitated problems. The capacitated problem is committed to ensuring the number of examined students does not exceed the capacity of the scheduled room. On the other hand, the un-capacitated problem disregards room capacity [9].

2.1.2 Course Timetabling

Course timetabling can be formally defined as “a multi-dimensional assignment problem in which students and teachers (or faculty members) are assigned to courses, course sections, or classes; events (individual meetings between students and teachers) are assigned to classrooms and times [10].” Course timetabling is a significant educational timetabling field. Course, lecture, or class timetabling is a multipart scheduling problem in which students are assigned to courses, and consequently, those courses must be allocated to specific rooms and timeslots [11]. Furthermore, course scheduling can be divided into subproblems like student scheduling, course scheduling, teacher assignment, and classroom assignment [12]. The differences between courses and exam timetabling are, firstly, that, commonly, each course has one assigned exam; secondly, the exam could be assigned to one room or divided across several rooms. On the other hand, courses must be scheduled in one room; nothing else [13]. University course timetabling is divided into curriculum-based and enrollment-based course timetabling. First, the issue is to develop a weekly lecture schedule and then use the enrollment-based approach to develop the timetable later on [14].

2.2 Timetabling Constraints

The constraints can be considered as borders when a feasible timetable is found. Constraints are classified into two types: hard and soft constraints. Once forming the timetable, the variation of the hard and soft constraints should be considered, as well as considering that these constraints differ from one institution to another.

•   Hard constraints: these cannot be violated, and hard constraints must be met for the solution to be valid for the problem.

•   Soft constraints: can be violated, they are not required, but their fulfillment is critical to producing a good quality timetable and is used to measure the quality of the solution. Every violation denotes a penalty for the solution that is added to the cost.

Fig. 2 lists common examples of both examination and course timetabling for more specifics; check [7,15], for examination constraints as well as [12,15] for university course constraints.

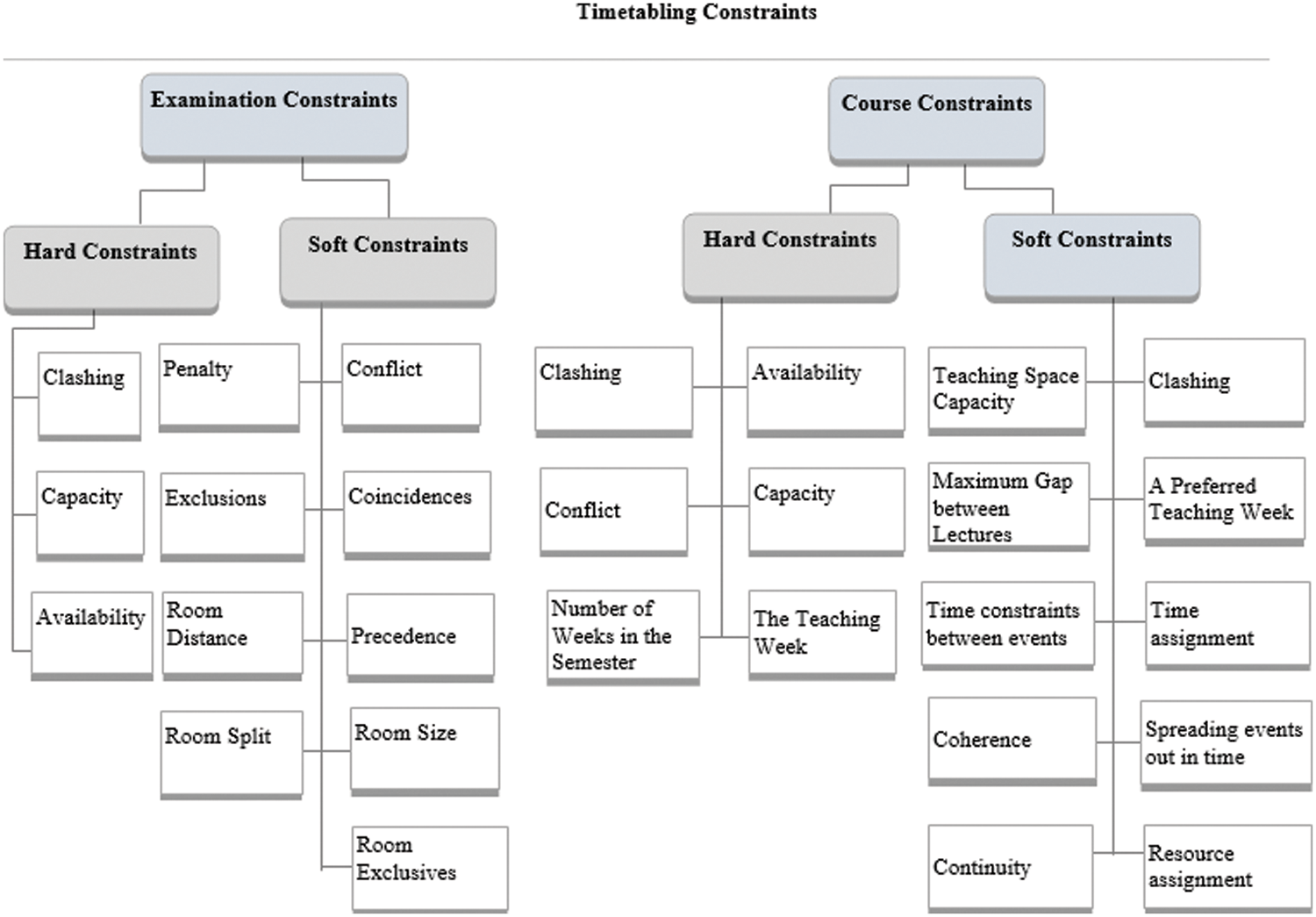
Figure 2: University timetabling scheduling constraints

3  University Timetabling Problem Methodologies

This section demonstrates different methodologies utilized in university timetabling using meta-heuristic optimization algorithms.

3.1 Timetabling Methodologies

The diverse proposed methods for solving university timetabling problems can be divided into four agreed categories, in addition to six extended categories:

•   Sequential methods

•   Cluster methods

•   Constraint-based methods

•   Meta-heuristic methods

•   Generalized search

•   Hybrid evolutionary algorithms

•   Multi-criteria approaches

•   Case-based reasoning techniques

•   Hyper heuristics

•   Adaptive approaches

The majority of approaches have been previously suggested to solve timetabling problems. In the following, only three substantial and significant timetabling approaches will be described in detail: heuristic algorithms, meta-heuristic algorithms, and hybridization methods. Fig. 3 illustrates the hierarchy and clarifies the common framework of university timetabling approaches.

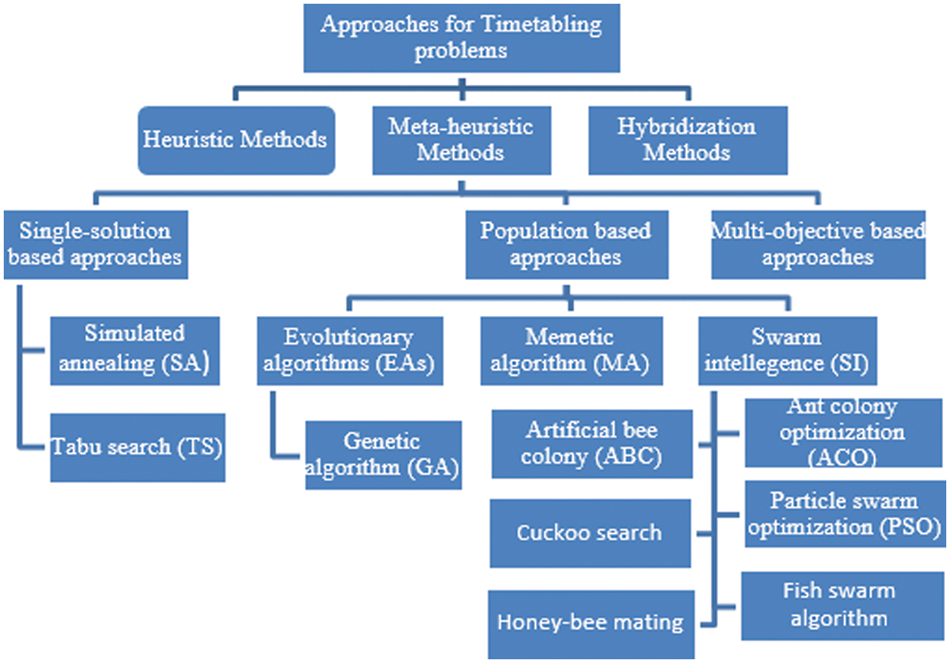
Figure 3: University timetabling scheduling methods

3.2 Heuristic Algorithms

Sequential heuristics algorithms are simple and easy methods to solve timetabling problems. The primary idea is to schedule the events by arranging them in a series, starting with the most difficult event [12]. It has proven capable of producing quick solutions. However, the performance of sequential heuristic approaches is relatively weak as compared to meta-heuristic efficiency [11]. Local search is one example of heuristic algorithms and is described as follows:

LS is a functional algorithm for solving combinatorial optimization problems (COPs). Most approaches that tackle NP/COPs problems include local search. Technically, local search takes the current best solution from the search space and repeatedly replaces it with a newer, better solution from the neighborhood [7]. Local search is presented to maximize the conditions between several candidate solutions in the search space. Because of the success of LS, recently, it has been applied to meta-heuristic algorithms such as PSO [16].

3.3 Meta-heuristic Algorithms

Meta-heuristic algorithms are elaborated approaches that are improved from the sequential heuristic method. Meta-heuristics have the capability to produce superior and better solutions as compared to sequential heuristic algorithms [12]. Broadly, in university timetabling, the initial solution is constructed using an appropriate heuristic mechanism, and the rest of the optimization process is carried out using an elected meta-heuristics algorithm. The performance of meta-heuristic algorithms may vary from one instance to another, depending on various factors. Therefore, the development of an overall comprehensive framework that remains stable and balanced under different circumstances with no need for expensive adaptation has been a research subject in recent years [17,18]. Diverse meta-heuristic approaches have been represented and developed lately, inspired by different fields; for example, analogy to scientific domains such as physics, biology, neurology, and sociology [7]. A meta-heuristic is categorized into single-solution and population-based approaches as follows:

3.3.1 Single-Solution Based Approaches

It addresses and handles one solution during the search process to obtain the best solution [11]. Instead of using a set of candidate solutions, it processes a single solution, picked up according to a set of criteria, and replaces it repeatedly with an improved solution until the termination step is accessed when the final conditional criterion is satisfied [17].

The efficiency of this approach depends on the definition of the neighborhood alternative candidate solutions to replace the current best one. Even though this notion represents the strength of this approach, the main shortcoming is that single-solutions are easily stuck in local optima as compared with the second category [11]. Some applicable single-solution based methods for solving university timetabling problems include:

•   Simulated Annealing (SA)

SA is considered an LS approach that stimulates the heating of solids in physics. It goes through a different strategy of origin local search, so instead of replacing the current solution frequently with another candidate, it creates a random initial solution and for each iteration, it is replaced by an alternative random solution, which increases the possibility of avoiding trapping in local optima [17].

•   Tabu Search (TS)

TS is based on stating a tabu list as a criterion. First, it starts from the initial result and moves toward a set of neighboring results to select the superior one. If the neighboring result is preferable to the available one, the algorithm will take that route. The transition from the current best result to the neighboring candidate result will be repeated until the termination condition is met [17].

3.3.2 Population Based Approaches

The population-based approaches first initiate a combination of population solutions. This initial set goes through numerous alterations and repetitions to obtain the optimal solution. For each restoration, a selection technique will be applied to choose the fittest solution from the presented population. After that, based on the implemented meta-heuristic algorithm, several modifications are performed to the selected solutions, so refinements are obtained to the solution. This procedure will continue until the optimal solution is obtained [17]. Usually, in university timetabling, the premier solution is formatted by utilizing a suitable heuristic approach. Nevertheless, the improvement was accomplished by using a meta-heuristic algorithm [12]. The following population-based approaches are examples of applicable algorithms for solving university timetabling problems:

Evolutionary Algorithms (EAs)

EAs are stochastic search approaches that imitate natural evaluation in addition to the social behavior of some species. EAs are population-based methods of assessing potential solutions. They consist of three phases: selection, regeneration, and replacement [19]. There are so many evolutionary algorithms available that have been successful and effective in solving optimization problems, like the well-known and commonly used genetic algorithm:

•   Genetic Algorithm (GA)

The genetic algorithm is a stochastic search technique inspired by molecular biology based on the natural evolutionary process and works on the process of natural selection [20]. GA has a great ability to search in large spaces, is a flexible algorithm, and is commonly characterized by robustly solving complex combinatorial problems [21]. The algorithm treats the solution as a chromosome carrying good and bad phenotypes, then uses the re-production technique.

Swarm Intelligence (SI)

Swarm intelligence mimics the social attitudes of species in nature, like bird flocks, beehives, and ant colonies. This kind of algorithm has proven to be effective and efficient in solving complicated optimization problems. A swarm is usually formed from a group or population of individuals that communicate and interact between individuals without any central control, yet leads to a final harmony in the whole colony [20]. The swarm’s formative behavior is based on some simple rules like:

•   central control of the individual’s behavior; decentralization reinforces the robustness of collective behavior, interactions, and performance.

•   Each individual in the swarm has a specified declared role based on the whole objective.

•   Individuals interact and communicate directly or indirectly through influencing a local, resulting in the emergence of intelligent global manners.

•   The swarm adopts a self-organization strategy.

The following are examples of popular and widely used swarm intelligence algorithms:

•   Particle Swarm Optimization (PSO)

PSO is inspirited by the coexistence of herds of birds or shoals of fish. In these swarms, there is a leader who has the best value of fitness to guide the whole swarm, so any individual moves are related to and based on the leader’s moves [20]. As a real-life example, in a herd of birds communicating during flight, each bird looks in a specific direction, and then the group will communicate together to identify and determine the bird at the best location. According to that, every bird speeds toward the superior bird’s location, utilizing velocity based on its immediate position. After that, it explores the search area from its fresh position. The birds can utilize their own expertise, which represents the local search process, as well as the expertise of the entire flock, which represents the global search [22].

•   Ant Colony Optimization (ACO)

The basic notion of the ACO algorithm is to find the shortest path from a food source to an ant hill by smelling pheromones. The colony is managed by hundreds of individuals. When collecting food, if there are two possible paths to access the food source, the ants choose randomly. Basically, half of them choose the first direction and the other half choose the other one. The shortest path obtains a huge amount of pheromone. So next time, the ants will recognize the shorter path by smelling the pheromones [20]. Looking at ACO, a random route or path creation is basically a mutation process, while pheromone concentration selection affords a technique for electing the shortest path, and crossover processes are not declared in this algorithm [23].

•   Artificial Bee Colony (ABC)

ABC mimics the natural behavior of bees during pollen collection. It is categorized into three bee sets: employed/forager bees; onlooker bees or observer bees; and scouts. The process starts by sending the scouts to randomly search around for promising areas. After searching, they return to the hive and express themselves by dancing. The information about the found site is vital, and this information guides the colony to evaluate the amount of energy needed to harvest. Based on that, the colony could send bees directly to the most promising place [20]. Both the scout and employed bees are mainly considered as mutation processes, where selection is based on the objective, which is the honey. There is no explicit crossover process [23].

Memetic Algorithm (MA)

The memetic algorithm is basically formed by hybridizing meta-heuristic algorithms that represent a global search with a local search [7]. A memetic algorithm is like a genetic algorithm, except the components that form the chromosome are called memes instead of genes. By the same token, there is a contrastive way to classify meta-heuristic algorithms. This standpoint divides meta-heuristics into three categories based on the hard and soft constraints considered according to declared requirements [18]:

•   One-stage optimization algorithms: where the satisfaction of both hard and soft constraints is conducted simultaneously.

•   Two-stage optimization algorithms: where the satisfaction of the soft constraints is only conducted when achieving the feasible timetable.

•   Algorithms that allow relaxations: where violations of the hard constraints are disallowed from the beginning by relaxing some other features of the problems, and then trying to satisfy the soft constraints.

3.3.3 Multi-Objective Based Approaches

A multi-objective optimization problem (MOP) is a process to simultaneously optimize two or more conflicting objectives. In university timetabling, sometimes it is needed to solve more than one constraint simultaneously. In this case, MOP is the best choice. For example, in exam timetabling problems, sometimes students can take exams in as many consecutive intervals as possible but at the same time reduce the schedule length and meet the difficult constraints like seat capacity and no overlapping exams. However, recent studies have been conducted successfully using multi-objective optimization algorithms in university timetabling problems [24–27], as well as in other applications [28].

3.4 Hybridization Methods

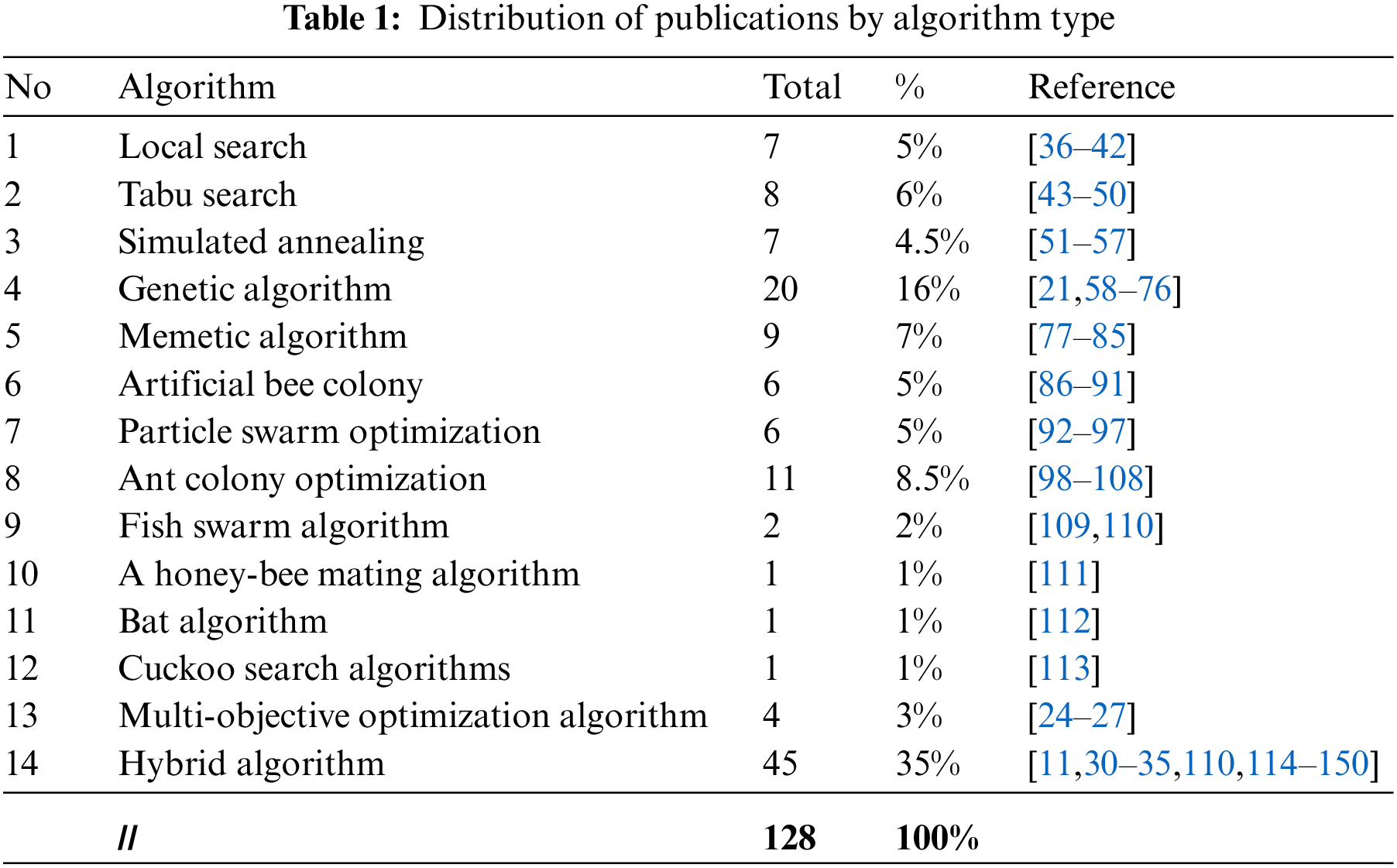
A hybrid algorithm is a combination of at least two algorithms complementing each other that are performed and executed together to generate a gainful synergy from their integration. In general, operating an effective and functional hybrid approach is a difficult mission [29]. The hybridization technique plays an outstanding role in creating a robust hybrid algorithm by integrating the features of each combined algorithm while simultaneously minimizing any substantial shortcomings [30]. The hybridization between single and population-based methods aims to utilize the preference features of population-based methods, which have enough capability to declare the potential promising zones in the exploration area, and single-based methods, which have enough capability to exploit the prospective areas [31]. For more information about this rising area, refer to the following references [32–35]. The allocation of the covered publications according to the adopted algorithm sort is presented in Table 1.

4  Optimization Algorithms Evaluation

Since university timetabling problems are categorized as NP-COP, the most probable way to solve and handle this kind of problem is through optimization algorithms. The following section clarifies some major concepts about optimization algorithms. To evaluate optimization algorithms, two phases should be explored: first, analyzing the algorithm; and second, measuring the total performance of an algorithm.

4.1 Optimization Algorithms Analysis

Optimization algorithms can be analyzed by different procedures. It follows two common and fundamental approaches: the exploration and exploitation method and the evolutionary operators’ method.

4.1.1 Exploration and Exploitation

Since most optimization algorithms are naturally inspired, they are analyzed according to their exploitation and exploration functionality in the search space. An exploitation process tries to create new solutions that are better than the existing ones, and the search process for better candidates is done on a local scale. From the same aspect, the exploration process tries to create solutions with enough variety from the existing solutions, and the search is done on a global level, making it less probable to get trapped in local mode. The exploration process indicates more efficiency than the exploitation process in the space search operation. But this comes with some limitations; since the search goes on a global scale, the time of convergence is affected, making it slower [23,151].

However, fulfilling this balance is still an open problem. Furthermore, such a balance depends on various factors; for instance, the setting of tuning and controlling parameters. Additionally, such a balance may not occur globally and may differ from one problem to another. It is consistent with “no-free-lunch (NFL)” theorems, which indicate that for a specific problem, one algorithm may record high performance; at the same time, it may perform badly for other problems. Essentially, there is no algorithm that has absolute priority over other algorithms [23]. To learn more about the interesting NFL theorem, refer to [152].

4.1.2 Evolutionary Operators

Crossover, mutation, and selection present the essential and primary evolutionary operators for optimization algorithms. Crossover and mutation processes drive variation to offer new solutions. In addition, the selection operator has a double role, choosing the best solutions from a subspace and reinforcing the self-organization and convergence processes. However, mostly all algorithms use the mutation and selection operators over the crossover operator [23].

4.2 Performance Measurement

Despite the massive number of studies and publications on diverse meta-heuristic algorithms, there is still a lack of qualified and dependable performance measures to compare between the distinct algorithms. Commonly, there are four prime approaches to comparing two algorithms.

•   First approach compares the accuracy of two algorithms when solving the same problem for a stable number of function evaluations.

•   Second approach compares the required function evaluations of two various algorithms for a stated accuracy.

•   Third approach compares the execution times for two algorithms.

•   Fourth approach equalizes the results of algorithms to generate a ratio for comparison [23].

5  Benchmarking

Many optimization algorithms claim superiority over other comparable algorithms. Consequently, benchmark functions can be used as indicators to determine the most powerful and reliable algorithms to prove their effectiveness [153]. No exact algorithm can beat all comparable algorithms in all test cases and conditions [154].

5.1 Experimental Settings

The evolutionary approaches provide experimental settings with very substantial issues since they can influence the expected outcomes of the experiments. The setting must be flawless to obtain an optimal output; otherwise, imperfect settings may lead to un-optimal results. In order to have an adjusted assessment between various algorithms, it is crucial to set the value of each algorithm to optimum in order to achieve the best possible result.

5.2 Benchmark Functions

Each benchmark function identifies its features, such as unimodal, multimodal, separable, or non-separable. It is noteworthy that the combination of characteristics defines the function of complexity [153]. The intent of the optimization tactic is to find the global optimum; thus, the zone around the local optimum must be avoided to prevent getting stuck in the local optimum as far as possible [153].

5.2.1 University Course Timetabling Benchmark Data

University course timetabling faces an absence of benchmark data. The International Timetabling Competition (ITC) 2007 encloses data for enrollment-based course timetabling and curriculum-based course timetabling. The following is an explanation of the recognized benchmark of course timetabling:

•   ITC2007 Track2-Enrollment-based Course Timetabling

This dataset compares twenty-four existing datasets; all feature at least one optimal solution with no hard or soft constraint infringements. The main shortcoming of this benchmark is un-reality of datasets; they were generated by the competition organizers [14].

•   ITC2007 Track3-Curriculum-based Course Timetabling

To date, there are twenty-one examples available. All data examples are from real life, not the same as in the previous track. They were collected by the University of Udine, and there is at least one functional solution for each example [14]. The datasets are available on the competition website: http://www.cs.qub.ac.uk/itc2007/index.htm.

•   The Purdue benchmark data

The University of Purdue offers access to real data on its official website. The datasets are available for each department of the university [14]. Purdue datasets are available at https://www.unitime.org/uct_datasets.php.

5.2.2 University Examination Timetabling Benchmark Data

The university examination timetabling benchmark datasets are interesting data. These have been gathered by researchers, which has led to some established diversity of benchmark problems. The following is a brief explanation of the examination timetabling benchmark:

•   The Toronto benchmark data

The incapacitated dataset for the examination timetabling problem is presented in [155]. This data contains a clash-free constraint as a hard constraint, in which the student cannot sit for two exams at the same time. Likewise, the soft constraint is to spread exams as consistently as possible throughout the examination period [143]. By the same token, 13 real-world problems are available. Two objectives are provided by the Toronto benchmark data; 1) to minimize the number of assigned time slots and 2) to minimize the average cost per student [14]. The studies in examination timetabling tasks directed to establishing diverse options for the problem are called Toronto a, Toronto b, Toronto c, Toronto d and Toronto e [145]. They are illustrated based on a set of objectives and formed as thus:

Toronto a Objective: To minimize the total of desired timeslots.

Toronto b Objective: To space out contradictory exams’ limited timeslots.

Toronto c Objective: To minimize the impact of assigning two exams to students on one day.

Toronto d Objective: To minimize assigning two exams respectively for students on one day and overnight.

Toronto e Objective: To minimize assigning more than one exam during the day.

•   The Nottingham benchmark data

The study [77] modified six data sets from Carter et al. [155] and presented them as benchmarks alongside the examination timetabling data from the University of Nottingham. The objective was to minimize the impact of assigning two consecutive exams to students [14].

•   The Melbourne benchmark data

Study [115] provided two new datasets with two time slots for five workdays from the University of Melbourne with the objective of minimizing assigning two exams to students on one day as well as overnight [14]. All the mentioned benchmark data can be assessed at http://www.cs.nott.ac.uk/~pszrq/data.htm.

•   The Purdue benchmark data

Müller [15] provided the newest benchmark in examination timetabling. Nine datasets from Purdue University were presented; each data contained 29 examination periods for all two hours long [14]. The Purdue benchmark datasets are available online at https://www.unitime.org/exam_datasets.php.

6  Discussion

This survey presents an extensive integral review of university timetabling cases by submitting four bases as platforms to form and organize the review, and consequently trying to conduct a compatible and functional outcome covering all timetabling cases. Firstly, the survey started by clarifying the nature of timetabling problems to accurately achieve the optimal timetable through the extracted functional and efficient guided solution. Secondly, the problems were classified to provide a good perspective of the intended objectives considering the stated constraints. Thirdly, indicating and observing the applied approaches for solving timetabling problems were indicated and observed to show the main junction of these methods, the concept, the primary mechanism, and illustrate the primary bifurcation of these approaches as well as the concept, the core mechanism, and features of each individual method. Finally, the standards and specifications to adopt the method of candidates were described to ensure the optimality of the selected method, which indicates accomplishing the possible timetable. Therefore, two important questions have been answered at this stage: what analytic methods have been used to assess, measure, and compare the approach’s performance? In addition, what kinds of benchmark datasets are utilized for the experimental tests? To elucidate the preferences over methods. Fig. 4 displays the number of publication types distributed in journals, conferences, reports, books, and thesis dissertations.

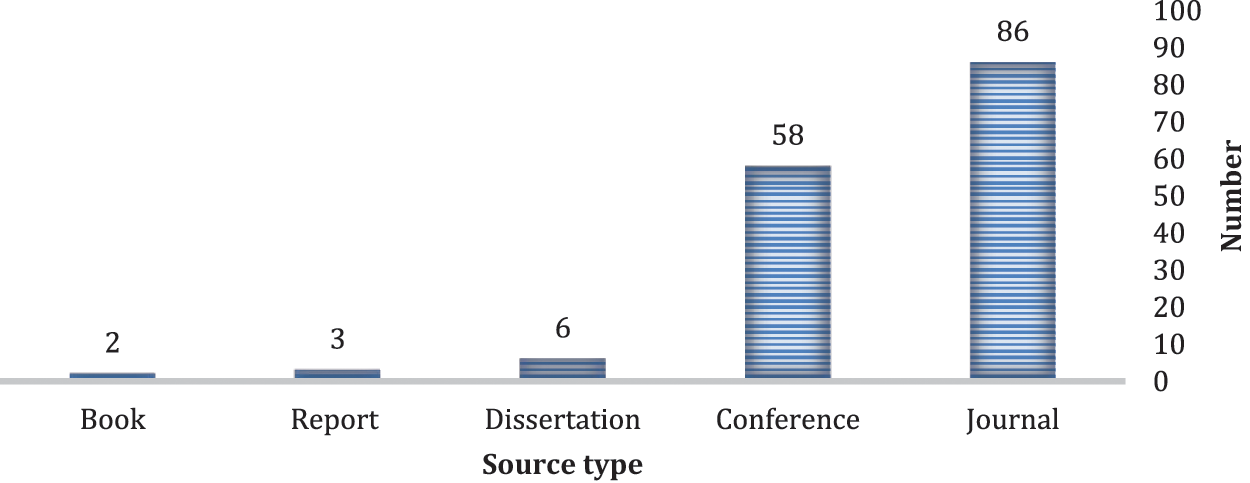
Figure 4: Number of publications by source type

The prime aim of this class of problems is to satisfy all problem constraints rather than optimizing a certain objective. The complication of this type of problem is progressively increasing with the growing number of increasing stated constraints. Every time more constraints are added, it gets harder to solve the problem, until it gets to a point where it is impossible to reach the optimal solution.

The most adjustment with the convergence dilemma is by conceding some of the stated constraints through the solving process to make it possible to reach a feasible solution. That is exactly why university timetabling is such a complex problem, because constraints differ from one institution to another. It should be considered that no timetable tackles all the hard and soft constraints as well as the indicated objectives. Only a few of these constraints are under control, while the rest are ignored. Therefore, a more general timetable is important. For this reason, the suggested timetable should further generalize and meet all the hard constraints and minimize (or maximize) a particular objective function that surrounds the soft constraints. The timetable cannot tackle all the hard and soft constraints as well as the indicated objectives. Most timetables can only handle part of the constraints and ignore the remaining ones.

A meta-heuristic is a technique for solving optimization problems that involves exploring the optimal solutions to a set of constraints and objectives, as well as suggesting candidate or alternate solutions to the stated problem. In general, meta-heuristics can be categorized into single-solution-based methods and population-based methods. Concerns about meta-heuristic algorithms have grown dramatically over the last decade. Despite the huge number of publications and studies, there is still a lack of performance measures for comparing different algorithms. The former clarified and illustrated meta-heuristic algorithms were selected based on their commonness and broad implementations. Fig. 5 illustrates the publication ratio distribution of the meta-heuristic algorithms used to optimize university timetabling problems. Performance and experimental outcomes have demonstrated operative success. In particular, the genetic algorithm as compared to other methods has shown great publication (16%). In recent years, more studies tend to implement hybrid methods due to their being fruitful in the final outcomes, with a 35% higher value as compared with the mentioned methods.

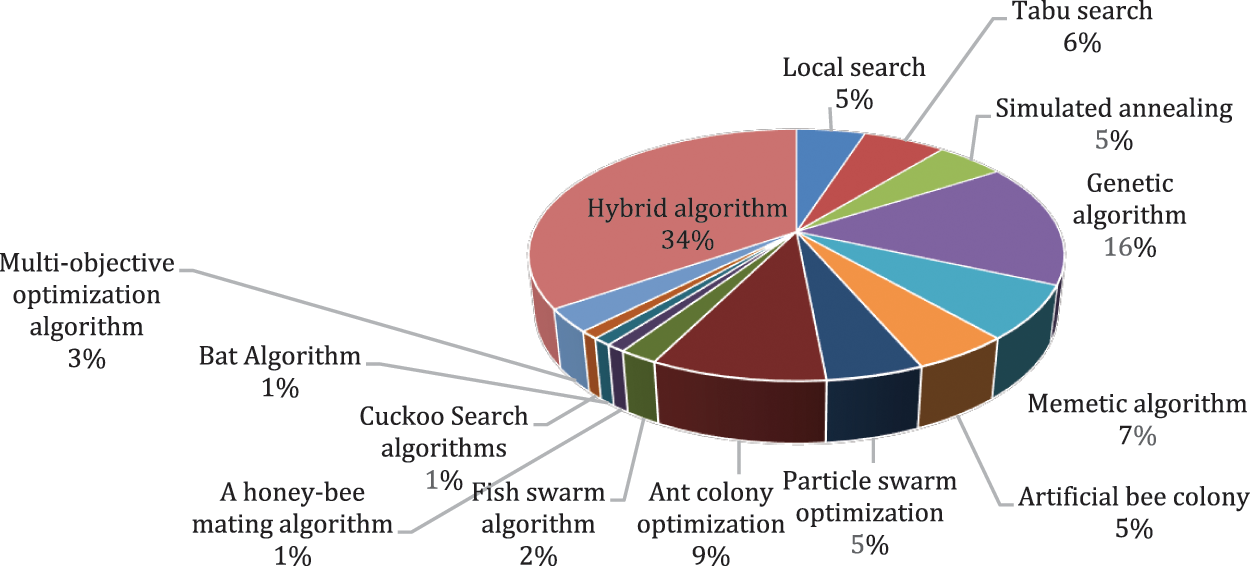
Figure 5: Publication of different meta-heuristic algorithms

The interest in swarm intelligence algorithms (SI) has been remarkable in the last decade. Swarm intelligence algorithms are efficient and reliable when applied to solving university timetabling problems. Swarm intelligence (SI) is one of the computational intelligence methods used to solve complex problems like university timetabling. Swarm intelligence deals with groups (collective behaviors) composed of a set of individuals (local interactions of the individuals with each other and with their environment) that coordinate using decentralized control and self-organization. Another confusing point about university timetabling is how to evaluate and examine different swarm intelligence algorithms against each other, considering each institution has specific stated objective functions and declared problem formulations, thus increasing the difficulty of performing a justified comparison. Comparing the algorithms in order to find the superior one is a vague concept since different algorithms achieve various objectives, and that revokes the standard criteria for formal evaluation and testing before comparison. In recent times, hybridization algorithms have attracted the interest of researchers because they provide an effective and outstanding performance in solving optimization problems by utilizing the advantage of a combination of population-based with a single-based methodology. The exploration process is the ability to expand the search over a broad area to reach the unvisited spaces, while the exploitation process focuses on the potentially promising spaces of suitable solutions to optimally utilize and converge. So, the search process must be in equilibrium between the exploitation and the exploration to reach the optimal solution.

7  Future Directions and Open Issues

This part shows numerous essential open research issues hindering the application of meta-heuristic algorithms in university timetabling. Several essential and primary approaches to handling university timetabling problems have not been included in this review because this study covered only some fundamental algorithms. It is noted that there is a gap between presumptive theories and factual practices concerning the employment of optimization tactics as a functional solution to university timetabling problems. Some evolutionary and swarm intelligence algorithms, like Biogeography-Based Optimization, Symbiotic Organisms Search, Grey Wolf Optimizer, Intelligent Water Drops Algorithm (IWD), Chicken Swarm Optimization (CSO), great deluge algorithm (GD), Monkey Algorithm, Bat Algorithm, Sheep Flocks Algorithm, Moth-Flame Optimization and Sine-Cosine Algorithm, Whale Optimization Algorithm, and Harris Hawks Optimization Algorithm, have never been utilized for solving university timetabling problems so far. In addition, multi-objective evolutionary algorithms are promising and have the capability to identify robust university course timetabling solutions. Therefore, multi-objective evolutionary algorithms are good choices to provide better approximation functions. This gap offers scope for researchers to examine and try out more modern optimization algorithms, in addition to running numerous analyses and comparisons over the conducted results to state and clarify the strengths and shortcomings of each algorithm and form a solid and rich database for future studies as a reference and guideline.

Additional recommended scopes for future studies are to keep up-to-date on the submitted novel meta-heuristic algorithms and explore more algorithms; summarize the concluded strengths and limitations for future utilization; hybridize further meta-heuristic algorithms and investigate the combination impact to emphasize the validity and qualified ability of the hybridization method; intensify the publication and research on systematic reviews and surveys to initiate a substantial platform and dependable background for future studies; generalize a global format and standard languages for timetabling; and develop university timetabling software fields; systems, and tools in general. However, there is still a lack of qualified performance measurements to compare between various algorithms. There is still a need for more real-world benchmark datasets to improve the analytical and experimental ways to evaluate the used approaches for solving university timetabling problems. Working on the evaluation techniques and finding a standard can exceed the ambiguous outcome when certain algorithms show preferable performance on some specific optimization problems and less achievement on other problems.

8  Conclusion

An increase in the number of publications addressing the university timetabling problem can be observed over the last decade. University timetabling is a non-polynomial-combinatorial optimization problem (NP-COP) which consists of two essential components: examination and course timetabling. The main goal of this kind of problem is to meet all the problem constraints rather than optimizing a particular objective. Viable solutions require high computational run time, which can increase exponentially with the problem size. Therefore, the use of meta-heuristic algorithms was explored here, along with the identification of open issues and challenges that must be addressed in the future to help solve this problem. The hybridization technique is able to achieve superior performance and robust efficiency by identifying the functional fittest solution for a particular timetabling problem. In addition, it can be concluded that multi-objective evolutionary algorithms can produce good and robust solutions. The intent of conducting this study was to investigate and explore the publishing rate in this field and to identify those issues which need further attention, and which seem promising. Moreover, we also aimed to identify which meta-heuristic algorithm had the highest publication rate. This survey outlined neglected topics in this domain as a foundation for future research, as well as emphasizing the common publishing platform as a standpoint indicator.

The limitations of this study were mainly in the collection of data from database sources, in addition to the search strategy used and the lack of pre-screening tools for the collected data. Moreover, the findings may be impacted by several factors that were not considered in this study. Lastly, the current study was not specifically designed to evaluate features related to datasets and validation measures used in optimization algorithms.

Funding Statement: This research work was supported by the University Malaysia Sabah, Malaysia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Schaerf, “A survey of automated timetabling,” Artificial Intelligence Review, vol. 13, no. 2, pp. 87–127, 1999. [Google Scholar]

 2.  A. Bashab, A. O. Ibrahim, E. E. AbedElgabar, M. A. Ismail, A. Elsafi et al., “A systematic mapping study on solving university timetabling problems using meta-heuristic algorithms,” Neural Computing and Applications, vol. 32, no. 23, pp. 17397–17432, 2020. [Google Scholar]

 3.  J. S. Tan, S. L. Goh, G. Kendall and N. R. Sabar, “A survey of the state-of-the-art of optimisation methodologies in school timetabling problems,” Expert Systems with Applications, vol. 165, Article no. 113943, 2021. http://doi.org/10.1016/j.eswa.2020.113943. [Google Scholar]

 4.  M. C. Chen, S. L. Goh, N. R. Sabar and G. Kendall, “A survey of university course timetabling problem: Perspectives, trends and opportunities,” IEEE Access, vol. 9, pp. 106515–106529, 2021. [Google Scholar]

 5.  A. Wren, “Scheduling, timetabling and rostering—A special relationship?” in Int. Conf. on the Practice and Theory of Automated Timetabling, Berlin, Heidelberg, Springer, pp. 46–75, 1995. [Google Scholar]

 6.  S. MirHassani and F. Habibi, “Solution approaches to the course timetabling problem,” Artificial Intelligence Review, vol. 39, no. 2, pp. 133–149, 2013. [Google Scholar]

 7.  T. Arbaoui, “Modeling and solving university timetabling,” Ph.D. Dissertation, Université de Technologie de Compiègne, 2014. [Google Scholar]

 8.  M. W. Carter and G. Laporte, “Recent developments in practical examination timetabling,” in Int. Conf. on the Practice and Theory of Automated Timetabling, Berlin, Heidelberg, Springer, pp. 1–21, 1995. [Google Scholar]

 9.  B. A. Aldeeb, N. M. Norwawi, M. A. Al-Betar and M. Z. B. Jali, “Solving university examination timetabling problem using intelligent water drops algorithm,” in Int. Conf. on Swarm, Evolutionary, and Memetic Computing, Cham, Springer, pp. 187–200, 2014. [Google Scholar]

10. M. W. Carter and G. Laporte, “Recent developments in practical course timetabling,” in Int. Conf. on Swarm, Evolutionary, and Memetic Computing, Berlin, Heidelberg, Springer, pp. 3–19, 1997. [Google Scholar]

11. C. W. Fong, H. Asmuni, B. McCollum, P. McMullan and S. Omatu, “A new hybrid imperialist swarm-based optimization algorithm for university timetabling problems,” Information Sciences, vol. 283, pp. 1–21, 2014. [Google Scholar]

12. S. Abdullah, “Heuristic approaches for university timetabling problems,” Ph.D. Dissertation, University of Nottingham Nottingham, Nottingham NG8 1BB, UK, 2006. [Google Scholar]

13. S. Petrovic and E. K. Burke, “University timetabling,” Ph.D. Dissertation, University of Nottingham, Nottingham NG8 1BB, UK, 2004. [Google Scholar]

14. S. Kristiansen and T. R. Stidsen, “A comprehensive study of educational timetabling-A survey,” Department of Management Engineering, Technical University of Denmark, DTU Management Engineering Report, no. 8, 2013. [Google Scholar]

15. T. Müller, “Reallife examination timetabling,” Journal of Scheduling, vol. 19, no. 3, pp. 257–270, 2016. [Google Scholar]

16. K. Kalita, R. K. Ghadai and S. Chakraborty, “A comparative study on the metaheuristic-based optimization of skew composite laminates,” Engineering with Computers, vol. 38, pp. 3549–3566, 2022. [Google Scholar]

17. J. Henry Obit, “Developing novel meta-heuristic, hyper-heuristic and cooperative search for course timetabling problems,” Ph.D. Dissertation, University of Nottingham, Nottingham NG8 1BB, UK, 2010. [Google Scholar]

18. R. Lewis, “A survey of metaheuristic-based techniques for university timetabling problems,” OR Spectrum, vol. 30, no. 1, pp. 167–190, 2008. [Google Scholar]

19. E. Elbeltagi, T. Hegazy and D. Grierson, “Comparison among five evolutionary-based optimization algorithms,” Advanced Engineering Informatics, vol. 19, no. 1, pp. 43–53, 2005. [Google Scholar]

20. L. Raudenská, “Swarm-based optimisation,” Quality Innovation Prosperity, vol. 13, no. 1, pp. 45–52, 2009. [Google Scholar]

21. E. A. Abdelhalim and G. A. El Khayat, “A utilization-based genetic algorithm for solving the university timetabling problem (uga),” Alexandria Engineering Journal, vol. 55, no. 2, pp. 1395–1409, 2016. [Google Scholar]

22. H. Asmuni, “Fuzzy methodologies for automated university timetabling solution construction and evaluation,” Ph.D. Dissertation, University of Nottingham, Nottingham NG8 1BB, UK, 2008. [Google Scholar]

23. X. -S. Yang, “Swarm intelligence based algorithms: A critical analysis,” Evolutionary Intelligence, vol. 7, no. 1, pp. 17–28, 2014. [Google Scholar]

24. S. N. Tung, J. B. Jaafar, I. A. Aziz, H. G. Nguyen and A. N. Bui, “Genetic algorithm for solving multi-objective optimization in examination timetabling problem,” International Journal of Emerging Technologies in Learning, vol. 16, no. 11, pp. 4–24, 2021. [Google Scholar]

25. A. Gülcü and C. Akkan, “Robust university course timetabling problem subject to single and multiple disruptions,” European Journal of Operational Research, vol. 283, no. 2, pp. 630–646, 2020. [Google Scholar]

26. S. Tung Ngo, J. Jafreezal, G. Hoang Nguyen and A. Ngoc Bui, “A genetic algorithm for multi-objective optimization in complex course timetabling,” in 10th Int. Conf. on Software and Computer Applications, Kuala Lumpur Malaysia, pp. 229–237, 2021. [Google Scholar]

27. A. Gülcü and C. Akkan, “Bi-criteria simulated annealing algorithms for the robust university course timetabling problem,” in Proc. PATAT, Vienna, Austria, pp. 129–136, 2018. [Google Scholar]

28. K. Vikram, U. Ragavendran, K. Kalita, R. K. Ghadai and X. Gao, “Hybrid metamodel—NSGA-III— EDAS based optimal design of thin film coatings,” Computers, Materials & Continua, vol. 66, no. 2, pp. 1771–1784, 2021. [Google Scholar]

29. C. Blum, J. Puchinger, G. Raidl and A. Roli, “A brief survey on hybrid metaheuristics,” in Proc. BIOMA, Ljubljana, Slovenia, pp. 3–18, 2010. [Google Scholar]

30. T. Ting, X. -S. Yang, S. Cheng and K. Huang, “Hybrid metaheuristic algorithms: Past, present, and future,” in Recent Advances in Swarm Intelligence and Evolutionary Computation, Cham: Springer, pp. 71–83, 2015. [Google Scholar]

31. S. Abdullah and M. Alzaqebah, “A hybrid self-adaptive bees algorithm for examination timetabling problems,” Applied Soft Computing, vol. 13, no. 8, pp. 3608–3620, 2013. [Google Scholar]

32. C. Blum and A. Roli, “Hybrid metaheuristics: An introduction,” in Hybrid Metaheuristics. Studies in Computational Intelligence, vol. 114, Berlin, Germany: Springer, pp. 1–30, 2008. [Google Scholar]

33. I. Fister, D. Strnad and X. -S. Yang, “Adaptation and hybridization in nature-inspired algorithms,” in Adaptation and Hybridization in Computational Intelligence, Cham: Springer, pp. 3–50, 2015. [Google Scholar]

34. G. R. Raidl, “A unified view on hybrid metaheuristics,” in Int. Workshop on Hybrid Metaheuristics, Berlin, Heidelberg, Springer, pp. 1–12, 2006. [Google Scholar]

35. G. R. Raidl, J. Puchinger and C. Blum, “Metaheuristic hybrids,” In: M. Gendreau and J. Y. Potvin (Eds.) Handbook of Metaheuristics, 2nd edition, vol. 146, Berlin, Germany: Springer, pp. 469–496, 2010. [Google Scholar]

36. M. Caramia, P. Dell’Olmo and G. F. Italiano, “New algorithms for examination timetabling,” in Int. Workshop on Algorithm Engineering, Berlin, Heidelberg, Springer, pp. 230–241, 2000. [Google Scholar]

37. E. K. Burke and J. P. Newall, “Enhancing timetable solutions with local search methods,” in Int. Conf. on the Practice and Theory of Automated Timetabling, Berlin, Heidelberg, Springer, pp. 195–206, 2002. [Google Scholar]

38. D. T. Anh, V. H. Tam and N. Q. V. Hung, “Generating complete university course timetables by using local search methods,” in Proc. RIVF’06, Ho Chi Minh City, Vietnam, pp. 67–74, 2006. [Google Scholar]

39. S. Yang and S. N. Jat, “Genetic algorithms with guided and local search strategies for university course timetabling,” IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), vol. 41, no. 1, pp. 93–106, 2011. [Google Scholar]

40. A. Abuhamdah, M. Ayob, G. Kendall and N. R. Sabar, “Population based local search for university course timetabling problems,” Applied Intelligence, vol. 40, no. 1, pp. 44–53, 2014. [Google Scholar]

41. J. A. Soria-Alcaraz, E. Özcan, J. Swan, G. Kendall and M. Carpio, “Iterated local search using an add and delete hyper-heuristic for university course timetabling,” Applied Soft Computing, vol. 40, pp. 581–593, 2016. [Google Scholar]

42. T. Song, S. Liu, X. Tang, X. Peng and M. Chen, “An iterated local search algorithm for the university course timetabling problem,” Applied Soft Computing, vol. 68, pp. 597–608, 2018. [Google Scholar]

43. L. Di Gaspero and A. Schaerf, “Tabu search techniques for examination timetabling,” in Int. Conf. on the Practice and Theory of Automated Timetabling, Berlin, Heidelberg, Springer, pp. 104–117, 2000. [Google Scholar]

44. R. Alvarez-Valdes, E. Crespo and J. M. Tamarit, “Design and implementation of a course scheduling system using tabu search,” European Journal of Operational Research, vol. 137, no. 3, pp. 512–523, 2002. [Google Scholar]

45. C. Aladag and G. Hocaoglu, “The effect of neighborhood structure and of move types in the problem of course timetabling with the tabu search algorithm,” in Proc. of the Fifth Statistics Conf., pp. 14–19, 2007. [Google Scholar]

46. C. H. Aladag, G. Hocaoglu and M. A. Basaran, “The effect of neighborhood structures on tabu search algorithm in solving course timetabling problem,” Expert Systems with Applications, vol. 36, no. 10, pp. 12349–12356, 2009. [Google Scholar]

47. Z. Lü and J. -K. Hao, “Adaptive tabu search for course timetabling,” European Journal of Operational Research, vol. 200, no. 1, pp. 235–244, 2010. [Google Scholar]

48. S. Abdullah and H. Turabieh, “On the use of multi neighbourhood structures within a tabu-based memetic approach to university timetabling problems,” Information Sciences, vol. 191, pp. 146–168, 2012. [Google Scholar]

49. A. Shakir, B. AL-Khateeb, K. Shaker and H. A. Jalab, “The effect of neighborhood structures on tabu search algorithm in solving university course timetabling problem,” in AIP Conf. Proc., vol. 1635, no. 1, pp. 657–664, Langkawi Kedah, Malaysia, American Institute of Physics, 2014. [Google Scholar]

50. F. H. Awad, A. Al-Kubaisi and M. Mahmood, “Large-scale timetabling problems with adaptive tabu search,” Journal of Intelligent Systems, vol. 31, no. 1, pp. 168–176, 2022. [Google Scholar]

51. J. M. Thompson and K. A. Dowsland, “Variants of simulated annealing for the examination timetabling problem,” Annals of Operations Research, vol. 63, no. 1, pp. 105–128, 1996. [Google Scholar]

52. M. Tuga, R. Berretta and A. Mendes, “A hybrid simulated annealing with kempe chain neighborhood for the university timetabling problem,” in 6th IEEE/ACIS Int. Conf. on Computer and Information Science (ICIS 2007), Melbourne, VIC, Australia, pp. 400–405, 2007. [Google Scholar]

53. E. Aycan and T. Ayav, “Solving the course scheduling problem using simulated annealing,” in 2009 IEEE Int. Advance Computing Conf., Patiala, India, pp. 462–466, 2009. [Google Scholar]

54. S. Ceschia, L. Di Gaspero and A. Schaerf, “Design, engineering, and experimental analysis of a simulated annealing approach to the post-enrolment course timetabling problem,” Computers & Operations Research, vol. 39, no. 7, pp. 1615–1624, 2012. [Google Scholar]

55. M. Cheraitia and S. Haddadi, “Simulated annealing for the uncapacitated exam scheduling problem,” International Journal of Metaheuristics, vol. 5, no. 2, pp. 156–170, 2016. [Google Scholar]

56. S. Zheng, L. Wang, Y. Liu and R. Zhang. “A simulated annealing algorithm for university course timetabling considering travelling distances,” International Journal of Computing Science and Mathematics, vol. 6, no. 2, pp. 139–151, 2015. [Google Scholar]

57. S. L. Goh, G. Kendall and N. R. Sabar, “Simulated annealing with improved reheating and learning for the post enrolment course timetabling problem,” Journal of the Operational Research Society, vol. 70, no. 6, pp. 873–888, 2019. [Google Scholar]

58. R. Weare, E. Burke and D. Elliman, “A hybrid genetic algorithm for highly constrained timetabling problems,” Technical Report, Department of Computer Science, University of Nottingham Nottingham, UK, 1995. [Google Scholar]

59. W. Erben and J. Keppler, “A genetic algorithm solving a weekly course-timetabling problem,” in Int. Conf. on the Practice and Theory of Automated Timetabling, Berlin, Heidelberg, Springer, pp. 198–211, 1995. [Google Scholar]

60. K. -E. Ellingsen and M. Penaloza, “A genetic algorithm approach for finding a good course schedule,” Technical Report, South Dakota School of Mines and Technology, USA, 2003. [Google Scholar]

61. S. Kazarlis, V. Petridis and P. Fragkou, “Solving university timetabling problems using advanced genetic algorithms,” in Proc. of the ICTA’05, Thessaloniki, greece, pp. 8–12, 2005. [Google Scholar]

62. M. Chiarandini, M. Birattari, K. Socha and O. Rossi-Doria, “An effective hybrid algorithm for university course timetabling,” Journal of Scheduling, vol. 9, no. 5, pp. 403–432, 2006. [Google Scholar]

63. S. Abdullah and H. Turabieh, “Generating university course timetable using genetic algorithms and local search,” in Third Int. Conf. on Convergence and Hybrid Information Technology, Busan, Korea (Southpp. 254–260, 2008. [Google Scholar]

64. S. N. Jat and S. Yang, “A guided search genetic algorithm for the university course timetabling problem,” in Int. Conf. on Scheduling: Theory and Applications (MISTA 2009), Dublin, Ireland, pp. 180–191, 2009. [Google Scholar]

65. P. Khonggamnerd and S. Innet, “On improvement of effectiveness in automatic university timetabling arrangement with applied genetic algorithm,” in Fourth Int. Conf. on Computer Sciences and Convergence Information Technology, Seoul, Korea (Southpp. 1266–1270, 2009. [Google Scholar]

66. O. M. K. Alsmadi, S. Za’er, D. I. Abu-Al-Nadi and A. Algsoon, “A novel genetic algorithm technique for solving university course timetabling problems,” in Int. Workshop on Systems, Signal Processing and their Applications, WOSSPA, Tipaza, Algeria, pp. 195–198, 2011. [Google Scholar]

67. S. R. Sutar and R. S. Bichkar, “University timetabling based on hard constraints using genetic algorithm,” International Journal of Computer Applications, vol. 42, no. 15, pp. 3–5, 2012. [Google Scholar]

68. O. I. Obaid, M. Ahmad, S. A. Mostafa and M. A. Mohammed, “Comparing performance of genetic algorithm with varying crossover in solving examination timetabling problem,” J. Emerg. Trends Comput. Inf. Sci., vol. 3, no. 10, pp. 1427–1434, 2012. [Google Scholar]

69. W. Chinnasri, S. Krootjohn and N. Sureerattanan, “Performance comparison of genetic algorithm’s crossover operators on university course timetabling problem,” in 2012 8th Int. Conf. on Computing Technology and Information Management (NCM and ICNIT), Seoul, Korea (Southpp. 781–786, 2012. [Google Scholar]

70. K. Kumar, R. S. Sikander and K. Mehta, “Genetic algorithm approach to automate university timetable,” International Journal of Technical Research (IJTR), vol. 1, no. 1, pp. 47–51, 2012. [Google Scholar]

71. A. O. Modupe, O. E. Olusayo and O. S. Olatunde, “Development of a university lecture timetable using modified genetic algorithms approach,” International Journal, vol. 4, no. 9, pp. 163–168, 2014. [Google Scholar]

72. M. Alwashahi, “Investigation and optimization of scheduling system in sohar university using genetic algorithm (GA),” International Journal of Computer Applications, vol. 126, no. 11, pp. 11–15, 2015. [Google Scholar]

73. S. S. Alves, S. A. Oliveira and A. R. R. Neto, “A recursive genetic algorithm-based approach for educational timetabling problems,” in Designing with Computational Intelligence, Cham: Springer, pp. 161–175, 2017. [Google Scholar]

74. M. Assi, B. Halawi and R. A. Haraty, “Genetic algorithm analysis using the graph coloring method for solving the university timetable problem,” Procedia Computer Science, vol. 126, pp. 899–906, 2018. [Google Scholar]

75. A. Sultan, “A genetic algorithm approach for timetabling problem: The time group strategy,” Journal of Information and Communication Technology, vol. 3, no. 2, pp. 1–14, 2020. [Google Scholar]

76. C. H. Wong, S. L. Goh and J. Likoh, “A genetic algorithm for the real-world university course timetabling problem,” in 2022 IEEE 18th Int. Colloquium on Signal Processing & Applications (CSPA), Selangor, Malaysia, pp. 46–50, 2022. [Google Scholar]

77. E. K. Burke, J. P. Newall and R. F. Weare, “A memetic algorithm for university exam timetabling,” in Int. Conf. on the Practice and Theory of Automated Timetabling, Berlin, Heidelberg, Springer, pp. 241–250, 1995. [Google Scholar]

78. E. K. Burke and J. L. Silva, “The design of memetic algorithms for scheduling and timetabling problems,” in Int. Conf. on the Practice and Theory of Automated Timetabling, Recent Advances in Memetic Algorithms, Berlin, Heidelberg, Springer, pp. 289–311, 2005. [Google Scholar]

79. S. N. Jat and S. Yang, “A memetic algorithm for the university course timetabling problem,” in 2008 20th IEEE Int. Conf. on Tools with Artificial Intelligence, Mashhad, Iran, pp. 427–433, 2008. [Google Scholar]

80. H. Turabieh and S. Abdullah, “Incorporating tabu search into memetic approach for enrolment-based course timetabling problems,” in 2009 2nd Conf. on Data Mining and Optimization, Kajand, Malaysia, pp. 115–119, 2009. [Google Scholar]

81. S. Abdullah, H. Turabieh, B. McCollum and P. McMullan, “A tabu-based memetic approach for examination timetabling problems,” in Int. Conf. on Rough Sets and Knowledge Technology, Berlin, Heidelberg, Springer, pp. 574–581, 2010. [Google Scholar]

82. M. Joudaki, M. Imani and N. Mazhari, “Using improved memetic algorithm and local search to solve university course timetabling problem (UCTTP),” in Proc. of the 2011 Int. Conf. on Artificial Intelligence ICAI 2011, Las Vegas NV, pp. 501–506, 2011. [Google Scholar]

83. A. Jula and N. K. Naseri, “Using CMAC to obtain dynamic mutation rate in a metaheuristic memetic algorithm to solve university timetabling problem,” European Journal of Scientific Research, vol. 63, no. 2, pp. 172–181, 2011. [Google Scholar]

84. M. A. Al-Betar, A. T. Khader and I. A. Doush, “Memetic techniques for examination timetabling,” Annals of Operations Research, vol. 218, no. 1, pp. 23–50, 2014. [Google Scholar]

85. Y. Lei, M. Gong, L. Jiao and Y. Zuo, “A memetic algorithm based on hyper-heuristics for examination timetabling problems,” International Journal of Intelligent Computing and Cybernetics, vol. 8, no. 2, pp. 139–151, 2015. [Google Scholar]

86. A. L. A. Bolaji, A. T. Khader, M. A. Al-Betar and M. Awadallah, “Artificial bee colony algorithm for curriculum-based course timetabling problem,” in Fifth Int. Conf. on Information Technology, Amman, Jordan, pp. 546–552, 2011. [Google Scholar]

87. M. Alzaqebah and S. Abdullah, “Comparison on the selection strategies in the artificial bee colony algorithm for examination timetabling problems,” Int. J. Soft Comput. Eng., vol. 1, no. 5, pp. 158–163, 2011. [Google Scholar]

88. A. L. A. Bolaji, A. T. Khader, M. A. Al-Betar and M. A. Awadallah, “A modified artificial bee colony algorithm for post-enrolment course timetabling,” in Int. Conf. in Swarm Intelligence, Berlin, Heidelberg, Springer, pp. 377–386, 2013. [Google Scholar]

89. M. Alzaqebah and S. Abdullah, “Artificial bee colony search algorithm for examination timetabling problems,” International Journal of Physical Sciences, vol. 6, no. 17, pp. 4264–4272, 2011. [Google Scholar]

90. F. C. Weng and H. Bin Asmuni, “An automated approach based on bee swarm in tackling university examination timetabling problem,” International Journal of Engineering & Computer Science, vol. 13, no. 2, pp. 8–23, 2013. [Google Scholar]

91. M. Alzaqebah and S. Abdullah, “An adaptive artificial bee colony and late-acceptance hill-climbing algorithm for examination timetabling,” Journal of Scheduling, vol. 17, no. 3, pp. 249–262, 2014. [Google Scholar]

92. S. -C. Chu, Y. -T. Chen and J. -H. Ho, “Timetable scheduling using particle swarm optimization,” in First Int. Conf. on Innovative Computing, Information and Control-Volume I (ICICIC’06), Beijing, China, pp. 324–327, 2006. [Google Scholar]

93. D. Qarouni-Fard, A. Najafi-Ardabili, M. -H. Moeinzadeh, S. Sharifian-R, E. Asgarian et al., “Finding feasible timetables with particle swarm optimization,” in 2007 Innovations in Information Technologies (IIT), Dubai, United Arab Emirates, pp. 387–391, 2007. [Google Scholar]

94. S. F. H. Irene, S. Deris and M. H. S. Zaiton, “A study on PSO-based university course timetabling problem,” in 2009 Int. Conf. on Advanced Computer Control, Singapore, pp. 648–651, 2009. [Google Scholar]

95. D. F. Shiau, “A hybrid particle swarm optimization for a university course scheduling problem with flexible preferences,” Expert Systems with Applications, vol. 38, no. 1, pp. 235–248, 2011. [Google Scholar]

96. H. Kanoh and S. Chen, “Particle swarm optimization with transition probability for timetabling problems,” in Int. Conf. on Adaptive and Natural Computing Algorithms, Berlin, Heidelberg, Springer, pp. 256–265, 2013. [Google Scholar]

97. R. -M. Chen and H. -F. Shih, “Solving university course timetabling problems using constriction particle swarm optimization with local search,” Algorithms, vol. 6, no. 2, pp. 227–244, 2013. [Google Scholar]

98. K. Socha, J. Knowles and M. Sampels, “A max-min ant system for the university course timetabling problem,” in Int. Workshop on Ant Algorithms, Berlin, Heidelberg, Springer, pp. 1–13, 2002. [Google Scholar]

99. K. Socha, M. Sampels and M. Manfrin, “Ant algorithms for the university course timetabling problem with regard to the state-of-the-art,” in Workshops on Applications of Evolutionary Computation, Berlin, Heidelberg, Springer, pp. 334–345, 2003. [Google Scholar]

100. K. A. Dowsland and J. M. Thompson, “Ant colony optimization for the examination scheduling problem,” Journal of the Operational Research Society, vol. 56, no. 4, pp. 426–438, 2005. [Google Scholar]

101. M. Ayob and G. Jaradat, “Hybrid ant colony systems for course timetabling problems,” in 2009 2nd Conf. on Data Mining and Optimization, Kajand, Malaysia, pp. 120–126, 2009. [Google Scholar]

102. T. Lutuksin, A. Chainual and P. Pongcharoen, “Experimental design and analysis on parameter investigation and performance comparison of ant algorithms for course timetabling problem,” Naresuan University Engineering Journal, vol. 4, no. 1, pp. 31–38, 2009. [Google Scholar]

103. M. A. Al-Betar and A. T. Khader, “A hybrid harmony search for university course timetabling,” in Proc. of the 4nd Multidisciplinary Conf. on Scheduling: Theory and Applications (MISTA 2009), Dublin, Ireland, pp. 157–179, 2009. [Google Scholar]

104. T. Lutuksin and P. Pongcharoen, “Best-worst ant colony system parameter investigation by using experimental design and analysis for course timetabling problem,” in 2010 Second Int. Conf. on Computer and Network Technology, Bangkok, Thailand, pp. 467–471, 2010. [Google Scholar]

105. C. Nothegger, A. Mayer, A. Chwatal and G. R. Raidl, “Solving the post enrolment course timetabling problem by ant colony optimization,” Annals of Operations Research, vol. 194, no. 1, pp. 325–339, 2012. [Google Scholar]

106. T. Thepphakorn, P. Pongcharoen and C. Hicks, “An ant colony based timetabling tool,” International Journal of Production Economics, vol. 149, pp. 131–144, 2014. [Google Scholar]

107. M. Mazlan, M. Makhtar, A. Khairi and M. A. Mohamed, “University course timetabling model using ant colony optimization algorithm approach,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 13, no. 1, pp. 72–76, 2019. [Google Scholar]

108. S. Aslan and C. Aci, “Solving university course timetabling problem using ant colony optimization: An example of mersin university engineering faculty,” in Int. Conf. on Advanced Technologies, Computer Engineering and Science (ICATCES’18), Safranbolu, Turkey, pp. 154–157, 2018. [Google Scholar]

109. H. Turabieh, S. Abdullah, B. McCollum and P. McMullan, “Fish swarm intelligent algorithm for the course timetabling problem,” in Int. Conf. on Rough Sets and Knowledge Technology, Berlin, Heidelberg, Springer, pp. 588–595, 2010. [Google Scholar]

110. H. Turabieh and S. Abdullah, “A hybrid fish swarm optimisation algorithm for solving examination timetabling problems,” in Int. Conf. on Learning and Intelligent Optimization, Berlin, Heidelberg, Springer, pp. 539–551, 2011. [Google Scholar]

111. N. R. Sabar, M. Ayob, G. Kendall and R. Qu, “A honey-bee mating optimization algorithm for educational timetabling problems,” European Journal of Operational Research, vol. 216, no. 3, pp. 533–543, 2012. [Google Scholar]

112. U. Limota, E. Mujuni and A. Mushi, “Solving the university course timetabling problem using bat inspired algorithm,” Tanzania Journal of Science, vol. 47, no. 2, pp. 674–685, 2021. [Google Scholar]

113. T. Thepphakorn and P. Pongcharoen, “Performance improvement strategies on cuckoo search algorithms for solving the university course timetabling problem,” Expert Systems with Applications, vol. 161, pp. 113732, 2020. [Google Scholar]

114. L. T. Merlot, N. Boland, B. D. Hughes and P. J. Stuckey, “A hybrid algorithm for the examination timetabling problem,” in Int. Conf. on the Practice and Theory of Automated Timetabling, Berlin, Heidelberg, Springer, pp. 207–231, 2002. [Google Scholar]

115. Z. N. Azimi, “Hybrid heuristics for examination timetabling problem,” Applied Mathematics and Computation, vol. 163, no. 2, pp. 705–733, 2005. [Google Scholar]

116. N. Nuntasen and S. Innet, “Application of genetic algorithm for solving university timetabling problems: A case study of Thai universities,” in Proc. SMO’07, Beijing, China pp. 128–133, 2007. [Google Scholar]

117. S. Abdullah, E. K. Burke and B. McCollum, “A hybrid evolutionary approach to the university course timetabling problem,” in IEEE Congress on Evolutionary Computation, Singapore, pp. 1764–1768, 2007. [Google Scholar]

118. S. Abdullah and A. R. Hamdan, “A hybrid approach for university course timetabling,” International Journal of Computer Science and Network Security, vol. 8, no. 8, pp. 127, 2008. [Google Scholar]

119. A. Abuhamdah and M. Ayob, “Hybridization multi-neighbourhoodparticle collision algorithm and great deluge for solving course timetabling problems,” in 2nd Conf. on Data Mining and Optimization, Kajand, Malaysia, pp. 108–114, 2009. [Google Scholar]

120. Y. Liu, D. Zhang and S. C. Leung, “A simulated annealing algorithm with a new neighborhood structure for the timetabling problem,” in Proc. of the First ACM/SIGEVO Summit on Genetic and Evolutionary Computation, Shanghai, China, pp. 381–386, 2009. [Google Scholar]

121. I. S. F. Ho, D. Safaai and M. H. S. Zaiton, “A combination of PSO and local search in university course timetabling problem,” in Int. Conf. on Computer Engineering and Technology, Singapore, pp. 492–495, 2009. [Google Scholar]

122. R. Nabeel, “Hybrid genetic algorithms with great deluge for course timetabling,” International Journal of Computer Science and Network Security, vol. 10, pp. 283–288, 2010. [Google Scholar]

123. M. Fukushima, “A hybrid algorithm for the university course timetabling problems,” Journal of Japan Society for Fuzzy Theory and Intelligent Informatics, vol. 22, no. 1, pp. 142–147, 2010. [Google Scholar]

124. A. Oner, S. Ozcan and D. Dengi, “Optimization of university course scheduling problem with a hybrid artificial bee colony algorithm,” in IEEE Congress of Evolutionary Computation (CEC), New Orleans, LA, USA, pp. 339–346, 2011. [Google Scholar]

125. H. Turabieh and S. Abdullah, “An integrated hybrid approach to the examination timetabling problem,” Omega, vol. 39, no. 6, pp. 598–607, 2011. [Google Scholar]

126. M. Alzaqebah and S. Abdullah, “Hybrid artificial bee colony search algorithm based on disruptive selection for examination timetabling problems,” in Int. Conf. on Combinatorial Optimization and Applications, Berlin, Heidelberg, Springer, pp. 31–45, 2011. [Google Scholar]

127. M. S. Kohshori, M. S. Abadeh and H. Sajedi, “A fuzzy genetic algorithm with local search for university course timetabling,” in The 3rd Int. Conf. on Data Mining and Intelligent Information Technology Applications, Macao, China, pp. 250–254, 2011. [Google Scholar]

128. A. Ghaffar, M. U. Sattar, M. Munir and Z. Qureshi, “Multi-objective fuzzy-based adaptive memetic algorithm with hyper-heuristics to solve university course timetabling problem,” in EAI Endorsed Transactions on Scalable Information Systems, Belgium: European Alliance for Innovation (EAIpp. e14–e14, 2022. [Google Scholar]

129. S. N. Jat and S. Yang, “A hybrid genetic algorithm and tabu search approach for post enrolment course timetabling,” Journal of Scheduling, vol. 14, no. 6, pp. 617–637, 2011. [Google Scholar]

130. M. A. Al-Betar, A. T. Khader and M. Zaman, “University course timetabling using a hybrid harmony search metaheuristic algorithm,” IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), vol. 42, no. 5, pp. 664–681, 2012. [Google Scholar]

131. K. Nguyen, P. Nguyen and N. Tran, “A hybrid algorithm of harmony search and bees algorithm for a university course timetabling problem,” International Journal of Computer Science Issues (IJCSI), vol. 9, no. 1, pp. 12, 2012. [Google Scholar]

132. R. Bellio, L. Di Gaspero and A. Schaerf, “Design and statistical analysis of a hybrid local search algorithm for course timetabling,” Journal of Scheduling, vol. 15, no. 1, pp. 49–61, 2012. [Google Scholar]

133. S. Abdullah, H. Turabieh, B. McCollum and P. McMullan, “A hybrid metaheuristic approach to the university course timetabling problem,” Journal of Heuristics, vol. 18, no. 1, pp. 1–23, 2012. [Google Scholar]

134. M. A. Ahandani, M. T. V. Baghmisheh, M. A. B. Zadeh and S. Ghaemi, “Hybrid particle swarm optimization transplanted into a hyper-heuristic structure for solving examination timetabling problem,” Swarm and Evolutionary Computation, vol. 7, pp. 21–34, 2012. [Google Scholar]

135. N. Chmeit, “Using simulated annealing and ant-colony optimization algorithms to solve the scheduling problem,” Computer Science and Information Technology, vol. 1, no. 3, pp. 208–224, 2013. [Google Scholar]

136. K. Shaker, S. Abdullah, A. Alqudsi and H. Jalab, “Hybridizing meta-heuristics approaches for solving university course timetabling problems,” in Int. Conf. on Rough Sets and Knowledge Technology, Berlin, Heidelberg, Springer, pp. 374–384, 2013. [Google Scholar]

137. K. Anwar, A. T. Khader, M. A. Al-Betar and M. A. Awadallah, “Harmony search-based hyper-heuristic for examination timetabling,” in 2013 IEEE 9th Int. Colloquium on Signal Processing and Its Applications, Kuala Lumpur, Malaysia, pp. 176–181, 2013. [Google Scholar]

138. A. L. A. Bolaji, A. T. Khader, M. A. Al-Betar and M. A. Awadallah, “University course timetabling using hybridized artificial bee colony with hill climbing optimizer,” Journal of Computational Science, vol. 5, no. 5, pp. 809–818, 2014. [Google Scholar]

139. C. K. Teoh, A. Wibowo and M. S. Ngadiman, “An adapted cuckoo optimization algorithm and genetic algorithm approach to the university course timetabling problem,” International Journal of Computational Intelligence and Applications, vol. 13, no. 1, pp. 1450002, 2014. [Google Scholar]

140. C. W. Fong, H. Asmuni and B. McCollum, “A hybrid swarm-based approach to university timetabling,” IEEE Transactions on Evolutionary Computation, vol. 19, no. 6, pp. 870–884, 2015. [Google Scholar]

141. R. P. Badoni and D. Gupta, “A hybrid algorithm for university course timetabling problem,” Innovative Systems Design and Engineering, vol. 6, no. 2, pp. 6066, 2015. [Google Scholar]

142. M. Alzaqebah and S. Abdullah, “Hybrid bee colony optimization for examination timetabling problems,” Computers & Operations Research, vol. 54, pp. 142–154, 2015. [Google Scholar]

143. S. Jaengchuea and D. Lohpetch, “A hybrid genetic algorithm with local search and tabu search approaches for solving the post enrolment based course timetabling problem: Outperforming guided search genetic algorithm,” in 2015 7th Int. Conf. on Information Technology and Electrical Engineering (ICITEE), Chiang Mai, Thailand, pp. 29–34, 2015. [Google Scholar]

144. A. El Hilali Alaoui, B. Dkhissi, J. Boukachour and R. Abounacer, “A hybrid ant colony algorithm for the exam timetabling problem,” Revue Africaine de la Recherche en Informatique et Mathématiques Appliquées, vol. 12, pp. 15–42, 2010. [Google Scholar]

145. M. Nugroho and G. Hermawan, “Solving university course timetabling problem using memetic algorithms and rule-based approaches,” IOP Conference Series: Materials Science and Engineering, vol. 407, no. 1, pp. 012012, 2018. [Google Scholar]

146. M. Forsberg, “Local search hybridization of a genetic algorithm for solving the university course timetabling problem,” M.S. Dissertation, KTH Royal Institute of Technology, Stockholm, Sweden, 2018. [Google Scholar]

147. I. AlHadid, K. Kaabneh and H. Tarawneh, “Hybrid simulated annealing with meta-heuristic methods to solve uct problem,” Modern Applied Science, vol. 12, no. 11, pp. 385–394, 2018. [Google Scholar]

148. A. Hambali, Y. Olasupo and M. Dalhatu, “Automated university lecture timetable using heuristic approach,” Nigerian Journal of Technology, vol. 39, no. 1, pp. 1–14, 2020. [Google Scholar]

149. A. Rezaeipanah, S. S. Matoori and G. Ahmadi, “A hybrid algorithm for the university course timetabling problem using the improved parallel genetic algorithm and local search,” Applied Intelligence, vol. 51, no. 1, pp. 467–492, 2021. [Google Scholar]

150. M. H. Cruz-Rosales, M. A. Cruz-Chávez, F. Alonso-Pecina, J. D. C. Peralta-Abarca, E. Y. Ávila-Melgar et al., “Metaheuristic with cooperative processes for the university course timetabling problem,” Applied Sciences, vol. 12, no. 2, pp. 542, 2022. [Google Scholar]

151. K. Hussain, M. N. M. Salleh, S. Cheng and Y. Shi, “Metaheuristic research: A comprehensive survey,” Artificial Intelligence Review, vol. 52, no. 4, pp. 2191–2233, 2019. [Google Scholar]

152. D. H. Wolpert and W. G. Macready, “No free lunch theorems for optimization,” IEEE Transactions on Evolutionary Computation, vol. 1, no. 1, pp. 67–82, 1997. [Google Scholar]

153. M. N. Ab Wahab, S. Nefti-Meziani and A. Atyabi, “A comprehensive review of swarm optimization algorithms,” PloS One, vol. 10, no. 5, pp. e0122827, 2015. [Google Scholar]

154. M. Eley, “Ant algorithms for the exam timetabling problem,” in Int. Conf. on the Practice and Theory of Automated Timetabling, Berlin, Heidelberg, Springer, pp. 364–382, 2006. [Google Scholar]

155. M. W. Carter, G. Laporte and S. Y. Lee, “Examination timetabling: Algorithmic strategies and applications,” Journal of the Operational Research Society, vol. 47, no. 3, pp. 373–383, 1996. [Google Scholar]