A Novel 2D Hyperchaotic with a Complex Dynamic Behavior for Color Image Encryption

1  Introduction

Image is an essential carrier of information. Due to the openness of the network environment, digital images are inevitably subject to various illegal attacks during the transmission process, and essential information in images will be stolen [1–3]. They are ensuring that privacy is not leaked, and the safe transmission of images in the network has become a significant research problem in the field of information security [4–7]. Many image protection methods have been proposed, such as image steganography, image encryption technology, image watermarking technology, and so on [8–13]. Image encryption technology is one of the most widely used technologies. Image encryption technology converts the original plaintext information into a noise image completely different from the plaintext information, thereby realizing image encryption [14–16].

Because of the large amount of image data and the strong correlation between adjacent pixels, traditional advanced encryption standard (AES), triple data encryption algorithm (3DES), and other methods are not suitable for image encryption, these methods cannot reduce the correlation of adjacent pixels in the image, and the efficiency is very slow [17]. The generation method and algorithm structure of the keystream determine the security of the image encryption algorithm [18–20]. With the introduction of chaos theory, because the sequence generated by a chaotic system has some good characteristics such as pseudo-randomness, initial value sensitivity, secret key sensitivity, ergodicity, etc., the sequence generated by the chaotic system is very suitable for generating the secret of the cryptographic system [21–25]. Therefore, the image encryption algorithm combined with chaos theory has become the mainstream research method in image encryption [26–28].

The chaos system is divided into a one-dimensional chaotic system, a two-dimensional chaotic system, and a high-dimensional chaotic system. A one-dimensional chaotic system has the characteristics of simple structure and fast generation of keystream [29–34]. For example, Li et al. used tent maps to generate keystreams in image encryption [30]. In order to expand the parameter space of the cryptosystem, Chen et al. used a new chaotic system to generate the key stream, composed of a logistic map, sine map, and Chebyshev map [33]. However, a one-dimensional chaotic system has few control parameters and a small parameter space in a chaotic state. Since a one-dimensional chaotic system has only one Lyapunov exponent, it can only exhibit chaotic behavior rather than hyperchaotic behavior. Hyperchaotic behavior is a more complex dynamical behavior compared with chaotic behavior. High-dimensional chaos has the characteristics of complex dynamic behavior and complex structure [35–38]. For example, Liu et al. proposed a new 3D chaotic system and generated an S-box for the encryption algorithm based on this chaotic system [36]. Wang et al. proposed a new spatiotemporal chaotic system, analyzed the performance of this spatiotemporal system, and proposed a new image encryption algorithm combined with this spatiotemporal system, which showed good security properties [38]. Due to the complex structure of the hyperchaotic system, the speed of generating the key stream is very slow, and it is challenging to realize this structure in practical applications.

In order to balance the performance of the high-dimensional and one-dimensional chaotic systems, it is the best choice to use a 2D chaotic system to generate a key stream. Many 2D chaotic systems have been proposed. Although they can exhibit excellent performance, they are pretty complex, and the parameter space in the hyperchaotic state is discontinuous [39,40]. Zheng et al. proposed a 2D logistic sine chaotic map (2D-LSMM), and designed a dynamic image encryption scheme combined with DeoxyriboNucleic Acid (DNA) coding. However, the parameter space of 2D-LSMM is very small which are μ1∈[0,4] and μ2∈[0,4] [41]. Teng et al. proposed a 2D cross-logistic-sin-sin (2D-CLSS), and proposed an image encryption strategy based on 2D-CLSS. However, the phase diagram distribution of 2D-CLSS is uneven and there is only one control parameter, which means that the sequences generated by 2D-CLSS will be in an aggregated state [42]. To overcome these shortcomings, this paper proposes a new 2D chaotic system called 2D-SSCDB, which has a simple structure but complex dynamic behavior. The 2D-SSCDB has ample parameter space, and the parameter space in the hyperchaotic state is continuous. These advantages show that the 2D-SSCDB is very suitable for generating keystreams.

Furthermore, to verify the practicality of the 2D-SSCDB, we propose a color image encryption algorithm based on the 2D-SSCDB. In the encryption algorithm, the secret key of the cryptosystem is generated from the plaintext. In the encryption stage, scrambling and diffusion are carried out simultaneously, which increases the algorithm’s security, and the attacker needs to break the scrambling and diffusion operations simultaneously. The experimental results verify that the 2D-SSCDB can be well applied in chaotic image encryption.

2  2D-SSCDB

In this paper, a 2D hyperchaotic system with simple structure, complex dynamic behavior and continuous chaotic parameter space is proposed, called 2D-SSCDB. The 2D-SSCDB is derived from Sine map, Logistic map, the defined of the 2D-SSCDB is shown in Eq. (1),

{xn+1=sin⁡(μxn(1−yn)+1),yn+1=sin⁡(η/(xn+yn)+1)(1)

where μ and η are the control parameters of the 2D-SSCDB, μ∈R+ and η∈R+. x0 and y0 are the initial values of the 2D-SSCDB.

2.1 Lyapunov Exponent Analysis

The Lyapunov exponent is one of the most effective methods to test whether the nonlinear dynamical system is in chaotic or hyperchaotic state. If a two-dimensional chaotic system has two positive Lyapunov exponents, the system is hyperchaotic in this parameter space. Hyperchaotic behavior has more complex dynamical behavior compared to chaotic behavior. The calculation formula of Lyapunov exponent is shown in Eq. (2),

λ=limT→+∞1T∑t=0T|f′(xt)|.(2)

The Lyapunov exponent analysis of the 2D-SSCDB is shown in Fig. 1, and compare the Lyapunov exponent with Logistic Map and cascade modulation couple with two 1D-chaotic map (2D-SCMCI) [39].

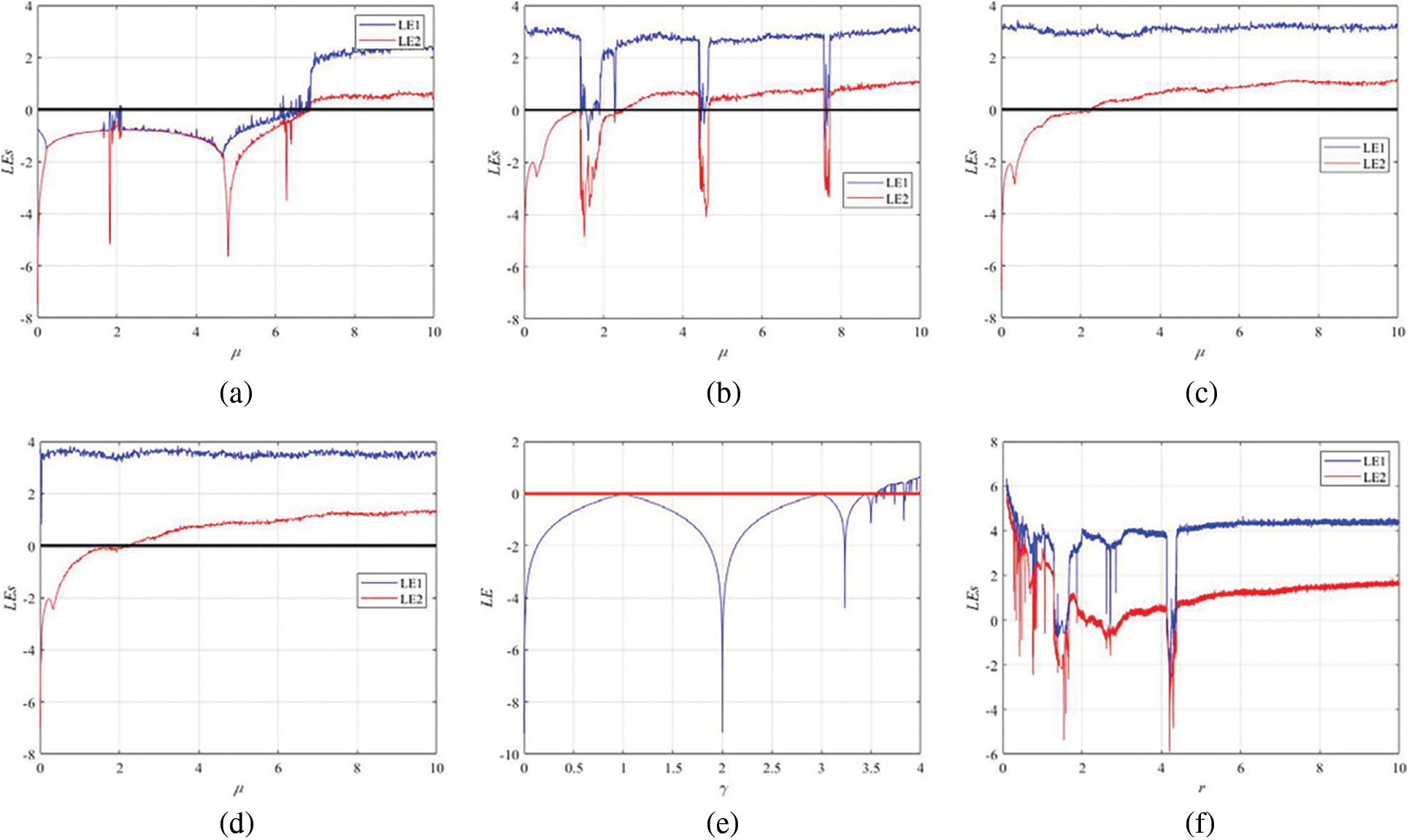
Figure 1: Lyapunov exponents (a) LEs of 2D-SSCDB with η=2. (b) LEs of 2D-SSCDB with η=5. (c) LEs of 2D-SSCDB with η=7.2. (d) LEs of 2D-SSCDB with η=15. (e) LEs of Logistic. (f) LEs of 2D-SCMCI

At η=2, the 2D-SSCDB exhibits weak dynamic behavior when μ≤6.921, the 2D-SSCDB exhibits strong dynamic behavior when μ>6.921. At η=5, the 2D-SSCDB presents a chaotic state, and the behavior of hyperchaotic states alternately appears. With η increasing gradually, the period window gradually disappears. At η=7.2, the period window disappears completely, when μ<2.151, the 2D-SSCDB presents a chaotic state, and when μ≥2.151, the 2D-SSCDB presents a hyperchaotic state. Thereafter, the 2D-SSCDB exhibits stable kinetic behavior with η increasing gradually. Compared with Logistic Map, the 2D-SSCDB has more complex dynamic behavior. Compared with the 2D-SCMCI, the parameter space of the 2D-SSCDB in hyperchaotic state is continuous. Therefore, the 2D-SSCDB has better expressiveness.

In order to generate chaotic sequences with excellent performance, the range of parameters we choose in the cryptosystem is η≥7.2, and μ≥3. At this time, the state of 2D-SSCDB is hyperchaotic, which means that the sequence generated by it has excellent randomness.

2.2 Phase Diagram Analysis

Phase diagram analysis describes the trajectory of a nonlinear dynamical system. The larger the area occupied by the phase diagram, the better the chaotic performance of the nonlinear dynamical system. The phase diagram analysis of the 2D-SSCDB is shown in Fig. 2. The initial value are x0=0.465651321, and y0=0.32131654. Phase diagram analysis shows that the 2D-SSCDB occupies a larger space compared to 2D-SCMCI [39] and 2D-SLMM [40]. Therefore, the 2D-SSCDB has better ergodicity and can take all the values of the phase space.

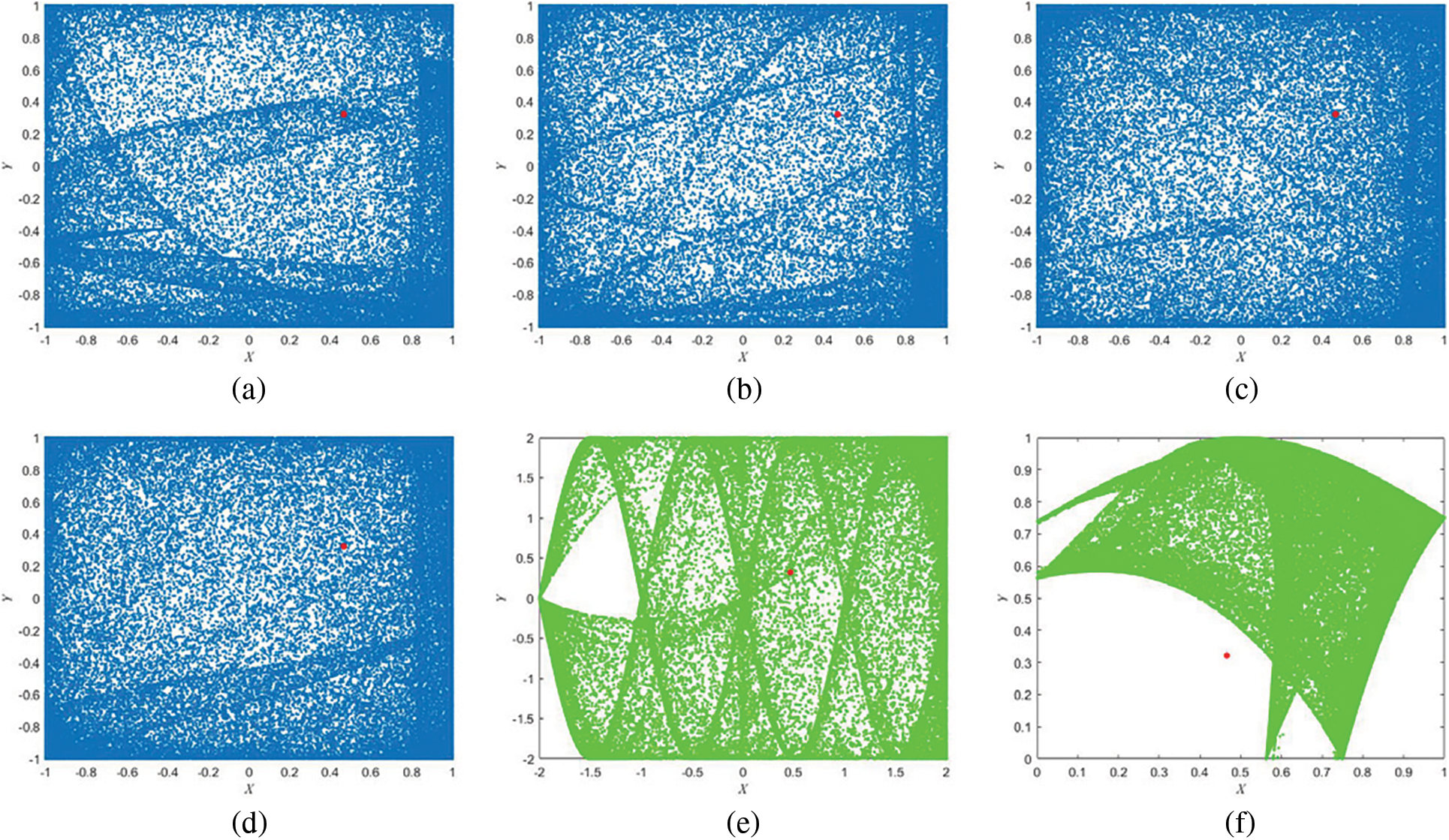
Figure 2: Phase diagram analysis. (a) η=2.8,μ=5 of 2D-SSCDB. (b) η=5,μ=5.5 of 2D-SSCDB. (c) η=7.2,μ=7.2 of 2D-SSCDB. (d) η=15,μ=8.9 of 2D-SSCDB. (e) 2D-SCMCI. (f) 2D-SLMM [40]

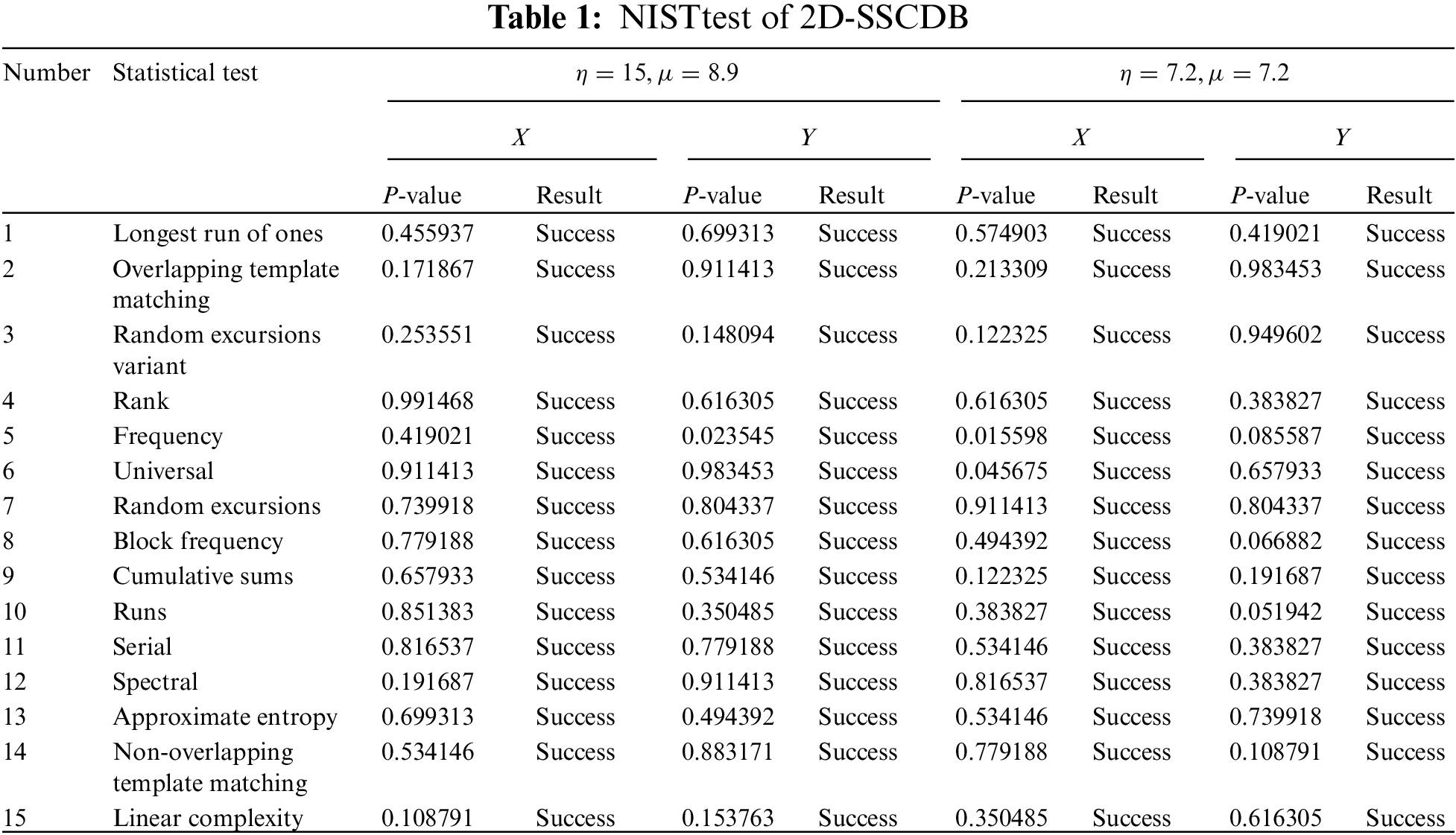
2.3 NIST Statistical Test Suite

The NIST statistical test suite was used to test the randomness of the sequences generated by the 2D-SSCDB.

NIST contains 15 tests, and when the P-value is greater than 0.01, the random sequence passes the test. The NIST test of the 2D-SSCDB is shown in Table 1, where x0=0.465651321 and y0=0.32131654. The parameters for the 2D-SSCDB are η=7.2,μ=7.2 and η=15,μ=8.9. NIST tests show that the sequences generated by the 2D-SSCDB have good randomness.

3  Color Image Encryption Algorithm by 2D-SSCDB

In order to explore the application of the 2D-SSCDB to image encryption, we propose a color image encryption algorithm based on 2D-SSCDB, which we call simple structure-color image encryption (SS-CIE). The SS-CIE is a symmetric encryption algorithm, and the decryption process is the reverse process of encryption. The SS-CIE is an encryption algorithm that performs scrambling and diffusion at the same time. This design structure increases the security of the algorithm.

3.1 Encryption

The plaintext image is P∈Mm×n×3, the red channel of the plaintext is PR∈Mm×n, the green channel of the plaintext is PG∈Mm×n, and the blue channel of the plaintext is PE∈Mm×n. The algorithm of the SS-CIE is described as follows,

Input: P (PR, PG, PG)

Output: C (C∈Mm×n×3)

Step 1: Connect the three channels of the plaintext in turn to obtain a new plaintext P∈Mm×3n, P=[PR,PG,PB].

Step 2: Get an initial fine-tuning key k by P, where k=∑i=1m∑j=13nP(i,j)/1010×π. If k=0, then we set k=100.

Step 3: Bring k into the Logistic iteration for 50 times to get the final fine-tuning key k1(k1=z50) by Eq. (3),

zn+1=3.99999×zn×(1−zn),n=1,2,3,…,50,z0=k.(3)

Step 4: Randomly give the initial key of the cryptosystem, x0 (x0∈(0,1)), y0 (y0∈(0,1)), μ (μ∈[3,+∞)) and η (η∈[7.2,+∞)). Set the new keys which are xn0=x0+k1, yn0=y0+k1, μn=μ+k1, and ηn=η+k1.

Step 5: Let xn0, yn0, μn and ηn be the initial values and parameters of the 2D-SSCDB, iteratively generate chaotic sequences are X and Y, where X∈M1×3mn and Y∈M1×3mn. It should be noted that the generated sequence needs to discard the initial sequence, so that the generated sequence is sufficiently chaotic, and the number of discarded sequences set in this paper is 300.

Step 6: Generate the encryption matrix of the cryptosystem D (D∈Mm×3n), D=floor(X×1010)mod256.

Step 7: Set a sorting function A=f(a,L), which can truncate the first L sequences from a one-dimensional vector a. Sort the intercepted sequence, and find the position of the sorted sequence in the original sequence, and return as A.

According to the sorting function, generate two sorting matrices S1 and S2, where S1=f (Y,m) and S2=f (Y(m+3n:end),3n).

Step 8: The encryption process is described as,

(1)   C(S1(1),S2(1))=(P(1,1)+D(S1(1),S2(1)))mod256.

(2)   C(S1(i),S2(1))=(P(i,1)+D(S1(i),S2(1))+C(S1(i−1),S2(1)))mod256, i=1,2,3,…,m.

(3)   C(S1(1),S2(i))=(P(1,i)+D(S1(1),S2(i))+C(S1(1),S2(i−1)))mod256, i=1,2,3,…,3n.

(4)   C(S1(i),S2(j))=(P(i,j)+D(S1(i),S2(j))+C(S1(i−1),S2(j−1)))mod256, i=1,2,3,…,m,j=1,2,3,,…,3n.

3.2 Decryption

The decryption algorithm is the inverse process of the encryption algorithm. The decryption algorithm is described as follows.

Input: C (C∈Mm×n×3), x0, y0, μ, η, and k1

Output: P (P∈Mm×n×3)

Step 1: Convert ciphertext C to new ciphertext C∈Mm×n×3→C∈Mm×3n.

Step 2: According to the secret keys x0, y0, μ, η, and k1, the encryption matrix D of the cryptosystem can be generated, and two sorting matrices S1 and S2 are generated.

Step 3:The decryption process is described as follows,

(1)   P(1,1)=(C(S1(1),S2(1))−D(S1(1),S2(1)))mod256

(2)   P(i,1)=(C(S1(i),S2(1))−D(S1(i),S2(1))−C(S1(i−1),S2(1)))mod256, i=1,2,3,…,m

(3)   P(1,i)=(C(S1(1),S2(i))−D(S1(1),S2(i))−C(S1(1),S2(i−1)))mod256, i=1,2,3,…,3n

(4)   P(i,j)=(C(S1(i),S2(j))−D(S1(i),S2(j))−C(S1(i−1),S2(j−1)))mod256, i=1,2,3,…,m,j=1,2,3,,…,3n

4  Performance Analysis

4.1 Visualization

The encryption simulation experiment is carried out using the image encryption algorithm based on chaos theory proposed in this paper.

Taking Lena as an example, the image encryption and decryption results are shown in Fig. 3. Taking Black as an example, the image encryption and decryption results are shown in Fig. 4. The initial keys for SS-CIE are set to x0=0.465651321, y0=0.32131654, μ=7.2, and η=7.2. Visual analysis shows that the SS-CIE is visually secure, and the ciphertext is transformed into an unrecognizable noise image.

Figure 3: Visualization of SS-CIE for Lena (512 × 512). (a) Plaintext of lena. (b) Ciphertext of lena. (c) Decrypted lena

Figure 4: Visualization of SS-CIE for black (512 × 512). (a) Plaintext of black. (b) Ciphertext of black. (c) Decrypted black

4.2 Key Analysis

Key analysis is divided into key sensitivity analysis and key space analysis. The secret key of SS-CIE are x0 (x0∈(0,1)), y0 (y0∈(0,1)), μ (μ∈[3,+∞)), η (η∈[7.2,+∞)), and k1, if the calculation accuracy of the computer is 10−15, the secret key space of x0, y0, μ, η, and k1 are 1015, 1015, 1015×1015, 1015×1015, and 1015. The secret key space of SS-CIE is

keyspace=1015×1015×(1015×1015)×(1015×1015)×1015=10105≈2348.

When the key space of the algorithm exceeds 2100, the algorithm is considered to be resistant to brute force attacks. So the SS-CIE can resist brute force attacks.

In order to test the key sensitivity of the image encryption algorithm in this paper, the key is changed 10−15, and the simulation results are shown in Fig. 5. The initial keys for SS-CIE are set to x0=0.465651321, y0=0.32131654, μ=7.2, and η=7.2. Key sensitivity analysis shows that the SS-CIE is sensitive to keys, and the decryption system also has good sensitivity.

Figure 5: Key sensitivity analysis of SS-CIE for Goldhill (576 × 702). (a) Correct key to decrypt. (b) Wrong key to decrypt with x0=x0+10−15. (c) Wrong key to decrypt with y0=y0+10−15. (d) Wrong key to decrypt with η=η+10−15. (e) Wrong key to decrypt with μ=μ+10−15

4.3 Histogram Analysis

The histogram can be used to visually see the distribution characteristics of the pixel value of an image. Taking Goldhill as an example, the histogram analysis of SS-CIE is shown in Fig. 6.

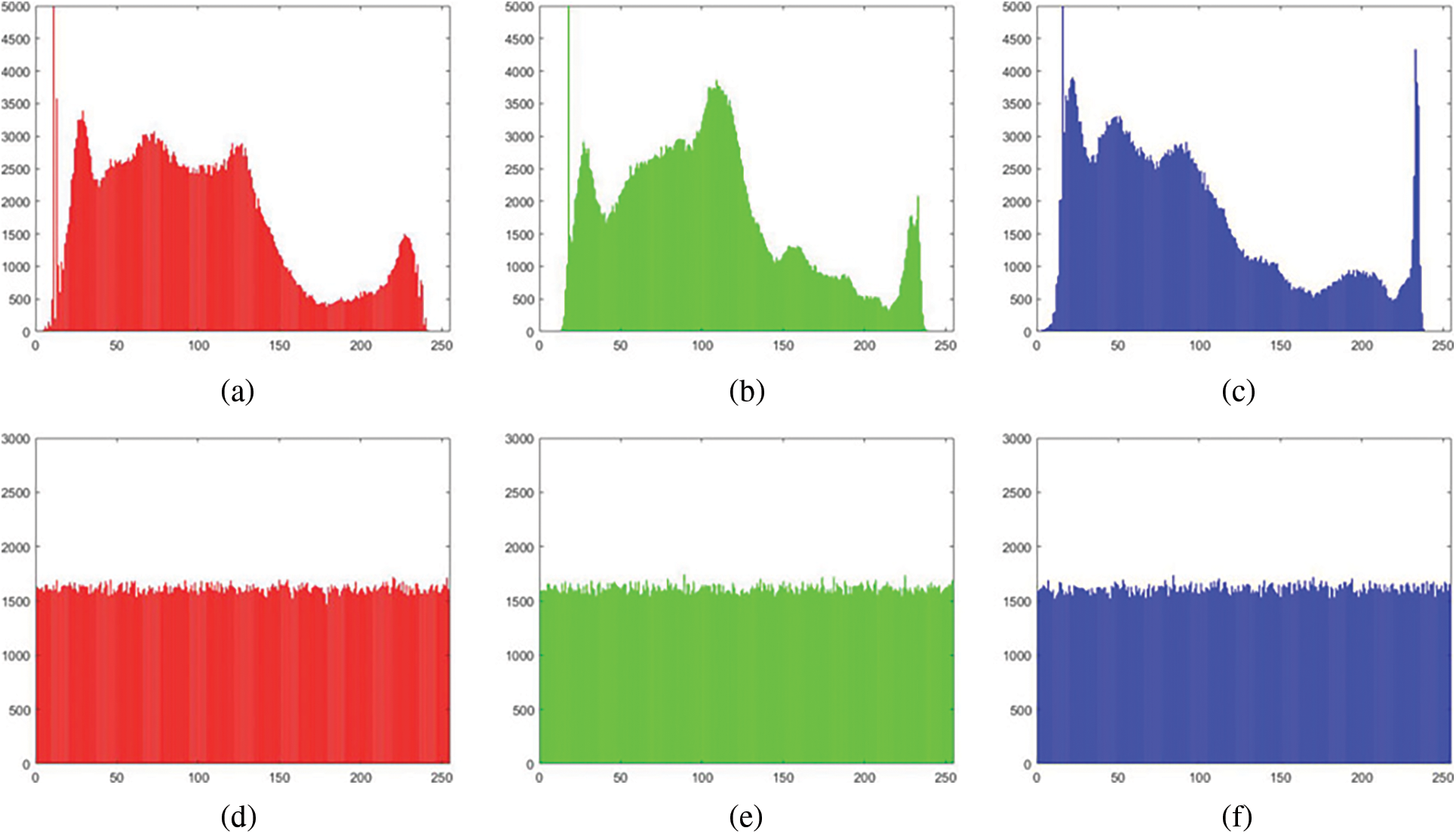
Figure 6: Histogram analysis of SS-CIE. (a) Histogram of R channel. (b) Histogram of G channel. (c) Histogram of B channel. (d) Histogram of encrypted R channel. (e) Histogram of encrypted G channel. (f) Histogram of encrypted B channel

Histogram analysis shows that the ciphertext histogram distribution of SS-CIE is uniform, which means that the ciphertext pixel value distribution is random, and the attacker cannot obtain any useful information from the ciphertext, so SS-CIE can Resist statistical attacks.

4.4 Correlation Analysis

Generally, the correlation between adjacent pixels of the raw unprocessed image is high. We hope that the correlation performance between adjacent pixels of the image will be reduced after encryption, so that the ciphertext image cannot be cracked through the correlation analysis of adjacent pixels. Taking Goldhill as an example, the correlation analysis of the SS-CIE is shown in Figs. 7 and 8.

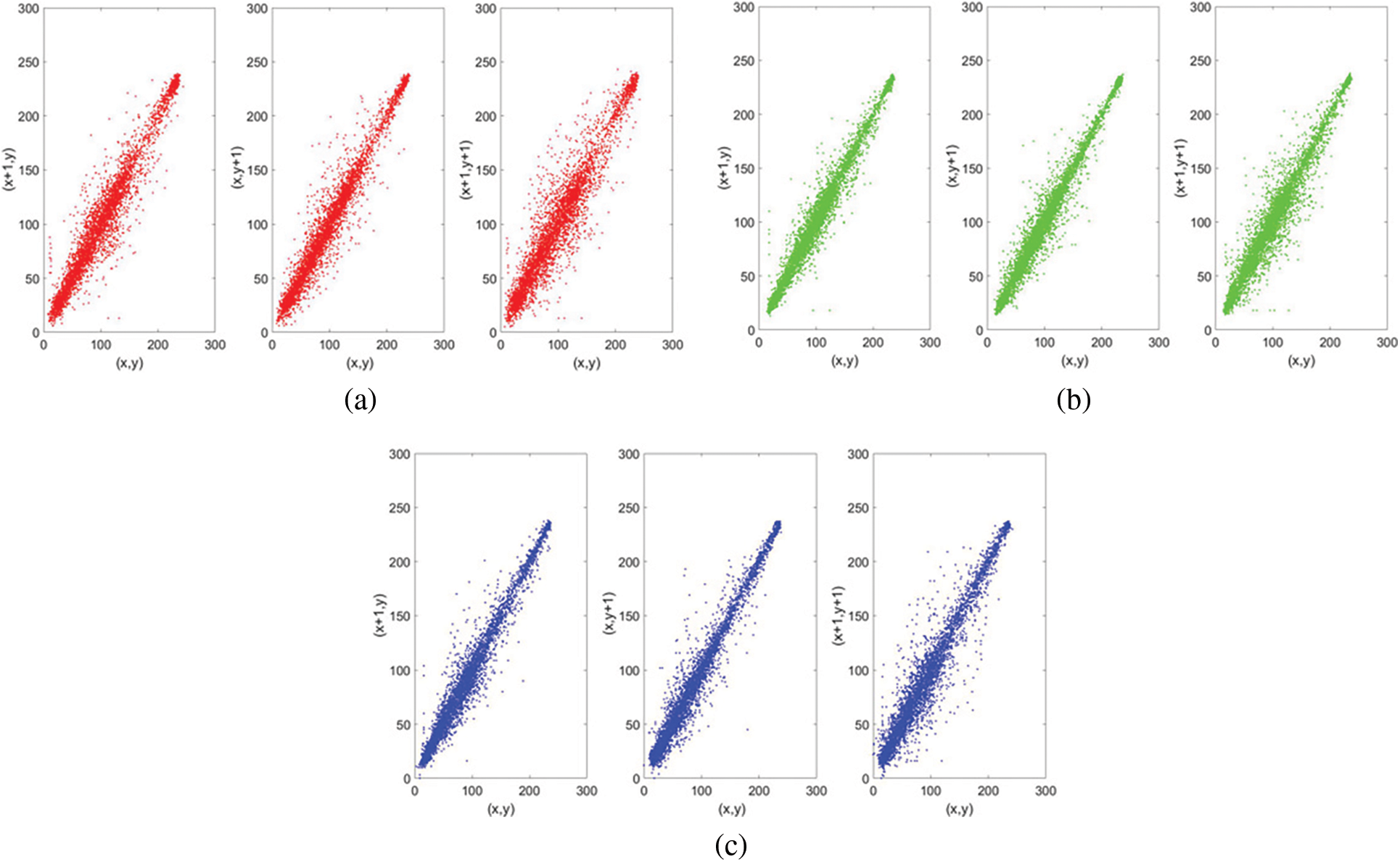
Figure 7: Correlation analysis of plaintext for SS-CIE. (a) Correlation of R channel. (b) Correlation of G channel. (c) Correlation of B channel

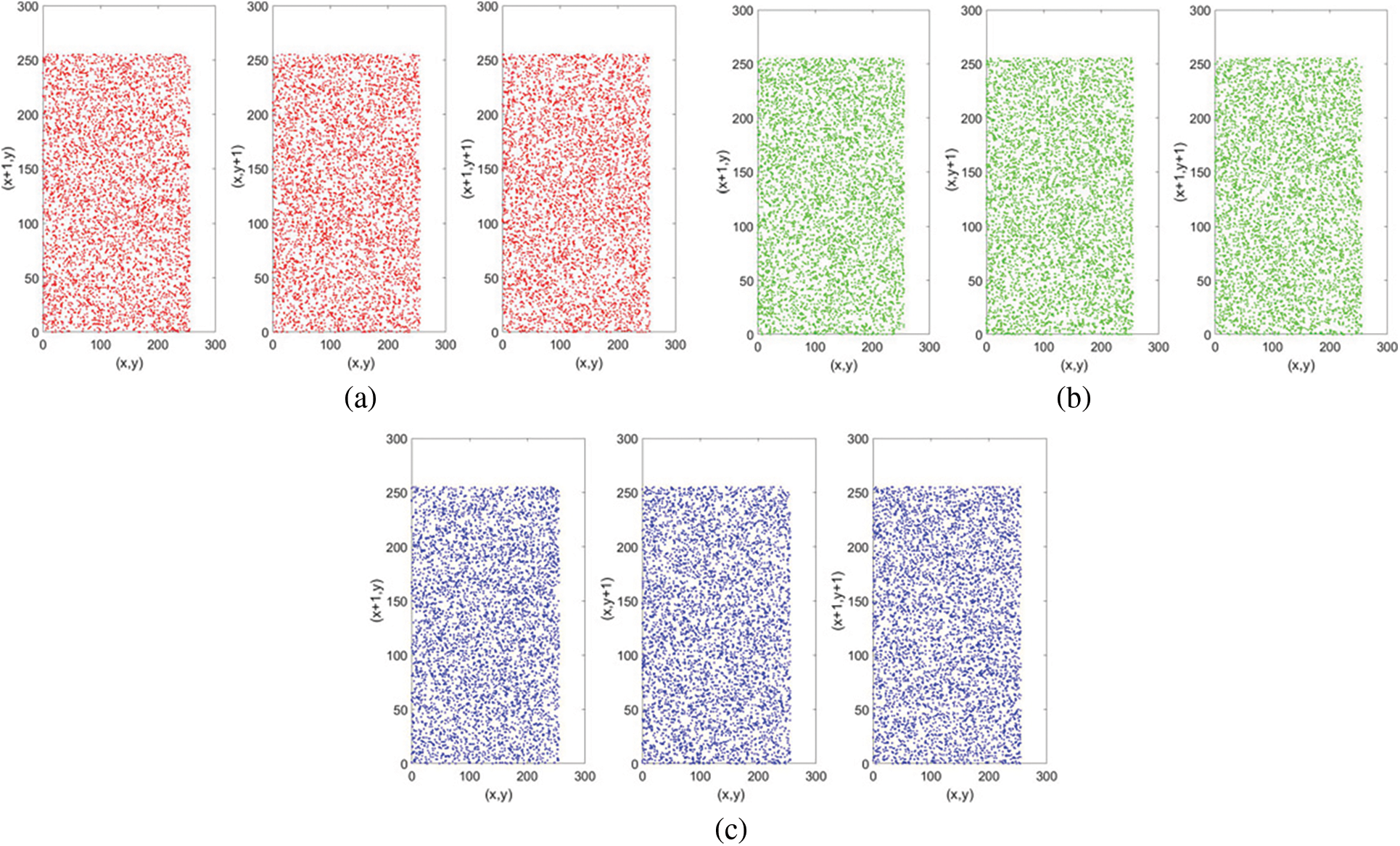
Figure 8: Correlation analysis of ciphertext for SS-CIE. (a) Correlation of encrypted R channel. (b) Correlation of encrypted G channel. (c) Correlation of encrypted B channel

When the adjacent correlation is small, the correlation image shows a divergent state. When the adjacent correlation is large, the image presents an aggregated state. Therefore, visually, the ciphertext of SS-CIE has less correlation. To further verify the accuracy of the correlation, the calculation formula of the correlation is

rρ=cov(x,y)D(x)⋅D(y).(4)

Table 2 is the correlation analysis results of SS-CIE. And compared with some classic algorithms (Refs. [43–45]), the comparison results are shown in Table 3.

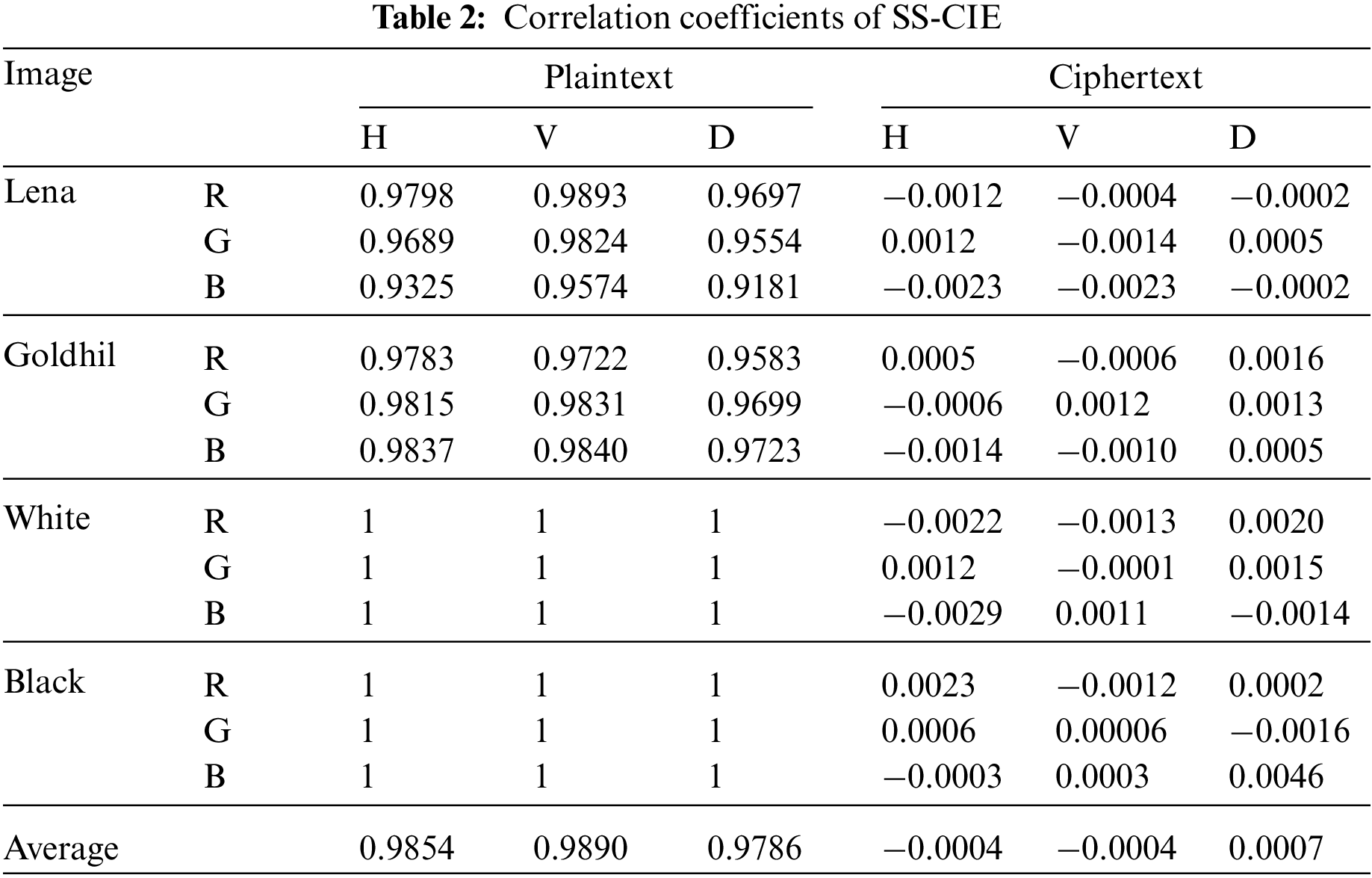
The correlation coefficient of the plaintext image is large, and the correlation is very strong. However, the correlation coefficient of adjacent pixels of the ciphertext image is very small, and the correlation is low. It shows that after the encryption of the algorithm in this paper, the ciphertext image can well resist the attack of statistical analysis. In addition, the correlation comparison with other algorithms shows that the SS-CIE is more resistant to statistical analysis.

4.5 Correlation Analysis of R, G, and B

Using the method of correlation analysis to analyze the correlation between the three channels, a safe algorithm can not only reduce the correlation between adjacent pixels, but also reduce the correlation between the three channels of the plaintext image. The correlation analysis of the three channels is shown in Table 4.

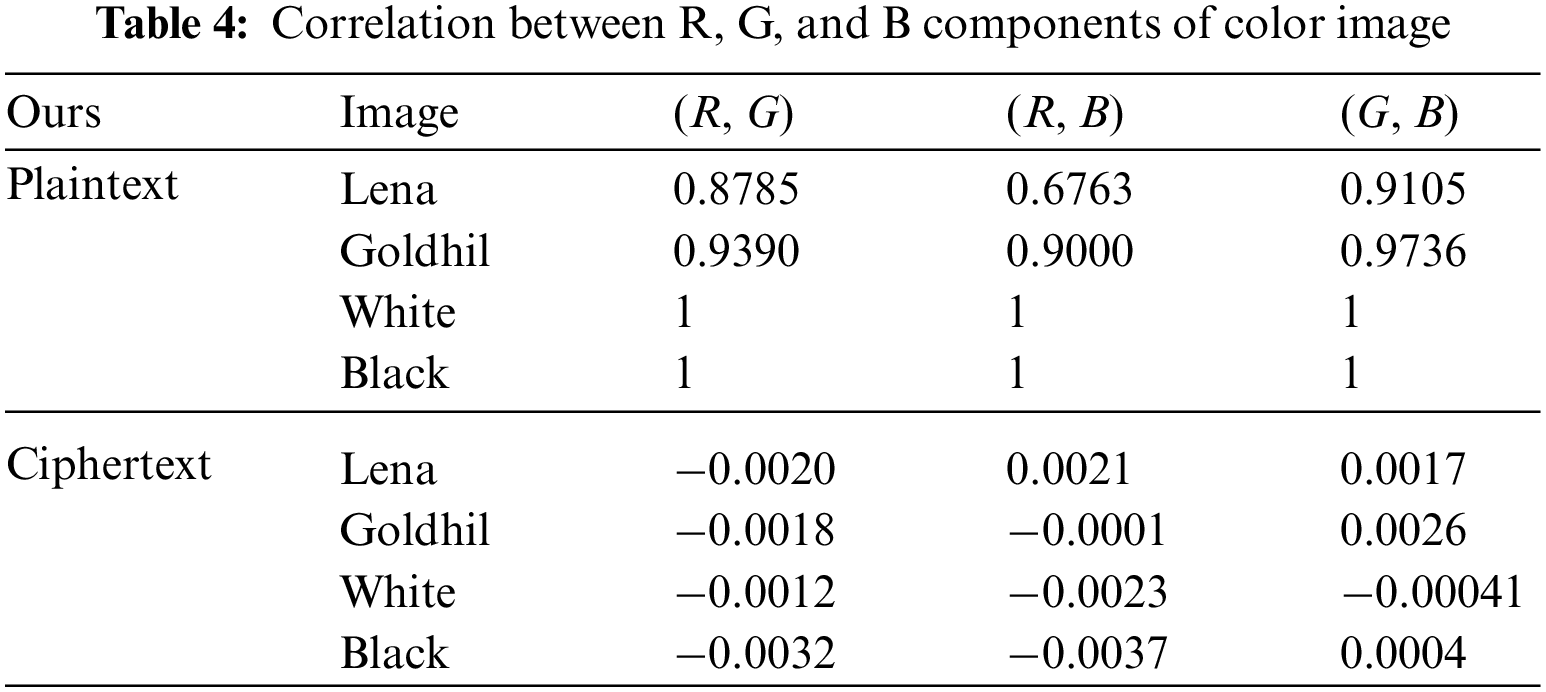
The experimental results show that the SS-CIE effectively reduces the correlation between the three channels, and the attacker cannot infer the information of the remaining channels through the ciphertext value of one channel, indicating that the algorithm has good security.

4.6 Information Entropy Analysis

The amount of information contained in an image can be reflected by information entropy. The greater the information entropy, the better the encryption effect of the algorithm and the more hidden information. The calculation formula of information entropy is,

H=∑i=0255p(gi)log2⁡1p(gi).(5)

The information entropy analysis of SS-CIE is shown in Table 5, and the information entropy comparison results with other algorithms are shown in Table 6 (Refs. [43–45]).

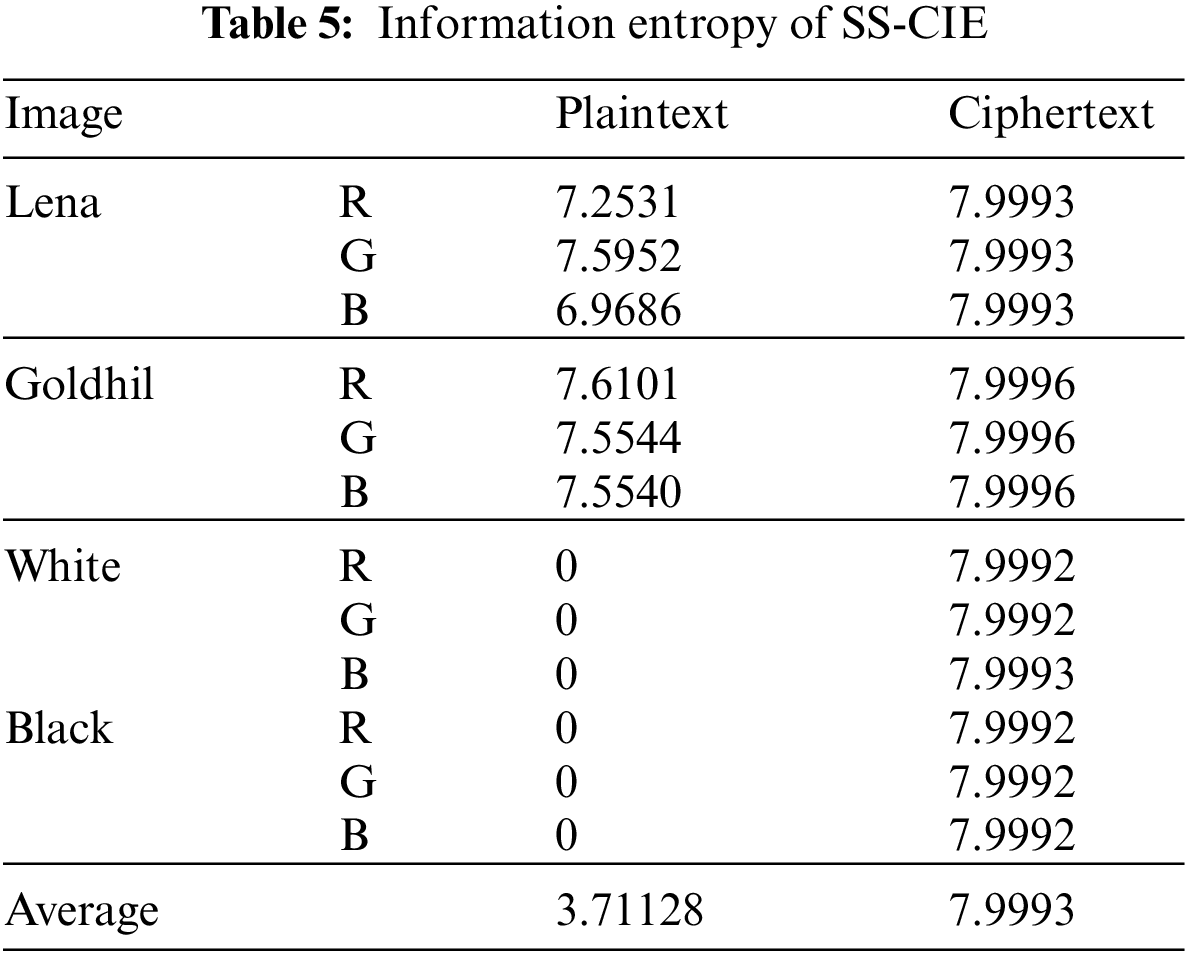
The information entropy analysis shows that the plaintext image carries a lot of information, while the ciphertext image obtained by the SS-CIE has a small amount of information (the information entropy is close to 8). The ciphertext image presents a random noise image. The information entropy comparison results show that the ciphertexts of SS-CIE have better randomness and less information, so the SS-CIE is more resistant to statistical attacks, and the algorithm has better security.

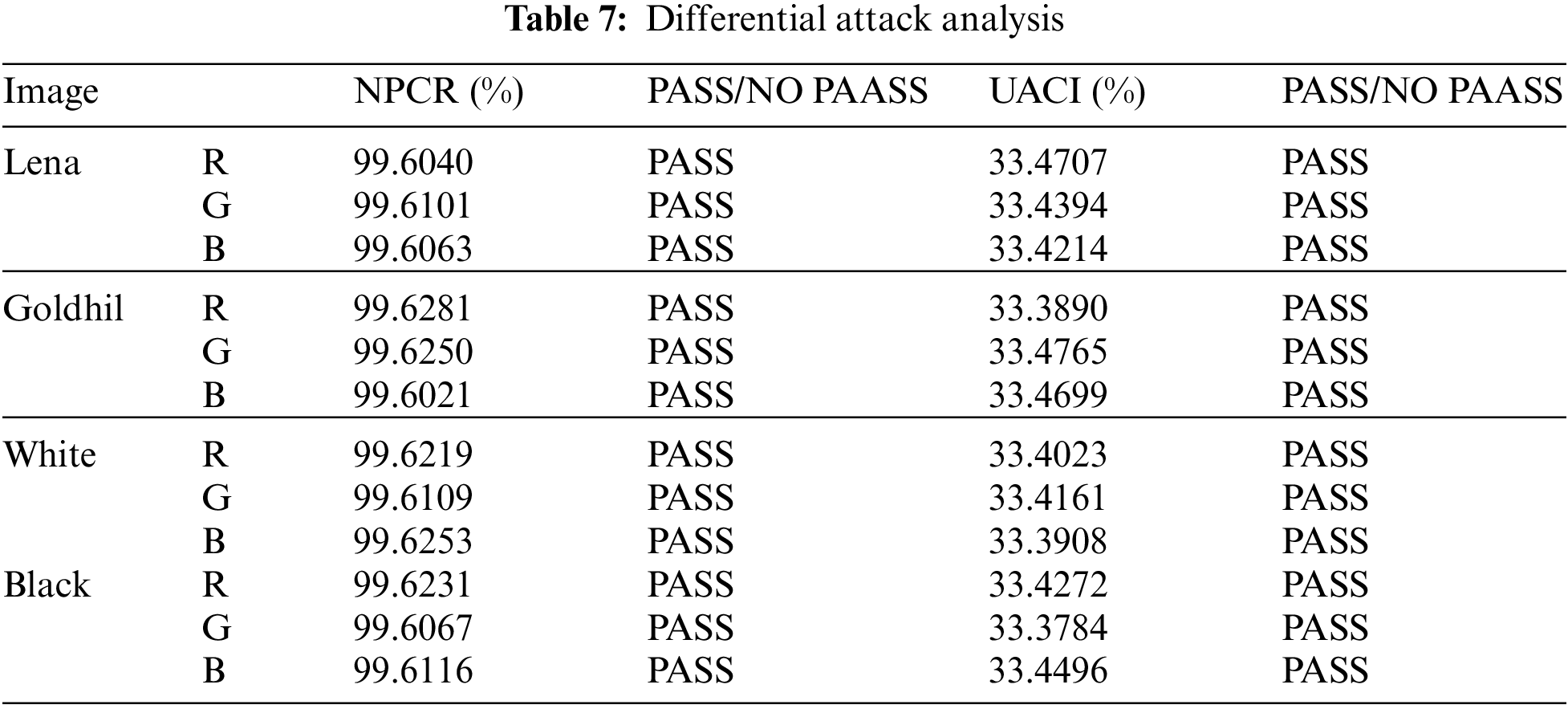
4.7 Differential Attack Analysis

A secure algorithm is sensitive to the plaintext. Even if the plaintext changes slightly, two distinct ciphertexts will still be obtained. NPCR and UACI are two indicators to evaluate the ability of the algorithm to resist differential attack. Wu et al. proposed in the Ref. [46] that when the value of NPCR exceeds 99.5893%, the value of UACI is between 33.3730% and 33.5541%, indicating that the algorithm can resist differential attacks. The ability of SS-CIE to resist differential attacks is shown in Table 7. Differential attack analysis shows that SS-CIE has excellent resistance to differential attacks, and the attacker cannot crack the algorithm by analyzing the characteristics of the two ciphertexts.

4.8 Robustness Analysis

There will be noise attacks and clipping attacks in the transmission of ciphertext. The effect of SS-CIE against clipping attack is shown in Fig. 9. The effect of SS-CIE against noise attack is shown in Fig. 10. Noise attack and clipping attack show that SS-CIE has good robustness.

Figure 9: Clipping attacks analysis. (a) Correlation of encrypted R channel. (b) Data lost of 50 * 50. (c) Data lost of 100 * 100. (c) Data lost of 200 * 200. (d) Decrypted image of (a). (e) Decrypted image of (b). (c) Decrypted image of (c)

Figure 10: Noise attacks analysis. (a) 0.1 salt & pepper. (b) 0.01 salt & pepper. (c) 0.001 salt & pepper. (d) Decrypted image of (a). (e) Decrypted image of (b). (c) Decrypted image of (c)

4.9 Efficiency Analysis

The running environment of the SS-CIE is Windows 10, matlab 2020, i3-10105F. The efficiency analysis is shown in Table 8. Efficiency analysis shows that SS-CIE requires about 1.0930 s to encrypt color images with 512 * 512. Compared with other algorithms, SS-CIE has higher efficiency. SS-CIE not only has high security, but also runs efficiently.

5  Conclusion

In this paper, a new 2D hyperchaotic system is proposed, called 2D-SSCDB. The 2D-SSCDB has a simple structure and can generate complex dynamic behavior. Through Lyapunov exponent, phase diagram analysis, NIST test, sensitivity analysis, and comparative analysis, it is verified that the 2D-SSCDB has good performance and can generate random numbers with better performance. In order to verify the practicability of the 2D-SSCDB, combined with the 2D-SSCDB system, we propose a color image encryption algorithm. Scrambling and diffusion are carried out at the same time in this algorithm. Through key analysis, information entropy analysis, statistical analysis, and other methods, it is verified that the cryptographic system has high security and can resist common attack methods. The 2D-SSCDB is a better candidate for keystream generation based on chaotic image encryption.

Funding Statement: Funds for New Generation Information Technology of the Industry-University-Research Innovation Foundation of China University (No.2020ITA03022).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  X. Huang, Y. Dong, H. Zhu and G. Ye, “Visually asymmetric image encryption algorithm based on SHA-3 and compressive sensing by embedding encrypted image,” Alexandria Engineering Journal, vol. 61, no. 10, pp. 7637–7647, 2022. [Google Scholar]

 2.  F. Yang, J. Mou, C. Ma and Y. Cao, “Dynamic analysis of an improper fractional-order laser chaotic system and its image encryption application,” Optics and Lasers in Engineering, vol. 129, pp. 106031, 2020. [Google Scholar]

 3.  S. Gao, R. Wu, X. Wang, J. Wang, Q. Li et al., “A 3D model encryption scheme based on a cascaded chaotic system,” Signal Processing, vol. 202, pp. 108745, 2023. [Google Scholar]

 4.  X. Wang, S. Gao, X. Ye, S. Zhou and M. Wang, “A new image encryption algorithm with cantor diagonal scrambling based on the PUMCML system,” International Journal of Bifurcation and Chaos, vol. 31, no. 1, pp. 2150003, 2021. [Google Scholar]

 5.  R. Anitha and B. Vijayalakshmi, “Image encryption using multi-scroll attractor and chaotic logistic map,” Computers, Materials and Continua, vol. 72, no. 2, pp. 3447–3463, 2022. [Google Scholar]

 6.  X. Wang and S. Gao, “A chaotic image encryption algorithm based on a counting system and the semi-tensor product,” Multimedia Tools and Applications, vol. 80, no. 7, pp. 10301–10322, 2021. [Google Scholar]

 7.  X. Li, J. Mou, L. Xiong, Z. Wang and J. Xu, “Fractional-order double-ring erbium-doped fiber laser chaotic system and its application on image encryption,” Optics and Laser Technology, vol. 140, pp. 107074, 2021. [Google Scholar]

 8.  B. Ma and Y. Q. Shi, “A reversible data hiding scheme based on code division multiplexing,” IEEE Transactions on Information Forensics and Security, vol. 11, no. 9, pp. 1914–1927, 2016. [Google Scholar]

 9.  X. Wang and P. Liu, “A new full chaos coupled mapping lattice and its application in privacy image encryption,” IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 69, no. 3, pp. 1291–1301, 2021. [Google Scholar]

10. S. Zhou, X. Wang, M. Wang and Y. Zhang, “Simple colour image cryptosystem with very high level of security,” Chaos, Solitons and Fractals, vol. 141, pp. 110225, 2020. [Google Scholar]

11. C. Wang, B. Ma, Z. Xia, J. Li, Q. Li et al., “Stereoscopic image description with trinion fractional-order continuous orthogonal moments,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 32, no. 4, pp. 1998–2012, 2022. [Google Scholar]

12. Q. Li, X. Wang, B. Ma, X. Wang, C. Wang et al., “Concealed attack for robust watermarking based on generative model and perceptual loss,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 32, no. 8, pp. 5695–5706, 2022. [Google Scholar]

13. X. Wang, X. Wang, B. Ma, Q. Li and Y. Shi, “High precision error prediction algorithm based on ridge regression predictor for reversible data hiding,” IEEE Signal Processing Letters, vol. 28, pp. 1125–1129, 2021. [Google Scholar]

14. X. Wang and S. Gao, “Application of matrix semi-tensor product in chaotic image encryption,” Journal of the Franklin Institute, vol. 356, no. 18, pp. 11638–11667, 2019. [Google Scholar]

15. S. Zhou, X. Wang, M. Wang, B. Ge, M. Wang et al., “A novel image encryption cryptosystem based on true random numbers and chaotic systems,” Multimedia Systems, vol. 28, no. 1, pp. 98–112, 2022. [Google Scholar]

16. L. Gong, K. Qiu, C. Deng and N. Zhou, “An image compression and encryption algorithm based on chaotic system and compressive sensing,” Optics and Laser Technology, vol. 115, pp. 257–267, 2019. [Google Scholar]

17. F. H. Hsiao, “Applying 3DES to chaotic synchronization cryptosystems,” IEEE Access, vol. 10, pp. 1036–1050, 2021. [Google Scholar]

18. N. Zhou, S. Pan, S. Cheng and Z. Zhou, “Image compression encryption scheme based on hyper-chaotic system and 2D compressive sensing,” Optics and Laser Technology, vol. 82, pp. 121–133, 2016. [Google Scholar]

19. L. Xu, Z. Li, J. Li and W. Hua, “A novel bit-level image encryption algorithm based on chaotic maps,” Optics and Lasers in Engineering, vol. 78, pp. 17–25, 2016. [Google Scholar]

20. X. Chai, X. Fu, Z. Gan, Y. Lu and Y. Chen, “A color image cryptosystem based on dynamic DNA encryption and chaos,” Signal Processing, vol. 155, pp. 44–62, 2019. [Google Scholar]

21. J. Wu, X. Liao and B. Yang, “Color image encryption based on chaotic systems and elliptic curve ElGamal scheme,” Signal Processing, vol. 141, pp. 109–124, 2017. [Google Scholar]

22. L. Wang, T. Dong and M. F. Ge, “Finite-time synchronization of memristor chaotic systems and its application in image encryption,” Applied Mathematics and Computation, vol. 347, pp. 293–305, 2019. [Google Scholar]

23. B. Liu, X. Ye and Q. Chen, “Generating infinitely many coexisting attractors via a new 3D cosine system and its application in image encryption,” IEEE Access, vol. 9, pp. 136292–136301, 2021. [Google Scholar]

24. W. Liu, K. Sun and C. Zhu, “A fast image encryption algorithm based on chaotic map,” Optics and Lasers in Engineering, vol. 84, pp. 26–36, 2016. [Google Scholar]

25. C. Cao, K. Sun and W. Liu, “A novel bit-level image encryption algorithm based on 2D-LICM hyperchaotic map,” Signal Processing, vol. 143, pp. 122–133, 2018. [Google Scholar]

26. R. Wu, S. Gao, X. Wang, S, Liu, Q. Li et al.,“AEA-NCS: An audio encryption algorithm based on anested chaotic system,” Chaos, Solitons and Fractals, vol. 165, pp. 112770, 2022. [Google Scholar]

27. M. Alawida, A. Samsudin, J. S. Teh and R. S. Alkhawaldeh, “A new hybrid digital chaotic system with applications in image encryption,” Signal Processing, vol. 160, pp. 45–58, 2019. [Google Scholar]

28. X. Chai, Z. Gan, K. Yuan, Y. Chen and X. Liu, “A novel image encryption scheme based on DNA sequence operations and chaotic systems,” Neural Computing and Applications, vol. 31, no. 1, pp. 219–237, 2019. [Google Scholar]

29. Y. Zhou, L. Bao and C. Chen, “A new 1D chaotic system for image encryption,” Signal Processing, vol. 97, pp. 172–182, 2014. [Google Scholar]

30. C. Li, G. Luo, K. Qin and C. Li, “An image encryption scheme based on chaotic tent map,” Nonlinear Dynamics, vol. 87, no. 1, pp. 127–133, 2017. [Google Scholar]

31. Y. Xiao, X. Tong, M. Zhang and Z. Wang, “Image lossless encoding and encryption method of SPECK based on 1D chaotic map,” Physica Scripta, vol. 97, no. 5, pp. 05521, 2022. [Google Scholar]

32. C. Zhu, G. Wang and K. Sun, “Improved cryptanalysis and enhancements of an image encryption scheme using combined 1D chaotic maps,” Entropy, vol. 20, no. 11, pp. 843, 2018. [Google Scholar]

33. J. Chen, F. Han, W. Qian, Y. Yao and Z. Zhu, “Cryptanalysis and improvement in an image encryption scheme using combination of the 1D chaotic map,” Nonlinear Dynamics, vol. 93, no. 4, pp. 2399–2413, 2018. [Google Scholar]

34. S. Dhall, S. K. Pal and K. Sharma, “Cryptanalysis of image encryption scheme based on a new 1D chaotic system,” Signal Processing, vol. 146, pp. 22–32, 2018. [Google Scholar]

35. M. Khan and A. Rasheed, “A fast quantum image encryption algorithm based on affine transform and fractional-order Lorenz-like chaotic dynamical system,” Quantum Information Processing, vol. 21, no. 4, pp. 134, 2022. [Google Scholar]

36. H. Liu, J. Liu and C. Ma, “Constructing dynamic strong S-box using 3D chaotic map and application to image encryption,” Multimedia Tools and Applications, 2022. https://doi.org/10.1007/s11042-022-12069-x. [Google Scholar]

37. S. Wang, Q. Peng and B. Du, “Chaotic color image encryption based on 4D chaotic maps and DNA sequence,” Optics and Laser Technology, vol. 148, pp. 107753, 2022. [Google Scholar]

38. X. Wang and J. Yang, “Spatiotemporal chaos in multiple coupled mapping lattices with multi-dynamic coupling coefficient and its application in color image encryption,” Chaos, Solitons and Fractals, vol. 147, pp. 110970, 2021. [Google Scholar]

39. J. Sun, “2D-SCMCI hyperchaotic map for image encryption algorithm,” IEEE Access, vol. 9, pp. 59313–59327, 2021. [Google Scholar]

40. Z. Hua, Y. Zhou, C. M. Pun and C. L. Chen, “2D sine logistic modulation map for image encryption,” Information Sciences, vol. 297, pp. 80–94, 2015. [Google Scholar]

41. J. Zheng and L. F. Liu, “Novel image encryption by combining dynamic DNA sequence encryption and the improved 2D logistic sine map,” IET Image Processing, vol. 14, no. 11, pp. 2310–2320, 2020. [Google Scholar]

42. L. Teng, X. Wang and Y. Xian, “Image encryption algorithm based on a 2D-CLSS hyperchaotic map using simultaneous permutation and diffusion,” Information Sciences, vol. 605, pp. 71–85, 2022. [Google Scholar]

43. X. Wu, K. Wang, X. Wang, H. Kan and J. Kurths, “Color image DNA encryption using NCA map-based CML and one-time keys,” Signal Processing, vol. 148, pp. 272–287, 2018. [Google Scholar]

44. X. Wang, H. Zhang and X. Bao, “Color image encryption scheme using CML and DNA sequence operations,” Biosystems, vol. 144, pp. 18–26, 2016. [Google Scholar]

45. X. J. Kang and Z. H. Guo, “A new color image encryption scheme based on DNA encoding and spatiotemporal chaotic system,” Signal Processing: Image Communication, vol. 80, pp. 115670, 2020. [Google Scholar]

46. Y. Wu, J. P. Noonan and S. Agaian, “NPCR and UACI randomness tests for image encryption,” Journal of Selected Areas in Telecommunications, vol. 1, no. 2, pp. 31–38, 2011. [Google Scholar]

47. X. Wang, Y. Su, C. Luo, F. Z. Nian and L. Teng, “Color image encryption algorithm based on hyperchaotic system and improved quantum revolving gate,” Multimedia Tools and Applications, vol. 81, no. 10, pp. 13845–13865, 2022. [Google Scholar]

48. Y. Wang, C. Quan and C. J. Tay, “Optical color image encryption without information disclosure using phase-truncated Fresnel transform and a random amplitude mask,” Optics Communications, vol. 344, pp. 147–155, 2015. [Google Scholar]

49. Y. Luo, R. Zhou, J. Liu, S. H. Qiu and Y. Cao, “An efficient and self-adapting colour-image encryption algorithm based on chaos and interactions among multiple layers,” Multimedia Tools and Applications, vol. 77, no. 20, pp. 26191–26217, 2018. [Google Scholar]