Energy Management System with Power Offering Strategy for a Microgrid Integrated VPP

1  Introduction

Recently, the concept of MG network and its applications have become important issues. The MG is regarded as a well-known promising schematic solution to guarantee a reliable energy supply from prosumers and to satisfy demand of either prosumers or consumers [1]. In general, the compositions of MG is the aggregation of the conventional generators, renewable energy systems, and Energy Storage Systems (ESS). For support of such different energy resource loads, MG is required to form a self-sufficient and flexible system which operates either in power grid-connected mode or in island mode. One of the main advantages of the MG is to supply an energy production sources such as distributed renewable energy resources (D-RES or DERs), energy storage facilities and energy flow/distribution management.

However, the intermittent utilization of RESs such as wind turbine (WT) and photovoltaic (PV) into power grid brigs about instability and unreliability problem of the power system. Such intermittent characteristics of RESs originated from the weather variation causes power imbalance and power-quality problem. To neutralize side effects of RESs’ usage and handle them properly, the EMS is regarded as a very essential option for not only controlling the power flow in MGs but also offering the lower operating cost. For those purposes, the EMS employed at the intelligent MG network has to be capable of delivering the optimal distribution of RESs and minimizing the operating cost as well.

Recently, the VPP has been believed to provide sustainable power-services to the customers by virtually connecting with distributed RESs, and battery storage units in MGs [2–5]. For this reason, it is regarded as the most promising and effective alternative for optimal control of heterogeneous DERs in the Urban Energy System (UES)s. Since the VPP is required to offer the dynamic operation and the optimization strategy to concerning prosumers in the power-grid network, the best economic operation scheduling with the optimal power flow control is the main objective function in the operation of VPP network. Besides economic operation and reliability, the scope of EMS’s objectives in VPP network has to include the sustainability of energy and the environmental impact. Therefore, the role of EMS becomes much important in achieving the optimized control and scheduling of DERs in VPP.

While MG has an ability of increasing the reliability, stability and reducing energy losses, MG technology has great concern of cost, efficiency and control issues. Moreover, the important benefit of MG is to be a controllable entity to the electrical network itself. On the other hand, it has a drawback such as geographical limits. For overcoming the drawback and concerning issues of MG, the VPP is considered as a novel technology to provide sustainable energy utilization, virtually operating for local distributed sources and providing auxiliary services for shared renewable sub-plants. Hence, the VPP can contain distributed renewable energy power plants (i.e., DERs), traditional fossil–fuel-fired power plants (i.e., Conventional Heat-power Plant (CHP)), energy storage facilities and dispatchable loads. VPP can consist of a hierarchical aggregation of MGs [6,7]. Such integration approach is a very efficient way of coordinating the various types of energy resources in order to increase the profits and minimize the overall maintenance cost [8]. Thus, the concept of MG integrated VPP is regarded as a best option to develop sustainable energy management system with the optimal scheduling controller. Therefore, the proposal of such MG integrated VPP model with EMS is the major aim of this paper.

However, a new objective related to the minimization of power fluctuations in the power flow exchanged with the utility network has taken a great interest in recent years [9]. Thus, an optimization problem of minimizing the power fluctuations in the power flow of the MG aggregated VPP becomes another open issue to be discussed. For a successful solution to such optimization problem, the supplementary objective of controlling the decisive variables of EMS has to be taken into account. This objective is to guarantee the minimum and stable power peaks and fluctuation in the power profile. Even if the power peaks and fluctuation is controlled by the properly selected optimization algorithm, this supplementary objective cannot be achieved easily. During the minimization of power fluctuation and peaks, the enforced curtailment of the power surplus of DERs has to be carried out. Therefore, it causes the unfairness problem of the power curtailment and the re-distribution to prosumers, which is still remains to be tackled over for the best network operation.

To achieve a fair power curtailment, the decentralized method is proposed in [10] and the centralized Distributed Optimal Power Flow (DOPF) strategies are proposed in [11–13]. An alternative approach of fair power curtailment combined DOPF is presented in [14] which suggests three equity redistribution principles such as egalitarian, proportional and uniform curtailment. While those fair redistribution approaches contributed on achieving a certain level of curtailment of the power peaks and fluctuation, the overall optimization profit of generating revenue on the energy market could not be sufficiently considered in those works. For fair DERs coordination in VPP by mitigating power fluctuation, the power offering strategy considering energy market should be applied to overcome uncertain and complex decision-making issues [15,16]. Moreover, the active curtailed power control to all involving DERs should be considered with the objective of optimized scheduling control algorithm of EMS for MG integrated VPP. Thus, the active and intelligent power offering strategy in VPP in energy market becomes a decision-making method to solve the intermittent issues of DERs. Such offering strategy is carried out by the EMS in charge of VPP, playing an interaction role between the VPP and the energy market. Therefore, the EMS has to be highlighted as a decision-making strategy to monitor and control the load demand and supply as far as the relationship between VPP and integrated MGs is concerned.

Optimization algorithms have been widely used to minimize the overall cost and reducing energy losses. Intelligently controlled optimizing scheduler could ensure the system stability and enable smooth aggregation of MGs into VPP, resulting in guaranteeing the reliability and efficiency of network, and reducing cost and CO2 emission. Meta-heuristic optimization algorithms based on nature-inspired concept such as Genetic Algorithms (GAs) [17], Particle Swarm Optimization (PSO) [18], ant colony optimization [19], Cuckoo Search Algorithm (CSA) [20] are used to find the better alternative solution given objective function. Among those algorithms, PSO has been applied to almost every area in optimization, computational intelligence, and design applications. It is known that PSO is better than traditional search algorithms and even better than genetic algorithms for many types of problems [21].

A previous study in [22] shows that the binary PSO algorithm is very feasible to offer the optimal search of dispatch, unit commitment problem and dynamic multi-objective functions in MG operation. Hence, the EMS with PSO incorporating an active power control strategy is a very attractive approach to offer the optimal scheduling controller in MG integrated VPP, resulting in providing the optimal control in operation and management of the usage of DERs. Thus, this paper proposes an intelligent operating strategy of MG integrated VPP to minimize power fluctuation and the overall operating cost of VPP revenue. The major aim of this paper is to find the optimized solution of overall operating cost and provide fair power curtailment. The role of optimization algorithm of EMS is to calculate and offer the reference power to the controllers for controlling the power flow of DERs in the MG integrated VPP. The optimal power offering is calculated and scheduled based on energy revenue and surplus power waste using meta-heuristic optimization method. This paper is organized as follows: Section 2 presents the MG integrated VPP model. Section 3 describes the EMS and the offering strategy. The simulation results of the proposed model are presented in Section 4. The conclusion is summarized in Section 5.

2  Microgrid Integrated Virtual Power Plant Model

2.1 VPP and MG

Microgrid has been playing a key player in the smart grid network, thanks to its scalability and flexibility. By virtue of advent of smart grid with intelligent algorithm, the aggregation of smart MGs and separate DERs into the VPP is a feasible alternative approach to act like a conventional central generator. While MG has benefit of being a controllable entity to the electrical network itself, it has a drawback of geographical limits. The VPP is believed to provide highly efficient power services to customers through virtually sharing of dispersed DERs, and battery storage units in MGs. Hence, the aggregation of DER in VPP can be done by cloud-based or software-based. For this reason, VPP is regarded as the most promising and effective method for controlling heterogeneous DERs in the UESs. Moreover, in order to deal with intermittent nature of increasing shared DER, both the intelligent power offering management and the hierarchical topology of aggregation of DERs are essential to guarantee the reliable provision of sustainable energies. Thus, the VPP with such aggregation topology with an intelligent offering strategy can enable small stand-alone DERs to participate in the energy market, and meanwhile, it can mitigate DERs’ penalties by intermittent energy generation.

The architecture of VPP is very similar to MGs as shown in Fig. 1. The main difference is the geographical location of DERs and other units. The units of MG are located closely each other and thus, MG has a confined geographical limit of network. However, those of VPP are located apart and virtually connected without geographical limit and thus, VPPs are always grid-connect network. For high energy sustainability and reliability of DERs, the EMS is very necessary in both MG and VPP [20,23]. Moreover, the proper aggregation topology with an intelligent offering strategy is inevitable to minimize the overall operating cost. Hence, the topology of VPP with aggregated MGs is regarded as a best option for enabling a MG to participate in the energy market and for improving the profitability in the energy revenue [21,24].

Figure 1: General architecture of (a) MG and (b) VPP

2.2 Basic Framework of the Proposed MG Integrated VPP Model

The VPP is regarded as an innovative technology for an effective integration and aggregation of the conventional RESs as well as dispersed DERs. It can manage the unexpectable energy resources to be re-distributed fairly with a rationally scheduled energy allocation. It should be noted that the approach of VPP integrated with multiple MGs is a very efficient way of coordinating the various types of energy resources and of improve the profitability in the energy market trade, which is eventually expected to develop a sustainable energy management system with the optimized scheduling controller.

Based on such topology concept, we proposed the basic framework of the MG integrated VPP model with the EMS as shown in Fig. 2. This framework is a key decision-maker to provide intelligent control of distributed renewable energy power plants (i.e., DERs such as PV, WT) and energy storage system (ESS, battery storage), as well as control of CHP and dispatchable loads. As shown in Fig. 2, the MG integrated VPP consists of multiple MGs with their own DERs, alongside independent dispersed DERs, ESSs and other dispatchable loads. With a hierarchical operation structure and aggregation topology, the proposed model can implement an intelligent EMS with power offering strategy most effectively.

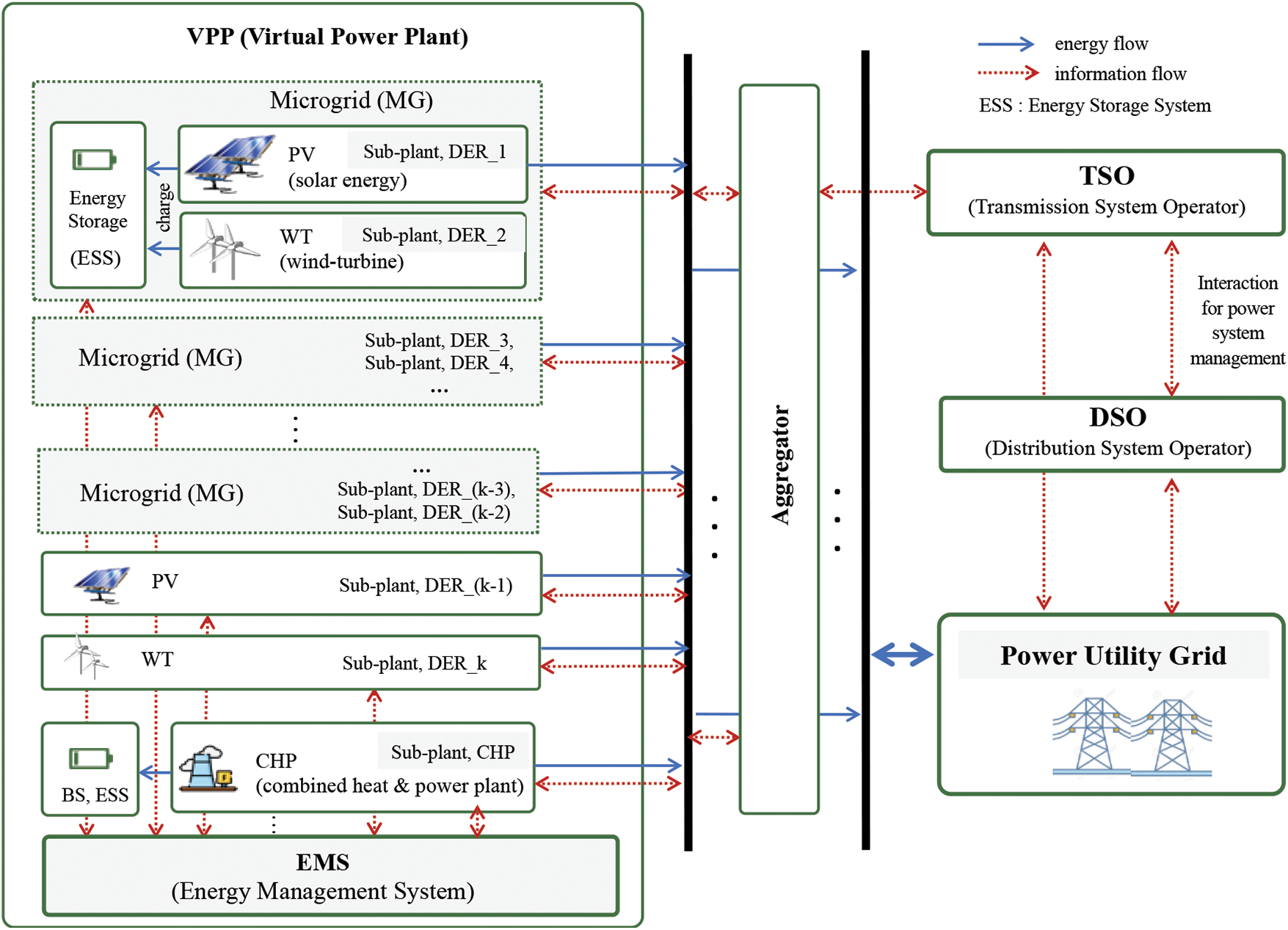
Figure 2: Basic framework of the MG integrated VPP model

The role of Aggregator in Fig. 2 is to coordinate all the power allocation of DERs belonging to VPP and to abate the power fluctuations caused by involved DERs, following the decision of the EMS and the power offering strategy. The former (unfairness) problem is derived from the unfair energy curtailment, allocation and re-distribution of the regenerated energy resources. The latter (uncertainty) problem is originated from either intermittent renewable energy availability or from the load demand. Both problems can be tackled over by the optimized scheduled decision of EMS which delivers the day-ahead scheduled reference power to the Aggregator and the fair power offering strategy, resulting in guaranteeing the reliable provision of sustainable energies to all entities in VPP. Such parameters related to control, monitoring and management of power flow is then reflected in the objective function of EMS in the proposed VPP model, aiming at finding the optimized solution for the minimum overall operating cost.

The Aggregator utilizes functionalities of both the Commercial VPP (CVPP) and the Technical VPP (TVPP). Based on economic parameters of sub-plants in VPP as well as technical power transmission scheduling reported from the TVPP, the CVPP manages to enable sub-plants to participate in energy market by delivering the power commitment scheduling to sub-pants. For the safety operation of VPP, the TVPP provides the information of real-time operation status of sub-plants in VPP [20,23]. Based on technical information such as DER’s ramp limit, capacity limit, energy storage situation etc., the TVPP delivers the technical power transmission scheduling to the CVPP and ensures the power scheduling and the maintenance of power balance by virtue of the power offering strategy for tackling down the unfair power re-distribution issue. In the proposed MG integrated VPP model, the role of the Transmission System Operator (TSO) is the same as that of the TVPP, and the operation procedure of the Distribution System Operator (DSO) is the same as that of the CVPP in Fig. 2.

3  Energy Management System

3.1 Objective Function of the EMS in VPP

Many studies on trying to resolve the issue of energy resource optimization in VPPs to either minimize the cost of VPP revenue or minimize the power fluctuation. However, the optimization dealing with objective functions is not considered yet as far as our knowledge is concerned. Hence, this paper takes these objectives into account so as to provide an optimized scheduler for ensuring smooth aggregation of MGs into VPP and for guaranteeing the overall network reliability of VPP. The objective function of the EMS in the proposed MG integrated VPP consists of the control parameters containing the energy load balance, the energy revenue and load surplus, which is aiming at determining the overall operating cost of the proposed VPP model.

Load Surplus: Let S(t),L(t), and G(t) be the surplus energy, the total load demand and the actual power generation at time t∈T, respectively, where t is the VPP service time as T={1,…,t,…,T}. The total amount of surplus energy S(t) can be defined as the difference between load demand L(t) and the actual power generation G(t), i.e., the sum of all the actual power generation by total K DERs (sub-plants). Let the actual generated power at either PV DER, WT DER or CHP at kth sub-plant in VPP be as P~PV,WT,CHP(k)(t).

S(t)=L(t)−G(t)=L(t)−∑kKP~PV,WT,CHP(k)(t)(1)

Energy Load Balance: To maintain the power balance between the load demand and the supply, the surplus energy should be 0 in the context of each generated power by DERs, the purchased power from the grid (Pbgrid(t)) and the sold power to the grid (Psgrid(t)) in the VPP at each time interval. Let Eq. (1) equals to 0, then:

L(t)−∑kKP~PV,WT,CHP(k)(t)−Pbgrid(t)+Psgrid(t)=0.(2)

Energy Revenue: In the energy market, the operating cost of the VPP can be determinized to establish the objective function. Let Ck as the maintenance cost at kth sub-plant (DERs) and Cbgrid(t), Csgrid(t) the unit cost of purchasing/selling from/to the main grid, respectively. Then, the objective function (f(t)) to be minimized can be determined as following:

f(t)=∑t=1T{S(t)+ℰ(t)}(3)

where ℰ(t) is the total energy revenue with consideration of the maintenance and the energy trading cost,

ℰ(t)=∑t=1T{∑kKP~PV,WT,CHP(k)(t)⋅Ck+Pbgrid(t)⋅Cbgrid(t)−Psgrid(t)⋅Csgrid(t)}.(4)

Then, the objective function can be defined as following:

Minf(t)=Min{∑t=1T[S(t)+ℰ(t)]}.(5)

To precisely calibrate the parameters of the objective function, the energy surplus equation in Eq. (1) should be replaced by the surplus energy fluctuation error function, that is

Se(t)=(S(t)−L(t)max(S(t),L(t)))2.(6)

Moreover, the actual generated power should be controlled by the power offering strategy in the VPP aggregator with EMS. Then, the actual power generation by DERs, P~PV,WT,CHP(k)(t), could be re-written as

P~PV,WT,CHP(k)(t)=PPV,WT,CHPmin+wk(t)⋅Pk,step(t)(7)

where wk(t) is the control co-efficiency to adjust step-size with the amount of Pk,step(t). And the unit power step size of kth sub-plant. Then, the total outpower is

P~gen(t)=∑kKP~PV,WT,CHP(k)(t)=∑kK(PPV,WT,CHPmin(t)+wk(t)⋅Pk,step(t))(8)

where

wk(t)≤[PPV,WT,CHPmax(t)−PPV,WT,CHPmin(t)Pk,step(t)]∈N0(9)

and the DER constraints can be defined as

PPV,WT,CHPmin(t)≤P~PV,WT,CHP(k)(t)≤PPV,WT,CHPmax(t).(10)

Finally, the objective function in Eq. (5) can be re-written as

minwf(w,t)minw∑t=1T[S(w,t)+ℰ(t)].(11)

3.2 Power Offering Strategy for Curtailment and Re-distribution

The power fluctuation due to the uncertainty and intermittency of the renewal energy resources by unpredictable weather conditions has to be mitigated by an intelligent algorithm for supplying stable energy distribution to all entities in VPP network. In order to handle the power fluctuation and unfair power curtailment, this paper considers the well-known situations such as Limited Power Control (LC), Power Reserved Control (PRC) and power Ramp Control (RC), each of which results in balancing the power generation and consumption [25]. Moreover, this paper applies three power curtailment and re-distribution strategies such as an Egalitarian reDistribution (ED), a Proportional Fair Curtailment (PFC) and a Uniform Curtailment (UC). If the power curtailment is done by the control and offering strategy, the actual generated power P~PV,WT,CHP(k)(t) can be re-written as

𝒫^PV,WT,CHP(k)(t)=P~PV,WT,CHP(k)(t)−P~curtail(k)(t)(12)

where P~curtail(k)(t) can be classified into three cases such as LC, PRC and RC. Then, the actual surplus energy S~(t) is

S~(t)=L(t)−G~(t)=L(t)−∑kK𝒫^PV,WT,CHP(k)(t).(13)

Moreover, the other issue has to be considered is the compensation to those sacrificial DERs’ for suffering enforced power curtailment by the EMS, in process of balancing the total load power fluctuation. The compensation price policy should be carefully determined in a reasonable and fair manner toward to all those DER sacrifices. Thus, the first term in Eq. (4) should be modified with consideration of the power curtailment parameter and the compensation price as following:

∑kK𝒫^PV,WT,CHP(k)(t)⋅Ck(t)=∑kKP~PV,WT,CHP(k)(t)⋅Ck−∑kKP~curtail(k)(t)⋅CCT(t)(14)

where the compensation price CCT(t) can be defined depending on the power curtailment and re-distribution policy such as ED, PFC and UD. Then, any relevant DER should turn the surplus generated energy into the battery storage system according to the amount of the curtailed power decided by the offering strategy. The curtailed and stored energy is re-distributed to meet the load demand or sold to the main grid, later.

When the total amount of to be curtailed power is decided, the EMS should decide which DER should be curtailed appropriately. For this purpose, we take into account three re-distribution techniques such as 1) ED; to decrease the same amount of power production, 2) PFC; to decrease power production with un-proportional to the amount of power generation, the more, the less, and 3) UC; to decrease the power production at the same limited level [13]. These strategies as illustrated in Fig. 3 are utilized in process of EMS operation. All three strategies could be used together or an appropriate strategy could be utilized judging from the load demand conditions such as LC, PRC and RC. Hence, the EMS should intelligently decide an active power control strategy with this power curtailment and re-distribution option, in finding the optimized solution of the objective function of the EMS.

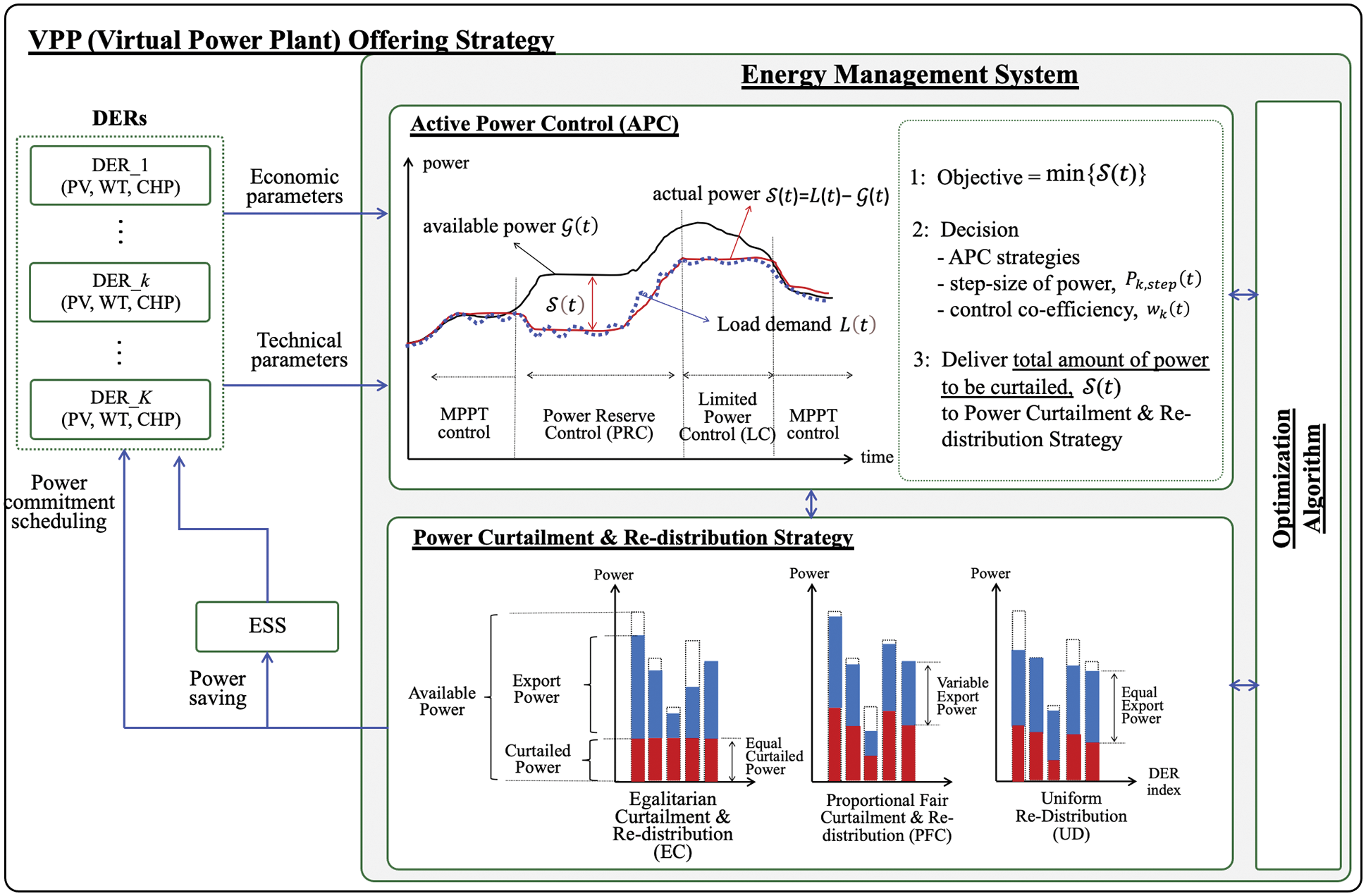
Figure 3: Proposed VPP offering strategy with EMS employing APC and power curtailment & re-distribution strategy

Now we can define the compensation price Ccs(t) to those sacrificial DERs as

𝒞CT(t)≈[CCT(t)G~(t)]⋅CCTunit(t)(15)

where CCTunit(t) is the unit price paid for curtailed DERs sacrifices at time interval t and depending on the re-distribution technique, it can be defined as

CCTunit(t)={CEDunit:ED suitable for LCCPFCunit:PFC suitable for PRC or RCCUCunit:UC suitable for LC.(16)

Then, Eqs. (4) and (5) and (11) should be re-written as

ℰ~(t)=∑t=1T{∑kK𝒫^PV,WT,CHP(k)(t)⋅Ck(t)+Pbgrid(t)⋅Cbgrid(t)−Psgrid(t)⋅Csgrid(t)}(17)

Minf~(t)=Min{∑t=1T[S(t)+ℰ~(t)]}(18)

Objectivefunction:minwf~(w,t)minw∑t=1T[S(w,t)+ℰ~(t)](19)

3.3 PSO of Optimizing the Objective Function of EMS in VPP

Among many optimization algorithms, it is known that PSO is better than other traditional search algorithms. Moreover, a previous study in [22] shows that the binary PSO algorithm is a very feasible solution to offer the optimal search of multi-objective functions in MG operation. Hence, in this paper, the PSO algorithm is applied to finding the solution of the objective function of EMS in VPP and thus, it offers the optimal scheduling controller in MG integrated VPP. The PSO is an optimization algorithm inspired by swarm intelligence of birds’ social behavior in flight. Each particle is characterized by a position and velocity vector that directs its movement which is guided by the optimal particles in the current moment [18]. Due to the simplicity of implementation with few parameters and less calculation complexity, PSO algorithm is very attractive to find the optimal solution. Based on basic procedure of the PSO in [20] can be modified and summarized as the pseudo code as follows.

4  Simulation Results and Discussion

The simulation results of the proposed MG integrated VPP with the EMS employing the power offering strategies are presented based on the MATLAB simulation platform. To evaluate the performance of the optimized EMS with the power offering strategy, it is assumed that the VPP consists of three MGs, each of which includes PV, WT and ESS (battery storage). The maximum limits of the generated power by PV and WT are 150 and 100 kW, respectively. The initial State of Charge (SOC) of the battery is set to 50%, and the range of SOC is set to 10%~90%. The electricity tariff is assumed as Table 1 during a typical weekday in which, the buying price and the selling price from the grid is respectively Cbgrid and Csgrid as defined in Eq. (17). The CCT1h is the compensation price paid for curtailed DERs sacrifices per hour during a day. It is noted that the power curtailment is optional countermeasures against the power fluctuation only if the generated power is higher than the load demand.

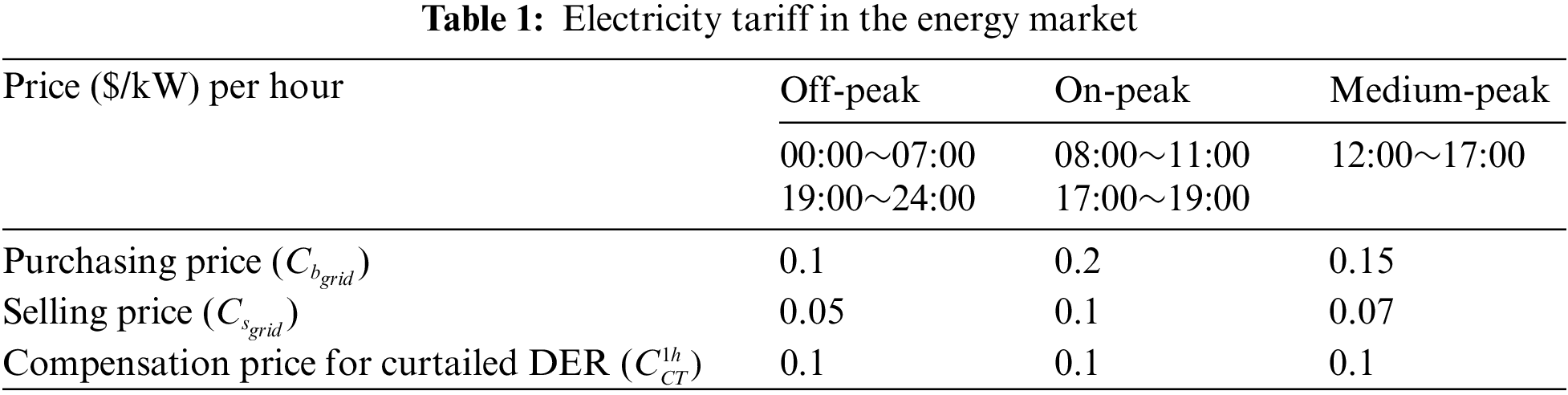
Thus, the power curtailment of DERs is carried out by the optimized decision of EMS with the active power control and offering strategy whether the load demand is higher than the total generated power or not. The curtailed power of DERs is to be charged into the corresponding MG’s battery storage (ESS) and then, it is to be discharged to the VPP or be sold to the power grid when the on-peak and medium-peak time. The EMS in VPP decides this operation by comparing the total cost of compensation price paid for those curtailed DERs with that of purchasing power from the grid. Hence, the compensation price at off-peak time is reasonably set as lower than the purchasing price at on-peak time and higher than the selling price at off-peak time, and thus, we set CCT1h to 0.1$/kW per hour without loss of generality. The overall cost of the electricity trade result can be varied according to the active power control and offering strategy such as ED, PFC and UC in Fig. 3 and it is dependent on the usage of the EMS with optimization algorithm.

Fig. 4 shows the power flow output results of DERs of each MGs, integrated into VPP, of which power curtailment and offering strategy are optimized by the PSO algorithm embedded in EMS with active power control strategy. In the off-peak time operation (either 00:00~7:00 or 19:00~24:00), the generated power by DERs in each MGs is managed and controlled to be charged into battery storage (ESS) and manage MGs to purchase shortage power from the grid, even if the load demand is affordable level for the VPP network. During the off-peak time, the curtailment and purchase is decided and managed by the EMS optimization algorithm based on the estimated overall operating cost of the energy market. The main reference decision of EMS is when to purchase power from the grid and to curtail power of DERs. Thus, the curtailed power of DERs will be utilized to meet the load demand by discharging the stored battery power during the on-/medium-peak period (8:00~18:00) where the load demand is lower than the generated power from DERs, i.e., the over-generated power supply case.

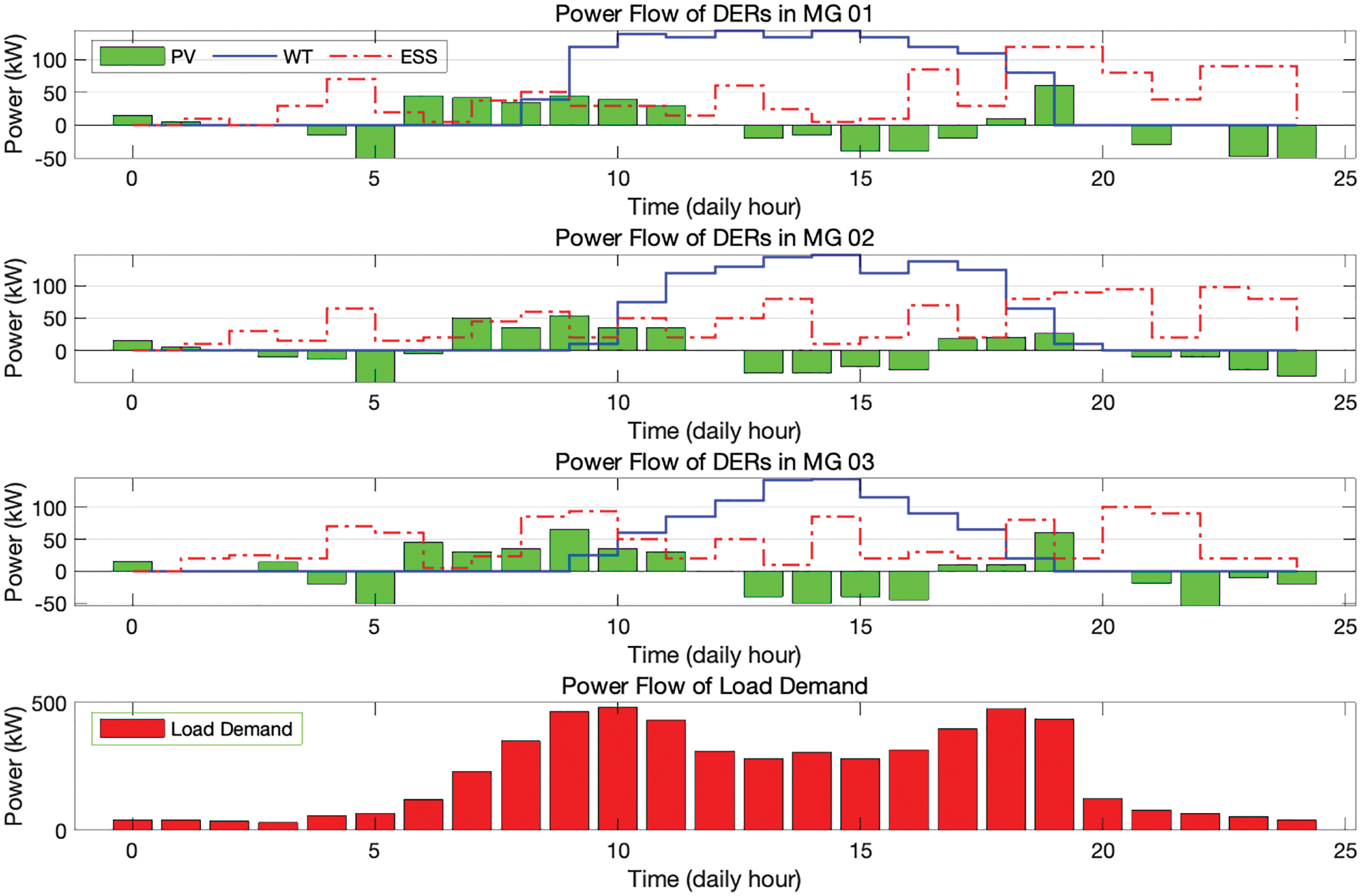
Figure 4: Optimized and scheduled power flow of DERs of MGs integrated VPP with the PSO-based EMS employing the power offering strategy; (a) MG1, (b) MG2, (c) MG3

With this strategy, the overall operating cost is saved since the selling price at both on-peak time and medium-peak time is much higher than that of off-peak time. This intelligent operation is decided by the EMS in VPP which compares the total cost of purchasing power from the grid with that of curtailed powers. Thus, it is reasonable that the compensation cost for the curtailed power at off-peak is lower than the purchasing price at on-peak time and higher than the selling price at off-peak time. On the other hand, the results of power flow obtained are shown in Fig. 5, when only MGs without EMS participate in the energy market. Fig. 5 shows that any surplus power throughout the day is likely to be charged into the ESS immediately. Thus, during the on-/medium-peak period, the re-generated power from DERs of MGs could be curtailed and stored into the battery, in contrast to the result of MGs with the proposed EMS. It is inferred that the curtailment operation of MGs only case is mainly dependent on the condition of the load demand, not on the overall operation cost of MGs.

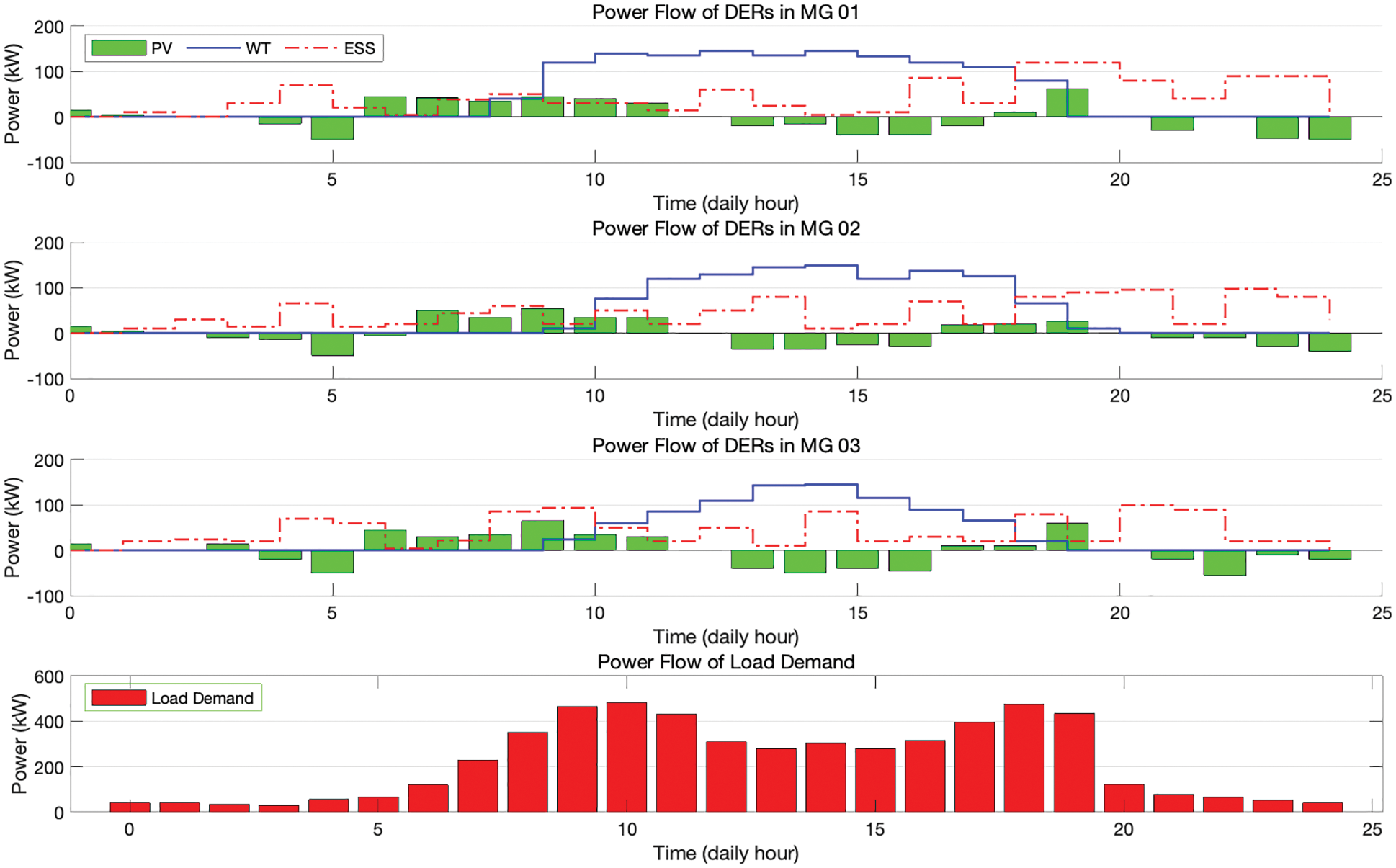
Figure 5: Power flow of DERs of MGs only without the EMS; (a) MG1, (b) MG2, (c) MG3

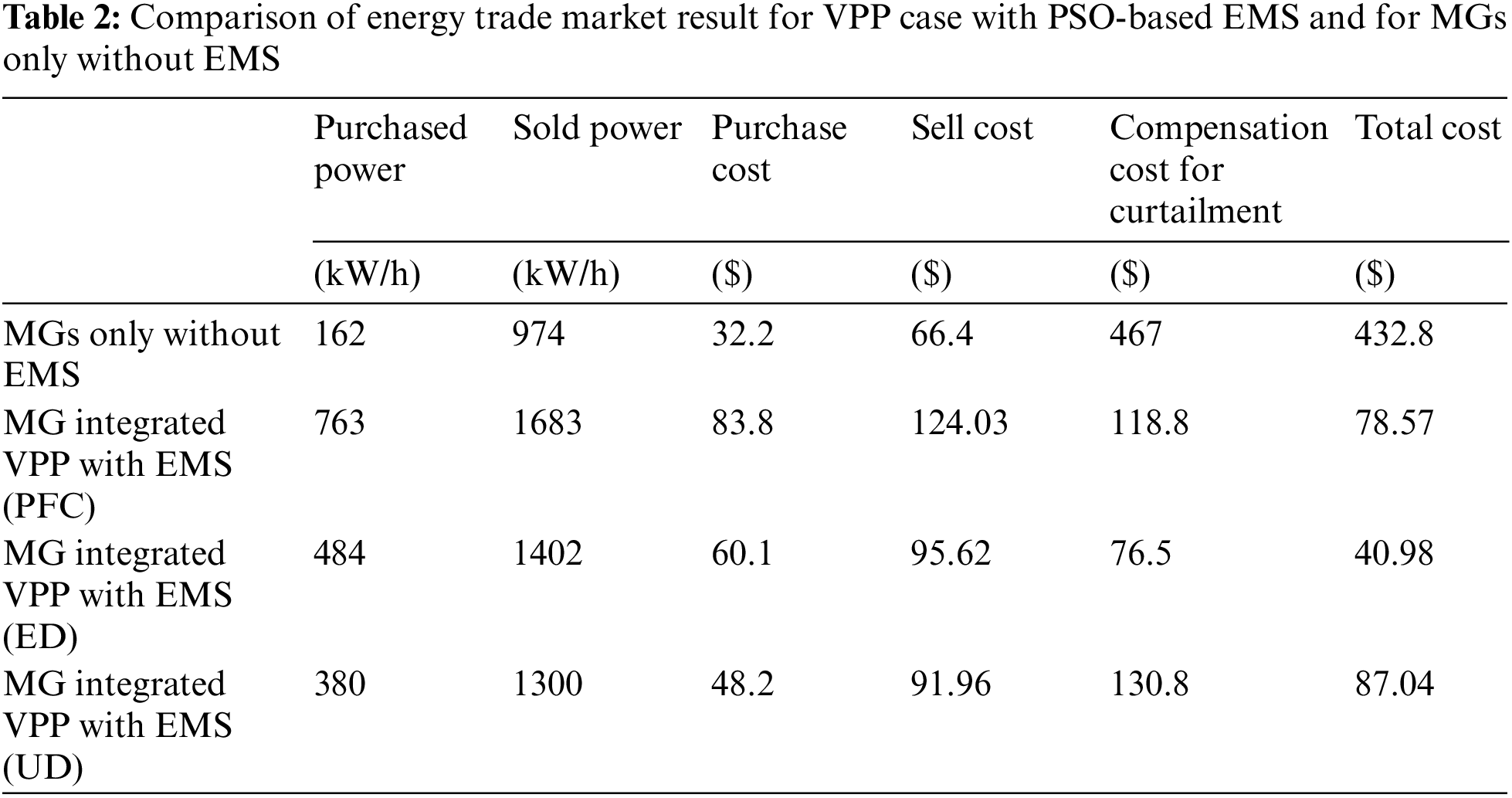
Fig. 6 shows the results of purchasing/selling power from/to the grid in case of VPP with the PSO-based EMS employing different offering strategies (PFC, ED and UC) and that of MGs only without EMS. It is presented that the case of VPP with PSO-based EMS follows the economic strategy which estimates the energy market trend of day time and decides the selling/purchasing time appropriately. Table 2 shows that the overall operating cost of MG integrated VPP with EMS employing the egalitarian re-distribution (ED) is much lower than that of MGs only without EMS, which is mainly resulted from the adoption of EMS optimization and active power offering strategy.

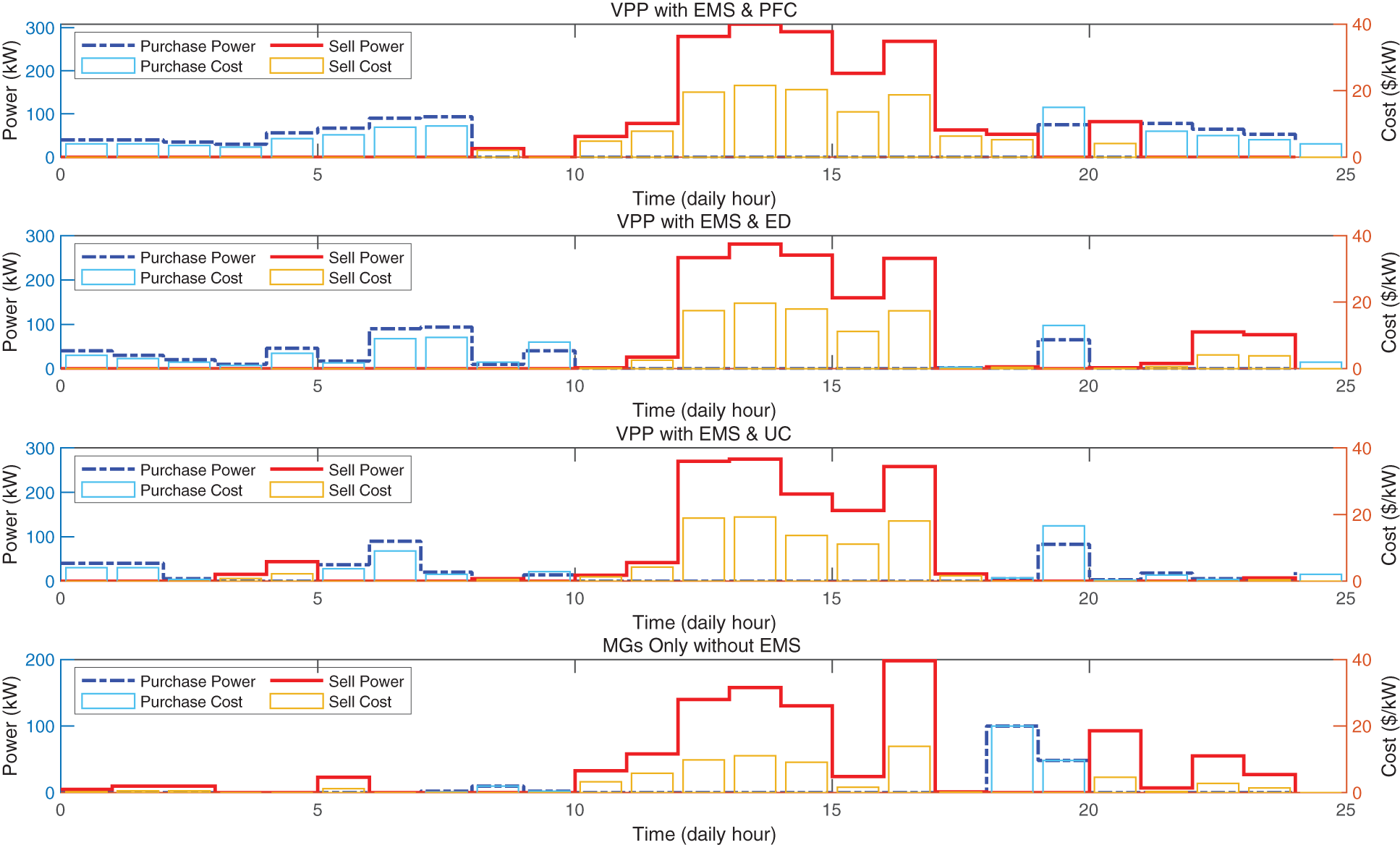
Figure 6: Purchasing power and selling power from/to the grid of VPP with PSO-based EMS employing different offering strategy and those of MGs only without EMS

The overall cost of VPP with PFC and UD offering strategies are slightly higher than that of VPP with ED, since the ED is most suitable for limiting the over-generated power. The reason why the ED power redistribution strategy outperforms the other two strategies could be found in Eq. (16). It is noted that the ED strategy is suitable for the limited power control case. From the obtained results, it is concluded that all MGs in VPP are managed to purchase/sell the power from/to the power grid compliant with the objective function, minw∑t=1T[S(w,t)+ℰ~(t)] as defined in Eq. (19).

Fig. 7 shows the total re-generated power by all the DERs and the actually offered power by either VPP or MGs only. In case of VPP with PSO-based EMS and ED offering strategy, all the generated power is not used to supply the load demand and it is managed by the optimized decision of EMS by curtailing those generated power according to the total operating cost or purchasing the power. The actual-offered power (blue solid line in Fig. 7) of VPP with EMS is higher than the available power (blue dotted line in Fig. 7) during 12:00~16:00 period, and surplus power is sold to the main grid. It is noted that the MG integrated VPP with EMS sell more power than that of MGs only case and purchase more power during the energy shortage period, i.e., off-peak time, because it is beneficial from the operating cost point of view.

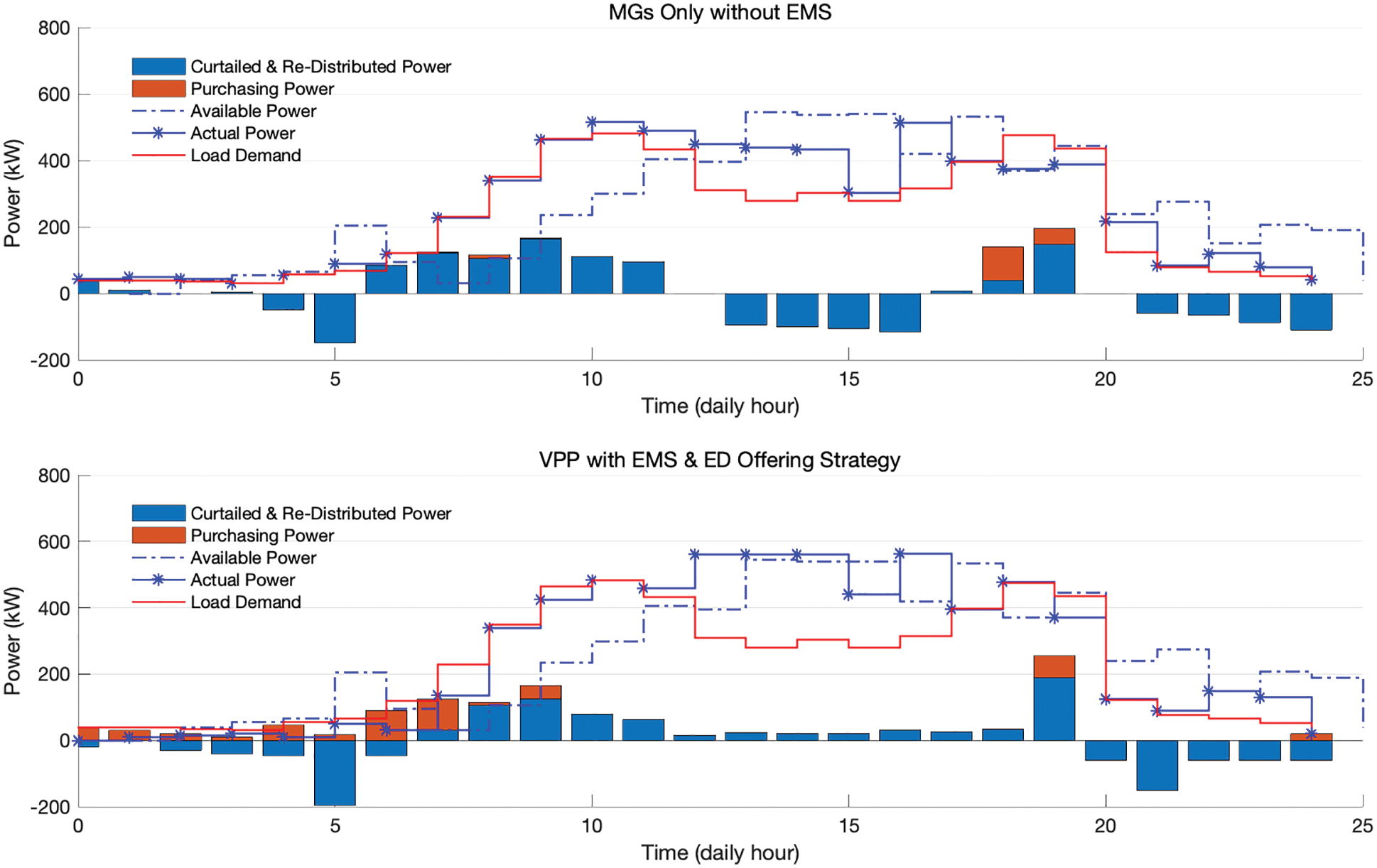
Figure 7: Actual-offered power and re-generated power flow of MGs only without EMS and those of VPP with PSO-based EMS employing the egalitarian re-distribution (ED) offering strategy

5  Conclusion

This paper presents the development of a new nature-inspired algorithm (PSO)-based EMS for the proposed MG integrated VPP model employing the proposed power offering strategy combined with the active power control, which is offered to maximize the overall operating cost of the VPP model. As an optimal scheduling controller of disperse DERs, PV, WT, and ESS, belonged to MGs in VPP, the PSO-based EMS plays a very decisive role in increasing the profit in the energy market for those involved DERs and in mitigating the power fluctuation and unbalance in power profile, by virtue of the proposed power offering strategy. With the optimized energy scheduling and the active power offering technique, the proposed MG integrated VPP model outperforms the conventional MGs only network model in the context of the overall cost and profit.

Simulation results show that the proposed VPP model with EMS could offer the efficient management of power flow and the curtailment/re-distribution of power control. The active power curtailment of DERs is carried out by the optimized decision of EMS with the active power offering strategy, which is not mainly based on the load demand condition but on the objective function, i.e., to minimize the overall cost and the power fluctuation. It is shown that the generated power by DERs of each MGs integrated into VPP in the off-peak time operation is managed to be curtailed by the optimized EMS’s decision. From the total operating cost comparison results of EMS employing three power offering strategies, the cost of PSO-based EMS employing ED is 40.98$, which is much lower than 432.8$ of MGs only without EMS. Thus, the PSO-based EMS with ED offering strategy is most suitable for limiting the over-generated power. Therefore, it is concluded that all the generated power of DERs is curtailed and managed by the optimized decision of EMS mainly based on the minimization of operating cost. It is inferred that the MG integrated VPP model with the proposed PSO-based EMS employing power offering strategies is a sufficient feasible option of providing the satisfactory energy services to all compositions of VPP.

Funding Statement: This research was supported by Research Funds of Mokpo National University in 2021.

Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.

References

    1. E. spina, J. Llanos, C. Burgos-Mellado, R. Cardenas-Dobson, M. Martinez-Gomez et al., “Distributed control strategies for microgrids: An overview,” IEEE Access, vol. 8, pp. 193412–193448, 2020. [Google Scholar]

    2. H. M. Rouzbahani, H. Karimipour and L. Lei, “A review on virtual power plant for energy management,” Sustainable Energy Technologies and Assessments, vol. 47, no. 11, pp. 101370, 2021. [Google Scholar]

    3. L. Baringo and M. Rahimiyan, Virtual power plants and electricity markets: Decision making under uncertainty. Switzerland AG: Springer Nature (e-Bookpp. 9–37, 2020. [Google Scholar]

    4. M. Rahimiyan and L. Baringo, “Strategic bidding for a virtual power plant in the day-ahead and real-time markets: A price-taker robust optimization approach,” IEEE Transaction on Power System, vol. 31, no. 4, pp. 2676–2687, 2016. [Google Scholar]

    5. M. Freire-Lizcano, L. Baringo and R. García-Bertrand, “Offering strategy of a price-maker virtual power plant,” in Proc. 2019 Int. Conf. on Smart Energy Systems and Technologies (SEST), Porto, Portugal, pp. 1–6, 2019. [Google Scholar]

    6. M. Pasetti, S. Rinaldi and D. Manerba, “A virtual power plant architecture for the demand-side management of smart prosumers,” Applied Sciences, vol. 3, no. 3, pp. 432, 2018. [Google Scholar]

    7. R. Khan, N. Islam, S. K. Das, S. M. Muyeen, S. I. Moyeen et al., “Energy sustainability-Survey on technology and control of microgrid, smart grid and virtual power plant,” IEEE Access, vol. 9, pp. 104663–104694, 2021. [Google Scholar]

    8. E. Ghiani, A. Serpi, V. Pilloni, G. Sias, M. Simone et al., “A multidisciplinary approach for the development of smart distribution networks,” Energies, vol. 11, no. 10, pp. 2530, 2018. [Google Scholar]

    9. D. Arcos-Aviles, D. Pacheco, D. Pereira, G. Garcia-Gutierrez, E. V. Carrera et al., “A comparison of fuzzy-based energy management systems adjusted by nature-inspired algorithms,” Applied Sciences, vol. 11, no. 4, pp. 1663, 2021. [Google Scholar]

  10. S. Yu, F. Fang, Y. Liu and J. Liu, “Uncertainties of virtual power plant: Problems and countermeasures,” Applied Energy, vol. 239, no. 7, pp. 454–470, 2019. [Google Scholar]

  11. S. Alyami, Y. Wang, C. Wang, J. Zhao and B. Zhao, “Adaptive real power capping method for fair overvoltage regulation of distribution networks with high penetration of PV systems,” IEEE Transaction on Smart Grid, vol. 5, no. 6, pp. 2729–2738, 2014. [Google Scholar]

  12. M. Liu, A. Procopiou, K. Petrou, L. Ochoa, T. Langstaff et al., “On the fairness of PV curtailment schemes in residential distribution networks,” IEEE Transaction on Smart Grid, vol. 11, no. 5, pp. 4502–4512, 2020. [Google Scholar]

  13. P. Lusis, L. L. H. Andrew, S. Chakraborty, A. Liebman and G. Tack, “Reducing the unfairness of coordinated inverter dispatch in PV-rich distribution networks,” in Proc. 2019 IEEE Milan PowerTech, Milan, Italy, pp. 1–6, 2019. [Google Scholar]

  14. D. Gebbran, S. Mhanna, Y. Ma, A. C. Chapman and G. Verbič, “Fair coordination of distributed energy resources with Volt-Var control and PV curtailment,” Applied Energy, vol. 286, no. 6, pp. 116546, 2021. [Google Scholar]

  15. A. Baringo, L. Baringo and J. M. Arroyo, “Day-ahead self scheduling of a virtual power plant in energy and reserve electricity markets under uncertainty,” IEEE Transaction on Power System, vol. 34, no. 3, pp. 1881–1894, 2019. [Google Scholar]

  16. A. J. Conejo, M. Carrión and J. M. Morales,“ Decision making under uncertainty in electricity Markets,” in: International Series in Operations Research and Management Science, vol. 1, New York Publisher: Springer, pp. 376–384, 2010. [Google Scholar]

  17. S. K. Jauhar and M. Pant, “Genetic algorithms, a nature-inspired tool: Review of applications in supply chain management,” in Proc. Fourth Int. Conf. on Soft Computing for Problem Solving, New Delhi, India, pp. 71–86, 2015. [Google Scholar]

  18. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. ICMM’95-Int. Conf. on Neural Networks, Piscataway, NJ, USA, pp. 1942–1948, 1995. [Google Scholar]

  19. A. Esmat, A. Magdy, W. ElKhattam, A. M. Elbaklym and A. Magdy, “A novel energy management system using ant colony optimization for micro-grids,” in Proc. The 3rd Int. Conf. on Electric Power and Energy Conversion Systems, Istanbul, Turkey, pp. 1–6, 2013. [Google Scholar]

  20. X. Yang, “Nature-inspired optimization algorithms,” in Academic Press, Elsevier Publisher, pp. 15–64, 2020. [Google Scholar]

  21. B. Dey, K. Shivam and B. Bhattacharyya, “Energy management of various microgrid test systems using swarm evolutionary algorithms,” in Distributed Energy Resources in Microgrids, London, UK: Elsevier, pp. 323–341, 2019. [Google Scholar]

  22. M. A. Hannan, M. G. M. Abdolrasol, M. Faisal, P. J. Ker, R. A. Begum et al., “Binary particle swarm optimization for scheduling MG integrated virtual power plant toward energy saving,” IEEE Access, vol. 7, pp. 107937–107951, 2019. [Google Scholar]

  23. G. Zhang, C. Jiang and X. Wang, “Comprehensive review on structure and operation of virtual power plant in electrical system,” IET Generation, Transmission & Distribution, vol. 13, no. 2, pp. 145–156, 2019. [Google Scholar]

  24. V. Mohan, J. G. Singh, W. Ongsakul and M. P. R. Suresh, “Performance enhancement of online energy scheduling in a radial utility distribution microgrid,” International Journal Electrical Power Energy System, vol. 79, no. Part 1, pp. 98–107, 2016. [Google Scholar]

  25. A. Sangwongwanich, Y. Yang and F. Blaabjerg, “Development of flexible active power control strategies for grid-connected photovoltaic inverters by modifying MPPT algorithms,” in Proc. 2017 IEEE 3rd Int. Future Energy Electronics Conf. and ECCE Asia (IFEEC 2017-ECCE Asia), Kaohsiung, Taiwan, pp. 87–92, 2017. [Google Scholar]