 Open Access
Open Access
ARTICLE
Optimal Strategies Trajectory with Multi-Local-Worlds Graph
1 School of Electronics and Information Engineering, Taizhou University, Taizhou, Zhejiang, 318000, China
2 China Industrial Control Systems Cyber Emergency Response Team, Beijing, 100040, China
3 School of Economics and Management, Weifang University of Science and Technology, Shouguang, Shandong, 262700, China
4 National Computer System Engineering Research Institute of China, Beijing, 102699, China
5 Department of Computer Science and Information Engineering, Asia University, Taiwan, Taichung, 413, China
6 Research and Innovation Department, Skyline University College, Sharjah, P.O. Box 1797, United Arab Emirates
7 Staffordshire University, Stoke-on-Trent, ST4 2DE, UK
* Corresponding Author: Xiaojing Zheng. Email:
Computers, Materials & Continua 2023, 75(1), 2079-2099. https://doi.org/10.32604/cmc.2023.034118
Received 06 July 2022; Accepted 14 December 2022; Issue published 06 February 2023
Abstract
This paper constructs a non-cooperative/cooperative stochastic differential game model to prove that the optimal strategies trajectory of agents in a system with a topological configuration of a Multi-Local-World graph would converge into a certain attractor if the system’s configuration is fixed. Due to the economics and management property, almost all systems are divided into several independent Local-Worlds, and the interaction between agents in the system is more complex. The interaction between agents in the same Local-World is defined as a stochastic differential cooperative game; conversely, the interaction between agents in different Local-Worlds is defined as a stochastic differential non-cooperative game. We construct a non-cooperative/cooperative stochastic differential game model to describe the interaction between agents. The solutions of the cooperative and non-cooperative games are obtained by invoking corresponding theories, and then a nonlinear operator is constructed to couple these two solutions together. At last, the optimal strategies trajectory of agents in the system is proven to converge into a certain attractor, which means that strategies trajectory are certainty as time tends to infinity or a large positive integer. It is concluded that the optimal strategy trajectory with a nonlinear operator of cooperative/non-cooperative stochastic differential game between agents can make agents in a certain Local-World coordinate and make the Local-World payment maximize, and can make the all Local-Worlds equilibrated; furthermore, the optimal strategy of the coupled game can converge into a particular attractor that decides the optimal property.Keywords
In the last 20 years, the theoretic study of complex adaptive systems has become a significant field. A broad range of complex adaptive systems has been studied, from abstract ones, such as the evolution of the economic system and the criticality of the complex adaptive system, to physical systems, such as city traffic designing and management decisions. These all have in common the property one cannot hope to explain their detailed structures, properties, and functions exactly from a mathematical viewpoint. By the 2010s, there were rich theories of stochastic differential games describing agent’s behavior of interacting coupled with the optimal strategies in a transitory deterministic structure, and there have been many random complex networks models describe the evolutionary law under specific logical rules in various fields, which makes complex adaptive system studying colorfully. These two problems are essential due to this management complex adaptive system.
On the one hand, Hachijo et al. [1] studied the agent’s interaction with others according to a Boolean game in random complex networks. Lera et al. [2] and Li et al. [3], on the other hand, reported that the agent interact with others according to certain games, such as a stochastic differential game, which has been studied by Javarone [4], Mcavoy et al. [5], Gächter et al. [6]. However, few scientific research results indicate that if these two problems are combined, the existing research cannot support the making-decision process in reality.
Suppose that the system configuration is a fixed graph; the interaction between agents happens in a certain Multi-Local-World graph. Invoke Hypothesis 1–2 specified in the following Section, the interaction between agents can be thought of as two categories: a cooperative game between homogenous agents in the same Local-World and a non-cooperative game between in-homogenous agents in different Local-Worlds. According to the theory of emergence, an exclusive phenomenon of the complex adaptive system of the non-cooperative game between agents in different Local-Worlds can be coarsened in size to the non-cooperative game
The most important thing to this problem should be not only the existence of a solution to the optimal strategy but also the property of the optimal strategy and the stability of the solution. However, several questions perplex us: all agents in this system are always partially intelligent, partially autonomous, and partial society. They interact with others according to the interactive rules of both cooperative and non-cooperative games. So, getting the corresponding optimal strategies is the most important and difficult thing due to these two mixed interactions. According to theories of operational research and game theory, for an arbitrary Super-Agent, the payoff coupled with a non-cooperative game with other Super-Agents always is not identical to the payoff coupled with the optimal problem that is the first process of the cooperative game to other Agents, even if the same strategy is considered. So, how to make up for this difference must be our purpose. As well known, whether the imputation mechanism designed is rational or not decides whether the solution is stable or not. To resolve this problem, an adjusted dynamical Shapley is constructed; whether the adjusted dynamical Shapley vector can make the solution stable or not is what we focus on if non-cooperative/cooperative games are considered together.
As far as this complex adaptive system coupled with those gaps introduced above is considered, a non-cooperative/cooperative stochastic differential game model for the agent’s dynamical, intelligent and social properties has been constructed. The corresponding solutions respective to these two models are obtained by invoking classic analytic methods and processes. At last, a nonlinear operator is constructed to pair the Nash strategies with Pareto strategies together so that each agent in the system can select its optimal strategies under certain conditions. Because of optimal dynamic optimal strategies, this complex adaptive system synchronizes locally but not globally, making this system more stable to operate and more innovative to fit for change. To ensure that the optimal strategies are stable and can converge into a certain attractor, an adjusted Shapley vector is introduced in the payoff distribution procedure to make all agents more rational and dynamically stable over a long period. The details of the model are specified in the next section. This paper considers a coexisting game of the stochastic differential cooperative game and stochastic differential non-cooperative game, which is more close to reality; furthermore, we design a rational payment distribution mechanism driven by an adjusted dynamical Shapley value, which is proven to be much more stable under certain conditions. These two innovations make this paper more interesting.
Following a complex adaptive system for Agent behavior and local topological configuration co-evolving, let’s consider.
Definition 1.
(1) Topological space
(2)
(3) A realization
(4) The interaction law of agents can be proposed based on following hypotheses:
Hypothesis 1. Several different Local-Worlds are large enough such that there are sufficient agents interact with the others within this Local-World, and who are small enough such that there exist sufficient Local-Worlds interact with others in this system.
Hypothesis 2. In a short time scale, each agent interacts with the others who are in the same Local World can be defined as a cooperative game, i.e., all agents pursue the maximized profit of the Local-World first, then distribute the system profit rationally. Each Local World interacts with the others according to the rule of a non-cooperative game such that the system is equilibrated. On a long time scale, the behaviors and configuration of the system can be converted into a certain attractor.
Due to this paper’s limited space and the process’s complexity, just 2-levels of the system are analyzed as an example. If the system’s levels are larger than or equal to 3, the results can be linearly extended directly. According to the property defined in Hypothesis 1 and 2, the system configuration can be described as Fig. 1.
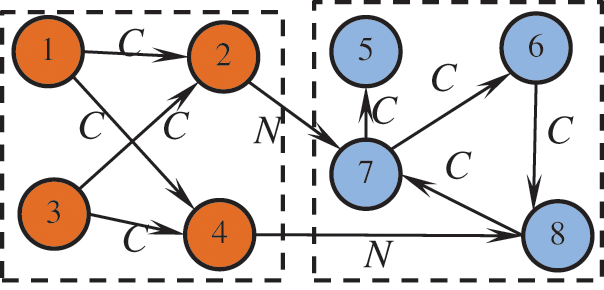
Figure 1: Interaction between agents in the dynamic topology of the complex adaptive system
Fig. 1 describes the dynamic property of the complex adaptive system with co-evolving behavior and local configuration. Where C represents “Cooperation games” happen in agents and N represents “Non-cooperation games” happen in agents. There are two local-worlds in this system. Suppose that an arbitrary agent should not pursue maximizing the current payoff. However, the payoff is maximized in a specific time scale, which means that an agent can give up the transitory benefit but the total payoff in the corresponding time scale—they think the payment is decided by a certain integral of the transitory objectivity function at a continuous time. Furthermore, the agent’s behavior is limited by the corresponding resource that is described as a stochastic dynamics equation such that agents’ objectivity will be changed synchronized, which should be described by a certain discount function
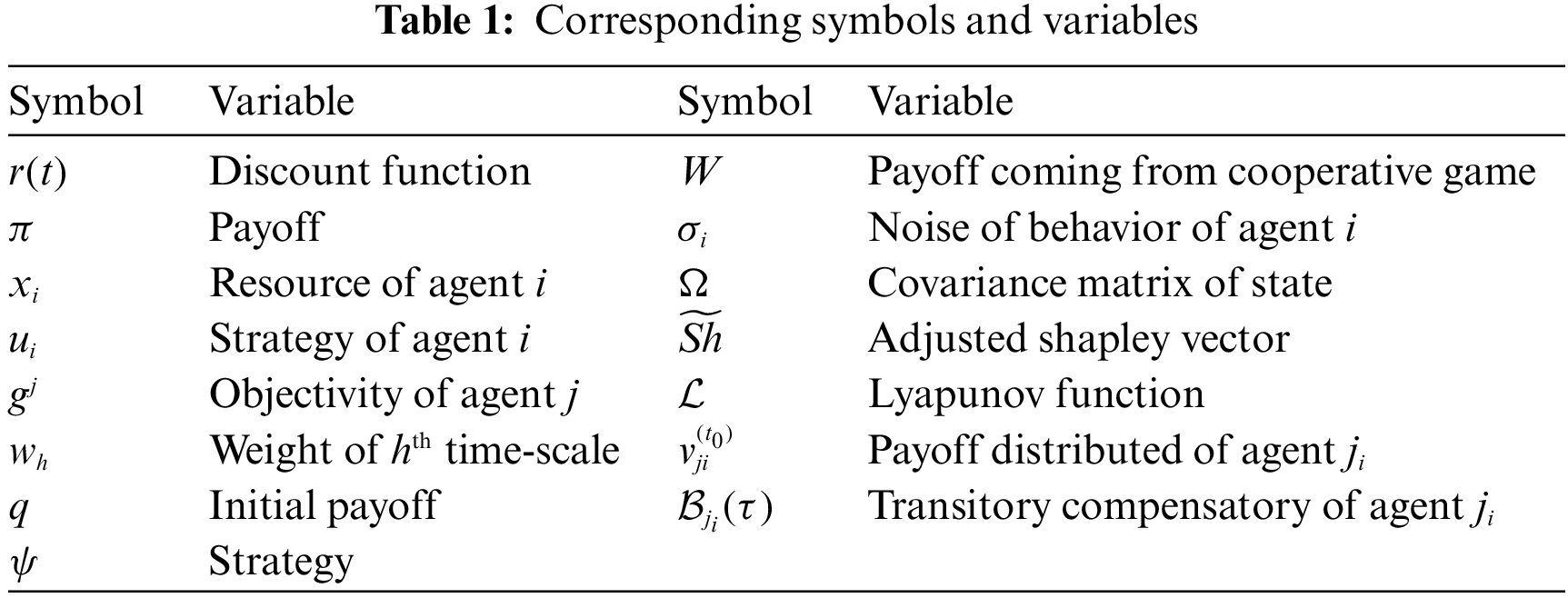
Firstly, some symbols and variables appeared in this paper should be listed in Table 1.
Suppose that there are m Local-Worlds in the system, denoted by Super-Agent i, and the
As well known, the property of a complex adaptive system of economy and management is random time-varying. In this paper, according to the economic and management system’s property, three different systems with the statistical property of agents’ behaviors, homogeneous exponent distribution, inhomogeneous exponent distribution, and Lévy distribution, are studied respectively, which should be shown as follow.
To analyze this problem effectively, we consider the Super-Agent’s behavior. For arbitrary Super-Agent, its state dynamics are characterized by the set of vector-valued differential equations
And the corresponding objectivities are
where,
describe three behaviors driven by the discount functions with homogeneous exponential distribution, inhomogeneous exponent distribution, and Lévy distribution, respectively.
Similarly, as for an arbitrary agent
where,
The set of vector-valued differential equations characterizes the state dynamics of Agent
Similarly, the state dynamics for inhomogeneous exponent distribution and Lévy distribution of agent
respectively. To simplify this problem, we consider the cooperative game between arbitrary Agents
Historical strategies and local topological configuration determine agents’ payoffs. When an agent
Invoke the models mentioned above, and it is easy to know: it is not only the payoff maximized should be considered, but also the optimal payoff should be maintained stably in a much longer time scale, which means that agents must give up the short-period objectivity to pursue to the long-period objectivity once these two different objects conflict. Furthermore, the optimal strategy would change as the environment changing, which the random dynamics and objectivity can reflect. It is easy to know that each agent would adapt to his current and historical state, the stats of other agents that interact with him, and the environment by using different strategies; when an agent makes a decision, he does consider not only the current state of the system but also the historic states coupling with the evolutionary property, which is important. An arbitrary agent in this complex adaptive system is intelligent because an arbitrary agent in this complex system can make a decision and update strategy relying on its historical states and other agents’ strategies that interact directly. When an agent decides, it must forecast the future state to keep the strategies from making mistakes. The future state can be obtained from the corresponding trend term of the state equation constrained. However, because of the floating term in the behavior dynamics equation, the future state cannot be forecasted precisely. So, the strategies of an arbitrary agent should be set to an adaptable interval to make up the wrong or incorrect decision, which makes the agent autonomous.
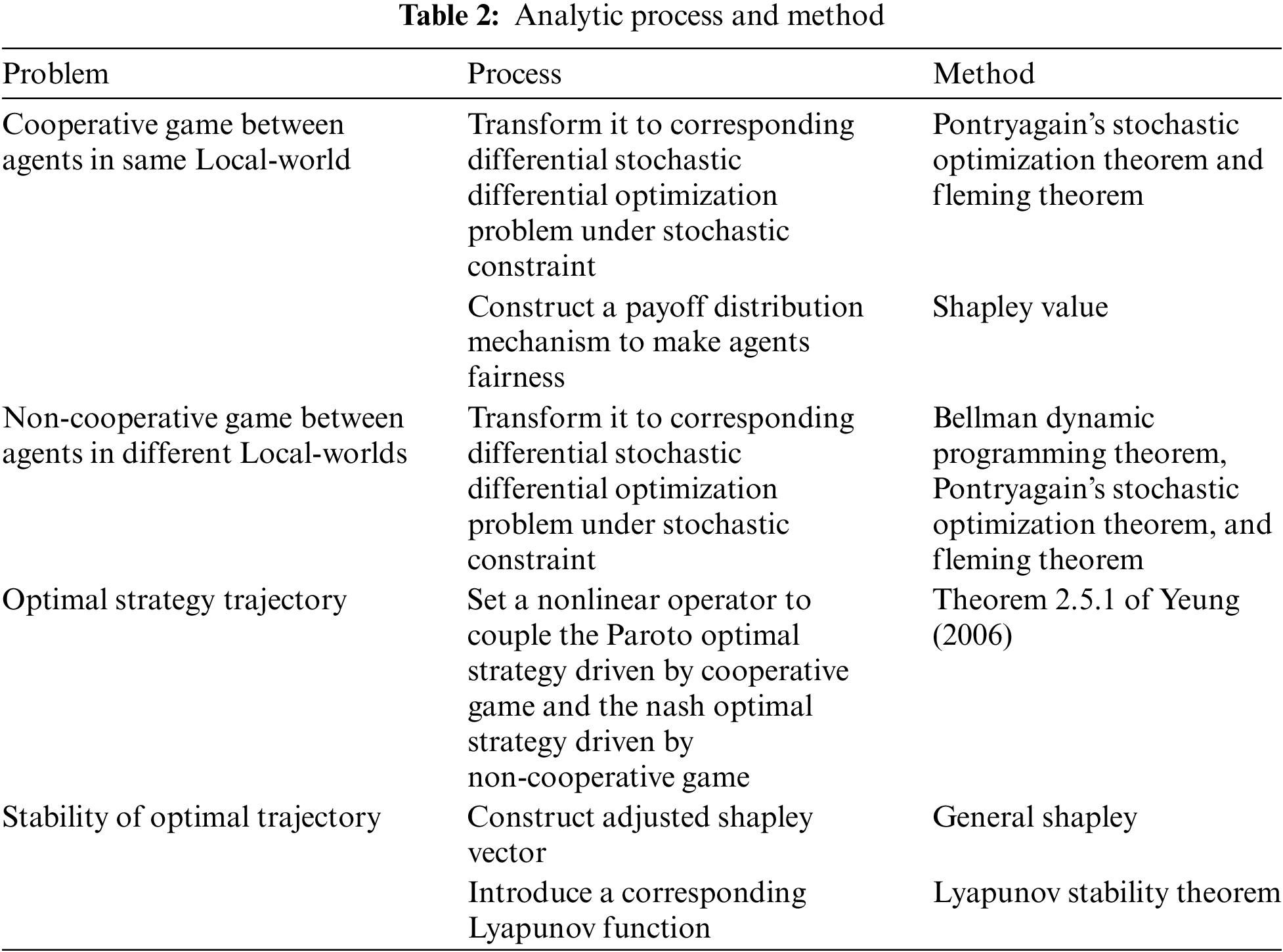
According to (1) and (2), an arbitrary super-agent interacts with others, which is a non-cooperative game. Similar, arbitrary agents interact with others in the same Local-World according to (4) and (5). The interaction is defined as a cooperative game. Considering the complexity, following analytic method should be invoked, as specified in Table 2.
There are two theorems would be given. When the system achieves equilibrium, the transitory payoff for an arbitrary agent in this complex adaptive system can be described as:
Theorem 1. For all
(1) The payoff of agent
(2) The payoff of agent
(3) The payoff of agent
However, it is clear from Theorem 1 that the optimal payoff of the agent
3.2 Transitory Compensatory of Arbitrary Agent
Theorem 2. On time
(1) The transitory compensatory agent
(2) The transitory compensatory agent
(3) The transitory compensatory agent
4 Behavior and the Equilibrium of the Agent in Multi-Local-Worlds Graph
4.1 The Cooperative Stochastic Differential Game Between Agents of Super-Agent
Regarding the cooperative stochastic differential game, two problems why an arbitrary agent will cooperate with others and how much it will get coupled with a certain optimal strategy must be considered. In this sense, the conflicts between coalition and individual rationality should be considered. Scientists insist that the essence of a cooperative stochastic differential game is to distribute the payoff between agents in the system after its profit is maximized. As mentioned above, two problems must be considered. The first is optimizing this system by invoking Bellman dynamic programming theorem, Pontryagain’s stochastic optimization theorem, and Fleming theorem, then transferring the optimal problem to a corresponding Hamilton-Jacobi-Isaacs equation, which has been resolved respectively by Chighoub et al. [10], Guo et al. [11], Gomoyunov [12]. The second one is constructing a payoff distribution procedure for all agents [13,14]. These papers discuss the properties and relationships among the kernel, the nucleolus, and the minimum core of the cooperative game. It is concluded that the Shapley value is a relatively feasible method for distributing the payoff among the agents in the system if coalition rationality constraint conditions and individual rationality constraint conditions are considered.
However, these conclusions lack analyzing of time-varied of the system, which makes the results far from reality. Furthermore, human behavior is very uncertain and cannot be recognized and take on the property of diversity, which means that every agent has different behaviors at a time, and he can select a strategy randomly, which makes the deterministic conclusions mentioned cannot fit for the real complex system and must be adjusted to satisfy this requirement. In this paper, we omit the diversity of the behavior and abstract them to a certain effort level. It means every agent’s behavior transfers the input to output by laboring and maximizing the output for a long time. In this sense, simplifying human behaviors is the most important thing one must study. This paper will analyze the system’s property according to this idea.
4.1.1 Payoff Maximized of the Sub-System
Because the first process is to optimize an arbitrary Local-World i, i.e., Super-Agent i and the corresponding optimal strategies can be expressed to a PDE, which has the following formation:
and
As far as the agent’s behavior of discount function with homogeneous exponential distribution is considered, this is the basic representation. If agent’s behavior satisfies the distribution function of in-homogenous exponential distribution and Lévy distribution, a similar representation will be copied except for the discount functions. So, it is concluded that the strategies are independent of the agent’s property if all agents have identical properties, i.e., all agents have the same distribution but have different parameters of the dynamics function. This result should be seen in Lemma 1 and the corresponding proof in Supplementary Material. Furthermore, the corresponding optimal strategies trajectory should be specified by Theorem 3 coupled with corresponding proofs in Supplementary Material for the discount function of the homogenous exponential distribution, Theorem 4, and Lemma 2, Lemma 3, Corollary 1 and Corollary 2 coupled with corresponding proofs in Supplementary Material for the discount function of the in-homogenous exponential distribution, and Corollary 3, Corollary 4 and Corollary 4 coupled with corresponding proofs in Supplementary Material for the discount function of Lévy distribution.
4.1.2 Dynamical Shapley Value for Distribution Coalition’s Payoff
Firstly, some necessary conditions should be introduced in this paper. As well known, an agent feels rational if the following conditions are all satisfied: (1) The sum of all agent’s payoff distributed must equal to the maximum payoff of this Local-World; (2) As far as each agent in this system is considered, the payoff distributed that he take part in the cooperation must be not less than the one that he does not take part in the cooperation. The former is called coalition rationality, and the latter is called an individual coalition. Many scientists provide a rational imputation payoff method, for example, Shapley value, to distribute payoff rationally between Agents in Super-Agent. It is proven right that dynamical Shapley has the property of joint stability and sub-game consistency [15]. In this sense, the agent’s payoff in arbitrary Local-World would be calculated, and so would the corresponding optimal strategies.
Condition 1: System rational constraint Dynamical Shapley value imputation vector
Satisfying,
(1)
(2)
Condition 2:
From these two conditions, it is easy to see that an arbitrary Agent feels rational if and only if the deviation among all possible payoffs is the least minimum.
It is concluded that the Shapley vector satisfies Condition 1 and Condition 2. According to the dynamical Shapley value and cooperative game theory, we can know the agent will take the strategy vector of
This kind of distribution fits the initial state but unfits for arbitrary time. The state is always changed dynamically, which makes the optimal strategies change randomly, too. Here, a dynamical imputation mechanism must be constructed to fit the real complex management system, i.e.,
where
The fairness of the concept is provided using the Theorem below.
Theorem 3. The transitory payoff distributed to the agent
where
The proof is finished by invoking Lemma 2 and Theorem 6 in Supplementary Material. The specification meaning should be seen in Remark 1 and Remark 2 in Supplementary Material. An example is given to specify this process in Zheng et al. [16], to explain the agent’s coordination strategy and effort level in the stochastic cooperative differential game framework. In fact, the rational payoff distributed and the corresponding compensatory is independent of the discount function; the distinction is in detail in the imputation process.
4.2 The Noncooperative Stochastic Differential Game Between Super-Agents
An Arbitrary Local-World is regarded as a Super-Agent, in this case, suppose that there are m Super-Agents in this system. According to Hypothesis 1–2, we can know, the interaction between these Super-Agents is a non-cooperative stochastic differential game
For an arbitrary Super-Agent i, its objective should be described as
The corresponding constraint equation should be:
There must exist a Nash equilibrium point for the system. Due to its complexity in resolving the optimal problem, another PDE is introduced to give the corresponding solution identical to the optimal strategy of the non-cooperative stochastic differential game.
Lemma 1. A set of controls
and
As far as other discount functions are considered, similar forms are reflected except for the discount function. The corresponding proof should invoke Lemma 3 and Corollary 3 in Supplementary Material.
4.3 Coupling Between the Noncooperative Game of Super-Agent and the Cooperative Game of Agent
So far, the optimal strategy coupled with a cooperative stochastic differential game between agents in a certain Local-World and the Nash optimal strategy coupled with a non-cooperative stochastic differential game between differential Local-Worlds has been obtained. However, there exists another paradox: the optimal strategy due to the cooperative stochastic differential game between Agents in a certain Super-Agent is not identical to the optimal strategy of the agent. This is because of complex interaction mixed as a Non-cooperative game and cooperative game, which means the most important research for obtaining the optimal strategy of the system is to find an algorithm to couple these two different optimal strategies together. According to Proposition 1, shown in Supplementary Material, it is evident that the optimal solution for the Cooperative game in Super-Agent is feasible. Let’s reconsider the essence of these two kinds of games. As far as the cooperative stochastic differential game between Agents in this Local-World is considered, the corresponding optimal strategy of arbitrary agents comes from a rationally distributed payoff. In fact, the total payoff comes from the non-cooperative stochastic differential game between Super-Agents.
So, it is the identical relationship between optimization and game theory shows that there is a mapping between the Nash optimal solution
According to the theory of calculus of variations, a nonlinear operator
Theorem 4. There must be a function
(1) As for the complex system of management with a discount function of the homogenous exponential distribution, we have
1)
2)
(2) As for the complex system of management with the discount function of the in-homogenous exponential distribution, we have
1)
2)
(3) As for the complex system of management with the discount function with Lévy distribution, we have
1)
2)
Theorem 4 couples the cooperative stochastic differential game between agents in an arbitrary Local-World and the non-cooperative stochastic differential game between Super-Agents. By invoking this result, the agent’s optimal strategy in the system must be obtained. The proof of Theorem 4 should invoke Proposition 1, Theorem 1, Theorem 5, and Theorem 6 in Supplementary Material.
5 The Stability of Agents’ Behaviour in Deterministic Multi-Local-World Graph
Section 4 shows us the Agent’s Nash-Pareto optimal solution of the complex system of management coupled with the game theory model in a Multi-Local-World graph. Scientists think the solution is stable if the optimal solution of a cooperative stochastic differential game is stable, which means the synchronism, coordination, and stability are all satisfied, which will be analyzed in this Section. However, stability must be discussed to promise the scientific character of the solution.
The stability of the cooperative stochastic differential game solution decides whether optimal equilibrium strategies are feasible or not. Intuitively, the stability of the solution of the corresponding Hamilton-Jacobi-Isaacs equation and the stability of the Shapley decide the stability of the optimal strategies. However, scientists have not yet discussed the attractor of these optimal strategies’ trajectory.
Definition 2. The following vector is the adjusted Shapley vector if
As for the sub-game
Introduce the adjusted Shapley vector compensatory program,
Obviously,
So,
The Nash-Pareto optimal solution of the cooperative stochastic differential game with the discount function of the homogenous exponential distribution is stable if the corresponding Shapley imputation and the corresponding compensatory mentioned in Theorem 4 and Theorem 5 in Supplementary Material are proven to be adjusted Shapley vectors, respectively. The detailed proof can be seen in Lemma 4 and Lemma 5, coupled with the proof in Supplementary Material. In this sense, the point of this problem is transferred to find the strong condition of this mapping.
We know that the dynamical distribution mechanism for payoff and the compensatory mechanism described describe the properties of three complex management systems, driven by agent behavior coupled with the homogeneous discount function of the exponential distribution
As for the first case, the payoff imputation is
and for
The corresponding compensatory is
The imputation is specified as
and for
By analyzing the above, it is evident that the imputation mechanism adjusted has the property of strong
6 The Attractor of Agents’ Behaviour in Deterministic Multi-Local-World Graph
Under the interaction between the agent and the external environment, the economic and management system constantly changes dynamically. If and only if Agent optimal strategy converges to a relatively constant value, the system tends to be stable and can be described as deterministic. Furthermore, if and only if the system state converges to a certain small region, the behavior strategy of each agent in the whole system will tend to a certain deterministic state, which will make the system converge to its attractor as defined by Definition 6 in Supplementary Material.
The convergence of system game results determines the state’s convergence in the process. If the system state equation
The convergence of a random differential game in a deterministic Multi-Local-World graph determines the property that each Agent behavior tends to a constant state in a relatively small time scale, which is proven by Lemma 6, Lemma 7, Lemma 8 and Theorem 8 coupled with corresponding proofs in Supplementary Material. If and only if the Agent behavior in the Multi-Local-World graph remains constant, external environment interference, internal non-leading factors, and fluctuations of those factors can make the innovation. Such innovation may lead to dynamic behaviors for Agent behavior, including creating new reactions with other agents in the same local domain and in different, breaking the relationship with other agents that have reacted with, eliminating by the system, creating new reaction relationships with new agents coming into the system. Those behaviors are the sources of system innovation. And then, the convergence analysis of Agent behavior in a relatively small time scale has very important value. Furthermore, such convergence is deterministic by constraint condition of Agent behavior describing the system characteristics (namely, the convergence of corresponding random differential equation of state dynamics equation). From such a Perspective, the problem will turn to attractor analysis of Eqs. (1) and (6).
The attractor of the equation is disused by introducing a corresponding Lyapunov function
For Eq. (18), we set
Suppose that
We can know there does exist some
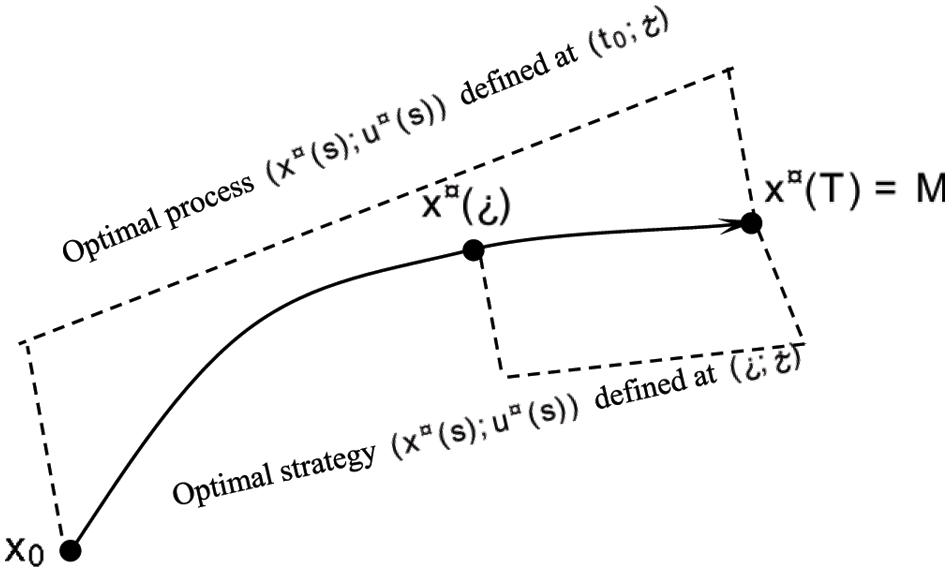
Figure 2: The property of the attractor of stochastic differential game
These optimal strategies are stable when some degree of disruptions are added sharply, as shown in Fig. 3.
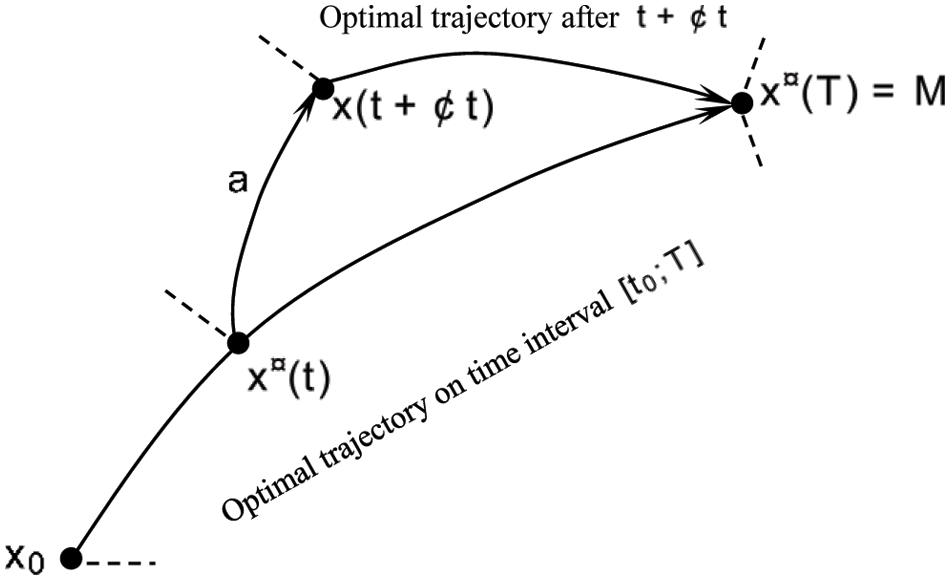
Figure 3: The property of attractor of the stochastic differential game when optimal strategy trajectory deviates
The optimal strategies strategy driven by adjusted Shapley value is more stable, as shown in Figs. 1 and 2. The proof is seen Sub-section in 6.2 and Appendix H in the Supplementary Material.
The interaction between Agents can be concluded with two kinds of stochastic differential games: cooperative and non-cooperative. The former happens between agents in the same Local-World. However, the latter happens between agents in different Local-World. Agent’s behavior is decided by two factors: the constraint condition driven by a stochastic dynamics equation on resources and the objectivity of payoff maximized within a specific time interval.
In this paper, three different behaviors with the discount function of the homogenous exponential distribution, in-homogenous exponential distribution, and Lévy distribution are analyzed, respectively. By analyzing, it is concluded that the optimal strategy according to the cooperative stochastic differential game in a certain Local-world and the non-cooperative stochastic differential game between different Local-worlds are obtained, respectively. The optimal strategy of a cooperative game is not consistent with the other. It is concluded that a nonlinear operator
where W is the agent’s optimal payoff coming from the cooperative stochastic differential game in a certain Local-World. The vector
The optimal strategy is described as a mapping of the optimal strategy of a cooperative game stochastic differential game, and the stability relies on the payoff distribution mechanism. In this paper, we construct an adjusted dynamical stochastic Shapley value
The adjusted dynamical stochastic Shapley payoff distribution procedure and the transitory payoff compensatory make the agent’s optimal strategy stable and sustained and make the Agents’ behavior such that the optimal strategy converge into a deterministic attractor.
Funding Statement: This paper is supported by the National Natural Science Foundation of China, (Grant Nos. 72174064, 71671054, and 61976064); the Natural Science Foundation of Shandong Province, “Dynamic Coordination Mechanism of the Fresh Agricultural Produce Supply Chain Driven by Customer Behavior from the Perspective of Quality Loss” (ZR2020MG004); and Industrial Internet Security Evaluation Service Project (TC210W09P).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. T. Hachijo, H. Gotoda, T. Nishizawa and J. Kazawa, “Early detection of cascade flutter in a model aircraft turbine using a methodology combining complex networks and synchronization,” Physical Review Applied, vol. 14, no. 1, pp. 14093, 2020. [Google Scholar]
2. S. C. Lera, A. Pentland and D. Sornette, “Prediction and prevention of disproportionally dominant agents in complex networks,” Proceedings of the National Academy of Sciences, vol. 117, no. 44, pp. 27090–27095, 2020. [Google Scholar]
3. A. Li, L. Zhou, Q. Su, S. P. Cornelius, Y. Liu et al., “Evolution of cooperation on temporal networks,” Nature Communications, vol. 11, no. 1, pp. 1–9, 2020. [Google Scholar]
4. M. A. Javarone, “Poker as a skill game: Rational versus irrational behaviors,” Journal of Statistical Mechanics: Theory and Experiment, vol. 2015, no. 3, pp. P3018, 2015. [Google Scholar]
5. A. Mcavoy, B. Allen and M. A. Nowak, “Social goods dilemmas in heterogeneous societies,” Nature Human Behaviour, vol. 4, no. 8, pp. 819–831, 2020. [Google Scholar]
6. S. Gächter, B. Herrmann and C. Thöni, “Culture and cooperation,” Philosophical Transactions of the Royal Society B: Biological Sciences, vol. 365, no. 1553, pp. 2651–2661, 2010. [Google Scholar]
7. A. J. Calvert, K. Ramachandran, H. Kao and M. A. Fisher, “Local thickening of the cascadia forearc crust and the origin of seismic reflectors in the uppermost mantle,” Tectonophysics, vol. 420, no. 1–2, pp. 175–188, 2006. [Google Scholar]
8. T. L. Friesz and K. Han, “The mathematical foundations of dynamic user equilibrium,” Transportation Research Part B-Methodological, vol. 126, pp. 309–328, 2019. [Google Scholar]
9. P. L. Querini, O. Chiotti and E. Fernádez, “Cooperative energy management system for networked microgrids,” Sustainable Energy Grids and Networks, vol. 23, pp. 100371, 2020. [Google Scholar]
10. F. Chighoub and B. Mezerdi, “The relationship between the stochastic maximum principle and the dynamic programming in singular control of jump diffusions,” International Journal of Stochastic Analysis, vol. 2014, pp. 1–17, 2014. [Google Scholar]
11. L. Guo and J. J. Ye, “Necessary optimality conditions for optimal control problems with equilibrium constraints,” Siam Journal on Control and Optimization, vol. 54, no. 5, pp. 2710–2733, 2016. [Google Scholar]
12. M. I. Gomoyunov, “On viscosity solutions of path-dependent Hamilton–Jacobi–Bellman–Isaacs equations for fractional-order systems,” arXiv preprint arXiv:2109.02451, 2021. [Google Scholar]
13. G. Giallombardo, F. Guerriero and G. Miglionico, “Profit maximization via capacity control for distribution logistics problems,” arXiv preprint arXiv:2008.03216, 2020. [Google Scholar]
14. D. Kosz, “Dichotomy property for maximal operators in a nondoubling setting,” Bulletin of the Australian Mathematical Society, vol. 99, no. 3, pp. 454–466, 2019. [Google Scholar]
15. Y. Filmus, J. Oren and K. Soundararajan, “Shapley values in weighted voting games with random weights,” arXiv preprint arXiv:1601.06223, 2016. [Google Scholar]
16. X. J. Zheng, X. S. Xu and C. C. Luo, “Agent behaviors and coordinative mechanism,” Kybernetes, vol. 41, no. 10, pp. 1586–1603, 2012. [Google Scholar]
17. D. W. Yeung and L. A. Petrosjan, Cooperative Stochastic Differential Games, New York, USA: Springer Science & Business Media, pp. 1586–1603, 2006. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools