Attribute-Based Authentication Scheme from Partial Encryption for Lattice with Short Key

1  Introduction

There are many attributes-based authentication schemes proposed in protocols related to wireless networks and information security, such as references [1–4]. However, most of the proposed authentication and key agreement protocols for wireless networks are based on traditional cryptosystems such as large integer decomposition and elliptic curves. With the rapid development of quantum computing, these authentication protocols based on traditional cryptography will be more and more threatened. These attribute-based authentication schemes will not be secure in the post-quantum era. At present, the widely used anti-quantum cryptosystem is an anti-quantum algorithm based on lattice cryptosystem and coding-related problems. With the rapid development of quantum computer, the anti-quantum algorithm based on lattice cryptosystem will attract more researchers. For the related security protocols based on lattice cryptosystem [5–7], the anti-quantum performance of the protocols is based on the related difficult problems such as the shortest vector and learning with errors in a lattice-based cryptosystem. The authentication and key agreement protocol based on lattice cryptosystem can also resist various threats brought by quantum computers in the post-quantum era, and can ensure the security of wireless networks, which is a hot issue in anti-quantum algorithms [8–15]. The difficult problem of a lattice-based cryptosystem is that it plays a key role in information security in wireless networks in the future quantum era [16–18]. Based on the difficult problems of lattice-based cryptosystem, many fully homomorphic encryption schemes [19–24] and public-key encryption schemes [25–27] are presented.

In the past decade, many schemes of anti-quantum authentication and security protocols based on the difficult problems of lattice cryptosystem have been proposed [28–34]. In 2016, Bansarkhani et al. [5]. Based on lattice cryptosystem, a new anti-quantum authentication signature protocol is proposed, and the authentication protocol is applied to block chain security. In 2018, Behina et al. [35]. From the difficult problem of lattice-based cryptosystem, an effective key searchable security authentication scheme is proposed, the key searchable security authentication scheme uses a new strategy to search keywords such as keys. In 2019, Fukumitsu et al. [7]. Based on the difficulty of lattice cryptosystem, a secure and efficient authentication signature protocol is proposed, which is proved to be secure in the random model, which is a three-round scheme with the public key aggregation with the security proof, A group signatures scheme without NIZK (Non-Interactive Zero Knowledge) base on lattice was designed [36], but this group signatures scheme requires a combination of attribute-based encryption and signatures. Ma et al. [10]. Based on lattice cipher, an effective anti-quantum authentication signature protocol for blockchains is proposed, which is a four-round scheme with the key aggregation and Tso et al. [12]. An effective anti-quantum blind signature protocol based on attributes from lattices is proposed, which is the attribute-based signature. In 2020, Kansal et al. [9]. Based on the difficulty of lattice cryptosystem, an effective anti-quantum authentication signature scheme is proposed, which is a round optimal secure authentication scheme. In 2020, Sun et al. [37]. Proposed an effective anti-quantum lattice cipher group signature authentication protocol based on zero knowledge proofs. Canard et al. [38]. Proposed an anti-quantum group signature authentication protocol with secure data fixed length based on lattice cryptosystem. The protocol is proved to be secure under the standard model. In 2020, Doss et al. [39]. Proposed a secure and effective meme optimization method based on lattice public key cryptosystem, which is used to transmit important medical privacy information in block chain and the internet of things that can resist the key exchange. The application of the attribute-based authentication scheme also includes hierarchical electronic voting for multiple regions, robust reversible audio watermarking for telemedicine and privacy protection, and much more [40]. At present, many scholars are studying anti-quantum secure signature and authentication protocols based on lattice cryptosystem, such as the quantum-resistant batch verifiable data privacy security authentication protocol of VANETs (Vehicular Ad Hoc Networks) using lattice [8].

Hence, it is of great significance to construct a secure authentication protocol based on the difficult problem of lattice cryptosystem. In this paper, an effective attribute-based authentication protocol is proposed, which supports full homomorphic encryption of information. The length of the public-private key pair in this protocol is short, and the corresponding computational overhead is reduced.

2  Preliminaries

2.1 Lattice

The general definition in these lattices can be expressed as: randomly select a prime number qs≥2 and a matrix B∈Zqn×m. The specific definition is as follows:

Λqs⊥(B)={e∈Zm:B⋅e=0 mod qs}

Λqsu(B)={e∈Zm:B⋅e=u mod qs}

2.2 The LWE Problem

Definition 1 (LWE Problem [17]). Enter a random integer qs=q(n)≥2 and a random Gaussian distribution σs=σ(n) in the Zqs, the LWE problem is possible to distinguish the following different distributions:

(B,Bu+y)and(B,x)

where B←$Zqn×m,u←$Zqn,y←$χm,x←$Zqm.

Connection with lattices. Suppose C=C(m)∈N. Some Gaussian distributions σ=σ(m)m∈N is called C-bounded as follow:

Pr[σ∈{−C,⋯,C−1,C}]=1.

There is a C-bounded Gaussian distribution σ such that solving the LWE problem is as same hard as under the worst-case lattice problems to the factor in O~(m⋅qs/C) [17,18].

2.3 Lattice Algorithms

Lemma 1 ([31]) SampleLeft:

Randomly select the matrixes C in Zqn×m and D in Zqn×m1, select a grid base TC of Λq⊥(C), a short vector v∈Zqn, and the parameter β.

Suppose G:=(C||D). The algorithm SampleLeft(C,D,TD,v,β) outputs the short vector u∈Zm+m1 over ΛG+v.

Lemma 2 ([31]) SampleRight:

Randomly select the matrixes C in Zqn×k, H in Zqk×m and D in Zqn×m, select a grid base TD of Λq⊥(D), a short vector v∈Zqn, and the parameter β.

Suppose G:=(C||D). The algorithm SampleRight(C,D,TD,v,β) the short vector u∈Zm+k over ΛG+v.

Lemma 3 [29] EvalPK and EvalCT:

1.    EvalPK: Randomly select the matrixes A1,A2,⋯,Al,B1,B2,⋯,Bt∈Zqn×m, and select a formula fγ:{0,1}l×Zqt→Zq, the algorithm EvalPK calculates matrix Afγ∈Zqn×m.

2.    Evalct: Randomly select the matrixes A1,A2,⋯,Al,B1,B2,⋯,Bt∈Zqn×m, and select a formula fγ:{0,1}l×Zqt→Zq, due to the ID∈{0,1}l and some vectors u1,u2,⋯,ul,v1,v2,⋯,vt∈Zqm, the algorithm Evalct calculates the vector ufγ∈Zqm.

3  Attribute-Based Authentication Scheme

Based on the partial hidden predicate encryption protocol based on the difficult problem of lattice cryptosystem, a new attribute-based anti-quantum authentication protocol (ABAS) is proposed. The partial implicit predicate encryption protocol based on lattice cryptosystem used in this paper is effective and anti-quantum secure, the detailed process of the scheme is shown in [28,29]. An algorithm for generating two user communication keys is added to our attribute-based anti-quantum authentication protocol, which is based on a symmetric key of a symmetric cryptosystem, and the key length can be controlled by selecting different parameters through the generation algorithm. The attribute-based authentication scheme for a predicate universe C, a symmetric cryptosystem communication key space ksc, and there are five other algorithms (ABAS.Setup, ABAS.Enc, ABAS.Keygen, ABAS.Dec).

In the section, it is proposed that the public key, common parameter, and master key of all users are generated by the algorithm ABAS.Setup. Where Aij,Bij,Pij, i represent the i component, j represents the common parameter of the j user, and IDj represents the identity of the j user. The specific process is as follows:

ABAS.Setup(1λ,1t,1l,1d,1Q): Given as input the important parameters λ, t, d, the length l and private attributes t respectively. The algorithm ABAS.Setup outputs some parameters and the most important core key of our attribute-based anti-quantum authentication protocol, the specific process of the ABAS.Setup is as follows:

1.    Randomly select some important parameters (q,m,n,s,u,ρ,N):

n≥d′(k)1/ε

q=O~(tnd)O(d)

m=O(nlog⁡q)

s=(tnlog⁡q)O(d)

2.    Choose some important random matrices:

IDj∈{0,1}l,j=1,2,⋯,z

Aij∈Zqn×mfori=1,2,⋯,l,j=1,2,⋯,z

Bij∈Zqn×mfori=1,2,⋯,t,j=1,2,⋯,z

Pij∈Zqn×mfori=1,2,⋯,N,j=1,2,⋯,z

3.    Sampling matrix with algorithm TrapGen [30]: randomly select some important parameters (1m,1n,q), the algorithm TrapGen outputs the (A,TA).

4.    The algorithm outputs some parameters and the most important core key of the scheme:

ABAS.mpk=({Aij}i∈[l],j∈[z],{Bij}i∈[t],j∈[z],A,{Pij}i∈[N],j∈[z],{IDj}j∈[z]),

ABAS.msk=(TA)

The private key of the scheme for the user is generated using those public parameters generated above, where SKj represents the private key of the j user.

ABAS.Keygen(ABAS.msk,fγjj): Randomly select the circuit of the j user fγjj and the most important core key of our attribute-based anti-quantum authentication protocol, output the private key skfγjjj of the j-th user. The specific process of the algorithm ABAS.Keygen is as follows:

1.    Compute the parameter (Afγjjj)j∈[z] with algorithm EvalPK.

(Afγjjj)j∈[z]=EvalPK({Aij}i∈[l],j∈[z],{Bij}i∈[t],j∈[z],fγjj})

2.    Sample a random subset Δ⊂[N] with |Δ|=u, and respectively compute the sum of subset ΔPΔj=∑i∈ΔPij,j=1,2,⋯,z.

3.    Sampling the key with algorithm SampleLeft: [K1jK2j]←SampleLeft(A,Afγjjj+γjG,TA,PΔj,s) where s is a Gaussian parameter, and

[A|Afγjjj+γjG][K1jK2j]=PΔj.

4.    Let SKj=[K1jK2j], j=1,2,⋯,z, and output the private key skfγjjj of the j-th user skfγjjj=(Δ,SKj), j=1,2,⋯,z.

Take Alice and Bob as an example, Alice and Bob are necessary to authenticate each other before finally generating a symmetric key for communication, which is jointly generated by the Alice private attributes xa and Bob private attributes xb. The symmetric key authentication for communication is as follows: if Alice and the first user communicate for the first time, the partial communication key associated with Alice should be negotiated first. The partial communication key associated with the Alice negotiation process is as follows: assuming that Alice is the initiator of the communication, Alice first uses the hash algorithm H1 to generate the message ma associated with private attributes xa, and then encrypts the message ma using the public key of Bob, then sends the ciphertext cIDa to Bob. The specific negotiation process is as follows:

ABAS.Enc(ABAS.mpk,(xa,IDa),H1). The ABAS.Enc algorithm gets as input ABAS.mpk, xa∈{0,1}t, the identification IDa∈{0,1}l and the hash function H1, out the ciphertext cIDa. The specific process of the algorithm ABAS.Enc is as follows:

1.    Sample a Gaussian parameter s←DZn,sB, two Gaussian parameters e←DZm,sB, ek′←DZm,sD and k∈[N].

2.    Choose a security hash function H1:{0,1}∗→{v1:v1∈{0,1}τ1}.

3.    Compute the message ma associated with xa: ma=H1(xa)

4.    Select a parameter b, and set b=[0,0,⋯,0,⌈q/2⌉ma]T∈Zqm. Compute

β0=ATs+e

β1,k=PkTs+ek′+b,k∈[N]

5.    Random sampling t matrices Ri′←${−1,1}m×m, Where i=1,2,⋯,t, compute:

vi=(Bi+xiaG)Ts+(Ri′)Te

6.    Random sampling l matrices Ri←${−1,1}m×m, where i=1,2,⋯,l, compute:

ui=(Ai+IDiaG)Ts+(Ri)Te

7.    Finally, out the encrypted ciphertext cIDa:

cIDa=(H1,IDa,β0,{β1,k}k∈[N],{ui}i∈[l],{vi}i∈[t])

ABAS.Dec(skfγbb,cIDa). The ABAS.Dec algorithm inputs ciphertext cIDa, the public part of the attribute IDa and own secret key skfγbb, output the partial communication key associated with Alice. The specific process is:

1.    Based on these parameters (IDa,{ui},{vi}), use Evalct to compute ufγbb:

ufγbb=Evalct({Aij,ui}i∈[l],j∈[z],{Bij,vi}i∈[l],j∈[z],fγbb,IDa).

2.    Compute:

η=∑k∈[N]β1,k−SKb(β0ufγbb).

3.    If

[Rd(η[1]),Rd(η[2]),⋯,Rd(η[m−1])]=0,

Then set μ=Rd(η[m]) and output μ. Otherwise, termination ⊥.

4.   Compute the partial communication key associated with Alice: ma=μ.

The partial communication key associated with the Bob negotiation process is as follows: Alice uses the hash function H1 to generate the data mb associated with private attributes xb, and then encrypts the message mb with Bob’s public key, and then sends the ciphertext cIDb to Bob. Then, Bob can use the hash algorithm H2 to generate the symmetric key for communication kscab.The specific process is as follows:

ABAS.Enc(ABAS.mpk,(xb,IDb),H1,H2). The ABAS.Enc algorithm gets as input ABAS.mpk, the attributes xb∈{0,1}t, IDb∈{0,1}l and the hash function H1 and H2, output the ciphertext cIDb. The specific process is as follows:

1.    Sample a Gaussian parameter s←DZn,sB, two Gaussian parameters e←DZm,sB and ek′←DZm,sD, where k=1,2,⋯,N.

2.    Compute the message mb associated with xb: mb=H1(xb)

3.    Select a parameter b′, and set b′=[0,0,⋯,0,⌈q/2⌉mb]T∈Zqm. Compute:

β0=ATs+e

β1,k=PkTs+ek′+b′,k∈[N]

4.    Random sampling t matrices Ri′←${−1,1}m×m, where i=1,2,⋯,t, compute:

vi=(Bi+xibG)Ts+(Ri′)Te

5.    Random sampling l matrices Ri←${−1,1}m×m, where i=1,2,⋯,l, compute:

ui=(Ai+IDibG)Ts+(Ri)Te

6.    Choose a hash algorithm H2:{0,1}∗→{v2:v2∈{0,1}τ2}.

7.    Compute the symmetric communication key with Bob: kscab=H2(ma,mb)

8.    Out the ciphertext

cIDb=(H2,IDb,β0,{β1,k}k∈[N],{ui}i∈[l],{vi}i∈[t])

ABAS.Dec(skfγaa,cIDb). The ABAS.Dec algorithm gets as input the ciphertext cIDb, the attribute IDb, the secret key skfγaa, and the hash function H2, output the authentication symmetric key. The specific process is as follows:

1.    Using (IDb,{ui},{vi}), apply the Evalct algorithm to compute:

ufγaa=Evalct({Aij,ui}i∈[l],j∈[z],{Bij,vi}i∈[l],j∈[z],fγaa,IDb)

2.    Compute

η=∑k∈[N]β1,k−SKa(β0ufγaa)

3.    Round computes each datum of η. If

[Rd(η[1]),Rd(η[2]),⋯,Rd(η[m−1])]=0

Then set μ′=Rd(η[m]) and output μ′. Otherwise, termination ⊥.

4.   Compute the partial communication key associated with Bob: mb=μ′.

5.   Compute the symmetric communication key with Bob: (kscab)′=H2(ma,mb).

Finally, the whole attribute-based authentication Scheme is over, and Alice and Bob can communicate securely with the authentication symmetric key (kscab)′=kscab.

4  Analysis

4.1 Correctness

The correctness of Alice to Bob’s partial authentication in the ABAS follows from our choice of parameters. The specific process is as follows:

ufγbb=Evalct({Aij,ui}i∈[l],j∈[z],{Bij,vi}i∈[l],j∈[z],fγbb,IDa)

=(Afγbbb+fγbb(x,IDa)⋅G)T⋅s+eEval.

If fγbb(x,IDa)=γbmodq, then

(β0ufγbb)=(AT(Afγbbb+γb⋅G)T)⋅s+(eeEval).

Compute

(SKb)T⋅(β0ufγbb)=PΔb⋅s+(SKb)T⋅(eeEval),

∑k∈[N]β1,k−(SKb)T⋅(β0ufγbb)=b+∑k∈[N]ek′−(SKb)T⋅(eeEval).

If the first m−1 coordinates of ∑k∈[N]ek′−(SKb)T⋅(eeEval) are less than q/4, which means that the correctness of Alice to Bob’s partial authentication.

Otherwise, if fγbb(x,IDa)=γb∗≠γbmodq, then setting γb′=γb∗+γb for γb∗, so

η=∑k∈[N]β1,k−(SKb)T⋅(β0ufγbb)=b+γb∗⋅(SKb)T⋅G+e∗.

Therefore, with overwhelming probability from the No.1 to No.m−1 parameters of η are less than q/4.

The security of Bob to Alice’s other partial authentication in the ABAS is the same as above.

So, the symmetric communication key of Bob and Alice is:

kscab=H2(ma,mb)=(kscab)′.

4.2 Security

The specific process of the security of Alice to Bob’s partial authentication in the ABAS is as follows:

Proof. First, we describe the auxiliary evaluation algorithms of the proof.

ABAS.Setup1∗: The specific process is as follows:

1.    Sampling matrix with algorithm TrapGen [30]: randomly select some important parameters (1m,1n,q), the algorithm TrapGen outputs the (A,TA).

2.    Random sample l parameters Ri←${−1,1}m×m, compute Ai=ARi−IDibG∈Zqn×m, where i=1,2,⋯,l.

3.    Random sample t parameters Ri′←${−1,1}m×m, compute Bi=ARi′−xiG∈Zqn×m, where i=1,2,⋯,t.

4.    Random choose some subsets Δ1∗,Δ2∗,⋯Δi′,∗,⋯,ΔQ′∗ the size of each subset is v, which has the unique index, where i′=1,2,⋯,Q′.

5.    Sample some random matrices Pkb∈Zqn×m make them satisfied with PΔi∗b=∑k∈Δi∗Pkb, where i′=1,2,⋯,Q′ and k=1,2,⋯,N.

6.    Sample the private key SKi∗←(DZ2m,s)m and compute:

Pkb,∗=[A|Afγib,∗b,∗b,∗+γib,∗G][K1,ib,∗K2,ib,∗]=[A|ARfγib,∗b,∗b,∗][K1,ib,∗K2,ib,∗]∀i∈[Q′]

7.   Output necessary public key of our scheme as

ABAS.mpk=({Aib}i∈[l],{Bib}i∈[t],A,{Pib}i∈[N])

And the most important core key of our scheme as

ABAS.msk=(TA,{Rib}i∈[l],{Rib,′}i∈[t],{SKib,∗}i∈[N])

ABAS.Enc1∗: The specific process is as follows:

1.    Sample a Gaussian parameter s←DZn,sB, two Gaussian parameters e←DZm,sB and ek′′←DZm,sD, where k=1,2,⋯,N.

2.    Select a parameter b′, and set b=[0,0,⋯,0,⌈q/2⌉kab]T∈Zqm. Compute:

β0=ATs+e

β1,k=(SKkb)Tβ0+ek′′+b,k∈[N].

3.    Compute the ui:

ui=(Ri)Tβ0,where,i=1,2,⋯,l.

4.    Random sampling t matrices Ri←${−1,1}m×m, compute the vi:

vi=(Ri′)Tβ0,Where,i=1,2,⋯,t.

5.    Final output the encrypted ciphertext

(H,IDa,β0,{β1,k}k∈[N],{ui}i∈[l],{vi}i∈[t]).

ABAS.KeyGen1∗: The ABAS.KeyGen1∗ has a special function that will be marked if some public and private key pairs have been questioned before. The specific process is as follows:

1.    Compute the key corresponding to fγbb as:

Afγbb←EvalPK({Aib},{Bib},fγbb)

2.     We know that Afγbb=ARfγbb−⟨x,f^(IDb)⟩G. For different key query, the specific process is as follows:

1)   A fγbb such that fγbb(x,f^(IDb))=0. Then:

[A|Afγbbb+ρG]=[A|ARfγbb+(ρ−⟨x,f^(IDb)⟩)G].

Let

SK←SampleRight(A,(ρ−⟨x,f^(IDb)⟩).G,Rfγbb,TG,∑k∈[N]ΔkPΔk,s).

Therefore that:

[A|Afγbbb+ρG][K1bK2b]=∑k∈[N]ΔkPΔk

Return [K1bK2b].

2)   The fγib,∗b,∗, such that ⟨x,f^∗(IDb,∗)⟩=γib,∗, in which case, return [K1,ib,∗K2,ib,∗].

ABAS.KeyGen2∗: In the realistic simulation, the algorithm ABAS.KeyGen2∗ will select the No.0 public-private key pair, while in algorithm ABAS.KeyGen1∗, the No.1 public-private key pair will be selected.

ABAS.Enc2∗: The game simulation ABAS.Enc2∗ random switch the ciphertext data β0. The algorithm ABAS.Enc1∗ will generate all the elements and data that need to be encrypted by itself.

ABAS.Enc3∗: The simulation ABAS.Enc3∗ random change these ciphertext data {ui},{vi}.

ABAS.Setup2∗: The real simulation ABAS.Setup2∗ random chose the public data {Bj}, A. The game simulation random chose the data Aib, Pib.

Now, we describe a sim algorithm, which claims that the result of the real algorithm is indistinguishable from game simulation through the following hybrids.

(1). The first case that satisfies indistinguishable situation is the following two simulation algorithm:

Algorithm 0: The realistic simulation.

Algorithm 1: The simulation ABAS.Setup1∗ replaces the game simulation ABAS.Setup. The simulation ABAS.Setup1∗ outputs some parameters and the most important core key of our attribute-based anti-quantum authentication protocol using (x,IDa) and {fγb,ib}i∈[Q′].

(2). The second case that satisfies indistinguishable situation is the following two simulation algorithm:

Algorithm 1: This algorithm is the same as algorithm 1 in the first case.

Algorithm 2: The game simulation ABAS.Enc1∗ replaces the ABAS.Enc. The ABAS.Enc1∗ compute the data β0, and the ABAS.Enc compute the public-private key pair of the scheme.

(3). The third case that satisfies indistinguishable situation is the following two simulation algorithm:

Algorithm 2: This algorithm is the same as algorithm 2 in the second case.

Algorithm 3: The game simulation ABAS.KeyGen1∗ replaces the ABAS.KeyGen, and using the lattice basis T of other matrices instead of A.

(4). The fourth case that satisfies indistinguishable situation is the following two simulation algorithm:

Algorithm 3: This algorithm is the same as algorithm 3 in the third case.

Algorithm 4: The algorithm ABAS.Enc2∗ replaces the ABAS.Enc1∗. The algorithm ABAS.Enc2∗ random switches the data β0, which is encrypted.

(5). The fifth case that satisfy indistinguishable situation is the following two simulation algorithm:

Algorithm 4: This algorithm is the same as algorithm 4 in the fourth case.

Algorithm 5: The game simulation ABAS.KeyGen2∗ replaces the ABAS.KeyGen1∗. The ABAS.KeyGen2∗ is mostly the same as the algorithm ABAS.KeyGen, except for the {fγb,ib,∗}i∈[Q′] corresponding to the public-private key pair.

(6). The sixth case that satisfy indistinguishable situation is the following two ism algorithm:

Algorithm 5: This algorithm is the same as algorithm 5 in the fifth case.

Algorithm 6: The game simulation ABAS.Enc3∗ replaces the ABAS.Enc2∗. The ABAS.Enc3∗ random change these ciphertext data {ui},{vi}.

(7). The seventh case that satisfy indistinguishable situation is the following two ism algorithm:

Algorithm 6: This algorithm is the same as algorithm 6 in the sixth case.

Algorithm 7: The game simulation ABAS.Setup2∗ replaces the ABAS.Setup1∗.

A detailed proof of indistinguishability (1) –(7) is provided in the references [23,29]. The security of Bob with Alice's other partial authentication in the ABAS is the same as above, this completes the security proof.

4.3 Performance Analysis

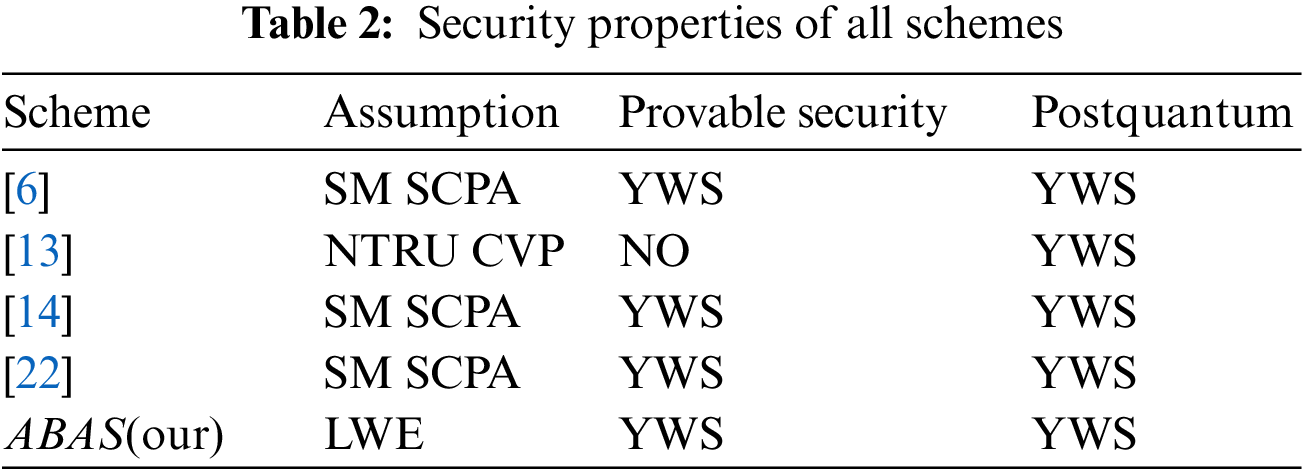
Next, we compare our attribute-based authentication scheme with other related secret key schemes [6,13,14,22]. We mainly focus on the computational costs, storage overhead, and several security properties.

As depicted in Table 1, we compare the storage overhead and other related secret key schemes. The public key parameter' size is m2log⁡q in [6], is 4nlog⁡q in [13], is (2l+9)m2log⁡q in [14], is 2lm2log⁡q in [22], and is 2n(t+l+k)log⁡q in our attribute-based authentication scheme. For the length of public-private key pair, our attribute-based authentication scheme based on the concealable partial predicate encryption, that is gates thereby further reducing the complexity of the formula. The length of public-private key pair in the attribute-based authentication scheme only related to the complexity of the formula, which helps to reduce the secret key length.

In Table 2, the SM represents the standard model, and the SCPA represents the selective chosen plaintext attack, the NTRU represents the number theory research unit, and the CVP represents the closest vector problem. We compare the security properties and other related secret key schemes, according to the Table 1, Li et al. [13] is more effectivie than our attribute-based authentication scheme over lattice in terms of computational storage, which is based on NTRU lattice, so it lacks provable security. Gentry et al. [22], Wang et al. [14] and Brakerski et al. [6] Schemes are slightly weaker than our attribute-based authentication scheme over lattice in terms of computational complexity and storage. Moreover, our scheme is based on partially hiding predicate encryption, so the key size is also efficient, and our scheme is provably security of (Q,poly) based on the LWE problem. Therefore, our attribute-based authentication scheme is more secure resistance to quantum computers than over schemes.

5  Citations

Based on the LWE hard problem over lattice cryptosystem, an anti-quantum authentication scheme for wireless networks is proposed in this paper. In the attribute-based authentication scheme, there is a certain correlation between the authenticated data and the attribute values of the users in the scheme. For the length of public-private key pair, in our attribute-based authentication scheme based on the concealable partial predicate encryption, that is gates thereby further reducing the complexity of the formula. The length of public-private key pair only related to the complexity of the formula in the scheme, which helps to reduce the secret key length. Future work, we will continue to explore and design anti-quantum authentication protocols based on lattice cryptosystem, which is an anti-quantum sublattice cipher security protocol that will run more efficiently and have less storage space.

Funding Statement: This work was supported by the Special Project for Scientific and Technological Cooperation of Jiangxi Province [no. 20212BDH80021].

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. M. Azees, P. Vijayakumar and L. J. Deboarh, “EAAP: Efficient anonymous authentication with conditional privacy-preserving scheme for vehicular ad hoc networks,” IEEE Transactions on Intelligent Transportation Systems, vol. 18, no. 9, pp. 2467–2476, 2017. [Google Scholar]

    2. J. Zhang, J. Cui, H. Zhong, Z. Chen and L. Liu, “PA-CRT: Chinese remainder theorem based conditional privacy-preserving authentication scheme in vehicular ad-hoc networks,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 2, pp. 722–735, 2021. [Google Scholar]

    3. H. Li, F. Guo, L. Wang, J. Wang, B. Wang et al., “A blockchain-based public auditing protocol with self-certified public keys for cloud data,” Security and Communication Networks, vol. 2021, no. 1, pp. 6623639–6623649, 2021. [Google Scholar]

    4. A. Yang, X. Tan, J. Baek and D. S. Wong, “A new ADS-B authentication framework based on efficient hierarchical identity-based signature with batch verification,” IEEE Transactions on Services Computing, vol. 10, no. 2, pp. 165–175, 2017. [Google Scholar]

    5. R. El Bansarkhani and J. Sturm, “An efficient lattice-based multi signature scheme with applications to bitcoins,” in Proc. of the Int. Conf. on Cryptology and Network Security (CANS 2016), vol. 10052 of LNCS, Milan, Italy, pp. 140–155, 2016. [Google Scholar]

    6. Z. Brakerski, D. Cash D, R. Tsabary and H. wee, “Targeted homomorphic attribute-based encryption,” in Proc. of Theory of Cryptography (TCC 2016), Beijing, China, pp. 330–360, 2016. [Google Scholar]

    7. M. Fukumitsu and S. Hasegawa, “A lattice-based provably secure multi signature scheme in quantum random oracle model,” in Proc. of the 14th Int. Conf. on Provable and Practical Security (ProvSec 2020), Singapore, Singapore, pp. 45–64, 2020. [Google Scholar]

    8. S. Mukherjee, D. S. Gupta and G. Biswas, “An efficient and batch verifiable conditional privacy-preserving authentication scheme for VANETs using lattice,” Computing, vol. 101, no. 12, pp. 1763–1788, 2019. [Google Scholar]

    9. M. Kansal and R. Dutta, “Round optimal secure multi signature schemes from lattice with public key aggregation and signature compression,” in Proc. of the 12th Int. Conf. on Cryptology in Africa (AFRICACRYPT 2020), Cairo, Egypt, pp. 281–300, 2020. [Google Scholar]

  10. C. Ma and M. Jiang, “Practical lattice-based multi signature schemes for blockchains,” IEEE Access, vol. 7, pp. 179765–179778, 2019. [Google Scholar]

  11. P. Dupont, J. Hesse, D. Pointcheval, L. Reyzin and S. Yakoubov, “Fuzzy password-authenticated key exchange,” in Proc. of the 37th Annual Int. Conf. on the Theory & Applications of Cryptographic Techniques (EUROCRYPT 2018), Tel Aviv, Israel, pp. 393–424, 2018. [Google Scholar]

  12. R. Tso, Z. Liu and Y. Tseng, “Identity-based blind multi signature from lattices,” IEEE Access, vol. 7, pp. 182916–182923, 2019. [Google Scholar]

  13. D. Li, H. Chen, C. Zhong, T. Li and F. Wang, “A new self-certified signature scheme based on ntrusing for smart mobile communications,” Wireless Personal Communications, vol. 96, no. 3, pp. 4263–4278, 2017. [Google Scholar]

  14. G. Wang, Z. Liu Z and D. Gu, “Ciphertext policy attribute-based encryption for circuits from LWE assumption,” in Proc. of the 21st Int. Conf. on Information and Communications Security (ICICS 2019), Beijing, China, pp. 278–396, 2019. [Google Scholar]

  15. N. Tahat, A. K. Alomari, O. M. Al-Hazaimeh and M. F. Al-Jamal, “An efficient self-certified multi-proxy signature scheme based on elliptic curve discrete logarithm problem,” Journal of Discrete Mathematical Sciences and Cryptography, vol. 23, no. 4, pp. 935–948, 2020. [Google Scholar]

  16. O. Regev, “On lattices, learning with errors, random linear codes, and cryptography,” in Proc. of the 37th Annual ACM Symp. on Theory of Computing, Association for Computing Machinery (STOC 2005), New York, NY, USA, pp. 84–93, 2005. [Google Scholar]

  17. O. Regev, “On lattices, learning with errors, random linear codes, and cryptography,” Journal of the ACM, vol. 56, no. 6, pp. 1–122, 2009. [Google Scholar]

  18. C. Peikert, “Public-key cryptosystems from the worst-case shortest vector problem,” in Proc. of the 41th Annual ACM Symp. on Theory of Computing, Association for Computing Machinery (STOC 2009), Bethesda, MD, USA, pp. 333–342, 2009. [Google Scholar]

  19. Z. Brakerski, A. Langlois, C. Peikert, O. Regev and D. Stehlé, “Classical hardness of learning with errors,” in Proc. of the 45th Annual ACM Symp. on Theory of Computing, Association for Computing Machinery (STOC 2013), New York, NY, USA, pp. 575–584, 2013. [Google Scholar]

  20. Z. Brakerski, C. Gentry and V. Vaikuntanathan, “(Leveled) fully homomorphic encryption without bootstrapping,” in Proc. of the 3rd Innovations in Theoretical Computer Science Conf. (ITCS 2012), Cambridge, MA, USA, pp. 309–325, 2012. [Google Scholar]

  21. L. Ducas and D. M. Fhew, “Bootstrapping homomorphic encryption in less than a second,” in Proc. of the 34th Annual Int. Conf. on the Theory & Applications of Cryptographic Techniques (EUROCRYPT 2015), Sofia, Bulgaria, pp. 617–640, 2015. [Google Scholar]

  22. C. Gentry, A. Sahai and B. Waters, “Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based,” in Proc. of the 33th Annual Int. Conf. on Cryptology (CRYPTO 2013), Santa Barbara, California, USA, pp. 75–92, 2013. [Google Scholar]

  23. S. Agrawal, “Stronger security for reusable garbled circuits, general definitions and attacks,” in Proc. of the 37th Annual Int. Conf. on Cryptology (CRYPTO 2017), Santa Barbara, CA, USA, pp. 3–35, 2017. [Google Scholar]

  24. R. Steinfeld, A. Sakzad and R. K. Zhao, “Practical MP-LWE-based encryption balancing security-risk versus efficiency,” Designs Codes and Cryptography, vol. 87, pp. 2847–2884, 2019. [Google Scholar]

  25. A. Lombardi, V. Vaikuntanathan and T. D. Vuong, “Lattice trapdoors and IBE from middle-product LWE,” in Proc. of the Theory of Cryptography Conf. (TCC 2019), Nuremberg, Germany, pp. 24–54, 2019. [Google Scholar]

  26. A. Pellet-Mary, G. Hanrot and D. Stehlé, “Approx-SVP in ideal lattices with pre-processing,” in Proc. of the 38th Annual Int. Conf. on the Theory & Applications of Cryptographic Techniques (EUROCRYPT 2019), Darmstadt, Germany, pp. 685–716, 2019. [Google Scholar]

  27. S. Gorbunov, V. Vaikuntanathan and H. Wee, “Functional encryption with bounded collusions via multi-party computation,” in Proc. of the 32nd Annual Int. Conf. on Cryptology (CRYPTO 2012), Santa Barbara, CA, USA, pp. 162–179, 2012. [Google Scholar]

  28. Y. Ishai and H. Wee, “Partial garbling schemes and their applications,” in Proc. of the Int. Colloquium on Automata, Languages, and Programming (ICALP 2014), Copenhagen, Denmark, pp. 650–662, 2014. [Google Scholar]

  29. S. Gorbunov, V. Vaikuntanathan and H. Wee, “Predicate encryption for circuits from lwe,” in Proc. of the 35th Annual Int. Conf. on Cryptology (CRYPTO 2015), Santa Barbara, CA, USA, pp. 503–523, 2015. [Google Scholar]

  30. C. Gentry, C. Peikert and V. Vaikuntanathan, “Trapdoors for hard lattices and new cryptographic constructions,” in Proc. of the 40th Annual ACM Symp. on Theory of Computing, Association for Computing Machinery (STOC 2008), Victoria (BCCanada, pp. 197–206, 2008. [Google Scholar]

  31. S. Agrawal, D. Boneh and X. Boyen, “Efficient lattice (H)IBE in the standard model,” in Proc. of the 29th Annual Int. Conf. on the Theory & Applications of Cryptographic Techniques (EUROCRYPT 2010), French Riviera, pp. 553–572, 2010. [Google Scholar]

  32. D. Cash, D. Hofheinz, E. Kiltz and C. Peikert, “Bonsai trees, or how to delegate a lattice basis,” Journal of Cryptology, vol. 25, no. 4, pp. 601–639, 2012. [Google Scholar]

  33. C. Baum, I. Damgård, V. Lyubashevsky, S. Oechsner and C. Peikert, “More efficient commitments from structured lattice assumptions,” in Proc. of the 11th Conf. on Security and Cryptography for Networks (SCN 2018), Amalfi, Italy, pp. 614–629, 2018. [Google Scholar]

  34. V. Lyubashevsky and G. Neven, “One-shot verifiable encryption from lattices,” in Proc. of the 36th Annual Int. Conf. on the Theory & Applications of Cryptographic Techniques (EUROCRYPT 2017), Paris, France, pp. 293–323, 2017. [Google Scholar]

  35. R. Behnia, M. O. Ozmen and A. A. Yavuz, “Lattice-based public key searchable encryption from experimental perspectives,” IEEE Transactions on Dependable Secure Compute, vol. 17, no. 6, pp. 1269–1282, 2018. [Google Scholar]

  36. S. Katsumata and S. Y amada, “Group signatures without NIZK: From lattices,” in Proc. of the 38th Annual Int. Conf. on the Theory & Applications of Cryptographic Techniques (EUROCRYPT 2019), Darmstadt, Germany, pp. 312–344, 2019. [Google Scholar]

  37. Y. Sun and Y. Liu, “A lattice-based fully dynamic group signature scheme without NIZK,” in Proc. of the Information Security and Cryptology (INSCYPT 2020), Guangzhou, China, pp. 359–367, 2020. [Google Scholar]

  38. S. Canard, A. Georgescu, G. Kaim, A. R. Langlois and J. Traoré, “Constant-size lattice-based group signature with forward security in the standard model,” in Proc. of the 14th Int. Conf. on Provable and Practical Security (ProvSec 2020), Singapore, Singapore, pp. 24–44, 2020. [Google Scholar]

  39. S. Doss, J. Paranthaman, S. Gopalakrishnan, A. Duraisamy, S. Pal et al., “Memetic optimization with cryptographic encryption for secure medical data transmission in IoT-based distributed systems,” Computers, Materials & Continua, vol. 64, no. 2, pp. 1577–1594, 2021. [Google Scholar]

  40. X. Zhang, X. Sun, X. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]