Enhanced Clustering Based OSN Privacy Preservation to Ensure k-Anonymity, t-Closeness, l-Diversity, and Balanced Privacy Utility

1  Introduction

A platform for users to exchange information with their peers is provided by an Online Social Network (OSN) [1]. Many recent emerging techniques like the Internet of Things (IoT) [2–5] are concerned with data security and privacy. Many third parties are interested in OSNs because of the incorporation of personally identifiable sensitive and non-sensitive data [6,7]. It raises the issue of personal data security and privacy [8]. In an OSN, several data security concerns like stalking, reputation slandering, private information leakage, tailored spamming, phishing, and so on are frequent [9]. Context-aware spamming is a well-known spamming attack. The network structure has also been utilized to launch OSN graph structural assaults such as the Sybil attack. These potential attacks can introduce botnet or malware into the network through user communication and third-party programs [10]. Security is a necessary but insufficient condition for protecting data privacy, i.e., security procedures alone do not ensure data privacy. An individual’s sensitive data might include their name, location detail, electronic mail, phone number, information concerning one’s Social Security Number (SSN), insurance information, health, and credit card details, financial records, personal images, videos, notes, and so on. Leaks of sensitive data may result in lawsuits, erosion of privacy, degrading reputation, personification, income loss, loss of consumer trust, brand harm, and other consequences. In some cases, theft and robbery can also be dangerous threats. If someone is found guilty of unlawful disclosure of information in the Indian context, the Indian Information Act-2000 provides for the penalty.

In contrast to the actual world, where data is transient, information on the internet stays indefinitely, posing a significant risk to online users’ privacy. When individuals share sensitive information online, they frequently ignore the associated consequences [11]. Privacy problems are sure to occur whenever and wherever Personal Identifiable Information (PII) is exchanged and maintained. As a result, maintaining privacy in an OSN domain essentially built for sharing has proven problematic. No unauthorized user should have access to the data owner’s sensitive information. If unauthorized users obtain access to the users’ sensitive attributes, they can dramatically violate data privacy. The OSN has various sensitive data fields and their consequences on data privacy when disclosed. Videos and photographs from the profiles might be manipulated and used to blackmail and defame [12]. In addition to revealing a great deal about a person, likes and interests can lead to opposing viewpoints being formed. The person can be determined using an address, which might lead to a criminal attack or burglary [13]. Individuals’ Social Security Numbers (SSNs) might be revealed by performing linkage of address, birthdate, and gender, leading to identity theft or personalization [14]. Email addresses and phone numbers may be used for targeted advertising, resulting in unwanted interruptions and spam. As a result, it is a significant problem for OSN to safeguard personal and sensitive data from unauthorized users while ensuring that actual data is available to legal users [15].

The protection of privacy and anonymization in OSNs has sparked considerable attention. Each OSN may be presented in graph form. OSN represents the end-user as a node and the edge between two such nodes as a link [16]. A user/node in the OSN graph can have several links/edges, such as attribute to attribute, user to user, and user to attribute. As a result, there are three phases to anonymizing any OSN graph: links, vertices, and user attributes. But the goal of any anonymization strategy is to avoid removing too much information that reduces the usability of the original graph that leads to the loss of its structural information. Identity disclosure is one of the critical objectives of unethical third parties and must be safeguarded for OSN privacy [17]. Naive anonymization methods replace random identifiers on identifiable attributes like the user’s name. This anonymized graph, however, can be exploited by attackers using its structural information. So, the OSN data should be made anonymous with good privacy preservation techniques before publishing so that only trustworthy promoters can use it. In OSN, two critical features must be preserved: knowledge about an individual’s sensitive information and end-user edge data [18,19]. Hence, preserving the privacy of this personal information is an open research issue [20,21]. K-anonymity privacy and l-diversity are two models for protecting privacy that has led to many strategies for anonymization in OSNs. But these conventions for protecting privacy only with limited scope, and they have not been able to keep all parts of social networks anonymous. Apart from this, yet another challenge for existing clustering-based OSN privacy preservation methods is the fixed clustering technique. Clustering large data sets using K-means is a well-known technique [22,23]. The K-means clustering algorithm splits the dataset with a fixed pre-defined number of clusters [24,25]. It is, however, more likely to group dissimilar users if the clusters created are small. Alternatively, if many clusters are selected, there is a greater likelihood of similar users being added to various groups. Therefore, it is highly required to have a mechanism that discovers the optimum number of clusters before forming actual clusters. The optimal number of clusters ensures the minimum IL with an improved Degree of Anonymization (DoA) because more enhanced and meaningful clusters are created.

The authors proposed a novel privacy preservation framework for the OSNs consisting of privacy for all network elements. The motivation of the proposed model is to provide all the privacy notions of OSNs using the graph properties to create an enhanced clustering approach. The proposed model acquires OSN data and applies the pre-processing to remove the noisy contents and attributes normalization without any IL. After pre-processing the input OSN data, different graph properties has selected for the initial cluster formation. The authors designed the enhanced clustering algorithm to ensure the minimum information loss with higher privacy preservation of attributes, edges, and nodes in the network. The authors modified the existing static K-means algorithm to discover the optimal number of clusters for the input OSN data using the multiple graph properties. A threshold is computed using various graph properties, and then the initial clusters are formed using that threshold. After forming clusters, the next phase is optimizing the clusters to achieve k-anonymity and higher privacy models, namely t-closeness and l-diversity. Authors developed unique lightweight techniques that meet all privacy criteria for clustered OSN data privacy. Research work is divided into the following sections. Section 2 examines the related works in terms of motivation and contributions. In Section 3, the design and methods of the proposed model are described. In Section 4, results from the simulation and system analysis are discussed. Section 5 concludes with recommendations for further work.

2  Related Work

Privacy preservation becomes the essential requirement to secure OSNs. This section aims to review the privacy preservation techniques in OSNs. As previously mentioned, the OSN is represented as a graph with vertices, links, and attributes. Therefore, securing these OSN components with minimum IL is vital. Further privacy preservation strategies are discussed, offered a research gap analysis, and then presented the contributions.

2.1 State-of-Art

The previous solution for Pervasive Social Network (PSN) privacy protection had presented in [26]. The anonymous authentication method had created to validate trust levels and pseudonyms to deliver a trustworthy PSN while protecting privacy. They used trusted authority to provide safe, anonymous authentication. A comparable mechanism for encrypted communication in PSN had described in [27]. With the help of a trusted authority, they created an anonymous authentication technique that uses group signatures to validate different trust levels and avoid privacy leaks. In [28], the authors have examined the identity revelation problem for weighted social graphs. With the assumption of understanding target vertex links, matching link weights, and vertex degrees, the weighted 1*-neighborhood threats are discovered. A private property known as probabilistic indistinguishability has been proposed. This property is achieved by the heuristic indistinguishable group anonymization (HIGA) algorithm. The authors of [29] examined the optimization between personalized data usefulness and latent privacy trade-off. They developed the data sanitization technique to preserve sensitive latent data while preserving many benefits of OSN data. In [30] presented a survey study on all contemporary privacy preservation strategies for OSNs. The constraints of privacy preservation strategies such as perturbation, creating the full alternative network, and naive anonymization have been examined. In [31], the authors have presented a hybrid privacy protection technique for OSN. Resilience, node identity, and privacy of location have been evaluated to overcome breaches of privacy. The decision process with the game-based Markov method had created to enhance data usage while maintaining robust privacy protection. The local differential privacy approach had introduced in [32] for OSN publishing to protect the structural information of the community. It assumes the edge probability reconstruction structural constraint and creates synthetic OSN information. Based on structure information, the author proposed a successful and rapid method of de-anonymizing social networks [33]. They developed a pairwise node similarity metric and an efficient method for matching nodes.

According to [34], k-anonymity was achieved through swarm intelligence in OSNs through clustering. The author initially devised the clustering approach to lower the IL by utilizing Particle Swarm Optimization (PSO). On the other hand, PSO-based clustering has a high computing cost; hence, a hybrid Genetic Algorithm (GA) and PSO-based algorithm (PSO-GA) have been developed for OSN clustering. Another recent study in [35] presented an OSN de-anonymization strategy to highlight the influence of user characteristics on de-anonymization accuracy. They assessed user attribute diversity and selected critical features to generate the multipartite graph. The multipartite graph had been partitioned into many communities. In [36], another privacy protection approach based on clustering for online social networks had proposed. They suggest clustering to provide privacy for all network components, including nodes, links, and attributes. The OSN nodes were grouped using similarity measures for k-anonymity assurance. The further l-diversity model was applied to strengthen the k-anonymity of OSN data. The feature learning methodology was recently developed in [37] to provide privacy preservation against poisoning. Before constructing an inferred social graph, they employed a feature learning technique to determine social relationships among social users. Authors exploited the inferred social graph to protect their privacy. Using a technique based on message replication and sensitive characteristics replacement, research in [38] proposes a privacy preservation technique during the message transmission phase. They calculated their reputation for privacy protection in OSN by analyzing each user’s social actions. In [39], the authors have suggested a differential privacy technique that merges the various series to provide privacy to all graph parts. The degree frequency was saved in the dK-1 series, the joint degree frequency was stored in the dK-2 series, and the connecting information between edges was kept in the dK-3 series. In [40], the authors have introduced the Customized Reliable Differential Privacy (CRDP) strategy to achieve customizable privacy for each user. They calculated the social distance for the shortest distance between two network users and used it to adjust the levels of privacy protection.

The authors of [41] sought to evaluate if a privacy-preserving data mining strategy could be effectively utilized in data mining for an OSN. The authors of [42] have included unlinkability for the weighted OSN data release. Two essential privacy models have been developed to prevent the connection of auxiliary information to a targeted individual. These models are highly probable: edge node unlinkability and weight unlinkability. In [43], the authors have developed a unique link-privacy maintained graph embedding system based on adversarial learning. The proposed approach focuses on reducing the accuracy of adversary prediction for sensitive attributes while allowing non-sensitive attributes in graph embedding, such as graph topology and node properties. The idea of dynamic privacy had established for the OSN in [44]. The authors suggest privacy propagation and accumulation as a method for private information to propagate in dynamic cyberspace. They created the associated ideas and procedures for maintaining privacy in OSNs.

2.2 Research Gap

The paper discusses the various research gaps in the underlying methods in the above section to justify the novelty of the proposed model. According to the above studies, achieving the complete privacy preservation of the OSN data is still a challenging research problem concerning the trade-off among the essential requirements such as system dynamics, minimum IL, computational efficiency, and higher DoA. The underlying methods have failed to achieve all these requirements while presenting the privacy preservation solution for OSNs. The research gaps that motivate the novel proposed model in this paper are summarized below.

Cryptography-based approaches achieved safe communications with a certain amount of anonymity, but not in all OSN components. In addition, they depended on trustworthy authorities to protect their privacy and secure communications.

Grouping/clustering-based approaches have shown acceptable results. However, they have not yet simplified or enhanced performance and privacy protection trade-off needs. It has been shown that swarm intelligence-based clustering algorithms can obtain the k-anonymity privacy principles in OSNs with high computational complexity. Hence, because of the low quality of anonymization, such clustering algorithms failed to accomplish high-level privacy protection in online social networks. The grouping was based on only one graph characteristic, limiting the privacy protection in OSNs.

Other OSN graph-based techniques failed to ensure privacy in all components, such as nodes, edges, and node characteristics. Attackers using such tactics can readily exploit the graph’s structural information by linking an anonymized OSN graph, which leads to IL.

Differential privacy and tailored privacy techniques for online social networks were discussed in the literature. On the other hand, different privacy approaches consider each data owner has identical privacy expectations and thus fail to accommodate various perspectives on privacy. On the other hand, a configurable privacy scheme initiates the creation process of differential privacy. It leads to an unanticipated correlation in new noises that compromise data privacy and leak sensitive information. All underlying methods discussed in the literature relied on the static computing environment to produce privacy protection in OSN.

The idea of the improved privacy preservation model for the OSN with limited scope had been introduced in the literature, but no provision to ensure the k-anonymization, t-closeness, and l-diversity.

2.3 Contributions

A novel enhanced privacy preservation framework is proposed in this paper to overcome the limitations of underlying methods. The authors recently addressed some of the problems mentioned in [45], where they obtained static clustering-based privacy preservation principles such as k-anonymization, l-diversity, and t-closeness. This study expands that technique to establish enhanced privacy preservation principles for OSN. The contributions listed below emphasize the uniqueness of the proposed framework.

•   A novel enhanced cluster-based anonymization for privacy preservation paradigm is developed, which employs numerous graph features for enhanced cluster formation to accomplish high-level privacy protection in OSNs while requiring reduced information loss and computational effort.

•   Research work uses a lightweight pre-processing approach to decrease data noise and complexity.

•   The threshold-based mechanism has been proposed for estimating the optimal number of clusters by enhancing the static k-means clustering algorithm. The proposed clustering achieves fully enhanced privacy preservation notions for OSN.

•   To assure k-anonymization privacy, the authors design a unique enhanced cluster optimization approach that uses OSN network features, eccentricity, and distance.

•   To improve the privacy of k-anonymized clusters, the authors design a unique one-pass technique that ensures enhanced clusters and has l-diversity and t-closeness to defend against similarity and attribute disclosure concerns.

•   The results of a performance analysis of the proposed model using comparable approaches on real-world datasets, altering the number of OSN users and size, are presented in the research work.

3  Proposed Methodology

This section discusses the proposed enhanced OSN privacy preservation framework’s design and methodology. The main objectives of the proposed model include (1) discovering the optimal number of clusters to divide the pre-processed OSN data into different groups and (2) ensuring the enhanced privacy preservation notions of k-anonymization, t-closeness, and l-diversity via a cluster’s optimization algorithm. Fig. 1 demonstrates the functionality of the proposed anonymization framework. The model consists of three phases Enhanced Clustering Phase (ECP), Enhanced k-Anonymity Phase (EAP), and Enhanced l-Diversity and t-Closeness Phase (EDCP). In the ECP phase, the input OSN data pre-processing, discovering the optimal number of clusters, and enhanced clusters are formed. The EAP phase enhances clusters utilizing OSN network features such as eccentricity and distance to improve the k-anonymity privacy notion.

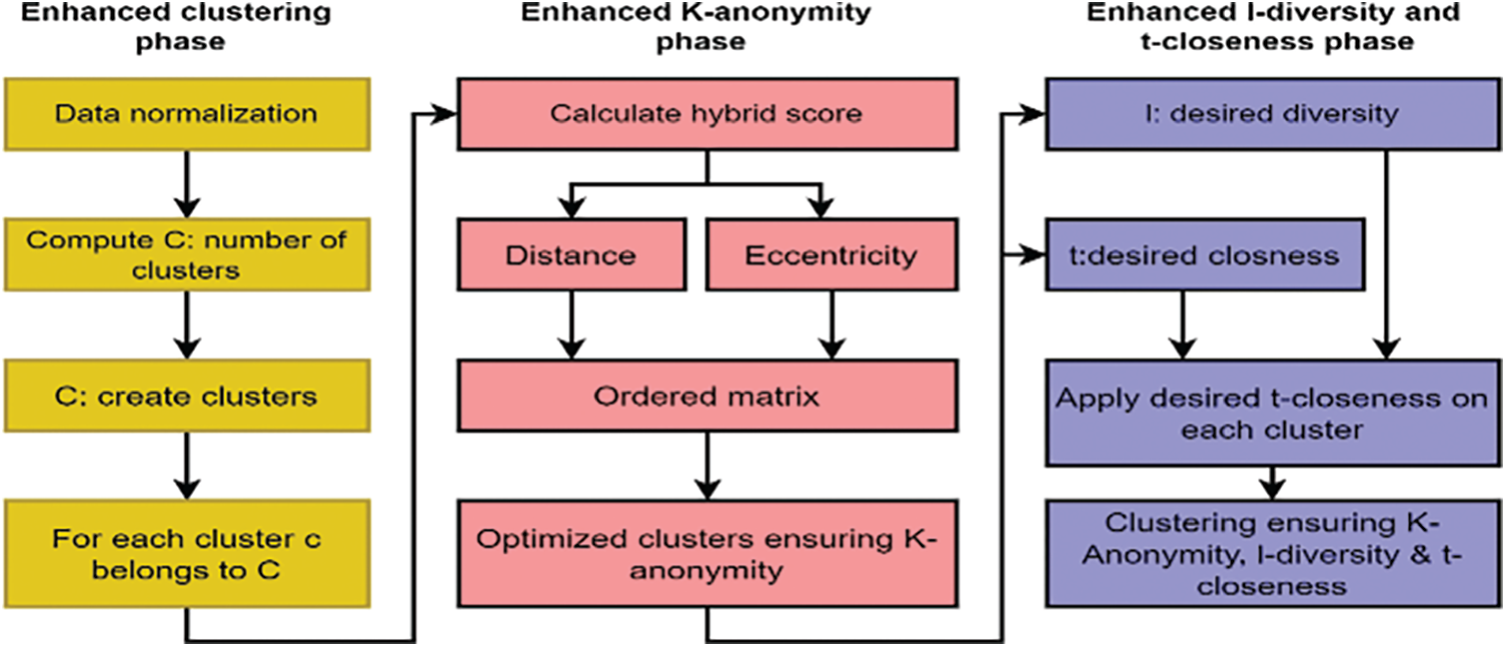
Figure 1: The architecture of the proposed enhanced privacy preservation framework for OSN

The outcome of the EAP phase is further given to the EDCP phase, where the one-pass algorithm optimizes clusters to guarantee the l-diversity and t-closeness privacy notions.

3.1 System Architecture

Consider the following: OSN is represented as a graph G, which has vertices V and edges E. V denotes OSN users, and E presents a friendship link that connects two vertices. Consider having n number of vertices V={v1,v2,…vn} in the OSN, where every vertex vi having m related attributes represented in A as A={a1i,a2i,…ami}. Because the edges are directed, all edges can be determined in OSN using Eq. (1):

E=n×(n−1)(1)

The study focuses on offering enhanced privacy preservation of OSN graph G by anonymizing every network element E, V, and A of OSN graph G to meet the proposed objectives listed below.

•   Instead of static clustering, split the OSN data into the optimal number of clusters based on the input dimensions and attributes.

•   To achieve all the privacy notions of k-anonymization, t-closeness, and l-diversity for the input OSN clusters.

•   To reduce sensitive information leakage, i.e., minimal IL, while maintaining high levels of privacy

3.2 Enhanced Clustering Phase (ECP)

As described above, this phase consists of OSN data pre-processing, discovering optimal cluster numbers using threshold, and forming enhanced clusters. Data pre-processing performs data normalization before clustering since raw data may contain outliers or messy data. The data normalization step’s goal is to improve the quality of OSN data using statistical attribute modeling. As a result of the statistical normalization of users and their vital properties, outliers or messy data are eliminated without needing a specific function. Thus, the data noise is discarded using the data normalization mechanism.

Fixed K-means clustering forms the c clusters by computing the euclidean distance between the attributes of two users with an estimation of centroids for each cluster. It is, however, more likely to group dissimilar users if the clusters created are small. Alternatively, if many clusters are selected, there is a greater likelihood of similar users being added to various groups. The threshold value T is determined using the mean of all the vertices’ Euclidean distances, as illustrated in Algorithm 1.

The needed number of clusters for the incoming OSN data is computed using the threshold T, along with their respective centroids value. The number of clusters is determined by combining the threshold value and the current Euclidean distance between two users’ Ai&Aj attributes. First, calculate the total distances between each data point in the dataset to determine the threshold value by Eq. (2).

d1(i)=∑i=1,j=1nEuclidean(Ai,Aj)(2)

After that, the mean function has applied to get the threshold value T as Eq. (3).

T=(d1n)n(3)

3.3 Enhanced K-Anonymization Phase (EAP)

The enhanced clustering of the OSN data failed to achieve the k-anonymization privacy notion as each cluster in the network does not satisfy the at-least k-user’s requirements. The k-anonymity requirement in a network requires at least k users in each cluster, i.e., every cluster Ci,i∈c in a network must have at least k users. Therefore, to verify that all clusters have the same size, it is necessary to optimize each cluster further based on a number of graph features such as eccentricity and distance. EAP consists of two main phases: computation of hybrid score matrix and k-anonymized enhanced clusters.

For each cluster i∈c, first discovered the number of CMs using the size (Ci) function. Then, we compute the hybrid score for jth user/vertex called Auid and centroid Acenti of the ith cluster. This hybrid score Hiuid for jth user/vertex called Auid in ith cluster is computed via the below sequence of equations. The distance measure duid,cent between attributes of the current user Auid and its corresponding centroid attributes Acenti is computed by Eq. (4):

duid,cent=∑r=1R|aruid−arcent|R(4)

where arcent defines the rthattribute of the current cluster centroid vertex and aruid defines the rthattribute of vertex uid. R specify the total count of attributes associated with each vertex in the network. The eccentricity of every vertex euid is computed as the number of friends (NF) value NFuid using Eq. (5).

euid=(1NFuid)×£s(5)

The minimum euid indicates the maximum eccentricity of the vertex. Eccentricity results are normalized by scaling factor £s. The scaling factor is computed by taking the mean of NFuid of all the vertices using Eq. (6)

£s=∑i=1nNFin(6)

Finally, the hybrid score for every vertex in the current cluster is computed using the weight management technique, as shown in Eq. (7).

Hiuid=(a1×duid,cent)+(a2×euid)(7)

where a1 and a2 are represents each graph property’s weights. It increases the likelihood of clusters having more identical vertices grouped. Matrix D stores each vertices hybrid score value one by one. Each vertex SD(i:,1) is joined to a current cluster Cj based on two constraints: (1) the vertex status must not be ‘assigned,’ and (2) the current cluster size must be less than or equal to n/k. These two criteria result in clusters of equal sizes that meet enhanced k-anonymity with the least amount of IL. It considerably decreases the possibility of leaking sensitive data about links, vertices, and their attributes.

3.4 l-Diversity and t-Closeness Phase (EDCP)

The enhanced l-diversity and t-closeness phase (EDCP) is designed to achieve the privacy models such as t-closeness and l-diversity for the enhanced clustered OSNs, as shown in Algorithm 2.

Algorithm 2 demonstrates the functioning of a one-pass algorithm that first assures the t-closeness notion with a predetermined threshold value t, then applies the l-diversity technique based on entropy. The underlying methods failed to ensure all three privacy levels: k-anonymization, t-closeness, and l-diversity for the OSNs. A novel one-pass algorithm was proposed to solve this problem, ensuring k-anonymized clusters are l-diversified and t-close. According to the notion of t-closeness, we categorized users into clusters based on the generated t-value. Based on Earth Movers’ Distance (EMD) [46] equal distance metrics, the t-value was calculated. The outcome of Algorithm 2 is the t-closeness and l-diversity ensured enhanced clusters for the input OSN data.

3.5 Edge Anonymizations

By employing the clustering approach described in this paper, the privacy of vertices and users and their properties are protected while sensitive information loss and computational overhead are minimized. The edges in OSNs are anonymized after the clusters are ensured to comply with the three principles of privacy preservation. We apply the approach in [36] for edge anonymization. The anonymization of edges was accomplished through super edges computation among clusters since each CH node represents a cluster head. In the proposed model, all edges of the weighted directed OSN network are anonymized. Finally, the enhanced privacy preservation ensures the k-anonymization, t-closeness, l-diversity, and edges anonymization with improved privacy and utility.

4  Result Analysis

The results of experimental work for performance analysis are presented in this section. We used MATLAB to develop and analyze the suggested model using cutting-edge methodologies. We conducted the studies on a Windows 10 computer with an Intel I3 processor and 4GB of RAM. A total of 25 instances were run for each scenario, and the results were averaged. The proposed approach had compared with two underlying OSN anonymization methods. It should be noted that PSO-GA refers to a hybrid swarm intelligence-based OSN clustering approach, whereas LECC refers to an l-diversity Equi-Cardinal (LECC) clustering approach. The Proposed Fixed Clustering model (PFC) and the Proposed Enhanced Clustering (PEC) are two variants of the proposed privacy preservation framework and evaluated with LECC and PSO-GA methodologies.

4.1 Datasets

The proposed and state-of-the-art techniques’ effectiveness was evaluated using two real-world datasets, Yelp [47] and Facebook [48]. Yelp’s dataset contains user reviews, where each user links to many other users and provides information about each user’s attributes. Friends and user files from this dataset are used in our experimental investigation. The user file contains a user ID and 18 user attributes. On the other hand, the Facebook OSN dataset build on a friends list from Facebook. Like the Yelp dataset, the Facebook dataset also consists of nodes (users), their attributes (features), and edges (circles). It consists of 4039 nodes in the network and 88234 edges among them. Attributes of each node in the dataset are already in pre-processed form. The performances of different privacy preservation techniques are analyzed by varying numbers of users for both datasets.

4.2 Performance Measures

Three parameters were taken into account to compare the proposed technique with state-of-the-art techniques: Degree of Anonymization (DoA), Execution Time (ET), and Information Loss (IL). During the OSN data anonymization, the ET represents the average execution time for each of the 25 scenarios considered. Counting the number of assigned users in a cluster has been used to calculate the DoA of every user; hence, user DoA is comparable to cluster DoA. The formulas for computing DoA, IL, and ET are referred to from [47]. Apart from these performance measures, we additionally computed the Average Mean of Inter-Cluster Distance (AMICD) and Average Sum of Squared Error (ASSE). The AMICD is the mean distance among all vertices in two distinct clusters. It is computed by Eq. (8).

AMICD=1|Ci||Cj|∑Aiuid∈Ci,Ajuid∈Cjdist(Aiuid,Ajuid)(8)

where, Ci, Cj are two clusters in the network. Aiuid and Ajuid attributes set of two users belongs to ith and jth clusters. Similarly, the ASSE is computed by estimating the Mean Square Error (MSE) among Aiuid and Ajuid attributes set of two users belongs to ith and jth clusters. It is computed by Eq. (9).

ASSE=∑Aiuid∈Ci,Ajuid∈Cjmse(Aiuid,Ajuid)(9)

4.3 Results Analysis Using Yelp Dataset

This section presents the experimental outcomes using different methods on the Yelp dataset. To analyze the effect of the number of users on the performances, we have varied the user density by keeping the fixed cluster size for static privacy preservation methods such as LECC, PSO-GA, and PFC. The clusters for the PEC are created based on a threshold. Yelp is an extensive dataset with more than 20,000 users/nodes. The user’s density varied from 2,000 to 20,000 users. We kept the cluster size 100 for LECC, PSO-GA, and PFC. This analysis aims to explain the efficiency of having the optimal number of clusters compared to static approaches. This section demonstrates the comparative results with DoA, IL, AMICD, ASSE, and ET parameters using Yelp Dataset.

Fig. 2 depicts how DoA has grown as user density has increased. DoA value grows almost exponentially, i.e., for 2,000 users, the DoA outcome is around 2,300, but for 20,000 users, the DoA outcome has climbed to roughly 20,000. The proposed model outperformed static approaches PSO-GA, LECC, and PFC in terms of DoA for each user-density scenario. Similarly, Fig. 3 demonstrates the IL results for each method.

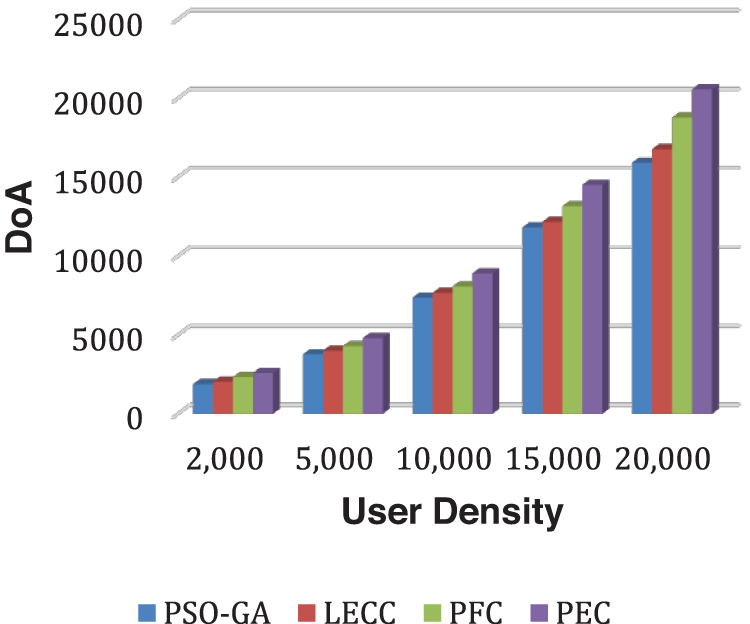
Figure 2: Analysis of DoA performance using yelp dataset

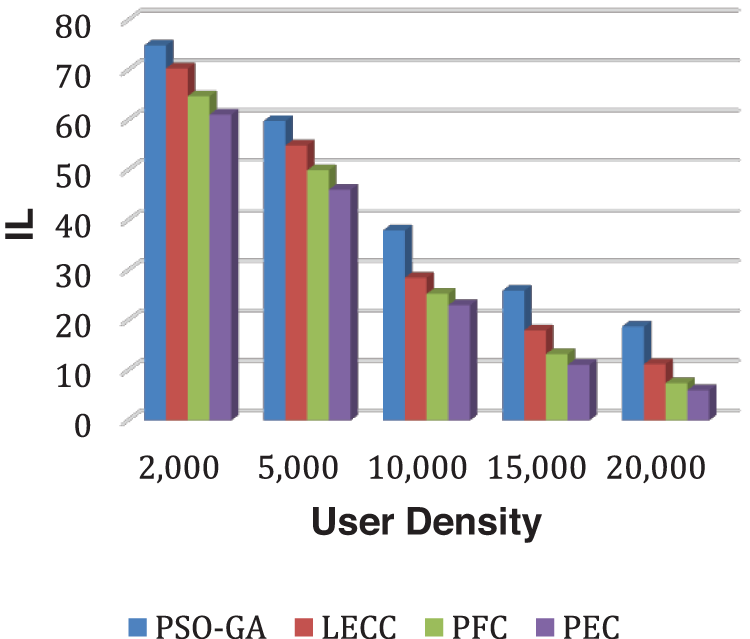
Figure 3: Analysis of IL performance using yelp dataset

The IL is contradictory to the DoA outcomes; therefore, with the increase in user density, the IL performance decreased. The technique with higher DoA and lower IL is declared an efficient privacy preservation solution. As a result of comparing all four methods, the proposed PEC framework outperformed all three fixed clustering methods. With the increase in user density, the privacy preservation performances like DoA and IL become efficient. Because of the increased number of users, the created clusters become more relevant and anonymized, resulting in higher DoA and lower IL. The PFC is a previously proposed model with fixed clustering [47]. The PEC shows the best performance among three static clustering methods: PSO-GA, LECC, and PFC, as the PEC model achieved the all-privacy notions of OSNs, including the k-anonymization, t-closeness, and l-diversity. PEC uses hybrid graph features to ensure the establishment of trustworthy and k-anonymous clusters, and then k-anonymous clusters optimize by maintaining l-diversity and t-closeness privacy ideas.

However, the PSO-GA and LECC suffered from the lack of complete privacy notions, leading to lower DoA and a higher possibility of IL.

The proposed enhanced privacy preservation framework, PEC, outperformed all four underlying techniques. PEC delivered a higher DoA than PSO-GA, LECC, and our previous proposed PFC model. PEC has calculated the ideal number of clusters based on enhanced clustering, which is the primary reason for improved performance. The current static models classified all OSNs into a predetermined 100 number of clusters. The fixed clustering leads to the problems of over-clustering or under-clustering, affecting performances like DoA and IL. After enhanced cluster formation, we achieved higher privacy notions using the proposed model that leads to reduced IL and higher DoA. Along with DoA and IL, AMICD and ASSE performance analysis of the privacy preservation notions becomes essential. Fig. 4 shows the AMICD performance analysis, and Fig. 5 shows the ASSE performance analysis for user density scenarios using different methods.

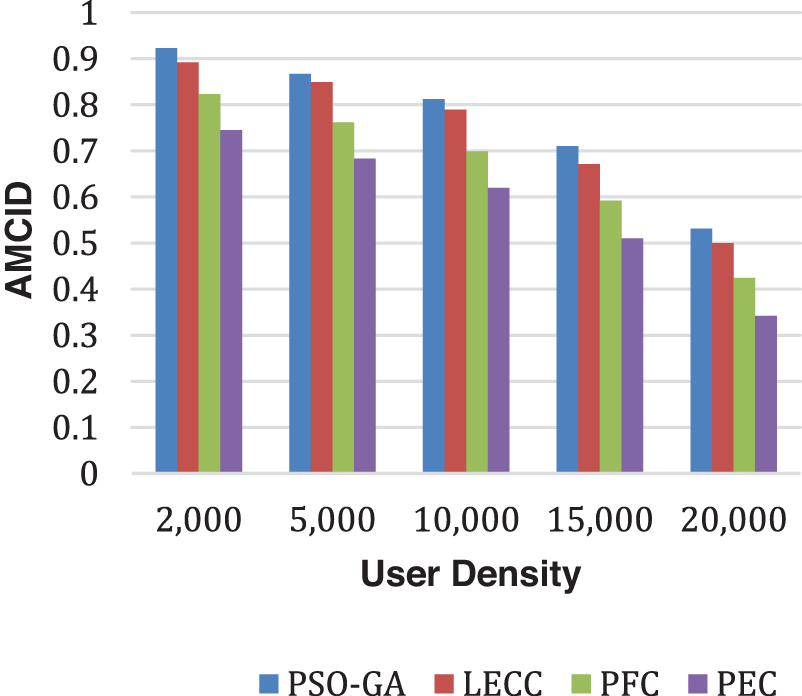
Figure 4: Analysis of AMICD performance using yelp dataset

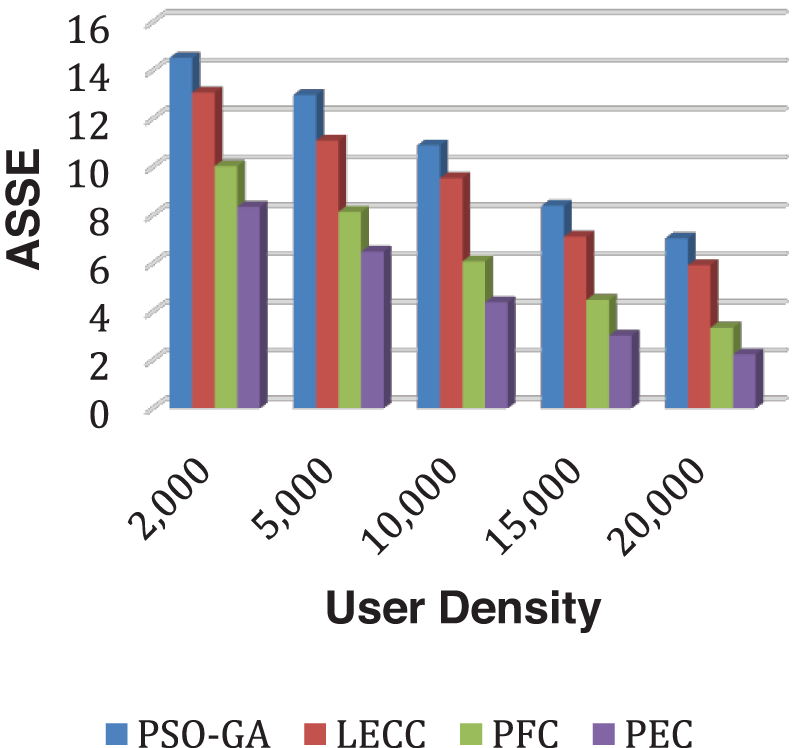
Figure 5: Analysis of ASSE performance using yelp dataset

LECC approach based on K-means clustering has provided privacy protection with the lowest ET of any strategy. The proposed technique is based on the LECC approach and includes data normalization, enhanced cluster generation, EAP with multiple graph attributes, and EDCP with higher privacy notions. Compared to LECC and PFC, including all privacy concepts with enhanced clustering necessitates more processing. However, compared to static techniques, the proposed model provides an enhanced approach to privacy protection with substantial performance savings. Fig. 6 shows the results of ET using each privacy preservation technique. As a result of the iterative optimization methodology, which takes a longer time to reach convergence, PSO-GA takes longer to build clusters than LECC, PFC, and PEC. It may be possible to negotiate processing time by using higher processing systems.

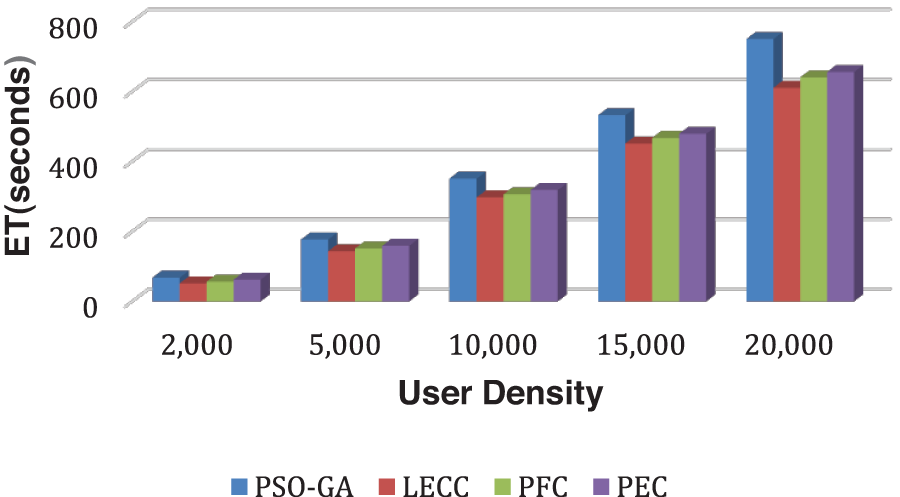
Figure 6: Analysis of ET performance using yelp dataset

4.4 Results Analysis Using Facebook Dataset

This section presents the analysis of the privacy preservation methods PSO-GA, LECC, PFC, and PEC using the Facebook dataset. The size of the Facebook dataset is relatively small compared to the Yelp dataset. As the dataset contains around 4000+ users, we varied the user densities from 1,000 to 4,000 and measured the results for each method. Figs. 7 and 8 demonstrate DoA and IL outcomes.

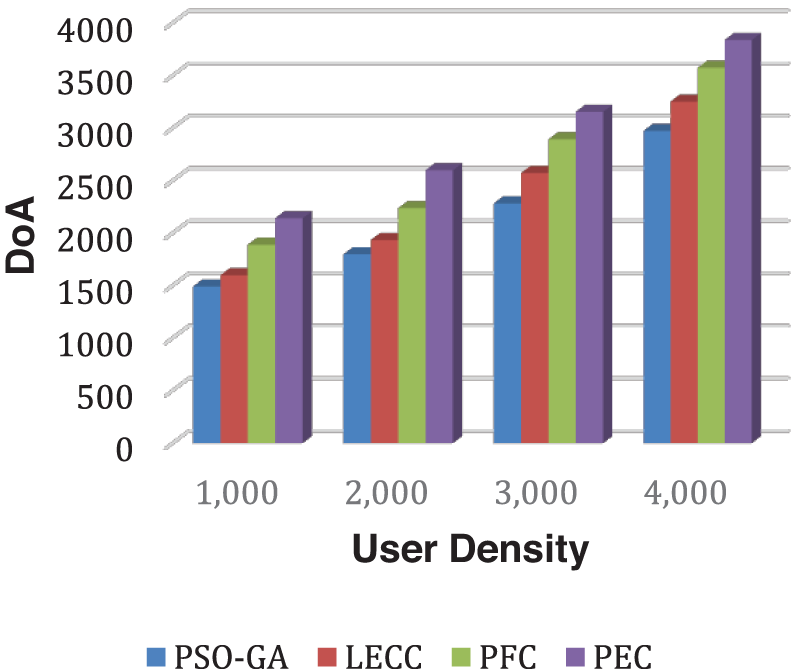
Figure 7: Analysis of DoA performance using the Facebook dataset

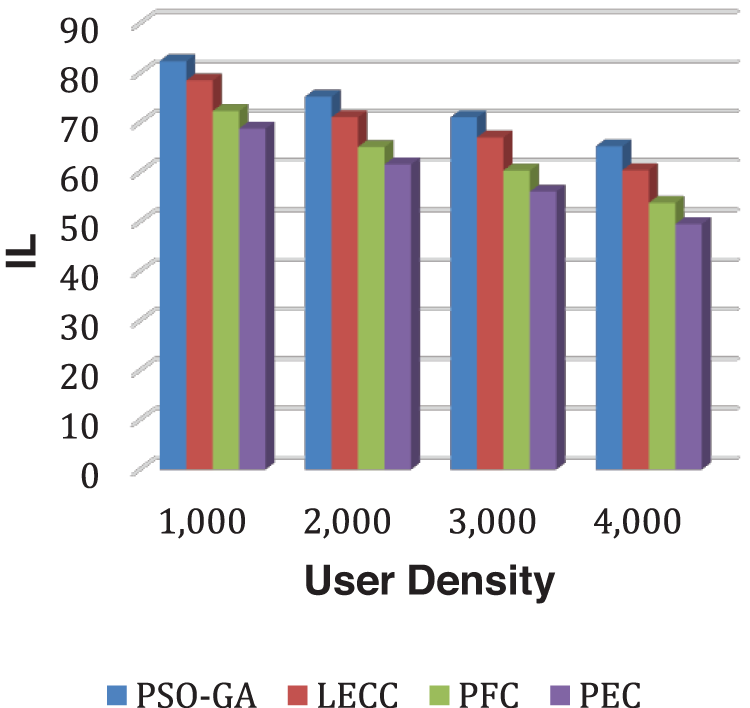
Figure 8: Analysis of IL performance using the Facebook dataset

As observed in all results of the Facebook dataset, the trend overlaps with the Yelp dataset. The proposed model significantly outperformed the underlying static privacy preservation models in terms of DoA, and IL parameters. The suggested model reduced IL by generating optimum clusters and exploiting several graph features for cluster optimization. Because of the scaled data points, the created clusters are more relevant, resulting in little IL. The static methods relied on a fixed number of clusters regardless of the user density, which significantly affects the overall performance. For this experiment, we set 70 clusters for each static method. The proposed enhanced approach internally discovered the optimal number of clusters according to input user density and then, with graph properties, performed clusters optimization to ensure the k-anonymization, t-closeness, and l-diversity. Therefore, it shows improved anonymization (DoA) with reduced IL. Figs. 9 and 10 show how AMICD, and ASSE decrease with increasing user density for each technique. It also accomplished the privacy preservation of all OSN graph elements and achieved higher-level privacy protection, including the t-closeness privacy concept.

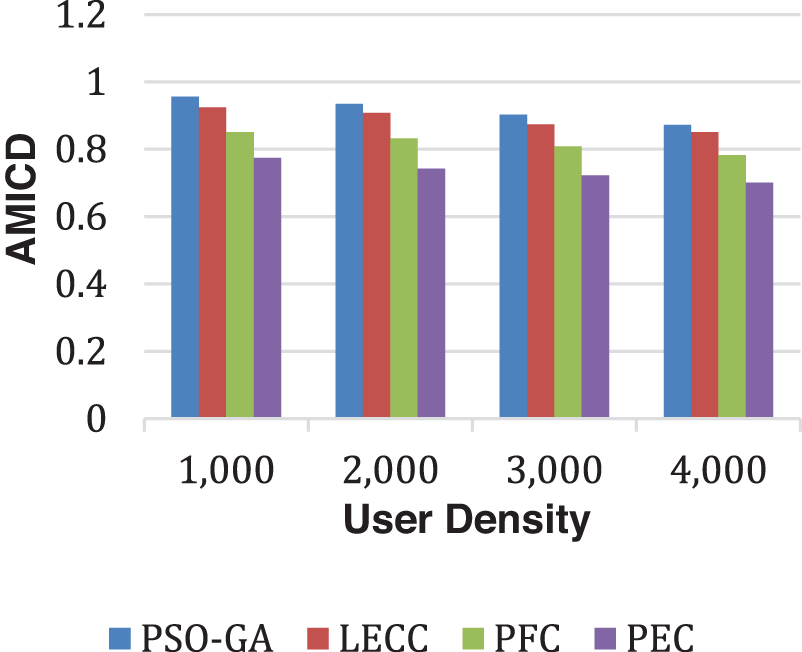
Figure 9: Analysis of AMICD performance using the Facebook dataset

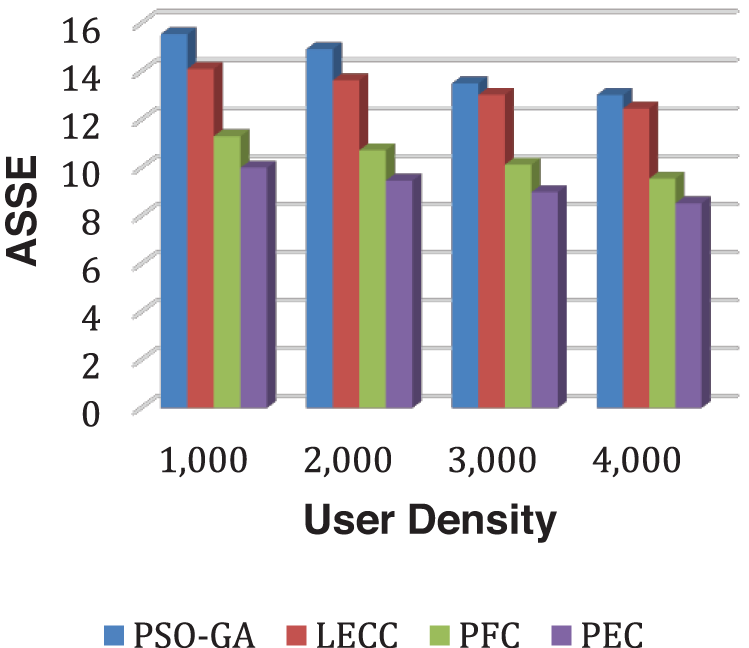
Figure 10: Analysis of ASSE performance using the Facebook dataset

In Fig. 11, we can observe that execution time significantly increases with user density. The proposed approach achieved the trade-off between computational and privacy preservation efficiency and underlying methods.

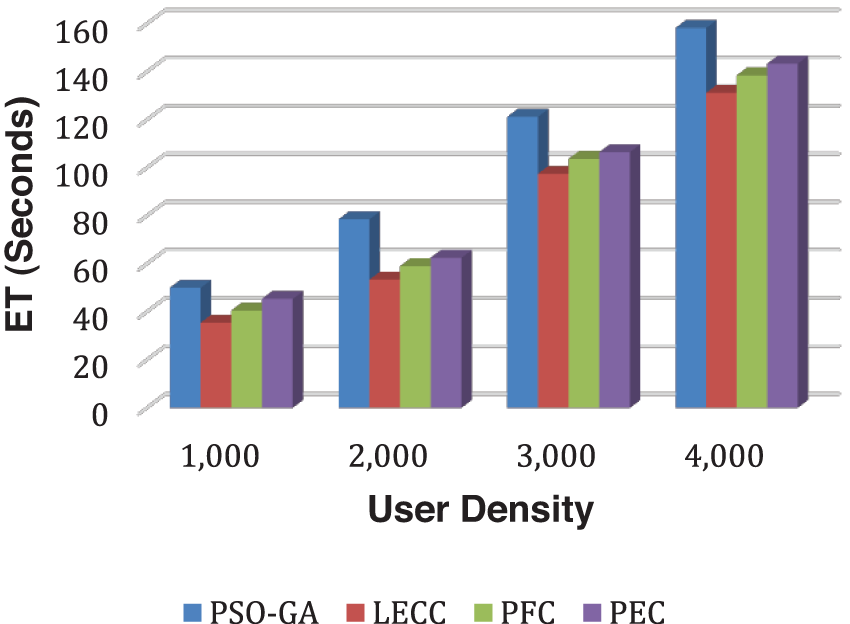
Figure 11: Analysis of ET performance using the Facebook dataset

4.5 Data Privacy and Utility Trade-Off

This section presents the comparative study of the static and enhanced privacy preservation models to claim that the proposed approach achieved data privacy and utility trade-off using two datasets. The data privacy and data utility trade-off are essential requirements for any privacy preservation technique. The underlying methods failed to produce a trade-off among them. The method should provide a higher DoA (data privacy) with minimum data utility (IL, AMICD, and ASSE).

The proposed enhanced privacy preservation model PEC produced higher DoA data privacy with reduced IL, AMICD, and ASSE utilities. The privacy preservation method uses enhanced clustering to compute clusters and has improved data privacy with efficient data utility parameters for both Yelp and Facebook datasets. According to the results achieved for Yelp datasets in the above section, Table 1 shows the average outcomes for each method for all parameters using the Yelp dataset.

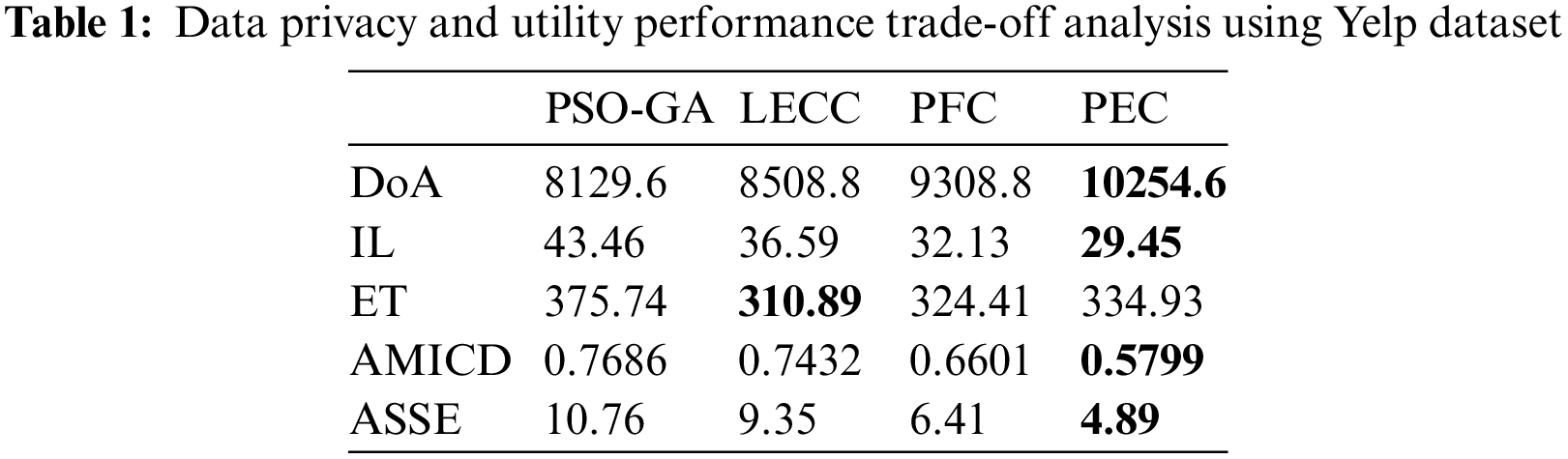
Table 2 shows the average results for each method for each parameter using the Facebook dataset.

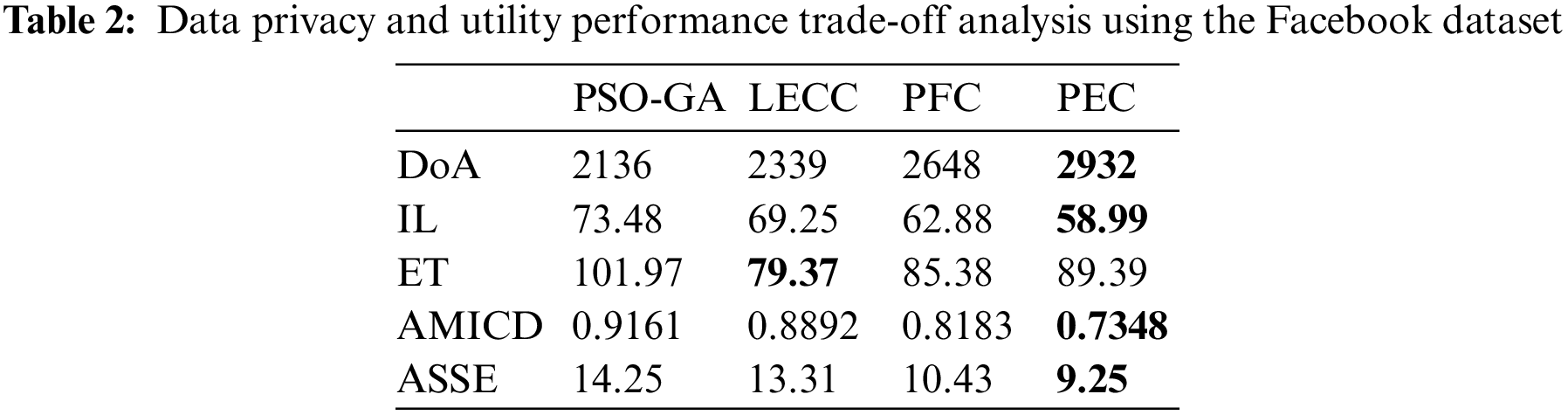
The proposed enhanced privacy preservation model improved four out of five parameters compared to underlying methods. It shows that the ET parameter belongs to the computational time, which is a little higher for PEC, but it also significantly improves the DoA and reduces the IL, AMICD, and ASSE. However, all static methods suffered from poor data privacy and data utility performances. The existing techniques, like PSO-GA and LECC, failed to achieve the trade-off among the five metrics. The PFC method is significantly better compared to PSO-GA and LECC. But dynamics of PEC outperformed PFC further as the existing models like LECC utilized the optimization algorithms, which required more time for convergence. The proposed model focused on establishing more reliable and stable clusters using the multiple graph properties. The stable clusters with dynamically discovered cluster numbers reduce the frequent clustering requirements. Therefore, it reduces the IL.

For the Yelp dataset, PEC improves the DoA performance by 10.16% compared to PFC and reduces IL, AMICD, and ASSE by 8.34%, 12.14%, and 23.71% compared to PFC, respectively. For the Facebook dataset, PEC improves the DoA performance by 10.72% compared to PFC and reduces IL, AMICD, and ASSE by 6.18%, 10.2%, and 11.31% compared to PFC, respectively. The enhanced privacy preservation approach PEC improves data privacy and utility parameters by approximately 10+% compared to our static model PFC, compromising additional 3%–4% computational requirements.

5  Conclusion, Limitations, and Future Work

Due to the growing use of ONS worldwide, several issues concerning the privacy preservation of sensitive information are arising. Privacy preservation becomes an essential need to secure OSNs from malicious users. The distributed nature of OSNs results in privacy preservation is a challenging task. The novel enhanced privacy preservation model proposed in this paper intends to address improving privacy preservation with minimum IL and computational complexity. To achieve improved privacy preservation, the authors have proposed an enhanced cluster mechanism where the number of clusters was computed. The optimal number of clusters for the OSNs leads to minimum IL with the highest level of anonymization compared to static clustering. Apart from this, the proposed work optimized the clusters to ensure the privacy preservation notions such as k-anonymization, t-closeness, and l-diversity. The experimental results proved the efficiency of the proposed model compared to underlying state-of-the-art privacy preservation methods. The DoA of the proposed model has improved by 25.35% compared to the underlying techniques. The IL proposed model has been reduced by 23.23%, respectively.

The system has the following limitations: 1) Although the proposed privacy preservation model delivered the best performances using different OSN datasets, applying optimization algorithms is still room for improvement. The proposed flexible clustering mechanism may lead to unreliable results in some instances due to the lack of an optimization mechanism. 2) The proposed model requires a semi-automatic process for privacy preservation. The proposed model has not explored the emergence of deep learning mechanisms for automatic privacy preservation requirements. 3) The proposed system performs well for static OSN datasets only, which is a system’s limitation; hence the system can be extended for dynamic OSN, where nodes and edges are added and deleted at runtime. Finding sensitive information and effectively implementing anonymization in dynamic real-world networks will be suggested in future work.

The exciting direction to extend the proposed work is to apply the various optimization algorithms to produce the optimized clusters without loss of information. The authors suggest introducing new privacy preservation notions to extend the proposed model.

Acknowledgement: We thank all those referees who contributed their time and suggestions to our work.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

    1. A. K. Jain, S. R. Sahoo and J. Kaubiyal, “Online social networks security and privacy: Comprehensive review and analysis,” Complex & Intelligent System, vol. 7, no. 5, pp. 2157–2177, 2021. [Google Scholar]

    2. B. Alhayani, A. S. Kwekha-Rashid, H. B. Mahajan, H. Ilhan, N. Uke et al., “5G standards for the industry 4.0 enabled communication systems using artificial intelligence: A perspective of smart healthcare system,” Applied Nanoscience, vol. 10, pp. 1–11, 2022. [Google Scholar]

    3. H. B. Mahajan, A. S. Rashid, A. A. Junnarkar, N. Uke, S. D. Deshpande et al., “Integration of healthcare 4.0 and blockchain into secure cloud-based electronic health records systems,” Applied Nanoscience,vol. 10, no. 9, pp. 1–14, 2022. [Google Scholar]

    4. A. Badarala and H. B. Mahajan, “Application of internet of things for smart precision farming: Solutions and challenges,” International Journal of Advanced Science and Technology, vol. 25, pp. 37–45, 2018. [Google Scholar]

    5. M. M. Rad, A. M. Rahmani, A. Sahafi and N. N. Qader, “Social internet of things: Vision, challenges, and trends,” Human-Centric Computer Information Sciences, vol. 10, no. 1, pp. 1–40, 2020. [Google Scholar]

    6. R. Gangarde, A. Sharma and A. Pawar, “Clustering approach to anonymize online social network data,” in Int. Conf. on Sustainable Computing and Data Communication Systems (ICSCDS) IEEE, Erode, India, pp. 1070–1076, 2022. [Google Scholar]

    7. R. Gangarde, D. Shrivastava, A. Sharma, T. Tandon, A. Pawar et al., “Data anonymization to balance privacy and utility of online social media network data,” Journal of Discrete Mathematical Sciences and Cryptography, vol. 25, no. 3, pp. 829–838, 2022. [Google Scholar]

    8. M. R. Prasad and S. Kumar, “Advance identification of cloning attacks in online social networks,” International Journal of Engineering & Technology, vol. 7, no. 3.10, pp. 83–87, 2018. [Google Scholar]

    9. S. S. Maria, Sá José, C. Miguel Ferreira and S. Serpa, “Science communication and online social networks: Challenges and opportunities,” Knowledge Management an International Journal, vol. 19, no. 2, pp. 1–22, 2020. [Google Scholar]

  10. S. Ali, N. Islam, A. Rauf, I. U. Din, M. Guizani et al., “Privacy and security issues in online social networks,” Future Internet, vol. 10, no. 12, pp. 114–125, 2018. [Google Scholar]

  11. Y. Xiang, E. Bertinos and M. Kutylowski, “Security and privacy in social networks,” Concurrent Computer Practical Experiment, vol. 29, no. 7, pp. 1–2, 2017. [Google Scholar]

  12. E. Kosta, C. Kalloniatis, L. Mitrou and S. Gritzalis, “Data protection issues pertaining to social networking under EU law,” Transforming Government People, Process and Policy, vol. 4, no. 2, pp. 193–201, 2010. [Google Scholar]

  13. L. Li, K. Ota, Z. Zhang and Y. Liu, “Security and privacy protection of social networks in big data era,” Mathematical Problems in Engineering, vol. 2018, pp. 1–2, 2018. [Google Scholar]

  14. C. Zhang, S. Wu, H. Jiang and Y. Wang, “Attribute-enhanced de-anonymization of online social networks,” in Int. Conf. on Computational Data and Social Networks, Cham, Ho Chi Minh City, Vietnam, Springer, pp. 256–267, 2019. [Google Scholar]

  15. P. K. Bhanodia, A. Khamparia, B. Pandey and S. Prajapat, “Online social network analysis,” in Hidden Link Prediction in Stochastic Social Networks. Hershey, PA, USA, IGI Global, pp. 50–63, 2019. [Google Scholar]

  16. M. Hay, G. Miklau, D. Jensen, D. Towsley and C. Li, “Resisting structural re-identification in anonymized social networks,” VLDB Journal, vol. 19, no. 6, pp. 797–823, 2010. [Google Scholar]

  17. X. Zheng, Z. Cai and Y. Li, “Data linkage in smart internet of things systems: A consideration from a privacy perspective,” IEEE Communication Maganize, vol. 56, no. 9, pp. 55–61, 2018. [Google Scholar]

  18. R. Gangarde, A. Pawar and A. Sharma, “Comparisons of different clustering algorithms for privacy of online social media network,” in IEEE Pune Section Int. Conf. (PuneCon), Pune, India, pp. 1–5, 2021. [Google Scholar]

  19. C. Sun, P. S. Yu, X. Kong and Y. Fu, “Privacy-preserving social network publication against mutual friend attacks,” in Proc.-IEEE 13th Int. Conf. on Data Mining Workshops, ICDMW, Dallas, TX, USA, pp. 883–890, 2013. [Google Scholar]

  20. J. Cheng, A. W. Fu and J. Liu, “K-isomorphism, privacy-preserving network publication against structural attacks,” in Proc. of the ACM SIGMOD Int. Conf. on Management of Data, Indiana, USA, pp. 459–470, 2010. [Google Scholar]

  21. Y. Zhang, A. O’Neill, M. Sherr and W. Zhou, “Privacy-preserving network provenance,” Proceedings of the VLDB Endowment, vol. 10, no. 11, pp. 1550–1561, 2017. [Google Scholar]

  22. A. K. Jain, “Data clustering: 50 years beyond K-means,” Pattern Recognition Letters, vol. 31, no. 8, pp. 651–666, 2010. [Google Scholar]

  23. S. K. Mydhili, S. Periyanayagi, S. Baskar, P. M. Shakeel and P. R. Hariharan, “Machine learning based multi-scale parallel K-means++ clustering for cloud-assisted internet of things,” Peer-to-Peer Network Application, vol. 13, no. 6, pp. 2023–2035, 2020. [Google Scholar]

  24. M. Nayak and B. Narain, “Predicting dynamic product price by online analysis: Modified K-means cluster,” in Computational Intelligence in Pattern Recognition, vol. 1120. Singapore: Springer, pp. 1–15, 2020. [Google Scholar]

  25. N. Chawla and A. Singh, “Cluster evaluation of online social network’s data by using K-means algorithm,” International Journal of Data Mining Emerging Technology, vol. 4, no. 2, pp. 83–91, 2014. [Google Scholar]

  26. Z. Yan, W. Feng and P. Wang, “Anonymous authentication for trustworthy pervasive social networking,” IEEE Transactions on Computational Social Systems, vol. 2, no. 3, pp. 88–98, 2015. [Google Scholar]

  27. W. Feng, Z. Yan and H. Xie, “Anonymous authentication on trust in pervasive social networking based on group signature,” IEEE Access, vol. 5, pp. 6236–6246, 2017. [Google Scholar]

  28. Q. Liu, G. Wang, F. Li, S. Yang and J. Wu, “Preserving privacy with probabilistic indistinguishability in weighted social networks,” IEEE Transaction Parallel Distribution System, vol. 28, no. 5, pp. 1417–1429, 2017. [Google Scholar]

  29. Z. He, Z. Cai and J. Yu, “Latent data privacy-preserving with customized data utility for social network data,” IEEE Transactions Vehicle Technology, vol. 67, no. 1, pp. 665–673, 2018. [Google Scholar]

  30. M. Siddula, L. Li and Y. Li, “An empirical study on the privacy preservation of online social networks,” IEEE Access, vol. 6, pp. 19912–19922, 2018. [Google Scholar]

  31. Y. Qu, S. Yu, L. Gao, W. Zhou and S. Peng, “A hybrid privacy protection scheme in cyber-physical social networks,” IEEE Transaction on Computational Society System, vol. 5, no. 3, pp. 773–784, 2018. [Google Scholar]

  32. P. Liu, Y. Xu, Q. Jiang, Y. Tang, Y. Guo et al., “Local differential privacy for social network publishing,” Neurocomputing, vol. 391, no. 1, pp. 273–279, 2020. [Google Scholar]

  33. Y. Shao, J. Liu, S. Shi, Y. Zhang and B. Cui, “Fast de-anonymization of social networks with structural information,” Data Science and Engineering, vol. 4, no. 1, pp. 76–92, 2019. [Google Scholar]

  34. N. Yazdanjue, M. Fathian and B. Amiri, “Evolutionary algorithms for k-anonymity in social networks based on clustering approach,” Computer Journal, vol. 63, no. 7, pp. 1039–1062, 2020. [Google Scholar]

  35. C. Zhang, H. Jiang, Y. Wang, Q. Hu, J. Yu et al., “User Identity de-anonymization based on attributes,” in Int. Conf. on Wireless Algorithms, Systems and Applications, Honolulu, HI, USA, pp. 458–469, 2019. [Google Scholar]

  36. M. Siddula, Y. Li, X. Cheng, Z. Tian and Z. Cai, “Anonymization in online social networks based on enhanced equi-cardinal clustering,” IEEE Transaction Computational Social Systems, vol. 6, no. 4, pp. 809–820, 2019. [Google Scholar]

  37. P. Zhao, H. Huang, X. Zhao and D. Huang, “P 3: Privacy-preserving scheme against poisoning attacks in mobile-edge computing,” IEEE Transactions Computational Social Systems, vol. 7, no. 3, pp. 818–826, 2020. [Google Scholar]

  38. A. Ibrahim, T. F. Al-Somani and F. Gebali, “Efficient scalable digit-serial inverter over GF( $2^{m}$ ) for ultra-low power devices,” IEEE Access, vol. 4, pp. 9758–9763, 2016. [Google Scholar]

  39. T. Gao and F. Li, “Protecting social network with differential privacy under novel graph model,” IEEE Access, vol. 8, pp. 185276–185289, 2020. [Google Scholar]

  40. Y. Qu, S. Yu, W. Zhou, S. Chen and J. Wu, “Customizable reliable privacy-preserving data sharing in cyber-physical social networks,” IEEE Transaction Network Science and Engineering, vol. 8, no. 1, pp. 269–281, 2021. [Google Scholar]

  41. A. Niimi and T. Arakawa, “Privacy-preserving data mining metrics for social networking services,” International Journal of Digital Society (IJDS), vol. 12, no. 1, pp. 1672–1677, 2021. [Google Scholar]

  42. K. M. Chong and A. Malip, “Trace me if you can: An unlinkability approach for privacy-preserving in social networks,” IEEE Access, vol. 9, pp. 143950–143968, 2021. [Google Scholar]

  43. K. Zhang, Z. Tian, Z. Cai and D. Seo, “Link-privacy preserving graph embedding data publication with adversarial learning,” Tsinghua Science and Technology, vol. 27, no. 2, pp. 244–256, 2022. [Google Scholar]

  44. T. Zhu, J. Li, X. Hu, P. Xiong and W. Zhou, “The dynamic privacy-preserving mechanisms for online dynamic social networks,” IEEE Transactions on Knowledge and Data Engineering, vol. 34, no. 6, pp. 2962–2974, 2022. [Google Scholar]

  45. R. Gangarde, A. Sharma, A. Pawar, R. Joshi, S. Gonge et al., “Privacy preservation in online social networks using multiple-graph-properties-based clustering to ensure k-anonymity, l-diversity, and t-closeness,” Electronics, vol. 10, no. 22, pp. 1–22, 2021. [Google Scholar]

  46. N. Li, T. Li and S. Venkatasubramanian, “t-closeness: Privacy beyond k-anonymity and l-diversity,” in 23rd Int. Conf. on Data Engineering, IEEE, Istanbul, Turkey, pp. 106–115, 2007. [Google Scholar]

  47. Yelp Dataset Challenge, 2019. [Online]. Available: https://www.yelp.com/dataset. [Google Scholar]

  48. J. Leskovec and K. Andrej, “Stanford large network dataset collection,” 2016. [Online]. Available: http://snap.stanford.edu/data/. [Google Scholar]