An Intelligent Admission Control Scheme for Dynamic Slice Handover Policy in 5G Network Slicing

1  Introduction

Since the evolution of the first generation (1G) wireless technology, there has been a dramatic growth in the telecommunications business. The industry’s expansion can be linked to a rise in need for network service industries from a variety of consumers. These services demand that network providers maintain a high level of QoS for users while efficiently utilizing available network resources. 5G wireless networks are expected to address users’ ever-increasing and diverse requirements. To address customers’ varying needs, 5G wireless networks leverage a variety of technologies, including Network Function Virtualization (NFV), Network Slicing, and Software Defined Network (SDN). Slicing of the network is the process of logically dividing the physical infrastructure or resources into multiple separate virtual networks customized to meet specific users’ unique requirements. While the terminology slicing, virtualization, cloud, edge computing, and programmable network are sometimes used interchangeably, their combination provides numerous opportunities for mobile network operators (MNOs) and service providers. It enables them to rapidly deploy new services, scale and adapt existing services to meet their needs, and serve as the foundation for an open ecosystem [1].

Mobility management refers to the capability of a call to remain connected while it is shifted from one cell to another. When a tenant moves from one area to other during a call, then, it is responsibility of the network to sustain the call while it is transferred after one coverage cell to the other. As soon as a call is relocated to an alternate cell which uses a similar network technology as utilized by the original, the procedure is called horizontal handoff. In contrast, when a call is transported to the cell that uses a separate technology, the procedure is called vertical handover. Inside the 5G networks, the calls will be able to move between slices that strengthen the identical use cases, revealed when intra-slice handover, or between slices that support distinct scenarios, known to be the inter-slice handover. In addition, 5G networks must include efficient algorithms that minimize call blocking or termination during handoffs and minimize the number of handoffs conducted to provide seamless connectivity during handover. Vertical handover algorithms in 5G networks incorporate several bandwidth reservation strategies to prioritize handoff calls and maintain acceptable QoS levels [2,3].

Through the introduction of 5G networks, the customers number requesting various network services is likely to grow tremendously. As the users of the network increases, then extra calls are expected to be blocked (ignored) or dropped when users change from one coverage region to another, necessitating the implementation of effective algorithms for call admission control to minimize the number of dropped or blocked calls and ensure that network resources are efficiently utilized. Additionally, because network users are more tolerant of dropped handoff calls, it is necessary to incorporate handoff call prioritization schemes into the call admission management algorithm. Further, the consequences of subscriber mobility at networks as well as handoff call prioritization must be investigated. 5G networks must include efficient algorithms that minimize call blocking or termination during handoffs and minimize the number of handoffs conducted to provide seamless connectivity during a handover. Vertical handover algorithms in 5G networks incorporate several bandwidth reservation strategies to prioritize handoff calls and maintain acceptable QoS levels [3].

In this paper, we investigate how to develop and evaluate an algorithm aimed at making handover decisions in 5G sliced networks. Ground truth that signifies the training sets accuracy classification approaches in the field of machine learning will be studied to check along with the selection of a most suitable technique. Therefore, we discuss the network model’s design and implementation of self-optimization Fuzzy Q-learning of the decision-making algorithm for slice handover. The fuzzy Q-Learning algorithm integrates action-state estimation coupled with action selection memory of into a single framework. By consolidating the state-action calculation and policy collection memory constructs into one frame, Fuzzy Q-Learning’s exploration activity is simpler. Consequently, the algorithm is better appropriate for planning issues such as multi-stage decision-making. The main contributions of our proposed scheme are as following:

•   Leveraging supervised learning algorithm as prior knowledge of additional capacity, ΔC(s,n). The knowledge enables the estimation of the limit of ΔC(s,n) along with its general behavior under varying traffic load conditions.

•   Leads to the objective to make the AC method of Q-learning learning easier to implement by encoded simpler the action selection in the term of Fuzzy logic management rules. The prior learning is for state analysis and evaluation, which can be revealed via fuzzy rules to guide the reinforcement learning.

•   We have compared the proposed fuzzy Q-learning methodology with the conventional approach with respect to the probability of blocking via utilizing an exploitation policy.

•   Finally, the results are evaluated for probability in the blocking in the three real-Internet topologies such as Abilene, Substrate, and USnet.

2  Literature Review

Studies have been undertaken on the Admission Control issue in 5G communication. Han et al. [4] present a utility-focused, multi-service approach to network slicing centred on Queuing Theory towards maximize network functionality. This approach accounts for impatient clients by utilizing distinct queues for two particular sorts of requests. Raza et al. [5] suggest an AC process that uses Big Data for traffic forecasting to boost public services providers’ profits. This methodology accepts slice requests in case when there is no risk of service interruption. Moreover, Salvat et al. [6] propose a heuristic-based admission control technique for maximizing user QoE. This strategy decides the acceptance for the slice requests dependent on the Radio Access Network (RAN) minimum as well as maximum rates of data rates along with the provided resources. In addition, Challa et al. [7] present an AC prototypical for optimizing resource monetization based on a formulation of the knapsack issue. Bega et al. [8] present a semi-Markov judgment process-based analytical model and a Q-learning related algorithm for performing AC on individual requests for slicing. Raza et al. [5] give an AC method based on reinforcement learning to maximize provider profit; this approach considers the flexibility of the 5G RAN after that prioritizes requests through varying latency needs and predicted profits. The proposed solution uses a Q-learning agent to determine which slices should be accepted to maximize income. Bega et al. [9] presented a DRL-based method for performing AC on individual RAN slicing that requests to optimize the infrastructure provider’s monetization.

Within 3GPP, we can relate to the current work that discusses the network slicing which is a significant element of 5G framework layout. To illustrate machine learning utilization, the works in [10] discuss the improvements in cognitive abilities. Machine learning entails an ability to adapt according to a complete infrastructure which is based upon the historical data, that ensures whether network management is able to monitor the key network parameters in 5G, and recognize configurable metrics, along with changing optimally their values for achieving the superior network outline, shown via a combination of key performance parameter indicators. Lastly, with the next generation for management of network and a key engine for 5G, and an introduction with cognitive network administration. There are also no strict specifications associated with the regular eMBB, mMTC, or URLLC slice of traffic types in [11]. The requirements are defined in a highly generic manner for the three basic types of traffic, eMBB, URLLC, and mMTC. As the number of different slices handled in one network is not constrained theoretically, the author restricts the number of different types of tenants (which corresponds to multiple interpretations of slices) to three types, primarily mMTC, eMBB, and URLLC, to make the study more tractable.

Salvat et al. offer a handover approach based on reinforcement learning in [6]. The method services a centralized reinforcement learning representative to manage network measurements from UEs and to use the data towards govern an optimal handover selection to optimize long-term utility. The proposed method is assessed and compared to traditional handover algorithms, and the outcomes indicate an increase of at least 20% in the proficiency of making the accurate handover decision. More and more, Chen et al. [12] recommend a Markov chain standard and sensitivity evaluation-based and threshold-based admission control approach for calling. The sensitivity analysis is used to constrain the number of recalculations conducted by the algorithm, altogether with Markov chain conjunction is utilized to derive the optimal policy.

3  Motivation and Problem Statement

Machine Learning (ML) is intended for a subset of applications for which it is impossible to create explicit algorithms with the desired performance. Learning methods are required when knowledge (like human skill) does not exist or is difficult to obtain. Nonetheless, ML algorithms can utilize training data or prior knowledge to construct useful models for a variety of applications. Several artificial intelligence strategies discussed to construct a self-optimizing AC for 5G. The proposed idea come under the well-known AI subject of machine learning, characterized by the emergence of two distinct learning algorithms.

Fuzzy logic enables the adoption of human awareness as if-then inference guidelines. A particular fuzzy if-then principle is expressed as follows: “If x equals to A, next y is equal of B”, where A along with B represent the linguistic principles (such as low, or medium, or high) specified with fuzzy sets X as well as Y, correspondingly. Input as well as output sharp values (for example the quality of signal and handoff choice) are denoted by x in addition to y. The if-condition for the rule “x is denoted with A” is also referred to as the rule’s antecedent, whereas the then-part of the rule “y = B” is known as the rule’s consequent. The antecedent, p, indicates the consequent, i.e., q, for an if-then rule. If p condition is true in binary logic, then q will also be true (p → q). However, according to fuzzy logic, when p will be true to certain extent of association, then q is too considered as true up to same degree [13].

The final phase of fuzzy interpretation process is defuzzification, which defines a single specific value as of a fuzzy output collection. An approach based on fuzzy logic appears ideal for managing the imprecision of real cellular networks (wireless) [14]. In fact, fuzzy system strategies have recently been presented as a means of managing handoff assessment algorithms. For example, the study illustrated in [15] provides a handoff choice method established on type-2 and fuzzy logic 3 that considers a range of access network along with features for user and chooses the network beside a highest value of satisfaction.

Moreover, a major primary limitation of Q-Learning is the inherent time needed, which is usually relatively long. Throughout each optimization iteration, the agent takes action to improve the correctness of the Q-estimates. An initial default rule should be founded (e.g., choose the random movements). The agent later sees this policy till it congregates with optimal Q* value corresponding to the state and its action. Depending upon the intricacy of the optimization situation, MNO expectations for higher convergence times may not be met.

In addition, it may be observed that the rules made by a for fuzzy logic may not be best possible. An optimization technique must be implemented in order to construct a precise knowledge base. Hence, this research studies self-optimization which focused on aspects concerning admission control. However, in certain applications for optimization, the continuous states-action spaces can result in highly complicated circumstances. To alleviate this issue, the integration of fuzzy rationality with Fuzzy Q-Learning is applied to discretize state as well as resultant action spaces. Consequently, instead of getting a vague number for states and their actions, the fuzzy logic restricts these numbers based on the requirements of each application exclusive of compromising time of convergence or state accuracy.

Q-learning based admission control can map every single state to the ideal action. Comparably, the Fuzzy Logic Control (FLC) can map every fuzzy set to the optimal action. Fig. 3 depicts a potential Learning-based optimization method, the agent of which executes the learning technique, where the instant reward might be any conventional KPI, for instance the ratio for call blocking or coverage of cell-edge, subject on the intended application. The basic Reinforcement Learning (RL) method is characterized as a Markov Decision Process (MDP) with state, action, and reward as its three components. The current environment is represented as a state st at every time slot t. The agent takes action at based on the state and a policy. The agent then receives reward rt, and the next state st+1 can be observed. The purpose of the RL agent remains to learn such a policy which maximizes the final cumulative reward. In this scheme, there is an additional component, critic that is used for evaluating the decisions by reward received and reward expectation. An agent attempts to learn as of its environment i.e., the optimal actions set to optimize the intended cumulative rewards as well as the performance of the overall system.

Rk=rk+γrk+1+γ2rk+2+γ3rk+3…=∑t=0∞γtrt+k(1)

where Rk represents the collective reward by k-th time moment (i.e., iteration). rt + k represents the immediate reward received for doing an action on the iteration (t + k). γ remains the discount component, with values approaching to 0 indicating that an agent attempts to maximize immediate benefits and values near to 1 showing that long-term high rewards are considered.

4  Proposed Idea

4.1 System Model

4.1.1 Supervised Learning

The scenario assumes that there are N cells designated n = 1…, N that are shared with S tenants labeled s = 1…, S. The total of Resource Blocks (RB) required by new Radio Access Bearers (RAB) and already declared RABs does not go beyond the amount of RBs available within a cell ρ(n). Therefore, the capability check requirement estimates if the calculated cell has satisfactory physical resources on the way to admit another RAB, which is expressed as given below:

∑s′=1SρG (s′,n)+Δρ≤ρ (n) αth(n)(2)

where ρG(s′,n) shows the average quantity of RBs for the n-th number cell designated to RABs for the s-th user. Δρ is the approximate RBs needed for the newly allowed RAB that is calculated with respect to the mandatory bit rate Rreq and the probable bit rate according to RB sˇ(n).

Δρ=Rreqsˇ(n)(3)

An upper limit for the RBs used by a tenant’s RABs in accordance with the ability stated in an SLA. For this instance, the capacity stands determined via a Scenario-Aggregated-Guaranteed-Bit-Rate i.e., (SAGBR), that establishes the guaranteed bit rate intended for the total amount of RABs for that tenant. The insignificant capacity part regarding tenant s, along with C(s), can be defined as a ratio of the SAGBR(s) around all cells to the grouped SAGBR of whole tenants:

C(s)=SAGBR(s)∑s′=1S SAGBR(s′)(4)

The per-tenant volume sharing check requirement can be stated: ρG(s,n)+Δρ≤ρ(n)αth(n).(C(s)+ΔC(s,n)). As, the previous condition assures that s-th tenant should be permitted to utilize a fraction for the RBs appearing in the n-th region of a cell specified by C(s), and also an additional label ΔC(s,n) that considers any remaining capacity received from the remaining tenants.

The development of supervised learning technique to exploit the learning of ΔC(s,n) takes two primary goals. First, the experience itself allow the determination of the limit of ΔC(s,n), in addition to its general behavior in various traffic aware situations. This indicates the second objective, which is to make the AC method for unsupervised learning easier to implement. As there are four variables to optimize themselves (that are ΔC(1, 1), with ΔC(1, 2), combined with ΔC(2, 1), and ΔC(2, 2)). Hence, the time of converge for an optimal solution will possibly be excessively long. Consequently, supervised learning can be applied to variables ΔC(s, n) for the sake of simplification, and the remaining will be preferred for optimization.

As a supervised learning technique applicable to the scale of this act. Therefore, an Adaptive-Neuro-Fuzzy-Inference-System (ANFIS) is planned. ANFIS is a type of ANN which contains a Takagi–Sugeno fuzzy interpretation engine, that only provides one single output (that is related to ΔC (s, n)) after the defuzzification stage. On the other hand, four inputs are considered, each of which corresponds to the suggested loads for each tenant within every cell, as extracted after the simulator. In addition, the fuzzy inference system (FIS) will be combine both grid panel along with subtractive clustering. Consider the most recent algorithm, in that each input contains as possible membership functions regarded as a number of discovered clusters. Fig. 1 identifies 10 clusters as an example, although a greater or fewer number of clusters could be detected depending on the trade-off among training error as well as training duration. The overall anticipated learning scheme is demonstrated in Fig. 2.

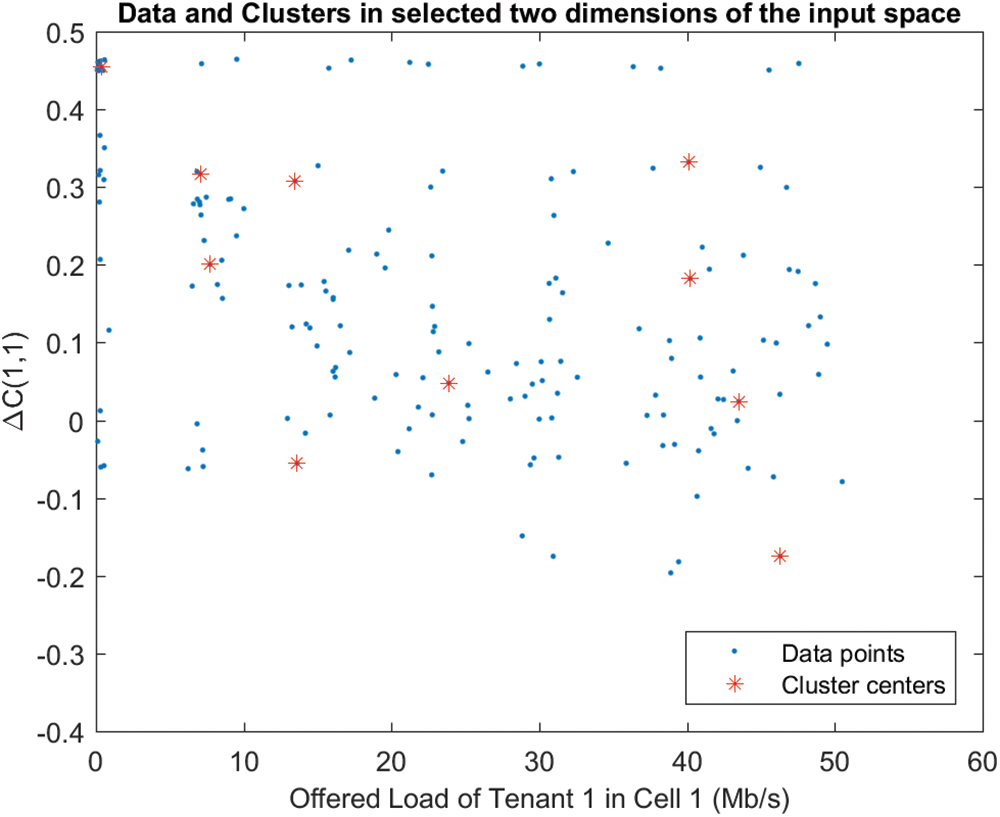
Figure 1: Subtractive clustering technique

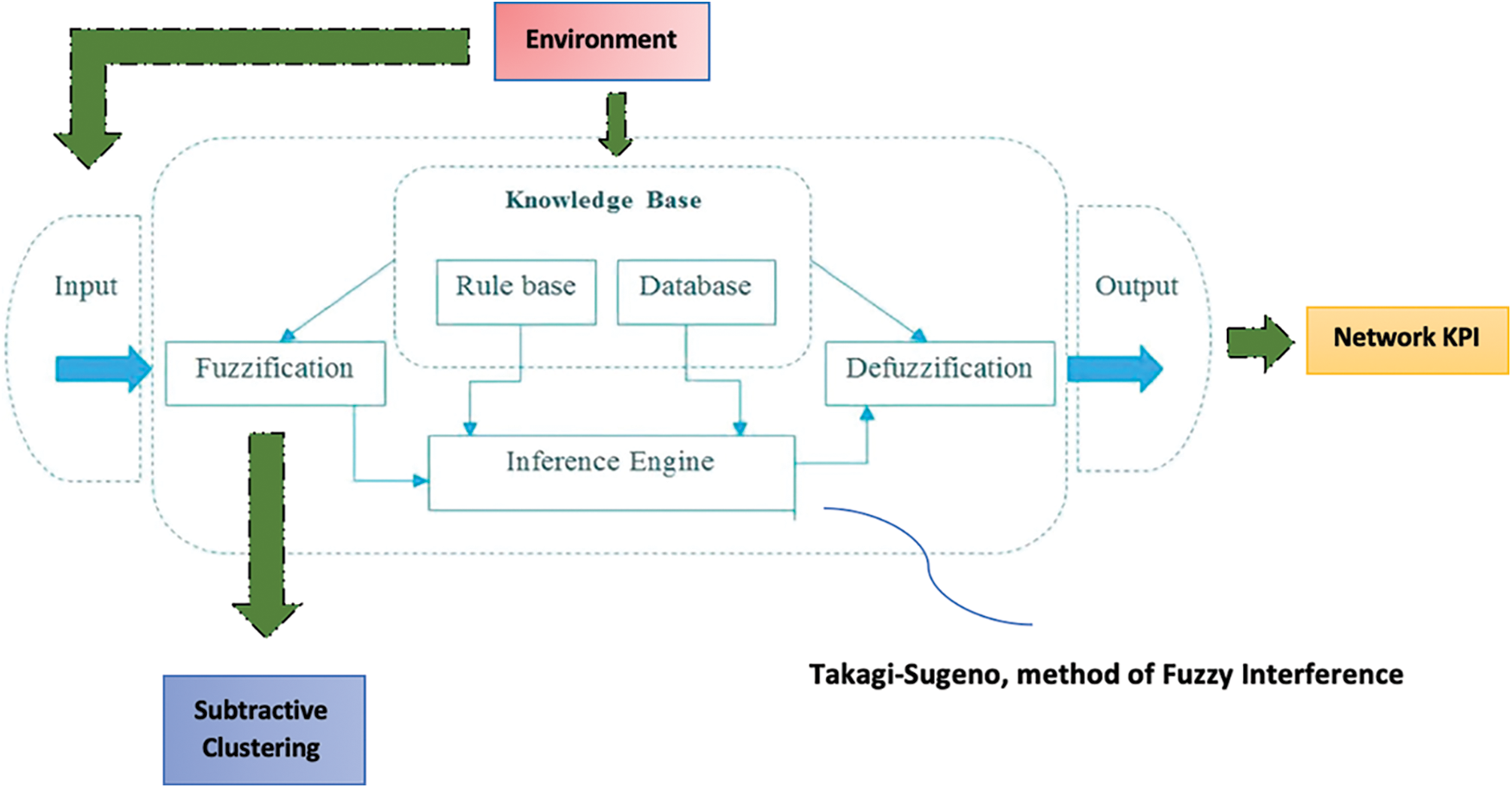
Figure 2: Supervised learning policy designed to exploit ∆C(s, n) knowledge

After that, once the input/output set of data gets trained using the aforementioned method, experience of ∆C (s, n) will be accessible to exactly exploit untaught input data. The subsequent phase will be to extract the ideal value i.e., ∆C (s, n) for a given traffic load condition in every optimization rehearsal for an unsupervised learning system, leaving a specific ∆C(s, n), that will be self-optimized for ease purpose.

4.1.2 Fuzzy Q-Learning

To attain self-optimization, each disseminated agent should understand which parameter tuning action is to take based on the current process state. Herein, the lines presented below provide an overview of the fundamentals for fuzzy Q-learning.

In brief, Q-learning provides a reinforcement learning strategy whose purpose is to increase an cumulative reward through environmental activities. Q-learning incrementally increases the size of a Q-function, revealed as Q(s, a), via calculating a discounted rewards in direction of future which are associated with actions among particular states s. This paper considers a fuzzy variant of Q-learning to reap the advantages of fuzzification. Fundamentally, fuzzy learning-based Q learning enables the discretization of state action spaces, avoiding the need to deal with continuous and consequently complex regions.

Fuzzy sets consist of components with varying degrees membership. In traditional set theory, a membership of items in the set is evaluated in terms of binary. In contrast, the fuzzy set theory allows for a detailed evaluation of an element’s set membership. A membership function expresses a statement’s degree for truth, that identifies the extent with which a statement is true. Moreover, the membership functions permit limited membership within a set. Typically, the mapping for input values to membership functions have being called “fuzzification.” In addition, Membership functions will be coupled with fuzzy “if... then” procedures to conclude, as in “if x will be larger and y is smaller, then z should be normal,” where “high/large,” “low,” as well as “normal” are considered membership functions for the identical fuzzy subsets.

4.1.3 Design and Optimization of the Fuzzy Sets

In this work, fuzzy sets can be viewed as a combination of states obtained by clustering the states, meaning that any state S can be categorized into a fuzzy set A: S∈A. Each state is assigned to one action a under the control of a neural network, S→a. The mapping rules are reasonable if the neural network is well-trained, hence it can be argued that the fuzzy logic controller uses the following mapping: A→a.

If states s1 and s2 and actions a1 and a2 exist, the following conditions are satisfied:

S1≠S2(5)

a1≠a2

The states s1 and s2 both belong to fuzzy set A: S1,S2∈A. And based on the rules of neural network mapping:

S1→a1(6)

S2→a2

There will be two distinct actions a1 and a2 for the same fuzzy set A in this circumstance. However, the fuzzy logic controller’s mapping rules must be uniquely determined. We define the function of FLC π and initialize it with zeros to address this problem:

π(A,a)=0∀A,a(7)

The value corresponding to the function is updated using the following formula:

π(A,a1)←π(A,a1)+1(8)

π(A,a2)←π(A,a2)+1

Thus, we employ a neural network for accomplishing a task with constantly update function π corresponding to the subsequent mapping rules, causing in the FLC with nearly identical functionality to the neural network. To make such rules which FLC learns after neural network as accurate as feasible, we also create a state s0 in the actual process. If the task can be performed under a control of the neural network, reset the preliminary state to s0; restart the control procedure, and update the function π; otherwise, establish a new state.

Furthermore, the self-optimization practice’s architecture is illustrated in Fig. 3, which is undoubtedly distributed. Moreover the optimizer Q-Learning unit, that fill in the Q-function in response to earned reward, the fuzzy reasoning controller monitors a set of states from environment in the form of inputs (i.e., recommended traffic loads altogether with ΔC(s, 1)) and a set of actions considered outputs (i.e., increase of ΔC(s, 1)). Firstly, it was intended to self-optimize ΔC(s, 1) and ΔC(s, 2), whereas supervised learning was used to optimize ΔC(s, 2). Nonetheless, due to the enormous time required for optimization, it was agreed for leaving ΔC(1, 1) as unique variable for self-optimization.

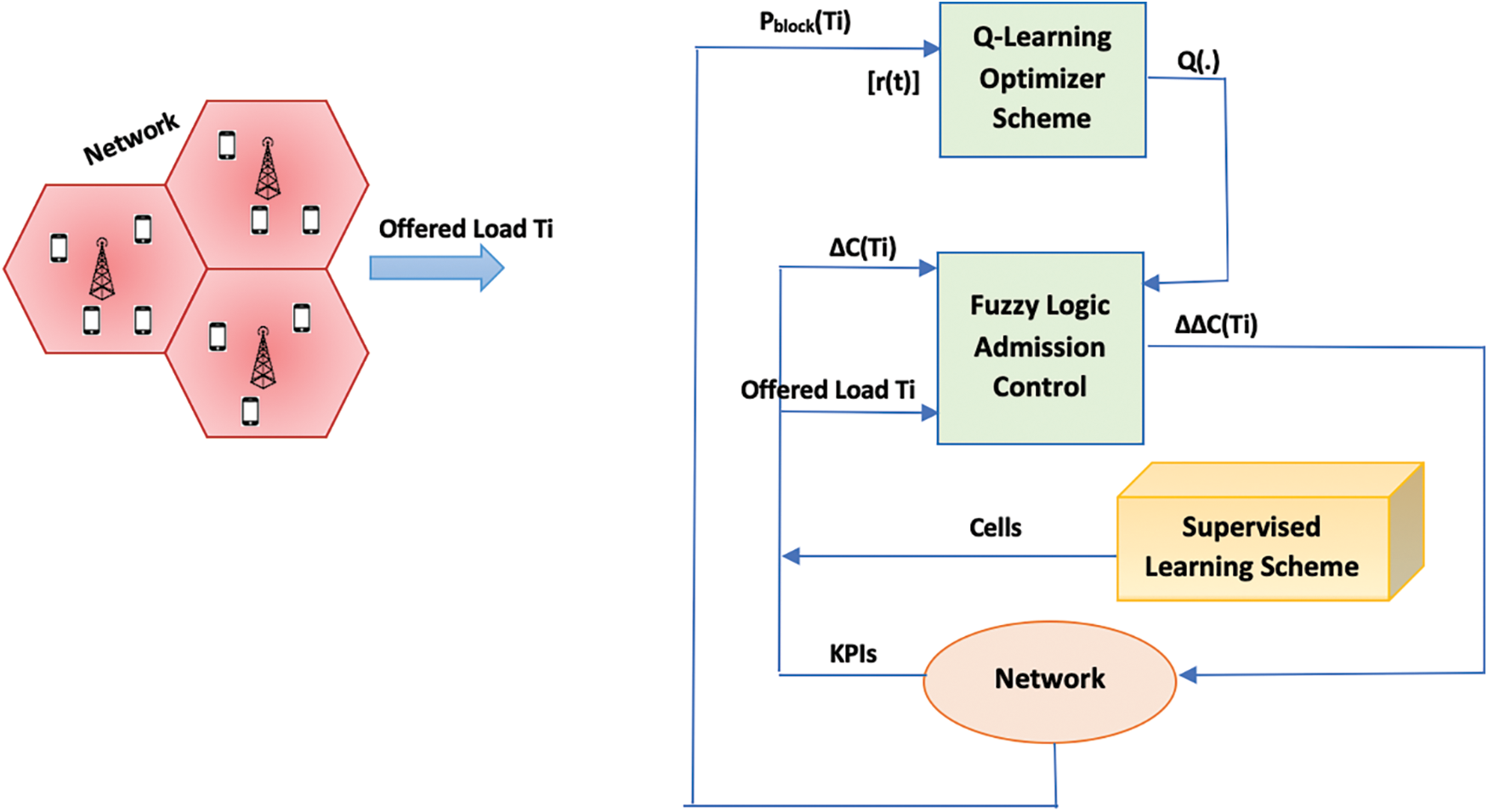
Figure 3: Architecture as well as proposed system model

Let’s start by identifying the notion of q-value. With each FIS rule, a[i, j] is called as the jth action for rule i as well as q[i, j] is defined as its accompanying q-value. i.e., quality value. As a result, the greater the value for q[i, j], the greater the trust in the specified tuning action corresponding to that value. The following easy requirement is used for initialize of q-values in an algorithm:

q[i,j]=0,1≤i≤N and 1≤j≤A(9)

Herein, the q[i, j] is regarded as the associated value to rule i along with action j. Similarly, N is considered to be the total mark for rules in conjunction with A which is s the number for available actions according to rules.

For each distinct activated rule, the action selection is performed following by exploration policy. In addition, the agent must select those actions that have generated highest rewards previously. Though, the agent discovers such action’s accomplishments by attempting the actions which were not selected in advance. After that, further exploitation phase, along with exploration policy must be considered to track an unfamiliar actions who bear maximum sustainable reward.

The CAC algorithm is in charge of determining whether a call should be accepted or rejected. A call is accepted into a resource-constrained network if and only if the slice contains sufficient bandwidth to allow the call without affecting the network’s agreements to other ongoing calls.

A={a={a1n,…,ain,a1h,…,aih}}(10)

With ain representing the action taken upon arrival of new calls and aih representing the action taken upon arrival of handoff calls.

ai={0,reject call1,accept call into slice 1U,accept call into slice U(11)

where ai is regarded an action for rule i. Normally, during the optimization process, is not fixed. Instead, it gradually decreases to values near to zero, indicating that the evaluation of prospective actions reduces. The subsequent determinant of the global action is as under:

a(t)=∑i=1Nαi(s(t)).ai(t)(12)

where a is the tuning action and αi(s(t)) is the activation function for rule i. In other words, αi(s(t)) reflects the factual accuracy of an input state s(t) in the t-th iteration.

αi(s(t))=∏i=1Mμi,j(xj(t))(13)

where M represents the FIS inputs. Moreover, μi,j(xj(t)) represents the membership function for the i-th rule and j-th input. For example, if we consider the first rule for all four inputs are labeled as low (L), and the activation function can be written as following:

αi(s(t))=μ11(x1(t)).μ12(x2(t)).μ13(x3(t)).μ14(x4(t))(14)

The Q-function can be determined using the activation functions and q-values of the particular rules:

Q(s(t),a(t))=∑i=1Nαi(s(t)).q[i,ai](15)

where Q(s(t), a(t)) is the Q-function value for state s with action a. The subsequent phase consists of allowing the system to expand to the subsequent state s(t + 1). On this stage, r(t + 1) is observed as a reward:

r(t)=r1(t)+r2(t)+k1(16)

where r(t) represents the overall reinforcement signal, r1(t) and r2(t) represent the reinforcement signal contributions of both tenants along the two cells, and k1 is a constant parameter. In particular, ri(t) signals are calculated as follows:

ri(t)=k2.log(1(Pblock(Ti)+k3).1000+1)(17)

where k2 and k3 are constant values and Pblock(Ti) is the tenant blocking probability for the scenario. Table 1 provides the parameters required to process the support signal. Furthermore, when blocking probability related with both tenants is zero, the maximum reward is obtained (which is 1).

After observing the reward of the later state r(t + 1), while the value for the new is denoted by Yt(s(t+1)) can be calculated as follows:

Yt(s(t+1))=∑i=1Nαi(s(t+1)).maxkq[i,ak](18)

The error signal between two sequential Q-functions will be utilized to update the q-values. It is expressed by:

ΔQ=r(t+1)+γYt(s(t+1))−Q(s(t),a(t))(19)

where Q represents the error signal, r(t + 1) represents the reward, γ represents the discount factor, and Q(s(t), a(t)) represents the previous state’s Q-function. γ is set to 0.7. Then, the q-values can be updated using a standard gradient descent algorithm:

q[i,ai]=q[i,ai]+η.ΔQ .αi(s(t))(20)

where η is the learning rate, and its value is set to 0.5, indicating that older knowledge is given equal weight to new information. The aforementioned practice is repeated starting from action assortment in anticipation of convergence is achieved. Algorithm 1 provides a summary of the algorithm discussed above.

4.2 Slicing Scenario

4.2.1 Assumptions

To implement the network model, some assumptions must be made. There are:

•   The MVNO prioritizes slices equally while allocating resources to maximize radio resource utilization.

•   Priority is assigned to users at each given slice according to their time for arrival.

•   Because the UEs mobility is not present. Hence, mMTC slice is unable to assist handoff calls.

•   In uRLLC and eMBB, handoff calls get priority as compared with new calls.

•   In a slice, users are spread uniformly.

The slices are known as mMTC, eMBB, uRLLC, or else slice 1, slice 2, and slice 3 in turn. If a call that is moved to another slice which supports a different use case, for example, when an eMBB call is assigned to an uRLLC slice, this is referred to as inter-slice handover. In another case, when a call is transferred to a slice that supports the same use case, for example, when an mMTC call is assigned to an mMTC slice, this kind of handover is known as intra-slice. Due to the fact that calls on behalf of uRLLC slices contains severe admission conditions, they cannot be allowed to any slices. Calls that are directed to eMBB have a demand that the uRLLC slice can meet, and hence can be assigned to an uRLLC slice. Because the conditions for mMTC slices are flexible and are likely met by both eMBB as well as uRLLC slices, they be capable of assigning to either slice. Calls are conceded to a slice when only if the slice has sufficient radio resources to meet the call’s constraints without interfering with other accepted calls; else, the call is likely transferred to another cell slice, blocked, or dropped. The use case of the sliced handover concept describes in Fig. 4.

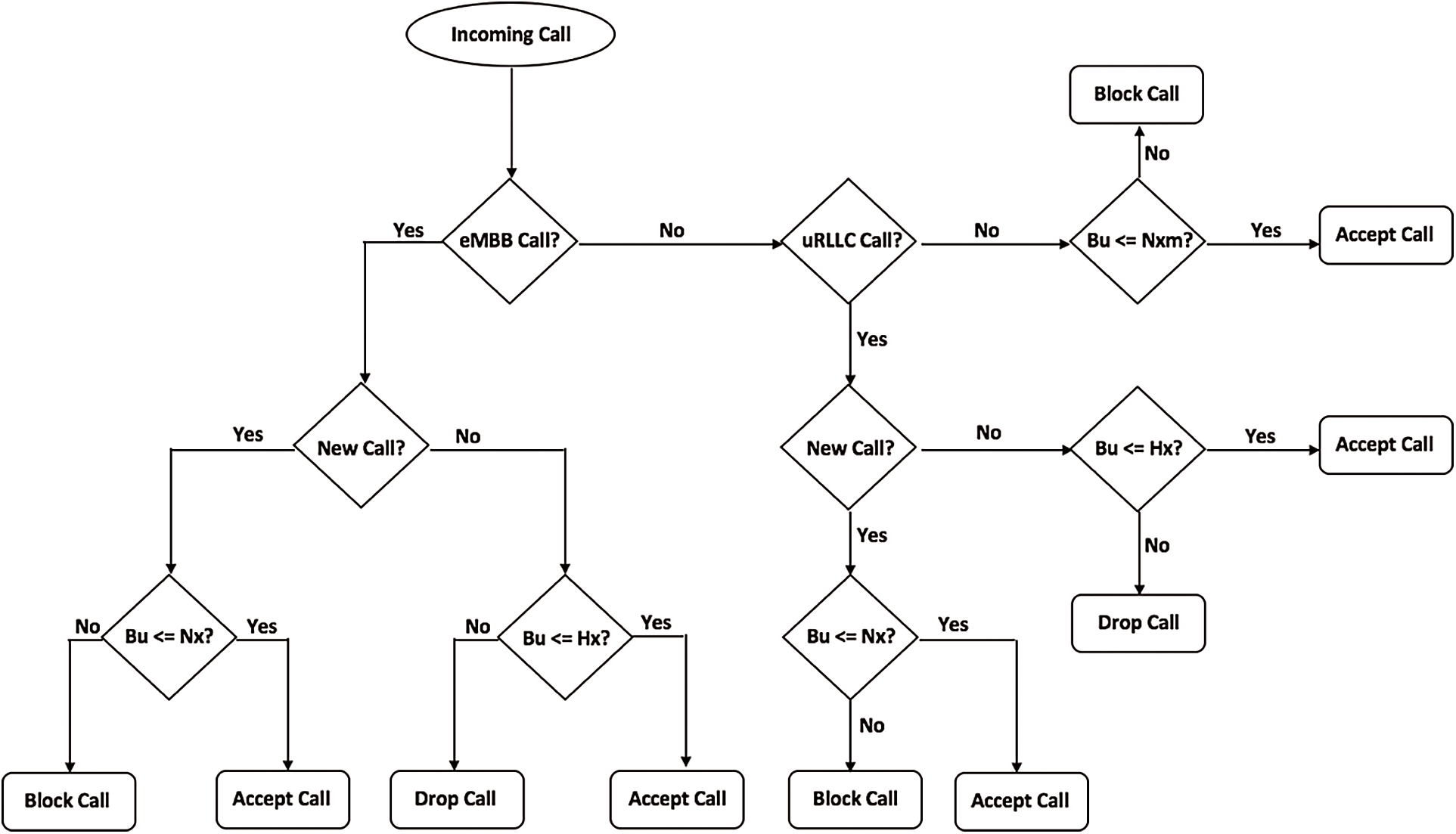
Figure 4: Use case of slice handover

Additionally, mMTC slice calls can be permitted into the uRLLC and eMBB slices, as the mMTC slice calls’ QoS requirements can be met in both the eMBB and uRLLC slices. eMBB slice calls can be permitted in the uRLLC slice since the uRLLC slice can satisfy its QoS requirements. Because no slice can satisfy the uRLLC slice’s QoS requirements, uRLLC slice calls cannot be handed over to any slice. There are some slice parameters are described in this work:

•   Threshold—Because wireless network users are more biased of stopped handoff calls compared with blocked calls (new), it is necessary to assign handoff calls a greater priority. To ensure that consumers’ QoS needs are met, a threshold will be established to prioritize handoff calls across new calls. The threshold can be static or dynamically set inside a slice. Because uRLLC and eMBB slices allow handoff calls, threshold values are set. A fixed threshold is applied in this research. When the slice is initialized during simulation, threshold value is provided as a metric.

•   Capacity—The term slice capacity refers to the maximum quantity of radio resources that a slice may provide. The MVNO’s overall capacity equals the sum of its 3 slices. The slice capacity changes according to the number of resources requested by the calls.

•   Basic Bandwidth Unit (BBU)—It explains the bandwidth conditions for calls. Several calls demanding services since slices have distinct BBU requirements due to their requirements. Because all bandwidth given by a slice is similar to its capacity. Therefore, handoff calls as well as new call are accepted only when there is sufficient bandwidth available.

•   Arrival Rate—The average calls that arrive in an available network is referred to as the call arrival rate. The rate with which calls arrive is determined by the poison distribution.

4.2.2 Experiment Setup

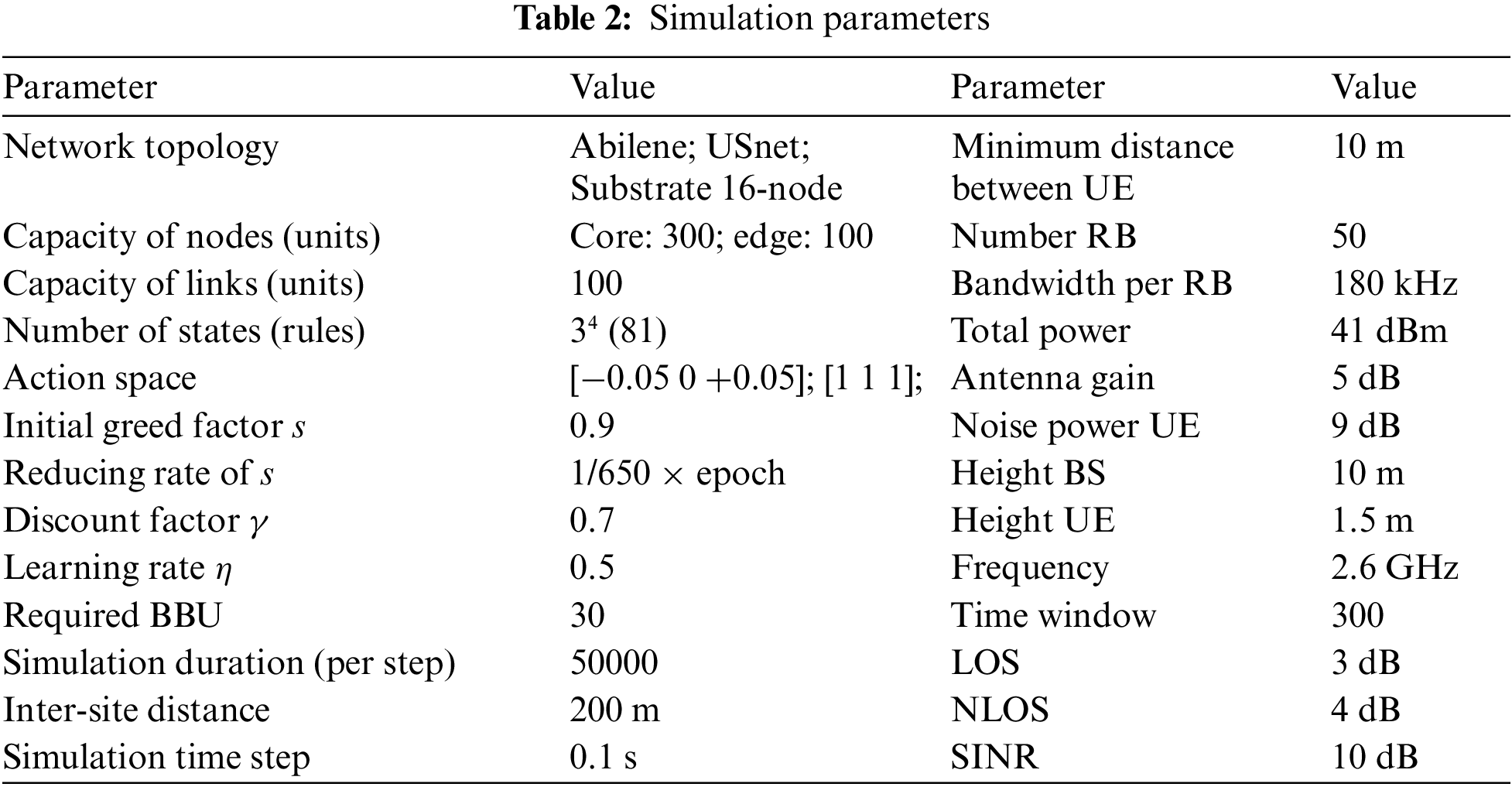
The architectural modules developed using Matlab 2021a and Python 3.8. The substrate network topology is generated by the simulator using Omnet++. Various topologies were utilized in the experiments, such as Abilene, US_Net, and 16-nodes networks topology. In this study, results are presented for an Abilene architecture consisting of 3 core nodes and 8 outer nodes with corresponding capacities of 300 and 100 processing units. Each link has a capacity of 100 bandwidth units. This topology’s results were comparable to those of the other topologies used in the performance evaluation. The bandwidth requirements for the virtual links in the eMBB, URLLC, and mMTC graphs are 3, 2, and 1, respectively. The details of the simulation topologies are given in Table 2. In addition, the simulation parameters and associated values utilized throughout the studies are summarized in Tables 1 and 2.

We represent the 5G core network substrate as an undirected graph with labels and weights: SN = {N, L}, where N denotes the node set, N={n1,n2,…,nm}, and L denotes the link set, L={(n1,n2),(n1,n3),…,(n1,nm)}. Each of the nodes ni ∈ N, has a processing capacity denoted by the symbol CPU (ni).

Consider an InP i that provides infrastructure services to the group of mobile virtual network operators, H={1,2,…,|H|}. Each MVNO consists of a number of slices is: Xh={1,2,…,|Xh|}. with each slice isolated from the rest of the network’s slices. A use case and capacity define each virtual network slice. The capacity for lice is known as the highest quantity for radio resources which the slice is able to deliver. Various studies reveal that radio sources are earmarked in provisions with time slots, code sequences, or frequency channels, depending upon multiplexing technology; nevertheless, this study, capacity is distributed in terms of Necessary Bandwidth Units (BBU). Hence, a use case implies a collection of essential services that contribute to standard needs i.e., eMBB. The MVNO might receive a requesting services call and transfer it to the slice keeping in view its requirements. For example, the video streaming apparatus can submit request for a service, and an MVNO will allow it to eMBB slice. Therefore, the MVNO analyze the slice limitation for load during admission of a call. If the current eMBB slice will be full, the call may be handled in the upcoming slice that meets the call’s parameters.

Each slice xh ∈ Xh belonging to an MVNO h has a capacity denoted by Cx; thus, the MVNO’s total capacity is: Ch=∑1XCx.Each slice has a list of users Uxh. Users are fully dependent upon that slice and are designated by: Uxh={1,2,…,|Uxh|}. Each user u ∈ U demands a bandwidth of Bu upon admission to the slice, and the slice distributes a fraction Fx of its total bandwidth to the user. Assuming uniform distribution of users, the likelihood of a user u ∈ U corresponding to a slice xh ∈ Xh that belongs to an MVNO h is:

ρb=1Xh(21)

Because users are less tolerant of dropped handoff calls in slices that support them (eMBB and uRLLC), handoff calls are prioritized over new calls in those that support them. A bandwidth reservation policy is therefore established. To ensure that consumers’ QoS requirements are met, a bandwidth reservation strategy is implemented that prioritizes handoff calls. The bandwidth reservation strategy that has been chosen is consistent with the guard channel technique. Since users are more sensitive to dropped handoff calls than blocked new ones, handoff calls are prioritized over new ones. Thresholds for new and handoff calls are defined as slice x with total capacity Cx. Let Tux be the rejection threshold for new calls from user u in slice x and Lx denote the load in each slice. The available bandwidth for new calls is indicated by: Nx=Tux−Lx. The available bandwidth for handoff calls is defined by: Hx=Cx−Lx. The bandwidth available for new calls on the mMTC slice that does not accept handoff calls is denoted by: Nxm=Cx−Lx. The Markov model represented the slice’s parameters. C is the slice’s total capacity; H denotes the bandwidth reserved for handoff calls; and λn, λh show the call arrival rate for new calls and handoff calls, respectively. And μn, μh denote the departure rate of new calls and handoff calls respectively. The current state determined by: Ω=(nu,x,hu,x,u=1,…,U,x=1,…,X), with nu,x and hu,x denoting the number of ongoing new and handoff call in the slices.

The admissible state for the network can be represented by a vector S. The acceptable states refer to a set of all possible numbers of new and handoff calls that can be admitted into the network simultaneously. The set of all possible states S is determined by:

S={∑u=1U∑x=1X(buhu,x+bunu,x≤Cx)∧∑u=1U∑x=1X(buhu,x≤Th)∧∑u=1U∑xX(buhu,x≤Tn)}(22)

with bu, Cx, Tn,Th denoting required bandwidth, slice capacity, new call threshold and threshold for handoff calls, respectively. The probability of P(s) of the system being in the state s(s ∈ Ω)is expressed by:

P(s)=1G(∏u=1U∏x=1X((ρnu,x)nu,xnu,x)((ρhu,x)hu,xhu,x))(23)

with ρnu,x and ρhu,x denoting the loads generated at the slices and they are given by:

ρnu,x=λn(u,x)μn(u,x)∀u,x(24)

ρhu,x=λh(u,x)μh(u,x)∀u,x(25)

The variable G is the normalization constant denoted by:

G=∑(s∈Ω)∏u=1U∏x=1X((ρnu,x)nu,xnu,x)((ρhu,x)hu,xhu,x)(26)

5  Performance Metrics

5.1 New Call Blocking Probability (NCBP)

NCBP represents the probability when a new call will be denied, which means it is blocked. A new call will be blocked when the slice is set up to concede it lacks the resources i.e., radio to admit it, i.e., if the maximum slice capacity is surpassed. Allowing Sbu ⊂ Ω to signify the state during which latest calls can be prevented, the blocking equation denoting the condition is as follows:

Sbu={s∈S:((bu+∑u=1Unu,xbu>Tn)∨(bu+∑u=1U(nu,x+hu,x)bu>Cx))∀x}(28)

As a result, the probability of recent call blocking is as follows:

Pb(S)=∑(s∈Sbu)P(s)(29)

5.2 Handoff Call Blocking Probability (HCBP)

HCBP denotes the probability for the handoff call declining, which means it is dropped. The handoff call will be declined when the slice constituted to acknowledge the call does not carry out sufficient bandwidth towards admitting it, i.e., when the slice’s highest capacity is overwhelmed. Sdu ⊂ Ω, define the state through which the calls in handoff are authorized to be dropped; the condition for dropping can be written as follows:

Sbu={s∈S:((bu+∑u=1Uhu,xbu>Tn)∨(bu+∑u=1U(nu,x+hu,x)bu>Cx))∀x}(30)

As a result, the handoff blocking probability is as follows:

Pd(S)=∑(s∈Sdu)P(s)(31)

6  Results and Discussion

6.1 New Call Blocking Probability (NCBP) and Handoff Call Blocking Probability (HCBP)

As it admits requests in the order in which they arrive while increasing the number of admissions by enabling resource exhaustion, first come first served is an admissions approach that is inimical to both fairness to SPs and profit to InP. The parameters of capacity and threshold were held constant in the scenario shown in Fig. 5a, but the call arrival rates were changed. There are 10 distinct call arrival rate values since the values are increased by 0.5 from 3 to 8 respectively. The rise in call arrival rate indicates that customers are making more calls, which increases the need for radio resources from networks. For the eMBB and uRLLC slices, the upcoming call rate is comparable, whereas the mMTC slice has a doubled rate. The arrival rate of the handoff call is taken to be the same as the arrival rate of the incoming call, and the departure rate for the slices is taken to be the same and maintained constant.

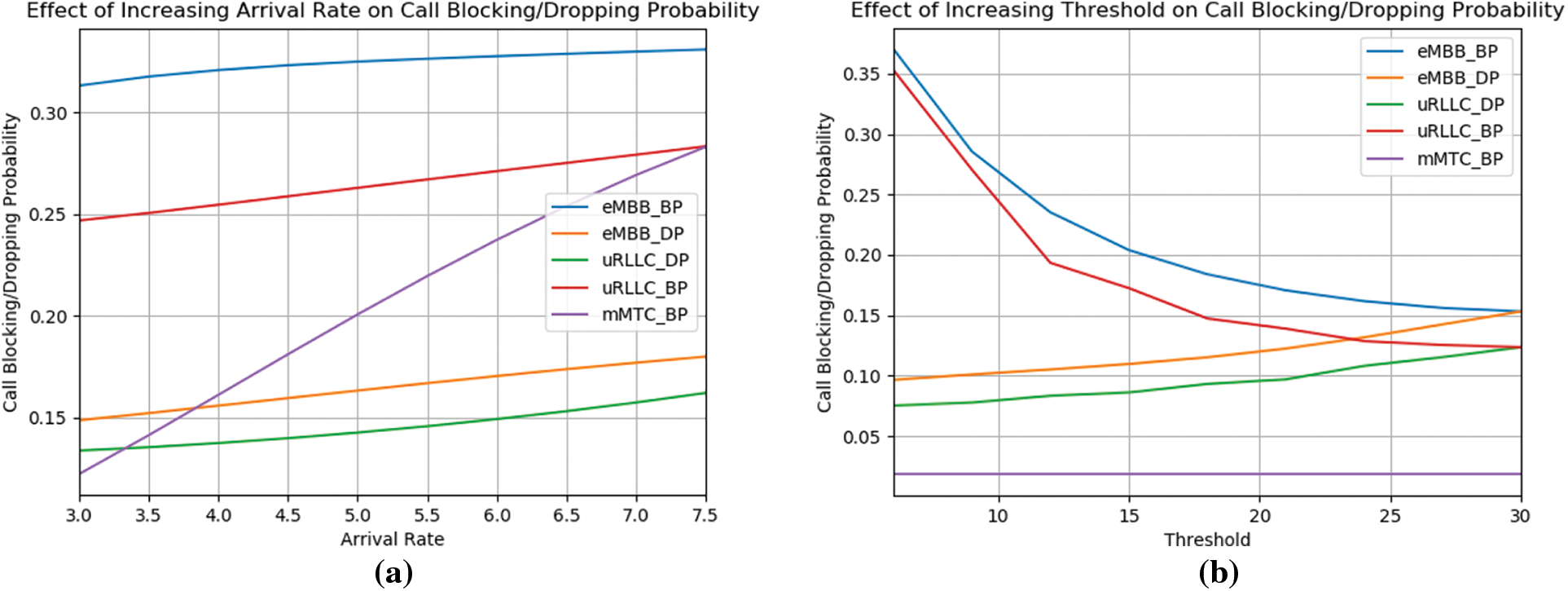
Figure 5: (a) Effect of the Increasing arrival rate on call blocking and dropping probability. (b) Effect of threshold Increasing on call dropping probability along with call blocking

In intra-slice handover, Fig. 5a shows the growing call arrival rate on the new call blocking and handoff call dropping probabilities. The graphs demonstrate that as the volume of incoming calls rises, the likelihood of call blocking and dropping increases as well. Due to the network’ limited radio resources derived from the graphs, as users place more calls, it becomes difficult for it to accept all of the calls demanding services. Due to the greatest BBU requirement for calls seeking services in the eMBB slice, it has the highest new call blocking probability of any slice. The mMTC slice has the lowest new call dropping probability while having a higher call arrival rate because calls requesting services in the slice have the lowest BBU needs and the slice has no threshold for new calls. Because bandwidth is reserved for handoff calls when using the intra-slice algorithm, the likelihood of a handoff call dropping is lower than the likelihood of a new call dropping. Due to the fact that calls for the uRLLC slice require less BBU than calls for the eMBB slice, uRLLC has the lowest handoff call dropping probability.

The rising threshold on the new call blocking and handoff call dropping probability is shown in Fig. 5b. The plots demonstrate that when the threshold rises, the new call blocking probability drop. This is so that the network can accept more new calls when the threshold for new calls rises. It should be observed from the findings that there is a modest increase in the chance of the handoff call dropping. More handoff calls are dropped when the threshold rises because less bandwidth is set aside for them. The mMTC slice’s blocking probability remains constant since there is no new call threshold for the slice. The likelihood of rejecting incoming calls at 30 (the maximum capacity) is the same as the probability of rejecting handoff calls. There is no bandwidth reservation when the threshold is similar to the slice capacity; hence, no priority is given to handoff calls.

Fig. 6 depicts the contours of the membership functions. For the recommended traffic stacks of both users, 3 Gaussian membership functions stay chosen and labeled Low (L), in combination with Medium (M), as well as High (H), in turn. For the variable ∆C (s, 1), 2 trapezoidal including 1 function i.e., triangular membership is utilized. Herein, we should consider that multiple strategies during the selection of an acceptable function for membership shape.

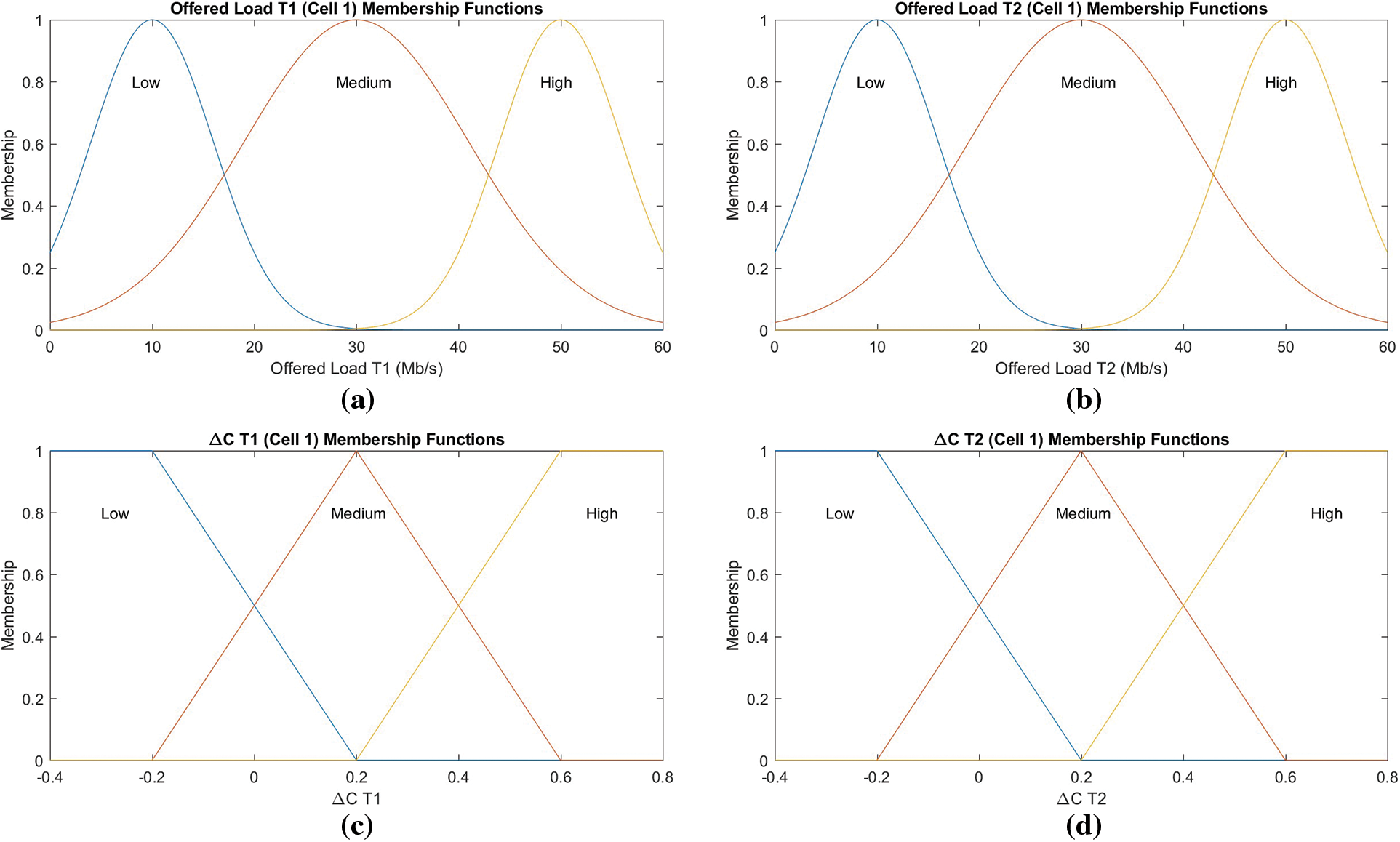
Figure 6: Fuzzy membership function (a) offered load T1, cell 1, (b) offered load T2, cell 1, (c) offered load T2, cell 1, (d) offered load T2, cell 2

The optimum outcome for every rule is defined through the action along with the maximum q-value. It can be seen that above average q-value during the entire optimization procedure relates t static action (i.e., 0), signaling that, from mid-to-long duration, this action would produce more rewards. Hence, best actions to accomplish are the expansion of ∆C (s, n). Moreover, the state’s number corresponds with the total rules number, and the related actions which are (∆C (s, n) = a + ∆C (s, n)) existing meant for each rule remain as follows: 1 increment (+0.05), its homologous decrement (−0.05), as well as the action (0) i.e., no-change.

As described in Fig. 7, exploration behaviors are observable attributed to the reason that a number of reinforcement signals do not provide anything close to the maximum reward. Therefore, the entire state-action space is entirely examined. It can be examined that as the blocking probability for both tenants remain 0, the reward or reinforcement acquired is high (i.e., equal to 1).

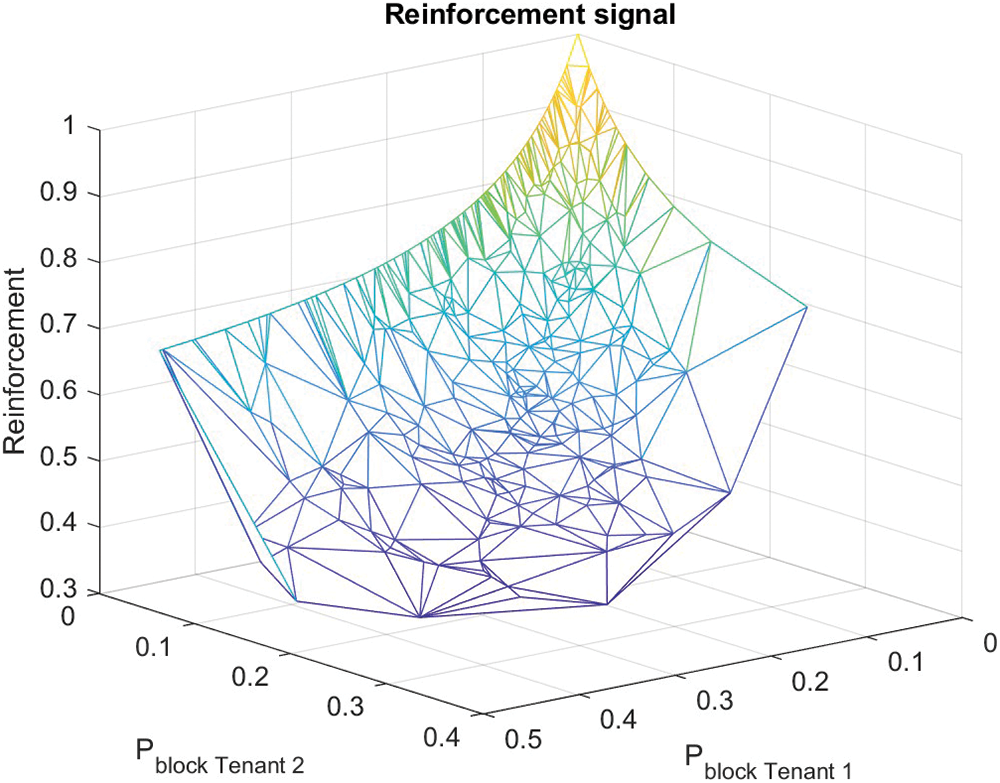
Figure 7: Illustration of reinforcement/reward signal

6.2 Comparation (With and Without Learning Method, Different Topologies)

After constructing the fuzzy assumption rule base using the proposed approach, the network performance will be weighed. In this scenario, the blocking probability of each user is used as the performance metric for the network. In addition, the results obtained by the proposed fuzzy Q-learning using the supervised learning method are compared to the scenario when (s, n) is fixed at 0. (designated as conventional Fuzzy Q-learning [14,15].

Fig. 8 represents the probability of blocking throughout the exploitation phase. It is noticed that the proposed approach achieves substantial improvements over the conventional fixed configuration approach, particularly in the T1 domain. Network performance is enhanced by utilizing supervised learning as prior knowledge of increased capacity, ∆C(s,n). However, this study includes any prospective activity that could provide higher rewards in the future, therefore the proposed approach is applicable. Regarding the results, the proposed fuzzy Q-learning approach reduced the blocking probability by 45.2%, compared to the conventional method while adopting an exploitation policy.

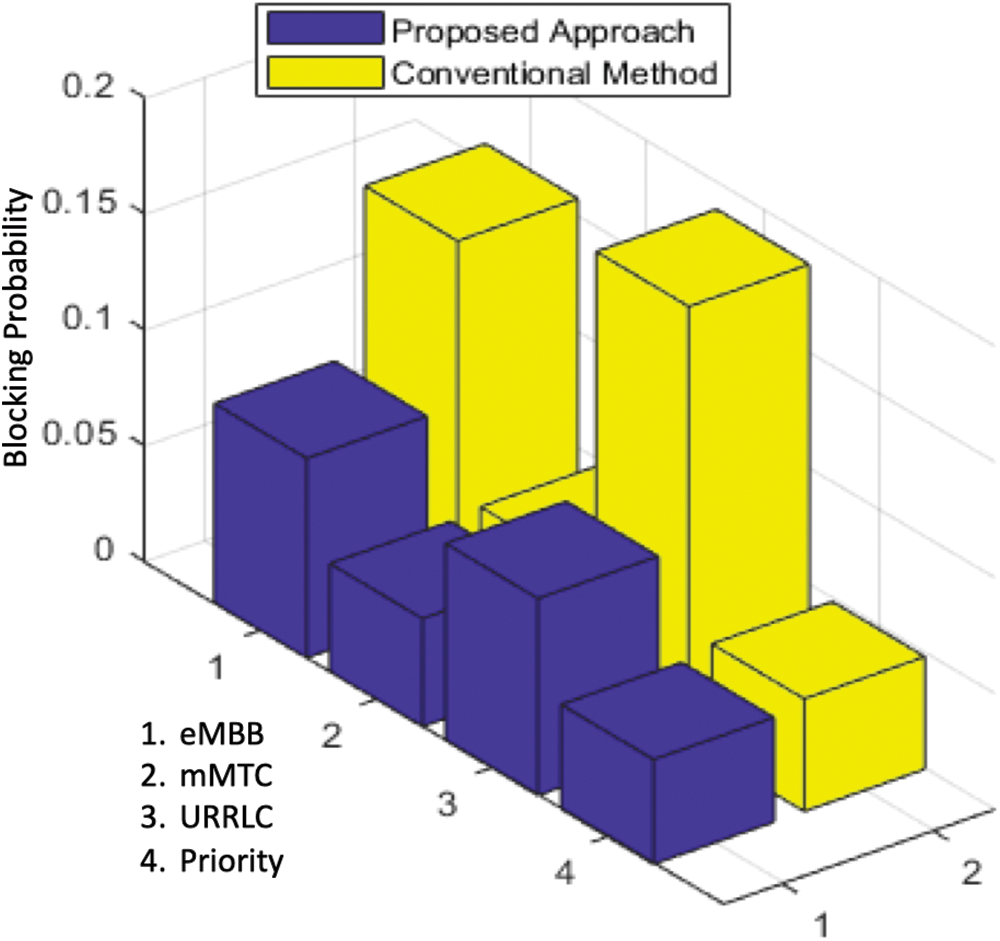
Figure 8: Comparation blocking probability in the exploitation phase

Fig. 9 displays the blocking probability obtained using the proposed method (leveraging supervised learning for Fuzzy Q-learning) for three different topologies. Based on the results, the Abilene topology achieved the lowest blocking probability. Abilene has less complexity with the least number of nodes compared to Substrate and USnet, both of them has 16 nodes and 23 nodes. This is simply due to the fact that in large networks, the agent has to process a large number of requests in order to gain rewards for learning. For instance, in the Abilene topology, 7 requests per time unit were sufficient for the agent to achieve satisfactory performance, however in the USnet topology, 25 requests per time unit were necessary which are larger as compared to the requests in the Abilene topology.

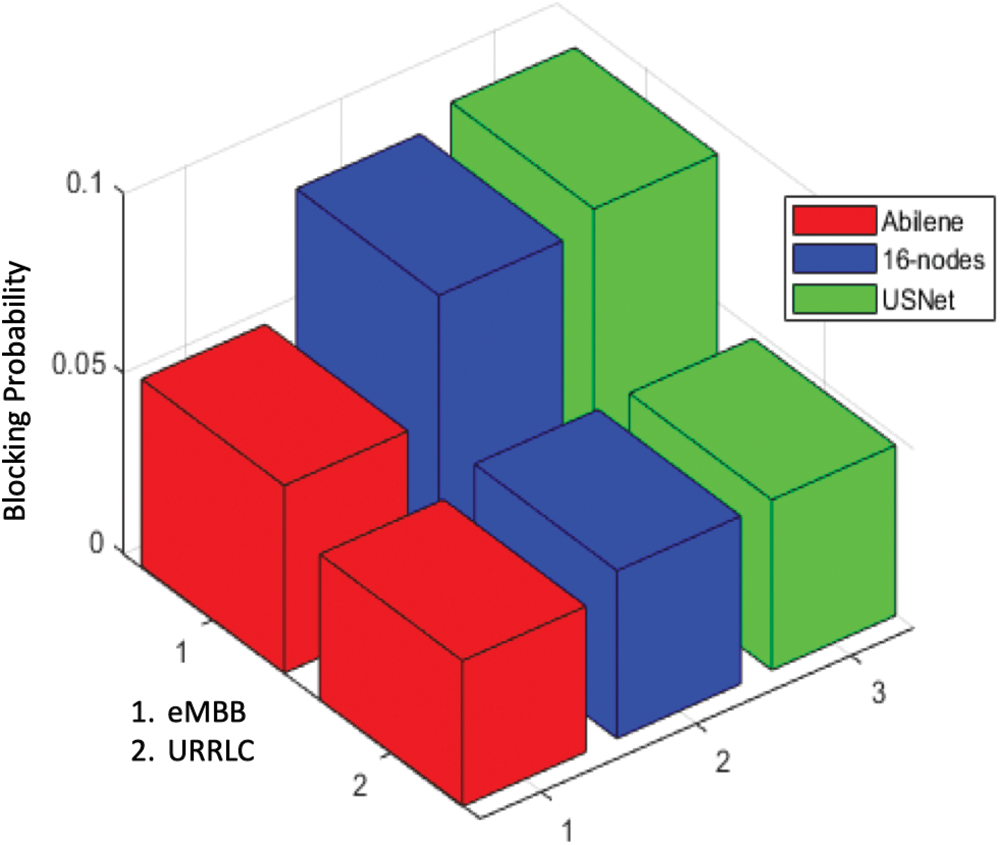
Figure 9: Comparation blocking probability in the different topologies

7  Conclusion

The study of QoS optimization for an intelligent admission control method of dynamic slice handover policy for 5G network slicing is among the major purposes of the presented work. In order to implement the suggested AI algorithm, accurate research of the self-optimized AC approach for adapting the proportion of resources utilized by for each subscriber was required. Among all prospective AI solutions, we proposed a fuzzy algorithm of Q-learning for the process of self-optimization because of its model-free method, which enables the development of an optimal action-selection policy. Utilizing a supervised learning algorithm as prior knowledge of additional capacity, fuzzy Q-learning was built ∆C(s,n). Knowledge allows estimation of the limit of ∆C(s,n) altogether with its general behavior under various traffic load situations. The analytical results from the simulations indicated that as the call arrival rate rises, the probability of blocking of the calls along with its dropping enhances. The rate at which probability increases with arrival frequency of a call indicates that the available network will not offer sufficient QoS to network subscribers. Consequently, the algorithm for slice handover was simulated, enabling calls to be directed to other slices. Slice handover considerably reduced call dropping as well as call dropping probability when call arrival rates remained constant, implying that network with handover slicing can provide a higher level of QoS to 5G network subscribers. In addition, the simulation results reveal that the proposed method offers a significant improvement over the standard fixed-configuration method. Utilizing supervised learning as prior knowledge of increased capacity improves network performance, ∆C(s,n). However, the scope of this study includes any prospective activity that may yield greater rewards in the future; thus, the proposed method is applicable. Regarding the results, the proposed fuzzy Q-learning approach decreased the probability of blocking by 45.2% compared to the conventional method while utilizing an exploitation policy. The future works include considering more parameters such as call acceptance ratio comparison.

Funding Statement: This work was supported partially by the BK21 FOUR program of the National Research Foundation of Korea funded by the Ministry of Education (NRF5199991514504) and by the MSIT (Ministry of Science and ICT), Korea, under the ITRC (Information Technology Research Center) support program (IITP-2023-2018-0-01431) supervised by the IITP (Institute for Information & Communications Technology Planning & Evaluation).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Y. Hao, D. Tian, G. Fortino, J. Zhang, I. Humar et al., “Network slicing technology in a 5G wearable network,” IEEE Communications Standards Magazine, vol. 2, no. 1, pp. 66–71, 2018. [Google Scholar]

2. X. Li, M. Samaka, H. A. Chan, D. Bhamare, L. Gupta et al., “Network slicing for 5G: Challenges and opportunities,” IEEE Internet Computing, vol. 21, no. 5, pp. 20–27, 2017. [Google Scholar]

3. V. Yajnanarayana, H. Rydén and L. Hévizi, “5G handover using reinforcement learning,” in 2020 IEEE 3rd 5G World Forum (5GWF), Bangalore, India, pp. 349–354, 2020. [Google Scholar]

4. B. Han, V. Sciancalepore, X. Costa-Perez, D. Feng, H. D. Schotten et al., “Multiservice-based network slicing orchestration with impatient tenants,” IEEE Transactions on Wireless Communications, vol. 19, no. 7, pp. 5010–5024, 2020. [Google Scholar]

5. M. R. Raza, A. Rostami, L. Wosinska and P. Monti, “A slice admission policy based on big data analytics for multi-tenant 5G networks,” Journal of Lightwave Technology, vol. 37, no. 7, pp. 1690–1697, 2019. [Google Scholar]

6. J. X. Salvat, L. Zanzi, A. Garcia-Saavedra, V. Sciancalepore, X. Costa-Perez et al., “Overbooking network slices through yield-driven end- to-end orchestration,” in ACM CoNEXT, pp. 353–365, 2018. [Google Scholar]

7. R. Challa, V. V. Zalyubovskiy, S. M. Raza, H. Choo, A. De et al., “Network slice admission model: Tradeoff between monetization and rejections,” IEEE Systems Journal, vol. 14, no. 1, pp. 657–660, 2019. [Google Scholar]

8. D. Bega, M. Gramaglia, A. Banchs, V. Sciancalepore, K. Samdanis et al., “Optimising 5G infrastructure markets: The business of network slicing,” in IEEE INFOCOM, Atlanta, GA, USA, pp. 1–9, 2017. [Google Scholar]

9. D. Bega, M. Gramaglia, A. Banchs, V. Sciancalepore, X. Costa-Perez et al., “A machine learning approach to 5G infrastructure market optimization,” IEEE Transactions on Mobile Computing, vol. 19, no. 3, pp. 498–512, 2020. [Google Scholar]

10. R. Li, Z. Zhao, Q. Sun, I. Chih-Lin, C. Yang et al., “Deep reinforcement learning for resource management in network slicing,” IEEE Access, vol. 6, pp. 74429–74441, 2018. [Google Scholar]

11. F. Kurtz, C. Bektas, N. Dorsch and C. Wietfeld, “Network slicing for critical communications in shared 5G infrastructures-An empirical evaluation,” in 2018 4th IEEE Conf. on Network Softwarization and Workshops, NetSoft, Montreal, QC, Canada, pp. 262–266, 2018. [Google Scholar]

12. H. Chen, C. C. Cheng and H. H. Yeh, “Guard-channel-based incremental and dynamic optimization on call admission control for next-generation QoS-aware heterogeneous systems,” IEEE Transactions on Vehicular Technology, vol. 57, no. 5, pp. 3064–3081, 2008. [Google Scholar]

13. MATLAB and Simulink-MathWorks, “Foundations of fuzzy logic,” https://es.mathworks.com/help/fuzzy/foundations-of-fuzzy-logic.html, Accessed Online: 20th Feb 2022. [Google Scholar]

14. K. Vasudeva, S. Dikmese, I. Guven, A. Mehbodniya, W. Saad et al., “Fuzzy-based game theoretic mobility management for energy efficient operation in hetnets,” IEEE Access, vol. 5, pp. 7542–7552, 2017. [Google Scholar]

15. B. Ma and X. Liao, “Speed-adaptive vertical handoff algorithm based on fuzzy logic in vehicular heterogeneous networks,” in 9th Int. Conf. on Fuzzy Systems and Knowledge Discovery (FSKD), Chongqing, China, pp. 371–375, 2012. [Google Scholar]