Smart Fraud Detection in E-Transactions Using Synthetic Minority Oversampling and Binary Harris Hawks Optimization

1  Introduction

Digital fraud is becoming more common due to the rising use of electronic cards for online and general purchases in e-banking. Most online frauds have rapidly routed to mobile and Internet channels. Bank card enrolment through smart mobile devices has become the main focus for fraud efforts which is the initial step in mobile transactions. Furthermore, fraudsters instantly change their techniques to avoid being noticed. As per data provided by the Reserve Bank of India (RBI), the number of fraud cases noted 4,071 by Indian lenders from April to September 2021, summed up to Rs 36,342 crore. As a result, the regulator is steadily touching the public to raise awareness about financial fraud. Researchers now concentrate more on fraudster activities and improve their techniques in a more advanced way. However, most algorithms are still incapable of solving all problems, necessitating the continued efforts of scientists or engineers to find more capable algorithms [1]. As a part of this advancement, feature selection plays a crucial role in lowering the dataset size by abolishing inessential features. Later, the optimal minimal feature subset is utilized for all the supervised learning algorithms. This feature selection process helps to minimize the training time of an algorithm. It also downsizes the storage complexity by omitting the inessential features. Thus, the selection of features is a conjunctional optimization problem. Many optimization algorithms were proposed to solve the problems encountered while exploring, exploiting, and conquering nature.

Many MH algorithms have been proposed in the literature to analyze the Feature Selection (FS) problem in various applications. MH algorithms are classified based on utilization of search space such as one & various neighbourhood structures, nature-inspired & non-natured inspired, dynamic & static objective functions, population & single-point based search, etc. Each of these algorithms has advantages and disadvantages in handling a specific problem. The following metrics must converge with any meta-heuristic model [2].

•   The exploration and exploitation capabilities of an algorithm determine its performance.

•   Hybridized algorithms are a combination of metaheuristics. The advantage of hybridization is to solve problems that occur in one method are addressed with another method.

•   Metaheuristics, unlike optimization algorithms, iterative methods, and simple greedy heuristics, can frequently find results with less computational effort regarding speed and convergence rate.

•   Metaheuristics algorithms demonstrate their robustness and are fed to a classifier.

The rest of this paper is written as follows. Firstly, Section 2 describes the digital transactional fraud detection mechanisms, i.e. existing works. Section 3 introduces the main essential concepts of feature selection techniques. Results are given in Section 4. Finally, the paper ended with a conclusion and future scope.

2  Literature Review

The amount of data available has grown in recent years using methods that make data collection feasible from several fields. It can increase computational complexity (space and time) while executing machine and deep learning algorithms. It reduces the algorithm’s efficiency when data has more redundancy. In classification tasks, irrelevant data reduces accuracy and performance significantly. Therefore, FS has secured prominence in the scientific area for advanced years. Advanced heuristics offer a collection of methods for creating heuristic optimization techniques. MH can be expressed as nature-behavioral and non-nature-behavioral. Again, nature-behavioral algorithms are derived into four categories such as evolutionary algorithms, swarm-based algorithms, physics-based algorithms, and human-based algorithms. This literature segment gives a broad survey of the most useful MH algorithms and highlights some of their areas in recent works.

Some hybrid algorithms have been reported to outperform native algorithms in feature selection. Zhang et al. [32] proposed a hybrid Aquila Optimizer with Arithmetic Optimization Algorithm (AO–AOA), which provides faster convergence in the best global search and produced better results than native methods. Wang et al. [33] combined the merits of both Differential Evolution (DE) and Firefly algorithm (FA). The author Zhang et al. [34] introduced hybrid AO and Harris Hawks Optimization algorithm (HHO), called IHAOHHO, to evaluate the performance of searching in optimization problems. The AO and HHO are the most recent CI algorithms that mimic the hunting behaviors of Aquila and harris hawks. As AO was proposed recently, there has been no work toward improvement. However, AO has been used to analyze and solve natural-world-based optimization problems. They verified IHAOHHO performance on seven benchmark functions to further verify IHAOHHO performance. It was applied to three well-known constrained engineering design problems: the three-bar truss, the speed reducer design problem, and the compression spring design problem. Mokshin et al. [3] explored a novel hybrid memetic approach called HBGWOHHO (i.e., BGWO and HHO) Optimization. The proposed hybrid approach outperforms the naive algorithm regarding AC%, some chosen features, and computational time. Seera et al. [35] improved and embedded HHO with Slap Swarm Algorithm (SSA), which developed a hybrid model called Improved HHO (IHHO). IHHO provides a faster convergence speed and maintains a better balance between exploration and exploitation.

Despite differences in optimization algorithms in MH, the process of optimization has been formulated into dual stages: Exploration (EXPO) and Exploitation (EXPL). These stages give broad coverage and analysis of the search region that is achieved by various finding solutions of the algorithm to solve searching and hunting problems, as mentioned in Table 1. The efficiency of any optimization depends only on the phases themselves. Comparing the proposed model BinHHO with other hybrid models, it works efficiently in terms of exploration and exploitation. The reason behind selecting these efficient methods is that BAO does the exploration process using two stages called Narrowed and Expanded modes. Whereas in BinHHO, the exploitation can be done using four phases. So, it explores the maximum search space, improves the convergence speed, avoids the local minima, and explores global optimization. When compared with other CI algorithms, BinHHO is efficient in exploitation.

3  Methodology

The proposed method is implemented in various phases. Firstly, the raw transactional data are preprocessed using Synthetic Minority Oversampling Technique (SMOTE). Optimization methods are used to select the perfect optimal reduced subset of features depending on the fit function. After that, conventional supervised learning models (KNN & SVM) depicts the performance of the metaheuristic feature selection method. The proposed approach is shown in Fig. 1.

Figure 1: Architecture for the proposed model

3.1 Dataset Sketch

The digital transaction fraud detection datasets from Kaggle and UCI repositories consist of anonymized credit card and payment transactions labelled as fraudulent or genuine. The two benchmark datasets, DTS1 [36] and DTS2 [37], are utilized in the proposed work. These datasets belong to payment type and European credit card, respectively. All these skewed datasets are highly imbalanced. In the above section (i.e., preprocessing), the conversion of all imbalanced datasets into balanced ones is done using SMOTE to improve the classification rate. A detailed summary of the two datasets is presented in the given Table 2.

3.2 Dataset Pre-Processing

Different experiments are done using real-world unique data sets to assess the model performance. The credit card fraud data has been accessed from the UCI machine learning repository. It is a highly imbalanced dataset. That means it gives less accuracy in classification. Therefore, it has used oversampling technique SMOTE to balance the data. SMOTE [38] is a familiar type of synthetic data generation technique. It deals with the imbalanced problems (i.e., class distribution) which arise in the classification. The SMOTE technique generates artificial instances between minority samples. These synthetic minority artificial instances are generated randomly by selecting one or more k-nearest neighbors for each sample in the space. This data can be used for various applications.

3.3 Optimal Feature Selection

MH algorithms started their enhancement process (optimization) with randomly generated candidate solutions. The produced collection of solutions is enhanced with a set of rules in the optimization process and repeatedly calculated by a defined objective function. Primarily, population-based methods seek the optimal solution to optimize the problems in a stochastic manner. So, obtaining a solution in one iteration is not guaranteed. Nonetheless, a fine collection of random solutions and repetition of the optimization process increase the probability of obtaining the optimal global solution for the specified problem. The details (Input & Parameter setting) of specified MH algorithms are depicted in Table 3.

3.3.1 The Binary Aquila Optimization Algorithm (BAO)

BAO [39] is a nature-inspirited and population-based optimization algorithm inspired by Aquila’s behavior in nature. This algorithm is inspired by different hunting strategies used by Aquila in nature and how they attack the target. This algorithm has different hunting strategies.

1. X1 → Expanded Exploration (EEXPO) → High sour with a vertical stoop.

2. X2 → Narrowed Exploration (NEXPO) → Contour flight with short glide attack.

3. X3 → Expanded Exploitation (EEXPL) → Low flight with a slow descent attack.

4. X4 → Narrowed Exploitation (NEXPL) → walking and grabbing the prey.

3.3.2 Binary Grey wolf Optimization (BGWO)

BGWO is a metaheuristic proposed by [40]. This algorithm has been an optimized search method and is inspired by the hunting technique of grey wolves mimicking the leadership. The Metaheuristic algorithm finds the best solution from all possible solutions using optimization. The grey wolves lived in vastly organized packs. The average harris hawks pack size is between 5 to 12. Each pack contains four distinct ranks of wolves. Alpha (α), Beta (β), Delta (δ), and Omega (ω) Wolves. The primary steps of the grey hunting process are:

Step1. Searching or Exploratory for the prey

Step2. Hunting, chasing, & proximate the prey

Step3. Following, encircling, and harassing the prey until it stops

Step4. Attacking or threatening the prey

The feature vector of size is 2N for different feature subsets, which enclose features within a large space that can be intensively explored. BGWO techniques are applied adaptively to examine the features in searching for optimal features. Hence, extracted features are merged with BGWO to evaluate the respective positions of the grey wolves as given [11] in Eq. (1).

Fitness =αγLg(T)+β|Cf−Lg||Cf|(1)

where γLg(T) = classification quality for rank attributes, Lg = (optimal feature subset) which represents relative to decision T, Cf represents total features truth set, α and β represent factors which impact the quality of classification and length of subset, α ∈ (0, 1] and β = 1 − α. Therefore, the fitness function optimizes the quality of classification, which is a ratio between unselected feature γLg(T) and total feature |Cf−Lg||Cf|. The preceding equation is easily transformed into a minimization problem by substituting the error rate for classification quality and selected feature ratio. The minimization problem can be written as Eq. (2).

Fitness =αEr(T)+β|Lg||Cf|(2)

where Er(T) = error rate for a classifier for rank attribute and for experiment considered β = 0.01.

3.3.3 Binary Version of Harris Hawk Optimization Algorithm (BinHHO)

BinHHO [41] is a nature-inspirited and also population-based approach. This algorithm mimics the Exploring, Exploiting, and attacking strategies of Harris hawks. Depending on the prey's evasion patterns, the hunting process takes a few seconds. The HHO algorithm is divided into two stages: Exploration (EXPO) and Exploitation (EXPL). The exploration stage refers to searching or investigating for target prey. The EXPL stage refers to updating the positions of harris hawks & target prey in the search space and attacking the target. Every operation involved in this attacking strategy is done in the EXPO and EXPL phases.

Exploration Phase

Harris Hawks are Intelligent Birds that track and detect their prey with powerful eyes. Here, harris hawk hunts randomly on specific sites and waits until it detects prey. If the prey is not found, the attacker waits, observes the situation, and monitors the site. The two strategies are followed by hawks to detect the prey. One is the position of other family members of harris. The second strategy is the target position. Harris hawk’s hunt randomly on specific sites and waits to detect prey. In the HHO algorithm, Harris Hawk is the best candidate solution in terms of prey. This phase expressed a mathematical model to alter the locality of the Harris Hawk in the search space by Eq. (3). This equation represents the solution generated based on random location and other hawks.

X(i+1)={Xrnd(i)−r1|Xrnd−2r2X(i)|q≥0.5Xtget(i)−Xp(i)−r3(LB+r4(UB−LB))q<0.5(3)

where X(i+1) represents the position vector, Xrnd(i) is a randomly selected hawk from the current population, X(i) is the hawk current position, ‘i’ is current iteration, Xtget(t) means the target position, Xp(i) is the average location of current hawk’s population, Lower Bound (LB), Upper Bound (UB). {r1, r2, r3, r4, q} are randomly generated numbers. Now determine the current population average position by Eq. (4).

Xp(i)=1N∑i=1Xj(i)(4)

The HHO EXPO process tends to distribute search agents across all desirable areas of search space while also enhancing the randomness in HHO.

Exploitation Phase

During the HHO EXPL process, search agents can exploit the closest optimal solutions. HHO originates four mechanisms to model the EXPL phase based on the distinct hunting scenarios and prey’s appropriate action (rabbit).

•   Exploit the rabbit when the rabbit’s energy is low. It can easily exploit or attack the rabbit.

•   Rabbit/prey energy decreases while escaping from the attacker (Hawk).

•   Suppose the energy level of the rabbit is high, and the hawk is chasing the rabbit.

•   The energy level is decreasing for the rabbit means that the hawk is continuously changing his position to catch a rabbit.

Based on the mechanisms, defined operations are to be performed, like decreasing rabbit energy in the algorithm, updating the position in the search space, and how to perform the exploitation phase. The main peculiarity of the meta-heuristic algorithm is that the exploitation phase can be done in four phases. It explores the maximum capacity in optimal feature selection. The mathematical model to calculate prey energy during escape is expressed in Eqs. (5) and (6).

E=2E0(1−iMaxT)(5)

E0=2r−1(6)

where E→ energy of the prey to escape, E0 → initial state of its energy inside the interval [−1,1], MaxT → maximum number of iterations, and i = current iteration. Here, the energy level of the rabbit is computed. If the rabbit is tired when the E0 value decreases from 0 to −1. When E0 increases from 0 to 1 means that the rabbit is strengthening. Then, update the rabbit position in the search space based on an obtained energy level. Firstly, compute the energy, compare it with the fitness value, and update the rabbit’s position in the search space. When the energy level (E) is ≥ 1, it means that the rabbit’s level of energy is higher and it can be escaped easily. The hawk search is used to explore the rabbit’s location. If the energy level of the rabbit is < 1, the rabbit is tired and has no energy to escape. Finally, apply the exploitation strategies to the rabbit. There are four strategies proposed in this algorithm to represent a hawk attack on the rabbit. Each time the rabbit will always try to escape from the attack.

Case1: Soft Roundup (SR) (E ≥ 0.5 & r ≥ 0.5)

The soft round-up depicts behavior using a given mathematical model [33]

X(i+1)=△X(i)−E| JXp(i)−X(i)|(7)

△X(i)=Xp(i)−X(i)(8)

where ∆X(t) = difference vector between position vector of prey and current location.

J=2(1−r5)(9)

Case2: Hard Roundup (HR) (E < 0.5 & r ≥ 0.5)

In this case, Harris Hawk performs a sudden attack. The math illustration for this behavior:

X(i+1)=Xp(i)–E|△X(i)|(10)

Case3: Soft Roundup w.r.t Progressive Rapid Dives (SRPD) (E ≥ 0.5 & r < 0.5)

Here, Harris Hawks encircle the rabbit softly and make it more tired before performing the unexpected attack. In this case of behavior, the mathematical model is

X(i+1)={Yif FUN(Y)<FUN(X(i))Zif FUN(Z)<FUN(X(i))(11)

where Y is already represented in Eq. (6) and Z = Y + S × LEF Y (D), LEFY means lavish flight.

Case 4: Hard Roundup w.r.t Progressive Rapid Dives (HRPD) (E < 0.5 & r < 0.5)

Here, Case 3 & 4 represents the intelligent behavior of harris hawks in the search space when trying to search and attack. The variable ‘r’ defines the prey that successfully escaped the attackers. So, the value for the ‘r’, i.e. random value.

If (r<0.5)

escaped before the attack.

If (r>0.5)

Not escaped before the attack.

Algorithm 1 is proficient in searching the binary search region. In BHHO, the hawk location is updated in multiple stages. The second step tells the S-shaped transfer function. Eqs. (12) or (13) are given to modify hawk’s old location or position Skd (i) to the new location ∆Skd (i+1). After that, BinHHO alters the newly available hawk position in the S-shaped as given by [41].

Skd(i+1)={1if rnd(0,1)<I(△Xkd(i+1))0otherwise(12)

Xkd(i+1)={¬Xkd(i)if rnd(0,1)<I(△Xkd(i+1))Xkd(i)otherwise(13)

The S-shaped transfer function is T(X), a random number in the range [0,1] represented as rnd (0,1]. Then, ¬S is called S’s complement.

Initially, the HHO technique intends to tackle problems that requires continuous optimization. On the other hand, feature selection is equivalent to the binary problem, which means every solution is referred to as binary points zero and one [42]. Finally, the BinHHO technique extracted the essential features of fraud identification.

4  Proposed Results & Discussions

The classifier parameters (i.e., Input) were adjusted using optimization algorithms to yield better classification accuracy. This process can be evaluated using popular supervised learning techniques called KNN and SVM. This work utilized three different distance functions, namely Minkowski Distance, Euclidean Distance, and The City block for KNN. These functions reflect the functionality of the KNN at different k-values. Here, the k value varies with the nearest neighbors, which can be represented as k ∈ {3,5,7,9}. The functionality of the SVM classifier is mapped to the linear, polynomial, and RBF kernel functions. And the kernel scale parameter (σ) was changed stepwise, i.e. from 1 to 5. The experimental results for digital transactional fraud detection on benchmark datasets (in Table 2) were presented in Tables 4 to 7, respectively. Subsequently, the compared performance of the classifiers with the performance metrics Accuracy (AC%), Sensitivity (SE), Specificity (SP), Precision (PR), Recall (RC), F1 Score (F1S%).

The results of the optimization techniques BAO, BGWO, and BinHHO have been applied to a KNN classifier that utilizes and implements various distance functions by differing K metrics, which is depicted in Tables 4 and 6. The approach BinHHO-KNN technique uses the Euclidean distance function, and K = 5 yielded a greater AC (%), SE, SP, PR, and F1S (%) of 99.94%,1,0.96, and 100%, respectively, considering the dataset DTS1. Subsequently, the optimal AC (%) and other metrics of the DTS2 were also accomplished in the BinHHO-KNN technique by Euclidean distance function with K = 5, and results were 99.95%, 0.99, 0.99, 1, and 99.84%. Similarly, Tables 5 and 7 show the performance of SVM classifiers based on kernel functions with kernel scale. Here the SVM classifier has also worked with the BinHHO feature optimization technique.

All the specified optimization algorithms are evaluated by the fitness/convergence function. A fitness function influences the behavior of algorithms in the search space or explores test data to maximize a convergence metric, which can be considered an optimization problem. So, Figs. 2 and 3 present the best convergence curve, confusion matrix, and roc curve for DTS1 & DTS2, respectively.

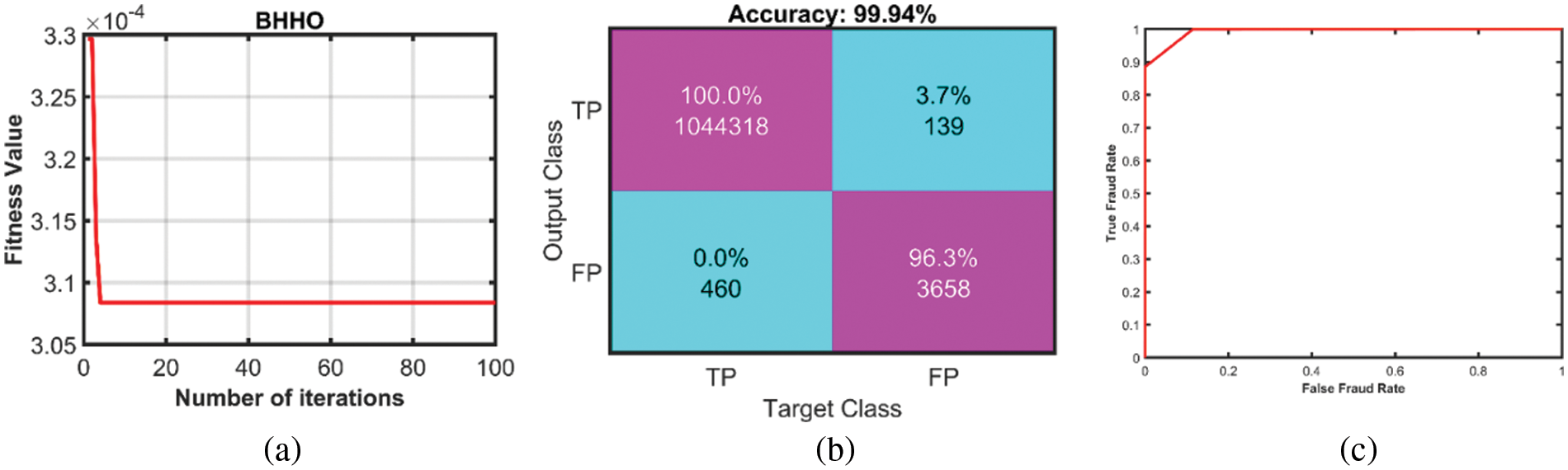
Figure 2: (a) Fitness curve (b) Confusion matrix and (c) ROC curve for DTS1

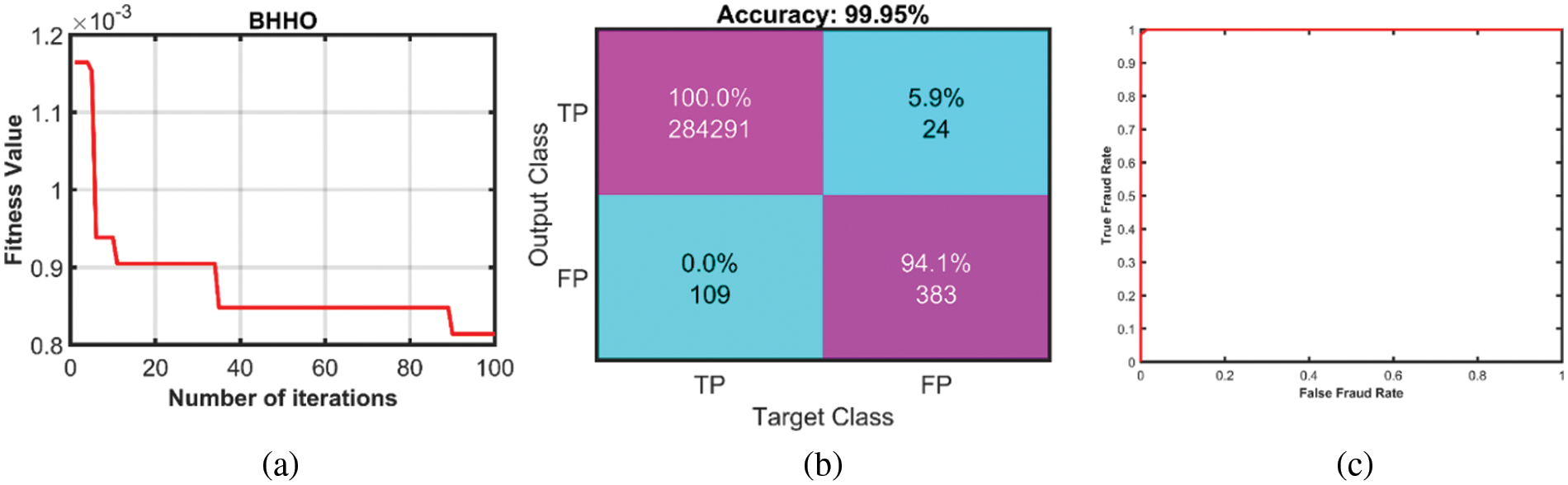
Figure 3: (a) Fitness curve (b) Confusion matrix and (c) ROC curve for DTS2

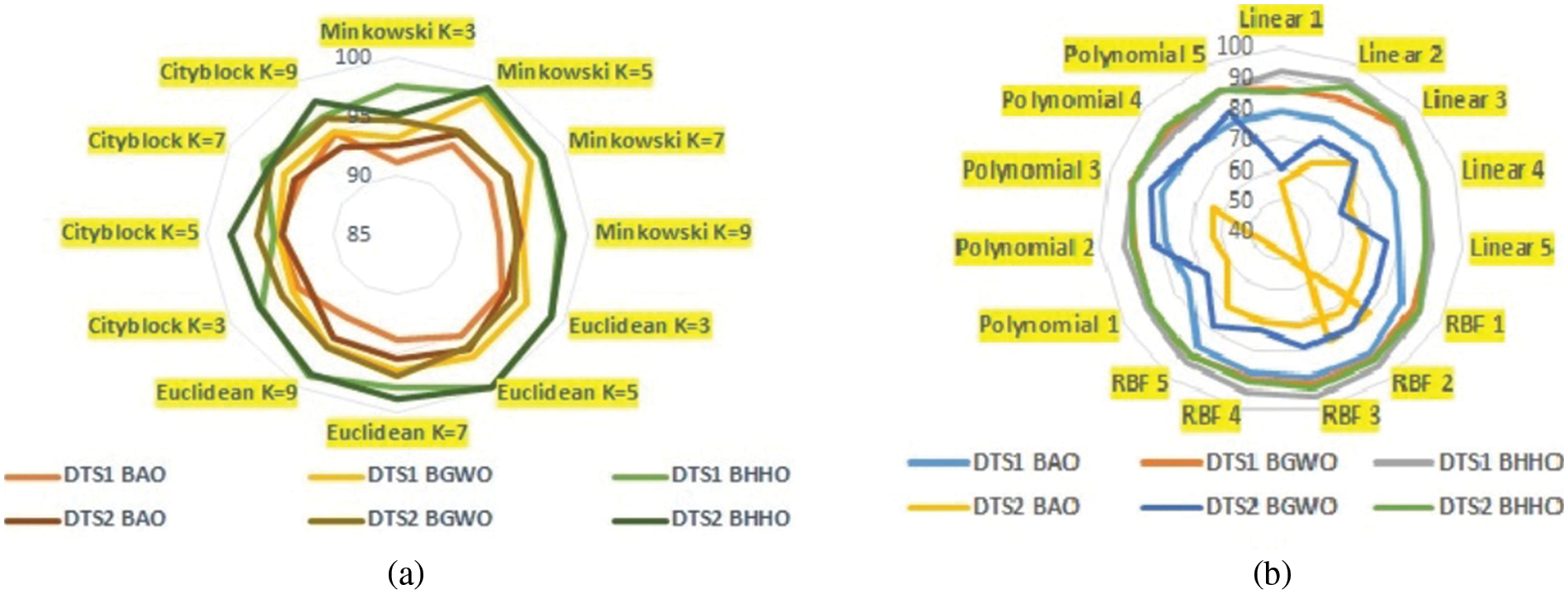
Figure 4: Proposed model: Comparison of accuracy (%)

In the dataset DTS1, the approach BinHHO-SVM achieved well at RBF using three as kernel scale (), i.e., AC (%), SE, SP, PR, and F1S of 95.87%, 0.94%, 0.95%, 0.96%, and 96.28% respectively. Also, the dataset DTS2 had the results of AC (%), SE, SP, PR, and F1S (%) as 92.8%, 0.92%,0.93%, 0.94%, and 95.02%, respectively. The results which got better are shown in tables (in Bold Font). The well-worked classifier KNN achieved a maximum classification accuracy of 99.94% and 99.95% from the DTS1 and DTS2, respectively.

Fig. 5 measure various optimization models for our proposed methodology, i.e., optimal feature selection techniques. Numerous algorithms focusing on the BinHHO feature selection technique require less problem-solving knowledge. Hence, these algorithms face the tough task of identifying the objective function by taking long hours to evaluate compared to proposed optimization techniques.

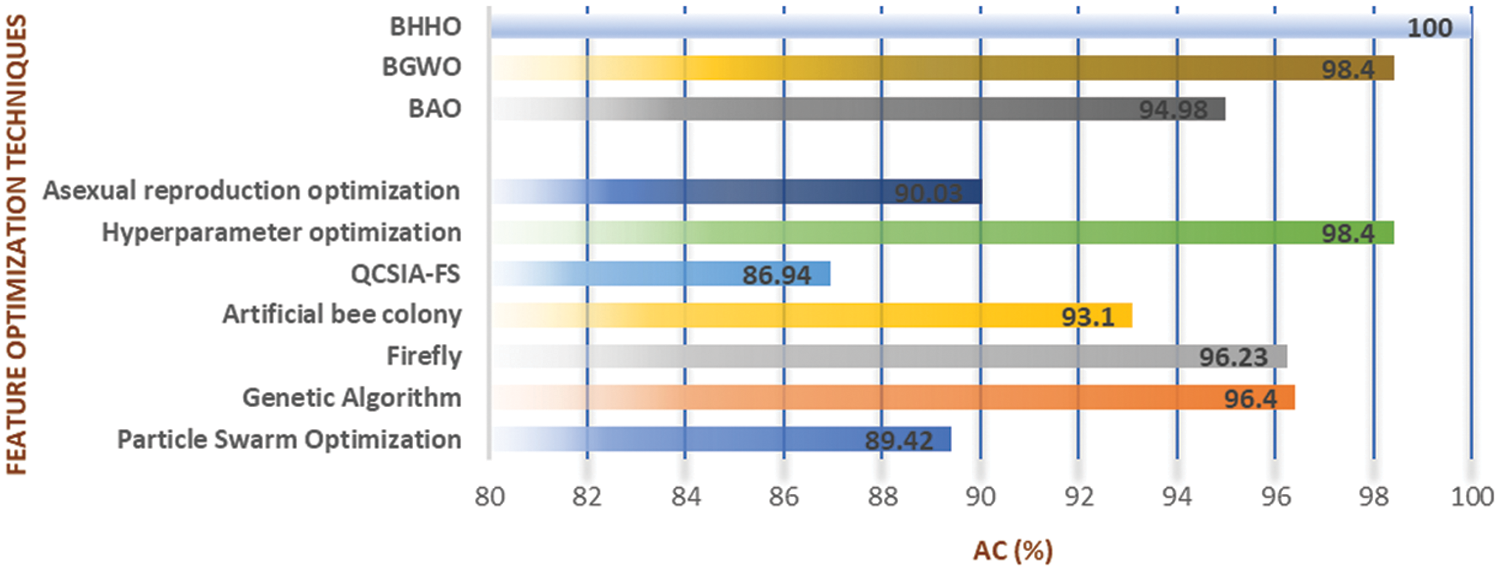
Figure 5: Comparison of various feature selection techniques

The proposed design exceeds the modern state-of-the-art methodology using supervised machine learning techniques SVM and KNN. Worse performance was achieved by entropy-based or non-linear feature-based methods. The proposed model upgraded the accuracy by comparing it with other feature selection techniques.

Fig. 6 contrast the proposed model for the detection of fraud with extant methodologies. The essential features generated by the proposed technique are utilized for classification. Hence, the features extracted by DTS1 & DTS2 make a significant impact on the accuracy of classification. The proposed optimized Bayesian KNN was used for detecting digital transactional fraud data, hence defining the level of depth with 99.95% accuracy, and only ten features were used. The overall performance of the BinHHO + KNN & BinHHO + SVM were represented in Fig. 4 as the radar graphs for visualization.

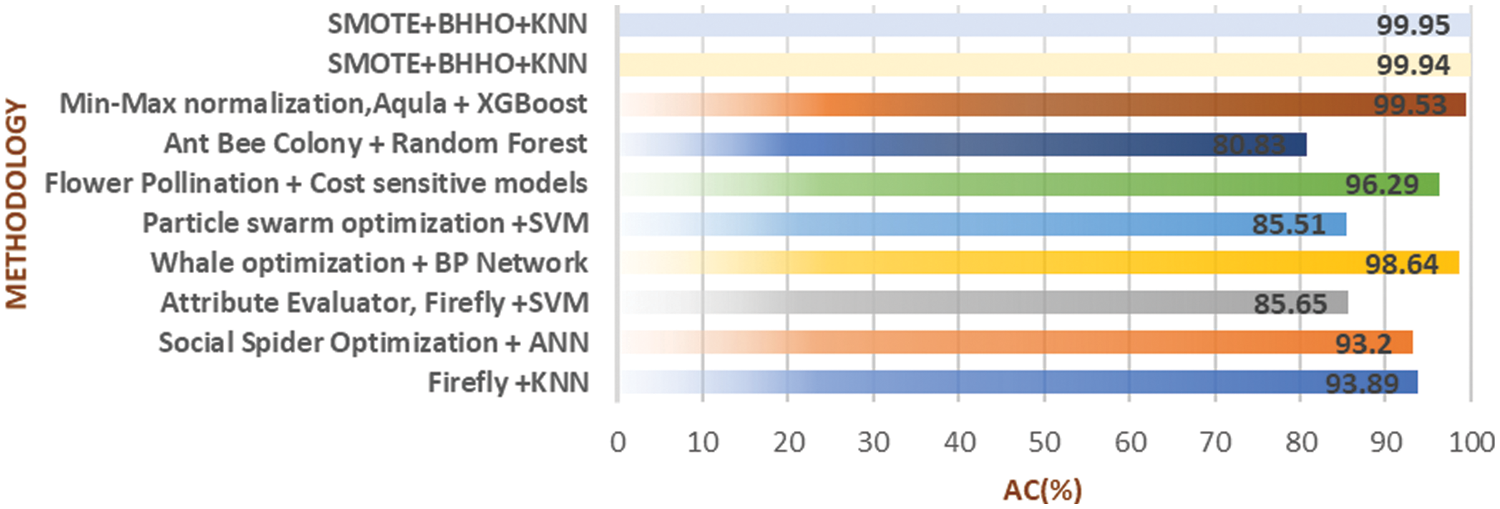
Figure 6: Comparison of the proposed method with state-of-art methods

5  Conclusion & Future Scope

This research presents a novel approach to classify fraud and non-fraud with feature selection in digital transaction fraud detection. The Synthetic Minority Oversampling Technique (SMOTE) was utilized for balancing the datasets and was tested to classify using a cross-validation approach (means of 10-fold). An intelligent way of identifying feature selection is determined using optimization techniques called BAO, BGWO, and BinHHO. BAO & BGWO have the drawback of a slow convergence rate and more time complexity than BinHHO. The Binary version of HHO (BinHHO) is a unique and efficient nature-inspired swarm-based approach and has achieved a good accuracy with both datasets. The following limitations of the proposed work provide suggestions for future research:

•   This proposed approach is best suited for blockchain applications in banking and finance, and similar advanced fields.

•   Other feature selection methods to be studied.

•   Apply to any deep learning models.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

1. Z. M. Gao, J. Zhao, S. R. Li and Y. R. Hu, “The improved mayfly optimization algorithm,” Journal of Physics: Conference Series, vol. 1684, no. 1, pp. 12077, 2020. [Google Scholar]

2. R. Al-Wajih, S. J. Abdulkadir, N. Aziz, Q. Al-Tashi and N. Talpur, “Hybrid binary grey wolf with harris hawks optimizer for feature selection,” IEEE Access, vol. 9, pp. 31662–31677, 2021. [Google Scholar]

3. A. V. Mokshin, V. V. Mokshin and L. M. Sharnin, “Adaptive genetic algorithms used to analyze behavior of complex system,” Communications in Nonlinear Science and Numerical Simulation, vol. 71, pp. 174–186, 2019. [Google Scholar]

4. Q. U. Ain, H. Al-Sahaf, B. Xue and M. Zhang, “Generating knowledge-guided discriminative features using genetic programming for melanoma detection,” IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 5, no. 4, pp. 554–569, 2020. [Google Scholar]

5. K. R. Opara and J. Arabas, “Differential evolution: A survey of theoretical analyses,” Swarm and Evolutionary Computation, vol. 44, no. 1–2, pp. 546–558, 2019. [Google Scholar]

6. D. Simon, “Biogeography-based optimization,” IEEE Transactions on Evolutionary Computation, vol. 12, no. 6, pp. 702–713, 2008. [Google Scholar]

7. S. Fukuda, Y. Yamanaka and T. Yoshihiro, “A probability-based evolutionary algorithm with mutations to learn Bayesian networks,” International Journal of Interactive Multimedia and Artificial Intelligence, vol. 3, no. 1, pp. 7, 2014. [Google Scholar]

8. E. H. Houssein, A. G. Gad, K. Hussain and P. N. Suganthan, “Major advances in particle swarm optimization: Theory, analysis, and application,” Swarm and Evolutionary Computation, vol. 6, no. 11, pp. 100868–100905, 2021. [Google Scholar]

9. C. Blum, “Ant colony optimization: Introduction and recent trends,” Physics of Life Reviews, vol. 2, no. 4, pp. 353–373, 2005. [Google Scholar]

10. S. Mirjalili, “Moth flame optimization algorithm: A novel nature inspired heuristic paradigm,” Knowledge-Based Systems, vol. 89, pp. 228–249, 2015. [Google Scholar]

11. J. Yedukondalu and L. D. Sharma, “Cognitive load detection using circulant singular spectrum analysis and binary harris hawks optimization based feature selection,” Biomedical Signal Processing and Control, vol. 79, no. 4, pp. 104006, 2022. [Google Scholar]

12. L. Abualigah, D. Yousri, M. Abd Elaziz, A. A. Ewees, M. A. Al Qaness et al., “Aquila optimizer: A novel metaheuristic optimization algorithm,” Computers & Industrial Engineering, vol. 157, no. 11, pp. 107250, 2021. [Google Scholar]

13. K. Zervoudakis and S. Tsafarakis, “A mayfly optimization algorithm,” Computers & Industrial Engineering, vol. 145, no. 5, pp. 106559, 2020. [Google Scholar]

14. J. S. Chou and D. N. Truong, “A novel metaheuristic optimizer inspired by behavior of jellyfish in ocean,” Applied Mathematics and Computation, vol. 389, pp. 125535, 2021. [Google Scholar]

15. M. Mafarja and S. Mirjalili, “Whale optimization approaches for wrapper feature selection,” Applied Soft Computing, vol. 62, no. 1, pp. 441–453, 2018. [Google Scholar]

16. H. Rezaei, O. Bozorg Haddad and X. Chu, “Grey wolf optimization (gwo) algorithm,” in Advanced Optimization by NatureInspired Algorithms. Springer, vol. 720, pp. 81–91, 2018. [Google Scholar]

17. F. A. Hashim, E. H. Houssein, M. S. Mabrouk, W. Al Atabany and S. Mirjalili, “Henry gas solubility optimization: A novel physicsbased algorithm,” Future Generation Computer Systems, vol. 101, pp. 646–667, 2019. [Google Scholar]

18. M. Dehghani, Z. Montazeri, S. Saremi, A. Dehghani, O. P. Malik et al., “Hogo: Hide objects game optimization,” International Journal of Intelligent Engineering Systems, vol. 13, no. 4–10, pp. 216–225, 2020. [Google Scholar]

19. H. S. Hosseini, “Otsu’s criterion based multilevel thresholding by a nature-inspired metaheuristic called galaxy based search algorithm,” in 2011 Third World Congress on Nature and Biologically Inspired Computing, Salamanca, Spain, pp. 383–388, 2011. [Google Scholar]

20. E. Rashedi, E. Rashedi and H. Nezamabadi Pour, “A comprehensive survey on gravitational search algorithm,” Swarm and Evolutionary Computation, vol. 41, no. 4, pp. 141–158, 2018. [Google Scholar]

21. A. Kaveh and S. Talatahari, “Charged system search for optimal design of frame structures,” Applied Soft Computing, vol. 12, no. 1, pp. 382–393, 2012. [Google Scholar]

22. R. V. Rao, V. Savsani and J. Balic, “Teaching–learning-based optimization algorithm for unconstrained and constrained realparameter optimization problems,” Engineering Optimization, vol. 44, no. 12, pp. 1447–1462, 2012. [Google Scholar]

23. M. Kumar, A. J. Kulkarni and S. C. Satapathy, “Socio evolution & learning optimization algorithm: A socio-inspired optimization methodology,” Future Generation Computer Systems, vol. 81, no. Suppl., pp. 252–272, 2018. [Google Scholar]

24. Y. Shi, “Brain storm optimization algorithm,” in Int. Conf. in Swarm Intelligence, Berlin, Heidelberg, Springer, pp. 303–309, 2011. [Google Scholar]

25. S. H. S. Moosavi and V. K. Bardsiri, “Poor and rich optimization algorithm: A new human-based and multi populations algorithm,” Engineering Applications of Artificial Intelligence, vol. 86, no. 12, pp. 165–181, 2019. [Google Scholar]

26. P. Agrawal, T. Ganesh and A. W. Mohamed, “A novel binary gaining-sharing knowledge-based optimization algorithm for feature selection,” Neural Computing and Applications, vol. 33, no. 11, pp. 5989–6008, 2021. [Google Scholar]

27. A. Azadeh, M. H. Farahani, H. Eivazy, S. Nazari Shirkouhi and G. Asadipour, “A hybrid meta-heuristic algorithm for optimization of crew scheduling,” Applied Soft Computing, vol. 13, no. 1, pp. 158–164, 2013. [Google Scholar]

28. I. B. Aydilek, “A hybrid firefly and particle swarm optimization algorithm for computationally expensive numerical problems,” Applied Soft Computing, vol. 66, no. 2, pp. 232–249, 2018. [Google Scholar]

29. I. Attiya, M. Abd Elaziz and S. Xiong, “Job scheduling in cloud computing using a modified harris hawks optimization and simulated annealing algorithm,” Computational Intelligence and Neuroscience, vol. 2020, no. 16, pp. 1–17, 2020. [Google Scholar]

30. Y. J. Zhang, Y. X. Yan, J. Zhao and Z. M. Gao, “Aoaao: The hybrid algorithm of arithmetic optimization algorithm with aquila optimizer,” IEEE Access, vol. 10, pp. 10907–10933, 2022. [Google Scholar]

31. S. Mahajan, L. Abualigah, A. K. Pandit and M. Altalhi, “Hybrid aquila optimizer with arithmetic optimization algorithm for global optimization tasks,” Soft Computing, vol. 26, no. 10, pp. 4863–4881, 2022. [Google Scholar]

32. L. Zhang, L. Liu, X. S. Yang and Y. Dai, “A novel hybrid firefly algorithm for global optimization,” PloS One, vol. 11, no. 9, pp. e0163230, 2016. [Google Scholar] [PubMed]

33. S. Wang, H. Jia, Q. Liu and R. Zheng, “An improved hybrid aquila optimizer and harris hawk’s optimization for global optimization,” Mathematical Biosciences and Engineering, vol. 18, no. 6, pp. 7076–7109, 2021. [Google Scholar] [PubMed]

34. Y. Zhang, R. Liu, X. Wang, H. Chen and C. Li, “Boosted binary harris hawks optimizer and feature selection,” Engineering with Computers, vol. 37, no. 4, pp. 3741–3770, 2021. [Google Scholar]

35. M. Seera, C. P. Lim, A. Kumar, L. Dhamotharan and K. H. Tan, “An intelligent payment card fraud detection system,” Annals of Operations Research, vol. 269, no. 3, pp. 1–23, 2021. [Google Scholar]

36. N. Rtayli and N. Enneya, “Enhanced credit card fraud detection based on SVM-recursive feature elimination and hyperparameters optimization,” Journal of Information Security and Applications, vol. 55, no. 3, pp. 102596, 2020. [Google Scholar]

37. V. S. Babar and R. Ade, “A review on imbalanced learning methods,” International Journal of Computer Applications, vol. 975, pp. 23–27, 2015. [Google Scholar]

38. M. H. Nadimi Shahraki, S. Taghian, S. Mirjalili and L. Abualigah, “Binary aquila optimizer for selecting effective features from medical data: A COVID-19 case study,” Mathematics, vol. 10, no. 11, pp. 1929, 2022. [Google Scholar]

39. E. Emary, H. M. Zawbaa and A. E. Hassanien, “Binary grey wolf optimization approaches for feature selection,” Neurocomputing, vol. 172, no. 1, pp. 371–381, 2016. [Google Scholar]

40. J. Too, A. R. Abdullah and N. Mohd Saad, “A new quadratic binary harris hawk optimization for feature selection,” Electronics, vol. 8, no. 10, pp. 1130, 2019. [Google Scholar]

41. H. Chantar, T. Thaher, H. Turabieh, M. Mafarja and A. Sheta, “Bhho-tvs: A binary harris hawks optimizer with time-varying scheme for solving data classification problems,” Applied Sciences, vol. 11, no. 14, pp. 6516, 2021. [Google Scholar]

42. T. Thaher, A. A. Heidari, M. Mafarja, J. S. Dong and S. Mirjalili, “Binary harris hawks optimizer for high-dimensional, low sample size feature selection,” in Evolutionary Machine Learning Techniques, Springer, pp. 251–272, 2020. [Google Scholar]