A Speech Cryptosystem Using the New Chaotic System with a Capsule-Shaped Equilibrium Curve

1  Introduction

Chaos theory has been applied in various areas of science and engineering such that found in nonlinear oscillatory systems [1,2], biological modelling [3,4], circuits [5–10], artificial neural network modelling [11,12], chemical modelling [13,14], fuzzy modelling [15,16], robotics [17], cryptosystem [18], audio encryption [19,20], image encryption [21–24], data hiding [25–27], watermarking [28], and Field Programmable Gate Array (FPGA) implementation [29]. A system is said to be chaotic when exhibiting high sensitivity to even small changes in the initial conditions [30].

By definition, dynamical systems with a positive Lyapunov index number are called chaotic [31]. In recent years, there is a great interest by researchers in finding a specific type of chaotic systems that has a closed curve of equilibrium points [32–38]. Thus far, many such chaotic systems have been reported in the chaos literature with equilibrium curves such as circles [34], butterflies [35], hearts [36], and apples [37], etc. These chaotic systems come with a curve of infinitely many equilibrium points, and hence these systems are equipped with hidden chaotic attractors.

Speech signal encryption is one of the most widely used techniques for ensuring the security of the verbal transmission of data. To address information security concerns, various cryptographic standards and protocols have been proposed, including speech encryption algorithms such as Data Encryption Standard (DES) [38], Triple Data Encryption Standard (3DES) [39], and the Rivest–Shamir–Adleman (RSA) algorithm [40].

Each standard encryption technique has pluses and minuses; however, these cryptographic techniques do not address the distribution of encryption keys. The signal being aperiodic, broadband, and spacious spectrum for housing the secret message, the use of chaotic systems in cryptography brought new life into encryption systems [41,42]. Several algorithms based on chaotic maps have been proposed in order to expand the range of parameters and improve the sensitivity of secret keys. The implementation of chaotic systems can be found in various technologies such as analog circuits [43], digital circuits [44] or FPGA [45,46].

This study presents a novel 3-D chaotic system consisting of six nonlinear terms. A novelty in our research work is that the proposed chaotic system exhibits a capsule-shaped equilibrium curve. In addition, an illustration of the system’s dynamic properties including signal plots and bifurcation diagram are given. For nonlinear dynamical systems, multi-stability refers to the coexistence of chaotic attractors for the same values of parameters but different values of initial states [21,22]. In this work, we show that the proposed chaotic system exhibits multi-stability with coexisting chaotic attractors. Finally, a speech encryption scheme is developed using the novel chaotic system with a capsule-shaped equilibrium curve and implementation on the FPGA platform. Simulation results revealed that the proposed encryption system utilizes 33% of the FPGA, with the maximum clock frequency at 178.28 MHz.

Section 2 presents the modelling of our proposed chaotic system with capsule equilibrium curve. In Section 3, we analyze the proposed system from the perspective of bifurcation and multi-stability properties. We show that the new chaotic system has two coexisting chaotic attractors for the same parameter set but different sets of initial sets. A speech encryption scheme based on the proposed system is introduced in Section 4. Finally, conclusions are dressed in Section 5.

2  A Novel Chaotic System with a Capsule Equilibrium Curve

This study proposed a 3-D chaotic dynamical system having six nonlinear terms.

{ξ˙=ζη˙=−ζ(αη+βη2+ξζ)ζ˙=ξ4−0.1ξ2η2+η2−0.5(1)

In the system (1), the state is designated by the three-dimensional vector K =(ξ,η,ζ). Noteworthy, the dynamics (1) consists of six nonlinear terms. We assume that all system constants α,β are positive.

To determine the equilibrium points of system (1), we solve the following set of equations:

ζ=0(2a)

−ζ(αη+βη2+ξζ)=0(2b)

ξ4−0.1ξ2η2+η2−0.5=0(2c)

Solving the equations (2a) and (2b), we get ζ=0. Combining this with (2c), we conclude that the system’s equilibrium points (S) are given by a curve residing on (ξ,η)−plane:

S={(ξ,η,ζ)∈R3|ζ=0,ξ4−0.1ξ2η2+η2−0.5=0}(3)

Fig. 1 shows the capsule-shaped equilibrium curve of the system (1) on the (ξ,η)−plane.

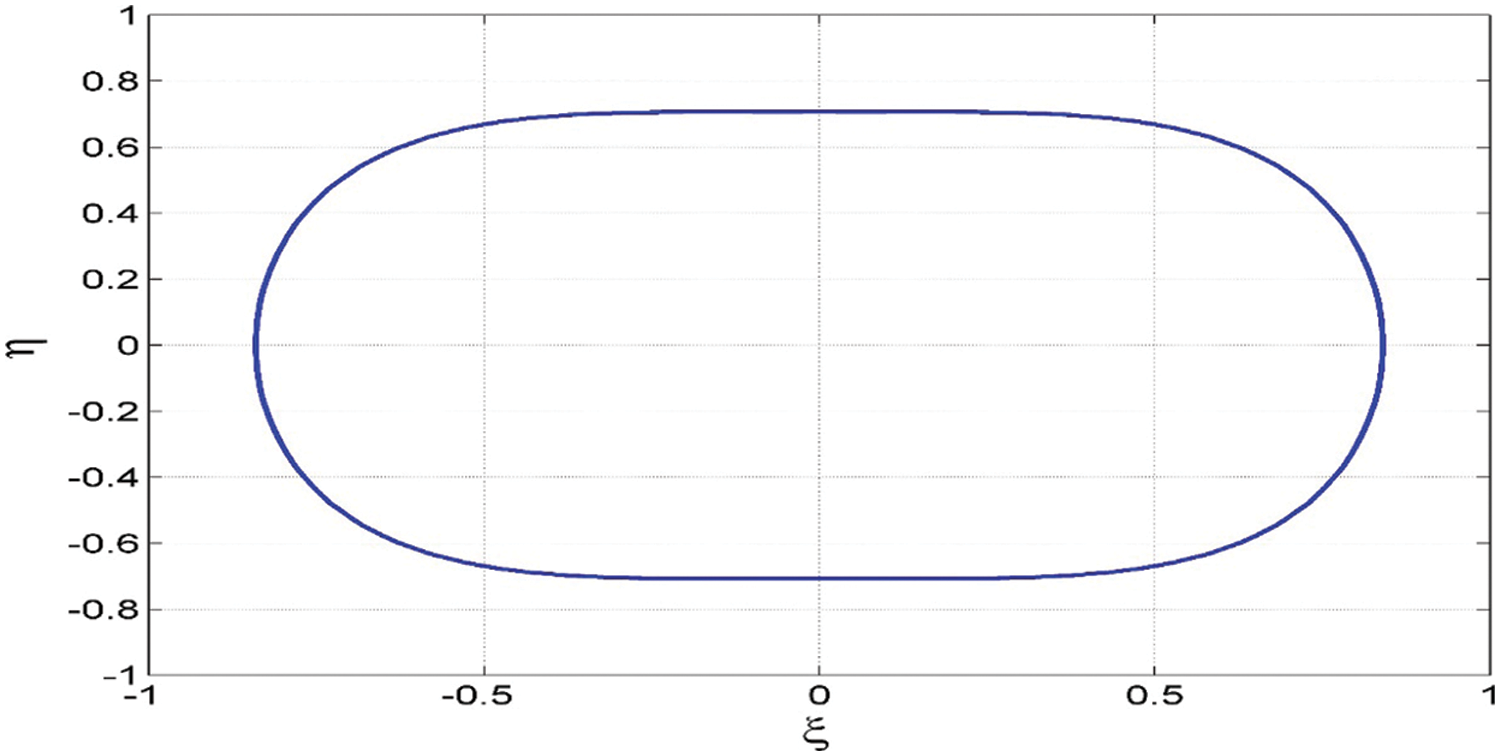
Figure 1: Equilibrium curve with capsule-shaped of the system (1) on the (ξ,η)−plane

MATLAB’s Lyapunov Index (LI) values spectrum analysis was used to establish the chaotic existence in the three-dimensional dynamical system (1) with the following values for tuning parameters:

α=8,β=3(4)

To perform time-series analysis for the system’s state K , the initial state of the system (1) takes up the following values:

ξ(0)=0.02,η(0)=0.01,ζ(0)=0.02(5)

Based on Wolf’s procedure [47], for T=1e4 seconds, the values of Lyapunov Exponent Index (LEI) belong to the dynamical system (1) (see Fig. 1) were found to be:

μ1=0.0468, μ2=0, μ3=−0.0993(6)

The chaotic property of system (1) is guaranteed following the positivity of LEI value for μ1.

The negative sum of all LEI values in (6) shows that the system (1) also has dissipative motion derived from its entire trajectories, which finally converges to the strange chaotic attractor. Since the proposed chaotic system (1) with a capsule-shaped equilibrium curve comes with infinitely many equilibrium points, we can immediately conclude the existence of a hidden chaotic attractor.

Moreover, the Kaplan-Yorke dimension for system (1) can be found as:

DKY=2+μ1+μ2|μ3|=2.4713(7)

The higher the value of DKY indicates that higher complexity in the chaotic system (1).

By fixing the parameter set (α,β)=(8,3) and K0 = (0.02, 0.01, 0.02), we determine the values of LI and signal plots for the system (1) using MATLAB.

Fig. 2 shows the LEI spectrum of the new chaotic system (1), while Fig. 3 shows the phase plots of the system (1).

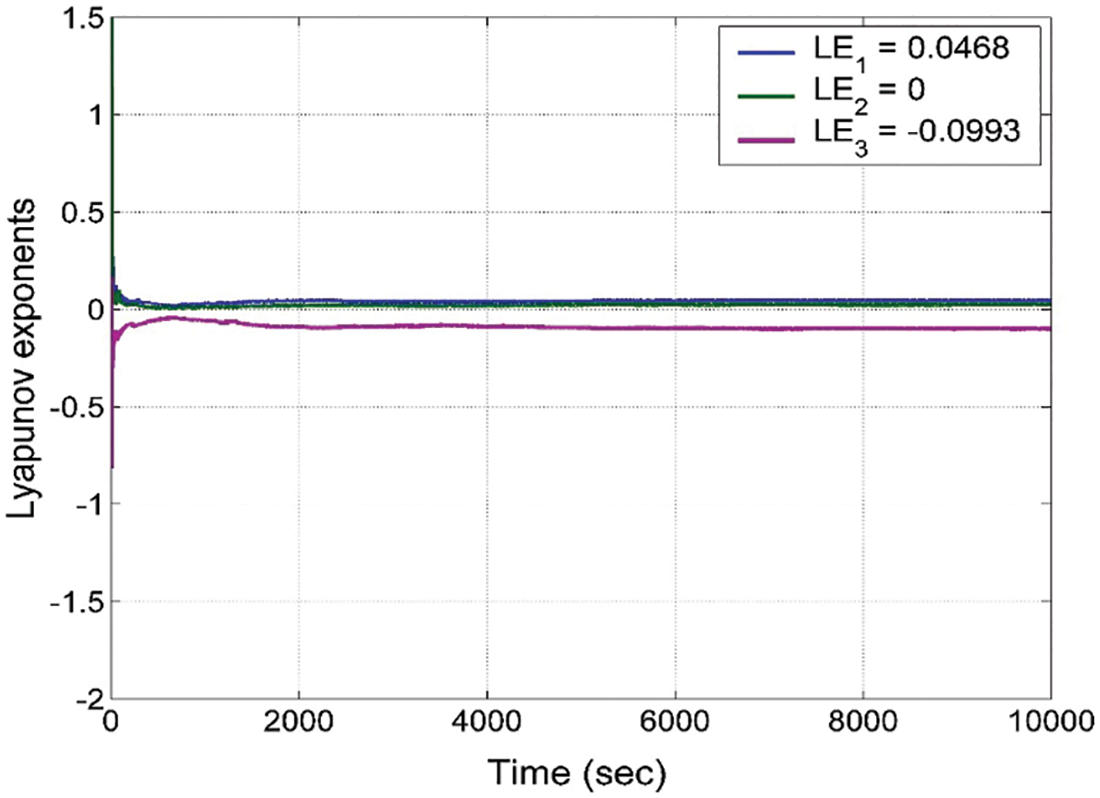
Figure 2: The spectrum of Lyapunov index values for the proposed 3-D chaotic system (1)

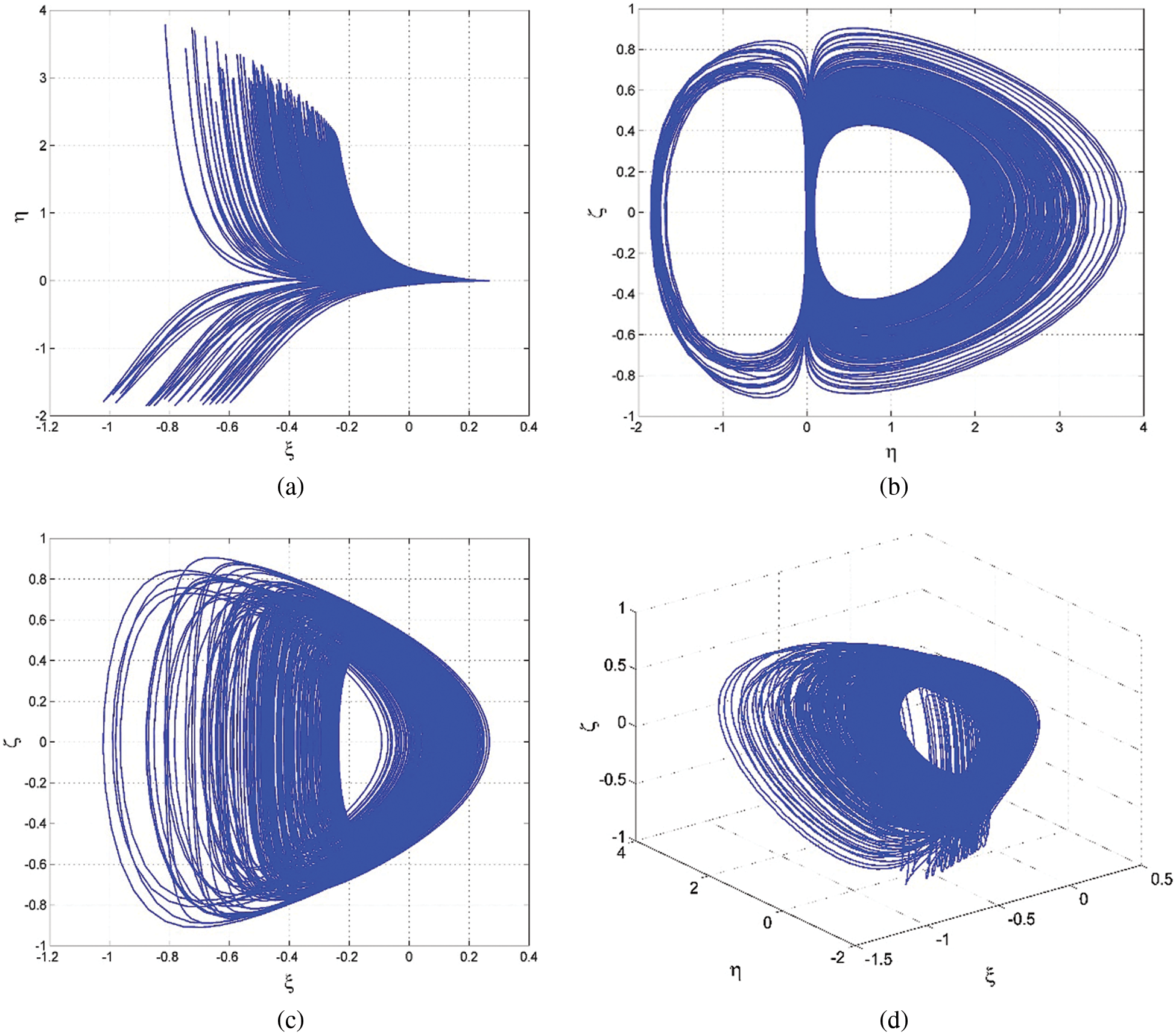
Figure 3: The signal plots for the proposed 3-D chaotic system (1)

3  Bifurcation Analysis and Multi-Stability of the New Chaotic System

3.1 Bifurcation Analysis

In this section, we use bifurcation diagrams to analyze the dynamics of the proposed chaotic system (1). Bifurcation analysis is useful for studying the qualitative properties of dynamical systems [48–51]. Our analysis concentrates on the parameter-dependent behavior of the proposed chaotic system (1) having capsule equilibrium and it is divided into two different cases.

For the first case, let β=3, the initial state at K 0=(0.02,0.01,0.02) and change α such that 6 ≤ α ≤ 10. For the second case, let α=8, the initial state at K 0=(0.02,0.01,0.02) and change β such that 2 ≤ β ≤ 6.

For both cases, we performed bifurcation analysis for the state variables ξ and ζ, and the corresponding largest Lyapunov exponent, respectively depicted in Figs. 4 and 5. It is observable from both settings that the system (1) exhibits robust chaos with a positive largest Lyapunov exponent runs through the entire region. Besides, it also indicates that the chaotic characteristics of system (1) increase with the decrease of the bifurcation parameter β.

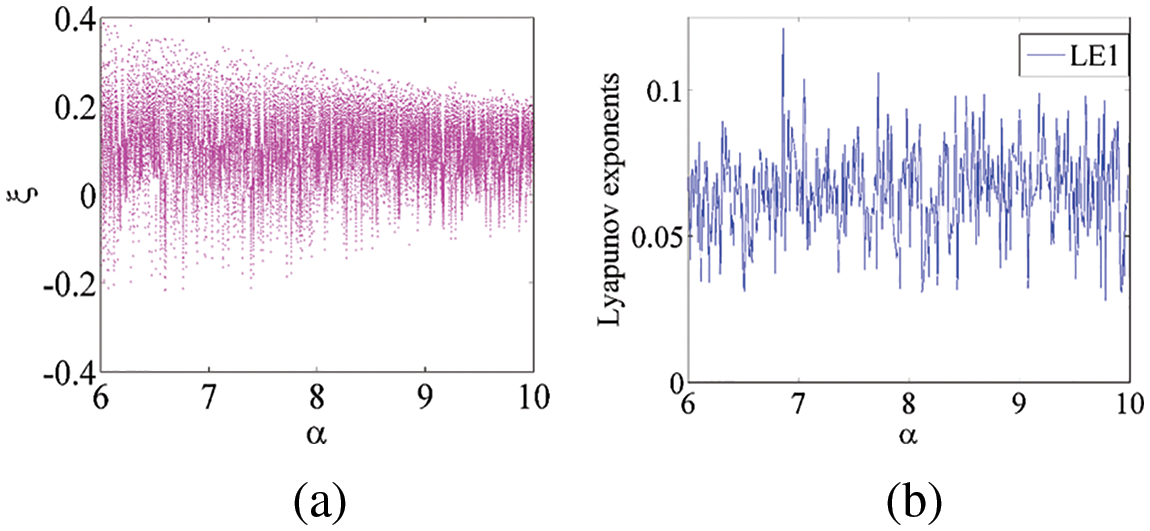
Figure 4: Dynamical analysis of the new chaotic system (1): (a) bifurcation diagram of ξ with reference to α; (b) largest Lyapunov exponent spectrum

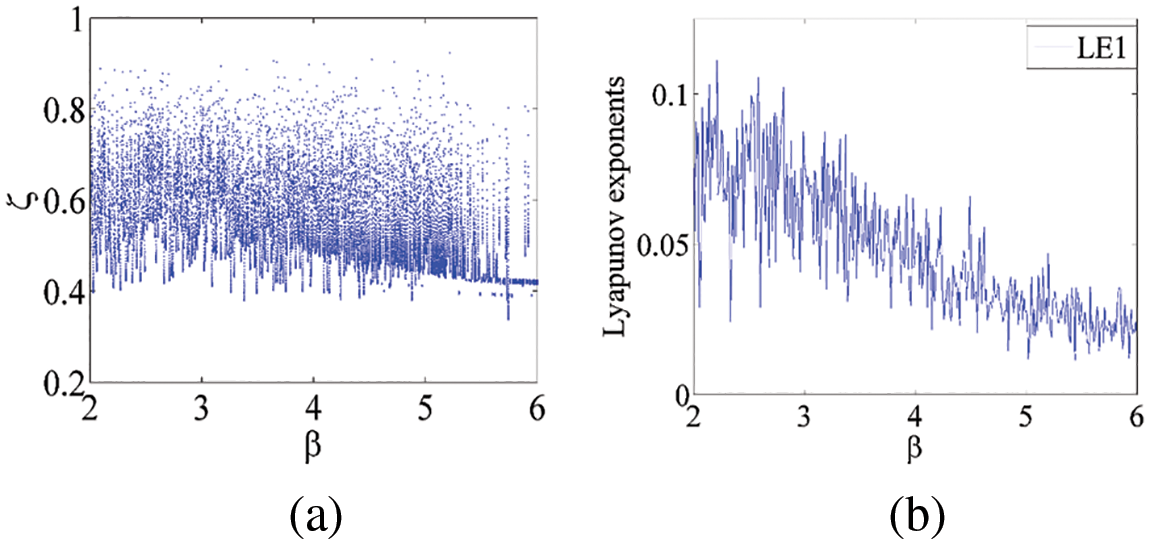
Figure 5: Dynamical analysis of chaotic system (1): (a) bifurcation diagram of ζ with reference to β; (b) largest Lyapunov exponent spectrum

3.2 Multi-Stability

Multi-stability is an intrinsic property of nonlinear dynamical systems, which reveals the abundant dynamic characteristics of the system (1), and has attracted much attention in recent years [18,19]. It means that two or more different kinds of attractors coexist together under the same parameter setting but with different initial states.

By fixing α=12, varying β in the region of [1,4] and selecting initial states to be K 0=(0.02,0.01,0.02) and Ω0=(−0.02,−0.01,−0.02), respectively. The coexisting bifurcation diagrams are plotted in Fig. 6. From Fig. 3, it is clear to observe that there exists a coexisting region of [1.5, 4]. For example, when β = 2.5, we discover that the system produces two types of coexisting chaotic attractors that can be shown in the respective Figs. 7a and 7b.

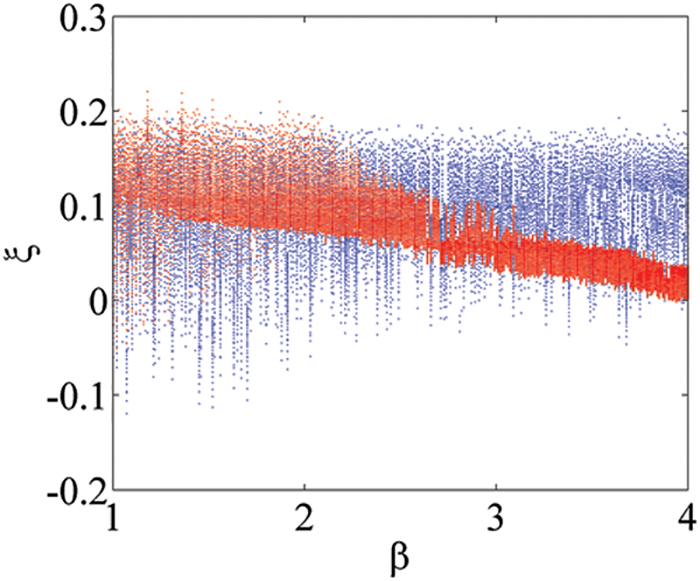
Figure 6: The coexisting bifurcation diagrams of the new system (1) with respect to β where α=12, K0=(0.02,0.01,0.02) (blue orbit) and Ω0=(−0.02,−0.01,−0.02) (red orbit)

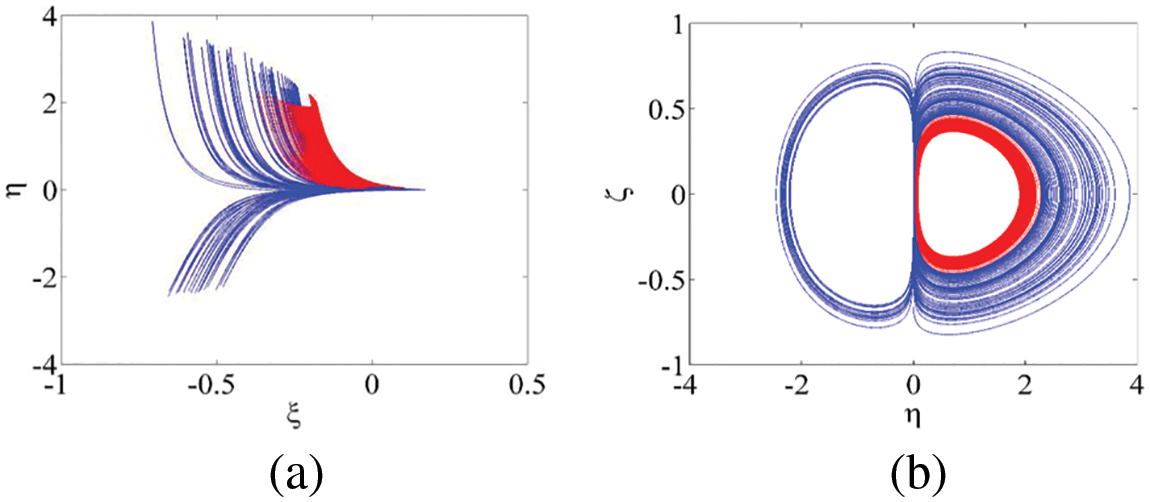
Figure 7: Phase portraits of the coexisting chaotic attractors in two different planes with α=12 and β=2.5 for the initial conditions K0=(0.02,0.01,0.02) (blue orbit) and Ω0=(−0.02,−0.01,−0.02): (a) ξ−η plane and (b) η−ζ plane

4  Speech Cryptosystem with FPGA Realization

4.1 The Proposed Speech Cryptosystem

This section illustrates the speech-based cryptosystem using the proposed 3-D chaotic system (1) with a capsule equilibrium curve. Fig. 8 shows the block diagram of the encryption system. In this cryptosystem, the two chaotic systems A and B are used as sources for chaos based key generators.

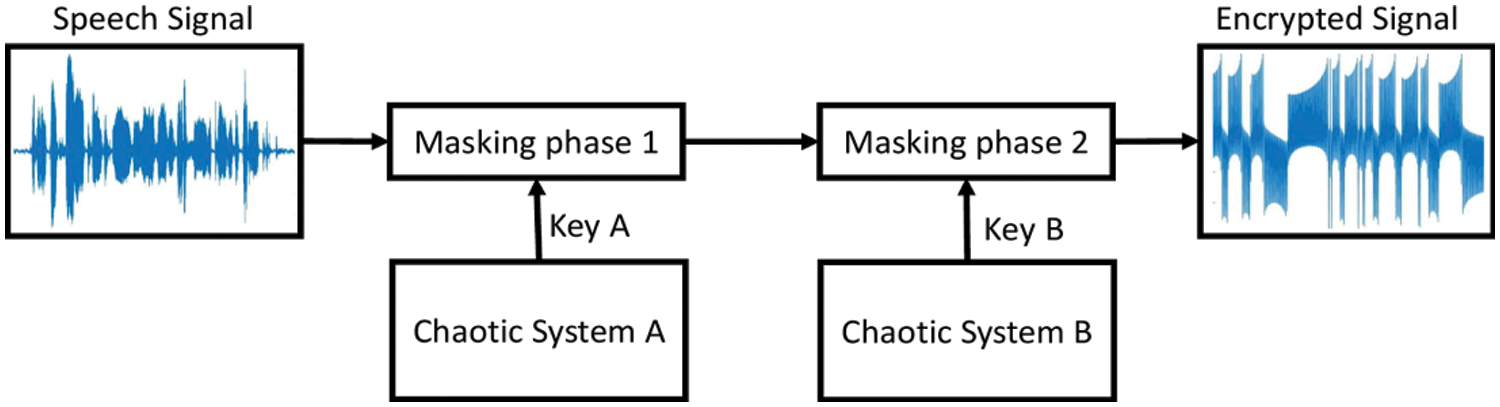
Figure 8: Block diagram of the proposed speech encryption

The encryption process consists of two phases. Firstly, the speech signal S(t) is masked based on the output of the chaotic system A as follows:

E1(t)=S(t)+ξA+ηA+ζA(8)

Then this signal is masked again using the second chaotic system B output, to produce the encrypted signal E2(t) as in (8) that is to be transferred through the channel

E2(t)=E1(t)+ξB+ηB+ζB(9)

We note that the outputs of systems A and B are managed to combine all state variables of the chaotic systems. As a result, the encrypted signal that carries the information becomes more complex than any individual state variable and cannot be predicted by the intruder.

In the decryption process (see Fig. 9), the proposed 3D chaotic system with capsule equilibrium curve in (1) is used in systems A and B as chaos-based key generators. Firstly, the received encrypted signal E2(t) is unmasked using the chaotic systems B as follows:

D1(t)=E2(t)−(ξB+ηB+ζB)(10)

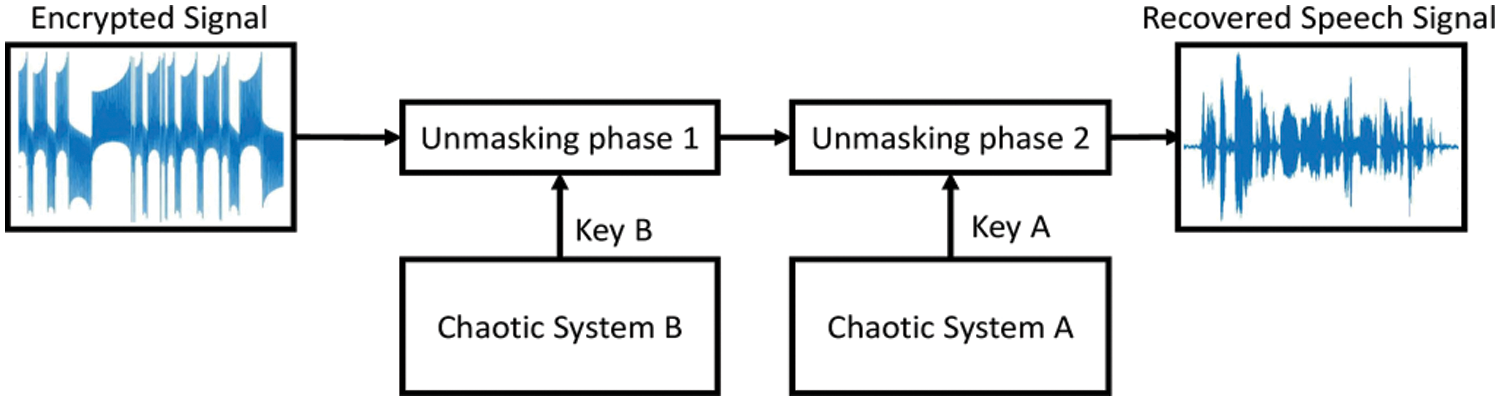
Figure 9: Block diagram of the proposed speech decryption

Then the un-masking of the produced signal D1(t) takes place using the output of the chaotic system A to produce the recovered speech signal D2(t) as follows:

D2(t)=D1(t)−(ξB+ηB+ζB)(11)

We assume that the key generators on the decryption side are identical and synchronized with the systems on the encryption side. Based on this assumption, the recovered signal D2(t) in (11) is similar to the original speech signal S(t).

4.2 Numerical Simulation

The simulation results were obtained using MATLAB/SIMULINK. Various tests were performed to examine the security and efficiency of the proposed system, such as waveforms, spectrogram analysis, Signal to Noise Ratio (SNR), and correlation tests. Speech signals have an 8000 Hz using eight quantization bits.

Fig. 10a shows the waveform in the original speech’s time domain, while Fig. 10b illustrates the encrypted speech waveform after the two phases of masking. On the other hand, the decrypted speech waveform in Fig. 10c matches the original speech waveform on the transmitter side.

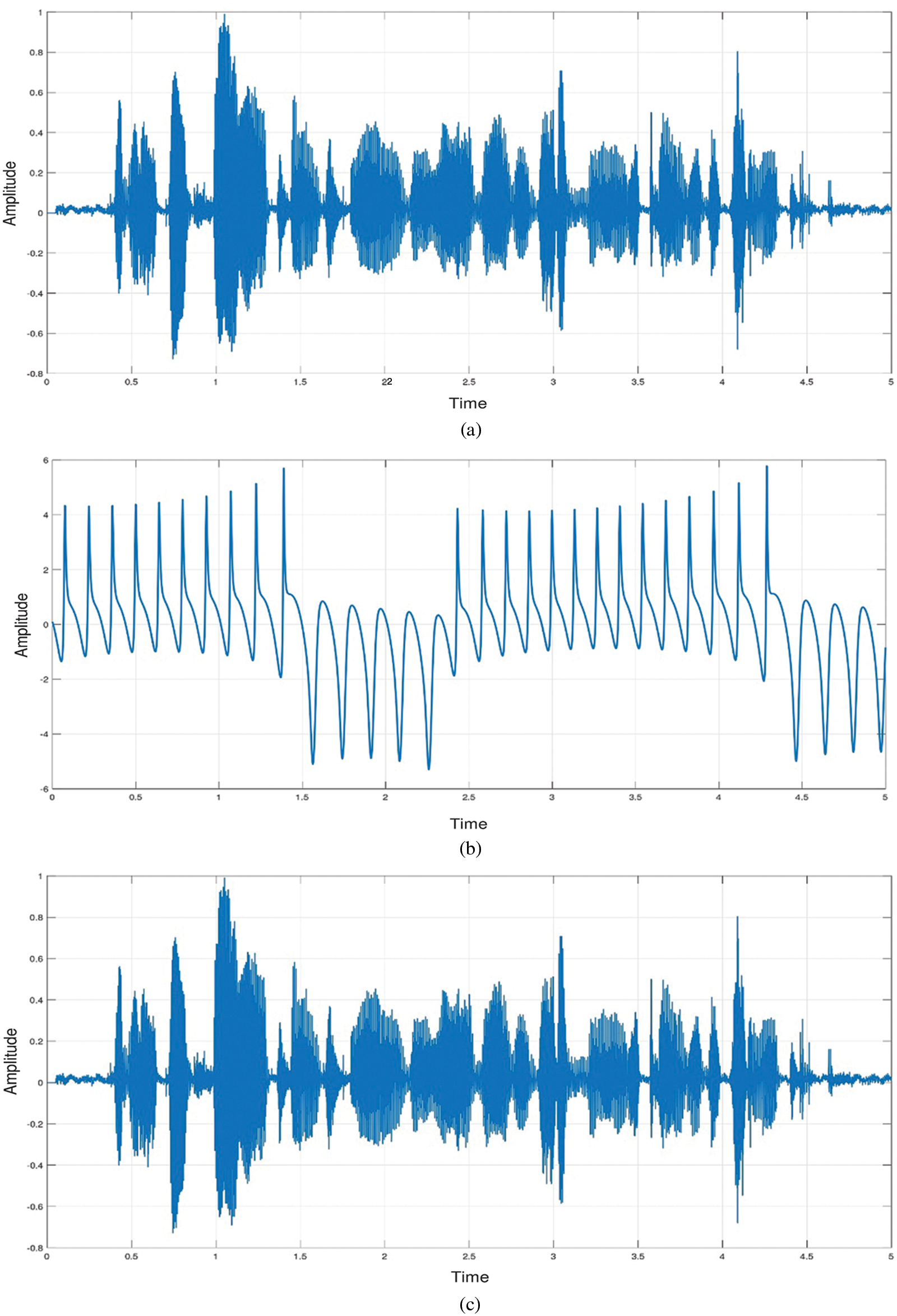
Figure 10: Waveform plots of (a) original speech, (b) encrypted speech, and (c) decrypted speech

4.3 Spectrogram Analysis

The proposed speech cryptosystem can be visually analyzed using the spectrogram’s distribution of energy in the time-frequency plane. As shown in Fig. 11, the spectrogram of the encrypted signal in Fig. 11b was distributed and very different from that of the original signals in Fig. 11a. Thus, the original signal became incomprehensible. Moreover, from the spectrogram plots, we can deduce that the decrypted speech signal in Fig. 11c is identical to that of the original speech as in Fig. 11a.

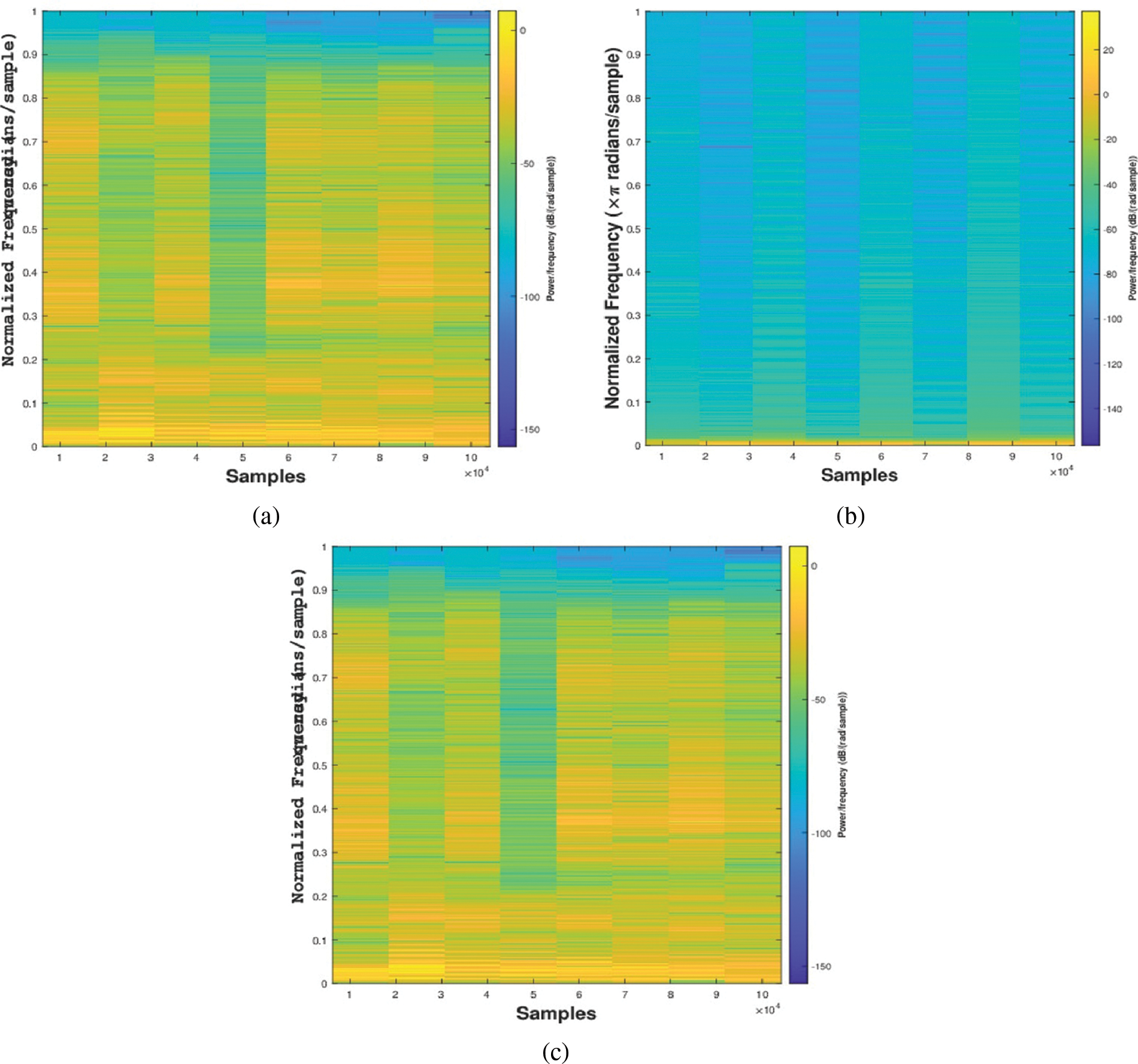
Figure 11: Spectrogram plots for (a) original speech, (b) encrypted speech, and (c) decrypted speech

4.4 Keyspace and Key Sensitivity Analysis

Noteworthy, the proposed chaotic system consists of two parameters and three initial conditions. The combination of these five parameters makes up the keyspace. They are responsible for the robustness of the proposed algorithm against many attacks. Based on key sensitivity test, it was shown that a slight change in one parameter alters the decrypted signal entirely. For example, Fig. 12 shows the effect of changing βvalue from 3 to 2.99999999999.

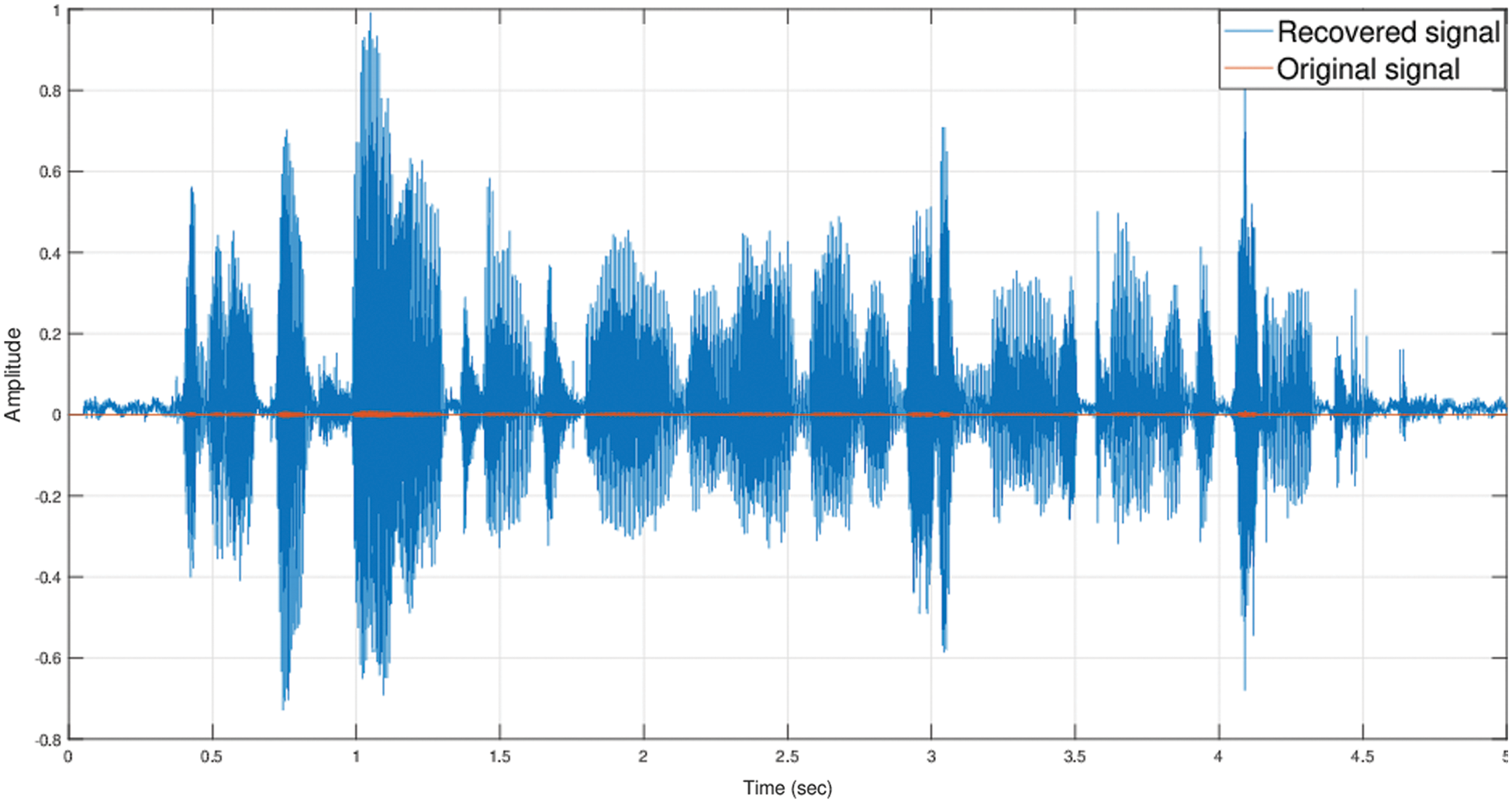
Figure 12: Decrypted speech signal with a little change in the parameter β

4.5 Statistical Tests

The Correlation Coefficient (CC) and Signal to Noise Ratio (SNR) are used to determine the strength of the proposed algorithm against statistical attacks. Table 1 shows the calculations of CC and SNR for four speech signals. The CC measures the numerical correlation having values in the range of −1 and 1. The smaller value of CC indicates a much better scrambled encrypted signal in comparison to the original speech signal. The SNR measures the ratio between the encrypted image and the original image. The highly negative value of SNR indicates an excellent quality of the encrypted speech signals.

4.6 Encryption Speed Analysis

Measuring the encryption speed of a speech signal is affected by the operating system, programming language, CPU frequency, and system complexity. The encryption speed results for a speech sample using the proposed speech cryptosystem are (0.12 s). Where the length of speech sample is (7.9 s) and the specifications of the used PC are; Intel(R) Core (TM) i7-8565U CPU @ 1.80 GHz hp LAPTOP-UFTCGPRC, 8 GB RAM, Windows11.

4.7 Algorithm Complexity Analysis

The algorithm complexity for the encryption of a speech signal consists of n samples is mainly determined by the following sub operations: masking phases 1 and 2. The complexity of each masking phase is O(n). Therefore, the overall complexity of the proposed speech cryptosystem is O(2n).

4.8 Statistical Randomness Tests

In this test, we analyze the randomness of the encrypted speech signal using NIST 800-22 test package provided by the National Institute of standards and technology (NIST) of the United States. Which is a statistical randomness test consisting of fifteen tests. This paper mainly tests the randomness of the original and the encrypted speech signals. The fifteen tests were applied to examine the randomness of each signal as shown in Table 2. The bit-stream of the original speech signal passed only 2 of the NIST tests. However, after applying our proposed speech signal (see Fig. 8), all tests were passed.

4.9 FPGA Realization

In this part of the study, the speech-based cryptosystem has been realized on the FPGA platform. The synthesizable Very High-Speed Integrated Circuit Hardware Description Language (VHDL) code was generated using a Hardware Description Language (HDL) coder. MATLAB toolbox is responsible for converting MATLAB/SIMULINK design into VHDL or Verilog code. The generated VHDL code has been tested using the QUARTUS program using CYCLON V FPGA chip. The Quartus includes full support for all popular methods of entering a description of the desired circuit into a Computer Aided Design (CAD) system, such as the Verilog, VHDL, and based on a schematic diagram.

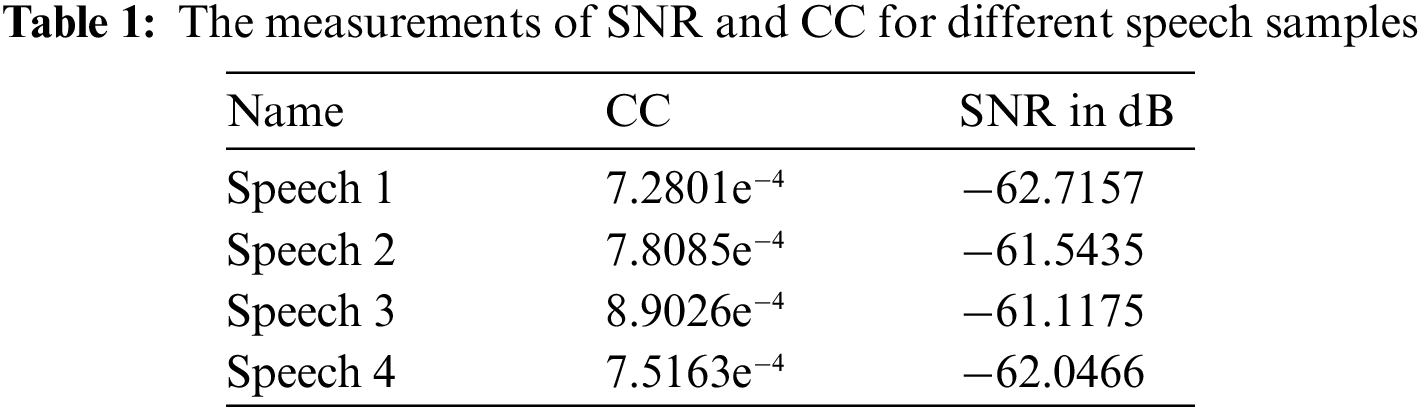
In this section, we illustrate in detail how to build the speech-based cryptosystem using the proposed 3D chaotic system with a capsule equilibrium curve (1) and its realization in MATLAB/SIMULINK to generate HDL-code. The study begins with the discretization of the novel 3D chaotic system with a capsule equilibrium, which is presented with differential equations in continuous time. The discrete form for the proposed 3D chaotic system using the forward Euler algorithm is shown in Eq. (12).

ξ[n+1]=ξ[n]+h.ζ[n]η[n+1]=η[n]+h.(−ζ(αη[n]+βη2[n]+ξ[n]ζ[n]))ζ[n+1]=ζ[n]_h.(ξ4[n]−0.1ξ2[n]η2[n]+η2[n]−0.5)(12)

The discretization step size parameter h is chosen to be 0.001 with n and n + 1 being the current state and the next state of the chaotic system.

Using Simulink, we can draw the top-level block diagram of the discretized 3D chaotic system (12) as in Fig. 13. This system consists of three main parts, one for each state variable. The initial conditions for the system are ξ[0] = 0.02, η[0] = 0.01, ζ[0] = 0.02. Each part has three inputs u(1), u(2), and u(3) represents ξ[n], η[n], and ζ[n] respectively. The output of each part is connected to the output block that passes the values of state variables to the workspace as time series.

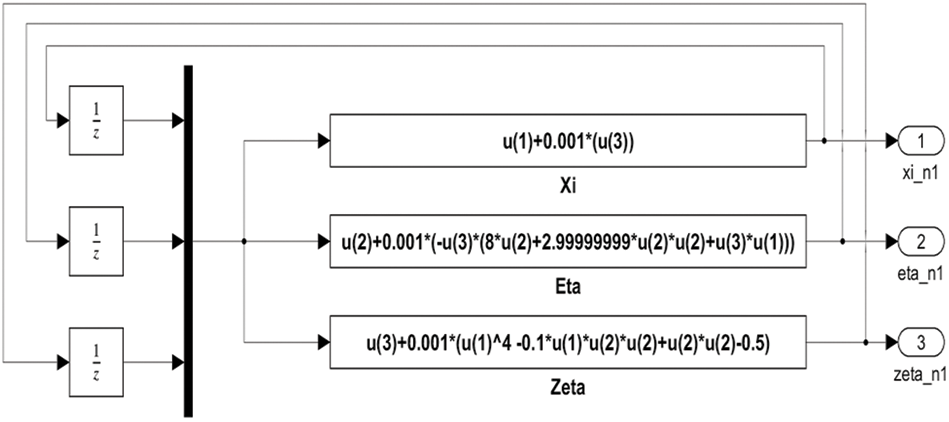
Figure 13: Simulink block diagram of the proposed 3D chaotic system

Figs. 14a–14c illustrate the chaotic attractors of the discretized 3D chaotic system (12).

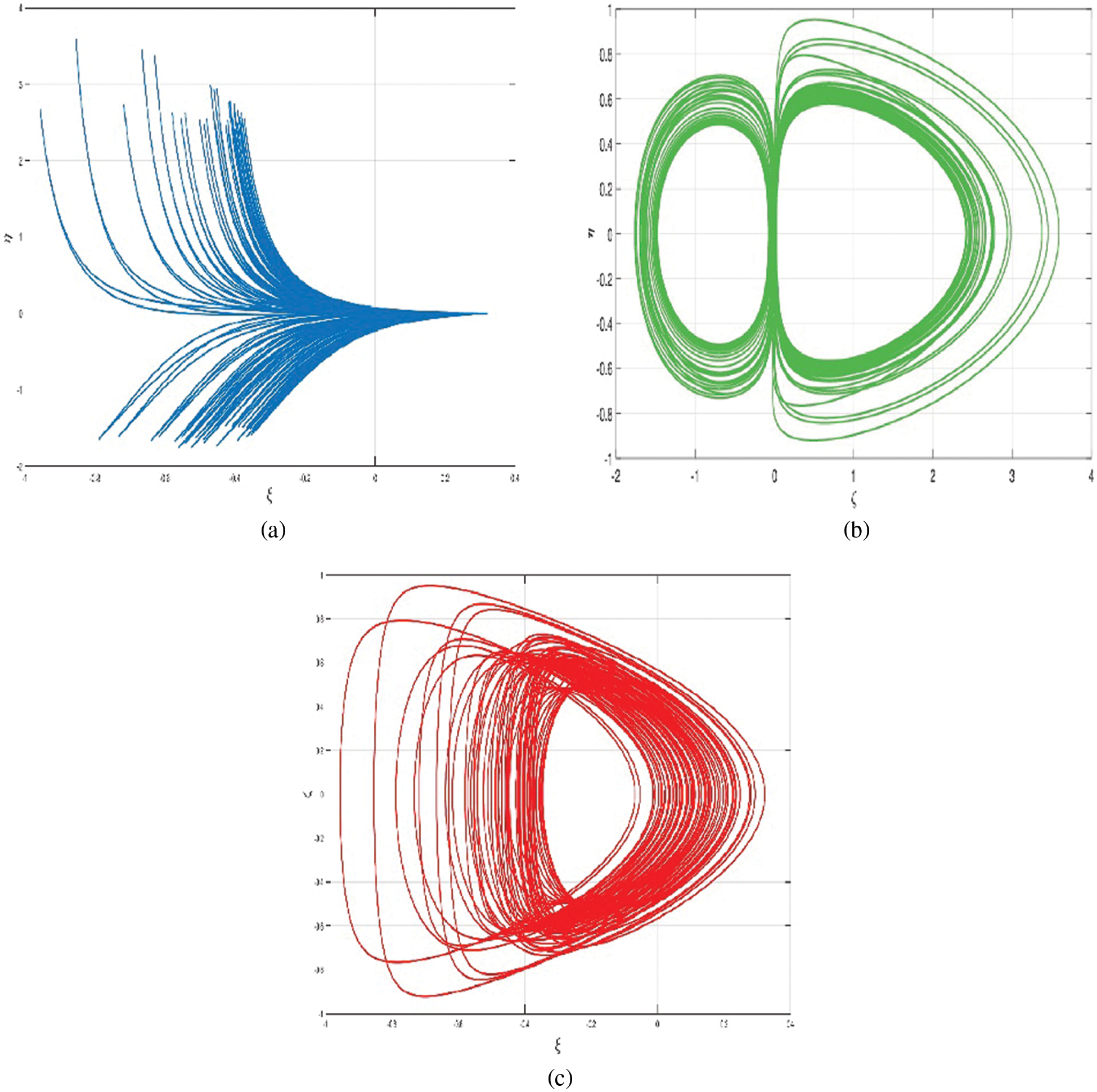
Figure 14: Simulation trajectories of discretized 3D chaotic system (12)

The top-level block diagram of speech encryption process is shown in Fig. 15a. This system consists of three inputs; clock, reset, and speech signal.

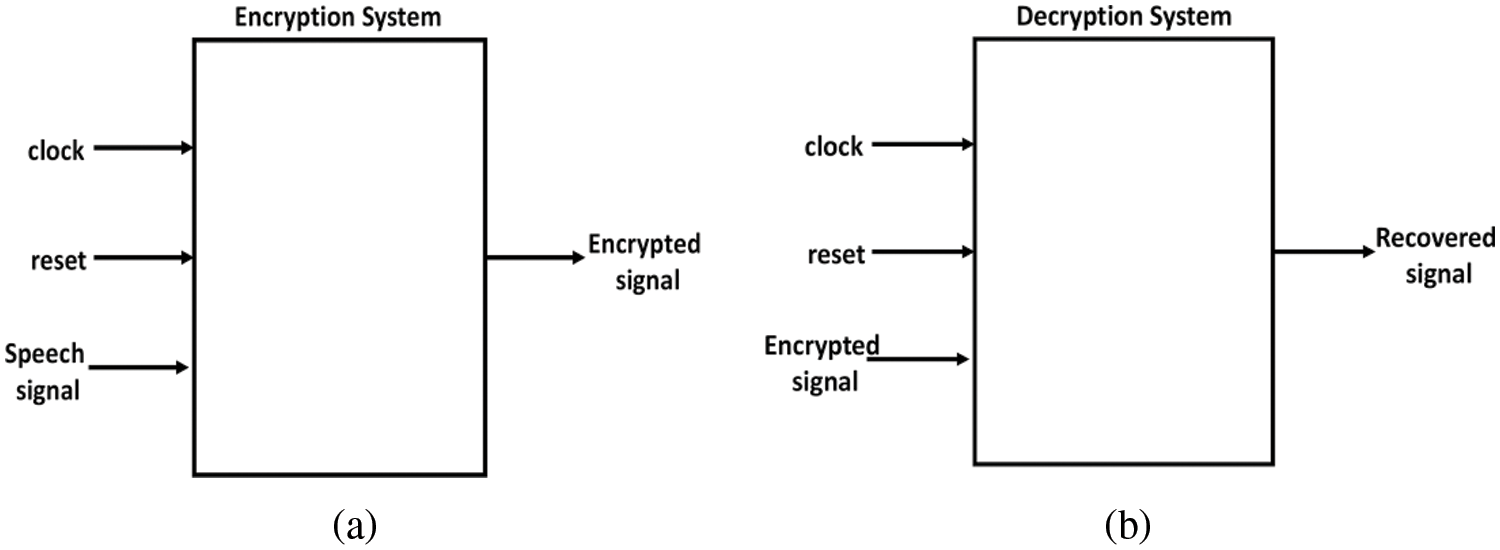
Figure 15: Top-level simulink blocks of: (a) speech encryption and (b) speech decryption system

Similarly, the top-level block diagram for the decryption is shown in Fig. 15b. The inputs of these systems are the encrypted signal, clock, and reset. The values of (α, β) parameters, the initial values of the three state variables, ξ[0]η[0]ζ[0] and step size h are assigned internally within the system.

Figs. 16a and 16b illustrate the internal Simulink blocks for the encryption/decryption systems. These systems mainly consist of the chaotic systems A and B, which are identical to each other, adders and subtracts.

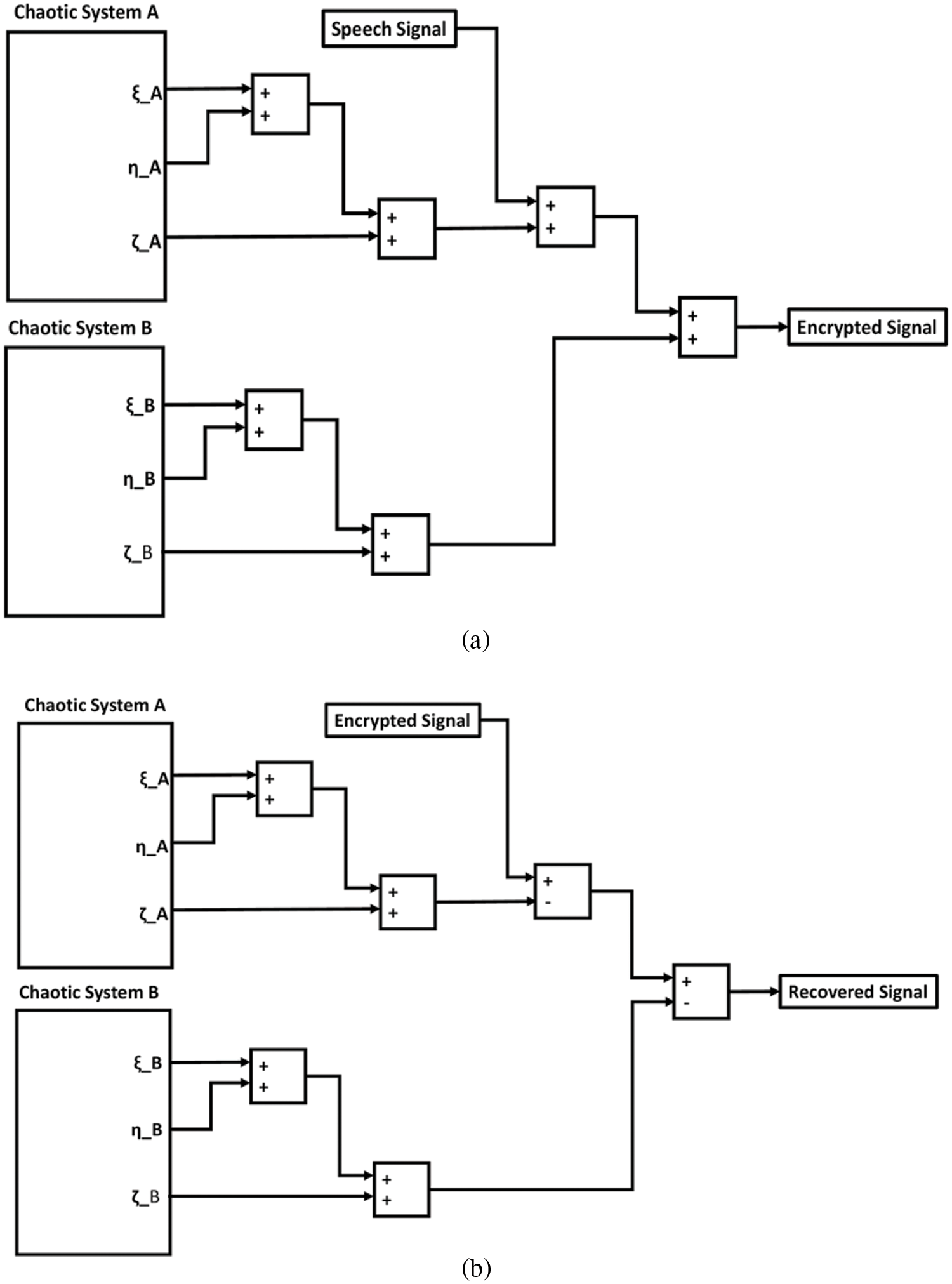
Figure 16: Detailed simulink blocks for (a) speech encryption and (b) speech decryption system

Then, the hardware implementation of the proposed cryptosystem is done using the VHDL code. Each system is realized on the FPGA Cyclon V platform as shown in Fig. 17.

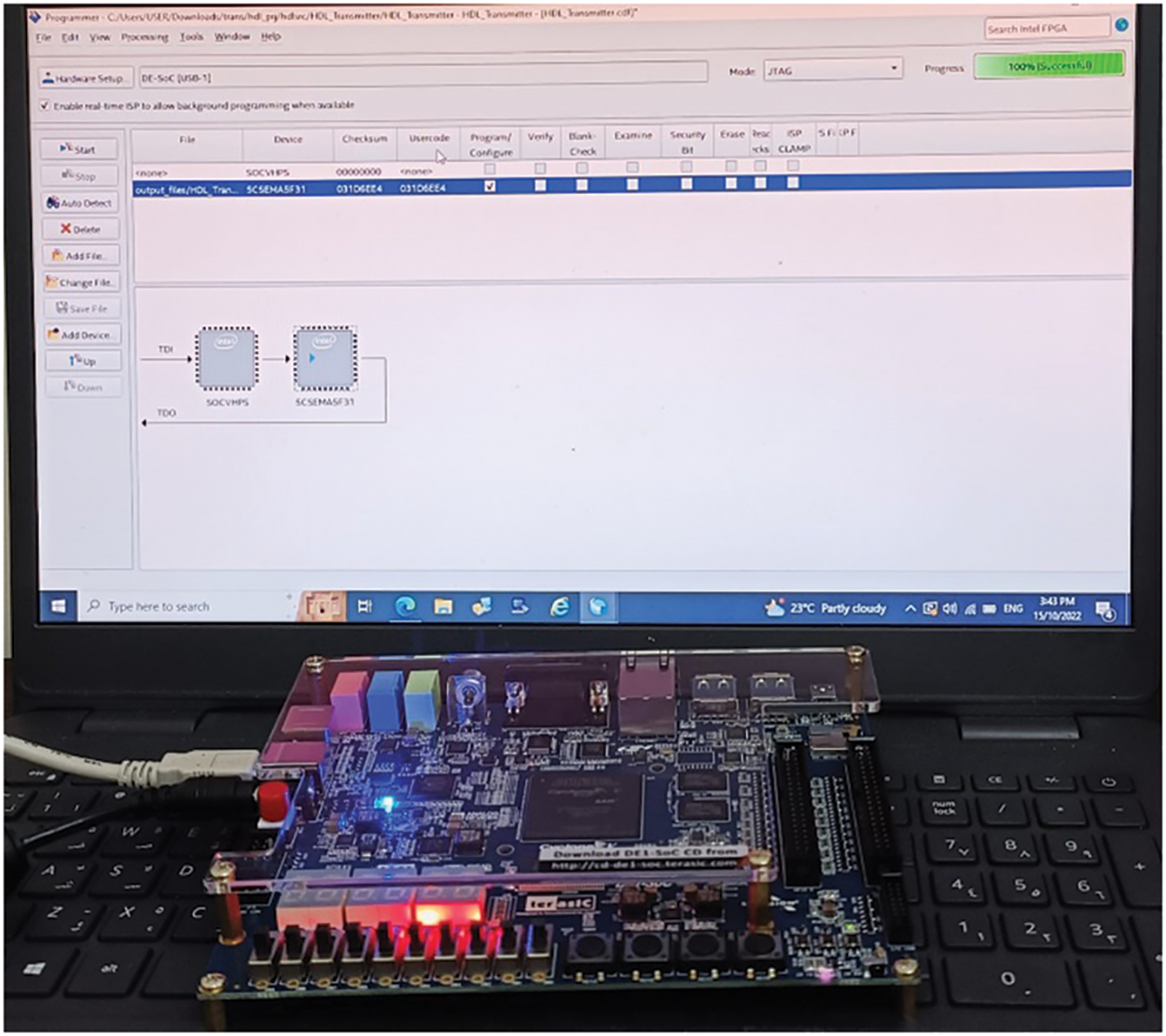
Figure 17: The FPGA implementation of the proposed encryption system

With regards to FPGA implementation, all variables and constants makes use of the 32-bit fixed-point arithmetic representation. This representation can be divided into three parts, 1-bit for the sign, 7-bits for the integer part, and 24-bits for the fractional part.

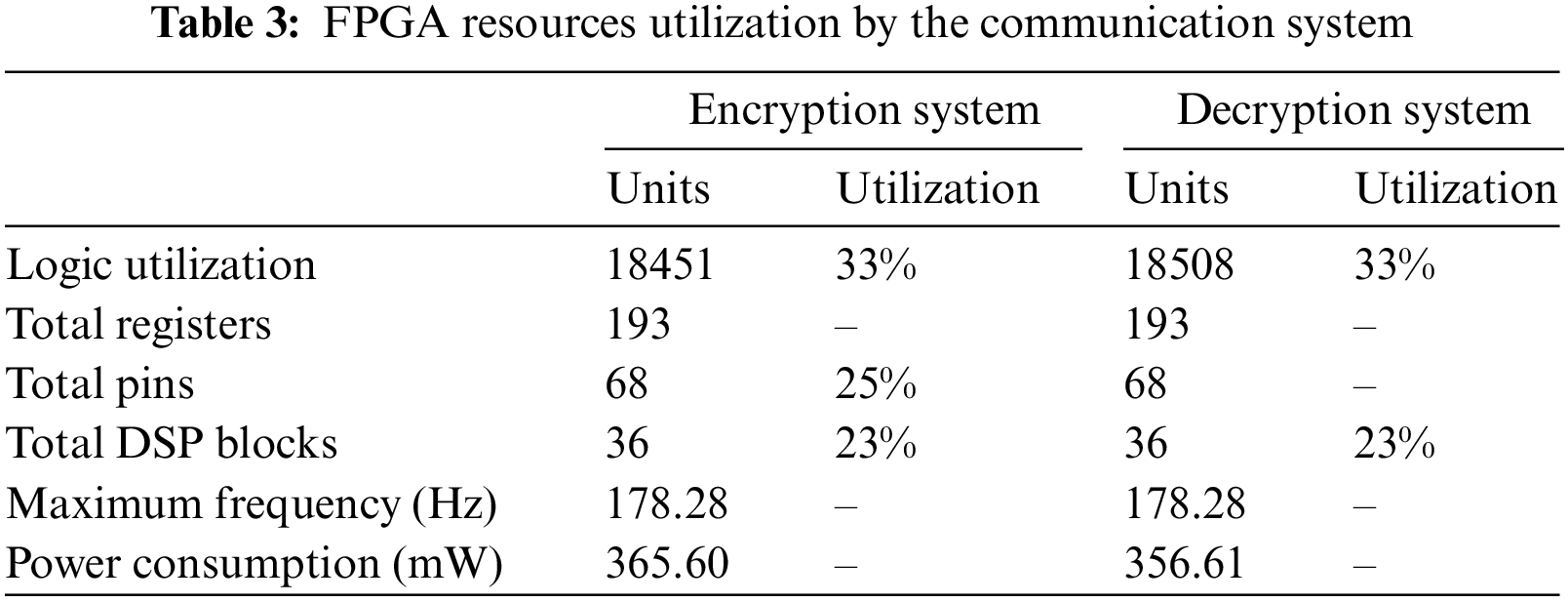
Table 3 reveals the amount FPGA resources utilization by the encryption and decryption systems. As shown in Table 3, both encryption and decryption systems require almost the same FPGA resources, which are 33% of Logic Utilization and 23% of Digital Signal Processors (DSP), while the maximum frequency and power consumption obtained as 178.28 MHz and 365.60 mW respectively.

5  Conclusion

This research describes a new chaotic dynamical system with a capsule equilibrium curve. The proposed chaotic system is made up of six nonlinear terms. The proposed chaotic system exhibits a hidden attractor and multi-stability with coexisting attractors. A detailed bifurcation analysis with respect to parameters was described for the proposed chaotic system with capsule equilibrium curve. Finally, we have proposed speech cryptosystem and algorithm, which is based on our novel chaotic system with a capsule equilibrium curve and follows its security evolution and implementation on the FPGA platform. The measures for encrypted and decrypted signal quality showed that the proposed algorithm has high quality of recovered speech signal. Experimental results showed that our speech encryption system utilized 33% of the Field Programmable Gate Array (FPGA), while the maximum clock frequency was 178.28 MHz.

Chaotic systems have several applications in science and engineering. In this work, we focused only on a speech encryption cryptosystem. As future research work, we plan to develop more engineering applications of our chaotic system such as watermarking, data hiding, steganography, etc.

Acknowledgement: The authors would like to thank the Universiti Sultan Zainal Abidin for supporting this project.

Funding Statement: This project is partially funded by the Center for Research Excellence, Incubation Management Center, Universiti Sultan Zainal Abidin via an internal grant UniSZA/2021/SRGS-IC/07.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. K. Benkouider, T. Bouden, A. Sambas, M. A. Mohamed, I. M. Sulaiman et al., “Dynamics, control and secure transmission electronic circuit implementation of a new 3D chaotic system in comparison with 50 reported systems,” IEEE Access, vol. 9, pp. 152150–152168, 2021. [Google Scholar]

2. C. Guo and A. C. J. Luo, “Bifurcation dynamics of complex period-1 motions to chaos in an electromagnetically tuned duffing oscillator,” International Journal of Dynamics and Control, vol. 10, no. 5, pp. 1361–1384, 2022. [Google Scholar]

3. S. Vaidyanathan, M. Feki, A. Sambas and C. H. Lien, “A new biological snap oscillator: Its modelling, analysis, simulations and circuit design,” International Journal of Simulation and Process Modelling, vol. 13, no. 5, pp. 419–432, 2018. [Google Scholar]

4. S. S. Sajjadi, D. Baleanu, A. Jajarmi and H. M. Pirouz, “A new adaptive synchronization and hyperchaos control of a biological snap oscillator,” Chaos, Solitons & Fractals, vol. 138, Article ID 109919, pp. 1–13, 2020. [Google Scholar]

5. V. T. Pham, D. S. Ali, N. M. G. Al-Saidi, K. Rajagopal, F. E. Alsaadi et al., “A novel mega-stable chaotic circuit,” Radioengineering, vol. 29, no. 1, pp. 140–146, 2020. [Google Scholar]

6. A. Sambas, S. Vaidyanathan, E. Tlelo-Cuautle, S. Zhang, O. Guillen-Fernandez et al., “A novel chaotic system with two circles of equilibrium points: Multistability, electronic circuit and FPGA realization,” Electronics, vol. 8, no. 11, Article ID 1211, pp. 1–13, 2019. [Google Scholar]

7. R. Wang, C. Li, S. Kong, Y. Jiang and T. Lei, “A 3D memristive chaotic system with conditional symmetry,” Chaos, Solitons and Fractals, vol. 158, Article ID 111992, pp. 1–15, 2022. [Google Scholar]

8. K. M. Owolabi, J. F. Gómez-Aguilar and B. Karaagac, “Modelling, analysis and simulations of some chaotic systems using derivative with Mittag–Leffler kernel,” Chaos, Solitons and Fractals, vol. 125, pp. 54–63, 2019. [Google Scholar]

9. S. B. Chen, H. Jahanshahi, O. A. Abba, J. E. Solís-Pérez, S. Bekiros et al., “The effect of market confidence on a financial system from the perspective of fractional calculus: Numerical investigation and circuit realization,” Chaos, Solitons and Fractals, vol. 140, Article ID 110223, pp. 1–15, 2020. [Google Scholar]

10. M. Messadi, K. Kemih, L. Moysis and C. Volos, “A new 4D memristor chaotic system: Analysis and implementation,” Integration, vol. 88, pp. 91–100, 2023. [Google Scholar]

11. W. A. Al-Musawi, W. A. Wali and M. A. A. Al-Ibadi, “New artificial neural network design for chua chaotic system prediction using FPGA hardware co-simulation,” International Journal of Electrical and Computer Engineering, vol. 12, no. 2, Article ID 1955, pp. 1–10, 2022. [Google Scholar]

12. M. Tuna, A. Karthikeyan, K. Rajagopal, M. Alcin and İ. Koyuncu, “Hyperjerk multiscroll oscillators with megastability: Analysis, FPGA implementation and a novel ANN-ring-based true random number generator,” AEU-International Journal of Electronics and Communications, vol. 112, Article ID 152941, pp. 1–20, 2019. [Google Scholar]

13. S. He, S. Banerjee and K. Sun, “Complex dynamics and multiple coexisting attractors in a fractional-order microscopic chemical system,” European Physical Journal: Special Topics, vol. 228, no. 1, pp. 195–207, 2019. [Google Scholar]

14. C. H. Miwadinou, A. V. Monwanou, J. Yovogan, L. A. Hinvi, P. N. Tuwa et al., “Modeling nonlinear dissipative chemical dynamics by a forced modified Van der Pol-Duffing oscillator with asymmetric potential: Chaotic behaviors predictions,” Chinese Journal of Physics, vol. 56, no. 3, pp. 1089–1104, 2018. [Google Scholar]

15. F. Sukono, A. Sambas, S. He, H. Liu, S. Vaidyanathan et al., “Dynamical analysis and adaptive fuzzy control for the fractional-order financial risk chaotic system,” Advances in Difference Equations, vol. 2020, no. 1, Article ID 674, pp. 1–12, 2020. [Google Scholar]

16. R. Hosseinzadeh, M. Zarebnia and R. Parvaz, “Hybrid image encryption algorithm based on 3D chaotic system and choquet fuzzy integral,” Optics and Laser Technology, vol. 120, Article ID 105698, pp. 1–14, 2019. [Google Scholar]

17. G. Grassi, “Chaos in the real world: Recent applications to communications, computing, distributed sensing, robotic motion, bio-impedance modelling and encryption systems,” Symmetry, vol. 13, no. 11, Article ID 2151, pp. 1–10, 2021. [Google Scholar]

18. S. Guo, R. Wu, X. Wang, J. Wang, Q. Li et al., “A 3D model encryption scheme based on a cascaded chaotic system,” Signal Processing, vol. 202, Article ID 108745, pp. 1–20, 2023. [Google Scholar]

19. R. Wu, S. Guo, X. Wang, S. Liu, Q. Li et al., “AEA-NCS: An audio encryption algorithm based on a nested chaotic system,” Chaos, Solitons & Fractals, vol. 165, no. 3, Article ID 112770, pp. 1–11, 2022. [Google Scholar]

20. M. Ahmad, B. Alam and O. Farooq, “Chaotic masking of voice bitstream using mixed sequences for authorized listening,” Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering, vol. 85, pp. 604–611, 2012. [Google Scholar]

21. A. Sambas, S. Vaidyanathan, X. Zhang, I. Koyuncu, T. Bonny et al., “A novel 3D chaotic system with line equilibrium: Multistability, integral sliding mode control, electronic circuit, FPGA implementation and its image encryption,” IEEE Access, vol. 10, pp. 68057–68074, 2022. [Google Scholar]

22. A. Sambas, S. Vaidyanathan, E. Tlelo-Cuautle, B. Abd-El-Atty, A. A. Abd El-Latif et al., “A 3-D multi-stable system with a peanut-shaped equilibrium curve: Circuit design, FPGA realization, and an application to image encryption,” IEEE Access, vol. 8, pp. 137116–137132, 2020. [Google Scholar]

23. M. Ahmad, S. Agarwal, A. Alkhayyat, A. Alhudhaif, F. Alenezi et al., “An image encryption algorithm based on new generalized fusion fractal structure,” Information Sciences, vol. 592, pp. 1–20, 2022. [Google Scholar]

24. L. Zhu, D. Jiang, J. Ni, X. Wang, X. Rong et al., “A stable meaningful image encryption scheme using the newly-designed 2D discrete fractional-order chaotic map and Bayesian compressive sensing,” Signal Processing, vol. 195, Article ID 108489, pp. 1–27, 2022. [Google Scholar]

25. X. Wang, X. Wang, B. Ma, Q. Li and Y. Q. Si, “High precision error prediction algorithm based on ridge regression predictor for reversible data hiding,” IEEE Signal Processing Letters, vol. 28, pp. 1125–1129, 2021. [Google Scholar]

26. C. Wang, B. Ma, Z. Xia, J. Li, Q. Li et al., “Stereoscopic image description with trinion fractional-order continuous orthogonal moments,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 32, no. 4, pp. 1998–2012, 2022. [Google Scholar]

27. B. Ma and Y. Q. Shi, “A reversible data hiding scheme based on code division multiplexing,” IEEE Transactions on Information Forensics and Security, vol. 11, no. 9, pp. 1914–1927, 2016. [Google Scholar]

28. Q. Li, X. Wang, B. Ma, X. Wang, C. Wang et al., “Concealed attack for robust watermarking based on generative model and perceptual loss,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 32, no. 8, pp. 5695–5706, 2022. [Google Scholar]

29. L. F. Avalos-Ruiz, C. J. Zuniga-Aguilar, J. F. Gomez-Aguilar, R. F. Escobar-Jimenez and H. M. Romero-Ugalde, “FPGA implementation and control of chaotic systems involving the variable-order fractional operator with Mittag–Leffler law,” Chaos, Solitons and Fractals, vol. 115, pp. 177–189, 2018. [Google Scholar]

30. A. Dali, S. Abdelmalek, A. Bakdi and M. Bettayeb, “A class of PSO-tuned controllers in Lorenz chaotic system,” Mathematics and Computers in Simulation, vol. 204, pp. 430–449, 2023. [Google Scholar]

31. C. Li, J. C. Sprott, X. Zhang, L. Chai and Z. Liu, “Constructing conditional symmetry in symmetric chaotic systems,” Chaos, Solitons and Fractals, vol. 155, Article ID 111723, pp. 1–27, 2022. [Google Scholar]

32. V. T. Pham, S. Jafari, X. Wang and J. Ma, “A chaotic system with different shapes of equilibria,” International Journal of Bifurcation and Chaos, vol. 26, no. 4, Article ID 1650069, pp. 1–5, 2016. [Google Scholar]

33. V. T. Pham, S. Jafari, C. Volos, A. Giakoumis, S. Vaidyanathan et al., “A chaotic system with equilibria located on the rounded square loop and its circuit implementation,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 63, no. 9, pp. 878–882, 2016. [Google Scholar]

34. T. Gotthans, J. C. Sprott and J. Petrzela, “Simple chaotic flow with circle and square equilibrium,” International Journal of Bifurcation and Chaos, vol. 26, no. 8, Article ID 1650137, pp. 1–8, 2016. [Google Scholar]

35. A. Sambas, S. Vaidyanathan, T. Bonny, S. Zhang, Y. Hidayat et al., “Mathematical model and FPGA realization of a multi-stable chaotic dynamical system with a closed butterfly-like curve of equilibrium points,” Applied Sciences, vol. 11, no. 2, Article ID 788, pp. 1–16, 2021. [Google Scholar]

36. V. T. Pham, S. Jafari and C. Volos, “A novel chaotic system with heart-shaped equilibrium and its circuital implementation,” Optik, vol. 131, pp. 343–349, 2017. [Google Scholar]

37. A. Sambas, S. Zhang, S. Vaidyanathan and Y. Hidayat, “Electronic circuit design of a novel chaotic system with apple-shaped curve equilibrium and multiple coexisting attractors,” Journal of Physics: Conference Series, vol. 1477, no. 2, Article ID 022015, pp. 1–12, 2020. [Google Scholar]

38. K. Merit and A. Ouamri, “Securing speech in GSM networks using DES with random permutation and inversion algorithm,” International Journal of Distributed and Parallel Systems, vol. 3, no. 4, Article ID 157, pp. 1–8, 2012. [Google Scholar]

39. Z. Chang and M. Woźniak, “Encryption technology of voice transmission in mobile network based on 3DES-ECC algorithm,” Mobile Networks and Applications, vol. 25, no. 6, pp. 2398–2408, 2020. [Google Scholar]

40. M. M. Rahman, T. K. Saha and M. A. A. Bhuiyan, “Implementation of RSA algorithm for speech data encryption and decryption,” International Journal of Computer Science and Network Security, vol. 12, no. 3, pp. 74–82, 2012. [Google Scholar]

41. J. M. Munoz-Pacheco, E. Zambrano-Serrano, C. Volos, S. Jafari, J. Kengne et al., “A new fractional-order chaotic system with different families of hidden and self-excited attractors,” Entropy, vol. 20, no. 8, Article ID 564, pp. 1–18, 2018. [Google Scholar]

42. V. H. Carbajal-Gomez, E. Tlelo-Cuautle, J. M. Muñoz-Pacheco, L. G. de la Fraga, C. Sanchez-Lopez et al., “Optimization and CMOS design of chaotic oscillators robust to PVT variations,” Integration, vol. 65, pp. 32–42, 2019. [Google Scholar]

43. T. Liu, H. Yan, S. Banerjee and J. Mou, “A fractional-order chaotic system with hidden attractor and self-excited attractor and its DSP implementation,” Chaos, Solitons and Fractals, vol. 145, Article ID 110791, pp. 1–12, 2021. [Google Scholar]

44. A. D. Pano-Azucena, E. Tlelo-Cuautle, J. M. Muñoz-Pacheco and L. G. de la Fraga, “FPGA-based implementation of different families of fractional-order chaotic oscillators applying Grünwald–Letnikov method,” Communications in Nonlinear Science and Numerical Simulation, vol. 72, pp. 516–527, 2019. [Google Scholar]

45. T. Bonny, R. Al Debsi, S. Majzoub and A. S. Elwakil, “Hardware optimized FPGA implementations of high-speed true random bit generators based on switching-type chaotic oscillators,” Circuits, Systems, and Signal Processing, vol. 38, no. 3, pp. 1342–1359, 2019. [Google Scholar]

46. T. Bonny, “Chaotic or hyper-chaotic oscillator? Numerical solution, circuit design, MATLAB HDL-coder implementation, VHDL code, security analysis, and FPGA realization,” Circuits, Systems, and Signal Processing, vol. 40, no. 3, pp. 1061–1088, 2021. [Google Scholar]

47. A. Wolf, J. B. Swift, H. L. Swinney and J. A. Vastano, “Determining lyapunov exponents from a time series,” Physica D: Nonlinear Phenomena, vol. 16, no. 3, pp. 285–317, 1985. [Google Scholar]

48. S. He, K. Sun, X. Mei, B. Yan and S. Xu, “Numerical analysis of a fractional-order chaotic system based on conformable fractional-order derivative,” European Physical Journal Plus, vol. 132, no. 1, pp. 1–11, 2017. [Google Scholar]

49. S. He, K. Sun, H. Wang, X. Mei and Y. Sun, “Generalized synchronization of fractional-order hyperchaotic systems and its DSP implementation,” Nonlinear Dynamics, vol. 92, no. 1, pp. 85–96, 2018. [Google Scholar]

50. A. Sambas, S. Vaidyanathan, I. Moroz, B. Idowu, M. A. Mohamed et al., “A simple multi-stable chaotic jerk system with two saddle-foci equilibrium points: Analysis, synchronization via active backstepping control and electronic circuit design,” International Journal of Electrical and Computer Engineering, vol. 11, no. 4, pp. 2941–2952, 2021. [Google Scholar]

51. S. F. Al-Azzawi, M. A. Mohamed, H. Rubiani, M. Mamat, J. Titaley et al., “Chaotic lorenz system and it’s suppressed,” Journal of Advanced Research in Dynamical and Control Systems, vol. 12, no. 2, pp. 548–555, 2020. [Google Scholar]