Residual Feature Attentional Fusion Network for Lightweight Chest CT Image Super-Resolution

1  Introduction

The ever-mutating COVID-19 has severely threatened human life and global economic security. Many relevant retrospective studies have demonstrated that chest computed tomography (CT) is an effective diagnostic method for COVID-19 [1]. However, the ionizing radiation of CT can pose a potential cancer risk to patients [2]. In order to effectively and accurately detect COVID-19 while protecting the health of patients, researchers have tried to reduce the radiation dose [3]. Nevertheless, lowering the radiation dose will reduce the image quality, leading to areas of pneumonia and indistinct lung parenchyma in CT scans, which further affects the final diagnosis [4]. Therefore, it is crucial to investigate super-resolution reconstruction algorithms to maintain good chest CT image resolution while reducing irradiation.

Image super-resolution (SR) aims at reconstructing degraded low-resolution (LR) images into high-resolution (HR) images, which can effectively restore image details and improve image quality. With the ongoing advancement of deep learning technology, deep learning-based methods have recently emerged as the current research hotspot for super-resolution reconstruction. Dong et al. [5] proposed a super-resolution convolutional neural network (SRCNN), the first convolutional neural network application in image super-resolution. Subsequently, Kim et al. [6] proposed a very deep super-resolution network (VDSR), which introduced a residual structure to solve the gradient disappearance and further deepened the network hierarchy to improve the reconstruction quality significantly. Since then, many methods, including enhanced deep super-resolution network (EDSR) [7], have achieved satisfactory results by increasing the network depth, demonstrating that deeper networks can help improve the quality of reconstructed images.

However, the methods mentioned above usually have huge model parameters and slow training and testing speeds [8], which do not apply to resource-constrained machines, such as medical imaging equipment used in hospitals, so designing a lightweight and efficient SR algorithm is vital. In addition, the algorithms mentioned above are designed based on natural images, whereas chest CT images have poor visual recognition and more complex textures than natural images, so it is not easy to ensure that the key information remains unchanged in chest CT images reconstructed by the above algorithm. To alleviate these issues, we propose a residual feature attention fusion network for lightweight CT image super-resolution (RFAFN), experiments demonstrate the outstanding performance of our method. As shown in Fig. 1, comparison with state-of-the-art (SOTA) methods, our network achieves better performance with fewer parameters. The main contributions of our paper can be summarized as follows:

Figure 1: Comparison with SOTA methods in terms of PSNR and parameters on CTtest1 at ×3 SR

1.    We design a contextual feature extraction block (CFEB) to efficiently extract image features, which is computationally cheaper while maintaining performance compared to ordinary residual blocks.

2.    We propose a feature-weighted cascading strategy (FWCS) that adaptively fuses feature information from adjacent levels. This strategy performs better than other feature information reuse methods at adjacent levels.

3.    We propose a global hierarchical feature fusion strategy (GHFFS) that can efficiently fuse features at different levels. Due to the retention of richer feature details, better image reconstruction results can be achieved by using GHFFS compared to other hierarchical feature exploitation methods.

2  Related Work

With the rapid development of deep learning, deep learning-based methods have become the mainstream of super-resolution. Dong et al. [5] proposed SRCNN to reconstruct HR images from LR images by learning a non-linear mapping relationship between the input to the ground truth, achieving better performance than previous work. However, SRCNN first requires a pre-upsampling operation to pre-process the LR images, making most of the next operations occur in high-dimensional space, which increases the computational cost. For better computational efficiency, Shi et al. [9] proposed an efficient sub-pixel convolutional neural network (ESPCN) by placing the upsampling layer at the end of the algorithm so that the feature extraction operation only occurs in the low-dimensional space, significantly reducing the computational effort and spatial complexity. Kim et al. [6] deepened the network and used the residual structure to design VDSR, further improving the reconstruction quality and demonstrating that increasing the network depth could improve the performance. Since then, scholars have continuously improved the performance of the algorithm through diverse and complex network design strategies such as residual learning [10], dense learning [11], and attention mechanism [12], among others.

Nevertheless, this improvement in reconstruction performance by deepening the network comes at the cost of a significant increase in computational resources and inference time [8], which limits the application of SR in practical scenarios. Numerous studies on lightweight SR algorithms have been carried out to address this challenge. Residual feature aggregation network (RFAnet) [13] achieves better performance with smaller parameters than networks such as very deep residual channel attention network (RCAN) [14] by exploiting the hierarchical feature of residual branching and introducing a spatial attention mechanism into the residual blocks. Deep recursive residual network (DRRN) [15] shares parameters through a recursive mechanism reducing the number of parameters and improving the reconstruction quality. Cascading residual network (CARN) [16] reduces the number of network parameters by adding 1×1 convolutional layers to the dense connection to compress the information in each layer. Information distillation network (IDN) [17] and information multi-distillation network (IMDN) [8] make better use of layered features by separating the processing of the current feature mapping to maintain the speed of real-time reconstruction. However, CT images are complex in texture and rich in semantic information. These above lightweight networks extract deep feature information by stacking the convolutional modules, so they cannot fully utilize the rich contextual information and different hierarchical levels of feature information in CT images.

Recently, medical image super-resolution has attracted the research interest of many scholars. Qiu et al. [18] proposed a multi-window back-projection residual network for super-resolution (MWSR); for one thing, multiple windows are used to refine the same feature maps simultaneously to obtain richer high and low-frequency information; for another, the inverse projection network is used to fully extract image features. Chen et al. [19] distinguished low-frequency and high-frequency information in images and established a medical image super-resolution algorithm based on dual-path residual information distillation (DRIDSR) to improve the resolution of lung CT images. In addition, some excellent super-resolution algorithms for CT images have been proposed [20,21]. However, most of the above medical image super-resolution studies do not consider computational complexity.

Compared with these algorithms, our RFAFN can fully extract the contextual feature information of CT images by designing CFEB, and can fully utilize the feature information at different levels by designing FWCS and GHFFS. In addition, thanks to the design of an efficient network structure, our RFAFN achieves excellent reconstruction performance while also making it lightweight.

3  Proposed Model

3.1 Network Architecture

Our RFAFN network framework is shown in Fig. 2. The proposed RFAFN consists of three main components: (1) a shallow feature extraction layer, (2) a deep feature extraction layer, and (3) a reconstruction layer (the red, yellow and blue dashed boxes in Fig. 2, respectively).

Figure 2: Schematic diagram of RFAFN

We define the input and output of our network as ILR and ISR respectively, thereby the process of generating ISR for our network can be expressed as follows:

ISR=HRFAFN(ILR),(1)

where HRFAFN is our RFAFN operation.

To be more precise, we first extract the shallow features from the input low-resolution CT image with a 3×3 convolution; the process can be expressed as follows:

F0=f3×3(ILR),(2)

where F0 is the extracted shallow feature, and f3×3 denotes a 3×3 convolution operation.

Then we stack multiple feature-weighted cascading groups (FWCG) in a chain-like manner and gradually fuse the features in each layer through a global hierarchical feature fusion strategy to obtain a deep feature extraction layer, which can be expressed as follows:

Fres=f3×3(OHFF(F0,F1,F2,..,Fk)),k=1,2,..n,(3)

where OHFF denotes the GHFFS operation, Fres is the extracted deep feature. Furthermore, Fk denotes the output feature of the kth FWCG operation, which can be obtained by the following formula:

Fk=Hk(Fk−1),k=1,2,..n.(4)

Finally, we can obtain ISR as follows:

ISR=HREC(Fres+F0)+HUP(ILR),(5)

where HREC denotes a reconstruction layer operation and HUP is a bilinear interpolation upsampling operation, referring to ESPCN [9]; we construct HREC using a 3×3 convolution and a sub-pixel operation.

3.2 Contextual Feature Extraction Block

The residual block (RB, shown in Fig. 3a), introduced by EDSR [7], is widely used in SR algorithms as a basic structure for image feature extraction. However, the number of parameters using RB is large, so it does not apply to the needs of lightweight networks. Inspired by RB, Liu et al. [22] constructed a shallow residual block (SRB, shown in Fig. 3b) by introducing residual learning into a 3×3 convolution, which greatly reduced the number of parameters, and related experiments also demonstrated the excellent effect of SRB in lightweight networks. Further, Peng et al. [23] constructed a deep residual block (DRB, as shown in Fig. 3c) in lightweight skip concatenated residual channel attention network (LCRCA) by doubling the number of convolutional layers and halving the number of filters, further improving the network performance by deepening the network hierarchy without increasing the computational complexity.

Figure 3: Comparison of different convolution blocks. (a) RB. (b) SRB. (c) DRB. (d) SCconv. Notice that the yellow block here represents the 3×3 convolution, the blue block represents the self-calibrated convolution branch, and the grey part represents the number of filters in the convolution layer

However, the textures of CT images are complex, and each pixel value represents the X-ray linear attenuation coefficient of the material in that region [24], so the rich contextual information embedded in CT images should not be ignored during feature extraction; we need a more efficient feature extraction block to extract the deep features of CT.

Liu et al. [25] proposed a self-calibrated convolution (SCconv), which provides a good solution to this problem. As shown in Fig. 3d, SCconv splits the convolution into two branches: one is the self-calibrated convolution for obtaining rich contextual features, and the other is the regular convolution for maintaining the original features. SCconv achieves significant results on the classification task. However, SCconv operates using 1×1 convolutions for channel downscaling before using 3×3 convolutions for feature extraction, making the spatial context poorly considered and affecting the extraction of deep semantic features, so it cannot be well applied to super-resolution tasks. In addition, SCconv has complex connections, which are not friendly to hardware acceleration. To solve these problems, we propose a CFEB, the structure of which is shown in Fig. 4.

Figure 4: The structure of CFEB. Notice that the grey part represents the number of filters in the convolutional layer

Specifically, firstly, a 3×3 convolution is used to extract coarse feature information, the process can be expressed as follows:

FmidCFEB=f3×31(FinCFEB),(6)

where FinCFEB∈RH×W×C is the input feature, FmidCFEB∈RH×W×C2 is the extracted feature information, and f3×3k is the kth3×3 convolution.

We then apply a series of convolutions to perform the feature transformation in two different branches: one is a reserved branch maintaining the information in the original feature space, and the other is a self-calibration branch that obtains rich contextual feature information for each spatial location. The process can be expressed as follows:

F1CFEB=f3×31g(FmidCFEB),(7)

F2CFEB=f3×32g(fS(F1CFEB)⊗f3×32(FmidCFEB)),(8)

where F1CFEB and F2CFEB are the features extracted from these two branches respectively. f3×3kg is the kth 3×3 group convolution, fS is the sigmoid function. Compared to SCconv obtaining the attention map through a complex up/down sampling operation, we use F1CFEB as the attention map to generate 3D attention weights to guide the feature transformation process in the original feature space, which is inspired by the pixel attention in PAN [26].

Finally, the outputs of the two operations are spliced in the channel dimension. To save the number of parameters, we use group convolutions in both branches, but this also weakens the expressive power of convolution [27], so we choose to use a 1×1 convolution and a squeeze-and-excitation block (SEB, which is from SEnet [28]) to enhance inter-group feature communication and inter-branch feature communication respectively for further improving the feature extraction power of CFEB. The final output FoutCFEB can be expressed as follows:

FoutCFEB=HSEB(f1×11(concat(F1CFEB,F2CFEB)))+FinCFEB,(9)

where f1×1k is the kth 1×1 convolution, concat(∗,∗) represents the concatenation of two feature maps in the channel dimension. HSEB is the operation of SEB, SEB models the interdependencies between channels to adaptively adjust the importance of each channel feature through four consecutive layers: global pooling →fully connected layer →fully connected layer →sigmoid layer, so that the network can focus on the features that are useful for the task.

Our proposed CFEB achieves superior performance while having fewer parameters. In subsequent ablation experiments, we shall elaborate on the performance of CFEB in our task.

3.3 Feature-weighted Cascading Strategy

In order to make full use of adjacent-level features and better maintain the diversity of feature mapping, Peng et al. [23] proposed the skip concatenation strategy (SC). As shown in Fig. 5a, adjacent-level features are fused through cascading and transported deeper into the network. Using SC, low-level features are connected to high-level features, and lower-level features can be reused. However, this single-stage fusion strategy has its limitations. Adjacent levels of feature information have different receptive fields, and these features may have significant inconsistencies in scale and semantics, so simply fusing them in cascade as the following stage input may affect the performance of the model.

Figure 5: Comparison of the two hierarchical feature cascading strategies. From left to right: (a) Skip concatenation (b) FWCS

We propose a FWCS to solve this problem. As shown in Fig. 5b, similar to SC, we first cascade the two adjacent levels of feature information at the channel level. Subsequently, unlike SC which directly employs 1×1 convolution for direct feature extraction and channel dimensionality reduction, we construct an AFFB to adjust the spatial and channel dimensionality information of adjacent hierarchical feature maps so that the network can focus more on information that is more important to the task.

In this paper, our FWCS consists of a series of CFEBs and AFFBs. Specifically, the input Finput is processed by the first CFEB to obtain the extracted features, this process can be expressed as follows:

FCFFB1=HCFFB1(Finput),(10)

where FCFFB1 is the output of the first CFEB, HCFFB1 is the first CFEB operation. The AFFB fuses the feature information of the two adjacent levels of Finput and FCFFB1, together with the second CFEB operation to generate FCFFB2, this process can be expressed as:

FCFFB2=HCFFB2(HAFFB1(Finput,FCFFB1)),(11)

where HAFFB1 is the first AFFB operation, and similarly, the feature information FCFFBk is obtained by the kth CFEB operation, this process can be expressed as follows:

FCFFBk=HCFFBk(HAFFBk−1(FCFFBk−1,FCFFBk−2)),k=3,4,…n.(12)

In order to better fuse feature information from adjacent levels and different receptive fields so that more representative features can be obtained, we design an AFFB inspired by selective kernel network (SKnet) [29]. AFFB and SKnet are designed with different motivations. SKnet is designed to improve feature extraction by generating the channel attention weight using the interdependence between channel dimensions, while AFFB is designed to enhance feature extraction by generating the spatial attention weight using the relationship between spatial features on the global level. We believe that guiding the network to focus on important spatial feature regions on different levels of features is more important for the task of super-resolution on the CT images. For example, our model should focus more on the edges and textures of the CT images.

The AFFB structure is shown in Fig. 6. First, we fuse two adjacent levels feature information Finput1 and Finput2 using element summation, this process can be expressed as follows:

Figure 6: Our proposed framework for AFFB

Ffusion=Finput1+Finput2,(13)

we then reduce the channel dimension of the fused feature information Ffusion by a 1×1 convolution layer to reduce the computational complexity of AFFB. Next, three 3×3 dilated convolutions with different dilated rates are used to collect as much information as possible from a larger receptive field without reducing the image size. To avoid the gridding effect [30], we set the dilated rate to {1, 2, 5} and add a residual connection. The process can be expressed as follows:

FISF=f3×3(f3×3g(f1×1(Ffusion)))+f1×1(Ffusion),(14)

where FISF denotes the integrated spatial feature information, f1×1 denotes a 1×1 convolution operation, f3×3g denotes a 3×3 dilated convolution group operation and f3×3 denotes a 3×3 convolution operation. Subsequently, we recover the channel dimension using the 1×1 convolution and obtain the attention weights of the two branches using the Softmax activation function [29], which can be expressed as:

W=concat(A1,A2)=fs(concat(f1×11(FISF),f1×12(FISF))),(15)

where A1 and A2 are the attention weights of these two branches, fs is the Softmax operation, f1×11 and f1×12 are two 1×1 convolution operations, respectively. Finally, the feature map Foutput can be formed as follows:

Foutput=f1×1(concat(A1⊗Finput1,A2⊗Finput2))(16)

where f1×1 is a 1×1 convolution used to smooth the extracted features.

Benefiting from AFFB, FWSC can effectively acquire sufficient contextual information, thus further enhancing the network’s ability to extract texture features from CT images while ensuring the pathological invariance of the reconstructed CT images. In subsequent ablation experiments, we shall elaborate on the performance of FWCS in our task.

3.4 Global Hierarchical Feature Fusion Strategy

For the reconstruction task of fine-grained images such as CT images, the feature refinement part is more required. As shown in Fig. 7a, most existing super-resolution networks stack multiple feature extraction modules in a chain-like manner to refine the extracted features [31], which does not make full use of the different levels of features. To solve this problem, several scholars [11,32] employ dense connection (DC) to exploit feature information from different layers, as shown in Fig. 7b, DC feeds the features of each layer to all subsequent layers so that the features of all layers are concatenated, this operation allows features to be reused and utilized more efficiently. However, DC makes the network more complex and bloated, which is unsuitable for lightweight tasks. Drawing on the idea of DC, as shown in Fig. 7c, RFAnet [13] proposes the RFA framework, which enables the fusion of features at each level by aggregating features from different residual blocks, and experimentally demonstrates that RFA plays a crucial role in the reconstruction of spatial details while reducing the number of parameters. Regrettably, this one-time fusion of all the different layers of features and direct downscaling from higher channels by a 1×1 convolution can lose partial information.

Figure 7: Comparison of different global hierarchical feature exploiting strategies. From left to right: (a) Chain-like strategy, (b) dense connection, (c) residual feature aggregation, and (d) GHFFS

In order to achieve a balance between performance and the number of parameters, we design a GHFFS to exploit feature information from each layer of the global network on a step-by-step basis. The process of GHFFS is shown in Fig. 7d. Firstly, we concatenate the features at adjacent levels to obtain feature information with double the number of channels. Further, we choose to squeeze the result of the concatenation with a 1×1 convolution. Specifically, when the input F0 is processed by the first FWCG, the extracted feature F1 can be obtained, the process can be expressed as:

FH1=f1×11(concat(F0,F1)),(17)

where FH1 is the feature information obtained by fusing F0 and F1, f1×11 represents the first 1×1 convolution operation. Similarly, the subsequent multiple feature fusion operations can be expressed as follows:

FHk=f1×1k(concat(FH(k−1),Fk)),k=2,3,..n,(18)

where Fk is the output feature of the kth FWCG. FHk and FH(k−1) are the output of the kth global hierarchical feature fusion operation and the output of the previous global hierarchical feature fusion operation, respectively.

In GHFFS, different levels of feature information can be interactively fused and then delivered to deeper parts of the network, which allows for better gradient propagation. The structure is much simpler as it reduces many long-range connections compared to dense connections, making it more suitable for lightweight networks. Compared to RFAnet [13], the progressive fusion of layered features preserves more image detail. We demonstrate the superior performance of our proposed GHFFS structure in subsequent ablation experiments.

4  Experiment

4.1 Datasets and Metrics

Our experimental data come from the public COVID-19 chest CT dataset by TCIA [33] and the public COVID-CT dataset constructed by Yang [34], which we denote as CT1 and CT2, respectively. CT1 contains nii-format chest CTs of 632 COVID-19 patients, from which we derive 7200 high-quality CT slices, 6400 of which are used as the training set, named CTtrain; 200 of which are used as the validation set, named CTvalid; the remaining 600 images are used to construct the test set, named CTtest1. CT2 contains 349 CT images of COVID-19 collected from COVID-19-related papers. To further validate the generalization of our network, we select 280 high-quality CT images from CT2 to construct the test dataset CTtest2.

We use two metrics, peak signal-to-noise ratio (PSNR) and structure similarity index (SSIM) [35], to evaluate the quality of the reconstructed images. PSNR indicates the ratio between the maximum signal and background noise, which is an image quality evaluation index based on the error sensitivity. SSIM is a metric that measures the similarity of two images in terms of luminance, contrast, and structure. In order to better evaluate the computational complexity of our model, as in many works [23], we calculate the Multi-Adds of the model with the set HR image size of 480×480.

4.2 Implementation Details

Due to the difficulty in obtaining high-low resolution paired data, similar to the previous work [36], we downsample the HR images via bicubic interpolation to obtain the corresponding LR images. The HR image blocks for ×2 SR, ×3 SR, and ×4 SR with dimensions of 96×96, 144×144 and 192×192, respectively, are randomly cropped out by us from the original HR images. We perform data augmentation by randomly rotating 90°, 180°, 270°, and horizontally flipping. We set the batch size to 64 and apply the Adam optimizer [37] with β1=0.9, β2=0.99 and ϵ=10−8 to train our network. The initial learning rate of the network is set to 5×10−4 and then halved every 5×104 iterations for a total of 3×105 iterations. We choose to use the L1 loss, which calculates the sum of all absolute differences between the true and predicted values; the formula can be expressed as follows:

L(θ)=1N∑i=1N⁡‖HLFIFN(ILRi)−IHRi‖1,(19)

where {ILRi,IHRi} is the ith LR-HR image pair in the batch, N is the batch size, and θ is the parameter of RFAFN. For our network, the number of FWCGs is set to 4, and the number of CFEBs is set to 3. All experiments in this paper are performed under the PyTorch framework on NVIDIA RTX 2080 Super GPUs.

4.3 Ablation Analysis

4.3.1 Efficiency of Contextual Feature Extraction Block

As described in Section 3.2, we propose CFEB as the base block of our network to extract CT image features. To verify the effectiveness of CFEB, we embed five basic feature extraction blocks into our network, which are (1) SRB, (2) DRB, (3) SCconv, (4) CFEB without SEB added, and (5) CFEB.

In Table 1, we can see that compared to SRB, DRB, and SCconv, the PSNR of our proposed CFEB achieves the best performance by 29.16 dB with similar parameters, which demonstrates the importance of contextual information for CT image reconstruction. Furthermore, we can see that the performance decreases by 0.04 dB with the removal of SEB on CFEB, which indicates the importance of adding a channel attention mechanism after group convolution to enhance inter-branch feature communication.

4.3.2 Efficiency of Feature-Weighted Cascading Strategy

As described in Section 3.3, we propose FWCS, which can make full use of the rich and diverse feature information of adjacent levels to enhance the performance of CT image reconstruction. To verify the effectiveness of FWCS, we construct our network using three different connection methods for ablation experiments, and the results are shown in Table 2. It can be seen that the parameters of the network with FWCS increase by 11.93K compared to the network with SC, but the slight increase in parameters leads to a significant increase in PSNR by 0.41 dB, which proves the effectiveness of FWCS in super-resolution tasks.

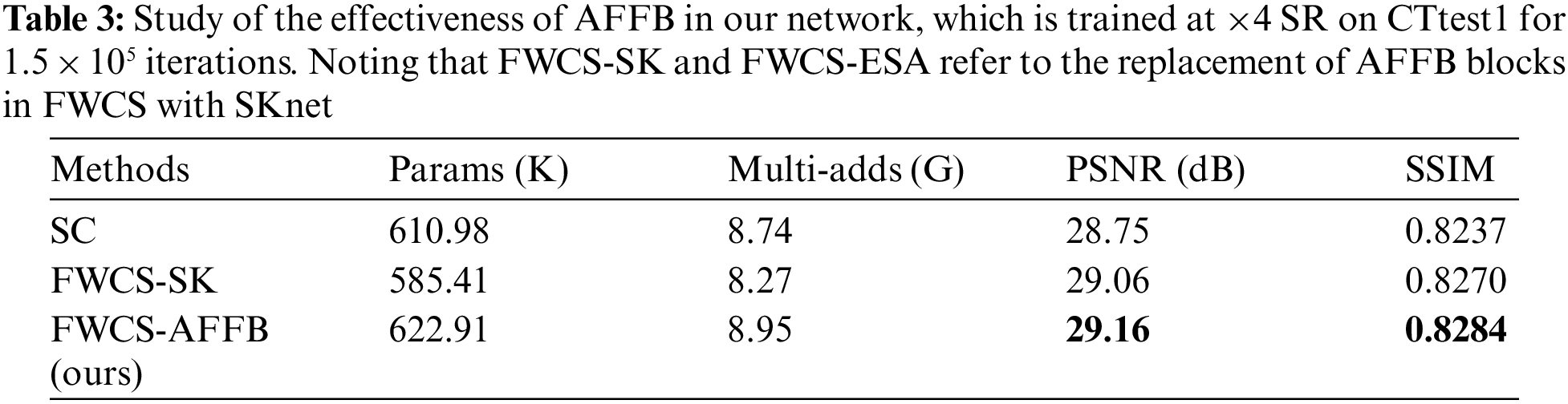
AFFB is the heart of our proposed FWCS, and we have previously described that our AFFB is constructed under the guidance of SKnet [29]. To this end, we embed SKnet in our network, and the experimental results are shown in Table 3. The networks embedded with SKnet and AFFB perform better than those without the attention mechanism, with an increase in PSNR by 0.31 dB and 0.41 dB, respectively, demonstrating that the attention mechanism plays an essential role in super-resolution tasks. Moreover, the PSNR of the network embedded with AFFB is improved by 0.1 dB compared with the network embedded with SKnet, which shows that our proposed AFFB performs better in our task than SKnet.

4.3.3 Efficiency of Global Hierarchical Feature Fusion Strategy

As described in Section 3.4, we adopt GHFFS to fully use the feature information in each layer, which improves the ability of the network to extract feature information. To verify the excellent performance of GHFFS, we refer to the different layered utilization strategies in Fig. 7, embedded in our network, and carry out ablation experiments in the results shown in Table 4. It can be seen that the network using the chained connections has the least parameters but the worst reconstruction results with the PSNR by 29.12 dB, although it has the least parameters, while our GHFFS achieves the best results with the PSNR by 29.16 dB. Compared with the suboptimal RFAFN-Dense, our network has 24.63K fewer parameters while increasing the PSNR on CTtest1 by 0.02 dB, which indicates the superior performance of our proposed GHFFS.

4.3.4 Discussion on Residual Learning Connections

Many previous studies [11,13,15,22] have demonstrated that residual learning connections can significantly enhance the flow of information details in a network and effectively mitigate the gradient disappearance problem. We use multi-level residual feature information in our network. Considering the modules to which the residual learning connections are applied, we classify the residual learning connections used into the block residual connection (BRC, see Fig. 4), the module residual connection (MRC, see Fig. 5b), the layer residual connection (LRC, see Fig. 2) and the global residual connection (GRC, see Fig. 2).

We have experimentally demonstrated the effectiveness of using multi-level residual learning connections, as shown in Table 5, which shows that the network with residual learning connections performs significantly better than the network without residual learning connections, and the network with multi-level residual connections is also better than the network with single-level residual connections. Finally, considering the performance of each method on CTtest1, we choose BRC, LRC, and GRC to construct our network, because in the experiment, the method has the best performance with the PSNR by 29.16 dB and the SSIM by 0.8284.

4.4 Comparison with State-of-the-Art Methods

To demonstrate the performance of RFAFN, we compare it with some of the SOTA lightweight super-resolution networks, including SRCNN [5], VDSR [6], IDN [17], CARN [16], IMDN [8], RFDN [22] and LCRCA [23]. For all the above networks, we use the source code published online by the authors and retrain it with the same dataset and training details as the RFAFN proposed in this paper.

4.4.1 Quantitative Results

As shown in Table 6, by comparing the performance of different super-resolution reconstruction algorithms at ×2 SR, ×3 SR, and ×4 SR, we can find that our proposed RFAFN outperforms the other methods in general.

Regarding performance, RFAFN outperforms the other methods on both test datasets, with a lower number of parameters but higher PSNR and SSIM metrics than the following best method RFDN. In addition, our RFAFN achieves optimal performance with a relatively small number of parameters and multi-adds compared with other excellent lightweight methods.

Notably, CTtest1 and CTtrain come from the same dataset CT1, so the test results on CTtest1 can reflect the training effect of the network well. However, the CT images we acquire in reality come from various sources, and the mapping relationship between these images and the corresponding high-resolution images will be more complicated. To test the practicality of our algorithm, we also tested on CTtest2, which is collected from some COVID-19 related papers, so it is a dataset closer to the actual application scenarios. In fact, the testing results of our method on CTtest2 also outperform other state-of-the-art methods, which proves the generalization performance of our method.

4.4.2 Visual Comparison

Considering that the accuracy of the CT image information can directly affect the doctor’s judgment, we also compare the visual quality of RFAFN with that of other algorithms. As can be seen from Figs. 8–10, the CT images reconstructed by bicubic interpolation are significantly blurrier. Compared with deep learning-based methods such as SRCNN, our method can generate texture details closer to the original image, and its visual quality is better than other networks. The diagnosis of COVID-19 can be greatly aided by using our method.

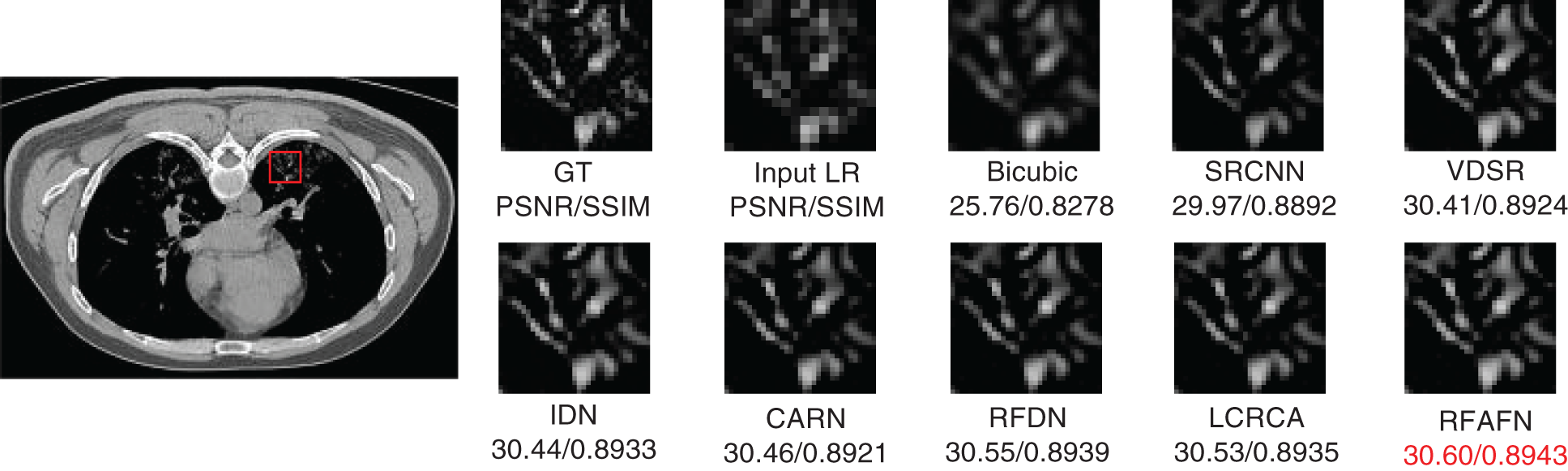
Figure 8: Visual comparison with other state-of-the-art lightweight methods on CTtest1 at ×2 SR

Figure 9: Visual comparison with other state-of-the-art lightweight methods on CTtest2 at ×3 SR

Figure 10: Visual comparison with other state-of-the-art lightweight methods on CTtest2 at ×4 SR

5  Conclusion

This paper proposes a lightweight residual feature attention fusion CT image super-resolution algorithm named RFAFN. In order to improve the feature extraction capability, we construct CFEB, which can perform more accurate feature extraction while reducing the network parameters. To make full use of the superior performance of CFEB, we construct FWCS using AFFB, which can fuse feature information from neighboring levels, better maintaining the diversity of feature mapping, and improving network performance. Finally, we utilize GHFFS to construct the proposed network for efficient and lightweight SISR. Extensive experiments demonstrate that our RFAFN outperforms other SOTA methods in quantity and quality while maintaining a moderate number of parameters. For example, the PSNR is 0.47 dB higher on CTtest2 at ×3 SR compared to the suboptimal method RFDN, but the number of parameters and multi-adds are reduced by 22K and 0.43G, respectively. Currently, the idea of structural reparameterization [38] is becoming a hot topic in deep learning research. In the future, we will explore the introduction of the structural reparameterization into our CT image reconstruction task to reduce the number of network parameters further while improving the reconstruction performance.

Funding Statement: This work was supported by the General Project of Natural Science Foundation of Hebei Province of China (H2019201378), the Foundation of the President of Hebei University (XZJJ201917) and the Special Project for Cultivating Scientific and Technological Innovation Ability of University and Middle School Students of Hebei Province (2021H060306).

Conflicts of Interest: The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

1. H. Alshazly, C. Linse, E. Barth and T. Martinetz, “Explainable COVID-19 detection using chest CT scans and deep learning,” Sensors, vol. 21, no. 2, pp. 455, 2021. [Google Scholar] [PubMed]

2. H. Hou, Q. Jin, G. Zhang and Z. Li, “CT image quality enhancement via a dual-channel neural network with jointing denoising and super-resolution,” Neurocomputing, vol. 492, no. 1, pp. 343–352, 2022. [Google Scholar]

3. J. Finance, L. Zieleskewicz, P. Habert, A. Jacquier, P. Parola et al., “Low dose chest CT and lung ultrasound for the diagnosis and management of COVID-19,” Journal of Clinical Medicine, vol. 10, no. 10, pp. 2196, 2021. [Google Scholar] [PubMed]

4. W. Tan, P. Liu, X. Li, Y. Liu, Q. Zhou et al., “Classification of COVID-19 pneumonia from chest CT images based on reconstructed super-resolution images and vgg neural network,” Health Information Science and Systems, vol. 9, no. 1, pp. 10, 2021. [Google Scholar] [PubMed]

5. C. Dong, C. C. Loy, K. He and X. Tang, “Learning a deep convolutional network for image super-resolution,” in Proc. European Conf. on Computer Vision, Zurich, Switzerland, pp. 184–199, 2014. [Google Scholar]

6. J. Kim, J. K. Lee and K. M. Lee, “Accurate image super-resolution using very deep convolutional networks,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, pp. 1646–1654, 2016. [Google Scholar]

7. B. Lim, S. Son, H. Kim, S. Nah and K. M. Lee, “Enhanced deep residual networks for single image super-resolution,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, pp. 1132–1140, 2017. [Google Scholar]

8. Z. Hui, X. Gao, Y. Yang and X. Wang, “Lightweight image super-resolution with information multi-distillation network,” in Proc. the 27th ACM Int. Conf. on Multimedia, Nice, France, pp. 2024–2032, 2019. [Google Scholar]

9. W. Shi, J. Caballero, F. Huszár, J. Totz, A. P. Aitken et al., “Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, pp. 1874–1883, 2016. [Google Scholar]

10. J. Li, F. Fang, K. Mei and G. Zhang, “Multi-scale residual network for image super-resolution,” in Proc. European Conf. on Computer Vision, Munich, Germany, pp. 517–532, 2018. [Google Scholar]

11. Y. Zhang, Y. Tian, Y. Kong, B. Zhong and Y. Fu, “Residual dense network for image super-resolution,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 2472–2481, 2018. [Google Scholar]

12. Y. Hu, J. Li, Y. Huang and X. Gao, “Channel-wise and spatial feature modulation network for single image super-resolution,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 30, no. 11, pp. 3911–3927, 2020. [Google Scholar]

13. J. Liu, W. Zhang, Y. Tang, J. Tang and G. Wu, “Residual feature aggregation network for image super-resolution,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Seattle, WA, USA, pp. 2356–2365, 2020. [Google Scholar]

14. Y. Zhang, K. Li, K. Li, L. Wang, B. Zhong et al., “Image super-resolution using very deep residual channel attention networks,” in Proc. European Conf. on Computer Vision, Munich, Germany, pp. 286–301, 2018. [Google Scholar]

15. Y. Tai, J. Yang and X. Liu, “Image super-resolution via deep recursive residual network,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition, Honolulu, HI, USA, pp. 2790–2798, 2017. [Google Scholar]

16. N. Ahn, B. Kang and K. -A. Sohn, “Fast, accurate, and lightweight super-resolution with cascading residual network,” in Proc. European Conf. on Computer Vision, Munich, Germany, pp. 252–268, 2018. [Google Scholar]

17. Z. Hui, X. Wang and X. Gao, “Fast and accurate single image super-resolution via information distillation network,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 723–731, 2018. [Google Scholar]

18. D. Qiu, Y. Cheng, X. Wang and X. Zhang, “Multi-window back-projection residual networks for reconstructing COVID-19 CT super-resolution images,” Computer Methods and Programs in Biomedicine, vol. 200, no. 8, pp. 105934, 2021. [Google Scholar] [PubMed]

19. Y. Chen, Q. Zheng and J. Chen, “Double paths network with residual information distillation for improving lung CT image super resolution,” Biomedical Signal Processing and Control, vol. 73, no. 1, pp. 103412, 2022. [Google Scholar] [PubMed]

20. T. Zhao, L. Hu, Y. Zhang and J. Fang, “Super-resolution network with information distillation and multi-scale attention for medical CT image,” Sensors, vol. 21, no. 20, pp. 6870, 2021. [Google Scholar] [PubMed]

21. H. Hou, Q. Jin, G. Zhang and Z. Li, “CT image quality enhancement via a dual-channel neural network with jointing denoising and super-resolution,” Neurocomputing, vol. 492, no. 1, pp. 343–352, 2022. [Google Scholar]

22. J. Liu, J. Tang and G. Wu, “Residual feature distillation network for lightweight image super-resolution,” in Proc. European Conf. on Computer Vision Workshops, Glasgow, UK, pp. 41–55, 2020. [Google Scholar]

23. C. Peng, P. Shu, X. Huang, Z. Fu and X. Li, “LCRCA: Image super-resolution using lightweight concatenated residual channel attention networks,” Applied Intelligence, vol. 52, no. 9, pp. 10045–10059, 2022. [Google Scholar]

24. C. H. McCollough, S. Leng, L. Yu and J. G. Fletcher, “Dual- and multi-energy CT: Principles, technical approaches, and clinical applications,” Radiology, vol. 276, no. 3, pp. 637–653, 2015. [Google Scholar] [PubMed]

25. J. -J. Liu, Q. Hou, M. -M. Cheng, C. Wang and J. Feng, “Improving convolutional networks with self-calibrated convolutions,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Seattle, WA, USA, pp. 10093–10102, 2020. [Google Scholar]

26. H. Zhao, X. Kong, J. He, Y. Qiao and C. Dong, “Efficient image super-resolution using pixel attention,” in Proc. European Conf. on Computer Vision Workshops, Glasgow, UK, pp. 56–72, 2020. [Google Scholar]

27. X. Zhang, X. Zhou, M. Lin and J. Sun, “Shufflenet: An extremely efficient convolutional neural network for mobile devices,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 6848–6856, 2018. [Google Scholar]

28. J. Hu, L. Shen, S. Albanie, G. Sun and E. Wu, “Squeeze-and-excitation networks,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 8, pp. 2011–2023, 2020. [Google Scholar] [PubMed]

29. X. Li, W. Wang, X. Hu and J. Yang, “Selective kernel networks,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 510–519, 2019. [Google Scholar]

30. S. Mehta, M. Rastegari, A. Caspi, L. Shapiro and H. Hajishirzi, “ESPNet: Efficient spatial pyramid of dilated convolutions for semantic segmentation,” in Proc. European Conf. on Computer Vision, Munich, Germany, pp. 552–568, 2018. [Google Scholar]

31. Z. Du, D. Liu, J. Liu, J. Tang, G. Wu et al., “Fast and memory-efficient network towards efficient image super-resolution,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, New Orleans, Louisiana, USA, pp. 853–862, 2022. [Google Scholar]

32. T. Tong, G. Li, X. Liu and Q. Gao, “Image super-resolution using dense skip connections,” in Proc. IEEE Int. Conf. on Computer Vision, Venice, Italy, pp. 4809–4817, 2017. [Google Scholar]

33. S. A. Harmon, T. H. Sanford, S. Xu, E. B. Turkbey, H. Roth et al., “Artificial intelligence for the detection of COVID-19 pneumonia on chest CT using multinational datasets,” Nature Communications, vol. 11, no. 1, pp. 4080, 2020. [Google Scholar] [PubMed]

34. X. Yang, X. He, J. Zhao, Y. Zhang, S. Zhang et al., “COVID-CT-Dataset: A CT scan dataset about COVID-19,” 2020. [Online]. Available: http://arxiv.org/abs/2003.13865 [Google Scholar]

35. Z. Wang, A. C. Bovik, H. R. Sheikh and E. P. Simoncelli, “Image quality assessment: From error visibility to structural similarity,” IEEE Transactions on Image Processing, vol. 13, no. 4, pp. 600–612, 2004. [Google Scholar] [PubMed]

36. Z. Wang, J. Chen and S. C. H. Hoi, “Deep learning for image super-resolution: A survey,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 43, no. 10, pp. 3365–3387, 2021. [Google Scholar] [PubMed]

37. D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” 2014. [Online]. Available: https://doi.org/10.48550/arXiv.1412.6980 [Google Scholar] [CrossRef]

38. X. Ding, X. Zhang, N. Ma, J. Han, G. Ding et al., “Repvgg: Making vgg-style convnets great again,” 2021. [Online]. Available: https://arxiv.org/abs/2101.03697 [Google Scholar]