Index-adaptive Triangle-Based Graph Local Clustering

1  Introduction

The graph is a fundamental and significant structure to model the real world [1,2]. A cluster in graph theory is a node-set with strong intra-relationship but slack inter-linkage [3], which corresponds to the group in social science (power or interest group) or the community in network science (chemical radical or molecule). Graph local clustering (GLC) takes a seed node with the graph topology as input and aims to output the local cluster without exploring the whole graph [4,5]. The locality of GLC makes it more scalable and attracts extensive attention in various fields [6–8]. To measure the quality of the cluster, several metrics have been proposed [9–12], and the most commonly used one [13] is conductance [14,15].

Motif-based Graph Local Clustering. Benson et al. [16] prove that the motif-conductance of a cluster on graph G is equivalent to the conductance of the cluster on the motif-weighted graph when the motif is in 3-order, i.e., wedge and triangle. Therefore, the problem of motif-conductance optimization on the original graph can be reduced to a two-phase process that first constructs the motif-weighted graph and then conducts the standard conductance optimization clustering algorithm. Motif-based Approximate Personalized PageRank (MAPPR) [17], the first MGLC algorithm, is devised in line with this two-phase framework. To begin with, MAPPR builds the motif-weighted graph by weighting each edge with the number of motif instances it is contained. Then, it utilizes the widely-used GLC algorithm PageRank Nibble (PRNibble) [5] as the kernel to obtain the cluster on the motif-weighted graph. Among the various higher-order motifs, the triangle has been illustrated to be significant and valuable in extensive applications, such as graph topology analysis [18,19], complex network mining [16,20], and spatial-temporal system optimization [21–23]. Therefore, motif-based graph local clustering (MGLC) [17], which aims to find the local cluster with the optimal motif-conductance, has been a significant task.

Despite effectiveness, the pre-processing phase brings limitations on both theoretical and practical aspects. For one thing, building the motif-weighted adjacency matrix should be prohibited not only on massive graphs but also for ad-hoc situations. For another, the algorithm with a fixed pre-processing phase would make the query suffer from a severe legacy and the service response far from satisfaction.

Purely Local Motif-based GLC. Though the deficiencies have been mitigated by a series of recent works, such as the purely localized version of MAPPR proposed by its authors [17] with only computing the node visited during the clustering process, the greedy seed expansion method Motif-based Local Expansion and Optimization (MLEO) [24] with optimizing local validation function to achieve locality, the approximation method with using sampling techniques to speed up the motif-weighted graph computation [25], the sparsification method Sampling-based Motif Graph Partition (SMGP) with constraining the exploration field within the k-hop neighborhood to reducing problem space [26]. As evidenced by our experiments, there is still no actual applicable method that achieves satisfying efficiency, e.g., less than 10 s [27,28], on graphs with billion edges, e.g., Orkut and Friendster [29].

Our Method. Focusing on the most common static situation in practical graph applications, we develop Index-adaptive Triangle-based Graph Local Clustering (TGLC+) in this work, which achieves comparable effectiveness w.r.t. state-of-the-art (SOTA) methods and much more efficient w.r.t. interactive analysis. TGLC+ achieves the advantages from three main aspects: (1) It follows the PRNibble framework as MAPPR to be effective; (2) it removes the pre-processing phase in the traditional two-phase framework to be efficient; and (3) it acquires and accumulates the higher-order information of graph topology with sampling and estimation, to achieve better effectiveness-efficiency trade-off to be practical and scalable. Besides applying to real massive graphs, TGLC+ is suitable for interactive applications, which could be time-sensitive, for the following reasons: (1) It can quickly respond to the query at any time, even the ad-hoc query, since it does not require pre-processing. (2) It can consecutively respond with better results during the interaction phase since it would be improved while running. The effectiveness and efficiency of TGLC+ are guaranteed by the theoretical analysis and demonstrated by extensive experiments on six real-world graphs.

Our Contributions. To our best knowledge, TGLC+ is the first purely local MGLC algorithm optimized for the static situation without building the exact motif-based adjacency matrix beforehand. It thus is applicable and scalable for real-world massive static graphs under interactive situations. In summary, we have made the following contributions:

-   We design the approximated triangle-based Monte-Carlo method, Triangle-based Random Walk (TRW) with wedge-sampling technique, and the determined triangle-based Forward Push method, Triangle-based Forward Push (TFP) with Brute-Force triangle enumeration method.

-   We combine them in a non-trivial way to propose Triangle-based Monte-Carlo Allocation (TMCA) and finally form a novel framework TGLC+ for the MGLC problem w.r.t. triangle for the static graph. TGLC+ is scalable to massive real-world graphs with theoretical guarantees, comparable to SOTA MGLC methods, and appropriate for interactive situations.

-   We conduct extensive experiments on six real-world benchmarks, demonstrating the advantages of TGLC+ on effectiveness, efficiency, and robustness with numerical and visual results.

2  Preliminaries

We take the triangle as the target motif, defined as the induced closed 3-order subgraph on graph G, i.e., △u,v,x∈G. We focus on the simple undirected unweighted connected graph G=(V,E). To make the symbol comprehensive, we use △ to represent the variables related to the triangle, such as triangle count or triangle conductance. The main notations used in this work are listed in Table 1. Before deriving our TGLC+ method, we first introduce essential and valuable concepts in the following part.

2.1 △ -Conductance

We define the △-conductance according to the original definition in MAPPR [17].

Definition 1. (△-Conductance) The △-cut of a node-set 𝒞 on graph G, denoted by ∂△(𝒞), is the number of triangles with at least one endpoint in 𝒞 and at least one endpoint in G∖𝒞. The △-volume of 𝒞, denoted by vol△(𝒞), is the number of endpoints of triangles in 𝒞. The △-conductance of 𝒞 w.r.t G is defined as:

Φ△(G,𝒞)=|∂△(𝒞)|min(vol△(𝒞),vol△(G∖𝒞)).(1)

For convenience, we use Φ△(𝒞) to represent Φ△(G,𝒞).

2.2 Two-phase MGLC Framework

2.2.1 Approximate Personalized PageRank (APPR)

Definition 2. (PPR) Given the unweighted graph G with adjacency matrix A and degree matrix D, the seed node u and the teleportation probability α, the PPR vector pu w.r.t u is defined as:

pu=(1−α)P⋅pu+α1→u,(2)

where P is the transition probability matrix defined as P=AD−1, 1→u is the one-hot vector u. The unique solution to (2) is given by pu=∑i=0∞α(1−α)i⋅Pi⋅1→u.

Since the exact PPR value is difficult to calculate because of the infinite summation in its definition form, the APPR is more studied and is widely used for local clustering.

Definition 3. (APPR) Given the PPR vector pu, the error bound ϵ and confidence δ, p^u is called APPR with ϵ-δ guarantee if:

P(|p^u−pu|<ϵ)≥1−δ.(3)

2.2.2 PageRank Nibble (PRNibble)

Based on the motif weighting phase, MAPPR conducts the standard PRNibble process to get the final clustering result. We introduce it under the Nibble framework here in detail.

Definition 4. (PRNibble) Given the graph G, the seed node u, and the measuring function ℳ𝒫, which takes G,u as input, PRNibble first outputs the proximity score vector q=ℳ𝒫(G,u) of all nodes on G u and then conduct the standard sweep process to acquire the clustering result.

Definition 5. (Sweep) Given the proximity score vector q output by the measure phase and the cluster quality metric Φ, the sweep phase of Nibble is defined as the following procedure. (1) Compute ordered sequence c=(v1,…,vn) s.t. q(vi)d(vi)≥q(vi+1)d(vi+1), where d is the degree vector. (2) Scan the c from left to right, and record each k-prefix node set 𝒞k with its quality score Φ(𝒞k). (3) Make the node set 𝒞∗, which achieves the first or global minimal quality score Φ(𝒞∗), as the sweep result, also the clustering result of the GLC task.

The effectiveness of PRNibble is guaranteed by the theoretical bounds on cluster quality and illustrated by empirical evaluations on various real networks. Therefore, we follow the standard PRNibble framework, apply the widely-used PPR as proximity score metric 𝒫, and take △-conductance as the cluster quality metric Φ in this work.

Efficiency Dilemma. Despite effectiveness, conducting MAPPR relies on computing the motif transition probability of each node u, and thus needs to enumerate all possible 3-node tuples containing u with O(d(u)2) complexity, which is unacceptable when there are some d(u) are large, 106 in Friendster.

2.3 Monte-Carlo and Local Push

APPR can be computed with two main categories of the method, i.e., the randomized Monte-Carlo simulation [30] and deterministic local push [5].

Monte-Carlo. It stimulates random walks from the seed node u with restarting probability α, which equals the teleportation probability, and uses the percentage of the walks that terminate at node v as the estimation of pu(v). The sufficient sampling times for satisfying performance in GLC tasks under real situations are usually much less than the theoretical requirement O(1ϵ2ln⁡1δ).

Local Push. It speeds up the computation by aggregating several randomized samples in one deterministic push operation and conducting an early stop policy. Though no theoretical guarantee exists, the typical local push method PRNibble performs well in GLC tasks.

3  Related Work

Motif has received much attention in biological, social, and ecological fields [31]. Meanwhile, the vital role motif has been revealed in the fields of brain science [32], web browsing [33], and text classification of unknown authors [34]. Motifs consisting of three and four dots are the most studied. Since the low-order structures of undirected networks in different domains are similar, researchers have proposed using several motifs as features to carve the network structure [35]. Though motif-based graph local clustering (MGLC) is closely related to extensive literature, such as graphlet computation [36–38], (semi) streaming algorithm [39–41], graph proximity computation [42–44], we only focus on the most relevant ones with our work and review them carefully in this part.

Locality Improvement. Since the pre-processing phase of MAPPR accesses the whole graph and thus loses the locality, some works are proposed to achieve locality to be more efficient. Motif-based Approximate Personalized PageRank Local version (MAPPRL) [17] is the first trial to be purely local, with only counting the motifs for the nodes visited during local clustering. Though purely local, MAPPRL is infeasible to deal with the GLC tasks where large degree nodes exist around the seed node since it should suffer from enumerating the motifs. With taking triangle as the motif, MLEO [24] proposes a novel local validation function called local triangle ratio to guide the expansion process greedily to be purely local. Like MAPPRL, MLEO needs to enumerate all triangles around the nodes in the current cluster at each expansion, making it less applicable for massive real-world graphs.

Efficiency Improvement. Despite several practical methods [30,36,45] and theoretical results [14,46,47] have been developed to make the graph algorithms more efficient, only a few have been applied to the MGLC problems, among which Sampling-based Motif Graph Partition (SMGP) is the most typical one. Following the same two-phase paradigm as MAPPR, SMGP is proposed to mitigate the efficiency limitation by estimating the motif-weighted matrix rather than exactly counting it. Though SMGP achieves a much better effectiveness-efficiency trade-off and is compatible with both graph global partition and local clustering tasks, it has the following limitations on GLC tasks. (1) SMGP still needs to precompute the approximate motif-weighted matrix, making it not index-free and thus infeasible to large graphs and dynamic graphs. (2) SMGP estimates the global motif-weighted matrix without considering the seed node and its local topology, making it vary among different seed nodes in effectiveness and efficiency and thus less applicable for GLC tasks.

Remark. For local tasks, the pre-processing phase computes much more information for unrelated points or edges, thus introducing extra and unnecessary costs. In summary, there is still no applicable method for MGLC tasks on real large graphs, even w.r.t. the triangle motif and static graphs.

4  Index-adaptive Triangle-based Method

To solve the problem of no actual practical method for MGLC tasks on real large graphs, we propose an Index-adaptive Triangle-based Graph Local Clustering (TGLC+) algorithm for MGLC w.r.t. triangle on the static graph. We provide the discussions and proofs in Appendix A.

4.1 Framework Overview

Following the standard Nibble two-phase framework and keeping in line with the PRNibble, together with the probably-approximately-correct (PAC) criterion, TGLC+ takes as input the graph data G, the seed node u, and the parameters α,ϵ,δ, outputs the local cluster with △-conductance. The algorithm is demonstrated by Algorithm 1. It produces the APPR vector p^u with estimated triangle-weighted matrix W^△ from TMCA (line 1) and then conducts the standard sweep procedure to get the clustering result (line 2).

Since we have clearly defined the sweep process in Definition 5, we focus on introducing the TMCA algorithm in this section. To begin with, we go through the core techniques in this work, TRW and TFP, and demonstrate their effectiveness and efficiency by proving the correctness and analyzing the complexity. Then, we propose the TMCA algorithm by combining these two techniques in a non-trivial adaptive way. Finally, we demonstrate the benefits and characteristics of TGLC+.

4.2 Triangle-based Random Walk (TRW)

To make the pure locality compatible with the effectiveness requirements, TGLC+ ought to produce an APPR vector consistent in the accurate motif-weighted graph, which is the triangle-weighted graph in this work, with only utilizing the original graph topology information. To achieve this, we carefully investigate the wedge sampling method [48] and the rejection sampling technique [49], making it applicable to take a step out following the target triangle-weighted transition probability distribution.

Wedge Sampling. To form the candidate wedge, the wedge sampling samples two nodes from the neighborhood of node u, i.e., the candidate node v and the check node x. Notice that each wedge that serves as a triangle candidate has an identical probability of being sampled. Besides, all triangles containing the node u must be a subset of all wedges obtained by the wedge sampling. Therefore, we can sample triangles (triangle candidates) independently and uniformly from a complete and compact sampling space. We form the fundamental sampling properties of wedge sampling with Prop. 1.

Proposition 1. (Wedge Sampling) Given the graph G and the node u, the wedge sampling method samples each wedge containing u w.p. 1d(u)2 and samples a triangle containing u w.p. 1d(u)2⋅V△∗.

Wedge Rejection Sampling. Based on the wedge sampling method, we have the same probability of getting each triangle candidate together with the unnecessary wedge. Towards this, we need a post-adjust operation to filter the wedge out and identify the triangle. We present the first core technique in this work, TRW, following the wedge rejection sampling manner with Algorithm 2. TRW first conducts the wedge sampling algorithm to get the candidate node v and check node x (line 2). Then, it records the trial by adding 1 to the counter E△(u,v) (line 3). If u,v,x forms a triangle, TRW records the success by adding 1 to counter E△(s)(u,v) and accepts candidate node v as one random walk step (line 4 - line 6). If not, repeat the sample and reject process (line 1). That is why this method is called rejection sampling.

With TRW, we can sample a triangle with uniform probability by only accessing the local topology information of node u on graph G. The following Prop. 2 and Cor. 1 illustrate the effectiveness and efficiency of TRW.

Proposition 2. (TRW Correctness) TRW takes a step out from u to v w.p. W△∗V△∗, where W△∗,V△∗ are the number of triangles containing edge (u,v) and node u.

The proposition illustrates that TRW samples a triangle from all triangles containing u uniformly according to the triangle-weighted transition probability, just the same as the standard random walk on the exact triangle-weighted graph. Thus, we could get the APPR vector by taking the TRW as the underlying random walk in the Monte-Carlo manner. Therefore, TRW provides the primary method to achieve scalability for MGLC tasks. Prop. 2 induces Cor. 1, which claims the TRW complexity.

Corollary 1. (TRW Complexity) TRW needs d(u)2V△∗ trials to step out from u on average.

Remark. To this end, we have the practical solution for taking a random walk step out according to the triangle weights without knowing the exact weights. Even on the static graph, there are some non-trivial problems in forming an effective and efficient algorithm for MGLC tasks. It is essential to notice that there are two most significant characteristics of the TRW, (1) it introduces the approximation error to the PPR vector, (2) it is not only pure local but also designed in an index-free manner. The related questions are: (1) whether and how we can bound the error to have little effectiveness loss, and (2) whether the index-free manner costs less and is necessary for the static graph. For the first question, we form Thm. 1 to claim the sampling budget for TRW.

Theorem 1. (TRW Monte-Carlo Sampling Budget) Given the graph G, node u, error bound ϵ, confidence δ, we need O(1ϵ2ln|V|δ) Monte-Carlo simulations to output the APPR vector p^u.

Based on the sampling budget claimed in Thm. 1, which determines the algorithm cost of the TRW-based Monte-Carlo method, we analyze the relations between the trivial Brute-Force search method and TRW and present our second core technique, Triangle-based Forward Push (TFP).

4.3 Triangle-based Forward Push (TFP)

Notice that, the exact triangle weights around the node u on graph G could be determined by enumerating each wedge containing u in a Brute-Force manner, whose complexity is O(d(u)2). If TRW-based Monte-Carlo needs more sampling budgets for node u than O(d(u)2) at some simulation step, index-free TRW should be less efficient and less effective than the Brute-Force search. Therefore, the determined Brute-Force search and the approximated wedge rejection sampling should be combined in an adaptive way, which is related to the graph’s local structure and the specific details of the algorithm, thus non-trivial indeed. To begin with, we revisit the TRW-based Monte-Carlo as a Depth First Search (DFS) process. Notice that the sampling budgets have been determined by Thm. 1, the total number of simulations is thus also determined. In the general Monte-Carlo process, though simulations could be conducted in parallel independently, the random walk steps in one simulation are strictly ordered and are not able to communicate to those in other simulations. The synchronous mechanism in DFS keeps the TRW-based Monte-Carlo method index-free. However, we will illustrate that it is unnecessary and propose a novel method in Breadth First Search (BFS) manner.

Adaptive Selection. Given the sampling budgets Q, we put all Q TRW Monte-Carlo simulations together in a layer-wise BFS manner and form the data structure EXP, where the node u in 𝓁 layer EXP[𝓁][u] denotes the random walks reach the u on the 𝓁-th step and the sampling trials. Given the node u on the 𝓁-th step, if the sampling budget EXP[𝓁][u] is less than its Brute-Force search cost, d(u)2, EXP[𝓁][u] times TRW should be executed to step out from node u. Otherwise, the determined Brute-Force search, i.e., Algorithm 3, should be applied to node u to get the exact triangle weights, and then the TFP is conducted to push the sampling budgets to the next layer to simulate a batched TRW. Since the triangle weighting algorithm is comprehensive, we focus on introducing the TFP technique in the following part.

Triangle-based Forward Push (TFP). Though the exact triangle weights and the corresponding probability are given, it is still challenging to directly push the sampling budgets forward while keeping equivalent with the result of a batch of accurate triangle-based random walks. To solve this problem, we devise the TFP technique based on the local push idea and demonstrate it with Algorithm 4. TFP firstly groups the batch of random walks by finding the integer multiple of the triangles around u as the node sampling budgets (line 1). Then, it pushes the budgets to the neighbors according to the triangle weights and forms the sampling budgets for the next layer, the (𝓁+1)-th layer (line 2–line 3). Finally, TFP subtracts the pushed budgets from the original one and gets the left trails which would be further handled by the TRW method (line 4). Prop. 3 and Cor. 2 illustrate the effectiveness and efficiency of TFP.

Proposition 3. (TFP Correctness) The TFP push result with nexpalloc trials is equivalent to the simulation result with nexpalloc TRW trials from the same node on expectation.

Corollary 2. (TFP Complexity) TFP only needs O(d(u)) cost to obtain the push result for arbitrary trials from node u at layer 𝓁.

To this end, we have investigated two typical situations and proposed two corresponding appropriate solutions, i.e., Triangle-based Random Walk (TRW) and Triangle-based Forward Push (TFP). Then, we can combine them adaptively and present Triangle-based Monte-Carlo Allocation (TMCA).

4.4 Triangle-based Monte-Carlo Allocation (TMCA)

We develop TMCA based on TRW and TFP to produce the APPR vector p^u with ϵ-δ guarantee and the estimated triangle-weighted matrix W^△. TMCA is demonstrated with Algorithm 5. First, TMCA initializes the auxiliary data structures, Brute-Force search cost for node u and layer-wise sampling budgets allocation EXP (line 1 – line 3). Next, it constructs the index structures, sampled △ counter E△, and exact △ counter W△*, which will be assigned and updated adaptively during the algorithm running (line 4–line 8). Then, TMCA allocates the initial sampling budgets, EXP, from the first layer to the L-th layer (line 9). Within each inter-layer allocation, TMCA adaptively conducts TFP in a determined Brute-Force manner or TRW in approximated Monte-Carlo manner, according to the corresponding conditions (line 10–line 15). Finally, the aimed APPR vector p^u and triangle-weighted matrix W^△ are estimated based on the constructed index structures (line 18). Precisely, p^u is estimated by assembled EXPEXP, the approximated L-hop transition probabilities with the PPR weights (line 16). W^△ is obtained by combining the estimations of triangle weights on edges from the TRW Monte-Carlo process and the exact value from the determined triangle weighting (Algorithm 3) process (line 17). In the following part, we present how to use the data accumulated during the running process to estimate the triangle-weighted matrix without introducing extra operations and costs.

Theorem 2. (TMCA Optimum) Given the graph G, node u, error bound ϵ, confidence δ, sampling budget 1ϵ2ln|V|δ, TMCA outputs the APPR vector p^u with no more cost than either purely randomized TRW Monte-Carlo method or purely deterministic TFP Brute-Force method.

Triangle-weighted Matrix Estimation. To produce the Φ△(𝒞) for candidate cluster 𝒞 during the sweep phase, the triangle-weighted matrix should be used to compute the △-conductance. Since we do not have the exact triangle-weighted matrix, which is the most critical requirement and core advantage of our Index-adaptive Triangle-based Graph Local Clustering (TGLC+) algorithm, it is essential to estimate the triangle-weighted matrix by only utilizing the information acquired during the TMCA procedure. Towards this, we propose the following Prop. 3 to introduce the method used to estimate the triangle weight for each edge in TMCA.

Proposition 3. (Triangle Weights Estimation) Given the check counter E△ and success counter E△(s) obtained from TMCA, E△(s)(u,v)E△(u,v) is an unbiased estimator of △u,vd(u), where d(u) is the degree of node u.

Notice that the exact triangle weights could be acquired for some edges since they have been processed by the triangle weighting method (Algorithm 3). Therefore, the estimated and exact triangle weights can be merged to use the information accumulated during the algorithm fully.

4.5 Properties and Advantages

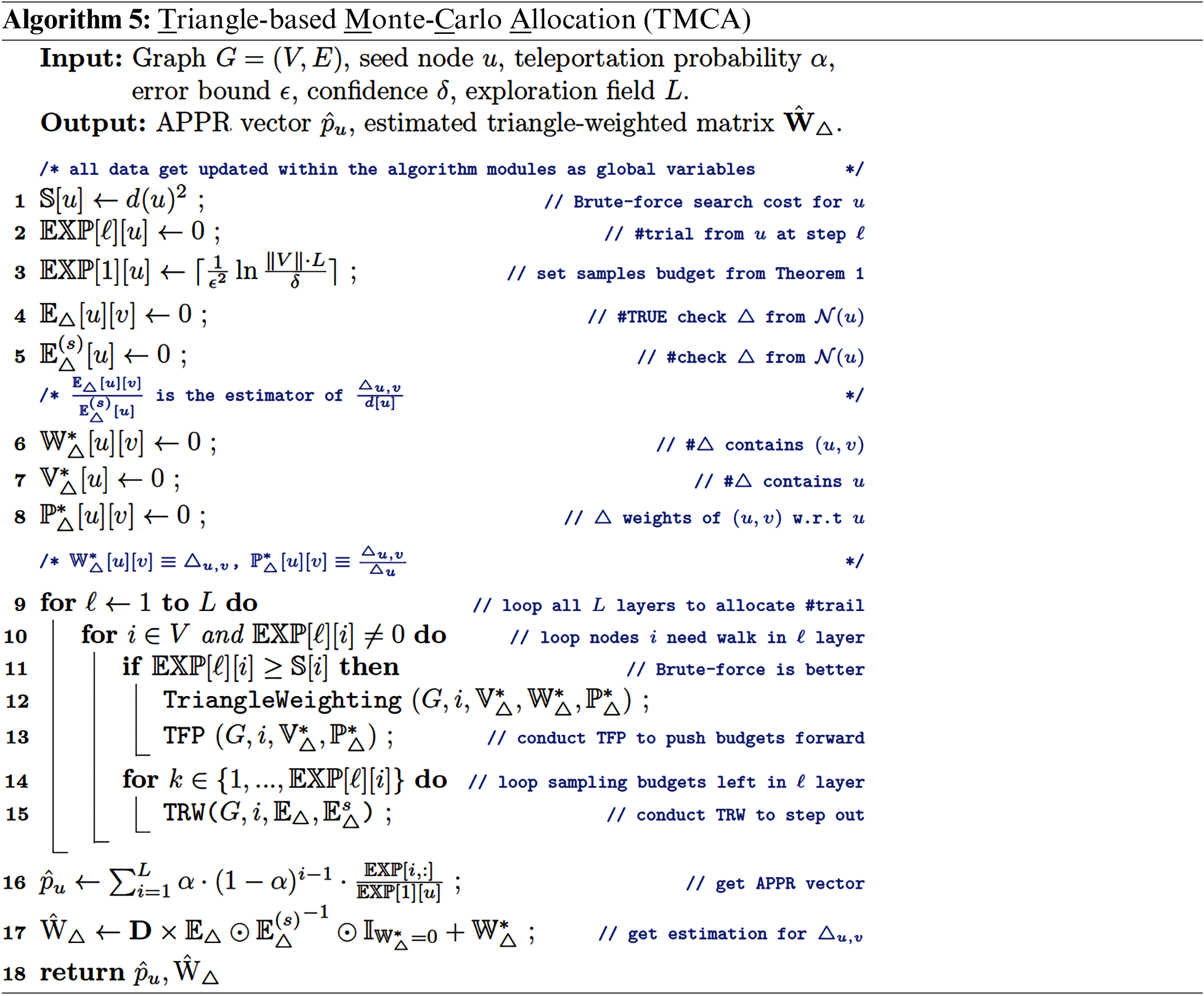
To this end, we have introduced two essential techniques in our proposed Index-adaptive Triangle-based Graph Local Clustering (TGLC+), i.e., Triangle-based Random Walk (TRW), Triangle-based Forward Push (TFP), and adaptively combine them to form the core algorithm Triangle-based Monte-Carlo Allocation (TMCA). Besides, we also present several fundamental operations, i.e., triangle weighting and triangle-weighted matrix estimation, which make the TGLC+ complete and applicable. To summarize, we present the most critical properties of TGLC+ from the following aspects.

Purely Local. TGLC+ can be conducted by only exploring the limited local field of the visited node u, i.e., the neighborhood 𝒩(u). The locality makes TGLC+ possible to be scalable on large-scale graphs.

Interaction Applicable. TGLC+ is the first MGLC algorithm to apply to ad-hoc queries. It is thus appropriate for interactive applications because it is free from constructing the triangle-weighted matrix and can output the clustering result at nearly any time during the algorithm.

Index-adaptive. Though it is unnecessary for TGLC+ to compute the triangle-weighted matrix beforehand, and thus can be conducted in an index-free manner, TGLC+ could also make use of the information accumulated during the algorithms and construct essential and optimal index adaptively. Therefore, besides the advantages of responding to ad-hoc queries, TGLC+ is also comparable with other two-phase methods, e.g., MAPPR and SMGP, for simultaneous queries on the same graph.

5  Experiments

Dataset. We conduct the experiments on six undirected real-world graphs with ground-truth communities, i.e., Amazon, DataBase systems and Logic Programming (DBLP), YouTube, LiveJournal, Orkut, and Friendster [29], whose sizes are from moderate to massive. Table 2 summarizes the statistics and presents the △-conductance distributions among the ground-truth communities with top-5000-quality1.

Methods for Comparison. Since we focus on achieving scalability by establishing a purely local and index-adaptive method, we compare our TGLC+ with the two SOTA purely local methods, i.e., MAPPRL and MLEO.

Implementation. Experiments are conducted on a machine with an Intel(R) Xeon(R) Gold 6126@2.60 GHz CPU and 500 GB memory. We implement all methods with native Python and run experiments with a single thread. We conduct each algorithm as below.

•   TGLC+: We set the teleportation probability of PPR, α∈{0.02,0.1,0.2,0.4} to get the appropriate α for the corresponding dataset. We vary the sample budget S from 0 to 105 with step 5,000 to get 20 evaluations for each test.

•   MAPPRL: We set the teleportation probability for each dataset with the corresponding TGLC+ optimal α. We vary the error bound ϵ from 10−3 to 10−13 with step 10−2, which covers the range suggested by [17], to get 5 evaluations for each test.

•   MLEO: We fix the cluster size parameter α=1 and get evaluations for each test every 3 s until it finishes or achieves the time budget, 3600 s.

Experiment Setting. We randomly choose 150 communities among the top-5000-quality clusters, which the experts annotate, and randomly choose two nodes from each chosen community to form the query set with size 300.

Evaluation and Demonstration. We use △-conductance and F1-score to evaluate the effectiveness of the methods on the first six datasets. We demonstrate the effectiveness with the mean and variance of the corresponding indicators. We present the effectiveness-efficiency trade-off curve to illustrate the characters of our TGLC+ and baselines.

5.1 Effectiveness Evaluation

The evaluation results are presented in Tables 3 and 4. For each dataset, the first row represents the mean, and the second row represents the standard deviation. We use * and bold font to indicate the best result. Generally speaking, our TGLC+ outperforms the baselines with both △-conductance and F1-score in most cases and is still comparable in the rest cases.

It is essential to see that TGLC+ provides effective results for all experiments, and MLEO gets less effective for the three largest datasets. However, MAPPRL is only applicable to the two smallest datasets. To explain this, we present the average degree d¯ in Table 2. Since all datasets except the two smallest ones have large d¯, MAPPRL and MLEO should fail under the time budget.

Besides, our TGLC+ performs the best with both △-conductance and F1-score metrics for YouTube, Orkut, and Friendster, which is rather challenging. In addition, TGLC+ achieves the best △-conductance with PPR teleportation probability α=0.02 in half of the tasks, which is consistent with the observation from MAPPR [17] to some extent.

5.2 Performance Evaluation

We illustrate the characters of TGLC+ with two baseline methods through the effectiveness-efficiency trade-off curves on DBLP in Fig. 1 and Friendster in Fig. 2. As demonstrated by the relative positions between curves, the performance of MLEO is dominated by our TGLC+ method on both two datasets, since its curve is entirely above the one of TGLC+, which means MLEO takes more time and get a less satisfying result. The curves of MAPPRL and TGLC+ are both lying on the bottom in Fig. 1, which means they perform well on the DBLP dataset. However, on Friendster, MAPPRL is prominently outperformed by our TGLC+ and behaves strangely. Thus, we discuss two weird but interesting phenomena to better analyze the experimental results.

Figure 1: DBLP trade-off curve

Figure 2: Friendster trade-off curve

Sharp Drop and Scattered Distribution. The sharp drop between the first two nodes on the green MLEO curve in Fig. 1 is not corresponding to the △-conductance optimization but to two different nodes and indicates that the performance of MLEO varies from different nodes even on the same graph. Meanwhile, MAPPRL is more aggregated and thus more robust. As for TGLC+, it concentrates on the 1 s time, and 0.06 △-conductance tightly and thus achieves the best robustness.

Non-monotonic Decrement. As the curve presents the trade-off between efficiency and effectiveness, it is reasonable to expect it to decrease monotonically since we should get better results with a longer running time. The abnormal rises of both the green MLEO curve and the blue MAPPRL curve in both two figures are mainly caused by the time-out records, indicating that these two methods could not be applicable for some nodes even on the same graph. Meanwhile, TGLC+ would be fine with this problem.

6  Conclusion and Discussion

In this work, we propose the first purely local and index-adaptive motif-based graph local clustering (MGLC) algorithm Index-adaptive Triangle-based Graph Local Clustering (TGLC+) based on the combination of Triangle-based Random Walk (TRW) in Monte-Carlo manner and Triangle-based Forward Push (TFP) in Brute-Force manner. TGLC+ achieves the optimal balance between the approximation and determination, thus performing better in both efficiency and effectiveness. Besides, TGLC+ is applicable for both ad-hoc and simultaneous query tasks, which makes it appropriate for interactive applications. TGLC+ bids fair to bring benefits to extensive applications, such as making the visualization detailed and the decision-making process timely. The efficiency and effectiveness of TGLC+ are guaranteed by theoretical analysis. Extensive experiments on six real-world graphs demonstrate the scalability and robustness of TGLC+. However, there are still several questions here, such as choosing the optimal parameter of PPR, and generalizing to more motifs, or arbitrary higher-order structures, which should be interesting for future works.

Acknowledgement: We thank Lv Fangrui, Wang Shijun, Huang Jin, and Li Lianbei from the Renmin University of China for their time and effort in discussing the ideas and algorithms. We thank Dr. Wu Jun for providing support on the core techniques and proof details. We also thank Pr. Chen Zheng from the Beijing Foreign Studies University for her kind encouragement and solid support.

Funding Statement: This work is partially supported by the Fundamental Research Funds for the Central Universities (No.2020JS005).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

1https://snap.stanford.edu/data/index.html#communities

References

1. S. Boccaletti, V. Latora, Y. Moreno, M. Chavez and D. -U. Hwang, “Complex networks: Structure and dynamics,” Physrep., vol. 424, no. 4, pp. 175–308, 2006. [Google Scholar]

2. Z. Lu, J. Wahlström and A. Nehorai, “Community detection in complex networks via clique conductance,” Scientific Reports, vol. 8, no. 1, pp. 1–16, 2018. [Google Scholar]

3. M. Girvan and M. E. Newman, “Community structure in social and biological networks,” Proceedings of the National Academy of Sciences of the United States of America, vol. 99, no. 12, pp. 7821–7826, 2002 [Google Scholar] [PubMed]

4. D. A. Spielman and S. -H. Teng, “Nearly-linear time algorithms for graph partitioning, graph sparsification, and solving linear systems,” in Proc. of the Thirty-sixth Annual ACM Symp. on Theory of Computing, Chicago, IL, USA, pp. 81–90, 2004. [Google Scholar]

5. R. Andersen, F. Chung and K. Lang, “Local graph partitioning using pagerank vectors,” in Proc. of 2006 47th Annual IEEE Symp. on Foundations of Computer Science (FOCS’06), Berkeley, CA, USA, pp. 475–486, 2006. [Google Scholar]

6. C. -S. Liao, K. Lu, M. Baym, R. Singh and B. Berger, “Isorankn: Spectral methods for global alignment of multiple protein networks,” Bioinformatics, vol. 25, no. 12, pp. 253–258, 2009. [Google Scholar]

7. S. Li, C. Gentile and A. Karatzoglou, “Graph clustering bandits for recommendation,” arXiv preprint, arXiv: 1605.00596, 2016. [Google Scholar]

8. Y. Feng, S. Yu, K. Zhang, X. Li and Z. Ning, “Comics: A community property-based triangle motif clustering scheme,” PeerJ Computer Science, vol. 5, no. 5, pp. 180, 2019. [Google Scholar]

9. J. Shi and J. Malik, “Normalized cuts and image segmentation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 22, no. 8, pp. 888–905, 2000. [Google Scholar]

10. M. E. Newman, “Modularity and community structure in networks,” Proceedings of the National Academy of Sciences of the United States of America, vol. 103, no. 23, pp. 8577–8582, 2006 [Google Scholar] [PubMed]

11. N. X. Vinh, J. Epps and J. Bailey, “Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance,” The Journal of Machine Learning Research, vol. 11, pp. 2837–2854, 2010. [Google Scholar]

12. S. G. Kobourov, S. Pupyrev and P. Simonetto, “Visualizing graphs as maps with contiguous regions,” in EuroVis (Short Papers), 2014. [Google Scholar]

13. J. Yang and J. Leskovec, “Defining and evaluating network communities based on ground-truth,” Knowledge and Information Systems, vol. 42, no. 1, pp. 181–213, 2015. [Google Scholar]

14. J. Cheeger, “A lower bound for the smallest eigenvalue of the Laplacian,” Problems in Analysis, vol. 625, no. 110, pp. 195–199, 1970. [Google Scholar]

15. I. J. Cox, S. B. Rao and Y. Zhong, “Ratio regions: A technique for image segmentation,” in Proc. of 13th Int. Conf. on Pattern Recognition, Vienna, Austria, vol. 2, pp. 557–564, 1996. [Google Scholar]

16. A. R. Benson, D. F. Gleich and J. Leskovec, “Higher-order organization of complex networks,” Science, vol. 353, no. 6295, pp. 163–166, 2016 [Google Scholar] [PubMed]

17. H. Yin, A. R. Benson, J. Leskovec and D. F. Gleich, “Local higher-order graph clustering,” in Proc. of the 23rd ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, Halifax, NS, Canada, pp. 555–564, 2017. [Google Scholar]

18. D. J. Watts and S. H. Strogatz, “Collective dynamics of ‘small-world’ networks,” Nature, vol. 393, no. 6684, pp. 440–442, 1998 [Google Scholar] [PubMed]

19. N. C. Krämer, V. Sauer and N. Ellison, “The strength of weak ties revisited: Further evidence of the role of strong ties in the provision of online social support,” Social Media + Society, vol. 7, no. 2, pp. 1–19, 2021. [Google Scholar]

20. S. Yao, “Application of data mining technology in financial fraud identification,” in Proc. of 2021 4th Int. Conf. on Information Systems and Computer Aided Education, Dalian, China, pp. 2919–2922, 2021. [Google Scholar]

21. S. Zhou, X. Yang and Q. Chang, “Spatial clustering analysis of green economy based on knowledge graph,” Journal of Intelligent & Fuzzy Systems (Preprint), vol. 23, no. 2, pp. 1–10, 2021. [Google Scholar]

22. K. H. Foysal, H. J. Chang, F. Bruess and J. W. Chong, “Smartfit: Smartphone application for garment fit detection,” Electronics, vol. 10, no. 1, pp. 97, 2021. [Google Scholar]

23. D. Zhu, G. Shen, J. Chen, W. Zhou and W. Kong, “A higher-order motif-based spatiotemporal graph imputation approach for transportation networks,” Wireless Communications and Mobile Computing, vol. 2022, no. 8, pp. 1–16, 2022. [Google Scholar]

24. W. Ma, L. Cai, T. He, L. Chen, Z. Cao et al., “Local expansion and optimization for higher-order graph clustering,” IEEE Internet of Things Journal, vol. 6, no. 5, pp. 8702–8713, 2019. [Google Scholar]

25. S. Huang, Y. Li, Z. Bao and Z. Li, “Towards efficient motif-based graph partitioning: An adaptive sampling approach,” in Proc. of 2021 IEEE 37th Int. Conf. on Data Engineering (ICDE), Chania, Greece, pp. 528–539, 2021. [Google Scholar]

26. A. Chhabra, M. F. Faraj and C. Schulz, “Local motif clustering via (hyper) graph partitioning,” arXiv preprint, arXiv: 2205.06176, 2022. [Google Scholar]

27. R. B. Miller, “Response time in man-computer conversational transactions,” in Proc. of the December 9-11, 1968, Fall Joint Computer Conf., San Francisco, CA, USA, Part I, pp. 267–277, 1968. [Google Scholar]

28. Z. Liu and J. Heer, “The effects of interactive latency on exploratory visual analysis,” IEEE Transactions on Visualization and Computer Graphics, vol. 20, no. 12, pp. 2122–2131, 2014 [Google Scholar] [PubMed]

29. J. Leskovec and R. Sosic, “Snap: A general-purpose network analysis and graph-mining library,” ACM Transactions on Intelligent Systems and Technology (TIST), vol. 8, no. 1, pp. 1–20, 2016. [Google Scholar]

30. D. Fogaras, B. Rácz, K. Csalogány and T. Sarlós, “Towards scaling fully personalized pagerank: Algorithms, lower bounds, and experiments,” Internet Mathematics, vol. 2, no. 3, pp. 333–358, 2005. [Google Scholar]

31. N. T. L. Tran, L. DeLuccia, A. F. McDonald and C. -H. Huang, “Cross-disciplinary detection and analysis of network motifs,” Bioinformatics and Biology Insights, vol. 9, pp. 23619, 2015. [Google Scholar]

32. O. Sporns, R. Kötter and K. J. Friston, “Motifs in brain networks,” PLoS Biology, vol. 2, no. 11, pp. 369, 2004. [Google Scholar]

33. F. Chierichetti, R. Kumar, P. Raghavan and T. Sarlos, “Are web users really markovian?,” in Proc. of the 21st Int. Conf. on World Wide Web, Lyon, France, pp. 609–618, 2012. [Google Scholar]

34. Y. Al Rozz and R. Menezes, “Author attribution using network motifs,” in Proc. of Int. Workshop on Complex Networks, Cambridge, UK, pp. 199–207, 2018. [Google Scholar]

35. P. Cunningham, M. Harrigan, G. Wu and D. O’CALLAGHAN, “Characterizing ego-networks using motifs,” Network Science, vol. 1, no. 2, pp. 170–190, 2013. [Google Scholar]

36. M. N. Kolountzakis, G. L. Miller, R. Peng and C. E. Tsourakakis, “Efficient triangle counting in large graphs via degree-based vertex partitioning,” Internet Mathematics, vol. 8, no. 1, pp. 161–185, 2012. [Google Scholar]

37. J. Tetek, “Approximate triangle counting via sampling and fast matrix multiplication,” arXiv preprint, arXiv: 2104.08501, 2021. [Google Scholar]

38. K. Paramonov, D. Shemetov and J. Sharpnack, “Estimating graphlet statistics via lifting,” in Proc. of the 25th ACM SIGKDD Int. Conf. on Knowledge Discovery & Data Mining, Anchorage, AK, USA, pp. 587–595, 2019. [Google Scholar]

39. B. W. Priest, R. Pearce and G. Sanders, “Estimating edge-local triangle count heavy hitters in edge-linear time and almost-vertex-linear space,” in Proc. of Int. 2018 IEEE High Performance Extreme Computing Conf. (HPEC), Waltham, MA, USA, pp. 1–7, 2018. [Google Scholar]

40. D. Fu, D. Zhou and J. He, “Local motif clustering on time-evolving graphs,” in Proc. of the 26th ACM SIGKDD Int. Conf. on Knowledge Discovery & Data Mining, Virtual Event, CA, USA, pp. 390–400, 2020. [Google Scholar]

41. C. Tsourakakis, C. Gkantsidis, B. Radunovic and M. Vojnovic, “Fennel: Streaming graph partitioning for massive scale graphs,” in Proc. of the 7th ACM Int. Conf. on Web Search and Data Mining, New York, NY, USA, pp. 333–342, 2014. [Google Scholar]

42. F. Chung, “The heat kernel as the pagerank of a graph,” Proceedings of The National Academy of Sciences of The United States of America, vol. 104, no. 50, pp. 19735–19740, 2007. [Google Scholar]

43. P. Li, I. Chien and O. Milenkovic, “Optimizing generalized pagerank methods for seed-expansion community detection,” Advances in Neural Information Processing Systems, vol. 32, pp. 11710–11721, 2019. [Google Scholar]

44. R. Yang, X. Xiao, Z. Wei, S. S. Bhowmick, J. Zhao et al., “Efficient estimation of heat kernel pagerank for local clustering,” in Proc. of the 2019 Int. Conf. on Management of Data, Amsterdam, Netherlands, pp. 1339–1356, 2019. [Google Scholar]

45. Q. Li, S. Zaman, W. Sun and J. Alam, “Study on the normalized Laplacian of a penta-graphene with applications,” International Journal of Quantum Chemistry, vol. 120, no. 9, pp. e26154, 2020. [Google Scholar]

46. S. Zaman, A. N. A. Koam, A. A. Khabyah and A. Ahmad, “The kemeny’s constant and spanning trees of hexagonal ring network,” Computers, Materials & Continua, vol. 73, no. 3, pp. 6347–6365, 2022. [Google Scholar]

47. S. Zaman, “Spectral analysis of three invariants associated to random walks on rounded networks with 2n-pentagons,” International Journal of Computer Mathematics, vol. 99, no. 3, pp. 465–485, 2022. [Google Scholar]

48. C. Seshadhri, A. Pinar and T. G. Kolda, “Wedge sampling for computing clustering coefficients and triangle counts on large graphs,” Statistical Analysis and Data Mining: The ASA Data Science Journal, vol. 7,no. 4, pp. 294–307, 2014. [Google Scholar]

49. M. T. Wells, G. Casella and C. P. Robert, “Generalized accept-reject sampling schemes,” Lecture Notes-Monograph Series, vol. 45, pp. 342–348, 2004. [Google Scholar]

Appendix A. TGLC+ Proofs and Analysis

Proof. (TRW Correctness) Given the node u, considering the node v∈𝒩(u), let △u,v=W△∗[u][v], let △u=V△∗[u]. TRW selects v as the candidate or check node w.p. 1d(u) since each neighbour of u has the same probability of being sampled. If node v is accepted by TRW as the sampled node with checked node x, there are △u,v possible choices for x. Thus, TRW accepts v w.p.

ℙ(u→v)=1d(u)⋅△u,vd(u)=△u,vd(u)2.(4)

Thus, the probability of TRW taking a step out from u to v∈V is

ℙ(u⇝v)=ℙ(u→v)∑v∈N(u)ℙ(u→v)=△u,vd(u)2⋅d(u)2∑v∈N(u)△u,v=△u,v∑v∈N(u)△u,v=△u,v△u,(5)

since △u=∑v∈𝒩(u)△u,v.

Proof. (TRW Complexity) Notice that the summation of Eq. (4) on the neighbors of the node u is the probability that TRW successfully takes a step out from u after one trial,

P(u⇝△)=∑v∈𝒩(u)△u,vd(u)2=△ud(u)2.(6)

Since each trial is i.i.d., the amount of trials TRW needs to achieve the first acceptance follows the Geometric distribution with parameter P(u⇝△). Thus, the complexity for TRW taking one step out is 1P1(u⇝△)=d(u)2△u.

Proof. (TRW Monte-Carlo Sampling Budget) As guaranteed by TRW, each TRW Monte-Carlo simulation from u stops at node v w.p. pu(v). According to Chernoff Bound, it takes O(1ϵ2ln⁡1δ) samples P(|p^u(v)−pu(v)|<ϵ)≥1−δ. To make this guarantee applied to all nodes v∈V and thus achieve ϵ-δ guarantee, we set δn be the confidence parameter. According to Union Bound, the theorem is established.

Proof. (TFP Correctness) Given the node u with nexpalloc trials, considering the node v∈𝒩(u), let △u,v=W△∗[u][v], let △u=V△∗[u]. According to Algorithm 4, TFP pushes nexpalloc⋅△u,v△u sampling budget to node v. According to Prop. 2, nexpalloc times TRW from node u should reach node v for nexpalloc⋅P(u⇝v)=nexpalloc⋅△u,v△u times. Therefore, TFP and TRW are equivalent on expectation.

Proof. (TFP Complexity) Since the exact triangle weights are obtained from Algorithm 3, TFP only needs to allocate the sampling budget to d(u) nodes directly with just naïve operations. Thus, the complexity of a single TFP is O(d(u)).

Proof. (TMCA Optimum) Given the node u, let △u,v=W△∗[u][v], let △u=V△∗[u], let { EXℙ[ 1 ][ u ],EXℙ[ 2 ][ u ],…,EXℙ[ L ][ u ] } denote its total sampling operations during the purely randomized TRW Monte-Carlo process to obtain the APPR vector p^u. Considering some layer 𝓁, according to Cor. 1, it takes TRW Monte-Carlo EXP[𝓁][u]⋅d(u)2△u to step out. If we conduct TFP for node u at layer 𝓁, according to Algorithm 3 and Algorithm 4, it costs d(u)2 to establish the exact triangle weights and d(u) to get the equivalent result as TRW. Guaranteed by Prop. 3, TFP and TRW are equivalent on expectation; thus, the arbitrary combination of these two methods would be correct and effective. Therefore, we could adaptively select TFP instead of TRW to achieve the optimal efficiency according to the condition EXP[𝓁][u]⋅d(u)2△u>d(u)2+d(u). Unfortunately, the fact that the triangle count △u for specific node u is unknown would cause the condition to be unpractical. From this, we make the relaxation and use the graph clustering coefficient ϕ¯ to represent the item d(u)2△u to induce the condition used in TMCA, i.e., EXP[𝓁][u]>ϕ¯−1⋅(d(u)2+d(u)). Thus, the theorem is established.

Proof. (Triangle Weight Estimation) Given the seed node u and the specific candidate node v, it is accepted by TRW and steps out through the edge eu,v w.p. △u,vd*(u), since the check node is sampled from the smaller one between 𝒩(u),𝒩(v), and there are exact △u,v containing eu,v. Thus, each count in E△(u,v) represents a Bernoulli trial w.p. △u,vd*(u), and each count in E△(s)(u,v) represents one success. Therefore, for each edge (u,v), the ratio of the success counts E△(s)(u,v), and the check counts E△(u,v) is the unbiased estimator for its exact triangle weight.