A Double-Compensation-Based Federated Learning Scheme for Data Privacy Protection in a Social IoT Scenario

1  Introduction

The smart wearable device is an Internet of Things (IoT) equipment for personal health monitoring. It can obtain the human body status in real-time and communicate with other IoT devices. After acquiring the physiological data, the device transmits the data to a mobile application or an intermediate router and finally to a cloud-based database. There have been various applications of social IoT in recent years [1,2]. The data application scenario for smart wearable devices is one of the most important. The physiological data on these devices also has significant commercial and application value.

Studies are emerging on the use of Artificial Intelligence (AI) techniques and various types of physiological data to assess users’ health levels comprehensively [3]. Among them, using machine learning techniques to evaluate indicator data for overall health has become the primary path of many studies. Gavhane et al. [4] used a multilayer perceptron network based on age, blood pressure, and heart rate data. This network can predict the occurrence of heart disease. Masuda et al. [5] developed a new practical system that estimates circadian rhythm. This system can estimate the time and heart rate (HR) value to reach the lowest point in the circadian rhythm. Li et al. [6] proposed a locally connected long and short-term memory denoising autoencoder framework (LC-LSTM-DAE). This framework can use the data collected by smart wearable devices to make more accurate predictions about users’ moods, health, stress, and other aspects. The application of AI technology facilitates users with training data automatically collected from smart wearable devices. The corresponding models were trained or predicted through cloud platforms or edge computing nodes, constituting a set of social IoT for medical services. The significance of its interactive process is that it reduces the time needed for diagnosis and provides an essential reference for subsequent treatment, evaluation, and feedback.

Data security [7–12] is a new issue with the development of the information era. Nowadays, smart wearable devices have been widely used in people's life to record personal health information, and their performance of privacy protection cannot be ignored. During the data analysis processing, it may make the data flow to the outside world and make it difficult for users to ensure the ownership of their data. These problems allow lawbreakers to easily access sensitive information and illegally exploit the data for profit. In 2016, the Mirai botnet [13] took control of many IoT devices and launched a Distributed Denial of Service (DDoS) attack with network traffic up to 620 gb/s, which emerged in most states in the USA. Another study showed that more than 6,000 open cameras are at risk of privacy breaches in streets, restaurants, and even hospitals in the USA.

These problems have been improved somewhat since federated learning was proposed [14–16]. Federated learning, regarded as a distributed method in the field, uses homomorphic methods to solve the problem of data privacy breaches. It is a privacy-preserving and data-sharing method. The subjects involve the participants and the central server. The participants only upload quantities that do not directly expose data features such as gradients or model parameters. The homomorphic encryption [17,18] method keeps the uploaded information from being leaked, effectively protecting the participant’s data privacy. At the same time, the participants collaborate to train the model so that it can apply in a broader range of situations.

As federated learning is still at an early stage, many issues still need to be resolved. In recent years, synchronous federated learning models [19] have been replaced by asynchronous models [20–22], which can improve the convergence speed and avoid time wastage. Differential privacy-based federated learning algorithms are used to reduce the cost of cryptography [23]. In addition, federated learning algorithms in heterogeneous environments [24,25] have been proposed to reduce the heterogeneity loss in federated learning. However, these methods still have various drawbacks, such as time delay, data heterogeneity, lack of incentive, loss of accuracy, and limitation to specific scenarios [26–28]. These drawbacks will be introduced in detail in Section 2.2 and the way our scheme would overcome the challenges will be explained in Section 3.

This paper aims to form a flexible federated learning scheme with better security and usability to protect sensitive data in smart wearable devices. We propose an asynchronous federated learning scheme based on double compensation. It is used for the horizontal federated learning scenario to solve the time delay problem and data heterogeneity. The scheme proposed in this paper generally has certain advantages over existing methods.

We summarize our main results and contributions as follows:

•   We propose an asynchronous federated learning scheme based on double compensation. The scheme uses the DC-ASGD method [29] based on second-order Taylor expansion as the delay compensation. It adds FedProx operators [30] to the objective function as the heterogeneity compensation. The two compensations are used for solving the time delay and data heterogeneity problems.

•   Our scheme performs a role reversal between the participants and the central server. The entire process is participant-centered making the update process more flexible and incentivizes participants. This design motivates the federated learning process.

•   We theoretically prove that the existing methods have previously mentioned problems, and our scheme can solve them and simplify the parameter update process.

•   Experiments show that our scheme can effectively improve the accuracy of asynchronous federated learning algorithms by about 5%, which is compromised for time delay and data heterogeneity problems.

Section 2 introduces the basic process of federated learning and the classic federated averaging (FedAvg) [27]. Besides, we discuss existing related work. In Section 3, we discuss the scheme’s design and the two compensations theoretically and present our scheme. In Section 4, we present comparative experiments in regular and heterogeneous scenarios respectively and discuss the experimental results. We summarize the findings of this paper and discuss future work in Section 5.

2  Background

As data becomes more commoditized and personalized, privacy protection becomes an increasing concern for data owners. However, to maximize the value of their data, such as using machine learning to make more accurate predictions and classifications, these data owners need to work together to ensure that the data is as well distributed as possible. This collaborative approach inevitably leads to the problem of privacy leakage. Federated learning [31], as a privacy-preserving approach in distributed learning scenarios, makes good use of homomorphic methods to solve this problem.

2.1 Federated Learning

The subject of federated learning includes the participant and the central server [15,32]. The participants are the data owners, usually enterprises, platforms, individuals, etc. who own the data. The data will involve privacy and confidentiality. The central server is the intermediate computing party, which does not own the data. It is mainly responsible for receiving the parameters of each participant, calculating the intermediate results, and issuing the new model parameters. The central server can be curious, as ordinary federation learning usually uses homomorphic privacy protection methods to prevent the leakage of intermediate results. However, it must be assumed to be honest to prevent malicious tampering during the computation and distribution process affecting the overall model effect. In exceptional cases, the central server can be omitted to form a point-to-point overall structure, but the computational cost is also increased.

The primary process of federated learning is divided into the following steps [32], Distribute model, Local training, Upload parameter, and Update and Syndicate, as shown in Fig. 1. The central server issues initial parameters to each participant. Each participant receives the model parameters from doing local training and uploads the model parameters or gradients to the central server after complementing the homomorphic operation. After receiving the model parameters, the central server performs specific calculations to obtain the optimized results, which are distributed to the participants. This process is repeated until the number of training rounds is reached, or convergence is achieved. Homomorphic privacy protection methods are essential for federated learning to carry out subsequent algorithm development. The standard methods are homomorphic encryption [17] and differential privacy [23].

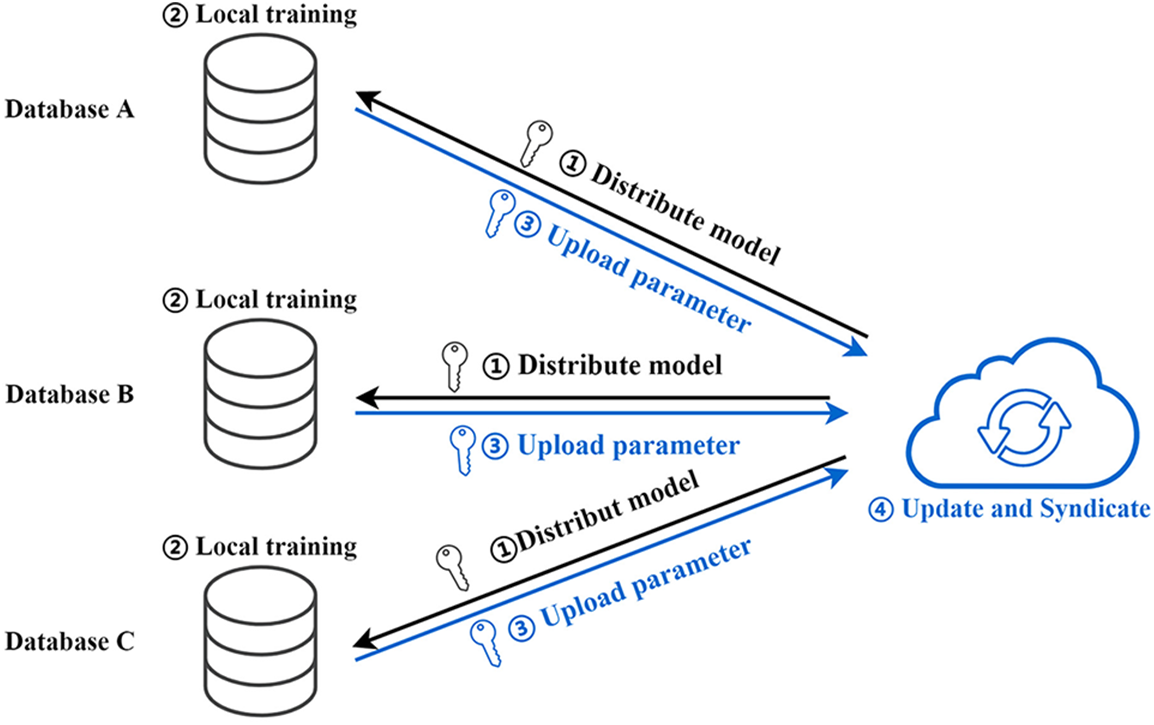
Figure 1: The basic process of federated learning

In addition, another essential factor in federated learning is data. Each participant has different amounts and types of data. The appropriate federated learning algorithm needs to be set up to enable better aggregating gradients, models, and other information according to these circumstances. Depending on the amount and type of data, the main types of federated learning are horizontal federated learning, vertical federated learning, and federated transfer learning.

Horizontal federated learning is also known as sample-partitioned federated learning [33,34]. In this scenario, the participants have the same data attributes and different data samples, represented as horizontal divisions in the data table. The federated learning for the data scenario used in this paper is horizontal. We use the smart wearable device to collect the same physiological data, and each participant has separate data samples from different users.

The mathematical description of the horizontal federated learning scenario is as follows. The set Di is the data owned by a participant, where i is the participant’s index. Then the data category and label category of the participant i will be (Xi,Yi). For two participants, i and j, there are:

Xi=Yj,Yi=Yj,Di∩Dj=∅orDi∩Dj≈∅(1)

Horizontal federated learning implies that each participant has a complete data type. The implementation relies on the results of the training of each participant. Suppose the overall objective function satisfies a linear relationship in a weighted average with the objective function of each participant, such as the MSE, Cross-Entropy, and other types of objective functions. Then the derivatives theoretically also satisfy such linear relationships. The theory is as follows.

Let the overall loss function be F(w), and the loss function of participant k be Fk(w). If the weighted average relationship is satisfied, then:

F(w)=∑pkFk(w)(2)

where pk is the weight assigned to participant k. pk is usually the ratio of the number of nodes nk owned by a participant to the total number of nodes N. By applying both sides of Eq. (2) simultaneously to the gradient of the model parameter w, the relationship between the overall gradient and the gradient of each participant is obtained as follows:

g(w)=∑pkgk(w)(3)

From Eq. (3), the gradient of the overall model can be obtained by a weighted average of the gradients calculated locally by each participant, which is the specific theory of the federal averaging algorithm FedAvg [27]. However, two aspects have been improved in implementing the algorithm: communication dissipation and computational complexity. The former is reduced by increasing the number of rounds trained locally. The latter reduces the computational cost using methods such as stochastic gradient descent (SGD) to simplify the gradient calculation. The improved FedAvg algorithm, which makes it challenging to use gradient averaging due to multiple calculations locally by the participants, uses a model averaging method.

2.2 Related Work

Smart wearable system is an crucial application scenario of social IoT. Compared with other data security scenarios, smart wearable systems do not have powerful computing and storage capabilities on the device side. In contrast, their data are real-time, distributed, and multi-typed. When designing the privacy protection scheme for this scenario, the existing data security technologies need to be improved. The following section describes some federated learning methods suitable for the smart wearable scenario and summarizes the limitations.

•   Asynchronous Federated Learning. Derived from asynchronous distributed learning, asynchronous federated learning enables participants in federated learning to upload training data at any time, rather than having to wait for all participants to finish uploading before computing in one training session. With the distributed and asynchronous nature of data in horizontal federated learning, asynchronous federated learning can save time and enable faster convergence of the model [26].

•   Federated Learning based on Differential Privacy. Differential privacy is homomorphic, and it has lower calculation costs. It can replace homomorphic encryption in federal learning for smart wearable devices for post-processing data. The local differential privacy method is usually used [35,36]. Abadi et al. proposed the Moments Accountant Algorithm to calculate the overall privacy cost of training a model containing a specific noise distribution and demonstrated that choosing the right noise strength and threshold can achieve a smaller privacy loss [37]. Mcmahan et al. proposed a language model based on long short-term memory (LSTM) networks and differential privacy [27], which has less impact on prediction accuracy and allows for user-level differential privacy.

•   Federated Learning in Heterogeneous Environments. There is a heterogeneity problem in federated learning with the non-independent identical distribution of data (Non-IID) [24,25]. If using the traditional FedAvg algorithm, it will have a significant impact on the results of the federated learning [28]. Li et al. conducted an in-depth study of this problem [14], suggesting that this impact can be measured using empirical mode decomposition (EMD) and proposing a strategy for building shared subsets. Zhao et al. provided a comprehensive survey of existing federated learning methods in a heterogeneous data environment and summarized three main approaches [28]: FedProx [38], FedNova [39], and Scaffold [40]. Among them, FedProx added standard terms to the loss function for local training. FedNova changed the way of updating and aggregating the central server. Scaffold adds drift to correct updates during local training. Zhao et al. comprehensively analyze these three methods and give the results in different environments using suppression decision trees for data heterogeneity methods [28].

The above solutions will have problems as follows. The current asynchronous federated learning assigns update weights by time lengthening [26] but ignores the decisive role of the distance of the model parameters. It also suffers from inaccurate time delay compensation, data heterogeneity, high communication costs, and insufficient incentives. Federated learning based on differential privacy reduces the cost of cryptography but still suffers from the loss of accuracy due to added noise. For the federated learning method in heterogeneous environments, it reduces the heterogeneity loss in the federated learning process. But as far as the current study is concerned, it can only be applied to specific scenarios, and its generalizability and portability are low.

3  Scheme Design

The asynchronous federated learning algorithm is emerging to solve the problem of time-consuming issues. It replaces the synchronous model with an asynchronous one, where the participants can join in updating the primary model and obtain the updated parameters at any time. For example, all n participants are trained for a fixed number of iterations. For a synchronous model, they would wait for all participants to finish training and perform one update. For an asynchronous model, they perform n updates in the order in which the parameters are uploaded after training. So, the asynchronous model converges much faster than the synchronous model and can be deployed as needed.

However, new issues arise. Updating for asynchronous federated learning has a different solid mathematical foundation than synchronous models. A common update method for multilayer neural networks is gradient descent, whose primary requirement is to update the original parameters. On the one hand, in asynchronous federated learning, as the master model is constantly being updated, the model parameters to be optimized by the participants are prone to mismatch with the existing model parameters of the central server. On the other hand, synchronous federated learning based on model updates also suffers from data heterogeneity due to the non-independent and homogeneous distribution of the participant’s data. This problem leads to difficulties in converging the aggregated model in the central server after each participant has been trained several times locally. Besides, motivating participants is also a hot issue of federated learning in current research.

We build on previous studies and propose an asynchronous federated learning scheme based on double compensation, which maximizes solving these problems and makes it more practical. The flow and effect of each component in our scheme are shown in Fig. 2.

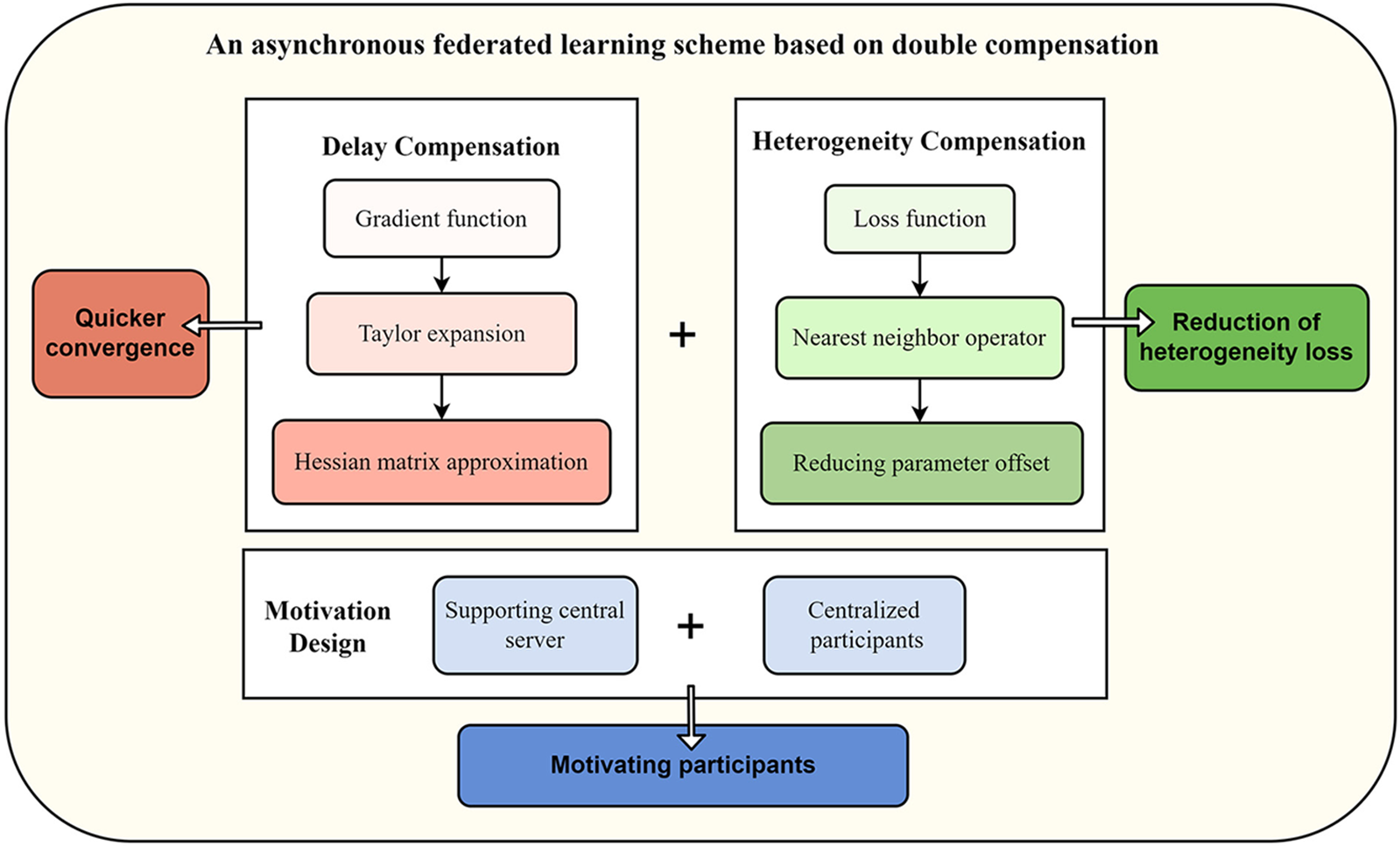
Figure 2: Design of the overall scheme

•   Delay Compensation. We use the DC-ASGD method to compensate for the losses in asynchronous distributed learning [29]. The method calculates the compensation by performing Taylor expansion on the gradient function, performing an approximation of the Hessian matrix in the process. Hence the model converges faster than traditional asynchronous distributed deep learning.

•   Heterogeneity Compensation. To alleviate the data heterogeneity problem, we use the FedProx algorithm for nearest neighbor optimization [38], whose main element is adding the regularized nearest neighbor operator to the loss function to reduce the bias of the model parameters during the training process. It was previously applied to synchronous federated learning after gradient averaging. However, the algorithm can also be used for asynchronous federated learning due to its derivation process's generality and context-specific nature.

•   Motivation Design. The scheme designs a motivating algorithm to enhance the positivity of the participants based on double compensations. The scheme performs a role reversal between the central server and the participants. The entire process is participant-centered, and participants will focus on completing their training. The central server or the coordinator is involved in a supporting role throughout the process. Thus, the motivation of participants is improved for better training.

3.1 Delay Compensation

3.1.1 The Problem of Time Delay in Federated Learning

The delay problem arises from asynchronous federated learning. The basic steps of asynchronous federated learning are as follows. First, the central server sends the initial model parameters to each participant. After local training, the participant individually sends the current model gradient to the central server. Finally, the central server returns the new model parameters directly to the participant after updating.

However, the asynchronous federated learning algorithm suffers from the time delay problem, depicted in Fig. 3. When the participant returns the trained gradient or model parameters at a time, the central server may have already performed multiple rounds of updates. The principle of the gradient descent algorithm is to update the original parameters. Therefore, the model no longer applies to the linear operations represented by FedAvg. The above analysis shows that the parameter changes resulting from the time delay of the training process are the key to preventing asynchronous federated learning from performing direct updates.

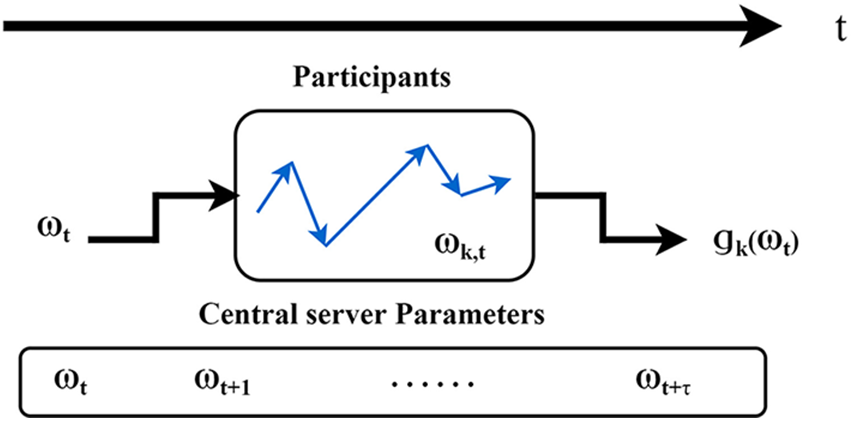
Figure 3: The problem of time delay in federated learning

3.1.2 Limitations of the FedAsync Algorithm

There is less existing research on asynchronous federated learning. Xie et al. proposed the FedAsync algorithm based on model averaging. It compensates for the loss during temporal asynchrony by weighting the parameters uploaded by the participants. The algorithm's update equation is:

ωt=αtωnew+(1−αt)ωt−1(4)

where αt is a variable obtained by performing a function on the time delay. The paper lists several forms of calculating αt: Constant, Hinge, Polynomial, etc.

As the algorithm is based on a failure function, the following problems will arise in its implementation. Firstly, for slower training participants, the algorithm suffers from underweighting. However, the faster training participants can not only participate in adjusting the model parameters several times but also have higher weights. So, the model formed by the final calculation will likely to be more biased towards these participants, resulting in poor model training. Secondly, the paper assumes intuitively that time delay correlates with error. When we revisit the asynchronous federated learning process, it can be found that the error occurs due to the update of the central server parameters. The actual correlation with the error should be the distance between ωt+τ and ωt.

3.1.3 Delay Compensation in the DC-ASGD Method

In the study of distributed deep learning, Zheng et al. propose the DC-ASGD method to compensate for the losses in asynchronous distributed learning [29]. The method calculates the compensation by performing Taylor expansion on the gradient function, performing an approximation of the Hessian matrix in the process. The final update equation obtained is:

gk(ωt+τ)=gk(ωt)−λtgk(ωt)⊙gk(ωt)⊙(ωt+τ−ωt)(5)

Zheng et al. also demonstrate that Eq. (5) can converge [29] faster than traditional asynchronous distributed deep learning. Distributed deep learning [41] and federated learning is similar in some respects, and the above derivation process is universal. We regard it as a more accurate description of the parameter relations for use in the asynchronous federated learning proposed in this paper.

3.2 Heterogeneity Compensation

3.2.1 Data Shorten the Convergence Time of the Model in Federated Learning

The difference between common distributed learning and federated learning lies in the different structures of the data sets. Distributed learning aims to improve the efficiency of machine learning, in which the data is planned to be divided so that each set has roughly the same structure. Federated learning is based on the user's privacy, and no changes can be made to the form of the data owned by the user. There is a Non-IID phenomenon in the data, which creates a data heterogeneity problem.

The different data structures result in the distributed model optimizing in different directions during training, while the linear relationship with the overall model breaks down and does not even converge. As a result, the simple FedAvg algorithm cannot be used. The rationale is explained as follows. In a Non-IID federated learning scenario with two participants, participant a has only two types of data, 1 and 2, and participant b has only two classes of data, 3 and 4. The directions of optimization that participants a and b wish to achieve when training the classification model are:

ωa=argminFa(ω)(6)

ωb=argminFb(ω)(7)

And the optimal solution of the overall model is:

ωcenter=argminFcenter(ω)(8)

There is a linear relationship between Fa(ω), Fb(ω), and Fcenter(ω): Fa(ω)+Fb(ω)=Fcenter(ω). Under the Independent and Identically Distributed (IID) condition, it is straightforward to find that E(ωa)=E(ωb)=E(ωcenter) satisfies the same linear relationship as the loss function calculating the overall model. However, under Non-IID, the expectation values of the three are not the same. The argmin() function is not an ordinary linear operation that cannot be averaged linearly. Therefore, attention needs to be paid to the heterogeneity of federated learning.

3.2.2 FedProx Algorithm

This paper uses the FedProx algorithm for nearest-neighbor optimization to alleviate the data heterogeneity problem [38]. The algorithm’s main element is adding the regularized nearest neighbor operator to the loss function to reduce the bias of the model parameters during the training process. In ρ2‖ωk−ωt‖2 synchronous federated learning, the FedProx algorithm constrains the relationship between the training and global models, reducing heterogeneous losses. Due to the iterative nature of the asynchronous algorithm, the algorithm plays another role. It reduces the losses due to the omission of higher-order terms in the Taylor expansion in 3.1. Also, Dou et al. propose that the update process of FedProx can be simplified by the chain rule as [30]:

gk(ωt)=ρ(ωt−ωk∗)(9)

where ωk∗ is the value of the model parameter for which the FedProx derivative is zero, and the process is referred to as implicit gradient descent. Dou et al. found that the result was applied to synchronous federated learning after gradient averaging. However, the algorithm can also be used for asynchronous federated learning due to its derivation process’s generality and context-specific nature.

3.3 Motivation Design

The scheme designs a motivating algorithm to enhance the positivity of the participants based on double compensations. The motivation for federated learning is a hot issue in current research [42–45]. It arises due to the lengthy training process, complex environment deployment, and excessive training restrictions of federated learning. For example, implementing federated learning in a 2B scenario requires the coordination of all participants to complete the environment deployment and continuous participation in each session.

However, the participants cannot see the training results at any time and can only follow the instructions of the agreement to complete the training within a fixed number of rounds. In the long term, their motivation can be severely dampened, leading to reduced participation and ineffective continuation of federated learning outcomes. The introduction of asynchronous federated learning has reduced the time cost of the federated learning system and made the update-issuance process more flexible. But it still requires participants to deploy a rigorous environment and conduct a fixed number of training rounds. It is a semi-normative learning process overall.

The scheme proposed in this paper performs a role reversal between the two parties. The entire process is participant-centered, and participants will focus on completing their training. The central server or the coordinator is involved in a supporting role throughout the process.

Inspired by Eq. (9) in 3.2.2, we consider ωk∗ a critical parameter with asynchronous nature. ωk∗ is independent of the training time and the number of training rounds, which is only related to the data structure owned by participant k. Thus, ωk∗ is not only applicable to asynchronous federated learning but can loosen the process of federated learning and lift the restriction of a fixed number of training rounds for the participants. At the same time, gradient descent is performed at the central server using the delay compensation in Section 3.1.

It results in a new federated learning scheme: the participants train to approximate convergence and the central server performs gradient descent. The new model has three motivational effects. First, the participants are motivated by being able to train themselves in appropriate values and see the results of their models at any time. Second, the participants’ autonomy increases by lifting the restrictions on training time and several training rounds; Third, participants’ initiative to join federated learning enhances. Because the central server acts as a supporting role to help the participants escape the local minimum trap and overfitting.

3.4 Description of the Scheme

From the illustrations in 3.1 and 3.2 with Eqs. (5) and (9), it follows that with the inclusion of the two compensations, the gradient of the existing model parameter ωt−1 of the central server for the data of participant k is:

gk(ωt−1)=gk(ωτ)−λtgk(ωτ)⊙gk(ωτ)⊙(ωt−1−ωτ)=ρ(ωτ−ωk∗)−λtρ2(ωτ−ωk∗)⊙(ωτ−ωk∗)⊙(ωt−1−ωτ)(10)

A gradient descent at the central server gives that:

ωt=ωt−1−ηgk(ωt−1)(11)

A system overview is illustrated in Fig. 4. It can be seen that the update process involves only the addition, subtraction and dot product operations of the three model parameters ωt, ωt−1 and ωk∗. It avoids finding the first and second-order derivatives and simplifies its update process.

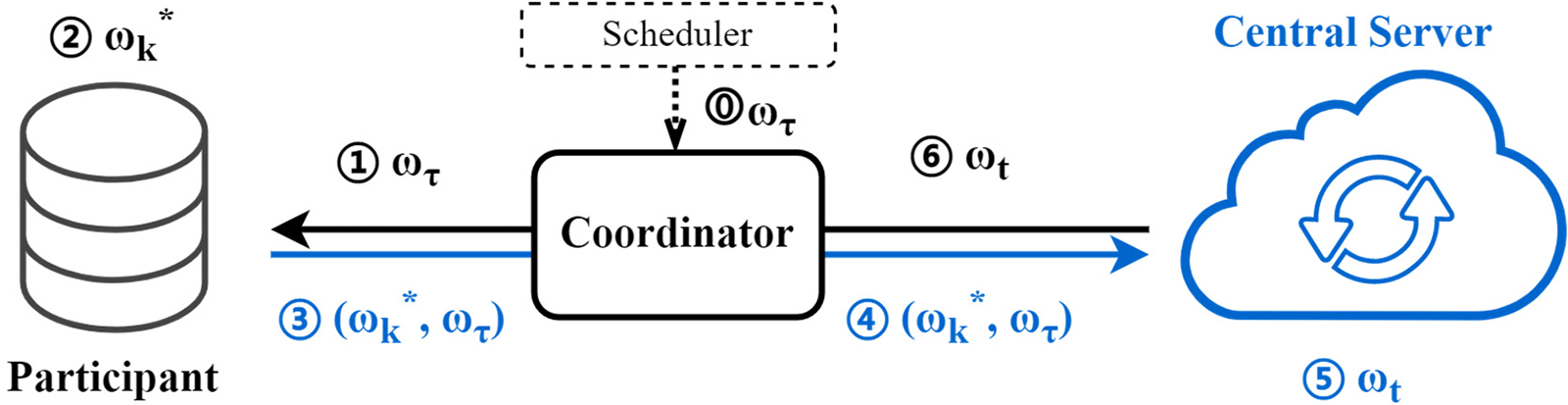
Figure 4: System overview. : scheduler initializes training through the coordinator. ①: participant receives model ωτ from the central server via the coordinator. ②: participant trains locally with a loss function containing the FedProx operator to obtain the parameter ωk∗. It computes local updates as Algorithm 1. ③: participant pushes the locally updated model to the central server via the coordinator. ④: central server receives an updated model from the coordinator. ⑤: central server updates the global model by the Eqs. (10) and (11) and makes it ready to read by the coordinator in step ⑥

The detailed algorithm is shown in Algorithm 1 (Table 1). Notations of the system is shown in Table 2. The central server initializes and distributes the model parameters, which are received and trained locally by each participant. When trained to approximate convergence, the trained parameters ωk∗ and the previously received parameters ωt are packaged and sent to the central server. The central server performs the updates of Eqs. (10) and (11) and returns them to that participant. The algorithm has both the stimulus effect stated in 3.3.1 and the loss compensation function in 3.1 and 3.2. It is suitable for flexible, efficient, and autonomous asynchronous federated learning scenarios.

4  Experiments

4.1 Data Sets

The data used in this paper were collected in the field and post-tabulated from smart wearable devices. Data from smart wearable devices are often private. Yet their data can be used to provide better services to users. The application of federated learning in smart wearable devices is essential. The data contained eight sets of screened characteristics related to cardiorespiratory fitness: rapid heart rate, blood oxygen variance, running time, heart rate rise speed, heart rate reserve, heart rate fall speed, resting heart rate, and maximum heart rate. The labels are derived from ratings of 800/1000 meters running performance on a physical test closely related to adolescent fitness, with four levels Excellent, Good, Pass, and Poor. The size of dataset was 5772 × 9, with a randomly divided training and test set ratio of 7:3.

In the simulation experiments, the training set was divided into M(M={2,4,6}) subsets used to simulate the M participants. To simulate different asynchronous federated learning environments, we randomly generated the computational order of the participant’s participation in the overall model. The starting point for studying more complex deep learning models is the multilayer perceptron network (MLP) [46], and the training model selected for this paper is always the MLP. Besides, all the simulation experiments were done in the python 3.7 environment.

4.2 Experimental Design

The specific setup and description of the simulation experiment are as follows.

•   Our method and the FedAsync method do not have similarities with the existing FedAsync method, and the parameters play different roles. This paper selects multiple sets of parameters for comparison experiments to obtain an overall comparison.

•   In the simulation experiments, we randomly generate a sequential list of participants involved in the overall model update to implement the asynchronous scenario. It can simulate asynchronous learning in a variety of training situations. The list length is set to 30. When the update proceeds to the participant of the sequential list, it will trace back the time or model parameters of the last participant update in the order of the list and follow the algorithm of this paper or FedAsync's steps to perform the update and the evaluation of the loss on the training and test sets.

•   To compare the convergence speed of the two methods more intuitively, we set each participant to enough rounds to allow comparison at the same training level. It satisfies the approximate convergence condition of the proposed method. In the experiments, the number of local training rounds for each participant is set to 1000.

•   For the comparison experiments of the FedAsync algorithm, we choose the more effective hinge update methods, whose failure functions are described in Eq. (12).

Sa,b(t−τ)={1,t−τ1a(t−τ−b)+1,Else(12)

•   In this experiment, the Fedprox operator was added to the loss functions of both algorithms. The Fedprox operator was set as the parameter ρ(ρ=1).

In the model training, we find that the optimal value of the step size η is related to the number of participants M. When M is bigger, the updated step size needs to be smaller. This design is because the training of participants leads to different directions of optimization. The more participants, the more dispersed the direction of optimization and complex the environment is. So, the step size needs to be reduced. We set the step size to η1 when M=1 and ηn=η1/n when M=n.

4.3 Results and Discussion

4.3.1 In Regular Scenarios

For different numbers of participants and training parameters, the loss descent images of this paper’s method and the FedAsync algorithm (FedAsync-hinge algorithm) are shown in Fig. 5. The data of the accuracies are shown in Table 3. As we mentioned in the experimental design in 4.2, we were unable to conduct comparative experiments controlling the same parameters. Therefore, our method sets fixed parameters λ(λ=1). While in the FedAsync-hinge algorithm, we have selected α(α={0.4,0.6,0.8}) for comparison experiments to get an overall performance comparison. Since only the update parameters are changed, the rise and fall of the three FedAsync-hinge’s loss descent angles are synchronized. While the proposed scheme in this paper changes the update method, and its loss descent angles have different starting points from the above three angles.

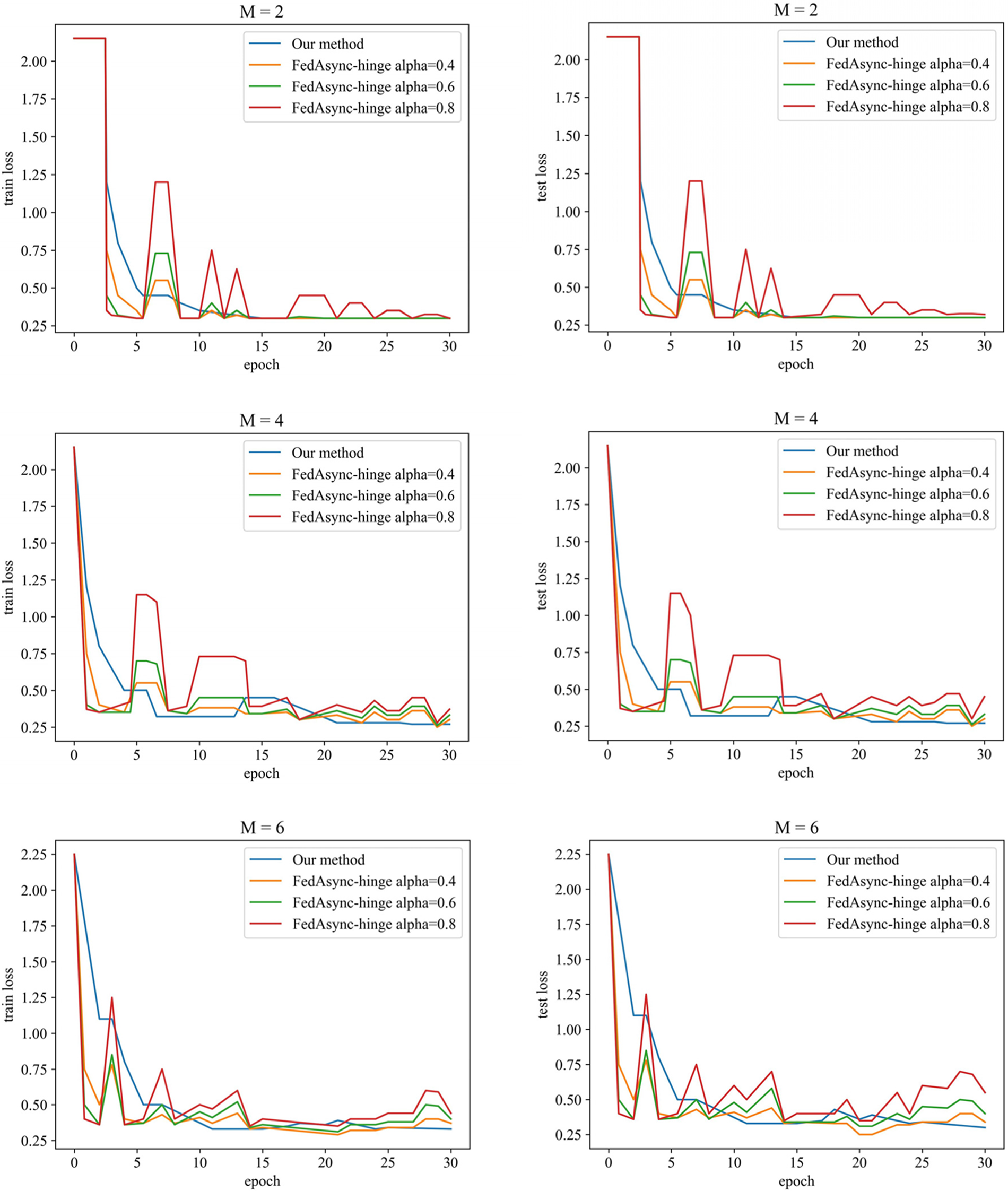
Figure 5: Loss reduction of two algorithms in different situations

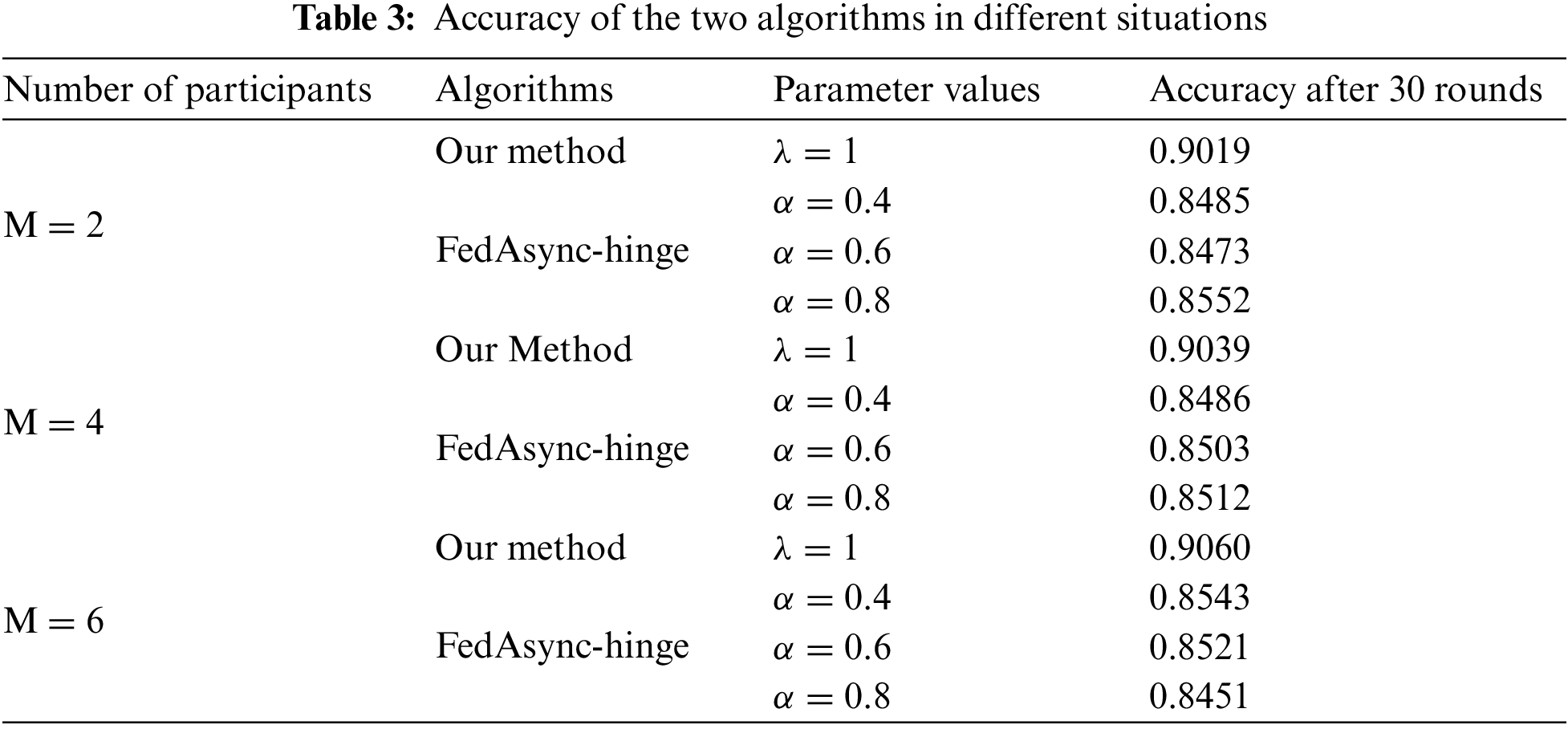
In Fig. 5, we can see that as the number of training rounds increases, the loss descent of this paper is more stable than that of FedAsync, and the final accuracy is higher. In Table 3, the accuracy of our method (after 30 rounds) usually is over 90% and is better than FedAsync by 5%. The results in regular scenarios show that solving the time delay problem can improve training accuracy while smoother the training process. It also proves the superiority of our delay compensation method, which uses the DC-ASGD method [29] based on second-order Taylor expansion as the delay compensation. The smoothness of the training process benefits from the participant being constantly motivated.

4.3.2 In Heterogeneous Scenarios

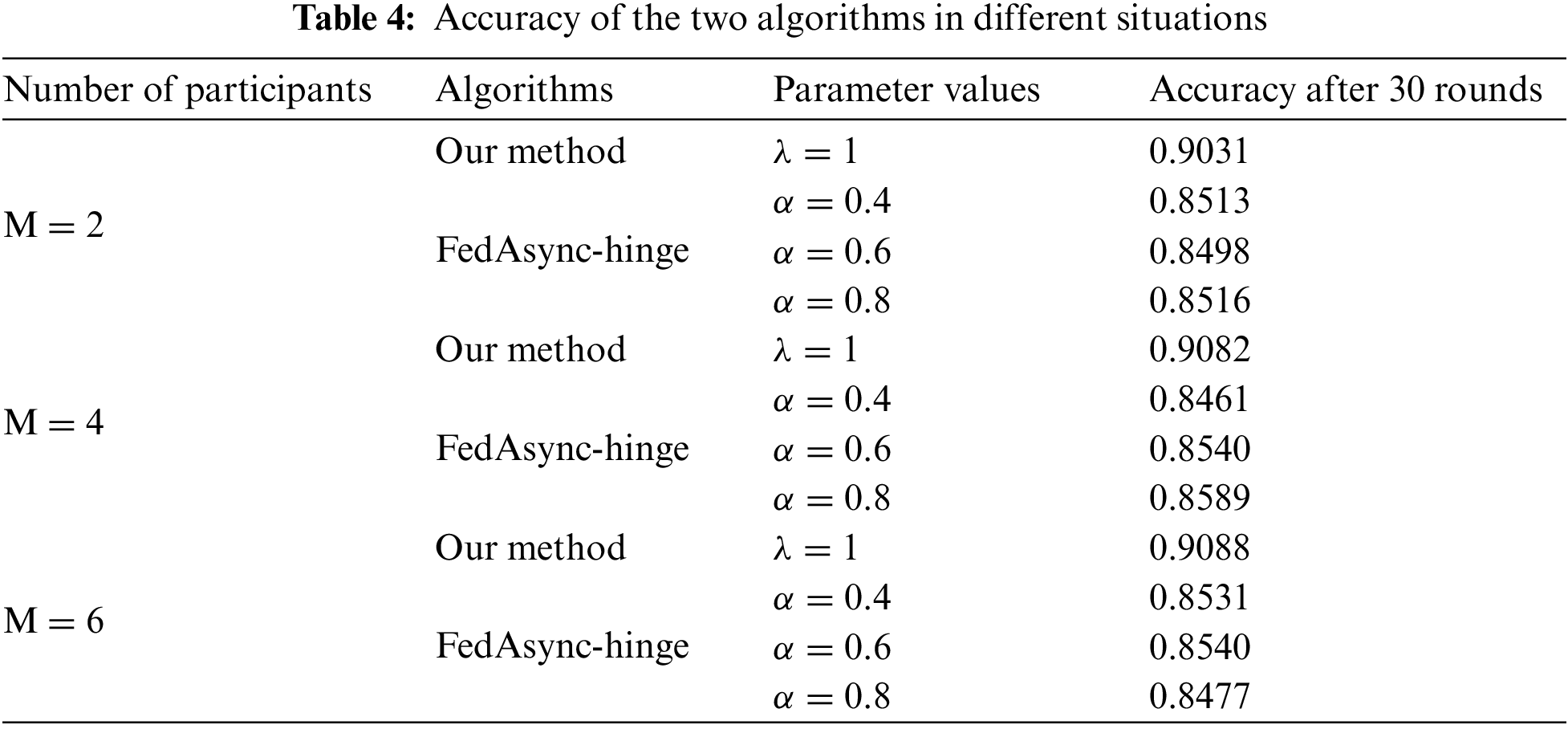
To make the data distribution of each participant as dispersed as possible to form a robust data heterogeneous environment, we group and arrange the datasets according to labels and divide them into participants. In a data heterogeneous environment, the loss reduction images and accuracy of our scheme and FedAsync-hinge algorithm are shown in Fig. 6 and Table 3.

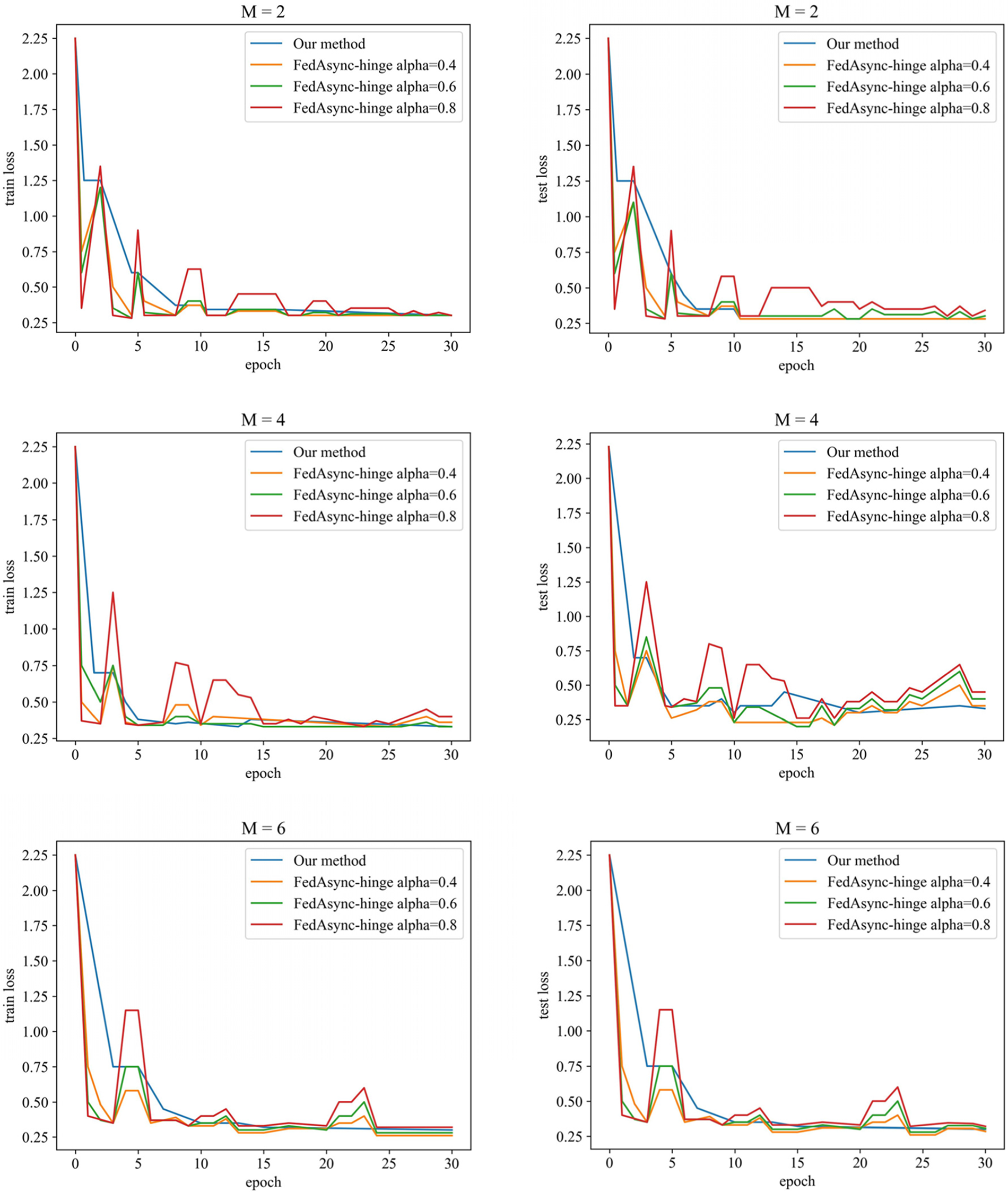
Figure 6: Loss reduction of two algorithms in heterogeneous scenarios

Fig. 6 shows that although the FedAsync-hinge algorithm also contains FedProx operators in its loss function, its performance in a more heterogeneous environment is still different than the scheme in this paper. The reason is that the FedAsync-hinge algorithm is based on a model averaging algorithm that replaces the underlying model during the update process and is more susceptible to the models of participation in a heterogeneous environment. As a result, its overall loss in training can have large ups and downs. In contrast, the scheme in this paper is based on a gradient descent approach, and the loss drop will be smoother. In terms of accuracy after 30 rounds, our method is about five percent higher than the FedAsync-hinge algorithm. Our scheme performs well even in data heterogeneous scenarios because FedProx operators [30] are added to the objective function as the heterogeneity compensation. In addition, our scheme updates the parameters based on swapping the roles of the participant and the central server, which motivates the federated learning processing. This motivation also plays a gainful role in the training process.

4.3.3 Evaluation of Our Scheme

Some measures of classification performance, including Precision, Recall, and F1−Score are calculated as follows.

Precision=TPTP+FP(13)

Recall=TPTP+FN(14)

F1−Score=2Precision∗RecallPrecision+Recall(15)

where TP (True Positive) represents the positive samples that the model correctly predicts. FP (False Positive) represents the negative samples that are correctly predicted by the model, and FN (False Negative) represents the positive samples that the model incorrectly predicts. Thus, Precision represents the percentage of samples correctly predicted as positive by the model, and Recall represents the probability of being correctly predicted among the actual positive samples. F1−Score is their summed average, and the higher its value is, the better the classification performance is. In this paper, we take F1−Score as a classification metric to measure our algorithm. Its results at M = 4 are shown in Table 5. Excellent, Good, Pass, and Poor represent the classification results of body mass data on the smart wearable device and are described in detail in 4.1.

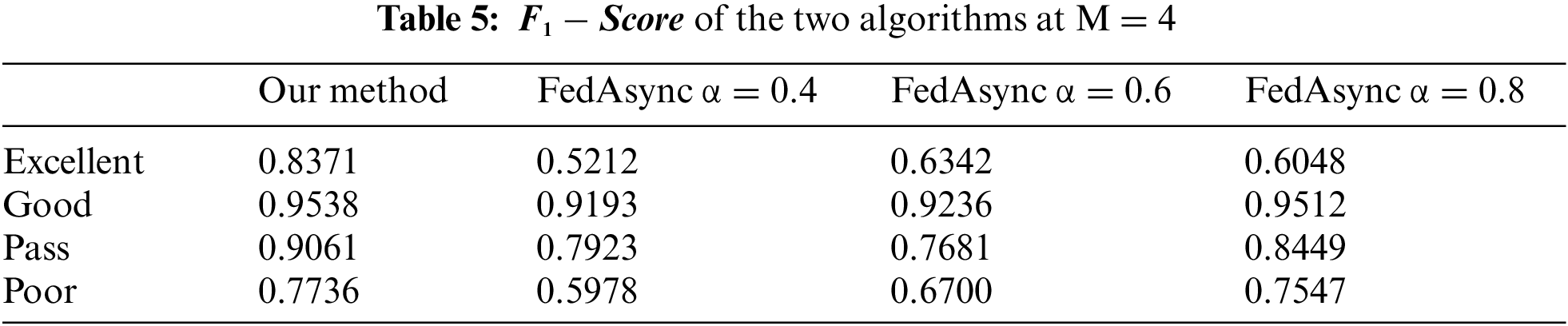
As seen above, the scheme proposed in this paper changes the updated method of federated learning. Both the FedAsync method and our method are related to scalar multiplication and addition operations of tensors. Although our method also involves two dot multiplication operations, the time complexity of both update methods is O(n) for the number of model parameters n. Meanwhile, the time consumed by the update process is small compared to the training time of all parties. For different scenarios, the training time and the overall model convergence time are different for each participant, so it is impossible to compare the time complexity.

In the scenario of this paper, the training loss with time is as Fig. 7. Our method and FedAsync-hinge method drop to the lowest in the 50 s, which shows that there is little difference in the time complexity of the two methods in this scenario. In addition, the loss of our method falls more smoothly during training, without ups and downs. It benefited from the scheme where we added time and heterogeneous compensation for the asynchronous federal learning environment, and the participants were more active in the training process.

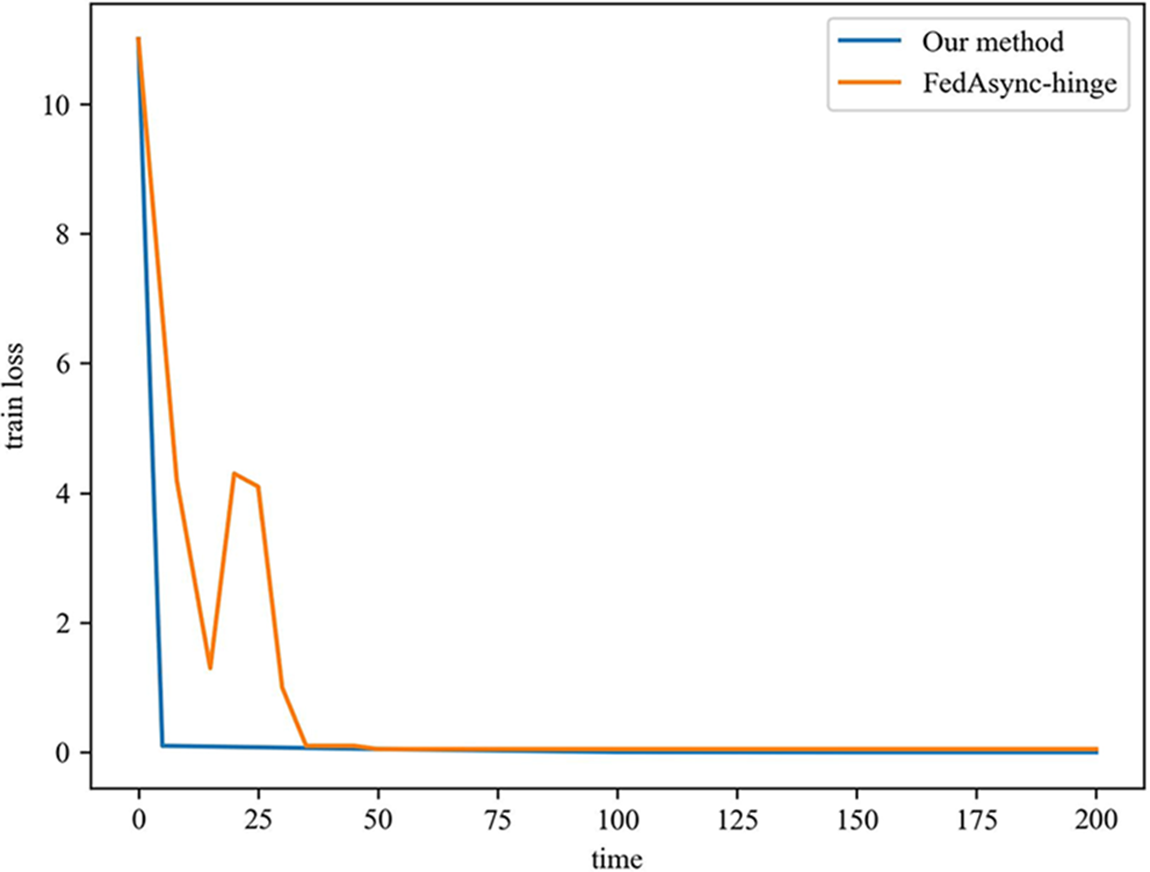
Figure 7: Comparison of two methods in training loss vs. time

In discussing space complexity, all three methods (Our method, the FedAsync method, and the asynchronous federated learning without two compensations) occupy the space of the order of magnitude of the model parameters with a complexity of O(n).

4.3.4 Discussion

This subsection explains the performance of the proposed work. Figs. 5 and 6 show the comparison of the federated learning scheme based on double compensation and the FedAsync algorithm in the smoothness of the decline of the loss value. Tables 3 and 4 compare the accuracy after 30 rounds of the two methods. The above experimental results show that the scheme in this paper has certain advantages over existing methods.

The research highlights of our method are listed as follows.

•   It solves two main problems: the time delay problem and the data heterogeneity problem. Both of these problems can lead to low accuracy.

•   The accuracy is about 5% higher on the training set than the FedAsync algorithm.

•   The convergence of our method is smoother during the training process, and it can adapt better in heterogeneous environments.

In terms of time complexity, the scheme in this paper and the other asynchronous federated learning algorithms only modify the update method of the central server. Therefore, consume the same order of magnitude of time for each round of training. Our method has a mathematical basis, reduces the number of parameters that need to be adjusted, and has good practicality. In contrast to methods such as FedAsync, which averages categories of models, the scheme in this paper uses a gradient descent method with better accuracy and mathematical basis, avoiding the influence of local models of the participants in the process of model averaging.

5  Conclusion and Future Work

In this paper, we proposed an asynchronous federated learning scheme based on double compensation to solve time delay and data heterogeneity problems. Our experiments showed that the proposed scheme converged more smoothly and was more accurate than the existing algorithm. It performs better in scenarios where data from smart wearable devices are analyzed and processed at scale. For federated learning, the current algorithms only consider the case of honest participants and central servers. In the future, we will continue to study the problem of security mechanisms for dishonest participants or central servers in the flexible federated learning environment proposed in this paper.

Funding Statement: This research is supported by the National Natural Science Foundation of China, No. 61977006.

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

1. A. P. Plageras, K. E. Psannis, C. Stergiou, H. Wang and B. B. Gupta, “Efficient IoT-based sensor BIG data collection-processing and analysis in smart buildings,” Future Generation Computer Systems, vol. 82, no. 1, pp. 349–357, 2018. [Google Scholar]

2. D. Li, L. Deng, B. B. Gupta, H. Wang and C. Choi, “A novel CNN based security guaranteed image watermarking generation scenario for smart city applications,” Information Sciences, vol. 479, no. 2, pp. 432–447, 2019. [Google Scholar]

3. Z. Zhang, R. Zhang, C. Chang, Y. Guo, Y. Chi et al., “iWRAP: A theranostic wearable device with real-time vital monitoring and auto-adjustable compression level for venous thromboembolism,” IEEE Transactions on Biomedical Engineering, vol. 68, no. 9, pp. 2776–2786, 2021. [Google Scholar] [PubMed]

4. A. Gavhane, G. Kokkula, I. Pandya and K. Devadkar, “Prediction of heart disease using machine learning,” in 2018 Second Int. Conf. on Electronics, Communication and Aerospace Technology, Coimbatore, India, pp. 1275–1278, 2018. [Google Scholar]

5. H. Masuda, S. Okada, N. Shiozawa, M. Makikawa and D. Goto, “The estimation of circadian rhythm using smart wear,” in 2020 42nd Annual Int. Conf. of the IEEE Engineering in Medicine & Biology Society, Montreal, QC, Canada, pp. 4239–4242, 2020. [Google Scholar]

6. B. Li and A. Sano, “Extraction and interpretation of deep autoencoder-based temporal features from wearables for forecasting personalized mood, health, and stress,” Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies, vol. 4, no. 2, pp. 1–26, 2020. [Google Scholar]

7. G. D. Samaraweera and J. M. Chang, “Security and privacy implications on database systems in big data era: A survey,” IEEE Transactions on Knowledge and Data Engineering, vol. 33, no. 1, pp. 239–258, 2021. [Google Scholar]

8. X. Liu, L. Xie, Y. Wang, J. Zou, J. Xiong et al., “Privacy and security issues in deep learning: A survey,” IEEE Access, vol. 9, pp. 4566–4593, 2021. [Google Scholar]

9. L. Malina, P. Dzurenda, S. Ricci, J. Hajny and G. Srivastava, “Post-quantum era privacy protection for intelligent infrastructures,” IEEE Access, vol. 9, pp. 36038–36077, 2021. [Google Scholar]

10. M. Binjubeir, A. A. Ahmed, M. A. B. Ismail, A. S. Sadiq and M. K. Khan, “Comprehensive survey on big data privacy protection,” IEEE Access, vol. 8, pp. 20067–20079, 2020. [Google Scholar]

11. H. Hu, L. Wang, Q. Hu, Y. Bu and Y. Zhang, “Deep-learning-based mobile group intelligence perception mechanism oriented to user privacy and data security in the internet of things,” IEEE Wireless Communications, vol. 29, no. 2, pp. 60–67, 2022. [Google Scholar]

12. I. Cvitić, D. Perakovic, B. B. Gupta and K. R. Choo, “Boosting-based DDoS detection in internet of things systems,” IEEE Internet of Things Journal, vol. 9, no. 3, pp. 2109–2123, 2021. [Google Scholar]

13. X. Zhang, O. Upton, N. L. Beebe and K. R. Choo, “IoT botnet forensics: A comprehensive digital forensic case study on Mirai botnet servers,” Forensic Science International: Digital Investigation, vol. 32, pp. 300926, 2020. [Google Scholar]

14. B. Li, P. Qi, B. Liu, S. Di, J. Liu et al., “Trustworthy AI: From principles to practices,” arXiv preprint arXiv:2110.01167, 2021. [Google Scholar]

15. J. Cheng, Z. Liu, Y. Shi, P. Luo and V. S. Sheng, “GrCol-PPFL: User-based group collaborative federated learning privacy protection framework,” Computers, Materials and Continua, vol. 74, no. 1, pp. 1923–1939, 2023. [Google Scholar]

16. S. Pouriyeh, O. Shahid, R. M. Parizi, Q. Z. Sheng, G. Srivastava et al., “Secure smart communication efficiency in federated learning: Achievements and challenges,” Applied Sciences, vol. 12, no. 18, pp. 8980, 2022. [Google Scholar]

17. S. Zhang, Z. Li, Q. Chen, W. Zheng, J. Leng et al., “Dubhe: Towards data unbiasedness with homomorphic encryption in federated learning client selection,” in 50th Int. Conf. on Parallel Processing, New York, United States, pp. 1–10, 2021. [Google Scholar]

18. Y. Liu, C. Xu, L. Xu, M. Lin, X. Zhang et al., “Verifiable privacy-preserving neural network on encrypted data,” Journal of Information Hiding and Privacy Protection, vol. 3, no. 4, pp. 151–164, 2021. [Google Scholar]

19. J. Zhao, R. Han, Y. Yang, B. Catterall, C. H. Liu et al., “Federated learning with heterogeneity-aware probabilistic synchronous parallel on edge,” IEEE Transactions on Services Computing, vol. 15, no. 2, pp. 614–626, 2021. [Google Scholar]

20. Z. Wang, G. Xia, J. Chen and C. Yu, “Adaptive asynchronous federated learning for edge intelligence,” in 2021 Int. Conf. on Machine Learning and Intelligent Systems Engineering, Chongqing, China, pp. 285–289, 2021. [Google Scholar]

21. Y. Lu, X. Huang, K. Zhang, S. Maharjan and Y. Zhang, “Blockchain empowered asynchronous federated learning for secure data sharing in internet of vehicles,” IEEE Transactions on Vehicular Technology, vol. 69, no. 4, pp. 4298–4311, 2020. [Google Scholar]

22. B. Gu, A. Xu, Z. Huo, C. Deng and H. Huang, “Privacy-preserving asynchronous vertical federated learning algorithms for multiparty collaborative learning,” IEEE Transactions on Neural Networks and Learning Systems, vol. 33, no. 11, pp. 6103–6115, 2022. [Google Scholar] [PubMed]

23. X. Wu, Y. Zhang, M. Shi, P. Li, R. Li et al., “An adaptive federated learning scheme with differential privacy preserving,” Future Generation Computer Systems, vol. 127, no. 8, pp. 362–372, 2022. [Google Scholar]

24. C. Briggs, F. Zhong and P. Andras, “Federated learning with hierarchical clustering of local updates to improve training on non-IID data,” in 2020 Int. Joint Conf. on Neural Networks, Glasgow, UK, pp. 1–9, 2020. [Google Scholar]

25. H. Wang, Z. Kaplan, D. Niu and B. Li, “Optimizing federated learning on non-IID data with reinforcement learning,” in IEEE INFOCOM 2020-IEEE Conf. on Computer Communications, Toronto, Canada, pp. 1698–1707, 2020. [Google Scholar]

26. C. Xie, S. Koyejo and I. Gupta, “Asynchronous federated optimization,” arXiv preprint arXiv:1903.03934, 2019. [Google Scholar]

27. B. McMahan, E. Moore, D. Ramage, S. Hampson and B. A. Arcas, “Communication-efficient learning of deep networks from decentralized data,” in Proc. of the 20th Int. Conf. on Artificial Intelligence and Statistics, New York, United States, pp. 1273–1282, 2017. [Google Scholar]

28. Y. Zhao, M. Li, L. Lai, N. Suda, D. Civin et al., “Federated learning with non-IID data,” arXiv preprint arXiv:1806.00582, 2018. [Google Scholar]

29. S. Zheng, Q. Meng, T. Wang, W. Chen, N. Yu et al., “Asynchronous stochastic gradient descent with delay compensation,” in Int. Conf. on Machine Learning, Amsterdam, Netherlands, pp. 4120–4129, 2017. [Google Scholar]

30. Y. Dou and X. Yuan, “Federation learning based on implicit stochastic gradient descent optimization,” Journal of Intelligent Systems, vol. 17, no. 3, pp. 488–495, 2021. [Google Scholar]

31. V. Mothukuri, R. M. Parizi, S. Pouriyeh, Y. Huang, A. Dehghantanha et al., “A survey on security and privacy of federated learning,” Future Generation Computer Systems, vol. 115, no. 4, pp. 619–640, 2021. [Google Scholar]

32. M. Aledhari, R. Razzak, R. M. Parizi and F. Saeed, “Federated learning: A survey on enabling technologies, protocols, and applications,” IEEE Access, vol. 8, pp. 140699–140725, 2020. [Google Scholar] [PubMed]

33. A. Hammoud, H. Otrok, A. Mourad and Z. Dziong, “On demand fog federations for horizontal federated learning in IoV,” IEEE Transactions on Network and Service Management, vol. 19, no. 3, pp. 3062–3075, 2022. [Google Scholar]

34. C. Feng, B. Liu, K. Yu, S. K. Goudos and S. Wan, “Blockchain-empowered decentralized horizontal federated learning for 5G-enabled UAVs,” IEEE Transactions on Industrial Informatics, vol. 18, no. 5, pp. 3582–3592, 2021. [Google Scholar]

35. P. C. M. Arachchige, P. Bertok, I. Khalil, D. Liu, S. Camtepe et al., “Local differential privacy for deep learning,” IEEE Internet of Things Journal, vol. 7, no. 7, pp. 5827–5842, 2019. [Google Scholar]

36. J. C. Duchi, M. I. Jordan and M. J. Wainwright, “Local privacy and statistical minimax rates,” in 2013 IEEE 54th Annual Symp. on Foundations of Computer Science, Berkeley, CA, USA, pp. 429–438, 2013. [Google Scholar]

37. M. Abadi, A. Chu, I. Goodfellow, H. B. McMahan, I. Mironov et al., “Deep learning with differential privacy,” in Proc. of the 2016 ACM SIGSAC Conf. on Computer and Communications Security, New York, United States, pp. 308–318, 2016. [Google Scholar]

38. T. Li, A. K. Sahu, M. Zaheer, M. Sanjabi, A. Talwalkar et al., “Federated optimization in heterogeneous networks,” in Proc. of Machine Learning and Systems, Austin, United States, vol. 2, pp. 429–450, 2020. [Google Scholar]

39. J. Wang, Q. Liu, H. Liang, G. Joshi and H. V. Poor, “Tackling the objective inconsistency problem in heterogeneous federated optimization,” in Advances in Neural Information Processing Systems, Online, vol. 33, pp. 7611–7623, 2020. [Google Scholar]

40. M. Noble, A. Bellet and A. Dieuleveut, “Differentially private federated learning on heterogeneous data,” in Proc. of the 25th Int. Conf. on Artificial Intelligence and Statistics, New York, United States, pp. 10110–10145, 2019. [Google Scholar]

41. Z. Tang, S. Shi, X. Chu, W. Wang and B. Li, “Communication-efficient distributed deep learning: A comprehensive survey,” arXiv preprint arXiv:2003.06307, 2020. [Google Scholar]

42. N. Ding, Z. Fang, L. Duan and J. Huang, “Incentive mechanism design for distributed coded machine learning,” in IEEE INFOCOM 2021-IEEE Conf. on Computer, Vancouver, Canada, pp. 1–10, 2021. [Google Scholar]

43. B. Luo, X. Li, S. Wang, J. Huang and L. Tassiulas, “Cost-effective federated learning design,” in IEEE INFOCOM 2021-IEEE Conf. on Computer Communications, Vancouver, Canada, pp. 1–10, 2021. [Google Scholar]

44. M. Tang and V. W. Wong, “An incentive mechanism for cross-silo federated learning: A public goods perspective,” in IEEE INFOCOM 2021-IEEE Conf. on Computer Communications, Vancouver, Canada, pp. 1–10, 2021. [Google Scholar]

45. N. Ding, Z. Fang and J. Huang, “Optimal contract design for efficient federated learning with multi-dimensional private information,” IEEE Journal on Selected Areas in Communications, vol. 39, no. 1, pp. 186–200, 2020. [Google Scholar]

46. L. T. Phong, Y. Aono, T. Hayashi, L. Wang and S. Moriai, “Privacy-preserving deep learning via additively homomorphic encryption,” IEEE Transactions on Information Forensics and Security, vol. 13, no. 5, pp. 1333–1345, 2017. [Google Scholar]