Phase-Field Simulation of δ Hydride Precipitation with Interfacial Anisotropy

1  Introduction

Zirconium alloy is widely used in nuclear fuel rod cladding for nuclear reactors, motivated by excellent mechanical properties, corrosion resistance, and low neutron adsorption cross-section [1]. In nuclear reactors, at constant temperatures, the concentration of hydrogen in a solid solution is lower than the final solid solubility of the hydride precipitate [2]. When the hydrogen concentration reaches its solid solution limit, the zirconium alloy absorbs hydrogen to produce brittle δ hydride [3]. The morphology affects the ductility and fracture toughness of zirconium alloy materials [4,5]. In the past decade, researchers have made great efforts to observe the morphology of δ hydride using high-resolution electron microscopy or bright field transmission electron microscopy, namely the morphology of needles and platelets [6,7]. Meanwhile, different environmental variables can also affect the distribution state of δ hydride. For example, the introduction of grain boundaries [8], internal stress [9], and external load [10] would alter the reorientation behavior [11] and precipitation habit plant of circumferential and radial hydride, resulting in a small amount of radial hydride precipitation at the grain boundary has the orientation relationship of {101¯7}α//{111}δ and radial δ hydride is precipitated when applied load.

The nature of the interface between the δ hydride and the zirconium matrix affects the morphology and orientation of the precipitate phase. However, due to the spatial and temporal limitations of the experimental process, it is difficult to study and analyze the relationship between the nature of the interface and the morphology of the precipitate phase in a continuous and quantitative manner. Therefore, the effect of interfacial anisotropy on the morphology of δ hydride precipitation has been less studied.

The phase-field method is a good remedy for the inability of experiments to observe the phase transformation process dynamically and continuously [12–14]. This method has been used to simulate and predict the microstructure and tissue morphology evolution during the phase transformation of materials by solving the controlling equations [15–17]. It helps to understand the precipitation mechanism of solid phase change processes [18–24]. The phase-field method has been widely used to simulate the microstructure of hydride in zirconium alloy [25–29]. Usually, the majority of research on stress-induced (internal stress and external load) nucleation, growth, stacking, and reorientation behavior of δ hydrides [30–33]. However, these theoretical achievements were based on a coherent interface between the precipitate phase and the matrix phase.

In fact, due to the difference in crystal structure between the hexagonal close-packed (HCP) matrix phase and the face-centered cubic (FCC) δ hydride precipitate phase. The semi-coherent or non-coherent interface produces interfacial energy difference, resulting in interfacial anisotropy, which ultimately affects the morphology of the δ hydride precipitated. Anisotropy has been extensively studied by previous authors. Ghosh et al. [34] used a three-dimensional phase field method to study the microstructural evolution of binary eutectic alloy with interphase boundary anisotropy during the solidification process. Cai et al. [35] simulated the critical orientation angle of the anisotropic structure of a needle-like Al4C3. Mao et al. [36] considered the anisotropic interfacial energy and elastic interaction to simulate the evolution of the precipitation morphology of β″ in Al-Mg-Si alloy. In this study, by incorporating an anisotropy function related to the precipitation angle in the interfacial energy and interfacial mobility, this paper aims to reveal the effect of anisotropy on the precipitation morphology of δ hydride in zirconium alloys.

2  Phase-Field Model

The phase-field simulation for δ hydride precipitation coupled with interfacial anisotropy in this work is based on the EasyPhase software package, a comprehensive phase field theory software package developed by Professor Yuhong Zhao’s research group [37]. The phase-field method expresses the precipitation process of the phase through continuous diffusion of the interface and uses both conserved field variables and non-conserved field variables to describe the microstructure evolution of the system [38,39]. The conserved field variable C is controlled by the Cahn-Hilliard equation [40] and the non-conserved field variable ηp is controlled by the Allen-Cahn equation [41], as shown in Eqs. (1) and (2) [42].

Cahn-Hilliard phase-field equation:

∂C∂t=∇⋅(M∇δFδC)+ξ(1)

Allen-Cahn phase-field equation:

∂ηp∂t=−L(φx,φy)δFδηp+ζp(p=1,2,3)(2)

where C is the concentration field indicating the composition. ηp is the order parameter, p=1,2,3 representing three different directional variants of hydride, where variants 2, 3 are obtained by rotating variant 1 by 120° and 240°. M is the diffusion mobility [43] of hydrogen atoms in zirconium. F is the total free energy of the system. L(φx,φy) is the interfacial mobility, φx, φy are the angles between the normal direction of hydride precipitation and the x and y axes, respectively. ξ and ζp are noise terms satisfying the up and-down dissipation theorem.

Total free energy of the system [44]:

F=∫[ f(C,ηp)+∑pκp2(∇ηp)2+λ2(∇C)2+Eel ]dV(3)

where F is the total free energy. f(C,ηp) is the chemical free energy density. The second and third terms are gradient energy. κp and λ are the gradient coefficients. κp and λ are positively correlated with γs/l in Shi et al. [45], where γs is the interfacial energy between the hydride and matrix phase, l is the interfacial thickness. Eel is the strain energy term. V is the system volume.

The chemical free energy density f(C,ηp) is expressed using a Landau polynomial:

f(C,ηp)=A12(C−C1)2+A22(C2−C)∑pηp2−A34∑pηp4+A46∑pηp6+A5∑p≠qηp2ηq2+A6∑p≠q,p≠rηp4(ηq2+ηr2)+A7∑η12η22η32(4)

where A1–A7 are image-only parameters with positive values. A1–A4 give locally smaller values of f at C=C1, ηp=0 and C=C2, ηeq=0, where ηeq is the equilibrium value of ηp in the ordered phase. A5–A7 ensures that two or more different variants are not produced at the same position. p,q,r are different variants of the hydride. C1 and C2 have the chemical free energy density minimum points at η=0 and η=±1, respectively.

The strain energy can be calculated according to the Khanchaturyan theory of micro-elastic strain energy [46–48]:

∫EeldV=12∫VCijklεij0(r)εkl0(r)d3r−12VCijkl∫Vεkl0(r)d3r∫Vεkl0(r′)d3r′−12fVd3k(2π)3niσ~ij0(k)Ωjk(n)σ~kl0(k)∗nl−σija∫Vεij0(r)d3r−V2Sijklσijaσkla(5)

where r is the space vector. fV denotes the infinite inverse space in which the integral f is computed as the principal value excluding k=0. εij0 is the hydride intrinsic strain. Ωjk(n) is the Green’s function tensor. Sijkl is the elastic flexural tensor. σ~ij0(k)=Cijklε~kl0(k), where ε~kl0(k) is the Fourier transform of εkl0(r). σija is the applied stress.

The lattice difference between the FCC δ hydride and the HCP matrix phase could lead to anisotropy. The anisotropic interfacial energy formulas (6) and (7) [49–51] are coupled by considering the anisotropy of semi-coherent and non-coherent interfaces (Due to the large lattice mismatch in the interface, this paper has only considered semi-coherent and non-coherent interfacial states when performing simulations in the 2D plane):

γs=γ1+(γ2−γ1)A(φx)(6)

A(φx)={ π2−φxπ2 (0≤φx≤π2)φx−π2π2(π2<φx≤π)(7)

where A(φx) is the anisotropic function, φx is the angle between the direction normal to the precipitation direction and the x-axis, as shown in Fig. 1. The anisotropic functions A(φx) in polar coordinates is shown in Fig. 2. A(φx)=1 for 0° direction, φx=0, which corresponds to the non-coherent interface and A(φx)=0 for 90° direction, φx=π2, which corresponds to the semi-coherent interface. The orientation relationship between the precipitate phase and the matrix phase in the x-axis direction [11¯0]δ||[112¯0]α compared to the orientation relationship in the y-direction [110]δ||[0001]α is the habit surface. Therefore, it is reasonable to consider a semi-coherent interface in the x-axis direction and a non-coherent interface in the y-axis direction. γ1,γ2 are the semi-coherent and non-coherent interfacial energy, respectively. It is calculated by first principles that γ1=3.8J/m2, γ2=7.4J/m2.

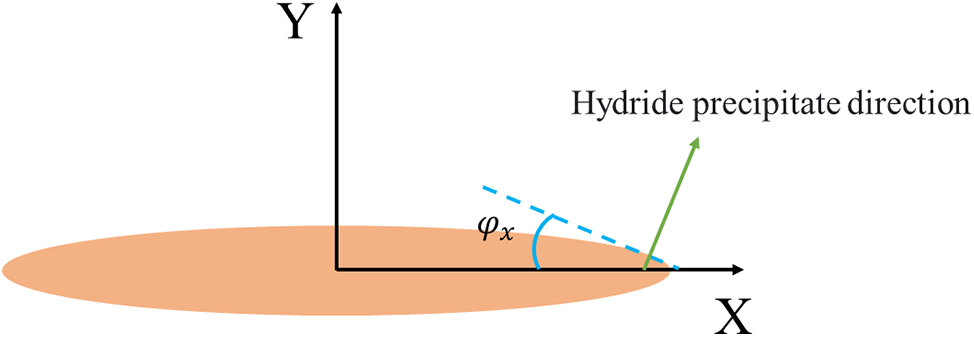
Figure 1: Schematic representation of the angle φx between the direction normal to the hydride precipitation direction at a point and the x-axis

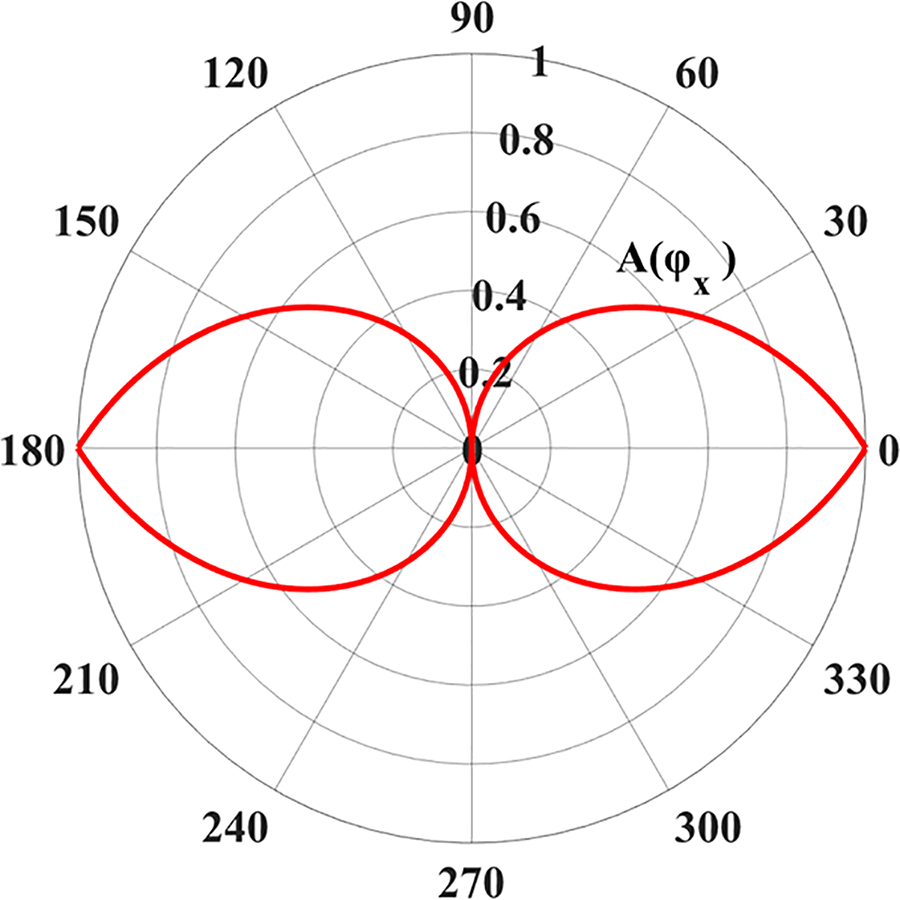
Figure 2: Anisotropic functions A(φx) in polar coordinates

In the KKS (Kim, Kim, and Suzuki) phase field model, interfacial mobility is related to interfacial energy [52]. The interfacial mobility L [53,54] is affected by the interfacial anisotropy. Following Hu et al. [55] who defined the anisotropic interfacial mobility using segmented functions, the anisotropic interfacial mobility L(φx,φy) is defined as follows:

L(φx,φy)=L0{ Ix(cos(φx))2+Iy(cos(φy))2   π2−φ0≤φx≤π2+φ01  { 0≤φx<π2−φ0π2+φ0<φx≤π(8)

φx=arcos(∂η∂x|∇η|),φy=arcos(∂η∂y|∇η|),|∇η|=(∂η∂x)2+(∂η∂y)2(9)

where Ix is the x-axis mobility coefficient and Iy is the y-axis mobility coefficient, representing the weighting of the x- and y-axis mobility, respectively. Ix=1.0, Iy=0.2, which is not fixed but can be adjusted according to actual data. L0 is the interfacial mobility coefficient.

The relevant parameters are shown in the following Table 1:

3  Simulation Results and Analysis

The crystal structure and lattice constant of the hydride precipitate phase and matrix phase are different, resulting in a semi-coherent or non-coherent interface. Differences in interfacial states will produce differences in interfacial energy, resulting in interfacial anisotropy of the hydride, which affects the precipitate morphology and orientation of the hydride. Fig. 3 is a schematic diagram of the hydride variants with different precipitation orientations. The formation of δ hydride favors the transition from HCP to FCC, splitting the stress-free transformation strain into three components and giving rise to three different structural variants obeying a triple symmetry relationship [58]. Variant 2 and variant 3 are obtained by rotating variant 1 by 120° and 240°, respectively. Fig. 4 shows the simulation diagram and experiment diagram of δ hydride. Periodic boundary conditions are used. The metallographic photo of hydride in zirconium alloy tubes is shown in Fig. 4d. The hydride observed in the experiment has different precipitated orientations. Fig. 4a shows the precipitation of slate-shaped hydride in the x-axis and y-axis directions under the action of isotropic interfacial energy. Fig. 4b shows the needle-like morphology of variant 1 hydride precipitation and variant 2 and variant 3 hydride precipitation parallelogram morphology under the action of anisotropic interfacial energy and interfacial mobility. Fig. 4c shows anisotropy hydride precipitation morphology at the concentration order parameter field. The formation of the hydride tip is due to the uneven distribution of hydrogen concentration in the matrix under the action of tensile and compressive strain, and there are local enrichment areas. The hydrogen content at the hydride tip is less, which is not enough to continue the nucleation of the hydride, so the shape of the tip is formed [23]. In the case of interfacial isotropy hydride without applied stress, the trend of hydride growth in the x-axis direction is significantly larger than that in the y-axis direction. X-axis direction is the habitual direction of δ hydride, and to minimize the stress around the matrix, the hydride tends to precipitate in the x-axis direction growth. However, there is no difference in precipitate orientation between the different variants. The anisotropic hydrides are less dependent on the plane of inertia, and the trend in precipitation growth of variant 1 hydride is not significant compared to that of variant 2 and variant 3 hydrides. The anisotropic hydrides have different precipitation orientations, which is consistent with experimental results and a more realistic situation, so anisotropy must be introduced. Subsequent studies have been directed towards anisotropy.

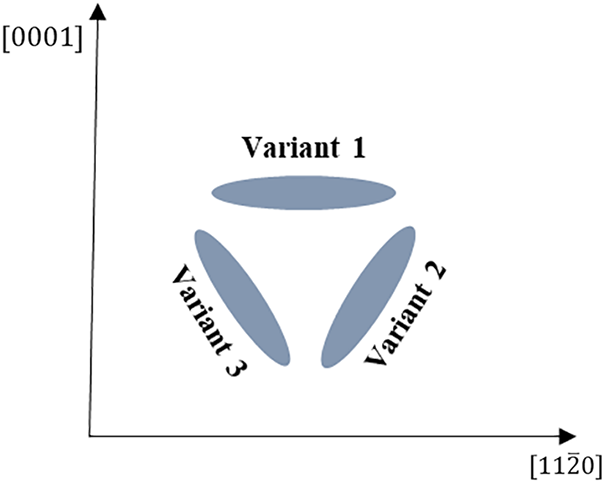
Figure 3: Schematic diagram of different precipitation orientation variants of hydrides

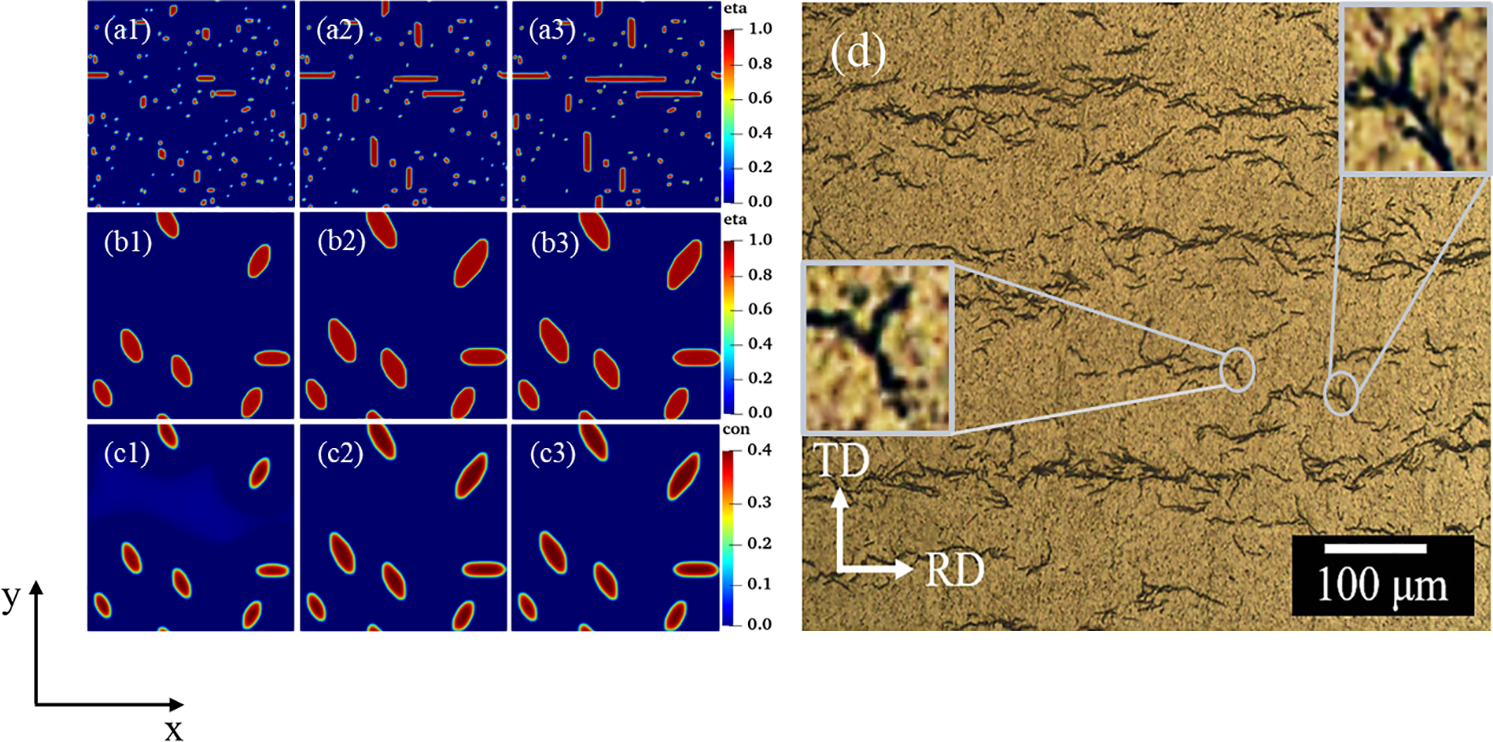
Figure 4: δ hydride simulation diagram and experiment diagram. (a), (b), (c) Hydride simulation diagram at time steps t = 4000, t = 10000, and t = 20000, (a1–a3) Isotropy hydride precipitation morphology. (b1–b3) Anisotropy hydride precipitation morphology at structural order parameter field. (c1–c3) Anisotropy hydride precipitation morphology at concentration order parameter field. (d) Hydride metallographic photograph of zirconium alloy tubes [59]

To obtain accurate hydride morphology characteristics, the different variants were simulated and tested individually. Fig. 5 shows the precipitated morphology, equivalent forces diagram, and the circumferential length and radial height curves with time for different time steps of the individual δ hydride. With the nucleation sites in the middle region. Fig. 5a shows the δ hydride of variant 1, which exhibits needle-like morphology with circumferential length (AB) and radial height (CD) of about 1215 and 345 nm at t = 20000, and aspect ratio (AB/CD) of 3.52. Fig. 5b shows the δ hydride of variant 2, which exhibits a parallelogram-like morphology with a circumferential length (AB) of about 1252 nm and a radial height (CD) of about 355 nm at t = 20000, with an aspect ratio of 3.53 and hydride precipitated deflection angle of θ1 =19°. Variant 3 is symmetrical with variant 2 and precipitates similar morphology, as shown in Fig. 5c. The circumferential length (AB) of variant 3 is approximately 1237 nm and the radial height (CD) is approximately 340 nm at time step t = 20000, with an aspect ratio of 3.64 and precipitated deflection angle of θ1 = 19°. As shown in Figs. 5d and 5e, the circumferential length is linear with time, and the radial height has a stepped change, which is due to the precipitation of hydride in a lateral stacking pattern [60], and there is an interval when measuring the radial height at a certain time. The equivalent stress is calculated using the VonMises equation [61], defined as:

σVM=12[(σxx−σyy)2+(σyy−σzz)2+(σzz−σxx)2]+3σxy2(10)

where σxx is the positive stress in the x-direction. σyy is the positive stress in the y-direction. σzz=v(σxx+σyy), where v is the Poisson’s ratio. σxy is the tangential stress. The stress of the acicular hydride is concentrated at the tip, the stress value in the inner and middle regions of the hydride is small, and the stress state inside the hydride is evenly distributed. The stress in the matrix on both sides of the hydride increases from the middle to the tip, and the stress in the matrix presents a cross-like distribution. The growth state and stress state of parallelogram-like shaped hydride is complicated. Stress in the matrix is concentrated at the tip, the middle region of the hydride is low, and the stress value on both sides is high. The stress state of the hydride in the matrix gradually decreases and then increases from both sides to the tip region, and the stress in the matrix shows a lateral H-shaped distribution.

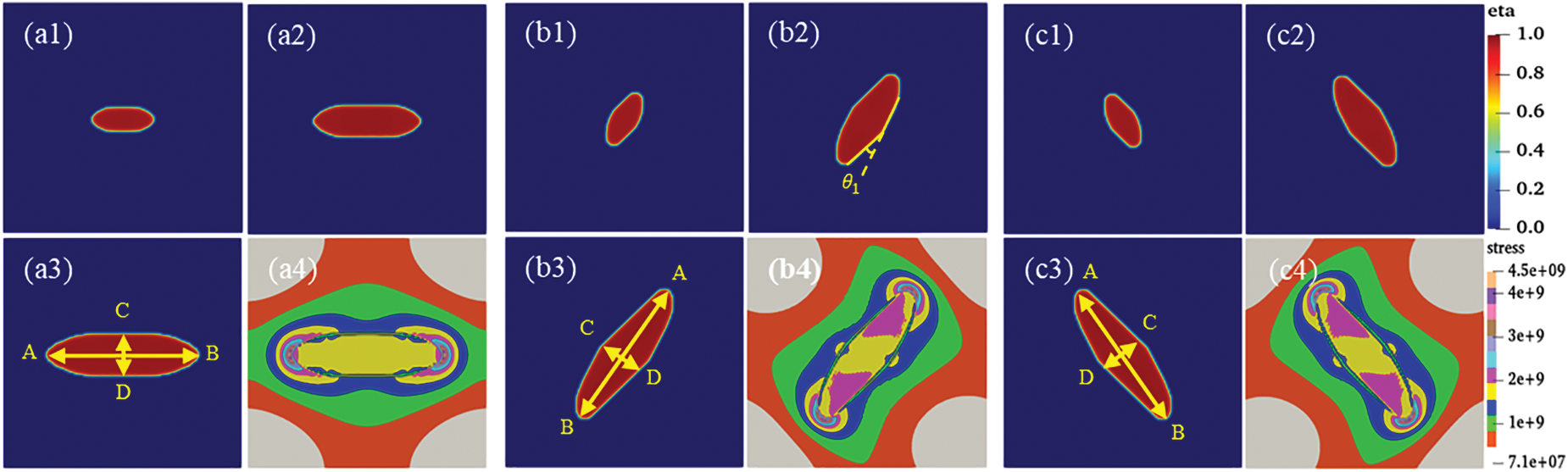
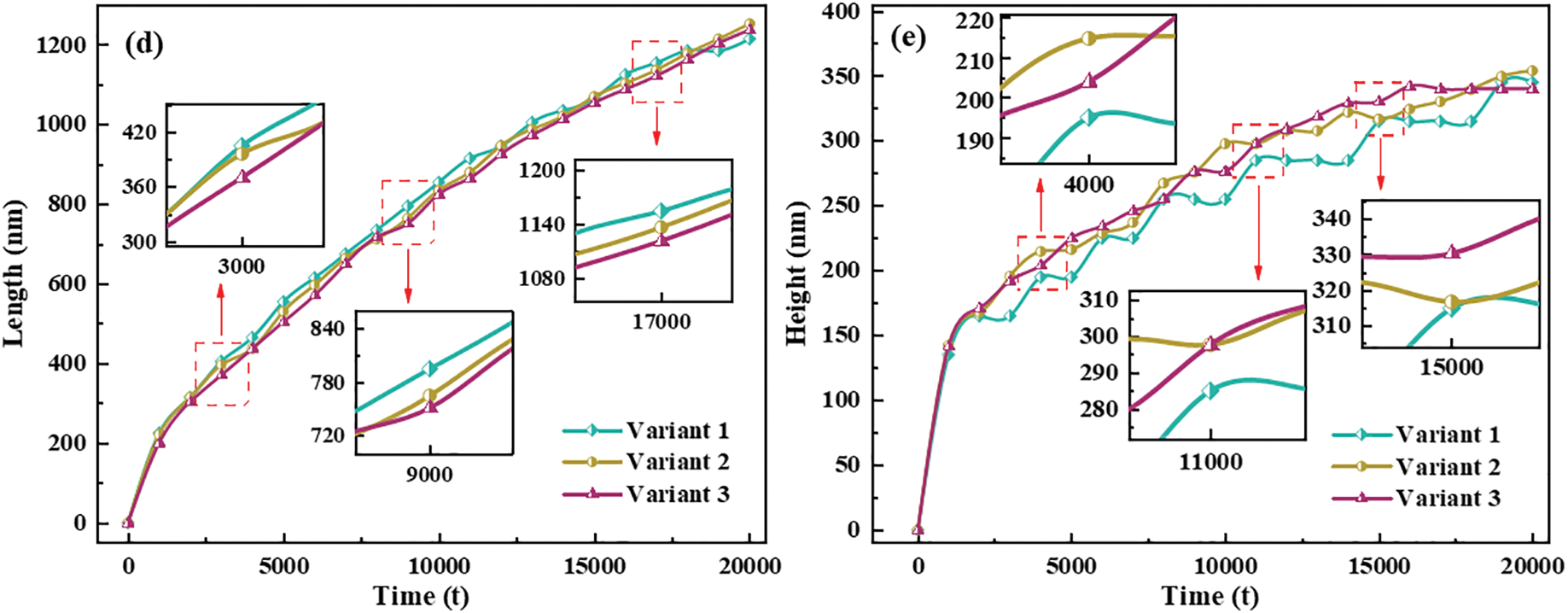
Figure 5: Individual hydride morphology, equivalent force diagram, and circumferential length and height variation curves for different time steps t. (a, b, c) Morphology of variant 1, variant 2 and variant 3, (a1, b1, c1) t = 4000, (a2, b2, c2) t = 10000, (a3, b3, c3) t = 20,000, (a4, b4, c4) Equivalent force diagram at t = 20,000. (d) Variant 1, variant 2, and variant 3 circumferential length (AB length) curve with t. (e) Variant 1, variant 2, and variant 3 radial height (CD height) curve with t

In general, the interfacial mobility coefficient is closely related to the interfacial energy. Therefore, anisotropic interfacial energy leads to the anisotropy of interfacial mobility. The change of hydride precipitated morphology is observed by changing the ratio of x and y-axis coefficients in interfacial mobility. Fig. 6 shows the hydride morphology and equivalent force diagrams for different anisotropic mobility ratios. The variation curves of circumferential length and radial height and aspect ratio of hydride with anisotropic mobility ratio are shown in Fig. 7. As the y-axis mobility ratio increases, the circumferential length peaks significantly at Iy=1.0, showing a process of increase and then decrease and finally increase. The radial height variation fluctuates less, but has the same trend. The circumferential length is approximately 675 nm for variant 1, variant 2 about 630 nm, and variant 3 about 520 nm at Iy=1.0. The radial height is approximately 160 nm for variant 1, variant 2 about 220 nm, and variant 3 about 190 nm at Iy=1.0. The variation in the aspect ratio of variant 1 hydride compared to variant 2 and variant 3 tends to be greater. Variant 1 has an aspect ratio of about 2.7 at Iy=0.2 and about 4.2 at Iy=1.0. Variant 2 and variant 3 have aspect ratios of about 2.2 and 2.1 at Iy=0.2 and about 2.8 and 2.7 at Iy=1.0, respectively, which is a smaller difference. The growth orientation of the hydride is gradually tilted toward the y-axis, and the variation of the hydride precipitated deflection angle with the ratio of anisotropic mobility is shown in Fig. 8. As the anisotropic mobility of variant 2 increases, the first precipitated deflection angle θ1 tends to decrease. The second precipitated deflection angle θ2 tends to increase. But the angle changes are small, with θ1 varying in the range of about 17°–18.5° and θ2 varying in the range of about 26.5°–28°. Variant 3 only precipitated the deflection angle θ1, which varies over a wide range of approximately 40°–45°. The stress is concentrated at the tip of the hydride, and the internal stress of variant 1 hydride is more powerful than variant 2 and variant 3 hydrides. Fig. 9 shows the curve of the equivalent stress of the hydride with time for different anisotropic mobility ratios. Stress around the hydride can hinder the growth of the precipitate phase. With the increase of anisotropic interfacial mobility, the rate of increase of equivalent stress decreased, then increased, and finally decreased. The rate of hydride precipitation showed a trend of acceleration, then slowdown, and then acceleration. Later the hydride growth state is stable, the equivalent stress values for different ratios also tend to be stable with little difference.

Figure 6: Hydride morphology and equivalent stress diagrams for different anisotropic interfacial mobility ratios at time step t = 20000. (a1) Ix=1.0, Iy=0.2, (a2) Ix=1.0, Iy=0.5, (a3) Ix=1.0, Iy=1.0, (a4) Ix=1.0, Iy=1.5, (a5) Ix=1.0, Iy=2.0. (b1–b5) Equivalent stress diagrams

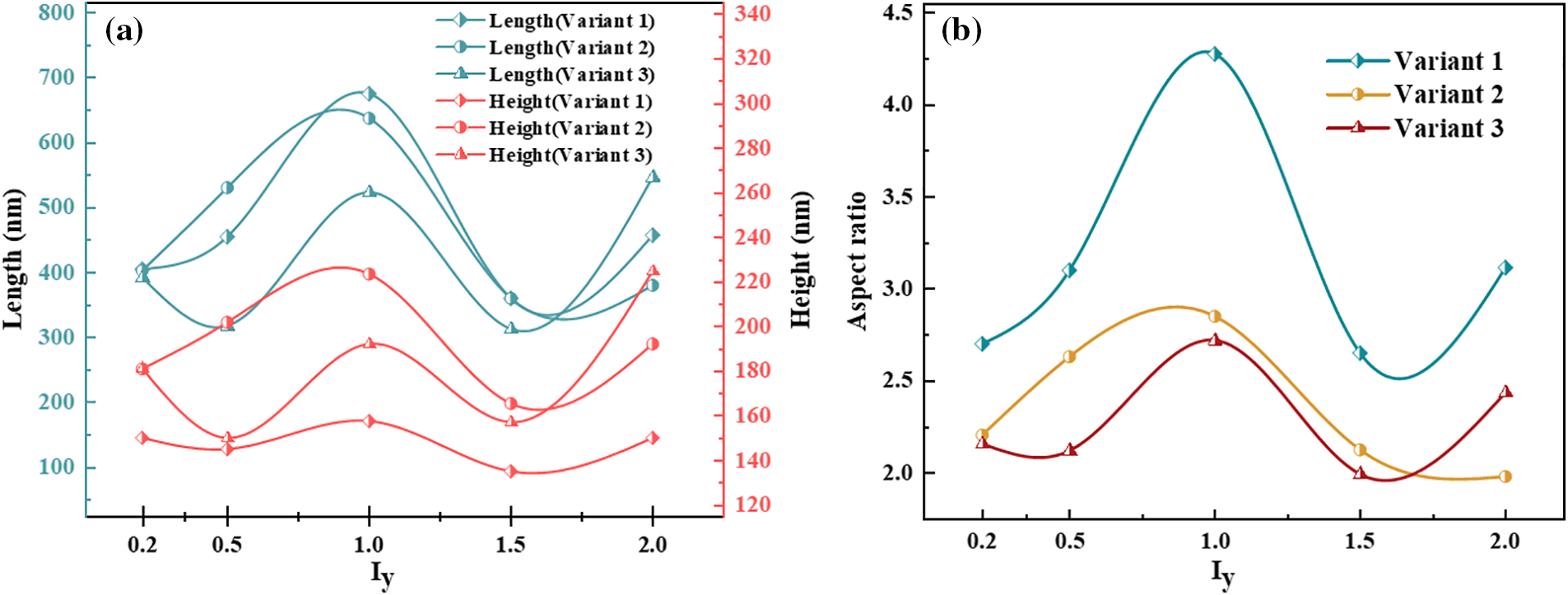
Figure 7: Variation of circumferential length and radial height and aspect ratio of hydride with anisotropic mobility ratios at time step t = 20000

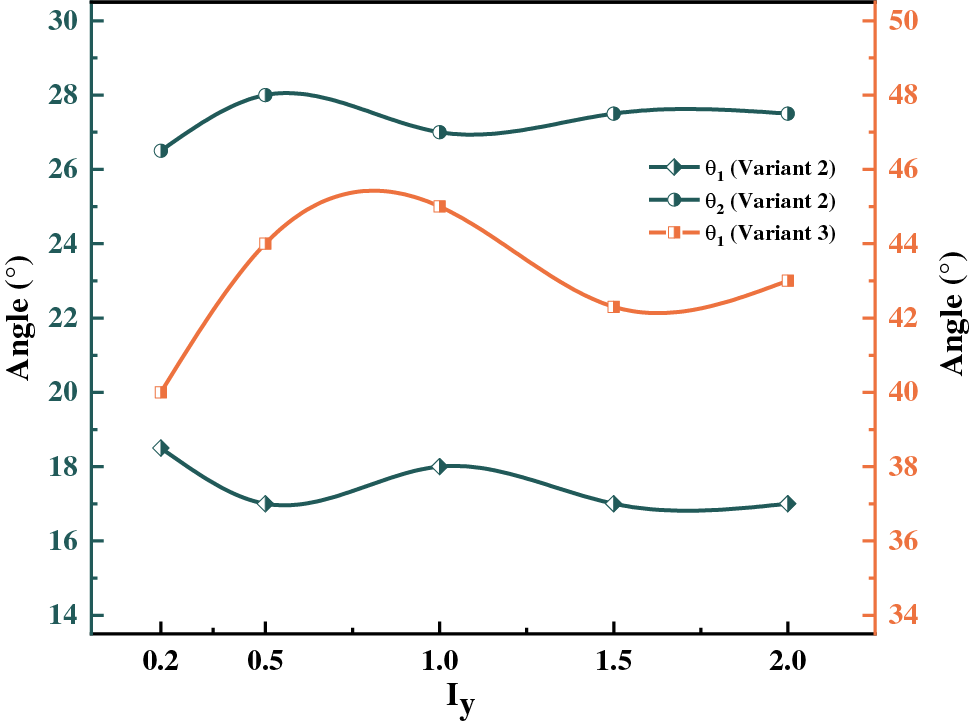
Figure 8: Variation curve of hydride precipitated deflection angle with anisotropic mobility ratios at time step t = 20000

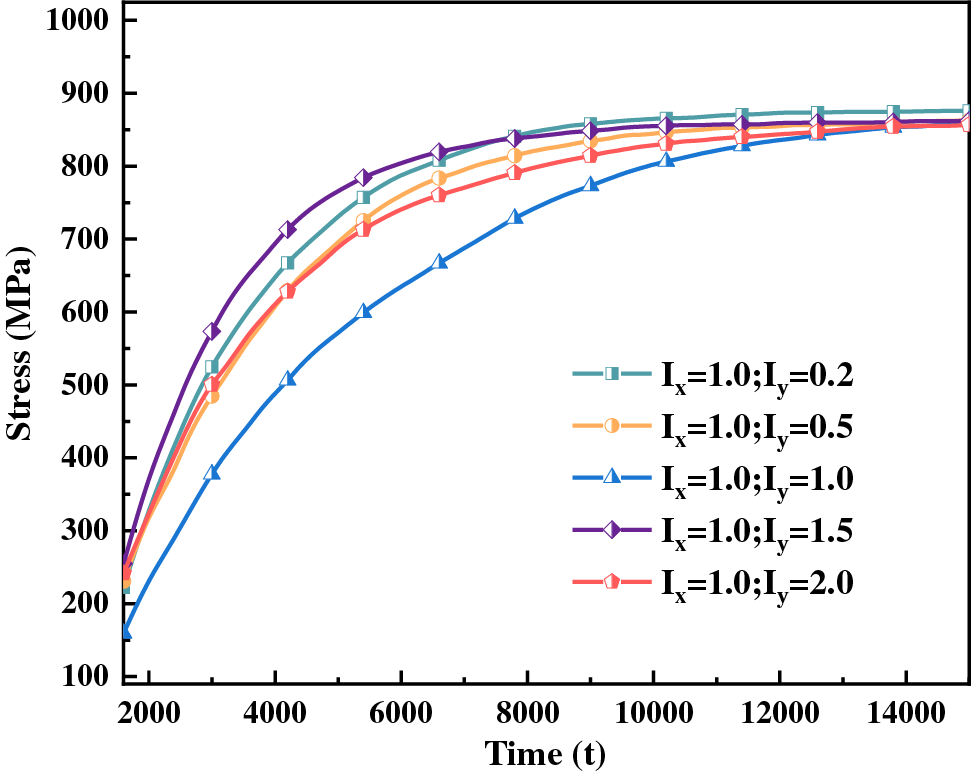
Figure 9: Hydride equivalent stress curve with time for different anisotropic interfacial mobility ratios

The magnitude of energy will affect the nucleation and growth of hydride. The gradient energy coefficient is related to interfacial energy, and the magnitude of anisotropic interfacial energy will affect the variation of gradient energy. Under the action of anisotropic interfacial energy, hydride forms parallelogram-like and needle-like morphology. Figs. 10 and 11 are isotropic and anisotropic hydride gradient energy diagrams and curves. Interfacial anisotropy results in a decrease in gradient energy. Due to the influence of interfacial anisotropy between the hydride and matrix phase, the structure change at the interface is larger than the concentration change. Therefore, the gradient energy related to the structure tends to decrease significantly compared with the gradient energy related to the concentration.

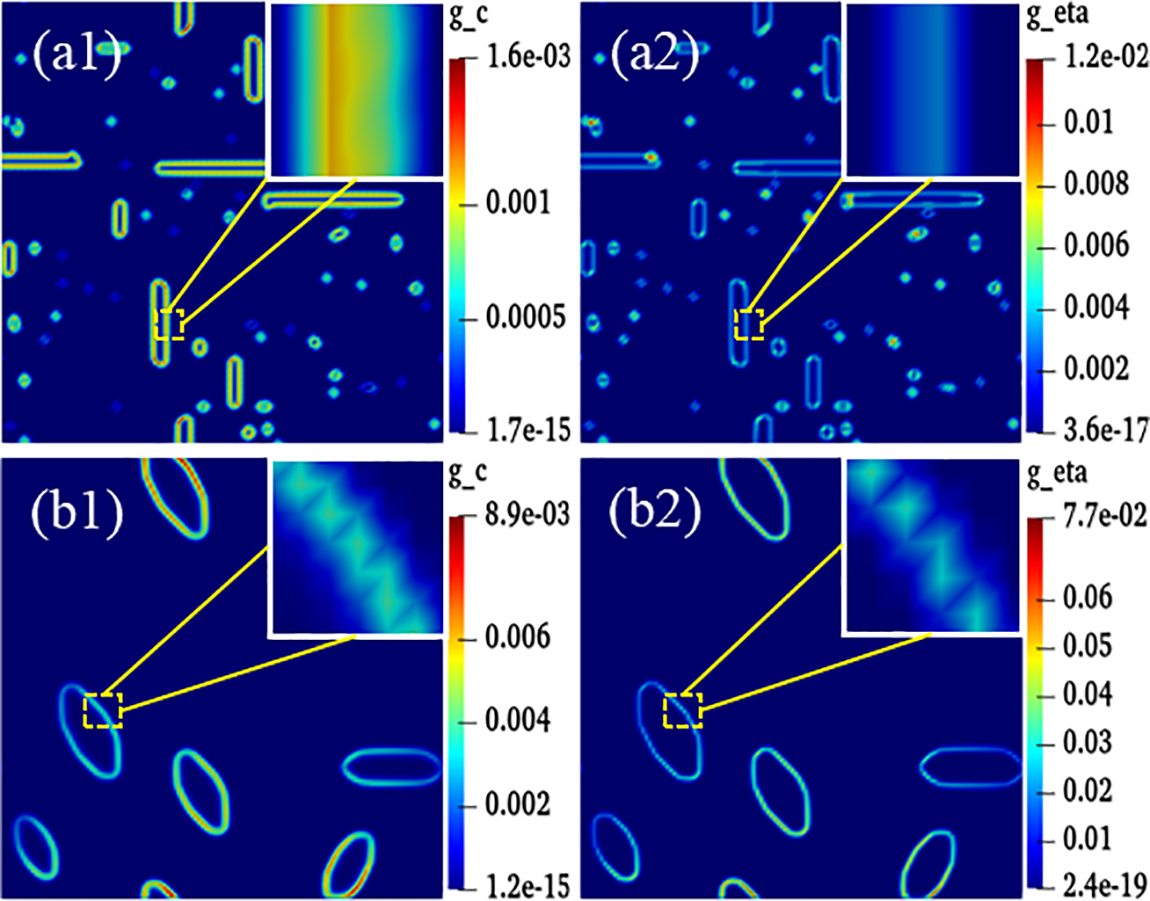
Figure 10: Gradient energy diagrams of isotropy and anisotropy hydrides at time step t = 20000. (a1–a2) Isotropy hydride, (a1) Concentration gradient energy, (a2) Structural gradient energy. (b1–b2) Anisotropy hydride, (b1) Concentration gradient energy, (b2) Structural gradient energy

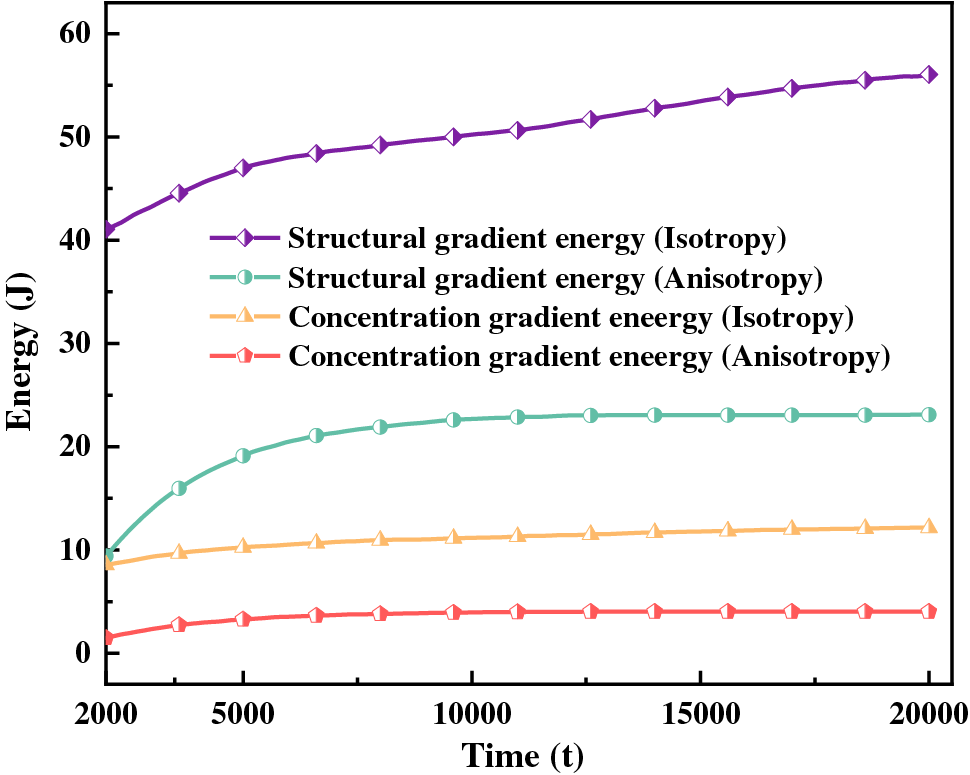
Figure 11: Gradient energy curves of isotropy and anisotropy hydrides

Interfacial anisotropy leads to different hydride morphology, and there are differences in the stress states around different hydride morphology. Fig. 12 shows the stress distribution of anisotropic hydride. The evolution of the equivalent stress with time step is shown in Fig. 12a. The stress distribution shows that the equivalent stresses are concentrated at the hydride tips, and the stresses are less at the sides and inside the hydride. Figs. 12b–12d show the positive stress in the x direction, the positive stress in the y direction, and the shear stress in the xy direction of the hydride, respectively. The stress value around the hydride is negative, which is manifested as compressive stress, and the positive stress value shows tensile stress. From Figs. 12b and 12c, it can be seen that σxx is negative and σyy is positive in the region on both sides of the hydride and at the tip of the hydride, σxx is positive and σyy is negative. The shear stress is caused by the hydride deflection precipitation, so the internal stress in the lateral precipitate hydride is larger than the internal stress in the precipitate hydride in the x-axis direction. For the lateral precipitate hydride, the shear stress is concentrated at the tip, negative inside the hydride and at the tip for variant 2, positive on both sides of the hydride, and the opposite for variant 3. The internal shear stress of the hydride precipitated along the x-axis is small, and the shear stress near the tip is evenly distributed.

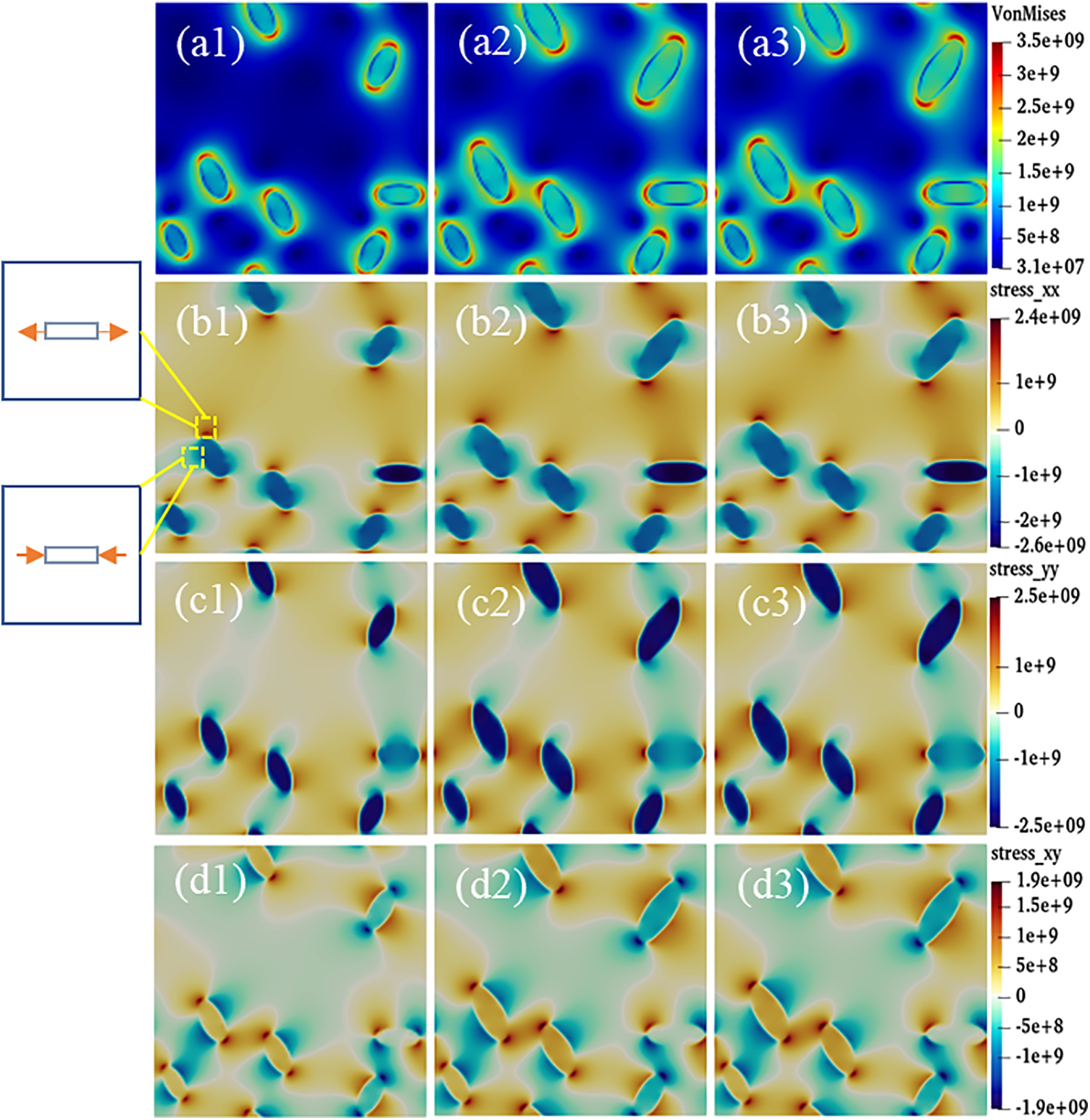
Figure 12: Anisotropic hydride stress distribution at time steps t = 4000, 10000, and 20000. (a1–a3) Equivalent stress, (b1–b3) σxx, (c1–c3) σyy, (d1–d3) γxy

4  Discussions

Under the effect of anisotropic interfacial energy and interfacial mobility, hydrides precipitate needle-like and parallelogram-like morphologies (Fig. 4b). Yuan et al. [6] obtained δ hydride by hydrogen permeation treatment of Zr-4 alloy, and the bright field image was observed using Transmission electron microscope (TEM) to obtain the hydride morphology in Fig. 13, where the parallelogram-like and needle-like morphology is the same as the simulation results. The stress state, aspect ratio, and precipitated deflection angle of the different hydrides were investigated by morphology observation of individual δ hydrides as shown in Fig. 5. Variant 1 hydrides have needle-like morphology and aspect ratios of approximately 3.52. Variant 2 and variant 3 hydrides have aspect ratios of approximately 3.5 and 3.64, respectively, and the precipitated deflection angle is θ1 = 19°, with parallelogram-like morphology.

Figure 13: Experimental morphology [6] and simulated morphology of hydride at time step t = 20000. (The yellow dotted line in the figure is labeled)

Interfacial isotropy assumes that the interface is coherent. However, in practice, the semi-coherent or non-coherent interfacial state between HCP and FCC crystal structures will generate anisotropy. The effect on hydride morphology was investigated by varying the y-axis anisotropic interfacial mobility, as shown in Fig. 6. It was found that the y-axis mobility coefficient Iy increased, the gradient energy at the interface showed a trend of decrease then increase and finally decrease, and the structural gradient energy varied more than that of the concentration gradient energy, as shown in Fig. 14. When Iy<Ix, with the increase of the y-axis interfacial anisotropy mobility coefficient, the gradient energy decreases, the trend of the semi-coherent relationship between the precipitate phase and the matrix phase increases, and the hydride precipitation rate is accelerated. However, the x-axis precipitate still dominates, and the hydride precipitate along the circumferential direction is obvious. The circumferential precipitated rate of variant 1 is accelerated and the aspect ratio increases, while the difference in aspect ratio of variant 2 and variant 3 are smaller, as shown in Fig. 7. When Ix<Iy<1.5Ix, as the y-axis mobility coefficient continues to increase, disincentives the x-axis interfacial mobility. X-axis directional interfacial energy increases and the trend of non-coherent relationship increases. The circumferential precipitation rate decreased, the circumferential length growth rate decreased, and the difference in hydride aspect ratio decreased. As the y-axis mobility coefficient continues to increase, when Iy>1.5Ix, the y-axis interfacial energy decreases, the trend of semi-coherent relationship again increases, and the hydride precipitation rate increases. The radial height growth rate of variant 2 and variant 3 are stronger than variant 1. Fig. 9 shows the hydride equivalent stress curve with time for different anisotropic interfacial mobility ratios. The stress state of the precipitate phase includes elastic stress caused by lattice distortion and volume stress caused by hydride precipitation, and the stress around the hydride will inhibit the growth and precipitation of the hydride. The stress state around hydride decreases with the increase of anisotropic mobility, then increases, and finally decreases. When the hydride growth reaches the limit, the stress value tends to be stable between 850–880 MPa.

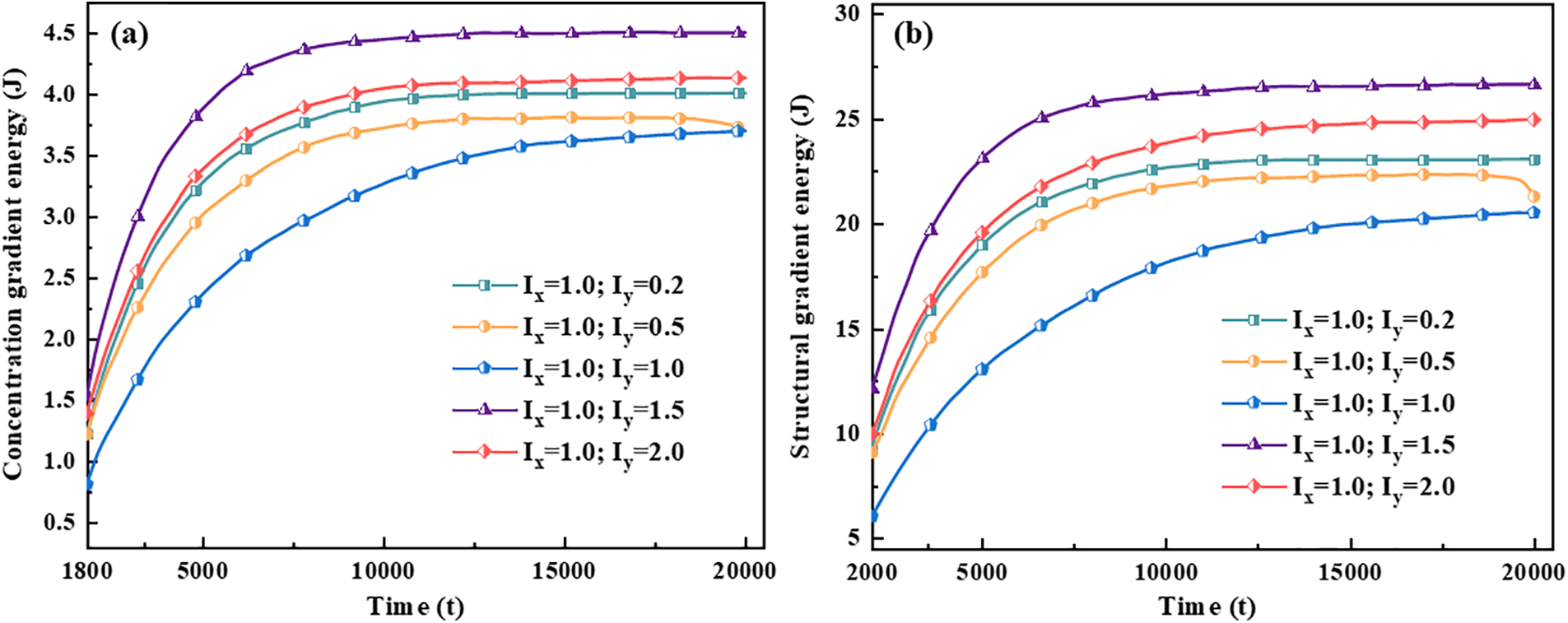
Figure 14: Gradient energy curves with time for different anisotropic mobility ratios. (a) Concentration gradient energy, (b) Structural gradient energy

Hydride precipitated morphology and orientation depend on the interfacial energy and interfacial mobility. The gradient energy coefficient is related to the interfacial energy [59,62]. Under the action of anisotropic interfacial energy and interfacial mobility, variant 1 hydride precipitates needle-like morphology, and variant 2 and variant 3 hydride precipitates parallelogram-like morphology. Figs. 10 and 11 show the gradient energy diagram and energy curve of the interfacial isotropy and anisotropy hydride in Fig. 3. The interfacial anisotropy gradient can be reduced compared to the interfacial isotropy. As the interfacial anisotropy adjusts the lattice mismatch, it reduces the energy difference due to the lattice mismatch, resulting in a lower gradient energy. The structural difference changes significantly compared to the concentration difference. Therefore, the structure gradient energy decreases significantly more than the concentration gradient energy. It shows that the non-coherent or semi-coherent interface conforms to the interfacial state between the precipitate hydride phase and the matrix phase. It is more advantageous to replace the coherent interface with a semi-coherent or non-coherent interface close to the real situation.

Differences in the precipitated morphology and growth characteristics of anisotropic hydride affect the change in the stress state around the hydride. Fig. 12 represents the stress state of the anisotropy hydride, where the equivalent force is concentrated at the tip. Due to the mismatch between the two phases lattice, the matrix is strained to accommodate the growing hydride. The matrix part around the hydride is compressed, the rest is stretched, and the hydrogen atoms tend to diffuse toward the tension zone [25]. The internal stress of the hydride precipitation in the x-axis direction is small, and the tensile stress and compressive stress at the tip are symmetrical. Since the regions above and below the hydride are in a compressed state, the hydrogen depletion region is formed, while the region near the hydride edge is in a stretched state, thus attracting hydrogen atoms. The tension region also tends to promote hydride precipitation, while compression impedes it, thus causing the hydride shape to be elongated.

5  Conclusions

In this study, phase-field simulation was performed on δ hydride coupled with interfacial anisotropy in zirconium alloys, and the effect of interfacial anisotropy on δ hydride precipitated morphology and stress state were analyzed. The main conclusions are as follows:

1.    The interfacial isotropic hydride precipitated morphology is slat-like. The addition of interfacial anisotropy, under the combined effect of interfacial energy and anisotropic interfacial mobility, transforms the hydride morphology from slat-like to parallelogram-like and needle-like morphology. This study optimizes the model to be closer to the real state, which is consistent with the experimental results.

2.    As the y-axis mobility coefficient Iy increases, when Ix<Iy<1.5Ix (Iy<Ix or Iy>1.5Ix), the gradient energy increases (decreases), and the non-coherent (semi-coherent) relationship between the interfaces increases. The growth rate of hydride circumferential length, radial height, and aspect ratio also decreases (increases), and the trend of the hydride growth decreases (increases). The stress state around the hydride tends to decrease, then increase, then decrease again. When the growth of the hydride reaches the limit, the stress value tends to be stable.

3.    The gradient energy coefficient is related to the interfacial energy. The anisotropy of the non-coherent or semi-coherent interface reduces the lattice mismatch between the precipitate phase and the matrix phase interface. Reduce the energy difference caused by lattice distortion, resulting in a decrease in gradient energy related to interfacial anisotropy. The semi-coherent or non-coherent interface instead of the coherent interface conforms to the real interfacial state between the precipitate phase and the matrix phase.

4.    The hydride morphology affects the stress state around the hydride. Due to the lattice mismatch between the two phases, the hydride in the matrix is under compression on both sides, hindering the absorption of hydrogen atoms. The tip and inside are stretched, promoting the absorption of hydrogen atoms, resulting in stress concentration at the tip and elongation of the hydride. At the same time, the uneven stress distribution around the hydride causes local enrichment of hydrogen concentration and produces tip morphology.

Acknowledgement: The authors especially acknowledge Prof. Sanqiang Shi of Hong Kong Polytechnic University and Dr. Zhihua Xiao of Peking University.

Funding Statement: The authors gratefully acknowledge financial support from the National Natural Science Foundation of China (Nos. 52375394, 52074246, 52275390, 52205429, 52201146), National Defense Basic Scientific Research Program of China (JCKY2020408B002, WDZC2022-12), Key Research and Development Program of Shanxi Province (202102050201011, 202202050201014), Science and Technology Major Project of Shanxi Province (20191102008, 20191102007) and Guiding Local Science and Technology Development Projects by the Central Government (YDZJSX2022A025, YDZJSX2021A027).

Author Contributions: Investigation: H.L. Nie, X.C. Shi, W.K. Yang, K.L. Wang, Y.H. Zhao; data collection: H.L. Nie, X.C. Shi, W.K. Yang; analysis and interpretation of results: H.L. Nie, X.C. Shi, W.K. Yang, K.L. Wang, Y.H. Zhao; draft manuscript preparation: H.L. Nie, X.C. Shi, W.K. Yang, K.L. Wang, Y.H. Zhao; software and funding: Y.H. Zhao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analysed during this study are included in this article and are available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. R. A. Holt, “In-reactor deformation of cold-worked Zr–2.5Nb pressure tubes,” Journal of Nuclear Materials, vol. 372, no. 2–3, pp. 182–214, 2008. [Google Scholar]

2. E. Lacroix, A. T. Motta and J. D. Almer, “Experimental determination of zirconium hydride precipitation and dissolution in zirconium alloy,” Journal of Nuclear Materials, vol. 509, pp. 162–167, 2018. [Google Scholar]

3. E. Zuzek, J. P. Abriata, A. San-Martin and F. D. Manchester, “The H-Zr (Hydrogen-Zirconium) system,” Bulletin of Alloy Phase Diagrams, vol. 11, no. 4, pp. 385–395, 1990. [Google Scholar]

4. A. Ishii, “Activation energy of homogeneous nucleation of Zr hydride: Density functional theory calculation,” Computational Materials Science, vol. 215, pp. 111769, 2022. [Google Scholar]

5. J. Bair, M. A. Zaeem and M. Tonks, “A review on hydride precipitation in zirconium alloys,” Journal of Nuclear Materials, vol. 466, pp. 12–20, 2015. [Google Scholar]

6. G. H. Yuan, G. Q. Cao, Q. Yue, L. Yang, J. H. Hu et al., “Formation of nanocrystalline δ-ZrHx in Zircoloy-4: Orientation relationship and twinning,” Journal of Alloys and Compounds, vol. 658, pp. 494–499, 2016. [Google Scholar]

7. M. A. Tunes, C. M. Silva and P. D. Edmondson, “Site specific dependencies of hydrogen concentrations in zirconium hydrides,” Scripta Materialia, vol. 158, pp. 136–140, 2019. [Google Scholar]

8. K. Une, K. Nogita, S. Ishimoto and K. Ogata, “Crystallography of zirconium hydrides in recrystallized zircaloy-2 fuel cladding by electron backscatter diffraction,” Journal of Nuclear Science and Technology, vol. 41, no. 7, pp. 731–740, 2004. [Google Scholar]

9. S. J. Wang, S. L. Li, R. G. Li, X. X. Zhang, Y. K. Wang et al., “Stress-induced reorientation of hydrides in Zr-1Nb-0.01Cu cladding tube studied by synchrotron X-ray diffraction and EBSD,” Journal of Nuclear Materials, vol. 558, pp. 153374, 2022. [Google Scholar]

10. Y. J. Jia and W. Z. Han, “Effect of external stress on hydride reorientation in zirconium,” Acta Materialia, vol. 235, pp. 118100, 2022. [Google Scholar]

11. W. Qin, J. L. Liang, Z. Q. Cheng, M. H. Shi, D. Gu et al., “Threshold stress of hydride reorientation in zirconium alloy nuclear fuel cladding tubes: A theoretical determination,” Journal of Nuclear Materials, vol. 563, pp. 153659, 2022. [Google Scholar]

12. X. L. Tian, Y. H. Zhao, T. Gu, Y. L. Guo, F. Q. Xu et al., “Cooperative effect of strength and ductility processed by thermomechanical treatment for Cu-Al-Ni alloy,” Materials Science and Engineering: A, vol. 849, pp. 143485, 2022. [Google Scholar]

13. Y. H. Zhao, B. Zhang, H. Hou, W. P. Chen and M. Wang, “Phase-field simulation for the evolution of solid/liquid interface front in directional solidification process,” Journal of Materials Science & Technology, vol. 35, no. 6, pp. 1044–1052, 2019. [Google Scholar]

14. Y. H. Zhao, “Editorial: Phase field method and integrated computing materials engineering,” Frontiers in Materials, vol. 10, pp. 1145833, 2023. [Google Scholar]

15. Y. H. Zhao, K. X. Liu, H. B. Zhang, X. L. Tian, Q. L. Jiang et al., “Dislocation motion in plastic deformation of nano polycrystalline metal materials: A phase field crystal method study,” Advanced Composites and Hybrid Materials, vol. 5, no. 3, pp. 2546–2556, 2022. [Google Scholar]

16. W. P. Chen, H. Hou, Y. Zhang, Y. T. Zhao, W. Liu et al., “Thermal and solute diffusion in α-Mg dendrite growth of Mg-5wt.%Zn alloy: A phase-field study,” Journal of Materials Research and Technology, vol. 24, pp. 8401–8413, 2023. [Google Scholar]

17. X. L. Tian, Y. H. Zhao, D. W. Peng, Q. W. Guo, Z. Guo et al., “Phase-field crystal simulation of evolution of liquid pools in grain boundary pre-melting regions,” Transactions of Nonferrous Metals Society of China, vol. 31, no. 4, pp. 1175–1188, 2021. [Google Scholar]

18. X. Q. Ma, S. Q. Shi, C. H. Woo and L. Q. Chen, “Simulation of γ-hydride precipitation in bi-crystalline zirconium under uniformly applied load,” Materials Science and Engineering: A, vol. 334, no. 1, pp. 6–10, 2002. [Google Scholar]

19. X. Q. Ma, S. Q. Shi, C. H. Woo and L. Q. Chen, “Phase-field simulation of hydride precipitation in bi-crystalline zirconium,” Scripta Materialia, vol. 47, no. 4, pp. 237–241, 2002. [Google Scholar]

20. X. Q. Ma, S. Q. Shi, C. H. Woo and L. Q. Chen, “Effect of applied load on nucleation and growth of γ-hydrides in zirconium,” Computational Materials Science, vol. 23, no. 1–4, pp. 283–290, 2002. [Google Scholar]

21. X. H. Guo, S. Q. Shi and X. Q. Ma, “Elastoplastic phase field model for microstructure evolution,” Applied Physics Letters, vol. 87, pp. 221910, 2005. [Google Scholar]

22. L. Thuinet, A. Legris, L. Zhang and A. Ambard, “Mesoscale modeling of coherent zirconium hydride, precipitation under an applied stress,” Journal of Nuclear Materials, vol. 438, no. 1–3, pp. 32–40, 2013. [Google Scholar]

23. J. Bair and M. A. Zaeem, “Effects of applied strain on formation, shape evolution, and reorientation of multiphase zirconium hydrides: A multiphase field modeling study,” arXiv:1706.01097v1, 2017. [Google Scholar]

24. M. J. Welland and S. M. Hanlon, “Prediction of the zirconium hydride precipitation barrier with an anisotropic 3D phase-field model incorporating bulk thermodynamics and elasticity,” Computational Materials Science, vol. 171, pp. 109266, 2020. [Google Scholar]

25. S. Wu, J. Sheng, C. Yang, X. M. Shi, H. B. Huang et al., “Phase-field model of hydride blister growth kinetics on zirconium surface,” Frontiers in Materials, vol. 9, pp. 916593, 2022. [Google Scholar]

26. B. Yoon and K. Chang, “Effect of number of variants of zirconium hydride on grain growth of zirconium,” Metals, vol. 10, no. 9, pp. 1155, 2020. [Google Scholar]

27. X. H. Guo, S. Q. Shi, Q. M. Zhang and X. Q. Ma, “An elastoplastic phase-field model for the evolution of hydride precipitation in zirconium. Part II: Specimen with flaws,” Journal of Nuclear Materials, vol. 378, no. 1, pp. 120–125, 2008. [Google Scholar]

28. T. W. Heo, K. B. Colas, A. T. Motta and L. Q. Chen, “A phase-field model for hydride formation in polycrystalline metals: Application to δ-hydride in zirconium alloys,” Acta Materialia, vol. 181, pp. 262–277, 2019. [Google Scholar]

29. X. H. Guo, S. Q. Shi, Q. M. Zhang and X. Q. Ma, “An elastoplastic phase-field model for the evolution of hydride precipitation in zirconium. Part I: Smooth specimen,” Journal of Nuclear Materialia, vol. 378, no. 1, pp. 110–119, 2008. [Google Scholar]

30. G. M. Han, Y. F. Zhao, C. B. Zhou, D. Y. Lin, X. Y. Zhu et al., “Phase-field modeling of stacking structure formation and transition of δ-hydride precipitates in zirconium,” Acta Materials, vol. 165, pp. 528–546, 2019. [Google Scholar]

31. W. Shin and K. Chang, “Phase-field modeling of hydride reorientation in zirconium cladding materials under applied stress,” Computational Materials Science, vol. 182, pp. 109775, 2020. [Google Scholar]

32. P. C. A. Simon, L. K. Aagesen, A. M. Jokisaari, L. Q. Chen, M. R. Daymond et al., “Investigation of δ zirconium hydride morphology in a single crystal using quantitative phase field simulations supported by experiments,” Journal of Nuclear Materials, vol. 557, pp. 153303, 2021. [Google Scholar]

33. A. Toghraee, J. Bair and M. A. Zaeem, “Effects of applied load on formation and reorientation of zirconium hydrides: A multiphase field modeling study,” Computational Materials Science, vol. 192, pp. 110367, 2021. [Google Scholar]

34. S. Ghosh and M. Plapp, “Influence of interphase boundary anisotropy on bulk eutectic solidification microstructures,” Acta Materialia, vol. 140, pp. 140–148, 2017. [Google Scholar]

35. Y. H. Cai, F. Wang, M. Selzer and B. Nestler, “Phase-field investigation on the growth orientation angle of aluminum carbide with a needle-like structure at the surface of graphite particles,” Modelling and Simulation in Materials Science and Engineering, vol. 27, no. 6, pp. 065010, 2019. [Google Scholar]

36. H. Mao, Y. Kong, D. Cai, M. J. Yang, Y. B. Peng et al., “β″ needle-shape precipitate formation in Al-Mg-Si alloy: Phase field simulation and experimental verification,” Computational Materials Science, vol. 184, pp. 109878, 2020. [Google Scholar]

37. Y. H. Zhao, H. Xing, L. J. Zhang, H. B. Huang, D. K. Sun et al., “Development of phase‐field modeling in materials science in China: A review,” Acta Metallurgica Sinica (English Letters), vol. 36, pp. 1749–1775, 2023. [Google Scholar]

38. Y. H. Zhao, “Understanding and design of metallic alloys guided by phase-field simulations,” npj Computational Materials, vol. 9, no. 1, pp. 94, 2023. [Google Scholar]

39. T. Xin, S. Tang, F. Ji, L. Q. Cui, B. B. He et al., “Phase transformations in an ultralight BCC Mg alloy during anisothermal ageing,” Acta Materialia, vol. 239, pp. 118248, 2022. [Google Scholar]

40. J. W. Cahn and J. E. Hilliard, “Free energy of a nonuniform system. I. Interfacial free energy,” The Journal of Chemical Physics, vol. 28, no. 2, pp. 258–267, 1958. [Google Scholar]

41. J. W. Cahn and S. M. Allen, “A microscopic theory for domain wall motion and its experimental verification in Fe-Al alloy domain growth kinetics,” Le Journal de Physique Colloques, vol. 38, no. C7, pp. C7-51–C7-54, 1977. [Google Scholar]

42. K. L. Wang, W. K. Yang, X. C. Shi, H. Hou and Y. H. Zhao, “Phase-field-method-studied mechanism of Cu-rich phase precipitation in AlxCuMnNiFe high-entropy alloy,” Acta Physica Sinica, vol. 72, no. 7, pp. 076102, 2023. [Google Scholar]

43. W. K. Yang, K. L. Wang, J. Q. Pei, X. C. Shi, H. Hou et al., “Dislocation loop assisted precipitation of Cu-rich particles: A phase-field study,” Computational Materials Science, vol. 228, pp. 112338, 2023. [Google Scholar]

44. L. Q. Chen and Y. H. Zhao, “From classical thermodynamics to phase-field method,” Progress in Materials Science, vol. 124, pp. 100868, 2022. [Google Scholar]

45. S. Q. Shi and Z. H. Xiao, “A quantitative phase field model for hydride precipitation in zirconium alloys: Part I. Development of quantitative free energy functional,” Journal of Nuclear Materials, vol. 459, pp. 323–329, 2015. [Google Scholar]

46. T. Z. Xin, Y. H. Zhao, R. Mahjoub, J. X. Jiang, A. Yadav et al., “Ultrahigh specific strength in a magnesium alloy strengthened by spinodal decomposition,” Science Advances, vol. 7, no. 23, pp. eabf3039, 2021. [Google Scholar] [PubMed]

47. W. K. Yang, X. A. Jiang, X. L. Tian, H. Hou and Y. H. Zhao, “Phase-field simulation of nano-α′ precipitates under irradiation and dislocations,” Journal of Materials Research and Technology, vol. 22, pp. 1307–1321, 2023. [Google Scholar]

48. A. G. Khachaturian, “Elastic strain caused by crystal lattice rearrangement,” in Theory of Structural Transformations in Solids, pp. 5821133, New York, USA: Wiley, 1983. [Google Scholar]

49. G. M. Han, Z. Q. Han, A. A. Luo and B. C. Liu, “Three-dimensional phase-field simulation and experimental validation of β-Mg17Al12 phase precipitation in Mg-Al-based alloys,” Metallurgical and Materials Transactions A, vol. 46, no. 2, pp. 948–962, 2014. [Google Scholar]

50. G. M. Han, Z. Q. Han, A. A. Luo, A. Sachdev and B. C. Liu, “Phase field simulation on morphology of continuous precipitate Mg17Al12 in Mg-Al alloy,” Acta Metallurgica Sinica, vol. 49, no. 3, pp. 277–283, 2013. [Google Scholar]

51. Y. H. Zhao, K. X. Liu, H. Hou and L. Q. Chen, “Role of interfacial energy anisotropy in dendrite orientation in Al-Zn alloys: A phase field study,” Materials & Design, vol. 216, pp. 110555, 2022. [Google Scholar]

52. S. G. Kim, W. T. Kim and T. Suzuki, “Phase-field model for binary alloys,” Physical Review E, vol. 60, no. 6, pp. 7186–7197, 1999. [Google Scholar]

53. J. B. Zhang, H. F. Wang, W. W. Kuang, Y. C. Zhang, S. Li et al., “Rapid solidification of non-stoichiometric intermetallic compounds: Modeling and experimental verification,” Acta Materialia, vol. 148, pp. 86–99, 2018. [Google Scholar]

54. W. W. Kuang, H. F. Wang, X. Li, J. B. Zhang, Q. Zhou et al., “Application of the thermodynamic extremal principle to diffusion-controlled phase transformations in Fe-C-X alloys: Modeling and applications,” Acta Materialia, vol. 159, pp. 16–30, 2018. [Google Scholar]

55. S. Y. Hu, J. Murray, H. Weiland, Z. K. Liu and L. Q. Chen, “Thermodynamic description and growth kinetics of stoichiometric precipitates in the phase-field approach,” Calphad, vol. 31, no. 2, pp. 303–312, 2007. [Google Scholar]

56. Z. H. Xiao, X. H. Guo, G. Y. Tang, S. Q. Shi and M. J. Hao, “A quantitative phase field model for hydride precipitation in zirconium alloys: Part II. Modeling of temperature dependent hydride precipitation,” Journal of Nuclear Materials, vol. 459, pp. 330–338, 2015. [Google Scholar]

57. W. H. Zhu, R. S. Wang, G. G. Shu, P. Wu and H. M. Xiao, “First-principles study of different polymorphs of crystalline zirconium hydride,” Journal of Physical Chemistry C, vol. 114, no. 50, pp. 22361–22368, 2010. [Google Scholar]

58. Y. F. Zhang, X. M. Bai, J. G. Yu, M. R. Tonks, M. J. Noordhoek et al., “Homogeneous hydride formation path in α-Zr: Molecular dynamics simulations with the charge-optimized many-body potential,” Acta Materialia, vol. 111, pp. 357–365, 2016. [Google Scholar]

59. Q. Yu, M. Reyes, N. Shah and J. Marian, “Kinetic model of incipient hydride formation in Zr clad under dynamic oxide growth conditions,” Material, vol. 13, no. 5, pp. 1088, 2020. [Google Scholar]

60. V. Perovic, G. C. Weatherly and C. J. Simpson, “Hydride precipitation in α/β zirconium alloys,” Acta Metallurgica, vol. 31, no. 9, pp. 1381–1391, 1983. [Google Scholar]

61. S. Q. Shi, X. N. Jing, X. H. Guo, X. Q. Ma and L. Q. Chen, Phase Field Simulation of Hydrogen Diffusion and Hydride Formation Pattern in Zirconium, Beijing, China: Atomic Energy Press, pp. 186–197, 2005. [Google Scholar]

62. B. Li, J. Lowengngrub, A. Ratz and A. Voigt, “Geometric evolution laws for thin crystalline films: Modeling and numerics,” Communications in Computational Physics, vol. 6, no. 3, pp. 433–482, 2009. [Google Scholar]