Nonlinear Components of a Block Cipher over Eisenstein Integers

1  Introduction

Cryptography was widely used in military, diplomatic, and government applications until the 1970s. In the 1980s, the telecommunications and financial industries installed hardware cryptographic devices. The mobile phone system was the first cryptographic application in the late 1980s. Nowadays, everyone uses cryptographic applications in their daily lives. Our daily lives commonly depend on the secure transmission of information and data. Online shopping, cell phone messages and calls, ATMs, electronic mail, facsimile, wireless media, and data transfer over the internet all require a system to maintain the secrecy and integrity of private information. Cryptography offers a mechanism for everyone to interact safely in a hostile environment. Sensitive data is significantly aided by cryptography. Communication is encrypted to guarantee that its meaning is hidden, preventing anybody who reads it from understanding something regarding it unless somebody else manages to decrypt it [1].

In cryptography, the S-box is crucial for ensuring secure communication. Shannon suggested the notion of an S-box in 1949 in [2]. S-boxes serve a pivotal role in causing confusion within the data. According to Shannon, concealing the relationship between the key and cipher text is referred to as confusion, while concealing the statistical link between plain text as well as cipher text is referred to as diffusion. In other words, the non-uniformity in the distribution of individual letters inside plain text should be redistributed into the non-uniformity in the distribution of much bigger structures in the encrypted text, which is substantially more difficult to decrypt [3]. The Rijndael algorithm is basically the same as an iterated block cipher but has a few extra features. Before we talk about the Rijndael algorithm, we will talk about an iterated block cipher shown in [4].

Many scholars employed diverse algebraic and statistical frameworks to confound data and produce S-boxes. In [5], the authors suggested S-boxes over the permutation of the symmetric group. In [6], Javeed et al. constructed the non-linear component of block cipher by means of a chaotic dynamical system and symmetric group. In [7], the authors described the S-box based on the subgroup of the Galois field. The author suggested a robust encryption system using a modified Chebyshev map, Advanced Encryption Standard (AES) S-boxes, and a symmetric group of permutations [8].

In [9], the authors proposed a new scheme for the construction of the S-box based on the linear fractional transformation (LFT) and permutation function. In [10], the authors proposed S-box over the Mobius group and finite field. The author proposed S-box on a nonlinear chaotic map in [11]. In [12], Sajjad et al. designed pair of nonlinear components of a block cipher over Gaussian integers. In [13,14], the authors constructed cyclic codes over quaternion integers, these quaternion structures can be helpful for the construction of S-boxes. The authors designed differential cryptanalysis of DES-like cryptosystems in [15]. Cassal-Quiroga et al. generated the dynamical S-boxes for block ciphers via an extended logistic map [16]. Tang et al. designed a new method of dynamical S-boxes based on discretized chaotic maps [17]. Chen et al. extended method for obtaining S-boxes based on three-dimensional chaotic Baker maps [18]. The authors constructed s-boxes using different maps over elliptic curves for image encryption [19]. Cavusoglu et al. [20] constructed S-box based on chaotic scaled zhongtang system. Siddiqui et al. developed a novel scheme of substitution-box design based on modified Pascal’s triangle and elliptic curve in [21]. Farhan et al. designed a new S-box generation algorithm based on the multistability behavior of a plasma perturbation model [22]. In [23], the authors approached the S-boxes and permutation, substitution, based encryption.

Eisenstein integers are named after German mathematician Ferdinand Eisenstein, who first introduced them in the 1850s while studying the theory of quadratic forms. Like ordinary complex numbers, Eisenstein integers can be added and multiplied together. However, their properties are different. Eisenstein integers have important applications in number theory, coding theory, data security, and algebraic geometry. They also have connections to other areas of mathematics, such as algebraic number theory and modular forms [24].

An S-box generator is appropriate for cryptographic purposes if it can efficiently make highly dynamic S-boxes with good cryptographic properties or tests like nonlinearity, bit independence criterion, strict avalanche criterion, linear approximation probability, and differential approximation probability. The key contributions of our proposed study are given below:

•   Propose an algorithm to generate pair of S-boxes by the cyclic group over the residue class of Eisenstein integers.

•   Security Analysis.

•   The advantages of the proposed algorithm over EI with some of the existing algorithms over EC.

This paper is structured as follows: Basic definitions, cyclic group over the residue class of Eisenstein integers, and some fundamental results are elaborated in Section 2. The scheme of the pair of new S-boxes is proposed in Section 3. Analysis of the proposed S-boxes including nonlinearity, bit independence criterion, strict avalanche criterion, linear approximation probability, and differential approximation probability investigated in Section 4. The comparison of the proposed S-boxes with some of the existing S-boxes are given in Section 5. Conclusions and future directions are given in Section 6.

2  Preliminaries

This section provides the key concepts and basic findings that will be used in the study of upcoming sections. First of all, we recall the definition of Eisenstein integers, cyclic group over a residue class of Eisenstein integers, and some fundamental results.

Eisenstein Integers

In [24], Eisenstein integers are a subset of complex numbers with real and vector parts.

1.   Z[ω]={b0+b1ω:b0,b1∈Z}, where Z is the set of integers.

2.   Multiplicative identity is 1.

3.   ω is the cube root of unity.

Let h=b0+b1ω be an element of the Eisenstein integer ring, then the conjugate of h is h¯=b0+b1ω2. Then the norm of h is given by

p=N(h)=hh¯=b02+b12−b0b1

An Eisenstein integer has only two parts, one is the scalar part b0 and the other is the vector part b1ω.

Addition of Two Eisenstein Integers

Let h=a1+b1ω and k=a2+b2ω be two Eisenstein integers then, the sum of two Eisenstein integers is also an Eisenstein integer defined as

h+k=(a1+b1ω)+(a2+b2ω)=(a1+a2)+ω(b1+b2)=a3+ωb3

Multiplication of Two Eisenstein Integers

Let h=a1+b1ω and k=a2+b2ω are two Eisenstein integers then, the multiplication of two Eisenstein integers is also an Eisenstein integer defined as

hk=(a1+b1ω)(a2+b2ω)=(a1a2−b1b2)+ω(a1b2+a2b1−b1b2)=(a1a2−b1b2,a1b2+a2b1−b1b2)=a4+b4ω

Theorem: In [24], the set of natural numbers for each odd rational prime p, there is a prime h∈Z[ω], such that N(h)=p=hh¯. In particular, p is not prime in Z[ω].

Theorem: In [24], if the norm of an Eisenstein integer N(h) is prime in Z, then the Eisenstein integer h is prime in Z[ω].

Definition: In [24], let Z[ω] be the set of Eisenstein integers and Z[ω]h be the residue class of Eisenstein integers over modulo h,h=a+bω. Then, the modulo function:

s:Z[ω]={c+dω:c,d∈Z}→Z[ω]h

Then, s(u)=z(modh)=u−[uh¯hh¯]h.

where z∈Z[ω]h and [.] are rounding to the nearest integer. The rounding of an Eisenstein integer can be done by rounding the real part and coefficients of the vector part separately to the closest integer.

Theorem: In [24], let h be an Eisenstein prime, and the number of Eisenstein integers modulo h is the norm of h. If ρ≠0 (mod h), then ρn(h)−1≡1(mod h).

Remark: The group generated b <ρ> in the above Theorem is named S.

3  Redesign of Pair of n×n S-boxes over Eisenstein Integers

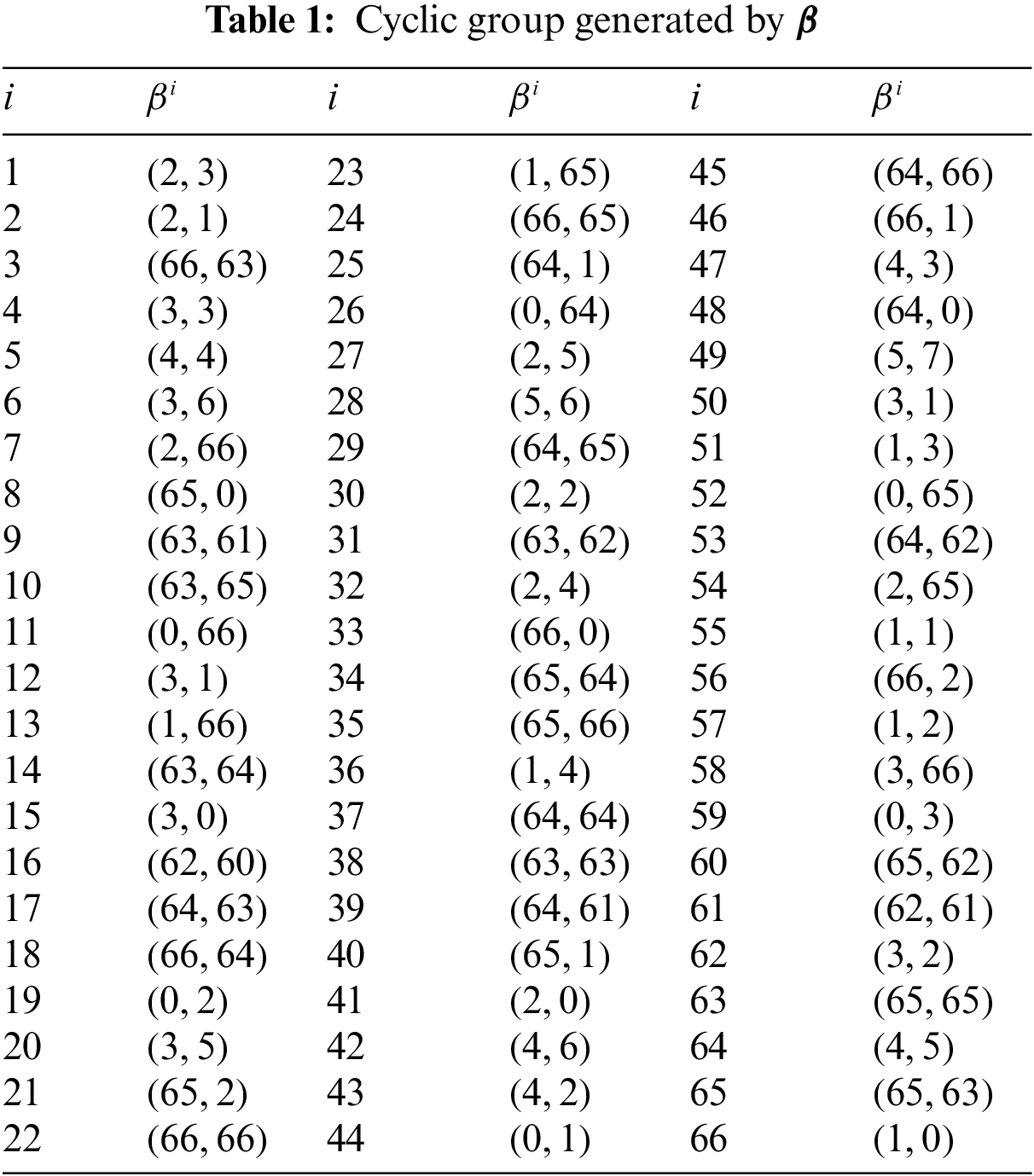
Multiple methods can be employed to cause confusion inside a security system. S-box is one of the most efficient cryptographic algorithms in use today. The S-boxes are generally formed using the EI class or the multiplicative cyclic group. As a result, it is feasible to create a variety of S-boxes across the residue class of EI, which presents a fantastic outlook for the development of secure and consistent cryptosystems. The subsequent procedures are useful for constructing S-boxes over the residue class of EI (Multiplicative cyclic group).

Step 1: Construct a cyclic group S of order p−1 over the residue class of EI.

Step 2: Apply permutation through affine mapping as:

f(x)=(ax+b)(mod2n)

where b∈S and a be the unit element of S.

Step 3: Separate real and vector parts of Step 2.

Step 4: Apply modulo 2n over the separated parts in Step 3.

Step 5: Select the first 2n non-repeated elements from the elements of Step 4.

Step 6: Get a pair of S-boxes.

The construction of S-boxes by Eisenstein integers provides us with better performance instead of S-boxes by using other structures like as chaotic maps, elliptic curves, finite fields, etc.

3.1 Pair of 4 × 4 S-boxes over the Residue Class of EI

Let h=2+9ω, p=n(h)=22+92−18=67, and β=2+3ω=(2,3), then the cyclic group generated by β is given in Table 1.

Apply the affine permutation mapping, f(x)=((63+61ω)x+(63+62ω))(mod16), separate real and vector parts, and select the first 16 non-repeating entries for real and vector parts, which are given in Tables 2 and 3.

3.2 Pair of 8 × 8 S-boxes over the Residue Class of EI

Example 1: Let h=81+71ω, p=n(h)=812+712−(81)(71)=5851, and β=2+3ω=(2,3), then apply the same procedure of 3.1, we get pair of S-boxes by affine mapping f(x)=((59+29ω)x+(14+8ω))(mod256) given in Tables 4 and 5.

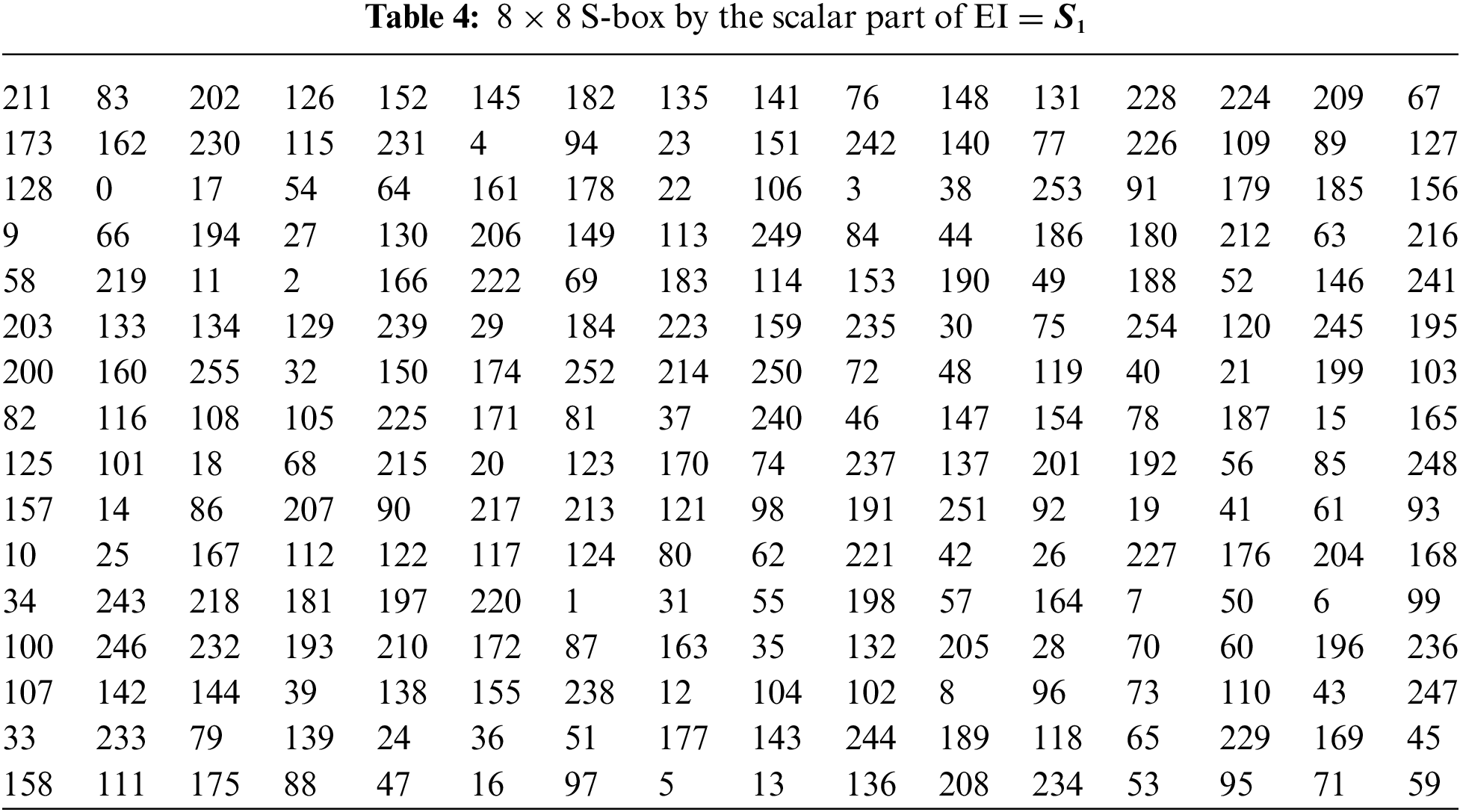
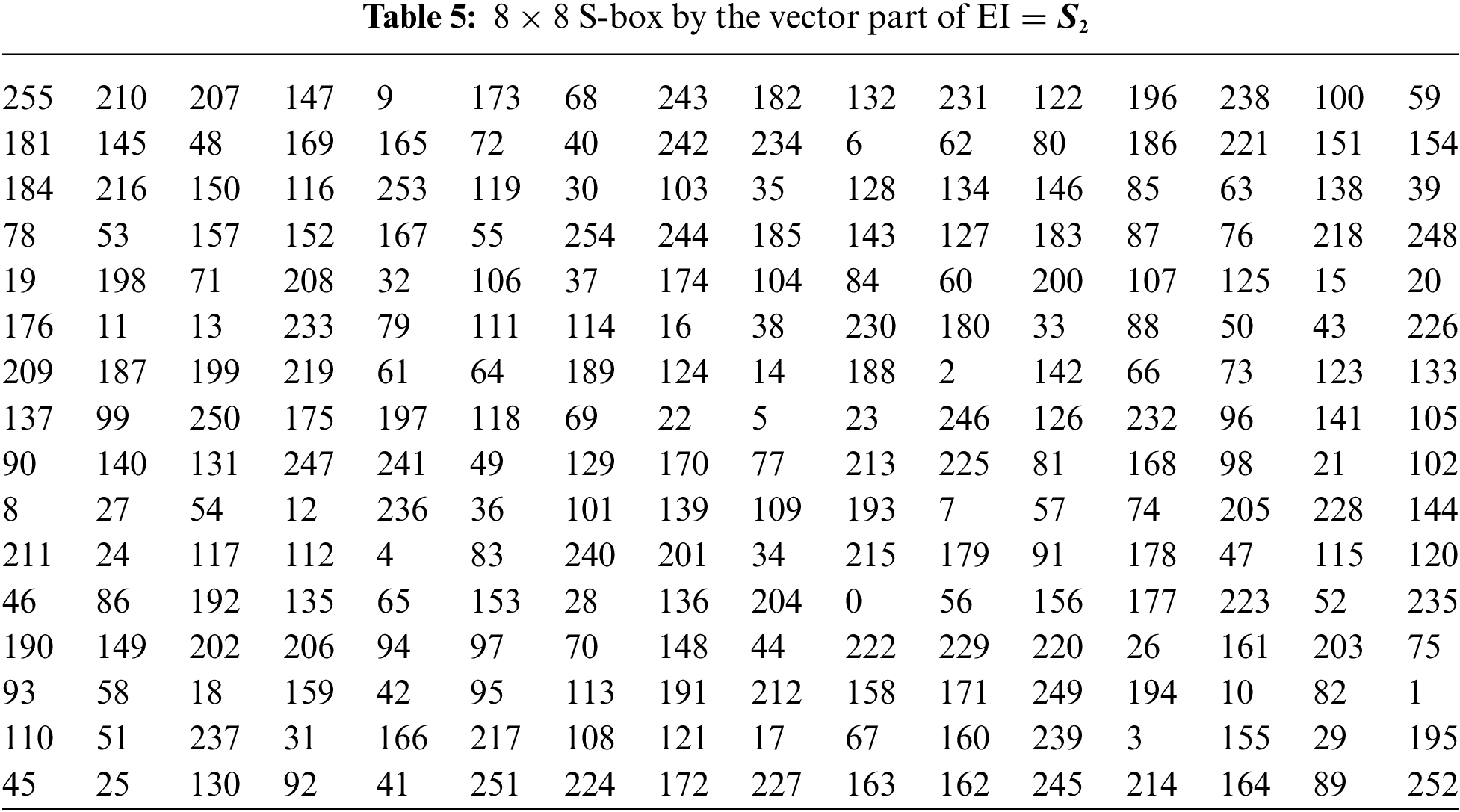
Example 2: Let h=81+71ω, p=n(h)=812+712−(81)(71)=5851, and β=2+3ω=(2,3), then apply the same procedure of 3.1, we get pair of S-boxes by affine mapping f(x)((59+29ω)x+(7+5836ω))(mod256) given in Tables 6 and 7.

4  Analysis of S-boxes

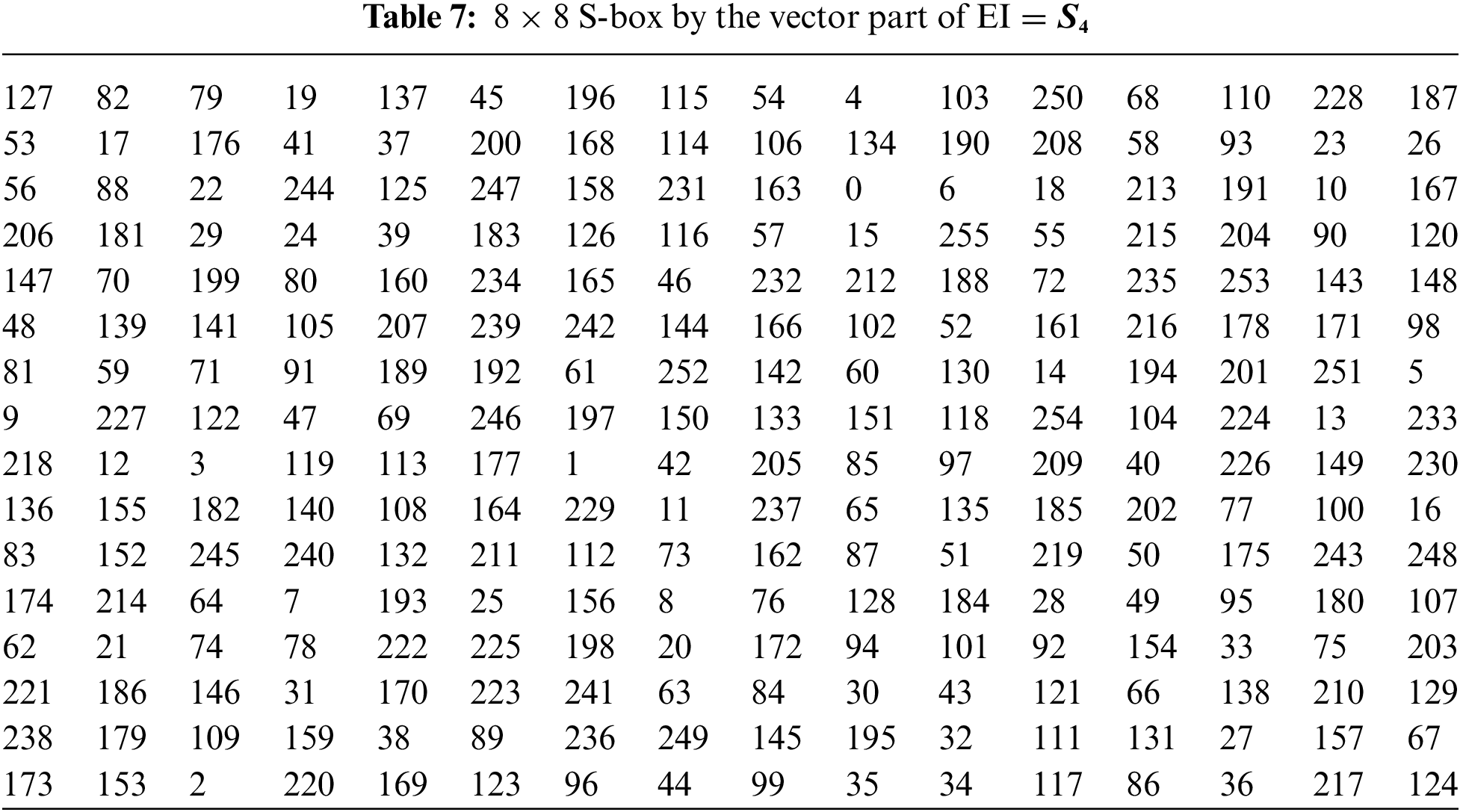
There are the following tests to analyze the properties of S-boxes.

4.1 Non-Linearity

The nonlinearity of the S-box refers to the property of the substitution box used in cryptographic algorithms, which is designed to introduce nonlinearity into the encryption process. In particular, the S-box is used in block ciphers to perform the substitution of plaintext bits with cipher text bits, and its nonlinearity is important for the security of the cipher. The nonlinearity of the S-box is usually measured using a metric called the “nonlinearity coefficient” or “nonlinearity index”. This metric quantifies the degree of nonlinearity introduced by the S-box and is based on the Walsh-Hadamard transform of the S-box. A high nonlinearity coefficient indicates that the S-box is highly nonlinear, which is desirable for cryptographic purposes. Nonlinear S-boxes make it more difficult for an attacker to find patterns or correlations between the plaintext and cipher text, which can be used to break the cipher [25]. To achieve high nonlinearity, S-boxes are often constructed using mathematical functions that are highly nonlinear, such as power functions or finite field operations. The upper bound of nonlinearity is N(f)=2n−1−2n2−1, for S-box. The optimal value of non-linearity is 120. The nonlinearity of the proposed S-boxes is given in Table 8.

The average non-linearity of proposed S-boxes is 107, 106.75, 107.0, and 106.75.

4.2 Bit Independent Criterion (BIC)

The bit independence criterion of an S-box is a measure of its resistance to linear and differential cryptanalysis attacks. Specifically, it refers to the property that no linear relationship exists between any two output bits of the S-box and any two input bits of the S-box. In other words, the bit independence criterion of an S-box ensures that changing one input bit or one output bit of the S-box will not affect the other output bits or input bits, respectively, in a linear way [26]. This property makes it more difficult for an attacker to analyze the S-box using linear or differential cryptanalysis. To achieve high bit independence, S-box designers often use mathematical structures, such as finite fields and Boolean functions, to construct the S-box lookup table. They also perform extensive testing and analysis to ensure that the S-box meets the required bit independence criteria and other cryptographic properties. The results of the BIC are given in Tables 9–12.

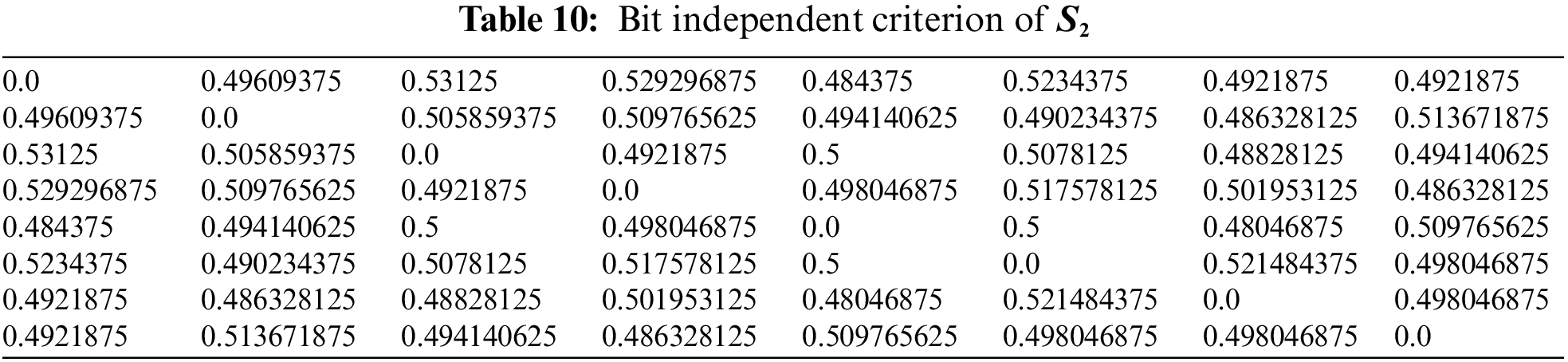
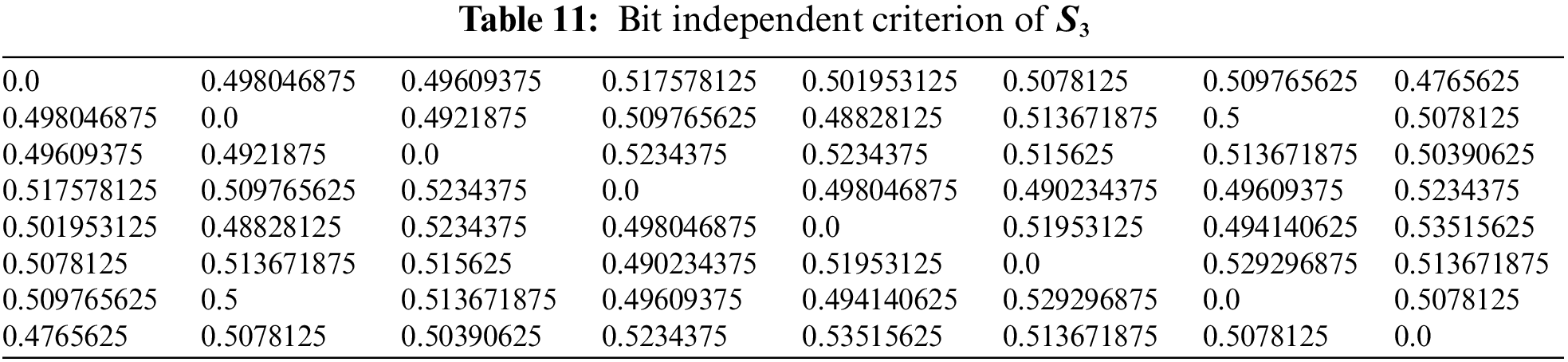
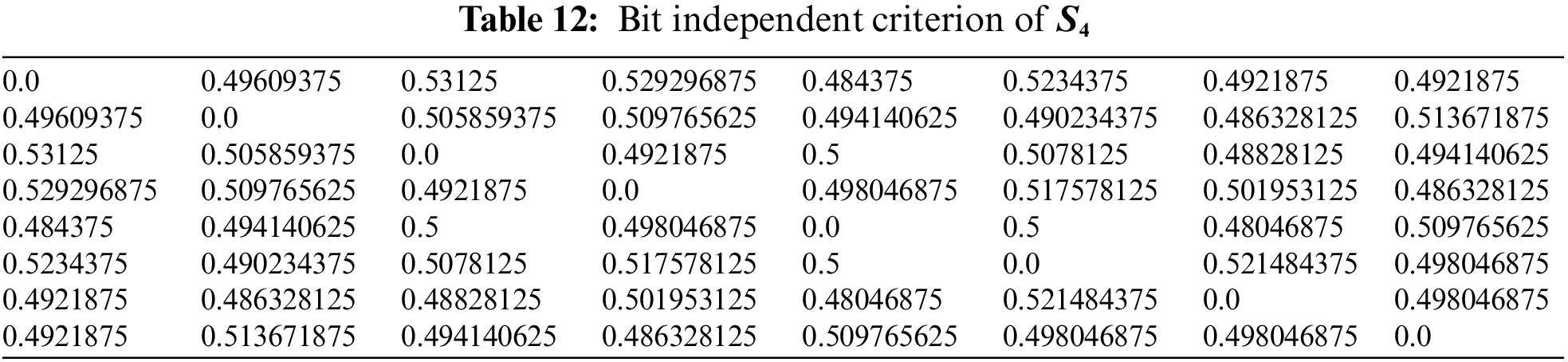
Hence S1, S2, S3 and S4 satisfied the bit-independent criterion close to the best possible value.

4.3 Linear Approximation Probability (LP)

The linear approximation probability for a substitution box (S-box) is a measure of the probability that a linear approximation of the S-box will hold. In other words, it is a measure of the correlation between a set of input bits and a set of output bits of the S-box [27]. The linear approximation probability of an S-box is defined as Pr[a⋅x=b⋅S(x)], where a and b are two-bit vectors of the same length as the input and output of the S-box, respectively, x is an input to the S-box, and S(x) is the output of the S-box. The symbol · denotes the bitwise inner product of the two-bit vectors. The linear approximation probability is a value between 0 and 1. A value of 0 means that there is no linear approximation of the S-box, while a value of 1 means that the linear approximation holds with certainty. We have calculated the linear approximation probability of the S-boxes S1, S2, S3 and S4. The maximum value of LP is 0.1484375, 0.1328125, 0.1484375, and 0.1328125.

4.4 Differential Approximation Probability (DAP)

The differential approximation probability for a substitution box (S-box) is a measure of the probability that a differential approximation of the S-box will hold. In other words, it is a measure of the correlation between a set of input differences and a set of output differences of the S-box. The differential approximation probability of an S-box is defined as Pr[Δx→Δy=Δu→Δv], where Δx and Δy are two input differences of the S-box, Δu, and Δv are the corresponding output differences, and → denotes the S-box operation. The differential approximation probability is a value between 0 and 1. A value of 0 means that there is no differential approximation of the S-box, while a value of 1 means that the differential approximation holds with certainty. The DAP results of the proposed work are given in Tables 13–16.

The maximum value of differential approximation probability for both S-boxes S1,S2,S3, and S2 is 0.046875, 0.0390625, 0.046875, and 0.0390625.

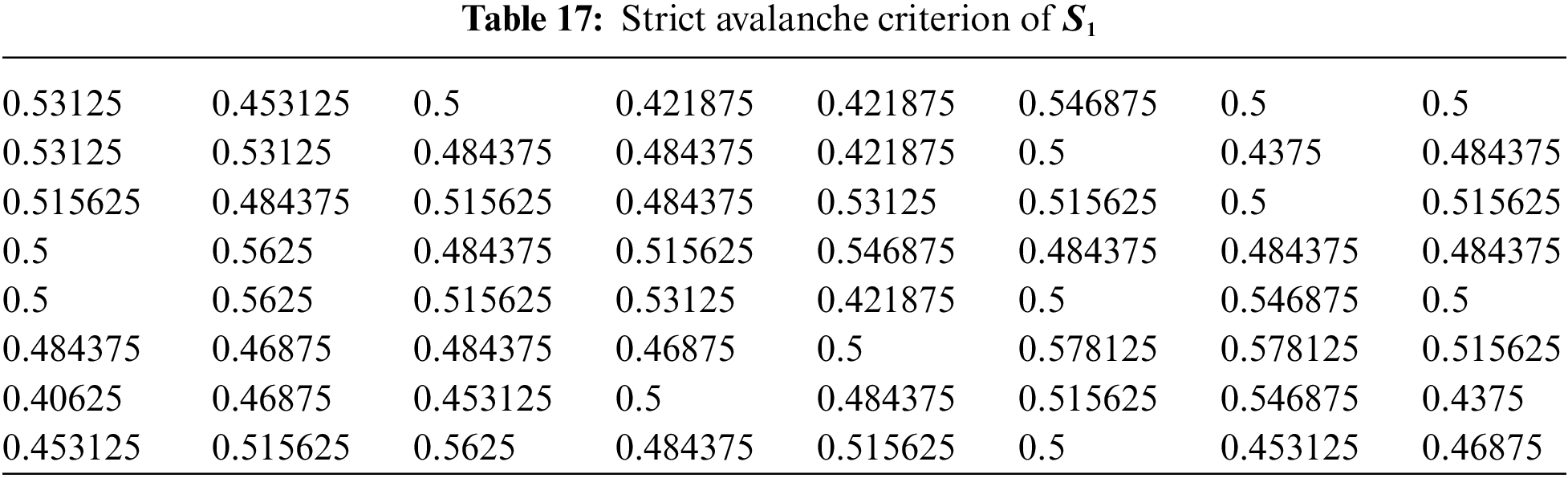
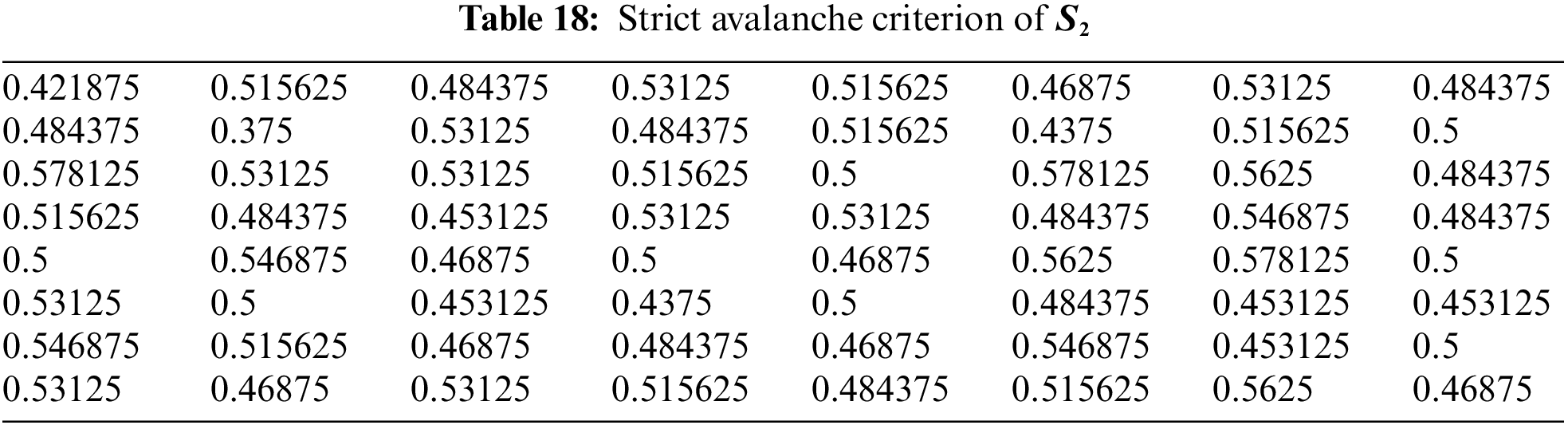
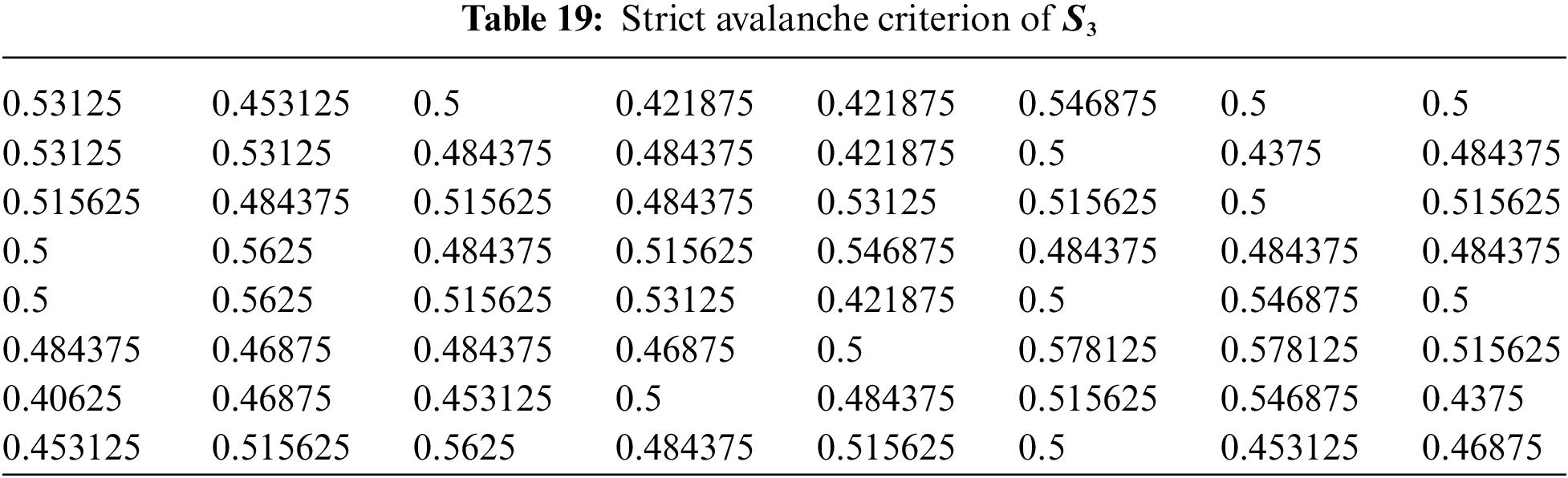
4.5 Strict Avalanche Criterion (SAC)

The Strict Avalanche Criterion (SAC) is a measure of the cryptographic strength of a substitution box (S-box). The SAC measures how much a change in one input bit affects the output bits on average, and is defined as follows: For every pair of input bits i and j, and for every pair of output bits k and l, the difference between the output bits when i and j are flipped is denoted by Δ{i,j}{k,l}. The SAC requires that the average over all pairs of input and output bits of the total number of output bit differences that occur when a single input bit is flipped is at least 1/2:

∑{i,j=1}{n}∑{k,l=1}{m}abs(Pr[Δ{i,j}{k,l}=1]−12)≤ε

where n is the number of input bits, m is the number of output bits, and ε is a small positive constant, typically set to 0.01 or smaller. The results in Tables 17–20 show that the value of the strict avalanche criterion of S-boxes based on the residue of a prime number is ~1/2.

5  Comparison

The former tests are performed on well-known S-boxes over EC, chaotic maps, and finite fields presented in [19–23,26,27] in order to compare them to the proposed S-boxes S1,S2,S3, and S4 over EI. Table 21 shows the results of the EC, chaotic maps (CM), and EI analyses for the various parameters. It is discovered that the proposed S-boxes have a higher nonlinearity value than EC, CM, and other S-boxes. The intriguing features of the proposed technique provide S-boxes pair at a time by fixing three parameters a,b, and p. However, the prime field, which is dependent on the EC via various techniques, provides one S-box at a time by fixing three parameters a,b, and p. Table 21 and Fig. 1 show the nonlinearity of the proposed S-box. The proposed S-box LAP results are lower than those presented in [19–23,26,27] and Fig. 2. As a result, the proposed S-boxes generate more data confusion and are more resistant to linear attack [17] than [19–23,26,27]. The proposed S-boxes’ SAC and BIC results are comparable to those of other S-boxes used in Table 21 and Fig. 2. As a result, the S-box generated by the proposed technique and the S-boxes shown in Table 21 cause equal magnitude diffusion in the data. The proposed DAP is comparable to the DAP of S-boxes in [19–23,26,27] and Fig. 2. Thus, when compared to the others, the proposed technique generates an S-box with high resistance to differential cryptanalysis [18]. Table 21 shows the analysis results of newly generated paired S-boxes by the EI cyclic group. Table 21 shows that the performance of paired S-boxes by the cyclic group over EI is comparable to that of S-boxes over EC.

Figure 1: Comparison of NL of proposed work with existing works

Figure 2: Comparison of BIC, SAC and LAP of proposed work with existing works

6  Conclusion and Future Directions

We propose a novel construction of substitution boxes by using affine mapping and fixing three parameters a, b, and p. By fixing the three parameters, the prime field dependent on the EC, chaotic maps, and Gaussian integers provide one S-box at a time. Here, the Prime p must be greater than or equal to 257 and belong to the cyclic group over the residue class of Eisenstein integers in order to produce cryptographically robust S-boxes. The newly proposed S-boxes are tested by using different available algebraic and statistical tests. Additionally, the proposed S-boxes cryptographic characteristics are contrasted with some of the currently used S-boxes over EC, Gaussian integers, and chaotic maps. The results indicate that the proposed algorithm can generate paired S-boxes with high resistance to linear and differential attacks.

The proposed S-boxes over the residue class of EI integers may extend to the S-boxes over the residue class of quaternion and octonion integers. These structures may also use for watermarking and image encryption.

Acknowledgement: The authors would like to thank the anonymous reviewers for their valuable comments. This work was financially supported by the Deanship of Scientific Research at King Khalid University in Saudi Arabia.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, for funding this work through the General Research Groups Program under Grant No. R.G.P.2/109/43.

Author Contributions: Study conception and design: M. S., and T. S.; data collection: M. S., and M. M. H.; analysis and interpretation of results: M. S., T. S., M. M. H., Z. B., and A. A.; draft manuscript preparation: M. S., and M. M. H. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. K. Ruohonen, “Mathematical cryptology,” Lecture Notes, vol. 1, no. 1, pp. 1–138, 2010. [Google Scholar]

2. C. E. Shannon, “Communication theory of secrecy systems,” The Bell System Technical Journal, vol. 28, no. 4, pp. 656–715, 1949. [Google Scholar]

3. M. M. Hoobi, “Strong triple data encryption standard algorithm using nth degree truncated polynomial ring unit,” Journal of Science, vol. 3, no. 3, pp. 1760–1771, 2017. [Google Scholar]

4. A. Fathy, I. F. Tarrad, H. F. A. Hamed and A. I. Awad, “Advanced encryption standard algorithm, issues and implementation aspects,” in Int. Conf. on Advanced Machine Learning Technologies and Applications, Berlin, Heidelberg, Springer, vol. 12, pp. 516–523, 2012. [Google Scholar]

5. A. Anees and Y. P. P. Chen, “Designing secure substitution boxes based on permutation of symmetric group,” Neural Computing and Applications, vol. 2, no. 11, pp. 7045–7056, 2020. [Google Scholar]

6. W. Gao, B. Idrees, S. Zafar and T. Rashid, “Construction of nonlinear component of block cipher by action of modular group PSL (2, Z) on projective line PL(GF(28)),” IEEE Access, vol. 8, pp. 136736–136749, 2020. [Google Scholar]

7. H. A. Ahmed, M. F. Zolkipli and M. Ahmad, “A novel efficient substitution-box design based on firefly algorithm and discrete chaotic map,” Neural Computing and Applications, vol. 31, pp. 7201–7210, 2019. [Google Scholar]

8. I. Hussain, A. Anees, A. H. Alkhaldi, M. Aslam, N. Siddiqui et al., “Image encryption based on Chebyshev chaotic map and S8 S-boxes,” Optica Applicata, vol. 49, no. 2, pp. 317–330, 2019. [Google Scholar]

9. L. C. N. Chew and E. S. Ismail, “S-box construction based on linear fractional transformation and permutation function,” Symmetry, vol. 12, no. 5, pp. 826–842, 2020. [Google Scholar]

10. B. Arshad, N. Siddiqui, Z. Hussain and M. E. U. Haq, “A novel scheme for designing secure substitution boxes (S-boxes) based on Mobius group and finite field,” Wireless Personal Communications, vol. 135, no. 124, pp. 3527–3548, 2022. [Google Scholar]

11. A. H. Zahid and M. J. Arshad, “An innovative design of substitution-boxes using cubic polynomial mapping,” Symmetry, vol. 11, pp. 1–10, 2019. [Google Scholar]

12. M. Sajjad, T. Shah and R. J. Serna, “Designing pair of nonlinear components of a block cipher over gaussian integers,” Computers, Materials & Continua, vol. 74, no. 1, pp. 1–20, 2023. [Google Scholar]

13. M. Sajjad, T. Shah, M. M. Hazzazi, A. R. Alharbi and I. Hussain, “Quaternion integers based higher length cyclic codes and their decoding algorithm,” Computers, Materials & Continua, vol. 73, no. 1, pp. 1177–1194, 2022. [Google Scholar]

14. M. Özen and M. Güzeltepe, “Cyclic codes over some finite quaternion integer rings,” Journal of the Franklin Institute, vol. 348, no. 7, pp. 1312–1317, 2011. [Google Scholar]

15. E. Biham and A. Shamir, “Differential cryptanalysis of DES-like cryptosystems,” Journal of Cryptology, vol. 4, no. 1, pp. 3–72, 1991. [Google Scholar]

16. B. B. Cassal-Quiroga and E. Campos-Cantón, “Generation of dynamical S-boxes for block ciphers via extended logistic map,” Mathematical Problems in Engineering, vol. 3, pp. 1–12, 2020. [Google Scholar]

17. G. Tang and X. Liao, “A method for designing dynamical S-boxes based on discretized chaotic map,” Chaos Solitons and Fractals, vol. 23, no. 5, pp. 1901–1909, 2005. [Google Scholar]

18. G. Chen, Y. Chen and X. Liao, “An extended method for obtaining S-boxes based on three-dimensional chaotic Baker maps,” Chaos Solitons and Fractals, vol. 31, no. 3, pp. 571–579, 2007. [Google Scholar]

19. S. Ibrahim and A. Alharbi, “Efficient image encryption scheme using Henon map, dynamic S-boxes and elliptic curve cryptography,” IEEE Access, vol. 8, pp. 194289–194302, 2020. [Google Scholar]

20. U. Çavuşoğlu, A. Zengin, I. Pehlivan and S. Kaçar, “A novel approach for strong S-box generation algorithm design based on chaotic scaled Zhongtang system,” Nonlinear Dynamics, vol. 87, no. 2, pp. 1081–1094, 2021. [Google Scholar]

21. N. Siddiqui, A. Naseer and M. E. U. Haq, “A novel scheme of substitution-box design based on modified Pascal’s triangle and elliptic curve,” Wireless Personal Communications, vol. 116, no. 4, pp. 3015–3030, 2019. [Google Scholar]

22. A. K. Farhan, R. S. Ali, H. Natiq and N. M. Al-Saidi, “A new S-box generation algorithm based on multistability behavior of a plasma perturbation model,” IEEE Access, vol. 7, pp. 124914–124924, 2021. [Google Scholar]

23. A. Belazi, M. Khan, A. A. A. El-Latif and S. Belghith, “Efficient cryptosystem approaches: S-boxes and permutation, substitution, based encryption,” Nonlinear Dynamics, vol. 87, no. 1, pp. 337–361, 2017. [Google Scholar]

24. K. Huber, “Codes over eisenstein-jacobi integers,” Contemporary Mathematics, vol. 168, no. 1, pp. 165, 1994. [Google Scholar]

25. C. Baudoin and F. X. Standaert, “Experimenting linear cryptanalysis,” in Advanced Linear Cryptanalysis of Block and Stream Ciphers. Amsterdam: IOS Press, pp. 1–28, 2011. [Google Scholar]

26. G. Jakimoski and L. Kocarev, “Chaos and cryptography: Block encryption ciphers based on chaotic maps,” IEEE Transactions on Circuits and Systems: Fundamental Theory and Applications, vol. 48, no. 2, pp. 163–169, 2001. [Google Scholar]

27. M. Khan and Z. Asghar, “A novel construction of substitution box for image encryption applications with Gingerbreadman chaotic map and S8 permutation,” Neural Computing and Applications, vol. 29, no. 4, pp. 993–999, 2018. [Google Scholar]