A Strengthened Dominance Relation NSGA-III Algorithm Based on Differential Evolution to Solve Job Shop Scheduling Problem

1  Introduction

The Job Shop Scheduling Problem (JSSP) refers to a class of problems where the objective is to optimize scheduling by arranging the processing sequence of operations within a set of tasks, while adhering to task-specific constraints and precedence relations among operations [1]. Job shop scheduling, as a critical component of the intelligent manufacturing industry, plays a vital role in resolving the conflicts between shop floor production and optimization objectives [2]. It facilitates the methodical advancement of production processes while adhering to constraints imposed by multiple resources. Concurrently, effective scheduling of the manufacturing process can significantly enhance resource utilization and production efficiency [3].

JSSP, a prominent focus in intelligent manufacturing research, exemplifies a classic NP-hard combinatorial optimization challenge, rendering its resolution exceedingly arduous [4]. Due to the excessive time costs associated with traditional exact methods for solving JSSP, they have become less practical. Therefore, researchers have turned to heuristic algorithms, such as the Firefly Algorithm [5], Gray Wolf Optimization (GWO) [6], NSGA-III Algorithm [7], and others to address these intricate problems. Drawing from the existing research, it becomes evident that heuristic algorithms are effective in solving JSSP, characterized by swift execution and superior optimization performance. As a result, they play a pivotal role in the domain of enterprise production scheduling. At the same time, those algorithms play an important role in the path planning of unmanned aerial vehicles [8], pedestrian and vehicle detection [9] and other fields. However, existing algorithms often suffer from issues such as excessive reliance on parameters, poor global search capability, and significant performance degradation when faced with complex scheduling problems. This paper aims to propose a high-performance algorithm that reduces the dependence on parameters and incorporates efficient search methods, allowing it to maintain efficient performance in complex multi-objective JSSP and achieve thorough exploration of the solution space.

In classical JSSP models, the primary optimization objective has traditionally focused on minimizing the single criterion of the makespan. However, with the advancement of factory automation, a single scheduling criterion can no longer meet the diverse production requirements. Therefore, in this paper, we consider a total of five objectives to solve the Multi-Objective Job Shop Scheduling Problem (MO-JSSP). These objectives encompass total flow time, total tardiness time, average machine idle time, and implementing a Just-in-Time (JIT) production mode, in addition to the traditional objective of makespan. When there are too many objectives, traditional algorithms struggle to find suitable trade-offs and equilibrium points among multiple objectives. Moreover, the solution space of MO-JSSP is vast, which may lead to computational complexity and long computation time for traditional optimization algorithms.

The NSGA-III algorithm, proposed by Deb et al. [7] in 2013, represents a significant category of meta-heuristic evolutionary algorithm. It, as a classical multi-objective optimization algorithm, can be applied to solve various multi-objective optimization problems. It has shown excellent performance, particularly when dealing with problems involving three or more objectives, and has garnered considerable attention from scholars worldwide. However, when addressing the MO-JSSP, traditional NSGA-III employs the Simulated Binary Crossover (SBX) operator as its crossover mechanism, leading to limitations, including constrained global search capability and susceptibility to premature convergence. Additionally, the dominance relation exhibits a poor balance between convergence and diversity, often leading to a concentration of solutions in a small portion of the Pareto front. To address these issues and achieve a more favorable equilibrium between the convergence and diversity aspect of multi-objective optimization problems, this paper introduces enhancements to the traditional NSGA-III. These algorithm improvements primarily concentrate on three key aspects: evolutionary genetic operator, dominance relation among non-dominated solution sets, and encoding and decoding methods tailored for job shop scheduling instances. Through experimental verification, the improved algorithm shows strong superiority in the MO-JSSP instances.

The main contributions of this paper are as follows:

•   Proposed hybrid constraint differential evolution and simulated binary crossover to enhance the searchability of NSGA-III and avoid premature convergence.

•   Introduced a new reinforced dominance relation to improve the convergence and diversity of the algorithm.

•   Designed effective encoding and decoding methods for MO-JSSP.

The rest of the paper is organized as follows: Section 2 presents the existing related research work. Section 3 introduces the model of MO-JSSP. Section 4 introduces the algorithm proposed in this paper. Section 5 conducts comparative tests on the performance of the algorithm. Section 6 provides a summary of the work in this paper and future research directions.

2  Related Work

JSSP has remained a focal point of research for numerous years, and scholars have undertaken extensive investigations to find efficient solutions. For the single-objective JSSP, the primary methods include mathematical programming and metaheuristics. For instance, Meng et al. [10] devised a novel integer linear programming approach for JSSP. Liu [11] proposed an enhanced metaheuristic algorithm that effectively improves the resolution capability of candidate solutions, leading to efficient solutions for the single-objective JSSP.

With the rapid development of the manufacturing industry and the increasing complexity of customer requirements, traditional single-objective JSSP struggles to accommodate today’s diverse production requirements. Consequently, more and more scholars have embarked on research into the multi-objective JSSP. For instance, Liu et al. [12] proposed a genetic algorithm based on a multi-population multi-objective framework to comprehensively consider scheduling problems with five interconnected workshops. The effectiveness of the proposed algorithm is evaluated by analyzing the evaluation metrics. Tan et al. [13] introduced an improved NSGA-II algorithm to address the dual-resource-constrained flexible job shop scheduling problem. It aims to alleviate production fatigue and enhance efficiency by jointly scheduling machines and workers. Xu et al. [14] presented a three-layer coded hybrid algorithm to solve MO-JSSP, accounting for job outsourcing and carbon emission, effectively addressing pressing environmental issues. Wang et al. [15] proposed a multi-objective dual-population algorithm capable of continuously improving scheduling solutions during optimization interaction. Based on previous research, it has been found that many algorithms contain a significant number of simple crossover and mutation operations, resulting in inefficient search patterns. Additionally, some algorithms tend to get trapped in local optima, which prevents them from finding the global optimum solution.

NSGA-III is considered a favorite algorithm for solving multi-objective problems due to its efficient crossover and mutation operations. These operations help overcome the inefficiency of simple crossover and mutation patterns found in many algorithms. Many scholars have dedicated their efforts to improving the NSGA-III algorithm for efficient resolution of MO-JSSP. Wu et al. [16] designed a flexible job shop scheduling model considering energy factors, combining a dual-control strategy with the NSGA-III algorithm to enhance the efficiency of the entire JSSP optimization process. Similarly, Sun et al. [17] proposed a multi-population co-evolution and natural selection NSGA-III algorithm, capable of effectively optimizing makespan and energy consumption in MO-JSSP. However, these algorithms are not suitable for handling MO-JSSP with a large number of objectives. They also have limitations in maintaining the diversity and distribution of solutions as they primarily rely on reference points for individual selection. They may struggle to provide a well-distributed set of solutions across the Pareto front.

In summary, the methods mentioned above have made notable advancements. However, they still possess certain limitations. As a result, researchers continue to explore new approaches to tackle the MO-JSSP. The objective of this paper is to present an enhanced NSGA-III algorithm that incorporates efficient crossover and mutation mechanisms, along with a more effective individual selection method. These enhancements will enable the algorithm to meet diverse production requirements and effectively solve the MO-JSSP problem.

3  Multi-Objective Job Shop Scheduling Model

3.1 Problem Description

MO-JSSP can be described as m processing machines {M1, M2, M3, …, Mm} for n jobs to be processed, of which each job i (i = 1, 2, …, n) has ni operations. The j-th operation of job i is processed on a specified machine M, according to a certain process sequence. Denote the j-th operation of job i by Oij. The processing time Tij for process Oij is determined by the specific performance of the machine π(Oij) being processed, and the delivery time of job i is Di. The scheduling task is to determine the optimal machining sequence of n jobs on each machine, subject to all constraints, such that the optimization objective of the scheduling model is optimal.

3.2 Multi-Objective Scheduling Optimization Model

This model evaluates the production efficiency of the entire scheduling model based on objectives such as makespan, flow time, tradiness time, average machine idle time and the Just-in-Time (JIT) production mode. The optimization objective set can be represented as min (f1, f2, f3, f4, f5), where minimizing the makespan and minimizing the total flow time aim to reduce job processing time and improve the overall efficiency of the production workshop. Minimizing total tardiness time and adhering to the JIT production mode are intended to maximize customer satisfaction by ensuring on-time delivery, thereby enhancing the company’s reputation. Minimizing average machine idle time aims to maximize machine utilization and shorten the overall project duration. The formulas for the objective functions are as follows:

Makespan:

f1=min(maxCi) i ∈ {1,2,…,n}(1)

Total flow time:

f2=min(∑i=1nCi)(2)

Total tradiness time:

f3=min(∑i=1nmax(0,(Ci−Di)))(3)

Average machine idle time:

f4=(∑i=1mCm−∑i=1nCi)/n(4)

Just in Time (JIT) production mode time:

f5=min(∑i=1n(0.5∗max(0,(EE−Ci))+0.5∗max(0,(Ci−TT))))(5)

S.T.

Sij2π(Oij)×Zij2π(Oij)−Sij1π(Oij)×Zij1π(Oij)≥Tij1π(Oij)×Zij1π(Oij)i∈{1,2,⋯n},j∈{1,2,⋯ni}(6)

Si(j+1)π(Oij)2×Zi(j+1)π(Oij)2−Sijπ(Oij)1×Zijπ(Oij)1≥Tijπ(Oij)1×Zijπ(Oij)1i∈{1,2,⋯n},j∈{1,2,⋯ni}(7)

∑i=1n∑j=1niZijπ(Oij)=1(8)

Ci in Eqs. (1) and (2) denotes the time taken by the i-th job to finish the last operation; Di in Eq. (3) represents the delivery period, which is set to be 1.5 times the completion time of the job on the machine; In Eq. (4), Cm represents the time required for the m-th machine to complete the last process of the i-th job; In Eq. (5), EE represents the earliest delivery date, which is set to be 1.2 times the processing completion time of the job on the machine, and TT represents the latest delivery date, which is set to 1.8 times the processing completion time of the job on the machine.

In Eqs. (6) and (7), S(i,j,π(Oij)) denotes the start time of Oij on the optional processing machine. Z(i,j,π(Oij)) is processed on this machine or not, yes is 1, otherwise 0. Eq. (6) enforces the machine constraint, ensuring that each machine can process only one operation at a time. Eq. (7) addresses the job process constraint, ensuring that different operations of a job cannot be processed simultaneously. Eq. (8) indicates that only one optional machine is selected for an operation, that is, the machine selected for Oij process is π (Oij).

4  NSGA-III-SD Algorithm for Solving MO-JSSP

4.1 Encoding

In scheduling, an effective encoding method is crucial for the overall optimization of scheduling solutions [18]. For JSSP, this paper employs a process-based encoding method. In this approach, a feasible sequence of operations is encoded as [1 2 2 4 3 1 1 2 3 3 4 4], where the number indicates the job number and the frequency of each number represents the number of operations for that job. For example, in the encoding scheme, the first “1” represents the first operation for job 1, the first “2” represents the first operation for job 2, and the second “2” represents the second operation for job 2. The total length of a sequence of operation codes corresponds to the total number of operations for the task. Fig. 1 provides an example of a feasible schedule for JSSP.

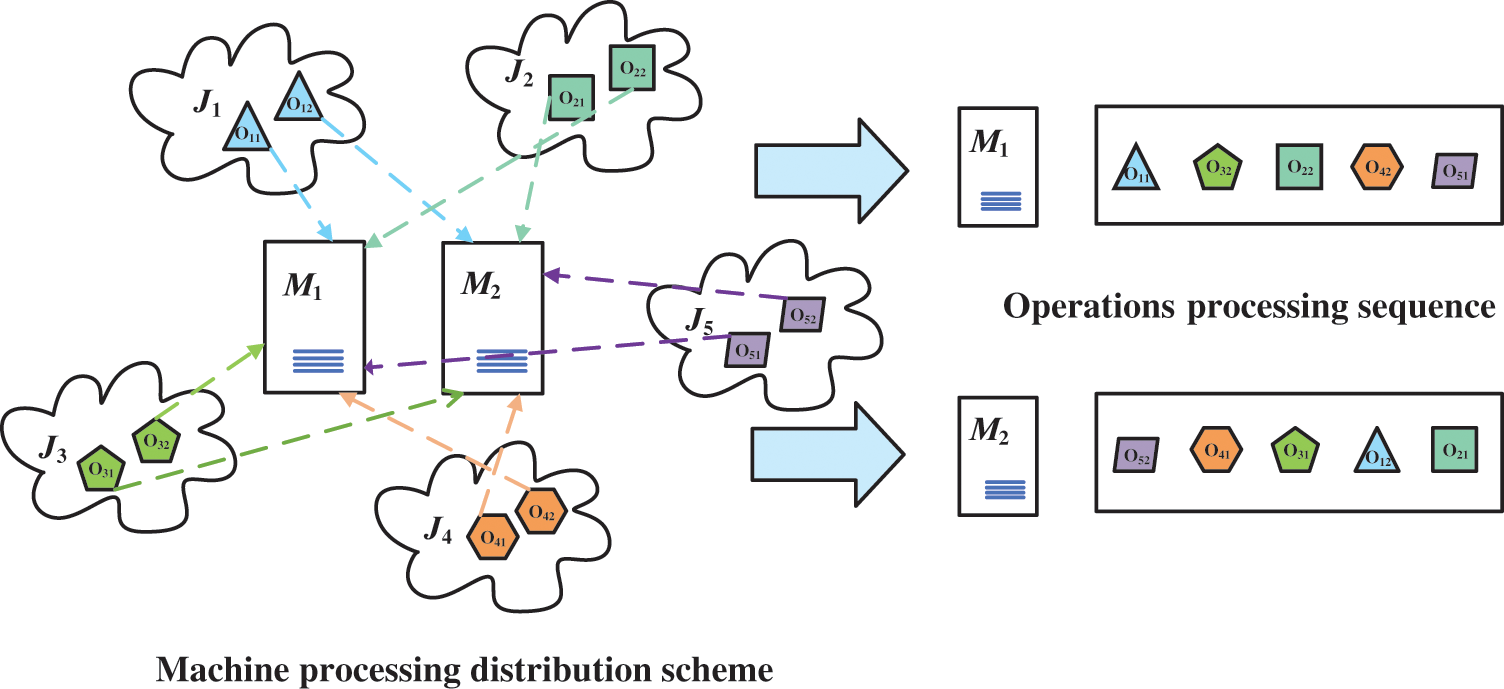
Figure 1: JSSP scheduling example

The key issue of JSSP in Fig. 1 is to properly handle the processing sequence of the operations on machines M1 and M2. For example, the processing sequence of O12 must be after O11. The processing sequence of M1 is {O11, O32, O22, O42, O51}, and the processing sequence of M2 is {O52, O41, O31, O12, O21}.

4.2 Decoding

Since the NSGA-III algorithm is primarily designed for solving continuous optimization problems and cannot be directly applied to typical discrete combinatorial JSSP, it is necessary to decode the solutions into operation code formats at the end of each iteration. Furthermore, it is essential to handle any illegal solutions generated during the decoding process. In this regard, the paper has devised an effective decoding method to facilitate the transition between the population positions in the continuous solution space and the discrete JSSP encoding of operations, as depicted in Fig. 2. The steps for achieving an effective decoding scheme are as follows:

Figure 2: Effective decoding scheduling scheme

(1) Obtain the individual position X=[x1,x2,…,xL] in the continuous solution space (L is the total number of processes in the procedure);

(2) The individual positions of the continuous solution are converted to job individual position codes by rounding down;

(3) Handle the generated illegal solutions effectively, following these steps:

  i) Determine whether the number of operations for each job equals the maximum allowed. If it does, no illegal solutions are generated.

  ii) If the number exceeds the maximum, identify the positions of all jobs with an excessive number of operations, and randomly replace the operations exceeding the maximum with operations from adjacent jobs, adjusting the counts accordingly.

  iii) If the number does not exceed the maximum, randomly select positions outside the index of the illegal job and fill the missing operations with operations from that job.

(4) Establish a valid correspondence between individual positions and operation encoding.

Fig. 2 shows an example of the FT06 illegal solution processing scheme. FT06 data set has a scale of 6 × 6. If the number of jobs in the encoding method exceeds the maximum number of operations for this job, it means that there is an illegal solution individual. The effective processing is completed according to the illegal solution processing steps, which can damage the processing sequence of other operations to a lesser extent.

After adopting this encoding and decoding scheme, each set of encoding schemes can be regarded as a chromosome, which facilitates the algorithm to perform corresponding crossover and mutation, thereby gradually optimizing the scheduling results. Moreover, the proposed approach in this paper allows for the rapid transformation of individual positions into valid discrete encodings, without introducing complex calculations that would burden the algorithm. It is a simple and efficient method.

4.3 Simulated Binary Crossover

The Simulated Binary Crossover (SBX) [19] first simulates the single-point crossover process in binary encoding and then applies this process to the chromosome genes in real-valued encoding. Genes from parent chromosomes are passed to the next generation through the SBX crossover, where the crossover probability is set to 1. Assuming that in the population, the parent chromosomes are P1 and P2, and two offspring are generated through SBX, resulting in chromosomes X1 and X2.

{X1=12(P1,i+P2,j)+βSBX2(P1,i−P2,j)(i∈(1,2,⋯N/2),j∈(N/2+1,⋯N))X2=12(P1,i+P2,j)−βSBX2(P1,i−P2,j)(i∈(1,2,⋯N/2),j∈(N/2+1,⋯N))(9)

In Eq. (9), βSBX is a random variable generated as:

βSBX={(2μ)1γ+1,μ≤0.5[2(1−μ)]−1γ+1,μ>0.5(10)

In Eq. (10), μ is a random number distributed evenly over the interval (0,1) and γ is the distribution index set to 20.

4.4 Polynomial Mutation

The probability of polynomial mutation is 1/D [20], where D represents the number of all operations. The form of the mutation operator is P′=P+X(ui−li), where the individual X obtained after the parent individual P is mutated is:

X={[2∗μ+(1−2∗μ)(1−δ1)γ+1]1γ+1−1,μ≤0.51−[2∗(1−μ)+2∗(μ−0.5)(1−δ2)γ+1]1γ+1,μ>0.5(11)

where δ1=P−liui−li,δ2=ui−Pui−li, μ is a random number uniformly distributed on the interval (0,1), ui and li are the upper and lower bounds of the i-th individual variable, and γ is the distribution index set to 20.

SBX and Polynomial mutation are the original evolutionary operators of NSGA-III. However, its overall search performance is poor and prone to premature convergence. Moreover, its dominance relation performs poorly in balancing convergence and diversity, often resulting in a small portion of the solution set being concentrated on the Pareto front. To enhance the algorithm’s performance, new evolutionary operators and dominance relations have been introduced based on experimental research, as described in the following text.

4.5 Constrained Differential Evolution Strategy

Introducing Differential Evolution (DE) into the algorithm’s evolution process can effectively enhance the diversity of solutions. However, it is important to note that traditional DE operators scale the difference vector based on the differences, which can result in mutation having a high degree of randomness and a lack of direction [21]. To control the variation intensity of each individual in the population, upper and lower limit parameter values are set for each variable in this paper. First, randomly select two different individuals in the population, use the two selected individuals to calculate the vector difference V, and then carry out the polynomial mutation of Eq. (12) on V with the probability Pm, and the mutation probability is 0.15. Then restrict the difference vector V, the restriction method is as Eq. (13).

Vi={Vi+(ui−li)∗((2μ)1γ+1−1),μ≤0.5Vi+(ui−li)∗[1−2∗(1−μ)]1γ+1,μ>0.5(12)

Vi={−υiifVi<−υiυiifVi>υiViotherwise(13)

υi=ui−li2i∈{1,2,⋯N}(14)

The specific constraint differential evolution strategy is shown in Algorithm 1.

The algorithm enhances the diversity of solutions by introducing a constrained differential evolution mechanism, which allows for better exploration of the search space. Additionally, by setting upper and lower parameter limits and using polynomial mutation, NSGA-III-SD can control the mutation intensity of individuals, thereby balancing the trade-off between exploration and exploitation during the search process and avoiding getting stuck in local optima. This evolutionary approach enables NSGA-III-SD to excel in global search and prevent premature convergence.

4.6 Strengthened Dominance Relation Strategy

Elimination and selection of individuals will inevitably occur during the evolution of algorithms. In multi-objective optimization, the pareto dominance relation is widely used to distinguish the superiority and inferiority of candidate solutions. Reviewing the existing dominance relations, there are four representative classes:

1. The first class of dominance relations aims to improve selection pressure by expanding the dominance region. Examples include methods like S-CDAS [22] and GPO [23].

2. The second class of dominance relations is based on the grid-based approach in the objective space, such as ∋− dominance [24] and pa∋− dominance [25].

3. The third class of dominance relations introduces a new dominance relation defined using fuzzy logic, as seen in L− dominance [26].

4. The fourth class of dominance relations is defined by a set of weight vectors, as seen in θ− dominance [27].

However, most existing dominance relations increase the algorithm’s selection pressure and struggle to balance the trade-off between convergence and diversity [28]. Therefore, this paper introduces a new dominance relation called Strengthened Dominance Relation (SDR) to reduce the selection pressure of NSGA-III while maintaining a good balance between convergence and diversity.

The SDR is defined as follows:

{Con(x)<Con(y),θxy≤θ¯Con(x)⋅θxyθ¯<Con(y),θxy>θ¯(15)

where Con(x)=∑i=1Mfi(x) is a measure to measure the degree of convergence of X, θxy=arccos⁡(f(x),f(y)) represents the acute angle between the target value of two candidate solutions. θ¯ represents the niche size of each candidate solution, and its size can be adaptively estimated according to the distribution of the candidate solution set. In this paper, the θ¯ size is set as follows:

{minq∈P∖{p}θpq|p∈P}(16)

where θpq denotes the acute angle between any pair of candidate solutions p and q. It is worth noting that to better handle JSSP where the ideal point is not the origin or where the number of targets is too large, the minimum and maximum values of each target in the population are normalized as the ideal and minimum points, respectively, before computing Con(x) and θxy.

According to the first equation in Eq. (15), if the angle between any x and a candidate solution y is less than θ¯, and if the convergence of x is smaller than the convergence of y, then x is said to dominate y. This implies that within each niche, due to the absence of non-dominated solutions with angles less than θ¯, the diversity of the non-dominated solution set is naturally maintained. Conversely, according to the second equation, if two candidate solutions x and y are not in the same location and if the convergence of y is much worse than that of x, x can still dominate y, where the probability of x dominating y is negatively correlated with the angle θxy. This ensures the convergence of the non-dominated solution set.

To better illustrate this process, Fig. 3 depicts the distribution of dominance region in a two-objective space. On the one hand, y1 is located within the niche range of x, indicating that its convergence performance is worse than that of x, and x dominates y1. On the other hand, y2 is located outside the niche range of x, indicating that its convergence performance is much worse than that of x, and x dominates y2. The dominance region of x consists of two parts, as given by Eq. (15). Individuals within the dominant region will be selected for the next iteration. Due to the adaptability of θ¯, the dominant region will also adaptively change.

Figure 3: SDR strategy solution set dominance relation distribution

The non-dominated region identified by SDR covers the entire Pareto front, while other dominance relations often shrink to a small region or fail to comprehensively cover the Pareto front. In comparison, SDR maintains a better balance between convergence and diversity. Additionally, SDR does not rely on aggregation functions or weight vectors but can adaptively select candidate solutions with better convergence and diversity. This adaptability allows SDR to handle Pareto front of various shapes.

4.7 NSGA-III-SD Algorithm

This algorithm operates within the framework of the NSGA-III algorithm and is executed as follows:

Step 1: Initialize the population and algorithm parameters.

Step 2: Generate the mating pool using tournament selection. Check if the evaluation count is less than or equal to one-third of the maximum evaluation count. If it is, use constrained differential evolution as the genetic operator to generate offspring population. Otherwise, use simulated binary crossover and polynomial mutation to generate offspring population.

Step 3: Merge the parent and offspring populations.

Step 4: Apply the SDR fast non-dominated sorting strategy to divide the merged population into non-dominated layers. Use the NSGA-III algorithm based on reference points to select suitable individuals from the last front to determine the next population.

Step 5: According to the encoding and decoding scheme, the individual position is converted into the operation encoding.

Step 6: Check if the termination condition is met. If yes, end the iteration. Otherwise, return to Step 2.

The specific NSGA-III-SD algorithm is detailed in Algorithm 2.

5  Experiment and Discussion

5.1 Test Date and Parameter Setting

This study employs a set of 20 widely recognized job shop scheduling test datasets to validate the algorithm’s effectiveness. These datasets are sourced from Fisher & Thompson (FT) [29], Lawrence (LA) [30], Adams & Balas & Zawack (ABZ) [31], and Storer & Wu & Vaccari Hard (SWV) [32]. FT datasets come in different sizes, including 6 × 6, 10 × 10, and 20 × 5. FT06 has processing time in the range [1,10], and FT10 and FT20 have processing time in the range [1,99]. The ABZ dataset is of size 20 × 15, with processing time in the range [10,40]. SWV dataset includes three different sizes: 20 × 10, 20 × 15, and 50 × 10. The processing time falls within the range [1,100]. LA dataset consists of six different sizes: 10 × 5, 15 × 5, 20 × 5, 15 × 10, 20 × 10, and 30 × 10. Processing time is in the range [5,99].

To validate the effectiveness of the NSGA-III-SD algorithm, it is compared with five advanced MOEAs: VaEA [33], SRA [34], MaOEACSS [35], NSGA-III [7], and NSGA-II [36]. The algorithm’s parameters align with the optimal configurations mentioned in the original paper. All algorithms share common crossover and mutation probabilities, set at 0.8 and 1/D [35], respectively, with D denoting problem dimensionality. Additionally, SRA employs a neighborhood size of 20, while MaOEACSS utilizes an environmental selection threshold set at 0. All codes are programmed using MATLAB 2019b, and the software is run on a system with an Intel(R) Core(TM) i9-9900K CPU @ 3.60 GHz and 64 GB RAM, operating on a Windows 10 system.

To ensure experimental fairness, consistent parameter settings are applied to all algorithms. According to the parameters mentioned by He et al. [35], all the parameters have been set as follows: initial population size N = 126, maximum number of iterations G = 100, number of runs R = 20, and number of evaluations E = N * G.

5.2 Performance Metric

To evaluate the quality, diversity, and distribution of the algorithm's solutions, two commonly used multi-objective evaluation metrics, Coverage of two sets (C) [37] and Hypervolume (HV) [38] are selected for analyzing the results. The specific introductions of these two metrics are as follows.

5.2.1 Coverage of Two Sets (C)

C(X1,X2)=|{a′′∈X2;∃a′∈X1:a′≻_a′′}|X2(17)

where X1 and X2 represent two different Pareto solution sets, C(X1,X2) denotes the ratio of solutions in X2 that are either dominated by or equal to solutions in X1, and its value ranges between 0 and 1. Specifically, when C(X1,X2)=1, it indicates that all solutions in X2 can be found in X1, and they are either dominated by or equal to solutions in X1. Conversely, when C(X1,X2)=0, it signifies that no solution in X2 is dominated by any solution in X1.

5.2.2 Hypervolume (HV)

HV(P,r)=∪x∈ppv(x,r)a(18)

In this equation, P represents the Pareto solution set obtained by each algorithm, and r is the reference point. x represents a normalized Pareto solution, and v represents the volume of the hypercube. The HV metric assesses the diversity and distribution of Pareto solutions within the objective space. A larger HV value signifies superior overall algorithmic performance.

5.3 Comparison Experiment

Table 1 provides a comparative analysis of the NSGA-III-SD algorithm against five other MOEAs, focusing on the C metric. All data represent the average outcomes from 20 independent runs for each algorithm, with superior results emphasized. A larger value of C means better convergence of the algorithm. The final row of the table contains statistical data on how frequently the NSGA-III-SD algorithm outperformed or underperformed the other comparison algorithms in terms of C value. Out of 20 test instances, the NSGA-III-SD algorithm obtained 19, 20, 20, 20, and 18 superior results, while VaEA, SRA, MaOEACSS, NSGA-III, and NSGA-II obtained 1, 0, 0, 0, and 2 superior results, respectively. It is evident that the NSGA-III-SD algorithm demonstrates strong performance and yields higher-quality solutions.

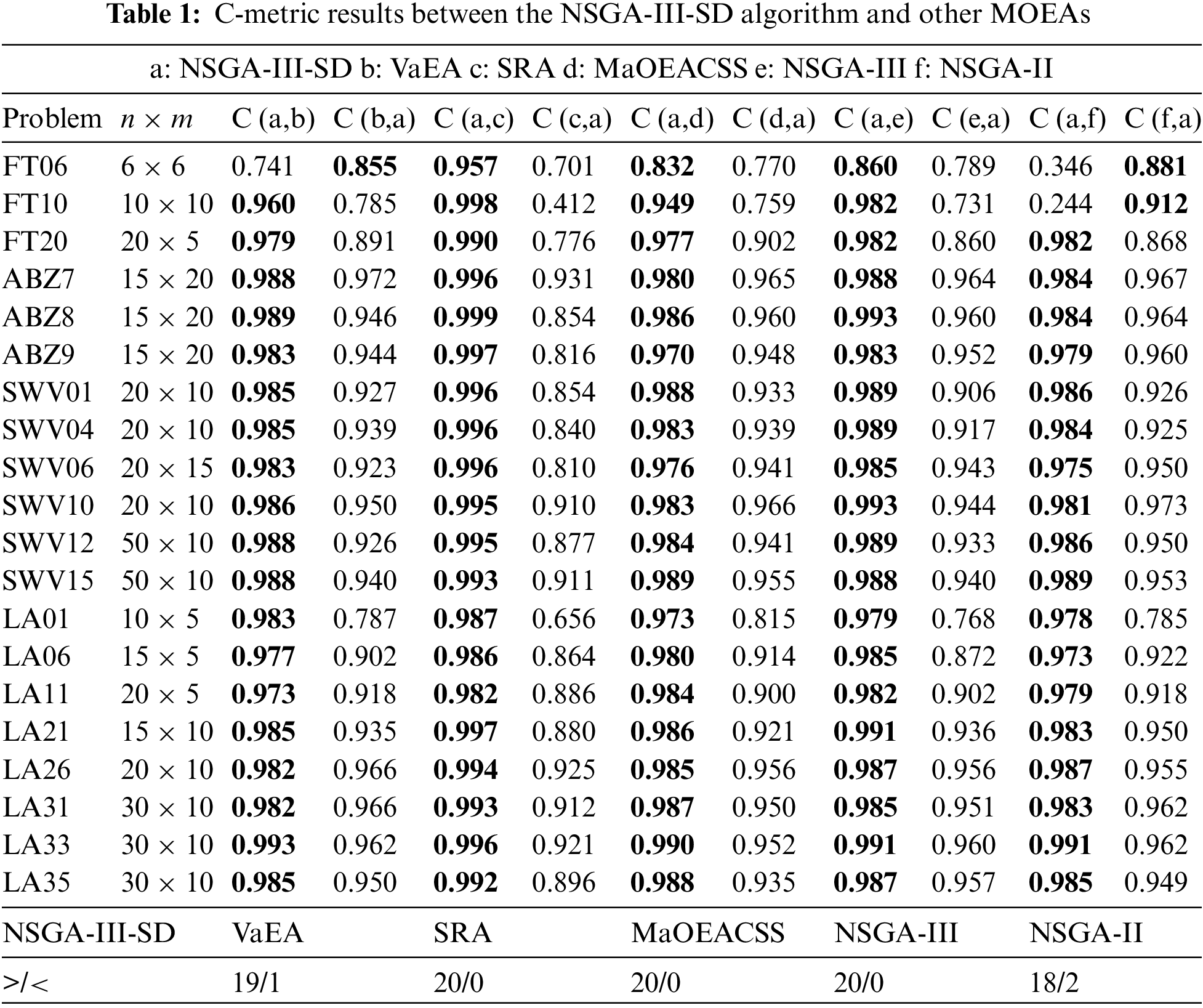
These comparative findings underscore the outstanding performance of the NSGA-III-SD algorithm in addressing MO-JSSP, attributed to its exceptional evolutionary strategy. Unlike the singular search approach of NSGA-III, NSGA-III-SD incorporates advanced evolutionary techniques like constrained differential evolution and simulated binary crossover. These techniques enable a diverse evolution mode and robust global exploration capability, mitigating the risk of premature convergence. The algorithm’s effective exploration of the solution space contributes to the production of higher-quality solutions and overall performance in addressing the MO-JSSP.

In addition to conducting a comparative analysis, we performed further analysis to provide a deeper understanding of the results. This section explores the algorithm’s performance across various datasets and problem complexities. Notably, the NSGA-III-SD algorithm consistently exhibited exceptional performance even when faced with an increasing number of jobs and machines. This indicates its robustness and scalability in handling most instances of the MO-JSSP. Furthermore, analysis reveals that the competitive edge of the NSGA-III-SD algorithm becomes increasingly prominent as problem complexity escalates. This suggests that the algorithm’s powerful capacity for exploratory endeavors remains potent when confronted with intricate and demanding problems. The effective exploration of the solution space and the ability to adapt to complex problems contribute to the NSGA-III-SD algorithm’s superior performance and the production of higher-quality solutions.

Following 20 independent runs of each algorithm, where the average HV values are computed, a Friedman rank-sum test is performed. Table 2 displays the ranks of all algorithms with a significance level of 0.05. Among all algorithms, NSGA-III-SD secures the second position, closely following SRA, and exhibits a remarkably low p-value of 3.2915E-16, indicating significant disparities in the outcomes across all algorithms. The HV metric serves as an indicator of the solution’s convergence and diversity. The high ranking of NSGA-III-SD implies that it attains superior convergence and diversity within its solution set.

The superiority of NSGA-III-SD can be attributed to its strategic utilization of the SDR approach during individual selection. This approach not only selects individuals with superior fitness but also takes advantage of individuals with potential benefits. In comparison to methods that solely rely on dominance relations for individual selection and elimination, SDR incorporates a niche technique based on candidate solutions. By autonomously determining the niche size according to the distribution of candidate solutions, NSGA-III-SD maintains a more favorable balance between convergence and diversity within each niche. This ability allows the algorithm to avoid solution overcrowding and enhance the diversity of the solution set, especially in complex MO-JSSP scenarios. Furthermore, NSGA-III-SD’s rank significantly surpasses that of NSGA-III, demonstrating a substantial improvement in the performance of the enhanced algorithm and effectively illustrating the effectiveness of various strategies.

In conclusion, the hybrid evolutionary approach of NSGA-III-SD exhibits enhanced search capability in solving MO-JSSP. Moreover, employing the SDR non-dominance ranking strategy, instead of the original sorting method in the NSGA-III algorithm, effectively balances the trade-off between population convergence and diversity.

Of course, this experimental study has certain limitations that should be acknowledged. One of the limitations is that the scalability of NSGA-III-SD has not been extensively tested, especially when dealing with hyperscale scheduling problems. Hyperscale problems may involve more complex constraints and decision variables, potentially impacting the performance of NSGA-III-SD. Therefore, further research can explore the performance of NSGA-III-SD on hyper-scale scheduling problems and evaluate its adaptability in handling highly discontinuous or non-convex Pareto front.

6  Conclusion

For the MO-JSSP with five objectives: makespan, total flow time, total tardiness time, average machine idle time, and just-in-time production mode, a strengthened dominance relation NSGA-III algorithm based on differential evolution, NSGA-III-SD, is proposed. NSGA-III-SD employs a constrained differential evolution strategy during the initial evolution stage to prevent premature convergence and enhance the trait of convergence. Furthermore, it replaces the original dominance relation of NSGA-III with the SDR non-dominance sorting strategy, effectively managing the trade-off between population convergence and diversity. The experimental results on MO-JSSP tests undeniably demonstrate the superior performance of NSGA-III-SD. It outperforms other algorithms in both the C metric and the HV metric, indicating higher-quality solutions as well as improved diversity and distribution of the solution set. These results highlight the strong overall performance and practical advantage of NSGA-III-SD in solving MO-JSSP.

The proposed algorithm has significant theoretical implications as it contributes to the understanding of multi-objective optimization in job shop scheduling. It provides insights into the effective utilization of a strengthened dominance relation and the integration of a constrained differential evolution strategy, contributing to the advancement of optimization algorithms in complex manufacturing systems.

Due to the need to maintain the Pareto front in NSGA-III-SD, the size of the set increases with the problem scale. Therefore, for hyperscale problems, NSGA-III-SD may have low convergence accuracy and require more computational resources. Future research can focus on designing more efficient evolutionary approaches to address this limitation.

In future work, we plan to further enhance the algorithm and expand its applications. We consider incorporating a dynamic resource allocation mechanism into the algorithm to solve the flexible job shop scheduling problem [39], or introducing a workshop allocation mechanism to address the distributed job shop scheduling problem [40].

Acknowledgement: Not applicable.

Funding Statement: This work was in part supported by the Key Research and Development Project of Hubei Province (Nos. 2020BAB1141, 2023BAB094), the Key Project of Science and Technology Research Program of Hubei Educational Committee (No. D20211402), the Teaching Research Project of Hubei University of Technology (No. XIAO2018001), and the Project of Xiangyang Industrial Research Institute of Hubei University of Technology (No. XYYJ2022C04).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Liang Zeng; data collection: Junyang Shi; analysis and interpretation of results: Shanshan Wang; draft manuscript preparation: Yanyan Li; manuscript proofreading: Weigang Li. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data is available on request from the authors. The data that support the findings of this study are available from the corresponding author, S. Wang, upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Z. He, B. Tang and F. Luan, “An improved african vulture optimization algorithm for dual-resource constrained multi-objective flexible job shop scheduling problems,” Sensors, vol. 23, no. 1, pp. 90, 2022. [Google Scholar] [PubMed]

2. C. N. Wang, G. Andrew Porter, C. C. Huang, V. Tinh Nguyen and S. Tam Husain, “Flow-shop scheduling with transportation capacity and time consideration,” Computers, Materials & Continua, vol. 70, no. 2, pp. 3031–3048, 2022. [Google Scholar]

3. A. Zhao, P. Liu, X. Gao, G. Huang, X. Yang et al., “Data-mining-based real-time optimization of the job shop scheduling problem,” Mathematics, vol. 10, no. 23, pp. 4608, 2022. [Google Scholar]

4. R. Braune, F. Benda, K. F. Doerner and R. F. Hartl, “A genetic programming learning approach to generate dispatching rules for flexible shop scheduling problems,” International Journal of Production Economics, vol. 243, pp. 108342, 2022. [Google Scholar]

5. K. Gayathri Devi, R. S. Mishra and A. K. Madan, “A dynamic adaptive firefly algorithm for flexible job shop scheduling,” Intelligent Automation & Soft Computing, vol. 31, no. 1, pp. 429–448, 2022. [Google Scholar]

6. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]

7. K. Deb and H. Jain, “An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: Solving problems with box constraints,” IEEE Transactions on Evolutionary Computation, vol. 18, no. 4, pp. 577–601, 2014. [Google Scholar]

8. Q. Ding and X. Xu, “Improved GWO algorithm for UAV path planning on crop pest monitoring,” International Journal of Interactive Multimedia and Artificial Intelligence, vol. 7, no. 5, pp. 30, 2022. [Google Scholar]

9. M. A. Mohammed, A. Lakhan, K. H. Abdulkareem, D. A. Zebari, J. Nedoma et al., “Homomorphic federated learning schemes enabled pedestrian and vehicle detection system,” Internet of Things, vol. 23, pp. 100903, 2023. [Google Scholar]

10. L. Meng, C. Zhang, Y. Ren, B. Zhang and C. Lv, “Mixed-integer linear programming and constraint programming formulations for solving distributed flexible job shop scheduling problem,” Computers & Industrial Engineering, vol. 142, pp. 106347, 2020. [Google Scholar]

11. C. Liu, “An improved harris hawks optimizer for job-shop scheduling problem,” The Journal of Supercomputing, vol. 77, no. 12, pp. 14090–14129, 2021. [Google Scholar]

12. S. C. Liu, Z. G. Chen, Z. H. Zhan, S. W. Jeon, S. Kwong et al., “Many-objective job-shop scheduling: A multiple populations for multiple objectives-based genetic algorithm approach,” IEEE Transactions on Cybernetics, vol. 53, no. 3, pp. 1460–1474, 2023. [Google Scholar] [PubMed]

13. W. Tan, X. Yuan, J. Wang and X. Zhang, “A fatigue-conscious dual resource constrained flexible job shop scheduling problem by enhanced NSGA-II: An application from casting workshop,” Computers & Industrial Engineering, vol. 160, pp. 107557, 2021. [Google Scholar]

14. W. Xu, Y. Hu, W. Luo, L. Wang and R. Wu, “A multi-objective scheduling method for distributed and flexible job shop based on hybrid genetic algorithm and tabu search considering operation outsourcing and carbon emission,” Computers & Industrial Engineering, vol. 157, pp. 107318, 2021. [Google Scholar]

15. C. Wang, X. Li and Y. Gao, “A novel collaborative evolutionary algorithm with two-population for multi-objective flexible job shop scheduling,” Computer Modeling in Engineering & Sciences, vol. 137, no. 2, pp. 1849–1870, 2023. [Google Scholar]

16. M. Wu, D. Yang, B. Zhou, Z. Yang, T. Liu et al., “Adaptive population NSGA-III with dual control strategy for flexible job shop scheduling problem with the consideration of energy consumption and weight,” Machines, vol. 9, no. 12, pp. 344, 2021. [Google Scholar]

17. X. Sun, Y. Wang, H. Kang, Y. Shen, Q. Chen et al., “Modified multi-crossover operator NSGA-III for solving low carbon flexible job shop scheduling problem,” Processes, vol. 9, no. 1, pp. 62, 2020. [Google Scholar]

18. C. Wang, Y. Wei, P. So, V. Nguyen and P. Phuc, “Optimization model in manufacturing scheduling for the garment industry,” Computers, Materials & Continua, vol. 71, no. 3, pp. 5875–5889, 2022. [Google Scholar]

19. L. Pan, W. Xu, L. Li, C. He and R. Cheng, “Adaptive simulated binary crossover for rotated multi-objective optimization,” Swarm and Evolutionary Computation, vol. 60, pp. 100759, 2021. [Google Scholar]

20. S. Dash, D. Joshi, A. Sharma and G. Trivedi, “A hierarchy in mutation of genetic algorithm and its application to multi-objective analog/RF circuit optimization,” Analog Integrated Circuits and Signal Processing, vol. 94, no. 1, pp. 27–47, 2018. [Google Scholar]

21. R. Denysiuk, L. Costa and I. E. Santo, “Many-objective optimization using differential evolution with variable-wise mutation restriction,” in Proc. of the 15th Annual Conf. on Genetic and Evolutionary Computation, Amsterdam, Netherlands, pp. 591–598, 2013. [Google Scholar]

22. H. Sato, H. E. Aguirre and K. Tanaka, “Self-controlling dominance area of solutions in evolutionary many-objective optimization,” in Asia-Pacific Conf. on Simulated Evolution and Learning, Berlin, Heidelberg, pp. 455–465, 2013. [Google Scholar]

23. C. Zhu, L. Xu and E. D. Goodman, “Generalization of pareto-optimality for many-objective evolutionary optimization,” IEEE Transactions on Evolutionary Computation, vol. 20, no. 2, pp. 299–315, 2016. [Google Scholar]

24. M. Laumanns, L. Thiele, K. Deb and E. Zitzler, “Combining convergence and diversity in evolutionary multiobjective optimization,” Evolutionary Computation, vol. 10, no. 3, pp. 263–282, 2002. [Google Scholar] [PubMed]

25. A. G. Hernández-Díaz, L. V. Santana-Quintero, C. A. Coello Coello and J. Molina, “Pareto-adaptive ε-dominance,” Evolutionary Computation, vol. 15, no. 4, pp. 493–517, 2007. [Google Scholar]

26. X. Zou, Y. Chen, M. Liu and L. Kang, “A new evolutionary algorithm for solving many-objective optimization problems,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 38, no. 5, pp. 1402–1412, 2008. [Google Scholar]

27. Y. Yuan, H. Xu, B. Wang and X. Yao, “A new dominance relation-based evolutionary algorithm for many-objective optimization,” IEEE Transactions on Evolutionary Computation, vol. 20, no. 1, pp. 16–37, 2016. [Google Scholar]

28. Y. Tian, R. Cheng, X. Zhang, Y. Su and Y. Jin, “A strengthened dominance relation considering convergence and diversity for evolutionary many-objective optimization,” IEEE Transactions on Evolutionary Computation, vol. 23, no. 2, pp. 331–345, 2019. [Google Scholar]

29. V. S. Jorapur, V. S. Puranik, A. S. Deshpande and M. Sharma, “A promising initial population based genetic algorithm for job shop scheduling problem,” Journal of Software Engineering and Applications, vol. 9, no. 5, pp. 208, 2016. [Google Scholar]

30. H. Gröflin and A. Klinkert, “A new neighborhood and tabu search for the blocking job shop,” Discrete Applied Mathematics, vol. 157, no. 7, pp. 3643–3655, 2009. [Google Scholar]

31. J. Adams, E. Balas and D. Zawack, “The shifting bottleneck procedure for job shop scheduling,” Management Science, vol. 34, no. 3, pp. 391–401, 1988. [Google Scholar]

32. R. H. Storer, S. D. Wu and R. Vaccari, “New search spaces for sequencing problems with application to job shop scheduling,” Management Science, vol. 38, no. 10, pp. 1495–1509, 1992. [Google Scholar]

33. Y. Xiang, Y. Zhou, M. Li and Z. Chen, “A vector angle-based evolutionary algorithm for unconstrained many-objective optimization,” IEEE Transactions on Evolutionary Computation, vol. 21, no. 1, pp. 131–152, 2017. [Google Scholar]

34. B. Li, K. Tang, J. Li and X. Yao, “Stochastic ranking algorithm for many-objective optimization based on multiple indicators,” IEEE Transactions on Evolutionary Computation, vol. 20, no. 6, pp. 924–938, 2016. [Google Scholar]

35. Z. He and G. G. Yen, “Many-objective evolutionary algorithms based on coordinated selection strategy,” IEEE Transactions on Evolutionary Computation, vol. 21, no. 2, pp. 220–233, 2017. [Google Scholar]

36. K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Transactions on Evolutionary Computation, vol. 6, no. 2, pp. 182–197, 2002. [Google Scholar]

37. A. Zhou, Y. Jin, Q. Zhang, B. Sendhoff and E. Tsang, “Combining model-based and genetics-based offspring generation for multi-objective optimization using a convergence criterion,” in 2006 IEEE Int. Conf. on Evolutionary Computation, Vancouver, BC, Canada, pp. 892–899, 2006. [Google Scholar]

38. L. While, P. Hingston, L. Barone and S. Huband, “A faster algorithm for calculating hypervolume,” IEEE Transactions on Evolutionary Computation, vol. 10, no. 1, pp. 29–38, 2006. [Google Scholar]

39. E. Moradi, S. M. T. Fatemi Ghomi and M. Zandieh, “An efficient architecture for scheduling flexible job-shop with machine availability constraints,” The International Journal of Advanced Manufacturing Technology, vol. 51, pp. 325–339, 2010. [Google Scholar]

40. S. Zhang, T. Hou, Q. Qu, A. Glowacz, S. Alqhtani et al., “An improved mayfly method to solve distributed flexible job shop scheduling problem under dual resource constraints,” Sustainability, vol. 14, no. 19, pp. 12120, 2022. [Google Scholar]