Enhancing Multicriteria-Based Recommendations by Alleviating Scalability and Sparsity Issues Using Collaborative Denoising Autoencoder

1  Introduction

Over recent decades, Recommender Systems (RS) have grown to be a pivotal solution in tackling the issues of the overwhelming amount of information, particularly within the dynamic landscape of e-commerce. These systems serve the essential function of providing personalized suggestions, encompassing a wide array of items and services, to individual users. This is achieved through the intricate analysis of users’ diverse information sources, including their explicit ratings, detailed reviews, historical purchasing patterns, and even implicit behavioral cues. Recommendation systems often employ content-driven and cooperation-driven filtering approaches. In the realm of content-driven filtering, the technique revolves around delving into the preferences and attributes of the present item, along with the historical choices of the active user [1]. This method essentially tailors’ recommendations based on the intrinsic qualities of items and the user’s demonstrated inclinations, creating a personalized tapestry of suggestions. On the other hand, the landscape of collaborative filtering (CF) has emerged as a potent force within the e-commerce industry, amassing notable achievements [2]. This method hinges on the power of collective wisdom, orchestrating recommendations by extrapolating from the user’s historical rating interactions. By identifying patterns in user behavior, CF techniques adeptly uncover latent connections among users with analogous preferences. This enables them to proficiently recommend items that remain unexplored within a user’s history but are anticipated to resonate with their tastes. Within the realm of collaborative filtering (CF) algorithms, we find a crucial categorization: Memory-focused CF and Model-centric CF. Memory-driven CF, in particular, operates by recognizing akin users or comparable items concerning the current user (or a designated target item). These proximate entities’ inclinations then serve as valuable inputs in shaping the recommendations provided [3]. In contrast, Model-based CF methodologies, celebrated for their enhanced precision, delve deeper by comprehensively comprehending users’ and items’ inherent attributes. This adeptness is cultivated during the model development phase, facilitated by the deployment of sophisticated machine-learning techniques. This encompasses the strategic use of methodologies like matrix factorization [4], factorization machines [5], and deep neural networks [6–9], all synergistically working to grasp and internalize users’ nuanced preferences.

The previously mentioned methodologies have conventionally been applied to solitary grading schemes. But depending only on these prove inadequate in capturing the diverse spectrum of user feedback, particularly in multifaceted service sectors like restaurants, hotels, and movies. In such contexts, users’ experiences are multidimensional and cannot be fully encapsulated through a single rating. In multi-criteria recommender systems, a more comprehensive approach is adopted. These systems enable users to provide feedback across various criteria, offering a nuanced evaluation of an item. For instance, within the realm of restaurants, a user might furnish ratings for distinct attributes such as taste, hygiene, ambiance, hospitality, and price, supplementing an overall rating. This augmentation of feedback affords multi-criteria recommender systems [10] a richer pool of information to draw upon. Consequently, these systems excel in suggesting items that align more accurately with users’ multifaceted preferences in comparison to their single-rating counterparts.

Several researchers have ventured into incorporating multi-criteria rating information within their recommendation frameworks [11,12]. However, the potential of applying diverse machine learning techniques to multi-criteria recommender systems remains largely untapped. This study introduces an innovative utilization of a deep learning method known as Stacked Autoencoder (SAE) [13]. In response to the intricacies of multi-criteria rating systems, we present an extended version of SAE that is tailored to address their unique demands. To adapt this technique effectively, modifications are implemented to both the interface component of the traditional network and the objective function. These adjustments are strategically introduced to simplify the comprehension of complex associations between multi-criteria evaluations and their respective aggregate ratings.

As RS is made to aid users in navigating through an enormous number of items, one of its main objectives is to scale up to actual datasets [14]. Conventional collaborative filtering techniques may encounter significant scalability challenges as the volume of items and users grows, leading to computational demands that surpass practical or acceptable thresholds [15]. User clustering via affinities in their user profiles is a popular technique for making recommender systems more scalable and reducing their time complexity. The intricacy of suggestions is only dependent on the size of the cluster when made by cluster representatives for the remaining cluster members [16,17]. Several model-based strategies [18] have been presented before addressing scalability and sparsity challenges in recommender systems. To realize the full potential of recommender system research, it is necessary to comprehend the most common methodologies applied to directly construct recommender algorithms or to pre-process recommendation datasets, as well as their advantages and disadvantages. As a result, our proposed methodology surpasses the performance benchmarks set by both contrasting single-score recommendation platforms with cutting-edge scalable recommendation systems utilizing diverse criteria.

In brief, this research offers the following major contributions:

_   The novel ESAE_KFCM has 2 offline stage, the sparse user-item multicriteria rating matrix undergoes a smoothing process to make the matrix complete without sparsity by estimating an intact rating of the item using an expanded stacked autoencoder that is not possible in a conventional autoencoder.

_   To attempt the problem of scalability and to generate the most excellent recommendations, a Kernel Fuzzy C-Means Clustering (KFCM) is utilized to cluster highly correlated users. Thereby, highly relevant users from multiple clusters alone are utilized in the online phase prediction of intact rating using the ESAE_KFCM approach that minimizes the time taken for recommendation generation and increases the prediction accuracy.

_   Extensive experiments on real-world multicriteria data sets from the Yahoo! Movies (YM) movie dataset and TripAdvisor (TA) travel dataset confirm that ESAE_KFCM outperforms the traditional recommender systems.

The structure of the work is as follows: The related work of the multicriteria-based recommender system is reviewed in Section 2. In Section 3, the proposed ESAE_KFCM approach is presented. The specifics of the experimental evaluation and results in terms of prediction accuracy and computation time are discussed in Section 4. Finally, the conclusion and future work of the paper is discussed in Section 5.

2  Related Work

Among the pioneering endeavors in the domain of recommendation systems employing multiple aspects is the work by Adomavicius et al. [10]. In their approach, they harnessed statistical methodologies to formulate an aggregation function that bridges the gap between diverse evaluative factors and the comprehensive overall assessment. This entails predicting multi-criteria ratings through conventional techniques [19,20] and subsequently utilizing the aggregation function to derive the overall rating, a process integral to the recommendation process. However, it is worth noting that this approach adheres to an established predilection for parameters consistently among all individuals. Lu et al. [21] presented a hybrid approach that amalgamates content-driven filtering and item-centric collaborative recommendation methods. This hybrid approach was devised to address the challenges posed by the cold-start problem and sparsity within the context of recommender systems employing multiple criteria. Nilashi has made significant contributions to the realm of multi-dimensional recommendation systems through a series of works, as evidenced in [22] and [23]. In [22], Nilashi et al. introduced algorithms rooted in fuzzy logic to enhance the precision of multi-dimensional recommendation systems. Continuing their exploration in [23], Nilashi et al. introduced a blended approach that utilizes the Ant K-means clustering technique. In this structure, essential elements are derived from each group of users through Principal Component Analysis. This information is then employed to facilitate the learning of the sequence linking global assessments and the harvested elements using Support Vector Regression (SVR). Zheng [12] introduced a set of three distinct approaches known as the ‘criteria chain.’ In the first approach, the prediction process commences with the initial criteria rating, which then serves as contextual information while forecasting the subsequent criteria rating, and so forth. Ultimately, SVR is employed to anticipate the complete assessment based on the sequence of criteria evaluations in addition to Preference learning methodology [24]. The alternative method involves employing Context-Aware Matrix Factorization (CAMF) [25] for predicting the eventual rating by incorporating the ratings of criteria as contextual hints. In the sequential approach, each evaluation factor is autonomously projected, and these anticipated assessments subsequently contribute as background information when predicting the overall assessment. However, relying on sequentially predicted criteria ratings could potentially lead to a cumulative loss in predictive accuracy when estimating the final overall rating [26–31]. Table 1 provides related works, offering insights into various algorithms and methodologies.

3  Proposed Method

The architectural view of the proposed ESAE_KFCM approach is depicted in Fig. 1. As specified in Fig. 1, the smoothening approach in the phase-I offline task utilizes a novel expanded stacked autoencoder that combines users’ multicriteria-based ratings given for the specific item to predict overall or intact rating value. Thus, the sparse matrix of multicriteria ratings is made into a filled matrix of intact ratings that yields an efficient way to predict the most relevant time and identify the highly correlated user. To perform user modeling, the Kernel Fuzzy C-Means Clustering (KFCM) approach is utilized to cluster the correlated users. In the online phase, the active user is recommended with the top-N most relevant item by the based rating prediction approach. The overall process of the proposed ESAE_KFCM approach is given in Algorithm 1.

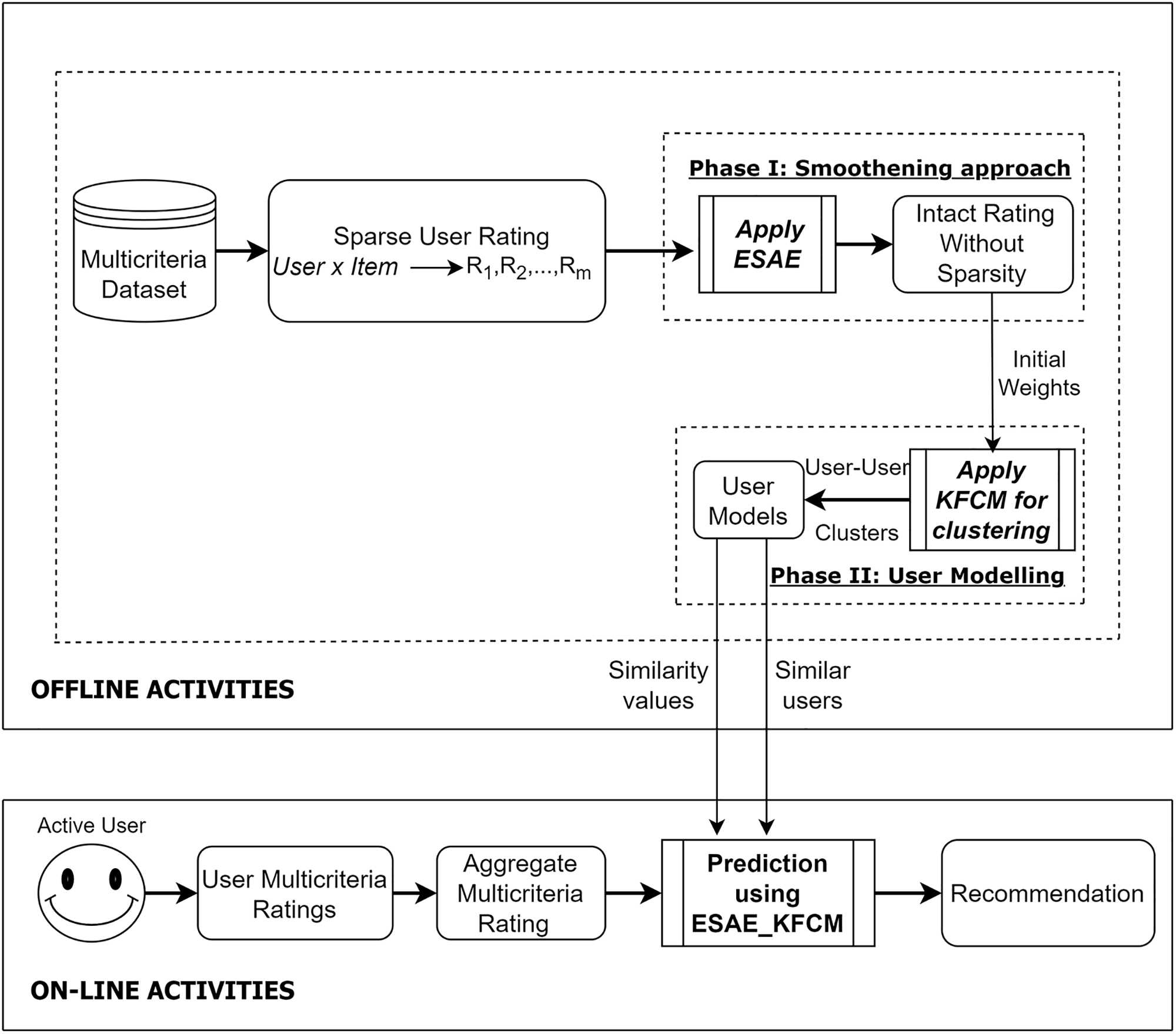
Figure 1: Proposed approach using ESAE_KFCM

The following data has been provided in a transaction database:

1. A collection of I users {Un|n=1,2,...,I}.

2. A collection of K diverse items {Im|m=1,2,...,K}.

3. A table of rating Rι of size [I×K] that contains data on the users’ history of multicriteria ratings of items o={n,m,rnm1,rnm2,rnm3,...,rnmq} where rnm1 implies the rating value for item m by user n under criteria 1 and q represents the total number of criteria. A zero is used to indicate the rating value of unavailable items.

3.1 Off-Line Task of the ESAE_KFCM

Two phases of the task are carried out offline, specifically, Phase I performs Smoothening, and User modeling is done in Phase II.

3.1.1 Smoothening-Expanded Stacked Denoising Autoencoder (ESAE) (Phase-I)

Here, the stacked denoising autoencoder is expanded to include a multicriteria of ratings given by the user for an item in the network. Consequently, the improved loss function is incorporated accordingly [27]. The user–item explicit preferences in the matrix of sparse multicriteria ratings are computed to a dense matrix of overall ratings using ESAE.

The count of neurons that comprise the first layer of a typical autoencoder is similar to the count of parameters in the input. The fact from each attribute is supplied to the appropriate neurons within the layer of input. But in the case of a multi-criteria context, any product will have multiple quality ratings that must be fed inside the network. As a consequence, the autoencoder was expanded by having an add-on layer that encompasses multi-criteria ratings. Particularly, denoising AE aims to prevent the latent layer from just learning the identification function and to compel it to find more robust features. Therefore, the expanded add-on layer serves as a first input layer that is corrupted with the addition of Gaussian noise and is subsequently connected to the intermediary layer containing item nodes. It is indeed connected to the successive T encoding layers to uncover the items’ hidden representation.

The final layer of encoding is allied to the T layers of decoding, which are employed to interpret the latent features learned from corresponding encoders. The items’ exact specific ratings are predicted as an output in the final decoding layer.

Let rmno be the optimum rating for an item m given by user n which is attained from rnm1,rnm2,rnm3,...,rnmq respectively as mentioned in Eq. (1).

rnmo=rnm1×wm1+rnm2×wm2+rnm3×wm3+......+rnmq×wmq(1)

where wm1,wm2,wm3,...,wmq are the multicriteria weights of the mth item. These unified optimum values of rating are given to the subsequent layers of the ESAE model. Finally, a justifiable and intact preference value R^ιn is predicted as in Eq. (2) by a completely connected network as depicted in Fig. 2.

R^ιn=ρ(G′(ρ(G{rmo}+s))+s′)(2)

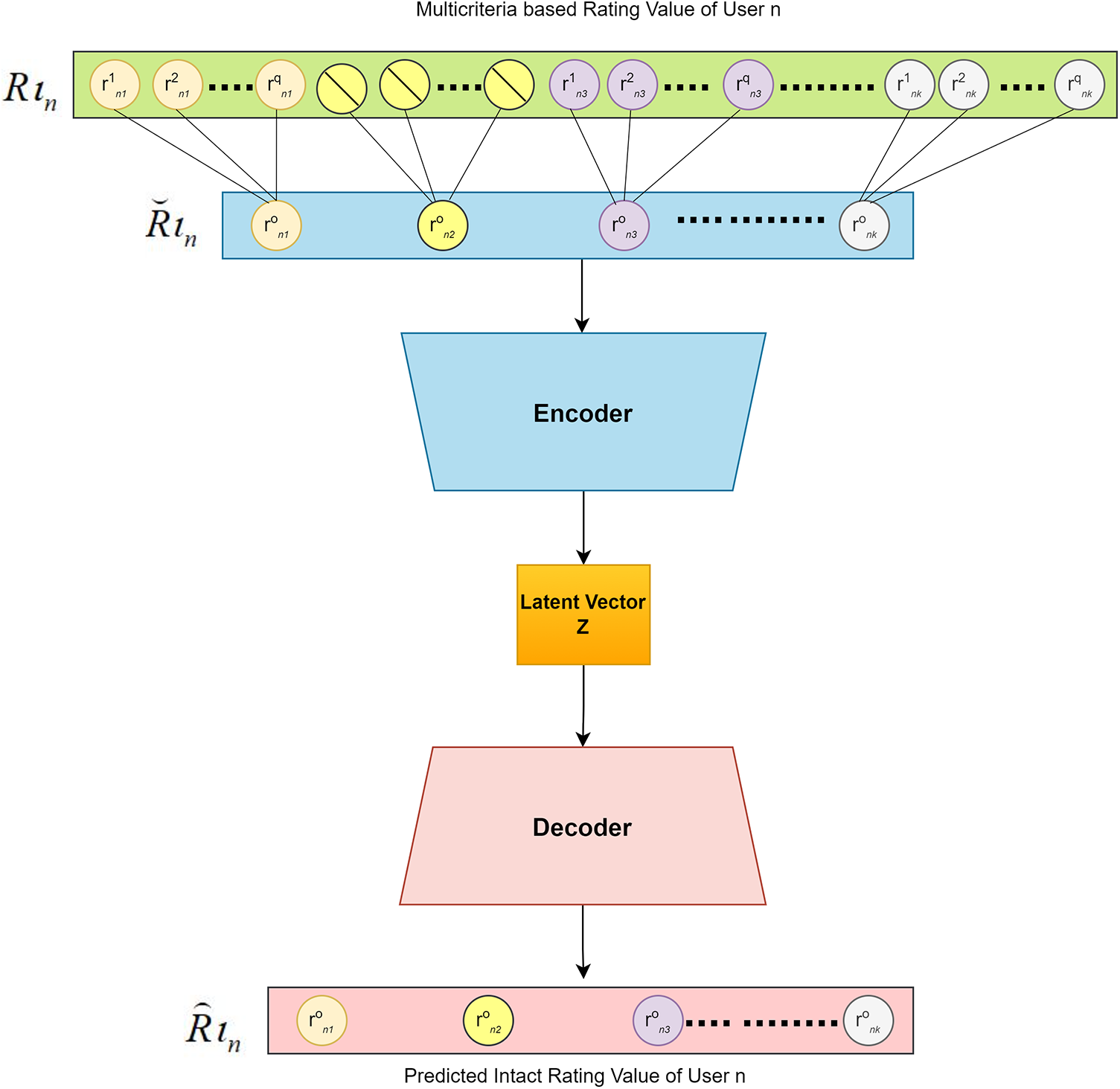
Figure 2: Structure of expanded stacked autoencoder (ESAE)

where R^ιn∈ℝK is the final predicted layer of intact rating value, G∈ℝH×K and G′∈ℝI×H are the weight matrices, rmo∈ℝK is the intact rating value of item m in the sparse R˘ιn, s∈ℝH and s′∈ℝK is the bias vectors and function ρ is the hyperbolic tangent.

The ESAE model is trained using the updated loss function below in Eq. (3) to gain a concise representation, since predicting the loss rate for the zero values in the rating vector Rιn results in obsolete. To prevent overfitting of the proposed ESAE model, the objective function combines regularization terms and is given away as in Eq. (3).

L(R^ι,R˘ι)=∑j∈Rι′(ESAE(R^ι)j−R˘ιj)2+β(‖G‖F2+‖G′‖F2+‖w‖F2+‖s‖F2+‖s′‖F2)(3)

where R^ι indicates an absolute array of intact ratings where R^ι=Rι″∪Rι‴, Rι″ comprises of known intact rating instances, Rι‴ comprises of the unknown instances, ‖G‖, ‖G′‖ are the vectors of weight of the ESAE model, ‖w‖ indicates the vectors of the weight of multicriteria rating of respective item, vectors of the weight of bias are ‖s‖,‖s′‖ and β is the regularization hyperparameter that controls how much learning has an impact on how generalizable the model is, so it is important to determine the right value, and β is defined by the outcomes of the experiment. The parameters are updated using the ADAM optimizer, a version of stochastic gradient descent. In an attempt to overwhelm the identity network, regularized dropouts via a probability p are additionally introduced at all layers. The forecasted instance j’s intact rating is ESAE(Rι′)j and R˘ιj, the real overall rating of instance j. From Eq. (3), it could be seen that the loss is computed using only the available rating instance set (Rι′).

Now the rating table R^ι is a completely smoothened matrix of users’ intact rating values for all the items that have been predicted from multicriteria ratings given for the item by the user. By this ESAE approach the accuracy of the intact rating prediction is improved which enhances Top-N recommendation.

3.1.2 User Modeling-Kernel Fuzzy C-Means Clustering (KFCM) (Phase-II)

Towards dealing with the scalability issue, the smoothened matrix R^ι using the ESAE approach as explained in Section 3.1.1 is clustered before the task of recommendation. This task is altered for ESAE_KFCM. The total amount of ratings given by the active user during the phase of recommendation is incredibly low. Prevalent clustering techniques like expectation maximization, similarity-based clustering, and k-means project the data over a scale of rating space that may be significantly larger. These clustering methods have the limitation that their prototypes are located in a highly-dimensional rating space, consequently, the descriptions are inadequate and informative (sparse user-item matrix). As a result, Zhang et al. [28] introduced a kernel fuzzy approach for clustering that is utilized in user modeling in ESAE_KFCM. The investigation demonstrates that fuzzy clustering is more resistant to outliers and noise than other approaches and can accept unequally sized clusters. In the phase of online, the most relevant users’ multicriteria rating vector alone is retrieved from the multiple clusters and the accurate unknown ratings are predicted using the ESAE approach with minimal recommendation time. The procedure of clustering is elucidated in Algorithm 2.

3.2 Recommendation Process by ESAE_KFCM in Online Phase

During the stage of the online recommendation process, the active user is recommended depending on the most correlated users obtained from multiple clusters generated by Section 3.1.2. This process of online recommendation is explained in Algorithm 3.

4  Experimental Evaluation

4.1 Dataset Description and Evaluation Metrics

The proposed ESAE_KFCM technique is tested using two real-time multicriteria data sets from the Yahoo! Movies (YM) movie sector dataset [11] and TripAdvisor (TA) [29] travel dataset sectors. The Yahoo Movies dataset has 6,078 users who rated a total of 976 movies has 62,156 ratings between 1 and 13. Each user assessed a movie based on 4 different criteria: Visuals, Direction, Acting, and Story. For experimenting, this 13-level scoring is converted to the standard 5-point format. Through web scraping on the Trip Advisor website with Beautiful Soup, a total of 60,216 records were gathered from 2500 hotels located in 93 different cities. Each hotel may be assessed based on multiple criteria such as service, value, cleanliness, rooms, staff, and quality of sleep. We sustain instances of users whose rating is at least five hotels and hotels that had at least five user ratings to extract the workable subset of data from TA. The extracted subset TA 5-5 has sparse data of 99.83% for 3550 hotels with 3160 users and 9374 instances of ratings. Similarly, YM 20-20, YM 5-5, and YM 10-10 subsets of data are extracted.

To assess the efficacy of the ESAE_KFCM approach, we employed prominent performance measures like, F1 score, Mean Absolute Error (MAE) [30], Good Predicted Items MAE (GPIMAE), Good Items MAE (GIMAE) [31], and computation time. Metrics for prediction accuracy, such as Mean Absolute Error (MAE), specified in Eq. (6), compare the actual ratings with the expected ratings.

MAE=∑n=1I∑m=1K|An,m−En,m|I∗K(6)

where I,K,An,m,En,m denotes the total user, total items, and actual, and expected ratings of user n for item m. High recall and precision levels are ideal for a model. Recall typically decreases as precision increases, and vice versa, due to the inverse correlation. To take into account recall (Ꞧ) and precision (₽), the metric F1 is defined in Eq. (7):

F1=2₽Ꞧ/₽+Ꞧ(7)

GPIMAE and GIMAE calculate the MAE in the system’s prediction of acceptable items and in those items, it forecasts to be good. As a result, they concentrate just on pertinent things rather than considering every item in the assessment subset. Therefore, the primary benefit of these measures is that they assess the algorithm solely for predictions that are pertinent to the user, i.e., for items that either ought to or will get placed on the list of recommendations.

4.2 Training Settings

The datasets TA 5-5, YM 20-20, YM 5-5, and YM 10-10 are divided into training data (60%), cross-validation (20%), and test data (20%) for the experiment. The proposed ESAE_KFCM paradigm is trained using Keras API in Python from the TensorFlow package. Utilizing the sci-kit-learn’s GridSearchCV feature, we investigate the potential effects of several distinct parameter values on the accuracy of the ESAE_KFCM model. Specifically, noise variance is altered with [0.1,0.2,0.3,0.4,0.5], number of hidden units [500,450,350,300,600], optimization technique as [‘Nadam’, ‘Adamax’, ‘Adam’, ‘Adadelta’, ‘Adagrad’, ‘RMSprop’, ‘SGD’], epoch with [100,200,240,280,300] and learning rate are assessed. Whenever the value of epoch value is 280, the ESAE model gets converged with corruption ratio = 0.4 and hidden units 450. Learning rates with altering values (0.002, 0.001, 0.01, 0.02, and 0.03) were tested and exposed that the learning rate η=0.02 is given better accuracy. Similar to this, a minibatch of size 50 is used to optimize the network using a Stochastic Gradient Descent Optimizer. Also, weight decay l2(0.001) is introduced for regularization, we chose hyperbolic tangents as a transfer function.

In this ESAE_KFCM technique, the optimum number of clusters (f) is found using the Silhouette Coefficient Method [43]. The max value of the silhouette coefficient (β), which indicates that the number of clusters formed is ideal, is 1. The first step in the experiment to find the optimum value for f is choosing the number of clusters to be assessed, which can range from 5 to 25. Based on the smallest possible clusters, the minimum f = 5. In the interim, the maximum f = 25. The value of β gives the second-highest optimum value at f = 22 and then starts to decline at f = 25. Since the higher f requires greater computing time, the subsequent f values do not proceed. The findings of the clustering assessment via the Silhouette Coefficient approach are displayed in Fig. 3. The ideal f value is indicated in Fig. 3, where the f = 16 yields the greatest value of the Silhouette Coefficient. As a result, the process of clustering will start with some clusters f equal to 16.

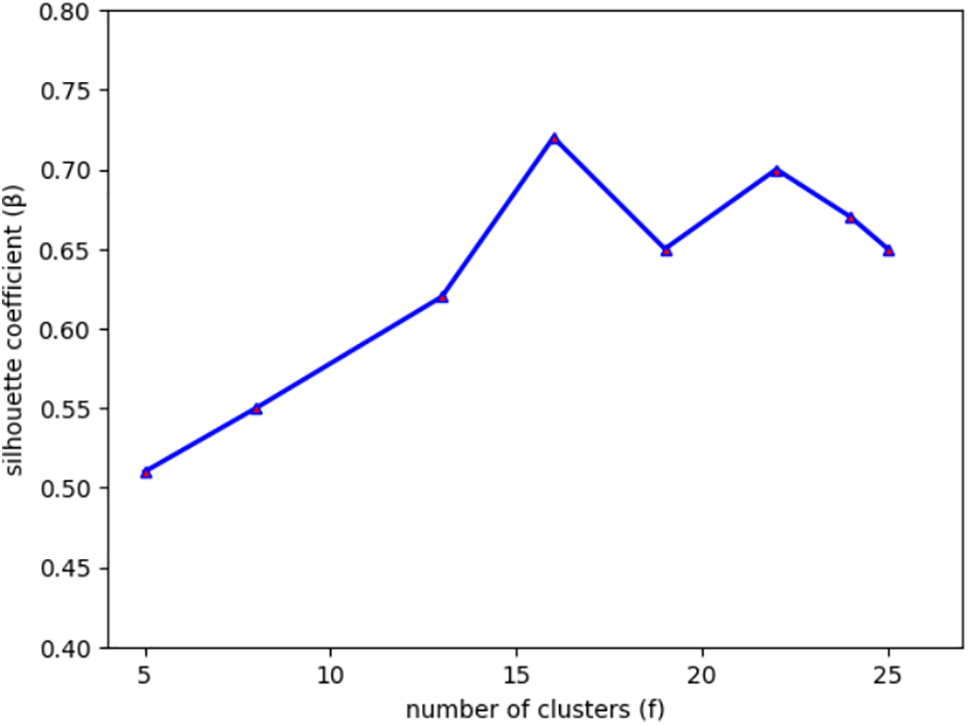
Figure 3: Results of silhouette coefficient (β)

4.3 Results and Discussion

The performance of ESAE_KFCM is assessed and compared with single and multicriteria rating-based models as baseline methods of recommendation as listed below:

1.    CDAE [8]: Collaborative DAE that uses a single rating system that incorporates latent factors for recommendation.

2.    Hybrid_AE [9]: CF-based neural network that uses a single rating system that combines user and item side information.

3.    Agg_CCA [12]: Aggregation approach that utilizes a multicriteria rating system to construct hybrid item and user-specific model.

4.    Context_CCC [12]: Estimates overall preference values based on contextual situations cast by multiple criteria rating system.

5.    Ind_CIC [12]: The BiasedMF algorithm was utilized to estimate the individual rating criteria as contexts by avoiding dependencies between multiple criteria ratings.

6.    ESAE_CF: This approach integrates the proposed ESAE approach with CF technique-based prediction for top-N item recommendation.

4.3.1 Performance Analysis of ESAE-Based Smoothening Process (Offline Phase)

Fig. 4 shows the MAE and smoothening time comparison of the ESAE with conventional models on all the working datasets. The efficiency of the ESAE model’s smoothening process in the offline phase is measured in terms of MAE and computational time.

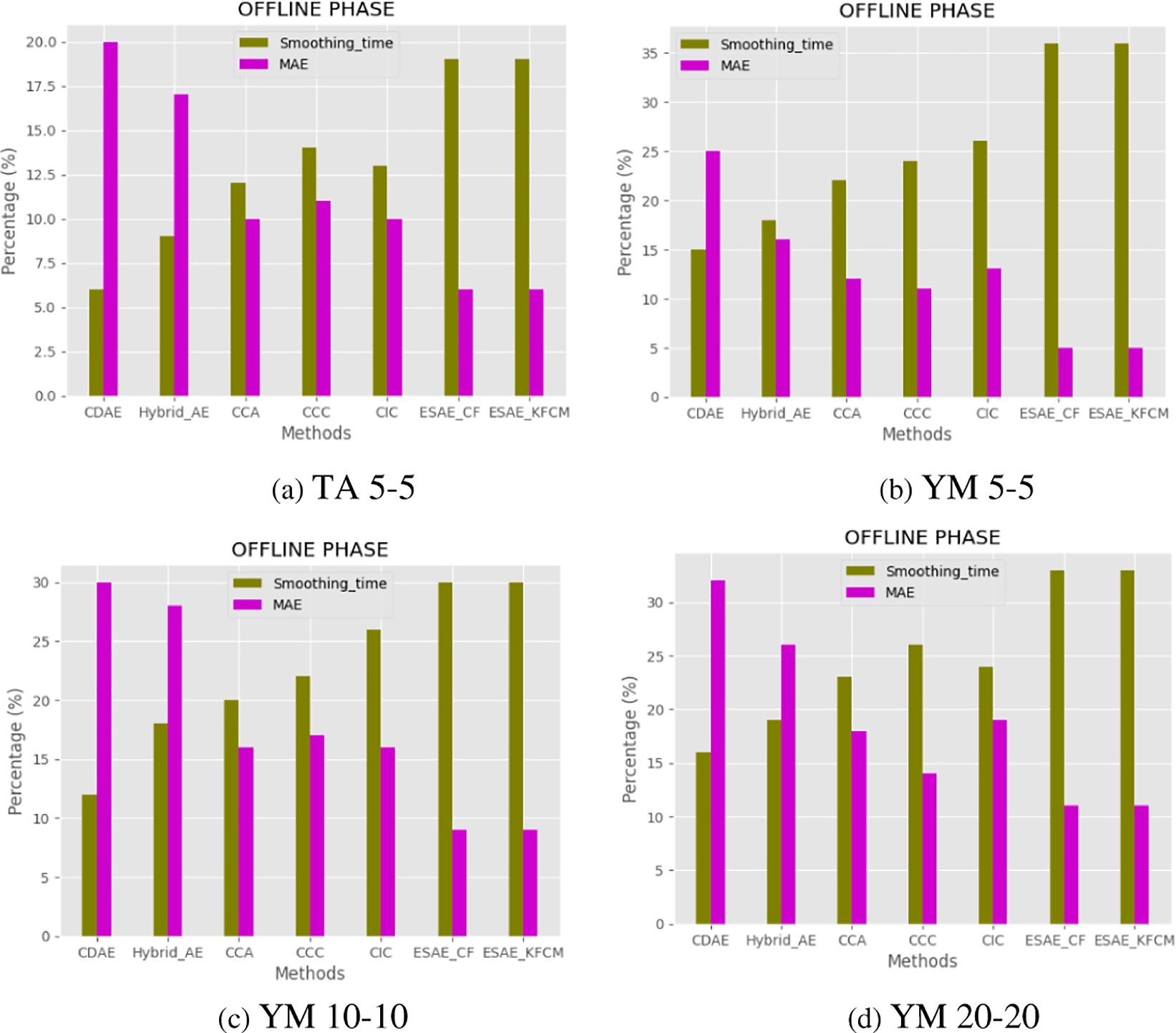
Figure 4: MAE comparison and smoothening time of the ESAE

•   CDAE and Hybrid_AE work on a single rating system where the smoothening process is done by autoencoder has average performance in MAE but the smoothening time is comparatively high.

•   Hybrid_AE outperforms the based smoothening technique since it incorporates the gain from side information to avoid the sparsity problem.

•   Agg_CCA and Context_CCC approaches utilize the CAMF_C method, which adopts criteria chains to anticipate the various criteria ratings one at a time and has better prediction accuracy than single rating systems such as CDAE and Hybrid_AE.

•   Ind_CIC outperforms Agg_CCA and Context_CCC in terms of prediction accuracy and the smoothening time was comparatively high.

•   As multicriteria ratings are considered for the smoothening process by utilizing an expanded stacked autoencoder in the ESAE_KFCM approach, the modeling time is comparatively elevated whereas outperforms MAE prediction accuracy compared to all the other models.

•   The smoothening approach is similar for both ESAE_CF and ESAE_KFCM. Subsequently, both have the same performance.

4.3.2 Performance Analysis of ESAE_KFCM Process (Online Phase)

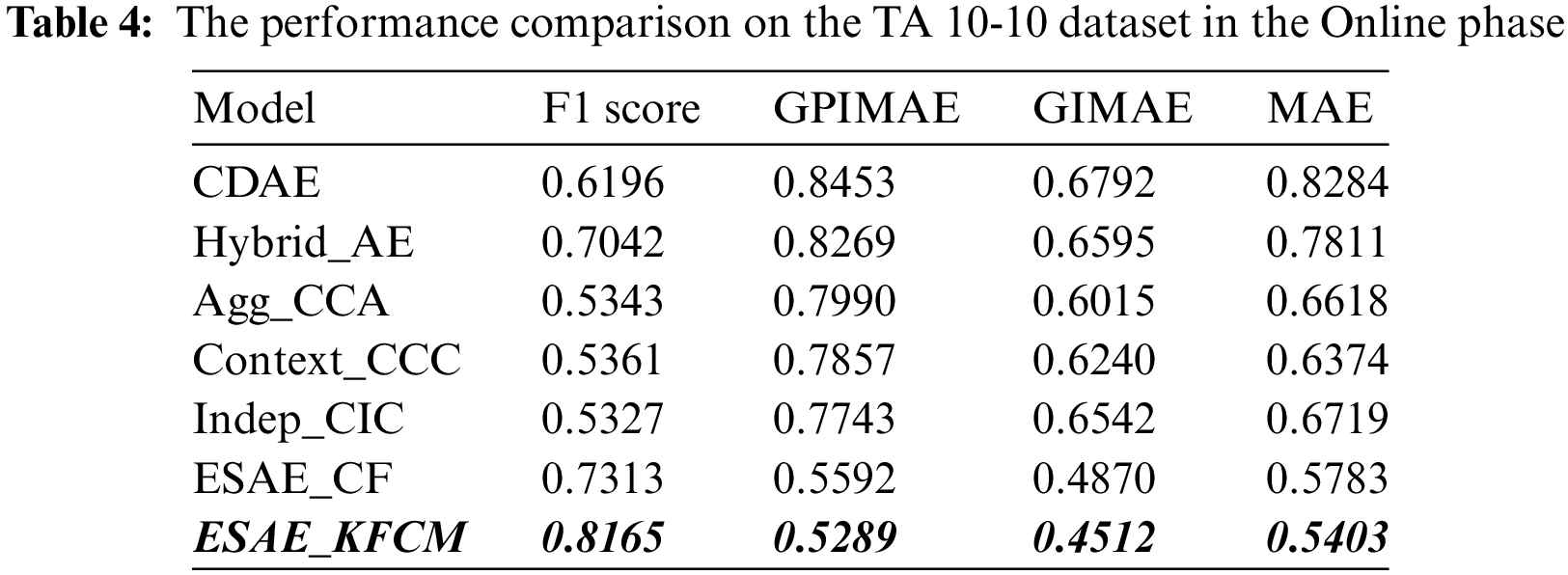
Subsequently completing the smoothening process, the dataset is clustered by the proposed Kernel Fuzzy C-Means Clustering (KFCM) approach. In the online phase the multicriteria rating vector of highly correlated users’ is alone considered for rating prediction using the ESAE approach. Thereby the proposed ESAE_KFCM approach gives the most relevant Top-N items as recommendations in minimal time and greater prediction accuracy. The time taken to recommend top-N items for the active user with the conventional model is depicted in Fig. 5. Tables 2–5 depict the results of accuracy measures in terms of MAE, F1 score, GPIMAE, and GIMAE, and the observations are listed as follows:

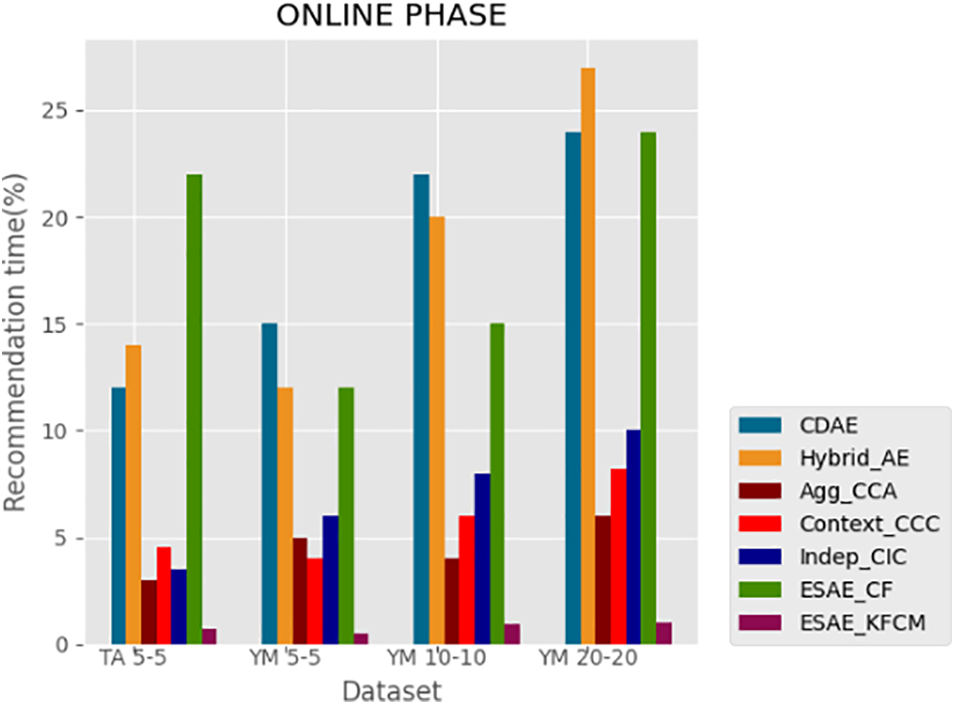
Figure 5: Recommendation time evaluation on the dataset

•   As depicted in Fig. 5, ESAE_KFCM constantly outperforms all the conventional models concerning recommendation time. Here the prediction of an intact rating takes only a minimal time for Top-N item recommendation since it inputs only the highly correlated multicriteria rating vector into the ESAE model fetched from multiple clusters in the online phase. Ind_CIC, Agg_CCA, and Context_CCC outperform CDAE and Hybrid_AE in terms of recommendation time since it works with the principle of dimensionality reduction technique. In ESAE_CF, the recommendation generation time is high compared to all the other models.

•   Ind_CIC, Agg_CCA, and Context_CCC comparatively have 17% higher errors than the ESAE_KFCM approach in terms of MAE, F1 score, GPIMAE, and GIMAE. Hybrid_AE outperforms CDAE in terms of prediction accuracy but has comparatively 21% high GPIMAE, and GIMAE. ESAE_CF outperform all the multicriteria rating-based recommendation system such as Ind_CIC, Agg_CCA, and Context_CCC in terms of F1 score, GPIMAE, and GIMAE for the existing user with modified multicriteria rating vector and new user with no rating vector.

•   The KFCM clustering process with some cluster (f) = 16 as mentioned in Fig. 4 on all the datasets has upgraded the prediction accuracy of 98.2% in Top-N recommendation with an average online recommendation generation time per item with 0.00428346 s accordingly.

•   ESAE_KFCM has an accurate prediction of intact ratings with less error in terms of GPIMAE, GIMAE, MAE and a 22% efficient F1 score compared to ESAE_CF, Ind_CIC, Agg_CCA, and Context_CCC in addition to minimized recommendation time and better decision support.

5  Conclusion and Future Enhancement

This work developed and estimated a scalable novel ESAE_KFCM model to enhance Top N recommendation by Kernel Fuzzy C-Means Clustering. In the KFCM technique, the method of clustering efficiently retrieves the highly correlated user from multiple clusters in the recommendation phase. In the offline phase, ESAE ESAE-based smoothening is performed by considering the multicriteria rating vector thereby overcoming the sparsity and enhancing prediction accuracy. Compared with the existing models, the proposed ESAE_KFCM model can make online recommendations using only the most similar users’ multicriteria rating vector retrieved from multiple clusters enhancing the high quality of Top-N item recommendation with minimal computation time. This model can be enhanced further by involving additional criteria like reviews, and user and item features to improve the accuracy of the recommendation process. Besides, variational or sparse autoencoders can be utilized for further investigation to enhance the Top-N recommendation.

Acknowledgement: We thank Vellore Institute of Technology, Chennai, for supporting us with the article processing charge (APC).

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Abinaya S; data collection: Uttej Kumar K; analysis and interpretation of results: Abinaya S, Uttej Kumar K draft manuscript preparation: Abinaya S, Uttej Kumar K. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The TripAdvisor datasets analyzed during the current study are available at https://www.kaggle.com/datasets/andrewmvd/trip-advisor-hotel-reviews, and Yahoo movies dataset, https://webscope.sandbox.yahoo.com/ accessed on 17 May 2023.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. Pazzani and D. Billsus, “Learning and revising user profiles: The identification of interesting web sites,” Mach. Learn, vol. 27, pp. 313–331, 1997. doi: 10.1023/A:1007369909943. [Google Scholar] [CrossRef]

2. G. Linden, B. Smith, and J. York, “Amazon. com recommendations: Item-to-item collaborative filtering,” IEEE Internet. Comput, vol. 7, no. 1, pp. 76–80, 2003. doi: 10.1109/MIC.2003.1167344. [Google Scholar] [CrossRef]

3. Z. Sun, X. Zhang, H. Li, Y. Xiao and H. Guo, “Recommender systems based on tensor decomposition,” Comput. Mater. Contin, vol. 66, pp. 621–630, 2020. doi: 10.32604/cmc.2020.012593. [Google Scholar] [PubMed] [CrossRef]

4. Y. Koren, “Factorization meets the neighborhood: A multifaceted collaborative filtering model,” in Proc. 14th ACM SIGKDD Int. Conf. Knowl. Discov. Data. Min., Las Vegas, Nevada, USA, 2008, pp. 426–434. [Google Scholar]

5. S. Rendle, “Factorization machines,” in 2010 IEEE Int. Conf. Data. Min., Sydney, NSW, Australia: IEEE, 2010, pp. 995–1000. [Google Scholar]

6. S. Abinaya and M. K. Kavitha Devi, “Trust-based context-aware collaborative filtering using denoising autoencoder,” in Pervasive. Comp. Soc Netw: Proc. ICPCSN 2021, Singapore, Springer, 2022, pp. 35–49. [Google Scholar]

7. S. Abinaya, A. S. Alphonse, S. Abirami, and M. K. Kavithadevi, “Enhancing context-aware recommendation using trust-based contextual attentive autoencoder,” in Neural. Proc. Letters, 2023, pp. 1–22. doi: 10.1007/s11063-023-11163-x. [Google Scholar] [CrossRef]

8. Y. Wu, C. DuBois, A. X. Zheng, and M. Ester, “Collaborative denoising auto-encoders for top-N recommender systems,” in Proc. 9th ACM Int. Conf. Web Search Data Min., 2016, pp. 153–162. [Google Scholar]

9. F. Strub, R. Gaudel, and J. Mary, “Hybrid recommender system based on autoencoders,” in Proc. 1st Workshop Deep Learn Recommender Syst., 2016, pp. 11–16. doi: 10.1145/2988450.2988456. [Google Scholar] [CrossRef]

10. G. Adomavicius and Y. Kwon, “New recommendation techniques for multicriteria rating systems,” IEEE Intell. Syst, vol. 22, no. 3, pp. 48–55, 2007. doi: 10.1109/MIS.2007.58. [Google Scholar] [CrossRef]

11. D. Jannach, Z. Karakaya, and F. Gedikli, “Accuracy improvements for multi-criteria recommender systems,” in Proc. 13th ACM Conf. Electron. Commer., 2012, pp. 674–689. [Google Scholar]

12. Y. Zheng, “Criteria chains: A novel multi-criteria recommendation approach,” in Proc. 22nd Int. Conf. Intell. User Interfaces, 2017, pp. 29–33. [Google Scholar]

13. S. Abinaya and M. K. Devi, “Enhancing top-N recommendation using stacked autoencoder in context-aware recommender system,” Neural. Process. Lett, vol. 53, pp. 1865–1888, 2021. doi: 10.1007/s11063-021-10475-0. [Google Scholar] [CrossRef]

14. A. Kumar and A. Sharma, “Alleviating sparsity and scalability issues in collaborative filtering based recommender systems,” in Proc. Int Conf Front Intell Comput: Theory Appl. (FICTA), Berlin Heidelberg: Springer, 2013, pp. 103–112. [Google Scholar]

15. M. Singh, “Scalability and sparsity issues in recommender datasets: A survey,” Knowl. Inf. Syst, vol. 62, pp. 1–43, 2020. doi: 10.1007/s10115-018-1254-2. [Google Scholar] [CrossRef]

16. S. Abinaya, K. Indira, S. Karthiga, and T. Rajasenbagam, “Time cluster personalized ranking recommender system in multi-cloud,” Math, vol. 11, no. 6, pp. 1300, 2023. doi: 10.3390/math11061300. [Google Scholar] [CrossRef]

17. M. K. Devi and P. Venkatesh, “Smoothing approach to alleviate the meager rating problem in collaborative recommender systems,” Future. Gener. Comput. Syst, vol. 29, no. 1, pp. 262–270, 2013. doi: 10.1016/j.future.2011.05.011. [Google Scholar] [CrossRef]

18. S. Bakshi, A. K. Jagadev, S. Dehuri, and G. N. Wang, “Enhancing scalability and accuracy of recommendation systems using unsupervised learning and particle swarm optimization,” Appl. Soft. Comput, vol. 15, pp. 21–29, 2014. doi: 10.1016/j.asoc.2013.10.018. [Google Scholar] [CrossRef]

19. Y. Zhang, Y. Zhuang, J. Wu, and L. Zhang, “Applying probabilistic latent semantic analysis to multi-criteria recommender system,” Ai. Commun, vol. 22, no. 2, pp. 97–107, 2009. doi: 10.3233/AIC-2009-0446. [Google Scholar] [CrossRef]

20. L. Liu, N. Mehandjiev, and D. L. Xu, “Multi-criteria service recommendation based on user criteria preferences,” in Proc. Fifth ACM Conf. Recomm. Syst., 2011, pp. 77–84. doi: 10.1145/2043932.2043950. [Google Scholar] [CrossRef]

21. Q. Shambour and J. Lu, “A hybrid multi-criteria semantic-enhanced collaborative filtering approach for personalized recommendations,” in In 2011 IEEE/WIC/ACM Int. Conf. Web. Intell. Intell. Agent. Technol., IEEE, vol. 1, 2011, pp. 71–78. [Google Scholar]

22. M. Nilashi, D. Jannach, O. bin Ibrahim, and N. Ithnin, “Clustering-and regression-based multi-criteria collaborative filtering with incremental updates,” Inf. Sci, vol. 293, pp. 235–250, 2015. doi: 10.1016/j.ins.2014.09.012. [Google Scholar] [CrossRef]

23. M. Nilashi, O. bin Ibrahim and N. Ithnin, “Hybrid recommendation approaches for multi-criteria collaborative filtering,” Expert. Syst. Appl, vol. 41, no. 8, pp. 3879–3900, 2014. doi: 10.1016/j.eswa.2013.12.023. [Google Scholar] [CrossRef]

24. R. S. Sreepada, B. K. Patra, and A. Hernando, “Multi-criteria recommendations through preference learning,” in Proc. 4th ACM IKDD Conf. Data. Sci., 2017, pp. 1–11. [Google Scholar]

25. M. Braunhofer, V. Codina, and F. Ricci, “Switching hybrid for cold-starting context-aware recommender systems,” in Proc. 8th ACM Conf. Recomm. Syst., 2014, pp. 349–352. [Google Scholar]

26. B. B. Sinha and R. Dhanalakshmi, “DNN-MF: Deep neural network matrix factorization approach for filtering information in multi-criteria recommender systems,” Neural. Comput. Appl, vol. 34, no. 13, pp. 10807–10821, 2022. doi: 10.1007/s00521-022-07012-y. [Google Scholar] [CrossRef]

27. D. Tallapally, R. S. Sreepada, B. K. Patra, and K. S. Babu, “User preference learning in multi-criteria recommendations using stacked auto encoders,” in Proc. 12th ACM Conf. Recomm Syst., 2018, pp. 475–479. [Google Scholar]

28. D. Q. Zhang and S. C. Chen, “Clustering incomplete data using kernel-based fuzzy c-means algorithm,” Neural. Process. Lett, vol. 18, pp. 155–162, 2003. doi: 10.1023/B:NEPL.0000011135.19145.1b. [Google Scholar] [CrossRef]

29. C. V. M. Krishna, G. A. Rao, and S. Anuradha, “Analysing the impact of contextual segments on the overall rating in multi-criteria recommender systems,” J. Big Data, vol. 10, no. 1, pp. 16, 2023. doi: 10.1186/s40537-023-00690-y. [Google Scholar] [PubMed] [CrossRef]

30. J. L. Herlocker, J. A. Konstan, L. G. Terveen, and J. T. Riedl, “Evaluating collaborative filtering recommender systems,” ACM Trans. Inf. Syst. (TOIS), vol. 22, no. 1, pp. 5–53, 2004. doi: 10.1145/963770.963772. [Google Scholar] [CrossRef]

31. F. Cacheda, V. Carneiro, D. Fernández, and V. Formoso, “Comparison of collaborative filtering algorithms: Limitations of current techniques and proposals for scalable, high-performance recommender systems,” ACM Trans. Web. (TWEB), vol. 5, no. 1, pp. 1–33, 2011. doi: 10.1145/1921591.1921593. [Google Scholar] [CrossRef]

32. Z. Shu, Y. Bai, D. Zhang, J. Yu, Z. Yu, and X. Wu, “Specific class center guided deep hashing for cross-modal retrieval,” Inf. Sci, vol. 609, pp. 304–318, 2022. doi: 10.1016/j.ins.2022.07.095. [Google Scholar] [CrossRef]

33. Z. Shu, K. Yong, D. Zhang, J. Yu, Z. Yu, and X. J. Wu, “Robust supervised matrix factorization hashing with application to cross-modal retrieval,” Neural. Comput. Appl, vol. 35, no. 9, pp. 6665–6684, 2023. doi: 10.1007/s00521-022-08006-6. [Google Scholar] [CrossRef]

34. P. N. Ramesh and S. Kannimuthu, “Context-aware practice problem recommendation using learners’ skill level navigation patterns,” Intell. Autom. Soft. Comput, vol. 35, no. 3, pp. 3845–3860, 2023. doi: 10.32604/iasc.2023.031329. [Google Scholar] [PubMed] [CrossRef]

35. L. Li, Z. Shu, Z. Yu, and X. J. Wu, “Robust online hashing with label semantic enhancement for cross-modal retrieval,” Pattern. Recognit, vol. 145, pp. 109972, 2024. doi: 10.1016/j.patcog.2023.109972. [Google Scholar] [CrossRef]

36. Z. Shu, K. Yong, J. Yu, S. Gao, C. Mao and Z. Yu, “Discrete asymmetric zero-shot hashing with application to cross-modal retrieval,” Neurocomputing, vol. 511, pp. 366–379, 2022. doi: 10.1016/j.neucom.2022.09.037. [Google Scholar] [CrossRef]

37. V. S. Devi and S. Kannimuthu, “Author profiling in code-mixed WhatsApp messages using stacked convolution networks and contextualized embedding-based text augmentation,” Neural. Process. Lett, vol. 55, no. 1, pp. 589–614, 2023. doi: 10.1007/s11063-022-10898-3. [Google Scholar] [CrossRef]

38. K. C. Raja and S. Kannimuthu, “Conditional generative adversarial network approach for autism prediction,” Comput. Syst. Sci. Eng, vol. 44, no. 1, 2023. doi: 10.32604/csse.2023.025331. [Google Scholar] [PubMed] [CrossRef]

39. S. Wu, F. Sun, W. Zhang, X. Xie, and B. Cui, “Graph neural networks in recommender systems: A survey,” ACM Comput. Surv, vol. 55, no. 5, pp. 1–37, 2022. doi: 10.1145/3535101. [Google Scholar] [CrossRef]

40. C. Gao et al., “A survey of graph neural networks for recommender systems: Challenges, methods, and directions,” ACM Trans. Recomm. Syst, vol. 1, no. 1, pp. 1–51, 2023. doi: 10.1145/3568022. [Google Scholar] [CrossRef]

41. Y. Gao et al., “Chat-REC: Towards interactive and explainable llms-augmented recommender system,” arXiv preprint arXiv:2303.14524, 2023. [Google Scholar]

42. Y. Deng, W. Zhang, W. Xu, W. Lei, T. S. Chua, and W. Lam, “A unified multi-task learning framework for multi-goal conversational recommender systems,” ACM Trans. Inf. Syst, vol. 4, no. 3, pp. 1–25, 2023. doi: 10.1145/3570640. [Google Scholar] [CrossRef]

43. H. Jiawei, K. Micheline, and P. Jian, “Dm concepts and techniques preface and introduction,” in S. Kusumadewi (Ed.Klasifikasi Status Gizi Menggunakan, 2012, vol. 3, pp. 6–11. [Google Scholar]