Privacy-Preserving Multi-Keyword Fuzzy Adjacency Search Strategy for Encrypted Graph in Cloud Environment

1  Introduction

The widespread existence of cloud computing and its powerful applications has brought great changes and convenience to people’s lives and work. With the continuous growth of data scale, outsourcing massive graph data to cloud servers is an important choice for data owners, and this can save space and cost [1,2]. The powerful computing and processing power of cloud computing has become an important reason for the favor of many outsourcing services [3,4]. Graph data is widely used in many fields, and the complex graph structure contains rich information [5,6]. As cloud servers are insecure and unreliable, the outsourced graph data cannot be directly stored in the cloud servers [7,8], otherwise there will be a risk of privacy information being leaked. Generally speaking, encrypting outsourcing data is a frequently used and effective strategy [9,10]. Accordingly, another problem is that it is very troublesome to process and operate the graph data outsourced to the cloud servers. In the existing adjacency queries for outsourced encrypted graphs, the requirement for multi-keyword fuzzy queries in query requests is ignored. This will expand the scope of the query and give the user more choices of query results. Therefore, it is very valuable to execute privacy-preserving adjacency query supporting multi-keyword fuzzy search on encrypted graphs in the cloud environment.

In graph data processing, an adjacency query is a very elementary and general operation. Many queries and other operations are performed based on adjacency queries [11–13]. The adjacency query supporting multi-keyword fuzzy search can take multiple keywords as query trapdoors, and finally get fuzzy query results. This allows users to get more diversified query results and meets more query scenarios [14,15]. Take an example of a scientific research cooperation graph, each vertex of the graph represents a researcher, and each edge represents that two vertices have cooperation. The adjacency query supporting multi-keyword fuzzy search is to process multiple keywords as query tokens to realize an adjacency query. To implement a multi-keyword fuzzy search, we use the Bloom filter to construct index and query tokens in the paper [16,17]. This work considers performing adjacency queries on encrypted graph of cloud servers. Considering the cost, it is not cost-effective to download all the graph data to execute the query locally. For this reason, it is urgent and necessary to study adjacency queries supporting multi-keyword fuzzy search on cloud servers.

Performing queries on encrypted data in the cloud environment, searchable encryption is a very effective processing mechanism [18–22]. Searchable encryption has become a useful cryptographic primitive in cryptography, and cloud servers cannot obtain sensitive information of outsourced data when performing queries. Searchable encryption has evolved over the years, with many extensions and enhancements [23–27]. It makes the query operation of outsourced data more convenient and secure. Due to the existing searchable encryption methods mainly studying processing techniques on text datasets, they cannot be utilized directly to implement adjacency queries supporting multi-keyword fuzzy search. Latterly some research results of graph-related ciphertext queries have been put forward [28–32]. The relevant query on ciphertext graph was studied in the literature [28], and the query idea of structured encryption and controlled disclosure was proposed. The research on subgraph queries on remote outsourcing graphs was studied in the pieces of literature [29–31], and the corresponding solutions were proposed. A graph encryption scheme was proposed to implement constrained shortest-distance query in the literature [32]. However, all these query schemes cannot solve the problem of adjacency queries supporting multi-keyword fuzzy search on cloud servers.

To solve this problem, we came up with a solution to perform a privacy-preserving adjacency query supporting multi-keyword fuzzy search on the encrypted graph in the cloud environment, which is named PAQM. In our proposed PAQM solution, cloud servers realize the adjacency query with the aid of encrypted index and encrypted query tokens. We first convert all graph vertices into vectors based on unary grammar. We then build a secure index based on the Bloom filter and symmetric encryption mechanism, and the index is sent to cloud servers. The encrypted query tokens are subsequently built in a similar way to build the index. Finally, cloud servers perform the adjacency query through the secure index and the encrypted query tokens. After the query, the encrypted query results are returned, and cloud servers can not know the privacy information about graph data and retrieval results. Through formal analysis and experimental evaluation, the proposed PAQM solution is proven to be secure and efficient.

The contributions of this work are summarized as follows:

(1) We propose a solution to solve this problem of privacy-preserving adjacency query supporting multi-keyword fuzzy search on the encrypted graph in the cloud environment.

(2) We prove the security of our proposed solution through formal analysis.

(3) The effectiveness of our solution is illustrated by experimental evaluation on real data sets.

The rest of the work is as follows. Section 2 introduces the related work. Section 3 analyzes and designs our PAQM solution. Section 4 proves the security of our PAQM solution. Section 5 shows the effectiveness of our PAQM solution through experimental analysis and evaluation. Finally, Section 6 summarizes our work.

2  Related Work

With the development and popularization of cloud computing and cloud services, a large number of data outsourcing has become a popular trend [33–35]. At the same time, the security of outsourced data has become an important issue to be urgently considered [36–38]. Considering the complexity of the cloud environment and the unreliability of cloud servers, the research on privacy protection of cloud outsourcing services has become a hot research area and a lot of research achievements have been made. Among them, searchable encryption is an important mechanism to solve the security problems of cloud outsourcing [39–40]. Due to different encryption methods, there are two modes: symmetric searchable encryption (SSE) [18–20] and asymmetric searchable encryption (ASE) [22]. In consideration of the higher efficiency of symmetric encryption, we adopt the idea of searchable symmetric encryption in this work.

A searchable encryption mechanism is a solution to the query problem on the remote server. This is of great use to queries and related operations on cloud outsourcing data [18–22]. Song et al. put forward the idea of searchable symmetric encryption for the first time and solved the problem of data query on remote servers [18]. Goh first proposed the concept of a security index-based on the Bloom filter to realize outsourcing queries [19]. Later Curtmola et al. proposed more efficient SSE solutions, one of which can achieve adaptive SSE security [21]. Boneh et al. studied the searchable encryption mechanism based on a public key cryptography algorithm and proposed the concept of public key encryption with keyword search for the first time [22]. With the vigorous development of encryption outsourcing technology, some extended searchable encryption schemes have emerged [23–27]. The problem of dynamic searchable symmetric encryption was studied in the literature [23], and the inverted index method of literature [21] was extended to effectively add and delete documents. Based on binary grammar and the Bloom filter, Wang et al. proposed a multi-keyword fuzzy query scheme for cloud outsourcing data for the first time [24]. Fu et al. implemented a multi-keyword fuzzy query on encrypted outsourcing data based on unary grammar and root extraction algorithm, which improved the query accuracy, but the cost would increase [25]. In the literature [26], a dynamic multi-keyword fuzzy search scheme was proposed, in which Bloom filter and unary grammar were used, and a dynamic update of file set and index was realized. Liu et al. proposed matrix-based multi-keyword fuzzy search schemes that supported approximate keyword matching in the literature [27]. In summary, the above schemes have studied the processing methods of searchable encryption on ciphertext text datasets, but for graph-structured data, these schemes cannot be exploited to implement adjacency query supporting multi-keyword fuzzy search.

Recently, the query problem on outsourcing graph data has attracted a lot of attention, and some research results have emerged [28–32]. The research [28] put forward the concept of structure encryption, which could perform query operations on data of any structure, and also studied the query scheme on graph structure data. Cao et al. proposed and solved the problem of subgraph queries on an outsourced graph for the first time [29]. In the query, two stages of filtering and verification were designed, and privacy information was also protected. Zhang et al. used frequent features to calculate similarity, formalized the query graph and each data graph as vectors, respectively, and realized privacy-protecting similar subgraph query problems [30]. Fan et al. studied the problem of subgraph isomorphism query of outsourced graph data and transformed the subgraph isomorphism query into a series of matrix operations, and the scheme reduced communication overhead and optimized the query process [31]. Shen et al. presented a graph encryption scheme that achieved the cloud-based approximate constrained shortest distance queries over encrypted graphs with privacy protection [32]. However, these research methods do not solve the problem of multi-keyword fuzzy adjacency query, so these schemes cannot solve the problem of adjacency query supporting multi-keyword fuzzy search in the cloud environment.

In the work, we propose a solution to realize adjacency query by using Bloom filter, unary grammar based on a searchable encryption mechanism. Our scheme can support multi-keyword fuzzy search on the encrypted graph and protect the privacy contents in the query process. The vertices in the outsourcing graph are firstly transformed into vectors by a unary grammar. The security index and query token are next built based on the generated vectors and transmitted to cloud servers. At last, cloud servers complete adjacency queries with the help of the index and query token. The security and effectiveness of the proposed solution are verified by formal analysis and experimental comparison.

3  Construction of PAQM Solution

3.1 Preliminary Information

With the increasing demand for security, the development of cryptography is also progressing. Among them, semantic security and indistinguishability proposed in the literature [41] are two important properties. In the work, we use the idea of semantic secure symmetric encryption to construct our scheme. We use kge to denote a symmetric secret key generation algorithm, and use Enc and Dec respectively denote a symmetric encryption algorithm and symmetric decryption algorithm [42].

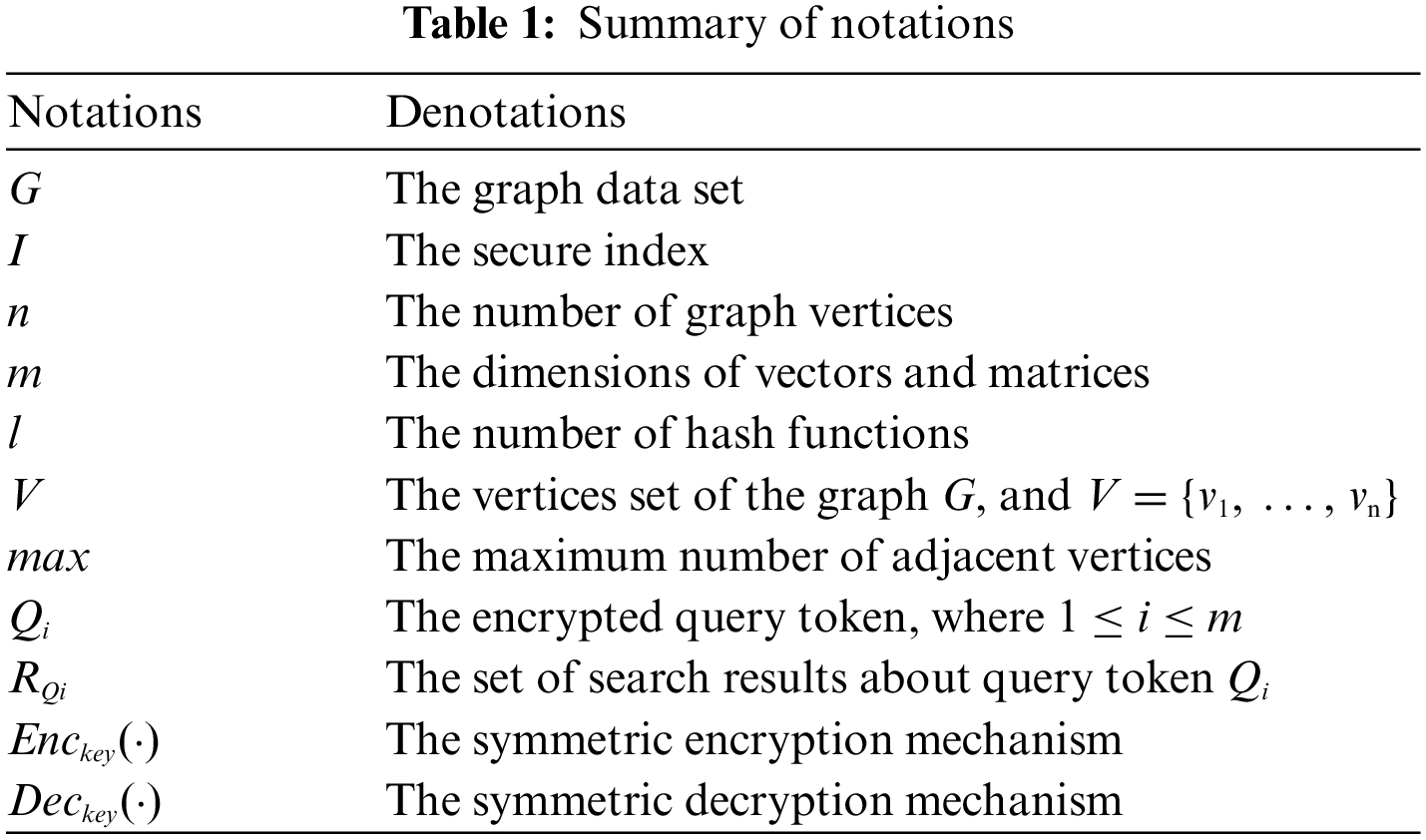
We utilize unary grammar and Bloom filter to implement multi-keyword fuzzy adjacency query in this scheme [16,17,25,43]. All graph vertex words are converted into vectors of equal length and mapped to a Bloom filter by Locality-Sensitive Hashing (LSH) functions [25,26]. We construct a Boolean filter for the set of adjacency-vertices of each graph vertex, initialize each bit of the Boolean filter to 0, and then map each element in the set of adjacency-vertices to its corresponding Boolean filter [17,26]. Some main notations used in this work are listed in Table 1.

3.2 Solution Overview

In a cloud outsourcing environment, the system structure of our adjacency query is shown in Fig. 1 which includes cloud servers, graph data owners, and users. The query and processing operations are implemented through the cloud servers with the help of the encrypted index and query tokens. To prevent the disclosure of private information, it is necessary to set the security conditions of our solution to ensure the security of the query process. In the work, we use the existing methods in searchable encryption for the search authorization and query control of users [21,23].

Figure 1: The system structure of adjacency query on encrypted graph

Our solution solves the adjacency query problem supporting multi-keyword fuzzy search on the outsourcing encryption graph and can achieve the following design purposes:

(1) Secure adjacency queries supporting multi-keyword fuzzy search. Data users can perform secure adjacency query supporting multi-keyword fuzzy search through cloud servers.

(2) Protecting private information. It will not disclose the privacy information at the time of query, and the security proof is given by formal analysis.

(3) Effectiveness of the scheme. Through comparative analysis, it is given that the cost of our proposed scheme is small and acceptable.

In the work, we adopt Bloom filter, LSH function, unary grammar, searchable encryption, etc., to build a query scheme. The set of adjacency vertices of each graph vertex will be mapped to a Bloom filter, and all Bloom filters are used to build the query index. The query index and query request are sent to cloud servers after symmetric encryption, and cloud servers perform adjacency queries supporting multi-keyword fuzzy search.

To achieve the adjacency queries supporting multi-keyword fuzzy search on cloud servers, the system process flow of our proposed methodology is as follows. We first carry out vector transformation for each graph vertex and construct a Bloom filter for its adjacent vertices. Each bit of the Bloom filter corresponds to an adjacency vertex information. Then all the Bloom filters are combined and arranged to construct the query index. Next, the query request is transformed into a vector, and cloud servers complete the query by calculating its inner product with the index. Following the previous idea of searchable symmetric encryption, we set cloud servers in our scheme to adopt an adaptive attack model [21,23]. In our scheme, only the user with the authorization key can obtain the encrypted query request [21]. Finally, we analyze and verify the correctness and effectiveness of the proposed methodology through formal security proof and experimental comparison.

3.3 Realization of PAQM Solution

The core task of our PAQM solution is to design and build a secure query index and query token, and then realize adjacency query on cloud servers. The execution process of the overall scheme architecture is shown in Fig. 2.

Figure 2: The execution process of the overall scheme architecture

Five algorithms are used in the scheme, and the content is introduced as follows:

keysGen(k): A security parameter k is used as input, and the algorithm returns the secret key SK = {S, M1, M2}. Here, S is an m-dimensional vector consisting of 0 and 1, and {M1, M2} are two randomly generated m-dimensional invertible matrices.

BloomfilteCon(G): Construct a Bloom filter for the set of adjacent points of each graph vertex. The data set of graph G is used as input. The results of outputs are the set of adjacency vertices vectors of graph vertices N = {N1, N2, …, Nn}, and Bloom filter set B.

IndextreeCon(N, B, SK): Constructing an index for cloud servers. The set of adjacency vertices vectors N, the Bloom filter set B, and the secret key SK are used as inputs, and the output is used as a secure index I for cloud queries.

QueryrequestCon(Ψ, SK): Constructing a Bloom filter for a query request Ψ. Each query component of the query request Ψ is mapped into the Bloom filter through several LSH functions. The query request Ψ, and the secret key SK are used as inputs, and the result of output is a Bloom filter Q.

Queryimplementation(I, Q)}: The index I and the query Bloom filter Q are used as inputs, and cloud servers implement the query task. After the query is completed, the query results are returned to the user.

In our solution design, k is used as a security parameter, and (Kge, Enc, Dec) is used as a symmetric encryption scheme. The specific construction process of our solution PAQM is described below.

3.3.1 Constructing Bloom Filter Set

Before outsourcing graph data to cloud servers, some data preprocessing is required. Firstly, the vertex data is extracted and processed according to the graph data, and then the graph vertex set V = {v1,…,vn} is constructed. At the same time, the set of adjacency vertices is obtained U = {U1, U2, …, Un}. To realize multi-keyword fuzzy query in the process of query, we use unary grammar to transform the vertex set, and then use Bloom filter to build index and query request. See Algorithm 1 for the specific process of constructing the Bloom filter. The vertex set V is first converted into vector form based on unary grammar. For example, the vertex keyword of a graph is “goods”, which is converted to a unary grammar set {g1, o1, o2, d1, s1}. Among them, “o1” is the first letter “o” in the word, and “o2” is the second letter “o” in the word. For each unary grammar set, we use 160-bit vectors to represent it. The elements of the vector are English letters, numbers and some common symbols. Of the components of the vector, the English letters are 26, repeated five times, and the other 30 elements are numbers and common symbols.

If the element of the keyword appears in the unary grammar set, it is placed 1 in the corresponding position and 0 in the other positions. For example, if “g1” appears, place 1 in the seventh position. The set of vectors that is converted by the vertices set is represented by C = {c1,…, cn}. The set of adjacency vertices vectors of graph vertices is expressed as N = {N1, N2, …, Nn}. We construct an m-bit Bloom filter for each set of adjacency vectors, and the value of each bit is 0. And then each vertex in the set is then mapped to this filter. Each vertex in the set is mapped to l positions by l hash functions, and its value is set to 1. In our scheme, we calculate the correlation score between adjacency vertices instead of 1 by the TF × IDF rule, which is a common ranked function used in information retrieval [39], and the formula is as follows:

Score(Q;Fd)=∑t∈Q1|Fd|⋅(1+ln⁡fd,t)⋅ln⁡(1+Nft)(1)

where Q represents a query keyword; fd,t represents the term frequency of the term t in the file Fd; ft represents the number of files containing the term t; N represents the total number of files; |Fd| represents the length of the file Fd, which is calculated by summing the number of index terms. In the adjacency query of a graph, the formula (1) is used to reflect the correlation between the vertex and its adjacency vertices. The formula we improved to calculate the correlation score between adjacency vertices is as follows:

Score(Q;j)=∑i∈Q1|Lj|⋅(1+ln⁡ui,j)⋅ln⁡(1+Nmi)(2)

where Q denotes query information. The ui,j denotes the weight of the edge between query vertex i and its adjacency vertex j, and |Lj| denotes the sum of weights of all edges which connect vertex j and its adjacency vertices. N denotes the number of vertices other than the queried vertices in the graph, and mi represents the number of vertices adjacent to the query vertex i. In this way, all graph vertex words are converted into 160-bit long vectors. This method can make the vector of slightly misspelled words close to the vector of correct words. At this time, the Euclidean distance can be used to measure the similarity between them. Finally, the Bloom filter set B is constructed through Algorithm 1.

By analyzing the BloomfilteCon algorithm, the time complexity of converting graph vertices into vectors is O(n), and the time complexity of constructing the Bloom filter for Ni is O(l·| Ni |) = O(l· max) (max is the maximum number of adjacency vertices for a vertex in the graph). Therefore, the time complexity of constructing all Bloom filters is O(l·max·n).

3.3.2 Constructing Adjacency Query Index

After the Bloom filters are constructed, we construct the query index through all the Bloom filters. We first generate the secret key SK = {S, M1, M2} by the key generation algorithm, and the security parameter is k. S is an m-dimensional random vector composed of 0 and 1, and S ∈ {0,1}m. M1 and M2 are two invertible matrix, and here, M1, M2 ∈ Rm*m. The index construction detail is described in Algorithm 2. To reduce query consumption, we construct the index based on a balanced binary tree. We build the query index tree in a bottom-up way, that is, we first construct leaf nodes, and then construct internal nodes layer by layer. For each adjacency vertices set Ni of the graph, a leaf node Ni is constructed, and the node content includes the set flag i and the corresponding vector Bi. Next, we build the inner nodes of the index tree. If the number of vertices n of the graph is an even number, that is, n = 2k (k ∈ [1,n/2]), every two leaf nodes N2k-1 and N2k construct a parent node Nx. The parent node stores a vector, and its value is Nk[j] = max{N2k-1[j], N2k[j]}. If n is an odd number, the first n-1 leaf nodes will generate parent nodes in pairs in order in the way just now. The nth leaf node and the parent node of the (n-1)th leaf node construct a new parent node. The construction method of other internal nodes is the same as that above until the root node of the index tree is generated.

To ensure the security of the query content, it is necessary to encrypt the outsourced data. For each node t in the index tree, its corresponding vector Bt is divided into two vectors {Bt1[i];Bt2[i]} by the vector S in the secret key SK. For each bit i in vector S, if S[i] = 0, we set Bt1[i] = Bt2[i] = Bt[i]. If S[i] = 1, Bt1[i] and Bt2[i] are set as two random values, and Bt[i] = Bt1[i] + Bt2[i]. Then, we use the matrices {M1, M2} in the secret key SK to perform matrix transformation on the vectors {Bt1, Bt2} to obtain the encrypted node vector It = {M1TBt1; M2TBt2}. When all nodes in the index tree are encrypted, the encrypted index tree I is obtained.

On the index constructing algorithm IndextreeCon, the time complexity of constructing all parent nodes is O(n), and the time complexity of encrypting index tree nodes is O(m·n). Therefore, the time complexity of constructing the encrypted index tree is O(m·n).

3.3.3 Performing Query

After the construction of the encrypted index is completed, the next step will be to consider the construction of the server-side query scheme. We first build a Bloon filter for a query request Ψ. Each constituent word of the query request is mapped to the Bloon filter by l LSH functions, and then a query vector Ψ’ is generated. Next, the query vector Ψ’ is encrypted. The query vector Ψ’ is divided into two parts {Ψ1’,Ψ2’} by the vector S. If S[i] = 0, Ψ1’[i] = Ψ2’[i] = Ψ’[i]. If S[i] = 1, Ψ’[i] = Ψ1’[i]+ Ψ2’[i], and here Ψ1’[i] and Ψ2’[i] are two randomly selected values. Then we encrypt the query vector {Ψ1’,Ψ2’} through the matrices {M1,M2}, and obtain the encrypted query token Q = {M1TΨ1’, M2TΨ2’}.

Based on the encrypted index tree and query token we constructed, we use the greedy depth-first search algorithm to execute the query [26,44]. Starting from the root node, the inner product of the index vector and the query vector is calculated to obtain the correlation score of the query. Then the query results are sorted based on the correlation score, and the k query results are obtained that are most relevant to the query token. The server completes the adjacency query operation in the cloud environment as described in Algorithm 3.

In the algorithm Queryimplementing, for the query token Q, starting from the root node of the index tree to execute the query. In the worst-case scenario, the time complexity of the query is O(n·log(n)), where n is the number of nodes in the index tree.

4  Security Analysis

For the query scheme we have constructed, we need to ensure the security of privacy information and the query process. We now introduce some concepts used in security analysis [21].

History: The interaction between cloud server and user, including outsourcing graph G and query token sets, represented as Hq = (G, Q1,…, Qq). The partial history is expressed as Hqt = (G, Q1,…, Qt), where t ≤ q.

View: Having the history Hq about the key SK, the access pattern is described as VSK(Hq) = (EncSK(G), I, Q1,…, Qq). The partial view is VSKt(Hq) = (EncSK(G), I, Q1,…, Qq), where t ≤ q.

Access Pattern: Having the history Hq about the key SK, a view is described as a tuple R(Hq) = (RQ1,…, QQq), where RQi (1 ≤ i ≤ q) is the retrieved result set of adjacency query matching to the query token Qi.

Search Pattern: Having the history Hq about the key SK, the search pattern is described as a binary symmetric matrix Πq, such that Πq[i,j] = 1 if Qi = Qj, and Πq[i,j] = 0, otherwise, for 1 ≤ i, j ≤ q.

Trace: Having the history Hq about the key SK, the trace is described as a tuple Tr(Hq) = (|EncSK(G)|, R(Hq), Πq), where |EncSK(G)| is the scale of the graph G, R(Hq) and Πq are the access pattern and the search pattern of the history Hq, respectively. The trace of partial history is described as Tr(Hqt) = (|EncSK(G)|, R(Hqt), Πqt), where t ≤ q.

With the help of the constructed secure index and encrypted query tokens, the cloud server executes adjacency queries and returns the encrypted query results to the user. Meanwhile, the cloud server cannot know the privacy information of query results and query tokens. In our solution design, we assume that our adjacency query scheme satisfies adaptive semantic security, where the server can make choices about query requests based on query results and query tokens from previous retrieval [21,23]. For the security analysis of this solution, we use a simulation-based approach and the conceptual ideas from existing searchable encryption schemes for analysis and verification [19,21]. In the security guarantee of our PAQM solution, the cloud server cannot obtain any content other than a trace, thus ensuring the security of our constructed solution. The security theorem of the PAQM solution we have built is described below.

Theorem 1. Our PAQM solution meets the adaptive semantic security.

Proof. To prove the security of our constructed PAQM solution, it is necessary to first define a polynomial-time simulator ξ such that for all q ∈ N, ξ can simulate the adversary A. For all 0 ≤ t ≤ q, given trace Tr(Hqt) of a partial history, ξ can generate a view (Vtq)* which is not distinguished from the view VtSK(Hq) of A.

For t = 0, on the partial history Tr(Hq0), ξ builds simulated index I* with the help of random strings to simulate the index I, both of which are equally large in scale. ξ simultaneously builds simulated outsourced encrypted graph data via random strings, with the same scale as the real graph data. In other partial views (Vtq)* (1 ≤ t ≤ q) scenarios, index I* will also be used to simulate the true index I. The index I* and I are indistinguishable, and the simulated encrypted graph is indistinguishable from the real graph data. Otherwise, the outputs of the symmetric encryption mechanism of semantic security can be distinguished from random strings of the same size. Thus, (Vq0)* is indistinguishable from V0SK(Hq).

For 1 ≤ t ≤ q, ξ will continue to use the previously built index I*, and Tr(Hqt) contains the search pattern matrix Πt for t query tokens. Next, we will describe how ξ builds the query tokens (Q1*,…, Qt*) contained in Tr(Hqt). In our scheme, we assume that ξ can reuse the query tokens (Q1*,…, Q t-1*) that are included in the view (Vqt-1)*, alternatively, ξ can rebuild these query tokens from Tr(Hqt-1). Below we will explain how to build Qt*.

To build Qt*, ξ first confirms whether Hqt-1 contains Qt* by verifying if Πt[t,j] = 1 (1 ≤ j ≤ t-1). If this verification is not valid, then ξ makes use of the learning from Tr(Hqt) about RQt. ξ picks an address at random from the index I*, ensuring that all selected addresses are pairwise different, and obtains the built query token Qt*. Otherwise, if Hqt-1 contains Qt*, ξ can retrieve the query information related to Qt* and assign it to Qt*. It ensures that if Hqt contains repeated query tokens, then the relevant query tokens that are involved in (Vtq)* are also the same.

The query tokens (Q1*,…, Qt*) in (Vtq)* are not distinguished from the query tokens (G, Q1,…, Qt) in VtSK(Hq), otherwise, the output of the symmetric encryption mechanism can be distinguished from a random string of equal length. Thus, for 0 ≤ t ≤ q, (Vtq)* and VtSK(Hq) are indistinguishable for a polynomial-time adversary. Therefore, this PAQM theorem has been proven to be of security.

5  Experimental Evaluations

This section conducts a performance analysis of our solution through an experimental comparison of the dataset of the Enron email network graph [45,46]. This experiment is implemented by the C program and executed on the server side and local platform. The server side is configured by the Linux system with about 6 CPU cores with 3.2 GHz and 16 GB of RAM. The local platform uses the Win10 system and is configured with an Intel Core 4 CPU of 2.8 GHz. In this scheme, the implementation of query operations is completed by the server on the cloud server side. The performance evaluation of index and query token construction is completed on the local platform. The index and query tokens built in our solution are processed through encryption, and the queries are executed on the cloud server based on secure index and query tokens, which guarantees the security of the private information in the queries.

To conduct a performance analysis on our construction scheme PAQM, we compared it with the multi-keyword fuzzy adjacency queries on plaintext graph data (denoted as MAQM). These two schemes are similar in terms of construction strategy, including index construction, token construction, and query methods. The difference is that one is ciphertext mode and the other is plaintext mode. The purpose of comparing and analyzing this construction scheme PAQM with the MAQM scheme is to evaluate the time cost, storage cost, and query efficiency of our proposed PAQM scheme. For experimental graph data, the difference in the number of vertices affects the change in the number of edges, which has a significant impact on experimental evaluation and analysis. The experimental analysis in the work can evaluate the cost and efficiency of the multi-keyword fuzzy adjacency queries of our PAQM scheme.

5.1 Constructing Secure Query Index

To realize security queries on the cloud server, it is necessary to construct a security index. We first convert the graph vertex set into vector form based on unary grammar. Then, the vector form of each set of adjacency vertices is constructed, and a Bloom filter is constructed for each set of adjacency vectors. Next, we build a secure index based on all Bloom filters. This section conducts experimental evaluation on index construction time and index construction scale and provides experimental results. The experimental analysis results of index construction time are given in Figs. 3a and 3b, where the horizontal axis direction of Fig. 3a represents the number of vertices in the graph dataset, and the horizontal axis direction of Fig. 3b represents the number of edges of the graph. The vertical axes of Figs. 3a and 3b represent the index construction time. Fig. 3a illustrates how index build time is affected by changes in the number of graph vertices, and Fig. 3b illustrates the impact of index construction time on the number of vertices in the graph.

Figure 3: Index construction time analysis on multi-keyword fuzzy adjacency search

From Fig. 3, it can be seen that there is an important correlation between index construction time and the number of vertices or edges in the graph. In both cases PAQM and MAQM, there is a basic linear correlation between index construction time and the number of graph vertices or edges. Generally speaking, an increase in the number of vertices in a graph will generally increase the number of edges, and the number of adjacency vertices of the graph vertices will also increase. This also increases the overhead for index building. For encrypted outsourcing graph data, the secure index is constructed in ciphertext. Therefore, the index construction cost of scheme PAQM is higher than that of scheme MAQM, but it also ensures the security of private information by increasing the time cost.

An experimental analysis of the index scale is given in Figs. 4a and 4b, where the horizontal axis direction indicates the number of vertices or edges of the graph, and the vertical axis directions of Figs. 4 a and 4b represent the size of the index. From the distribution trend of the experimental graph, it can be seen that the index scale of scenario PAQM and scenario MAQM changes roughly linearly with the number of vertices in the graph. The index building overhead for our proposed PAQM scheme is slightly higher than that of MAQM, but the additional overhead is necessary as the PAQM scheme addresses the issue of secure queries for outsourced graph data.

Figure 4: Index construction size analysis on multi-keyword fuzzy adjacency search

5.2 Performing Query

After the secure index and query token are constructed, the cloud server follows the idea of the query algorithm and utilizes the index and query token to achieve multi-keyword fuzzy adjacency queries. This experimental evaluation mainly compares and analyzes the query time cost to verify the effectiveness of this scheme. The results of the query times performed by the cloud server are shown in Figs. 5a and 5b, where the horizontal axis direction represents the number of vertices or edges about the graph, and the vertical axis directions of Figs. 5a and 5b represent the query time consumed. From the experimental results, it can be observed that the time consumed by the query increases approximately linearly with the number of vertices or edges on the graph. In the query experiment, our PAQM scheme achieves security protection in the query at the cost of increasing query time. The PAQM scheme takes slightly more time than the scheme MAQM, but the difference in time is acceptable, so it is feasible to query the efficiency of our query scheme.

Figure 5: Query time analysis on multi-keyword fuzzy adjacency search

In short, the PAQM scheme we constructed is evaluated through experimental analysis and comparison. Index construction is implemented on the local platform, and the time and scale of index construction are analyzed. The total time and storage costs of our experiment are acceptable under the condition of implementing a query function and security guarantee. As the number of graph vertices increased, it showed an approximate linear trend. The query processing process is implemented by the server on the cloud platform, and the query time shows an approximate linear trend with the increase in the number of graph vertices.

In short, the PAQM scheme we constructed is evaluated through experimental analysis and comparison. Index construction is implemented on the local platform, and the time and scale of index construction are analyzed. The total time and storage costs of our experiment are acceptable under the condition of implementing a query function and security guarantee. As the number of graph vertices increased, it showed an approximate linear trend. The query processing process is implemented by the server on the cloud platform, and the query time shows an approximate linear trend with the increase in the number of graph vertices.

6  Conclusion

In this work, we provide a new approach to realize the secure adjacency query supporting multi-keyword fuzzy search on encrypted graphs in the cloud environment. In the solution, we use some mechanisms such as unary grammar, Bloom filter, searchable encryption, and so on. We first convert the vertex set into vector form based on unary grammar, and then we construct the Bloom filter for each set of adjacency vectors. Next, we construct the query index based on a balanced binary tree through all the Bloom filters to realize a multi-keyword fuzzy query. Secondly, we have conducted a formal security analysis of the query scheme we have constructed. Finally, we provided experimental comparisons and analysis to demonstrate the effectiveness of our proposed scheme. As our future research direction, we will integrate big data analysis technology and tools with massive graph data, and conduct research and exploration on the query and other processing of encrypted graph data based on protecting privacy information.

Acknowledgement: We would like to thank all the members of the research team for their hard work and contribution to this study. We also want to thank the editors and reviewers for their opinions and suggestions on this work.

Funding Statement: This research was supported in part by the Nature Science Foundation of China (Nos. 62262033, 61962029, 61762055, 62062045 and 62362042), the Jiangxi Provincial Natural Science Foundation of China (Nos. 20224BAB202012, 20202ACBL202005 and 20202BAB212006), the Science and Technology Research Project of Jiangxi Education Department (Nos. GJJ211815, GJJ2201914 and GJJ201832), the Hubei Natural Science Foundation Innovation and Development Joint Fund Project (No. 2022CFD101), Xiangyang High-Tech Key Science and Technology Plan Project (No. 2022ABH006848), Hubei Superior and Distinctive Discipline Group of “New Energy Vehicle and Smart Transportation”, the Project of Zhejiang Institute of Mechanical & Electrical Engineering, and the Jiangxi Provincial Social Science Foundation of China (No. 23GL52D).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: B. Wu, X. Chen, J. Huang; data collection: C. Zhang, J. Wang; analysis and interpretation of results: J. Yu, Z. Zhao, Z. Mei; draft manuscript preparation: B. Wu, X. Chen, J. Huang, Z. Zhao, Z. Mei. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Please contact the author for information about the data used in the study in this work.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. X. Zhu, E. Ayday and R. Vitenberg, “A privacy-preserving framework for conducting genome-wide association studies over outsourced patient data,” IEEE Transactions on Dependable and Secure Computing, vol. 20, no. 3, pp. 2390–2405, 2023. [Google Scholar]

2. J. Sampe, M. S. Artigas, G. Vernik, I. Yehekzel and P. G. Lopez, “Outsourcing data processing jobs with lithops,” Outsourcing Data Processing Jobs with Lithops, vol. 11, no. 1, pp. 1026–1037, 2023. [Google Scholar]

3. Y. Ren, Z. Song, S. Sun, J. K. Liu and G. Feng, “Outsourcing LDA-based face recognition to an untrusted cloud,” IEEE Transactions on Dependable and Secure Computing, vol. 23, no. 3, pp. 2058–2070, 2023. [Google Scholar]

4. S. Huang, J. Xie, A. F. Nahhas and M. M. A. Muslam, “A cloud computing based deep compression framework for UHD video delivery,” IEEE Transactions on Cloud Computing, vol. 11, no. 2, pp. 1562–1574, 2023. [Google Scholar]

5. S. K. Pati, A. Banerjee and S. Manna, “Gene selection of microarray data using heatmap analysis and graph neural network,” Applied Soft Computing, vol. 135, pp. 110034, 2023. [Google Scholar]

6. L. Song, C. Wang, J. S. Fan and H. M. Lu, “Elastic structural analysis based on graph neural network without labeled data,” Computer-Aided Civil and Infrastructure Engineering, vol. 38, no. 10, pp. 1307–1323, 2023. [Google Scholar]

7. Z. Cui, Z. Lu, L. T. Yang, J. Yu, L. Chi et al., “Privacy and accuracy for cloud-fog-edge collaborative driver-vehicle-road relation graphs,” IEEE Transactions on Intelligent Transportation Systems, vol. 24, no. 8, pp. 8749–8761, 2023. 10.1109/TITS.2023.3254370 [Google Scholar] [CrossRef]

8. Y. Lv, W. Shi, W. Zhang, H. Lu and Z. Tian, “Do not trust the clouds easily: The insecurity of content security policy based on object storage,” IEEE Internet of Things Journal, vol. 10, no. 12, pp. 10462–10470, 2023. [Google Scholar]

9. C. Xu, R. Wang, L. Zhu, C. Zhang, R. Lu et al., “Efficient strong privacy-preserving conjunctive keyword search over encrypted cloud data,” IEEE Transactions on Big Data, vol. 9, no. 3, pp. 805–817, 2023. [Google Scholar]

10. S. Ghosh, S. H. Islam, A. Bisht and A. K. Das, “Provably secure public key encryption with keyword search for data outsourcing in cloud environments,” Journal of Systems Architecture, vol. 139, pp. 102876, 2023. [Google Scholar]

11. H. Groh, L. Ruppert, P. Wieschollek and H. P. A. Lensch, “GGNN: Graph-based GPU nearest neighbor search,” IEEE Transactions on Big Data, vol. 9, no. 1, pp. 267–279, 2023. [Google Scholar]

12. L. Chang, X. Feng, K. Yao, L. Qin and W. Zhang, “Accelerating graph similarity search via efficient GED computation,” IEEE Transactions on Knowledge and Data Engineering, vol. 35, no. 5, pp. 4485–4498, 2023. [Google Scholar]

13. C. Zygowski and A. Jaekel, “Optimal path planning strategies for monitoring coverage holes in wireless sensor networks,” Ad Hoc Networks, vol. 96, pp. 1–13, 2020. [Google Scholar]

14. B. Kay, P. Date and C. D. Schuman, “Neuromorphic graph algorithms: Extracting longest shortest paths and minimum spanning trees,” in NICE’20: Neuro-inspired Computational Elements Workshop, Heidelberg, Germany, pp. 1–6, 2020. [Google Scholar]

15. Y. Zheng, R. Lu, Y. Guan, S. Zhang, J. Shao et al., “Efficient and privacy-preserving similarity query with access control in eHealthcare,” IEEE Transactions on Information Forensics and Security, vol. 17, pp. 880–893, 2022. [Google Scholar]

16. P. K. Vairam, P. Kumar, C. Rebeiro and V. Kamakoti, “FadingBF: A bloom lter with consistent guarantees for online applications,” IEEE Transactions on Computers, vol. 71, no. 1, pp. 40–52, 2022. [Google Scholar]

17. M. Yang, D. Gao, C. H. Foh, Y. Qin and V. C. M. Leung, “A learned bloom lter-assisted scheme for packet classi cation in software-defined networking,” IEEE Transactions on Network and Service Management, vol. 19, no. 4, pp. 5064–5077, 2022. [Google Scholar]

18. D. X. Song, D. Wagner and A. Perrig, “Practical techniques for searches on encrypted data,” in 2000 IEEE Symp. on Security and Privacy, Berkeley, California, USA, pp. 44–55, 2000. [Google Scholar]

19. E. Goh, “Secure indexes,” IACR Cryptology ePrint Archive, vol. 2003, pp. 216, 2003. [Google Scholar]

20. Y. Chang and M. Mitzenmacher, “Privacy preserving keyword searches on remote encrypted data,” in Third Int. Conf. on Applied Cryptography and Network Security (ACNS 2015), New York, NY, USA, pp. 442–455, 2005. [Google Scholar]

21. R. Curtmola, J. A. Garay, S. Kamara and R. Ostrovsky, “Searchable symmetric encryption: Improved definitions and efficient constructions,” Journal of Computer Security, vol. 19, no. 5, pp. 895–934, 2011. [Google Scholar]

22. J. Baek, R. Safavi-Naini and W. Susilo, “Public key encryption with keyword search revisited,” in Computational Science and Its Applications-ICCSA 2008, Perugia, Italy, pp. 1249–1259, 2008. [Google Scholar]

23. S. Kamara, C. Papamanthou and T. Roeder, “Dynamic searchable symmetric encryption,” in CCS'12: Proc. of the 2012 ACM Conf. on Computer and Communications Security, Raleigh, NC, USA, pp. 965–976, 2012. [Google Scholar]

24. B. Wang, S. Yu, W. Lou and Y. T. Hou, “Privacy-preserving multi-keyword fuzzy search over encrypted data in the cloud,” in 2014 IEEE Conf. on Computer Communications, (INFOCOM 2014), Toronto, Canada, pp. 2112–2120, 2014. [Google Scholar]

25. Z. Fu, X. Wu, C. Guan, X. Sun and K. Ren, “Toward efficient multi-keyword fuzzy search over encrypted outsourced data with accuracy improvement,” IEEE Transactions on Information Forensics and Security, vol. 11, no. 12, pp. 2706–2716, 2016. [Google Scholar]

26. H. Zhong, Z. Li, J. Cui, Y. Sun and L. Liu, “Efficient dynamic multi-keyword fuzzy search over encrypted cloud data,” Journal of Network and Computer Applications, vol. 149, no. 1, pp. 102469, 2020. [Google Scholar]

27. Q. Liu, Y. Peng, J. Wu, T. Wang and W. Wang, “Secure multi-keyword fuzzy searches with enhanced service quality in cloud computing,” IEEE Transactions on Network and Service Management, vol. 18, no. 2, pp. 2046–2062, 2021. [Google Scholar]

28. M. Chase and S. Kamara, “Structured encryption and controlled disclosure,” in 16th Int. Conf. on the Theory and Application of Cryptology and Information Security, Singapore, pp. 577–594, 2010. [Google Scholar]

29. N. Cao, Z. Yang, C. Wang, K. Ren and W. Lou, “Privacy-preserving query over encrypted graph-structured data in cloud computing,” in 2011 Int. Conf. on Distributed Computing Systems, Minneapolis, Minnesota, USA, pp. 393–402, 2011. [Google Scholar]

30. Y. Zhang, S. Su, Y. Wang, W. Chen and F. Yang, “Privacy-assured substructure similarity query over encrypted graph-structured data in cloud,” Security and Communication Networks, vol. 7, no. 11, pp. 1933–1944, 2014. [Google Scholar]

31. Z. Fan, B. Choi, J. Xu and S. S. Bhowmick, “Asymmetric structure-preserving subgraph queries for large graphs,” in 31st IEEE Int. Conf. on Data Engineering, Seoul, South Korea, pp. 339–350, 2015. [Google Scholar]

32. M. Shen, B. Ma, L. Zhu, R. Mijumbi, X. Du et al., “Cloud-based approximate constrained shortest distance queries over encrypted graphs with privacy protection,” IEEE Transactions on Information Forensics and Security, vol. 13, no. 4, pp. 940–953, 2018. [Google Scholar]

33. X. Xia, C. Yuan, R. Lv, X. Sun, N. N. Xiong et al., “A novel weber local binary descriptor for fingerprint liveness detection,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 50, no. 4, pp. 1526–1536, 2020. [Google Scholar]

34. X. Li, H. Ye, T. Li, W. Wang, W. Lou et al., “Efficient and secure outsourcing of differentially private data publishing with multiple evaluators,” IEEE Transactions on Dependable and Secure Computing, vol. 19, no. 1, pp. 67–76, 2022. [Google Scholar]

35. Z. Wu, R. Wang, Q. Li, X. Lian, G. Xu et al., “A location privacy-preserving system based on query range cover-up or location-based services,” IEEE Transactions on Vehicular Technology, vol. 69, no. 5, pp. 5244–5254, 2020. [Google Scholar]

36. A. Jebali, S. Sassi, A. Jemai and R. Chbeir, “Secure data outsourcing in presence of the inference problem: A graph-based approach,” Journal of Parallel And Distributed Computing, vol. 160, pp. 1–15, 2022. [Google Scholar]

37. X. Zhang, J. Zhao, C. Xu, H. Wang and Y. Zhang, “DOPIV: Post-quantum secure identity-based data outsourcing with public integrity verification in cloud storage,” IEEE Transactions on Services Computing, vol. 15, no. 1, pp. 334–345, 2022. [Google Scholar]

38. S. Peng, L. Zhao, A. Y. Al-Dubai, A. Y. Zomaya, J. Hu et al., “Secure lightweight stream data outsourcing for internet of things,” IEEE Internet of Things Journal, vol. 74, no. 3, pp. 841–858, 2015. [Google Scholar]

39. C. Wang, N. Cao, K. Ren and W. Lou, “Enabling secure and efficient ranked keyword search over outsourced cloud data,” IEEE Transactions on Parallel and Distributed Systems, vol. 23, no. 8, pp. 1467– 1479, 2012. [Google Scholar]

40. K. Fan, Q. Chen, R. Su, K. Zhang, H. Wang et al., “MSIAP: A dynamic searchable encryption for privacy-protection on smart grid with cloud-edge-end,” IEEE Transactions on Cloud Computing, vol. 11, no. 2, pp. 1170–1181, 2023. [Google Scholar]

41. S. Goldwasser and S. Micali, “Probabilistic encryption,” Journal of Computer and System Sciences, vol. 28, no. 2, pp. 270–299, 1984. [Google Scholar]

42. O. Goldreich, “Encryption schemes,” in The Foundations of Cryptography, vol. 2. Cambridge, UK: Cambridge University Press, pp. 373–496, 2004. [Google Scholar]

43. W. T. Wong, D. W. Cheung, B. Kao and N. Mamoulis, “Secure kNN computation on encrypted databases,” in Proc. of the ACM SIGMOD Int. Conf. on Management of Data, Providence, Rhode Island, USA, pp. 139–152, 2009. [Google Scholar]

44. Z. Xia, X. Wang, X. Sun and Q. Wang, “A secure and dynamic multi-keyword ranked search scheme over encrypted cloud data,” IEEE Transactions on Parallel and Distributed Systems, vol. 27, no. 2, pp. 340–352, 2016. [Google Scholar]

45. B. Klimt and Y. Yang, “Introducing the enron corpus,” in First Conf. on Email and Anti-Spam, Mountain View, California, USA, pp. 1–2, 2004. [Google Scholar]

46. J. Leskovec, K. J. Lang, A. Dasgupta and M. W. Mahoney, “Community structure in large networks: Natural cluster sizes and the absence of large well-defined clusters,” Internet Mathematics, vol. 6, pp. 29–123, 2009. [Google Scholar]