VKFQ: A Verifiable Keyword Frequency Query Framework with Local Differential Privacy in Blockchain

1  Introduction

With the emergence and development of Bitcoin, blockchain technology has evolved beyond digital currencies and has demonstrated significant potential in various fields including finance, the Internet of Things, and healthcare. Blockchain functions as a distributed ledger, maintained by equal participants known as blockchain nodes. When new transactions occur, they are broadcast to all nodes, and the blockchain system utilizes a consensus algorithm to package these transactions into a new block. The consensus process is verified by nodes across the network. Data are stored within blocks, which are linked together through the hash value of the previous block in the block header, creating a chained structure. Consequently, any alteration of data within a block will result in a change in the hash value of that block, ensuring the integrity and immutability of the blockchain.

The decentralized, tamper-proof, and traceable features of blockchain technology allow for secure data sharing. This means that data can be securely shared between different systems, organizations, or individuals. For instance, electronic medical records can be shared across healthcare organizations, making medical services accessible; moreover, transaction information can be shared amongst organizations, facilitating inter-organization money transfers. One of the main problems in data sharing is how to protect individual privacy while allowing efficient data queries. In the context of blockchain, data are uploaded for sharing, and the data requester (DR) can query the blockchain to retrieve the data they need. However, even if the data are anonymized before being uploaded, there is still a risk of privacy leakage. Attackers may use external data sources to perform matching analysis or employ methods like linear programming to reconstruct the anonymized data and infer the privacy information it contains [1].

In this paper, we study verifiable KF queries with local differential privacy in blockchain. Data on blockchain is expanding rapidly these days; in November 2023, for example, over 18.71 million blocks were generated in Ethereum (https://etherscan.io/txs). As storing all the data would put high storage and computing pressure on blockchain nodes, a typical blockchain network contains two classes of nodes: Full nodes and light nodes. The full node stores the complete block, but the light node only holds the block header including the consensus proof and the block hash. There are three roles in blockchain-based sharing systems: Data owner (DO), DR, and cloud service provider (SP). As illustrated in Fig. 1, the SP acts as a full node, storing the data used for sharing and trading, and providing query services. The DR joins the blockchain as a light node. The trustworthiness of the SP is not absolute, and there is a potential risk of tampering. To address this concern, the full node maintains an ADS, which enables query processing and data verification. On the other hand, the light node only maintains the root hash of ADS for data verification. When returning query results to the DR, the SP provides a VO as well. This allows the DR to verify the accuracy of the result based on the held root hash and the received VO.

Figure 1: KF queries with local privacy in blockchain

A KF query aims to find the occurrences of a given keyword such that the value of the numeric attribute falls in a specified range. In many practical applications, numerical attributes, such as a patient’s temperature and heart rate are publicly available, while keyword attributes, such as the medicines purchased by a patient, need to be privacy-protected. Specifically, each data object oi generated by the DO contains both numeric attributes vi∈V and keyword attributes ki∈K. A local differential privacy perturbation is applied to ki, with vi held constant. The DR may be interested in the statistics of keywords; for instance, he/she may issue a query to find the frequency of a keyword ki with the numerical value falls in a range; i.e., how many data objects are associated with ki while vi is it in the given range?

Example 1. In a blockchain-based smart healthcare system, patients share their medical records, including body metrics like temperature, blood pressure, and heart rate, as well as symptom information such as dizziness, cough, and chest tightness. Healthcare organizations want to count the frequency of specific symptoms. For instance, a query Q=<[40,43],convulsive> is issued to query the number of patients with body temperatures between 40–43 degrees who exhibit the symptom “convulsive”. In this scenario, patients with symptoms of “convulsions” do not want their private information to be exposed.

Example 2. In blockchain-based investor behavior analysis, investors share information about their investments in various financial products. The blockchain systems store the investment amount and the name of the investor. Financial regulators may need to count the number of times an investor has invested within a particular investment amount range. For example, a query Q=<[100000,200000],IntelCapital> is to find the number of times an investor named “Intel Capital” has invested between 10–20 w. The investor “Intel Capital” wants its personal information to be kept private.

Although some researchers have studied the privacy protection problem in blockchain, most of them employ anonymous communication to anonymize users, preventing attackers from linking transaction information with user addresses. However, there is a “trilemma” for such anonymous communication-based approaches [2]. Some researchers use cryptographic algorithms to safeguard user identity information, but they do not consider supporting the query processing. There are also some studies on verifiable query processing in blockchains, e.g., numerical range queries and Boolean queries [3–5]. For inter-block queries, current approaches improve search efficiency through skip list [6] and sliding window indexes [7]. Although these approaches [3–7] allow for efficient queries and guarantee the correctness and integrity of the results, they do not use local differential privacy. Moreover, existing approaches cannot support KF queries. The proposed ADS are variants of the Merkle tree, the VO size of which is O(f⋅logfD). The VO size is high for large fanouts.

To this end, we propose a verifiable keyword frequency query framework with local differential privacy in blockchain (VKFQ), which aims to protect DOs’ privacy on keyword attributes and support efficient and verifiable query processing for KF queries. The framework protects the DO’s privacy of personal data using the local differential privacy technique [8] before the data are uploaded to the blockchain. It also facilitates the calculation of the frequency of a keyword on blockchain data. The framework consists of two main parts: A utility-optimized local differential privacy data-sharing model and a VB-cm ADS. In the data sharing model, each DO independently adds noise to their data object locally, ensuring that the impact of individual data objects on the statistical analysis of the overall dataset remains within the privacy budget (i.e., the upper limit of the privacy loss, lower privacy budget means stronger privacy protection). The perturbed data are then broadcast to the blockchain network. The VB-cm ADS is an inter-block index tree that combines the CM-sketch [9] and the Verkle tree [10]. The CM-sketch is used to summarize the frequency of keywords; as a result, each numerical attribute’s value vi is associated with a CM-sketch CMi. The CM-sketch has the advantage of small size, thereby reducing the ADS storage cost as well as the VO size. A frequency estimate cnt~j can be calculated for the given keyword kj based on the sketches. To further reduce the VO size, the VB-cm ADS uses the Verkle tree as the foundation index structure, the VO size of which is O(logfD).

The main contributions of this paper are as follows:

•   To the best of our knowledge, we are the first to address the verifiable KF query problem in blockchain. Our goal is to support efficient and verifiable query processing while protecting the DO’s privacy. Each data object has both numerical attributes and keyword attributes where the keyword attribute is sensitive and needs to be privacy-protected.

•   We propose the VKFQ framework for the KF query, which protects the DO’s keyword using a utility-optimized local differential privacy technique. The framework calculates the estimate of a keyword’s frequency and is efficient in query time and VO size.

•   We propose the VB-cm tree as the ADS to support efficient query processing while ensuring privacy protection. The VB-cm tree integrates the CM-sketch with the Verkle tree, to reduce the storage cost and the VO size. Each leaf node stores the fixed-size CM-sketch to summarize the frequency information of a large number of keywords. We propose a query scheme based on the VB-cm tree.

•   We conduct extensive experiments to evaluate the efficiency of the VKFQ framework. The experimental results demonstrate that there is a nearly one-order reduction in VO size. The query time and ADS size are lowered by 52.38% and 46.81%, respectively, in comparison to the Merkle B+ tree. The VO size is reduced by more than one order of magnitude.

The rest of the paper is structured as follows. The related work is shown in Section 2. In Section 3, the problem is formulated and the general idea and the preliminaries are presented. Section 4 presents the local differential privacy data sharing model. Section 5 presents the VB-cm ADS. Section 6 describes the experimental design and the results, and the paper’s conclusion is provided in Section 7.

2  Related Work

2.1 Privacy Protection in Blockchain

In recent years, extensive research has revealed the risk of privacy leakage in blockchain. For instance, within the Bitcoin system, each node stores the complete history of transaction information to prevent “double spending” and maintain decentralization. Moreover, Ober et al. [11] found that it is possible to link user addresses to transactions by analyzing the Bitcoin transactions. Reid et al. [12] suggested that incorporating external information, such as email addresses and IP addresses, can potentially expose a user’s identity and compromise anonymity. Koshy et al. [13] demonstrated this concept by mapping nearly 1000 Bitcoin addresses to their respective owner IPs using anomalous relay behavior, thus establishing the ownership relationship between Bitcoin addresses and IP addresses. One common approach to preserving privacy is the anonymizing communication such as Tor [14]. However, these communication networks face a “trilemma” [2] where only two of the three objectives, strong anonymity, minimal bandwidth overhead, and low latency, can be met. Biryukov et al. [15] suggested that while some latency can be tolerated in blockchain, integrating Tor introduces new security vulnerabilities, such as the use of DDoS mechanisms to control the flow of user information, thereby hindering the achievement of strong anonymity.

Yang et al. [16] have summarized the commonly used privacy-preserving methods in blockchain, particularly in cryptocurrencies. For instance, Maurer et al. [17] utilized hybrid coins to mix and split transactions, ensuring anonymity. ZeroCoin [18], on the other hand, employed zero-knowledge proofs to preserve user identity information privacy. Similarly, MonroeCoin [19] uses ring signatures to ensure user anonymity. Additionally, several privacy-preserving methods rely on cryptographic techniques. Zhang [20] proposed the VPFT algorithm, which utilizes a crypto-lottery algorithm to secure consumers’ personal information data. However, it does not provide how the encrypted data can be recovered once stored on the blockchain, making it impossible to query the data. Otherwise, Guo et al. [21] proposed a grid location coordinate privacy protection scheme. Attribute encryption as well as order-preserving encryption are employed to safeguard user location privacy. While this scheme allows querying based on the order of encrypted values, the encryption method is more complex than ordinary encryption, and it is more susceptible to statistical analysis attacks due to retaining the ordering information, thereby making it insufficiently secure.

In addition, smart contracts in blockchain can be used for privacy protection, for example, Raj et al. [22] used smart contracts for access control such that only authorized entities had access to a patient’s medical data. Lu et al. [23] proposed secure data storage protocols that used group signature schemes, proxy re-encryption schemes, and smart contracts to achieve privacy protection. However, smart contracts may have security vulnerabilities caused by code errors and cannot be modified after deployment.

2.2 Verifiable Queries in Blockchain

Verifiable queries in blockchain already enable range queries on numerical attributes [3] and keyword Boolean queries [4,5]. Zhang et al. [3] proposed a method that combines the MB and SMB trees, using the larger MB tree as the primary index and the smaller SMB tree to index newly inserted objects, thus enabling batch merging. Dai et al. [4] designed a lightweight verifiable query for account balances and transaction history in the Bitcoin system. They improved the straw man method to ensure that the query results satisfy the correctness and integrity of the data. But the method results in large intermediate data storage overhead. The keyword query scheme under the blockchain hybrid storage framework was proposed in [5]. This scheme overcomes the storage problem caused by a large amount of intermediate data and maintains the complete ADS on the SP, while the chain maintains part of the ADS. The keywords are organized using the idea of an inverted index. If the smart contract only stores the root summary of the MB tree, updating a new data item requires regenerating the proof, which will result in high overhead, even though only the SP needs to send an authenticatable proof of update to the smart contract. If a trapdoor is used to ensure that the DO does not change its commitment when updating the data, the password pairing operation during verification will be much slower than the password operation for hashing.

The vchain framework proposed by Xu et al. [6] works for both keyword Boolean queries and numerical value range queries. By changing the block structure, the attDigest field is added as a digest of the whole record (i.e., the value after encrypting the plaintext using a public key), which is packed and uploaded to the chain by miners. All collection elements are stored in Merkle tree nodes to support boolean queries for keywords, which leads to expensive storage overhead. In contrast, for numerical range queries, numerical attributes are converted to keywords based on the prefix tree. Because vchain becomes linear at worst when searching between blocks, vchain+ [7] is designed, which uses a Sliding Window Accumulator (SWA) index to achieve efficient search. The sliding window idea is used to divide the query into fixed-length subqueries and then construct a Merkle-Trie tree, avoiding the problem of possible failure of inter-block skiplist.

However, all the above approaches do not consider privacy protection and cannot address the KF query problem. Because the problem addressed is different from ours, existing approaches cannot be applied to the KF query.

3  Preliminaries

3.1 General Idea

Definition 1 (KF queries). Each data object is represented as oi=<vi,ki> containing both the numerical attribute’s value vi and the keyword ki. Given a set of data objects {o1,o2,⋯,om} and the query Q=<[p,q],kj>, KF query returns the total frequency of kj such that vi falls in the query range L=[p,q]; hence, the query result is Result=cnt~j where cnt~j=∑icnt~i,j and cnt~i,j represents the frequency estimate of ki satisfying vi∈[p,q].

We formulated the KF query in Definition 1. In this paper, we focus on privacy protection on keyword attributes, while assuming that the numerical attributes are publicly available. Let K={k1,k2,…,kD} represent the set of keywords where D denotes the keyword size. Let U={u1,u2,…,un} be the set of DOs where each DO ui produces a data object oi=<vi,ki> that contains both numeric attribute vi∈V and keyword attribute ki∈K. Before submitting the data oi to the blockchain network, DO retains vi publicly available and performs privacy protection on ki by adding noise. Specifically, ki is first encoded into a discrete number xi∈[D] and then perturbed into yi. As a result, oi becomes oi=<vi,yi>.

After receiving m data objects {o1,o2,⋯,om} from the DO, the SP aims to compute the keyword frequency on each vi: Fi={vi,(k1,cnti,1),(k2,cnti,2),…,(kD,cnti,D)}. The pair (k2,cnti,2) denotes that the frequency of keyword k2 is cnti,2 when the numerical attribute’s value is vi. To achieve this, the SP does the aggregation operation on {o1,o2,⋯,om}. Because each keyword ki has been transformed to yi by the DO, the SP can only estimate the keyword’s frequency based on received data objects. We use Fi′={vi,(k1,cnti,1′),(k2,cnti,2′),…,(kD,cnti,D′)} to denote the frequency estimate on vi. Let F′={F1′,F2′,…} be the set of frequency estimate Fi′ on each vi.

Because the data query often involves multiple blocks in real applications, to enable inter-block query processing, SP stores Fi′ of each block in the block header. In this way, SP only needs to query the information on the block header instead of scanning all data objects in the block. However, the size of Fi′ is proportional to the size D of keywords. To reduce the size of the block header as well as the VO size, SP uses CM-sketch to compress Fi′ into CMi. Hence, the SP stores {vi,CMi} instead of Fi′ in the block header. If the DR issues a query on the frequency of a keyword kj, the SP will calculate the frequency estimate cnt~i,j by performing the hash mapping of kj and obtaining corresponding bits in CMi.

To support the KF query, we design the VB-cm tree as the ADS. VB-cm tree is constructed on CMi and vi from each block header and uses vi as the search key. Given the query Q=<[p,q],ki> issued by a DR, the SP conducts the query processing on the VB-cm tree to obtain the frequency estimate {(vi,cnt~i,j)} such that vi∈[p,q]. It returns cnt~j, which is the sum of all cnt~i,j to the DR. Also, a VO is returned from the SP to the DR. The DR will verify the correctness and integrity of the query result.

Goals. We need to protect the DO’s privacy. Blockchain is a peer-to-peer network; there is a risk of dishonest nodes (e.g., the SP) tampering with the data, leading to inaccurate query results. To address these concerns, we propose a VKFQ framework that enables the DO to obfuscate keyword information before uploading data to the blockchain network. The blockchain network can then return VO along with the query result, which can be used by the DR to verify the accuracy of the result. The goals of the verifiable KF query under local differential privacy are as follows:

•   Privacy: Given a keyword, blockchain nodes including the SP and DR cannot identify the DO who have uploaded the data associated with this keyword based on the data stored in blockchain.

•   Correctness: Because the SP computes the frequency estimate cnt~j based on {(vi,cnt~i,j)}, the DR can verify that {(vi,cnt~i,j)} are not tampered with.

•   Integrity: The DR can verify that all vi falling in the query range [p,q] are contained in {(vi,cnt~i,j)}.

•   Query efficiency: The time it takes from when a DR initiates a query to when the DR verifies the query results is reduced.

•   Storage overhead: We want to reduce the ADS size and the VO size, and keep the VO size constant even with large volumes of data.

3.2 Preliminary

3.2.1 Differential Privacy

Differential privacy [8] is a technique aimed at safeguarding individual privacy by preventing the disclosure of sensitive personal information during the analysis of personal data, even if an attacker possesses information from other external data sources. The fundamental principle of this technique is to protect personal privacy by introducing noise or perturbation to the data, ensuring that any single modification made by an individual does not significantly impact the overall result. The mathematics of differential privacy is rooted in probability and randomization functions. If a randomized algorithm A, used to perturb the information, satisfies ε-differential privacy, then the inequality exp(−ε)≤Pr[A(S)=O]Pr[A(S′)=O]≤exp(ε) holds if and only if. Given a dataset S, each data point is replaced with a data point that did not originally exist in S, resulting in the modified dataset S′. The meaning of the inequality is as follows. First, the datasets S and S′ are used as inputs to the algorithm A, respectively. Next, the two probabilities that make the output of the algorithm O are compared. The ratio is in the range [exp(−ε),exp(ε)].

3.2.2 CM-Sketch

The probabilistic data structure called CM-Sketch allows for fast estimation of frequency information for elements in large-scale data streams approximately while conserving memory space. It utilizes a two-dimensional matrix to encode a significant amount of element count information. Each row of the matrix consists of an array of counters, with each element being mapped to a specific array using a different hash function. The mapped bits are then incremented by 1. For the estimation of the number of a given element, similar to sketch updating, the counts of the bits of the element in each row are checked. Due to potential hash conflicts and the possibility of different elements being mapped to the same bit, the count in the corresponding bit is also incremented. As a result, the estimated value for the element is determined by taking the smallest value among all the counters. CM-Sketch sacrifices a certain level of accuracy within an acceptable range, which allows for a trade-off between space overhead and accuracy. The width of the two-dimensional array controls the element counting error, while the height controls the probability of the element computation error not exceeding the counting error.

3.2.3 RSA-Based Vector Commitment

Vector Commitment (VC) is a cryptographic primitive used for committing a message (m1,m2,…,mq) and verifying whether the opened message at a specific location is the original committed message, i.e., proving that the opened mi is the i-th element in the message. The requirement for position-specific binding is to ensure that it is not possible to open two commitments with different values at the same position for security purposes. RSA-based vector commitment includes the following functions:

Key Generation Function KeyGen(1k,l,q), which generates the public parameter pp based on the security parameter k and the number q⋅(l+1) of bits of the prime number, and the length q of the message to be committed. This public parameter is used for encryption and decryption operations of the vector commitment.

Commitment Generation Function commitpp(m1,m2,…,mq), which commits to a message (m1,m2,…,mq) using a public parameter pp. The output is a commitment C as well as additional information aux=message.

Open Function Openpp(m,i,aux), an operation is performed by the committer to generate a proof π based on the input. This proof can be used to verify that the i-th committed element in the message is m.

Verification Function Verifypp(C,m,i,π), the output of this function will be either 1 or 0. It will be 1 only if π is a valid proof of C, where m is equal to mi, and C is indeed generated by message (m1,m2,…mq).

4  Utility-Optimized Local Differential Privacy Data Sharing Model

Using differential privacy to encrypt personal data can protect individual privacy and minimize the impact of privacy leakage on the overall data analysis results. The differential privacy method perturbs the dataset before posting it, making it impossible for attackers to determine whether the queried information is from the original or perturbed dataset. That is, an attacker cannot infer from the posted data whether a particular piece of data exists in the original dataset, thereby protecting the privacy of individuals. Modifying certain data will not have much impact on the distribution of the output of a certain algorithm, i.e., for a certain statistical value, the probability of outputting the same statistical value will not change significantly.

Specifically, the purpose of privacy protection in this paper is to collect useful information while ensuring that the keyword information uploaded by the DO is resistant to differential attacks. Useful information is the frequency of keyword appearances, which can be applied to data analysis. SP can collect this useful information from the blockchain network. However, the SP is not entirely trustworthy, and an SP or DR is able to perform a differential attack to localize sensitive information to a DO by using the information obtained from multiple queries. Thus utility-optimized local differential privacy protection is performed before the DO uploads the data. This is because in K there is a portion of sensitive keywords Ks and another portion of non-sensitive keywords KN, and KN=K∖Ks. Undifferentiated perturbation of all data using the local differential privacy technique would ignore differences in sensitivity between keywords, thereby providing less protection for sensitive keywords and adding additional risk. On the other hand, overprotection of non-sensitive keywords can lead to distortion or blurring, affecting the estimation results. Therefore, the DO perturbs the keywords locally and then broadcasts the processed data objects to the SP, which then aggregates the data objects to achieve secure data sharing. As mentioned above, the whole process is divided into two phases: Perturbation and aggregation.

4.1 Perturbation

In the perturbation phase, the numerical attributes vi are preserved, and the keyword attribute ki is obfuscated. After presetting the set of hash functions H, the privacy budget ε, and the allowed failure probability δ, we encode ki as a discrete number xi∈[D], representing a keyword in K. Then xi is obfuscated into a three-dimensional (3D) array, i.e., yi=(yi[1],yi[2],yi[3]).

We set yi[1]=H in the 3D array where H is a hash function randomly selected from H. The output range of the hash function is [1,g], indicating that the output of this hash function is any one of the values in {1,2,3,…,g}, where g=−3eεδ−eε−1(1−δ)(eε+δ−9eεδ−1)+eε+3δ−12δ [24]. Let yi[2]=bi, where bi represents the value of xi after perturbation. yi[3] takes the value of 0 or 1 as the sign of xi. The calculation results of yi[2] and yi[3] depend on whether xi is sensitive information or not. Specifically, if xi represents a sensitive keyword, at this point yi[3]=0, and bi is set to hi with probability M=eε+gδ−δeε+g−1. Here hi=H(xi), which is calculated by DO based on a hash function randomly selected. Also, hi is perturbed to some other value in the range [1,g] with probability N=1−δeε+g−1. That is, when xi represents a sensitive keyword, there is a probability of M for xi to be perturbed into H(xi). The hash collision probability, i.e., the probability that another xj representing a sensitive keyword is perturbed to become H(xi), is 1gM+(1−1g)N=1g. If xi represents a non-sensitive keyword, a local differential privacy perturbation computation is also needed to ensure that xi has the same probability of 1g to be perturbed to H(xi). yi[2] takes random values from [1,g]. If yi[2]=hi, we set yi[2] to the original xi and set yi[3] to 1. If yi[2]≠hi, then yi[2] is kept constant and yi[3] is set to 0. That is, the non-sensitive keyword has a probability of 1g to be retained at the original value xi. Thus, the DO obtains yi after the perturbation on ki. The data object oi=<vi,yi>. Then oi is sent to the blockchain system.

4.2 Aggregation

In the aggregation phase, SP calculates the corresponding frequency estimates of the privacy-protected keywords based on the data uploaded by the DO. In the blockchain network, the uploading of the perturbed keyword frequency information by the DOs is equivalent to broadcasting in the peer-to-peer network. When the SP receives the data {o1,o2,⋯,om} shared by m DOs, the data that have the same numerical attributes are grouped to become {vi,yi,1,yi,2,…,yi,m}. The frequency estimate for each keyword in K can be computed from the set of 3D arrays Yi={yi,1,yi,2,…,yi,m} therein.

We initialize an all-0 array arri=(ai(k1),ai(k2),…,ai(kD)) of length equal to the collection of keywords K for counting, and compute each 3D array yi,t in turn. For the 3D array of yi,t[3]=1, we add 1 to the corresponding ai(yi,t[2]) in arri. This means that yi,t is obtained from the non-sensitive keyword; hence, the value of yi,t[2] is the original xi,t. Therefore, the frequency estimate of the non-sensitive keyword kj∈KN is cntj′=g⋅ai(kj). For the 3D array that satisfies condition yi,t[3]=0, if yi,t[2]=Hi,x(kj), we add 1 to the corresponding bit ai(kj) of arri, where Hi,t=yi,t[1]. So the frequency estimate of the sensitive keyword kj∈KS is cntj′=ai(kj)−m/gM−1/g. In this way, the SP obtains the local differential privacy-protected keyword frequencies {vi,(k1,cnti,1′),(k2,cnti,2′),…,(kD,cnti,D′)}.

5  VB-cm ADS

The VB-cm tree combines the ideas of the Verkle tree and CM-sketch for efficient and verifiable KF queries. The VB-cm tree has the following advantages. First, it enables fast queries among blocks and reduces the storage cost of the ADS structure. Second, it supports the verification of the correctness and integrity of the query results.

Specifically, after the SP obtains the data with the perturbed keywords and numerical attributes, it uses the CM-sketch to map these keywords evenly to diffchildren with numerical attributerent rows. This reduces the possibility of hash conflicts and also compactly records the frequency. Because we consider inter-block queries, we deposit the sketch CM as well as the numerical attribute value v into children with numerical attributthe block header. In this way, we can construct the ADS on sketches and numerical attribute values, instead of the original data objects recorded in each block, thereby supporting fast inter-block KF queries. The block header also contains information such as the previous block hash value Prehash, the TimeStamp of the block generation and the digest value MerkleRoot of the block body, which is packaged with the block body and uploaded to the blockchain. Fig. 2 shows the contents of the block header and the structure of the VB-cm tree.

Figure 2: VB-cm tree

The VB-cm tree is constructed on CM and v, which are extracted from the block header of multiple blocks. The data <vi,CMi> are sorted according to the numerical attribute vi in ascending order. The VB-cm tree is constructed layer by layer upwards where each leaf node stores <vi,CMi>. When a query Q=<[p,q],kj> is issued, the CM in the leaf node is obtained by first starting from the root node and working down layer by layer according to the numerical attribute until a matching leaf node is queried. We get the corresponding bits of the keywords satisfying the query conditions using hash mapping and calculate the minimum of multiple bits as the frequency estimate of the keyword. The VO is generated during the query process and returned to the DR along with the query result. The DR performs the verification process to prove that the returned result is correct and not tampered with.

Compared with the traditional ADS such as the Merkle B+ tree and the Verkle B+ tree, the proposed VB-cm tree is more effective in reducing the query time and VO size. In query time, hashing is employed instead of traversing after finding the block containing the keywords. This allows for a speedy retrieval of the KF data. For VO size, the sketch is utilized to express keyword information rather than the key-value pair. Moreover, a smaller number of nodes are inserted into VO.

5.1 ADS Structure

There are three types of nodes in the proposed VB-cm tree: Leaf node, intermediate node and root node. The VB-cm tree adds the following fields to nodes: 1) CM, a CM-sketch to record the keywords and frequencies, 2) R, an array to record the range of numerical attributes of the child nodes, 3) π and Comm, to record the inputs and outputs of the vector commitment function for verification. Specifically, π is a proof of the node, Comm is a commitment of its child nodes. Each leaf node contains the sketch CM, the numerical attribute value v and the proof π. Each intermediate node contains the commitment Comm, the range R and the proof π. The root node contains the range R and the commitment Comm.

The field π in the leaf node and intermediate node is calculated by the Open Function based on the parent node. The Comm field in the intermediate node and the root node is computed from the information of all its child nodes based on the Commitment Generation Function. The R field aggregates the range of numerical attributes of the child nodes: R=[rangeA,rangeB]. For the first layer of intermediate node N, its numerical range is aggregated by the numerical attribute N.child.v of its children nodes, that is, N.rangeA=min(v0,v1,v2,…), N.rangeB=max(v0,v1,v2,…). If N is a node of other layers, N.R is the aggregation of the numerical ranges of its child nodes N.child, i.e.,

N.rangeA=min(N.child0.rangeA,N.child1.rangeA,N.child2.rangeA,…)(1)

and

N.rangeB=max(N.child0.rangeB,N.child1.rangeB,N.child2.rangeB,…).(2)

Example 3. Consider the VB-cm tree where node N has three children with numerical attribute ranges N.child0.R=[3,4],N.child1.R=[6,7] and N.child2.R=[8,9], respectively. Then the range of numerical attributes of this node N is N.R=[3,9]. Suppose the commitments of the three children are N.child0.Comm=100, N.child1.Comm=200, and N.child3.Comm=300, constituting the message=("100"|"[3,4]","200"|"[6,7]","300"|"[8,9]"). Then the commitment of node N is N.Comm=commitpp(message). The proof of the first child node of node N is N.child0.π=Openpp("100"|"[3,4]",0,message), and so on for the rest of the child nodes, where pp=KeyGen(1k,l,3).

Algorithm 1 describes the construction process of the VB-cm tree. The construction starts from the leaf node layer by layer upwards. We use cnt_node to denote the number of nodes in the current layer of the tree. We use a specific node N as an example. If N is a leaf node, then the message consists of CM fields and v fields, and the list of numerical attributes Numlist consists of v. Otherwise, the message consists of Comm fields and R fields, and Numlist consists of R. The “|” means concatenates two strings (lines 3–7). The numerical attributes range R of the parent node is obtained from the maximum and minimum values of Numlist. The commitment Comm of the parent node is obtained from the Commitment Generation Function based on the message. π of node N and all its sibling nodes is generated by the Open Function (lines 8–14). From this, the nodes at each level are constructed iteratively until R and Comm of the root node are computed. So far, the whole tree has been constructed.

5.2 Query Processing

Given a range [p,q] of numerical attributes and the keyword kj as query conditions, the result of a KF query is an estimate cnt~jof all the frequency of keyword kj with the vj falling in the range [p,q]. That is, cnt~j=∑icnt~i,j where cnt~i,j represents the frequency estimate of ki satisfying vi∈[p,q]. A VO is also generated during the query process and returned to the DR along with the query result to verify.

Note that the VB-cm tree retains the ordered and linkable structure of the leaf nodes like the B+ tree. Hence, we conduct a depth-first query to find the left-most and right-most leaf nodes based on the query range [p,q]. Then all leaf nodes in the middle are within the query range. For each leaf node within the query range, we need to get cnt~i,j for the keyword kj and accumulate to get the final result cnt~j. We obtain cnt~i,j from the CM-sketch in each leaf node. Also, VO is constructed bottom-up for subsequent verification. The VO contains the π, Comm (or CM) of each node in the path from root to the leaf node within [p,q], as well as the sequence number seq, which indicates that the current node is the seq-th child of its parent node.

Algorithm 2 describes the process of the query processing and the generation of the VO. The top-down query starts from the root node and performs node pruning based on the query range [p,q]. The node’s range R is compared with [p,q]. If p is smaller than rangeB, the query continues downward from this node. Otherwise, the query goes downward with the rightmost node. If q is larger than rangeA, we continue the query down from this node. Otherwise, we query down with the leftmost node. When the query reaches the leaf node, we compare [p,q] with v in the leaf node and obtain the left boundary leaf node Np and the right boundary leaf node Nq (lines 2–7). All nodes between Np and Nq are called result nodes. Thus, based on the queried keyword ki and the corresponding CM of the result nodes, the frequency estimates are obtained and then accumulated to get the query result cnt~i (lines 8–9). For each leaf node between Np−1 and Nq+1, the path from this leaf node to the root is added into VO. Specifically, we add the information including Comm (CM), R (v), π, and the sequence number seq in each node, into VO (lines 10–16).

Example 4. In Fig. 2, the numbers next to each node in the figure are the numerical attributes. Suppose the query range L of numerical attributes is [4,11] and the keyword is “Alice”. We perform the query down from the root node. We get two boundary leaf nodes in the range L with numerical attributes 5 and 10 with subscripts 2 and 4, respectively. The leaf nodes with subscripts 2∼4 have numerical attributes of 5, 7, and 10, all of which satisfy the numerical attribute query condition. So we read CM2∼CM4 to estimate the frequency of the keyword “Alice” and calculate their sum. For each leaf node with subscripts 1∼5, we need to add the nodes in the path from the root to such a leaf node into the VO for the result verification. In this way, we get VO=[[[CM1,1,π1,3], [Comm9,0,π9,R9]], [[CM2,2,π2,5], [Comm9,0,π9,R9]],[[CM3,0,π3,7], [Comm10,1,π10,R10]],[[CM4,1,π4,10], [Comm10,1,π10,R10]],[[CM5,1,π1,14],[Comm10,1,π10,R10]]].

5.3 Verification

The verification process contains correctness verification and integrity verification, which is achieved by traversing VO. Recall that VO is returned to the DR along with the query result. Commroot is in the root of the VB-cm tree and stored in the block header; hence, the DR can verify the query result by using the root commitment in the block header and VO to perform verification calculations. Because cnt~j=∑icnt~i,j, we need to verify the correctness and integrity of {(vi,cnt~i,j)}.

Algorithm 3 describes the process of verification. Based on VO obtained during the query process and Commroot owned by the DR, each item in VO is verified one by one using the Verification Function in the vector commitment. VO is a 3D array. The first dimension corresponds to the path of leaf nodes, with the length of the number of leaf nodes between Np−1 and Nq+1 (line 2). The second dimension corresponds to the nodes in the path, and the length depends on the layer height of the VB-cm tree. It is to be traversed from back to front, which in terms of the structure of the tree is a top-down verification (line 4). The third dimension corresponds to Comm (CM in the leaf node), R (v in the leaf node), the sequence number seq, and π in each node, which are all used as inputs to the Verification Function (line 5). When performing the correctness verification, we assign Commroot to C before traversing each path (line 3), and C is assigned to the next Comm (or CM) for the following verification by using the Verification Function (lines 5–6). The verification will continue only if the output of the above function is true after each call. If a false is returned, the result is proved to have been tampered with (line 8). After correctness verification, we can ensure that the data obtained are untampered with. So we can get four numerical attributes v of four boundary nodes from VO: Np, Nq, Np−1 and Nq+1. Only if p∈[Np−1.v,Np.v] and q∈[Nq.v,Nq+1.v], the result of the query is proved to have integrity (lines 9–12).

Example 5. We first verify the answer’s correctness. According to the VO obtained in Example 4, and the Commroot saved in the root node, we calculate Verifypp(Commroot,Comm9,0,π9). If the output is 1, we then calculate Verifypp(Comm9,CM2,2,π2), and so on until all the items in the VO are traversed and return true, proving that the data are untampered with. If the Verification Function has any one output of 0, i.e., the algorithm returns false, we can infer that the data have been tampered with. If the function returns true for every call, we can verify the integrity. According to the [CM1,1,π1,3], [CM2,2,π2,5], [CM4,1,π4,10], [CM5,1,π1,14] in VO, we can verify that 4∈[3,5], and 11∈[10,14]; hence,the integrity is proved.

5.4 Security Analysis

Privacy protection. There are potential security vulnerabilities in the system. The SP, as a full node, can locate the DO through the data stored in the blockchain to obtain address information. In addition, the DR can also be an attacker that performs a data reconstruction attack by launching multiple query requests to the SP. That is, an attacker can construct inequalities with KF information and solve linear equations with the goal of noise minimization to solve the approximate solution of the data object saved by the SP, which leads to personal privacy disclosure. Our approach uses the local differential privacy technique to allow the DO to do the noise addition to the data locally. The SP and the DR are unable to determine whether the data is real data from the DO, and therefore it is not possible to determine from which DO the real data was sent. From this, it can be concluded that the user’s privacy is protected to minimize security vulnerabilities.

Correctness and integrity of the query result. For the correctness of the query result, DR can extract all the CM-sketches in the VO and obtain cnt~j by summing up each cnt~i,j, and compare with the Result. If cnt~j is the same with Result, the query result is proved to be correct. For the integrity of the query result, DR can compare the four boundary leaf nodes in VO with the query range [p,q]. The integrity of the query result is proved if p∈[Np−1.v,Np.v] and q∈[Nq.v,Nq+1.v].

6  Evaluation

6.1 Experimental Setup

The value v of each data object on the numerical attribute is a random value in (0,232−1). The keyword is randomly generated using the website (https://contenttool.io/zh/random-word-generator). We set the number of DOs in the range [30,40,50,60,70], with the default value of 50. The number of leaf nodes is 42,43,44,45, and 46, with the default value of 44. The dataset size D is in the range [50,100,150,200,250], and the default value is set to 100. The query range L=[p,q] is randomly generated where the ratio of |q−p| in 232−1 is in the range [1% ,2% ,3% ,4% ,5% ], and the default ratio is 3% . The privacy budget ε in the local differential privacy model is set to 3.0, and the allowed failure probability δ is set to 10−3 [24]. We use MurmurHash3 in CM-sketches. We set the number of hash functions per CM-sketch to 8, i.e., the number of rows is 8 and each row is 100 bits.

We run all algorithms on a PC with Inter(R) Core(TM) i7-7700HQ CPU (2.80 GHz) and a RAM of 8 GB. The operating system is Windows 10 and the program code is written using Python 3.8. We measure the performance of the approaches using the following metrics: 1) Query time, the time from the beginning of the query to the end of getting the result verified as correct and integral, 2) Verification time, the time to verify the results after getting them, 3) ADS size, number of bytes occupied by the ADS, and 4) VO size, number of bytes occupied by VO. We compare our proposed VB-cm tree with the Merkle B+ tree and the Verkle B+ tree.

6.2 Experimental Results

6.2.1 Query Time

Figs. 3a–3c plot the query time as a function of the number of leaf nodes, the width of the query range, and the dataset size, respectively. The query time grows when the number of leaf nodes increases because it takes longer to perform the search and generate a larger VO. When the width of the query range becomes larger, all approaches see an increase in query time. This is because expanding the query range will result in more leaf nodes in the query results. More time is consumed for verification. When the dataset increases, the query time increases for the Merkle B+ tree and Verkle B+ tree but remains essentially unchanged for the VB-cm tree. The VB-cm tree performs best and the Merkle B+ tree performs worst in Fig. 3. The average query time of the Verkle B+ tree and the Merkle B+ tree is 1.52 times and 2.10 times that of the VB-cm tree, respectively. The main reason for the best performance of the VB-cm tree is the use of CM-sketch, which saves more time when querying the KF by hash mapping than traversing the keywords. The Verkle B+ tree performs better than the Merkle B+ tree because the Merkle B+ tree needs to obtain the hash of all the sibling nodes to generate the VO, whereas the Verkle B+ tree only needs information about the nodes in the path.

Figure 3: Query time

6.2.2 Verification Time

Fig. 4 shows the verification time of the three approaches. The VB-cm tree outperforms the other two approaches. The average verification time of the Verkle B+ tree and the Merkle B+ tree is 1.98 times and 2.67 times longer than that of the VB-cm tree, respectively. This is because both the VB-cm tree and the Verkle B+ tree use the same Verification Function to read VO for verification, and the verification time is proportional to the size of VO. VB-cm tree has the shortest verification time because it uses CM-sketch to aggregate the frequency information of a large number of elements in a fixed-size matrix compared to the counter. The verification time increases with the number of leaf nodes and the width of the query range because more nodes are added to the VO. When the dataset becomes larger, the verification time of the VB-cm tree remains essentially unchanged, and the verification time of the Merkle B+ tree and the Verkle B+ tree increases. This is because the VB-cm tree uses CM-sketch to ensure that VO size is constant.

Figure 4: Verification time

6.2.3 VO Size

Fig. 5 shows the size of VO. The VB-cm tree performs best and the Merkle B+ tree performs worst. The average VO size of the Verkle B+ tree and the Merkle B+ tree is 9.28 times and 14.9 times larger than that of the VB-cm tree, respectively. This is because the VO size of the Merkle tree is O(f⋅logfD) while that of the Verkle tree is O(logfD). Moreover, the VB-cm tree stores the CM-sketches in the leaf nodes, instead of each keyword and its frequency. When the number of leaf nodes increases, the VO size becomes larger for all three methods. This is because more leaf nodes satisfy the query range. Fig. 5b shows the effect of the width of the query range. Fig. 5c shows the effect of dataset size. The VO size remains unchanged with the dataset size for the VB-cm tree due to the CM-sketch.

Figure 5: VO size

6.2.4 ADS Size

Fig. 6a plots the ADS size as a function of the number of leaf nodes. When the number of leaf nodes increases, the ADS size becomes larger. This is because as the increase of leaf nodes in the tree structure, the data contained in the tree increases along with the number of layers, so the bytes occupied by ADS also increase. Fig. 6b shows the effect of dataset size. When the dataset size becomes larger, the size of the Merkle B+ tree and Verkle B+ tree becomes larger, and the size of the VB-cm tree remains the same. This is the VB-cm tree that uses a fixed-size CM-sketch to record the frequency of multiple keywords. The average ADS size of the Verkle B+ tree and the Merkle B+ tree is 1.89 times and 1.88 times larger than that of the VB-cm tree, respectively.

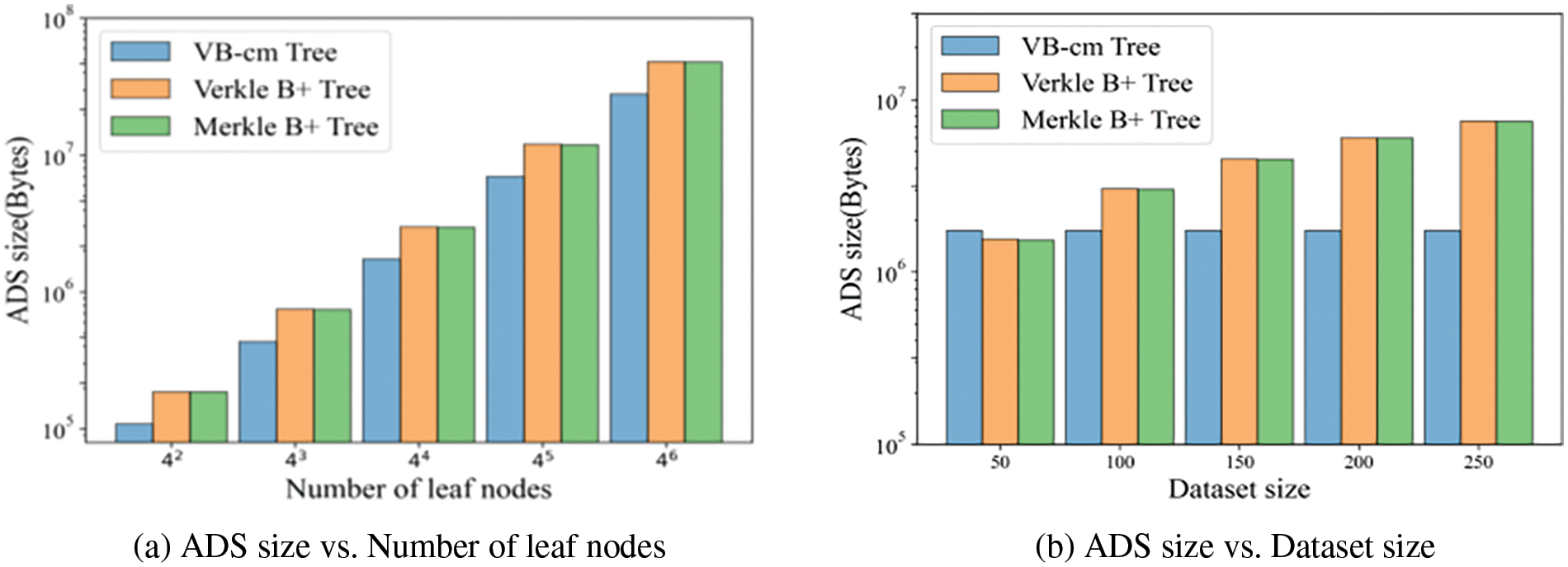
Figure 6: ADS size

6.2.5 Summary

The VB-cm tree performs better than the Merkle B+ tree and the Verkle B+ tree on the four metrics. This is because the VB-cm tree stores the frequency information using a CM-sketch of a fixed size without the need to store the keywords and their complete frequency information. The CM-sketch uses hash mapping in the query process, which saves more time than traversing the counters. In addition, the VB-cm tree incorporates the structure of a Verkle tree. To verify the content in a leaf node, the VO contains the nodes in the path from the leaf node to the root without the sibling nodes. As the dataset size increases, the superiority of the VB-cm tree is more obvious. Specifically, the query time, verification time, and VO size grow slightly while those of the other two ADS increase apparently. So we can conclude that the system has good scalability.

7  Conclusion

In this paper, we have proposed the VKFQ framework for efficient and verifiable KF queries with privacy protection in blockchain. Sensitive data keywords get differential privacy processing. We have proposed the VB-cm tree as the ADS. The VB-cm tree combines the CM-sketch and the Verkle tree to reduce storage costs and VO size. The CM-sketch serves as a summary of the frequency of keywords, from which an estimate of the frequency of keywords is derived. We have presented the query processing and result verification in detail. Extensive experimental results have demonstrated the efficiency of the proposed framework. For instance, there is more than one order of magnitude reduction in the VO size.

The suggested framework is compatible with blockchain architectures that are already in place, like Ethereum. We can add the VB-cm tree to the block where the root is stored in the block header, to support KF queries. The limitation of the framework is that the ADS can only handle KF queries. There are several future directions. We may think about using different kinds of privacy protection techniques such as data encryption technology in our framework. It is also interesting to extend the proposed framework to handle other query operators, i.e., skyline queries and k-nearest neighbor queries.

Acknowledgement: We would like to express thanks to the editor and anonymous reviewers for their appreciated comments that enhanced the worth of the research paper.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Study conception and design: Y. Ji and B. Yin; data collection: Y. Ji; analysis and interpretation of results: Y. Ji and B. Yin; draft manuscript preparation: Y. Ji and K. Gu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analyzed during this study are included in this article and are available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. I. Dinur and K. Nissim, “Revealing information while preserving privacy,” in Proc. Twenty-Second ACM SIGMOD-SIGACT-SIGART Symp. on Prin. of Dat. Syst., New York, NY, USA, 2003, pp. 202–210. [Google Scholar]

2. D. Das, S. Meiser, E. Mohammadi, and A. Kate, “Anonymity trilemma: Strong anonymity, low bandwidth overhead, low latency-choose two,” in 2018 IEEE Symp. on Secur. and Priv. (SP), San Francisco, CA, USA, 2018, pp. 108–126. [Google Scholar]

3. C. Zhang, C. Xu, J. Xu, Y. Tang, and B. Choi, “Gem2-tree: A gas-efficient structure for authenticated range queries in blockchain,” in 2019 IEEE 35th Int. Conf. on Data Eng. (ICDE), Macao, China, 2019, pp. 842–853. [Google Scholar]

4. X. Dai et al., “LVQ: A lightweight verifiable query approach for transaction history in bitcoin,” in 2020 IEEE 40th Int. Conf. on Distrib. Computing Syst. (ICDCS), Singapore, 2020, pp. 1020–1030. [Google Scholar]

5. C. Zhang, C. Xu, H. Wang, J. Xu, and B. Choi, “Authenticated keyword search in scalable hybrid-storage blockchains,” in 2021 IEEE 37th Int. Conf. on Data Eng. (ICDE), Chania, Greece, 2021, pp. 996–1007. [Google Scholar]

6. C. Xu, C. Zhang, and J. Xu, “vChain: Enabling verifiable boolean range queries over blockchain databases,” in Proc. 2019 Int. Conf. on Manag. of Data (SIGMOD), New York, NY, USA, 2019, pp. 141–158. [Google Scholar]

7. H. Wang, C. Xu, C. Zhang, J. Xu, Z. Peng and J. Pei, “vChain+: Optimizing verifiable blockchain boolean range queries,” in IEEE 38th Int. Conf. on Data Eng. (ICDE), Kuala Lumpur, Malaysia, 2022, pp. 1927–1940. [Google Scholar]

8. T. Murakami and Y. Kawamoto, “Utility-optimized local differential privacy mechanisms for distribution estimation,” in Proc. 28th USENIX Conf. on Secur. Symp., ser. SEC’19, Santa Clara, CA, USA, 2019, pp. 1877–1894. [Google Scholar]

9. G. Cormode, “Data sketching,” Commun. ACM, vol. 60, no. 9, pp. 48–55, 2017. [Online]. Available: https://api.semanticscholar.org/CorpusID:8697904 (accessed on 02/02/2024). [Google Scholar]

10. J. Kuszmaul, “Verkle trees,” 2019. [Online]. Available: https://api.semanticscholar.org/CorpusID:218475793 (accessed on 02/02/2024). [Google Scholar]

11. M. Ober, S. Katzenbeisser, and K. Hamacher, “Structure and anonymity of the bitcoin transaction graph,” Future Internet, vol. 5, no. 2, pp. 237–250, 2013. doi: 10.3390/fi5020237. [Google Scholar] [CrossRef]

12. F. Reid and M. Harrigan, “An analysis of anonymity in the bitcoin system,” in 2011 IEEE Third Int. Conf. on Priv., Secur., Risk and Trust and 2011 IEEE Third Int. Conf. on Soc. Comput., Boston, MA, USA, 2011, pp. 1318–1326. [Google Scholar]

13. P. Koshy, D. Koshy, and P. Mcdaniel, “An analysis of anonymity in bitcoin using P2P network traffic,” in Financial Cryptography, 2014. [Online]. Available: https://api.semanticscholar.org/CorpusID:225868 (accessed on 02/02/2024). [Google Scholar]

14. R. Dingledine, N. Mathewson, and P. Syverson, “Tor: The second-generation onion router,” in 13th USENIX Secur. Symp. (USENIX Security 04), San Diego, CA, USA, USENIX Association, Aug. 2004. [Google Scholar]

15. A. Biryukov and I. Pustogarov, “Bitcoin over tor isn’t a good idea,” in 2015 IEEE Symp. on Secur. and Priv., San Jose, CA, USA, 2015, pp. 122–134. [Google Scholar]

16. C. Yang, J. Chen, B. Zeng, and L. Liao, “Overview of blockchain privacy protection,” in 2022 IEEE 8th Int. Conf. on Big Data Secur. on Cloud (BigDataSecurityIEEE Int. Conf. on High Perf. and Smart Computing (HPSC) and IEEE Int. Conf. on Intell. Data and Secur. (IDS), Jinan, China, 2022, pp. 212–217. [Google Scholar]

17. F. K. Maurer, T. Neudecker, and M. Florian, “Anonymous coinjoin transactions with arbitrary values,” in 2017 IEEE Trustcom/BigDataSE/ICESS, Sydney, NSW, Australia, 2017, pp. 522–529. [Google Scholar]

18. I. Miers, C. Garman, M. Green, and A. D. Rubin, “Zerocoin: Anonymous distributed e-cash from bitcoin,” in 2013 IEEE Symp. on Security and Privacy, Berkeley, CA, USA, 2013, pp. 397–411. [Google Scholar]

19. N. van Saberhagen, “Cryptonote v 2.0,” 2013. [Online]. Available: https://api.semanticscholar.org/CorpusID:2711472 (accessed on 02/02/2024). [Google Scholar]

20. J. Zhang, “Research on business model governance and consumer privacy protection path of e-commerce industry based on blockchain technology,” in 2023 Int. Conf. on Distrib. Computing and Electrical Circuits and Electron. (ICDCECE), Ballar, India, 2023, pp. 1–6. [Google Scholar]

21. L. Guo and Z. Yan, “A privacy protection scheme for blockchain aggregation platform based on attribute-based and order-preserving encryption,” in 2023 8th Int. Conf. on Computer and Commun. Systems (ICCCS), Guangzhou, China, 2023, pp. 414–423. [Google Scholar]

22. A. Raj and S. Prakash, “A privacy-preserving authentic healthcare monitoring system using blockchain,” Int. J. Softw. Sci. Comput. Intell., vol. 14, no. 1, pp. 1–23, Oct. 2022. doi: 10.4018/IJSSCI.310942. [Google Scholar] [CrossRef]

23. J. Lu, J. Shen, P. Vijayakumar, and B. B. Gupta, “Blockchain-based secure data storage protocol for sensors in the Industrial Internet of Things,” IEEE Trans. Industr. Inform., vol. 18, no. 8, pp. 5422–5431, 2022. doi: 10.1109/TII.2021.3112601. [Google Scholar] [CrossRef]

24. Y. Zhang, Y. Zhu, Y. Zhou, and J. Yuan, “Frequency estimation mechanisms under (ϵ,δ) -utility-optimized local differential privacy,” IEEE Trans. Emerg. Topics Comput., pp. 1–12, 2023. [Google Scholar]