Reinforcement Learning Based Quantization Strategy Optimal Assignment Algorithm for Mixed Precision

1  Introduction

The quantization algorithm compresses the original network by reducing the numerical bit width [1] and improving the computation speed on neural network accelerators [2]. On one hand, different layers have different redundancy and accuracy requirements to bit width. Therefore, assigning the same bit width to all layers will result in a loss of accuracy. On the other hand, when different layers use flexible bit widths, the mixed-precision search space is exponential in the number of layers. It is not realistic to search for the appropriate bit width for each layer and computation resource is insufficient [3].

Therefore, it is necessary to use mixed precision quantization for different layers to reduce the computational resource while keeping the model accuracy basically unchanged, and effectively balance the contradiction between accuracy and computational performance.

However, there is a lack of an effective approach to determine the bit widths of different parts of the network. Traditional methods either examine only a small, artificially designed search space or utilize tedious neural structure searches to explore huge search spaces. These methods are not effective in obtaining optimal quantization schemes. So, it is necessary to automatically obtain the optimal bit width assignment scheme through the automatic neural network model mixed precision computational assignment technology.

So, there are two technical bottlenecks that need to be solved:

Technical Bottleneck 1: How to choose the appropriate bit width? The bit width should be set as low as possible to reduce the computational cost.

Technical Bottleneck 2: How to improve the quantization accuracy? The loss of accuracy due to quantization should be as small as possible.

Aiming at these two technical bottlenecks, this paper proposes a quantization strategy optimal assignment algorithm for mixed precision, which uses reinforcement learning to automatically predict the quantization bit width assignment strategy of each layer of a given model. The simulation software that simulates neural network accelerator inference is used as an environment to obtain the execution speed feedback of the model to guide the agent to meet the resource constraints. Finally, after quantization retraining, different quantization strategy optimal assignment methods are realized, and the quantization strategies suitable for all layers are output. The quantization strategy optimization technology based on reinforcement learning can minimize computational resource consumption and data access bandwidth requirements while maintaining computational accuracy.

2  Related Work

Quantization represents network weights with fewer bits, such as converting the data type computed by an algorithm from 32-bit floating-point to 8-bit or 4-bit low-bit integers [4]. Quantization algorithms quantize both parameters (i.e., weights) and activations of each layer in a neural network model to reduce the total memory footprint of the model during inference [5–7]. Mixed precision quantization designs a certain policy to reasonably allocate the weights and activations of each layer of the model. This allows mixed precision quantization to achieve the best compromise between the performance and accuracy of deep neural networks, and has therefore been widely studied.

The parameters of a neural network model are typically stored in a 32-bit floating-point data format [8]. By converting floating-point parameters into 1, 2, 4, or 8-bit integer data, model operation efficiency can be improved and model deployment can be promoted on embedded devices [9]. However, the reduction of the data bit width leads to a loss of accuracy, and the lower the bit width, the greater the accuracy loss. In addition, the parameters of different layers of the model have different sensitivity to the data bit width, among which the parameters that contribute to the accuracy need a higher quantization bit width, and the parameters that contribute less to the high accuracy can give a lower bit width [10]. Given the overall accuracy requirements of the model, the bit width assignment technology of the neural network model searches for and assigns appropriate bit widths to different layers to achieve the optimal quantization effect. However, there are many convolutional weights and activations in the model, and the number of bit widths can be selected, so the bit width search space refers to orders of magnitude, and manual search is very difficult [11].

Reinforcement Learning is a technique that directly learns control strategies from high-dimensional raw data [12]. The machine trained by reinforcement learning has reached or exceeded the level of human intelligence in many fields such as Alpha Go, video games, robotics, and ChatGPT. Researchers in the field propose some hybrid bit width automatic search methods to solve this problem, among which optimization-based methods/reinforcement learning-based methods and gradient descent-based methods have received active attention from researchers.

For example, a Lagrange multiplier [13] has been proposed for mixed precision search, which treats mixed precision quantization as an extreme value problem of function f(x1, x2,...) under the constraint of g(x1, x2,...) = 0. Each channel in a single layer is solved according to the Lagrange multiplier method. However, this method can only be used for each layer, and secondly, it cannot be allocated according to the specified optional quantization bit width, but only according to the calculated quantization bit width. Wang et al. of Massachusetts Institute of Technology (MIT) proposed a Hardware-Aware Automated Quantization (HAQ) method based on reinforcement learning [14]. For a certain layer of convolution, the delay and energy feedback provided by the hardware are included in the reward function based on reinforcement learning through the hardware accelerator. When looping, the quantization bit width is updated once in each reinforcement learning action according to the reward to make the bit width accuracy better than the bit width generated by the previous action. The gradient descent-based method also achieves good results. For example, Yu et al. of the University of Science and Technology Beijing proposed a new Differentiable Neural Architecture Search (DNAS) framework [15]. During the training process, the weights and activations of different layers are adjusted in their respective bit width search spaces, and their optimal bit widths are automatically explored based on the gradient descent of complexity loss. Compared with the reinforcement learning-based method, this method improves the bit width search speed and avoids separate training structures, but does not explore the root cause of the sensitivity of different layers of the model to bit width sensitivity, which may lead to suboptimal results.

To sum up, there are some challenges in these methods:

Challenge 1: Most of the methods do not consider the adaptability to the hardware.

Challenge 2: These methods either still require a lot of computational resources or are very sensitive to hyperparameters or even initialization.

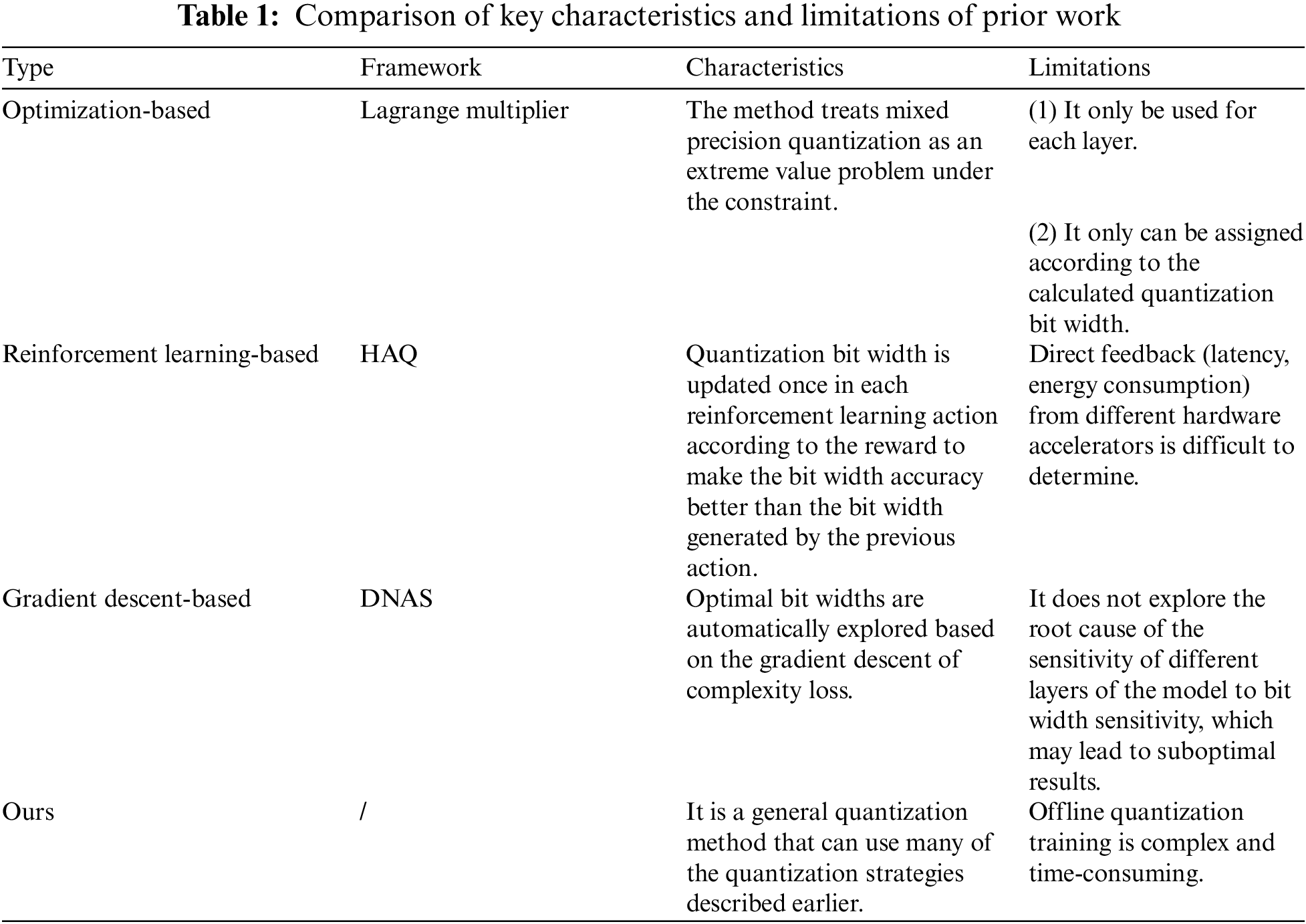
Above all, we added a table comparing key characteristics and limitations of Lagrange multiplier, HAQ and DNAS to highlight their differences and limitations. At the same time, the descriptions of the potential shortcomings of our framework have also been addressed in the comparison table, which is shown in Table 1.

Because the operation efficiency and accuracy of the quantized neural network model on different accelerators may be quite different, it is necessary to incorporate the accuracy and speed feedback of hardware feedback into the optimization function of bit width search. Therefore, this paper proposes a simple and fast mixed precision search technique.

3  Proposed Algorithm

The mixed precision automatic bit width assignment technology sets different quantization bit widths for the convolution weights and activations of different layers of the model to achieve the optimal balance between model accuracy and efficiency. Traditional neural network model quantization methods adopt uniform quantization bit widths for the weights and activations of the entire network model. However, the contribution of the internal layers of the neural network model to the prediction is not exactly the same, so it is necessary to adopt different quantization bit widths for different convolutional layers with different accuracy requirements to achieve the best balance between accuracy and efficiency.

The proposed method determines a hardware-aware mixed precision quantization strategy adapted to low bit width. Since a brute force approach is not feasible for deep networks, as the search space for mixed precision is exponential complexity in the number of layers. The proposed algorithm is a novel solution which uses mixed precision quantization to reduce the parameter size as well as computational complexity of neural network models. Our challenge is a similar factorial complexity for determining layer-wise finetuning order when quantizing the model to a target precision. Our works use execution speed feedback as metrics to measure computation complexity.

3.1 Structure

In this paper, a mixed precision quantization bit width assignment framework adapted to low bit widths is proposed, and reinforcement learning is used to automatically predict mixed precision that satisfies hardware resource constraints.

For each layer, the standard deviation of the weights is used in the state-space design to measure the distribution difference of the data, and the agent receives the layer configuration and statistical information feedback from the hardware as an observation, and then outputs the action behavior of the layer, that is, the quantization bit width of the weight and activation. When all layers are quantified, the execution speed feedback of simulated neural network accelerator inference is used as an environment to limit the action space of the agent to guide the agent to meet resource constraints. Then, according to the new quantization width, the model is briefly retrained to restore performance, and the accuracy of the retrained quantization model is used as the reward function to guide the agent to carry out deep reinforcement learning training. Finally, different quantization width optimal assignment methods are realized after training, and the quantization accuracy suitable for all layers is output. The overall structure is shown in Fig. 1.

Figure 1: Overall structure

As shown in Fig. 1, this paper uses reinforcement learning to automatically search for a large quantization design space in a loop. Given the number of computing resources of the neural network accelerator, an optimal quantization strategy selection method is proposed. The agent integrates the simulation of the accelerator into the neural network model parameter update process of reinforcement learning, so that the agent can receive direct feedback from the hardware. The mixed precision quantization framework of the whole neural network model for reinforcement learning is divided into two processes: Reinforcement learning process and quantization retraining process. The former contains state-space design, reward function design and reinforcement learning training strategy, the latter contains hardware feedback strategy and symmetric quantization strategy, respectively.

3.2 Reinforcement Learning Process

3.2.1 State-Space Design

In reinforcement learning, learners and decision-makers are called agents, and everything outside the agent is the environment, and the agent and environment interact at each step in a series of discrete time steps. At each time step, the agent receives the state of the environment, on the basis of which an action is selected to execute, and the agent receives a reward value and is in a new state.

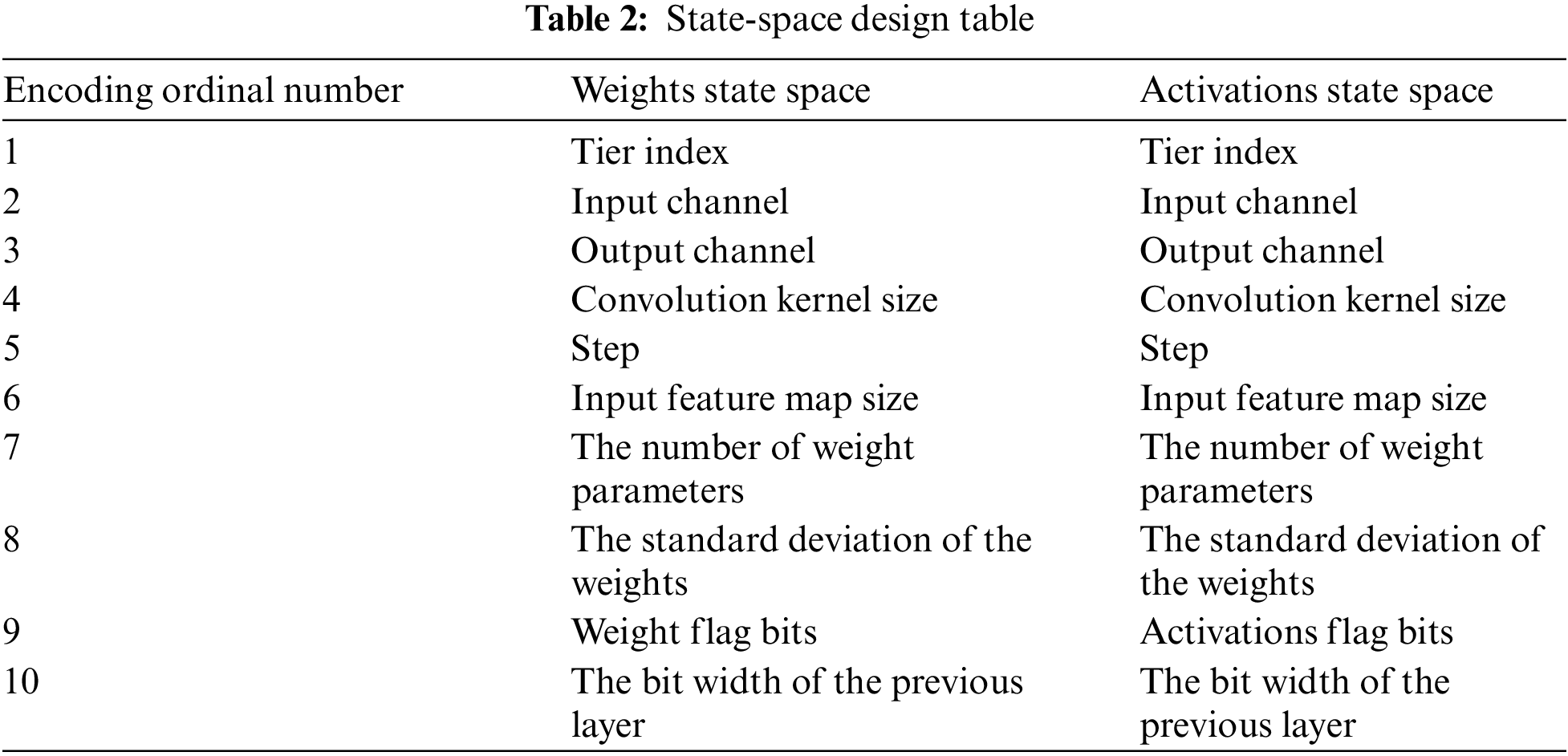
Since our agent processes neural networks in a layer-by-layer fashion, the state-space design is the set of each layer of weights/activations of all possible environmental states, as shown in Table 2.

3.2.2 Reward Function Design

After all layers have been quantized, the quantization model is periodically fine-tuned, and the model accuracy after short-term retraining is used as the reward value of the agent. Define a function reward whose reward is directly related to precision:

where cost_ratio=timeofcurrentbittimeoffull8bit is the compression ratio. acc_limit is the given precision constraint value. acc_orgin is the top-1 accuracy of the full 8 bit-precision model before quantization on the training set, and acc_quant is the accuracy of the quantization model after finetuning. δ is to prevent the occurrence of zero risk, which can be set to 0.0001.

3.3 Quantization Retraining Process

3.3.1 Hardware Feedback Strategy

After the agent provides actions for all layers, the amount of resources used by the quantized model is measured, and the feedback comes directly from the delay calculation table of the hardware accelerator [16], which is used as an environment to obtain direct feedback from the hardware to guide the agent to determine the quantization strategy selection from the nuances between different layers and meet the resource constraints. The speedometer is inferred from the speed evaluation model established in advance by different models on different hardware accelerators.

To adapt to existing accelerators, the hybrid bit width search space of weights is (1,4,8) and activation is (2,4,8). The weight bit width of the next layer is equal to the activation bit width of the previous layer.

After the agent provides actions to all layers, the quantization model measures the number of resources that will be used. If the current quantization cost exceeds the target constraint, the bit width of each layer is reduced sequentially until the resource constraint is finally satisfied. The order in which the action space is restricted is shown in the following pseudocode:

The proposed method encourages the agent to meet the computing resource budget by constraining the action space. The execution speed feedback comes directly from the hardware.

3.3.2 Symmetric Quantization Strategy

The quantization algorithm used in this paper is based on the neural network quantization software proposed by Xi’an Microelectronics Technology Institute [17]. The quantization software generates a guide file for the neural network accelerator to map floating-point data into low-precision data. The schematic diagram of the quantization software is shown in the Fig. 2.

Figure 2: Schematic diagram of quantization software

The quantization software uses the layers as the basic processing unit. A pseudo-quantization operation is inserted into the weight and output of each layer [18]. Firstly, the distribution and range of input, weight, and output data of each layer of the neural network model are analyzed in advance. Then, each floating-point value is represented by a low-bit integer. The output of the current layer is used as the input of the next layer. Note here that the activation threshold is calculated from the activation equalization of a set of quantization calibration images.

4  Numerical Simulation and Results Analysis

In this section, simulation experiments are carried out to verify the proposed method’s effectiveness. First, we describe the architecture of the proposed method in Section 4.1. Second, quantization perceptual hyperparameter selection experiment is conducted in Section 4.2. Then, most importantly, experimental results are given from three aspects in Section 4.3: Quantization strategy assignment results, hybrid bit width search results and comparison with previous work. In addition, we perform the ablation study of the proposed algorithm itself from the perspectives of standard deviation and optimized reward in Section 4.4. The experiments were carried out on Ubuntu 18.04. The Central Processing Unit (CPU) is Intel(R) Core(TM) i7-8700K, 3.70 GHz, the Graphics Processing Unit (GPU) is NVIDIA GeForce GTX1070, Deep Learning Framework is Pytorch 1.7.0, Compute Unified Device Architecture (Cuda) is 10.1. The execution speed feedback comes directly from TIANJI NPU4.0 neural network accelerator proposed by Xi’an Microelectronics Technology Institute [19].

4.1 Experimental Architecture

The experimental architecture is shown in Fig. 3, which uses datasets and models as input, hybrid bit width search is performed on classification tasks through reinforcement learning and simple quantization retraining. It converts the initial training models such as Open Neural Network Exchange (ONNX), TensorFlow, and Caffe provided by third parties into a PyTorch format. Based on the optimal bit width obtained by search, single quantization retraining is carried out again to update the weights of the model. This completes the training phase. In the testing phase, the model with mixed bit width configuration is deployed on the inference platform to obtain accuracy calculation results. To evaluate the effectiveness of the proposed algorithm across a variety of Deep Neural Networks (DNNs), three neural network test models MobileNet-V2, ResNet-50 and LeNet are selected in different target classification task.

Figure 3: Experimental architecture

4.2 Hyperparameter Selection

To adapt to existing accelerators, the weight bit width of the next layer is equal to the activation bit width of the previous layer. And when the activation bit width of the upper layer is 2-bits, the weight of the next layer can only be 1-bit. After all layers are quantified, if the current quantization policy exceeds the resource budget, resource constraints are applied. Update activations and weights layer by layer in reverse order, modifying the weights of this layer while changing the activations of the previous layer.

There are many hyperparameters in the hybrid bit-width framework, such as the initial value of the learning rate, the rate decay, the training set size, and the quantization retraining epochs. Fig. 4 lists only the most important quantization perception hyperparameters—the results of experiments with different quantization retraining epochs. In this experiment, two sets of fixed mixed precision quantization strategies of LeNet model were carried out on the Modified National Institute of Standards and Technology (MNIST) dataset. The accuracy after quantization retraining was used as the evaluation index. The initial value of learning rate is 0.01, the learning rate decay is 0.8, the number of quantization retraining is 100, and the training set size is 200. Repeating the experiment 3 times, selecting the average statistical results.

Figure 4: Accuracy with different quantization retraining epochs

Fig. 4 shows that with the increase of quantization retraining epochs, the accuracy of different mixed precision quantization strategies increases, and the accuracy is lower than that of the first group because the quantization width of the second group of mixed precision quantization strategies is lower and more difficult to quantize.

4.3 Experimental Results

In this section, we first present our quantization strategy assignment results for MobileNet-V2 on ImageNet, and LeNet on MNIST. Then we present our hybrid bit width search results for MobileNet-V2 on UCMerced LandUse. Finally, comparison with prior work is carried out.

4.3.1 Quantization Strategy Assignment Results

The maximum compression ratio is set to 0.6, and the episodes of Reinforcement Learning (RL) training is set to 50. The number of quantization retraining epochs for this experiment is set to 100. Repeat the experiment 3 times, selecting the average statistical results.

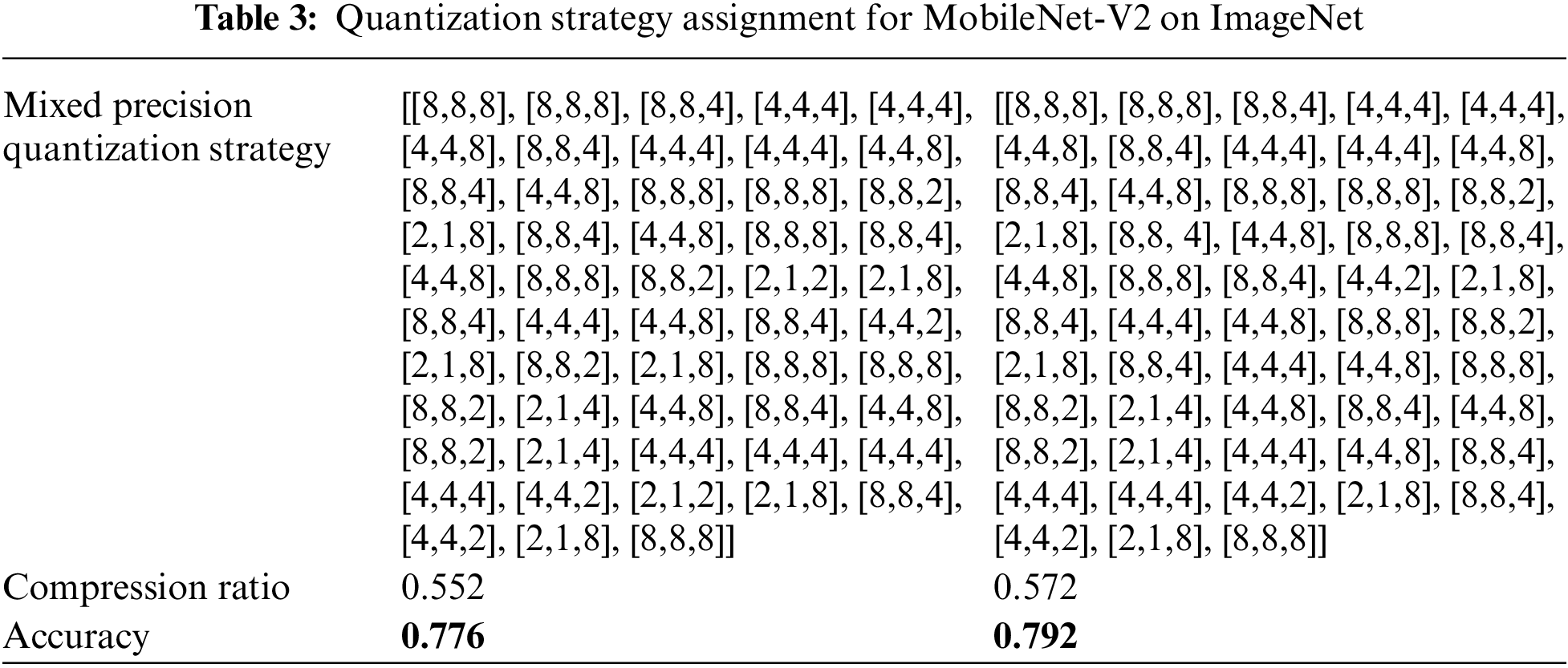
For MobileNet-V2 on ImageNet dataset, Table 3 shows the two sets of hybrid bit width assignment strategies with the best accuracy in multiple iterations. Due to the excessive number of layers in the MobileNet-V2 model, the hybrid bit width quantization strategy representation is simplified to layer by layer input/weight/activation bit width-[layer 1 [input, weight, activation], layer 2 [input, weight, activation]... Layer n [input, weight, activation]]. It can be seen from Table 3 that after replacing the dataset and model, the influence of low bit-to-width ratio on model accuracy is also reflected.

For the LeNet model, a speedometer with dimension 6 * 3 * 3 is established. 3 * 3 is the total number of combinations assigned bit widths of each convolutional layer, with a weight distribution of 1/4/8 bit and an activation distribution of 1/4/8 bit. In multiple iterations, select the two sets of mixed precision quantization strategies with the best accuracy. The intra-layer/inter-layer bit width assignment of different strategies and the corresponding evaluation metrics are shown in Table 4.

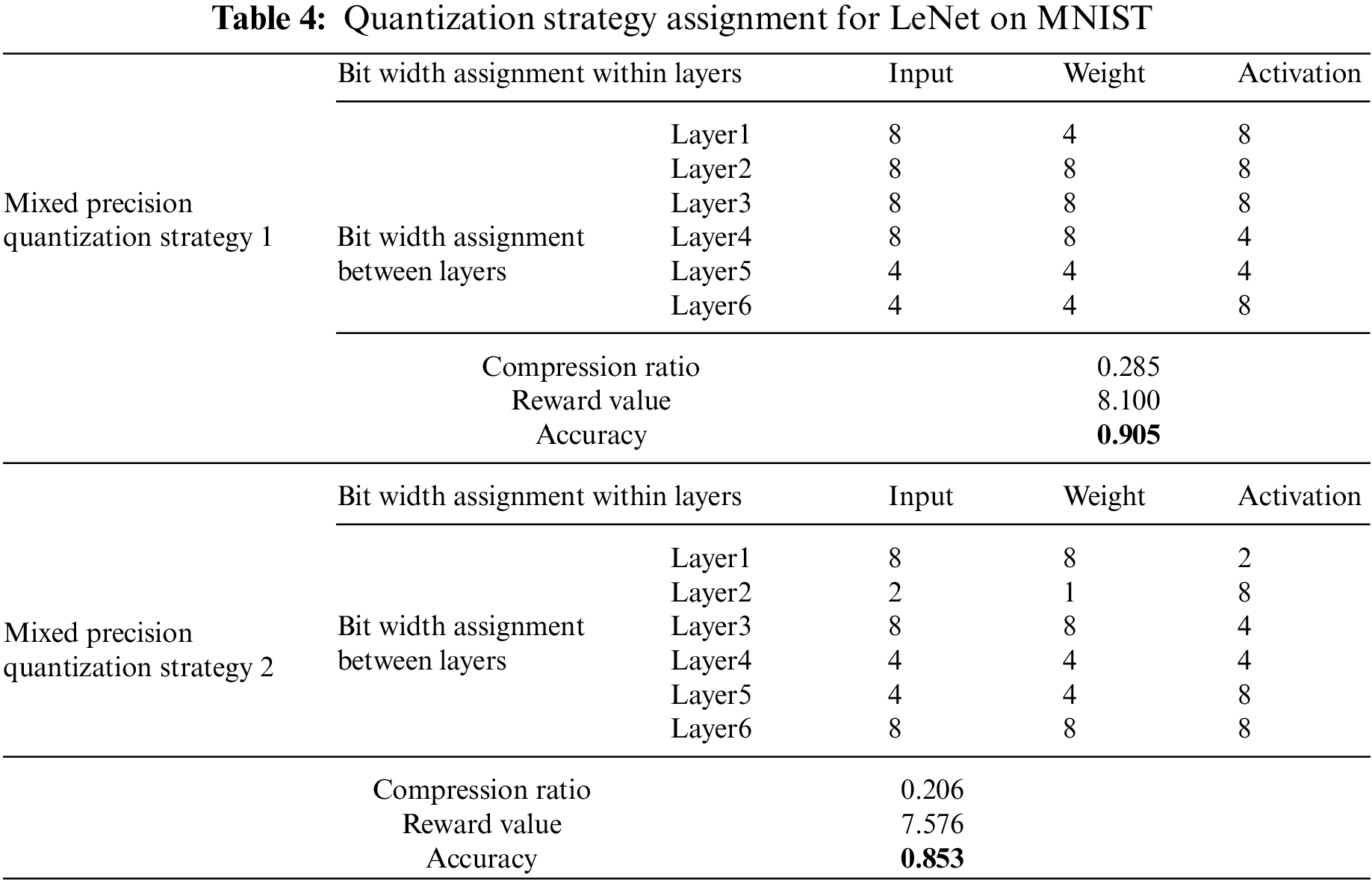
Experiments of LeNet on the MNIST dataset show that a group of hybrid bit width strategies with low compression ratio have low accuracy. It shows that the greater the proportion of low bit width, the greater the accuracy of the model. The larger the reward value, the higher the model’s accuracy, which shows that the more accurate the positive feedback is based on the accuracy of the quantized model after retraining, the more effective it can guide the agent to carry out deep reinforcement learning training, and the bit width strategy that satisfies the hardware resources can be obtained.

4.3.2 Hybrid Bit Width Search Results

To further verify the effectiveness of reinforcement learning in mixed-precision search, this section details the evolution of reward, loss, and evaluation metrics in RL training process. Evaluation metrics include the compression ratio of the search hybrid bit width and the accuracy of retrained quantization model. In order to fully improve the accuracy of the retrained quantization model, the maximum compression ratio of the search bit width is increased to 0.9, and the episodes of reinforcement learning training is set to 30. Moreover, the goal of mixed precision search technique is to find a suitable hybrid bit width assignment strategy in the complex bit width selection space. The bit width search of each time only requires simple quantization retraining, so the epochs of quantization retraining for this experiment is set to 30.

The hybrid bit width search experiment of MobileNet-V2 on UCMerced LandUse dataset is shown in Figs. 5–7. It can be seen from Fig. 5 that, due to the new design of the reward function, the reward becomes larger as the RL training episodes increase, and the reward value reaches a maximum of 9.053 at the 30th iteration. This fully demonstrates that this reward function, as an evaluation criterion of the agent’s task execution, can encourage the agent to make good action decisions and discourage the agent from making action decisions that lead to bad outcomes. This constantly updates the mixed-precision quantization strategies to get as many rewards as possible.

Figure 5: The evolution of reward in RL training

Figure 6: The evolution of compression ratio and accuracy in RL training

Figure 7: The evolution of loss varying different RL learning in quantization retraining

Fig. 6 shows that with the increase of RL trainings episodes, the accuracy of retrained quantization model is increasing, which reaches a maximum of 0.776 at the 30th iteration, and the error with the accuracy of 0.800 of the full-precision model is 2.5%. Meanwhile, the compression ratio of the best accuracy reaches 0.775. In particular, at the 15th iteration, the accuracy reaches 0.724, but the compression ratio reaches 0.848. In order to achieve the goal of lower compression ratio and higher accuracy, reinforcement learning once again exerts powerful decision-making capabilities. This gradually reduces the compression ratio and maintains a consistently increasing accuracy.

According to the mixed-precision quantization framework, the model assigned new quantization widths is briefly retrained to restore performance, and the accuracy of the retrained model is used as the reward to guide the agent to carry out deep reinforcement training. To illustrate the role of quantization retraining, Fig. 7 shows the evolution of loss varying seven different RL learning. On the one hand, the loss value in each RL training decreases steadily with the increase of the epochs of quantization retraining. Although there is a tendency to become larger in some places, this is due to the robustness of model training. On the other hand, with the increase of the order of 1, 3, 8, 13, 17, 25 and 30 for different RL training episodes, the overall range of loss values also decreases. Furthermore, it is shown that the accuracy of the evaluated model steadily increases in the RL training process.

4.3.3 Comparison with Prior Work

In order to verify the effectiveness of the improved quantization strategy assignment method, the comparative experiments with related works are carried out. Experiments are performed on target classification task. We compare with the full-precision MobileNet-V2, ResNet-50 and LeNet, and popular state-of-the-art hybrid bit width search methods including Parameterized Clipping activation (PACT) [20], Han et al. [21], HAQ [14], Reinforcement Learning approach for deep Quantization (ReLeQ) [22], DoReFa [23] and Alternating Direction Method of Multipliers (ADMM) [24]. Above all, we apply these methods to search for optimal hybrid bit widths.

The comparative experiment for MobileNet-V2 on ImageNet dataset is shown in Table 5. We compare our framework with PACT and Han that uses fixed number of bits without hardware feedback. And HAQ, ReLeQ that uses flexible number of bits with hardware feedback. It can be seen from Table 5, our method performs similarly to the full-precision baseline on the same hardware platform.

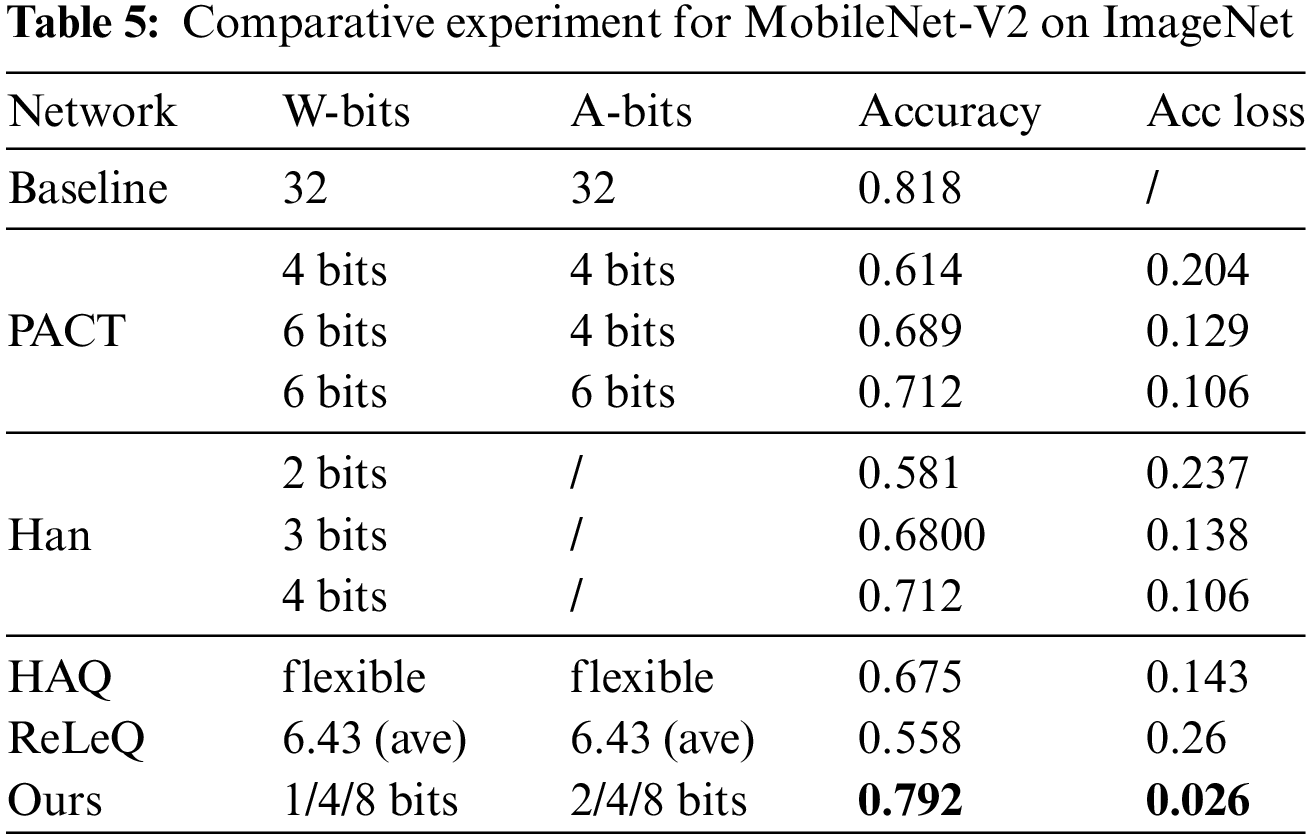
Table 6 shows the comparative experiment for ResNet-50 on ImageNet. Here, we add the traditional method DoReFa that uses fixed number of bits without hardware feedback as a comparison. Under 1, 2, 4, 8 mixed precision configuration, the quantized ResNet-50 has also achieved relatively small quantization errors by 0.024 than all comparative methods shown. It has certain performance competitive advantages.

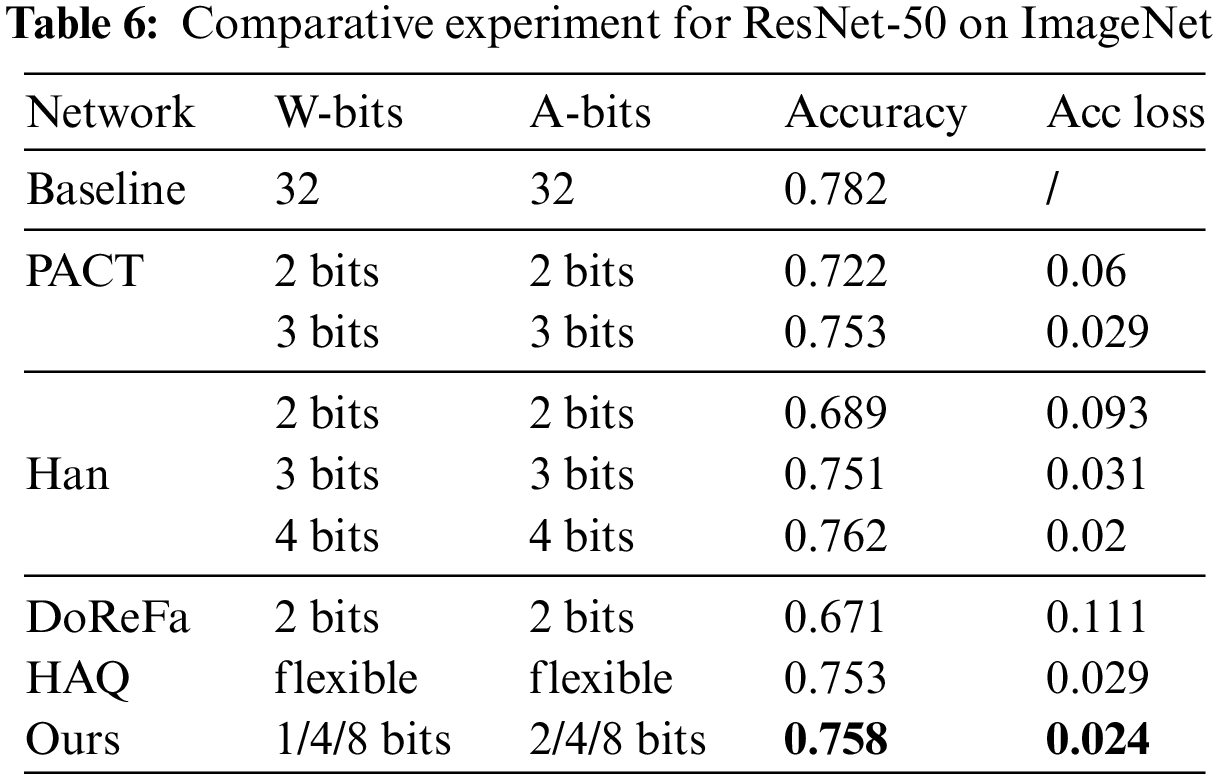
For comparison, Table 7 records the comparative experiment for LeNet on MNIST with prior work. Our method achieves minimum quantization variations of 0.055 and 0.003 compared to the full-precision baseline at the two-bit width allocation schemes, respectively. Again, in Table 7, we notice that a group of hybrid bit width strategies of our method with high average bit width have low accuracy. It indicates that the greater the proportion of low bit width, the greater the accuracy of the model.

4.4 Ablation Study

4.4.1 W/ and W/O Standard Deviation

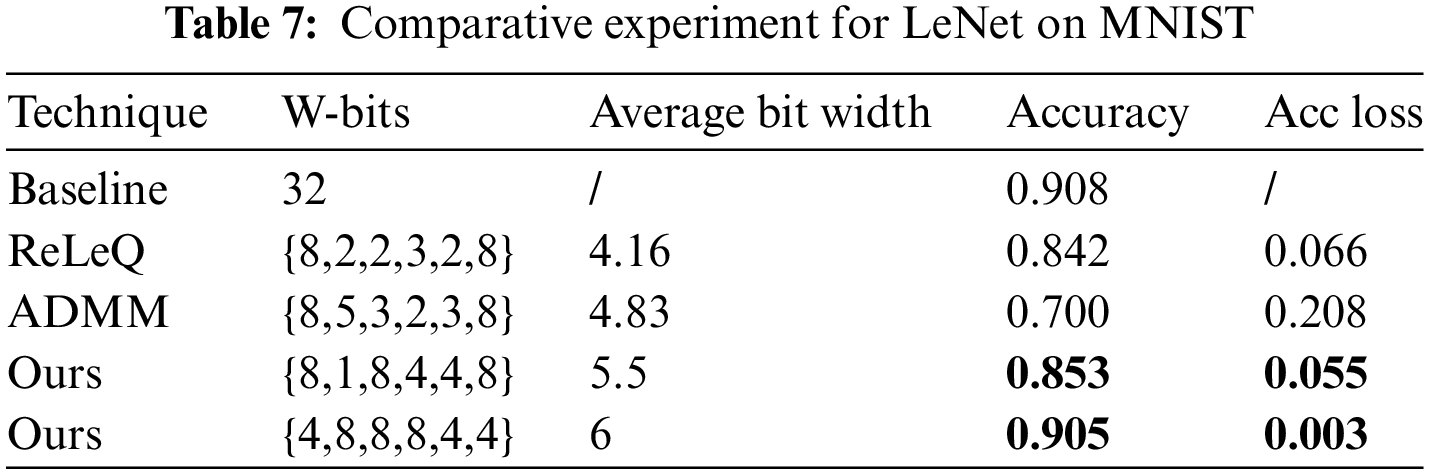
The design adds the standard deviation of weights to the state-space design. The number of searches is set to 50, the number of quantization retraining is set to 100, in order to make the comparison with the addition of the weight standard deviation more obvious, the hybrid bit width assignment strategy with the best verified accuracy is shown in the following table for the two models of MobileNet-V2 and LeNet.

The hybrid bit width assignment strategies selected in Table 8 are all have low bit width, that is, there is a combination of 2-bit input and 1-bit weight in one or more layers. Experiments show that reinforcement learning can fully measure the distribution differences of data in different layers in the mixed precision quantization bit width search process. Although the compression ratio of the model is slightly increased, the quantization deployment accuracy of the model is improved in the limited search space, and a suitable quantization bit width assignment strategy is found for each layer.

4.4.2 Comparison between Optimized Reward Function

The goal of reinforcement learning is to obtain optimal decisions so that the agents controlling the mixed-precision quantization strategies receive the greatest rewards. The design of reward function is a crucial component of reinforcement learning as indicated in Section 3.2. In this paper, we incorporate reinforcement learning techniques by proposing a special parametric reward formulation. To evaluate the effectiveness of the proposed reward formulation, we have compared the mixed-precision search effect of the models before and after the reward function optimization in Table 9.

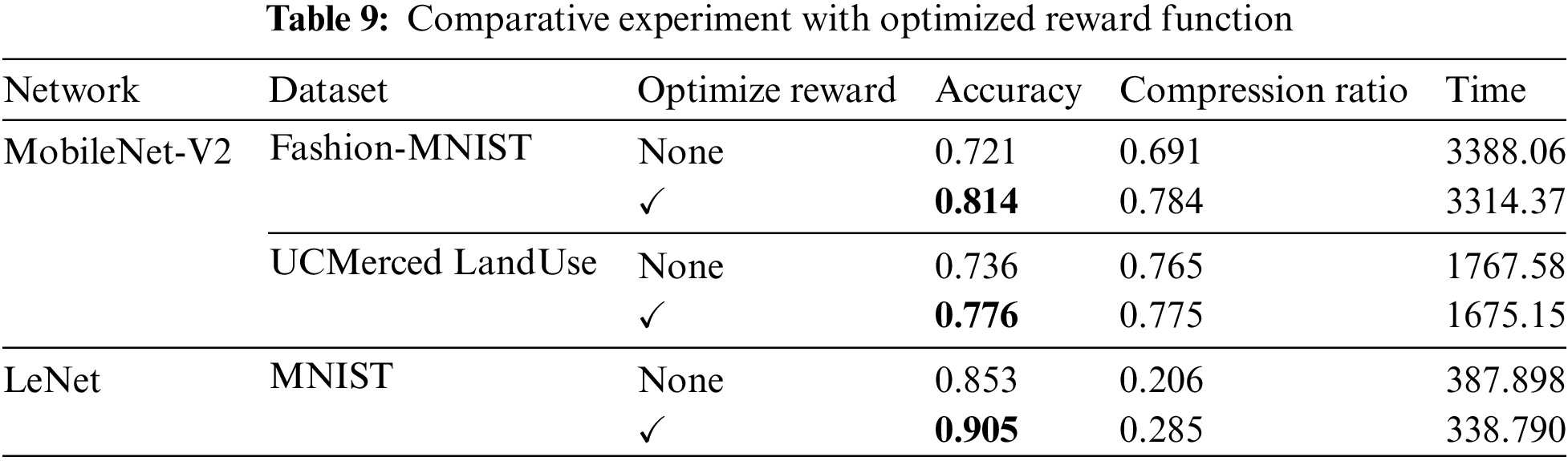
Table 9 shows the accuracy and compression ratio results of MobileNet-V2 and LeNet, where “✔” indicates that the corresponding reward function has been optimized. It can be seen from the comparative results that no matter which model is evaluated, no matter which dataset is based on, although the compression ratio of the quantization strategy searched by the optimized reward function is slightly higher, the accuracy of retrained quantization model becomes higher. Under the condition that the hardware resources are satisfied, the proposed reward formulation is consistently achieving higher accuracy during the reinforcement learning training episodes. Our agent gave quite different quantization strategies for accelerators.

5  Conclusion

In conclusion, a quantization strategy optimal assignment algorithm for mixed precision is proposed, and reinforcement learning is used to automatically predict the optimal bit width that meets the constraints of hardware resources. The proposed method improves the classification accuracy loss of 2.6%, 2.4% and 0.3% on the MobileNet-V2, ResNet-50 and LeNet compared to the full-precision baseline, respectively. It effectively achieves the compromise between the performance and accuracy of deep neural networks.

Future research opportunities stemming from the findings presented include: (1) Mixed-precision search based on reinforcement learning can be applied to tasks such as detection, semantic segmentation, and speech recognition, etc.; (2) The execution speed feedback can also be obtained from other localized embedded neural network accelerators. These can be widely deployed on various embedded computing platforms with low power consumption and limited resources; (3) Even though we have shown benefits of ours as compared to DNAS or HAQ, it may be possible to combine these methods for more efficient AutoML search. We leave this as part of future work.

Acknowledgement: I would like to express my sincere gratitude to Prof. Ma Zhong for his guidance and support. Our conversations inspired me to write the entire work and complete it successfully. I also want to thank the research team for their collaboration and help during gathering data for my research project.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Y. Wang, Z. Ma; data collection: C. Yang, L. Wei; analysis and interpretation of results: Y. Wang, Y. Yang; draft manuscript preparation: Y. Wang, Z. Ma. All authors approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Z. Ma, upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. P. Hu, X. Peng, H. Y. Zhu, M. M. S. Aly, and J. Lin, “OPQ: Compressing deep neural networks with one-shot pruning-quantization,” in Proc. AAAI Conf. Artif. Intell., Feb. 4–9, 2021, pp. 7780–7788. [Google Scholar]

2. L. Jiang, X. J. Wang, Z. T. Liu, X. Y. Xie, and Q. Heng, “Design and implementation of convolutional neural network based on FPGA,” Microelectron. Comput., vol. 35, no. 8, pp. 132–136, 2018. [Google Scholar]

3. Q. F. Ding and M. X. Liu, “Research on physical layer security performance of massive MIMO relay system based on mixed-ADC,” Acta Electron. Sin., vol. 49, no. 6, pp. 1142–1150, 2021. doi: 10.12263/DZXB.20200217. [Google Scholar] [CrossRef]

4. R. Zhao, Y. Hu, J. Dotzel, C. D. Sa, and Z. R. Zhang, “Improving neural network quantization without retraining using outlier channel splitting,” in Proc. 36th Int. Conf. Mach. Learn. (ICML), Long Beach, California, USA, Jun. 9–15, 2019. [Google Scholar]

5. Z. C. Liu, Z. Q. Shen, M. Savvides, and K. T. Cheng, “ReActNet: Towards precise binary neural network with generalized activation functions,” in Proc. Eur. Conf. Comput. Vis. (ECCV), Glasgow, UK, 2020, pp. 143–159. [Google Scholar]

6. E. Meller, A. Finkelstein, U. Almog, and M. Grobman, “Same, same but different-recovering neural network quantization error through weight factorization,” in Proc. 36th Int. Conf. Mach. Learn. (ICML), Long Beach, CA, USA, vol. 97, Jun. 9–15, 2019. doi: 10.48550/arXiv.1902.01917. [Google Scholar] [CrossRef]

7. X. Cheng, Z. Rao, Y. Chen, and Q. Zhang, “Explaining knowledge distillation by quantifying the knowledge,” in Proc. Conf. Comput. Vis. Pattern Recognit. (CVPR), Jun. 16–20, 2020, pp. 12925–12935. [Google Scholar]

8. K. K. E. Steven, L. M. Jeffrey, B. Deepika, A. Rathinakumar, S. M. Dharmendra and S. Modha, “Learned step size quantization,” in Proc. Int. Conf. Learn. Representations, ICLR, AddisAbaba, Ethiopia, Apr. 26–30, 2020. [Google Scholar]

9. Z. Wei, X. J. Zhang, Z. M. Zhuo, Z. Y. Ji, and Y. H. Li, “PPO-based automated quantization for reram-based hardware accelerator,” J. Comput. Res. Dev., no. 3, pp. 518–532, 2022. doi: 10.7544/issn1000-1239.20210551. [Google Scholar] [CrossRef]

10. Y. J. Wang, Z. Ma, and C. J. Yang, “A new mixed precision quantization algorithm for neural networks based on reinforcement learning,” in Proc. 6th Int. Conf. Pattern Recognit. Artif. Intell., PRAI, Haikou, China, Aug. 18–20, 2023, pp. 1016–1020. [Google Scholar]

11. L. Wei, Z. Ma, and C. J. Yang, “Activation redistribution based hybrid asymmetric quantization method of neural networks,” Comput. Model. Eng. Sci., vol. 138, no. 1, pp. 981–1000, 2024. doi: 10.32604/cmes.2023.027085. [Google Scholar] [CrossRef]

12. Z. Ma, Y. J. Wang, Y. D. Yang, Z. P. Wang, L. Tang and S. Ackland, “Reinforcement learning based satellite attitude stabilization method for non-cooperative target capturing,” Sens., vol. 18, no. 12, pp. 4331, 2018. doi: 10.3390/s18124331. [Google Scholar]

13. R. Banner, Y. Nahshan, and D. Soudry, “Post training 4-bit quantization of convolutional networks for rapid-deployment,” in Proc. 33rd Conf. Neural Inf. Process. Syst., NeurIPS, Vancouver, Canada, Dec. 8–14, 2019, pp. 7950–7958. [Google Scholar]

14. K. Wang, Z. Liu, Y. Lin, J. Lin, and S. Han, “HAQ: Hardware-aware automated quantization with mixed precision,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Long Beach, CA, USA, Jun. 16–20, 2019, pp. 8612–8620. [Google Scholar]

15. H. B. Yu, Q. Han, J. B. Li, J. P. Shi, G. L. Cheng and B. Fan, “Search what you want: Barrier panelty NAS for mixed precision quantization,” in Proc. Eur. Conf. Comput. Vis. (ECCV), Glasgow, UK, 2020, pp. 1–16. [Google Scholar]

16. W. He, Y. X. Zhu, H. Wang, and Z. K. Huang, “Accelerator design and implementation for automatic searching neural network,” Microelectron. Comput., vol. 38, no. 11, pp. 88–94, 2021. [Google Scholar]

17. Y. J. Wang, Z. Ma, and Z. M. Yang, “Sequential characteristics based operators disassembly quantization method for LSTM layers,” Appl. Sci., vol. 12, no. 24, pp. 12744, 2022. doi: 10.3390/app122412744. [Google Scholar] [CrossRef]

18. X. Zeng et al., “Addressing irregularity in sparse neural networks through a cooperative software/hardware approach,” IEEE Trans. Comput., vol. 69, no. 7, pp. 968–985, 2020. doi: 10.1109/TC.2020.2978475. [Google Scholar] [CrossRef]

19. Y. Ma, S. Y. Bi, and F. Jiao, “A CNN accelerator with high bandwidth storage,” Chinese Invention Patent, CN20210921363.9, Aug. 11, 2021. [Google Scholar]

20. J. Choi, Z. Wang, S. Venkataramani, I. J. Chuang, and K. Gopalakrishnan, “PACT: Parameterized clipping activation for quantized neural networks,” 2018. doi: 10.48550/arXiv.1805.06085. [Google Scholar] [CrossRef]

21. S. Han, H. Z. Mao, and W. Dally, “Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding,” in Proc. Int. Conf. Learn. Representations, ICLR, San Juan, Puerto Rico, May 2–4, 2016. [Google Scholar]

22. A. T. Elthakeb, P. Pilligundla, F. Mireshghallah, A. Yazdanbakhsh, and H. Esmaeilzadeh, “ReLeQ: A reinforcement learning approach for deep quantization of neural networks,” IEEE Micro, vol. 40, no. 5, pp. 37–45, 2020. doi: 10.1109/MM.2020.3009475. [Google Scholar] [CrossRef]

23. S. C. Zhou, Y. X. Wu, Z. K. Ni, X. Y. Zhou, H. Wen and Y. H. Zou, “DoReFa-Net: Training low bitwidth convolutional neural networks with low bitwidth gradients,” 2016. doi: 10.48550/arXiv.1606.06160. [Google Scholar] [CrossRef]

24. S. Ye et al., “A unified framework of DNN weight pruning and weight clustering/quantization using ADMM,” 2018. doi: 10.48550/arXiv.1811.01907. [Google Scholar] [CrossRef]