On Multi-Granulation Rough Sets with Its Applications

1  Introduction

According to the very rapid growth of data and the high incidence of Internet broadcasting, it has become a seriously urgent issue to extract useful information to make decisions. To do this accurately, quickly, and cost less, researchers need to work together in this field to unify their research framework. Many researchers have solved some of the problems of data sharing without a general conceptual framework governing their techniques. Some of them have used old mathematical techniques; some have used modern statistical methods; and others have developed hybrid methods between mathematics, statistics, and computer science.

In 1982, Pawlak defined the seminal theory of rough sets [1], which can be recognized as a pioneering mathematical framework designed to address the challenges posed by uncertainty, incompleteness, and imprecision within the realm of knowledge representation. Pawlak’s conceptualization delineates an approximation structure, denoted as AS = (℧,R), where ℧ represents a universal set and R denotes an equivalence relation imposed upon ℧. The equivalence classes that arise within ℧ are commonly referred to as the knowledge base. The lower approximation of a subset A of ℧ is the union of all equivalence classes wholly included in A, while the upper approximation is established as the intersection of all equivalence classes that intersect A in a non-trivial manner. Consequently, a rough set is elegantly expressed as a dual entity, comprising both the lower approximation and the upper approximation of set A, each a precise set in its own right. Recognizing the limitations of equivalence relations in the context of various applications in the real world, Pawlak’s classical rough set theory necessitated a process of generalization. This generalization endeavor unfolds on two fronts: Firstly, it involves the substitution of the equivalence relation with alternative relations such as tolerance relations [2,3], similarity relations [4], characteristic relations [5,6], and arbitrary binary relations [7]. Second, it involves replacing the partition caused by the equivalence relation with a covering mechanism. This makes it easier to approximate any subset of the universe [8]. These versatile frameworks fall under the rubric of granular computing, representing mathematical models that offer innovative solutions to a diverse array of challenges spanning data mining, machine learning, pattern recognition, and cognitive science. Nonetheless, certain challenges persist, necessitating further extensions.

In 2006, Qian et al. [9] defined the concept of multi-granular computing as a paradigm that advocates the utilization of rough sets not in isolation, but as an ensemble of relations acting upon the same universal set. This novel approach, known as multi-granular computing, supersedes the utilization of a single relation typically employed within a single granular setting, as elucidated in references [9–11]. Within the realm of mathematics, one of the most pivotal branches is topology, which serves as an indispensable tool for representing intricate relationships between objects or features, particularly when dealing with complex relational structures. Pawlak astutely emphasized the profound interconnection between topology and rough set theory, underlining the conviction that the topological space of rough sets constitutes a fundamental cornerstone within this domain. The convenience of this relationship has led researchers to undertake a comprehensive investigation into its features and practical uses and its real-world applications (see [12–14]). In 2013, Qian et al. investigated a new theory on MGRS from the topological point of view by inducing n-topological structures on the universe set ℧ from n-equivalence relations on ℧. They studied the multi-granulation topological rough structure and its topological properties (see [15]). This study focuses on enhancing the accuracy measure of rough sets by containment neighbourhoods, specifically in the context of a medical application. Additionally, the study aims to compare two different types of rough approximations that are based on neighbourhoods, for new applications at the same research point (see [16–20]). Topology has many applications in life problems [21–25].

Multi-source information fusion based on rough set theory involves integrating information from multiple sources using rough set theory. Rough set theory is used to handle inexact and uncertain information. It has been applied in various domains, such as parallel computing, neural network modeling, and information entropy. The combination of several rough set models and the use of rough set theory to measure uncertainty in an information system are some of the key aspects discussed in the literature. Zhang et al. [26,27] have presented an application of rough set theory for multi-source information fusion. The approach involves integrating heterogeneous data from multiple sources. Rough set theory is considered an efficient tool for dealing with uncertainty in the context of information fusion. They lay the foundation for integrating rough sets into decision support systems, emphasising data fusion techniques. It explores how rough set theory can effectively handle uncertainty in multi-source information, providing a comprehensive review of decision support applications. Focusing on the integration of rough sets and intelligent systems, it provides insights into the synergies between rough set theory and intelligent systems, offering applications in knowledge representation and decision-making. They provide a comprehensive overview of the role of rough set theory in data fusion. It systematically categorises and analyses existing approaches, shedding light on the strengths and challenges of employing rough sets for integrating information from multiple sources. They focused on practical applications; it explores how rough set theory can be effectively applied in multi-source information fusion scenarios. It discusses real-world examples and showcases the utility of rough sets in handling uncertainties arising from different information sources.

Rough set theory has found practical application in the domain of decision support systems, specifically within the context of data fusion. This theoretical framework proves to be a proficient tool for effectively managing information characterized by imprecision and uncertainty. Numerous scholarly inquiries have delved into the utilization of rough set theory within decision support systems, with a particular emphasis on information fusion scenarios. Notably, Han et al. [28] created an evaluation method based on rough set theory for figuring out what happens when data is missing in decision fusion. Furthermore, academic literature extensively explores the application of rough set theory in knowledge acquisition pertaining to incomplete information systems, showcasing its relevance in constructing decision support models [29–31]. Recognized for its efficacy, rough set theory is deemed instrumental in amalgamating disparate data from diverse sources, concurrently offering a means to quantify uncertainty in the information fusion process [32].

Huang et al. [33] stood as a pivotal contribution in the domain of rough set theory, specifically exploring the integration of multi-granulation and fuzzy sets for applications in feature selection. It enriches the theoretical foundations of rough set theory by integrating concepts from multi-granulation and fuzzy sets. The novel framework introduced opens avenues for more expressive and adaptable modelling of uncertainty in real-world datasets. Secondly, the application of these concepts to feature selection showcases the practical utility of the proposed methodology. This not only enhances the understanding of data representation but also provides a valuable tool for data scientists and practitioners.

Chen et al. [34,35] introduced a novel variable precision multigranulation rough set model that extends traditional rough set theory by accommodating variable precision granules. The authors delve into the mathematical foundations of this model, elucidating the principles governing the variable precision within granules. The study also explores the practical implications of this model, particularly in the realm of attribute reduction, demonstrating its effectiveness in handling uncertainty and imprecision in real-world datasets.

The multi-granularization decision-theoretic rough set (MG-DTRS) helps with cost-sensitive decision-making in multi-view and multi-level situations. One shortcoming of the MG-DTRS model is the use of subjectively assigned probability parameters (α and β) to compute three areas. Adaptive MG-DTRS (AMG-DTRS) is introduced in this study to overcome this issue. The suggested AMG-DTRS model uses a compensation coefficient ζ to provide adaptability in acquiring probabilistic thresholds. The research also examines three mean AMG-DTRS models, providing a new perspective on multi-granulation information fusion. The following analysis compares the proposed AMG-DTRS model to existing MGRS models, highlighting its advantages and generalizations. The paper also shows that the proposed framework may explicitly derive several existing MGRS models from (MG-DTRS), MGRS, and VP-MGRS models. These discoveries strengthen granular computing’s information fusion framework [36].

This work presents a novel approach that combines topology and rough set theory to address the challenge of exchanging multi-source, variable, and large-scale data in a more efficient manner. Additionally, we engage in the development of algorithms that are derived from the extraction of knowledge from the aforementioned data. The structure of this work is as follows: Sections 2 provides an exposition of the essential concepts and features of generic topology, along with an introduction to certain notions pertaining to information systems. In Sections 3, we present two methodologies for generalised multi-granulation, which can be classified into two distinct groups. The initial strategy involves the establishment of a novel approximation space with the objective of reducing the boundary region. Conversely, the second approach employs the notion of minimal neighbourhoods. In Sections 4 of our study, we utilise our findings to address the issue of attribute reduction in medical information systems. The conclusion and potential avenues for future research are outlined in Sections 5

2  Preliminaries

We provide the basic definitions and results on topological structures and rough sets. In classical rough set theory, the approximation structure is defined as (℧,R) where ℧ is non-empty finite set and R is an equivalence relation on ℧.

Definition 2.1. [1]. Let (℧,R) be a classical approximation structure. The lower and upper approximations of a given set Y⊆℧ are defined as follows:

R_Y={y:[y] R⊆Y}, R¯Y={y:[y] R∩Y≠ϕ}, where [y]R is the equivalence class of y∈℧ with respect to the equivalence relation R. The accuracy measure of the approximation is denoted by

αR(Y)=cardR_YcardR¯Y

Lemma 2.2. The boundary region of Y is given by R¯Y−R_Y, R_Y is called the positive region while ℧−R¯Y is called the negative region.

Definition 2.3. [37]. Let (℧,τ) be a topological structure, then the τ-closure of a subset A1⊆℧ is defined as follows: cl(A1)τ = ∩{F⊆℧:A1⊆F and F∈τc}.

Definition 2.4. [37]. Let (℧,τ) be a topological structure, then the τ-interior of a subset A1⊆℧ is defined as follows: int(A1)τ=∪{G⊆℧:G⊆A1 and G∈τ}.

Pawlak pointed out in [1] that lower approximations correspond to interiors and upper approximations correspond to closures. This idea has prompted the researchers to study the theory of rough sets from a topological point of view to know more about rough sets.

Definition 2.5. [37]. If ℧ is a finite universe and R is a binary relation on ℧, then we define the right neighborhood of x∈℧ as follows: RN(x)={y:xRy}.

Definition 2.6. [38]. Let ℧ be a non-empty set. A basis for a topology on ℧ is a collection β of subsets of ℧ such that:

1.    For every x∈℧, there is at least one basis element B containing x.

2.    If x belongs to the intersection of two basis elements B1 and B2, then there is a basis element B3 containing x such that B3⊆B1∩B2.

Definition 2.7. [37]. Let τ be a topology on a finite set ℧, with base β, then the rough membership function is μXτ=|{∩Bx}∩X||{∩Bx}|,x∈℧ where Bx is any member of β containing x.

Theorem 2.8. [38]. Let (℧,τ) be a topological space, A⊆℧ then x∈cl(A)τ if and only if G∩A≠ϕ, ∀G∈τ and x∈G.

The idea of multi-granulation is based on using multi-relation instead of a single relation to obtain a better approximation. Thus, we start by giving the definition of multi-granular rough sets based on equivalence relations.

Definition 2.9. [15]. Let (℧,τ1),(℧,τ2),…,(℧,τn) be n topological structures induced by equivalence relations R1,R2,…,Rn, respectively, and X⊆℧. Then, we define mint and mcl operators of X with respect to, where Γ={τ1,τ2,…,τn}, respectively, as follows:

mint(X)=∪{A∈τi|∨(A⊆X),i≤n}

mcl(X)=∪{A∈τi|∧(A∩X≠∅),i≤n}

3  MGRS Based on Topological Structure

In this section, we introduce a new theory on MGRS from the point of view of topological structures. We generate topological structures from arbitrary relations suitable for real life problems in other branches like artificial intelligence, knowledge discovery, machine learning and data mining. Also, we propose that it might be considered an extension or generalization of the Pawlak rough set framework, and we introduce a new algorithmic method for the reduction of attributes in the information (decision) system.

Theorem 3.1. Let R be a binary relation on the nonempty set ℧. ∀p∈℧, ∃RN(p)⊆℧, the family τ={X⊆℧:∀p∈X,RN(p)⊆X} forms a topology on ℧.

Proof.

Obviously ∅,U belong to τ;

Suppose that {Xi:i∈N} is a family of sets in τ, p∈∪i∈I Xi. Then ∃Xi0,p∈Xi0,i0∈N. Hence, RN(p)⊆Xi0 which leads to RN(p)⊆∪i∈N Xi. Thus ∪i∈N Xi∈τ;

Let X1,X2∈τ, p∈X1∩X2. Then, p∈X1 and p∈X2 which leads to RN(p)⊆X1 and RN(p)⊆X2. Therefore, RN(p)⊆X1∩X2 and X1∩X2∈τ;

The following example illustrates Theorem 3.1.

Example 3.2. Let U = {a, b, c, d} be a non empt set and R = {(a, a), (a, b), (b, b), (b, a) (c, c), (c, d), (d, b)} be an arbitrary relation. Then, RN(a) = {a, b}, RN(b) = {a, b}, RN(c) = {c, d}, RN(d) = {b}. Hence, τ={U,∅,{a,b},{c,d},{b},{b,c,d}} forms a topology on ℧.

Remark 3.3. From Theorem 3.1, we can generate many topological structures from any finite number of arbitrary relations. So, we are ready for the following definition of the approximation structure.

Definition 3.4. Let (℧,R) be a knowledge base, where R is a family of binary relations R1,R2,R3,…,Rn on the universe ℧ and τ1,τ2,τ3,…,τn are induced topologies on ℧ by the binary relations. Then, the multi-lower approximation and multi-upper approximation of the set X⊆℧ are defined as, respectively,

MLA(X)=∪i=1nint(X)τi

MUA(X)=⋂i=1ncl(X)τi

The pair (MLA(X),MUA(X)) is called a MGRS of X.

When LA(X)=X, resp., MUA(X)=X, we say that X is a lower definable, resp., an upper definable set in the MGRS model. If the set X is both lower definable and upper definable, we say the set X is definable.

Lemma 3.5. Suppose that (℧,R) and τ1,τ2,τ3,…,τn are induced topologies on ℧. Then for X⊆℧, i∈N, we have:

1.    int(X)τi=int(MLA(X))τi,

2.    cl(X)τi=cl(MUA(X))τi

Proof.

1.    Since MLA(X)=∪i=1nint(X)τi=∪i=1nGi, where Gi is the greatest open set with respect to τi contained in X. So, int(MLA(X))τi=int(∪i=1nGi)τi=Gi, where Gi is the greatest open set contained in X and Gi⊆∪i=1nGi. Hence, int(X)τi=int(MLA(X))τi.

2.    Since MUA(X)=⋂i=1ncl(X)τi=⋂i=1nFi, where Fi is the smallest set with respect to τi containing X. Then, cl(MUA(X))τi=cl(⋂i=1nFi)τi=Fi where Fi is the smallest closed set such that ⋂i=1nFi⊆Fi. Therefore, cl(X)τi=cl(MUA(X))τi.

Proposition 3.6. Assume that (℧,R) is a knowledge base where R is a family of binary relations R1,R2,R3,…,Rn on the universe ℧ and τ1,τ2,τ3,…,τn are induced topologies on ℧ by the binary relations. For X1,X2⊆℧, the following properties hold:

1.    MLA(∅)=∅;

2.    MUA(∅)=∅;

3.    MLA(℧)=℧;

4.    MUA(℧)=℧;

5.    MLA(X1)⊆X1;

6.    X1⊆MUA(X1);

7.    If X1⊆X2⇒ MLA(X1)⊆MLA(X2);

8.    If X1⊆X2⇒ MUA(X1)⊆MUA(X2);

9.    MLA(MLA(X1))=MLA(X1);

10.   MUA(MUA(X1))=MUA(X1);

11.   MLA(X1∩X2)=MLA(X1)∩MLA(X2);

12.   MUA(X1∪X2)=MUA(X1)∪MLA(X2);

Proof. We will prove 7,8,9,10,11 and 12 parts. The proof of the other parts is clear from Definition 3.1.

7. Let x∈MLA(X1)⇒x∈∪i=1nint(X1)τi. Then, there exists open set Gio such that x∈Gio⊆X1 for some i0∈N. Since X1⊆X2, hence, x∈Gio⊆X1 for some i0∈N. So x∈∪i=1nint(X2)τi, x∈MLA(X2). Therefore, MLA(X1)⊆MLA(X2).

8. Let x∈MUA(X1)⇒x∈⋂i=1nint(X1)τi. Then, for all open set G, x∈G∩X1≠∅. Since X1⊆X2, then x∈G∩X2≠∅ for all i∈N and x∈MUA(X2). Therefor, MUA(X1)⊆MUA(X2).

9. MLA(MLA(X1))=∪i=1nint(MLA(X1)τi=∪i=1nint(X)τi=MLA(X1).

10. MUA(MUA(X1))=⋂i=1ncl(MUA(X1))τi=⋂i=1ncl(X1)τi=MUA(X1);

11. Since X1∩X2⊆X1, X1∩X2⊆X2. So by (7), MLA(X1∩X2)⊆MLA(X1), MLA(X1∩X2)⊆MLA(X2) and MLA(X1∩X2)⊆MLA(X1)∩MLA(X2). Assume that x∉MLA(X1∩X2)⇒x∉∪i=1nint(X1∩X2)τi. Hence, x∉int(X1)τi and x∉int(X2)τi. Therefore, x∉int(X1)τi∩int(X2)τi. Then MLA(X1)∩MLA(X2)⊆MLA(X1∩X2) and MLA(X1∩X2)=MLA(X1)∩MLA(X2).

12. Since X1⊆X1∪X2, X2⊆X1∪X2. By (8), we get MUA(X1)⊆MUA(X1∪X2), MUA(X2)⊆MUA(X1∪X2) and MUA(X1)∪MUA(X2)⊆MUA(X1∪X2). On the other hand, Let x∈MUA(X1∪X2)⇒x∈⋂i=1ncl(X1∪X2)τi. So x∈⋂i=1ncl(X1)∪⋂i=1ncl(X2) and x∈MUA(X1)∪MUA(X2). Therefore, MUA(X1∪X2)⊆MUA(X1)∪MUA(X2). So MUA(X1∪X2)=MUA(X1)∪MLA(X2).

Example 3.7. Suppose that (℧,R) is knowledge base since R is a family of binary relations R1,R2,R3,…,Rn on the universe ℧={a,b,c,d}, where R1 = {(a, a), (a, b), (b, c), (b, d), (c, a), (d, a)}, R2={(b,b),(c,d),(c,a),(d,b),(d,c)} and R3 = {(a, a), (b, c), (b, d), (c, c)}. Then, by Theorem 3.1, the induced topologies are τ1 = {{a, b}, {c, d}, {a}, {a, c, d}, U, ∅}, τ2={{a,d},{b,c},{b},{a,b,d},U,∅} and τ3 = {{a}, {c, d}, {c}, {a, c, d}, {a, c}, U, ∅}. Let X1={a,b,c}, X2={b,c,d}. Then, the approximation of two sets is presented in the following Tables 1 and 2.

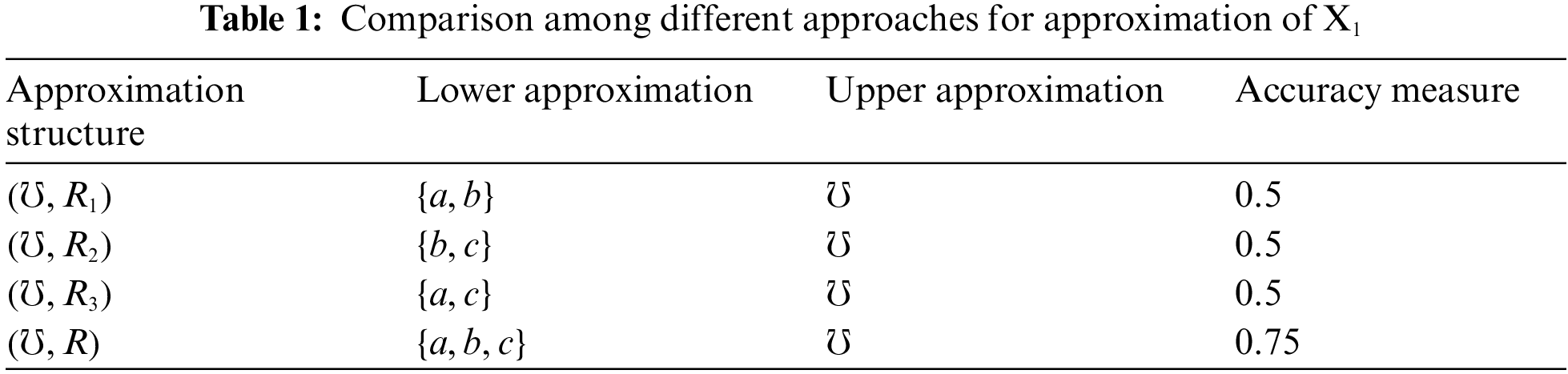
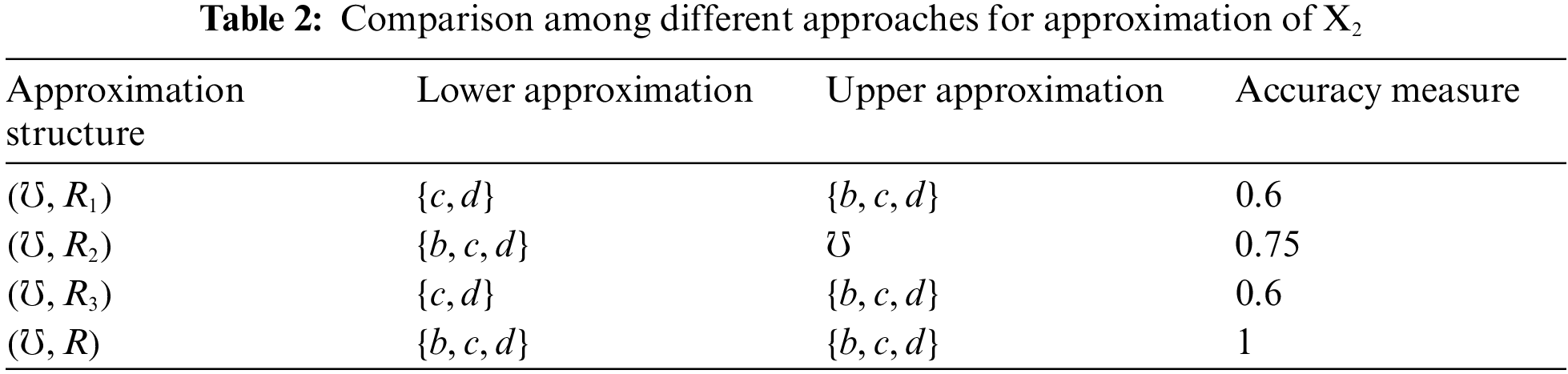
Remark 3.8. From Example 3.7, we note that the accuracy measure of our approximation structure is higher than the other approaches, as our approach is considered a generalization for the others.

3.1 Multi-Granulation of Rough Set Based on Neighborhood Concept

Definition 3.9. Let R1,R2,R3,…,Rn be binary relations on the nonempty set ℧. We define the minimal neighborhood MN:U→P(U) as MN(x)=⋂i=1nRNi(x),∀x∈℧, where RNi(x)right neighborhood x∈℧.

Theorem 3.10. If R1,R2 is two binary relations on the nonempty set ℧, then, the family

Bi=12={MN(x):x∈℧} form a topological base for ℧.

Proof. Since x1∈MN(x1) for every x1∈℧. So, suppose that β1,β2∈Bi=12, e∈β1∩β2. Then β1=MN(x1),β2=MN(x2) for x1,x2∈℧. Hence, e∈β1∩β2 if and only if e∈β1=MN(x1) and e∈β2=MN(x2). Obviously, e∈MN(e)⊆MN(x1) and e∈MN(e)⊆MN(x2). So, ∃β3=MN(e)∈Bi=12 such that e∈β3⊆β1∩β2.

Corollary 3.11. Suppose that R1,R2,R3,…,Rn be family of binary relations on the nonempty set ℧. Then, the collection of neighborhoods Bi=1n={MN(x):x∈℧} form a topological base for ℧ and the structure (℧,τMN) is called generalized multi-granular rough based topological structure GMRTS.

Theorem 3.12. Suppose that R1,R2,R3,…,Rn be a family of binary relations on the nonempty set ℧. If any relation Ri0 is an identity, then generalized multi-granular rough based topological structure GMRTS (℧,τMN) is the same topology generated by Ri0.

Proof. Since Ri0,i0∈{1,2,3,…,n} is an identity relation. Then RNi0(x)=x,∀x∈℧. Thus, N(x)=RNi0(x), ∀x∈℧ and the base Bi=1n={MN(x):x∈℧} is equal the base generated by Ri0. So, topological structure GMRTS (℧,τMN) is the same topology generated by Ri0.

Example 3.13. Let ℧={b1,b2,b3,b4,b5,b6} and R1,R2,R3 be family of relations on ℧ definedas: R1={(b1,b1),(b1,b2),(b3,b3),(b3,b5),(b5,b5),(b6,b3),(b6,b6)}, R2={(b1,b1),(b1,b2),(b2,b1),(b2,b2),(b3,b3),(b3,b4),(b4,b4)}, R3 = {(b2,b1)(b2,b2),(b3,b3), (b3,b4), (b4,b4),(b4,b5),(b4,b6), (b5,b5),(b5,b6)(b6,b4),(b6,b5),(b6,b6)}. Then MN(b1)={b1,b2}, MN(b2)={b1,b2}, MN(b3)={b3}, MN(b4)={b4}, MN(b5)={b5}, MN(b6)={b6}. Hence, Bi=1n={{b1,b2},{b3},{b4},{b5},{b6}} is the base of generalized multi-granular rough structure GMRTS. In Table 3, there is a comparison among different approximations of the set B={b1,b4,b6}.

The reduction process of data is very important since we express the whole data by a part of it with conservation of the structure of the whole data. So we introduce an algorithm for relation reduction by removing the superfluous relations and expressing the hole data of the universe by fewer number of relations. In this algorithm, we remove the redundant bases that generated from the superfluous relations. This reduction may be helpful in the process of decision-making.

This algorithm is shown by the following example:

Example 3.14. That ℧={b1,b2,b3,b4,b5,b6} and X={B1,B2,B3} be a family of bases induced by any arbitrary relations R1,R2,R3, respectively, where B1={{b1,b2,b3},{b4,b5,b6}}, B2={{b1,b2,b3,b4,b6},{b5}} and B3 = {(b1,b4), (b2,b5)}, (b3,b6)}}. Then ⋂i=1nBi={{b1},{b2},{b3},{b4},{b5},{b6}}. If we remove B1 from X, then B2∩B3={{b1,b4},{b2},{b3,b6},{b5}}≠⋂i=1nBi. Hence, R1 belongs to the reduct. Similarly, we find that R3 that belongs to the reduct, but R2 is redundant relation and can be omitted. So, the reduct ={R1,R3}.

4  Real Life Applications

The data used in this study is based on the collected data of the following paper [14].

4.1 Clinical Data Description

Patients with digestive disease have become so many of these lesions due to the high number of fast foods, which contain high calories, as well as processed meat. As a direct result of this food, many people suffer from excessive infusion and the subsequent diseases of the digestive system, the most serious of which are stomach and colon cancers. Because of the eradication of the stomach, the food directly goes to the intestine, causing confusion in the absorption. The patients have some violent symptoms after the meal, such as dizziness, headache, colic and increasing the blood sugar. After a period, the patient has the highest and most dangerous complications, such as high cholesterol and clogged arteries leading to heart attacks.

Hereditary nonpolyposis colorectal cancer (HNPCC) is the most common type of intrinsic stomach and colon cancer syndrome. HNPCC, also known as Lynch syndrome, raises the risk of stomach and colon cancer, as well as other malignancies. People with HNPCC are more likely to develop stomach and colon cancer before the age of 50. FAP (familial adenomatous polyposis) is an uncommon condition that causes hundreds of polyps to grow in the inner layer of your stomach, colon, and rectum. People who consume unprocessed FAP have a significantly higher chance of acquiring stomach and colon cancer before the age of 40.

4.2 Analysis of the Problem

Our aim in this study is to find recommendations for patients and show them appropriately greeted approach combines treatment and exercise to reach results and explain the function of every presentation of the positive and negative impact on the patient. The decision of the Physician for the medical reports is the continuation of the medical tests, which are all for another or off medical analysis. The patient’s condition is stable and insensitive to a healthy style of workout.

4.3 Problem Formulation

According to the medical reports requested by the doctor for patients in this case, the following attributes:

1) Liver Functions: Of type S. GPT (Natural percent between 0 to 45 U/L) and of the type S. GOT (Natural percent between 0 to 37 U/L).

2) Kidney Functions: The measurements of uric acid in the blood (Uric Acid varies between 3 to 7 mg/dl).

3) Fat Percentage: Fats in the blood are divided into two types, the cholesterol level has a natural a range of less than 200 mg/dl. The border range is between 200 to 240 mg/dl. The critical a range of it that causes arteriosclerosis or heart disease is higher than 240 mg/dl. Second, the so-called triglycerides range that has reference up to 150 mg/dl.

4) Heart Efficiency: We measured the enzyme (Serum LDH) has a range of reference between 0 to 480 U/L.

5) Signs of Tumors: We tested the digestive system through the scale (CEA) and normal Non-smoking rooms if it was less than 5 mg/ml. The other measure is so-called CA 19.9 and extent of reference from 0 to 39 U/ml.

6) Viruses Hepatitis: Test the patient’s immunity against viruses of type B (HBC) and of type C (Highly infectious) furthermore is positive or negative.

7) Blood Sugar: The patient’s measurement of sugar after fasting for 6 hours, an hour after eating, and then two hours after eating. The results of the seven patients were collected from official files in the physician, which was done after six months of surgery (see Table 4).

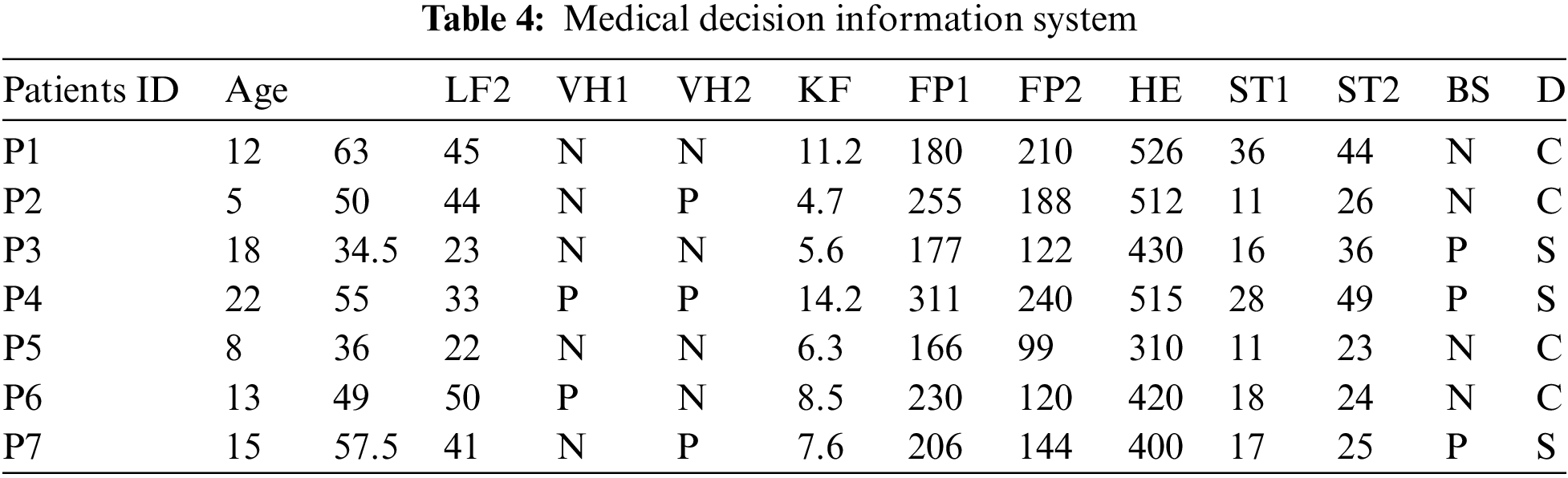
We define a suitable relation for every attribute and apply our approach to this data as follows:

Rage = {(p1,p2): Jfage(p1) − fage(p2)j ≤3 },

RLF1={(p1,p2):fFL1(p1) and fFL1(p2)≤45 or fFL1(p1) and fFL1(p2)>45},

RLF2={(p1,p2):fFL2(p1) and fFL2(p2)≤37 or fFL2(p1) and fFL2(p2)>37},

RVH1={(p1,p2):fVH1(p1)=fVH1(p2)},

RVH2={(p1,p2):fVH2(p1)=fVH2(p2)},

RKF={(p1,p2):3≤fKF(p1) and fKF(p2)≤7,fKF(p1) and fKF(p2)≤ 3o or fKF(p1) and fKF(p2)>7},

RFP1 = {(p1,p2): 200 ≤ fFP1(p1) and fFP1(p2) ≤ 240, fFP1(p1) and fFP1(p2) ≤ 200 or fFP1(p1) and fFP1(p2) > 240},

RFP2={(p1,p2):fFP2(p1) and fFP2(p2)≤150 or fFP2(p1) and fFP2(p2)>150},

RHE={(p1,p2):fHE(p1) and fHE(p2)≤480 or fHE(p1) and fHE(y)>480},

RST1={(p1,p2):fST1(p1) and fST1(p2)≤5 or fST1(p1) and fST1(p2)≤15 or fST1(p1) and fST1(p2)>15},

RST2={(p1,p2):fST2(p1) and fST2(P2)≤39 or fST2(p1) and fST2(p2)>39},

RBS={(p1,p2):fBS(p1)=fBS(p2)}. Thus, we compute relations as follows:

R1={(p1,p7),(p6,p7),(p1,p6),(p2,p5),},

R2={(p1,p2),(p1,p4),(p1,p6),(p1,p7),(p2,p4),(p2,p6),(p2,p7),(p6,p7),(p3,p5)},

R3={(p1,p2),(p,p7),(p1,p6),(p6,p7),(p3,p4),(p3,p5)},

R4={(p4,p6),(p1,p2),(p3,p5),(p5,p7)},

R5={(p1,p3),(p1,p5),(p4,p7),(p2,p4)},

R6={(p2,p3),(p2,p5),(p1,p7),(p1,p6),(p5,p6)},

R7={(p1,p3),(p1,p5),(p6,p7),(p2,p4),(p5,p6)},

R8={(p3,p5),(p1,p2),(p6,p7),(p2,p4),(p1,p4)},

R9={(p3,p6),(p3,p7),(p6,p7),(p1,p2),(p2,p4)},

R10={(p2,p5),(p1,p3),(p1,p4),(p6,p7),(p4,p6)},

R11={(p2,p3),(p5,p6),(p6,p7),(p1,p4),(p3,p4)},

R12={(p1,p2),(p5,p6),(p3,p4),(p3,p7),(p2,p6)}.

By calculating the neighborhood for every element, we get Bi=112 = {{p1}, {p2}, {p3}, {p4}, {p5}, {p6}, {p7}} as a topological base for approximation structure (℧,τMN). So, if we take the set of patients with condition C (need more check up), PC={p1,p2,p5,p6}. Therefore, the lower approximation intMN(PC) and upper approximation clMN(PC) are equal to PC={p1,p2,p5,p6} and the accuracy measure is 100. When we apply the algorithm of reduction, we get redcut(R)={R7,R11,R12} and accuracy measure of the approximation remain 100. After reduction, the table of information is reduced to be as in Table 5 and has the same structure as the original data in Table 4, where {R7,R11,R12} represent the attributes {FP1,ST2,BS}, respectively. From this reduct we get the decision rules to be used in the decision making in the future tests by a decision program.

4.4 Results Analysis

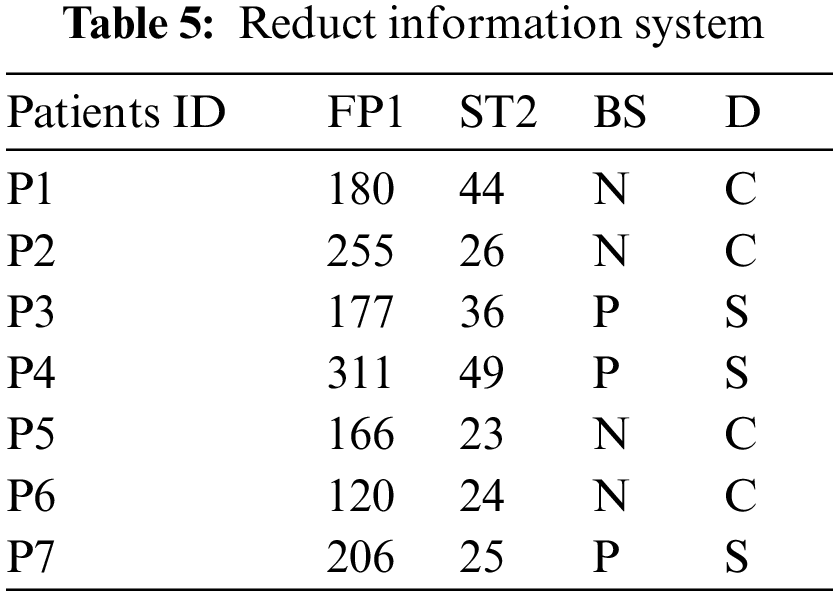
This method of dividing patient data from the results of the 12 medical examinations has been reduced to only three tests to be sufficient to make the right decision for these patients. There are other alternatives for decision-making. Using the pathological method of data analysis and division, we have been able to find more than one reduction in medical examinations and every patient can choose the appropriate alternative in terms of financial capacity and likelihood.

5  Conclusions and Future Works

The amount of research papers available online on the topological application is growing and this growth has generated a need for a unifying theory to compare the results. Also, we need new techniques and tools that can intelligently and automatically extract implicit information from these data. These tools and technicalities are the subjects of future research trends using general topological concepts. It may be inferred that the incorporation of topology in the construction of knowledge base concepts facilitates the generation of comprehensive outcomes, which encompass several logical statements that unveil concealed linkages within data. Furthermore, this integration potentially contributes to the formulation of precise rules.

In future papers, we hope to study more generalizations using topological concepts such as near sets. And apply these generalized concepts to realistic medical data of large sizes. The topic of multivariate data reduction can also be studied using generalized topological concepts, developing a unifying theory of topological generalizations that uses rough concepts. Scaling up to design topological software to handle big dimensional classification problems.

Acknowledgement: None.

Funding Statement: This research is funded by Zarqa University, Jordan.

Author Contributions: Study conception and design: Radwan Abu-Gdairi (RG), R. Mareay (RM). M. Badr (MB); data collection: RG, RM and MB; analysis and interpretation of results: RG, RM and MB; draft manuscript preparation: RG, RM and MB. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data are contained within the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Z. L. Pawlak, “Rough sets,” Int. J. Comput. Inf. Sci., vol. 11, no. 5, pp. 341–356, 1982. doi: 10.1007/BF01001956. [Google Scholar] [CrossRef]

2. G. Cattaneo, “Abstract approximation spaces for rough theories,” Rough Sets Knowl. Discov., vol. 1, pp. 59–98, 1998. [Google Scholar]

3. A. Skowron and J. Stepaniuk, “Tolerance approximation spaces,” Fund. Inform., vol. 27, pp. 245–253, 1996. doi: 10.3233/FI-1996-272311. [Google Scholar] [CrossRef]

4. R. Slowinski and D. Vanderpooten, “A generalized definition of rough approximations based on similarity,” IEEE Trans. Knowl. Data Eng., vol. 12, no. 2, pp. 331–336, 2000. doi: 10.1109/69.842271. [Google Scholar] [CrossRef]

5. J. W. Grzyma la-Busse, “Characteristic relations for incomplete data: A generalization of the indiscernibility relation,” in Int. Conf. Rough Sets Current Trends Comput., Berlin, Heidelberg, Springer, 2004, pp. 244–253. [Google Scholar]

6. Y. S. Qi et al., “Characteristic relations in generalized incomplete information system,” in 1st Int. Workshop Knowl. Discov. Data Min. (WKDD 2008), IEEE, 2008, pp. 519–523. [Google Scholar]

7. M. Kondo, “On the structure of generalized rough sets,” Inform. Sci., vol. 176, no. 5, pp. 589–600, 2006. doi: 10.1016/j.ins.2005.01.001. [Google Scholar] [CrossRef]

8. W. Zhu and F. Y. Wang, “Reduction and axiomization of covering generalized rough sets,” Inform. Sci., vol. 152, no. 9, pp. 217–230, 2003. doi: 10.1016/S0020-0255(03)00056-2. [Google Scholar] [CrossRef]

9. Y. H. Qian and J. Y. Liang, “Rough set method based on multi-granulations,” in 2006 5th IEEE Int. Conf. Cogn. Inform., 2006, pp. 297–304. [Google Scholar]

10. Y. Qian, J. Liang, Y. Yao, and C. Dang, “MGRS: A multi-granulation rough set,” Inf. Sci., vol. 180, no. 6, pp. 949–970, 2010. doi: 10.1016/j.ins.2009.11.023. [Google Scholar] [CrossRef]

11. L. A. Zadeh, “Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic,” Fuzzy Set Syst., vol. 90, no. 2, pp. 111–127, 1997. doi: 10.1016/S0165-0114(97)00077-8. [Google Scholar] [CrossRef]

12. A. S. Salama, “Generalizations of rough sets using two topological spaces with medical applications,” International Information Institute (Tokyo) Inform., vol. 19, no. 7A, pp. 2425, 2016. [Google Scholar]

13. A. Salama, “Generalized topological approximation spaces and their medical applications,” J. Egypt. Math. Soc., vol. 26, no. 3, pp. 412–416, 2018. doi: 10.21608/joems.2018.2891.1045. [Google Scholar] [CrossRef]

14. S. E. D. S. Hussein, A. S. Salama, and A. K. Salah, “Topological approaches for generalized multi-granulation rough sets with applications,” Ital. J. Pure Appl. Math., vol. 293, pp. 293–311, 2023. [Google Scholar]

15. G. Lin, J. Liang, and Y. Qian, “Topological approach to multigranulation rough sets,” Int. J. Mach. Learn. Cyber., vol. 5, no. 2, pp. 233–243, 2014. doi: 10.1007/s13042-013-0160-x. [Google Scholar] [CrossRef]

16. T. M. Al-Shami, “An improvement of rough sets’ accuracy measure using containment neighborhoods with a medical application,” Inform. Sci., vol. 569, no. 4, pp. 110–124, 2021. doi: 10.1016/j.ins.2021.04.016. [Google Scholar] [CrossRef]

17. I. Alshammari, T. M. Al-shami, and M. E. El-Shafei, “A comparison of two types of rough approximations based on neighborhoods,” J. Intell. Fuzzy Syst., vol. 41, no. 1, pp. 1393–1406, 2021. doi: 10.3233/JIFS-210272. [Google Scholar] [CrossRef]

18. A. A. Azzam, R. A. Hosny, B. A. Asaad, and T. M. Al-Shami, “Various topologies generated from neighbourhoods via ideals,” Complex., vol. 2021, pp. 1–11, 2021. doi: 10.1155/2021/4149368 [Google Scholar] [CrossRef]

19. W. Q. Fu, T. M. Al-shami, and E. A. Abo-Tabl, “New rough approximations based on neighborhoods,” Complex., vol. 2021, pp. 1–6, 2021. doi: 10.1155/2021/6666853 [Google Scholar] [CrossRef]

20. O. G. Elbarbary, A. S. Salama, A. Mhemdi, and T. M. Al-Shami, “Topological approaches for rough continuous functions with applications,” Complex., vol. 2021, pp. 1–12, 2021. 10.1155/2021/5586187 [Google Scholar] [CrossRef]

21. G. Wang, T. Li, P. Zhang, Q. Huang, and H. Chen, “Double-local rough sets for efficient data mining,” Inform. Sci., vol. 571, no. 2–3, pp. 475–498, 2021. doi: 10.1016/j.ins.2021.05.007. [Google Scholar] [CrossRef]

22. M. K. El-Bably and T. M. Al-Shami, “Different kinds of generalized rough sets based on neighborhoods with a medical application,” Int. J. Biomath., vol. 14, no. 8, pp. 292, 2021. doi: 10.1142/S1793524521500868. [Google Scholar] [CrossRef]

23. R. Mareay, R. Abu-Gdairi, and M. Badr, “Modeling of COVID-19 in view of rough topology,” Axioms, vol. 12, no. 7, pp. 663, 2023. doi: 10.3390/axioms12070663. [Google Scholar] [CrossRef]

24. A. A. El-Atik, Y. Tashkandy, S. Jafari, A. A. Nasef, W. Emam and M. Badr, “Mutation of DNA and RNA sequences through the application of topological spaces,” AIMS Math., vol. 8, no. 8, pp. 19275–19296, 2023. doi: 10.3934/math.2023983. [Google Scholar] [CrossRef]

25. M. Badr, R. Abu-Gdairi, and A. A. Nasef, “Mutations of nucleic acids via matroidal structures,” Symmetry, vol. 15, no. 9, pp. 1741, 2023. doi: 10.3390/sym15091741. [Google Scholar] [CrossRef]

26. P. Zhang et al., “Multi-source information fusion based on rough set theory: A review,” Inform. Fusion, vol. 68, no. 4, pp. 85–117, 2021. doi: 10.1016/j.inffus.2020.11.004. [Google Scholar] [CrossRef]

27. F. Yang and P. Zhang, “MSIF: Multi-source information fusion based on information sets,” J. Intell. Fuzzy Syst., vol. 44, no. 3, pp. 1–10, 2023. doi: 10.3233/JIFS-222210. [Google Scholar] [CrossRef]

28. S. Han, X. Jin, and J. Li, “An assessment method for the impact of missing data in the rough set-based decision fusion,” Intell. Data Anal., vol. 20, no. 6, pp. 1267–1284, 2016. doi: 10.3233/IDA-150242. [Google Scholar] [CrossRef]

29. Y. Qian, S. Li, J. Liang, Z. Shi, and F. Wang, “Pessimistic rough set based decisions: A multi-granulation fusion strategy,” Inform. Sci., vol. 264, no. 9, pp. 196–210, 2014. doi: 10.1016/j.ins.2013.12.014. [Google Scholar] [CrossRef]

30. S. Widz and D. Slezak, “Rough set based decision support—models easy to interpret,” in: G. Peters, P. Lingras, D. Slezak, Y. Yao, editors. Rough Sets: Select. Methods Appl. Manag. Eng., Springer, London, pp. 95–112, 2012. doi: 10.1007/978-1-4471-2760-4. [Google Scholar] [CrossRef]

31. R. Słowiński, S. Greco, and B. Matarazzo, “Rough-set-based decision support,” in Search Methodologies: Introductory Tutorials in Optimization and Decision Support Techniques, pp. 557–609, 2014. [Google Scholar]

32. W. Wei and J. Liang, “Information fusion in rough set theory: An overview,” Inform. Fusion, vol. 48, no. 4, pp. 107–118, 2019. doi: 10.1016/j.inffus.2018.08.007. [Google Scholar] [CrossRef]

33. Z. Huang and J. Li, “Covering based multi-granulation rough fuzzy sets with applications to feature selection,” Expert. Syst. Appl., vol. 238, no. 1, pp. 121908, 2024. doi: 10.1016/j.eswa.2023.121908. [Google Scholar] [CrossRef]

34. J. Chen and P. Zhu, “A variable precision multi-granulation rough set model and attribute reduction,” Soft Comput., vol. 27, no. 1, pp. 85–106, 2023. [Google Scholar]

35. W. Wei, J. Liang, Y. Qian, and F. Wang, “Variable precision multi-granulation rough set,” in 2012 IEEE Int. Conf. Granul. Comput., IEEE, 2012, pp. 536–540. [Google Scholar]

36. P. Zhang, T. Li, C. Luo, and G. Wang, “AMG-DTRS: Adaptive multi-granulation decision-theoretic rough sets,” Int. J. Approx. Reason., vol. 140, pp. 7–30, 2022. doi: 10.1016/j.ijar.2021.09.017. [Google Scholar] [CrossRef]

37. E. F. Lashin, A. M. Kozae, A. A. Abo Khadra, and T. Medhat, “Rough set theory for topological spaces,” Int. J. Approx. Reason., vol. 40, no. 1–2, pp. 35–43, 2005. doi: 10.1016/j.ijar.2004.11.007. [Google Scholar] [CrossRef]

38. J.R. Munkres, Topology a First Course. London: Prentice Hall, 1974. [Google Scholar]