A Multi-Strategy-Improved Northern Goshawk Optimization Algorithm for Global Optimization and Engineering Design

1  Introduction

The growing complexity of optimization problems, combined with the limitations of traditional algorithms, has underscored the need for developing meta-heuristic algorithms in recent years [1]. Focusing solely on inputs and outputs, metaheuristic algorithms excel in solving a broad spectrum of complex optimization problems across different fields. Applications range from path planning [2], and scheduling [3,4], to image threshold segmentation [5], and feature extraction and selection [6]. The inspiration behind metaheuristic algorithms stems from natural phenomena such as evolution, fundamental physicochemical laws, and the intelligent behaviors of swarms. By simulating these behaviors to construct models, these algorithms approximate the global optima of nonlinear, non-convex, discontinuous, and discrete complex optimization problems, thus achieving high-quality solutions at lower computational costs.

Metaheuristic algorithms are categorized into four types: Evolutionary, swarm intelligence-based, physicochemical law-grounded, and social or human behavior-modeled. The Genetic Algorithm (GA) [7] is notably the most influential among evolution-based algorithms. is notably the most influential among evolution-based algorithms. Mimicking Darwin’s evolution process, GA assesses organism fitness to their environments and uses genetic operators—selection, crossover, mutation—to iteratively improve solution quality, effectively solving optimization problems. Evolutionary algorithms, applicable broadly and independent of gradient information, are marked by high computational costs and slow convergence. Swarm intelligence algorithms replicate group information exchange capabilities and characteristics. For example, the particle swarm optimization (PSO) [8] mirrors birds’ predation behavior, simplifying optimization problem-solving to a quest for nourishment. Leveraging population and evolution concepts, these algorithms facilitate complex solution space exploration via individual cooperation. A common trait of swarm intelligence algorithms is their vulnerability to local optima, resulting in quicker convergence at the risk of settling for suboptimal solutions. Algorithms grounded in physical and chemical principles, like the Simulated Annealing algorithm (SA) [9] and Sine and Cosine Algorithm (SCA) [10], offer superior convergence accuracy. However, these algorithms have notable drawbacks, such as an excessive dependency on parameter settings, slow convergence rates, and applicability to only specific types of optimization problems. Algorithms inspired by social or human behaviors, like the Brain Storm Optimization Algorithm (BSOA) [11] and Tabu Search (TS) [12], derive their search strategies from the simulation of human behaviors in social interactions, learning, competition, and cooperation, aiming to solve complex optimization problems. The design of their search strategies significantly influences the convergence speed and stability of these algorithms.

Swarm intelligence algorithms offer significant benefits and potential for solving real-world engineering problems. As a result, numerous novel and enhanced swarm intelligence algorithms have been developed to address practical challenges. Introduced in the early 1990s, the Ant Colony Algorithm (ACO) [13] mimics ants’ foraging behavior to find the shortest path. It uses stochastic state transitions and pheromone updates, effectively solving the Traveling Salesman Problem. After 2000, swarm intelligence algorithms gained researchers’ attention for their fast convergence and robust stability. The Grey Wolf Optimizer (GWO) [14] was proposed in 2014, followed by the Whale Optimization Algorithm (WOA) [15] in 2016, igniting a surge in swarm intelligence algorithm proposals and improvements. In recent years, algorithms including the Dragonfly Algorithm (DA) [16], Aquila Optimizer (AO) [17], Harris Hawks Optimization (HHO) [18], Hunger Games Search (HGS) [19], Prairie Dog Optimization Algorithm (PDO) [20], Dwarf Mongoose Optimization Algorithm (DMO) [21], Chimp Optimization Algorithm (ChOA) [22], Beluga Whale Optimization (BWO) [23], have been introduced and shown effectiveness in various benchmarks and specific problems. The introduction of these algorithms has markedly facilitated solving complex engineering challenges in the real world.

Dehghani et al. [24] proposed the NGO in 2022, building on the simulation of the Northern goshawk’s predation behavior, featuring a mathematically simple model and rapid computation speeds, finding application across numerous domains. Yu et al. [25] enhanced NGO’s performance through methods such as leader mutation and sine chaos mapping, proposing a Chaotic Leadership Northern Goshawk Optimization (CLNGO), effectively addressing rolling bearing fault diagnosis issues. Youssef et al. [26] introduced an Enhanced Northern Goshawk Optimization (ENGO) for smart home energy management, incorporating Brownian motion in the first phase and Levy flight strategy in the second phase of NGO, which, although improving global search capability to some extent, rendered the algorithm prone to convergence difficulties. Liang et al. [27] improved NGO by integrating a polynomial interpolation strategy and multi-strategy opposite learning method, evaluating its performance using multiple benchmark function test sets, achieving noteworthy results, albeit the search methodologies of these strategies were relatively singular compared to others. El-Dabah et al. [28] employed NGO for identifying Photovoltaic (PV) model parameters. Satria et al. [29] introduced a hybrid algorithm, Chaotic Northern Goshawk, and Pattern Search (CNGPS), merging NGO with pattern search to improve convergence accuracy in PV parameter identification, reducing early-stage local optima’s impact and preventing premature convergence. Zhong et al. [30] optimized the hyperparameters of the Bi-directional Long Short Term Memory (BILSTM) network for facial expression recognition using NGO, with the proposed NGO-BILSTM model achieving an accuracy of 89.72%. Tian et al. [31] extended NGO into a multi-objective version to address multi-objective Disassembly Line Balancing Problems (DLBP) in remanufacturing, significantly contributing to solving DLBP issues. Wang et al. [32] refined NGO using Tent chaotic mapping, adaptive weight factor, and Levy flight strategy, applying the novel algorithm to tool wear condition identification, reaching an accuracy of 97.9%. Zhan et al. [33] expanded NGO into Multi-objective Northern Goshawk Optimization Algorithm (MONGO) for environmentally oriented disassembly planning of end-of-life vehicle batteries, aiming to maximize disassembly efficiency and quality. Bian et al. [34] combined NGO with Henry Gas Solubility Optimization (HGSO) to create the eXtreme Gradient Boosting Northern Goshawk (XGBNG) model, which predicts the compressive strength of self-compacting concrete with unparalleled accuracy. Wang et al. [35] applied NGO to address buyer-seller behavior models in the electric power trading system, effectively enhancing the rational reutilization of electricity in private electric vehicles. Ning et al. [36] proposed an Artificial Neural Network (ANN) model optimized by NGO, resulting in the NGO-ANN model with high predictive accuracy.

Despite the emergence of numerous NGO variants, they exhibit limitations and excel only in specific problems. This reality persists regardless of the type or extent of modifications researchers apply to any algorithm, as each harbors its inherent constraints. The No Free Lunch (NFL) theorem [37] elucidates that for any optimization algorithm, the expected performance across all possible problems is equivalent, signifying that no algorithm can universally attain the global optimum for every problem. This theorem has led researchers to work on improving existing algorithms and introducing new ones and their enhanced versions. Based on this principle, it is imperative to continuously propose new algorithms and adapt these proposals to address the characteristics of different types of problems to tackle both current and forthcoming optimization challenges [38]. NGO exhibits exceptional performance across a variety of optimization problems; however, it is undeniable that limitations remain. The research improvements on NGO have not transcended beyond optimization initialization, parameter enhancement, and mutation strategies. These strategies effectively ameliorate the algorithm’s convergence speed and, to some extent, its global search capability, yet their impact on the precision of NGO’s convergence is minimal. This article, starting from the NFL theorem and focusing on the minimization of functions as the problem type, addresses the issue of suboptimal convergence accuracy inherent in both NGO and its enhancements. Innovatively, this work integrates STA [39] into NGO, proposing a multi-strategy improved version, INGO, aimed at augmenting the algorithm’s local exploitation capacity. The performance of NGO is evaluated on two public test sets and one engineering problem. The contribution of this study is not limited to presenting an optimization algorithm with superior performance but also lies in the in-depth exploration of strategies for algorithm improvement, offering new insights and methodologies for future related research. Furthermore, through the application case of UAV path planning, the potential of INGO in practical engineering problems is showcased, further demonstrating its value as an effective tool for engineering design and global optimization. Following is a summary of the paper’s main contributions:

(1)   This study synthesizes the high convergence accuracy of physics-based algorithms and the rapid convergence speed of swarm intelligence algorithms by incorporating the STA into the optimization process of NGO, thereby proposing a novel algorithm with superior performance, denoted as INGO.

(2)   In the initialization phase, INGO utilizes Tent chaotic mapping to seed the population, thereby augmenting population diversity and boosting the chances of circumventing local optima in pursuit of superior solutions.

(3)   The integration of the BWO’s whale fall strategy and the T-distribution variation strategy as mutation strategies significantly augments the global search capability of NGO.

(4)   The incorporation of the STA facilitates sampling and comparison within the vicinity of the optimal solution in each iteration of the NGO, thereby enhancing the precision of solution convergence.

(5)   The performance of INGO was tested and evaluated using 53 benchmark functions and a path planning scenario of UAV.

The structure of this paper is as follows: Section 2 delineates the foundational principles and models of NGO. Section 3 outlines the development of the INGO algorithm. Section 4 reports on the evaluation of the algorithm’s efficacy through testing on 53 benchmark functions. Section 5 elaborates on the deployment of this algorithm in UAV path planning and shares the outcomes. Section 6 offers a concluding summary of the paper.

2  Northern Goshawk Optimization (NGO)

Inspired by the predatory behavior of the northern goshawk, NGO takes each northern goshawk as an individual of a population and abstracts the predatory behavior into two stages. The first stage is to explore and attack prey, which reflects the group behavior by identifying the position of the current best solution and influencing each individual to update their position through the optimal solution, representing the global exploration ability. The second stage is the escape behavior of prey, symbolizing the local exploitation ability.

2.1 Initialization of the Algorithm

NGO considers each northern goshawk as an individual of a population, that is, a viable solution, and searches for the best value in the viable solution space by moving. Like most swarm intelligence algorithms, NGO generates initial populations by randomly generating initial populations. In the mathematical model, each individual represents a D-dimensional vector, N individuals constitute the entire population, and the population is an N × D matrix. The mathematical model of the population is given by formula (1):

X=[X1⋮Xi⋮XN]N×M=[x1,1⋯x1,j⋯x1,M⋮⋱⋮⋱⋮xi,1⋯xi,j⋯xi,M⋮⋱⋮⋱⋮xi,1⋯xi,j⋯xi,M]N×M(1)

Here, the population N and individual’s position are represented by X and Xi, respectively, Xi,j denotes the value on the jth dimension and M are the number of individuals and the largest dimension. The objective function is represented by the fitness function.

2.2 Prey Identification and Attack

The search and attack of prey is the first stage of the NGO in each iteration, which simulates the optimal solution as prey and each individual launches the attack it. In this stage, every individual identifies the location of the current best solution and updates their position based on this optimal solution. The main purpose is to enable the northern goshawk individual to search the feasible solution space more widely. Thus, global search is carried out. Formulas (2)–(4) represent the mathematical model for the initial phase.

Pi=XZ(2)

xi,jnew1={xi,j+r(pi,j−I∗xi,j),Fpi<Fixi,j+r(xi,j−pi,j),Fpi≥Fi(3)

Xi={xinew1,Finew1<FiXi,Finew1≥Fi(4)

where i=1,2,⋯,N, the value of I can be 1 or 2 and r=rand(0,1).. Pi is a candidate solution. FPi is its objective function value. xinew1 is the new position of the first stage, xi,jnew1 is its jth dimension. Finew1 represents objective function value of the first stage.

2.3 Chase and Escape Operation

The second stage is the chase and escape of prey, and the local exploitation is carried out by simulating the local activities of prey to affect the individual position of the northern goshawk. The position updating formula of the second stage is shown in formulas (5)–(6):

xi,jnew2=xi,j+R(2r−1)xi,j(5)

Xi={xinew2,Finew2<FiXi,Finew2≥FiZ=1,2,⋯I,⋯N(6)

where xinew2 is the new position of the second stage and xi,jnew2 is its value in jth dimension. Finew2 represents objective function value of the second stage. R is the hunting radius. The expression of R is shown in formula (7):

R=0.02(1−tT)(7)

where t denotes the iteration number, and T signifies the maximum iteration number. R will diminish as the iteration count increases, indicating that the hunting radius of the NGO contracts in the later stages of iteration, thereby enhancing the algorithm’s local exploitation capability. This mechanism is pivotal to NGO achieving superior optimization accuracy compared to many other.

Each iteration within the NGO process encompasses these two phases. The prevailing optimal solution serves as a beacon for other members to gravitate towards improved outcomes. Upon reaching the maximum iteration limit, the algorithm concludes. Fig. 1 illustrates the flowchart of the standard NGO.

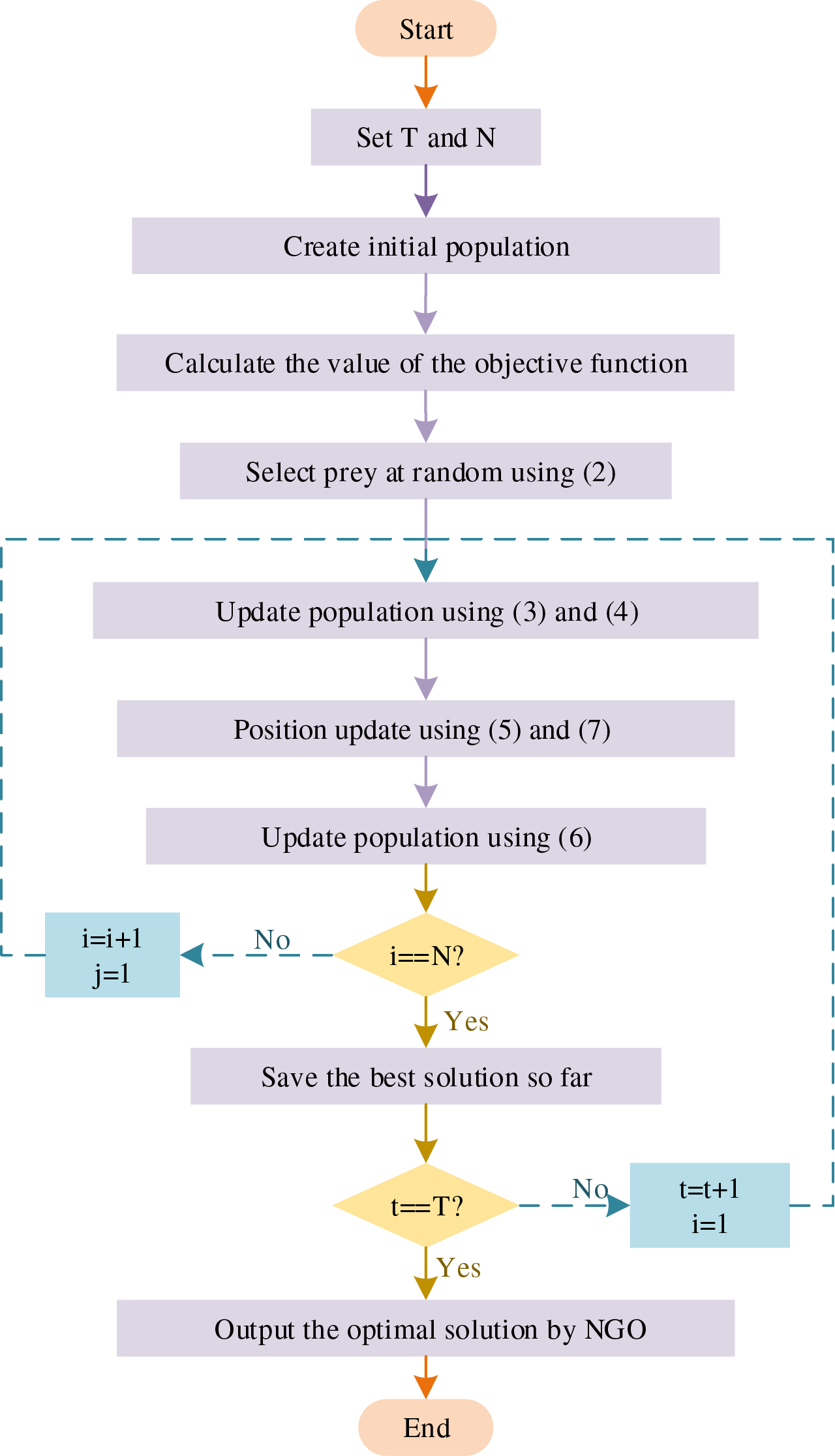
Figure 1: The flowchart of the northern Goshawk algorithm

3  The Proposed Algorithm: INGO

The essence of swarm intelligence algorithm lies in the algorithm’s capability to explore and exploit. The improvement of the so-called swarm intelligence algorithm is to help algorithms to strike a balance between the exploration and exploitation. This facilitates the algorithm’s capacity to not only broadly search the feasible solution space but also to refine its approach in achieving a closer approximation to the optimal solution with greater accuracy. Based on previous research, this section presents four effective improvement strategies for function optimization of NGO. By combining all four strategies, the NGO is strengthened in terms of its ability to explore and exploit.

3.1 Tent Chaotic Mapping

Given the lack of prior knowledge about the global optimal solution for the optimization problem, it is advisable to distribute the population evenly throughout the search space. However, the randomly generated initial population is frequently distributed unevenly, thereby impacting the diversity of the population. Although the intelligent algorithm is insensitive to the initialization method and there are no notable disparities among the methods of population initialization after enough iterations [40], using a more uniform initialization technique will improve the algorithm’s exploration ability during the early iteration.

Chaotic sequence is used to generate initial population instead of randomly generated initial population in this paper. Tent mapping is widely used in the initial improvement of swarm intelligent algorithm due to its ability to generate more uniform chaotic sequence [41]. The iterative formula of tent mapping operator adopted is shown as formula (8):

Xt+1={2Xt,Xt∈[0,0.5]2(1−Xt),Xt∈(0.5,1](8)

3.2 Whale Fall

The convergence speed of NGO is quick, which it also makes the local optimal value affecting the algorithm tremendously in the early stage, resulting in the low global search ability of it. In the first stage of NGO search, there is a phenomenon of rapid convergence, and it is quite probable to fall into local optimality. Therefore, improving the global exploratory ability is of great significance to improve NGO performance.

Targeted addition of some strategies is often an effective technique to improve the global exploratory capability of the algorithm. Whale fall refers to the phenomenon wherein a whale dies and its body descends to the bottom of the ocean and it is one of the main reasons life in the deep ocean flourishes. The whale fall phenomenon was introduced into the beluga optimization algorithm. The BWO gives a model of the falling behavior of the whale after death in each iteration. An updated position is established by using the beluga whale’s position and the length of its fall, along with a tiny probability.

Taking into account NGO’s inclination to get stuck in local optimum, this paper incorporated the whale fall phenomenon into the first stage search of it, representing the behavior of the northern goshawk, which has a very small probability of falling or was affected by other random individuals for other reasons after the large-scale exploration behind the first stage search, assists the algorithm in increasing its chances of breaking free from local optimal values. Formula (9) expresses the mathematical model of the whale fall.

Xi(t+1)=r1Xi(t)−r2XR(t)+r3Xstep(9)

where r1,r2,r3∈(0,1) are random numbers, XR is random individuals, and the mathematical expression of Xstep is illustrated in formula (10):

Xstep=(ub−lb)e(−ct/T)(10)

{C=2WfNWf=0.1−t20T(11)

In the process of each iteration of the NGO, the whale landing operation is carried out after the completion of the prey discovery and attack stage, which can better conduct a global search, so that the algorithm approaches the global optimal solution with a greater probability.

3.3 T-Distribution Variation

Variation is the most common strategy used for swarm intelligence algorithms to fall into local optimality. Cauchy variation and Gaussian variation are common. According to the characteristics of the NGO, this paper adopts T-distribution mutation strategy [42] to improve its weaknesses. The algorithm’s iteration count serves as the degree of freedom for the T-distribution. Following each individual’s completion of the initial two search stages, a variation operation is performed on the optimal solution. The fitness value of the optimal solution before and after variation is compared to re-evaluate the optimal solution and retain it. The variation formula is shown in formula (12):

Xi(new)=(T+1)Xi(12)

Here, T is a T-distribution. The mathematical formula for the T-distribution is shown in formula (13):

fz(x)=Γ(t+12)nπΓ(t2)(1+x2t)−t+12(13)

Here, t is the number of iterations.

During the initial phase of iteration, the T-distribution resembles the Cauchy distribution, mitigating the impact of local extremities. This alteration increases the likelihood of the algorithm breaking free from local optima, thereby boosting its global exploratory capabilities. In the subsequent phases, the T-distribution approaches the characteristics of a Gaussian distribution, facilitating improved local exploitation and enhanced convergence precision for the algorithm, while simultaneously quickening the rate of convergence.

3.4 Added the State Transition Algorithm (STA)

Algorithm fusion is the trend of swarm intelligence algorithm improvement recently. The main purpose is to combine the advantages of various algorithms so that new algorithms have stronger exploration and exploitation ability. STA is a competitive intelligent algorithm proposed by Zhou in 2012. It uses the state space expression as the framework to design four transformation operators, considering the process of the feasible solution iteration as a process of state transition. Based on the current optimal solution, some state transition operator is run, and the candidate solution set is generated by generating neighborhood and sampling in the neighborhood, and then compared with the current best solution, a new optimal solution is obtained.

STA utilizes the state space expression as a framework to simulate the iterative updating process of the solution, as shown in formula (14):

xt+1=Atxt+Btutyt+1=f(xt+1)(14)

Here, xt=[x1,x2,⋯xi,⋯,xn]T represents a candidate solution, At and Bt are state transition matrices, which can be random matrices, ut is the state function. f(xt) is the objective function.

The expression of the rotation transformation operator is shown in formula (15):

xt+1=xt+α1n‖xt‖2Rrxt(15)

Here, Rr∈Rn×n is the random matrix uniformly distributed between [−1,1]. ‖⋅‖2 is the norm. α>0 is the rotation factor.

The expression of translation transformation operator is shown in formula (16):

xt+1=xt+βRtxt−xt−1‖xt−xt−1‖2(16)

Here, Rr∈R is the random number uniformly distributed between [0,1]. β>0 is the translation factor.

The expression of expansion transformation operator is shown in formula (17):

xt+1=xt+γRext(17)

Here, Re∈Rn×n is the value of non-zero element following the random diagonal matrix of Gaussian distribution. γ>0 is the expanding factor.

The expression of axesion transformation operator is shown in formula (18):

xt+1=xt+δRaxt(18)

Here, Ra∈Rn×n is the value of non-zero element, which follows the sparse random diagonal matrix of Gaussian distribution. δ>0 is the axial factor. The axesion transformation operator improves the ability to search in a certain dimension.

For the existing optimal solution, a neighborhood is constructed through a candidate solution set generated by a specific transformation operator. Sampling within this neighborhood is executed via a defined sampling method, from which the superior solution is identified. Subsequently, optimal solutions undergo updates through greedy mechanisms; namely, comparing the derived solutions with the current optimal and selecting the most advantageous one. The greedy mechanism is shown in formula (19):

xt={xtnew,if f(xtnew)<f(xt)xt,other(19)

Aimed at the characteristics of NGO, which has high search speed but low search accuracy, STA is introduced into NGO to enhance its convergence accuracy, so that it could get better optimization results when solving function optimization problems. STA possesses strong local exploitation capability and is capable of thoroughly exploring the surrounding space of the current optimal solution. Upon discovering the best outcome during each NGO iteration, STA employs its four transformation operators to explore the vicinity of the optimal solution, thereby guaranteeing enhanced local exploitation of the algorithm.

3.5 The Pseudo-Code and Flowchart of INGO

Algorithm 1 outlines INGO’s pseudo-code. At line 3, the Tent chaotic map initializes the population. Line 11 updates positions through the whale fall strategy, and line 18 applies the T-distribution for variations. STA’s utilization for neighborhood searches of the optimal solution is marked at line 20.

Fig. 2 displays the flowchart of INGO. Upon setting the algorithm’s maximum iterations T and population size N, execution commences. Initially, population generation via Tent chaotic mapping, individual fitness evaluation, and sorting to identify the optimum position sets the stage. Subsequent phases leverage prey identification and the attack strategy for positional updates and the whale-fall technique to enhance escape from local optima. The NGO’s chase and escape mechanism then refines accuracy, followed by a T-distribution variation to intensively explore the solution space. Conclusively, sampling near the optimum with the state transition algorithm identifies a superior solution, ensuring progression to the next iteration once neighborhood superiority is confirmed. The algorithm concludes once it fulfills the stopping criteria.

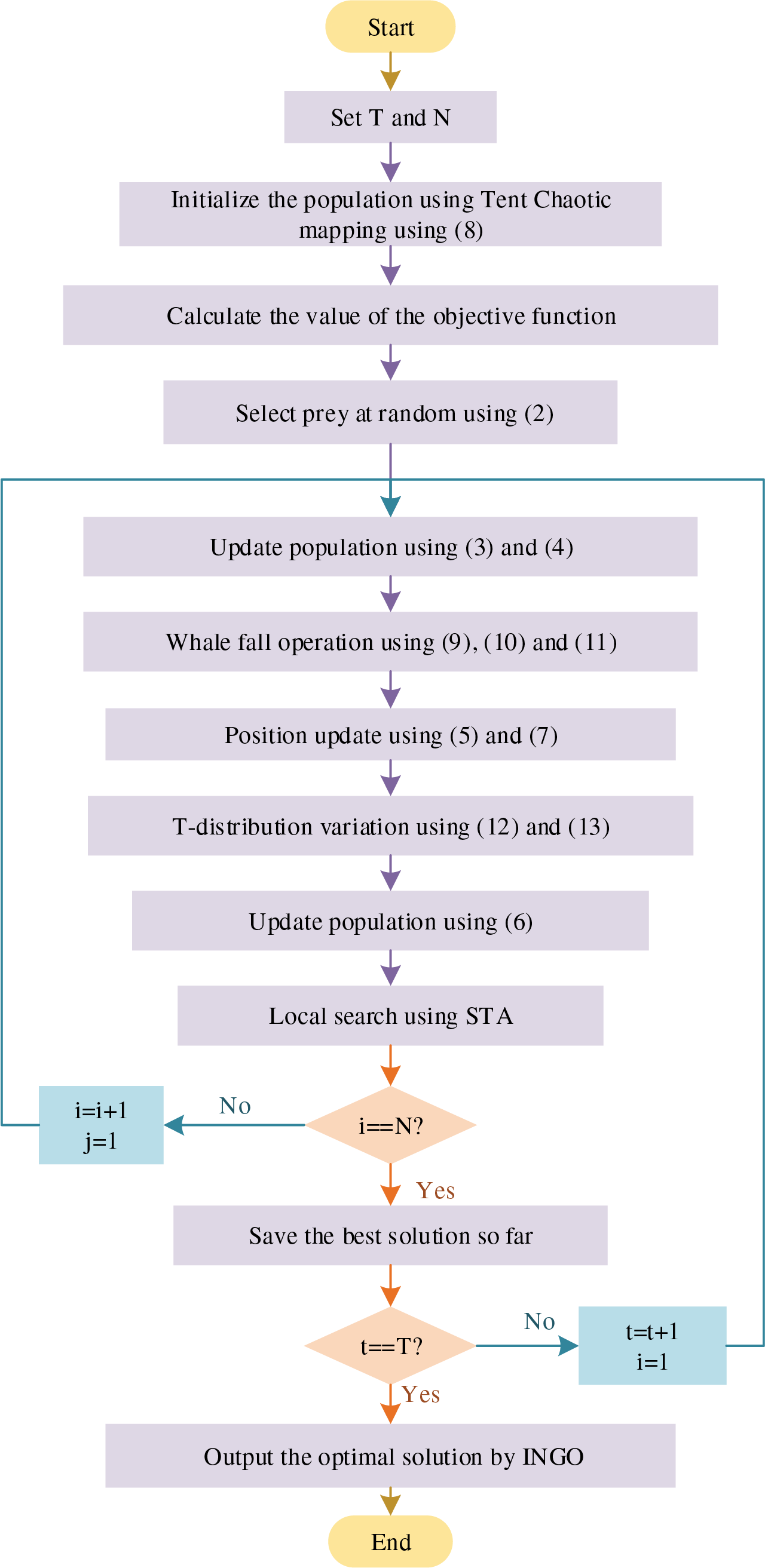
Figure 2: Flowchart of the INGO

4  Experimental Results

4.1 Experimental Setup

This section mainly analyzes the performance of INGO. Firstly, the effectiveness of the strategy is analyzed by gradually adding the strategy, secondly, the scalability of the algorithm is verified by testing on different dimensions, and finally, the algorithm is compared with other algorithms on 23 benchmark functions [43] and CEC2017 test set [44]. The algorithms involved in the comparison of these 53 benchmark functions are: AO, Hunter–prey Optimization (HPO) [45], Sand Cat Swarm Optimization (SCSO) [46], HHO, WOA, GWO, SCA, DA, Salp Swarm Algorithm (SSA) [47], BWO and an Improved Northern Goshawk Optimization (INGOfu) [48]. These algorithms can be categorized into four types: Classical swarm intelligence algorithms that are widely applied (GWO, WOA, DA, SSA), which have garnered significant attention from researchers; physics-based algorithms (SCA), with SCA often being utilized in conjunction with other swarm intelligence algorithms; recently developed competitive swarm intelligence algorithms (AO, HPO, SCSO, HHO), which, when compared with newer algorithms, can better highlight the performance of INGO; and the improved NGO algorithm (INGOfu). The diversity of the types of algorithms involved in the comparison provides a better and more comprehensive assessment of INGO’s performance. The population of all algorithms is 50, with a maximum iteration count of 1000 and a dimension of 30. The information and parameters of the algorithms used in this paper are given in Table 1. Run the algorithm independently for 30 times and compare the mean value and standard deviation. All algorithm tests were carried out on Windows 10(64-bit), Intel(R) Core(TM) i7-11800H, CPU@2.30 GHz, RAM:16 G MATLAB 2021b.

4.2 The Impact of Optimization Strategies on Algorithm

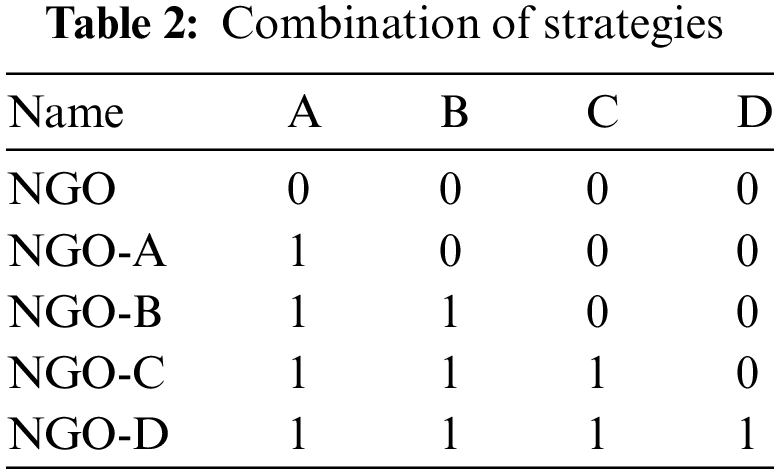
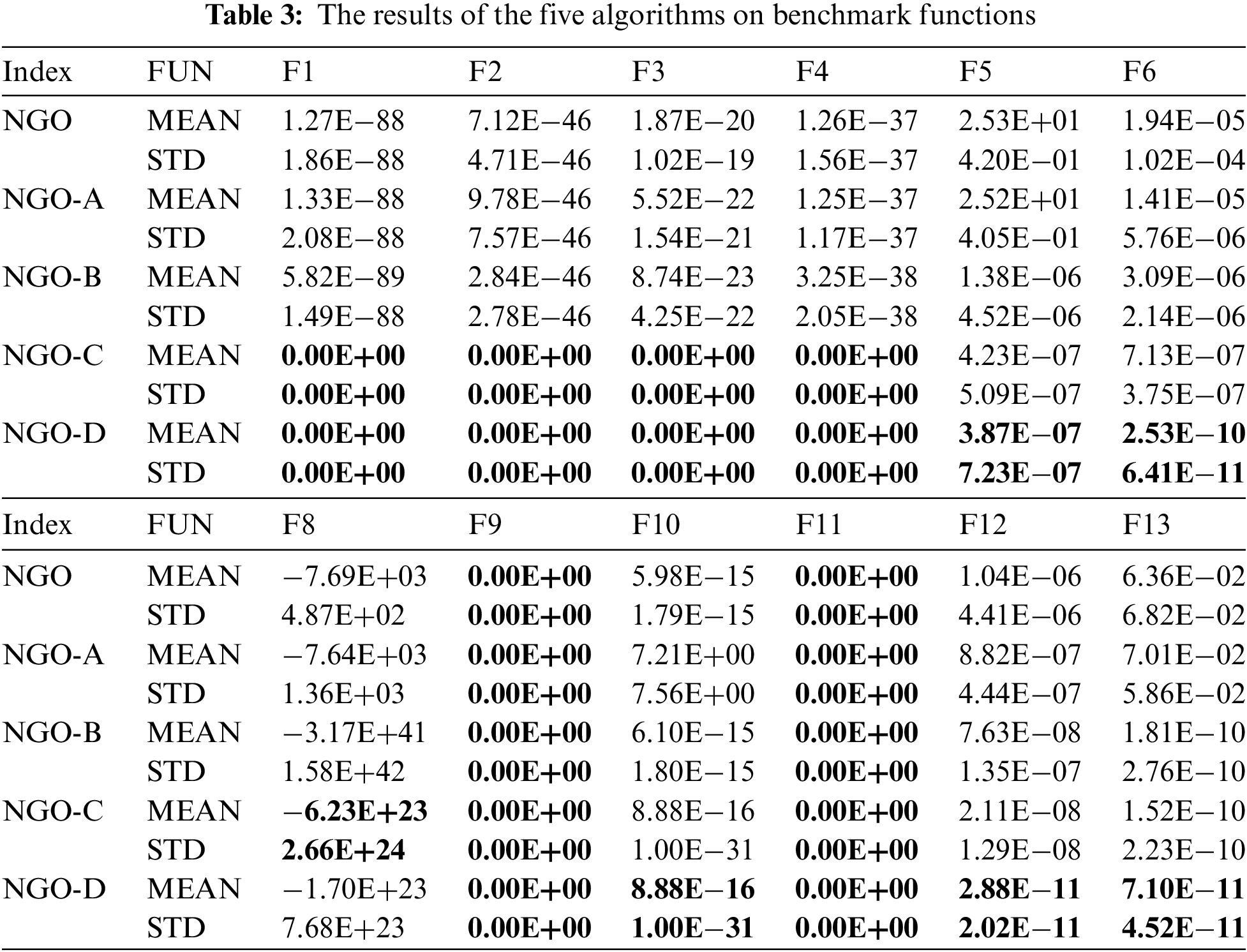
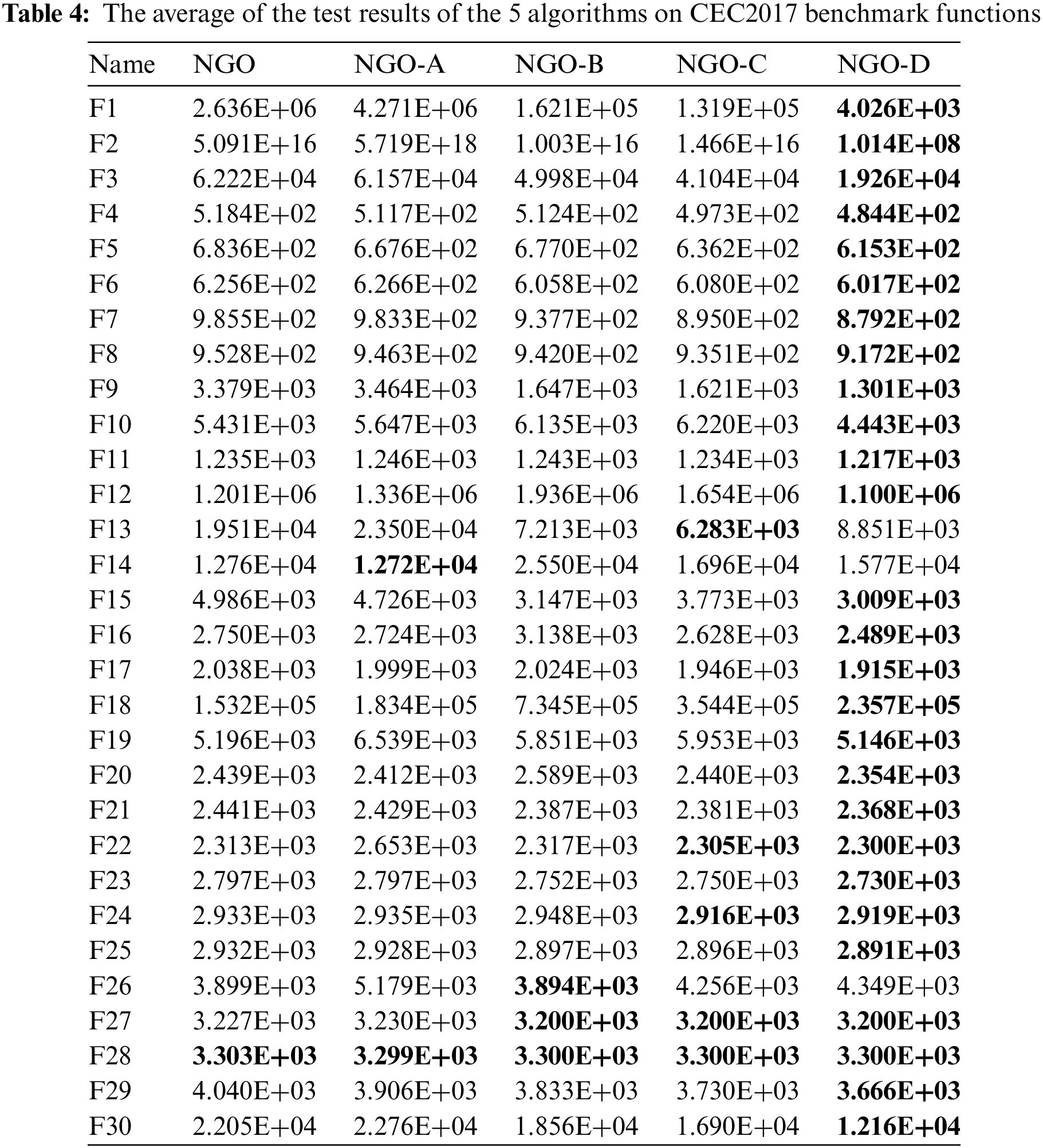
A set of experiments is set up in this section to analyze the effect of the four strategies introduced in INGO algorithm on the algorithm. Four strategies are added to NGO successively, and different combinations are shown in Table 2, where A represents tent chaotic mapping strategy, B represents whale fall strategy, C represents T-distribution variation strategy, D represents neighborhood search strategy, 1 represents these strategies are added to the NGO algorithm, and four new algorithms are obtained: NGO-A, NGO-B, NGO-C and NGO-D. NGO-D is equivalent to our proposed INGO algorithm. At the same time, NGO and these four algorithms were compared and tested on part of the benchmark functions. Table 3 shows the average and standard deviation test results of the 12 functions F1–F6 and F8–F13 out of 23 benchmark functions of 5 different algorithms. It is worth mentioning that, all the five algorithms F14–F23 have obtained the optimal values. Table 4 displays the performance outcomes of five algorithms across 30 functions within the CEC2017 test suite, with the reported results reflecting the mean of 30 independent trials. The data reveal a progressive improvement in algorithmic performance correlating with the incremental integration of strategies, thereby validating the efficacy of the four strategies. This enhancement signifies their collective capability to augment the algorithm’s search efficiency.

4.3 The Impact of Problem Dimensions

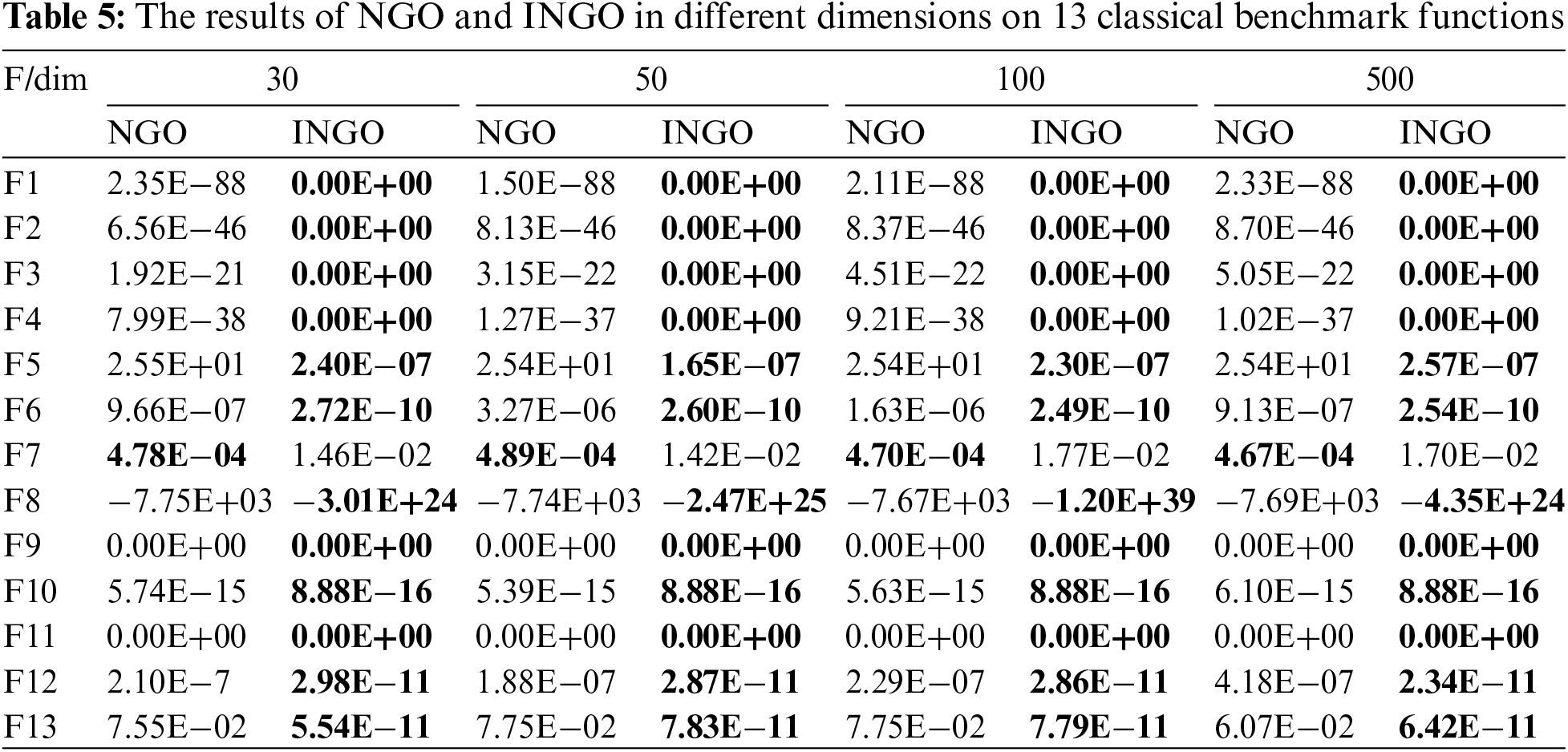
The dimensionality of optimization problems exerts a discernible influence on the operational efficiency of algorithms. The intricacy of high-dimensional optimization problems serves as a more effective measure for assessing an algorithm’s performance. In this section, the first 13 functions of 23 benchmark functions (F1–F13) are used to conduct dimensional tests on INGO. The performance of NGO and INGO was tested on four dimensions: 30, 50, 100 and 500. Table 5 shows the test results. The results show that the performance of both algorithms deteriorates with the increase of dimension, while INGO is less affected and can still find better solutions except for function F7, which proves that after the improvement of four strategies, INGO still has a strong development and exploration ability even when dealing with high-dimensional problems.

4.4 Comparison with Other Algorithms on 23 Classical Benchmark Functions

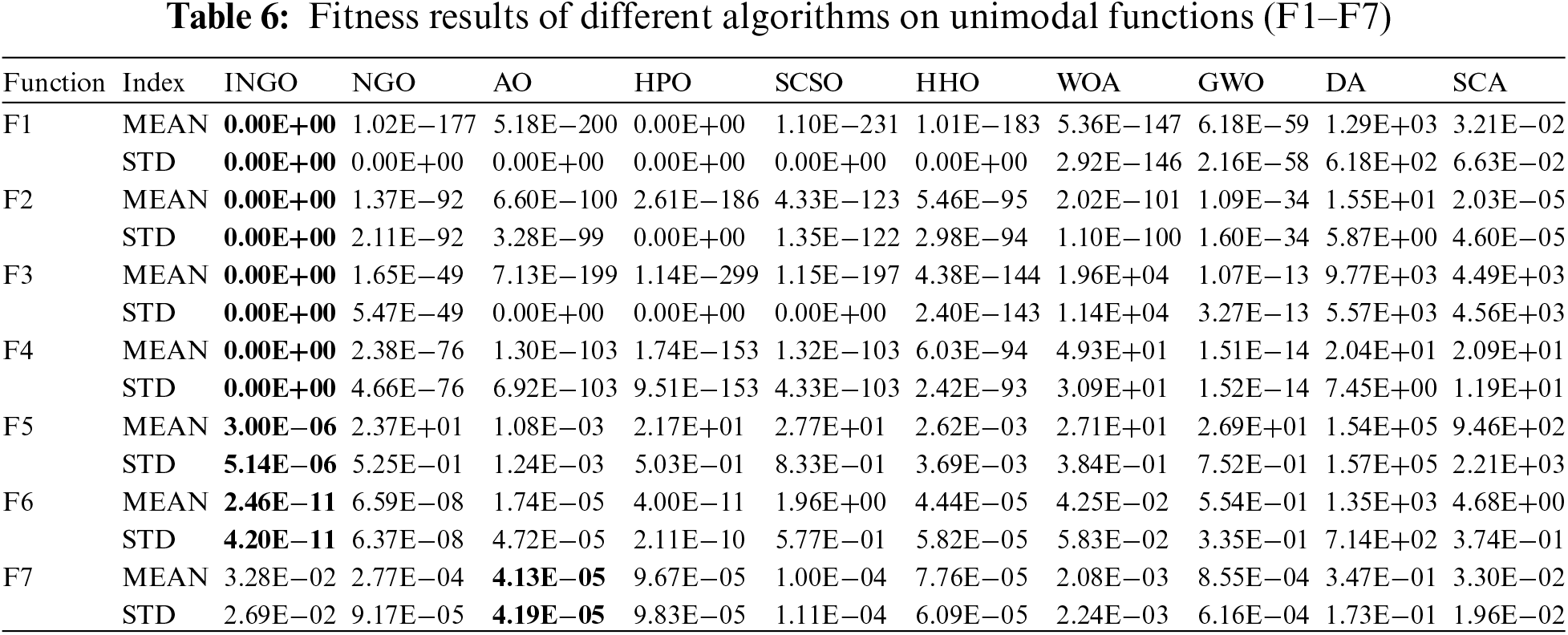
INGO’s function optimization performance is tested using 23 classic benchmark functions. There are 7 single-peak functions (F1–F7), 6 multi-peak functions (F8–F13) and 10 fixed-dimension multi-peak test functions (F14–F23). The algorithm’s exploitation ability is verified using unimodal functions. Multimodal function is used to reveal the algorithm’s exploration ability. INGO is compared with the NGO, AO, HPO, SCSO, HHO, WOA, GWO, SCA and DA.

Table 6 presents the test results for functions F1–F7, encompassing both mean and standard deviation values. In a comparative analysis involving the initial seven benchmark functions against nine alternative algorithms, INGO consistently achieved the theoretical optimal value of zero across the first four functions and secured the leading position for functions F5 and F6, culminating in a composite ranking of first place. This underscores INGO’s superior exploratory capabilities over the existing NGO algorithm, alongside enhanced local convergence precision, attributed to the refined integration of the STA strategy that bolsters INGO’s local exploratory proficiency. Notably, INGO’s performance was subpar on function F7, a function whose complexity escalates linearly with dimensionality and emulates noise encountered in real-world scenarios. This underperformance on such problems indicates a deficiency in INGO’s learning capacity during the optimization process, marked by an inability to make dynamic adjustments during the search. Future enhancements of the algorithm could consider the incorporation of dynamic parameter adjustments to facilitate adaptive modifications, thereby augmenting its optimization efficacy.

The test results for the multimodal functions F8–F13 are displayed in Table 7. Across these six multimodal functions, INGO consistently ranks first in comprehensive comparisons with other algorithms, indicating its superior exploratory capabilities and broader search scope within the feasible solution space. This is attributed to the enhanced global search ability of the algorithm, which is a result of the T-distribution mutation and the improved whale landing behavior strategies. Notably, INGO’s performance on F12 was slightly inferior to that of HPO, ranking second.

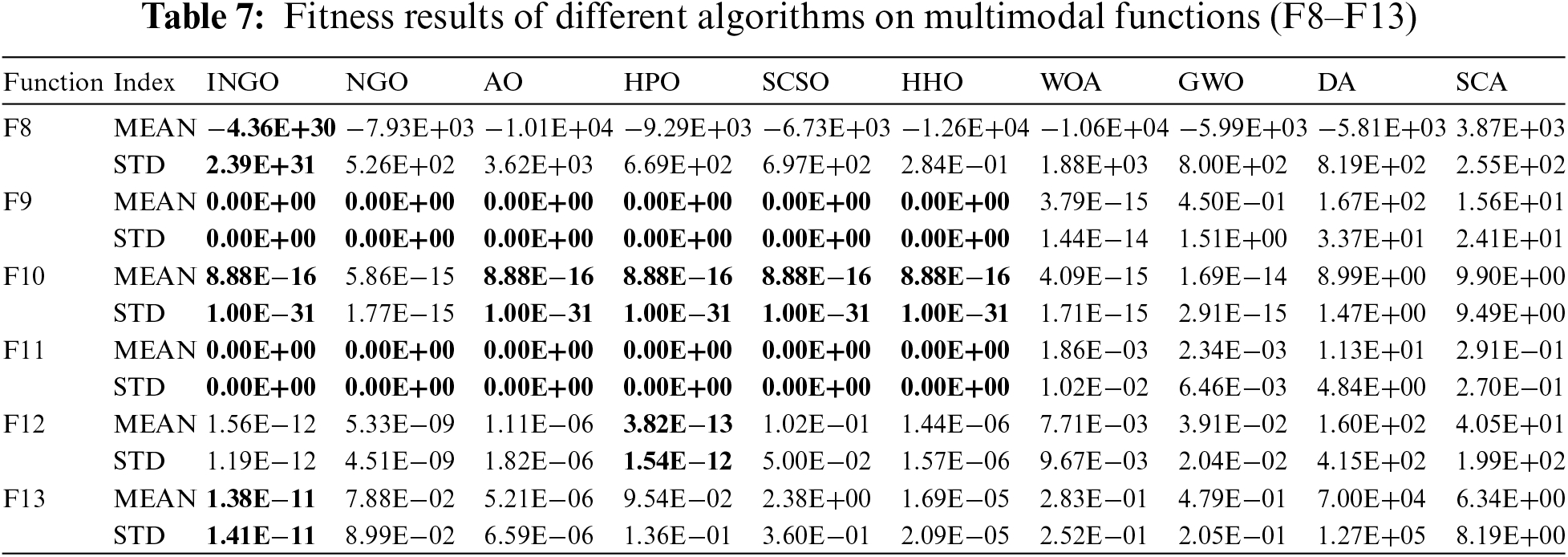
The experimental outcomes for functions F14–F23 are detailed in Table 8. The optimization results of INGO and NGO are infinitely close to the theoretical optimal values, demonstrating their superior optimization precision and stability over other algorithms. Across these ten functions, INGO consistently ranked first, with both NGO and INGO achieving the theoretical optimal values on seven of the test functions. This underscores the unique advantage of these two algorithms in addressing the optimization problems of fixed-dimensional multimodal functions. Although the original NGO algorithm matched INGO in achieving the optimal mean values across the ten functions, INGO exhibited a lower standard deviation, indicating greater reliability. This aspect is one of the key factors in evaluating algorithm performance.

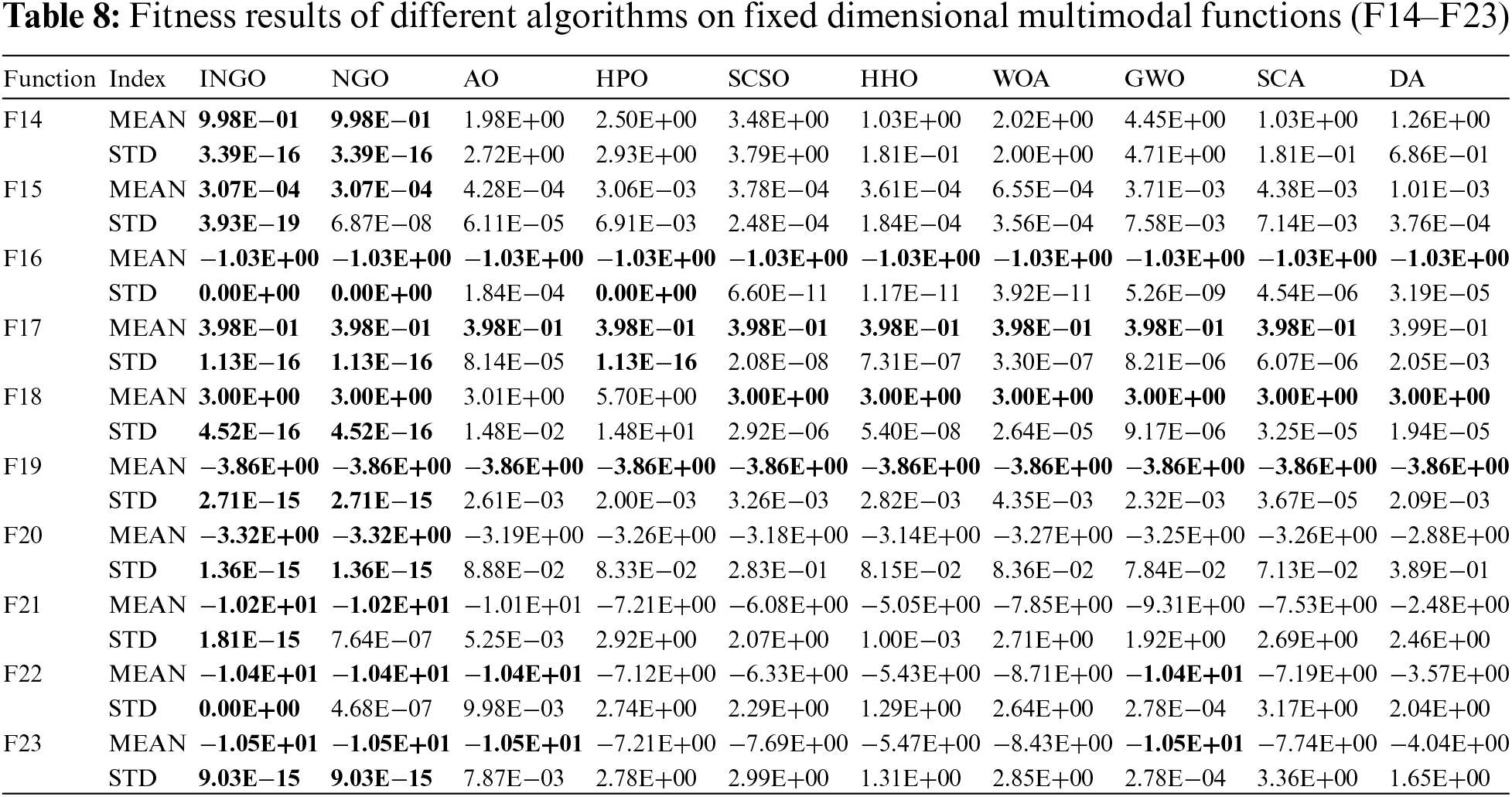
Convergence curves offer a more intuitive reflection of an algorithm’s optimization process. The partial convergence curves for unimodal and multimodal functions are depicted in Figs. 3 and 4, respectively. These figures reveal that, among the first thirteen test functions, INGO consistently provides more accurate solutions than its algorithmic counterparts. Furthermore, INGO exhibits a faster convergence rate on the majority of these functions, indicative of the positive impact derived from the integration of Tent chaotic mapping. This inclusion significantly enhances the diversity of the initial population, thereby broadening and equalizing the search across the feasible solution space in the early phases of iteration. Such observations underscore the efficacy of this strategy in augmenting the NGO algorithm.

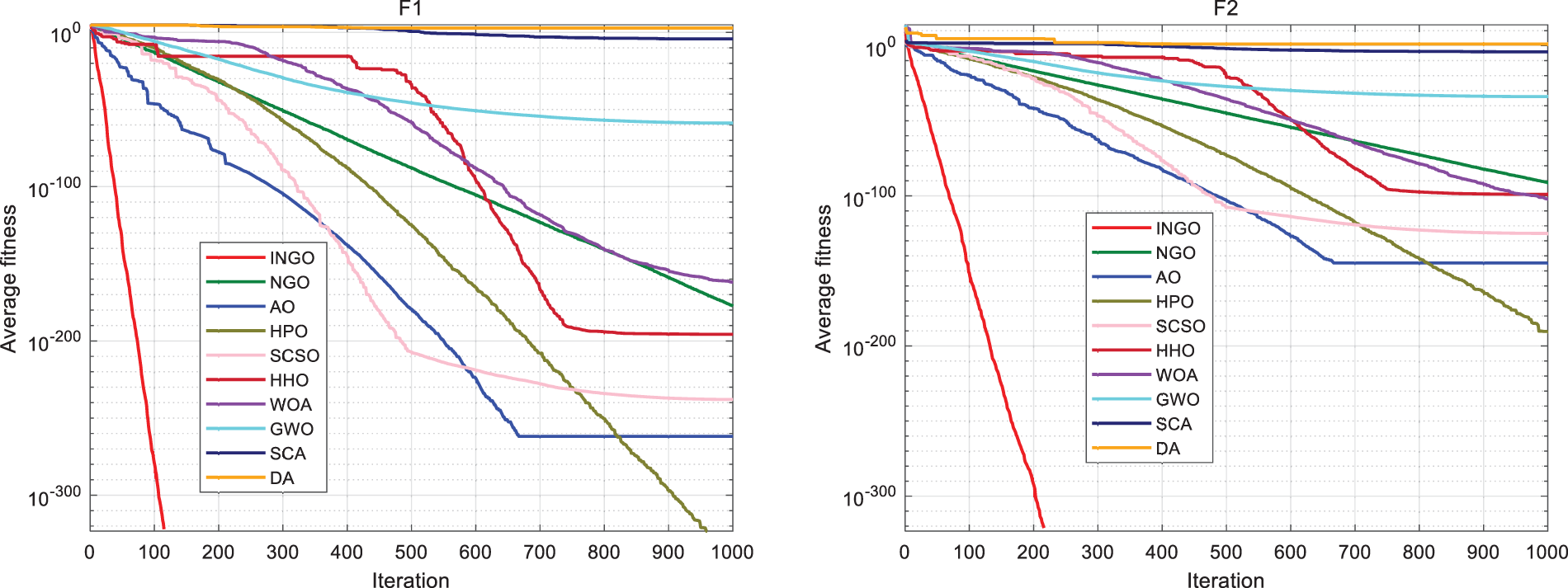
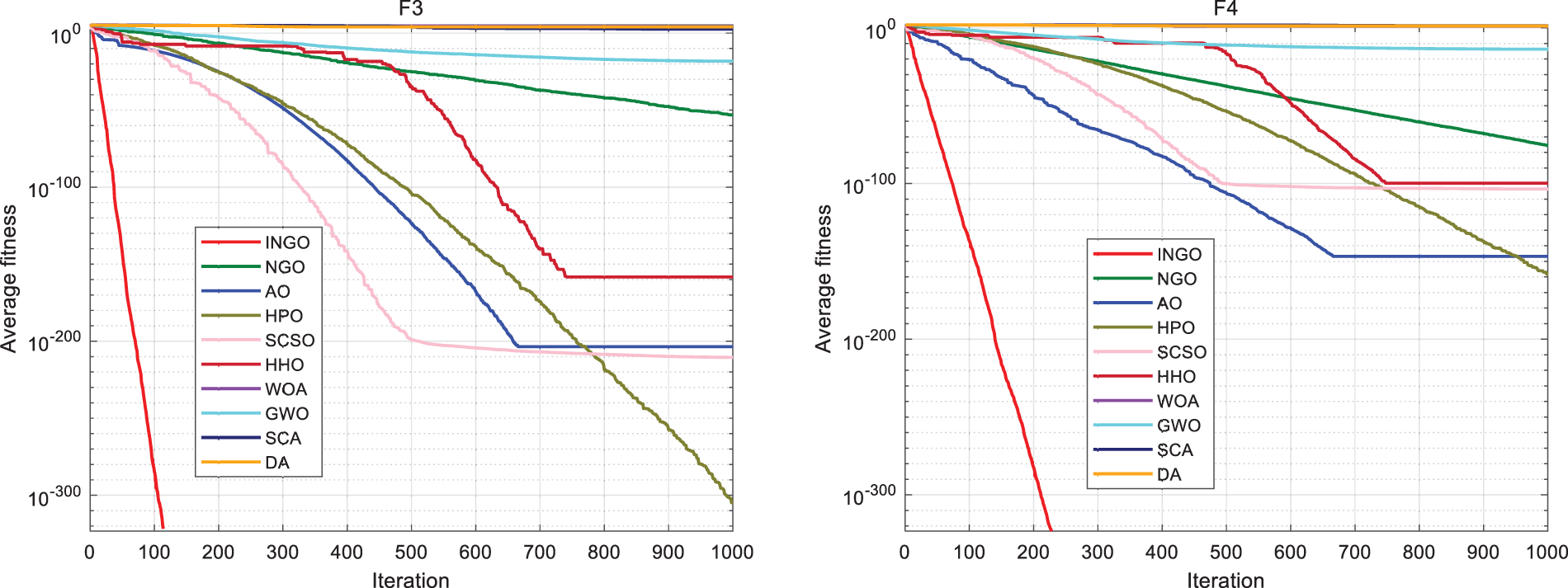
Figure 3: Iteration curve of unimodal function

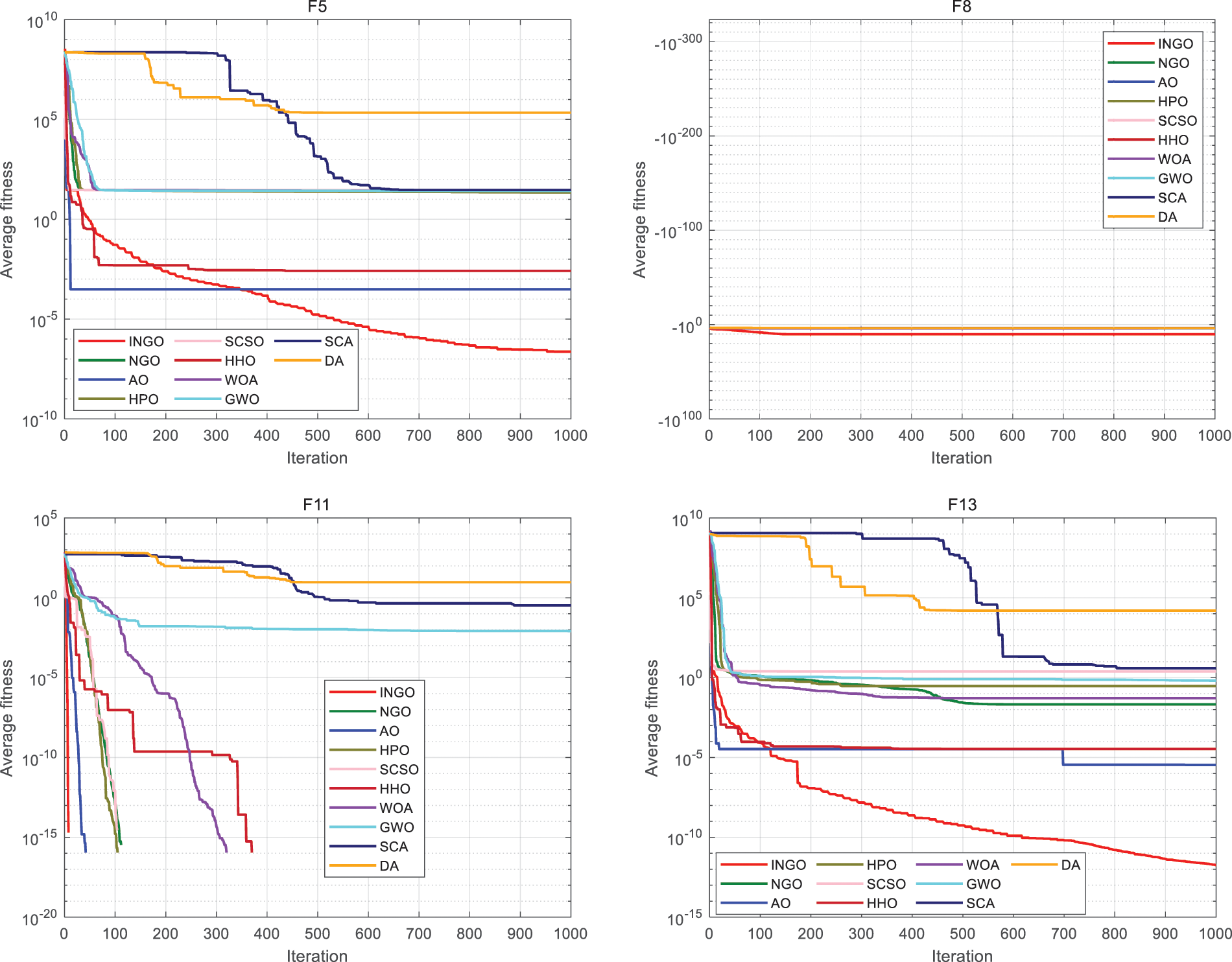
Figure 4: Iteration curve of multimodal function

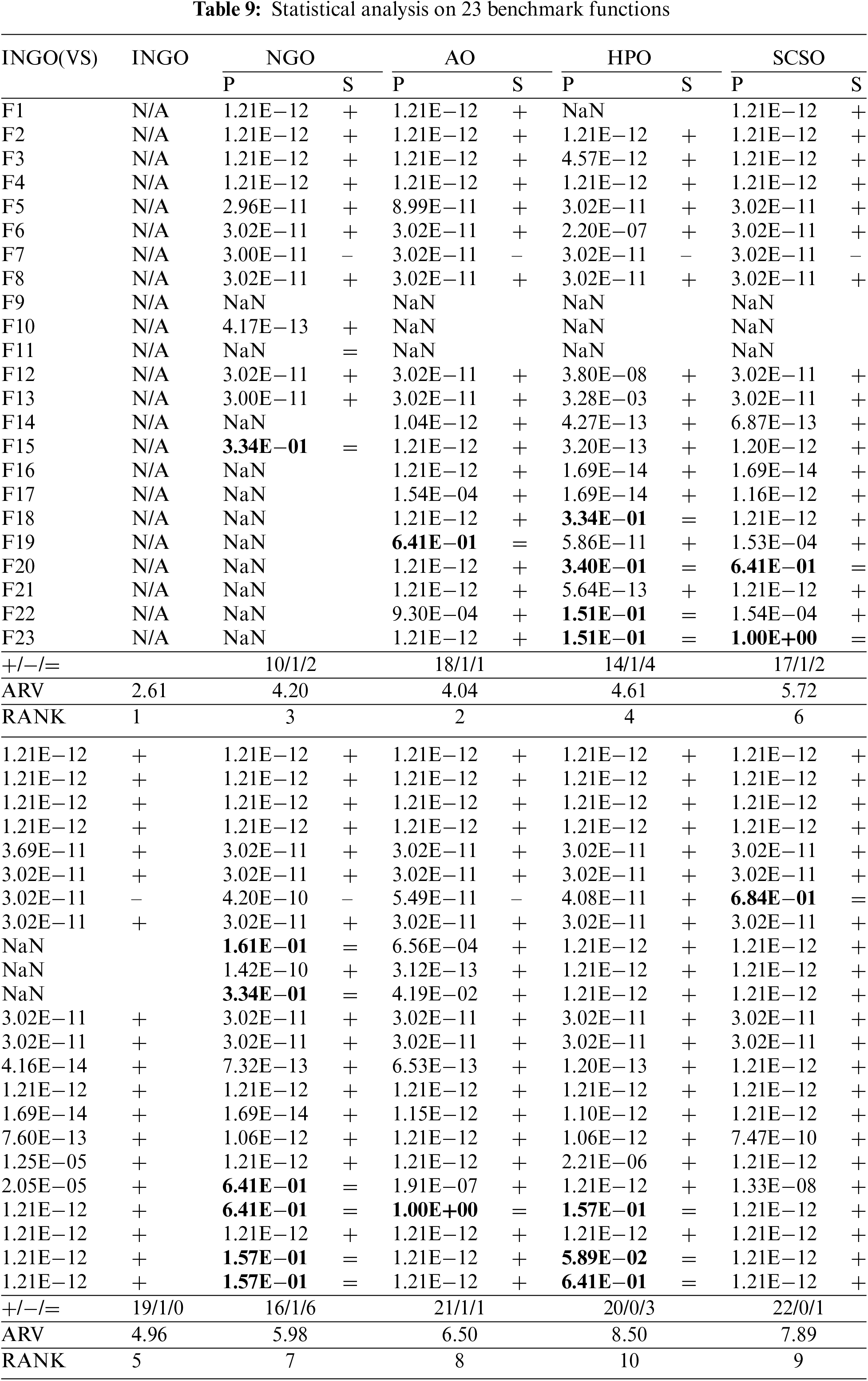
To mitigate the impact of randomness on the evaluation of algorithm performance, we employed two statistical tests: The Wilcoxon signed-rank sum and the Friedman tests. Table 9 displays the statistical analysis results for 23 benchmark functions. Within the context of the Wilcoxon rank-sum test at a significance level of 0.05, data points with p-values exceeding 0.05 have been highlighted, with an aggregate statistical analysis conducted. The notation “=” denotes no significant difference in performance between INGO and the comparison algorithms on the given problem; “+” signifies that INGO outperformed the comparison algorithms; “−” indicates that the comparison algorithms surpassed INGO; “NaN” suggests that both algorithms produced identical outcomes across all 30 independent runs, evidencing no performance variation for the specified function problem. Out of a total of 207 results, INGO achieved 157 instances of “+”, 7 of “−”, 20 of “=”, and 23 of “NaN”. Results from the Friedman tests demonstrate that INGO possessed the lowest Average Ranks (AVR) value of 2.61, thereby securing the top rank amongst ten algorithms in a comprehensive comparison.

4.5 Comparison with Other Algorithms on CEC2017 Benchmark Functions

INGO’s performance was tested and evaluated using the IEEE CEC2017 test set from the Conference on Evolutionary Computation 2017, which contains 30 test functions. CEC2017 has greater computational complexity than the common 23 reference functions and CEC2014. Moreover, the wide range of function types demonstrates that CEC2017 effectively assesses algorithm performance. In this test set, NGO, AO, HPO, SCSO, SSA, BWO, HHO, DA and INGOfu are compared. Table 10 records the results of 10 different algorithms in CEC2017. The result shows that INGO ranks the first overall on 30 test functions, while 28 functions of INGO rank the first among 10 algorithms. NGO’s original algorithm is narrowly ahead of INGO in only one function F26. The convergence curves of 10 different algorithms on the CEC2017 test set is shown by Fig. 5. It can be seen that INGO algorithm with four improved strategies has better exploration and exploitation ability, and stronger stability and robustness than other algorithms. Additionally, the performance on functions F26 and F28 did not achieve optimal results. Function F26, a high-dimensional nonlinear minimization problem, along with F28, which exhibits rotational characteristics, posed significant challenges. The suboptimal performance on these two functions indicates certain limitations within INGO’s search strategy, suggesting deficiencies in refining search operations and escaping local optima, or a lack of flexibility in adaptive adjustment of search strategies. This necessitates the enhancement of the algorithm’s adaptive adjustment capabilities, for instance, through the implementation of adaptive dynamic adjustment mechanisms to dynamically balance exploration and exploitation. Such improvements will guide future modifications to INGO.

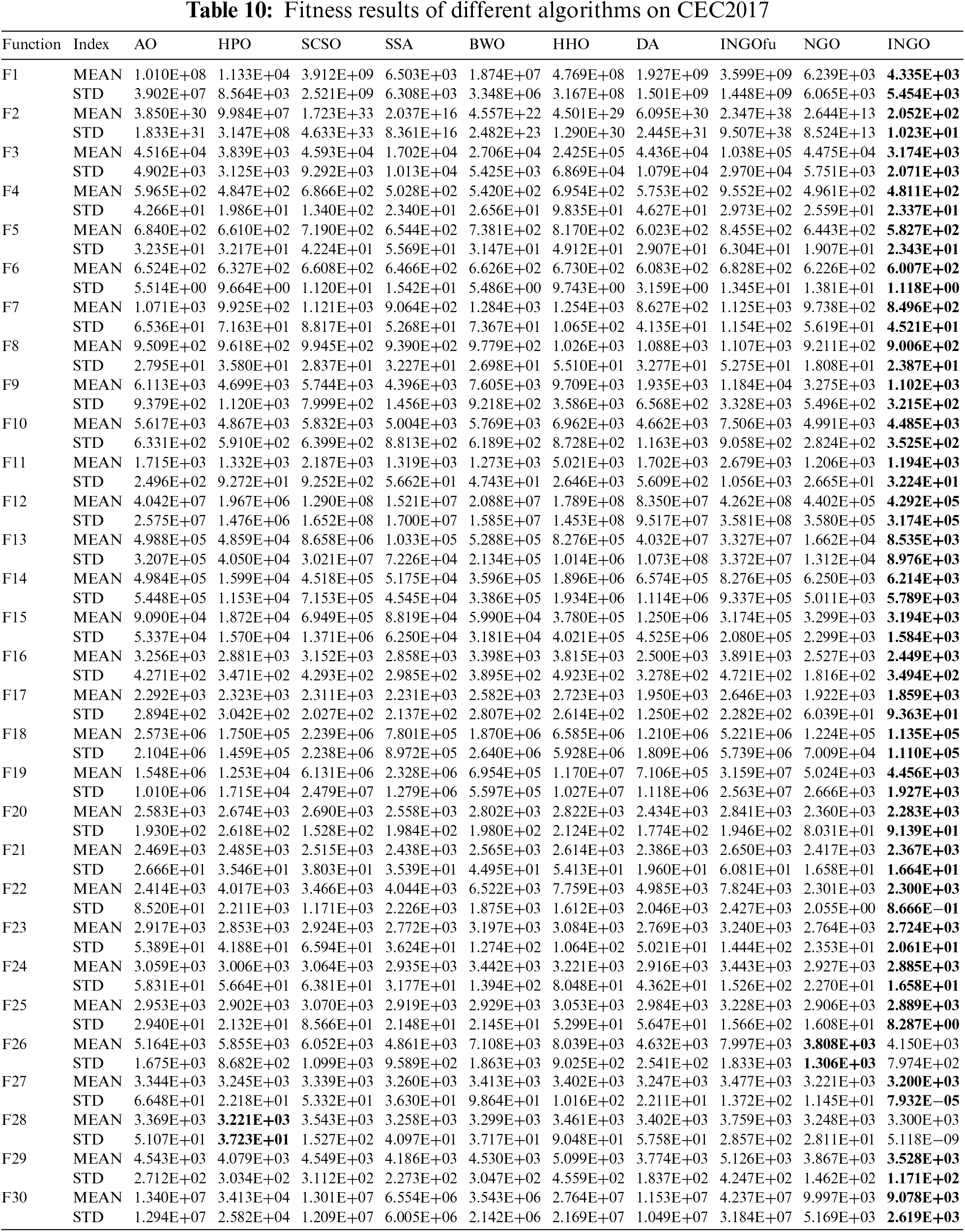
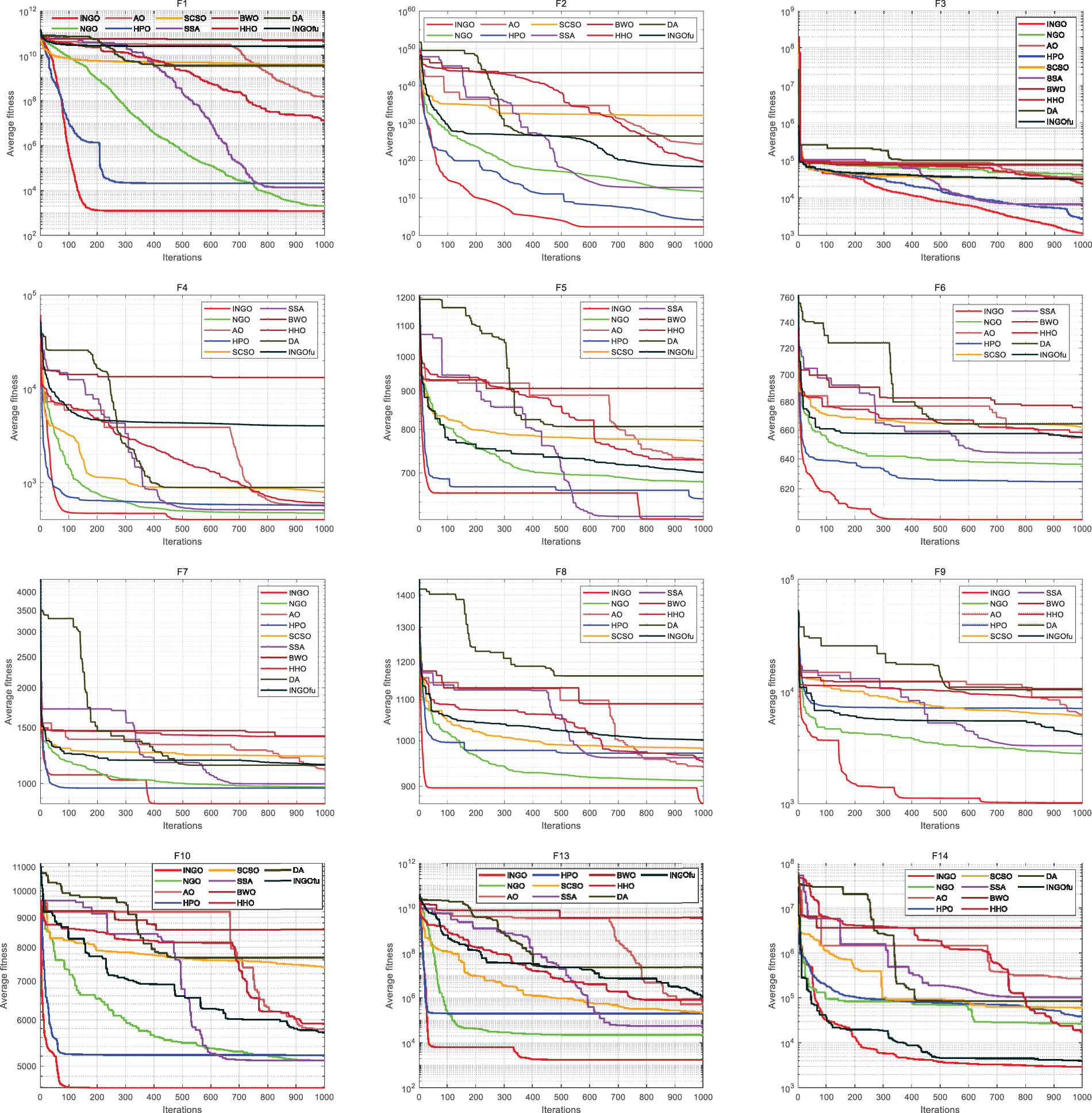
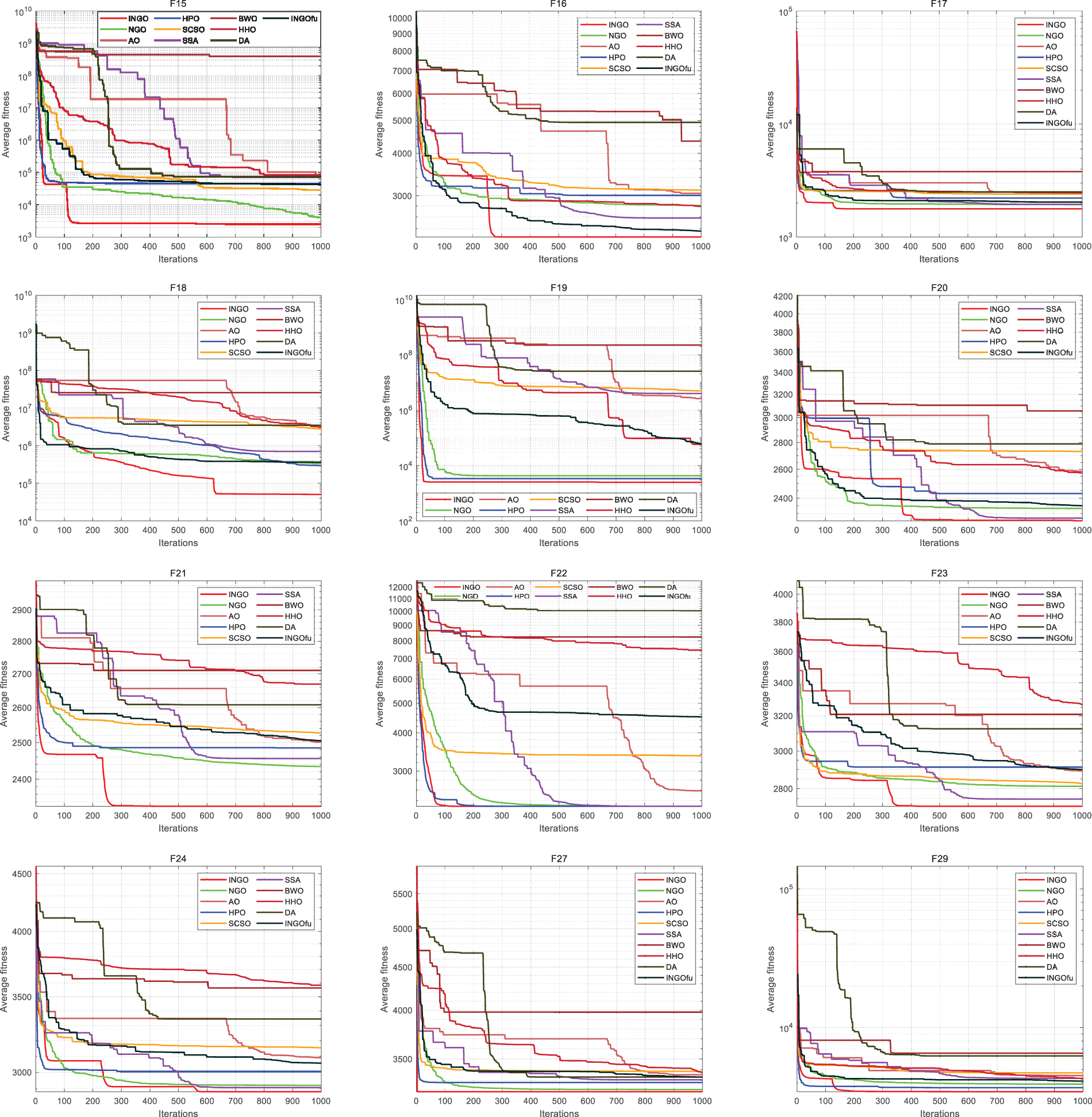
Figure 5: Iteration curve of CEC2017

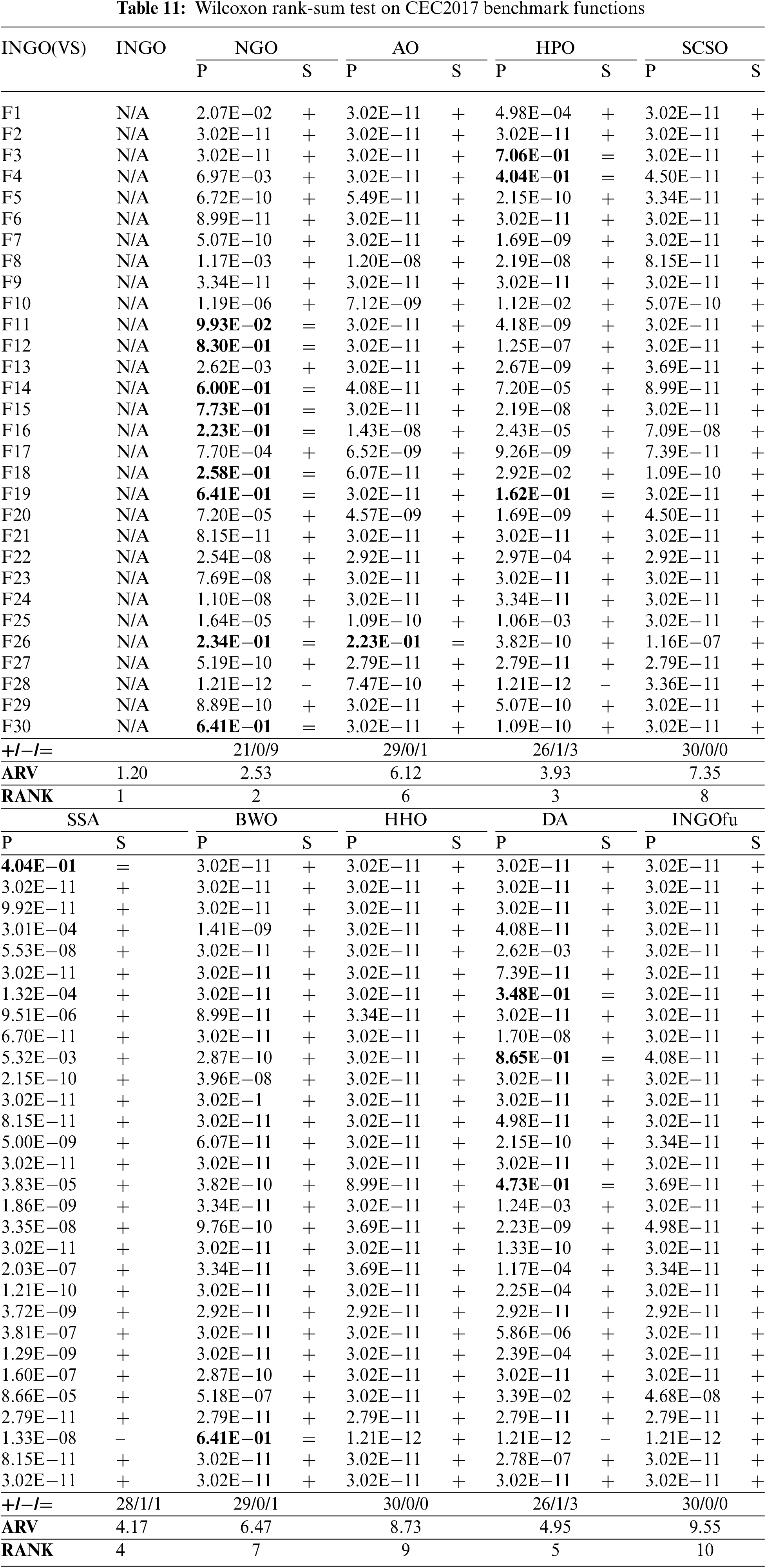
Table 11 presents the statistical analysis outcomes of ten distinct algorithms evaluated on the CEC2017 test suite. Out of a total of 270 results, INGO achieved 249 instances of “+”, 3 instances of “−”, and 18 instances of “=”, with the lowest AVR value of 1.20, securing the first position. This suggests that INGO has achieved more favorable optimization outcomes in comparison to the nine other algorithms evaluated.

5  Test of UAV Flight Path Planning Problem

5.1 The Introduction of the Problem

To verify INGO’s performance in solving real-world problems, the algorithm is tested on a UAV flight path planning problem. UAV path planning represents a constrained optimization challenge where Swarm Intelligence (SI) finds widespread application [49–53].

Constrained optimization problems are typically addressed using the penalty function approach and the multi-objective approach [54]. The penalty function method has been widely used because of its simple execution. Its main idea is to construct the penalty adaptation function by incorporating penalty terms into the objective function and then solve this new unconstrained optimization problem.

UAV path planning is actually a multi-constraint combinatorial optimization problem [55], and constraints are dealt with in the form of penalty function, as shown in formula (20):

F(x)=f(x)+γ∑i=1n⁡δik(x)⋅o(δi(x))o(δi(x))={1,δi(x)>00,δi(x)≤0(20)

Here, F(x) represents the objective function with penalty, f(x) represents the original objective function, γ is the penalty parameter of the constraint condition. In addition, k∈(1,2) and γ≫1 are the penalty parameters, δi(x) is the inequality constraint condition, n represents the number of inequality constraints.

To plan UAV flight path using Swarm Intelligent Optimization algorithm, the objective function should be determined first, and the total flight path evaluation function composed of the flight path length function, flight height function and angle cost function should be optimized. The total cost function is taken as the objective function of the algorithm. The indexes affecting UAV performance mainly include track length, flight altitude, minimum step length, corner cost, maximum climb angle, etc. [56]. Considering the three factors of track length, flight altitude and maximum turning angle, the total cost function is shown in formula (21):

{F(x)=w1f(L)+w2f(H)+w3f(Jturn)+⋯∑i=1nwi=1(21)

Here, F(x) is the total cost function, f(L) is the cost function of the trajectory length, f(H) is the cost function of the flight height, f(Jturn) is the cost function of the UAV turning angle, and wi is the percentage of each cost function.

In the route planning problem processed by swarm intelligent algorithm, n nodes are selected from a complete route, where the distance between the ith node and the (i+1)th node is denoted as ‖l(i+1)−l(i)‖2, and the coordinates of the two nodes are denoted as (xi,yi,zi) and (xi+1,yi+1,zi+1), labeled as l(i) and l(i+1), respectively. The mathematical model of track length of Lpath is shown in formula (22):

Lpath=∑i=1n−1‖l(i+1)−l(i)‖2(22)

The mathematical model of the standard deviation of flight altitude Hheight is shown in formula (23), where Hheight is the standard deviation cost function of altitude, z¯ is the average altitude, and z(i) is the height of the ith node:

{Hheight=1n∑i=0n−1(z(i)−z¯)2z¯=1n∑i=0n−1z(i)(23)

The mathematical model of turning angle Jturn is shown in formula (24), where Φ is the maximum turning angle, θ is the current turning angle, and ai is the track vector of section i:

{cos⁡θ=aiTai+1|ai||ai+1|Jturn=∑i=1n(cos⁡Φ−cos⁡θi)(24)

5.2 Analysis of Experimental Results

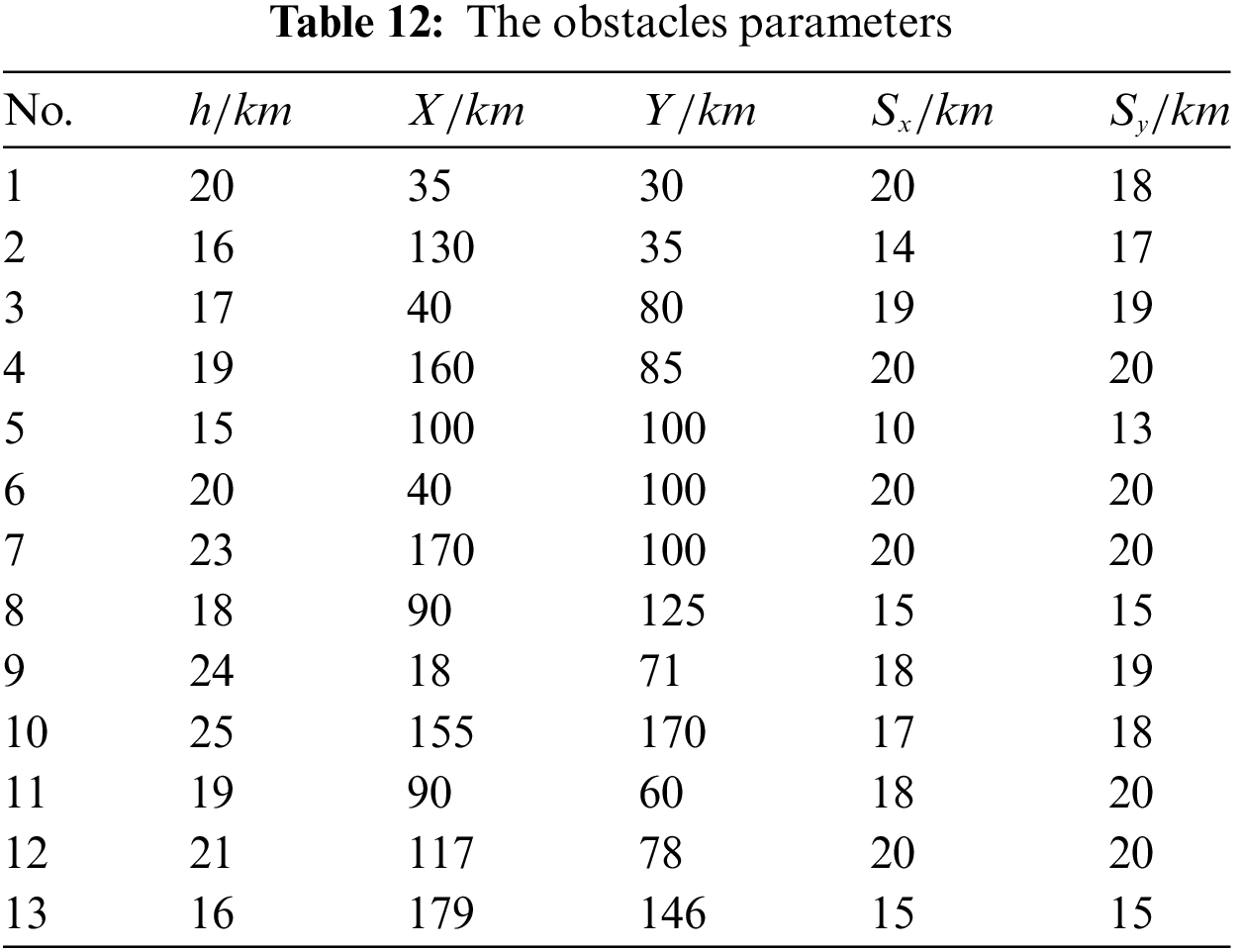
To fully test the performance of the algorithm, the flight space is set to 250∗250∗60 km in the simulation and visualization process, and the coordinates of the starting and ending points are (10,10,10) and (210,210,20), respectively, and multiple peaks are added to the environment model to act as obstacles, with their parameters detailed in Table 12.

Under identical conditions, the INGO’s outcomes are compared to those of NGO, SSA, BWO, DA and ChOA through 30 repetitions of the experiment. Table 13 displays the findings. The algorithm demonstrates its optimization ability and stability by achieving the minimum mean fitness value and standard deviation, with the optimal value of INGO being 217.2375 and the mean value being 224.1206. The results are superior when compared to other algorithms. It is noteworthy that, in contrast to other foundational algorithms such as SSA and BWO, the NGO algorithm does not exhibit rapid characteristics in the context of UAV trajectory planning problems under this mathematical model, despite its capability to achieve higher precision. The enhanced INGO algorithm, compared to the original NGO algorithm, demonstrates improvements in both speed and accuracy for such problems, validating the effectiveness of our four strategies for algorithmic enhancement. However, within the framework of the NGO algorithm, even the speed performance of INGO remains inferior compared to other algorithms. Therefore, at this stage, INGO is more apt for addressing static UAV trajectory planning problems that disregard temporal influences but demand cost minimization. Additionally, exploring ways to enhance INGO’s speed performance in these problems constitutes a potential direction for our future considerations.

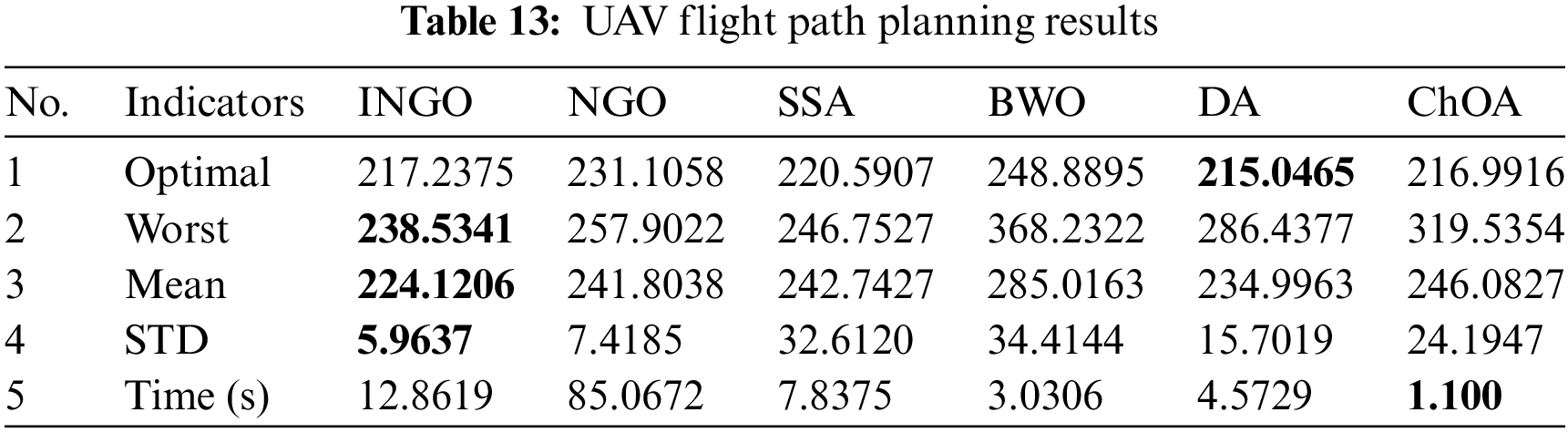
Fig. 6 shows the convergence curves of the six algorithms. Compared with other algorithms, INGO gets a smaller fitness value. Compared to NGO, which can approximate the optimal solution in nearly 10 iterations, it has a faster rate of convergence.

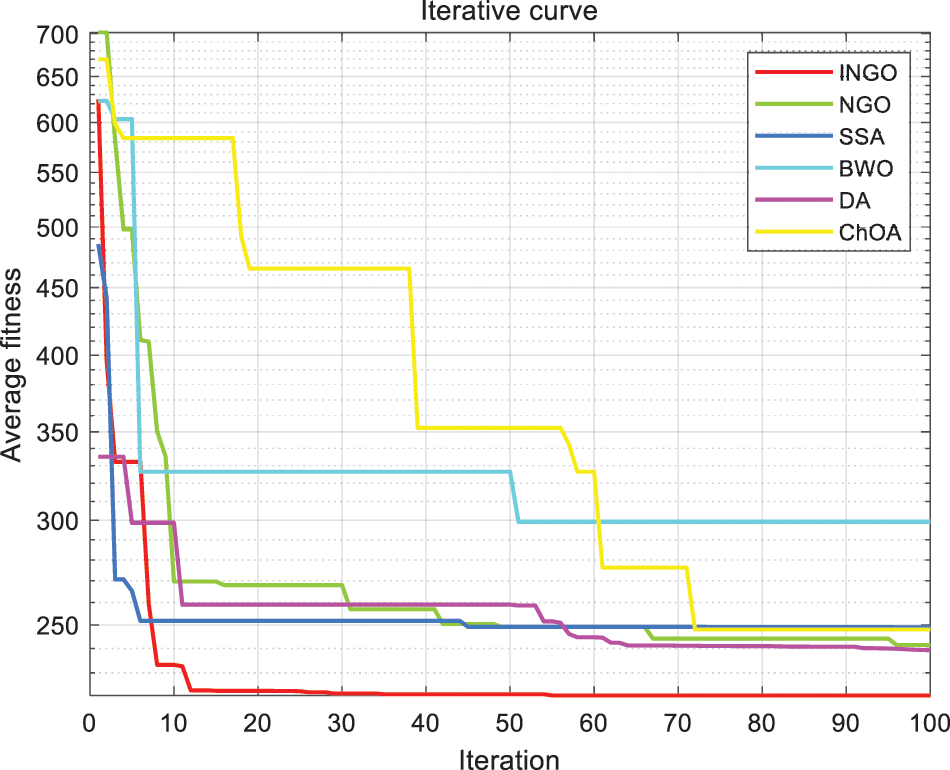
Figure 6: Fitness values change with the iteration

Figs. 7 and 8 show that swarm intelligence algorithm can plan a reasonable flight path for UAV in the case of obstacles and complete the goal of flight path planning. And the planned flight path is at a more stable and suitable altitude. The above experimental results show that INGO has good performance in this kind of problem and can effectively solve the UAV flight path planning problem under this environmental model.

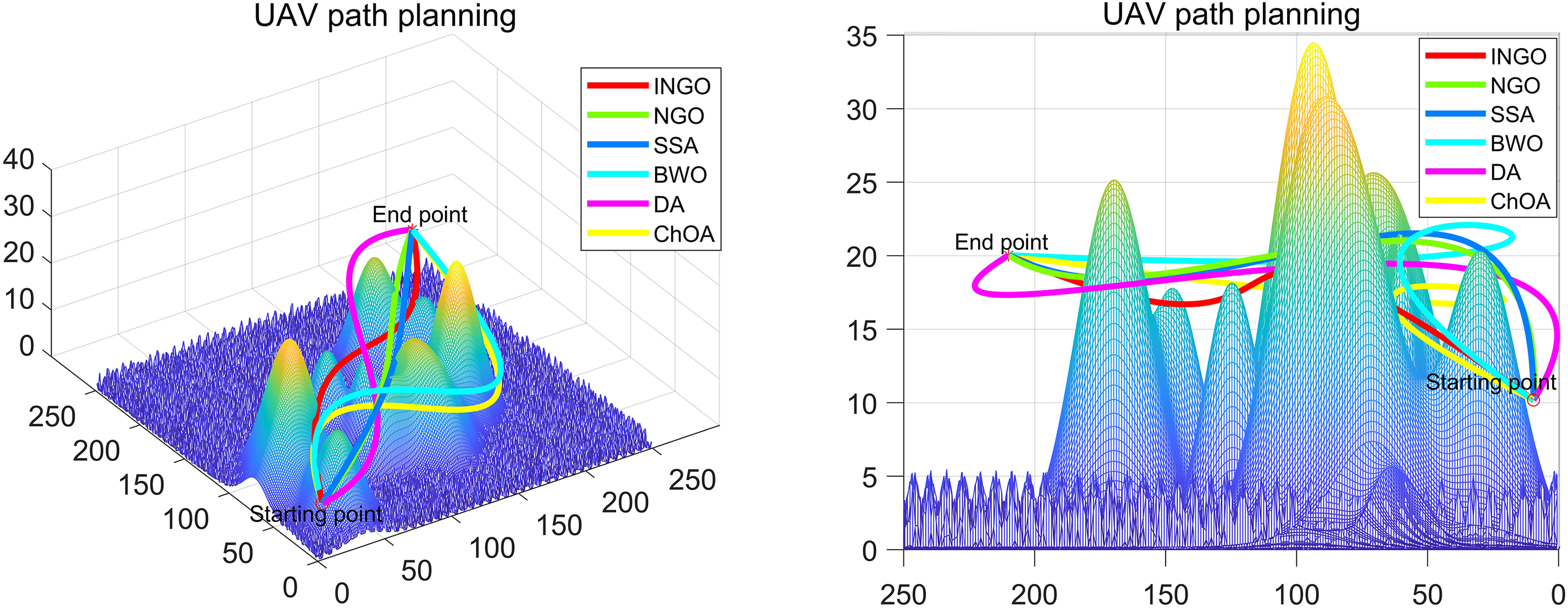
Figure 7: UAV path planning with different algorithms

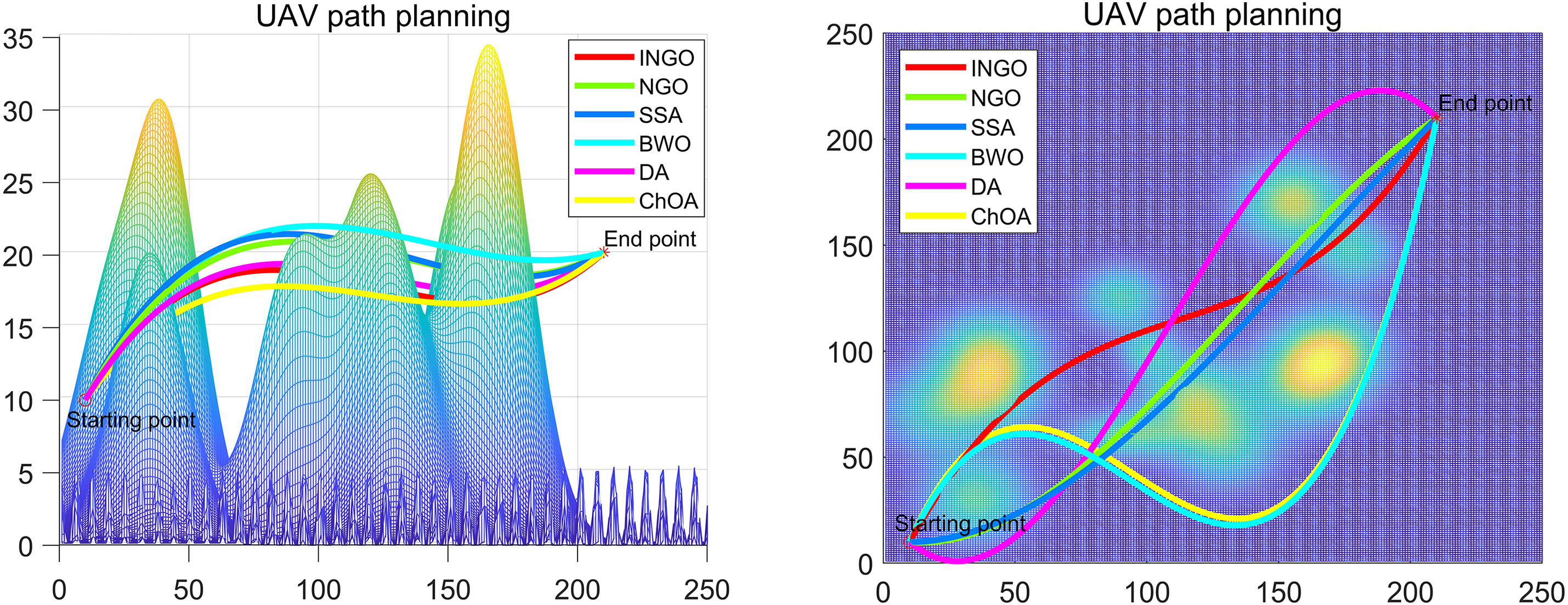
Figure 8: Front view and top view of UAV path planning

6  Conclusion

Within the realm of function optimization, the NGO algorithm exhibits diminished convergence accuracy and a propensity for entrapment in local optima. This paper proposes four strategic enhancements aimed at harmonizing the exploratory and exploitative abilities of NGO. First, introducing tent chaotic mapping aims to uniformly distribute the initial population, increasing diversity. Next, incorporating whale fall phenomena and T-distribution variations increases the algorithm’s chance of escaping local optima, reducing the risk of falling into local minima. Lastly, integrating the state transition algorithm’s neighborhood search capability strengthens INGO’s local utilization. INGO’s performance, assessed on public test sets and UAV trajectory planning, was compared with classic and new algorithms. Statistical methods analyzed the experimental results, summarizing the algorithm’s strengths and areas for improvement. The findings show that INGO has higher convergence accuracy and a better ability to escape local extremes in function optimization.

Moving forward, our efforts will focus on three main avenues: Firstly, we aim to integrate various optimization strategies into advanced intelligent optimization algorithms, creating competitive solutions for real-world problems. Secondly, considering INGO’s limitations, we will explore the inclusion of adaptive adjustment strategies to enhance algorithmic performance. Lastly, we will extend the application of INGO to tackle more sophisticated engineering scenarios, such as the complex task of UAV trajectory planning that involves additional constraints, broadening our approach to encompass a wider spectrum of intricate engineering problems.

Acknowledgement: The authors wish to acknowledge the editor and anonymous reviewers for their insightful comments, which have improved the quality of this publication.

Funding Statement: This work was in part supported by the Key Research and Development Project of Hubei Province (No. 2023BAB094), the Key Project of Science and Technology Research Program of Hubei Educational Committee (No. D20211402), and the Open Foundation of Hubei Key Laboratory for High-Efficiency Utilization of Solar Energy and Operation Control of Energy Storage System (No. HBSEES202309).

Author Contributions: Study conception and design: Mai Hu, Liang Zeng; Data collection: Chenning Zhang, Quan Yuan and Shanshan Wang; Analysis and interpretation of results: All authors; Draft manuscript preparation: Mai Hu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data and materials are available.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. L. Abualigah et al., “Meta-heuristic optimization algorithms for solving real-world mechanical engineering design problems: A comprehensive survey, applications, comparative analysis, and results,” Neural Comput. Appl., vol. 34, no. 6, pp. 1–30, 2022. doi: 10.1007/s00521-021-06747-4. [Google Scholar] [CrossRef]

2. S. Aggarwal and N. Kumar, “Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges,” Comput. Commun., vol. 149, no. 12, pp. 270–299, 2020. doi: 10.1016/j.comcom.2019.10.014. [Google Scholar] [CrossRef]

3. L. L. Li, Z. F. Liu, M. L. Tseng, S. J. Zheng, and M. K. Lim, “Improved tunicate swarm algorithm: Solving the dynamic economic emission dispatch problems,” Appl. Soft Comput., vol. 108, no. 5, pp. 107504, 2021. doi: 10.1016/j.asoc.2021.107504. [Google Scholar] [CrossRef]

4. E. H. Houssein, A. G. Gad, Y. M. Wazery, and P. N. Suganthan, “Task scheduling in cloud computing based on meta-heuristics: Review, taxonomy, open challenges, and future trends,” Swarm Evol. Comput., vol. 62, no. 3, pp. 100841, 2021. doi: 10.1016/j.swevo.2021.100841. [Google Scholar] [CrossRef]

5. D. Zhao et al., “Ant colony optimization with horizontal and vertical crossover search: Fundamental visions for multi-threshold image segmentation,” Expert. Syst. Appl., vol. 167, no. 1, pp. 114122, 2021. doi: 10.1016/j.eswa.2020.114122. [Google Scholar] [CrossRef]

6. Z. Sadeghian, E. Akbari, H. Nematzadeh, and H. Motameni, “A review of feature selection methods based on meta-heuristic algorithms,” J. Exp. Theor. Artif. Intell., vol. 78, no. 2, pp. 1–51, 2023. doi: 10.1080/0952813X.2023.2183267. [Google Scholar] [CrossRef]

7. S. Mirjalili, “Genetic algorithm,” in Evolutionary Algorithms and Neural Networks, Springer, Cham, 2019, vol. 780, pp. 43–55. doi: 10.1007/978-3-319-93025-1_4. [Google Scholar] [CrossRef]

8. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. ICNN’95-Int. Conf. on Neural Netw., Perth, WA, Australia, IEEE, 1995, pp. 1942–1948. doi: 10.1109/ICNN.1995.488968. [Google Scholar] [CrossRef]

9. R. A. Rutenbar, “Simulated annealing algorithms: An overview,” IEEE Circuits Devices Mag., vol. 5, no. 1, pp. 19–26, 1989. doi: 10.1109/101.17235. [Google Scholar] [CrossRef]

10. S. Mirjalili, “SCA: A sine cosine algorithm for solving optimization problems,” Knowl. Based Syst., vol. 96, no. 63, pp. 120–133, 2016. doi: 10.1016/j.knosys.2015.12.022. [Google Scholar] [CrossRef]

11. A. R. Jordehi, “Brainstorm optimisation algorithm (BSOAAn efficient algorithm for finding optimal location and setting of FACTS devices in electric power systems,” Int. J. Electr. Power Energy Syst., vol. 69, no. 10, pp. 48–57, 2015. doi: 10.1016/j.ijepes.2014.12.083. [Google Scholar] [CrossRef]

12. F. Glover, “Tabu search: A tutorial,” Interfaces, vol. 20, no. 4, pp. 74–94, 1990. doi: 10.1287/inte.20.4.74. [Google Scholar] [CrossRef]

13. M. Dorigo, M. Birattari, and T. Stutzle, “Ant colony optimization,” IEEE Comput. Intell. Mag., vol. 1, no. 4, pp. 28–39, 2006. doi: 10.1109/MCI.2006.329691. [Google Scholar] [CrossRef]

14. S. Mirjalili, S. M. Mirjalili, and A. Lewis, “Grey wolf optimizer,” Adv. Eng. Softw., vol. 69, pp. 46–61, 2014. doi: 10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]

15. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Adv. Eng. Softw., vol. 95, no. 12, pp. 51–67, 2016. doi: 10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

16. S. Mirjalili, “Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems,” Neural Comput. Appl., vol. 27, no. 4, pp. 1053–1073, 2016. doi: 10.1007/s00521-015-1920-1. [Google Scholar] [CrossRef]

17. L. Abualigah, D. Yousri, M. Abd Elaziz, A. A. Ewees, M. A. Al-Qaness and A. H. Gandomi, “Aquila optimizer: A novel meta-heuristic optimization algorithm,” Comput. Ind. Eng., vol. 157, no. 11, pp. 107250, 2021. doi: 10.1016/j.cie.2021.107250. [Google Scholar] [CrossRef]

18. A. Heidari, S. Mirjalili, H. Faris, I. Aljarah, M. Mafarja and H. Chen, “Harris hawks optimization: Algorithm and applications,” Future Gener. Comput. Syst., vol. 97, pp. 849–872, 2019. doi: 10.1016/j.future.2019.02.028. [Google Scholar] [CrossRef]

19. Y. Yang, H. Chen, A. A. Heidari, and A. H. Gandomi, “Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts,” Expert. Syst. Appl., vol. 177, no. 8, pp. 114864, 2021. doi: 10.1016/j.eswa.2021.114864. [Google Scholar] [CrossRef]

20. A. E. Ezugwu, J. O. Agushaka, L. Abualigah, S. Mirjalili, and A. H. Gandomi, “Prairie dog optimization algorithm,” Neural Comput. Appl., vol. 34, no. 22, pp. 20017–20065, 2022. doi: 10.1007/s00521-022-07530-9. [Google Scholar] [CrossRef]

21. J. O. Agushaka, A. E. Ezugwu, and L. Abualigah, “Dwarf mongoose optimization algorithm,” Comput. Methods Appl. Mech. Eng., vol. 391, pp. 114570, 2022. [Google Scholar]

22. M. Khishe and M. R. Mosavi, “Chimp optimization algorithm,” Expert. Syst. Appl., vol. 149, no. 1, pp. 113338, 2020. doi: 10.1016/j.eswa.2020.113338. [Google Scholar] [CrossRef]

23. C. Zhong, G. Li, and Z. Meng, “Beluga whale optimization: A novel nature-inspired metaheuristic algorithm,” Knowl. Based Syst., vol. 251, no. 1, pp. 109215, 2022. doi: 10.1016/j.knosys.2022.109215. [Google Scholar] [CrossRef]

24. M. Dehghani, Š. Hubálovský, and P. Trojovský, “Northern goshawk optimization: A new swarm-based algorithm for solving optimization problems,” IEEE Access, vol. 9, pp. 162059–162080, 2021. doi: 10.1109/ACCESS.2021.3133286. [Google Scholar] [CrossRef]

25. S. Yu and J. Ma, “Adaptive composite fault diagnosis of rolling bearings based on the CLNGO algorithm,” Processes, vol. 10, no. 12, pp. 2532, 2022. doi: 10.3390/pr10122532. [Google Scholar] [CrossRef]

26. H. Youssef, S. Kamel, M. H. Hassan, J. Yu, and M. Safaraliev, “A smart home energy management approach incorporating an enhanced northern goshawk optimizer to enhance user comfort, minimize costs, and promote efficient energy consumption,” Int. J. Hydrogen Energy, vol. 49, no. 57, pp. 644–658, 2024. doi: 10.1016/j.ijhydene.2023.10.174. [Google Scholar] [CrossRef]

27. Y. Liang, X. Hu, G. Hu, and W. Dou, “An enhanced northern goshawk optimization algorithm and its application in practical optimization problems,” Mathematics, vol. 10, no. 22, pp. 4383, 2022. doi: 10.3390/math10224383. [Google Scholar] [CrossRef]

28. M. A. El-Dabah, R. A. El-Sehiemy, H. M. Hasanien, and B. Saad, “Photovoltaic model parameters identification using northern goshawk optimization algorithm,” Energy, vol. 262, pp. 125522, 2023. doi: 10.1016/j.energy.2022.125522. [Google Scholar] [CrossRef]

29. H. Satria, R. B. Syah, M. L. Nehdi, M. K. Almustafa, and A. O. I. Adam, “Parameters identification of solar PV using hybrid chaotic northern goshawk and pattern search,” Sustainability, vol. 15, no. 6, pp. 5027, 2023. doi: 10.3390/su15065027. [Google Scholar] [CrossRef]

30. J. Zhong, T. Chen, and L. Yi, “Face expression recognition based on NGO-BILSTM model,” Front. Neurorobot., vol. 17, pp. 1155038, 2023. doi: 10.3389/fnbot.2023.1155038. [Google Scholar] [PubMed] [CrossRef]

31. G. Tian et al., “Hybrid evolutionary algorithm for stochastic multiobjective disassembly line balancing problem in remanufacturing,” Environ. Sci. Pollut. Res., vol. 55, no. 24, pp. 1–16, 2023. doi: 10.1007/s11356-023-27081-3. [Google Scholar] [PubMed] [CrossRef]

32. J. Wang, Z. Xiang, X. Cheng, J. Zhou, and W. Li, “Tool wear state identification based on SVM optimized by the improved northern goshawk optimization,” Sensors, vol. 23, no. 20, pp. 8591, 2023. doi: 10.3390/s23208591. [Google Scholar] [PubMed] [CrossRef]

33. C. Zhan et al., “Environment-oriented disassembly planning for end-of-life vehicle batteries based on an improved northern goshawk optimisation algorithm,” Environ. Sci. Pollut. Res., vol. 30, no. 16, pp. 47956–47971, 2023. doi: 10.1007/s11356-023-25599-0. [Google Scholar] [PubMed] [CrossRef]

34. J. Bian, R. Huo, Y. Zhong, and Z. Guo, “XGB-Northern goshawk optimization: Predicting the compressive strength of self-compacting concrete,” KSCE J. Civil Eng., vol. 28, no. 4, pp. 1–17, 2024. doi: 10.1007/s12205-024-1647-6. [Google Scholar] [CrossRef]

35. X. Wang, J. Wei, F. Wen, and K. Wang, “A trading mode based on the management of residual electric energy in electric vehicles,” Energies, vol. 16, no. 17, pp. 6317, 2023. doi: 10.3390/en16176317. [Google Scholar] [CrossRef]

36. M. Ning et al., “Revealing the hot deformation behavior of AZ42 Mg alloy by using 3D hot processing map based on a novel NGO-ANN model,” J. Mater. Res. Technol., vol. 27, pp. 2292–2310, 2023. doi: 10.1016/j.jmrt.2023.10.073. [Google Scholar] [CrossRef]

37. D. H. Wolpert and W. G. Macready, “No free lunch theorems for optimization,” IEEE Trans. Evol. Comput., vol. 1, no. 1, pp. 67–82, 1997. doi: 10.1109/4235.585893. [Google Scholar] [CrossRef]

38. S. Gupta and K. Deep, “A novel random walk grey wolf optimizer,” Swarm Evol. Comput., vol. 44, no. 4, pp. 101–112, 2019. doi: 10.1016/j.swevo.2018.01.001. [Google Scholar] [CrossRef]

39. X. Zhou, C. Yang, and W. Gui, “State transition algorithm,” arXiv preprint arXiv:1205.6548, 2012. [Google Scholar]

40. A. Tharwat and W. Schenck, “Population initialization techniques for evolutionary algorithms for single-objective constrained optimization problems: Deterministic vs. stochastic techniques,” Swarm Evol. Comput., vol. 67, pp. 100952, 2021. doi: 10.1016/j.swevo.2021.100952. [Google Scholar] [CrossRef]

41. Y. Li, M. Han, and Q. Guo, “Modified whale optimization algorithm based on tent chaotic mapping and its application in structural optimization,” KSCE J. Civil Eng., vol. 24, no. 12, pp. 3703–3713, 2020. doi: 10.1007/s12205-020-0504-5. [Google Scholar] [CrossRef]

42. J. H. Liu and Z. H. Wang, “A hybrid sparrow search algorithm based on constructing similarity,” IEEE Access, vol. 9, pp. 117581–117595, 2021. doi: 10.1109/ACCESS.2021.3106269. [Google Scholar] [CrossRef]

43. P. N. Suganthan et al., “Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization,” KanGAL Rep., 2005. [Google Scholar]

44. G. Wu, R. Mallipeddi, and P. N. Suganthan, “Problem definitions and evaluation criteria for the CEC 2017 competition on constrained real-parameter optimization,” Tech. Rep, National University of Defense Technology, Changsha, Hunan, China and Kyungpook National University, Daegu, South Korea and Nanyang Technological University, Singapore, 2017. [Google Scholar]

45. I. Naruei, F. Keynia, and A. Sabbagh Molahosseini, “Hunter-prey optimization: Algorithm and applications,” Soft Comput., vol. 26, no. 3, pp. 1279–1314, 2022. doi: 10.1007/s00500-021-06401-0. [Google Scholar] [CrossRef]

46. Seyyedabbasi and F. Kiani, “Sand cat swarm optimization: A nature-inspired algorithm to solve global optimization problems,” Eng. Comput., vol. 39, no. 4, pp. 2627–2651, 2023. doi: 10.1007/s00366-022-01604-x. [Google Scholar] [CrossRef]

47. S. Mirjalili, A. H. Gandomi, S. Z. Mirjalili, S. Saremi, H. Faris and S. M. Mirjalili, “Salp swarm algorithm: A bio-inspired optimizer for engineering design problems,” Adv. Eng. Softw., vol. 114, pp. 163–191, 2017. doi: 10.1016/j.advengsoft.2017.07.002. [Google Scholar] [CrossRef]

48. X. Fu, L. Zhu, J. Huang, J. Wang, and A. Ryspayev, “Multi-threshold image segmentation based on the improved northern goshawk optimization,” Comput. Eng., vol. 49, no. 7, pp. 232–241, 2023. [Google Scholar]

49. H. S. Yahia and A. S. Mohammed, “Path planning optimization in unmanned aerial vehicles using meta-heuristic algorithms: A systematic review,” Environ. Monit. Assess., vol. 195, no. 1, pp. 30, 2023. doi: 10.1007/s10661-022-10590-y. [Google Scholar] [PubMed] [CrossRef]

50. Y. Wu, “A survey on population-based meta-heuristic algorithms for motion planning of aircraft,” Swarm Evol. Comput., vol. 62, no. 6, pp. 100844, 2021. doi: 10.1016/j.swevo.2021.100844. [Google Scholar] [CrossRef]

51. J. Tang, H. Duan, and S. Lao, “Swarm intelligence algorithms for multiple unmanned aerial vehicles collaboration: A comprehensive review,” Artif. Intell. Rev., vol. 56, no. 5, pp. 4295–4327, 2023. doi: 10.1007/s10462-022-10281-7. [Google Scholar] [CrossRef]

52. R. A. Saeed, M. Omri, S. Abdel-Khalek, E. S. Ali, and M. F. Alotaibi, “Optimal path planning for drones based on swarm intelligence algorithm,” Neural Comput. Appl., vol. 34, no. 12, pp. 10133–10155, 2022. doi: 10.1007/s00521-022-06998-9. [Google Scholar] [CrossRef]

53. Yao et al., “IHSSAO: An improved hybrid salp swarm algorithm and aquila optimizer for UAV path planning in complex terrain,” Appl. Sci., vol. 12, no. 11, pp. 5634, 2022. doi: 10.3390/app12115634. [Google Scholar] [CrossRef]

54. G. Guo and Y. Wang, “Constrained-handling techniques based on evolutionary algorithms,” J. Hunan Univ. (Nat. Sci.), vol. 19, no. 4, pp. 15–18, 2006. [Google Scholar]

55. Y. Chen, D. Pi, and Y. Xu, “Neighborhood global learning based flower pollination algorithm and its application to unmanned aerial vehicle path planning,” Expert. Syst. Appl., vol. 170, pp. 114505, 2021. doi: 10.1016/j.eswa.2020.114505. [Google Scholar] [CrossRef]

56. Z. Yu, Z. Si, X. Li, D. Wang, and H. Song, “A novel hybrid particle swarm optimization algorithm for path planning of UAVs,” IEEE Internet Things J., vol. 9, no. 22, pp. 22547–22558, 2022. doi: 10.1109/JIOT.2022.3182798. [Google Scholar] [CrossRef]