Magnificent Frigatebird Optimization: A New Bio-Inspired Metaheuristic Approach for Solving Optimization Problems

1  Introduction

In the realm of scientific inquiry, optimization problems present a crucial challenge, defined by an objective function and constraints, with multiple feasible solutions. The quest for the optimal solution among these options is recognized as optimization. Across various domains like mathematics, engineering, industry, and economics, a myriad of optimization problems necessitate tailored solutions [1]. Approaches to solving these problems are broadly categorized into deterministic and stochastic methods [2]. Deterministic strategies, subdivided into gradient-based and non-gradient-based methods, excel in addressing linear, convex, continuous, and differentiable problems, particularly those with lower dimensions [3,4]. However, deterministic approaches falter in tackling higher-dimensional, non-linear, non-convex, and discontinuous problems often encountered in real-world applications, compelling the exploration of stochastic techniques [5,6].

Among stochastic approaches, metaheuristic algorithms stand out for their efficacy in navigating complex problem spaces through random search and trial-and-error processes [7]. Renowned for their conceptual simplicity, universality, and effectiveness in handling intricate, high-dimensional, non-deterministic polynomial (NP)-hard, and non-linear problems, metaheuristic algorithms have garnered substantial research interest [8]. These algorithms initiate optimization by randomly generating a set of candidate solutions, which are iteratively refined based on algorithmic instructions, ultimately converging to the best solution [9].

An effective metaheuristic algorithm must strike a delicate balance between global exploration and local exploitation [10]. Global exploration entails a comprehensive search of the problem space to avoid local optima and identify the main optimal region, while local exploitation focuses on refining solutions in promising areas to converge towards a global optimum. Despite the stochastic nature of metaheuristic algorithms, they provide near-optimal solutions without guaranteeing a global optimum [11]. Consequently, the quest for more effective optimization solutions has spurred the continual design of new metaheuristic algorithms.

The No Free Lunch (NFL) theorem underscores the necessity for diverse metaheuristic algorithms, as no single algorithm universally excels across all optimization problems [12]. While an algorithm may converge to a global optimum for one problem, it may fail for another. Therefore, the NFL theorem fosters ongoing exploration in metaheuristic algorithm design to devise more effective optimization strategies.

Although numerous metaheuristic algorithms have been designed and introduced, based on the best knowledge obtained from the literature review, it is confirmed that no metaheuristic algorithm has been designed based on simulating the natural behavior of magnificent frigatebirds. This is observed although the kleptoparasitic behavior of the magnificent frigatebird is an intelligent strategy that has a special potential for designing a new metaheuristic algorithm. Therefore, the originality and novelty of the design of the proposed approach are guaranteed.

The primary contribution of this paper is the introduction of Magnificent Frigatebird Optimization (MFO), a novel metaheuristic algorithm inspired by the behavior of magnificent frigatebirds in nature. Key features of MFO include its emulation of frigatebirds’ kleptoparasitic behavior and its mathematical modeling, which encompasses exploration and exploitation phases. Evaluation of MFO’s performance on standard benchmark functions demonstrates its efficacy in optimization tasks, outperforming twelve established metaheuristic algorithms.

The remainder of this paper unfolds as follows: Section 2 provides a literature review, Section 3 introduces and models the proposed MFO approach, Section 4 presents simulation studies and results, Section 5 evaluates the effectiveness of MFO for handling optimization tasks in real-world applications, and Section 6 concludes with reflections and suggestions for future research directions.

2  Literature Review

Metaheuristic algorithms are derived from a vast array of natural phenomena, encompassing the behaviors of living organisms, fundamental principles in physics, mathematics, and human decision-making strategies. These algorithms are typically organized into five primary categories: swarm-based approaches, which draw from the collective behavior observed in groups of animals, insects, or aquatic life; evolutionary-based approaches, which are inspired by the concepts of natural selection and genetics; physics-based approaches, which model various physical laws and phenomena; human-based approaches, which emulate human behavior and social dynamics in problem-solving scenarios, and mathematics-based approaches, which employ mathematical concepts and operators.

Swarm-based metaheuristic algorithms emulate the collective behaviors of animals, insects, and birds in nature. Notable examples include Particle Swarm Optimization (PSO) [13], Ant Colony Optimization (ACO) [14], Artificial Bee Colony (ABC) [15], and Firefly Algorithm (FA) [16]. These algorithms simulate behaviors such as foraging and communication, offering efficient search strategies for optimization problems. Frilled Lizard Optimization (FLO) is a recently published swarm-based approach whose design is inspired by the sit-and-wait strategy observed in frilled lizards during hunting [17]. Additionally, algorithms like the African Vultures Optimization Algorithm (AVOA) [18], White Shark Optimizer (WSO) [19], Beluga whale optimization [20], and Emperor Penguin Optimizer (EPO) [21] draw inspiration from various animal behaviors to enhance optimization performance.

Evolutionary-based metaheuristic algorithms are inspired by biological concepts such as natural selection and genetic evolution. Genetic Algorithm (GA) [22] and Differential Evolution (DE) [23] are prominent examples, mimicking reproduction and survival processes observed in nature. Other algorithms like Genetic Programming (GP) [24] leverage biological principles to explore optimization spaces effectively.

Physics-based metaheuristic algorithms simulate physical laws and phenomena to navigate optimization landscapes. Simulated Annealing (SA), for instance, replicates the annealing process in metallurgy, while algorithms like Spring Search Algorithm (SSA) [25] and Gravitational Search Algorithm (GSA) [26] simulate forces and transformations from physics. These algorithms capitalize on physical principles to guide search processes efficiently. Equilibrium Optimizer (EO) [27], and Water Flow Optimizer (WFO) [28] are other examples of physics-based metaheuristic algorithms.

Human-based metaheuristic algorithms model human behaviors and decision-making strategies. Teaching-Learning Based Optimization (TLBO) [29] mirrors the educational environment, while Following Optimization Algorithm (FOA) [30] replicates societal influences on individual progress. Language Education Optimization (LEO) [31] and Election Based Optimization Algorithm (EBOA) [32] draw inspiration from language learning and electoral processes, respectively. These algorithms harness human-centric strategies to tackle optimization challenges.

Mathematics-based metaheuristic algorithms have been developed by using the concepts and operators of mathematics. Arithmetic Optimization Algorithm (AOA) [33] and One-to-One Based Optimizer (OOBO) [34] are examples of algorithms of this group that are inspired by mathematics.

Despite the wealth of existing metaheuristic algorithms, none have been specifically designed based on the natural behavior of magnificent frigatebirds. The kleptoparasitic behavior of these birds presents an intelligent strategy ripe for algorithmic exploration. Thus, this paper introduces a new metaheuristic algorithm inspired by the mathematical modeling of magnificent frigatebird behavior, addressing a notable gap in existing research.

3  Magnificent Frigatebird Optimization

3.1 Inspiration

The Magnificent Frigatebird Optimization (MFO) is introduced in this section, drawing inspiration from the behavior of magnificent frigatebirds in their natural habitat. These seabirds, found in tropical and subtropical waters off the coasts of America, exhibit distinctive characteristics such as kleptoparasitic behavior. An image of the magnificent frigatebird is shown in Fig. 1.

Figure 1: Magnificent frigatebird took from: free media wikimedia commons

The magnificent frigatebird exhibits a kleptoparasitic strategy, engaging in behavior where it aggressively attacks and pecks at other seabirds, compelling them to relinquish their prey. Subsequently, the frigatebird swiftly descends towards the discarded food, seizing the prey before it descends to the water’s surface. This kleptoparasitic behavior stands out prominently among the natural tendencies of the magnificent frigatebird. Leveraging the mathematical modeling of this kleptoparasitic behavior forms a foundational aspect of the design of the Magnificent Frigatebird Optimization (MFO), as elaborated below.

3.2 Initialization

MFO is a population-based metaheuristic algorithm designed for iterative optimization processes. Each magnificent frigatebird in the MFO population represents a candidate solution, with its position in the problem-solving space modeled as a vector according to Eq. (1). The initial positions of the frigatebirds are determined within specified bounds using Eq. (2).

X=[X1⋮Xi⋮XN]N×m=[x1,1⋯x1,j⋯x1,m⋮⋱⋮⋰⋮xi,1⋯xi,j⋯xi,m⋮⋰⋮⋱⋮xN,1⋯xN,j⋯xN,m]N×m(1)

Xi:xi,j=lbj+r⋅(ubj−lbj),i=1,2,…,N, j=1,2,…,m,(2)

where X is the population matrix of the proposed MFO, N denotes the number of magnificent frigatebirds, m represents the number of decision variables, Xi is the ith magnificent frigatebird (i.e., a candidate solution), xi,j denotes its jth variable, r is a random number from the interval [0,1], lbj is a lower bound and ubj is an upper bound on the jth decision variable.

Subsequently, the objective function corresponding to each frigatebird’s position is evaluated that the set of these evaluated values for the objective function can be represented using a vector according to Eq. (3).

F=[F1⋮Fi⋮FN]N×1=[F(X1)⋮F(Xi)⋮F(XN)]N×1,(3)

where F is the vector of values of the objective function and Fi is the value of the objective function for the ith magnificent frigatebird (i.e., the candidate solution).

In the design of MFO, in each iteration, each magnificent frigatebird is updated in two phases of exploration and exploitation described below.

3.3 Phase 1: Selecting, Attacking, and Pecking at Seabirds Carrying Prey (Exploration Phase)

The kleptoparasitic behavior of the magnificent frigatebird is a defining characteristic of this species. This strategy begins with the magnificent frigatebird attacking another seabird that is carrying prey. The frigatebird repeatedly pecks at the seabird, forcing it to release the prey. This aggressive interaction results in substantial and abrupt movements of the magnificent frigatebird as it maneuvers to intercept the dropped prey. These significant displacements are mathematically modeled in the Magnificent Frigatebird Optimization (MFO) algorithm to simulate global search and exploration within the problem-solving space.

In the design of MFO, each magnificent frigatebird considers the positions of other population members that have achieved better objective function values as the targets, akin to seabirds carrying prey. The positions of these targeted birds for each frigatebird are determined using Eq. (4). The algorithm assumes that each magnificent frigatebird randomly selects one of these potential targets and initiates an attack. The movement of the magnificent frigatebird towards the selected seabird is then mathematically modeled, resulting in a new position, which is calculated using Eq. (5). If the new position yields an improved objective function value, this new position replaces the previous one as per the rules defined in Eq. (6).

CSi={Xk,Fk<Fiandk∈{1,2,…,N}},wherei=1,2,…,N,(4)

xi,jP1=xi,j+(1−2ri,j)⋅(SSi,j−Ii,j⋅xi,j),(5)

Xi={XiP1,FiP1≤Fi,Xi,else,(6)

where CSi is the set of presumed food-carrying seabirds for the ith magnificent frigatebird, Xk denotes the kth row of the matrix X which has a better objective function value than the ith one, where CSi is the set of presumed food-carrying seabirds for the ith magnificent frigatebird, SSi represents the selected food-carrying seabird for the ith magnificent frigatebird, SSi,j gives its jth dimension, XiP1 is the new position calculated for the ith magnificent frigatebird based on the first phase of the proposed MFO, xi,jP1 gives its jth dimension, FiP1 denotes its objective function value, ri,j are random numbers from the interval [0,1], and Ii,j are numbers which are randomly selected as 1 or 2.

3.4 Phase 2: Diving towards the Dropped Prey (Exploitation Phase)

In the second stage of the kleptoparasitic behavior, the magnificent frigatebird dives toward the prey released by the attacked seabird, catching it before it reaches the water’s surface. This behavior is simulated in the Magnificent Frigatebird Optimization (MFO) algorithm through small, precise displacements near the bird’s current position. These minor adjustments are mathematically modeled to facilitate local search and exploitation within the problem-solving space.

In the design of MFO, these displacements are assumed to occur within a neighborhood centered around the magnificent frigatebird, with a radius defined by (bestj−xi,jt), where bestj represents the best-known position in the jth dimension, xi,j is the current position of the ith bird in the jth dimension, and t is a control parameter. To model this process, a new position for each magnificent frigatebird is calculated based on its simulated movement toward the abandoned prey, using Eq. (7). If this new position yields an improved value for the objective function, it replaces the bird’s previous position according to the update rule in Eq. (8). This method ensures that the MFO algorithm effectively performs local search, refining solutions and enhancing the optimization process by exploiting promising areas in the search space.

xi,jP2=xi,j+(1−2ri,j)⋅bestj−xi,jt(7)

Xi={XiP2,FiP2≤FiXi,else(8)

where XiP2 is the new position calculated for the ith magnificent frigatebird based on the second phase of the proposed MFO, xi,jP2 represents its jth dimension, bestj is the jth dimension of the best member, FiP2 denotes its objective function value, ri,j are random numbers from the interval [0,1], and t is the iteration counter.

3.5 Repetition Process, Flowchart, and Pseudo-Code of MFO

Upon completing the first iteration, the Magnificent Frigatebird Optimization (MFO) algorithm updates the positions of all magnificent frigatebirds by applying both the exploration and exploitation phases. After these updates, the algorithm proceeds to the next iteration using the newly acquired values. This iterative process continues, adhering to the guidelines set forth by Eqs. (4) to (8) until the predetermined maximum number of iterations is reached.

Throughout each iteration, the best solution found so far is continually updated based on the latest results. At the end of the entire iterative process, MFO provides the best solution obtained during its execution as the final solution to the problem. The steps of the MFO implementation are presented in the form of a flowchart in Fig. 2, and its pseudo-code is presented in Algorithm 1.

Figure 2: Flowchart of the proposed MFO

3.6 Computational Complexity of MFO

In this subsection, the computational complexity of MFO is evaluated. The preparation and initialization process of MFO has a complexity equal to O(Nm), where N is the number of magnificent frigatebirds and m is the number of decision variables of the problem. Each magnificent frigatebird is updated in each iteration during two phases of exploration and exploitation. Therefore, the process of updating magnificent frigatebirds has a complexity equal to O(2NmT), where T is the maximum number of iterations of the algorithm. Therefore, the computational complexity of MFO is O(Nm(1+2T)).

4  Simulation Studies

In this section, the effectiveness of the Magnificent Frigatebird Optimization (MFO) algorithm in addressing optimization problems is thoroughly evaluated. For this assessment, a set of twenty-three standard benchmark functions, which include unimodal, high-dimensional multimodal, and fixed-dimensional multimodal types [35] is utilized. The mathematical model, the best value (which is denoted by the symbol Fmin), and information about these functions are provided in Appendix A and Tables A1 to A3. The performance of MFO is compared against twelve well-known metaheuristic algorithms: Genetic Algorithm (GA) [22], PSO [13], GSA [26], TLBO [29], Multi-Verse Optimization (MVO) [36], Grey Wolf Optimizer (GWO) [37], Whale optimization Algorithm (WOA) [38], Marine Predators Algorithm (MPA) [39], Tunicate Swarm Algorithm (TSA) [40], Rivest-Shamir-Adleman (RSA) [41], AVOA [18], and WSO [19]. The values of the control parameters of the metaheuristic algorithms are specified in Table 1. The optimization results are reported using six statistical indicators: mean, best, worst, standard deviation, median, and rank. The ranking criterion of the metaheuristic algorithms for each of the benchmark functions is the value of the mean index.

4.1 Results for Unimodal Objective Functions

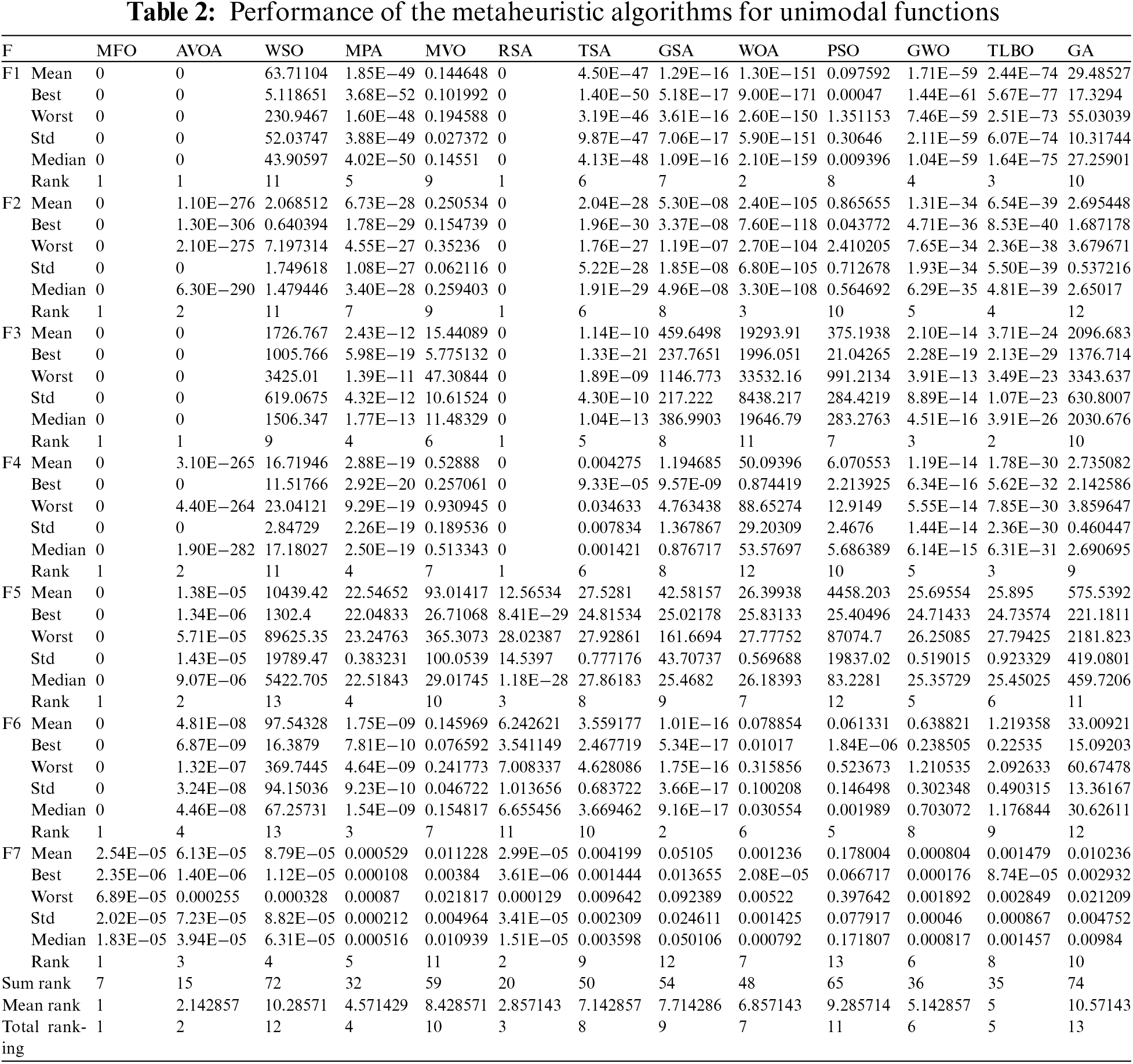
Table 2 illustrates the performance outcomes for unimodal functions F1 through F7, comparing MFO with various competing algorithms. Since unimodal functions F1 to F7 are devoid of local optima, they provide an ideal testbed for evaluating the local search and exploitation efficiencies of metaheuristic algorithms. Impressively, MFO exhibits exceptional exploitation capabilities, successfully converging to the global optimum for functions F1, F2, F3, F4, F5, and F6. Notably, MFO outperforms all other algorithms as the leading optimizer for function F7. These results highlight MFO’s proficiency in managing unimodal functions, surpassing its competitors with its strong exploitation prowess.

4.2 Results for High-Dimensional Multimodal Objective Functions

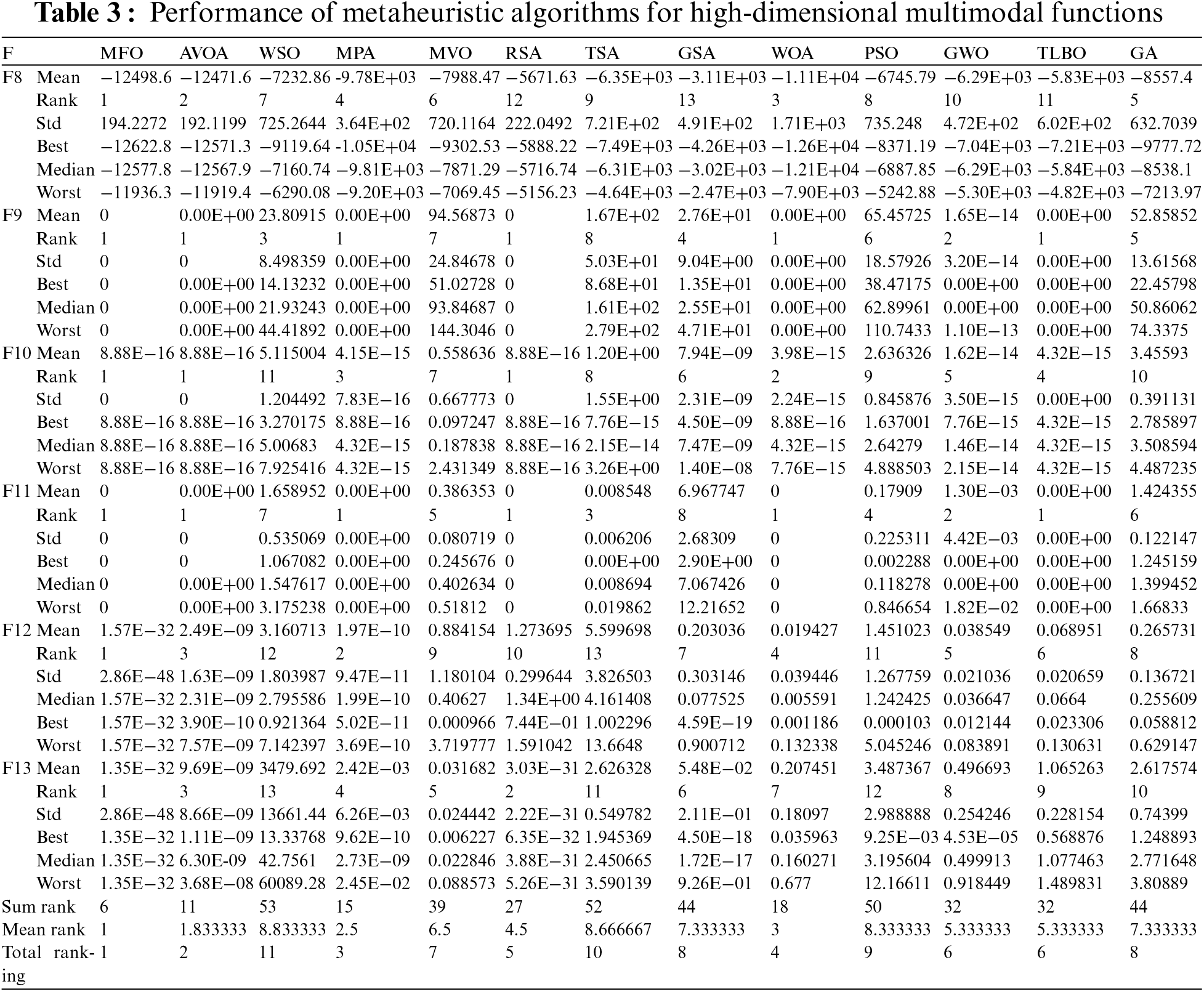
Table 3 showcases the performance results for functions F8 to F13, evaluated using the MFO algorithm and its competing counterparts. These functions, characterized by numerous local optima alongside the primary optima, serve as ideal benchmarks for assessing the global search and discovery capabilities of metaheuristic algorithms. The findings underscore MFO’s exceptional discovery abilities, particularly its successful convergence to the global optimum for functions F9 and F11, and its effective identification of the primary optimal region within the problem-solving space. Furthermore, MFO distinguishes itself as the leading optimizer for functions F8, F10, F12, and F13. These results highlight MFO’s superior performance in managing high-dimensional multimodal functions, showcasing its robust exploration capabilities and its ability to consistently outperform other algorithms.

4.3 Results for Fixed-Dimensional Multimodal Objective Functions

Table 4 presents the outcomes of evaluating the MFO algorithm alongside its competitors for functions F14 to F23. These functions are designed to test the balance between exploration and exploitation in metaheuristic algorithms. The results highlight MFO’s effectiveness, establishing it as the top optimizer across all functions F14 to F23. Even in cases where MFO matches other algorithms in mean index value, it consistently outperforms them in the standard deviation (std) index, indicating more reliable and consistent performance. These findings emphasize MFO’s exceptional capability to balance exploration and exploitation, yielding superior results in comparison to other algorithms when dealing with multi-modal functions of fixed dimensions.

The convergence curves of MFO and the competing algorithms in handling functions F1 to F23 are drawn in Fig. 3. The convergence analysis shows that when dealing with unimodal functions F1 to F7, where these functions have no local optimum, MFO has identified the main optimum region in the initial iterations and is converging towards the global optimum with high exploitation ability. When dealing with multimodal functions F8 to F23, where these functions have local optima, the convergence curves show that MFO with the exploration ability, during successive repetitions of the algorithm, has tried to identify the main optimal area by escaping from local optima and then, relying on the exploitation ability, until the last iterations of the algorithm, it goes through the process of convergence towards better solutions.

Figure 3: Convergence curves of MFO and the competing algorithms for F1 to F23

4.4 Statistical Analysis

In this subsection, using a statistical analysis, it is checked whether the superiority of MFO compared to the competing algorithms is significant from a statistical point of view. For this purpose, the Wilcoxon sign-rank test is used, which is a non-parametric statistical test and has an application to determine a significant difference between the averages of two data samples. In this test, using an index called p-value, it is determined whether there is a significant difference between the performance of the two algorithms or not.

The results of implementing the Wilcoxon sign-rank statistical analysis on the performance of MFO and the metaheuristic algorithms are presented in Table 5. Based on the obtained results, in the cases where the p-value is less than 0.05, MFO has a significant statistical superiority compared to the corresponding competing algorithm. Therefore, it can be seen that MFO has a significant statistical superiority against twelve competing metaheuristic algorithms in handling the evaluated benchmark functions.

5  Application of MFO to Real-World Optimization Problems

In this section, the effectiveness of the MFO proposed approach in dealing with real-world applications is investigated. For this purpose, MFO has been implemented on four engineering design issues: tension/compression spring (TCS) design, welded beam (WB) design, speed reducer (SR) design, and pressure vessel (PV) design. The full description and mathematical model of these problems are provided for TCS in [38], WB in [38], SR in [42,43], and PV in [44].

The results of employing MFO and the competing algorithms in solving the aforementioned engineering problems are reported in Tables 6 and 7. Based on the simulation results, MFO has provided the best design for the TCS problem with the values of the design variables equal to (0.051689061 0.356717739 11.28896583) and the value of the corresponding objective function equal to 0.012665233. In dealing with the WB problem, MFO has presented the best design with the values of the design variables equal to (0.778027075 0.384579186 40.3122837200) and the value of the corresponding objective function equal to 5882.901334. In solving the SR problem, the proposed approach of MFO has provided the best design with the values of the design variables equal to (3.5 0.7 17 7.3 7.8 3.350214666 5.28668323) and the value of the corresponding objective function equal to 2996.348165. MFO has presented the best design of the PV problem with the values of the design variables equal to (0.20572964 3.470488666 9.03662391 0.20572964) and the value of the corresponding objective function equal to 1.724852309.

It can be concluded from the simulation results that MFO has provided a superior performance compared to the competing algorithms by providing better designs and better values for statistical indicators in solving four engineering design problems. Also, the values obtained for the p-value index from the Wilcoxon statistical analysis show that MFO has a significant statistical advantage compared to the competing algorithms. Based on the simulation results, MFO has an acceptable efficiency in handling optimization problems in real-world applications.

6  Concluding Remarks and Future Works

This paper introduces a novel metaheuristic algorithm called Magnificent Frigatebird Optimization (MFO), inspired by the natural behaviors of magnificent frigatebirds. MFO draws its fundamental principles from the kleptoparasitic behavior exhibited by these birds in the wild. The theory behind MFO is elucidated and mathematically formulated into two distinct phases: exploration, which simulates the frigatebird’s attack on food-carrying seabirds, and exploitation, which mimics its diving towards abandoned prey. The efficacy of MFO in solving optimization problems is evaluated across twenty-three standard benchmark functions, encompassing both unimodal and multimodal types. Results indicate MFO’s proficiency in exploration, exploitation, and maintaining a balance between the two, leading to favorable solutions for optimization tasks. Comparative analysis against twelve established metaheuristic algorithms highlights MFO’s superior performance across a range of benchmark functions. Also, the application of MFO to four engineering design problems showed the effective capability of the proposed approach in handling optimization problems in real-world optimization applications.

Moreover, future research avenues include extending MFO to binary and multi-objective optimization problems, as well as exploring its applicability in various scientific domains and real-world applications.

Acknowledgement: Many thanks to the Republic of Kazakhstan and the Committee of Science, Ministry of Science and Higher Education of the Republic of Kazakhstan, for their financial support for research and the promotion of science on a global scale.

Funding Statement: This research is funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. AP19674517).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Tareq Hamadneh, Khalid Kaabneh, Frank Werner, Gulnara Bektemyssova, Dauren Umutkulov; data collection: Khalid AbuFalahah, Galymzhan Shaikemelev, Frank Werner, Dauren Umutkulov; analysis and interpretation of results: Khalid Kaabneh, Khalid AbuFalahah, Gulnara Bektemyssova, Zeinab Monrazeri, Mohammad Dehghani; draft manuscript preparation: Zeinab Monrazeri, Mohammad Dehghani, Tareq Hamadneh, Galymzhan Shaikemelev, Sayan Omarov. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are availale within the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. S. Assiri, A. G. Hussien, and M. Amin, “Ant lion optimization: Variants, hybrids, and applications,” IEEE Access, vol. 8, pp. 77746–77764, 2020. doi: 10.1109/ACCESS.2020.2990338. [Google Scholar] [CrossRef]

2. P. Coufal, Š. Hubálovský, M. Hubálovská, and Z. Balogh, “Snow leopard optimization algorithm: A new nature-based optimization algorithm for solving optimization problems,” Mathematics, vol. 9, no. 21, pp. 2832, 2021. doi: 10.3390/math9212832. [Google Scholar] [CrossRef]

3. A. A. Al-Nana, I. M. Batiha, and S. Momani, “A numerical approach for dealing with fractional boundary value problems,” Mathematics, vol. 11, no. 19, pp. 4082, 2023. doi: 10.3390/math11194082. [Google Scholar] [CrossRef]

4. W. G. Alshanti, I. M. Batiha, M. M. A. Hammad, and R. Khalil, “A novel analytical approach for solving partial differential equations via a tensor product theory of Banach spaces,” Partial Differ. Equ. Appl. Math., vol. 8, pp. 100531, Dec. 2023. [Google Scholar]

5. S. Mirjalili, “The ant lion optimizer,” Adv. Eng. Softw., vol. 83, pp. 80–98, 2015. doi: 10.1016/j.advengsoft.2015.01.010. [Google Scholar] [CrossRef]

6. I. Boussaïd, J. Lepagnot, and P. Siarry, “A survey on optimization metaheuristics,” Inf. Sci., vol. 237, pp. 82–117, 2013. doi: 10.1016/j.ins.2013.02.041. [Google Scholar] [CrossRef]

7. R. G. Rakotonirainy and J. H. van Vuuren, “Improved metaheuristics for the two-dimensional strip packing problem,” Appl. Soft Comput., vol. 92, no. 1, pp. 106268, 2020. doi: 10.1016/j.asoc.2020.106268. [Google Scholar] [CrossRef]

8. T. Dokeroglu, E. Sevinc, T. Kucukyilmaz, and A. Cosar, “A survey on new generation metaheuristic algorithms,” Comput. Ind. Eng., vol. 137, no. 5, pp. 106040, 2019. doi: 10.1016/j.cie.2019.106040. [Google Scholar] [CrossRef]

9. M. Dehghani et al., “Binary spring search algorithm for solving various optimization problems,” Appl. Sci., vol. 11, no. 3, pp. 1286, 2021. doi: 10.3390/app11031286. [Google Scholar] [CrossRef]

10. K. Hussain, M. N. Mohd Salleh, S. Cheng, and Y. Shi, “Metaheuristic research: A comprehensive survey,” Artif. Intell. Rev., vol. 52, no. 4, pp. 2191–2233, 2019. doi: 10.1007/s10462-017-9605-z. [Google Scholar] [CrossRef]

11. K. Iba, “Reactive power optimization by genetic algorithm,” IEEE Trans. Power Syst., vol. 9, no. 2, pp. 685–692, 1994. doi: 10.1109/59.317674. [Google Scholar] [CrossRef]

12. D. H. Wolpert and W. G. Macready, “No free lunch theorems for optimization,” IEEE Trans. Evol. Comput., vol. 1, no. 1, pp. 67–82, 1997. doi: 10.1109/4235.585893. [Google Scholar] [CrossRef]

13. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. IEEE Int. Conf. Neural Netw., Perth, WA, Australia, Nov. 27–Dec. 01, 1995, pp. 1942–1948. [Google Scholar]

14. M. Dorigo, V. Maniezzo, and A. Colorni, “Ant system: Optimization by a colony of cooperating agents,” IEEE Trans. Syst. Man Cybern. B, vol. 26, no. 1, pp. 29–41, 1996. doi: 10.1109/3477.484436. [Google Scholar] [PubMed] [CrossRef]

15. D. Karaboga and B. Basturk, “Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems,” in Proc. IEEE Int. Fuzzy Syst. Conf., Berlin, Heidelberg, Germany, 2007, pp. 789–798. [Google Scholar]

16. X.-S. Yang, “Firefly algorithms for multimodal optimization,” in Proc. 5th Int. Conf Stoch. Algorithms Found. Appl., Berlin, Heidelberg, Germany, 2009, pp. 169–178. [Google Scholar]

17. I. A. Falahah et al., “Frilled lizard optimization: A novel bio-inspired optimizer for solving engineering applications,” Comput. Mater. Contin., vol. 79, no. 3, pp. 3631–3678, 2024. doi: 10.32604/cmc.2024.053189. [Google Scholar] [CrossRef]

18. B. Abdollahzadeh, F. S. Gharehchopogh, and S. Mirjalili, “African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems,” Comput. Ind. Eng., vol. 158, no. 4, pp. 107408, 2021. doi: 10.1016/j.cie.2021.107408. [Google Scholar] [CrossRef]

19. M. Braik et al., “White shark optimizer: A novel bio-inspired meta-heuristic algorithm for global optimization problems,” Knowl.-Based Syst., pp. 108457, 2022. [Google Scholar]

20. C. Zhong, G. Li, and Z. Meng, “Beluga whale optimization: A novel nature-inspired metaheuristic algorithm,” Knowl.-Based Syst., vol. 251, no. 1, pp. 109215, 2022. doi: 10.1016/j.knosys.2022.109215. [Google Scholar] [CrossRef]

21. G. Dhiman and V. Kumar, “Emperor penguin optimizer: A bio-inspired algorithm for engineering problems,” Knowl.-Based Syst., vol. 159, no. 2, pp. 20–50, 2018. doi: 10.1016/j.knosys.2018.06.001. [Google Scholar] [CrossRef]

22. D. E. Goldberg and J. H. Holland, “Genetic algorithms and machine learning,” Mach. Learn., vol. 3, no. 2, pp. 95–99, Oct. 1988. doi: 10.1023/A:1022602019183. [Google Scholar] [CrossRef]

23. R. Storn and K. Price, “Differential evolution–A Simple and efficient heuristic for global optimization over continuous spaces,” J. Glob. Optim., vol. 11, no. 4, pp. 341–359, Dec. 1997. doi: 10.1023/A:1008202821328. [Google Scholar] [CrossRef]

24. W. Banzhaf, P. Nordin, R. E. Keller, and F. D. Francone, “Genetic programming: An introduction,” in the Automatic Evolution of Computer Programs and its Applications, 1st ed., San Francisco, California, USA: Morgan Kaufmann, 1998, pp. 496. [Google Scholar]

25. M. Dehghani et al., “A spring search algorithm applied to engineering optimization problems,” Appl. Sci., vol. 10, no. 18, pp. 6173, 2020. doi: 10.3390/app10186173. [Google Scholar] [CrossRef]

26. E. Rashedi, H. Nezamabadi-Pour, and S. Saryazdi, “GSA: A gravitational search algorithm,” Inf. Sci., vol. 179, no. 13, pp. 2232–2248, 2009. doi: 10.1016/j.ins.2009.03.004. [Google Scholar] [CrossRef]

27. A. Faramarzi, M. Heidarinejad, B. Stephens, and S. Mirjalili, “Equilibrium optimizer: A novel optimization algorithm,” Knowl.-Based Syst., vol. 191, pp. 105190, 2020. doi: 10.1016/j.knosys.2019.105190. [Google Scholar] [CrossRef]

28. K. Luo, “Water flow optimizer: A nature-inspired evolutionary algorithm for global optimization,” IEEE Trans. Cybern., vol. 52, no. 8, pp. 7753–7764, 2021. doi: 10.1109/TCYB.2021.3049607. [Google Scholar] [PubMed] [CrossRef]

29. R. V. Rao, V. J. Savsani, and D. Vakharia, “Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems,” Comput.-Aided Des., vol. 43, no. 3, pp. 303–315, 2011. doi: 10.1016/j.cad.2010.12.015. [Google Scholar] [CrossRef]

30. M. Dehghani, M. Mardaneh, and O. P. Malik, “FOA: Following’ optimization algorithm for solving power engineering optimization problems,” J. Oper. Autom. Power Eng., vol. 8, no. 1, pp. 57–64, 2020. [Google Scholar]

31. P. Trojovský, M. Dehghani, E. Trojovská, and E. Milkova, “Language education optimization: A new human-based metaheuristic algorithm for solving optimization problems,” Comput. Model. Eng. Sci., vol. 136, no. 2, pp. 1527–1573, 2023. doi: 10.32604/cmes.2023.025908. [Google Scholar] [CrossRef]

32. M. Dehghani et al., “A new ‘Doctor and Patient’ optimization algorithm: An application to energy commitment problem,” Appl. Sci., vol. 10, no. 17, pp. 5791, 2020. doi: 10.3390/app10175791. [Google Scholar] [CrossRef]

33. L. Abualigah et al., “The arithmetic optimization algorithm,” Comput. Methods Appl. Mech. Eng., vol. 376, no. 2, pp. 113609, 2021. doi: 10.1016/j.cma.2020.113609. [Google Scholar] [CrossRef]

34. M. Dehghani, E. Trojovská, P. Trojovský, and O. P. Malik, “OOBO: A new metaheuristic algorithm for solving optimization problems,” Biomimetics, vol. 8, no. 6, pp. 468, 2023. doi: 10.3390/biomimetics8060468. [Google Scholar] [PubMed] [CrossRef]

35. X. Yao, Y. Liu, and G. Lin, “Evolutionary programming made faster,” IEEE Trans. Evol. Comput., vol. 3, no. 2, pp. 82–102, 1999. doi: 10.1109/4235.771163. [Google Scholar] [CrossRef]

36. S. Mirjalili, S. M. Mirjalili, and A. Hatamlou, “Multi-verse optimizer: A nature-inspired algorithm for global optimization,” Neural Comput. Appl., vol. 27, no. 2, pp. 495–513, 2016. [Google Scholar]

37. S. Mirjalili, S. M. Mirjalili, and A. Lewis, “Grey wolf optimizer,” Adv. Eng. Softw., vol. 69, pp. 46–61, 2014. [Google Scholar]

38. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Adv. Eng. Softw., vol. 95, no. 12, pp. 51–67, 2016. doi: 10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

39. A. Faramarzi, M. Heidarinejad, S. Mirjalili, and A. H. Gandomi, “Marine predators algorithm: A nature-inspired metaheuristic,” Expert. Syst. Appl., vol. 152, no. 4, pp. 113377, 2020. doi: 10.1016/j.eswa.2020.113377. [Google Scholar] [CrossRef]

40. S. Kaur, L. K. Awasthi, A. L. Sangal, and G. Dhiman, “Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization,” Eng. Appl. Artif. Intell., vol. 90, no. 2, pp. 103541, 2020. doi: 10.1016/j.engappai.2020.103541. [Google Scholar] [CrossRef]

41. L. Abualigah, M. Abd Elaziz, P. Sumari, Z. W. Geem, and A. H. Gandomi, “Reptile search algorithm (RSAA nature-inspired meta-heuristic optimizer,” Expert Syst. Appl., vol. 191, no. 11, pp. 116158, 2022. doi: 10.1016/j.eswa.2021.116158. [Google Scholar] [CrossRef]

42. A. H. Gandomi and X. -S. Yang, “Benchmark problems in structural optimization,” in Computational Optimization, Methods and Algorithms, Berlin, Germany, Heidelberg: Springer, 2011, pp. 259–281. [Google Scholar]

43. E. Mezura-Montes and C. A. C. Coello, “Useful infeasible solutions in engineering optimization with evolutionary algorithms,” in A. Gelbukh, Á. de Albornoz, H. Terashima-Marín, Eds., MICAI 2005: Advanced Artificial Intelligence, Springer: Berlin, Heidelberg, 2005, pp. 652–662. doi: 10.1007/11579427_66 [Google Scholar] [CrossRef]

44. B. Kannan and S. N. Kramer, “An augmented Lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design,” J. Mech. Des., vol. 116, no. 2, pp. 405–411, 1994. doi: 10.1115/1.2919393. [Google Scholar] [CrossRef]

Information about the Test Objective Functions

The information about the objective functions used in the simulation section is presented in Tables A1 to A3.