Heterogeneous Task Allocation Model and Algorithm for Intelligent Connected Vehicles

1  Introduction

1.1 Background

Intelligent Connected Vehicle (ICV) is the new generation vehicle that takes vehicles as the main body and main nodes, combined with intelligent control and Internet of Vehicle communication technology, to enable information sharing and cooperative control between vehicles and external nodes, and achieve safe, orderly, efficient, and energy-saving driving of vehicles. The ultimate goal of ICV is fully autonomous driving. ICVs provide some application services such as driving safety, traffic information services, etc. These services will generate “big” data and computing tasks through their own sensors and interaction with other external network devices during driving. These computing tasks have unique computing and data processing requirements, while also being limited by the computing capability of the vehicle itself. These tasks often require the assistance of network devices with greater computing power to handle real-time information processing, especially in emergency situations such as collision avoidance at intersections or in remote areas [1]. While edge computing and cloud computing offer potential solutions, highly variable traffic environments can cause network connections to change rapidly, requiring computing paradigms capable of handling dynamic tasks [2].

Compared with cloud and edge computing, dispersed computing paradigms exhibit higher task allocation efficiency due to their ability to select optimal computing device locations based on task requirements. Dispersed computing is the introduction of the concept of networked computation points (NCPs) [3]. NCPs is a class of wireless heterogeneous devices with computing capability. The cloud centers, base stations, mobile terminals with computing capability, etc., all of these devices are at the same level. They play the role of NCPs in the dispersed computing network. This distributed network system based on dispersed computing resources not only satisfies the computing tasks offloading, but also shares resource information of various computing nodes in the network when facing computing task requests. From the perspective of task users, NCPs need to meet the computing resource requirements of computing tasks, ensure task completion, and enable task users to obtain as many advantageous computing resources as possible. From the perspective of NCPs themselves or the entire system, limited by the idle computing resources that NCPs can provide, NCPs not only need to distribute task requests to other NCPs when they exceed their computing capability, but also need to attract tasks from other overloaded nodes when they still have idle resources, in order to improve the effective utilization of computing resources [4,5].

Dispersed computing uses the idle computing resources provided by NCPs to facilitate computing resource cooperation in ad-hoc networks. This approach aligns with the concept of vehicle ad-hoc networks [6]. Meanwhile, vehicular tasks that rely on dispersed computing require access to the computing capabilities of NCPs. Assigning tasks in a dynamic and heterogeneous network environment presents several challenges that must be considered. Considering the significant differences in data size and computational complexity among different vehicle tasks in practice. Efficient scheduling and allocation of heterogeneous tasks are crucial for dispersed computing. Likewise, NCPs vary greatly in both computing resources and communication capabilities. Coordination of task offloading strategies and NCP resource allocations is essential. Thus, it is imperative to design an efficient and joint task allocation mechanism.

1.2 Motivation and Contributions

This paper will examine the way in which the matching problem between task ICVs and NCPs in a dispersed computing environment. In response to the latency and data rate requirements of specific ICV services, when vehicle tasks exceed their own computing capabilities or have other requirements, it is necessary to utilize other NCPs with idle resources in the dispersed computing system to accomplish task computing that the vehicle itself is unable to achieve. On this basis, computing task offloading and resource allocation algorithms should be designed. To solve the problem of maximizing the utilization of dispersed computing resources suitable for ICV services, it is necessary to establish a selection strategy between task ICVs and NCPs based on the preference lists. Furthermore, a many-to-many matching algorithm should be designed to achieve efficient matching between tasks and resources.

To address the aforementioned challenges, our paper makes several contributions to this field. The following specific revisions could be made for each numbered contribution:

1) We establish a dispersed network consisting of multiple ICVs and NCPs. By leveraging idle computing resources shared by NCPs based on task requirements, we establish the problem formulations for maximizing the comprehensive resource utilization rate and task completion efficiency, and we prove the problem is a Non-deterministic Polynomial-hard Problem (NP-hard).

2) We propose a preference mechanism to construct a preference list for both task ICVs and NCPs based on their different requirements and optimize the scheduling of both ICVs and NCPs.

3) We design a many-to-many matching algorithm that transforms ICVs-NCPs matching into task-resource matching. We also prove the stability of the solution and the upper bound of the algorithm’s computational time complexity.

In the paper, the research contents are as follows. In Section 2, we review the related work of resource allocations. In Section 3, we present the system model and problem formulation. In Section 4, we present the preference mechanism and many-to-many matching algorithm for ICVs and NCPs. In Section 5, we validate our model and algorithm by numerical simulations. Finally, in Section 6, we propose the conclusions and prospects.

2  Related Work

2.1 Task Allocation

Since 2018, the Autonomous Networks Research Group at the University of Southern California has been conducting research on dispersed computing. Yang et al. [7] proposed a maximum weight strategy for the directed acyclic graph (DAG) scheduling problem in dispersed networks, and proved the effectiveness of the proposed strategy. Nguyen et al. [8] proposed corresponding optimal scheduling strategies for end-to-end transmission delays in dispersed computing systems using secure copy. The delay is fitted as the optimal quadratic regression function for file size. Hu et al. [9] duplicated and split computationally intensive tasks (videos) to improve the throughput of dispersed computing systems under different task loads comprehensively. Ghosh et al. [10,11] proposed a dispersed computing network architecture based on container orchestration. This system enables efficient task offloading among NCPs. Kao et al. [12] proposed an online learning algorithm to achieve a better task offloading policy than best offline by continuously learning the performance of unknown computing nodes. Coleman et al. [13] synthesized a set of NCPs into a dispersed computing network framework for distributed execution of complex tasks on a group basis. The scalability of the proposed framework is also discussed so that it has general attributes. The Autonomous Networks Research Group is the main participant in the dispersed computing project. The researches mentioned above are based on DAG and provides a reference for follow-up researchers from the perspective of dispersed computing architecture.

Researchers from other institutions have investigated the theory and applications of dispersed computing. Rahimzadeh et al. [14] proposed a dispersed computing task scheduling system for image stream processing. Compared with traditional algorithms, its processing efficiency on real images has been greatly improved. Aiming at minimizing the total energy consumption of dispersed computing systems, Wu et al. [15] proposed a bilateral matching algorithm to rationally allocate computing resources and achieve the optimal selection of task offloading nodes. Zhou et al. [16] considered the feasibility of task allocation and resource scheduling in dispersed computing systems. The proposed system is proved through mathematical theory that is stable and feasible. A resilient resource allocation method when the dispersed network has failed nodes is further proposed in [17]. Even if the network degrades, task completion is still guaranteed.

2.2 Computing Resource Allocation

From the existing research results, energy consumption, latency, and resource utilization are still the key and difficult fields of computing resource allocation research. According to the research objectives of this paper, the focus is on reviewing existing research results from two aspects: delay-driven resource allocation and resource utilization-driven resource allocation.

Zhou et al. [18] aimed at the problem of computing resource allocation between vehicles and user devices, they proposed a stable matching algorithm based on the two-sided matching game with the goal of minimizing network delay (including transmission and task processing delay) and adopted a pricing mechanism to achieve stable matching between users and vehicles. Wang et al. [19] proposed a delay minimization algorithm for task allocation, computing resources, and transmission resources allocation between edge devices, multi-layer heterogeneous mobile edge servers, and cloud servers. The proposed algorithm can minimize the total computation and transmission time of edge computing networks. Fan et al. [20] aimed to reduce the response delay of all tasks. They designed an online reinforcement learning algorithm to solve the resource coupling problem of dynamic tasks in the fog computing environment. Guo et al. [21] established an edge node-oriented throughput model. With the objective of minimizing the packet average delay, a delay-sensitive resource allocation algorithm based on dominant role evaluation is proposed. Wan et al. [22] addressed research on vehicle task offloading and computing resource allocation in mobile edge environments. In order to minimize the total latency of task transmission and computation, they investigated the model and algorithm based on a multi-layer matching strategy. Wu et al. [23] proposed an extended deep-Q-learning algorithm to enable intelligent vehicular nodes to learn the dynamic environment and predict the optimal minimum contention window.

Resource utilization is one of the important metrics for computing resource providers to assess system costs. Since the dispersed resources of NCPs are all very limited, it is especially important to allocate and optimize dispersed resources and utilize them rationally. Wang et al. [24] proposed a detailed multi-layer computing model and optimization method. The purpose is to use a multi-layer computing system to effectively combine fog computing and edge computing to achieve effective task offloading and resource allocation. In order to provide low latency services to heterogeneous users in the industrial internet of things. Kumar et al. [25] established a game theory-based resource utilization maximization allocation model. The allocation of computing resources to multiple users is achieved by minimizing the service cost through virtual pricing of invoking edge servers. Yi et al. [26] proposed a branch-and-price greedy algorithm to realize the multi-dimensional computation resource allocation. They jointly optimized latency and resource utilization in the paper. Dispersed computing serves as a complement to other computing paradigms. Relevant studies of other computing paradigms can provide inspiration when designing task offloading and resource allocation algorithms for dispersed computing [27,28].

In summary, most of the existing research on dispersed computing has ignored the heterogeneity of NCP and tasks. In addition, the dispersed computing scenario has its special characteristics compared to other application scenarios. Tasks such as traffic safety and autonomous driving directly involve human life safety, and the latency and reliability requirements for task processing are almost perfect, and they must be based on the completion of the task. Finally, none of the above references considers the waste of computing resources. This is particularly important for resource constrained scenarios. The allocation of computing resources in ICVs scenarios has its particularity, and existing research has provided various computing resource allocation schemes, with optimization goals focused on energy consumption and latency. In addition, how to better utilize NCPs computing resources in a dispersed computing network environment is also a worthwhile research question. The summary of the literature work is shown in Table 1.

3  System Model and Problem Formulation

3.1 System Model

Referring to the dispersed computing network framework proposed in [3], we model a dispersed computing network for heterogeneous ICVs applications, and the model is established on the dispersed computing layer between the application layer and the physical layer, see Fig. 1 below. We assume that there are n ICVs and m NCPs in the dispersed computing network, V and P are used to represent the collection of task ICVs and NCPs, respectively:

Figure 1: Dispersed computing network for heterogeneous ICV tasks

V={v1,…,vi,…,vn}P={p1,…,pj,…,pm}(1)

where n < m. Let N = {1, 2, …, n}, M = {1, 2, …, m}. The arrival of ICVs and NCPs obeying the Poisson process. For a certain ICV, other ICVs with no tasks and available resources can also be NCPs.

cvi,ri represents that vehicle vi can divide the task size into ri units based on the different tasks, with each unit having a data volume of cvi,ri. Each NCP pj is considered as a resource pool, and bpj,rj represents that the computing resources in the resource pool of NCP pj can be divided into rj resource units, with each unit having a computing resource of bpj,rj. Corresponding to different task requests of vehicle vi based on different resources. Each resource unit can only execute task requests from one vehicle task unit at the same time, and each vehicle can use multiple resource units from the same NCP or between different NCPs. Therefore, the matching problem between vehicle tasks and NCPs is transformed into a many-to-many matching problem between task unit cvi,ri and resource unit bpj,rj. The task matrix of all vehicles and the resource matrix of NCPs are represented as:

𝒞=[C1,…,Cn]T(2)

ℬ=[B1,…,Bm]T(3)

where Ci={cvi,1,…,cvi,ri}, Bj={bpj,1,…,bpj,rj}.

Considering the total task volume of task vehicles in a batch and the total resources that NCPs can provide, we can obtain:

∑i=1nCi≤∑j=1mBj(4)

Specifically, for a certain task vehicle, the relationship between its task volume and required resource volume can be expressed as:

Ci≤∑j=1qBj,1≤q<m(5)

Therefore, the resource utilization rate corresponding to the execution of ICV tasks can be expressed as:

Q1=∑i=1n∑j=1mxijCi(Bj)i(6)

where xij is a binary variable that represents the matching relationship between task ICVs and NCPs. xij = 1 represents that ICV vi has a task executing computation at NCP pj. Otherwise, xij = 0. (Bj)i is the total resource unit corresponding to pj paired with vi. Furthermore, considering the particularity of ICV tasks, their execution time should not exceed the strong time delay constraint required by the task. Therefore, the execution time efficiency of ICV tasks can be expressed as:

Q2=1n∑i=1ntit(ci)(7)

where ti and t(ci) represent the task execution time and task delay constraints of vi, respectively.

3.2 Problem Formulation

Referring to the characteristics that ICV task allocation should have, the goal of this study is to maximize the quality of task completion. Based on the above proposed dispersed computing network for heterogeneous ICV applications, considering latency and resource utilization, the optimization problem of maximizing resource utilization is modeled as:

maxRQ=Q1+Q2−1(8)

s.t.∑i=1nxij≤Bj,∀j∈P(8a)

∑j=1mxij≤Ci,∀i∈V(8b)

∑i=1nCi≤∑j=1mBj,∀i∈V,j∈P(8c)

Ci≤∑j=1qBj,∀i∈V,j∈P,q<M(8d)

(cvi,ri)j≤bpj,rj,∀i∈V,j∈P(8e)

ri∈Z+,rj∈Z+,∀i∈V,j∈P(8f)

xij∈{0,1},∀i∈V,j∈P(8g)

ti<t(ci),∀i∈V(8h)

where R is the set of all task scheduling strategies. Eqs. (8a) and (8b) ensure that the number of matching pairs does not exceed the number of vehicle task units and NCP resource units. Eq. (8c) indicates that the total number of vehicle tasks is less than the total number of resource units that the NCP can provide. Eq. (8d) represents the resource units of the vehicle task count not exceeding q(≥1) NCPs, which depends on the results of preference matching. The calculation of preference values will be introduced in the next section. Eq. (8e) ensures that the data size unloaded from task vehicle v to NCP p does not exceed the currently available resource size of p. Eq. (8f) ensures that the number of task units for vehicle segmentation and the number of resource units for point segmentation are positive integers. Eq. (8h) is a time constraint to ensure that the task execution time is less than the allowed threshold. Obviously, the problem described by Eq. (8) and their constraints is NP-hard.

Theorem 1: Problem (8) is NP-hard.

Proof: Optimization problem (8) is a mixed integer nonlinear problem. By using the constraint method, the constrained optimization problem (8) can be transformed into a 0–1 knapsack problem to prove that (8) is NP-hard.

Regarding question (8), consider a special case where ti=t(ci),∀i∈V. In this case, it means that the time spent executing each task is exactly equal to the delay threshold of the task. At this point, problem (8) can be transformed into the following special form:

maxxi∈{0,1}1∑j=1m′Bj∑i=1nxi⋅Ci(9)

s.t.∑i=1nxi⋅Ci≤∑j=1m′Bj(9a)

Given N items with their values {v1,…,vn} and weights {w1,…,wn}, we want to determine which items to package to maximize the total value and satisfy the total weight constraint, that is:

maxxi∈{0,1}∑i=1nxi⋅Ci(10)

s.t.∑i=1nwi⋅μi≤B(10a)

Problem (10) is a common expression of the 0–1 knapsack problem, and Problem (9) can be reduced to (10) by the following encoding:

{Ci=μi∑j=1m′Bj=B(11)

where m′,m′≤m is the number of all matched NCPs.

By providing input (8)–(10) can be accurately solved, resulting in:

(10)≤P(9)≤P(8)(12)

Since the 0–1 knapsack problem is an NP-hard problem, problem (8) is at least as difficult as the 0–1 knapsack problem, that is, problem (9) is NP-hard. By considering both Steps 1 and 2, it can be proven that problem P4–1 is NP-hard. Theorem 4–1 has been proven.

3.3 Rationality Assumptions

1) Only the matching between the current round of vehicles and NCPs is considered, and only the latest preference values of the current round are saved in the preference list for each vehicle and NCP.

2) The information sent between the vehicle and the NCP is genuine and there are no malicious messages or attack threats.

3) Communication loss is not considered, and idle resources can be fully utilized.

4) The NCP must enable secure, mission-responsive resource sharing [3].

4  Algorithm Design and Characteristic Analysis

According to the original optimization problem is NP-hard, problem (8) can be divided into two sub problems, namely the NCP scheduling of task vehicles in each batch and the problem of minimizing the execution delay of ICV tasks. Consider a two-layer iterative optimization process, in which the task execution time obtained from the previous iteration is used to solve the scheduling problem and obtain the NCP scheduling result. Then, the obtained point scheduling is used to solve the delay minimization problem. The two sub-problems affect each other and ultimately obtain the optimal overall performance result.

4.1 User Scheduling Based on Preferences

When determining a pairing relationship between ICVs and NCPs, they can possess specific preferences based on their own conditions and be sorted by the degree of satisfaction. And the most suitable matching object is selected according to the preference list. Next, we will discuss the ICV-to-NCPs-based vehicle preference management architecture.

Preference principles: plays a task publisher role in dispersed computing. The preferences of ICV can be divided into two points: Firstly, to ensure task completion, i.e., the computing resources of the requested pairing NCPs are not less than the computing resources required for task completion. The second is task completion time. The closer of the communication distance, the shorter the signal transmission time. The stronger the computing capacity, the shorter the time to complete the computing task. Therefore, ICV prefers NCP with close range and high computing capacity.

We propose a preference model that considers different preference principles. The preference evaluation value of ICVs for NCPs can be calculated as:

RijV=I+W⋅Ej⋅ϕ(vi,pj)ψ(vi,pj)+1,if(li−lj)≤Li(13)

ϕ(vi,pj)=1−Ci−BjBj,Bj>Ci2(13a)

ψ(vi,pj)=(li−ljLi)2(13b)

where Ei is the preference initial value of NCPs. W is the weight factor that reflects the reliability of network preference transmission. Once preferred matching devices are more reliable than new ones. Eq. (13a) is called resource function, which indicates the adaptability of task required resources Ci and NCP resources Bj, and always positive. Eq. (13b) is the normalized distanced function. li−lj=(xi−xj)2+(yi−yj)2 is the Euclidean distance from vi to pj, Li is the maximum transmission range of vi. Eq. (13) indicates vi preference pj depends on resource adaptation and distance between them. The farther the distance, the lower the preference. RijV=0 when li−lj>Li. When the amount of resources owned by pj is closer to the number of resources required by vi, vi prefers pj more, which means simpler matching choices. Eq. (13) can be calculated by executing Algorithm 1.

NCP plays a task performer role in the network. The preference of NCP is also divided into two points: one is auxiliary task completion; NCP will prefer tasks more that can be completed. The second is resource conservation. As a provider of computing resources, NCP applies the fewest resources to complete the most tasks, minimizing the waste of computing resources as much as possible.

Similarly, the preference of NCP is usually determined by the preference evaluation value. The preference evaluation value of NCPs for vehicles can be calculated as:

RijP=Wψ(pj,vi)+1−Wϕ(pj,vi),if(li−lj)≤Li(14)

ϕ(pj,vi)=1−|Ci−Bj|Bj(14a)

ψ(pj,vi)=(lj−liLi)2(14b)

Eq. (14) is different from (13). The function φ(*) in (13a) indicates that task vehicles prefer NCPs with strong computing capability. The function φ(*) in (14a) indicates that NCPs prefer task vehicles with similar capability requirements. According to (14), we can obtain the preference sequence of all NCPs regarding vehicles.

According to Algorithm 1, the preference sequence vector of vi about pj can be expressed as:

R(vi)=(Ri1v,Ri2v,…,Rimiv),mi<m(15)

where Rijv indicates that pj is ranked by vi in the Rijv-th position. mi<m is the number of NCPs that finally fulfill the preference requirements of vi. The algorithm of preference sequence calculation of R(pj) is similar to R(vi), and we will not be introduced in detail. The preference sequence vector of pj about vi can be expressed as:

R(pj)=(R1jp,R2jp,…,Rnjjp)T,nj<n(16)

The preference list is established as:

R(V)=[Rijv]n×m(17)

R(P)=[Rijp]m×nT(18)

where the preference value that does not form a preference relationship in the matrix is represented by 0. Note that the preference matrices R(V) and R(P) are incomplete, and the original optimization problem (8) can be transformed into:

maxR⁡Q=Q1+Q2−1s.t.(8a)∼(8h)∀i∈R(V),j∈R(P)(19)

The constraints in (19), the selection of task ICVs and NCPs have changed from the original set to selecting from a preference list.

4.2 Many-to-Many Matching Algorithm

The problem (19) is the NP-hard problem can be solved by methods such as heuristic algorithms, it has limitations in reducing latency and complexity. The heterogeneity of dispersed computing networks makes the problem more difficult to solve. Thus, there is an urgent need for a method that can satisfy the characteristics of reliability, low latency, and low complexity. Therefore, we propose Algorithm 2 based on preference matching to solve the optimization problem described in (19).

4.3 Performance Analysis of Algorithm

According to Theorem 1, the optimization problem (8) is an NP-hard. However, the solving process and complexity of the problem (15) have been simplified by defining Algorithm 1 and Algorithm 2.

Theorem 2: If the preference sequence matrix of R(V) and R(P) are strict, then the matching solution f1 of the optimal problem (8) obtained by Algorithm 2 is stable.

Proof: Suppose the matching solution is not stable, then matching pairs ps∈f1(vi),pj∈f1(vr) are existing, where vi,vr∈V,pj,ps∈P. And since the preference sequence matrix of R(V) and R(P) are strict, there is tijv≻tisv in the matrix R(V), which means that pj forms a matching pair pj∈f1(vi) with vi earlier than ps. This contradicts the hypothesis that pj∈f1(vr). Therefore, there is no unstable matching pair in the matching solution calculated by Algorithm 2, i.e., the matching solution f1 is stable.

Theorem 3: If the preference sequence matrix of R(V) and R(P) are strict, then the matching solution f1 of the problem (8) obtained by Algorithm 2 is optimal for the task vehicle.

Proof: Suppose that there is a non-optimal matching pair (vi, pj) in the match f1. It means that (vi, ps) is an optimal matching pair. But ps is matching with vr. That is tisv≻tijv,trsv≻tr∗v and trsp≻tisp.

In the stable matching f1′, there must be a matching pair (vi, ps). Suppose vr is matching with pq at this time, where pq≠ps. And trsv≻tr∗v indicates that (vr, ps) must exist in the matching f1′. This contradicts with (vi, ps) in f1′. According to the above results, the assumptions are not tenable. The matching solution is optimal for task vehicle. Proof done.

Theorem 4: The time complexity of preference algorithm is O(nm).

Proof: During the preference computation, memory consumption is negligible and only computation cost is considered. Each NCPs receives the information (length m) from each ICV. The time consumption of is plausibility check is less than the length of the information table, as the maximum time of plausibility check is O(m). n ICVs send task and preference match, that is, each NCP performs n check at most. Thus, the total time complexity of the preference algorithm is O(nm). Proof done.

5  Numerical Evaluations

In this section, datasets were constructed based on different ICV task types, and an experimental platform was built based on Python and MATLAB/Simulink using a laptop with Intel i5-6200U CPU@2.4 GHz. The correctness and effectiveness of the proposed algorithm were verified through numerical simulation experiments.

5.1 Simulation Experiment Setup

Within an area of 2000 m × 2000 m, ICVs and NCPs are randomly dispersed as shown in Fig. 2. There are fixed numbers of 150, 300 and 50 ICVs for each of the three task types. The initial number of three types of NCP is 150, 300, and 20, respectively. Fig. 2 shows the distribution of ICVs with heterogeneous task types and NCPs with heterogeneous computing capabilities at a certain moment, where all task ICVs are randomly dispersed on the roads of the block, N-1 and N-2 NCPs are randomly dispersed within the region, and N-3 NCPs are randomly dispersed in the center of 20 out of 25 blocks.

Figure 2: Task completion rate under different numbers of NCPs

Each vehicle randomly sends tasks to NCPs based on their types and requirements, so ICVs and NCPs are categorized into three types. Type-1 vehicles (V-1): tasks of autonomous driving; Type-2 vehicles (V-2): tasks of traffic safety; Type-3 vehicles (V-3): tasks of vehicular entertainment. Type-1 NCPs (N-1): Large quantity, small computing resources, near the task vehicle, such as smartphones. Type-2 NCPs (N-2): The quantity, computing resources, and distance all are medium. Such as personal computers. Type-3 NCPs (N-3): Small quantity, large computing resources, far away from the vehicle. Such as terminal servers. The important characteristics of ICVs and NCPs are specified in Table 2, Some parameters in Table 2 refer to [29].

To evaluate the performance of the matching algorithm proposed in this paper, several types of algorithms were selected for comparison:

Traditional matching game algorithm: only considering the preferences between the task ICV and NCP, the task vehicle initiates a request, and the NCP responds and chooses to accept or reject, with the aim of obtaining a stable match.

Greedy algorithm: Select NCPs nearby for task vehicles until the task requirements are met.

Alternating Direction Method of Multipliers (ADMM) algorithm [30]: A distributed algorithm that alternately updates variables.

5.2 Simulation Results and Analysis

By and large, our proposed matching algorithm has demonstrated good performance and can effectively complete the computational tasks of a dispersed computing network.

1) Task completion ratio: In terms of task completion ratio, we fixed the number of N-3 in our simulation. As we increased of N-1 and N-2, the task completion ratio approached 100%. By observing Fig. 3, it can be seen that when the number of NCPs and corresponding types of ICVs is 2:1, the task completion rate can reach 100%. In real life, N-1 (such as smartphones) is much more common than N-2. Therefore, increasing the number of N-1 is more realistic than increasing N-2. Obviously, it is superior to the matching algorithm proposed by [31].

Figure 3: Task completion rate under different numbers of NCPs

2) Resource utilization rate of NCPs: As shown in Fig. 4, we demonstrate the resource utilization rate under different numbers of NCPs. In general, the resource utilization rate corresponding to V-2 is lower compared to the other two types of ICVs. When the number of NCPs is 300/300/20, the utilization rate of V-2 is higher than that of V-3. The reason is that the increase in N-1 provides more options for V-1 and V-2, and the quantity of V-1 is relatively less, so the resource utilization rate of V-2 will increase more. When the total number of NCPs is 770. Compared to the scenario with 150/600/20, the number of NCPs is 450/300/20 has the highest overall resource utilization rate. This is because N-1 has a lower computational capacity, and as per Algorithm 2, it allows for a wider range of matches. N-1 can also choose a more suitable vehicle for pairing.

Figure 4: The utilization rate of computing resources to complete various tasks

3) Delay of vehicle tasks: In Fig. 5 and Fig. 6, the simulation results of delay of vehicle tasks show that increasing the number of N-2 outperforms increasing N-1 in terms of total delay. The average delay of V-1 decreases regardless of whether N-1 or N-2 is increased (Fig. 5). Comparing two scenarios with the same number of NCPs (150/600/20 and 450/300/20), The delay for V-1 decreased by 6.50% and for V-2 decreased by 5.40%, while the delay for V-3 increased by 3.00%. When the number of NCPs is 150/600/20, the increase of N-2 will be prioritized to be allocated resources by V-3. As a result, the average delay of V-2 increases, and the average delay of V-3 decreases. However, it can be observed from Fig. 7 that the normalized delay performance gradually reduces. The total delay for all vehicles decreased by 1.86% (Fig. 6). When comparing the two scenarios 150/600/20 and 450/300/20, V-2, V-3 and total delay all increase except for V-1.

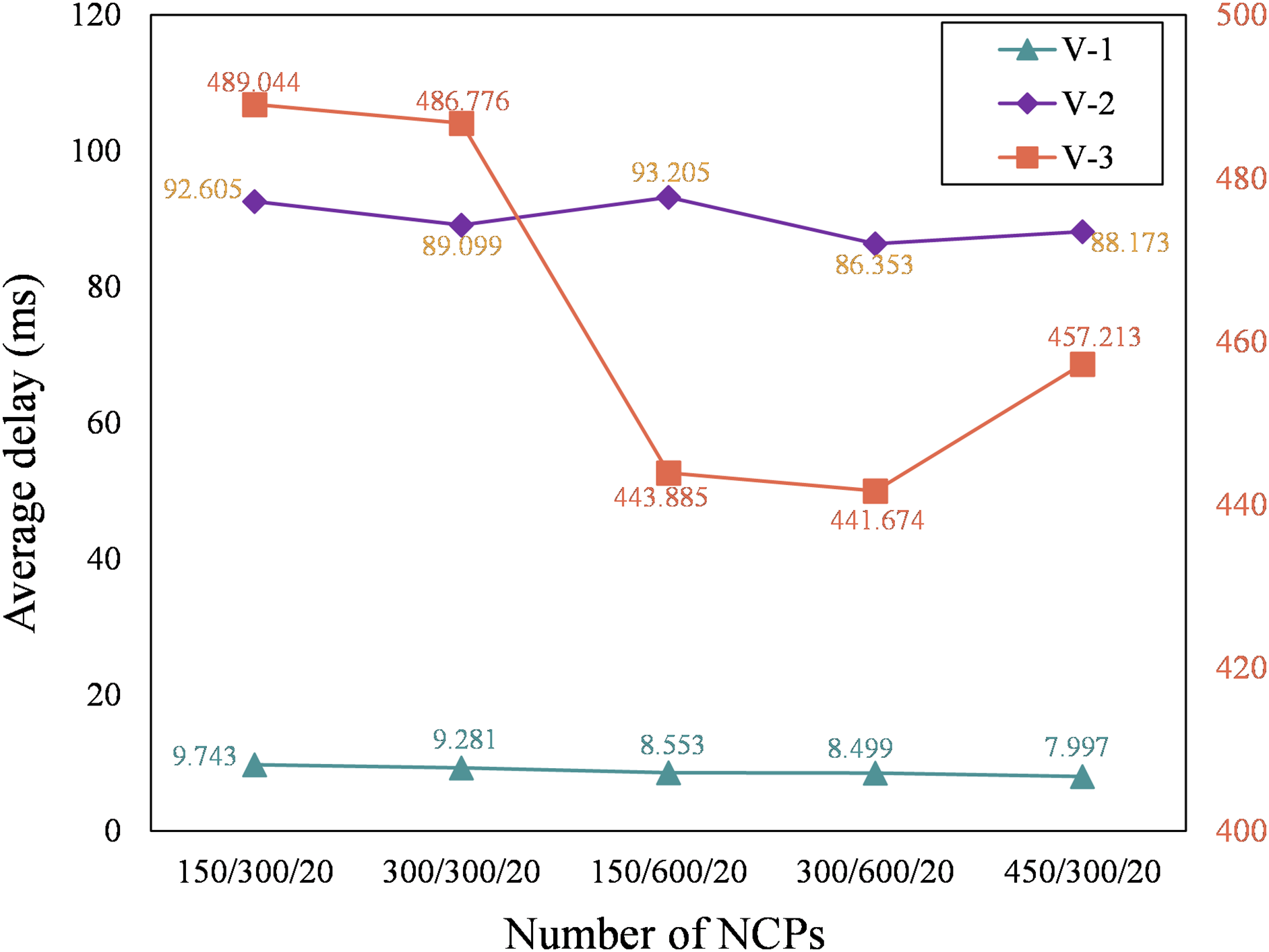
Figure 5: The average delay corresponding to completing different vehicle tasks

Figure 6: The total delay corresponding to completing different vehicle tasks

Figure 7: Performance indicators under different numbers of NCPs

4) Total performance: Fig. 7 shows the performance indicators after normalizing resources and latency according to Eq. (8). It can be seen that as the number of NCPs increases, the impact on latency performance is not significant. The reason is that although the optimization of latency performance is considered in the goal, latency also appears as a constraint condition, with time thresholds for each type of task. The resource performance target increases with the increase of NCPs, which is obvious because the increase of NCPs means that there are more matching objects available for selection.

At the same time, the increase in resource NCPs near the task ICVs also indirectly affects the time consumption and transmission delay in the matching process. When the number of NCPs is the same, the latency index in the 450/300/20 scenario is better than that in the 150/600/20 scenario. After adding computational resource indicators, 450/300/20 has better performance. This is due to the fact that N-1 NCPs have fewer idle resources, making it easier to find matching objects in the matching process based on effective resource utilization. When matching tasks with the same amount of data, even if it causes resource waste, its effective utilization rate is higher.

5) Performance comparison with other algorithms

We will conduct numerical experiments to compare the algorithm proposed in this paper with traditional matching games, greedy algorithms, and ADMM algorithms, and explore the effectiveness of the proposed algorithm, as shown in Figs. 8 to 9. Based on the previous experiments, the initial number of NCPs is set to 450/300/20, and the number of ICVs is the same as before.

Figure 8: Comparison of resource and delay performance with other algorithm

Figure 9: Comparison of total performance with other algorithm

Figs. 8 to 9 show the numerical experimental comparison results between the proposed algorithm and existing algorithms in this paper. As shown in the figure, traditional matching games perform worse than greedy algorithms in various performance indicators when there are fewer NCPs. As the number of NCPs increases, the performance indicators of traditional matching games perform better than greedy algorithms. This is because greedy algorithms prioritize selecting NCPs closer in distance, which can match task ICVs to NCPs faster and reduce queuing waiting time. As the number of NCPs increases, the number of NCPs with lower adaptability around the task ICV also increases, so their performance indicators will fluctuate with the changes in NCPs. Overall, whether it is traditional matching games or greedy algorithms, the many-to-many matching algorithm based on mutual preferences proposed in this paper is more effective in various performance indicators.

The overall performance index of the ADMM algorithm gradually approaches the many-to-many matching algorithm based on mutual preferences as the number of NCPs increases. The reason is that the ADMM algorithm decomposes the original optimization problem into several sub problems and solves them in parallel, resulting in a small error between the final result and the optimal result. The many-to-many matching algorithm based on the preferences of both parties can maintain performance indicators close to ADMM in the case of a large number of computing NCPs. As shown in the above chart, the proposed method can better improve the performance of the system when the number of NCPs is small, and the algorithm with fewer NCPs is better than the ADMM algorithm. This is fully in line with the characteristics of dispersed computing networks, which fully utilize the available dispersed resources in the surrounding area when resources are limited, and maximize the Quality of Services (QoS) requirements of tasks. The characteristics of the ADMM algorithm are strong computing power and fast convergence speed. However, the computational time complexity of each iteration of the proposed algorithm is O(N2M), while the computational time complexity of the ADMM algorithm is O(N4). Compared to ADMM, the proposed algorithm significantly reduces complexity. The proposed algorithm requires the most 15 iterations to obtain the optimal solution, and although ADMM also has the characteristic of fast convergence speed, it converges to the optimal state after 18 iterations (Fig. 10). Therefore, from the perspective of computational complexity and iteration speed, the proposed algorithm also has advantages.

Figure 10: Number of iterations

Compared with previous studies [30,31], the innovation of the model and algorithm proposed in this chapter lies in: 1) Considering the heterogeneity of tasks and NCPs in dispersed computing scenarios, which conforms to the characteristics of task offloading and allocation based on dispersed computing; 2) Unlike literature [30], the optimization objective of this chapter is to maximize task completion rate with optimal resource utilization as the constraint. Compared with research that only focuses on network throughput, this approach focuses more on the utilization of limited resources in dispersed computing environments; 3) For the three common application scenarios in the dispersed computing network scenario, considering the coexistence of the three types of applications, it has a more complex topology compared to the single task QoS requirement in Reference [30], but it can also achieve good task completion rate.

6  Conclusion and Future Work

This paper investigates how to ensure the minimum latency of ICV tasks and the maximum resource utilization of NCPs in dispersed computing networks. Firstly, we establish an optimization model for the correlation between the two parties through NCPs serving task ICVs. Secondly, in the optimization model, factors such as resource constraints of NCPs are considered. By introducing two factors: resource adaptability and communication range, a preference sequence between ICVs and NCPs is established. The task allocation problem can be transformed into a many-to-many matching problem. A resource preference based many-to-many matching algorithm is proposed, which ensures the application requirements of task ICVs through the matching and resource allocation of both. Finally, by comparing with different optimization schemes, the proposed algorithm has advantages in performance such as task completion rate, convergence, and resource utilization, which proves its superiority and effectiveness. The results show that the average task completion rate of the proposed scheme is greater than 95.8%, and the average resource utilization rate is greater than 83.6%. In terms of resource utilization performance and total performance, the proposed scheme is at least 9.6% and 4.0% better than the reference scheme, respectively.

In the future, this research can be further improved in the following ways: i) The proposed algorithm can be verified with real data; ii) We can expand the preference list by introducing time variables and historical preference values to update the preference list over time.

Acknowledgement: The authors would like to thank the editors and reviewers for their valuable work, as well as the supervisor and family for their valuable support during the research process.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Grant No. 62072031), the Applied Basic Research Foundation of Yunnan Province (Grant No. 2019FD071), and the Yunnan Scientific Research Foundation Project (Grant 2019J0187).

Author Contributions: The authors confirm contribution to the paper as follows: write the main manuscript text, design the methodology, conduct a research and investigation process, specifically perform the experiments and data collection/analysis, polish the language of the manuscript, search for relevant reference, and summarize the related work: Neng Wan; provide guidance on experimental ideas, supervise and lead the planning and execution of research activities: Guangping Zeng, Xianwei Zhou. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analyzed during this study are included in this article and are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. García-Valls, A. Dubey, and V. Botti, “Introducing the new paradigm of social dispersed computing: Applications, technologies and challenges,” J. Syst. Archit., vol. 91, no. 7, pp. 83–102, Nov. 2018. doi: 10.1016/j.sysarc.2018.05.007. [Google Scholar] [CrossRef]

2. S. Yuan, G. Xia, J. Chen, and C. Yu, “Toward dispersed computing: cases and state-of-the-art,” in Proc. 17th Int. Conf. Mobility Sens Netw, Exeter, UK, Dec. 2021, pp. 710–717. [Google Scholar]

3. M. R. Schurgot, M. Wang, A. E. Conway, L. G. Greenwald, and P. D. Lebling, “A dispersed computing architecture for resource-centric computation and communication,” IEEE Commun. Mag., vol. 57, no. 7, pp. 13–19, 2019. doi: 10.1109/MCOM.2019.1800776. [Google Scholar] [CrossRef]

4. A. Paulos et al., “Priority-enabled load balancing for dispersed computing,” in Proc. IEEE 5th Int. Conf. Fog. Edge Comput., Melbourne, Australia, May 2021, pp. 1–8. [Google Scholar]

5. N. Hu, Z. Tian, X. Du, N. Guizani, and Z. Zhu, “Deep-Green: A dispersed energy-efficiency computing paradigm for green industrial IoT,” IEEE Trans. Green Commun. Netw., vol. 5, no. 2, pp. 750–764, Jun. 2021. doi: 10.1109/TGCN.2021.3064683. [Google Scholar] [CrossRef]

6. Z. Niu, H. Liu, X. Lin, and J. Du, “Task scheduling with UAV-assisted dispersed computing for disaster scenario,” IEEE Syst. J., vol. 16, no. 4, pp. 6429–6440, Dec. 2022. doi: 10.1109/JSYST.2021.3139993. [Google Scholar] [CrossRef]

7. C. S. Yang, R. Pedarsani, and A. S. Avestimehr, “Communication-aware scheduling of serial tasks for dispersed computing,” IEEE ACM Trans. Netw., vol. 27, no. 4, pp. 1330–1343, Aug. 2019. doi: 10.1109/TNET.2019.2919553. [Google Scholar] [CrossRef]

8. Q. Nguyen, P. Ghosh, and B. Krishnamachari, “End-to-end network performance monitoring for dispersed computing,” in Proc. Int. Conf. Comput., Netw. Commun., Maui, HI, USA, Mar. 2018, pp. 707–711. [Google Scholar]

9. D. Hu and B. Krishnamachari, “Throughput optimized scheduler for dispersed computing systems,” in Proc. 7th IEEE Int. Conf. Mob. Cloud Comput. Services Eng., Newark, CA, USA, Apr. 2019, pp. 76–84. [Google Scholar]

10. P. Ghosh, Q. Nguyen, and B. Krishnamachari, “Container orchestration for dispersed computing,” in Proc. 5th Int. Workshop Container Technol. Container Clouds, New York, NY, USA, Dec. 2019, pp. 19–24. [Google Scholar]

11. P. Ghosh et al., “Jupiter: A networked computing architecture,” in Proc. IEEE/ACM 14th Int. Conf. Utility Cloud Comput., Leicester, UK, Dec. 2021, pp. 1–8. [Google Scholar]

12. Y. H. Kao, K. Wright, P. H. Huang, B. Krishnamachari, and F. Bai, “MABSTA: Collaborative computing over heterogeneous devices in dynamic environments,” in Proc. IEEE INFOCOM, Toronto, ON, Canada, Jul. 2020, pp. 169–178. [Google Scholar]

13. J. Coleman, E. Grippo, B. Krishnamachari, and G. Verma, “Multi-objective network synthesis for dispersed computing in tactical environments,” in Proc. SPIE Conf. Signal Process. Sensor/Inf. Fusion Target Recog. XXXI, Orlando, FL, USA, Apr. 2022, pp. 132–137. [Google Scholar]

14. P. Rahimzadeh et al., “SPARCLE: Stream processing applications over dispersed computing networks,” in Proc. 2020 IEEE 40th Int. Conf. Distrib. Comput.Syst., Singapore, Nov. 2020, pp. 1067–1078. [Google Scholar]

15. H. Wu et al., “Resolving multitask competition for constrained resources in dispersed computing: A bilateral matching game,” IEEE Internet Things J., vol. 8, no. 23, pp. 16972–16983, Dec. 1, 2021. doi: 10.1109/JIOT.2021.3075673. [Google Scholar] [CrossRef]

16. C. Zhou, C. Gong, H. Hui, F. Lin, and G. Zeng, “A task-resource joint management model with intelligent control for mission-aware dispersed computing,” Chin. Commun., vol. 18, no. 10, pp. 214–232, Oct. 2021. doi: 10.23919/JCC.2021.10.016. [Google Scholar] [CrossRef]

17. C. Zhou, L. Zhang, G. Zeng, and F. Lin, “Resilience mechanism based dynamic resource allocation in dispersed computing network,” IEEE Internet Things J., vol. 10, no. 8, pp. 6973–6987, Apr. 2023. doi: 10.1109/JIOT.2022.3228256. [Google Scholar] [CrossRef]

18. Z. Zhou, P. Liu, J. Feng, Y. Zhang, S. Mumtaz and J. Rodriguez, “Computation resource allocation and task assignment optimization in vehicular fog computing: A contract-matching approach,” IEEE Trans. Veh. Technol., vol. 68, no. 4, pp. 3113–3125, Apr. 2019. doi: 10.1109/TVT.2019.2894851. [Google Scholar] [CrossRef]

19. P. Wang, Z. Zheng, B. Di, and L. Song, “HetMEC: Latency-optimal task assignment and resource allocation for heterogeneous multi-layer mobile edge computing,” IEEE Trans. Wireless Commun., vol. 18, no. 10, pp. 4942–4956, Oct. 2019. doi: 10.1109/TWC.2019.2931315. [Google Scholar] [CrossRef]

20. Q. Fan, J. Bai, H. Zhang, Y. Yi, and L. Liu, “Delay-aware resource allocation in fog-assisted IoT networks through reinforcement learning,” IEEE Internet Things J., vol. 9, no. 7, pp. 5189–5199, Apr. 2022. doi: 10.1109/JIOT.2021.3111079. [Google Scholar] [CrossRef]

21. S. Guo, K. Zhang, B. Gong, W. He, and X. Qiu, “A delay-sensitive resource allocation algorithm for container cluster in edge computing environment,” Comput. Commun., vol. 170, no. 4, pp. 144–150, Mar. 2021. doi: 10.1016/j.comcom.2021.01.020. [Google Scholar] [CrossRef]

22. N. Wan, T. Luo, G. Zeng, and X. Zhou, “Minimization of VANET execution time based on joint task offloading and resource allocation,” Peer-to-Peer Netw. Appl., vol. 16, no. 1, pp. 71–86, Jan. 2023. doi: 10.1007/s12083-022-01385-6. [Google Scholar] [CrossRef]

23. Q. Wu, S. Shi, Z. Wan, Q. Fan, P. Fan and C. Zhang, “Towards V2I age-aware fairness access: A DQN based intelligent vehicular node training and test method,” Chin. J. Electron., vol. 32, no. 6, pp. 1230–1244, Nov. 2023. doi: 10.23919/cje.2022.00.093. [Google Scholar] [CrossRef]

24. K. Wang et al., “Task offloading with multi-tier computing resources in next generation wireless networks,” IEEE J. Sel. Areas Commun., vol. 41, no. 2, pp. 306–319, Feb. 2023. doi: 10.1109/JSAC.2022.3227102. [Google Scholar] [CrossRef]

25. S. Kumar, R. Gupta, K. Lakshmanan, and V. Maurya, “A game-theoretic approach for increasing resource utilization in edge computing enabled internet of things,” IEEE Access, vol. 10, pp. 57974–57989, 2022. doi: 10.1109/ACCESS.2022.3175850. [Google Scholar] [CrossRef]

26. C. Yi, S. Huang, and J. Cai, “Joint resource allocation for device-to-device communication assisted fog computing,” IEEE Trans. Mobile Comput., vol. 20, no. 3, pp. 1076–1091, Mar. 2021. doi: 10.1109/TMC.2019.2952354. [Google Scholar] [CrossRef]

27. M. S. Alzboon, M. Mahmuddin, and S. Arif, “Resource discovery mechanisms in shared computing infrastructure: A survey,” in Proc. Int. Conf. Rel. Inf. Commun. Technol., Johor, Malaysia, Sep. 2019, pp. 545–556. [Google Scholar]

28. A. D. S. Veith, M. Dias de Assunção, and L. Lefèvre, “Latency-aware strategies for deploying data stream processing applications on large cloud-edge infrastructure,” IEEE Trans. Cloud Comput., vol. 11, no. 1, pp. 445–456, Jan. 2023. doi: 10.1109/TCC.2021.3097879. [Google Scholar] [CrossRef]

29. Y. Li, B. Yang, H. Wu, Q. Han, C. Chen and X. Guan, “Joint offloading decision and resource allocation for vehicular fog-edge computing networks: A contract-stackelberg approach,” IEEE Internet Things J., vol. 9, no. 17, pp. 15969–15982, Sep. 2022. doi: 10.1109/JIOT.2022.3150955. [Google Scholar] [CrossRef]

30. Y. Wang, X. Tao, X. Zhang, P. Zhang, and Y. T. Hou, “Cooperative task offloading in three-tier mobile computing networks: An ADMM framework,” IEEE Trans. Veh. Technol., vol. 68, no. 3, pp. 2763–2776, Mar. 2019. doi: 10.1109/TVT.2019.2892176. [Google Scholar] [CrossRef]

31. H. Hui, F. Lin, L. Meng, L. Yang, and X. Zhou, “Many-to-many matching based task allocation for dispersed computing,” Computing, vol. 105, no. 7, pp. 1497–1522, Jan. 2023. doi: 10.1007/s00607-023-01160-2. [Google Scholar] [CrossRef]