A Task Offloading Strategy Based on Multi-Agent Deep Reinforcement Learning for Offshore Wind Farm Scenarios

1  Introduction

Under the new power system, offshore wind power is an important means for China to realize the goals of “2030 carbon peak” and “2060 carbon neutral” [1,2]. Offshore wind energy technology holds abundant resources and promising prospects, poised to become a cornerstone of future green energy [3]. Climate change and the increasing demand for renewable energy are driving the rapid development of offshore wind farms [4]. Beyond offering new opportunities for the energy industry, offshore wind power reduces greenhouse gas emissions, lowers energy costs, and fosters economic growth [5]. Ensuring the efficient operation of offshore wind farms has made real-time monitoring and optimization strategies crucial [6]. Traditional monitoring methods rely heavily on sensor networks and remote data transmission, which are often costly and susceptible to disruptions from marine environments [7]. Edge computing represents an emerging computing architecture placing computational resources near data sources to reduce latency and enhance responsiveness [8]. Task offloading plays a critical role in edge computing by shifting computational tasks from central data centers to edge nodes near data sources, effectively reducing data processing delays [9]. Therefore, addressing how task offloading strategies and resource allocation schemes can mitigate data processing latency and improve system responsiveness and real-time capabilities in offshore wind farms is a pressing issue.

Deep Reinforcement Learning (DRL) has gradually been applied to task offloading [10,11]. In [12], the authors investigate a Multiple Input Multiple Output (MIMO) system with a stochastic wireless channel, employing the DDPG method for handling continuous action DRL. However, DDPG’s performance overly relies on the critic network, making it sensitive to critic updates and resulting in poor stability and slow convergence during computational offloading. In [13], the authors addressed the cost of offloading from user devices and pricing strategies for MEC servers, proposing a MADRL algorithm to solve profit-based pricing problems. Nevertheless, the Deep Q-Network (DQN) algorithm used faces instability in handling complex task offloading scenarios, which hinders performance assurance. In [14], the authors studied joint optimization schemes for wireless resource coordination and partial task offloading scheduling. To address the slow convergence issue caused by high-dimensional actions in DDPG, noise exploration is introduced in the action outputs of participating networks. However, similar to DDPG, this method also requires traversing the entire action space, limiting its practical application effectiveness. In [15], the authors formulated optimization problems such as latency, energy consumption, and operator costs during offloading as Markov Decision Processes (MDPs). They propose a DRL-based solution but encounter challenges with low efficiency in experience replay utilization, leading to suboptimal learning efficiency. In [16], the authors modelled the resource allocation problem as a Markov game and propose a generative adversarial LSTM framework to enhance resource allocation among unmanned aerial vehicles (UAVs) in machine-to-machine (M2M) communication. The study successfully addresses scenarios where multiple UAVs act as learning agents. However, the computational complexity of this algorithm may constrain its implementation in large-scale M2M networks, particularly in scenarios involving high-speed moving UAVs. While existing literature has made some strides in applying Deep Reinforcement Learning to task offloading, it still faces numerous challenges. Addressing these challenges, this study introduces a novel task offloading strategy combining Adaptive Genetic Algorithm and Deep Deterministic Policy Gradient algorithm (AGA-DDPG), aimed at enhancing operational efficiency and reducing maintenance costs in offshore wind farms.

In summary, operational challenges faced by offshore wind farms, particularly in computational offloading and edge computing, remain substantial. Existing research predominantly focuses on onshore environments, resulting in limited exploration of offloading strategies in marine settings. Studies involving multiple users and multiple MEC servers encounter exponential growth in state and action spaces, leading to slow convergence in problem resolution. Moreover, current binary offloading models lack flexibility and efficiency, potentially leading to increased operational costs and reduced efficiency. In response to the aforementioned issues, this paper proposes a task offloading strategy based on multi-agent deep reinforcement learning for offshore wind farm scenarios. The specific contributions are as follows:

1. Innovative task offloading strategy: We introduce a novel approach utilizing UAVs as airborne MEC servers to optimize computational resource allocation under dynamic network conditions, significantly improving monitoring and maintenance efficiency in offshore wind farms.

2. Development of AGA-DDPG algorithm: We develop the AGA-DDPG model, which enhances the traditional Deep Deterministic Policy Gradient algorithm using an Adaptive Genetic Algorithm to overcome slow convergence in high-dimensional action spaces, thereby improving overall task offloading performance.

3. Multi-agent system framework: This study models the task offloading problem as a Multi-Agent Deep Reinforcement Learning challenge, providing a framework for centralized training and decentralized execution tailored for dynamic offshore environments, representing significant technological advancements for practical applications.

4. Empirical validation and performance evaluation: Through extensive simulation experiments, we validate the effectiveness of our proposed algorithms and demonstrate significant reductions in overall operational costs compared to existing methods, thereby offering practical solutions for the sustainable development of offshore wind farms.

Through these innovations, this research not only advances theoretical developments in task offloading and edge computing but also provides crucial technological support and implementation guidelines for enhancing the efficient operation of offshore wind farms worldwide.

2  Related Work

MEC is being applied in multiple fields, such as healthcare, agriculture, industry, the Internet of Vehicles, and the IoT [17]. MEC’s computing offloading technology involves offloading computing tasks to MEC servers with strong computing power. However, with the rapid increase of IoT terminal devices, MEC servers also face a shortage of their own resources [18]. Some researchers focused on improving the resource utilization of MEC servers to alleviate computational pressure [19]. On the other hand, some studies focused on the collaborative approach of multiple MEC servers [20]. The algorithms for task offloading can be divided into traditional algorithms and DRL-based algorithms.

2.1 Conventional Methods for Task Offloading

Heuristic algorithms are widely used for task offloading. For instance, Chen et al. [21] proposed a heuristic algorithm-based multi-user capability-constrained time optimization method. It provides a viable solution for optimizing workflow completion time under energy constraints. However, heuristic algorithms are noted for their high complexity and are not well-suited for long-term task offloading strategies. Vijayaram et al. [22] introduced a distributed computing framework for efficient task computation offloading and resource allocation in mobile edge environments of wireless IoT devices. Task offloading is treated as a non-convex optimization problem and solved using a meta-heuristic algorithm. Similarly, Karatalay et al. [23] investigated energy-efficient resource allocation in device-to-device (D2D) fog computing scenarios. They proposed a low-complexity heuristic resource allocation strategy to minimize overall energy consumption due to limited transmission power, computational resources, and task processing time. Nevertheless, heuristic algorithms exhibit poor adaptability and may not achieve the effectiveness of DRL over extended operational periods.

2.2 DRL-Based Methods for Task Offloading

To meet the high demands brought by the explosive growth of computationally intensive and delay-sensitive tasks on mobile user devices. Li et al. [24] proposed a content caching strategy based on Deep Q-Network (DQN) and a computation offloading strategy based on a quantum ant colony algorithm. The content caching solution addresses latency and round-trip load issues associated with repeated requests to remote data centers. However, DQN algorithms face challenges related to convergence. Chen et al. [25] utilized drones to assist in task offloading, aiming to minimize the weighted sum of average latency and energy consumption. Their study highlighted slow convergence due to the high-dimensional action space involved in maneuvering drones for efficient offloading. Guo et al. [26] applied task offloading to emergency scenarios by leveraging the computational capabilities of redundant nodes in large-scale wireless sensor networks, employing a DDPG algorithm to optimize computation offloading strategies. Similarly, Truong et al. [27] formulated the optimization problem as a reinforcement learning model to minimize latency and energy consumption, proposing a DDPG-based solution. They noted challenges arising from the high-dimensional action space and low utilization of historical experience data, which contribute to slow convergence. Similarly, Ke et al. [28] proposed a DLR strategy based on actor-network and critic network structure. This strategy adds a noise after the output action of the actor-network to avoid the complexity brought by high-dimensional action space. To highlight the contribution of this article, we present Table 1.

3  System Model and Problem Description

3.1 Network Model

As shown in Fig. 1, offshore wind farms are in remote areas with no cellular coverage, so this paper proposes a space-air-maritime integrated network (SAMIN) to provide network access, task offloading, and other network functions for offshore Wind Turbine Generator (WTG). In the SAG-IoT network, there are three network segments, i.e., the maritime segment, the aerial segment, and the space segment. The WTGs constitute the maritime segment, and the maritime segment uploads the WTG data and the computational tasks to be performed. In the aerial segment, flying UAVs can be used as edge servers to provide task offloading to maritime users. The flying UAVs, such as the Facebook Aquila, can fly for months without charging by using solar panels. In the space segment, one or more LEO satellites provide full coverage of the area of interest, and connect UAVs processing data to cloud servers via a satellite backbone.

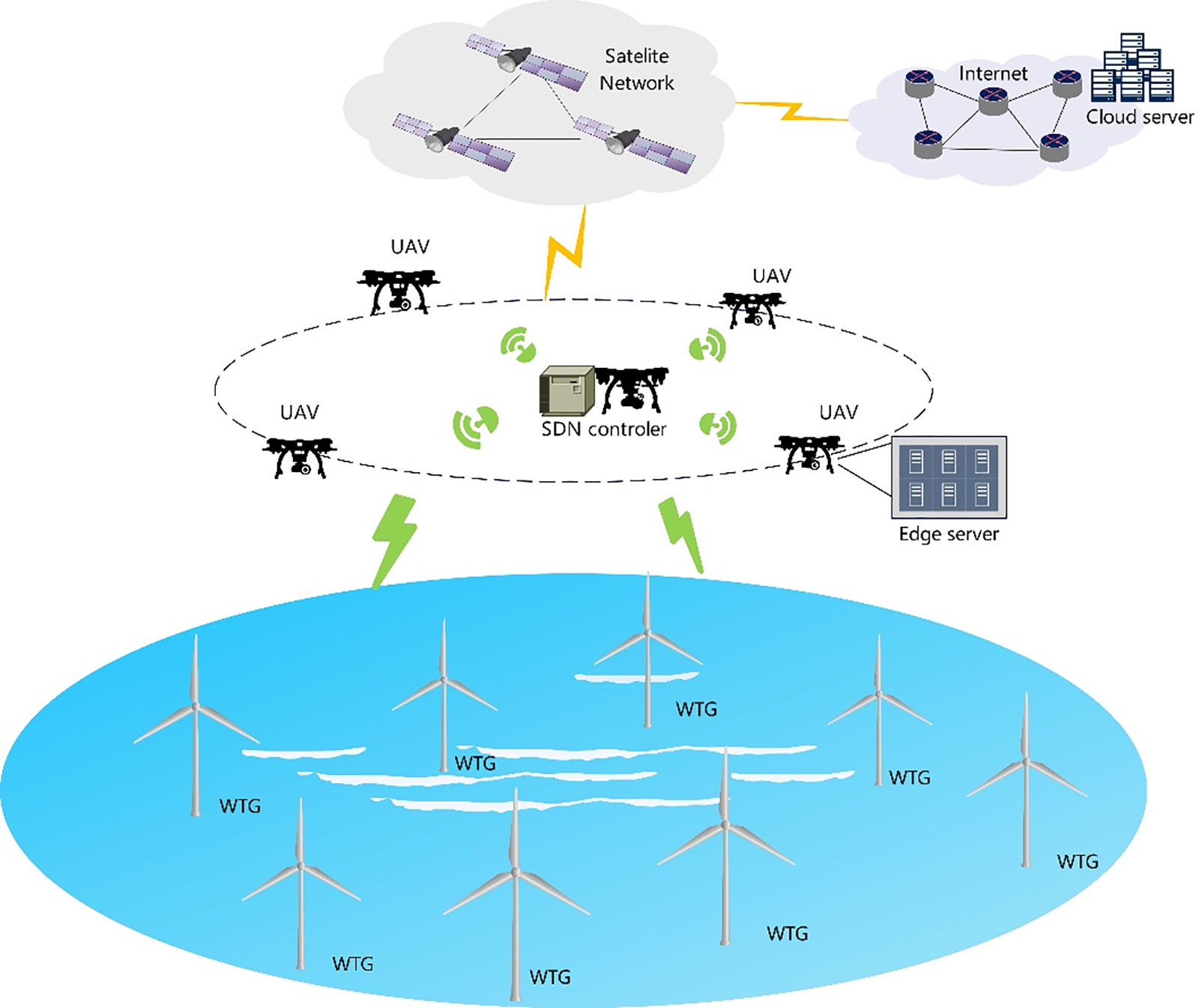
Figure 1: Computational model for multi-MEC collaboration in wind farms

The MEC scenario is assisted by multiple UAVs, consisting of n WSNs and m UAVs equipped with edge servers, with WSNs consisting of monitoring devices for wind turbines and multiple data sensors. To accommodate the complexity associated with the changing network environment in the MEC environment, software-defined networking SDN technology has been applied to the system [29]. The SDN controller is used to centrally train and issue control commands to maintain communication with the MEC server cluster. The set of WSNs is denoted as N= {1, 2, . . . , n}, n∈N, and the set of MEC servers is denoted as M= {1, 2, . . . , m}, m∈M [30]. The data processing tasks are defined as Tk={Ik,Fk,τkmax}. Here, Ik, Fk and τkmax are the task date size, task computational complexity, and maximum delay time to complete the task, respectively [31]. The continuous task processing period T={1, 2, . . .} is divided into multiple time slots, and the size of the time slots is τ0. To simulate the realism of the WTG data, the data processing task is randomly generated at the beginning of each time slot. To improve the task offloading efficiency and offloading flexibility, it is assumed that the data processing tasks are divisible and that the offloading ratio decision is determined by the parameter γ, which indicates that the local server offloads the computing tasks with ratio γ to other servers. Next, the local MEC server is referred to as the offloading user. The symbols are summarized in Table 2.

3.2 Communications Model

It is assumed that the communication mode between MEC servers follows orthogonal frequency division multiple access (OFDMA) [32–34]. It is assumed that the total bandwidth of the connection between MECs is set to Bi, which can be divided into E subchannels. Assuming that the channel state between MEC servers in each time slot is time-varying and obeys a Markov distribution, the channel state can be modeled as follows:

hm(t)=ℏe1Dmδm∗Pm(1)

where ℏe is the path loss coefficient and Dm is the distance between the MEC servers. Pm is a predefined transfer probability matrix for the channel state.

For example, the channel states between MEC servers are [64,128,192,256,512]. Assuming that the current channel state hm(t) is 192, the next time slot channel state hm(t+1) will be shifted to other states, e.g., 256, with a state transfer probability, in this way, the ever-changing channel states in the MEC environment will be modeled.

From the channel state model, the transmission rate between MEC servers can be obtained as:

Ri,j=βBilog2⁡(1+pn|hm(t)|2N0)(2)

where Bi is the transmission bandwidth, β is the bandwidth allocation ratio, pn is the transmission power, and N0 is Gaussian white noise.

3.3 Computational Model

When there is no abnormality in the motor set, the computation task is offloaded to the local MEC server for computation. In this paper’s formulation, the right superscript i represents the offloading user and the right superscript j represents the offloading target MEC server. The local time delay and energy consumption are expressed as follows:

Ti=Fkfi(3)

Ei=KiFkfi(4)

where fi is the computational power of the MEC server and Ki is the device correlation coefficient of the MEC.

When abnormalities occur in the WTG, the local server is overloaded with computational pressure and offloads the computational tasks with a ratio of γ to other servers for computation, and the local servers are referred to as offloaded users in the following. From the above, we can obtain the transmission delay for offloading the user offloading task to the target MEC server as follows:

Ti,j=IKRi,j(5)

The energy consumption is expressed as follows:

Ei,j=pi,jTi,j(6)

The delay calculated on the target MEC server is expressed as follows:

Tj=FKfj(7)

The energy consumption calculated on the target MEC server is expressed as follows:

Ej=KjFk(fj)2(8)

where fj denotes the computational resources allocated by the MEC server to the offloaded users.

3.4 Description of the Problem

When abnormalities occur in a wind turbine, a rapid response to the abnormal state is needed. On the one hand, the computation speed of the data processing task has real-time requirements; on the other hand, we need to consider the service life of the equipment because the equipment is required to run for a long time in the WTG anomaly monitoring environment. Therefore, it is necessary to consider the delay and energy consumption requirements, and the overall overhead of the system is expressed as the weighted sum of the delay and energy consumption. The overall delay and energy consumption of the system can be expressed as follows:

Ttotal=(1−γ)TmL+γ(TmMT+TmMC)(9)

Etotal=(1−γ)EmL+γ(EmMT+EmMC)(10)

Thus the overall overhead of the system can be obtained as follows:

Um=anTtotal+(1−an)Etotal(11)

where an is the weighting factor between delay and energy consumption.

To reduce the overall system overhead and efficiently use the system channel and computational resources, the system’s optimal objective is transformed into a problem of minimizing the overall system overhead. Then the system optimization problem is formulated as P1.

minΓi,Υi,Pi,j∑mMUmm∈M(12)

0≤fi≤fimax(13)

0≤am≤1(14)

Ttotal≤τKmax(15)

0≤γ≤1(16)

pi,j≥pi,jmax(17)

where Eq. (13) is a constraint on MEC computing resources, Eq. (14) is a weighting constraint on the ratio between delay and energy consumption, Eq. (15) indicates that the task processing time must be less than the maximum allowed processing delay, Eq. (16) is a constraint on the task offloading ratio, Eq. (17) is a constraint on the transmission power, Γi is the MEC server number selected by the agent, Υi is the task offload ratio selected by the agent, and pi,j is the transmission power allocation.

P1 indicates that Um is minimized after offloading operations. In the offloading action, pi,j and Υi are continuous variables, while Γi is an integer variable. The feasible region formed by the optimization objective and constraints is non-convex. This can lead to the existence of multiple local minima, thereby complicating the optimization process. Additionally, P1 involves selecting a subset of MEC servers from a large set to offload tasks, which can be viewed as a combinatorial optimization problem. The goal is to identify the optimal server combination that minimizes overall system costs while adhering to various constraints. This is a mixed integer programming problem. It is not practical to use a specific mathematical derivation. Therefore, we introduced DRL to the optimization problem of task offloading.

4  MADRL-Based Task Offloading Strategy

4.1 MADRL-Based Task Offloading Model

P1 involves the complex task offloading optimization problem within a MEC environment involving multiple servers and users. This scenario can effectively be modeled as a Markov Decision Process (MDP). In this framework, the state space (S) includes parameters such as the computational loads of individual servers, task statuses, and device energy levels. The action space (A) encompasses decisions like selecting target MEC servers for task offloading, determining task offloading proportions, and allocating transmission power. The Transition Function (T) governs how the system state evolves from one moment to the next based on chosen actions, while the Reward Function (R) provides feedback by penalizing system overhead costs to minimize overall expenditure. The data collected by the WSNs change dramatically when a WTG anomaly occurs, while the channel state also changes at any time. To address this challenge and inspired by [35], we model problem P1 as a MADRL-based task offloading model. The offloading user is designated as an agent in MADRL. In the offshore wind network, a centralized training and distributed computing architecture is used. The SDN controller trains the agents in a centralized manner. The network parameters are periodically distributed to the agents. The MADRL-based computing framework is shown in Fig. 2.

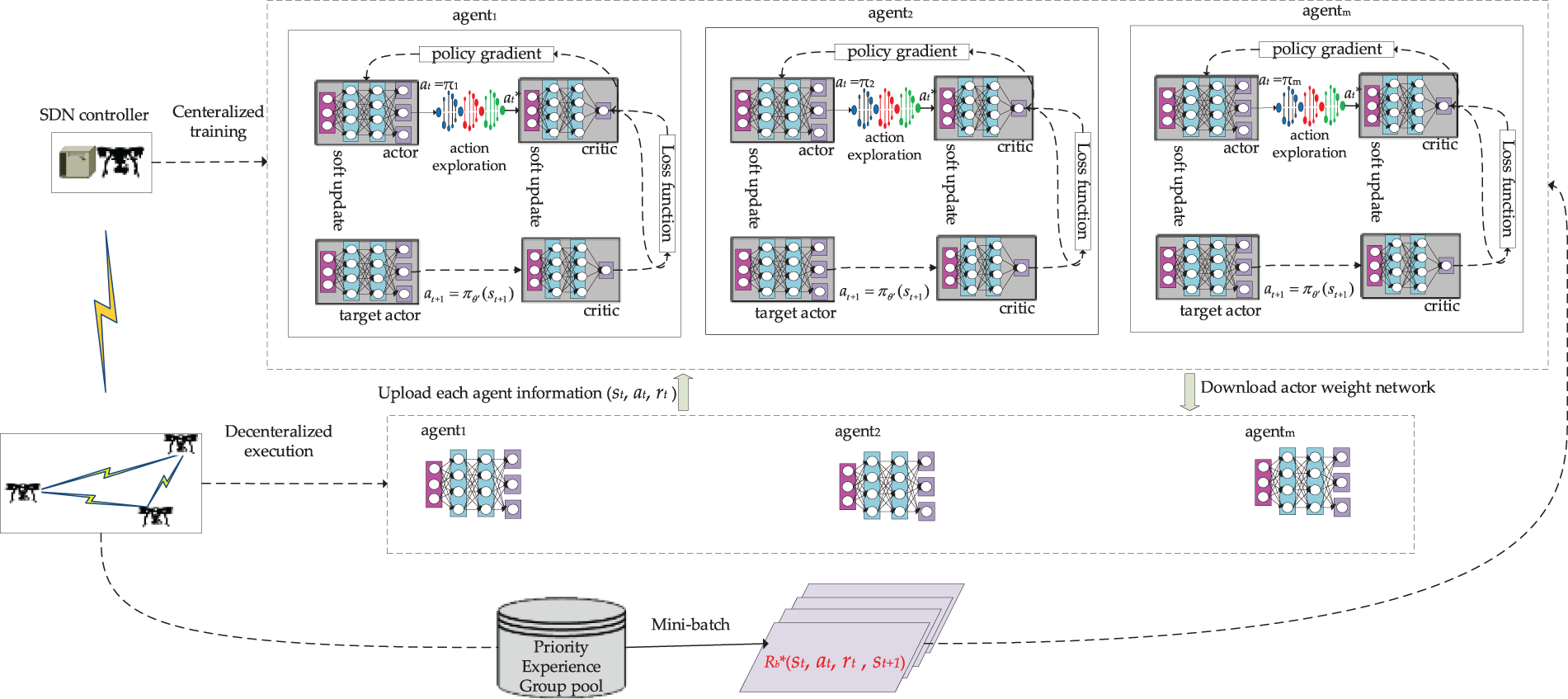
Figure 2: The computing framework based on MADRL

The state space, action space, and reward functions in MADRL are shown below.

4.1.1 State Space

At the beginning of each time slot, all agents receive computational tasks from nearby WSNs. They also consider the available computing resources of all MEC servers during the current time slot. This indicates how much processing capacity is available for task execution, directly influencing the decision of whether tasks should be processed locally or offloaded to MEC servers. Additionally, there is information about the current network status, including channel conditions and potential device failures. These factors directly impact the efficiency and stability of task transmission within the network. To efficiently use the computational resources of the system and the channel resources in the MEC environment, the state space is defined as:

St={TK,FM,At1,At2,…Atm−1,Atm+1,…AtM}(18)

where TK denotes the task, FM is the computational power of all MECs in the current time slot, and the goal of the system is to minimize overall overhead, therefore requiring collaboration among all agents, which requires actions from other agents.

4.1.2 Action Space

The action space aims to maximize expected long-term returns by efficiently utilizing available resources. Firstly, agents decide which MEC server to offload computational tasks to, based on factors such as server computing power, reliability, and geographical location, which impact task processing efficiency and latency. Secondly, agents determine the proportion of tasks to be offloaded to the chosen MEC server, taking into account its current workload and processing capabilities to ensure system balance and performance optimization. Lastly, agents allocate appropriate transmission power for tasks offloaded to MEC servers, directly influencing the stability and efficiency of data transmission. To efficiently utilize the spectrum, the transmission power of offloaded users is allocated. The appropriate offload ratio is selected based on the computing resources of the MEC cluster. The action space is represented as follows:

At={Γi,Υi,Pi,j}(19)

where Γi is the MEC server number selected by the agent, Υi is the task offload ratio selected by the agent, and Pi,j is the transmission power allocation.

The variable of the action space is normalized. For example, suppose that Pi,jmax is 20 MHz when the agent selects the action as [0.03,0.6,0.6]. Then it means that the agent chooses to offload 60% of its computational tasks to the MEC server numbered 3 and allocate 12 MHz transmission power for the current task.

4.1.3 Reward Function

The reward space quantifies the feedback agents receive based on their actions, guiding them towards making optimal decisions step by step. In this study, the reward is designed to encourage efficient task offloading and resource utilization. The reward function describes the relationships among multi-agent systems. In this system, the goal of optimization is to minimize the overall system overhead, so there is a cooperative relationship between agents. However, when the target MEC servers of two offloading users are consistent, there is a resource competition relationship between the agents. The goal of DRL is to maximize the expected long-term rewards, while the system goal is to minimize the overall system overhead. Therefore, we use the negative value of the overall cost as the reward after the decision. The reward function for individual agent i can be defined as follows:

rti=−Um(20)

The overall reward for agents is as follows:

rt=∑i=1m−Umm∈M(21)

The main goal of the system is to maximize overall rewards.

4.2 DRL-Based Online Computational Offloading Algorithm

DRL is an online algorithm that generates historical experience through constant interaction with the environment and uses it to learn. It uses deep neural networks based on reinforcement learning to fit state value functions and strategies π. It aims to maximize expected long-term returns through deep learning [36,37]. The proposed algorithm AGA-DDPG is an improvement of DDPG. First, intelligence acquires its current state from the MEC environment. Then, the agent’s executor network outputs the offloading action based on the acquired state St. After that, the MEC environment provides immediate rewards rt based on the offloading action at. Finally, the critic network scores the offload action. It is recorded as the action state value Q. The experience groups (St, at, rt, St+1) are also collected and their priority is calculated. The prioritized experience groups will be stored in the playback memory pool. The actor and critic networks are trained based on the experience sets in the replay memory pool. The two important parts of the AGA-DDPG algorithm are the actor-critic network and the AGA exploration of the action space.

4.2.1 Actor-Critic Network

The algorithm improves upon the DDPG, which is an online algorithm. The output of the offloading policy π is a deterministic action at. The purpose of the offloading strategy π is to enable the output action at to maximize expected long-term rewards. The actor-network fits the offloading policy π using deep learning techniques.

at=πθ(st)(22)

And the actor target network outputs the next actions based on the next states.

at+1=πθ′(st+1)(23)

The critic network in AGA-DDPG is a deep neural network (DNN) used to fit the Q-value function of state actions. The Q-value is the expected reward for the current action, so it can evaluate the quality of the output actions of the actor-network in the current state.

Qω(s,πθ(st))(24)

The critic target network is used to fit the Q-value function of state action at the next state.

Qw′(st+1,πθ′(st+1))(25)

After the MEC environment gets the action output from the actor-network, it will calculate the reward under the current action. The ultimate goal of AGA-DDPG is to maximize the expected long-term reward:

yt=rt+λQω′(st+1,πθ′(st+1))(26)

where λ is the discount factor.

We use minimizing loss values to update the parameters of critical networks.

Loss=1M∑t(yt−Qω(st,at))2(27)

And policy gradient is used to update actor-network parameters.

∇πθJ=1M∑i∇wQw(si,πθ(si))∇θπθ(si)(28)

The output action is unstable due to the quickly changing parameters of the online network. Therefore, we used soft update to update the target network making the output action more stable.

θ′=τθ+(1−τ)θ′(29)

ω′=τω+(1−τ)ω′(30)

where τ is soft updated parameter.

4.2.2 Exploring the Action Space with AGA

In traditional DDPG, the action space is explored using a greedy strategy, which requires traversing all action spaces, resulting in low learning efficiency and slow network training speed [38]. Therefore, instead of scoring the output of the action directly by the actor-network, we use the AGA to score the actions at∗ obtained after exploring the action space in the critic network in the AGA-DDPG algorithm.

First, the actor networks output actions at and (W–1) randomly generated offloading decision scheme form the initial population, where W is the population size. The initialized population is represented as follows:

Ai(0)=(ai,1(0),ai,2(0),ai,3(0),…,ai,n(0))i=1,2,3,…,W−1(31)

The steps of the AGA algorithm, as illustrated in Fig. 3, are described as follows:

Step 1: Initialize algorithm parameters, including the number and size of sub-populations, the number of iterations, crossover and mutation probabilities, adaptive control parameters, etc.

Step 2: Randomly generate an initial population and divide it into multiple sub-populations, assigning independent threads to each sub-population.

Step 3: Each sub-population executes basic genetic operations in parallel, which include fitness evaluation, selection, crossover and mutation, and preservation of elite individuals.

Step 4: Check the current iteration count; if it reaches the maximum number of iterations, merge the sub-populations and output the optimal solution set. Otherwise, proceed to Step 5.

Step 5: Determine if the sub-populations meet the migration condition. If so, each sub-population completes a migration communication operation and then proceeds to Step 3 to continue the iteration. If the migration condition is not met, directly proceed to Step 3.

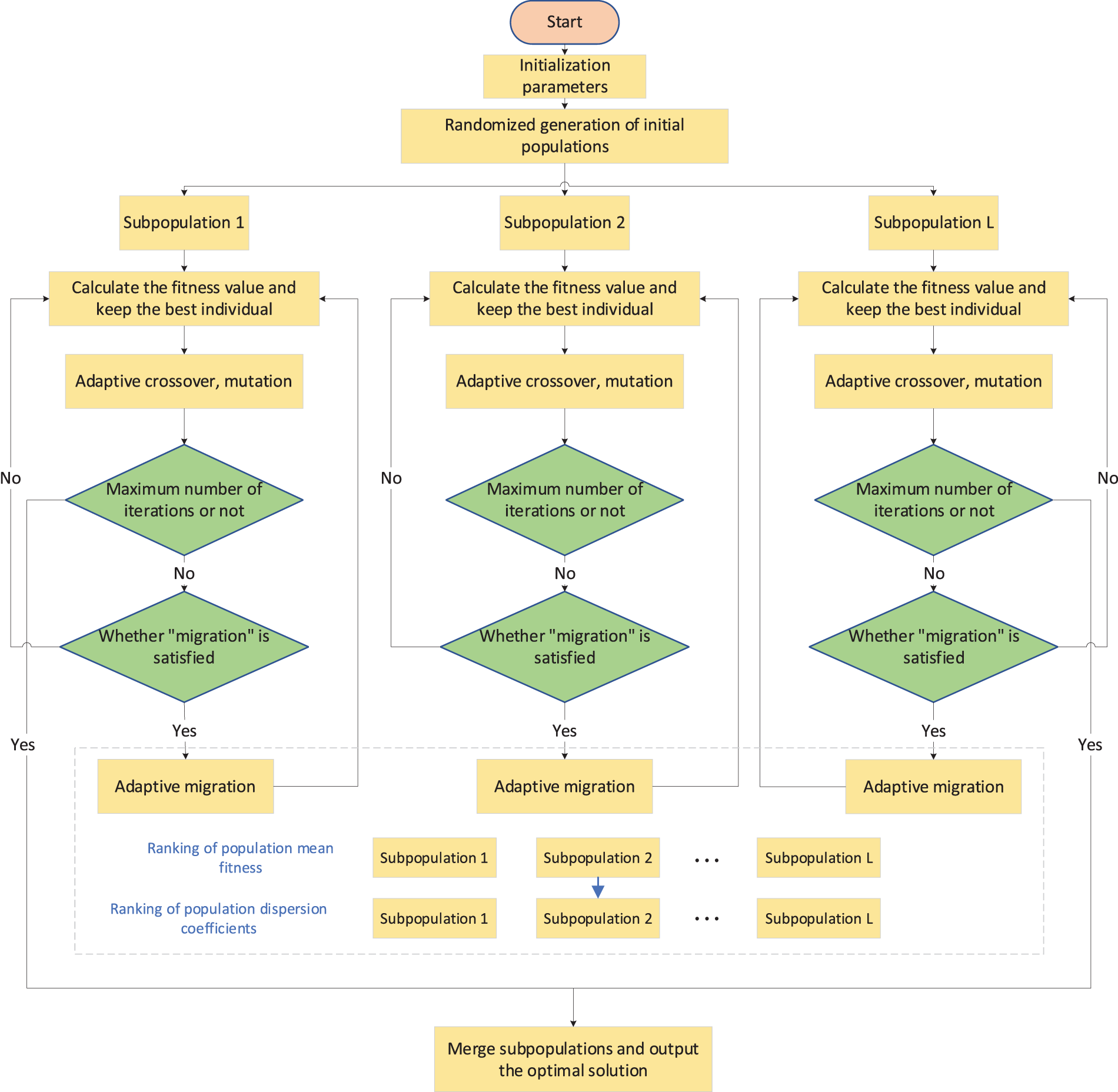
Figure 3: Sketch map of AGA

4.3 Prioritized Experience Replay

The experience replay technique is a key technique in DRL, which enables an agent to remember and use past experiences for learning. In the traditional deep reinforcement learning DDPG, experience replay groups are drawn using random sampling [39]. However, this approach ignores the importance of different values and experience groups for training. Therefore, we use the PER [40] technique to extract experience replay groups. Different experience groups have different importance, and experience groups with higher importance are drawn for training with a higher probability.

The calculation of priority in PER is the core problem. Because the replay probability of different experience replay groups needs to be calculated according to the priority. TD-error is used as an important indicator to evaluate the priority of experience. The neural network can’t estimate the true value of the action accurately when the absolute value of TD-error is high. At this time, giving it a higher weight helps the neural network to reduce the probability of wrong predictions. In addition, the overall task overhead is an important indicator to adjust whether the network is well-trained or not. Therefore, the calculation of priority takes into account the absolute value of TD-error and the overall task overhead. Scoring the experience group is as follows:

scoretφ=δ|δtφ|+(1−δ)z(t)φ)(32)

where δ is the score control parameter, |δtφ| is the absolute value of TD-error, and z(t)φ is a function related to the overall task overhead.

After obtaining Eq. (32) again, the experience group is sorted from smallest to largest, and the order number of the experience group is rank(φ) = {1,2,3. . .}. Define the sampling values according to the order number.

valueφ=1rank(φ)(33)

Based on the sampling values we can obtain the sampling probability from the following equation:

pφ=valueφ∑Rb=1Rbvalueφ(34)

The experience replay groups generated in each training round are assigned priority according to the PER method. Experience groups with higher scores will receive higher sampling probabilities to effectively use more training-worthy replay experience groups. It can increase the training speed of the network in this way.

The MADRL-based online task offloading algorithm (AGA-DDPG) is shown in Algorithm 1.

4.4 Complexity Analysis of AGA-DDPG

The comparative solution is the DDPG algorithm, so it is necessary to analyze the computational complexity of DDPG. Referring to [41], the time complexity of DDPG can be expressed as follows:

2×∑i=0InA,inA,i+1+2×∑j=0JnC,jnC,j+1=O [∑i=0InA,inA,i+1+∑j=0JnC,jnC,j+1](35)

In the above equation, I and J respectively represent the number of fully connected layers in the actor-network and critic network of the DDPG algorithm. Where nA,i and nC,j represent the number of neurons in the i-th layer of the actor-network and the j-th layer of the critic network. The proposed algorithm AGA-DDPG incorporates the AGA exploration process in the actor-network and critic network. AGA is an optimization process, so the time complexity of AGA-DDPG can be expressed as follows:

2×∑i=0InA,inA,i+1+2×∑j=0JnC,jnC,j+1+∑k=0KK×W=O [∑i=0InA,inA,i+1+∑j=0JnC,jnC,j+1+∑k=0KK×W](36)

where K is the number of iterations for AGA exploration Similarly, W is the size of the initialization population in the AGA algorithm.

5  Results

5.1 Simulation Parameter Setting

The simulation experiment environment we ussed was PyTorch 1.12.1 with Python 3.9. The simulation scenario is a circular area with a radius of 1000 m, the number of user nodes at the edge is 50, and the number of MEC servers is 10. The MEC computing power is randomly generated at 11 GHz~15 GHz.

For the deep neural network, the actor and critic networks at each agent consist of a four-layer fully connected neural network and two hidden layers. The numbers of neurons in the two hidden layers are 400 and 300. The neural network activation function uses the ReLu function, while the output function of the actor-network is a sigmoid function. The soft update coefficient of the target network is τ = 0.01 and the memory size of the history experience group is set to Ω = 3 × 1025.

The simulation parameters are shown in Table 3.

To verify the performance of the proposed algorithm, AGA-DDPG was compared with the following algorithms:

1.    LC scheme: All calculation tasks are calculated in local MEC.

2.    RC scheme: The offloading action is selected randomly, including the task division ratio, bandwidth allocation, and selected MEC server number.

3.    Twin Delayed Deep Deterministic Policy Gradient (TD3): TD3 was developed from the shortcomings of DDPG. Its core idea is that the critic network should update faster than the actor-network. When the critic network is well-trained, it can effectively guide the actor-network to improve its learning. Its actor-network and critic network use the same structure as the proposed algorithm.

4.    DDPG: The improved DDPG algorithm was selected as one of the comparative algorithms, which facilitates the verification of the effectiveness of the DDPG algorithm. The structure of the participant network and critic network of DDPG was the same as that of AGA-DDPG, and the empirical group extraction method used random extraction.

5.2 Convergence Performance

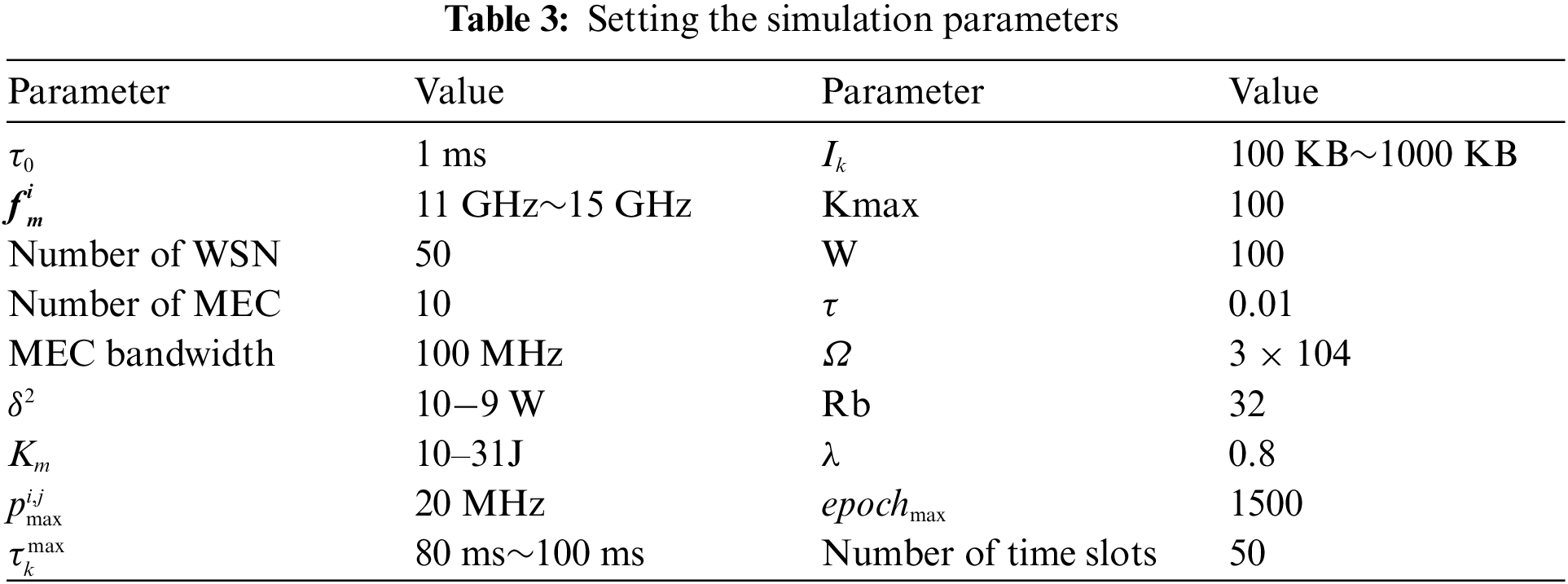
Simulation experiments are conducted for the proposed algorithm AGA-DDPG. It aims to maximize the expected long-term reward of the system. Network convergence can be judged when the overall average reward of the system tends to be stable while considering the learning rate as a hyperparameter that affects the learning efficiency of DRL. Therefore, the average reward variation of the actor-network and the critic network is plotted for different learning rates.

Fig. 4 shows the effect of different learning rates on the average reward under the AGA-DDPG algorithm. When training starts, compared to performing all local computations, the cost savings from starting to offload computational tasks to other MEC servers are rapidly increasing. As training progresses, the average reward slowly increases over the long term with large fluctuations. When the number of training episodes reaches 400, the system stabilizes. The average reward basically stops increasing, and network training is completed. When the training effect was better, the actor-network learning rate (A_LR) and critic-network learning rate (C_LR) were 0.01 and 0.05, respectively. This is because the update of the actor-network depends on the critic network, so A_LR is biased lower than C_LR. We use the same learning rate in the following simulation settings.

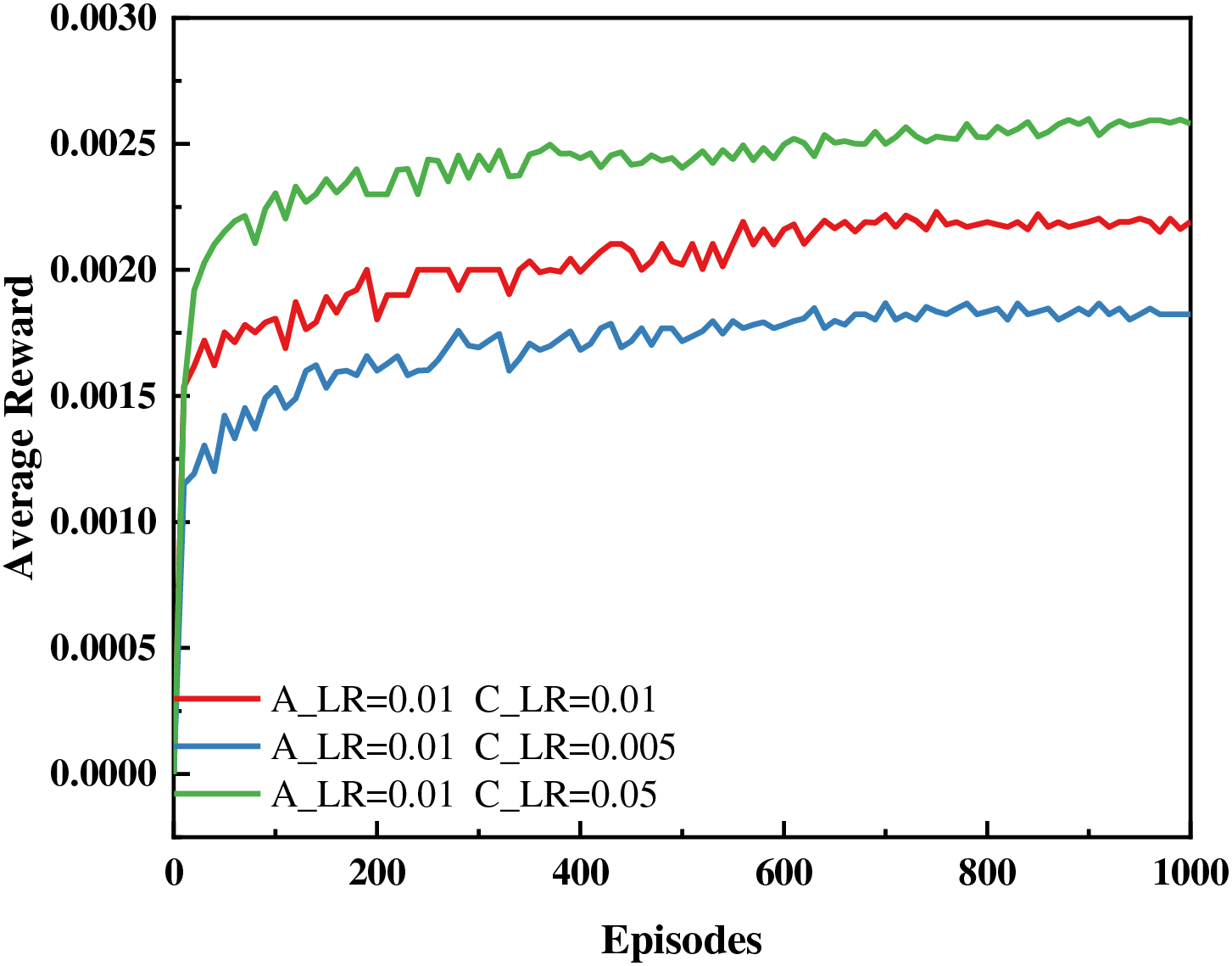
Figure 4: Average reward of the system under the AGA-DDPG algorithm

For DRL, the loss value of the network is an important indicator for determining whether the network converges. Therefore, we present the loss value change curves for the critic network.

Fig. 5 represents the variation in the loss values of the critic network with the number of iterations in the proposed algorithm. The critical network decreases sharply at the beginning of training and then enters a period of intense fluctuations. During this period, the critical network learns from historical experience and constantly updates its own parameters. After training for 400 episodes, the critical network tends to stabilize. Due to the constantly time-varying channel state, the loss value fluctuates slightly within an acceptable range. The convergence performance of the critic network and actor-network is interdependent. When critical converges, it provides better guidance for actor networks. The critical network fits the actor network’s output action expectation reward function. When the actor-network convergence occurs, its output actions are more accurate, and the reward value of environmental feedback is greater.

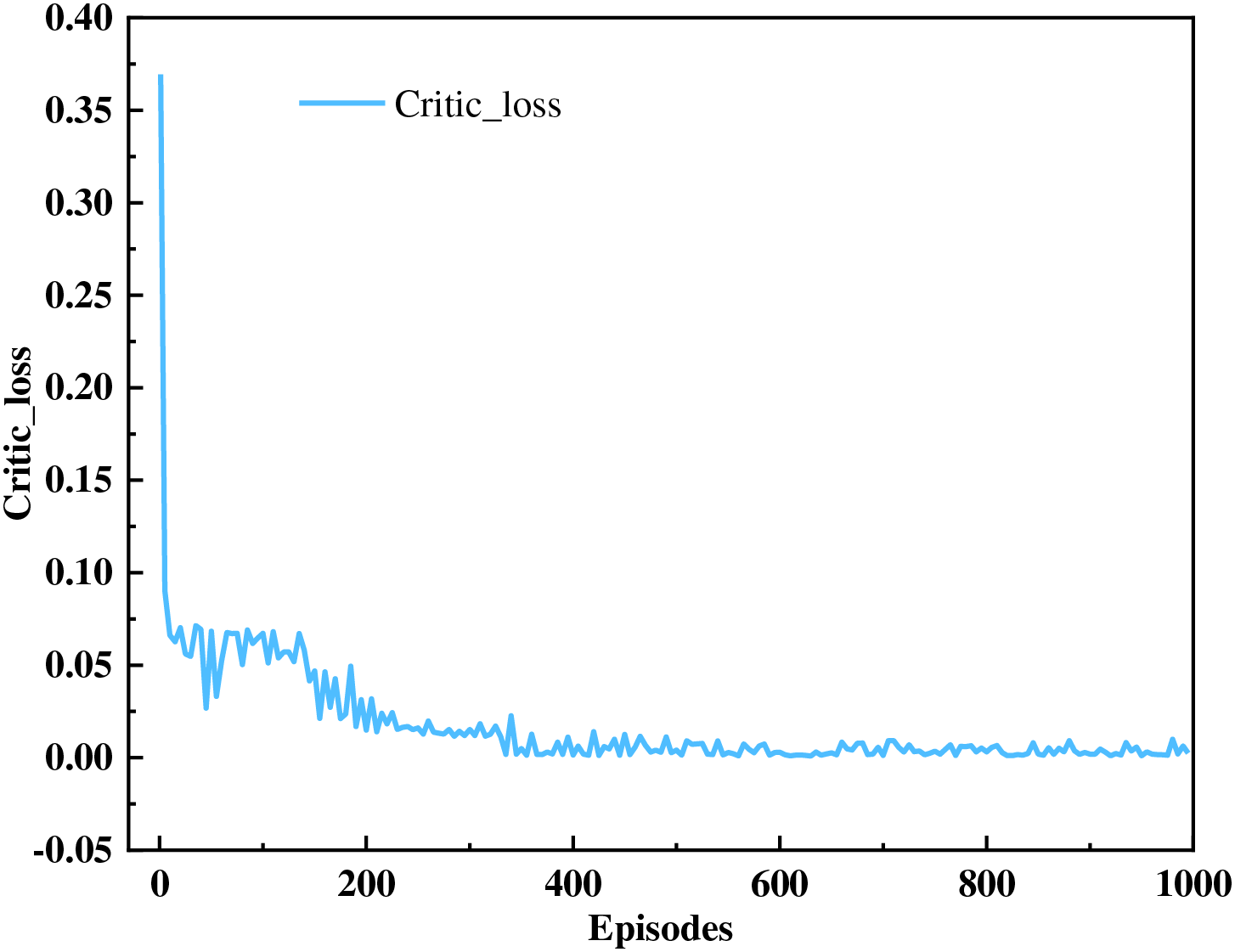
Figure 5: Critic network loss value

5.3 Model Optimization

AGA-DDPG integrates an AGA exploration process between the actor and critic networks and incorporates a prioritized concept within the experience replay buffer to determine the sampling probabilities of experiences. To validate the improvements of AGA-DDPG over traditional DDPG, we compared the performance of AGA-DDPG, DDPG, and Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithms.

Fig. 6 illustrates the variation of latency and energy consumption with training epochs for the three algorithms when the number of nodes in the WSN is 50. AGA-DDPG shows a rapid decrease in energy consumption and latency at the beginning of training, which is also observed to some extent in the other two approaches. However, AGA-DDPG demonstrates a faster convergence rate compared to the other two methods. As training progresses, tasks are effectively offloaded to different MEC servers, thereby improving the system’s resource utilization. In contrast to AGA-DDPG, both DDPG and TD3 exhibit poorer stability. AGA-DDPG not only demonstrates stability, as shown in Fig. 6, but also achieves quicker decreases in energy consumption and latency early in training compared to the other algorithms. This can be attributed to two main factors. Firstly, we employ AGA to explore the action space between the actor and critic networks, maximizing the actor network’s output of better actions each time. Secondly, the inclusion of prioritization to determine the sampling probabilities of experience batches ensures that batches with higher value are sampled with higher probability, avoiding unnecessary training on batches with lower value.

Figure 6: (a) Impact of algorithm improvements on delay; (b) Impact of algorithm improvements on energy

5.4 Performance Analysis

The weight coefficients am of delay and energy consumption have an impact on the performance of the algorithm. To analyze this impact, we analyzed the delay and energy consumption under the condition of changing weight coefficients.

Fig. 7 shows the influence of the weight coefficient on the average delay and average energy consumption of the system. As am gradually increases, AGA-DDPG tends to focus more on the delay cost paid by the system, while paying less attention to energy consumption. In contrast, as am gradually decreases, the proportion of delay in the overall system overhead decreases, and the system tends to pay more attention to energy consumption. In WTG anomaly monitoring, more emphasis is placed on reducing delays, as the ultimate goal is real-time monitoring to avoid WTG failures. Therefore, the parameter am is set to 0.6 to ensure that more attention is given to delay. This decision aligns with the characteristics of WTG anomaly detection applications, where timeliness is critical. It ensures that the monitoring system can promptly detect and respond to anomalies in wind turbines, thereby enhancing system reliability and efficiency. Furthermore, simulation results may illustrate the performance trends of the system as parameter am varies. For example, one may observe that with higher values of am, system latency decreases while energy consumption increases, whereas lower values of am may lead to slight increases in latency but effective control over system energy consumption.

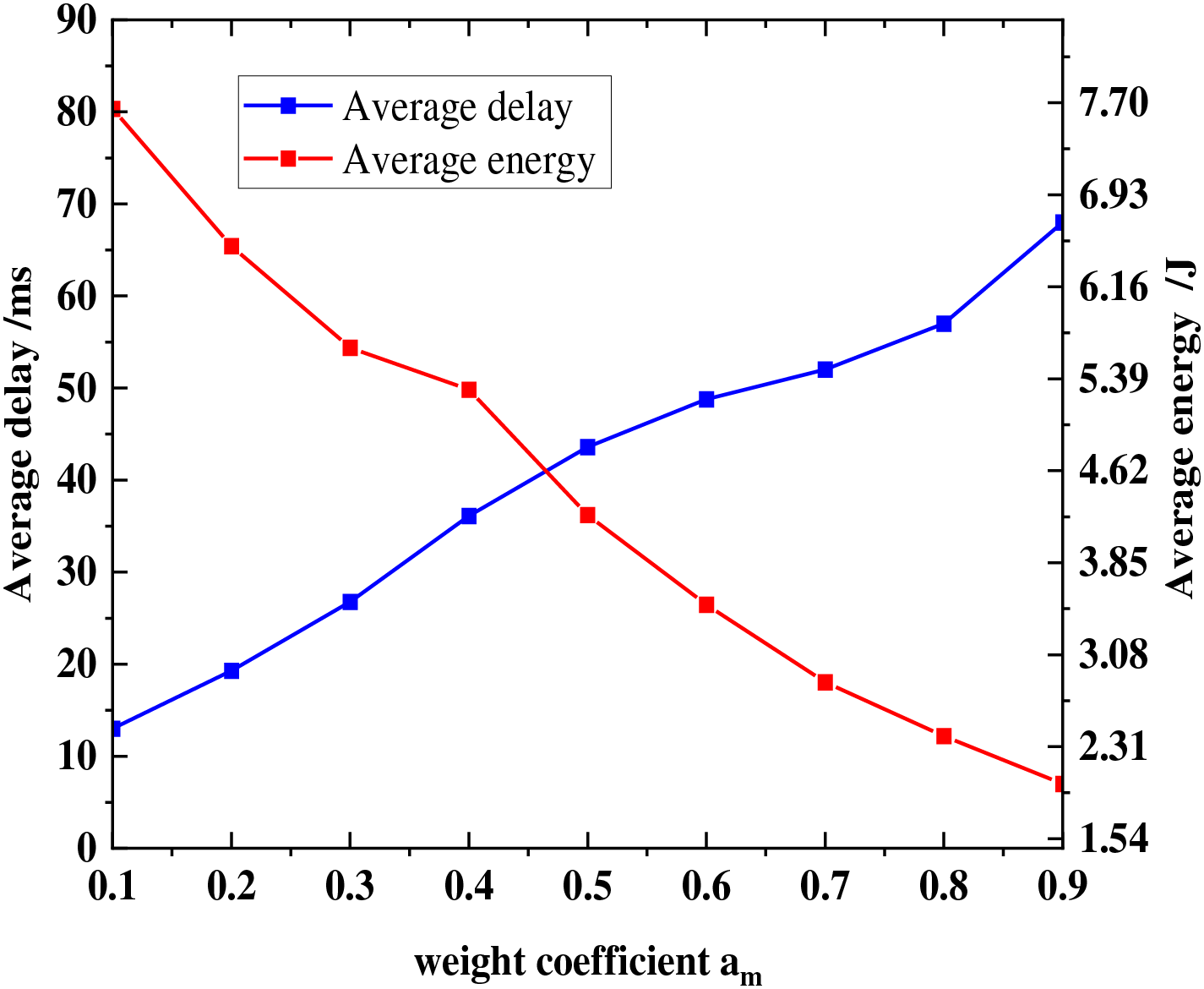
Figure 7: The influence of the weight coefficient am on the average delay and average energy consumption of the system

Fig. 8 shows the impact of the different schemes on the energy consumption and delay for WSNs ranging from 10 to 50. For the MEC solution, when the number of WSNs is low, the local server has fully sufficient capacity to handle it, and the produced energy consumption and latency start to increase linearly with the number of WSNs. However, when the number of WSNs increases to 30, the local MEC server appears to be under more calculation pressure and will incur more waiting delays. This indicates that even with the use of MEC, performance bottlenecks may occur under high load conditions. The random offloading scheme and MEC present similar tendencies but are more volatile. The random offloading generates more energy consumption and latency than does the MEC scheme. This is because random offloading requires additional latency and energy consumption for transmission compared with MEC when offloading tasks to other MEC servers. This additional overhead significantly increases the overall cost. When the number of WSNs is small, the delay and energy consumption generated by DDPG are similar to those generated by TD3, indicating the relatively stable performance of both algorithms in smaller-scale networks. However, as the number of WSNs increased, the performance of the AGA-DDPG algorithm gradually improved. This is attributed to AGA-DDPG’s better optimization of the trade-off between energy consumption and latency in multi-sensor network environments, achieved through dynamically adjusting task offloading strategies to adapt to varying load conditions. In addition, to further demonstrate the effectiveness of AGA-DDPG, the overall overhead of all algorithms is shown in Fig. 9.

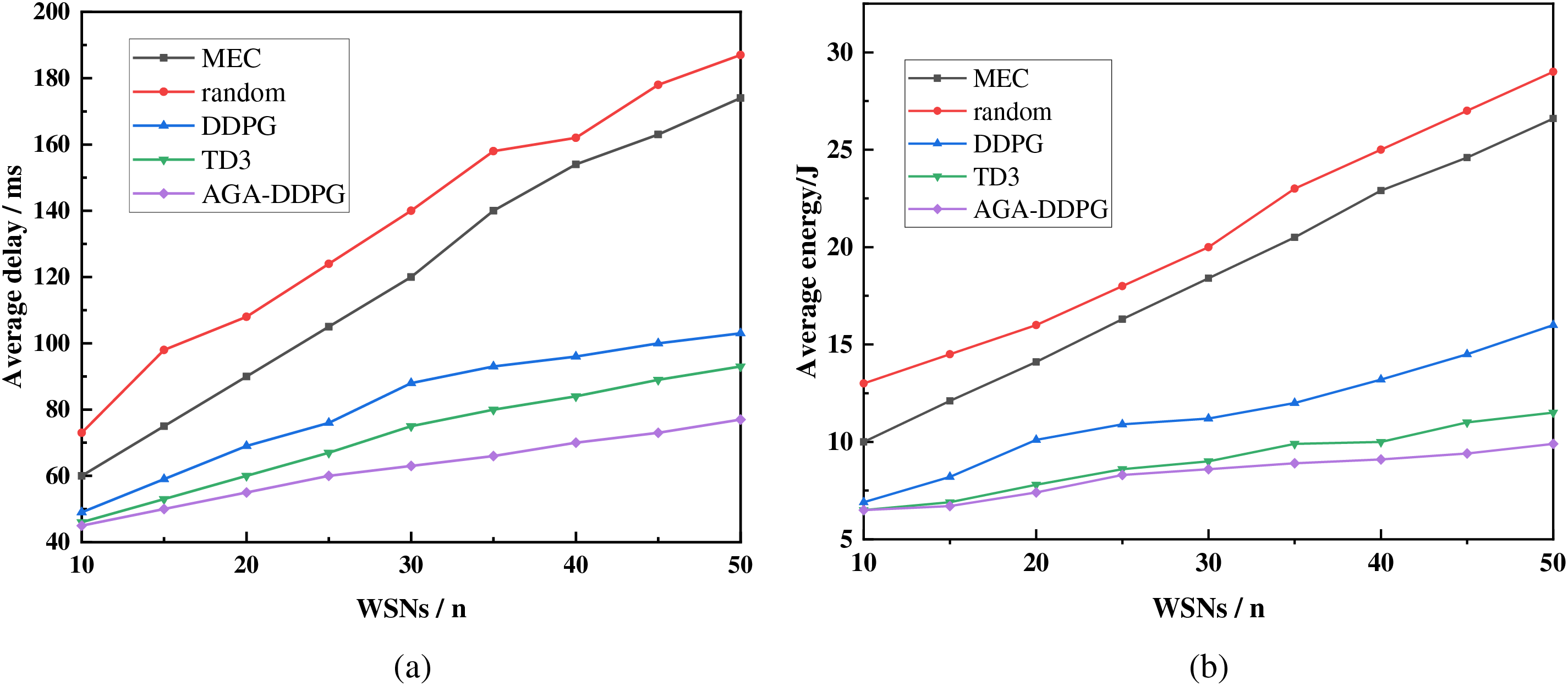
Figure 8: (a) Impact of the number of WSNs on average delay; (b) Impact of the number of WSNs on average energy consumption

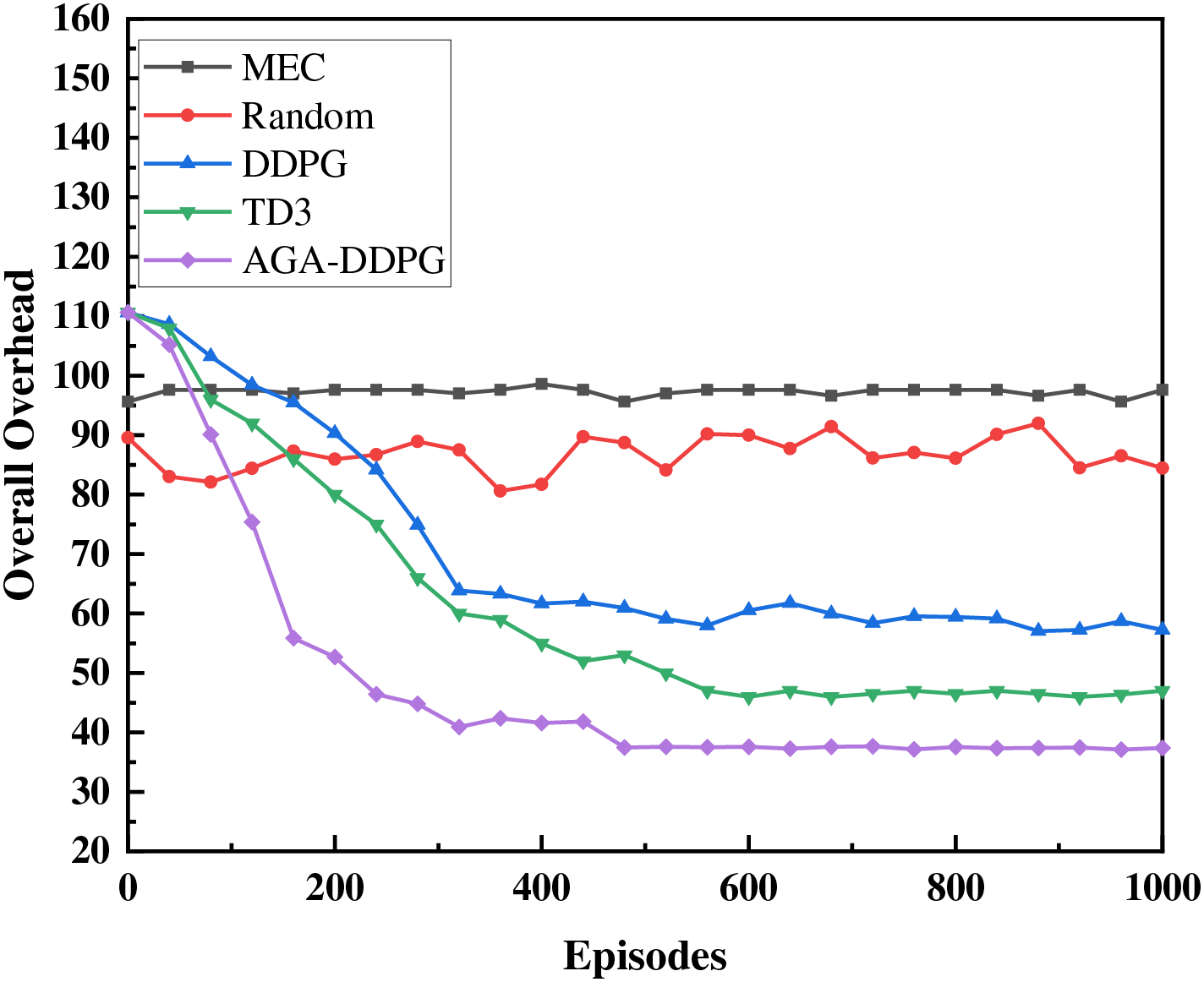
Figure 9: Overall overhead comparison of all solutions

The overall overhead changes little when the tasks are all computed on the local MEC server, but more system overhead is produced. This suggests that local MEC can efficiently handle tasks but may encounter performance bottlenecks due to resource constraints. The random offload scheme shows greater volatility because this approach does not consider the offload object resource situation. If the offload object has more sufficient computational resources, the system overhead is lower than that of the local MEC. In contrast, if the offloading object does not have enough arithmetic power, it does not work better and causes network blockage and energy consumption. TD3 and DDPG have a significant effect on the overall overhead reduction but exhibit slow convergence and unstable convergence. TD3 demonstrates superior performance compared to DDPG but converges slower than AGA-DDPG, reflecting the optimization and resource utilization advantages of the AGA-DDPG algorithm. Simulation results indicate that AGA-DDPG significantly reduces overall overhead compared to local MEC, random offloading, TD3, and DDPG algorithms, achieving savings of 61.8%, 55%, 21%, and 33%, respectively. This underscores AGA-DDPG’s ability to more effectively optimize resource allocation in task offloading decisions, thereby lowering system costs.

6  Conclusions

In this paper, the task offloading strategies to offshore wind farm operations address network congestion and high latency issues in cloud-based maintenance methods. Firstly, we propose the use of UAVs installed with MEC servers at offshore wind farms, marking a novel approach to task offloading services and addressing the scarcity of edge servers in offshore wind environments, thus filling a significant gap in the existing literature. Secondly, the implementation of the MADRL framework enables centralized training of agents with decentralized execution, crucial for dynamic offshore environments. Finally, by introducing the AGA to explore the action space of DDPG, we mitigate the slow convergence of DDPG in high-dimensional action spaces. Experimental results demonstrate that our proposed AGA-DDPG algorithm offers significant advantages over other methods in terms of overall cost savings.

While this research demonstrates the potential of new task offloading strategies for offshore wind farms, we acknowledge discrepancies between simulation environments and real-world conditions that may impact algorithm performance. Additionally, our model relies on idealized assumptions such as fixed task sizes and ideal communication conditions, limiting its applicability and generalizability in real-world settings. Future work should involve field experiments for validation, broader performance evaluations, and integration with IoT and big data analytics to further enhance algorithm efficiency and applicability in practical scenarios. These efforts will contribute to advancing the use of edge computing in offshore wind farms and other offshore environments, providing reliable technical support for future intelligent operations and resource management.

Acknowledgement: The authors would like to express their gratitude for the valuable feedback and suggestions provided by all the anonymous reviewers and the editorial team.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China under grant 61861007; in part by the Guizhou Province Science and Technology Planning Project ZK [2021]303; in part by the Guizhou Province Science Technology Support Plan under grant [2022]264, [2023]096, [2023]409 and [2023]412; in part by the Science Technology Project of POWERCHINA Guizhou Engineering Co., Ltd. (DJ-ZDXM-2022-44); in part by the Project of POWERCHINA Guiyang Engineering Corporation Limited (YJ2022-12).

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Zeshuang Song and Xiao Wang; methodology, Xiao Wang and Zeshuang Song; software, Zeshuang Song and Qing Wu; validation, Zeshuang Song and Yanting Tao; formal analysis, Linghua Xu and Jianguo Yan; investigation, Yaohua Yin; writing—original draft preparation, Zeshuang Song; writing—review and editing, Zeshuang Song and Xiao Wang; visualization, Zeshuang Song and Qing Wu; supervision, Xiao Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: According to the edge tasks offloading in the real world, we used Python language to simulate and validate our proposed method; the data source mainly comes from laboratory simulations, rather than real-life datasets, so we feel that there is no need to present these simulated data.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Qin, C. Qu, M. Song, Q. Wang, and L. Huang, “Planning of MTDC system for offshore wind farm clusters considering wind power curtailment caused by failure,” (in Chinese), Smart Power, vol. 51, no. 6, pp. 21–27, 2023. [Google Scholar]

2. J. Zhang and W. Hao, “Development of offshore wind power and foundation technology for offshore wind turbines in China,” Ocean Eng., vol. 266, no. 5, Dec. 2022. doi: 10.1016/j.oceaneng.2022.113256. [Google Scholar] [CrossRef]

3. H. M. Toonen, and H. J. Lindeboom, “Dark green electricity comes from the sea: Capitalizing on ecological merits of offshore wind power?” Renew. Sustain. Energ. Rev., vol. 42, pp. 1023–1033, 2015. doi: 10.1016/j.rser.2014.10.043. [Google Scholar] [CrossRef]

4. J. Chen and M. H. Kim, “Review of recent offshore wind turbine research and optimization methodologies in their design,” J. Mar. Sci. Eng., vol. 10, no. 1, Jan. 2022. doi: 10.3390/jmse10010028. [Google Scholar] [CrossRef]

5. Y. S. Hamed et al., “Vibration performance, stability and energy transfer of wind turbine tower via PD controller,” Comput. Mater. Contin., vol. 64, no. 2, pp. 871–886, 2020. doi: 10.32604/cmc.2020.08120. [Google Scholar] [CrossRef]

6. Y. Song et al., “Remotely monitoring offshore wind turbines via ZigBee networks embedded with an advanced routing strategy,” J. Renew. Sustain. Energy, vol. 5, no. 1, Jan. 2013. doi: 10.1063/1.4773467. [Google Scholar] [CrossRef]

7. R. Flagg et al., “Cabled community observatories for coastal monitoring-develo** priorities and comparing results,” in Global Oceans 2020: Singapore–US Gulf Coast, Biloxi, MS, USA, 2020, vol. 3, pp. 1–8. doi: 10.1109/IEEECONF38699.2020.9389268. [Google Scholar] [CrossRef]

8. H. Kobari, Z. Du, C. Wu, T. Yoshinaga, and W. Bao, “A reinforcement learning based edge cloud collaboration,” in 2021 Int. Conf. Inf. Commun. Technol. Disaster Manag. (ICT-DM), Hangzhou, China, 2021, pp. 26–29. doi: 10.1109/ICT-DM52643.2021.9664025. [Google Scholar] [CrossRef]

9. P. Zhang, Z. He, C. Cui, C. Xu, and L. Ren, “An edge-computing framework for operational modal analysis of offshore wind-turbine tower,” Ocean Eng., vol. 287, no. 1, Nov. 2023. doi: 10.1016/j.oceaneng.2023.115720. [Google Scholar] [CrossRef]

10. Z. Wu, Z. Yang, C. Yang, J. Lin, Y. Liu and X. Chen, “Joint deployment and trajectory optimization in UAV-assisted vehicular edge computing networks,” J. Commun. Netw., vol. 24, no. 1, pp. 47–58, Sep. 2021. doi: 10.23919/JCN.2021.000026. [Google Scholar] [CrossRef]

11. S. Yu, X. Chen, Z. Zhou, X. Gong, and D. Wu, “When deep reinforcement learning meets federated learning: Intelligent multitimescale resource management for multiaccess edge computing in 5G ultradense network,” IEEE Internet Things J., vol. 8, no. 4, pp. 2238–2251, Feb. 2021. doi: 10.1109/JIOT.2020.3026589. [Google Scholar] [CrossRef]

12. J. Xue, Q. Wu, and H. Zhang, “Cost optimization of UAV-MEC network calculation offloading: A multi-agent reinforcement learning method,” Arxiv Ad Hoc Netw., vol. 136, 2022. doi: 10.1016/j.adhoc.2022.102981. [Google Scholar] [CrossRef]

13. Z. Chen and X. Wang, “Decentralized computation offloading for multi-user mobile edge computing: A deep reinforcement learning approach,” EURASIP J. Wirel. Commun. Netw., vol. 2020, no. 1, Sep. 2022. doi: 10.1186/s13638-020-01801-6. [Google Scholar] [CrossRef]

14. X. Zhang, W. Wu, S. Liu, and J. Wang, “An efficient computation offloading and resource allocation algorithm in RIS empowered MEC,” Comput. Commun., vol. 197, pp. 113–123, 2023. doi: 10.1016/j.comcom.2022.10.012. [Google Scholar] [CrossRef]

15. X. Wang, Z. Lu, S. Sun, J. Wang, L. Song and M. Nicolas, “Optimization scheme of trusted task offloading in IIoT scenario based on DQN,” Comput. Mater. Contin., vol. 74, no. 1, pp. 2055–2071, 2023. doi: 10.32604/cmc.2023.031750. [Google Scholar] [CrossRef]

16. Y. H. Xu, X. Liu, W. Zhou, and G. Yu, “Generative adversarial LSTM networks learning for resource allocation in UAV-Served M2M communications,” IEEE Wirel. Commun. Lett., vol. 10, no. 7, pp. 1601–1605, 2021. doi: 10.1109/LWC.2021.3075467. [Google Scholar] [CrossRef]

17. P. K. R. Maddikunta et al., “Incentive techniques for the internet of things: A survey,” J. Netw. Comput. Appl., vol. 206, Oct. 2023. doi: 10.1016/j.jnca.2022.103464. [Google Scholar] [CrossRef]

18. Z. Gao, L. Yang, and Y. Dai, “Fast adaptive task offloading and resource allocation via multiagent reinforcement learning in heterogeneous vehicular fog computing,” IEEE Internet Things J., vol. 10, no. 8, pp. 6818–6835, 2023. doi: 10.1109/JIOT.2022.3228246. [Google Scholar] [CrossRef]

19. M. Gao, R. Shen, L. Shi, W. Qi, J. Li and Y. Li, “Task partitioning and offloading in DNN-task enabled mobile edge computing networks,” IEEE Trans. Mob. Comput., vol. 22, no. 4, pp. 2435–2445, 2023. doi: 10.1109/TMC.2021.3114193. [Google Scholar] [CrossRef]

20. H. Zhou, Y. Long, S. Gong, K. Zhu, D. T. Hoang and D. Niyato, “Hierarchical multi-agent deep reinforcement learning for energy-efficient hybrid computation offloading,” IEEE Trans. Veh. Technol., vol. 72, no. 1, pp. 986–1001, 2023. doi: 10.1109/TVT.2022.3202525. [Google Scholar] [CrossRef]

21. L. Chen, Y. Liu, Y. Lu, and H. Sun, “Energy-aware and mobility-driven computation offloading in MEC,” J. Grid Computing, vol. 21, no. 2, Jun. 2023. doi: 10.1007/s10723-023-09654-1. [Google Scholar] [CrossRef]

22. B. Vijayaram and V. Vasudevan, “Wireless edge device intelligent task offloading in mobile edge computing using hyper-heuristics,” EURASIP J. Adv. Signal Process, vol. 2022, no. 1, Dec. 2022. doi: 10.1186/s13634-022-00965-1. [Google Scholar] [CrossRef]

23. O. Karatalay, I. Psaromiligkos, and B. Champagne, “Energy-efficient resource allocation for D2D-assisted fog computing,” IEEE Trans. Green Commun. Netw., vol. 6, no. 4, pp. 1990–2002, Dec. 2022. doi: 10.1109/TGCN.2022.3190085. [Google Scholar] [CrossRef]

24. F. Li, H. Yao, J. Du, C. Jiang, Z. Han and Y. Liu, “Auction design for edge computation offloading in sdn-based ultra dense networks,” IEEE Trans. Mob. Comput., vol. 21, no. 5, pp. 1580–1595, May 2022. doi: 10.1109/TMC.2020.3026319. [Google Scholar] [CrossRef]

25. Z. Chen, L. Lei, and X. Song, “Multi-agent DDPG enpowered uav trajectory optimization for computation task offloading,” in Int. Conf. Commun. Technol. (ICCT), Nanjing, China, Nov. 2022, pp. 608–612. doi: 10.1109/ICCT56141.2022.10073166. [Google Scholar] [CrossRef]

26. Z. Guo, H. Chen, and S. Li, “Deep reinforcement learning-based one-to-multiple cooperative computing in large-scale event-driven wireless sensor networks,” Sensors, vol. 23, no. 6, Mar. 2023. doi: 10.3390/s23063237. [Google Scholar] [PubMed] [CrossRef]

27. T. P. Truong, N. N. Dao, and S. Cho, “HAMEC-RSMA: Enhanced aerial computing systems with rate splitting multiple access,” IEEE Access, vol. 10, pp. 52398–52409, 2022. doi: 10.1109/ACCESS.2022.3173125. [Google Scholar] [CrossRef]

28. H. Ke, J. Wang, L. Deng, Y. Ge, and H. Wang, “Deep reinforcement learning-based adaptive computation offloading for MEC in heterogeneous vehicular networks,” IEEE Trans. Veh. Technol., vol. 69, no. 7, pp. 7916–7929, Jul. 2020. doi: 10.1109/TVT.2020.2993849. [Google Scholar] [CrossRef]

29. M. R. Haque et al., “Unprecedented Smart algorithm for uninterrupted sdn services during DDoS attack,” Comput. Mater. Contin., vol. 70, no. 1, pp. 875–894, 2022. doi: 10.32604/cmc.2022.018505. [Google Scholar] [CrossRef]

30. H. Ke, H. Wang, and H. Sun, “Multi-agent deep reinforcement learning-based partial task offloading and resource allocation in edge computing environment,” Electronics, vol. 11, no. 15, Aug. 2022. doi: 10.3390/electronics11152394. [Google Scholar] [CrossRef]

31. X. Zhang, Z. He, Y. Sun, S. Yuan, and M. Peng, “Joint sensing, communication, and computation resource allocation for cooperative perception in fog-based vehicular networks,” in 13th Int. Conf. Wirel. Commun. Signal Process. (WCSP), Changsha, China, 2021, pp. 1–6. [Google Scholar]

32. S. Liu, S. Yang, H. Zhang, and W. Wu, “A federated learning and deep reinforcement learning-based method with two types of agents for computation offload,” Sensors, vol. 23, no. 4, Feb. 2023. doi: 10.3390/s23042243. [Google Scholar] [PubMed] [CrossRef]

33. C. You, K. Huang, H. Chae, and B. H. Kim, “Energy-efficient resource allocation for mobile-edge computation offloading,” IEEE Trans. Wirel. Commun., vol. 16, no. 3, pp. 1397–1411, 2016. doi: 10.1109/TWC.2016.2633522. [Google Scholar] [CrossRef]

34. L. Kang, Y. Wang, Y. Hu, F. Jiang, N. Bai and Y. Deng, “JUTAR: Joint user-association, task-partition, and resource-allocation algorithm for MEC networks,” Sensors, vol. 23, no. 3, Feb. 2023. doi: 10.3390/s23031601. [Google Scholar] [PubMed] [CrossRef]

35. A. M. Seid, J. Lu, H. N. Abishu, and T. A. Ayall, “Blockchain-enabled task offloading with energy harvesting in multi-uav-assisted IoT networks: A multi-agent drl approach,” IEEE J. Sel. Areas Commun., vol. 40, no. 12, pp. 3517–3532, Dec. 2022. doi: 10.1109/JSAC.2022.3213352. [Google Scholar] [CrossRef]

36. Q. Luo, T. H. Luan, W. Shi, and P. Fan, “Deep reinforcement learning based computation offloading and trajectory planning for multi-uav cooperative target search,” IEEE J. Sel. Areas Commun., vol. 41, no. 2, pp. 504–520, Feb. 2023. doi: 10.1109/JSAC.2022.3228558. [Google Scholar] [CrossRef]

37. H. Huang, Q. Ye, and Y. Zhou, “Deadline-aware task offloading with partially-observable deep reinforcement learning for multi-access edge computing,” IEEE Trans. Netw. Sci. Eng., vol. 9, no. 6, pp. 3870–3885, Nov. 2022. doi: 10.1109/TNSE.2021.3115054. [Google Scholar] [CrossRef]

38. X. Deng, J. Yin, P. Guan, N. N. Xiong, L. Zhang and S. Mumtaz, “Intelligent delay-aware partial computing task offloading for multiuser industrial internet of things through edge computing,” IEEE Internet Things J., vol. 10, no. 4, pp. 2954–2966, Feb. 2023. doi: 10.1109/JIOT.2021.3123406. [Google Scholar] [CrossRef]

39. S. Cao, S. Chen, H. Chen, H. Zhang, Z. Zhan and W. Zhang, “Research on hybrid computation offloading strategy for MEC based on DDPG,” Electronics, vol. 12, no. 3, Feb. 2023. doi: 10.3390/electronics12030562. [Google Scholar] [CrossRef]

40. C. Li, W. Gao, L. Shi, Z. Shang, and S. Zhang, “Task scheduling based on adaptive priority experience replay on cloud platforms,” Electronics, vol. 12, no. 6, Mar. 2023. doi: 10.3390/electronics12061358. [Google Scholar] [CrossRef]

41. G. Zhang, S. Ni, and P. Zhao, “Learning-based joint optimization of energy delay and privacy in multiple-user edge-cloud collaboration MEC systems,” IEEE Internet Things J., vol. 9, no. 2, pp. 1491–1502, 2022. doi: 10.1109/JIOT.2021.3088607. [Google Scholar] [CrossRef]