Real-Time Implementation of Quadrotor UAV Control System Based on a Deep Reinforcement Learning Approach

Nomenclature

1  Introduction

Quadrotors stand out as a common variety of UAVs, distinguished by features such as exceptional maneuverability, compact dimensions, Vertical Take-Off and Landing (VTOL) capabilities, and ease of interaction [1]. They are utilized in diverse fields, such as homeland security [2], atmospheric sampling [3], search-and-rescue operations [4], and military applications like battlefield surveillance and airspace patrolling [5]. Additionally, innovative uses have emerged, with quadrotors equipped with Micro Electrical Mechanical Sensors (MEMS) for applications in Internet of Things (IoT) and Mobile Edge Computing (MEC) architectures [6]. However, the complex dynamics of quadrotors, characterized by non-linearity, underactuation, and coupling, pose significant challenges in control system design. To address these challenges, researchers have developed control theories for both single and multi-agent systems, like consensus algorithms [7], cooperative control [8], and decentralized decision-making [9], focusing on enhancing the maneuverability and stability of individual quadrotors and improving collaboration among multiple UAVs.

In the field of single-agent control, quadrotors have been subjected to various methods and control techniques. Several of these employ linear methods, including PID [10], Linear Quadratic Regulator (LQR) [11], and Model Predictive Control (MPC) [12]. This category of controllers is simple and relatively easy to implement but has limited operating regions. To address this limitation, more complex controllers based on nonlinear approaches have been introduced, including SMC [13,14], Backstepping [15,16], Adaptive control [17,18], and H∞ control [19,20], with many advanced and hybrid versions of each. As shown in [21], the authors conducted a study that summarizes several attitude stabilization methods, including PID, LQR, MPC, Feedback Linearization, and SMC, offering guidance for selecting suitable quadrotor control strategies, considering both quantitative and qualitative considerations. The effectiveness of conventional control algorithms in diverse systems frequently hinges on subjective parameter selection informed by a comprehensive grasp of the model and experimental surroundings. In intricate situations, achieving a balance between accuracy, robustness, and efficiency in a single control function can be significantly challenging.

Besides the previously mentioned controllers, data-driven methods have become increasingly prominent in robotics and control systems due to recent advancements in computing power and the accessibility of vast amounts of data. Artificial intelligence (AI), including supervised, unsupervised, and reinforcement learning techniques, has undergone rapid advancements over the last few years. Various domains in robotics, including path planning [22], simultaneous localization and mapping (SLAM) [23], perception, and control, among others, have now integrated AI techniques into their applications. Furthermore, Deep Reinforcement Learning (DRL) has garnered significant attention within control theory due to its ability to handle high-dimensional state and action spaces and to learn directly from interaction with the environment without requiring an explicit model. It has shown impressive results in terms of accuracy and robustness across a large variety of tasks and applications. From various perspectives, DRL has the potential to offer significant advantages over traditional control methods, along with many other data-driven approaches.

Motivated by several factors including adaptability, learning from interaction, scalability, and performance, our work introduces several key innovations that differentiate it from existing approaches. We propose a novel framework that combines the Twin-Delayed Deep Deterministic Policy Gradient, an off-policy, model-free, actor-critic algorithm, with Simulated Annealing, a metaheuristic optimization technique. This framework is designed to control both the position and attitude of a quadrotor system, with the aim of overcoming the limitations of existing methods. The effectiveness of our approach is demonstrated through a comprehensive comparison with high-performance nonlinear controllers such as SMC and Backstepping, across various path-following scenarios. This study contributes to the field by introducing a robust, scalable, and adaptable control solution that bridges the gap between traditional control methods and modern AI-driven techniques.

The subsequent sections of the document are organized as follows: Section 2 furnishes relevant techniques used in UAVs control systems, encompassing convolutional approaches and, in particular, RL algorithms. Section 3 explores the investigated control approaches, providing a concise overview of reinforcement learning fundamentals. The spotlight is on the SA-RL algorithm, highlighting its role in optimizing hyperparameters for improved UAV control performance. Additionally, the section unfolds the formulation of the reward function and the proposed network’s architecture. Finally, Section 4 summarizes the simulation results, offering an extensive comparative analysis with the SMC and Backstepping controllers. It also delves into the real-world implementation and outlines the identified limitations and findings.

2  Related Works

While recent research has primarily focused on integrating AI algorithms for autonomous flights, questions remain regarding the performance and limitations of intelligent control strategies compared to traditional UAVs control methods. This section offers a review of the literature from both perspectives, complemented by related research on the optimization of reinforcement learning hyperparameters.

Deployed to quadrotor control systems, several data-based approaches and techniques have demonstrated promising performance, especially when combined with traditional controllers. In [24], the authors presented a data-enabled predictive control algorithm for nano-quadcopter position control, utilizing input/output measurements for trajectory prediction without system identification. The proposed approach exhibited reliable performance and successful trajectory tracking compared to MPC. Additionally, this paper [25] introduced a data-driven model-free adaptive control method based on improved SMC to address dynamic modeling and parameter identification challenges for quadrotor trajectory tracking. This method incorporates an adaptive update law and saturation function to mitigate chattering and employs inner and outer loop control structures for position and attitude control, demonstrating effectiveness, feasibility, and high accuracy in trajectory tracking validated through simulation. Furthermore, in [26], the authors presented a data-driven approach using the Koopman operator and extended dynamic mode decomposition for quadrotor UAV control, utilizing rotation matrices to accurately represent nonlinear dynamics. Leveraging this model, a linear model predictive controller operating at 100 Hz effectively tracked agile trajectories with high accuracy.

More relevant to the work presented in this paper, data-driven AI control systems, particularly RL approaches, have been extensively explored for UAVs and quadrotor control. As reported in [27], these algorithms are highly effective in optimizing controller parameters. In their study, the authors introduced an RL algorithm called Learning Automata to fine-tune the parameters of the X,Y,Z positions and the attitude PID controllers. The results obtained were notably promising compared to other applied strategies. Referring to [28], the authors introduced a low-level RL control framework combined with Global Positioning System (GPS) to counteract external forces. This controller outperformed a standalone RL control algorithm in tasks involving stationary hovering and path-following, reducing the error by 75% during outdoor experiments.

Moreover, in [29], the authors used the Deep Deterministic Policy Gradient (DDPG) algorithm to address the trajectory tracking issue quadrotors in three distinct ways. They incorporated instantaneous path information, integrated a mechanism to anticipate path curves, and computed the optimum speed based on the sloping nature of the path. Additionally, improvements were introduced to this technique as demonstrated in [30], a novel algorithm was proposed that leverages an integral compensator coupled with the deterministic policy gradient approach. The authors enhanced the actor-critic structure by implementing a two-phase learning protocol, which includes both online and offline training phases. In [31], the Recurrent Deterministic Policy Gradient method was introduced as a unique technique crafted to adjust weights based on previous paths, rather than at the end of each episode. It found application in obstacle avoidance agents, complementing the path-following strategy of the DDPG agent outlined in [29].

Furthermore, in their recent work [32], the authors addressed the challenge of selecting state and control weighting matrices for LQR control of a quadrotor. They employed DDPG to update the Q matrix, achieving faster response times while minimizing integral square error. The proposed controller outperforms four commonly used methods regarding the rise time, the settling time, and the time of flight. The authors concluded that this approach holds promise for application in other control problems and enhancing control efficiency.

Another RL-based method was employed for autonomous agent flight training. In [33], the off-policy Deep Q Network (DQN) algorithm was utilized to learn an agent a high-level control policy using low-resolution images captured from a downward-facing camera. This training aimed to achieve autonomous landing for a quadrotor. In the study presented in [34], the DQN algorithm using mean squared error of the Euclidean distance within the reward function, and the Adadelta optimizer, yielded the best performance in quadrotor flight when evaluated alongside Q-learning and SARSA (State-Action-Reward-State-Action). This evaluation encompassed a combination of optimizers (RMSProp, Adadelta, SGD, and Adam) and reward functions (Euclidean distance and its mean square error). Furthermore, on-policy algorithms were introduced as control strategies for quadrotors. In [35], the authors introduced a quadrotor control system at a lower level, employing the Proximal Policy Optimization (PPO) algorithm. The subsequent presentation included the outcomes of two practical experiments, aimed at validating the system’s proficiency in tasks such as maintaining a stationary position and following a predefined path. Another study [36] also investigated the use of PPO and TD3 for UAV control, comparing their performance in terms of stability, robustness, and trajectory accuracy across various UAV designs and scenarios. The results demonstrate that both algorithms effectively manage UAV control challenges in dynamic environments.

Additionally, RL algorithms were employed in conjunction with traditional linear and non-linear controllers to achieve high accuracy and robustness. In [37], a hybrid RL control system for micro-quadrotors is proposed, which combines PD-RL and LQR-RL. In terms of convergence rate and control performance, this hybrid strategy outperforms the original Probabilistic Inference for Learning Control (PILCO), a method recognized for being among the fastest model-based RL algorithms. In a separate study, outlined in [38], a Feedforward Neural Network (FFNN) was trained to serve as a predictive model for a quadrotor’s entire translational dynamics. This FFNN was subsequently integrated into the MPC framework, resulting in a neural network-based MPC. This controller effectively reduces the average path-following error by 40% in comparison to the performance of classic PID controllers. Furthermore, in [39], the authors conducted experiments involving the training of a Crazy-Fly Quadrotor using model-based RL with MPC. This approach enabled the training of a network to directly map Pulse Width Modulation (PWM) signals from sensors, facilitating autonomous flight based on experimental data.

While the previously discussed works employed RL algorithms as the primary control strategy or in conjunction with traditional controllers, a benchmark between these different approaches was less conducted in recent studies. In [40], two distinct quadrotor controllers were proposed and compared. The nonlinear controller, based on feedback linearization learned using Fitted Value Iteration, demonstrated superior performance when compared to an RL agent. Notably, it held the advantage of not requiring prior mathematical knowledge of the quadrotor model. In the work presented by the authors of [41], a method for controlling a quadrotor with a trained neural network was introduced. This approach employed another RL technique, denoted as NN+PD, which was considered more suitable for quadrotor control than previously employed methods. In addition to simulations, the efficiency of the obtained policy was evaluated in comparison to the DDPG and the Trust Region Policy Optimization (TRPO) in real-world implementations. In another study, detailed in [42], different options for reward functions were explored, and their influence on the controller efficiency were considered. This examination was performed while utilizing the model-free RL algorithm PPO. Subsequently, the results were compared to those obtained using a classic PD controller for motion control of a quadrotor.

Recent advancements in reinforcement learning for UAV control have addressed several complex challenges, including disturbance estimation, sample efficiency, collision avoidance, and multi-objective optimization in dynamic environments. In [43], the authors introduced the Constrained Distributional REinforced-Disturbance-estimator integrated with a Stochastic Model Predictive Controller to enhance quadrotor trajectory tracking performance amidst uncertain aerodynamic effects. This framework effectively identifies uncertainties, achieving optimal convergence rates and a 70% improvement in accumulative tracking errors compared to recent methods. Similarly, in [44], the authors presented a hybrid RL framework combining meta-learning (Reptile algorithm) and generative adversarial imitation learning to improve training efficiency and adaptability in UAV trajectory planning without the need for complex reward functions. In [45], a performance-designated RL-based enclosing control scheme was proposed to achieve target approximation while ensuring collision avoidance by using adaptive performance functions and barrier functions. Multi-agent and cooperative strategies have also been explored to extend UAVs’ operational lifecycle and enhance mission performance; for instance, in [46], the authors formulated a multi-objective optimization problem for UAV-based base stations using a DRL model assisted by particle swarm optimization to balance energy efficiency, user fairness, and coverage rate. Additionally, in environments where communication and radar are compromised, Fei et al. [47] proposed the FRDDM-DQN algorithm, integrating a Faster R-CNN model and a Data Deposit Mechanism to enhance autonomous navigation and collision avoidance by efficiently extracting obstacle information from images and optimizing training procedures. Moreover, Huang et al. [48] introduced a spatial–temporal integrated framework using a 4-D Multiple-Input–Multiple-Output (MIMO) radar to improve micro-UAV trajectory tracking and prediction under low signal-to-noise ratio (SNR) conditions. The framework jointly optimizes target detection and tracking, coupled with a transformer-based prediction model, achieving superior accuracy in trajectory prediction compared to conventional methods. Together, these studies highlight the continuous evolution of RL-based control strategies and advanced detection and prediction frameworks for UAVs, emphasizing robust disturbance estimation, adaptive learning frameworks, cooperative multi-agent systems, and enhanced trajectory prediction in complex environments. However, while these studies focus on integrating RL with other techniques to address specific challenges such as disturbance estimation, navigation, or prediction accuracy, our work is distinct in developing the SA-TD3 framework specifically for optimizing hyperparameters in quadrotor control tasks, offering improved stability and precision in both high and low-level control scenarios through novel reward functions and actor-critic structures.

Hyper-parameter Optimization (HPO) remains a major concern still under investigation by researchers. The significant sources of variance and the challenges associated with fine-tuning hyper-parameter selection for deep and reinforcement learning algorithms have been widely discussed in recent years. In [49], the authors addressed this issue by utilizing computational complexity and classification accuracy as competing objectives. They presented a Multi-Objective SA approach, yielding superior outcomes through fine-tuning the hyperparameters for Convolutional Neural Networks (CNNs) in object identification tasks. Similarly, in [50], the authors proposed an algorithm based on simplified swarm optimization to tune the hyperparameters of the LeNet CNN model. This algorithm was rigorously tested on three datasets and demonstrated superior performance when compared to both the standard LeNet model and a variant optimized using particle swarm optimization. Another study conducted in [51], a novel algorithm RFEPPO is presented to address the HPO issue, the authors treat the hyper-parameters tuning as a sequential decision problem and employ an agent to sequentially choose hyper-parameters that are updated using a PPO-based method and a surrogate model in which the results demonstrate the relevance of the advocated algorithm. In [52], the authors aimed to enhance both robustness and training efficiency in comparison to Bayesian optimization. They introduced an approach, which employed a framework employing a genetic algorithm with variable-length distributed components to fine-tune hyper-parameters through evolution. Furthermore, they identified appropriate RL structures that yielded higher rewards in fewer episodes across various applications.

As far as we know, the most similar approach to the one conducted in this study is proposed in [53]. In that work, SA was employed to optimize hyperparameters for a well-known unsupervised model called Latent Dirichlet Allocation (LDA). The experimental findings demonstrated that SA-LDA surpasses the performance of the conventional LDA model. This practical examination was conducted using datasets comprising clients feedback from the hotel, movie and mobile sectors. Another relevant paper [54], presents a more efficient and practical RL-based relay selection technique for Underwater Acoustic (UWA) networks. This technique considers both transmission delay and channel quality. Notably, the learning process parameters are dynamically adjusted using SA to enhance convergence speed and achieve higher performance. In contrast to the SA-RL approach described in this paper, our objective is to automate and integrate hyperparameter tuning into the training process of RL algorithms designed for continuous action and observation spaces. This systematic adaptation is aimed at ensuring training convergence and stability for an RL agent. We then apply this approach to perform complex path following and stabilization tasks, which to our best understanding, has not been investigated in this particular manner before.

In reviewing the current landscape of UAV control approaches, a comparative analysis has been conducted to highlight the distinctive methodologies and performance metrics associated with various techniques. Table 1 presents an overview of selected UAV control strategies, detailing their underlying advantages, and limitations.

3  Methodology

This section of the paper outlines the techniques explored for controlling a quadrotor system and explains the methodology used to train an accurate control policy. It presents the various approaches, offering a comprehensive understanding of the research. Additionally, it discusses the process of developing the policy, including the innovative techniques employed.

3.1 The Investigated Approaches

In this work, we explore the utilization and outcomes of an RL agent trained without expert assistance in hyper-parameter tuning. We apply this approach to two distinct quadrotor control configurations, as illustrated in Fig. 1.

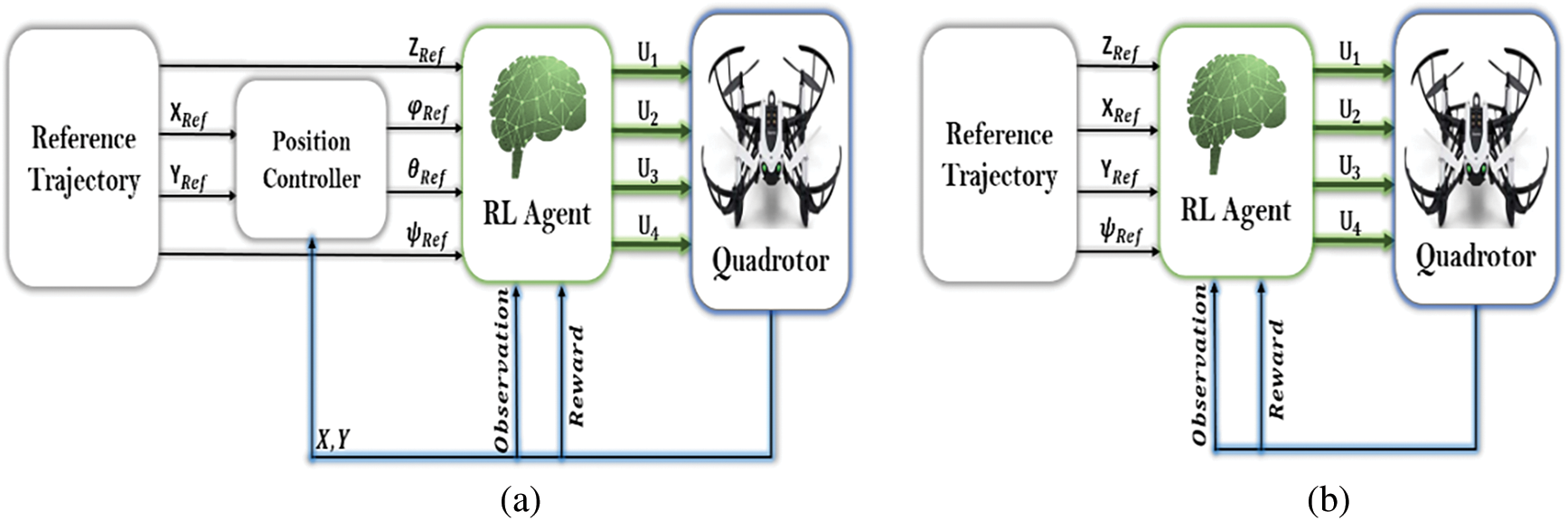
Figure 1: Quadrotor control levels, (a) RL low-level control system, (b) RL control system

We begin with the RL low-level (attitude) controller, as shown in Fig. 1a. This phase of control is critical for ensuring the drone’s stability and maneuverability, enabling it to perform a variety of tasks and missions effectively. Here, an RL agent generates four input commands based on attitude and altitude references (φRef,θRef,ψRef, ZRef).

The second controller, depicted in Fig. 1b, is an RL agent trained to execute a wide range of tasks, from simple hovering to complex autonomous navigation. It uses desired positions and orientation (XRef, YRef,ZRef, ψRef) as references and addresses the challenge of coupled dynamics to take full control of the quadrotor system without separating orientation and position control levels.

In the field of quadrotor UAV control, our work introduces several key contributions and innovations, which are primarily reflected in:

•   Presentation of a novel framework that combines Simulated Annealing with Reinforcement Learning to address the challenges of hyperparameter tuning in reinforcement learning for quadrotor control, ensuring stable and rapid training convergence.

•   Introduction of a simple and mixed reward function that enhances the agent’s ability to understand and adapt to the complex dynamics of the quadrotor, resulting in improved stability and precision in attitude and position control.

•   Proposal of an actor-critic network architecture that incorporates high-order observable states to enhance the RL agent’s comprehension of the quadrotor’s complex dynamics.

•   Performance comparison of the proposed approaches with two non-linear controllers under different scenarios, with results provided and discussed.

•   Finally, practical implementation of the trained RL agents to control a real quadrotor and follow a predefined trajectory.

3.2 Quadrotor Dynamics

Training RL agents in simulation environments before deploying them in the real world offers a safe, cost-effective, and rapid learning process. While simulations cannot fully replicate the complexity of the real world, they serve as a crucial initial phase in the development and refinement of agents before real-world testing.

In order to produce an accurate mathematical model of a quadrotor system, it is necessary to assume that it possesses a symmetry and rigidity in its structure, the thrust is generated by four motors, each connected to rigid propellers of equal size, and the aerodynamic forces (drag and lift) are proportionate to the speed of the rotor’s rotation, where the dynamics of the quadrotor are modeled using two frames: the body frame, and the inertial frame, with its origin located at the quadrotor’s center of the mass, as illustrated in Fig. 2.

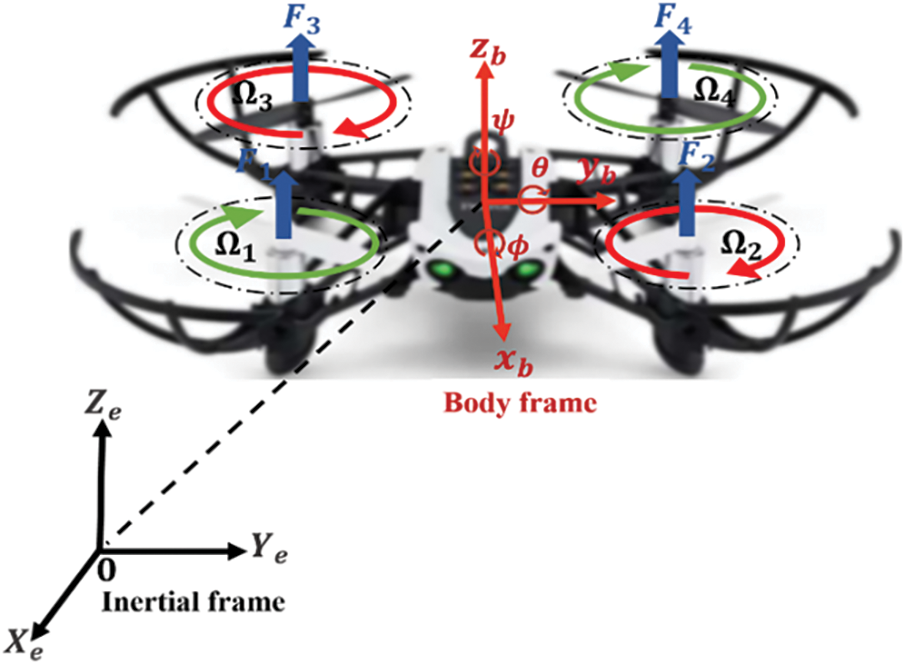
Figure 2: The quadrotor inertial and body frames

The appropriate lift forces (F1,F2,F3 and F4) can be generated by regulating the rotor’s speed, which enhances the quadrotor’s various motions and rotations. The pitch motion is attained by creating a differential thrust force between the front and rear motors, varying (Ω1 and Ω2) or (Ω3 and Ω4) leading to rotation around the yb-axis. Roll motion is generated through differential thrust throughout the right and left propellers’ rotation speeds, adjusting (Ω1 and Ω3) or (Ω2 and Ω4) resulting in rotation around the xb-axis. While the yaw motion occurs when either (Ω1=Ω4) >or< (Ω2 = Ω3) causing a rotation in the clockwise or anti-clockwise direction.

One of the approaches employed for deriving the dynamic model of a quadrotor system is based on the Euler-Lagrangian equation, and its equations of motion are summarized as follows [55]:

{x¨=U1m(cos(φ)sin(θ)cos(ψ)+sin(φ)sin(ψ))y¨=U1m(cos(φ)sin(θ)sin(ψ)+sin(φ)cos(ψ))z¨=U1m(cos(φ)cos(θ))−gφ¨=−(Jzz−Jyy)θ˙ψ˙+U2Jxxθ¨=−(Jzz−Jxx)φ˙ψ˙+U3Jyyψ¨=−(Jyy−Jxx)φ˙θ˙+U4Jzz(1)

This set of equations describes the motion of the quadrotor in 3D space, considering forces and torques applied to it. The terms represent the linear accelerations in the x,y and z directions and the angular accelerations in roll (φ), pitch (θ), and yaw (ψ) axes.

where:

{U1=b(Ω12+Ω22+Ω32+Ω42)U2=l.b(Ω42−Ω22)U3=l.b(Ω32−Ω12)U4=d(Ω12−Ω22+Ω32−Ω42)(2)

The command inputs Ui(i=1,2,3 and 4) denote respectively the lift force, the moments of roll, pitch and yaw. While each rotor’s speed is represented by Ωi(i=1,2,3 and 4). All of the symbols and physical parameters applied for this model are provided in Table 2.

3.3 Reinforcement Learning Background

We consider the conventional RL setup (see Fig. 3), where an agent interacts with an environment E in discrete timesteps. At each timestep t the agent takes an action at, receives an observation xt, and obtains a scalar reward rt. We assume that the environment under investigation is entirely observable, therefore st=xt. While the actions are real-valued, denoted as at∈RN.

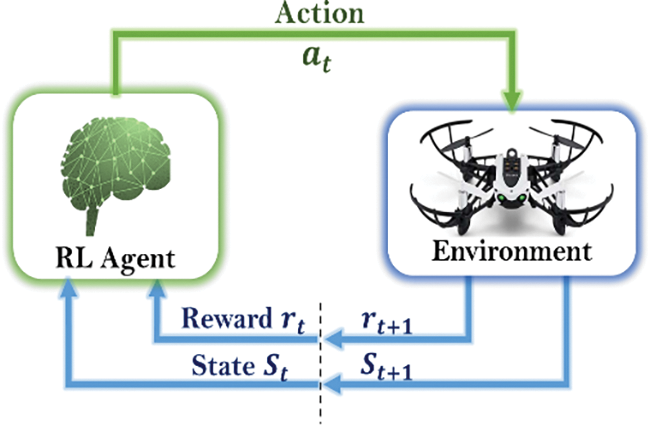
Figure 3: Standard RL setup

A policy, denoted as π, represents the agent’s behavior, mapping states to a probability distribution over actions, defined as π:S⟶P(A). The environment E can also be stochastic and is typically modeled as a Markov Decision Process (MDP). This MDP includes a state space S, an action space A=RN, an initial state distribution p(s1), transition dynamics p(st+1|st,at), and a reward function r(st,at).

The return from a state is calculated as the sum of discounted future rewards with a discounting factor γ∈[0,1]:

Rt=∑i=tTγi−tr(si,ai)(3)

It should be noted that the return is stochastic and depends on the chosen actions, which, in turn, influence the policy. This return defines the cumulative reward at time t for a given sequence of actions ai taken in states si. The discount factor γ ensures that future rewards are weighted less than immediate rewards.

In RL, the goal is to acquire a policy that promotes the predicted return from the initial distribution:

J=Eπ,s0[∑t=0∞γtr(st,at,st+1)|at=π(.|st)](4)

where J represents the expected return to maximize when following a policy π from an initial state s0. It calculates the total discounted reward that an agent can expect to accumulate over time.

Therefore, the state value function Vπ(s) that quantifies the expected return starting from state s and following policy π is defined by:

Vπ(s)=Eπ[∑t=0∞γtr(st,at,st+1)|at∼π(.|st),s0=s](5)

This function mainly reflects the long-term reward achievable from state s under the given policy.

Many RL algorithms make use of the action-value function, that reflects the expected outcome of making an action at in state st and then following policy π, it helps in evaluating the quality of specific actions in given states as:

Qπ(s,a)=Eπ[∑t=0∞γtr(st,at,st+1)|at∼π(.|st),s0=s,a0=a](6)

Given the transition dynamics and the reward function, the Bellman equation is a recursive relationship that holds for all states and shows that the optimum Q-value can be calculated by maximizing over the actions as:

Qπ∗(st,at)=∑s′p(s′|st,at)[r(st,at)+γ.maxa′Qπ∗(s′,a′)](7)

When the next state of st is represented by s′, the optimum state-value and policy are:

Vπ∗(st)=maxa⁡∑s′p(s′|st,at)[r(st,a)+γ.Vπ∗(s′)](8)

This equation defines the optimal state value function Vπ∗(st) as the maximum expected return that can be obtained by taking the best action a in state st. It considers the immediate reward and the optimal value of the next state.

3.4 SA-RL Approach

The reinforcement learning approach investigated in this work is Twin-Delayed Deep Deterministic Policy Gradient (TD3), developed based on the DDPG algorithm. Both algorithms support environments with continuous observation and action spaces, which is the case for our subject.

DDPG is an off-policy, model-free, actor-critic algorithm that employs deep function approximators, allowing it to learn policies in high-dimensional and continuous action spaces. Using the same network architecture and hyper-parameters, this technique efficiently handles over twenty simulated applications, encompassing popular problems such as cart-pole swing-up, dexterous manipulation, legged locomotion, and car driving [56]. It is capable of developing policies that perform comparably to planning algorithms while having complete access to the domain’s dynamics and derivatives. However, DDPG does have several limitations, including training instability, high variance in estimates, and sensitivity to hyper-parameters.

To address these limitations, in [57], the authors introduced several modifications to the original DDPG algorithm, resulting in the Twin-Delayed Deep Deterministic Policy Gradient (TD3). This technique combines the strengths of DPG and deep reinforcement learning by employing a deterministic policy with twin Q-networks, rather than one. It introduces a delay and target policy smoothing to mitigate the over-estimation of the value function and adjusts the target network update frequency to enhance learning stability and prevent overfitting. These modifications were intended to enhance the stability, robustness, and performance of the algorithm, making it more suitable for addressing challenging continuous control problems.

Nevertheless, a significant challenge in training DRL agents lies in the optimization of hyperparameters, as it significantly influences the entire learning process. This tuning process often necessitates exhaustive trials, demanding a high level of knowledge and computing resources for every assignment or task. While TD3 may be less sensitive to hyperparameter variations than DDPG, its performance can still be affected, and careful tuning to find the optimal hyperparameter configuration remains essential and a challenging task under researcher’s scopes.

To alleviate this issue, we introduce an automated framework (see Fig. 4), that initiates training with randomly assigned parameters. It then systematically tunes four critical hyperparameters which significantly impact the learning process, these include: the Noise Variance, the Variance Decay Rate, the Discount Factor and the Minibatch Size. We employ the SA optimization algorithm, a suitable technique that addresses global optimization problems. These problems involve objective functions that are not directly provided and can only be assessed through costly computational simulations as is often the case in reinforcement learning [58].

Figure 4: The SA-RL framework

The objective function represented below, with β a positive weight and Ar the average reward, is designed to enhance the average reward and guarantee consistent performance throughout all training episodes.

O(j)=−β(Ar)(9)

Initially, a random set of parameters, denoted as αrandom, serves as the current solution. From its neighborhood, a new solution j is then produced to initiate the training using the TD3 algorithm. The objective function’s assessment assists SA in deciding whether to accept the new solution or assign it with an acceptance probability p determined by the degree of worsening and the current temperature of the system ck.

The cooling schedule employed follows a linear decay model, where the temperature decreases as ck=c0−λ.k. Here, c0=10 is the initial temperature, λ = 0.2 is the decay rate, and k is the iteration count. This linear cooling strategy balances exploration and exploitation throughout the optimization process. A higher initial value of ck promotes broader exploration by increasing the likelihood of accepting suboptimal solutions in the early stages. This helps in avoiding local minima and ensures a thorough search of the hyperparameter space. As ck decreases, the acceptance probability of suboptimal solutions diminishes, which guides the algorithm toward convergence. The chosen linear decay rate λ is crucial to maintaining this balance, ensuring sufficient exploration in the early stages and efficient convergence in the later stages.

In the TD3 component, target networks are updated using a soft update mechanism to stabilize training. The target networks, denoted as θitarget and ϕtarget are updated as follows:

θitarget←τθi+(1−τ)θitarget(10)

ϕtarget←τϕ+(1−τ)ϕtarget(11)

where τ is the soft update parameter that controls the rate of updates. The updates occur every d=2 steps, which reduces the variance and prevents the problem of overestimation bias common in Q-learning algorithms. This update strategy ensures a smooth and stable learning process, promoting more reliable convergence of the actor and critic networks.

As summarized in Algorithm 1, with j and α are two points in the solution space representing TD3 training parameters, Lk is the number of transitions generated at iteration k, and CLevel is a pivotal factor to select the used control strategy.

3.5 Network Structures

The structure proposed for the critic neural network involves two paths. The action path, which consists of a single hidden layer with 128 neurons, is then combined with the state path that comprises three hidden layers with 256, 256, and 128 neurons, respectively. The state vector is represented with s1 {Orientation rates, Orientation errors, Altitude velocity, and Altitude error} or s2 {Linear velocities, Position errors, Yaw rate, and Yaw error}, depending on whether it’s for low or high control levels. Finally, an additional hidden layer with 128 neurons to generate the Q value, as shown in Fig. 5a.

Figure 5: The proposed networks, (a) critic network, (b) actor network

The actor network is structured with four feed-forward hidden layers, as depicted in Fig. 5b. All layers for both architectures use the Rectified Linear Unit as the activation function, except for the action output layer, which employs the Sigmoid activation function.

The proposed neural networks with the hyperparameters displayed in Table 3 brings the following enhancements:

•   By having a distinct action path and a more complex state path that later combine, the model can efficiently capture the nuances in both action and state spaces, leading to more accurate Q-value predictions. The action path is simpler, focusing on the action’s immediate impact, while the state path is more complex, enabling a deeper understanding of the environment’s dynamics.

•   The actor network’s deep hierarchical structure allows it to capture complex nonlinear relationships in the state-action space, leading to more precise control policies. The use of four hidden layers ensures that the network can model intricate dependencies between states and actions.

•   The proposed structure balances model complexity and computational efficiency, which is crucial for real-time implementation on hardware-constrained platforms like UAVs. The choice of layer sizes and activation functions was made to optimize learning without introducing unnecessary computational overhead.

3.6 Reward Function

The reward function formulation is a critical and distinctive aspect of reinforcement learning. It should be carefully crafted to offer clear and consistent feedback on the quality of the agent’s actions, ensuring that the optimal policy aligns with the desired behavior.

After testing various types of rewards, both continuous and discrete, we devised a mixed strategy that guides the quadrotor’s dynamics across various states. This strategy imposes penalties on unfavorable results while providing incentives for precise path-tracking behaviors, taking into account the tracking error and its derivative. The reward structure is illustrated in Fig. 6, where k serves as a positive weight, motivating the agent to minimize tracking errors in both following and performance stages defined by a limit distance to the target position.

ri=−k⋅sign(ei.ei˙)(12)

where i={x,y,z,φ,θ,ψ}, and sign(ei.ei˙) reflects the policy behaviour, whether the error is increasing or decreasing depending on whether the product of ei and ei˙ is positive (bad situation) or negative (good situation).

Figure 6: Reward function representation

The total reward for each control level is calculated as follows:

rLow−Level=rφ+rθ+rψ+rz(13)

rPosition−Control=rx+ry+rz+rψ(14)

4  Results and Discussion

We will use MATLAB/SIMULINK to demonstrate and discuss the results of the proposed framework, as well as the performance of its best-trained agents in tasks such as hovering from randomly initialized configurations and following predefined paths. Additionally, in this section, we will evaluate the control strategy by comparing it to SMC and Backstepping controllers in various path-following scenarios. Then, the application and testing of a trained SA-TD3 agent on altitude control for a Parrot Mambo mini drone will be carried out to validate the adaptability and potential real-world applicability of the proposed RL approach.

4.1 Low-Level Control System

Starting with the low-level RL controller shown in Fig. 1a, the desired state is specified using the Euler angles φRef,θRef,ψRef and the altitude ZRef. An agent, trained using the algorithm detailed in Section 3, ensures that the quadrotor follows the high-level controller’s orientation and altitude commands by generating precise control inputs U1,U2,U3 and U4.

Fig. 7 illustrates the significant training sessions recorded from fifty iterations of the proposed SA-TD3 approach, along with the best-trained agent’s performance in stabilizing from random initialization and attitude following tasks. These outcomes are interpreted as follows:

•   Indeed, numerous runs in the initial iterations bear a resemblance to the first one, where the set of training parameters demonstrated subpar performance. This is a plausible outcome considering the significance of these parameters for the learning algorithm, and the use of random values often leads to unsatisfactory results.

•   By the 10th iteration, the parameters generated by the SA displayed a slow training behavior, requiring more than 3900 episodes to start learning the environment’s dynamics and ending up with high reward variance in a local minimum.

•   At the 25th iteration, even theses parameter values were suitable and led to a successful training, they did not perform well in terms of balance between exploitation and exploration, stability and learning speed. After the 4500th episode, the algorithm shifted towards exploring new actions, leading to divergence and a loss of stability.

•   The final iteration yielded the best results, achieving the highest rewards and successfully balanced speed with stability within the training algorithm.

Figure 7: (a) Most significant SA-TD3 low-level training sessions, (b) best agent on attitude stabilization task from 20 random configurations, (c) best agent on attitude tracking task

These results effectively illustrates the progressive optimization of the TD3 algorithm’s performance through the SA process. As the SA iteratively refines the hyperparameters, there is a noticeable improvement in the rewards achieved by the agent, which underscores the algorithm’s enhanced learning efficiency. Moreover, the later iterations, especially the 45th, demonstrate not only higher rewards but also increased stability, as indicated by the reduced variability in performance. This consistent upward trend in both reward magnitude and reliability highlights the success of the SA-TD3 approach in developing a robust and efficient low-level control strategy for the quadrotor UAV.

4.2 Position Control System

As displayed in Fig. 1b, an RL agent was trained to address the underactuation issue in a quadrotor control system. In this setup, no inner and outer loops are provided to separate the position control from the orientation control levels. Instead, the agent directly maps control commands from the observation state space to ensure both stabilization and path following of a predefined trajectory. The most significant training sessions recorded at this control level, along with the performance of its best agent, are presented in Fig. 8.

Figure 8: (a) Most significant SA-TD3 low-level training sessions, (b) best agent on position stabilization task from 20 random configurations, (c) best agent on position tracking task

For this level of control, SA-TD3 consistently yielded similar overall results, as the impact of these parameters on the training process is likely to be similar across a majority of environments and tasks. The sets of parameters generated by SA exhibited multiple learning features, as outlined below:

•   In the initial iterations (1st and 5th), where SA explored the random solution space of training parameters neighborhood randomly, the training algorithm struggled to converge and learn the environment dynamics.

•   By the 20th iteration, SA had identified suitable parameter values, albeit slightly later, resulting in a stable and coherent training process.

•   At the 40th iteration, the TD3 agent achieved a high level of reward by the 4500th episode. However, this set of parameters led to an overall unstable and variant training session.

•   The last 5 iterations performed the best, showcasing stability, speed, and reaching the highest rewards. The 50th iteration is depicted in Fig. 8a.

The results of the SA-TD3 approach for both the position stabilization and position tracking tasks demonstrate its effectiveness and robustness in controlling quadrotor UAVs under different conditions. In the position stabilization task (see Fig. 8b), the agent successfully stabilized the quadrotor across all axes from 20 random initial configurations. The trajectories converge smoothly to the reference values within approximately 3 s, indicating rapid stabilization with minimal overshoot and efficient handling of diverse initial states. For the position tracking task (see Fig. 8c), the agent was tested on following dynamic trajectories. The actual positions (X,Y and Z) closely follow the reference paths over a 20 s duration, demonstrating precise tracking capabilities. The SA-TD3 approach shows strong adaptability and performance, achieving both stable hovering and accurate path tracking, thereby confirming its suitability for high-precision quadrotor control tasks in dynamic environments.

In order to evaluate the efficiency of the SA-TD3 best trained agents, we conduct a comparison with the Backstepping and the SMC using the Integral Square Error (ISE) metric for three paths: ellipsoid, square and circular reference trajectories, as illustrated in Fig. 9 and detailed in Table 4, where the lowest recorded metrics are highlighted in green.

Figure 9: (a) Position and orientation for the ellipsoid trajectory, (b) position and orientation tracking errors for the ellipsoid trajectory, (c) 3D ellipsoid trajectory, (d) position and orientation for the square trajectory, (e) position and orientation tracking errors for the square trajectory, (f) 3D square trajectory, (g) position and orientation for the circular trajectory, (h) position and orientation tracking errors for the circular trajectory, (i) 3D circular trajectory

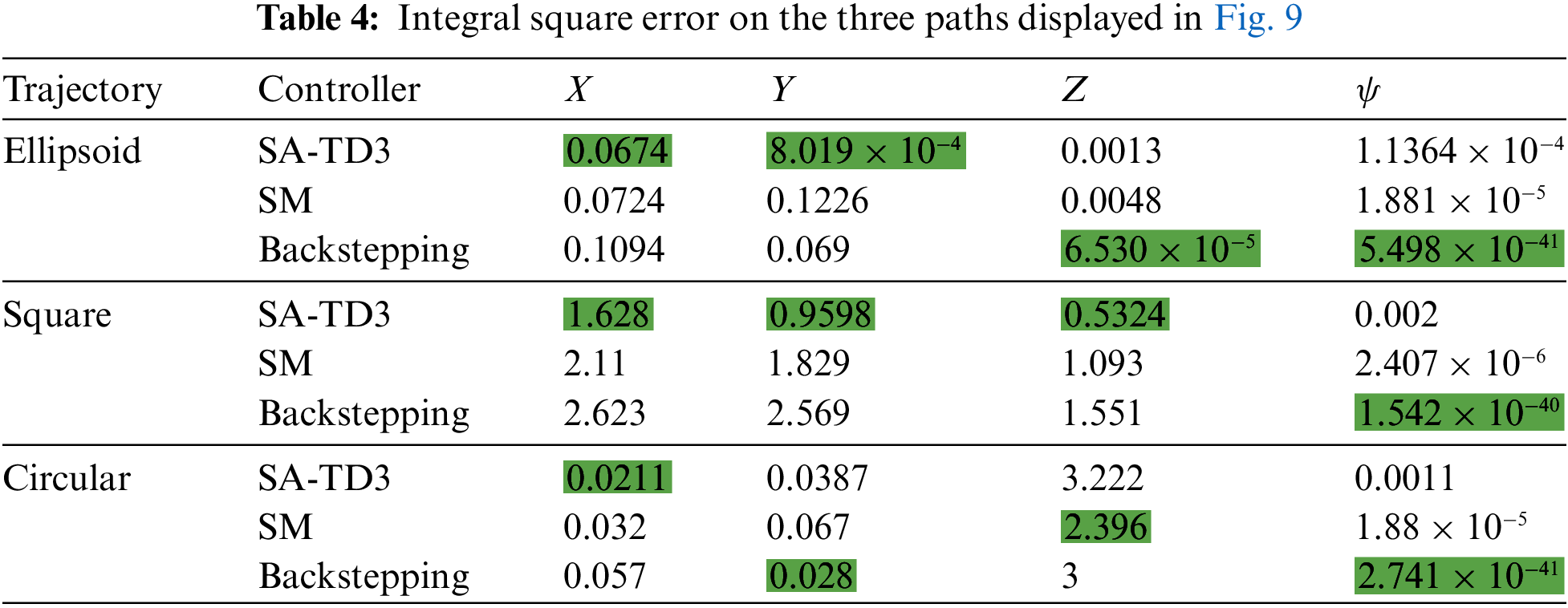
For the ellipsoid trajectory, the SA-TD3 controller exhibits the lowest ISE values for the X and Y-axes (0.0674, 8.019×10−4, respectively), indicating superior tracking accuracy compared to the SM and Backstepping controllers. While the Z-axis ISE for SA-TD3 is slightly higher (0.0013) than that of Backstepping (6.530×10−5), SA-TD3 still maintains an overall balanced performance with minimal error accumulation.

In the square trajectory, the SA-TD3 controller significantly outperforms both SM and Backstepping with lower ISE values in the X,Y, and Z-axes (1.628, 0.9598, and 0.5324, respectively), reflecting its capability to handle sharp directional changes with minimal error. In contrast, the SM and Backstepping controllers exhibit notably higher ISE values, indicating less effective control.

For the circular trajectory, the SA-TD3 controller achieves the lowest ISE value for the X-axis (0.0211), outperforming SM (0.032) and Backstepping (0.057), indicating more precise control. For the Y-axis, the Backstepping controller has the best performance with the lowest ISE (0.028), followed by SA-TD3 (0.0387) and then SM (0.067). Regarding the Z-axis, the SM controller exhibits the best performance (2.396), followed by Backstepping (3), while the SA-TD3 controller shows higher error accumulation (3.222).

Notably, the same control parameters were used for the SM and Backstepping controllers in all trajectories. Further tuning could potentially improve their performance. In contrast, the SA-TD3 agent exhibited a high level of adaptability in position tracking. Minor adjustments to the reward function could further enhance its orientation (ψ) tracking.

The optimal TD3 hyperparameters (Minibatch size, Discount factor, Noise variance, Variance Decay Rate) that were fine-tuned using the SA algorithm for both the low-level and position control systems are indicated in green within Table 5, alongside the other training parameters used in this study.

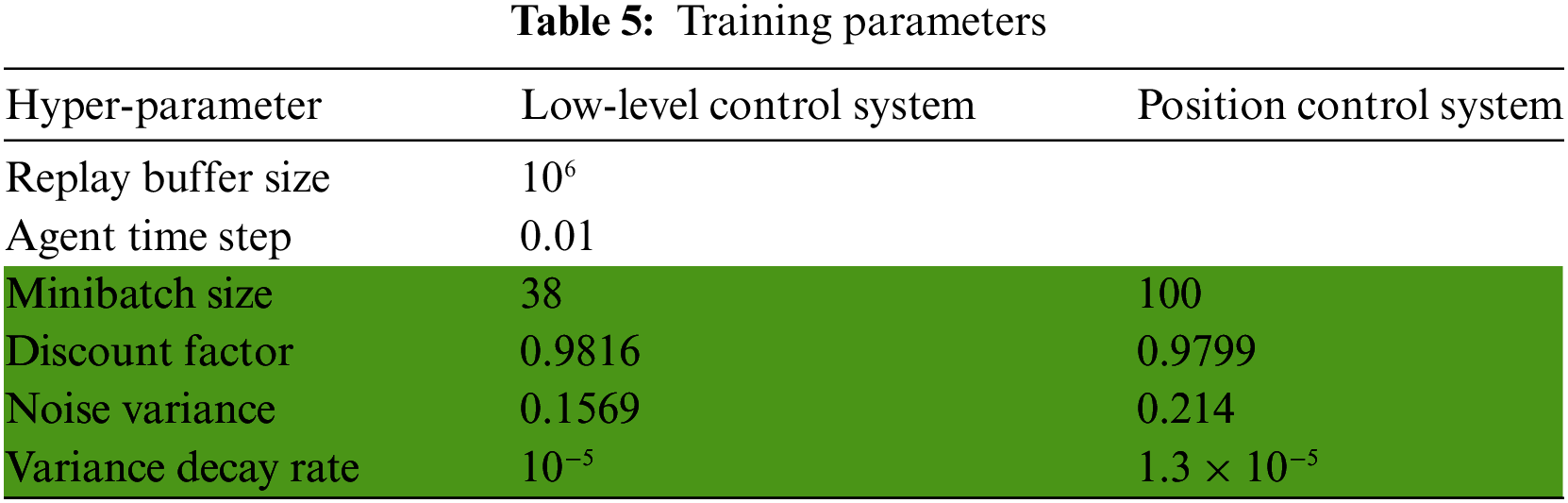
As is the case with most optimization techniques, sensitivity to initial parameter choices remains challenging. To address this issue, in this work, the hyperparameter solution space has been deliberately restricted to reduce the overall calculation time, emphasizing efficiency in the optimization process. Based on a combination of a literature review of recent studies and practices in reinforcement learning, highlighted in Section 2, particularly those involving DDPG, TD3, and similar algorithms, along with prior knowledge in quadrotor control systems, the restricted solution space for the TD3 training parameters are presented in Table 6.

4.3 Real-Time Implementation

This section provides the experimental findings aimed to substantiate the efficiency of the revealed RL approach for tracking both the position and orientation of quadrotors. The chosen setup is the Mambo mini-drone from Parrot’s low-cost quadrotors, this UAV is supplied with a gyroscope, an accelerometer, an ultrasonic sensor and pressure sensors for both altitude and attitude measurements. Furthermore, high-resolution vertical camera capturing images at a rate of 60 frames per second, along with an IMU are equipped in this quadrotor.

The RL agent was trained with the SA-TD3 approach in the Matlab/Simulink environment, then converted into C code, uploaded, and assessed on the Mambo through low energy 4.0 Bluetooth device (see Fig. 10).

Figure 10: The deployment framework

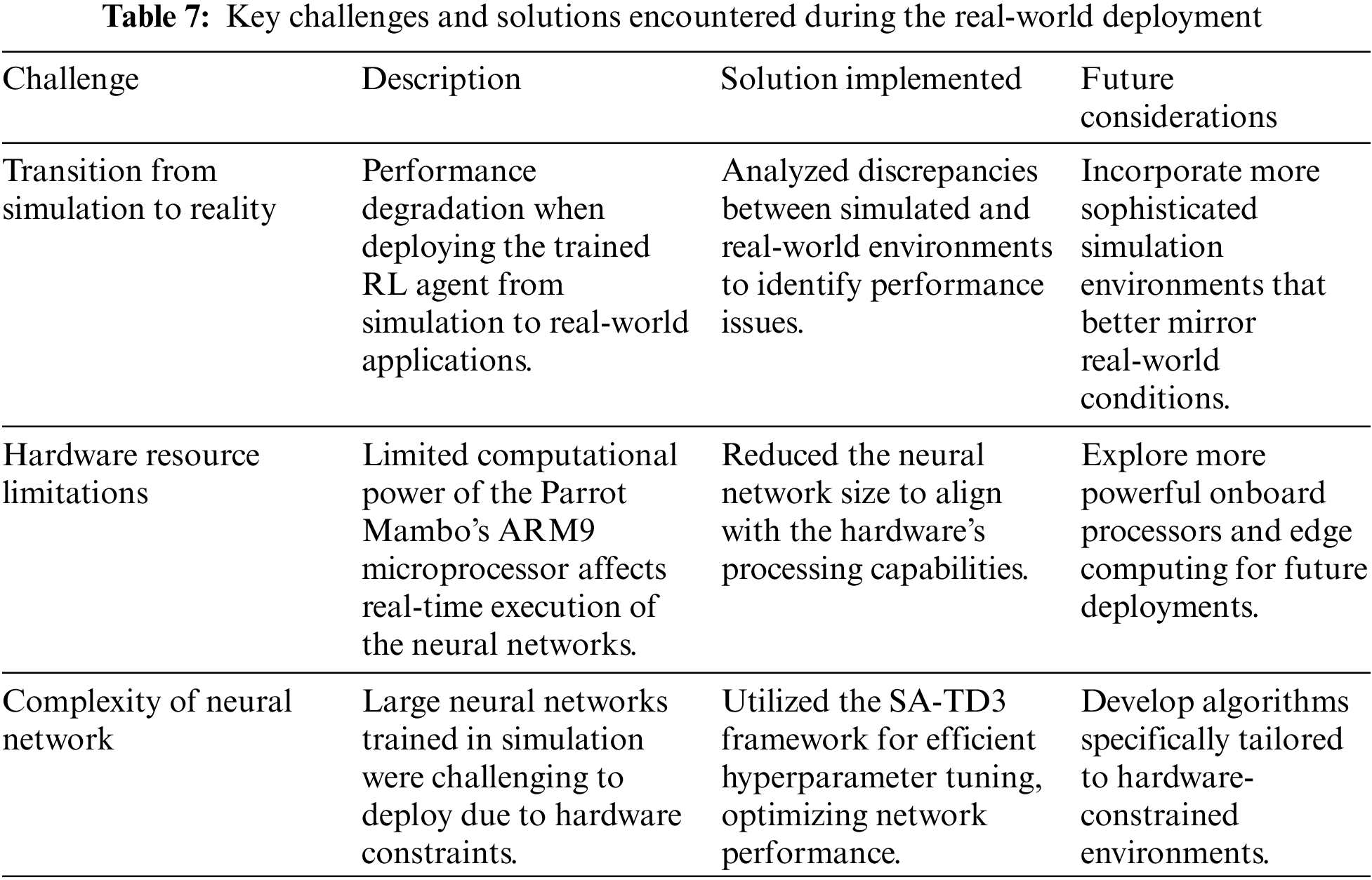
Transitioning from a simulated environment to real-world applications in the field of autonomous quadrotor control presents multiple obstacles. While training RL agents in simulations provides a safe and controlled environment, applying the acquired policies to actual quadrotors can be quite complicated. When deployed in a real-world setting, even well-trained agents can exhibit surprising behaviors, as minor disparities between the simulation and reality can have significant effects. These challenges became evident when we attempted to deploy the trained agent to control the Parrot Mambo mini-drone, which had demonstrated remarkable results during validation in simulation environment.

The issues encountered during the deployment of the trained agent prompted a thorough investigation into the main factors contributing to the performance degradation. One plausible explanation that emerged was the size of the trained neural network employed. In simulated environments, where computational resources are typically abundant, training and validating large neural networks is feasible. Yet, real-world applications posed challenges due to the finite computing power of the quadrotor’s onboard hardware, particularly the ARM9 microprocessor. Despite being compact and energy-efficient, it struggled to efficiently execute the intricate computations required by the neural network, resulting in unexpected performance issues during flight operations. To address this hardware limitation, efforts were made to reduce the neural network size. However, achieving stable attitude and position control with smaller neural networks remained challenging due to the nonlinear, unstable, and coupled dynamics of quadrotor systems. The SA-TD3 framework was particularly beneficial in this context, as the SA component allowed for more efficient tuning of the RL agent’s hyperparameters, optimizing the agent’s performance despite the reduced computational resources.

The video clips of all experiments conducted in this study can be found at https://drive.google.com/file/d/1yc3TABiUxhs80G3DgiliXGGaDxZD7eBb/view?usp=sharing (accessed on 13 November 2024).

To validate these assumptions, we conducted an empirical test aimed at reducing the computational load on processor. We decided to streamline the actor neural network, focusing on training an agent solely for the altitude control of the quadrotor while retaining PID controllers for the X and Y position and attitude control. The neural network used in this scenario, underwent significant simplification, featuring only two hidden layers, each comprised of five neurons, while still effectively managing the quadrotor’s altitude control.

These experiments were based on two scenarios. The first illustration, as depicted in Fig. 11, throughout a series of tests, the agent exhibited remarkable responsiveness in tracking various altitude references. Whether tasked with ascending to specific heights or gracefully descending, the agent consistently showcased its ability to maintain an accurate altitude profile.

Figure 11: Altitude tracking

The second test (see Fig. 12), illustrates the agent’s competence in preserving the altitude of the Parrot Mambo mini-drone while adhering to a predefined trajectory. This experiment, which mimics real-world scenarios where quadrotors are tasked with navigating specific paths, highlights the agent’s adeptness in seamlessly blending altitude control with trajectory tracking. The agent’s ability to uphold a consistent altitude throughout intricate maneuvers signifies its potential to excel in demanding applications such as surveillance of uneven terrains, inspection of infrastructure, and precise cargo delivery.

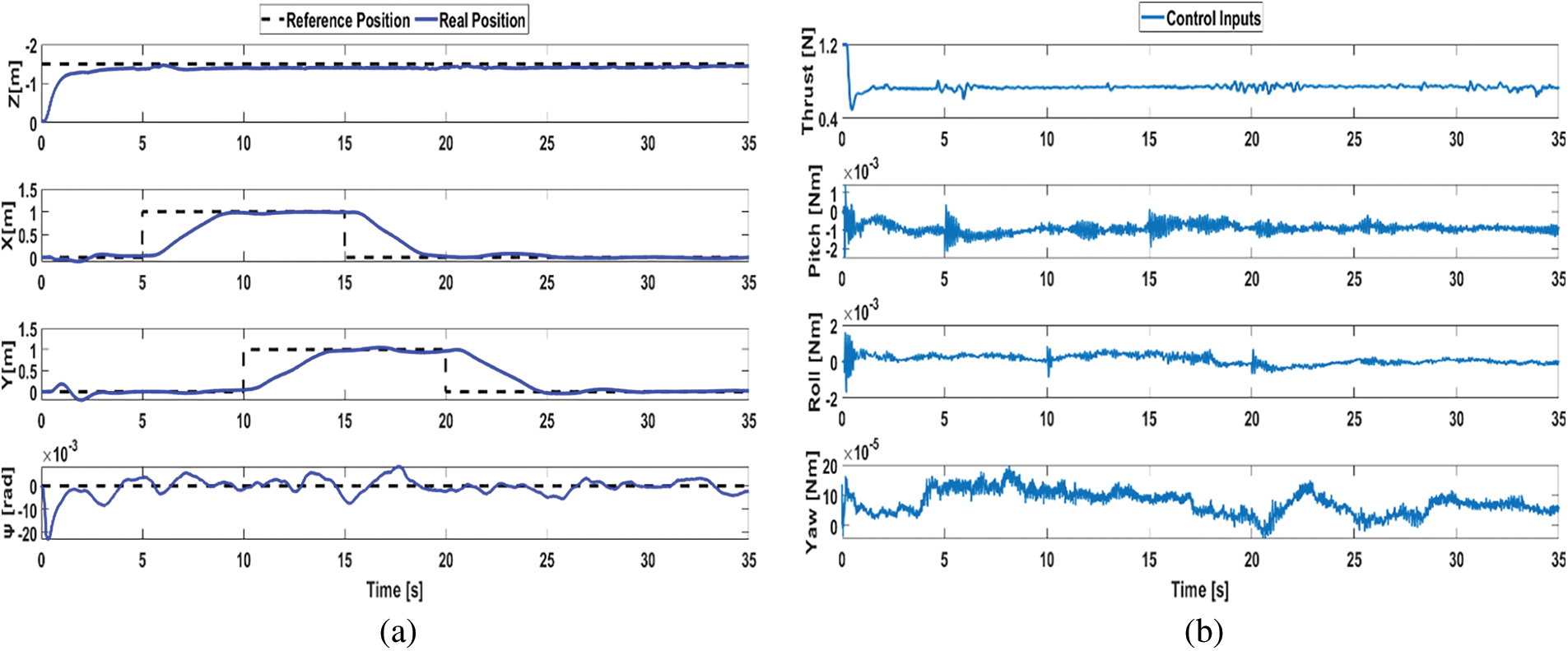
Figure 12: (a) Real trajectory tracking, (b) the experimental control inputs

Despite the inherent challenges (summarized in Table 7) posed by the Parrot Mambo mini-drone’s lower cost and less precise sensors, which can significantly affect the controller performance, the trained agent exhibited a very acceptable level of robustness and accuracy in altitude maintaining and tracking scenarios, further highlighting the potential of this approach in overcoming real-world intricacies.

5  Conclusion

This study presented an autonomous quadrotor control approach leveraging a Deep Reinforcement Learning framework enhanced by a Simulated Annealing-Twin Delayed Deep Deterministic Policy Gradient algorithm for efficient hyperparameter tuning. The custom-designed reward function and the proposed SA-TD3 framework demonstrated superior performance in attitude and position control compared to traditional non-linear controllers such as Backstepping and SMC. Empirical validation using real-time implementations on a low-cost Parrot Mambo mini-drone showcased the method’s precision and adaptability, even within resource-constrained environments.

Despite the promising results, the approach faces challenges related to computational intensity and time consumption, particularly in complex tasks with high-dimensional state and action spaces. The hyperparameter optimization process also contributes to the computational demands. Addressing these issues may benefit from incorporating parallel and distributed computing techniques, careful selection of SA temperature parameters, and tailored initial state space constraints specific to the application domain.

In future work, we aim to delve into the domain of high-end, sophisticated quadrotors to investigate potential strategies using advanced onboard processors, edge computing, and optimized algorithmic implementations. This broadened perspective will enable us to explore diverse scenarios and tasks comprehensively. Furthermore, we intend to undertake a comparative examination encompassing a wider array of data-driven methodologies, including alternative RL algorithms, neural network-based control strategies, and data-enabled MPC, in conjunction with the approach presented in this study.

Acknowledgement: The authors would like to acknowledge the Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia. The authors also would like to acknowledge ESTACA’Lab, S2ET, Laval, France.

Funding Statement: This work is supported by Princess Nourah Bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R135), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.

Author Contributions: Conceptualization, Taha Yacine Trad and Kheireddine Choutri; data curation, Kheireddine Choutri and Taha Yacine Trad; methodology, Kheireddine Choutri; software, Taha Yacine Trad; supervision, Mohand Lagha, Raouf Fareh and Souham Meshoul; validation, Fouad Khenfri, Kheireddine Choutri, Mohand Lagha, Hadil Shaiba and Souham Meshoul; writing—original draft, Taha Yacine Trad and Kheireddine Choutri; writing—review and editing, Fouad Khenfri, Souham Meshoul, Raouf Fareh, Hadil Shaiba and Mohand Lagha. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. K. Choutri, M. Lagha, S. Meshoul, M. Batouche, Y. Kacel and N. Mebarkia, “A multi-lingual speech recognition-based framework to human-drone interaction,” Electronics, vol. 11, no. 12, 2022, Art. no. 1829. doi: 10.3390/electronics11121829. [Google Scholar] [CrossRef]

2. P. S. Gohari, H. Mohammadi, and S. Taghvaei, “Using chaotic maps for 3D boundary surveillance by quadrotor robot,” Appl. Soft Comput., vol. 76, pp. 68–77, 2019. doi: 10.1016/j.asoc.2018.11.051. [Google Scholar] [CrossRef]

3. E. Kuantama, R. Tarca, S. Dzitac, I. Dzitac, T. Vesselenyi and I. Tarca, “The design and experimental development of air scanning using a sniffer quadcopter,” Sensors, vol. 19, no. 18, 2019, Art. no. 3849. doi: 10.3390/s19183849. [Google Scholar] [PubMed] [CrossRef]

4. G. A. Cardona, J. Ramirez-Rugeles, E. Mojica-Nava, and J. M. Calderon, “Visual victim detection and quadrotor-swarm coordination control in search and rescue environment,” Int. J. Electr. Comput. Eng., vol. 11, no. 3, 2021, Art. no. 2079. doi: 10.11591/ijece.v11i3.pp2079-2089. [Google Scholar] [CrossRef]

5. R. Kapoor, A. Shukla, and V. Goyal, “Analysis of multiple antenna techniques for unmanned aerial vehicle (UAV) communication,” in IOT with Smart Systems, Springer, 2022, vol. 2, pp. 347–357. doi: 10.1007/978-981-16-3945-6. [Google Scholar] [CrossRef]

6. K. Choutri, M. Lagha, S. Meshoul, and S. Fadloun, “Path planning and formation control for UAV-enabled mobile edge computing network,” Sensors, vol. 22, no. 19, 2022, Art. no. 7243. doi: 10.3390/s22197243. [Google Scholar] [PubMed] [CrossRef]

7. Q. Hou and J. Dong, “Distributed dynamic event-triggered consensus control for multiagent systems with guaranteed l_2 performance and positive inter-event times,” IEEE Trans. Autom. Sci. Eng., vol. 21, no. 1, pp. 746–757, 2022. doi: 10.1109/TASE.2022.3231845. [Google Scholar] [CrossRef]

8. K. Choutri, M. Lagha, and L. Dala, “Distributed obstacles avoidance for UAVs formation using consensus-based switching topology,” Int. J. Comput. Digit. Syst., vol. 8, no. 2, pp. 167–178, 2019. doi: 10.12785/ijcds/080208. [Google Scholar] [CrossRef]

9. Q. Hou and J. Dong, “Cooperative fault-tolerant output regulation of linear heterogeneous multiagent systems via an adaptive dynamic event-triggered mechanism,” IEEE Trans. Cybern., vol. 53, no. 8, pp. 5299–5310, 2022. doi: 10.1109/TCYB.2022.3204119. [Google Scholar] [PubMed] [CrossRef]

10. S. Wang, A. Polyakov, and G. Zheng, “Quadrotor stabilization under time and space constraints using implicit PID controller,” J. Franklin Inst., vol. 359, no. 4, pp. 1505–1530, 2022. doi: 10.1016/j.jfranklin.2022.01.002. [Google Scholar] [CrossRef]

11. R. Thusoo, S. Jain, and S. Bangia, “Path planning of quadrotor using A* and LQR,” in Recent Developments in Electrical and Electronics Engineering, Springer, 2023, pp. 227–238. doi: 10.1007/978-981-19-7993-4_19. [Google Scholar] [CrossRef]

12. M. Okasha, J. Kralev, and M. Islam, “Design and experimental comparison of PID, LQR and MPC stabilizing controllers for parrot mambo mini-drone,” Aerospace, vol. 9, no. 6, 2022, Art. no. 298. doi: 10.3390/aerospace9060298. [Google Scholar] [CrossRef]

13. H. Ahn, M. Hu, Y. Chung, and K. You, “Sliding-mode control for flight stability of quadrotor drone using adaptive super-twisting reaching law,” Drones, vol. 7, no. 8, 2023, Art. no. 522. doi: 10.3390/drones7080522. [Google Scholar] [CrossRef]

14. A. -W. Saif, K. B. Gaufan, S. El-Ferik, and M. Al Dhaifallah, “Fractional order sliding mode control of quadrotor based on fractional order model,” IEEE Access, vol. 11, no. 5, pp. 79823–79837, 2023. doi: 10.1109/ACCESS.2023.3296644. [Google Scholar] [CrossRef]

15. A. A. Mian and W. Daobo, “Modeling and backstepping-based nonlinear control strategy for a 6 DOF quadrotor helicopter,” Chin. J. Aeronaut., vol. 21, no. 3, pp. 261–268, 2008. doi: 10.1016/S1000-9361(08)60034-5. [Google Scholar] [CrossRef]

16. J. Wang, K. A. Alattas, Y. Bouteraa, O. Mofid, and S. Mobayen, “Adaptive finite-time backstepping control tracker for quadrotor UAV with model uncertainty and external disturbance,” Aerosp. Sci. Technol., vol. 133, no. 15, 2023, Art. no. 108088. doi: 10.1016/j.ast.2022.108088. [Google Scholar] [CrossRef]

17. R. Pérez, G. Galvan, A. Vázquez, S. Melo, and D. Alabazares, “Attitude control of a quadcopter using adaptive control technique,” Adapt. Robust Control Syst., 2017. doi: 10.5772/intechopen.71382. [Google Scholar] [CrossRef]

18. M. B. Artuc and I. Bayezit, “Robust adaptive quadrotor position tracking control for uncertain and fault conditions,” Proc. Inst. Mech. Eng., Part G: J. Aerosp. Eng., vol. 237, no. 14, 2023, Art. no. 09544100231181869. doi: 10.1177/09544100231181869. [Google Scholar] [CrossRef]

19. A. Jafar, S. Fasih-UR-Rehman, S. Fazal-UR-Rehman, N. Ahmed, and M. U. Shehzad, “A robust h control for unmanned aerial vehicle against atmospheric turbulence,” in 2016 2nd Int. Conf. Robotics Artif. Intell. (ICRAI), IEEE, 2016, pp. 1–6. doi: 10.1109/ICRAI.2016.7791234. [Google Scholar] [CrossRef]

20. F. W. Alsaade, H. Jahanshahi, Q. Yao, M. S. Al-zahrani, and A. S. Alzahrani, “A new neural network-based optimal mixed H2/H∞ control for a modified unmanned aerial vehicle subject to control input constraints,” Adv. Space Res., vol. 71, no. 9, pp. 3631–3643, 2023. doi: 10.1016/j.asr.2022.02.012. [Google Scholar] [CrossRef]

21. M. Rinaldi, S. Primatesta, and G. Guglieri, “A comparative study for control of quadrotor UAVs,” Appl. Sci., vol. 13, no. 6, 2023, Art. no. 3464. doi: 10.3390/app13063464. [Google Scholar] [CrossRef]

22. S. A. Mokhtari, “Fopid control of quadrotor based on neural networks optimization and path planning through machine learning and PSO algorithm,” Int. J. Aeronaut. Space Sci., vol. 23, no. 3, pp. 567–582, 2022. doi: 10.1007/s42405-022-00461-8. [Google Scholar] [CrossRef]

23. S. Rauniyar, S. Bhalla, D. Choi, and D. Kim, “EKF-SLAM for quadcopter using differential flatness-based LQR control,” Electronics, vol. 12, no. 5, 2023, Art. no 1113. doi: 10.3390/electronics12051113. [Google Scholar] [CrossRef]

24. E. Elokda, J. Coulson, P. N. Beuchat, J. Lygeros, and F. Dörfler, “Data-enabled predictive control for quadcopters,” Int. J. Robust Nonlinear Control, vol. 31, no. 18, pp. 8916–8936, 2021. doi: 10.1002/rnc.5686. [Google Scholar] [PubMed] [CrossRef]

25. D. Yuan and Y. Wang, “Data driven model-free adaptive control method for quadrotor formation trajectory tracking based on rise and ismc algorithm,” Sensors, vol. 21, no. 4, 2021, Art. no. 1289. doi: 10.3390/s21041289. [Google Scholar] [PubMed] [CrossRef]

26. S. S. Narayanan, D. Tellez-Castro, S. Sutavani, and U. Vaidya, “SE(3) koopman-MPC: Data-driven learning and control of quadrotor uavs,” IFAC-PapersOnLine, vol. 56, no. 3, pp. 607–612, 2023. doi: 10.1016/j.ifacol.2023.12.091. [Google Scholar] [CrossRef]

27. S. R. B. dos Santos, S. N. Givigi, and C. L. N. Júnior, “An experimental validation of reinforcement learning applied to the position control of UAVs,” in 2012 IEEE Int. Conf. Syst., Man, Cybern. (SMC), IEEE, 2012, pp. 2796–2802. doi: 10.1109/ICSMC.2012.6378172. [Google Scholar] [CrossRef]

28. C. -H. Pi, W. -Y. Ye, and S. Cheng, “Robust quadrotor control through reinforcement learning with disturbance compensation,” Appl. Sci., vol. 11, no. 7, 2021, Art. no. 3257. doi: 10.3390/app11073257. [Google Scholar] [CrossRef]

29. B. Rubí, B. Morcego, and R. Pérez, “Deep reinforcement learning for quadrotor path following with adaptive velocity,” Auton. Robots, vol. 45, no. 1, pp. 119–134, 2021. doi: 10.1007/s10514-020-09951-8. [Google Scholar] [CrossRef]

30. Y. Wang, J. Sun, H. He, and C. Sun, “Deterministic policy gradient with integral compensator for robust quadrotor control,” IEEE Trans. Syst., Man, Cybern.: Syst., vol. 50, no. 10, pp. 3713–3725, 2019. doi: 10.1109/TSMC.2018.2884725. [Google Scholar] [CrossRef]

31. B. Rubí, B. Morcego, and R. Pérez, “Quadrotor path following and reactive obstacle avoidance with deep reinforcement learning,” J. Intell. & Robotic Syst., vol. 103, no. 4, pp. 1–17, 2021. doi: 10.1007/s10846-021-01491-2. [Google Scholar] [CrossRef]

32. V. Kashyap and R. Vepa, “Reinforcement learning based linear quadratic regulator for the control of a quadcopter,” in AIAA SCITECH 2023 Forum, 2023, Art. no. 0014. doi: 10.2514/6.2023-0014. [Google Scholar] [CrossRef]

33. R. Polvara et al., “Autonomous quadrotor landing using deep reinforcement learning,” 2017, arXiv:1709.03339. doi: 10.48550/arXiv.1709.03339. [Google Scholar] [CrossRef]

34. Y. Z. Jembre et al., “Evaluation of reinforcement and deep learning algorithms in controlling unmanned aerial vehicles,” Appl. Sci., vol. 11, no. 16, 2021, Art. no. 7240. doi: 10.3390/app11167240. [Google Scholar] [CrossRef]

35. C. -H. Pi, K. -C. Hu, S. Cheng, and I. -C. Wu, “Low-level autonomous control and tracking of quadrotor using reinforcement learning,” Control Eng. Pract., vol. 95, no. 4, 2020, Art. no. 104222. doi: 10.1016/j.conengprac.2019.104222. [Google Scholar] [CrossRef]

36. A. G. De Almeida, E. L. Colombini, and A. Da Silva Simões, “Controlling tiltrotors unmanned aerial vehicles (UAVs) with deep reinforcement learning,” in 2023 Latin American Robotics Symp. (LARS2023 Brazilian Symp. Robotics (SBR2023 Workshop Robotics Education (WRE), IEEE, 2023, pp. 107–112. doi: 10.1109/LARS/SBR/WRE59448.2023.10333034. [Google Scholar] [CrossRef]

37. J. Yoo, D. Jang, H. J. Kim, and K. H. Johansson, “Hybrid reinforcement learning control for a micro quadrotor flight,” IEEE Control Syst. Lett., vol. 5, no. 2, pp. 505–510, 2020. doi: 10.1109/LCSYS.2020.3001663. [Google Scholar] [CrossRef]

38. B. Jiang, B. Li, W. Zhou, L. -Y. Lo, C. -K. Chen and C. -Y. Wen, “Neural network based model predictive control for a quadrotor UAV,” Aerospace, vol. 9, no. 8, 2022, Art. no. 460. doi: 10.3390/aerospace9080460. [Google Scholar] [CrossRef]

39. N. O. Lambert, D. S. Drew, J. Yaconelli, S. Levine, R. Calandra and K. S. Pister, “Low-level control of a quadrotor with deep model-based reinforcement learning,” IEEE Robot. Autom. Lett., vol. 4, no. 4, pp. 4224–4230, 2019. doi: 10.1109/LRA.2019.2930489. [Google Scholar] [CrossRef]

40. H. Bou-Ammar, H. Voos, and W. Ertel, “Controller design for quadrotor UAVs using reinforcement learning,” in 2010 IEEE Int. Conf. Control Appl., IEEE, 2010, pp. 2130–2135. doi: 10.1109/CCA.2010.5611206. [Google Scholar] [CrossRef]

41. J. Hwangbo, I. Sa, R. Siegwart, and M. Hutter, “Control of a quadrotor with reinforcement learning,” IEEE Robot. Autom. Lett., vol. 2, no. 4, pp. 2096–2103, 2017. doi: 10.1109/LRA.2017.2720851. [Google Scholar] [CrossRef]

42. Z. Jiang and A. F. Lynch, “Quadrotor motion control using deep reinforcement learning,” J. Unmanned Veh. Syst., vol. 9, no. 4, pp. 234–251, 2021. doi: 10.1139/juvs-2021-0010. [Google Scholar] [CrossRef]

43. Y. Wang and D. Boyle, “Constrained reinforcement learning using distributional representation for trustworthy quadrotor UAV tracking control,” IEEE Trans. Autom. Sci. Eng., pp. 1–18, 2024. doi: 10.1109/TASE.2024.3432405. [Google Scholar] [CrossRef]

44. S. Jiang, Y. Ge, X. Yang, W. Yang, and H. Cui, “UAV control method combining reptile meta-reinforcement learning and generative adversarial imitation learning,” Future Internet, vol. 16, no. 105, 2024. doi: 10.3390/fi16030105. [Google Scholar] [CrossRef]

45. Y. Xia, X. Shao, Z. Mei, and W. Zhang, “Performance-designated reinforcement learning enclosing control for UAVs with collision-free capability,” IEEE Trans. Intell. Transp. Syst., vol. 25, no. 9, pp. 12644–12656, Sep. 2024. doi: 10.1109/TITS.2024.3384431. [Google Scholar] [CrossRef]

46. H. Ma et al., “Improved DRL-based energy-efficient UAV control for maximum lifecycle,” J. Franklin Inst., vol. 361, no. 6, 2024. doi: 10.1016/j.jfranklin.2024.106718. [Google Scholar] [CrossRef]

47. W. Fei, X. P. Zhu, Z. Zhou, and T. Yang, “Deep-reinforcement-learning-based UAV autonomous navigation and collision avoidance in unknown environments,” Chin. J. Aeronaut., vol. 37, no. 3, pp. 237–257, 2024. doi: 10.1016/j.cja.2023.09.033. [Google Scholar] [CrossRef]

48. D. Huang, Z. Zhang, X. Fang, M. He, H. Lai and B. Mi, “STIF: A spatial-temporal integrated framework for end-to-end micro-UAV trajectory tracking and prediction with 4-D MIMO radar,” IEEE Internet Things J., vol. 10, no. 21, pp. 18821–18836, Nov. 1, 2023. doi: 10.1109/JIOT.2023.3244655. [Google Scholar] [CrossRef]

49. A. Gülcü and Z. Kuş, “Multi-objective simulated annealing for hyperparameter optimization in convolutional neural networks,” PeerJ Comput. Sci., vol. 7, no. 3, 2021, Art. no. e338. doi: 10.7717/peerj-cs.338. [Google Scholar] [PubMed] [CrossRef]

50. W. -C. Yeh, Y. -P. Lin, Y. -C. Liang, C. -M. Lai, and C. -L. Huang, “Simplified swarm optimization for hyperparameters of convolutional neural networks,” Comput. & Ind. Eng., vol. 177, no. 6, 2023, Art. no. 109076. doi: 10.1016/j.cie.2023.109076. [Google Scholar] [CrossRef]

51. Z. Ma, S. Cui, and I. Joe, “An enhanced proximal policy optimization-based reinforcement learning method with random forest for hyperparameter optimization,” Appl. Sci., vol. 12, no. 14, 2022, Art. no. 7006. doi: 10.3390/app12147006. [Google Scholar] [CrossRef]

52. M. Kiran and M. Ozyildirim, “Hyperparameter tuning for deep reinforcement learning applications,” 2022, arXiv:2201.11182. [Google Scholar]

53. N. Pathik and P. Shukla, “Simulated annealing based algorithm for tuning LDA hyper parameters,” in Soft Computing: Theories and Applications. Springer, 2020, pp. 515–521. doi: 10.1007/978-981-15-4032-5_47. [Google Scholar] [CrossRef]

54. Y. Zhang et al., “Reinforcement learning based relay selection for underwater acoustic cooperative networks,” Remote Sens., vol. 14, no. 6, 2022, Art. no. 1417. doi: 10.3390/rs14061417. [Google Scholar] [CrossRef]

55. R. Benotsmane and J. Vásárhelyi, “Towards optimization of energy consumption of tello quad-rotor with MPC model implementation,” Energies, vol. 15, no. 23, 2022, Art. no. 9207. doi: 10.3390/en15239207. [Google Scholar] [CrossRef]

56. T. P. Lillicrap et al., “Continuous control with deep reinforcement learning,” 2015, arXiv:1509.02971. [Google Scholar]

57. S. Fujimoto, H. Hoof, and D. Meger, “Addressing function approximation error in actor-critic methods,” in Int. Conf. Mach. Learn., PMLR, 2018, pp. 1587–1596. [Google Scholar]

58. D. Delahaye, S. Chaimatanan, and M. Mongeau, “Simulated annealing: From basics to applications,” in Handbook of Metaheuristics. Springer, 2019, pp. 1–35. doi: 10.1007/978-3-319-91086-4_1. [Google Scholar] [CrossRef]