An Improved LZO Compression Algorithm for FPGA Configuration Bitstream Files

1  Introduction

SRAM-based FPGA (Static Random-Access Memory-based Field-Programmable Gate Array) is a field-programmable gate array that uses SRAM cells to store its configuration data. SRAM-based FPGAs allow users to change the interconnections and behaviour of their internal logic circuits by loading different bitstream files to implement different hardware functions. With the advantages of rich logic resources, fast computing speed and strong parallel processing capability, SRAM-based FPGAs are widely used in significant fields such as communications, consumer electronics, automotive electronics, industrial control, military and aerospace applications, especially in application areas that require rapid development and flexible adaptation to different functions. With the emergence of commercial space industry, SRAM-based FPGAs can meet the requirements of high performance, low cost and many other requirements, and have been widely applied aerospace products.

In order to cope with the demand for a significant increase in the storage capacity of bitstream files in aerospace electronic systems, bitstream file compression technology has received widespread attention. Fig. 1 shows the architecture of space electronic equipment applying bitstream file compression technology, consisting of an SRAM-based FPGA, a scrubbing engine, and non-volatile memory. The original files can be compressed on the ground during the product development phase and then stored in the non-volatile memory of the avionics equipment. When it is necessary to configure or scrub the FPGA, the controller can first decompress the bitstream file and then write the decompressed bitstream file into the FPGA’s configuration memory with a specific format. Bitstream file compression not only significantly reduces the storage resource requirements but also decreases the upload time from the ground to the satellite. This is particularly beneficial for the Low Earth Orbit (LEO) Internet constellation systems, as it can greatly enhance the upgrade efficiency of the constellation software. At the same time, considering that the bitstream file storage of the FPGA in the spaceborne electronic system needs the master and backup to realize the on-orbit scrubbing and configuring, the storage pressure is further increased.

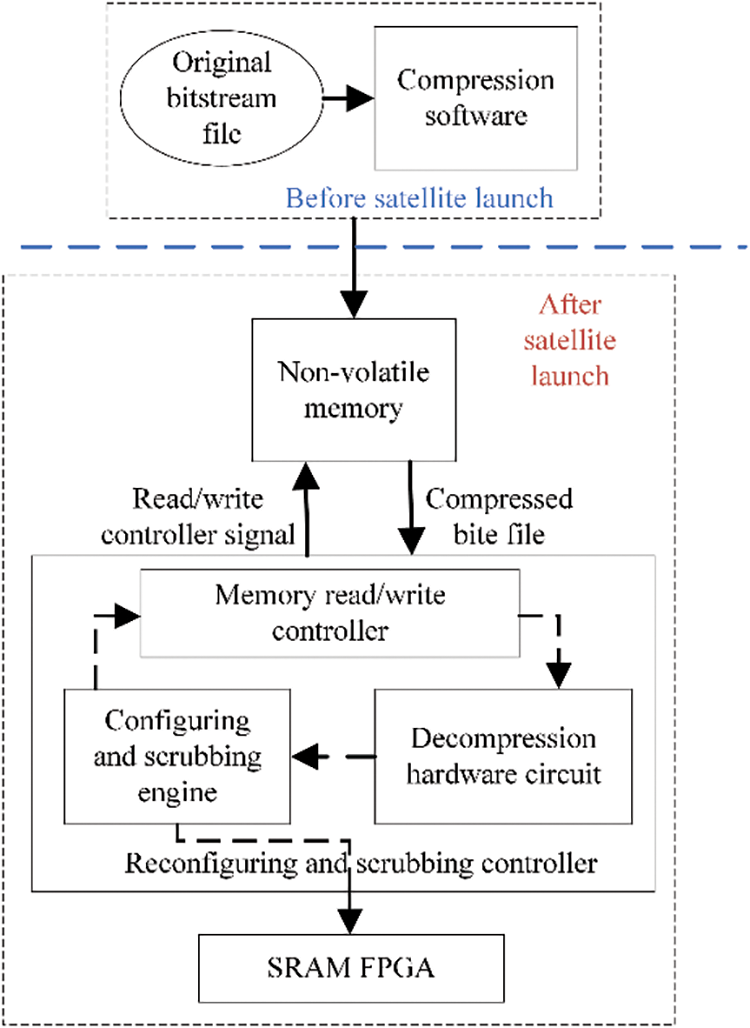
Figure 1: Schematic diagram of aerospace electronic system application for bitstream file compression

In order to cope with the demand for a significant increase in the storage capacity of bitstream files in aerospace electronic systems, bitstream file compression technology has received widespread attention. Fig. 1 shows the architecture of space electronic equipment applying bitstream file compression technology, consisting of an SRAM-based FPGA, a scrubbing engine, and non-volatile memory. The original files can be compressed on the ground during the product development phase and then stored in the non-volatile memory of the avionics equipment. When the FPGA is configured or scrubbed, the configuring and scrubbing controller first decompresses the bitstream file and then writes the decompressed bitstream file in a specific format to the FPGA’s configuration memory. Bitstream file compression not only significantly reduces the storage resource requirements but also decreases the upload time from the ground to the satellite. This is particularly beneficial for the Low Earth Orbit (LEO) Internet constellation systems, as it can greatly enhance the upgrade efficiency of the constellation software.

Commercial compression software can be used for bitstream file compression, but it is not suitable for on-orbit applications. For example, FPGA device manufacturers can use the LZ77 algorithm for bitstream file compression, but the compressed bitstream files do not support the implementation of configuration memory (CM) scrubbing policies [1,2], which affects the on-orbit reliability of the device. The main purpose of currently available bitstream file compression algorithms is to improve the Compression Ratio (CR). There are two approaches to achieve this: one is to improve existing compression algorithms, and the other is to use multiple compression algorithms in combination. Nevertheless, both suffer from the problem of overly complex decompression, which is not suitable for resource-constrained aerospace electronic devices.

Considering the requirements of the master and backup storage of FPGA bitstream files in spaceborne electronic systems, the compression ratio of bitstream files must be controlled within 50%, the ability of fast compression and decompression is required, and the hardware cost of the decompression circuit must be minimized. This paper focuses mainly on low resource consumption and high decompression speed, and conducts a comparative study of various compression algorithms. Based on the inherent characteristics of bitstream file data formats, this paper proposes an improved Lempel Ziv Oberhumer (LZO) compression and decompression algorithm, effectively simplifying the compression format. Corresponding hardware implementation circuits have also been designed.

The remainder of this paper is structured as follows. Section 2 introduces related works. Section 3 describes the data format characteristics of bitstream files, proposes the refined compression and decompression algorithms. Section 4 presents the results of experimental validation, designs a decompression hardware circuit with low resource expenditure. The concluding section synthesizes the findings of this paper.

2  Related Work

Because errors in bitstream files can result in functional anomalies and potentially severe device damage, the use of lossless compression algorithms is imperative [3,4]. When compressing bitstream files in aerospace electronic systems, it is necessary to meet the requirements of easy hardware implementation, low resource overhead, and fast decompression speed. General lossless compression algorithms employ specific encoding techniques, such as the Run-Length Encoding (RLE), Huffman coding and Dictionary-based Code Compression (DCC). In [5], Huffman encoding and DCC algorithms were proposed, but the focus was on the Virtex series. One of the typical algorithms in DCC is the LZ algorithm, which includes LZ77 and LZ78. To further improve compression ratios and efficiency, the LZO, LZSS, and LZW algorithms have been proposed [6–10]. Reference [11] enhanced the traditional LZW algorithm for bitstream file compression among others. The novel architecture, as proposed in [12], utilizes an LZSS compression engine for bitstream file compression. Some studies have shown that combining multiple compression algorithms can improve CR. Reference [13] combined RLE and Golomb to design RG-1 and RG-2 coding to improve CR, but did not introduce the corresponding decompression methods and did not analyze the hardware implementation cost of decompression. Based on DCC, the authors proposed the separate split LUT algorithm and the separate split LUT+BIT masking algorithm, which take the LUT size and the number of lines in the LUT as inputs to segment the bitstream file [14]. The CR was improved by 23% in [15] through the adoption of multiple bitstream compression algorithms. Reference [16] suggested the integration of the LZ77 algorithm with Golomb coding for FPGA bitstream compression. Some studies have found that segmented bitstream files can be fine-grained compressed. In [17], a lossless compression technique for FPGA cloud-based bitstream configuration files is presented. The technology divides the file into three parts. Based on this, it uses neural networks to select the most appropriate compression algorithm for each segment based on the characteristics of that segment.

Previous research mainly focused on reducing the CR to reduce the compressed file size and improve the compression speed. However, due to the limited hardware resources and high reliability requirements of aerospace electronic systems, it is necessary to investigate a compression algorithm that is easy to implement in hardware and has the characteristics of low cost and fast decompression. In [18], it is proposed that a low resource overhead compression and decompression circuit based on ANS (Asymmetric Numeral Systems) lossless compression algorithm. Although the hardware circuit overhead is significantly reduced, the compression ratio is greater than 50%.

LZO uses two rounds of hash computation to identify suboptimal matches, replacing the traditional exhaustive search for the best match. This method can effectively reduce compression time without significantly affecting the Compression Ratio (CR). LZO is one of the fastest compression algorithms in the LZ series, with a compression speed approximately 39 times that of LZSS and 26 times that of LZW. However, the trade-off for achieving this speed compared to LZSS and LZW is a reduction in Compression Ratio (CR) by about 10%.

The CR of LZO is closely tied to the data structure of the files being compressed. The LZO algorithm matches previously compressed data with the current data being compressed to find duplicate patterns or data sequences. When the LZO algorithm finds a match, it records the matching length and the number of bytes backtracked from the current position, which is called the offset. LZO needs to transmit the matching length and the offset as the compressed file. The closer the characters that are repeated in the original file, the smaller the offset; the longer the repeated string, the larger the matching length. A small offset and a large matching length are favorable for the CR of LZO. The abundance of FPGA resources often results in bitstream files with numerous ‘0’ characters, favoring LZO’s CR. Our findings indicate that, in the context of bitstream file compression, the LZO’s CR has increased by approximately 5% compared to LZW, which is an acceptable margin in practical applications.

Regarding the hardware cost associated with decompression circuits, LZ77 series algorithms can utilize text as a dictionary and employ a fixed-size sliding window for compression, without the need for the original dictionary during decompression. Therefore, the decompression circuit is more straightforward to implement compared to those of LZ78 and LZW. Within the LZ77 series, LZO eschews the exhaustive string matching search, simplifying the logic of the decompression circuit and enhancing decompression speed in comparison to LZSS.

Fig. 2 depicts the compression and decompression process of the LZO algorithm. The algorithm operates on a byte-level basis for both its input and output. It employs a hash function constructed using bit-wise exclusive OR (XOR) and shift operations on four-byte sequences. This mechanism is designed to facilitate rapid data retrieval within the dictionary, ensuring efficient compression. Let’s consider a hypothetical input of four bytes, denoted as ABCD. The corresponding hash operation, as shown in Eq. (1), is used to generate hash values that can be quickly looked up in a hash table. This can help determine potential matches for compression.

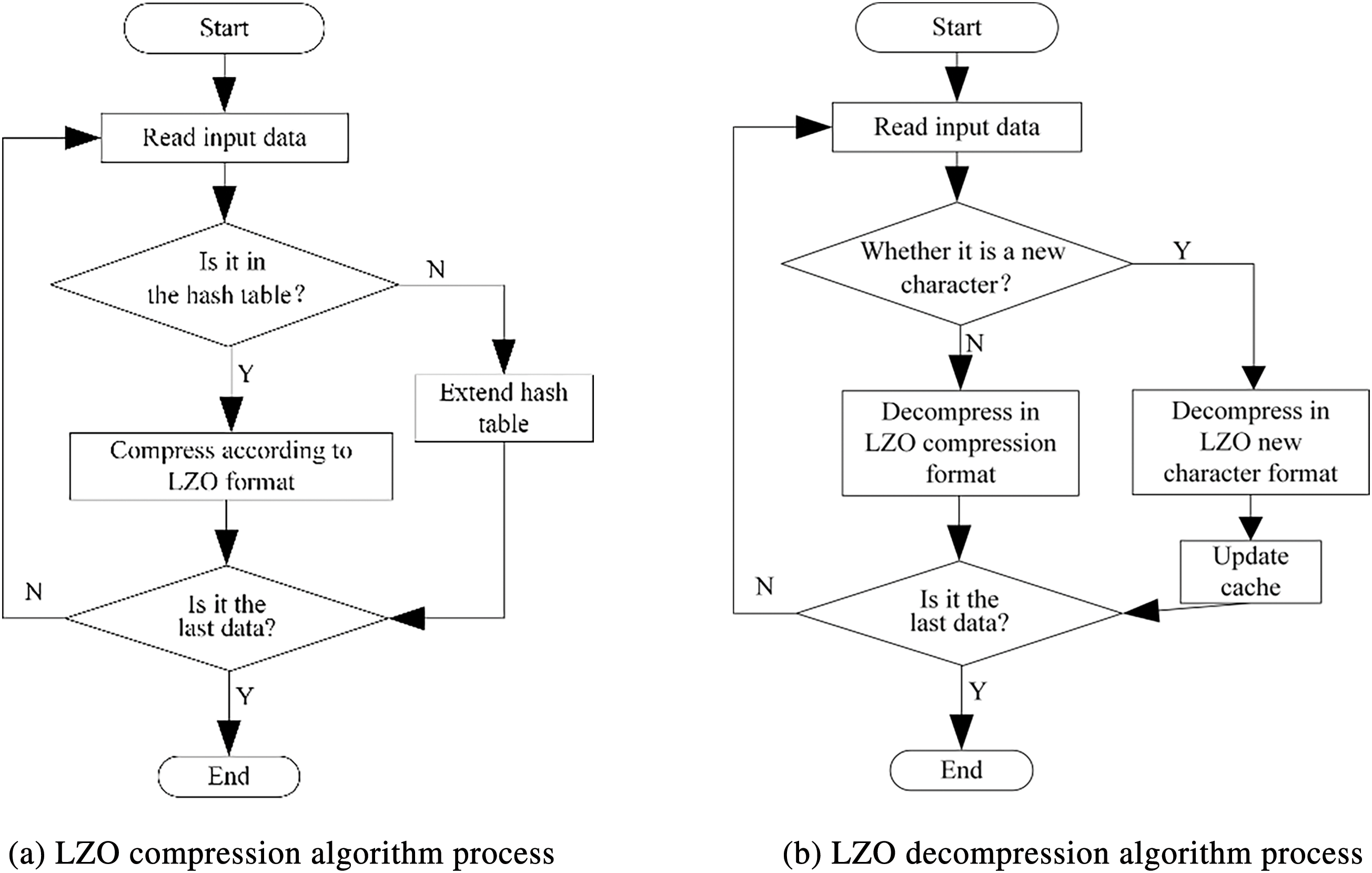
Figure 2: Compression and decompression process of LZO algorithm

H=(0x21∗(((((D<<6∧C)<<5)∧B<<5)∧A))>>5)&0x3FFF (1)

The specific compression implementation steps of LZO are shown in Table 1, with an example of encoding the string “AAABAAABAAABADAAAB”.

The specific decompression implementation steps of LZO are shown in Table 2, with an expamle of decoding the string “(05)hAAABAAB (6E)h(00)hAD (74)h(00)h”.

When employing the LZO algorithm for compressing FPGA bitstream files in aerospace electronic equipment, two primary challenges arise. The first one is hardware and timing overhead needs optimization. Based on the differences in offset and match length, the LZO algorithm’s compression format can be divided into five types, supporting a maximum offset of 48 kB. This requires that the decompression circuit should contain a minimum 48 kB data cache and a logic circuit capable of parsing various compression formats. The second point is the reduction of the impact of simplified compression formats on CR. By leveraging the intrinsic features of FPGA bitstream files to refine the LZO algorithm, a more bitstream-tailored compression format can be engineered to ameliorate the aforementioned issue.

In light of these challenges, the key of this research is based on the LZO algorithm to investigate the format of bitstream files, statistically analyze the distribution characteristics of offset and matching length of bitstream files, design a simplified compression format, propose low-cost compression and decompression algorithms suitable for aerospace electronics to improve compression speed and reduces hardware complexity without affecting CR.

3  Algorithm Design

3.1 Algorithm of Bitstream File Format

SRAM-based FPGA can be considered as a two-layer architecture, consisting of CM and user-programmable logic. The user-programmable logic includes Configuration Logic Blocks (CLB), IO Blocks (IOB), Block Memories (BRAM), Digital Clock Management modules (DCM), DSP48s, and other resources (such as processor cores, PCIe, high-speed interfaces, etc.). The CLB is interconnected by General Routing Matrices (GRM), which is an array of routing switches located at the intersection of horizontal and vertical routing channels [19]. One CLB is equivalent to two slices.

CM determines the specific functions and connection relationships of the user-programmable logic. By loading the configuration bitstream file, the device can be programmed to perform specific user-defined functions. The configuration bitstream file is a binary file that describes the usage and interconnection relationships of FPGA resources. The FPGA bitstream file can be divided into three parts: header file, configuration data, and end part. The header file mainly contains information such as project name, device model, and generation date. The configuration data consists of a large number of configuration frames, each of which contains a fixed number of configuration bits. Each configurable resource in the FPGA is defined by one or more configuration bits [20]. The end section contains load control words, several empty operators and some control command words. FPGA logic resources are very abundant, whose proportion of configuration frames and configuration bits related to user functional circuits is relatively small. In most cases, many configuration bits in the configuration data are 0. Taking a certain V5 FPGA design as an example, the slice resources account for 74%, FF resources account for 26%, LUT resources account for 51%, BRAM resources account for 25%, DSP48 resources account for 69%, and PLL resources account for 16%. However, the number of 0 bytes accounts for about 69%, indicating that a large amount of configuration frame data has similar content.

Based on the above analysis, it can be inferred that the offset of compressible strings in bitstream files is mostly small. To verify this conclusion, we developed a statistical analysis program based on the traditional LZO algorithm. Five FPGA projects based on four commonly used models of XC7VX690T, XC7K325T, XC5VFX130T, and XC4VX55 were randomly selected, which are research subjects for verification in this paper. All these projects were applied in on-board electronic systems, including FPGA software such as on-board communication, data transmission and processing, system control, navigation, and attitude control. This study involved calculating the offset, which was categorized into three different ranges: less than or equal to 2 kB, between 2 and 16 kB, and greater than 16 kB but less than the maximum supported 48 kB. This statistical analysis is shown in Table 3.

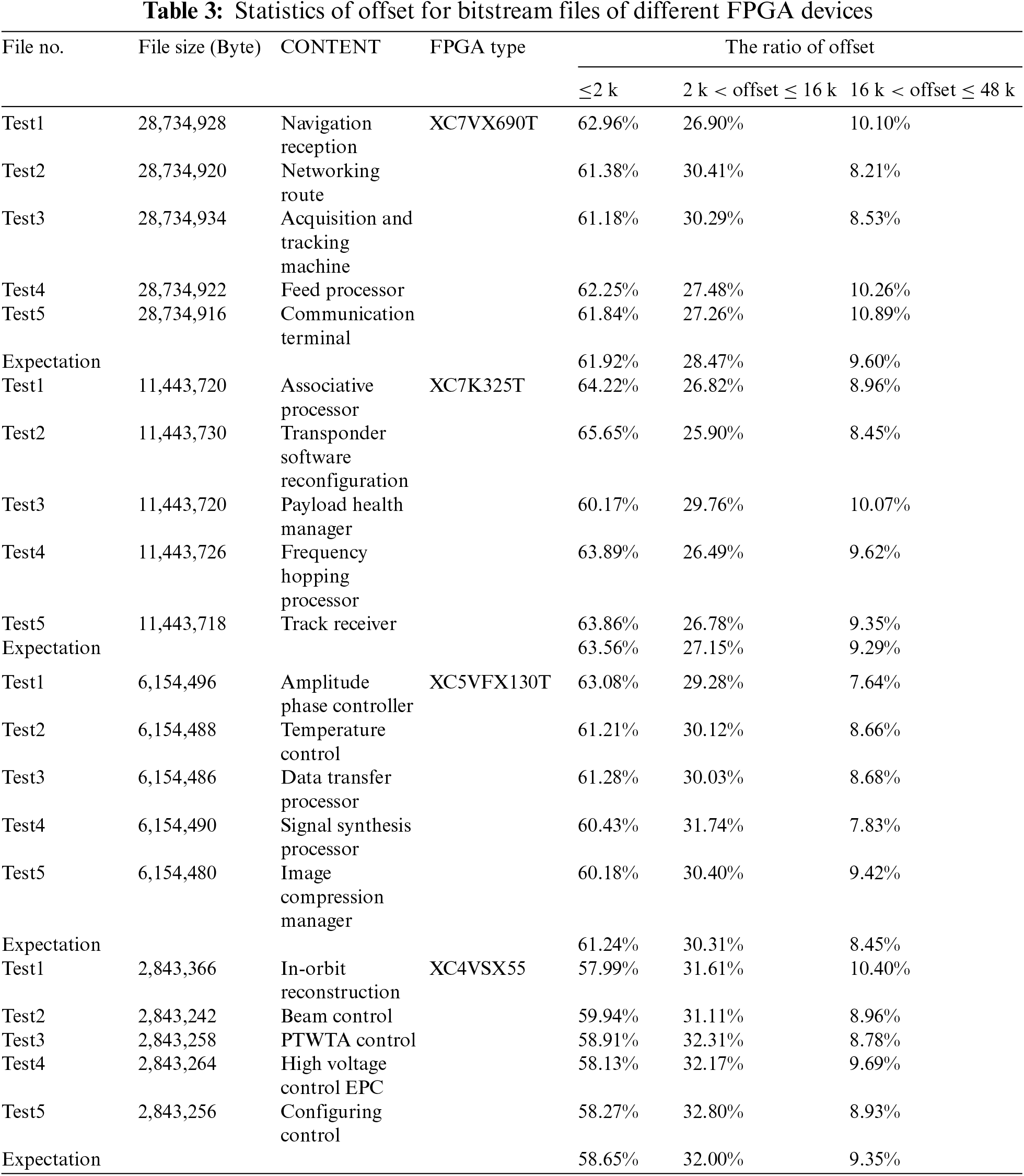
For four types of FPGAs, the proportional distribution of three different offsets was compared and analyzed, as shown in Fig. 3. The statistical results show that the proportion of duplicate strings with an offset greater than 16 kB but under 48 kB is less than 10%. By capping the offset to within 16 kB, it is possible to enhance both compression and decompression speeds, curtail decompression resource expenditures, and maintain a negligible effect on the overall CR.

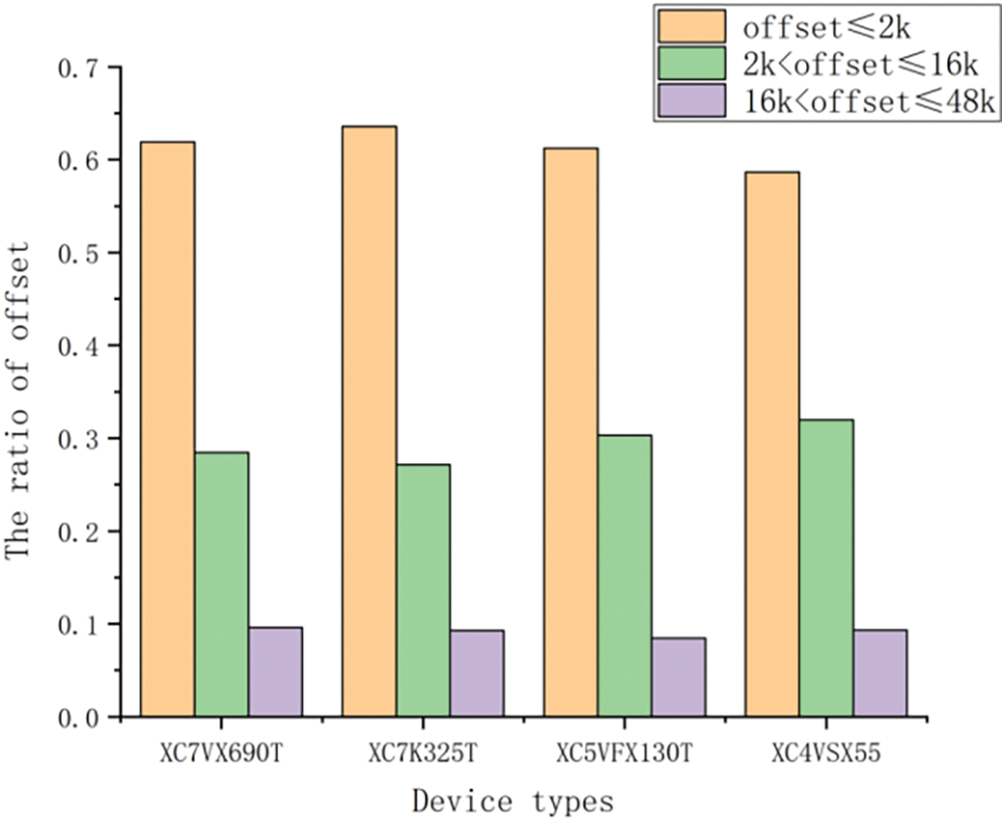
Figure 3: Proportion of back offset in bitstream files of different FPGA devices

3.2 Compression Format Design

Fig. 4 shows the compression format of the five traditional LZO algorithm, where ‘length’ is the matching length, ‘offset’ is the matching distance, and ‘nlen 2bit’ is the remaining 2 bits, that is, if the length of the new character is less than or equal to 3, the position of the new character length is recorded. The length of Format-1, Format-2, and Format-3 is less than or equal to 8 bytes. The length of Format-4 and Format-5 is greater than 8 bytes. The offset of Format-1 is less than or equal to 2 k the offset of Format-2 is less than or equal to 16 k, and the offset of Format-3 is 15 bits. However, since the range of the second compression format is between 0 and 16 k, in order to increase the range of the offset, the offset range of the third compression format is greater than 16 k and less than or equal to 48 k. The offset of Format-4 is less than or equal to 16 k, and the repetition length is not limited. The offset of Format-5 is greater than 16 k and less than 48 k, and the repeat length is not limited, either. The previous study explained the proportion of duplicate strings with a matching distance greater than 16 k but less than 48 k is less than 10%. Considering the existence of a large number of continuous empty characters in the bitstream file, abandoning this part of the string in compression has minimal impact on compression rate. The above two points provide ideas for optimizing compression formats.

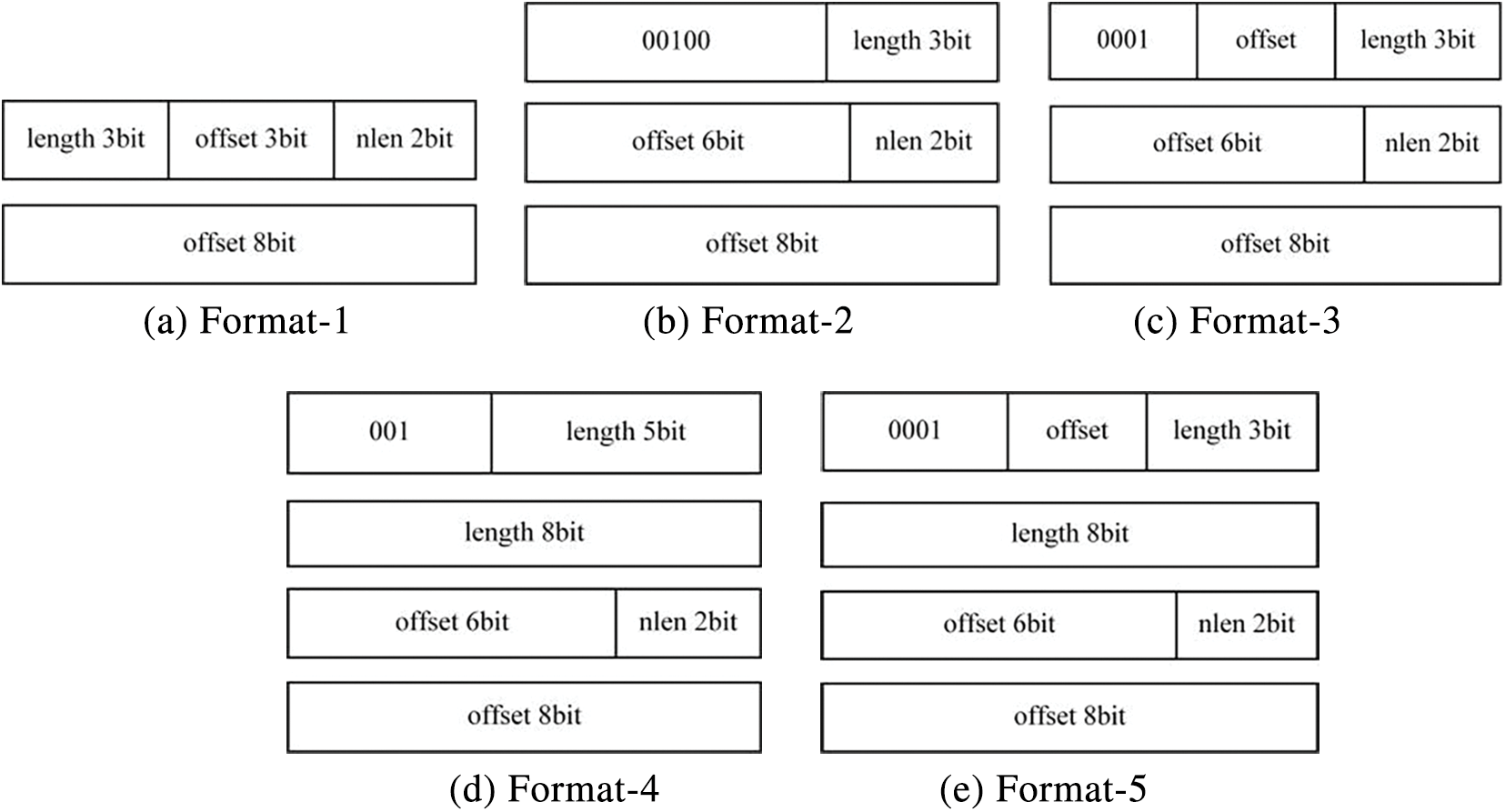
Figure 4: Five compression formats of LZO

(1) The maximum matching distance of the traditional LZO compression algorithm is 48 k, which requires at least 48 k deep cache storage to ensure that the compressed data is correctly decompressed. In order to reduce the hardware resource cost of the decompression circuit and improve the compression and decompression speed, reducing the matching distance of the storage format is very effective. In general, the depth of a hash dictionary memory is 16 k. Considering the very small percentage in bitstream files with matching distances between 16 and 48 k, Setting the match distance length to 16 k can satisfy the application requirements of bitstream files, ensure the dictionary capacity, and have a minimal impact on the compression ratio.

(2) The matching distances of Format-3 and Format-5 are greater than 16 k and less than 48 k, so these two formats will not be adopted. The distance range of Format-2 and Format-4 is the same, but the difference lies in the matching length. Format-4 contains more compact matching length information compared to Format-2, but has more bytes. Therefore, to avoid wasting bits, Format-2 and Format-4 will be merged. For the traditional LZO algorithm, when the number of new characters is greater than 3 bytes, the first character is less than or equal to 15. Hence, in this article, the compression Format-3 and Format-5 are eliminated from the encoding scheme, and the first character range of new characters can be set to be less than or equal to 31, making the format more compact.

Based on the above analysis, a simplified storage format encoding for FPGA bitstream files has been designed, with only two storage formats and a matching distance of less than or equal to 16 k. This is a customized and more compact compression format encoding for bitstream files. Compression Format-1, as shown in Fig. 5a, is designed for offset less than 2 k and matching length less than or equal to 8. This format mirrors the first compression format of the traditional LZO algorithm. Compression Format-2, as shown in Fig. 5b, accommodates offset ranging from greater than 2 k to a maximum of 16 k, without imposing any limitations on the repeat length. This format is an innovative fusion of LZO’s compressed Format-2 and Format-4. It offers a space-saving advantage by conserving up to one character for the encoding of identical strings, as compared to the traditional Format-4.

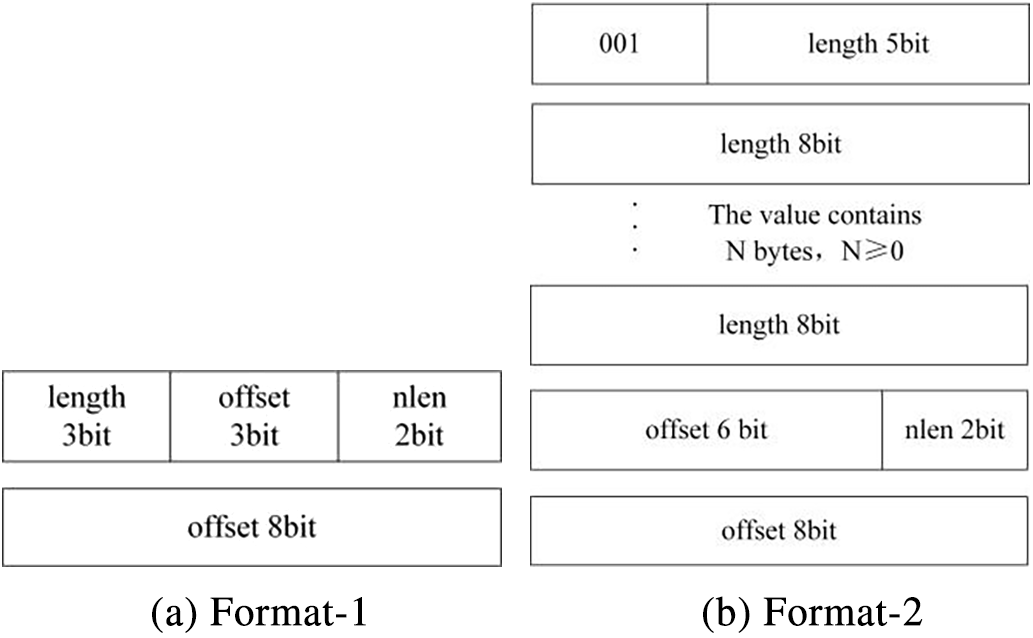
Figure 5: Simplified compression formats of LZO-ours

The compressed bitstream file is interspersed with segments of new and compressed characters. The LZO algorithm delineates two formats for new characters, as illustrated in Fig. 6. In comparison, the proposed compact character compression format is designed to counteract any potential reduction in CR that may result from limiting the offset. Fig. 7 introduces a novel character format, comprising a count of new characters and the specific characters themselves. In Fig. 7, ‘character’ is an 8-bit binary number, and ‘num’ represents the number of bits. The meanings of length and offset are the same as those in Fig. 5. The first new character format is applicable when the count of new characters does not exceed 3. In this scenario, the count is embedded within the last two bits of the penultimate byte of the preceding compressed format. The second new character format imposes no restrictions on the length of the new characters. A distinctive feature of this format is that the first byte value of the character must be less than 31, serving as a delimiter to differentiate between the new character format and the compressed format segments. In comparison to the LZO compression format, which utilizes a first byte value less than 15, the format introduced in this article offers a more compact representation. This innovation is aimed at enhancing the space efficiency of the compressed bitstream files.

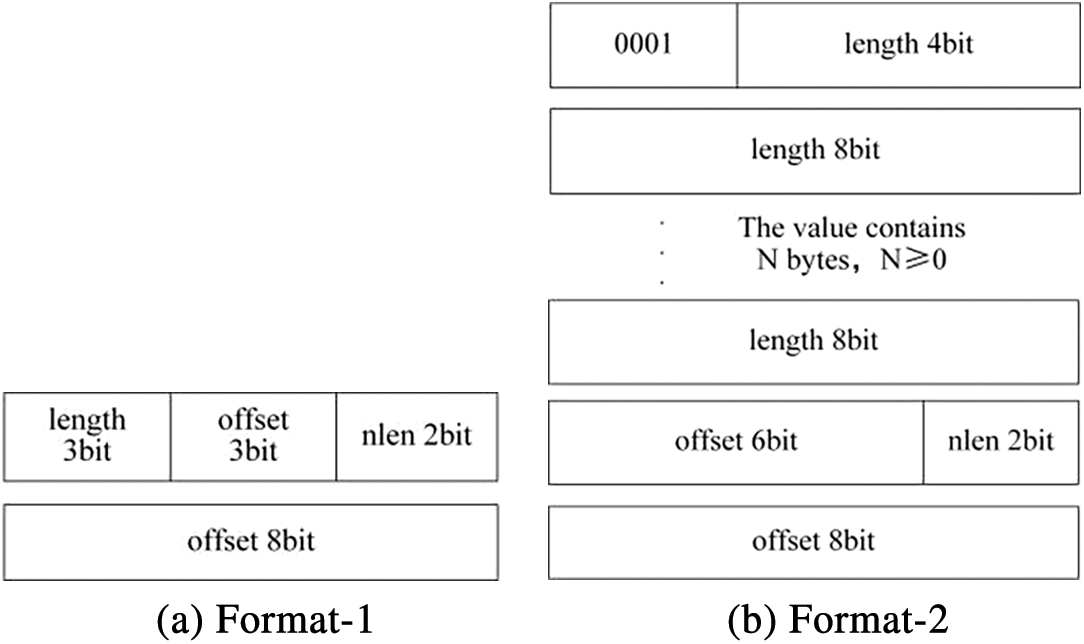
Figure 6: The new character format of LZO

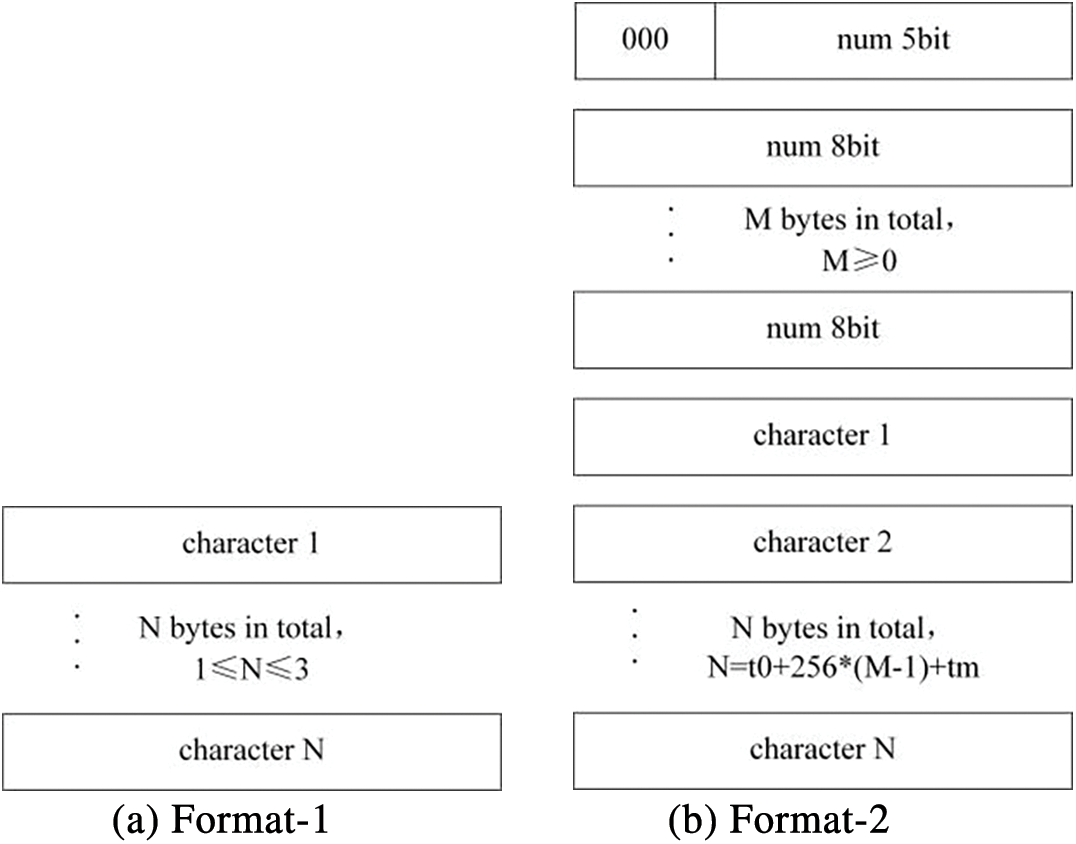
Figure 7: The new character format of LZO-ours

3.3 Our New LZO Algorithm

The compression algorithm presented in this article consists of a set of five core functions, each carefully designed to facilitate the compression process of bitstream files. These functions include bitstream input, hash table management, new character processing, duplicate character processing, and data output. The specific encoding process is shown in Fig. 8. The characteristic of this algorithm is its ability to quickly determine the appropriate encoding type, which is achieved by utilizing dual-hash operations and character comparison techniques. After determining the encoding type, the algorithm proceeds to encode the data according to the previously described compression format and the new character format.

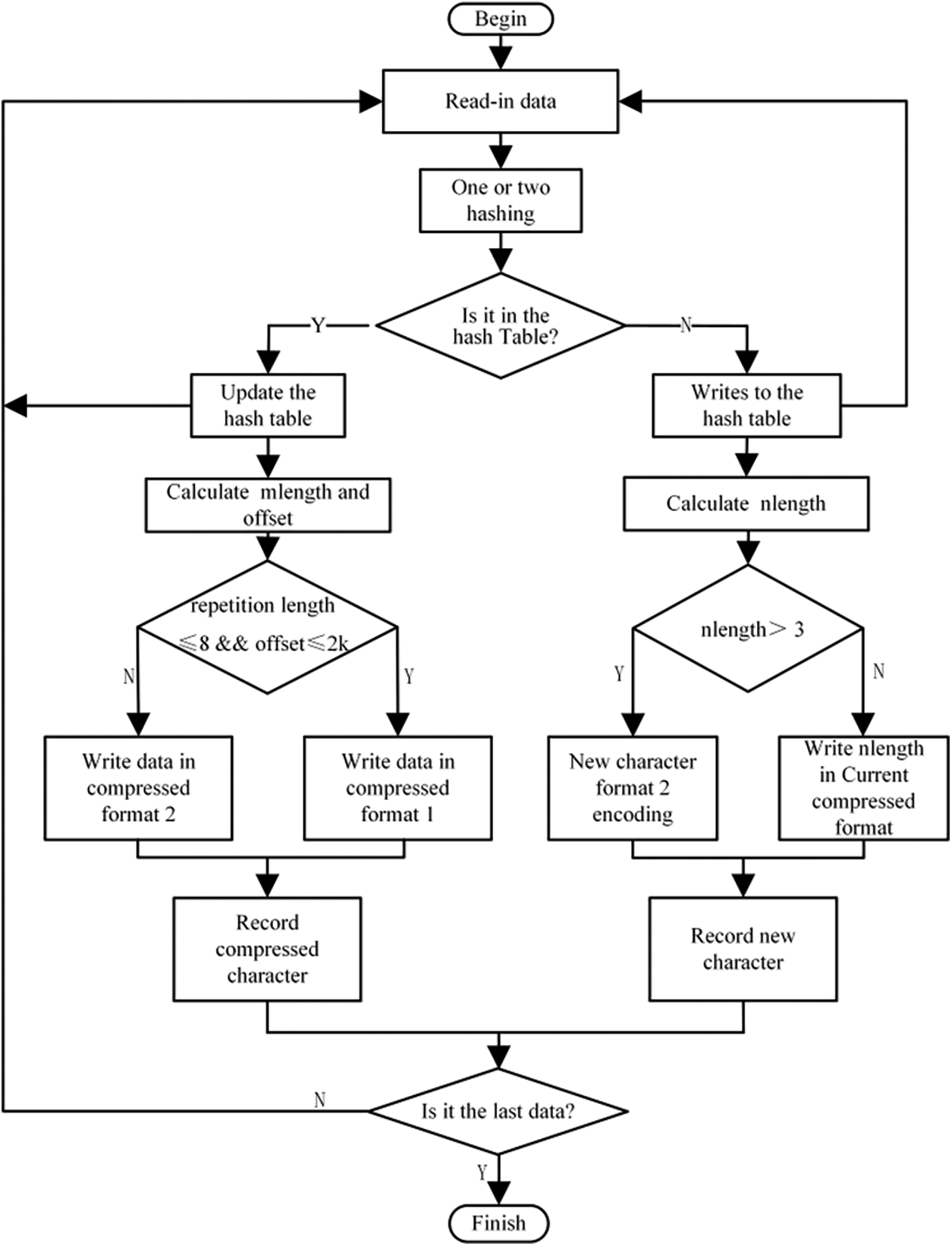
Figure 8: Compression algorithm design flowchart

The key step in the compression process of bitstream files is to determine the character type, that is, to determine whether the input character is a new character. The specific method involves performing the first hash operation on the input data, using the resulting hash value as an index to access the hash table, and then using the data retrieved from the hash table as an address to read the corresponding data from the bitstream file. If the data matches with the input data, it means that the input data is in the hash table and not a new character; otherwise, the process performs a second hash operation and retrieves the data based on the result of the second hash operation. If the data retrieved for the second time matches, it means it is not a new character; otherwise, it is determined to be a new character. Once determined to be a new character, update the index of that character in the hash table and continue reading data in byte units. Subsequently, repeat the above operation until the input data is in the hash table indicating the end of the new character. After that, calculate the length of the new character and encode it according to the new character format. If it is a duplicate character, update the index of the character in the hash table and continue reading data in bytes. Repeat the above operation until the input data is no longer in the hash table, indicating the end of the repeated character. Calculate the matching length and the matching distance. If the matching length is less than or equal to 3 and the matching distance is greater than 2 k, it is considered a new character and encoded according to the new character format; otherwise, calculate the matching length and the matching distance, and compress the data according to the compression format.

Decompression serves as the antonym to compression and involves a quartet of functions that work together to reconstruct the original data from its compressed form. The constituent functions of this process include reading compressed bitstream files, determining character types, caching a 16 kB dictionary, and decoding and outputting data. A schematic representation of the overall data flow during the decompression process is shown in Fig. 9.

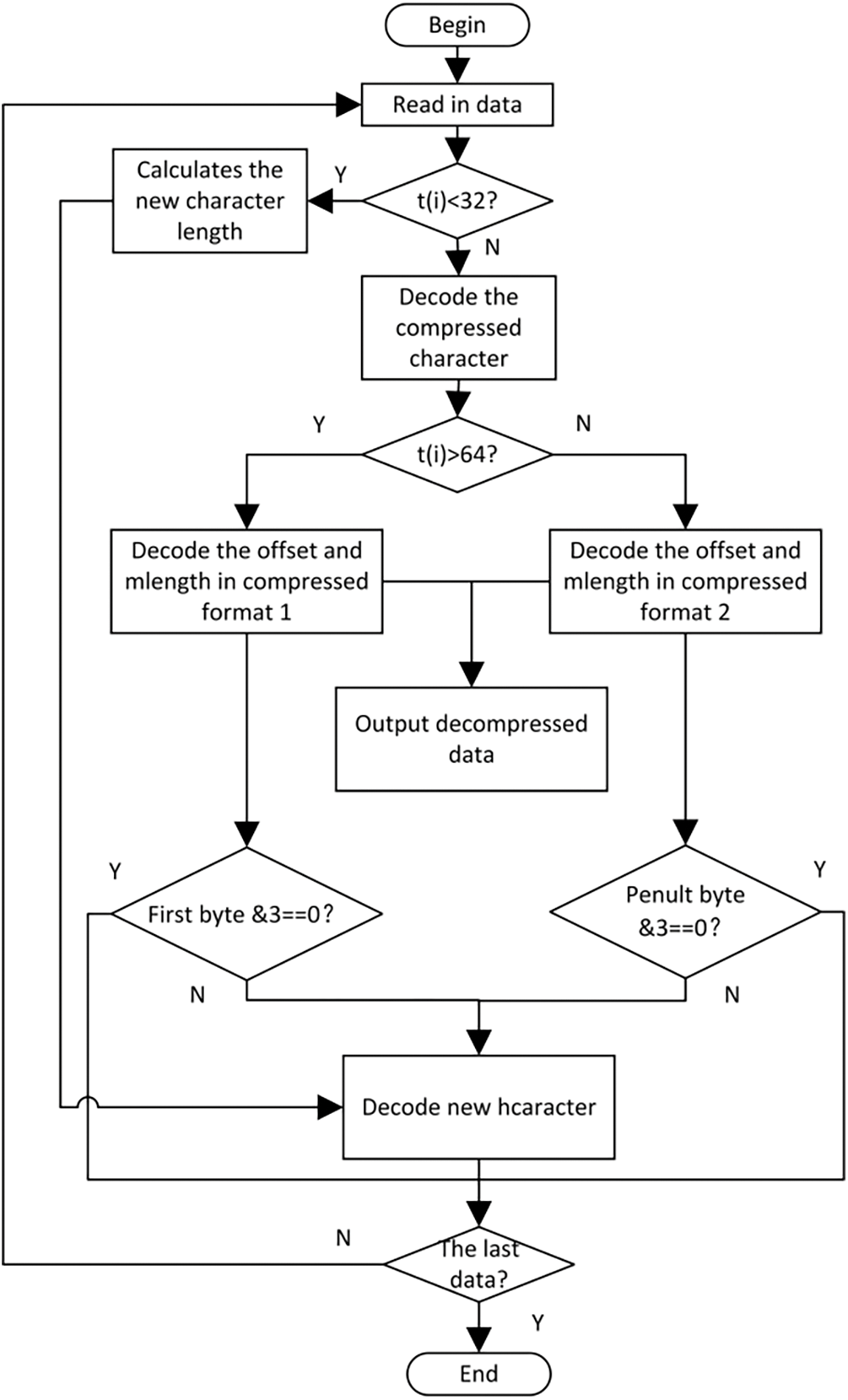
Figure 9: Decompression algorithm design flowchart

In the decompression process, the first character type judgement is made first. Each time a character is read. The data currently being read can be expressed as t(i), where i represents the index of the decompression file corresponding to the current character. If the first character satisfies 0 ≤ t(i) < 32, it is judged as a new character, otherwise it is judged as a duplicate character. For a new character, the length of the new character must be calculated. If 16 < t(i) < 32, the length of the new character is t(i) + 3; if t(i) = 16 and t(i+1) ≠ 0, the length of the new character is 34 + t(i+1); if t(i) = 16 and t(i+1) = 0, continue reading the following characters until the t(i+n) is not 0, then the length of the new character is (n-1) × 255 + 34 + t(i+n). Follow that, the new character is outputted continuously based on the calculated length. After the data has been outputted completely, the process returns to the judgment mechanism.

For repeated characters, it is necessary to judge the compression format. If t(i) ≥ 64, calculate the matching length and matching distance according to the compression format 1, and then perform the judgment of the new character information in the compression format 1. If the last two digits of t(i+1) are not 0, it is the length of the new character, and after the decompression of the data is completed, the new character is output. Otherwise, determine whether compression is finished, the end of the output data and the data length, otherwise continue reading the data and repeat the above operation. If 32 ≤ t(i) < 64, calculate the matching length and matching distance according to compression format 2, and then perform the new character information judgment in compression format 2. If the last two bytes of the penultimate byte are not 0, it is the length of the new character, and after decompression of the data is completed, the new character is output. Otherwise, judge whether the compressed bitstream file has completed all processing, if not, continue reading the data and repeat the above operation.

4  Experimental Verification

This experiment uses a Windows 10 64-bit platform and Intel(R)Core(TM)i7-8750H 2.21 GHz CPU. The development tool of the test algorithm is Microsoft Visual Studio 2010, which is realized by C language. We use the LZ4 [21,22], which is used in Xilinx’s Bitstream file dealing, original LZO, LZO-ours, and LZW algorithms to compress the bit-stream file in Table 3. The comparison results of compression time and compression rate are shown in Table 4.

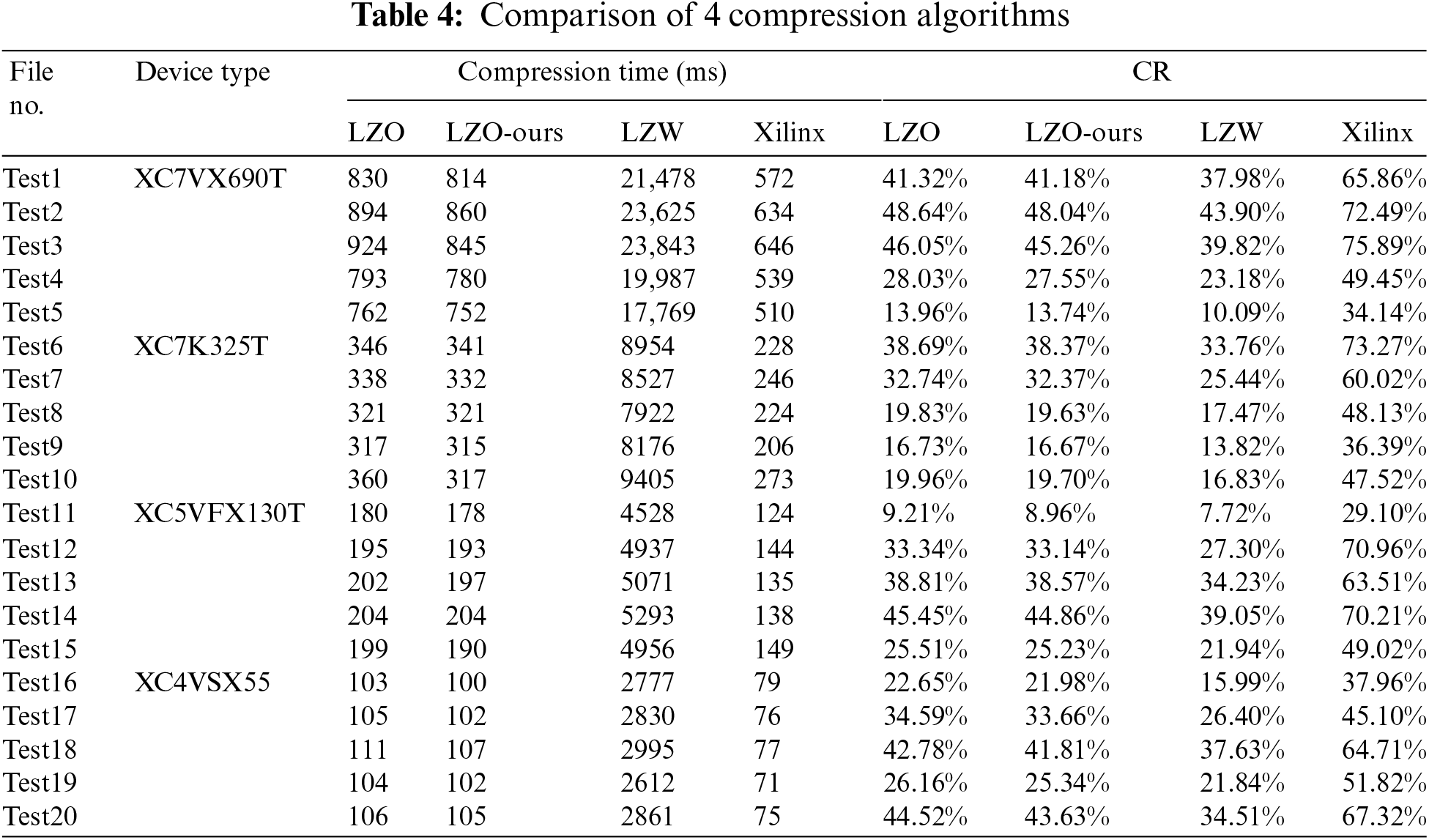
The CR comparison of different serial FPGA bitstream files is shown in Fig. 10a. The data indicates the CR of LZO, LZO-ours and LZW is less than 50%, with that of LZW is the lowest. And the CR of the LZO-ours is lower than that of the traditional LZO algorithm, with an average reduction of 0.47%. As shown in Fig. 10b, Xilinx has the lowest compression time, but it has no absolute advantage compared with LZO and LZO-ours, while the compression time of LZW is almost 30 times that of them. Compared with the traditional LZO algorithm, the average compression time of LZO-ours algorithm is reduced by 11.95 ms.

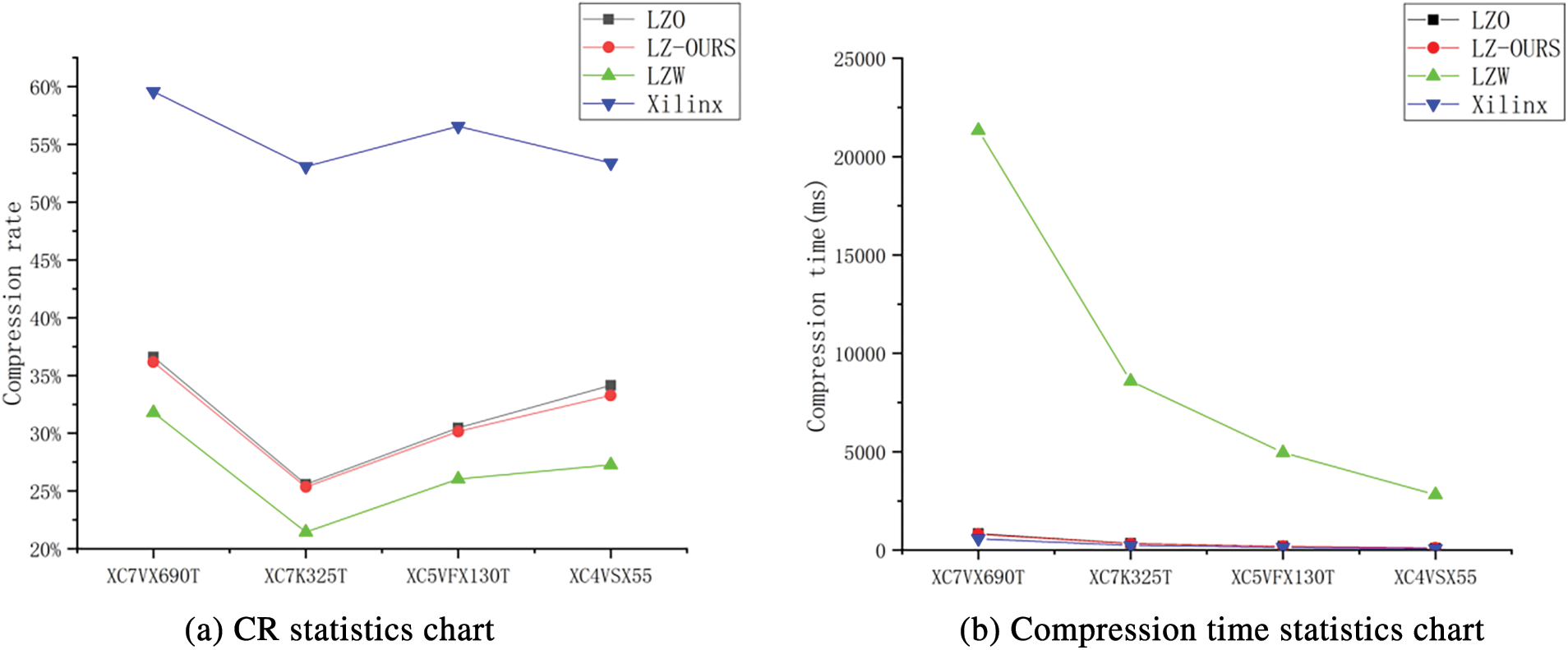
Figure 10: Statistics of CR and compression time for traditional LZO and ours improved LZO

Based on the analysis above, this paper proposes a decompression hardware circuit architecture, as shown in Fig. 11. This circuit architecture comprises several integral modules: a Character Type Judgment Module, a New Character Decoding Module, a Compressed Character Decoding Module, an SRAM Controller Module, a Data Caching Module, and a Data Output Control Module. And this systematic approach ensures an efficient decompression process. Upon receiving input data, the Character Type Judgment Module initially ascertains whether the data corresponds to a new or a duplicate character. In the case of new characters, the New Character Decoding Module calculates the character length, which is then directly outputted via the Data Output Control Module and cached for subsequent use. These characters are sequentially written to the SRAM starting from address zero, with the cached data stored in the Data Caching Module. Duplicate characters are processed by the Compressed Character Decoding Module, which identifies the compression format and computes the offset and matching length. These values are utilized to extract and decompress the data from the SRAM, which is then outputted and written into the Data Cache Module, overwriting from address zero. Concurrently, the Data Cache Module updates the address pointers for the previously written new characters. The SRAM Controller Module oversees the operational, generation, and control mechanisms for data and address read/write functions. The Data Caching Module integrates a SRAM16384x8 block alongside associated control cache logic. Given the variability in decompressed data length and the count of new characters, the Data Output Control Module incorporates a valid decision signal for output data. A feedback circuit is also engineered to govern the input signal, allowing character input to proceed only after the decompression of a specific segment of compressed characters. The decompression process adeptly compresses the matching length, offset, and previously decompressed data within the format.

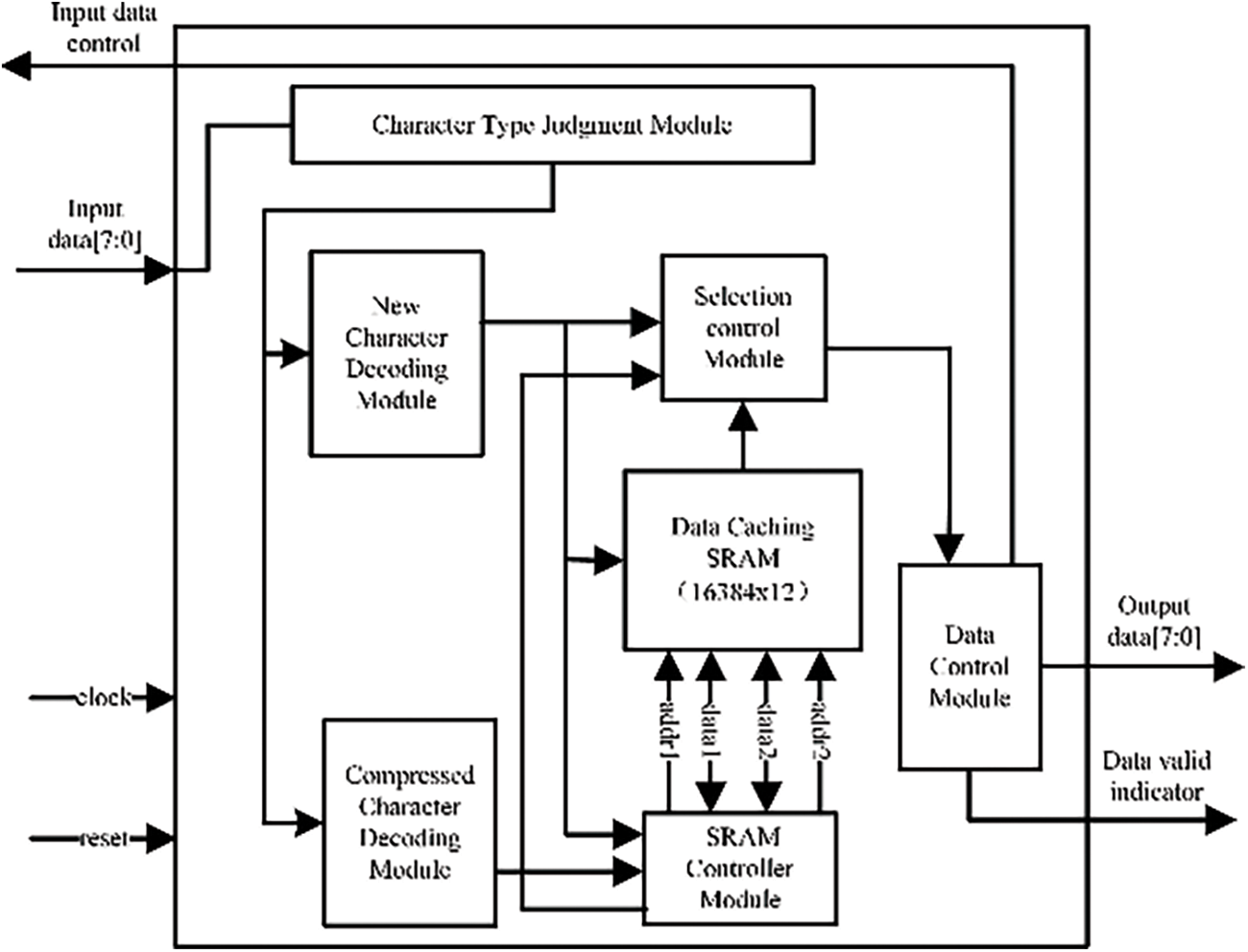
Figure 11: Decompression circuit architecture

The decompression hardware circuit proposed within this article has been meticulously implemented and validated using XC4VSX55 devices. A comprehensive assessment of the resource utilization rates is represented in Table 5. And the operating frequency is 138.1 MHz. When comparing the LZO-ours algorithm with the LZO algorithm, it can be observed that the resource consumption is about 40% of the LZO algorithm, except for the IO resources.

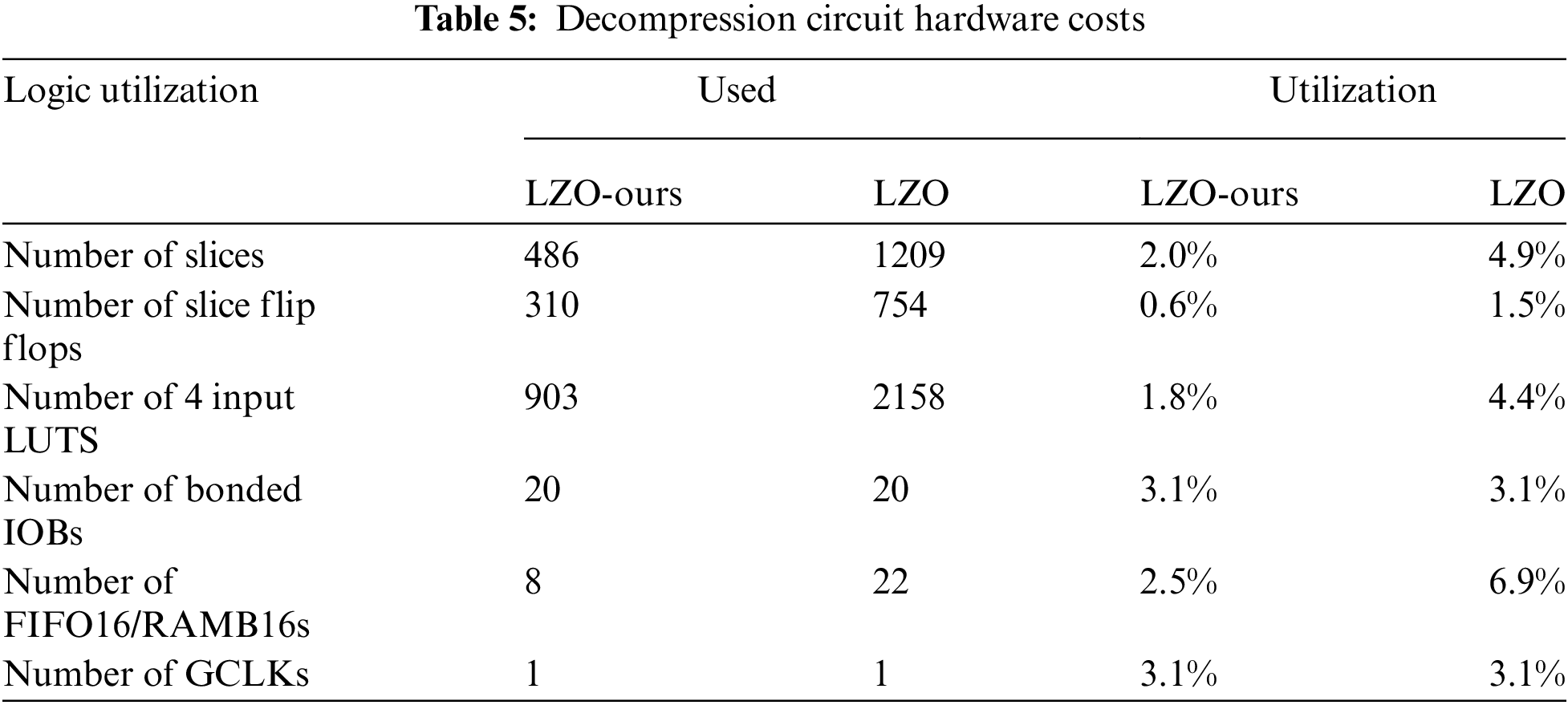
In FPGA/ASIC design, the access time of SRAM increases with the depth. The SRAM depth used in the decompression hardware circuit is only 30% of that used in the LZO compression algorithm, which improves the maximum operating frequency of the circuit. In addition, although the data stored in the SRAM is updated in real time, the data as a whole is updated every 16,384 clock cycles, which is three times the SRAM update rate of the LZO algorithm. Thus, this can further reduce the risk of Single Event Upset (SEU) in the SRAM storage data for space utilization.

5  Conclusions

The research objective of this paper is to design a bitstream file compression algorithm tailored for space applications, aiming to increase the speed of compression and decompression processes while achieving minimal or no loss in CR, and emphasizing the minimization of resource consumption. After conducting an in-depth comparative study of mainly several bitstream file compression technologies, it has been determined that the LZO compression algorithm is more suitable for the research objectives. However, the LZO algorithm has certain limitations in space applications. To address these issues, this paper analyzes these limitations and proposes an improved scheme that utilizes a custom compression format leveraging the unique characteristics of bitstream files. Utilizing a statistical analysis program, the research reveals that configuration data contains a significant number of redundant bits. Furthermore, it finds that during the compression process of configuration bitstream files, the proportion of repeated strings with an anagram distance between 16 and 48 k is less than 10%. Capitalizing on this insight, the paper introduces an optimized LZO algorithm and its corresponding decompression hardware design. These are intended to enhance the compression rate and curtail the resource requirements of the decompression circuit, without compromising the compression ratio. The experimental results demonstrate that the refined LZO algorithm achieves a 3% increase in compression speed, a 0.47% reduction in the compression ratio, and a reduction in the decompression hardware cost by approximately 35% compared to the original algorithm. This makes the algorithm exceptionally suitable for FPGA reconstruction systems in space-based electronic equipment, where resource constraints are stringent.

Building on the above research findings, future work plans will focus on the robust design of decompression circuits-resistant SEUs. This endeavor aims to enhance the stability and reliability of decompression circuits in the challenging environment of space, thereby providing more robust technical support for space electronics.

Acknowledgement: Sincere thanks to all the supervisors, colleagues and friends who contributed to this paper. Your support is so important, and your wisdom is amazing.

Funding Statement: This work was supported in part by the National Key Laboratory of Science and Technology on Space Microwave (Grant Nos. HTKJ2022KL504009 and HTKJ2022KL5040010).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Xiaoling Lai, Jian Zhang, Yangming Guo, Ting Ju, Qi Zhu, Guochang Zhou. Data collection and analysis: Xiaoling Lai, Jian Zhang, Ting Ju. Draft manuscript preparation: Xiaoling Lai, Jian Zhang, Qi Zhu. Supervision: Yangming Guo, Guochang Zhou. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. T. Toba, K. Shimbo, T. Uezono, F. Nagasaki, and K. Kawamura, “Soft error high speed correction by interruption scrubbing method in FPGA for embedded control system,” in 2017 IEEE 2nd Inform. Technol. Networ. Electr. Automat. Cont. Conf. (ITNEC), IEEE, 2017, pp. 634–641. [Google Scholar]

2. M. Berg, C. Poivey, D. Petrick, D. Espinosa, A. Lesea and K. A. LaBel, “Effectiveness of internal versus external SEU scrubbing mitigation strategies in a Xilinx FPGA: Design, test, and analysis,” IEEE Trans. Very Large Scale Integr. (VLSI) Syst., vol. 55, no. 4, pp. 2259–2266, 2008. doi: 10.1109/TNS.2008.2001422. [Google Scholar] [CrossRef]

3. X. Qin, C. Muthry, and P. Mishra, “Decoding-Aware compression of fpga bitstreams,” IEEE Trans. VLSI Syst., vol. 19, no. 3, pp. 411–419, 2011. doi: 10.1109/TVLSI.2009.2035704. [Google Scholar] [CrossRef]

4. T. Takagi et al., “Tag-less compression for FPGA configuration data,” in Proc. of SASIMI 2022, 2022, pp. 81–82. [Google Scholar]

5. Z. Li and S. Hauck, “Configuration compression for virtex FPGAs,” in 9th Annual IEEE Symp. Field-Programm. Custom Comput. Mach. (FCCM’01), IEEE, 2001, pp. 147–159. [Google Scholar]

6. J. Yan, J. Yuan, P. H. W. Leong, W. Luk, and L. Wang, “Lossless compression decoders for bitstreams and software binaries based on high-level synthesis,” IEEE Trans. Very Large Scale Integr. (VLSI) Syst., vol. 25, no. 10, pp. 2842–2855, 2017. doi: 10.1109/TVLSI.2017.2713527. [Google Scholar] [CrossRef]

7. A. Dandalis and V. K. Prasanna, “Configuration compression for FPGA-based embedded systems,” IEEE Trans. Very Large Scale Integr. (VLSI) Syst., vol. 13, no. 12, pp. 1394–1398, 2005. doi: 10.1109/TVLSI.2005.862721. [Google Scholar] [CrossRef]

8. J. Fang, J. Chen, J. Lee, Z. Al-Ars, and H. P. Hofstee, “An efficient high-throughput LZ77-based decompressor in reconfigurable logic,” J. Signal Process. Syst., vol. 92, no. 9, pp. 931–947, 2020. doi: 10.1007/s11265-020-01547-w. [Google Scholar] [CrossRef]

9. T. Wang, L. Tang, R. Li, S. Wang, and H. Yang, “Lightweight lossless compression algorithm for fast decompression application,” in 2021 Int. Conf. UK-China Emerg. Technol. (UCET), IEEE, 2021, pp. 258–263. [Google Scholar]

10. M. Safieh and J. Freudenberger, “Efficient VLSI architecture for the parallel dictionary LZW data compression algorithm,” IET Circ., Dev. Syst., vol. 13, no. 5, pp. 576–583, 2019. doi: 10.1049/iet-cds.2018.5017. [Google Scholar] [CrossRef]

11. M. Hubner, M. Ullmann, and J. Becker, “Realtime configuration code decompression for dynamic FPGA self reconfiguration: Evaluation and implementation,” Int. J. Embed. Syst., vol. 1, no. 3–4, pp. 263–273, 2005. doi: 10.1504/IJES.2005.009955. [Google Scholar] [CrossRef]

12. R. Iša and J. Matoušek, “A novel architecture for LZSS compression of configuration bitstreams within FPGA,” in 2017 IEEE 20th Int. Symp. Des. Diagnost. Electr. Circ. Syst. (DDECS), IEEE, 2017, pp. 171–176. [Google Scholar]

13. J. Satheesh Kumar, G. Saravana Kumar, and A. Ahilan, “High performance decoding aware FPGA bit-stream compression using RG codes,” Clust. Comput., vol. 22, no. Suppl 6, pp. 15007–15013, 2019. doi: 10.1007/s10586-018-2486-3. [Google Scholar] [CrossRef]

14. J. S. Kumar, O. Prakash, Y. Gopal, A. Rai, and A. Ranjan, “Effective bitstream compression approaches for high speed digital systems,” e-Prime-Adv. Elect. Eng. Electr. Energy, vol. 5, 2023, Art. no. 100221. doi: 10.1016/j.prime.2023.100221. [Google Scholar] [CrossRef]

15. P. N. Matte and D. D. Shah, “Cascading of compression algorithm to reduce redundancy in FPGAs configuration bitstream-a novel technique,” Int. J. Appl. Eng. Res., vol. 13, no. 5, pp. 2872–2878, 2018. [Google Scholar]

16. Y. Gao, H. Ye, J. Wang, and J. Lai, “FPGA bitstream compression and decompression based on LZ77 algorithm and BMC technique,” in 2015 IEEE 11th Int. Conf. ASIC (ASICON), IEEE, 2015, pp. 1–4. [Google Scholar]

17. J. Wang, Y. Kang, Y. Feng, Y. Li, W. Wu and G. Xing, “Lossless compression of bitstream configuration files: Towards FPGA cloud,” in 2021 IEEE Int. Conf. Parallel Distrib. Process. Appl. Big Data Cloud Comput. Sustain. Comput. Commun. Soc. Comput. Netw. (ISPA/BDCloud/SocialCom/SustainCom), IEEE, 2021, pp. 1410–1421. [Google Scholar]

18. M. Pastuła, P. Russek, and K. Wiatr, “Low-cost ANS encoder for lossless data compression in FPGAs,” Int. J. Electron. Telecommun., vol. 70, Mar. 2024, pp. 219–228. [Google Scholar]

19. P. Adell, G. Allen, G. Swift, and S. McClure, “Assessing and mitigating radiation effects in Xilinx SRAM FPGAs,” in 2008 Eur. Conf. Radiat. Effec. Compon. Syst., 2008. [Google Scholar]

20. XAPP538 (v1.0“Soft error mitigation using prioritized essential bits,” Apr. 4, 2012. Accessed: Aug. 15, 2014. [Online]. Available: https://www.eeweb.com/wp-content/uploads/articles-app-notes-files-soft-error-mitigation-using-prioritized-essential-bits-1339781673.pdf [Google Scholar]

21. Xilinx. “Xilinx LZ4 compression and decompression,” 2021. Accessed: Jun 8, 2023. [Online]. Available: https://xilinx.github.io/Vitis_Libraries/data_compression/2021.1/source/L2/lz4.html [Google Scholar]

22. T. Beneš, M. Bartík, and P. Kubalík, “High throughput and low latency LZ4 compressor on FPGA,” in 2019 Int. Conf. ReConFigurable Comput. FPGAs (ReConFig), Cancun, Mexico, IEEE, 2019, pp. 1–5. [Google Scholar]