A Dynamic Social Network Graph Anonymity Scheme with Community Structure Protection

1  Introduction

With the rise of online social network platforms (e.g., Google, Twitter, and Facebook), people can interact and make friends with other like-minded people. During the interaction, the network-centric graph data is formed. The data mining and data analysis of social networks for third parties can yield rich and accurate information such as users’ interests. However, the original social network graph often contains users’ sensitive information (e.g., hobbies, relationships, and profiles). Directly releasing the real graph data jeopardizes the users’ privacy, as Ferri et al. pointed out in [1], 90% of users are concerned about their sensitive information being leaked. For instance, malicious adversaries can obtain users’ private information by identifying unique identifiers (e.g., names) that represent their identities. Therefore, it is crucial to anonymize users’ identities and their edge relationships before publishing the social network graphs [2].

The common anonymization methods mainly consist of clustering generalization [3], graph editing [4], and differential privacy [5–7]. The clustering generalization divides all nodes in the original graph into multiple groups and anonymizes nodes in each group. The graph editing achieves the anonymization of the original graph by modifying nodes and edges randomly. The differential privacy perturbs the original graph by adding the appropriate noisy nodes/edges. However, these methods primarily concentrate on the anonymization of static graphs. Social network graphs are evolving over time, with new nodes, edges, and changing relationships between users. This evolution introduces a unique challenge, i.e., the original graph at each timestamp is anonymized independently using a static graph anonymization method. Although the nodes and edges in each anonymized graph are protected, adversaries with strong background knowledge can still perform differential analysis on the sequence of published anonymized graphs, allowing them to re-identify nodes or infer sensitive relationships. For instance, if an adversary has access to a sequence of anonymized graphs over a period of time and knows that a specific user was added at a certain timestamp, he/she can compare the anonymized graph at the last timestamp with that at the current timestamp to re-identify the identity of the newly introduced node (see adversary model in Section 3.1 for more details).

Therefore, to achieve effective dynamic anonymization of social network graphs, we need to solve the following challenges:

i) Complicated and cumbersome anonymization process. Existing researches [8,9] mitigate re-identification attacks on evolving graph snapshots using clustering generalization, that is, nodes are grouped at each timestamp and connected within groups to meet k-anonymity, and edges between groups are anonymized in an isomorphic way. However, this method needs to continually re-cluster groups at each timestamp, which is complicated and cumbersome.

ii) Dynamic protection of community structures. Existing methods neglect the dynamic protection of community structures [10,11], focusing only on nodes and edges, which reduces the utility of anonymized graphs. For instance, people cluster by interests, and these communities change over time with shifting interests [12]. Without dynamic protection of community structures, anonymized graph structures can diverge from the original, leading to low utility.

iii) Precise measure of graph utility. Using a single metric cannot fully represent the utility of an anonymized graph. Most researchers often use multiple metrics to assess how closely the anonymized graph resembles the original, but these metrics only capture differences from a single perspective.

To address the above challenges, we propose DSNGA-CSP, a dynamic social network graph anonymity scheme with community structure protection. At each updated timestamp, DSNGA-CSP categorizes communities based on changes in the original graph and only partitions community subgraphs for a specific category, avoiding redundant operations. Intra-community nodes and edges are anonymized using a novel k-composition anonymity method, while inter-community edges are anonymized using edge isomorphism. DSNGA-CSP protects nodes’ identities, edge relationships, and community structure at each timestamp, simultaneously. To measure utility more accurately, we propose an information loss metric based on original information preservation and anonymous information changes. Extensive experiments evaluate DSNGA-CSP on both static and dynamic graphs. Results show that DSNGA-CSP improves the utility of anonymized static graphs and outperforms other methods in terms of privacy and utility for anonymized dynamic graphs.

The main contributions are as follows:

1) A dynamic graph anonymization scheme (DSNGA-CSP) is proposed, which protects nodes’ identities and edge relationships in the original graph for each timestamp, and it achieves the dynamic protection of original graph structures.

2) A novel k-composition anonymity method is proposed, which achieves k-automorphism of each community subgraph, and the edge relationships between communities achieve isomorphic anonymity.

3) A new information loss metric is proposed to measure the utility of anonymized dynamic graphs from two perspectives, and it is more accurate than other similar alternatives.

4) All experiments are completed on multiple real datasets, and the measured results demonstrate the effectiveness of DSNGA-CSP.

The remaining parts of this paper are organized as follows: Section 2 presents related work. Section 3 gives preliminaries. Section 4 introduces the proposed DSNGA-CSP scheme in detail. Section 5 presents the experimental comparison and analysis. Section 6 discusses the implications and limitations of our work. Section 7 gives the conclusion and future work.

2  Related Works

In this section, we review related works on privacy-preserving static graph anonymity, privacy-preserving dynamic graph anonymity, and community structure protection. We summarize these works in a literature review matrix table (Table 1, which provides a comparison of the main techniques, key features, and limitations.

2.1 Static Graph Anonymity

Privacy-preserving data publishing has emerged as a prominent research focus [22]. Currently, the anonymous publishing of social network graphs has received a lot of attention and attracted many researchers to develop advanced methods. k-anonymity [23], as a promising technique, ensures that each node in the anonymized graph is indistinguishable from at least k−1 other nodes based on certain key attributes. If an adversary possesses private attributes of a target node, k-anonymity can prevent him from re-identifying the target node from at least k query results, as there are no significant differences among these results. Xiang et al. [13] proposed a tree-based k-degree anonymity (TKDA) method, which dynamically modifies edges in the original graph using a depth-first traversal algorithm. Lin et al. [14] proposed a novel k-degree anonymity method, which clustered groups of nodes through a greedy partitioning algorithm and then added edges for each group to increase the degree of the node to the maximum. Kaur et al. [15] proposed k-NeuroSVM, which classifies nodes in the original graph using Neural Networks (NN) and SVM into various groups. They add reasonable noise nodes into each group to meet the k-degree anonymity requirement while maintaining similarity with the original graph. However, these degree-based methods cannot completely resist re-identification attacks from an adversary with knowledge about the structural subgraph of a target node. To defend against this attack, k-isomorphism anonymity method [16] is proposed, which makes each node in the anonymized graph have corresponding k same neighborhood subgraphs. This prevents adversaries from accurately recognizing the identity of the target node due to the indistinguishability of queried neighborhood subgraphs. Zhang et al. [17] proposed GPPS, which achieves the indistinguishability of 1-neighborhood structures of each node in the anonymized graph. However, this method cannot guard against structural subgraph attacks beyond the 1-neighborhood range. Ren et al. [18] proposed a (α,β,l,k)-anonymity method, which can effectively resist the combination attack including d-neighborhood attack, homogeneity attack, and background knowledge attack.

The above researches indicate that the k-isomorphism anonymity method is popular for protecting nodes’ identities and edge relationships. However, this method removes all edges between k isomorphic subgraphs, which decreases the utility of the anonymized graph. k-automorphism anonymity [19] is considered as a good solution. It retains the edges between k isomorphic subgraphs as much as possible, which reduces the loss of the original edges. Therefore, this paper obtains the anonymized dynamic graphs with better utility based on the k-automorphic anonymity method.

2.2 Dynamic Graph Anonymity

In real life, social network graphs are dynamic. The static graph anonymization methods mentioned above cannot be directly applied to dynamic graph anonymization. The main reason is that the adversary can easily re-identify nodes’ identities and edge relationships through differences between anonymized graphs at adjacent timestamps. As the research presented in [20], Zhang et al. proposed DSNDG-KIODA, which only considers nodes’ degree anonymization at the corresponding timestamp. The newly added/removed nodes/edges can be re-identified by differences in node structures between two anonymized graphs at adjacent timestamps. To address this issue, Hoang et al. proposed two time-varying attribute degree anonymity methods ((k,l)-sad, kw-tad) [8,9] based on clustering generalization, which can simultaneously protect users’ identities and their sensitive attributes. However, clustering anonymization needs to repeatedly cluster changed groups at different timestamps, making the overall anonymization process inconvenient. Therefore, based on this challenge, this paper minimizes the redundant operations of the original graph anonymization at updated timestamps, facilitating the process of dynamic graph anonymization.

2.3 Community Structure Protection

The community structure is an important feature of a social network graph, and it is necessary to preserve the structural features of the original graph while achieving the anonymization of nodes’ identities and edge relationships. Zhang et al. [10] proposed a graph perturbation method (PrivCom) based on node-level differential privacy (node-DP), which maximally preserves the community structure of the original graph by a Katz index-based graph feature extraction algorithm. Based on deep learning techniques, Xiang et al. [11] proposed a graph generation model (CPGAN) with community structure protection, and this model presents good scalability on large graphs. With the aim of protecting community structures and node attributes, Ren et al. [21] proposed a kt-security anonymity method by combining k-anonymity and t-closeness to achieve anonymous publishing of the original graph. However, the above methods only can guarantee the protection of graph structures on static graphs, while they are ineffective for the dynamic protection of community structures of the original graph at different timestamps. Therefore, this paper considers the protection of the original graph structure at each timestamp, ensuring that the changed community structures over time can be protected dynamically.

Based on the above issues, this paper proposes a dynamic social network graph anonymity scheme with community structure protection (DSNGA-CSP). DSNGA-CSP achieves anonymization of nodes’ identities and edge relationships. To improve the utility of anonymized dynamic graphs, we preserve more structural information from the original graph at each timestamp. Additionally, a new information loss metric is defined to measure the utility of anonymized dynamic graphs more accurately.

3  Preliminaries

This section introduces the adversary model with a special example and provides the problem definition.

3.1 Adversary Model

Given an original graph sequence G={Gt1,⋯,Gtw} during time periods t1∼tw, to protect identities of users, data provider publishes the anonymized versions G′={Gt1′,⋯,Gtw′} of the original graph sequence. By monitoring the published anonymized graphs, an adversary can extract all nodes’ information (e.g., degree and subgraph structure) from G′. When the adversary masters the real information related to nodes and edges in the original graph (e.g., the user’s name and the friendship between two users with real names at a specific timestamp), he/she can re-identify nodes’ identities and edge relationships by observing the difference between two anonymized graphs at adjacent timestamps. The following example illustrates the aforementioned adversary attack:

Fig. 1 represents a 2-degree anonymous graph sequence being published during time periods t1∼t3. That is, each node in each anonymized graph has the indistinguishable degree with at least k−1 other nodes in the anonymized graph. To obtain 2-degree anonymous graphs, the solid red lines in (d)–(f) are added, respectively. Although each graph in (d)–(f) meets 2-degree anonymity, the adversary can easily re-identify the real identities of v9 and v2 by comparing the difference among three anonymized graphs. For instance, the adversary is convinced that v9 is a newly added node at timestamp t2 by observing Gt1′ and Gt2′, and v2 is a deleted node at timestamp t3 by observing Gt2′ and Gt3′. Similarly, the adversary can infer that the edge (v5,v7) is a newly added edge at timestamp t2 by observing Gt1′ and Gt2′. Suppose the adversary knows that Alice is a new user added to the graph Gt2 at timestamp t2, he can re-identify v9 as Alice. In the same way, the real identity of v2 and the real connection of (v5,v7) can also be completely re-identified by him.

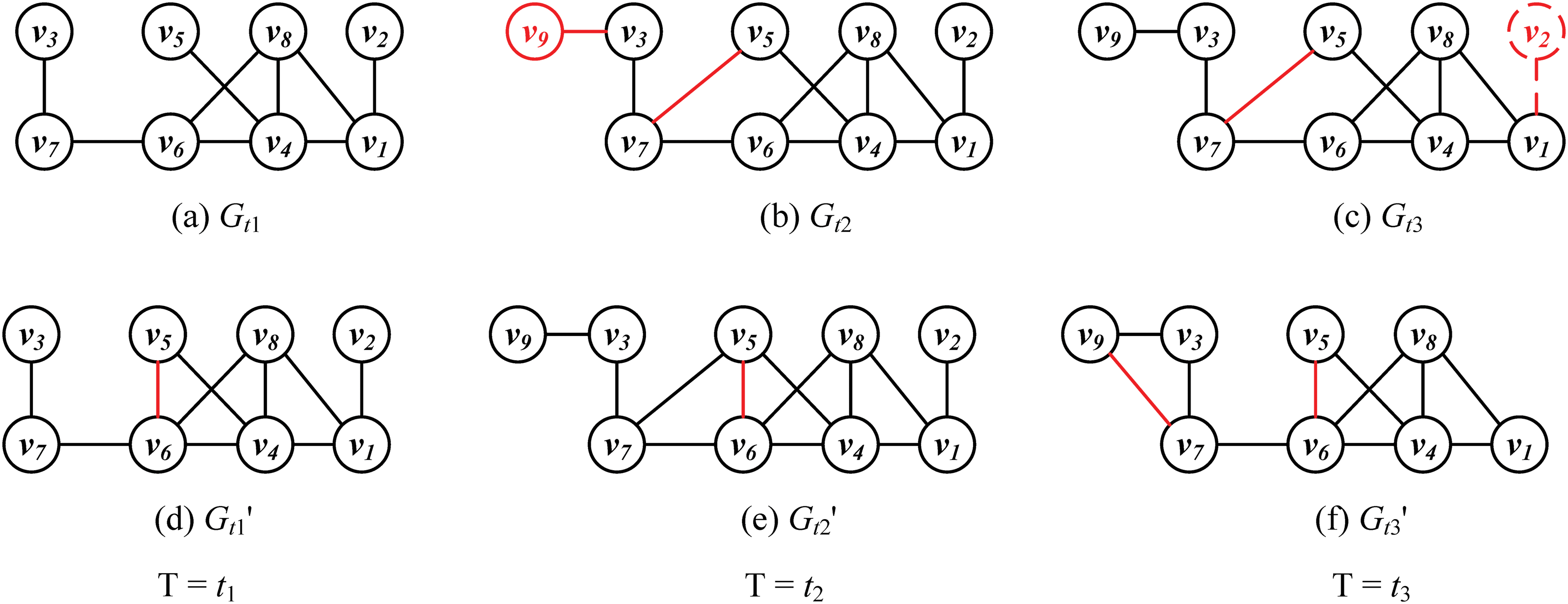
Figure 1: A 2-degree anonymous graph sequence is published during the time periods t1∼t3. (a)–(c) are three original graphs corresponding to three timestamps, respectively, and (d)–(f) are their anonymized graphs. The node v9 is a newly added node at timestamp t2, v2 is a deleted node at time t3, and (v5,v7) is a newly added edge at timestamp t2

3.2 Problem Definition

Problem statement. Given w undirected and unlabeled graphs {Gt1,⋯,Gtw} during the time periods t1∼tw, and {Gt1′,⋯,Gtw′} are their anonymized graphs. No third party or service provider can re-identify a user’s sensitive information from w anonymized graphs. However, the third party can still perform graph-related analysis and mining tasks.

This paper considers the protection of the original graph structure, so we first detect communities of the original graph at each timestamp. Then, based on graph isomorphism and graph automorphism, we obtain w anonymized graphs. Since the graph automorphism method reflects the symmetry of the graph, it can effectively resist re-identification attacks from adversaries due to the indistinguishability of the graph structure. Therefore, we anonymize community subgraphs by the graph automorphism method at each timestamp, preserving both nodes’ identities and real edge relationships. Graph isomorphism is a more generalized form of graph automorphism. We protect real edge relationships between communities through isomorphic anonymization, ensuring the indistinguishability of these edge relationships for adversaries. The definitions of graph isomorphism and graph automorphism are provided below:

Definition 1 (Graph isomorphism). Let G(V,E) and G′(V′,E′) be two graphs. G is isomorphic to G′, if and only if there exists a bijective function f:V→V′, such that for each edge (vi,vj)∈E, there is an edge (f(vi),f(vj))∈E′.

Definition 2 (Graph automorphism). Given a graph G(V,E), an automorphism of G is an bijective function h on the node set V, such that for each edge (vi,vj)∈E, the edge (h(vi),h(vj))∈E. In other words, a graph automorphism maps the graph to itself, preserving the edge relationships between nodes under the function h.

For an automorphic community subgraph, its anonymity level depends on the number of isomorphic subgraphs (i.e., k) within it. A k-automorphic graph is defined as follows:

Definition 3 (K-automorphic graph). Given a graph G′(V′,E′), G′ is called a k-automorphic graph if two conditions are met for each node vi′∈V′: a) There exists k−1 automorphic functions {h1,⋯,hk−1} of G′, and b) hp(vi′)≠hq(vj′), where vi′≠vj′,p≠q.

In this paper, we achieve the anonymous publishing of w original graphs. Thus, we give the definition of anonymous publishing of dynamic graphs as follows:

Definition 4 (Anonymous publishing of dynamic graphs). Let {Gt1(Vt1,Et1),…,Gtw(Vtw,Etw)} be w original graphs during the time periods t1∼tw, where Vti is the set of nodes in Gti, and Eti is the set of edges. We say that {Gt1′(Vt1′,Et1′),⋯,Gtw′(Vtw′,Etw′)} are anonymized graphs corresponding to the w original graphs if there exists a dynamic graph anonymization mechanism M, such that: a) Vti→Vti′,Eti→Eti′, and b) Vti∩M(Vti)≠∅,Eti∩M(Eti)≠∅, where M(Vti) represents the set of nodes in Gti′, and M(Eti) represents the set of edges in Gti′. These w anonymized graphs are then sequentially published to a third party for data analysis.

4  The DSNGA-CSP Scheme

This section introduces the proposed DSNGA-CSP scheme in detail. As shown in Fig. 2, DSNGA-CSP mainly consists of the following two stages:

Phase 1: Dynamic initial anonymity. In this phase, all nodes in Gt1 are first detected as multiple disjoint communities through the CDME algorithm [24]. To preserve more original graph structure at the initial timestamp, we perform intra-community and inter-community anonymity, respectively. This paper effectively resists the re-identification attack on nodes’ identities and edge relationships in the following way. For intra-community anonymity, each community subgraphs are anonymized by the proposed k-composition anonymity method. For inter-community anonymity, the original edges between communities are anonymized by an edge isomorphism method.

Phase 2: Dynamic changing anonymity. For each updated timestamp, all nodes in the original graph are detected as multiple disjoint communities using the DCDME algorithm [24]. Based on the changes in community structure caused by changed nodes and edges mentioned in [24], we divide the detected communities into three categories: 1) Communities not involving changed nodes and edges (NonCC_NonNE); 2) Communities involving changed nodes and edges, while not changing community structure (NonCC_NE); 3) Communities involving changed nodes and edges, and changing community structure (ChanC_NE). For intra-community anonymity, 1) the community subgraphs corresponding to NonCC_NonNE are anonymized by obtaining their anonymized community subgraphs at the last timestamp; 2) the community subgraphs corresponding to NonCC_NE are anonymized by achieving k-automorphism along with the newly added nodes and edges; 3) the community subgraphs corresponding to ChanC_NE are anonymized by the proposed k-composition anonymity method. For inter-community anonymity, follows the dynamic initial anonymity stated.

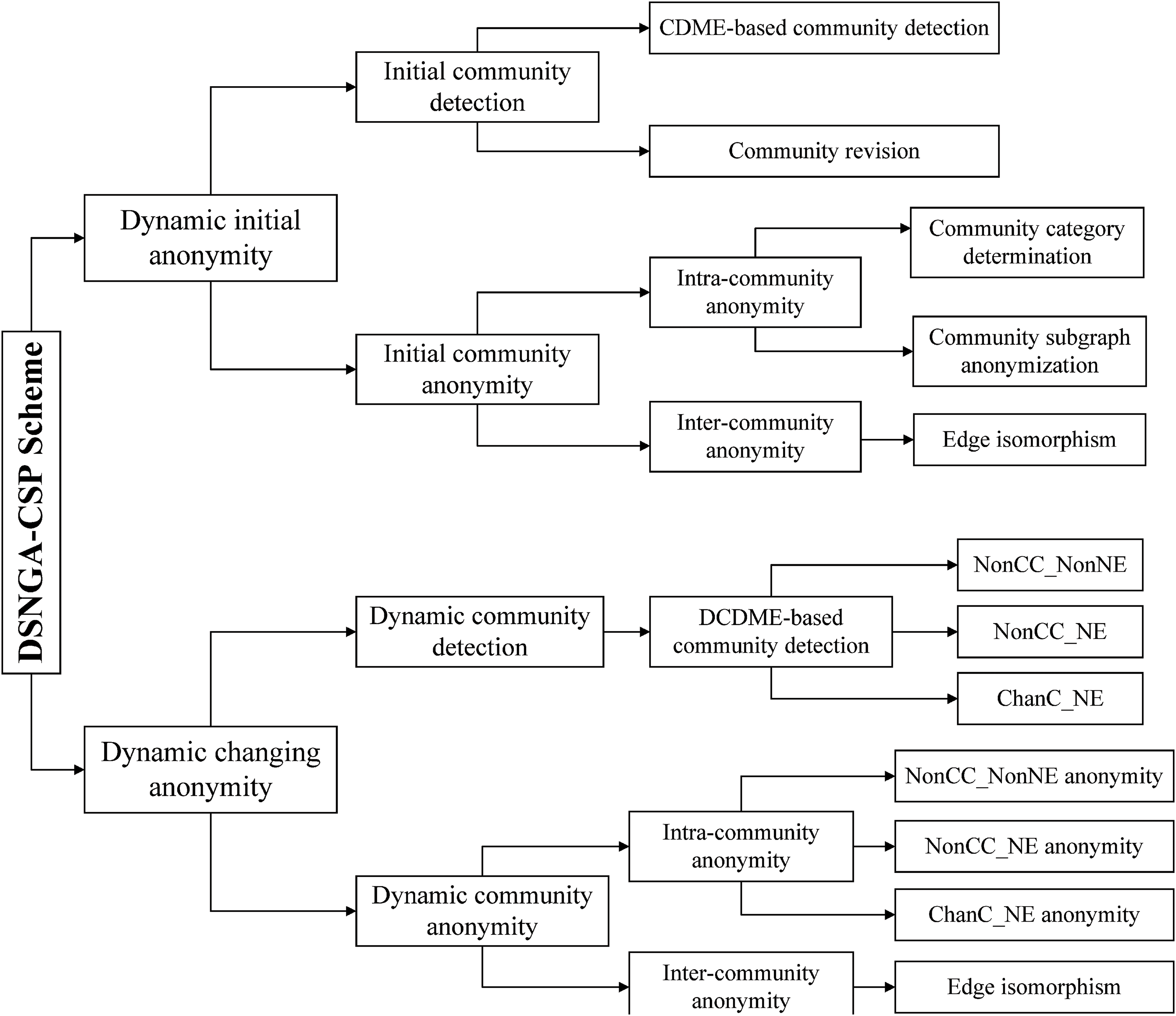
Figure 2: The flowchart of DSNGA-CSP

4.1 Dynamic Initial Anonymity

In this section, the anonymized graph Gt1′ is obtained at the initial timestamp t1. The anonymization process is detailedly described in the following two subsections: initial community detection and initial community anonymity.

4.1.1 Initial Community Detection

The CDME algorithm [24] is used to detect the community structure of Gt1, and the detected communities are recorded as Ct1∗={Ct1_1∗,⋯,Ct1_m∗}, where m is the total number of communities. Due to the anonymity requirement of subsequent community subgraphs, each community needs to contain at least k nodes. Thus, the communities in Ct1∗ are revised by two methods: adding fake nodes and merging invalid communities. Assume the communities that need to be revised are Ct1_inv∗={Ct1_inv_1∗,⋯,Ct1_inv_p∗}, where p is the number of these communities. Two methods are detailed below:

1) For the first method, if the number of nodes in a community Ct1_inv_i∗,i∈{1,⋯,p} is higher than the number of fake nodes needed to be added, fake nodes are added to Ct1_inv_i∗ until the number of nodes reaches k.

2) For the second method, if the number of nodes in Ct1_inv_i∗ is not greater than the number of fake nodes needed to be added, Ct1_inv_i∗ is merged with a community Ct1_mer∗ belonging to the rest of Ct1∗. To reduce the loss of community structure of Gt1, this method selects Ct1_mer∗ that has the most connected edges with Ct1_inv_i∗. If the number of nodes in the merged community is still less than k, the merged community continues to implement the above two methods until its number is met.

At the initial timestamp, we assume the ultimately detected communities are represented as Ct1={Ct1_1,⋯,Ct1_l}, where l is the number of communities. In addition, we assume Gt1∗ is a graph that only consists of all community subgraphs, excluding edge connections between them.

4.1.2 Initial Community Anonymity

This subsection anonymizes all community subgraphs corresponding to Ct1 (i.e., intra-community anonymity) and edge relationships between these communities (i.e., inter-community anonymity). The intra-community anonymity involves two steps: community category determination and community subgraph anonymization. The first step divides the detected communities into three categories by Algorithm 1, and the second step anonymizes community subgraphs formed by these three categories of communities, respectively. The inter-community anonymity is achieved by an edge isomorphism method described in Algorithm 4.

The key steps of Algorithm 1 are: 1) Since the graph partitioning method can affect the utility of the anonymized graph directly, this paper partitions all community subgraphs by two graph partitioning algorithms [25]: METIS_PartGraphKway and METIS_PartGraphRecursive (lines 1–2). 2) We determine the category of the current community based on k. If a community can be partitioned into k blocks by the above two algorithms, we use a common subgraph computation function in a network graph arithmetic package (e.g., igraph) to obtain two common subgraphs of k block subgraphs from two types of partitioning. The scales of these two common subgraphs are then computed using the function Scale(⋅), respectively. If the two scales are equal, the category of this community is decided by a characteristic of the METIS program. Ultimately, the detected communities are divided into three categories: non-partitioned communities, kway-partitioned communities, and recursive-partitioned communities (lines 3–27).

Function Scale(⋅): The function is used to compute the scale of common subgraph Gcomm1 or Gcomm2, i.e., the sum of the number of nodes and edges in Gcomm1 or Gcomm2. Here, the Scale(⋅) function serves as a metric to measure the overall size of Gcomm1 or Gcomm2, and it is applicative to measure different characteristics for different types of networks or applications, such as density or cohesion.

Three categories of community subgraphs are anonymized as follows:

a) For each community in Ct1non, the nodes are pairwise connected to obtain the anonymized community subgraph. Assume the anonymized community subgraphs related to Ct1non are recorded as CGt1non_a={CGt1_1non_a,⋯,CGt1_l1non_a}.

b) For each community in Ct1kwa and Ct1rec, the community subgraph is anonymized by the proposed k-composition anonymity method. The k-composition anonymity method involves three key phases: partition, isomorphism, and composition. To facilitate the understanding, a community Ct1_ikwa,i∈1,2,⋯,l2 in Ct1kwa is selected as a case to introduce the process of k-composition anonymity. Assume the anonymized community subgraphs related to these two categories of communities are recorded as CGt1kwa_a={CGt1_1kwa_a,⋯,CGt1_l2kwa_a} and CGt1rec_a={CGt1_1rec_a,⋯,CGt1_l3rec_a}, respectively.

In the partition phase, Ct1_ikwa is partitioned into k blocks by the METIS_PartGraphKway algorithm, and the partitioned blocks are represented as Bt1_ikwa={Bt1_i_1kwa,⋯,Bt1_i_kkwa}.

In the isomorphism phase, k block subgraphs corresponding to Bt1_ikwa achieve isomorphism anonymization. Algorithm 2 presents the process, and the key steps involved are: 1) Rank the nodes in each block using the function Rank(⋅)., and record them in order (line 1). 2) Obtain the adjacency matrices of k blocks and compute their sum (lines 2–15). 3) To ensure the utility of anonymized block subgraphs, we use the function Inf_edg(⋅) to compute the influence of original edges, selecting those with higher influence for isomorphism anonymization in each block, thereby minimizing the addition of fake edges. (lines 16–26). 4) After performing the above steps, BGt1_ikwa_a (i.e., k block anonymized subgraphs) is obtained (line 27).

Function Rank(⋅): Based on depth-first search, the function ranks nodes in BGt1_i_jkwa(j=1,⋯,k) using node degrees. To facilitate isomorphism anonymization for inter-block edges, the node with the most cross edges (i.e., edges connecting different blocks) is ranked first, and it and the backtracking node (labeled as 0) are recorded in a list. Then, using depth-first traversal, we select the neighbor of the current node with the highest degree as the next to be ranked and traverse it, recording both nodes in the list. If all neighbors have been visited, the backtracking node becomes the new current node; otherwise, the unvisited neighbor with the highest degree is selected next. This process continues until all nodes in BGt1_i_jkwa are visited, obtaining the ranked block BGt1_i_jkwa. This ranking facilitates consistent node ordering, crucial for effective isomorphism anonymization.

Function Inf_edg(⋅): The function is used to obtain highly influential edges in Gt1∗. It computes edge influence by two metrics [26]: NC, the number of triangles an edge participates in, and MNP, the number of shortest paths traversing the edge. The influence of one edge is computed as NC∗(MNP+1) [26]. The top 50% of edges with the highest influence are then recorded in matrix math_e. This ensures that influential edges are preserved, thereby maintaining the utility of the anonymized subgraphs.

In the composition phase, the inter-block crossing edges achieve isomorphism anonymization. Algorithm 3 describes the details, and the key steps involved are: 1) Obtain all inter-block crossing edges (lines 1–5). 2) For each cross edge, find the mapping positions of its two endpoints in the two blocks. Then, connect two nodes with the same mapping positions in the other pairs of blocks with the same block interval (lines 6–18). 3) After anonymizing all crossing edges, the anonymized community subgraph corresponding to Ct1_ikwa is obtained as CGt1_ikwa_a (line 19).

Algorithm 4 describes the process of inter-community anonymity. The edges between non-partitioned communities, as well as those between non-partitioned communities and partitioned communities, achieve the inter-community 2-isomorphism anonymity. The edges between partitioned communities achieve the inter-community k-isomorphism anonymity. In practice, since the nodes within communities are densely connected and sufficiently numerous, almost all community subgraphs can be partitioned into k blocks. Thus, in essence, the edges between communities achieve k-isomorphism anonymity. In this paper, the anonymization of edges between three categories of communities is introduced as follows:

1) Obtain all the edges between communities (lines 1–5). 2) The edges between three categories of communities achieve isomorphism anonymity, respectively (lines 6–25).

i) The edges between non-partitioned communities are anonymized by the function Ef_nn(⋅). The function divides nodes involved in Elnon_non into two node sets according to the involved two non-partitioned communities, and the node set with the smaller number is supplemented by adding other nodes from the corresponding community. Based on the degree (i.e., the number of edges involved Elnon_non) of nodes, two node sets are ranked in ascending order to achieve the same node mapping. Then, two pairs of nodes with the same mapping are connected in Gt1∼.

ii) The edges between non-partitioned and partitioned communities are anonymized by the function Ef_nb(⋅). For each edge in Elnon_b, the position of an endpoint within its belonging block is found, and then the current edge is added to Gt1∼. If other edges in Elnon_b meet: a) an endpoint of the edge has the same position index; b) two endpoints of the edge are not connected in Gt1∼, these edges are also added to Gt1∼. The remaining nodes in the current non-partitioned community are sequentially connected with nodes in other blocks with the same mapping position.

iii) The edges between partitioned communities are anonymized by the function Ef_bb(⋅). For each edge in Elb_b, the positions of two endpoints within their belonging blocks are found, and the subsequent anonymization process is similar to that of Ef_nb(⋅).

3) Obtain the anonymized graph Gt1′ of Gt1 at the initial timestamp t1 (line 26).

4.2 Dynamic Changing Anonymity

In this section, the anonymized graph Gti′ is obtained at timestamp ti,i=2,⋯,w, and the anonymization process includes two steps: dynamic community detection and dynamic community anonymity.

4.2.1 Dynamic Community Detection

This section detects multiple disjoint communities at timestamp ti, and the detected communities are divided into three categories: NonCC_NonNE,NonCC_NE,ChanC_NE.

Before detecting communities, the isomorphic nodes and edges related to removed nodes and edges at timestamp ti are first removed from Gti. The reason is to prevent the adversary from re-identifying the real identities of removed nodes and real edge relationships through two anonymized graphs at adjacent timestamps. Assume the current original graph is Gti∗ after removing all isomorphic nodes and edges related to removed nodes and edges from Gti. Based on dynamic community detection mentioned in [24], we divide the detected communities from Gti∗ into three categories as follows:

1) The original graph structure may cause changes from these cases: adding nodes between communities, adding edges between communities, deleting nodes in a community, deleting nodes between communities, and deleting edges in a community. Thus, the subgraph formed by these changes at timestamp ti is re-detected communities using the DCDME algorithm [24], and the detected communities are recorded as Cti3∗={Cti_13∗,⋯,Cti_ht33∗}, where ht3 is the number of communities in Cti3∗. Then, all communities in Cti3∗ are revised by two methods mentioned in initial community detection, and the revised Cti3∗ is recorded as ChanC_NE:Cti3={Cti_13,⋯,Cti_h33}, where h3 is the number of communities in Cti3.

2) The original graph structure may not cause changes from these cases: adding edges in a community, adding nodes in a community, and deleting edges between communities. Since some communities involved in the above changes have satisfied the requirement for the number of nodes within the community at the timestamp ti−1. Thus, these communities are recorded as NonCC_NE:Cti2={Cti_12,⋯,Cti_h22}, where h2 is the number of communities in Cti2.

3) The remaining communities involved nothing about changed nodes/edges are recorded as NonCC_NonNE:Cti1={Cti_11,⋯,Cti_h11}, where h1 is the number of communities in Cti1.

Assume the communities at timestamp ti are recorded as Cti=Cti1∪Cti2∪Cti3. Similarly, according to Algorithm 1, these communities are also divided into three categories: Ctinon={Cti_1non,⋯,Cti_L1non},Ctikwa={Cti_1kwa,⋯,Cti_L2kwa}, and Ctirec={Cti_1rec,⋯,Cti_L3rec}, where L1+L2+L3=h1+h2+h3.

4.2.2 Dynamic Community Anonymity

For the communities in Cti, this subsection achieves both intra-community anonymity and inter-community anonymity to obtain the anonymized graph Gti∼ at timestamp ti.

For intra-community anonymity, the community subgraphs formed by Cti1, Cti2, and Cti3 achieve k-automorphic anonymity, respectively, and the process is as follows:

1) For each community in Cti1, the community subgraph is anonymized by finding the anonymized community subgraph corresponding to the community at the last timestamp. Assume these anonymized community subgraphs are recorded as CGti1_a={CGti_11_a,⋯,CGti_h11_a}.

2) For each community in Cti2, the community subgraph is anonymized by the process presented in Algorithm 5, and the key steps involved are: 1) Obtain newly added nodes for each community in Cti2 (lines 1–2). 2) Determine the category of the current community, and then anonymize the community subgraph according to three different cases (lines 3–26). 3) Obtain all anonymized community subgraphs corresponding to Cti2 (line 27). Assume these anonymized community subgraphs are recorded as CGti2_a={CGti_12_a,⋯,CGti_h22_a}.

3) For each community in Cti3, the community subgraph is anonymized by applying k-composition anonymity method directly. Assume these anonymized community subgraphs are recorded as CGti3_a={CGti_13_a,⋯,CGti_h33_a}.

For inter-community anonymity, the edges between communities in Cti1, Cti2, and Cti3 are achieved isomorphic anonymization, and the process is as follows:

1) Merge CGti1_a, CGti2_a, and CGti3_a into the graph Gti∼.

2) Since the community subgraphs formed by Cti1 and Cti2 are neither split nor merged, the edges between these communities are anonymized by taking their anonymized state at the last timestamp into Gti∼. The removed edges between communities in Cti1 and Cti2 do not exist in Gti, so their isomorphic edges are not added to Gti∼. This prevents adversaries from re-identifying these removed edges due to their indistinguishability from their isomorphic edges.

3) The communities in Cti3 are re-detected, so the inter-community edges related to these communities are anonymized in the same way as the anonymization of inter-community edges at the initial timestamp (see Algorithm 4).

4.3 Information Loss

This section provides a new information loss metric. The main reason is: 1) the single graph metric cannot fully measure the information loss of an anonymized graph; 2) current research on measuring the utility of anonymized graphs is almost only from a single perspective, which is the difference between the anonymized graph and the original graph. Thus, we define a new metric from two perspectives: original information preservation and anonymous information change. The former measures the retention of original information in the anonymized graph, while the latter measures the information changes required to achieve anonymity. To unify measurement, this paper takes the inverse of anonymous information change and combines it with original information preservation to determine the information loss of an anonymized graph. The higher the defined metric, the smaller the distortion of the anonymized graph.

Definition 5 (Information loss). At timestamp ti, given a graph Gti, and Gti′ is the anonymized graph of Gti. The information loss ILti consists of two parts: original information preservation IRti and anonymous information change ICti. ICti is determined by two factors: NCti and ECti, which represent the node difference and edge difference between the original graph and the anonymized graph, respectively. ILti is calculated as follows:

ILti=IRti+1ICti(1)

IRti=12(|∪j=1nNGti(vj)∩NGti′(vj)|∑j=1ndegGti(vj)+|∪j=1nNGti(vj)∩NGti′(vj)|∑j=1ndegGti′(vj))(2)

ICti=NCti+ECti(3)

NCti=|ND(Gti′)∪ND(Gti)|−|ND(Gti′)∩ND(Gti)|(4)

ECti=|E(Gti′)∪E(Gti)|−|E(Gti′)∩E(Gti)|(5)

where NGti(vj) is the neighbors of node vj in Gti, NGti′(vj) is the neighbors of vj in Gti′, ND(Gti) and E(Gti) are all nodes and edges in Gti, respectively, and ND(Gti′) and E(Gti′) are all nodes and edges in Gti′, respectively.

According to Definition 5, the information loss of the anonymized graphs over w timestamps is calculated as follows:

IL=1w∑i=1wILti(6)

For IL, it reflects the average information loss of w anonymized graphs during the time periods t1∼tw. And the larger IL, the better the average utility of w anonymized graphs.

4.4 Privacy Analysis

This section proves that DSNGA-CSP can achieve the anonymity of dynamic social network graphs. Specifically, we prove that anonymized graphs obtained by DSNGA-CSP over w timestamps guarantee the anonymization of nodes’ identities and edge relationships in dynamic original graphs, which can effectively resist re-identification attacks from adversaries. The theorem states as follows:

Theorem 1. Let G={Gt1,⋯,Gtw} be w original graphs during the time periods t1∼tw, G′={Gt1′,⋯,Gtw′} is w anonymized graphs obtained by DSNGA-CSP. For each anonymized graph Gti′, the intra-community anonymity achieves k-automorphism, and the inter-community anonymity achieves k-isomorphism.

Proof of Theorem 1. Taking Gti′(i∈{1,⋯,w}) as an example. At timestamp ti,Gti is first detected as multiple disjoint communities. We first prove that the intra-community anonymity of Gti′ achieves k-automorphism. For communities in Cti1, each community subgraph is anonymized by finding its corresponding anonymized subgraph at timestamp ti−1. Since these anonymized community subgraphs were already k-automorphic at timestamp ti−1, the intra-community anonymity of Cti1 satisfies k-automorphism. For communities in Cti2, the anonymity of these community subgraphs satisfies k-automorphism, and the reasons are as follows: 1) Each newly added node belonging to Ctinon is connected pairwise with other nodes in the current community to achieve k-automorphic anonymity. 2) Newly added nodes/edges belonging to Ctikwa or Ctirec are first assigned to k partitioned blocks at timestamp ti−1, and then these k blocks are performed isomorphism and composition algorithms to achieve k-automorphic anonymity of the current community. For communities in Cti3, the anonymity of community subgraphs formed by these communities also satisfies k-automorphism. Since these communities are re-detected at timestamp ti, the community subgraphs formed by Ctinon,Ctikwa, and Ctirec are re-anonymized in the same way with the perturbation of the initial graph. The intra-community anonymity at the initial timestamp satisfies k-automorphism, so the intra-community anonymity related to these communities also satisfies k-automorphism. Next, we prove that the inter-community anonymity of Gti′ achieves k-isomorphism. As described in Algorithm 4, almost all inter-community edges achieve k-isomorphism at the initial timestamp. The inter-community edges related to Cti1 and Cti2 are anonymized by retaining their k-isomorphic state at timestamp ti−1, and the inter-community edges related to Cti3 are re-anonymized to satisfy k-isomorphism. In summary, the anonymized dynamic graphs obtained by DSNGA-CSP satisfy intracommunity k-automorphism and inter-community k-isomorphism. □

According to Theorem 1, this section provides the probability that the anonymized dynamic graphs defend against re-identification attacks, and the lemma is described as follows:

Lemma 1. DSNGA-CSP can resist re-identification attacks from adversaries. If an adversary only has access to a real node and its edge information within the community or real edge information between communities, the probability that he re-identifies the node’s identity and edge relationships does not exceed 1/k.

Proof of Lemma 1. Given w anonymized graphs G′={Gt1′,⋯,Gtw′} during the time periods t1∼tw. For an intra-community real node and its edge information, or inter-community real edge information, we can always find k−1 other information in Gti′(i={1,⋯,w}) matching them. Thus, assume that a query function Q is used to search an intra-community subgraph structure in Gti′. If the query result R(Gti′,Q) is not empty, there always exists k identical results in R(Gti′,Q). The adversary cannot re-identify the identity of the node and its edge relationships from the subgraph structure with a probability greater than 1/k. Similarly, the probability that the adversary re-identifies inter-community edge relationships does not exceed 1/k. □

5  Experiments and Analysis

In this section, the effectiveness of the proposed DSNGA-CSP scheme is evaluated through experimental comparison and analysis. Section 5.1 introduces datasets. Section 5.2 presents metrics. Section 5.3 explores the performance of DSNGA-CSP.

5.1 Datasets

Five real-world datasets are used in this paper, consisting of two static graph datasets and three dynamic graph datasets. The primary reason for choosing these datasets is their extensive use in prior studies, making them suitable benchmarks for comparison. The two static datasets, with well-documented properties and distinct community structures, help evaluate the effectiveness of our anonymization method in protecting community structures. The three dynamic datasets cover diverse social network scenarios, with varying time spans and edge changes. Shorter time span datasets simulate frequent social changes, while longer ones evaluate performance under long-term dynamics. These datasets allow us to test DSNGA-CSP’s effectiveness, particularly in resisting re-identification attacks and ensuring utility across different temporal characteristics. The statistics and properties of these datasets are presented in Tables 2 and 3, respectively.

Static graph datasets

1) Ca-GrQc [27]: a collaboration network about Arxiv General Relativity. It denotes an author vp co-authored a paper with author vq if there exists an undirected edge from vp to vq.

2) Ca-HepTh [27]: a collaboration network about Arxiv High Energy Physics Theory. An undirected edge (vp,vq) in this graph indicates that an author vp has co-authored a paper with author vq.

Dynamic graph datasets

1) Infectious SocioPatterns [28]: an infectious socio patterns dynamic contact network. An edge (vp,vq) in this graph represents close-range face-to-face proximity between the concerned persons. This paper selects data from the first half of May in 2009 as the dataset Inf_SocPatterns_1, and the second half of May and the first half of June of the same year as the dataset Inf_SocPatterns_2.

2) Email-Eu-core-temporal [29]: an email communication network spanning 803 days. An edge (vp,vq,ti) in this graph represents a person vp who sent an e-mail to person vq at time ti.

3) CollegeMsg [30]: a college messaging temporal network spanning 193 days. An edge (vp,vq,ti) in this graph represents a user vp who sent a private message to the user vq at time ti.

Data preprocessing. To better evaluate DSNGA-CSP, the aforementioned datasets are preprocessed by the following steps: 1) Converting directed graphs to undirected graphs; 2) Removing duplicate edges and loops; 3) Avoiding publishing impractical graphs with very few edges at certain timestamps, each of three dynamic graphs is split into 20 new graphs by merging continuous raw graphs, and all generated new graphs have a similar number of edges.

5.2 Metrics

This section introduces utility metrics and a privacy metric, which are used to evaluate the performance of anonymized graphs obtained by DSNGA-CSP. The utility metrics include two categories: graph analysis metrics and community structure metrics. The first focuses on general graph characteristics, while the second focuses on graph structural features. The first focuses on general graph characteristics to ensure fundamental structural properties like connectivity and centrality are preserved, which is essential for maintaining graph utility in various network analyses. The second focuses on graph structural features, key features representing clusters of users with similar interests or strong interactions. Preserving these structures ensures the anonymized graph remains useful for community-related studies. The privacy metric measures the uncertainty within the anonymized graph, quantifying the difficulty for adversaries to re-identify nodes or infer relationships. These metrics comprehensively evaluate both utility and privacy, providing a well-rounded understanding of the effectiveness of DSNGA-CSP. The metrics used in this paper are as follows:

Graph analysis metrics

1) Average Path Length (APL): the metric measures the average length of all shortest paths in a graph.

2) Average Clustering Coefficient (ACC): the metric is the average of the local clustering coefficients of nodes in a graph, quantifying how close the neighbors of a node are to being a clique.

3) Eigenvector Centrality (EC): the metric quantifies the importance of a node in a graph, and it depends on the neighbors connected with the node. To avoid the influence of acyclic graphs, a constant is added to the denominator position for subsequent error rate calculation.

4) Transitivity (T): the metric measures the number of triangles in a graph.

5) Average Degree (AVD): the metric measures the average degree of all nodes in a graph.

Community structure metrics

The community structure metrics used include: variation of information (VI) [31], adjusted rand index [32], normalized mutual information (NMI) [31], rand index [33], and modularity (mod) [34]. For VI and mod, the optimal value is 0, while for the rest, 1 is the optimal value. To better understand the results of the evaluation, metrics with an optimal value of 1 are inverted. Therefore, the smaller the measurement of these community structure metrics, the smaller the structural changes in the anonymized graph. Moreover, the first four metrics usually require that the two graphs being measured have the same nodes. Thus, we use the induced subgraph of the original and anonymized graphs with the same nodes to approximately measure these metrics.

Privacy metric

The privacy of the anonymized graph is assessed using a metric (i.e., Shannon entropy [35]) introduced in our previous work [36]. Entropy can be used to measure the uncertainty of the anonymized graph, thereby quantifying the degree to which the original graph is anonymized. If the anonymized graph has high uncertainty, it also has high privacy.

5.3 Experimental Evaluation

Implementation. To verify whether community structure protection can enhance the utility of anonymized graphs, we first evaluate our anonymization method on two static graph datasets, under scenarios involving community detection and those without. We then evaluate the performance of DSNGA-CSP on two dynamic graph datasets. All experiments are conducted on a PC with an Intel Core i5-10500 CPU, 64 GB RAM, and Windows 10 operating system. All schemes are achieved using the R programming language.

Competitors. We compare two static graph anonymity schemes using the k-composition anonymity method. One scheme, DC, detects the communities of the original graph and then performs k-composition anonymity for each community, while the other, Non−DC, applies k-composition anonymity directly to the original graph without community detection. Then, the proposed DSNGA-CSP scheme is compared with two dynamic graph anonymity schemes TAKG and CTKGA reported in [8] and [9], respectively. Since DSNGA-CSP focuses on anonymity in dynamic undirected graphs, it is compared with TAKG and CTKGA applied to undirected graphs.

5.3.1 Experimental Evaluation on Static Graphs

For graph analysis metrics, an error rate between the anonymized graph and the original graph is computed to measure the utility of the anonymized graph. This error rate reflects the degree to which the anonymized graph is close to the original graph based on these metrics. Moreover, the smaller the error rate, the better the utility of the anonymized graph. The average error rate at different anonymity levels is calculated as follows:

Error_rate=1kc∑j=1kc|Mj′−Mj|Mj(7)

where kc is the number of anonymity level k(k∈{2,5,10,15,20}), Mj is the result of a graph analysis metric for the original graph at the j-th anonymity level, and Mj′ is the corresponding result for the anonymized graph at the same anonymity level.

Figs. 3–6 present the experimental results of two categories of graph analysis metrics on two static graph datasets Ca-GrQc and Ca-HepTh. The horizontal axis represents the measured metrics. For graph analysis metrics, the vertical axis represents Error_rate, while for community structure metrics, it represents the average measurement error between original and anonymized graphs at different anonymity levels k.

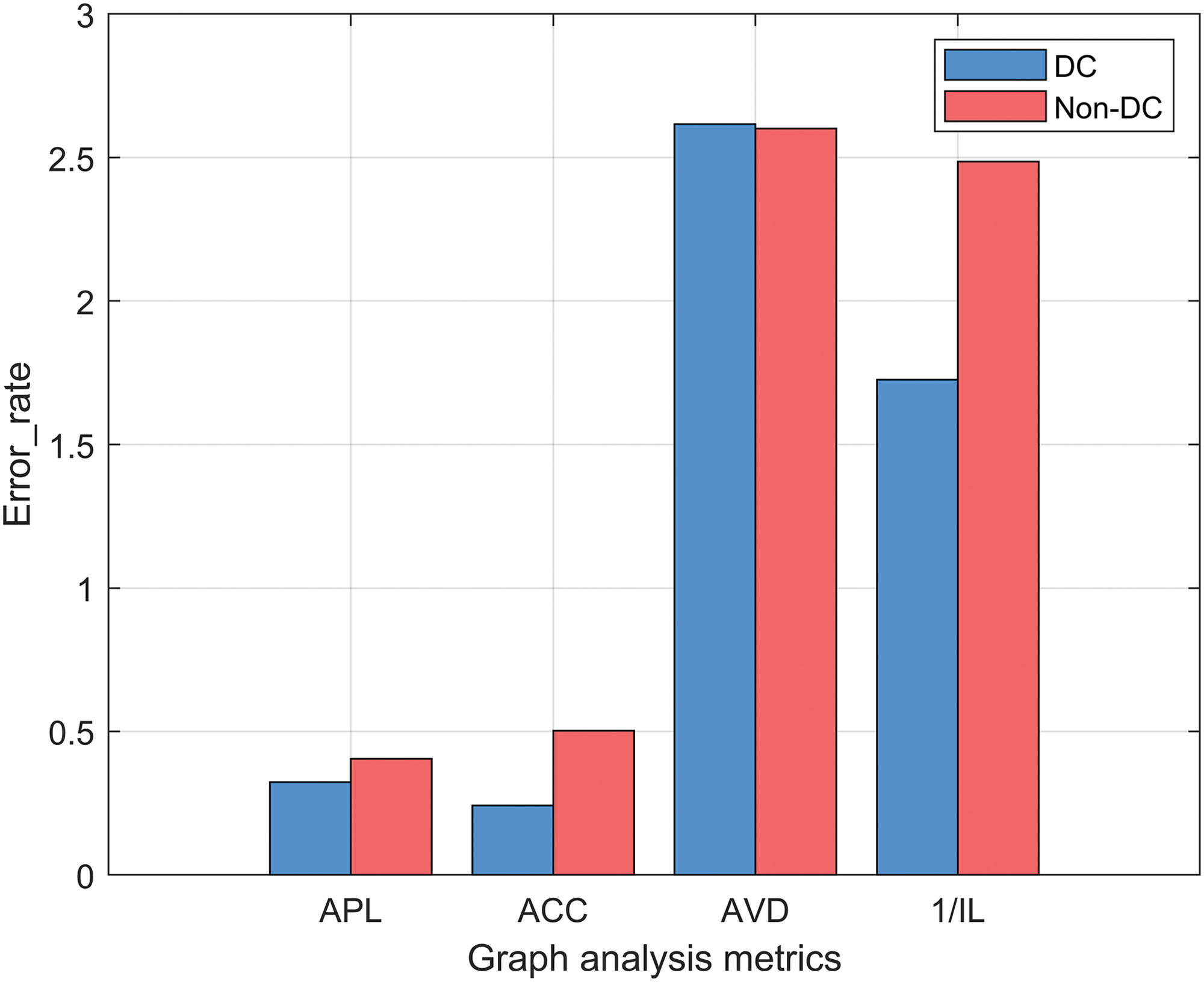
Figure 3: Comparison of Error_rate on Ca-GrQc dataset

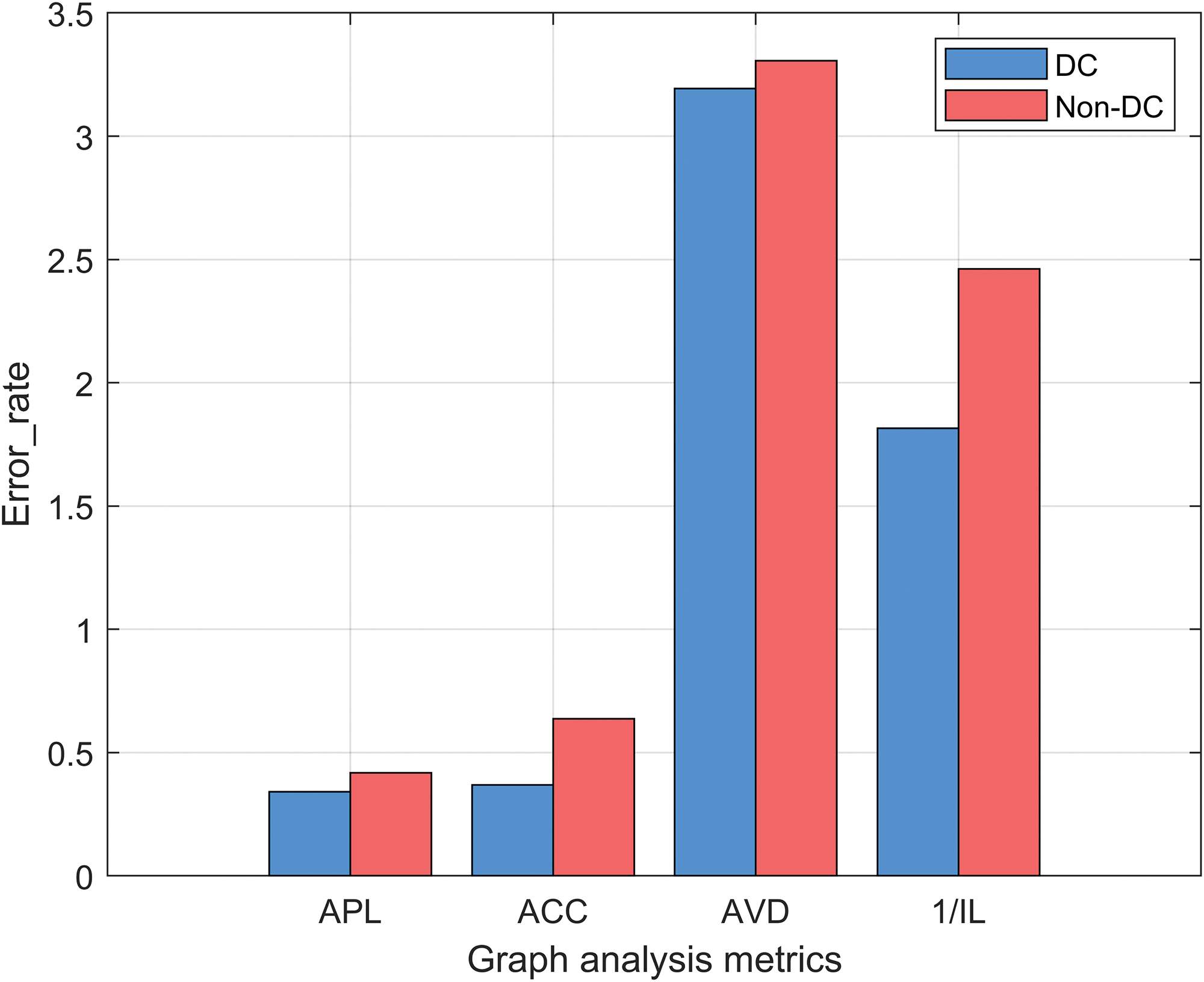
Figure 4: Comparison of Error_rate on Ca-HepTh dataset

Figure 5: Comparison of community structure metrics on Ca-GrQc dataset

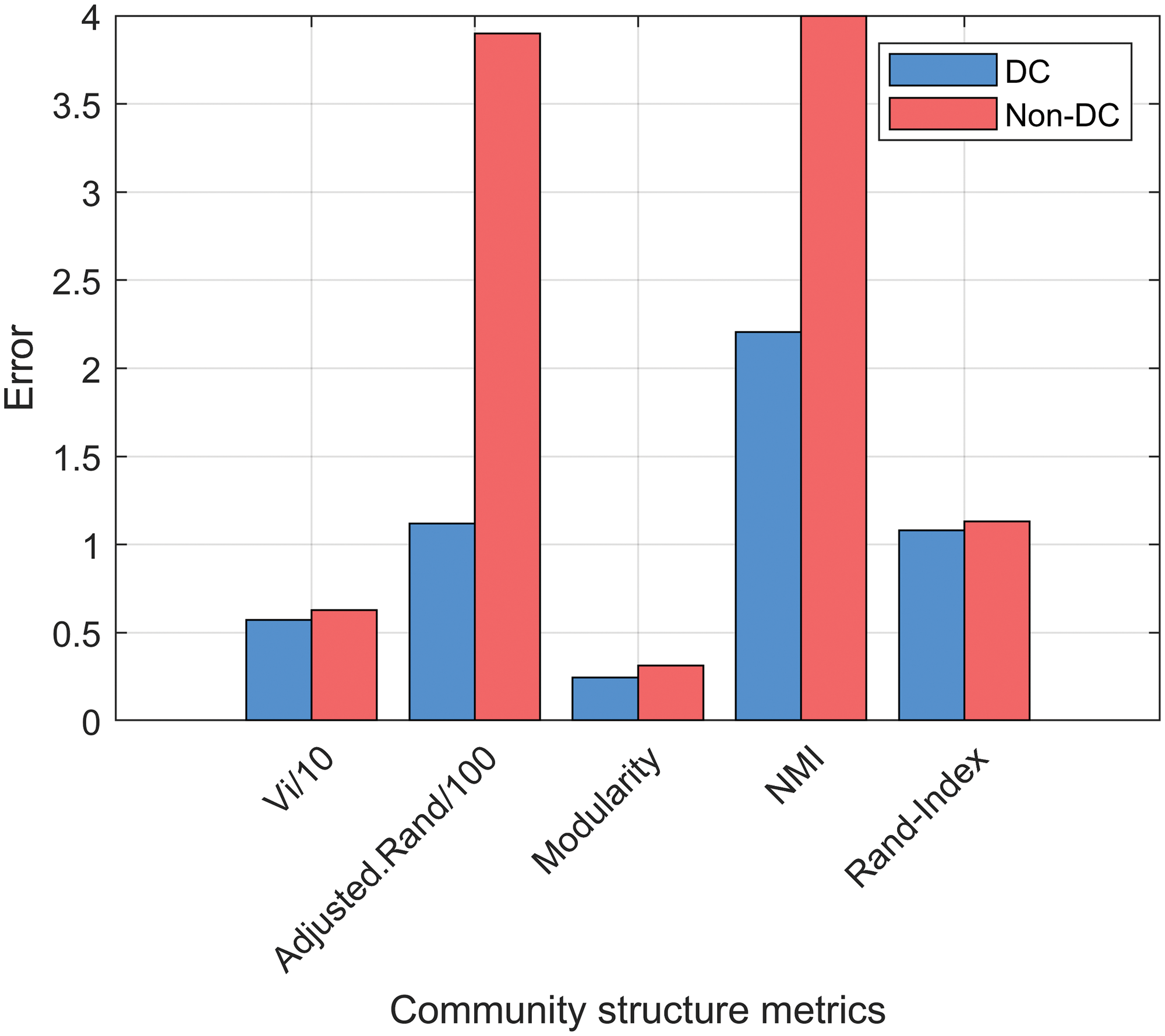
Figure 6: Comparison of community structure metrics on Ca-HepTh dataset

Graph analysis metrics results. As shown in Figs. 3 and 4, the results of DC are almost entirely superior to those of Non–DC. In the Ca-GrQc dataset, the result of DC is slightly higher than that of Non–DC in terms of AVD. This is because both intra-community and inter-community edges need to achieve isomorphic anonymization in DC, which may result in more changes in nodes’ degrees. However, due to the fairly close results, the measurement difference between the two schemes can be negligible.

Community structure metrics results. As shown in Figs. 5 and 6, all results of DC are superior to those of Non–DC. It indicates that k-composition anonymity under community detection can effectively reduce the destruction of structural features of the original graph.

5.3.2 Experimental Evaluation on Dynamic Graphs

For graph analysis metrics, refer to the description in Section 5.3.1. In this paper, since the anonymization of dynamic graphs sequentially publishes 20 anonymized graphs for each dataset, the average error rate for each graph analysis metric is calculated as follows:

Error_rate=120∗kc∑j=1kc∑i=120|Mj_ti′−Mj_ti|Mj_ti(8)

where Mj_ti is the result of a graph analysis metric at timestamp ti for the original graph at the j–th anonymity level, and Mj_ti′ is the corresponding result for the anonymized graph at the same anonymity level and timestamp. Meanwhile, this study selects k∈{2,5,10,15,20} for the first two datasets, and k∈{2,5,7,10,15} for the latter two datasets.

For four dynamic graph datasets, Figs. 7–10 present the experimental results of graph analysis metrics, Figs. 11–14 present the experimental results of community structure metrics, and Fig. 15 presents the experimental results of the privacy metric. For graph analysis metrics and community structure metrics, the presentation of coordinate axes refers to 5.3.1. For privacy metric, the horizontal axis represents datasets, and the vertical axis represents the average entropy at different timestamps and anonymity levels k.

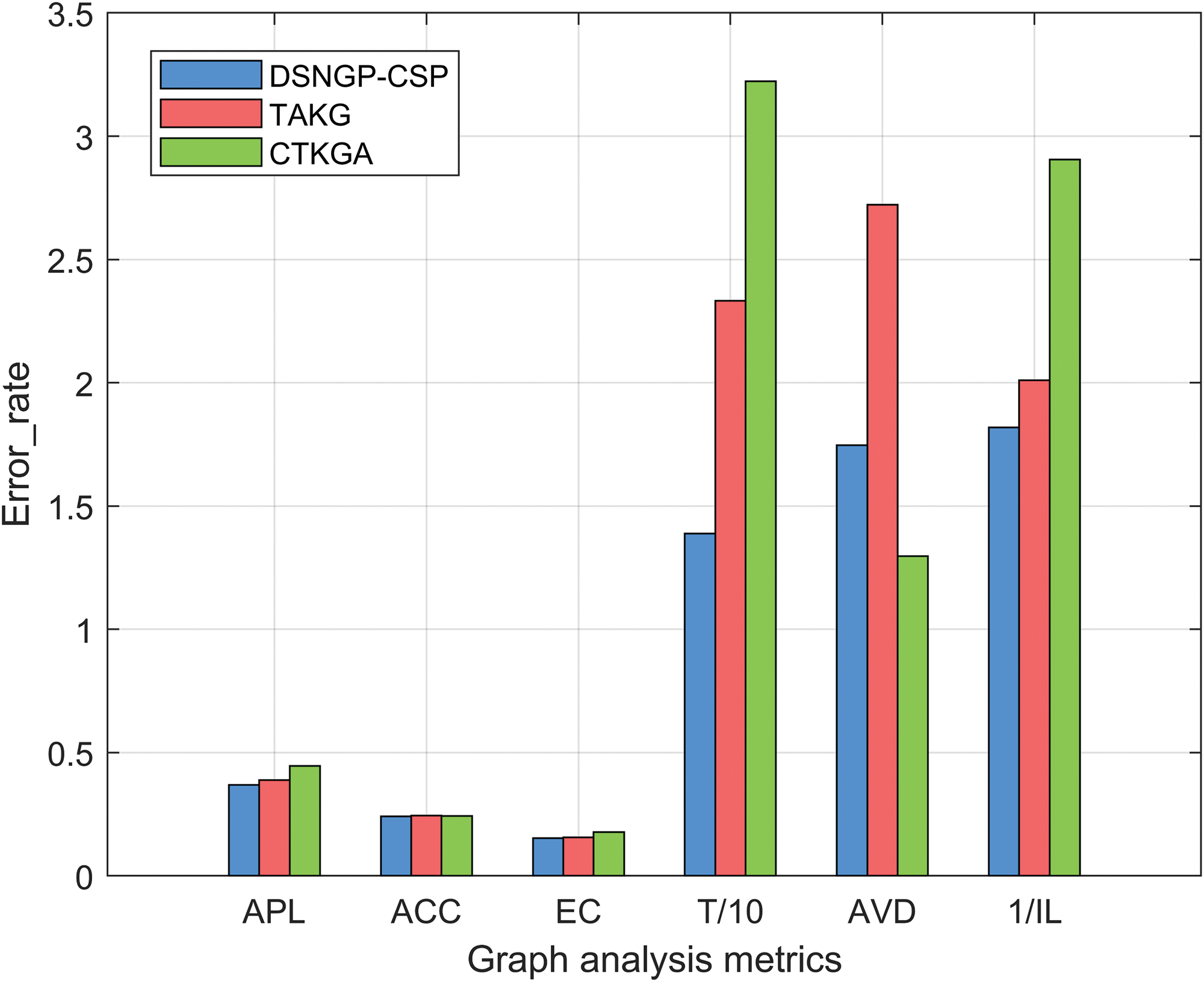
Figure 7: Comparison of Error_rate on Inf_SocPatterns_1 dataset

Figure 8: Comparison of Error_rate on Inf_SocPatterns_2 dataset

Figure 9: Comparison of Error_rate on CollegeMsg dataset

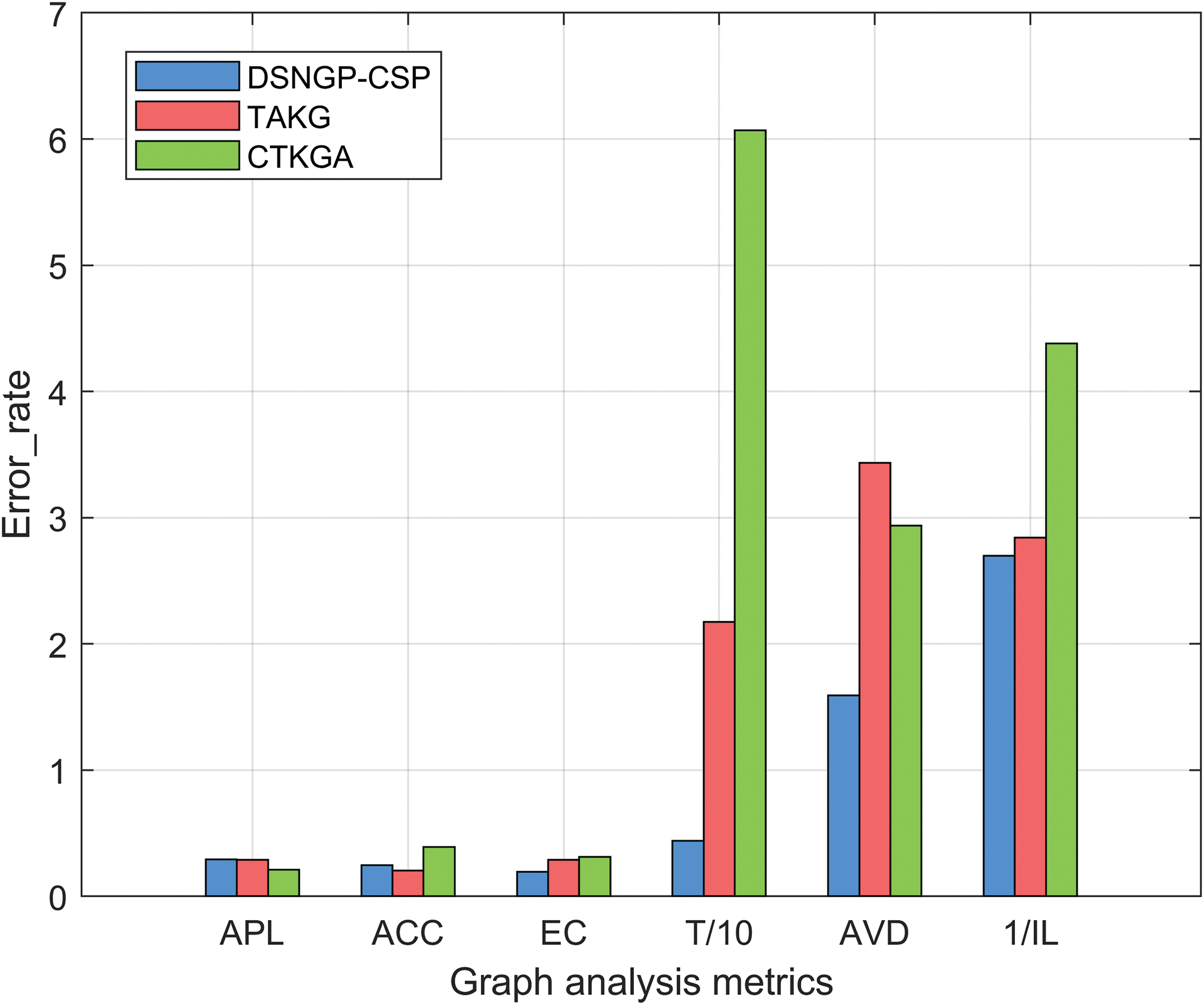
Figure 10: Comparison of Error_rate on Email-Eu-core-temporal dataset

Figure 11: Comparison of community structure metrics on Inf_SocPatterns_1 dataset

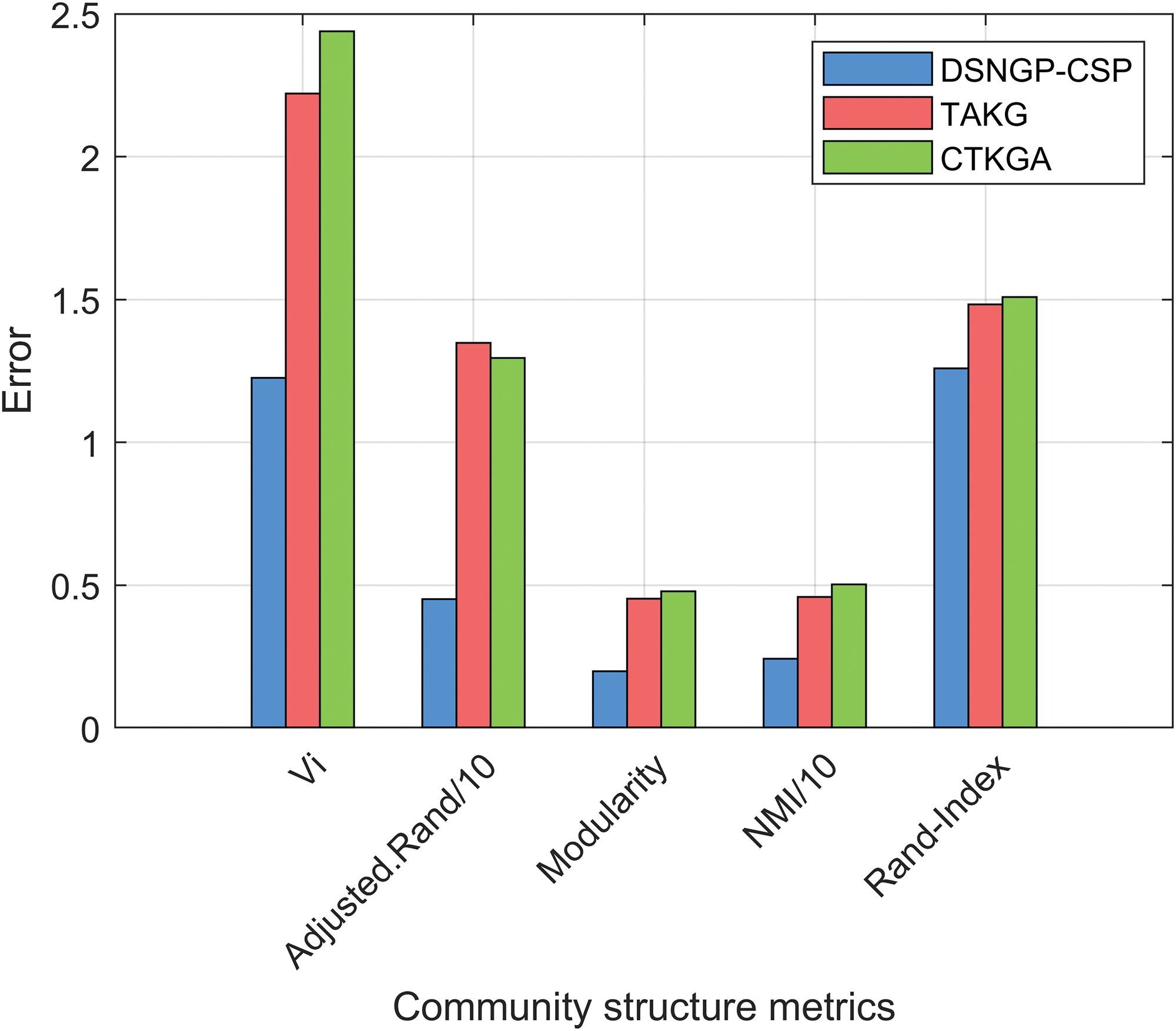
Figure 12: Comparison of community structure metrics on Inf_SocPatterns_2 dataset

Figure 13: Comparison of community structure metrics on CollegeMsg dataset

Figure 14: Comparison of community structure metrics on Email-Eu-core-temporal dataset

Figure 15: Comparison of Shannon entropy metric on four dynamic graph datasets

Graph analysis metrics results. Similar results are presented in Figs. 7 and 8 because the datasets used come from the same dynamic graph dataset. For ACC and EC, the results of DSNGA-CSP are close to those of TAKG and CTKGA. For APL, the result of DSNGA-CSP is better than that of CTKGA but slightly inferior to that of TAKG. The reason is that DSNGA-CSP removes more edges when anonymizing edges between three different categories of communities. For T and IL, DSNGA-CSP shows better results compared to TAKG and CTKGA. Notably, DSNGA-CSP maintains a number of triangles in the anonymized graph closest to the original graph, and the results of IL show that DSNGA-CSP causes fewer changes in nodes and edges compared to TAKG and CTKGA during anonymization. For AVD, the result of DSNGA-CSP is lower than that of TAKG but higher than that of CTKGA. This is because CTKGA clusters nearly all nodes in the original graph into groups with the size of k, allowing each node to achieve anonymity with fewer changes for its degree.

As shown in Fig. 9, for APL, the result of DSNGA-CSP is lower than that of CTKGA but slightly higher than that of TAKG, with similar analysis to that mentioned above. For the remaining metrics, the results of DSNGA-CSP show significant advantages compared with those of TAKG and CTKGA. In Fig. 10, DSNGA-CSP shows a slight disadvantage for the results of APL, but it does not significantly impact the utility of the anonymized graph. For ACC, the result of DSNGA-CSP is lower than that of CTKGA but slightly higher than that of TAKG. This is because TAKG achieves isomorphism of intra-cluster nodes by connecting all node pairs within each cluster, leading to tighter connections between intra-cluster nodes and their neighbors. However, the excessive addition of fake edges may significantly reduce the utility of the anonymized graph. For other metrics, the results of DSNGA-CSP are superior to those of TAKG and CTKGA.

Community structure metrics results. As shown in Figs. 11–14, nearly all results of DSNGA-CSP are superior to those of TAKG and CTKGA, with only a few results being close. Overall, DSNGA-CSP performs better for all community structure metrics. Additionally, it demonstrates that DSNGA-CSP can preserve more structural features of the original graph when achieving anonymous publishing of dynamic graphs. This also validates that dynamically protecting the community structure can enhance the utility of anonymized dynamic graphs.

Privacy metric results. As shown in Fig. 15, DSNGA-CSP outperforms TAKG and CTKGA on four datasets. This is because TAKG and CTKGA produce anonymized graphs where nodes have similar features, leading to smaller differences in intra-cluster and inter-cluster information. This increases the likelihood that an adversary can identify original information. Moreover, although clustering more groups in TAKG and CTKGA can make re-identification attacks more difficult, the privacy of the anonymized graphs obtained by these two schemes is inferior to that of DSNGA-CSP, due to the homogenized network structure and increased non-significant information in the anonymized graphs.

6  Discussion, Implication and Study Limitation

Summary of DSNGP-CSP. In this study, we propose a novel dynamic social network graph anonymity scheme, DSNGP-CSP, which demonstrates significant improvements in privacy protection and graph utility. Our experiments show that DSNGP-CSP effectively maintains community structures, while reducing the risk of privacy breaches compared to existing methods like TAKG and CTKGA. These findings indicate that incorporating community structure preservation into dynamic graph anonymization can enhance both privacy and graph utility, thereby overcoming a major limitation of traditional static anonymization methods.

Implications. The implications of our research are broad. Our method can be directly applied to social network platforms that need to publish anonymized graph data for research purposes, while still preserving user privacy. Furthermore, by integrating community structure preservation, our approach can also help improve the quality of downstream tasks, such as recommendation systems and social network analysis, which often rely on graph structure quality.

Study Limitations. There are two limitations in our work. Firstly, our approach relies on the pre-defined parameter k, which may limit adaptability across different types of social networks and may cause inappropriate partitioning of some community subgraphs, affecting the effectiveness of graph structure protection. Here, we envision an adaptive mechanism that involves setting a reasonable privacy threshold and quantifying network characteristics using metrics like community density and average degree. The value of k could then be adjusted based on how closely these quantified features align with the set threshold. This would make the scheme more flexible for various network types. Additionally, our approach has limitations when handling large-scale datasets, which impacts its scalability and performance. As the size of social network data grows, the computational overhead for community detection and edge anonymization becomes increasingly demanding. This limitation highlights the need for developing efficient optimization strategies or employing distributed computing techniques. These improvements would ensure that DSNGP-CSP can effectively scale to very large networks while maintaining performance and utility.

7  Conclusions and Future Work

This paper proposes DSNGA-CSP, a scheme for publishing dynamic social network graphs while preserving community structure based on k-automorphism. DSNGA-CSP detects three categories of communities at each timestamp and only partitions community subgraphs for a specific category at updated timestamps, avoiding a complex and cumbersome anonymization process. By detecting communities at each timestamp, we anonymize community subgraphs using a proposed k-composition method and inter-community edges using edge isomorphism, thereby achieving dynamic protection of community structures. Additionally, we introduce a novel information loss metric that measures graph utility based on original information preservation and anonymous information changes, providing a more precise metric for evaluating the utility of published dynamic graphs. Experimental results demonstrate that DSNGA-CSP outperforms other state-of-the-art methods in generating anonymized dynamic graphs with high utility and privacy.

Despite the advantages of k-anonymity in dynamic graph publishing, it still has limitations in protecting user privacy comprehensively, including vulnerability to sophisticated re-identification attacks and dependency on parameter k for privacy levels. Differential privacy, known for its robust mathematical guarantee, can offer a high level of privacy protection without relying on a single parameter to determine the privacy level, and it resists sophisticated adversarial attacks by adding random noise to nodes or edges. Hence, our future work will explore how to protect the privacy of dynamic social network graphs using differential privacy technology.

Acknowledgement: None.

Funding Statement: This work is supported by the Natural Science Foundation of China (No. U22A2099) and the Innovation Project of Guangxi Graduate Education (YCBZ2023130).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Yuanjing Hao; data collection: Mingmeng Zhang; analysis and interpretation of results: Yuanjing Hao, Xuemin Wang, Long Li; draft manuscript preparation: Yuanjing Hao, Liang Chang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are openly available in Stanford Large Network Dataset Collection at https://snap.stanford.edu/data/ (accessed on 25 November 2024).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. F. Ferri, P. Grifoni, and T. Guzzo, “New forms of social and professional digital relationships: The case of Facebook,” Soc. Netw. Anal. Min., vol. 2, no. 2, pp. 121–137, 2012. doi: 10.1007/s13278-011-0038-4. [Google Scholar] [CrossRef]

2. Y. Li, M. Purcell, T. Rakotoarivelo, D. Smith, T. Ranbaduge and K. S. Ng, “Private graph data release: A survey,” ACM Comput. Surv., vol. 55, no. 11, pp. 1–39, 2023. doi: 10.1145/3569085. [Google Scholar] [CrossRef]

3. A. Hoang, B. Carminati, and E. Ferrari, “Cluster-based anonymization of knowledge graphs,” in Applied Cryptography and Network Security, M. Conti, J. Zhou, E. Casalicchio, and A. Spognardi, Eds., Rome, Italy: Springer, 2020, vol. 12147, pp. 104–123. [Google Scholar]

4. R. K. Langari, S. Sardar, S. A. A. Mousavi, and R. Radfar, “Combined fuzzy clustering and firefly algorithm for privacy preserving in social networks,” Expert. Syst. Appl., vol. 141, 2020, Art. no. 112968. doi: 10.1016/j.eswa.2019.112968. [Google Scholar] [CrossRef]

5. H. Huang, D. Zhang, F. Xiao, K. Wang, J. Gu and R. Wang, “Privacy-preserving approach PBCN in social network with differential privacy,” IEEE Trans. Netw. Serv. Manag., vol. 17, no. 2, pp. 931–945, 2020. doi: 10.1109/TNSM.2020.2982555. [Google Scholar] [CrossRef]

6. X. Jian, Y. Wang, and L. Chen, “Publishing graphs under node differential privacy,” IEEE Trans. Knowl. Data Eng., vol. 35, no. 4, pp. 4164–4177, 2023. doi: 10.1109/TKDE.2021.3128946. [Google Scholar] [CrossRef]

7. N. Fu, W. Ni, S. Zhang, L. Hou, and D. Zhang, “GC-NLDP: A graph clustering algorithm with local differential privacy,” Comput. Secur., vol. 124, 2023, Art. no. 102967. doi: 10.1016/j.cose.2022.102967. [Google Scholar] [CrossRef]

8. A. Hoang, B. Carminati, and E. Ferrari, “Time-aware anonymization of knowledge graphs,” ACM Trans. Priv. Secur., vol. 26, no. 2, pp. 1–36, 2022. doi: 10.1145/3563694. [Google Scholar] [CrossRef]

9. A. T. Hoang, B. Carminati, and E. Ferrari, “Privacy-preserving sequential publishing of knowledge graphs,” in 37th IEEE Int. Conf. Data Eng. (ICDE), Chania, Greece, IEEE, 2021, pp. 2021–2026. [Google Scholar]

10. S. Zhang, W. Ni, and N. Fu, “Community preserved social graph publishing with node differential privacy,” 20th IEEE Int. Conf. Data Min. (ICDM), Sorrento, Italy: IEEE, 2020, pp. 1400–1405. [Google Scholar]

11. S. Xiang, D. Cheng, J. Zhang, Z. Ma, X. Wang and Y. Zhang, “Efficient learning-based community-preserving graph generation,” in 38th IEEE Int. Conf. Data Eng. (ICDE), Kuala Lumpur, Malaysia, IEEE, 2022, pp. 1982–1994. [Google Scholar]

12. S. Ranjkesh, B. Masoumi, and S. M. Hashemi, “A novel robust memetic algorithm for dynamic community structures detection in complex networks,” World Wide Web (WWW), vol. 27, no. 1, 2024, Art. no. 3. doi: 10.1007/s11280-024-01238-7. [Google Scholar] [CrossRef]

13. N. Xiang and X. Ma, “TKDA: An improved method for k-degree anonymity in social graphs,” in IEEE Symp. Comput.Commun. (ISCC), Rhodes, Greece, IEEE, 2022, pp. 1–6. [Google Scholar]

14. S. H. Lin and R. Xiao, “Towards publishing directed social network data with k-degree anonymization,” Concurr. Comput. Pract. Exp., vol. 34, no. 24, 2022, Art. no. e7226. doi: 10.1002/cpe.7226. [Google Scholar] [CrossRef]

15. H. Kaur, N. Hooda, and H. Singh, “k-anonymization of social network data using neural network and SVM: K-neurosvm,” J. Inf. Secur. Appl., vol. 72, 2023, Art. no. 103382. doi: 10.1016/j.jisa.2022.103382. [Google Scholar] [CrossRef]

16. J. Cheng, A. W. Fu, and J. Liu, “K-isomorphism: Privacy preserving network publication against structural attacks,” in Proc. ACM SIGMOD Int. Conf. Manage. Data (SIGMOD), Indianapolis, IN, USA: ACM, 2010, pp. 459–470. [Google Scholar]

17. H. Zhang, L. Lin, L. Xu, and X. Wang, “Graph partition based privacy-preserving scheme in social networks,” J. Netw. Comput. Appl., vol. 195, 2021, Art. no. 103214. doi: 10.1016/J.JNCA.2021.103214. [Google Scholar] [CrossRef]

18. X. Ren and D. Jiang, “A personalized (α,β,l,K)-anonymity model of social network for protecting privacy,” Wirel. Commun. Mob. Comput., vol. 2022, no. 1, 2022, Art. no. 7187528. [Google Scholar]

19. L. Zou, L. Chen, and M. T. Özsu, “K-automorphism: A general framework for privacy preserving network publication,” Proc. VLDB Endow., vol. 2, no. 1, pp. 946–957, 2009. doi: 10.14778/1687627.168773. [Google Scholar] [CrossRef]

20. X. Zhang, J. Liu, J. Li, and L. Liu, “Large-scale dynamic social network directed graph K-in&out-degree anonymity algorithm for protecting community structure,” IEEE Access, vol. 7, pp. 108371–108383, 2019. doi: 10.1109/ACCESS.2019.2933151. [Google Scholar] [CrossRef]

21. W. Ren, K. Ghazinour, and X. Lian, “kt-safety: Graph release via k-anonymity and t-closeness,” IEEE Trans. Knowl. Data Eng., vol. 35, no. 9, pp. 9102–9113, 2023. doi: 10.1109/TKDE.2022.3221333. [Google Scholar] [CrossRef]

22. G. S. Kumar, K. Premalatha, G. U. Maheshwari, and P. R. Kanna, “No more privacy concern: A privacy-chain based holomorphic encryption scheme and statistical method for privacy preservation of user’s private and sensitive data,” Expert. Syst. Appl., vol. 234, 2023, Art. no. 121071. doi: 10.1016/j.eswa.2023.121071. [Google Scholar] [CrossRef]

23. L. Sweeney, “k-anonymity: A model for protecting privacy,” Int. J. Uncertain. Fuzziness Knowl. Based Syst., vol. 10, no. 5, pp. 557–570, 2002. doi: 10.1142/S0218488502001648. [Google Scholar] [CrossRef]

24. Z. Sun et al., “Dynamic community detection based on the matthew effect,” Physica A, vol. 597, 2022, Art. no. 127315. doi: 10.1016/j.physa.2022.127315. [Google Scholar] [CrossRef]

25. G. Karypis and V. Kumar, “A fast and high quality multilevel scheme for partitioning irregular graphs,” SIAM J. Sci. Comput., vol. 20, no. 1, pp. 359–392, 1998. doi: 10.1137/S1064827595287997. [Google Scholar] [CrossRef]

26. M. Kiabod, M. N. Dehkordi, and B. Barekatain, “TSRAM: A time-saving k-degree anonymization method in social network,” Expert. Syst. Appl., vol. 125, pp. 378–396, 2019. doi: 10.1016/j.eswa.2019.01.059. [Google Scholar] [CrossRef]

27. J. Leskovec, J. M. Kleinberg, and C. Faloutsos, “Graph evolution: Densification and shrinking diameters,” ACM Trans. Knowl. Discov. Data., vol. 1, no. 1, 2007. doi: 10.1145/1217299.1217301. [Google Scholar] [CrossRef]

28. L. Isella, J. Stehlé, A. Barrat, C. Cattuto, J. Pinton and W. V. Den Broeck, “What’s in a crowd? analysis of face-to-face behavioral networks,” J. Theor. Biol., vol. 271, no. 1, pp. 166–180, 2011. doi: 10.1016/j.jtbi.2010.11.033. [Google Scholar] [CrossRef]

29. A. Paranjape, A. R. Benson, and J. Leskovec, “Motifs in temporal networks,” in Proc. Tenth ACM Int. Conf. Web Search Data Min. (WSDM), Cambridge, UK: ACM, 2017, pp. 601–610. [Google Scholar]

30. P. Panzarasa, T. Opsahl, and K. M. Carley, “Patterns and dynamics of users’ behavior and interaction: Network analysis of an online community,” J. Assoc. Inf. Sci. Technol., vol. 60, no. 5, pp. 911–932, 2009. doi: 10.1002/asi.21015. [Google Scholar] [CrossRef]

31. L. Danon, A. Díaz-Guilera, J. Duch, and A. Arenas, “Comparing community structure identification,” J. Stat. Mech., vol. 2005, no. 9, 2005, Art. no. P09008. doi: 10.1088/1742-5468/2005/09/P09008. [Google Scholar] [CrossRef]

32. L. Hubert and P. Arabie, “Comparing partitions,” J. Classif., vol. 2, pp. 193–218, 1985. doi: 10.1007/BF01908075. [Google Scholar] [CrossRef]

33. W. M. Rand, “Objective criteria for the evaluation of clustering methods,” J. Am. Stat. Assoc., vol. 66, no. 336, pp. 846–850, 1971. doi: 10.1080/01621459.1971.10482356. [Google Scholar] [CrossRef]

34. M. Kiabod, M. N. Dehkordi, and B. Barekatain, “A fast graph modification method for social network anonymization,” Expert. Syst. Appl., vol. 180, 2021, Art. no. 115148. doi: 10.1016/j.eswa.2021.115148. [Google Scholar] [CrossRef]

35. I. Wagner and D. Eckhoff, “Technical privacy metrics: A systematic survey,” ACM Comput. Surv., vol. 51, no. 3, pp. 1–38, 2018. [Google Scholar]

36. Y. Hao, L. Li, L. Chang, and T. Gu, “MLDA: A multi-level k-degree anonymity scheme on directed social network graphs,” Front. Comput. Sci., vol. 18, no. 2, 2024, Art. no. 182814. doi: 10.1007/s11704-023-2759-8. [Google Scholar] [CrossRef]