 Open Access
Open Access
ARTICLE
MATD3-Based End-Edge Collaborative Resource Optimization for NOMA-Assisted Industrial Wireless Networks
1 College of Information Engineering, Shenyang University of Chemical Technology, Shenyang, 110142, China
2 State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang, 110016, China
3 Key Laboratory of Networked Control Systems, Chinese Academy of Sciences, Shenyang, 110016, China
* Corresponding Author: Chi Xu. Email:
(This article belongs to the Special Issue: Advanced Communication and Networking Technologies for Internet of Things and Internet of Vehicles)
Computers, Materials & Continua 2025, 82(2), 3203-3222. https://doi.org/10.32604/cmc.2024.059689
Received 14 October 2024; Accepted 05 December 2024; Issue published 17 February 2025
Abstract
Non-orthogonal multiple access (NOMA) technology has recently been widely integrated into multi-access edge computing (MEC) to support task offloading in industrial wireless networks (IWNs) with limited radio resources. This paper minimizes the system overhead regarding task processing delay and energy consumption for the IWN with hybrid NOMA and orthogonal multiple access (OMA) schemes. Specifically, we formulate the system overhead minimization (SOM) problem by considering the limited computation and communication resources and NOMA efficiency. To solve the complex mixed-integer nonconvex problem, we combine the multi-agent twin delayed deep deterministic policy gradient (MATD3) and convex optimization, namely MATD3-CO, for iterative optimization. Specifically, we first decouple SOM into two sub-problems, i.e., joint sub-channel allocation and task offloading sub-problem, and computation resource allocation sub-problem. Then, we propose MATD3 to optimize the sub-channel allocation and task offloading ratio, and employ the convex optimization to allocate the computation resource with a closed-form expression derived by the Karush-Kuhn-Tucker (KKT) conditions. The solution is obtained by iteratively solving these two sub-problems. The experimental results indicate that the MATD3-CO scheme, when compared to the benchmark schemes, significantly decreases system overhead with respect to both delay and energy consumption.Keywords
The progression of wireless communication technology facilitates Industry 4.0, leveraging industrial wireless networks (IWNs) to boost the efficiency of conventional industries [1,2]. An increasing number of industrial end devices (iEDs) require instant processing for latency-sensitive and computational demanding tasks, driving the demand for advanced computation and communication resources. In traditional cloud computing, tasks are offloaded to cloud servers to compensate for the scarcity of computing resources. However, the quantity of data produced by numerous iEDs, when uploaded to the cloud server for computing, imposes a considerable strain on the network load. Thus, multi-access edge computing (MEC) has become a viable solution and is widely adopted in IWNs [3,4]. The deployment of MEC servers within industrial base stations (iBSs) effectively mitigates device resource constraints and significantly alleviates excessive pressure on network load [5].
While MEC is an effective solution to the lack of computation resources in iEDs, task offloading to MEC servers introduces latency and energy concerns. Traditional orthogonal multiple access (OMA) techniques are constrained by limited orthogonal communication resources, which largely hampers the number of devices that can be accommodated for industrial mission offloading [6,7]. Besides, non-orthogonal multiple access (NOMA) technology significantly mitigates delay and energy consumption issues. By enabling simultaneous data transmission among devices within the same resource block and using successive interference cancellation (SIC) to separate signals, NOMA surpasses OMA in supporting more devices [8]. Nevertheless, considering the constrained computation and communication resources, it is challenging to efficiently utilize the resources to reduce task processing latency and energy consumption in NOMA-assisted MEC systems. Alternatively, most current research leans heavily on centralized scheduling strategies. In contrast, multi-agent deep reinforcement learning (MADRL) is a promising distributed approach applied in IWNs for enhanced decision-making [9].
Existing literature often adopts single OMA or NOMA for MEC systems, where optimization theory or single-agent deep reinforcement learning (DRL) is employed for resource allocation. In contrast, this paper combines OMA and NOMA technology and employs multi-agent DRL (MADRL) for joint task offloading and resource allocation. Specifically, this paper constructs an IWN model based on hybrid multiple access schemes with respect to OMA and NOMA, and formulates the system overhead minimization (SOM) problem. Accordingly, we combine the multi-agent twin delayed deep deterministic policy gradient (MATD3) and convex optimization, namely MATD3-CO for iterative optimization.
The key achievements in this paper can be summarized as follows:
• We study an end-edge collaborative computing scenario for IWNs with hybrid multiple access schemes with respect to OMA and NOMA, where iEDs covered by multiple iBSs share the total system bandwidth resources. Task offloading rate is improved by considering the factors affecting NOMA efficiency, i.e., sub-channel allocation, intra-edge interference, and inter-edge interference.
• With full consideration of resources and NOMA efficiency, the SOM problem is formulated in terms of sub-channel allocation, task offloading ratio and computation resource allocation. To tackle this mixed-integer non-convex problem, we divide it into two sub-problems, i.e., joint sub-channel allocation and task offloading sub-problem, and computation resource allocation sub-problem.
• To approximate the optimal solution, we propose the MATD3-CO scheme. Specifically, we employ MATD3 to optimize the joint sub-channel allocation and task offloading sub-problem due to its non-convexity. Furthermore, we employ convex optimization to solve the computation resource allocation sub-problem, and derive the closed-form expression by the Karush-Kuhn-Tucker (KKT) condition. The solution is obtained by iteratively solving these two sub-problems.
The remaining work of this paper is as follows. Section 2 presents the related works. Section 3 describes the NOMA-assisted system model. Section 4 establishes the SOM problem. Section 5 proposes the MATD3-CO scheme. Section 6 evaluates the experimental outcomes, and Section 7 summarizes this work.
In recent years, numerous studies offered solutions to the technical hurdles faced by NOMA-assisted MEC systems. For instance, Ding et al. introduced a generic hybrid NOMA-MEC offloading strategy. They considered two special OMA and pure NOMA offloading scenarios to minimize both delay and energy consumption in MEC offloading process [10]. Albogamy et al. devised an efficient conjugate gradient-based approach for optimizing downlink power allocation in NOMA systems, maximizing the maximum weighted sum rate across users [11]. Besides, Muhammed et al. explored the intricacies of allocating resources in downlink NOMA networks. They significantly improved the energy efficiency of the system based on strict power constraints and quality of service (QoS) criteria [12]. Huang et al. assessed the effectiveness of three MEC offloading approaches: pure OMA, pure NOMA, and hybrid NOMA. Their findings highlighted the potential of hybrid NOMA in decreasing the energy consumption associated with MEC offloading [13]. Fang et al. developed a binary search algorithm to minimize delay in multi-user NOMA-assisted MEC systems through power allocation of data transmission [14]. Wu et al. optimized task allocation and resource scheduling in NOMA-MEC networks to minimize energy consumption, considering task delays and server capabilities [15]. Ding et al. optimized both power and time allocation simultaneously to lower the energy expenditure for computation offloading. Closed-form solutions guided the choice between OMA, pure NOMA, or hybrid NOMA [16]. Indeed, Wu et al. devised a distributed and efficient algorithm to reduce overall computation task latency by optimizing both offloaded workloads and transmission time concurrently in NOMA networks [17]. Pham et al. introduced collaborative game theory to resource optimization in NOMA MEC networks, minimizing both computational overhead through cooperative and competitive approaches [18]. Xu et al. developed a DRL-based multi-priority offloading strategy to minimize delay for MEC-enhanced IWNs with high-concurrent heterogeneous industrial tasks [19].
Moreover, MADRL [20] performed well in fully cooperative, competitive and mixed relationship scenarios. Yu et al. proposed a multi-agent deep deterministic policy gradient (MADDPG) framework to minimize the cost of task processing latency and device energy consumption by optimizing UAV routes and IoT device offloading decisions [21]. Luo et al. suggested a framework for mobile crowd computing in networks, utilizing physical layer security and MATD3 algorithm to optimize task offloading and assignment while minimizing computing costs [22]. Xu et al. proposed a digital twin-driven collaborative optimization scheme based on MADRL, which minimizes task processing time by optimizing task offloading ratio, power allocation, and resource allocation [23]. On this basis, Xu et al. further considered cache storage and blockchain consensus for digital twin-assisted MEC networks [24]. Cai et al. introduced a computation offloading method based on MADRL, aimed at meeting the diverse needs of various tasks in heterogeneous systems [25]. Li et al. proposed a MADRL framework aimed at minimizing weighted energy consumption in MEC networks, addressing communication and computation uncertainties by optimizing UAV trajectory, task partition, and resource allocation [26]. Xiao et al. developed a collaborative algorithm based MADRL aimed at optimizing resource allocation in MEC networks, surpassing existing mainstream methods in multiple aspects [27]. Cao et al. proposed a new MADRL scheme to support multi-channel communication and task computation in Industry 4.0 of MEC, significantly reducing task processing time and improving channel utilization [28]. Zhou et al. proposed a MADRL framework for collaborative optimization in MEC, which improves system performance, learning efficiency, and reliability by 50% through joint optimization of beam forming and offloading strategies [29].
Fig. 1 depicts the IWN with NOMA and OMA to support process monitoring and industrial control. There are
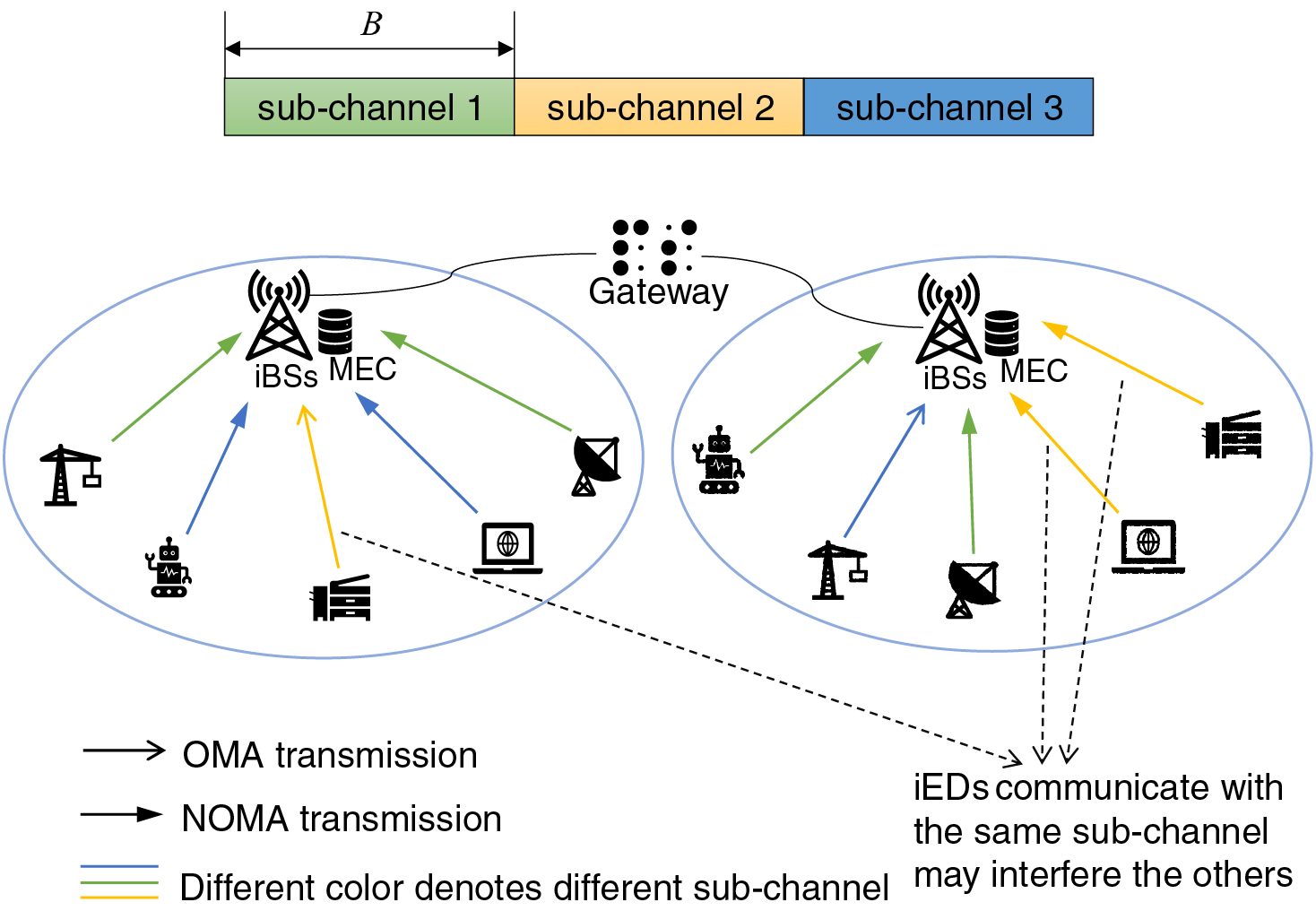
Figure 1: System model
Let time be slotted, denoted by
The communication model is constructed based on the NOMA principle, where the sub-channel allocation decision is denoted as
where
Let the transmission power of
where
According to the NOMA principle,
Let
where
Due to the constrained computation resources of iEDs, some tasks are offloaded to iBSs for edge computing. The task offloading ratio from
where
Let
Then, the energy consumption while computing the task partially at
where
In the computation offloading case, the primary components of the time needed to finish the computation task of
The completion time for
The energy consumption
where
4 Problem Formulation and Transformation
With the above system model, we further formulate the SOM problem. Firstly, we designate the system overhead as the weight sum of latency and energy consumption as
where
Then, the objective function is formulated by
Herein,
where
In the SOM problem, constraints (1)–(3) state that the sub-channel allocation, constraint (8) declares the proportion of tasks to be offloaded, and constraints (11) and (12) require that the overall allocation of computation resources cannot exceed the computation power of iESs.
Obviously, SOM is a mixed integer optimization problem that is NP-hard and typically requires exponential time complexity to find the optimal solution [32]. Moreover, since system dynamics over time generate a myriad of system states, it is challenging to implement one-time optimization strategies in practice. Thus, we reformulate the original problem as follows:
First, the SOM problem can be rewritten as
where
By analyzing (18), we find that the system overhead depends on the computation resource allocation
4.2.1 Joint Sub-Channel Allocation and Task Offloading Sub-Problem
4.2.2 Computation Resource Allocation Sub-Problem
5 The Proposed MATD3-CO Scheme
With the decoupled sub-problems, we develop MATD3-CO to approach the optimal solution. Fig. 2 depicts the framework for addressing the SOM problem.
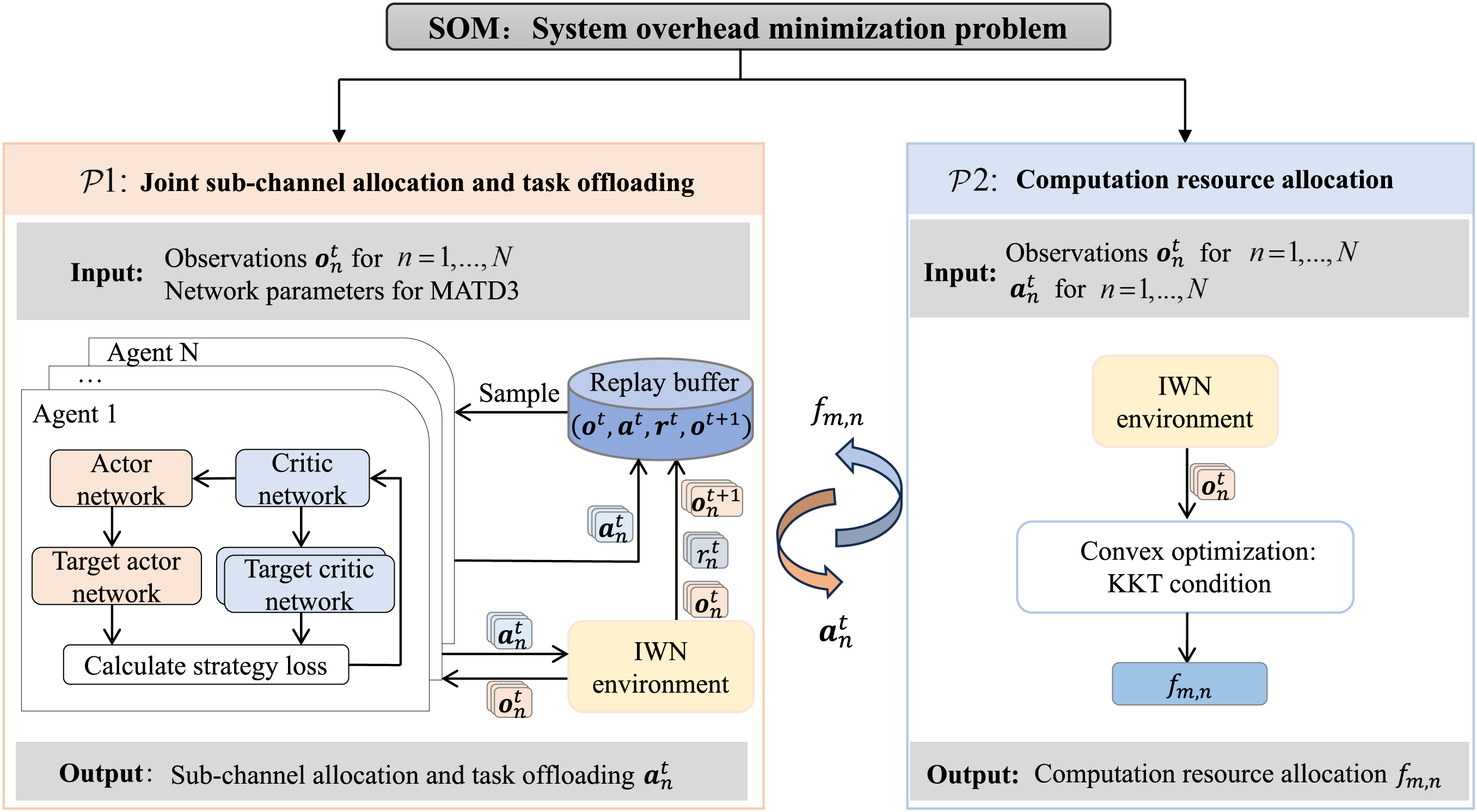
Figure 2: The framework to solve the SOM problem
For
5.1 Joint Sub-Channel Allocation and Task Offloading Based on MATD3
5.1.1 Multi-Agent MDP Modeling
In the IWN, we treat each iBS as an agent for its decision-making in order to obtain the minimum system overhead. The detailed three key elements of agent
1) Observation: At each time slot
where
2) Action: According to the current observations, each agent decides its sub-channel and offloading ratio strategy. The actions of agent
The set of actions for
3) Reward Function: In the multi-agent MDP scenario,
The set of rewards of
In MATD3, each agent aims to maximize its expected reward, represented by
To track the MDP, we employ DRL algorithm. First, TD3 is an improved version of deep deterministic policy gradient (DDPG), with enhanced stability and convergence compared to DDPG. Unlike DDPG, which only uses one Q-value network, the key of TD3 is the introduction of two independent critics trained to minimize the squared error between two different Q-values. Meanwhile, TD3 also incorporates techniques such as delay policy updates and target network smoothing, further enhancing the stability of the algorithm. By extending the TD3 to multi-agent environments, namely MATD3, we can facilitate the mean overestimation and error accumulation problems in the MADDPG. For this purpose, we use centralized training and distributed execution method, where centralized training enhances collaboration between agents by obtaining global data, while trained distributed execution agents make independent decisions based on local data.
Specifically, each iBS is considered as an agent that maintains its networks and learns individual policies based on local observations. Each agent comprises the following DNNs: a DNN implementing the actor
MATD3 is centralizedly trained by the industrial gateway, as summarized in Algorithm 1. Specifically, within this framework, critics of each agent are managed by the industrial gateway, which enables them to access global state and action information while ensuring full visibility of this information for all agents. All iBSs act as agents to perform actions through a decentralized observation mode, collect experience in interacting with the environment, and upload this experience to the industrial gateway for centralized training. The industrial gateway processes this data to calculate gradients, and then feeds back the updated model parameters to iBSs.

The training process of the neural network alternates with the interaction process. Each agent outputs an action
where
The actor network is updated in a delayed manner, i.e., updating the critic network many times before updating it, with an update cycle of
The target network is soft updated with an update cycle of
where
5.2 Computation Resource Allocation Based on Convex Optimization
The variables associated with all iBSs are independent. Therefore, we can further divide
where
Theorem 1.
Proof of Theorem 1. The partial derivatives of the objective function
where
We introduce the Lagrange multipliers
Based on the KKT condition, the following equation is obtained:
Solve the system of equations to get the optimal solution for task
5.3 Algorithmic Complexity Analysis
Since the computation resource allocation problem has a closed-form solution, the complexity originates primarily from MATD3, which is predominantly influenced by the neural network architecture and the sheer quantity of the parameters. All networks utilize DNNs, and their computation complexity is formulated as
where
During the intensive training phase,
During the phase of distributed implementation, each agent makes independent decisions. The actors’ computation complexity is
This section evaluates experimentally the performance of MATD3-CO.
Let a scalable IWN have different numbers of iBSs and iEDs, where the radio coverage radius of the iBSs is 100 m. All iEDs are evenly distributed over the coverage area and at least 5 m away from iBSs. During the experiment, we set the tasks to be randomly generated within a fixed range. The key parameters are set in Table 1. The configuration for the parameters of DNNs is given as follows. The actor network has 300 and 100 neurons in its first and second hidden layers, respectively. The size of the last layer is adjusted to match the action dimension of iBSs. Meanwhile, two critics adopt a consistent structure, each housing 300, 100 and 1 neurons across their three hidden layers. During the training phase, the learning rate of the actors and critics is
6.1.2 Benchmark Schemes for Comparison
The following experiments involve several benchmark DRL schemes:
• MATD3-CO: the proposed scheme employing MATD3 and convex optimization to iteratively approach the optimal solution.
• MATD3: a scheme based on MATD3 algorithm.
• MADDPG: a scheme based on MADDPG algorithm.
• DDPG: a scheme based on DDPG algorithm.
Reward measures the effectiveness of DRL-based algorithms. Fig. 3 illustrates the trend of reward convergence for all schemes, highlighting that as the number of iterations increases, the rewards of all schemes gradually increase and converge after a certain number of iterations. Moreover, as demonstrated in Fig. 3, we can see that the two TD3-based schemes converge more stable than the DDPG-based schemes, due to the introduction of two critic networks to address the overestimation problem, as well as the delayed updating of the actor networks. DDPG converges poorly in a multi-agent environment. Additionally, the three MADRL-based schemes perform better than the single-agent DDPG schemes in a multi-agent environment, obtaining higher reward. During the initial 400 episodes, the proposed scheme yields higher reward, primarily attributed to the optimal allocation of computation resources in making system decisions. The proposed MATD3-CO scheme yields the highest reward after convergence and a more stable reward curve.
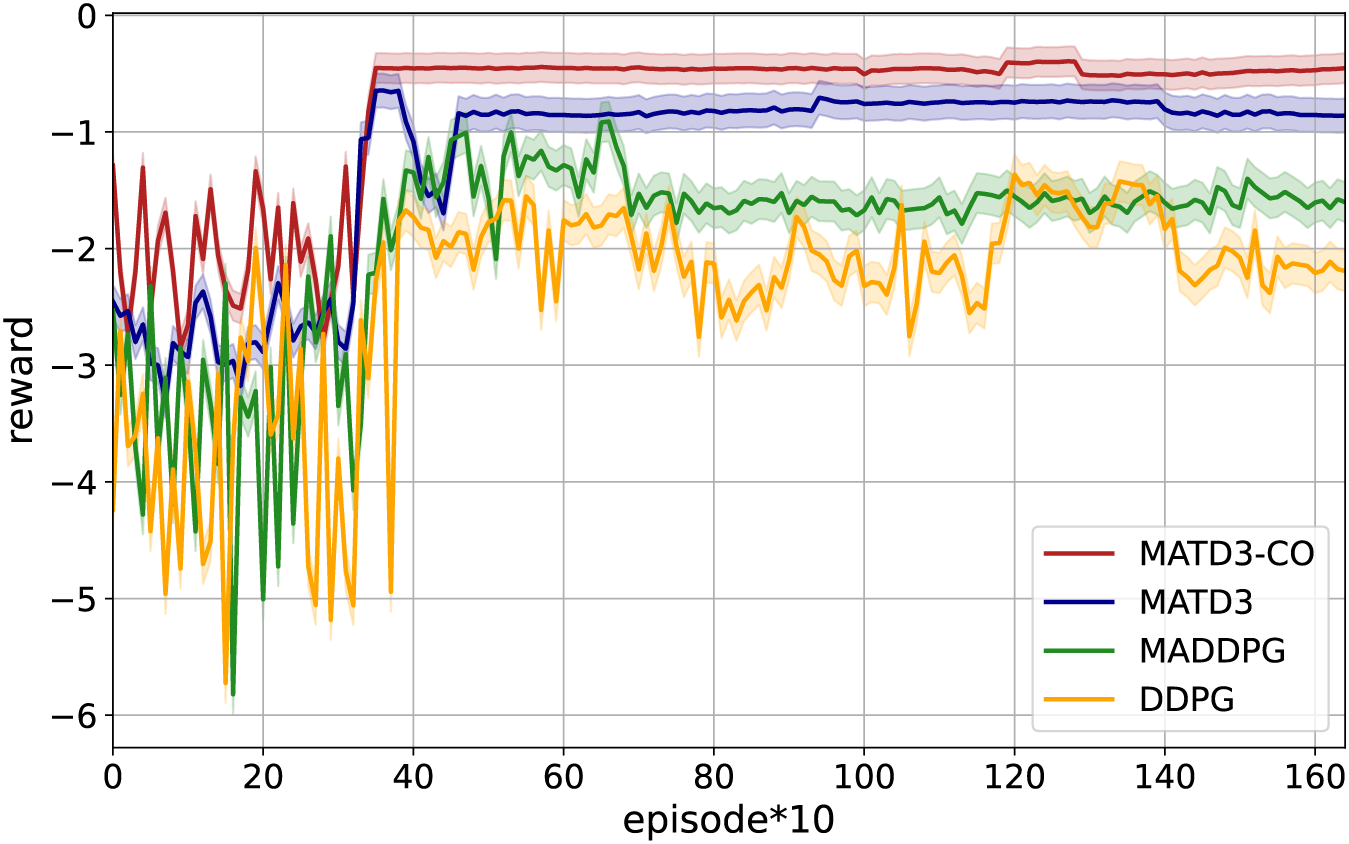
Figure 3: Reward vs. number of iterations for data training:
Fig. 4 shows the comparison of delay and energy consumption performance with different schemes. The results demonstrate that as the iteration count rises, the delay and energy consumption of all schemes decrease, and converge after a certain number of iterations. However, our proposed solution demonstrates superior performance in both delay and energy consumption. Therefore, MATD3-CO is superior to the other schemes.
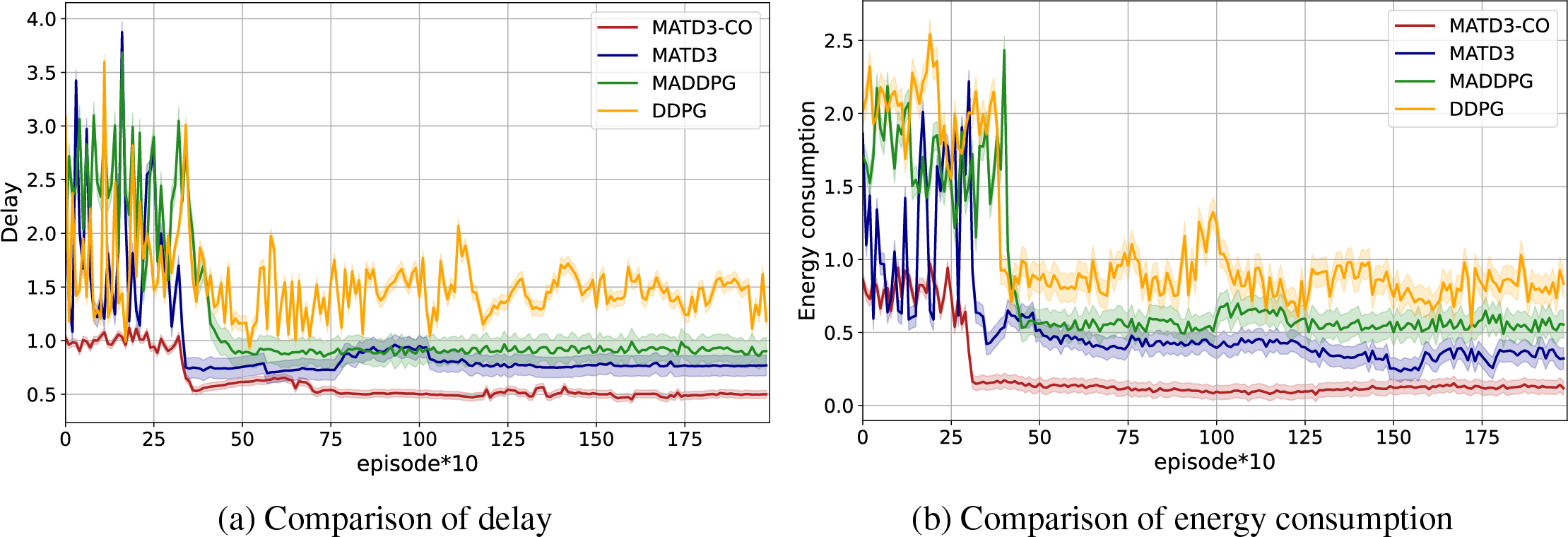
Figure 4: (a) Comparison of delay; (b) Comparison of energy consumption
Fig. 5 depicts the effect of the number of iEDs on system overhead under different schemes. When the number of iEDs is small (e.g., M = 15), we can see that there are fewer tasks that need to be computed, so the system overhead of all schemes is almost the same and very small. This is because there are sufficient resources to handle the tasks of iEDs. As the number of iEDs increases, the system costs under all schemes also rise. The reasons for this situation are as follows. When more iEDs are connected to the system, iEDs compete for limited computation resources, resulting in increased computation delay and energy consumption. In addition, due to limited channel resources, more iEDs sharing the same sub-channel increases the transmission delay and energy consumption for offloading tasks to iBSs. Overall, these factors lead to a regular increase in system overhead. As the number of iEDs increases further, the performance gap between different schemes also widens. Among all schemes, the system overhead of MATD3-CO consistently remains the smallest. This experimental result indicates that MATD3-CO is more suitable for more complex IWN environments.
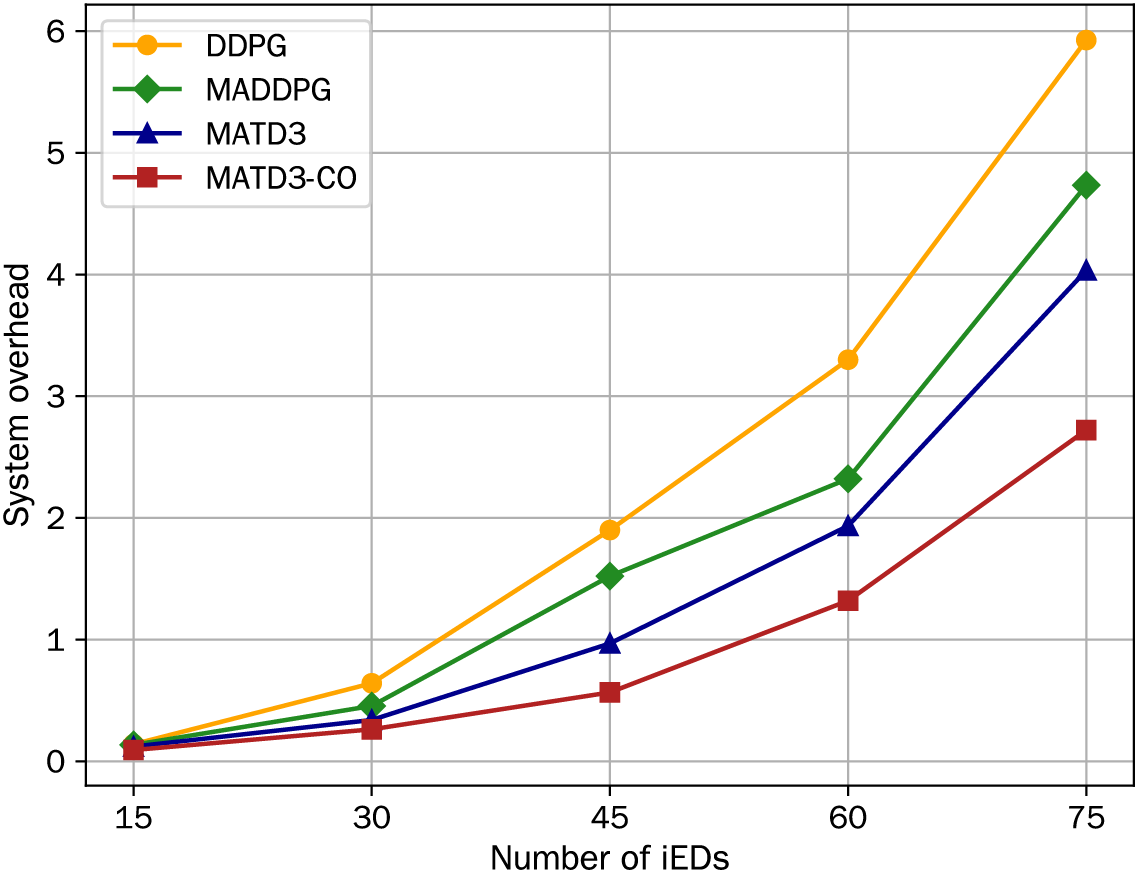
Figure 5: System overhead vs. number of iEDs:
Fig. 6 presents how system overhead is affected by the number of iBSs, where the number of iBSs is set to 3 and 4. For a fixed number of iEDs, increasing the number of iESs leads to a slight decrease in system overhead. This trend is consistent across different schemes. The reason is that more iESs only reduce the edge computing delay of tasks, while the energy consumption and offloading delay to iESs remain unchanged, and they account for the percentage of total system overhead. Meanwhile, the system overhead of MATD3-CO is lower than that of MATD3.
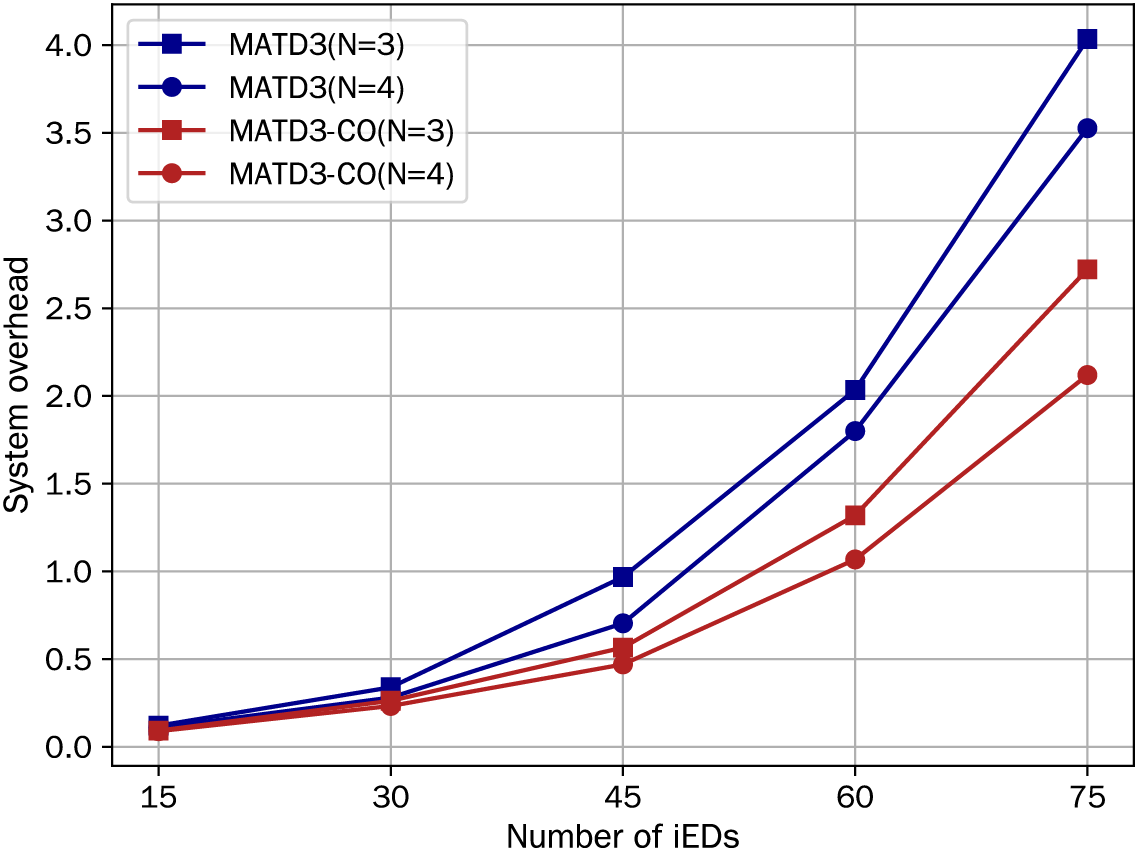
Figure 6: System overhead vs. number of iESs:
Fig. 7 illustrates the effect of sub-channel bandwidth on system overhead. In this evaluation, we increase the sub-channel bandwidth in the system from 4 to 20 MHz and set the task size to
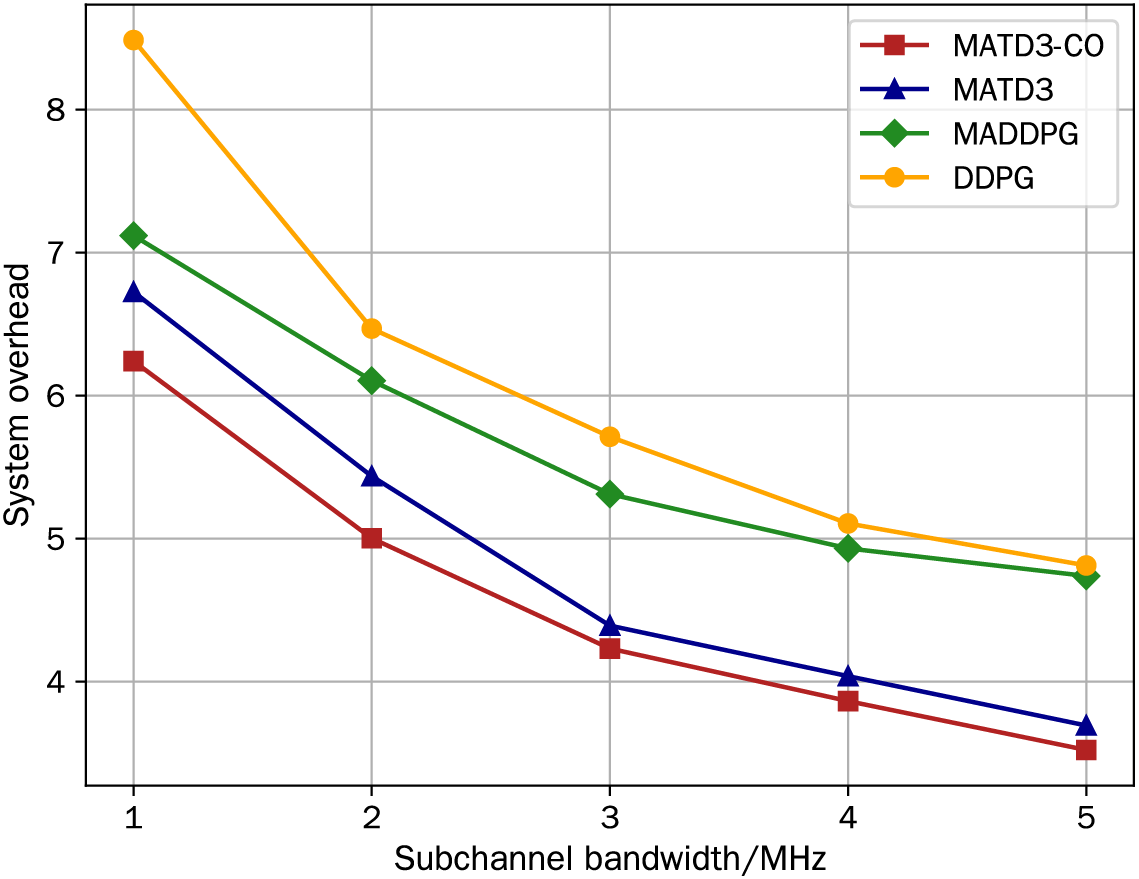
Figure 7: System overhead vs. sub-channel bandwidth:
Fig. 8 illustrates the impact of task size changes on system overhead. For this evaluation, the task size
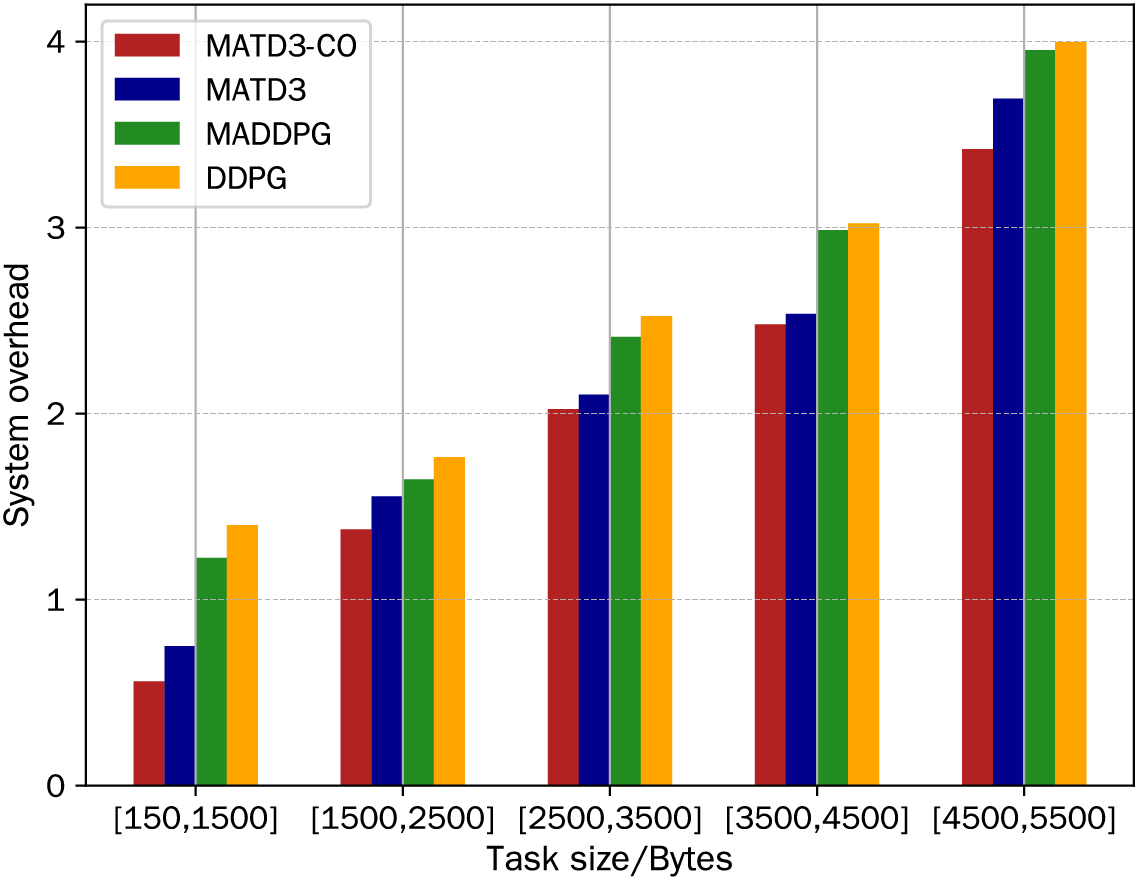
Figure 8: System overhead vs. task size:
In this paper, we investigated the problem of end-edge cooperative resource optimization for IWN with hybrid multiple access scheme. We established communication and computation models under this network model and fully considered the factors affecting the NOMA transmission rate under the constraint of limited computation and communication resources. We defined the weighted sum of task processing delay and energy consumption as the system overhead and formulated the system overhead minimization problem by jointly optimizing the sub-channel allocation, task offloading ratio, and computation resource allocation. To track this problem, we proposed MATD3-CO scheme to iteratively approach the optimal solution. The experimental results demonstrated that the proposed scheme converges well and effectively reduces the system overhead.
Future works will consider more constraints on the computation resource of iESs, the transmission power of iEDs, the cache of iEDs, and so on. Correspondingly, we will apply more algorithms for solutions, such as game-theoretic and other machine learning algorithms.
Acknowledgement: The authors would like to thank the editor and the reviewers for their time and effort in reviewing this paper.
Funding Statement: This work was supported by the National Natural Science Foundation of China under Grants 92267108, 62173322 and 61821005, and the Science and Technology Program of Liaoning Province under Grants 2023JH3/10200004 and 2022JH25/10100005.
Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Ru Hao, Chi Xu, Jing Liu; analysis and interpretation of results: Ru Hao, Chi Xu; draft manuscript preparation: Ru Hao, Chi Xu. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data are contained within this paper.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. C. Xu, H. Yu, X. Jin, C. Xia, D. Li and P. Zeng, “Industrial internet for intelligent manufacturing: Past, present, and future,” Front Inf. Technol. Electron. Eng., vol. 25, no. 9, pp. 1173–1192, Sep. 2024. doi: 10.1631/FITEE.2300806. [Google Scholar] [CrossRef]
2. L. D. Xu, W. He, and S. Li, “Internet of things in industries: A survey,” IEEE Trans. Ind. Inform., vol. 10, no. 4, pp. 2233–2243, Nov. 2014. doi: 10.1109/TII.2014.2300753. [Google Scholar] [CrossRef]
3. Y. Yu, “Mobile edge computing towards 5G: Vision, recent progress, and open challenges,” China Commun., vol. 13, no. S2, pp. 89–99, 2016. doi: 10.1109/CC.2016.7405725. [Google Scholar] [CrossRef]
4. X. Liu, C. Xu, H. Yu, and P. Zeng, “Multi agent deep reinforcement learning for end-edge orchestrated resource allocation in industrial wireless networks,” Front Inf. Technol. Electron. Eng., vol. 23, no. 1, pp. 47–60, Feb. 2022. doi: 10.1631/FITEE.2100331. [Google Scholar] [CrossRef]
5. P. Guan, X. Deng, Y. Liu, and H. Zhang, “Analysis of multiple clients behaviors in edge computing environment,” IEEE Trans. Veh. Technol., vol. 67, no. 9, pp. 9052–9055, Sep. 2018. doi: 10.1109/TVT.2018.2850917. [Google Scholar] [CrossRef]
6. J. Ding and J. Cai, “Two-side coalitional matching approach for joint MIMO-NOMA clustering and BS selection in multi-cell MIMO-NOMA systems,” IEEE Trans. Wirel. Commun., vol. 19, no. 3, pp. 2006–2021, Mar. 2020. doi: 10.1109/TWC.2019.2961654. [Google Scholar] [CrossRef]
7. W. Feng et al., “Hybrid beamforming design and resource allocation for UAV-aided wireless-powered mobile edge computing networks with NOMA,” IEEE J. Sel. Areas Commun., vol. 39, no. 11, pp. 3271–3286, Nov. 2021. doi: 10.1109/JSAC.2021.3091158. [Google Scholar] [CrossRef]
8. P. Wang, J. Xiao, and L. Ping, “Comparison of orthogonal and non-orthogonal approaches to future wireless cellular systems,” IEEE Veh. Technol. Mag., vol. 1, no. 3, pp. 4–11, Sep. 2006. doi: 10.1109/MVT.2006.307294. [Google Scholar] [CrossRef]
9. S. Hwang, H. Kim, H. Lee, and I. Lee, “Multi-agent deep reinforcement learning for distributed resource management in wirelessly powered communication networks,” IEEE Trans. Veh. Technol., vol. 69, no. 11, pp. 14055–14060, Nov. 2020. doi: 10.1109/TVT.2020.3029609. [Google Scholar] [CrossRef]
10. Z. Ding, D. Xu, R. Schober, and H. V. Poor, “Hybrid NOMA offloading in multi-user MEC networks,” IEEE Trans. Wirel. Commun., vol. 21, no. 7, pp. 5377–5391, Jul. 2022. doi: 10.1109/TWC.2021.3139932. [Google Scholar] [CrossRef]
11. F. R. Albogamy, M. A. Aiyashi, F. H. Hashim, I. Khan, and B. J. Choi, “Optimal resource allocation for NOMA wireless networks,” Comput. Mater. Contin., vol. 74, no. 2, pp. 3249–3261, 2023. doi: 10.32604/cmc.2023.031673. [Google Scholar] [CrossRef]
12. A. J. Muhammed, Z. Ma, Z. Zhang, P. Fan, and E. G. Larsson, “Energy-efficient resource allocation for NOMA based small cell networks with wireless backhauls,” IEEE Trans. Commun., vol. 68, no. 6, pp. 3766–3781, Jun. 2020. doi: 10.1109/TCOMM.2020.2979971. [Google Scholar] [CrossRef]
13. W. Huang and Z. Ding, “New insight for multi-user hybrid NOMA offloading strategies in MEC networks,” IEEE Trans. Veh. Technol., vol. 73, no. 2, pp. 2918–2923, Feb. 2024. doi: 10.1109/TVT.2023.3318151. [Google Scholar] [CrossRef]
14. F. Fang, Y. Xu, Z. Ding, C. Shen, M. Peng and G. K. Karagiannidis, “Optimal resource allocation for delay minimization in NOMA-MEC networks,” IEEE Trans. Commun., vol. 68, no. 12, pp. 7867–7881, Dec. 2020. doi: 10.1109/TCOMM.2020.3020068. [Google Scholar] [CrossRef]
15. Y. Wu, B. Shi, L. P. Qian, F. Hou, J. Cai and X. S. Shen, “Energy-efficient multi-task multi-access computation offloading via NOMA transmission for IoTs,” IEEE Trans. Ind. Inform., vol. 16, no. 7, pp. 4811–4822, Jul. 2020. doi: 10.1109/TII.2019.2944839. [Google Scholar] [CrossRef]
16. Z. Ding, J. Xu, O. A. Dobre, and H. V. Poor, “Joint power and time allocation for NOMA-MEC offloading,” IEEE Trans. Veh. Technol., vol. 68, no. 6, pp. 6207–6211, Jun. 2019. doi: 10.1109/TVT.2019.2907253. [Google Scholar] [CrossRef]
17. Y. Wu, K. Ni, C. Zhang, L. P. Qian, and D. H. K. Tsang, “NOMA-assisted multi-access mobile edge computing: A joint optimization of computation offloading and time allocation,” IEEE Trans. Veh. Technol., vol. 67, no. 12, pp. 12244–12258, Dec. 2018. doi: 10.1109/TVT.2018.2875337. [Google Scholar] [CrossRef]
18. Q. V. Pham, H. T. Nguyen, Z. Han, and W. J. Hwang, “Coalitional games for computation offloading in NOMA-enabled multi-access edge computing,” IEEE Trans. Veh. Technol., vol. 69, no. 2, pp. 1982–1993, Feb. 2020. doi: 10.1109/TVT.2019.2956224. [Google Scholar] [CrossRef]
19. C. Xu, P. Zhang, H. Yu, and Y. Li, “D3QN-based multi-priority computation offloading for time-sensitive and interference-limited industrial wireless networks,” IEEE Trans. Veh. Technol., vol. 73, no. 9, pp. 13682–13693, Sep. 2024. doi: 10.1109/TVT.2024.3387567. [Google Scholar] [CrossRef]
20. T. T. Nguyen, N. D. Nguyen, and S. Nahavandi, “Deep reinforcement learning for multiagent systems: A review of challenges, solutions, and applications,” IEEE Trans. Cybern., vol. 50, no. 9, pp. 3826–3839, Sep. 2020. doi: 10.1109/TCYB.2020.2977374. [Google Scholar] [PubMed] [CrossRef]
21. K. Yu, Q. Cui, Z. Zhang, X. Huang, X. Zhang and X. Tao, “Efficient UAV/satellite-assisted IoT task offloading: A multi-agent reinforcement learning solution,” in 2022 27th APCC, Jeju Island, Republic of Korea, 2022, pp. 83–88. [Google Scholar]
22. X. Luo, Y. Liu, H. H. Chen, and Q. Guo, “PHY security design for mobile crowd computing in ICV networks based on multi-agent reinforcement learning,” IEEE Trans. Wirel. Commun., vol. 22, no. 10, pp. 6810–6825, Oct. 2023. doi: 10.1109/TWC.2023.3245637. [Google Scholar] [CrossRef]
23. C. Xu, Z. Tang, H. Yu, P. Zeng, and L. Kong, “Digital twin-driven collaborative scheduling for heterogeneous task and edge-end resource via multi-agent deep reinforcement learning,” IEEE J. Sel. Areas Commun., vol. 41, no. 10, pp. 3056–3069, Oct. 2023. doi: 10.1109/JSAC.2023.3310066. [Google Scholar] [CrossRef]
24. C. Xu, P. Zhang, X. Xia, L. Kong, P. Zeng and H. Yu, “Digital twin-assisted intelligent secure task offloading and caching in blockchain-based vehicular edge computing networks,” IEEE Internet Things J., pp. 1–16, 2024. doi: 10.1109/JIOT.2024.3482870. [Google Scholar] [CrossRef]
25. J. Cai, H. Fu, and Y. Liu, “Multitask multi objective deep reinforcement learning-based computation offloading method for industrial internet of things,” IEEE Internet Things J., vol. 10, no. 2, pp. 1848–1859, Jan. 2023. doi: 10.1109/JIOT.2022.3209987. [Google Scholar] [CrossRef]
26. B. Li, R. Yang, L. Liu, J. Wang, N. Zhang and M. Dong, “Robust computation offloading and trajectory optimization for multi-UAV-assisted MEC: A multiagent DRL approach,” IEEE Internet Things J., vol. 11, no. 3, pp. 4775–4786, Feb. 2024. doi: 10.1109/JIOT.2023.3300718. [Google Scholar] [CrossRef]
27. Y. Xiao, Y. Song, and J. Liu, “Collaborative multi-agent deep reinforcement learning for energy-efficient resource allocation in heterogeneous mobile edge computing networks,” IEEE Trans. Wirel. Commun., vol. 23, no. 6, pp. 6653–6668, Jun. 2024. doi: 10.1109/TWC.2023.3335597. [Google Scholar] [CrossRef]
28. Z. Cao, P. Zhou, R. Li, S. Huang, and D. Wu, “Multiagent deep reinforcement learning for joint multichannel access and task offloading of mobile-edge computing in Industry 4.0,” IEEE Internet Things J., vol. 7, no. 7, pp. 6201–6213, Jul. 2020. doi: 10.1109/JIOT.2020.2968951. [Google Scholar] [CrossRef]
29. H. Zhou, Y. Long, S. Gong, K. Zhu, D. T. Hoang and D. Niyato, “Hierarchical multi-agent deep reinforcement learning for energy-efficient hybrid computation offloading,” IEEE Trans. Veh. Technol., vol. 72, no. 1, pp. 986–1001, Jan. 2023. doi: 10.1109/TVT.2022.3202525. [Google Scholar] [CrossRef]
30. Z. Song, Y. Liu, and X. Sun, “Joint radio and computation resource allocation for NOMA-based mobile edge computing in heterogeneous networks,” IEEE Commun. Lett., vol. 22, no. 12, pp. 2559–2562, Dec. 2018. doi: 10.1109/LCOMM.2018.2875984. [Google Scholar] [CrossRef]
31. V. D. Tuong, T. P. Truong, T. V. Nguyen, W. Noh, and S. Cho, “Partial computation offloading in NOMA-assisted mobile-edge computing systems using deep reinforcement learning,” IEEE Internet Things J., vol. 8, no. 17, pp. 13196–13208, Sep. 2021. doi: 10.1109/JIOT.2021.3064995. [Google Scholar] [CrossRef]
32. B. Yang, X. Cao, J. Bassey, X. Li, and L. Qian, “Computation offloading in multi-access edge computing: A multi-task learning approach,” IEEE Trans. Mobile Comput., vol. 20, no. 9, pp. 2745–2762, Sep. 2021. doi: 10.1109/TMC.2020.2990630. [Google Scholar] [CrossRef]
33. Y. Yang, L. Chen, W. Dong, and W. Wang, “Active base station set optimization for minimal energy consumption in green cellular networks,” IEEE Trans. Veh. Technol., vol. 64, no. 11, pp. 5340–5349, Nov. 2015. doi: 10.1109/TVT.2014.2385313. [Google Scholar] [CrossRef]
34. F. Wang, J. Xu, X. Wang, and S. Cui, “Joint offloading and computing optimization in wireless powered mobile-edge computing systems,” IEEE Trans. Wirel. Commun., vol. 17, no. 3, pp. 1784–1797, Mar. 2018. doi: 10.1109/TWC.2017.2785305. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF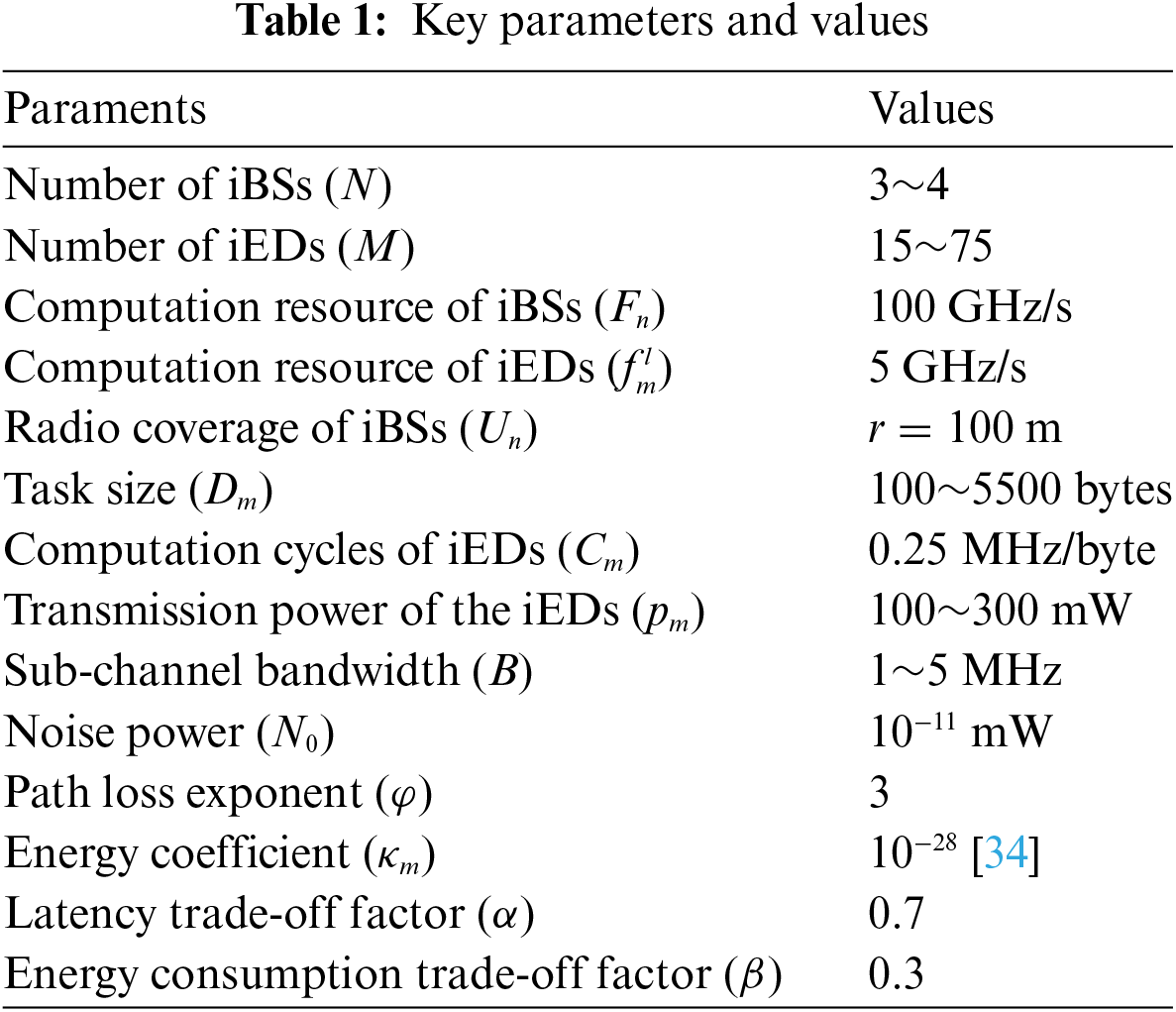
 Downloads
Downloads
 Citation Tools
Citation Tools