LSBSP: A Lightweight Sharding Method of Blockchain Based on State Pruning for Efficient Data Sharing in IoMT

1  Introduction

As people increasingly incorporate smart devices into various aspects of their lives from medical technologies and wearables to entertainment, these devices not only enhance daily experiences but also generate vast amounts of valuable data. However, this rapid digital integration brings elevated security and privacy concerns, particularly in the Internet of Medical Things (IoMT). IoMT devices, which often linked through multiple interfaces, are especially vulnerable to security breaches, presenting significant risks in sectors handling sensitive data.

To address these concerns, there is an urgent need for robust frameworks that safeguard IoMT data. Blockchain technology, with its decentralized, immutable, and traceable characteristics, offers a promising solution. The BFLDL scheme [1] integrates blockchain with federated learning, providing a secure, privacy-preserving approach for applications like deepfake detection. Beyond cryptocurrency, blockchain is increasingly recognized as a foundational technology in the digital economy, extending to areas like smart homes [2], smart cars [3], and the IoMT [4] among others. Despite its wide applicability, blockchain technology encounters significant scalability challenges. Traditional blockchains like Bitcoin and Ethereum, are limited to processing only 7 and 15 transactions per second (TPS), respectively [5]. Such throughput is inadequate for modern applications requiring processing capabilities exceeding 100,000 TPS. The main bottleneck is that all nodes must maintain a complete copy of the ledger.

Sharding technology is recognized as an effective approach to tackle this issue. However, current research on sharding technology faces several challenges when applied to modern sectors. First, there is substantial overhead associated with bootstrapping blockchain sharding states. Sharding technology utilizes a reshuffle committee that periodically updates the verification members in each shard to prevent malicious nodes from gaining control and to enhance security. This reconfiguration, however, increases the time overhead of state synchronization during the sharding process. Second, the blockchain ledger’s continuously growing data capacity poses further challenges. For instance, in the IoMT sector, the growing number of health-conscious individuals results in large volumes of data generated by medical devices. The medical blockchain struggles to process this large capacity of data, imposing a significant burden on the network, and the overhead incurred during the blockchain bootstrap phase becomes increasingly substantial. Lastly, the practical value of excessively old data stored across different shards diminishes, leading to increased validation costs. The involvement of numerous historical transactions and complex verification logic results in relatively high costs for validating outdated data.

To tackle these challenges, this paper presents a Lightweight Sharding method of Blockchain based on State Pruning (LSBSP) aimed at enhancing data sharing efficiency in the IoMT. LSBSP optimizes state management by utilizing a dual-shard architecture, comprising snapshot shards for accelerated transaction processing and full shards to ensure data integrity. This approach significantly reduces both storage and computational demands across network nodes, promoting more efficient operation within the network. The main contributions of this paper are:

•   We present a lightweight blockchain sharding method tailored to address the significant challenges of state bootstrapping load and time overhead in efficient data sharing, where both safety and efficiency are paramount.

•   We introduce a block state pruning technique that optimizes resource utilization during initialization and reconfiguration phases. This technique reduces storage disk space requirements and enhances transaction execution efficiency, which is essential for managing large data volumes.

•   Extensive simulation experiments validate the effectiveness of the LSBSP scheme. The results demonstrate its superior performance in key areas, including system storage capacity, throughput, and latency, outperforming other comparative approaches.

The rest of this article is organized as follows: Section 2 reviews the relevant background literature. We introduce the problem formulation in Section 3. In Section 4, we present the definition and proposed algorithm. Section 5 conducts mathematical analysis and discussion. The experimentation evaluation is illustrated in Sections 6, and 7 concludes the paper with insights and directions for future work.

2  Related Work

2.1 Blockchain Sharding Method

Sharding technology is recognized as a promising solution for addressing scalability issues in blockchains. Luu et al. [6] introduced the Elastico protocol, which divides the network into smaller committees to process distinct sets of transactions in parallel. However, Elastico faces challenges with cross-shard transactions, potentially leading to rejection and deadlocks. To address this, Kokoris-Kogias et al. [7] proposed OmniLedger, combining RandHound with the verifiable random function (VRF) algorithm. Rapidchain initially proposed a public blockchain sharding method capable of resisting up to 1/3 of Byzantine participants by leveraging the cuckoo rule and employing efficient cross-shard transaction verification technology routing [8]. However, both methods above require storing the complete blockchain ledger [9].

To enhance blockchain security, Federated Learning (FL) is often combined with blockchain technology to create a trusted environment for secure data transmission and privacy protection [10,11]. Zhen et al. [12] propose a blockchain architecture that leverages deep reinforcement learning for dynamic state storage to boost the performance of blockchain-based crowd sourcing systems. This architecture is designed to increase the blockchain’s throughput and the proportion of non-malicious nodes, thus enhancing its resistance to attacks. Free2Shard proposes a dynamic self-allocation strategy to maintain a favorable ratio of honest to hostile nodes in each shard [13]. PolyShard [14] uses polynomial-coding to address scalability, security, and decentralization challenges. Li et al. [15] presented a secure and efficient blockchain sharding scheme that combines hybrid consensus with dynamic management, enhancing scalability and security while optimizing performance and preserving resilience against attacks. Reticulum [16] introduces a two-layer sharding design, comprising “control” and “process” shards, manage security and liveness attacks separately while dynamically adjusting transaction throughput, significantly improving scalability without compromising security.

Vakili et al. [17] introduced a service composition approach for cloud-based IoT environments that leverages Grey Wolf Optimization and MapReduce frameworks. The optimization framework aligns with blockchain sharding’s goal of enhancing system efficiency through resource allocation strategies. Integrating Vakili et al.’s optimization principles could help improve transaction handling and load distribution across blockchain shards, addressing similar challenges of large-scale, decentralized environments that require rapid processing and adaptability.

For cross-shard transactions, when coordinating intra-shard and cross-shard consensus protocols, transaction ordering may expose the system to attacks. Haechi [18] introduces a final fairness algorithm to accommodate consensus speed differences across shards, ensuring global fair ordering, which enhances system consistency and parallel processing capabilities. The global order provided by Haechi ensures strong consistency between shards and improves parallelism in handling cross-shard conflicting transactions. Xu et al. [19] propose the X-shard method, which decomposes transactions into sub-transactions to reduce processing delays. Tao et al. [20] introduce a distributed sharding system based on smart contracts to resolve conflicts among miners in large shards. GriDB designs an off-chain mechanism for cross-shard operations, ensuring database service verification [21].

These studies contribute to enhancing blockchain security and reducing cross-shard communication overhead. However, the growing size of state ledgers increases the time for bootstrapping the ledger, impacting transaction processing efficiency.

2.2 Blockchain Storage Technology

The burgeoning growth of blockchain ledger sizes presents substantial computational and storage challenges for new nodes, with the sizes of Bitcoin and Ethereum ledgers exceeding 500 and 700 GB, respectively [22]. This data storage issues have garnered substantial attention. Traditionally, new nodes are required to download all blocks and re-execute transactions, leading to redundant computations and inefficient hardware utilization [23].

Recent approaches focus on reducing storage consumption through on-chain and off-chain methods. Light node technology, such as Simplified Payment Verification (SPV), stores only essential transaction data, minimizing the need for full node storage. CoinPrune introduces block pruning, allowing nodes to sync with recent snapshots of the ledger [24], however, this approach overlooks potential validation failures. FHFBOA optimizes storage by transforms the storage challenge into a multi-objective optimization problem [25].

To address data redundancy, Chunk2vec [26] introduces an advanced similarity detection scheme that utilizes deep learning and Approximate Nearest Neighbor Search. This method identifies similar data chunks across a predefined similarity threshold by analyzing fingerprint feature vectors. Furthermore, deep learning plays a crucial role in ensuring integrity and security in blockchain storage. Heidari et al. [27] reviewed deep learning-based methods for deepfake detection, highlighting their effectiveness in authenticity verification and combating malicious alterations. These techniques could be adapted to enhance blockchain storage by providing robust mechanisms for data integrity across distributed networks.

Coding techniques also enhance storage efficiency, such as erasure-correcting codes [28]. Qi et al. propose a Byzantine fault-tolerant storage engine leveraging error correction and replication modes [29]. Huang et al. [30] proposed the SnapshotPrune scheme, which improves the synchronization strategy based on the existing snapshot model to accommodate the UTXO pruning strategy, enabling nodes in the Bitcoin blockchain to quickly achieve state synchronization. Kumar et al. [31] aimed to improve the security of industrial image and video data by utilizing the distributed storage capabilities of IPFS and the tamper-proof nature of blockchain. S-BDS [32] constructs a storage sharding scheme for IoT data based on blockchain, replacing the Merkle tree in the blockchain data layer with Insertable Vector Commitment (IVC) to effectively reduce communication congestion. Additionally, Yang et al. [33] proposed a blockchain-based file storage mechanism that limits the selfish behavior of nodes.

Existing research often focuses solely on blockchain sharding technology without considering the impact of ledger capacity, or concentrates on optimizing blockchain ledger capacity while neglecting scalability issues. There is currently a lack of work that integrates blockchain sharding technology with ledger capacity management. To address this, the LSBSP solution aims to tackle the issues of blockchain ledger expansion and limited scalability, making it more suitable for blockchain systems in scenarios such as the IoMT. A comparison of related work is shown in Table 1.

3  Problem Formulation

3.1 Challenges and Solutions

Using the sharing of EHR data as an example, the current exchange healthy data faces several critical challenges that urgently need to be addressed.

C1: Stringent Security Requirements.

Medical data carries sensitive information such as personal privacy, health conditions, and potential treatment plans, thus necessitating extremely high security standards. In the process of medical data sharing, multiple and stringent security measures must be implemented to ensure the integrity and privacy of the data remain intact and uncompromised.

C2: Pursuit of Efficient Data Processing.

In the medical field, the accuracy and timeliness of data are critical for diagnosis and treatment. Therefore, the efficiency of medical data processing is of utmost importance. It must be capable of quickly and accurately acquiring, analyzing, and transmitting data to support rapid medical decision-making and service response.

C3: Massive Data Volume Challenge.

With the continuous advancement of medical technology and the increasing level of informatization, medical data is experiencing explosive growth. This data includes vast amounts of medical records, high definition imaging data, and complex genomic sequencing information, resulting in enormous data volumes. Therefore, medical blockchain data sharing systems need efficient data storage and management capabilities to support quick access to massive amounts of data.

Based on the analysis of the challenges in medical data sharing, the proposed solution of the LSBSP scheme is as follows:

S1: Enhancing Data Security

Utilizing the immutability of blockchain and powerful consensus algorithms, the aim is to ensure the integrity and privacy of medical data during the sharing process, significantly enhancing data security.

S2: Improving Data Sharing Efficiency

By employing blockchain sharding technology, the aim is to enhance the processing and transmission efficiency of medical data. This approach addresses the high demands for data accuracy and timeliness in the medical field, supporting rapid medical decision-making and prompt service responses.

S3: Reducing Storage Requirements for Verification Nodes

Through snapshot-based state pruning, the objective is to reduce the storage requirements of blockchain verification nodes. This effectively lowers the data storage burden on validators, accommodating the explosive growth of medical data.

3.2 Safety EHR Sharing Instances

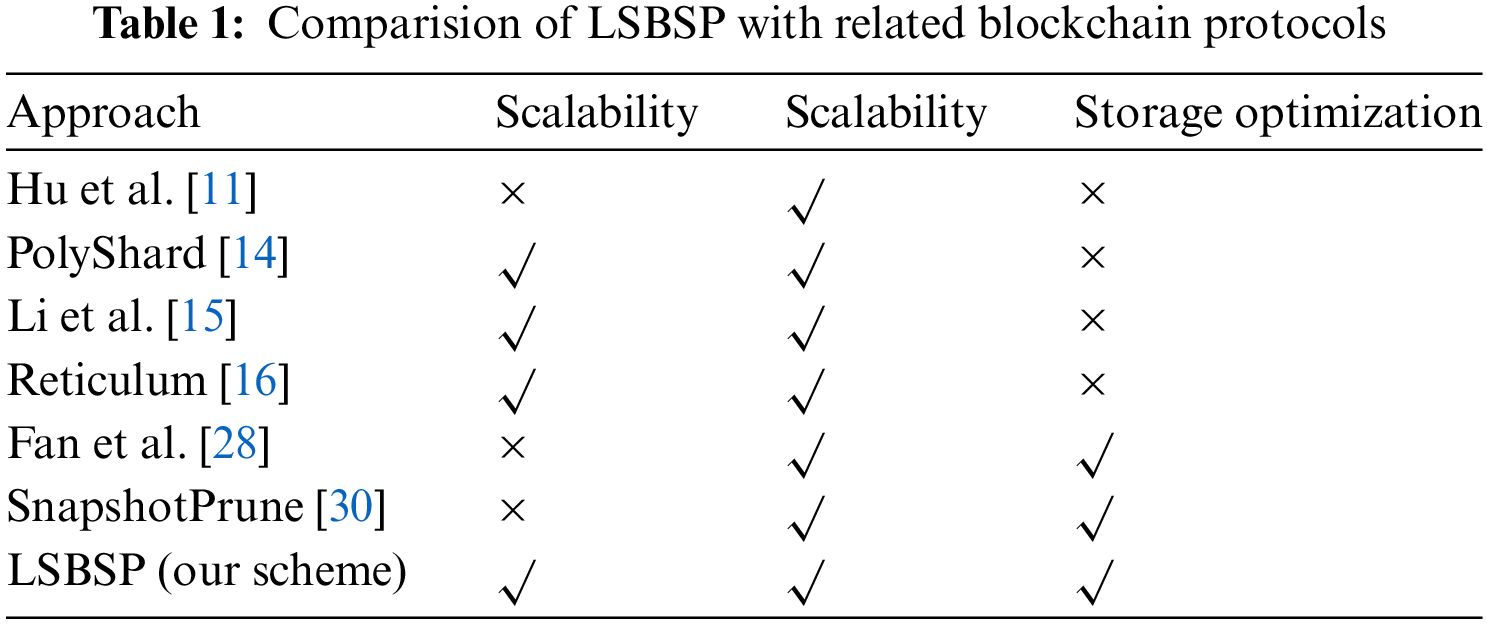
Fig. 1 illustrates a secure and efficient EHR sharing instance that combines blockchain sharding technology. This model can be divided into three phases: data generation, data management, and data utilization.

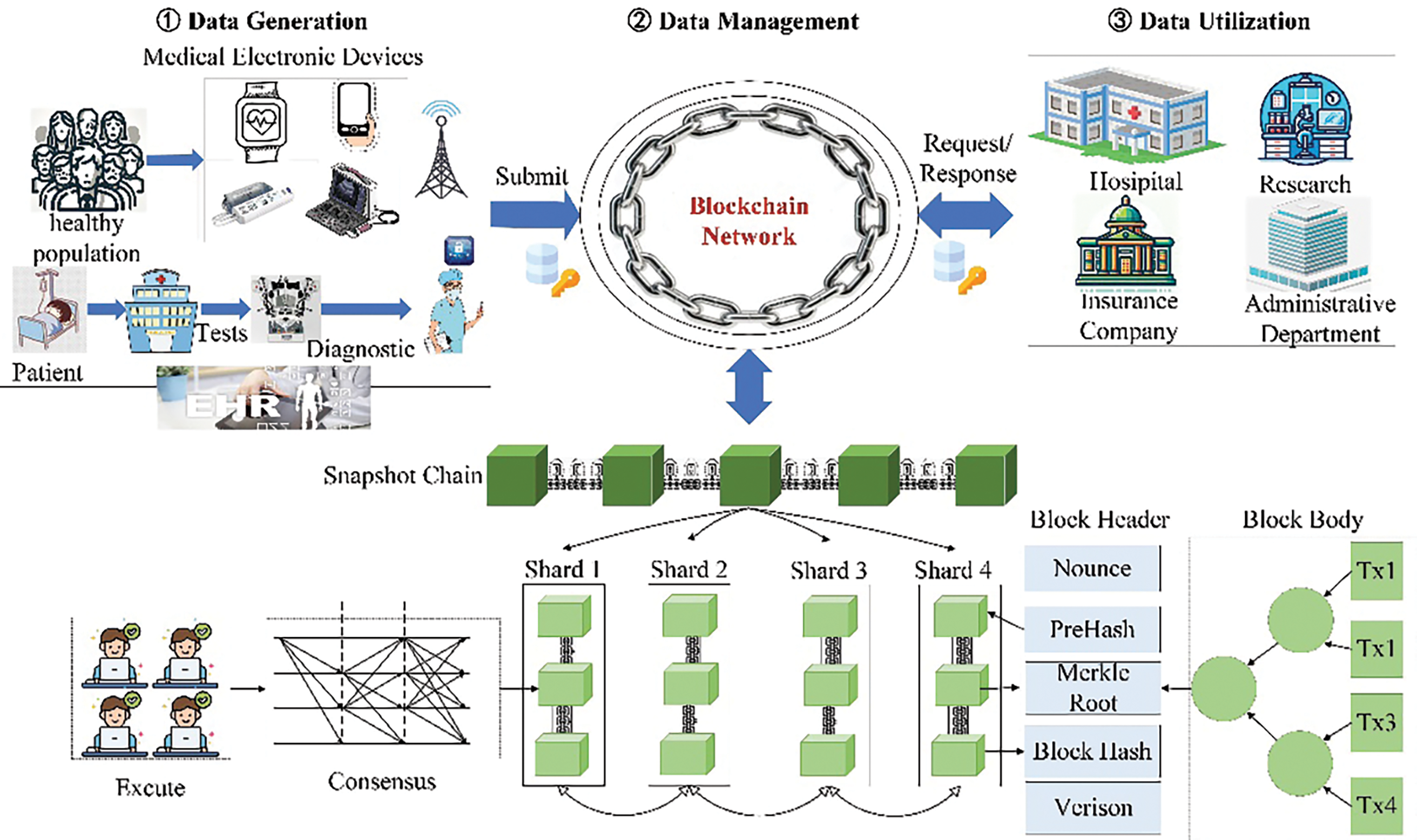
Figure 1: A safety EHR sharing instances

In the data generation phase, two prominent trends emerge alongside the growing emphasis on health issues. First, patients undergo a series of medical examinations upon admission, enabling doctors to make diagnoses based on the results. Second, individuals in sub-health states actively utilize various portable medical devices to track their health status. These electronic health records (EHRs) are invaluable to both patients and society. To ensure the secure sharing of EHRs, blockchain technology can be employed to manage this data. Data providers upload information to the blockchain after obtaining the patient’s consent, thus safeguarding sensitive data and improving processing efficiency.

During the blockchain data management phase, the sharding method can be adopted to improve scalability. All transactions are structured in the form of a Merkle tree, with leaf nodes containing EHR information. If any changes occur to the EHRs, the Merkle root R will be altered, ensuring data integrity through cryptography. Let LNi represent the leaf nodes containing EHR data, the Merkle root R is a hash function applied iteratively on all leaf nodes:

R=H(H(LN1)||H(LN2)||⋯||H(LNi)).(1)

All nodes in a shard will execute the transaction and reach consensus. The consensus algorithm guarantees that no unauthorized modifications to the EHRs can occur. By employing the sharding method, the scalability of the blockchain is significantly enhanced, ensuring quick access to data.

In the data utilization phase, relevant individuals and institutions can apply for access to pertinent data via the blockchain. With access to comprehensive medical histories, healthcare providers can make more accurate and timely diagnoses. Sharing EHRs eliminates the need for redundant tests and examinations. When patients transition between different healthcare providers, their complete medical records are readily available, reducing unnecessary procedures and lowering healthcare costs. Furthermore, shared EHR data enables healthcare specialists to collaborate more effectively. This coordinated approach ensures that all aspects of a patient’s health are considered, leading to more cohesive and efficient treatment plans.

4  Our Proposed Approach

To reduce the storage requirements for network nodes as large volumes of data are generated, we have innovatively proposed a lightweight blockchain sharding method based on state pruning (LSBSP) for secure data management and sharing.

4.1 The Overview LSBSP Model

The implementation of sharding technology significantly boosts the performance of blockchain systems. Let S be the set of all shards. Each node n∈N belongs to exactly one shard s∈S.

N=∪s∈SNswithNs∩Ns′=∅for s≠s′,(2)

where Ns is the set of nodes in shard s.

Let T be the set of all transactions with each transaction tx∈TX handled by exactly one shard s∈S.

TX=∪s∈STXs with TXs∩TXs′=∅ for s≠s′,(3)

where TXs is the set of transactions managed by shard s.

Each shard processes transactions in defined timeframes, or epochs. Let E be the set of epochs, where for each epoch e∈E, each shard s∈S generates a block Bs,e of transactions TXs.

Bs,e={tx∈TXs|txisincludedinepoche}.(4)

Fig. 2 shows an overview of LSBSP. This model incorporates a dual-chain structure consisting of MainChain(MC) and SnapshotChain(SC). The MC serves as storage for the entire blockchain’s state, while the SC packages data from the MC at fixed intervals. In LSBSP, shards are categorized into Fshards and Sshards based on different sources of state bootstrapping. Nodes in Fshard bootstrap their ledgers from the MC, whereas Sshards load the latest snapshot and chaintail. The adoption of this dual-chain and dual-shard design facilitates the balance between shard data storage costs and transaction throughput, thereby reducing transaction verification failures and the transaction waiting time of clients. Specifically, within a single epoch, the LSBSP executes transaction processing through the following sequential steps:

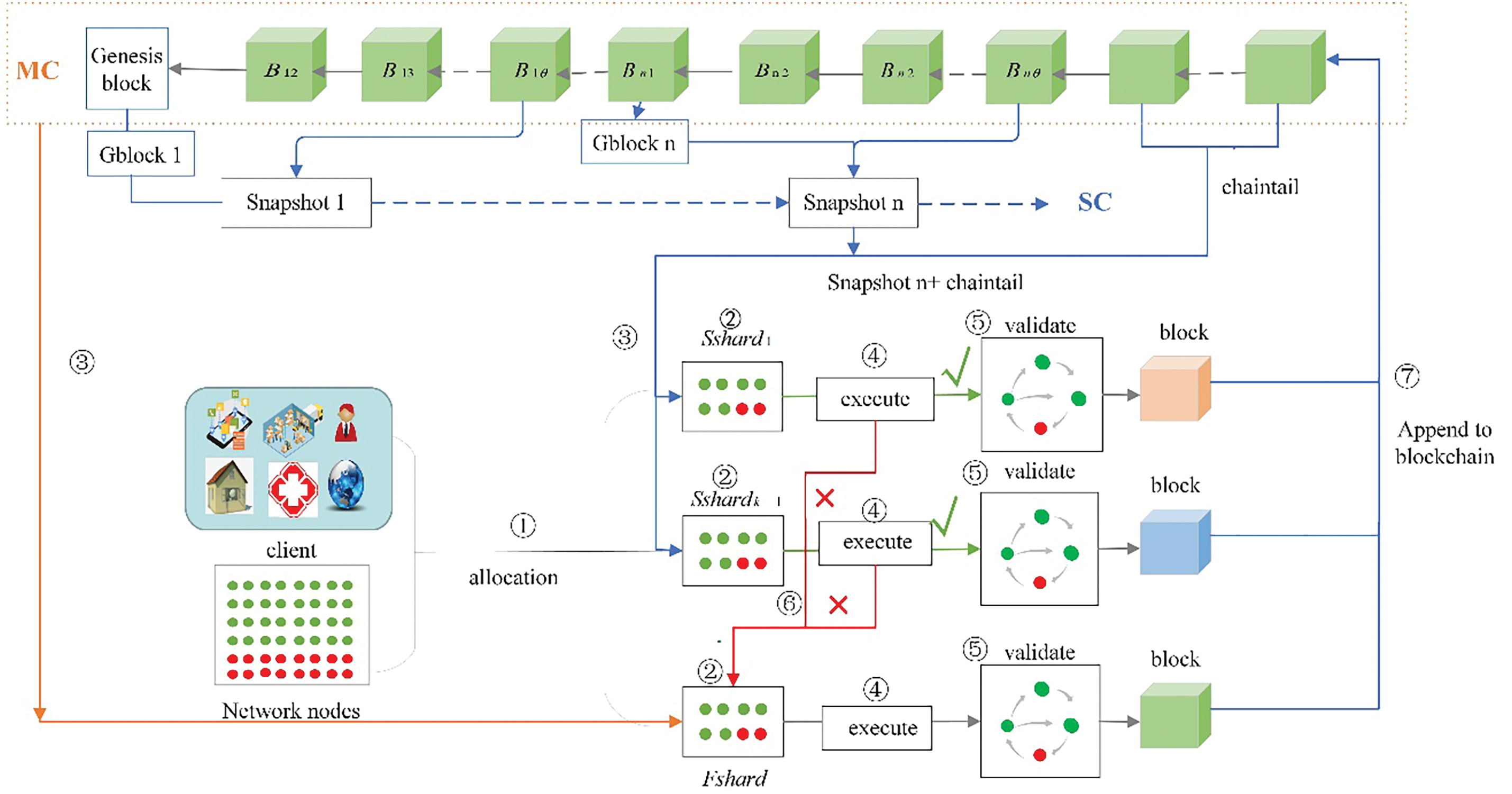
Figure 2: An overview of LSBSP

Step①: Transaction generation and node assignment. A transaction tx is initiated by a client and broadcast across the network, the network nodes are randomly allocated into different shards by an algorithm.

Step②: Configuration of the shards. The LSBSP configuration’s specification of k−1 Sshards for snapshot-based state storage and one Fshard for full ledger storage, nodes are evenly distributed among these shards.

Step③: State initialization. In this step, the validators in Sshard begin by loading the ledgers LSshard. This ledger includes crucial information such as the latest snapshot and chaintail, which are essential for ensuring the integrity and consistency of the blockchain state. Simultaneously, validators in Fshard load the ledgers directly from MC.

Step④: Transaction Execution. Transactions are executed in parallel across the shards. Successful executions in Sshard move to Step 5, while failures are redirects to Fshard, subsequently leading to step 6.

Step⑤: The transaction tx is verified through sequential execution and consensus within the shard. Once verified, the valid block Bvalid is appended with signatures from the verifiers, confirming its validity. Following this, the process proceeds to Step 7.

Step⑥: Transaction Processing in Fshard. Fshard re-executes the transactions that failed in Sshard and subsequently returns to Step 5 for verification.

Step⑦: Update. The valid block Bvalid is appended to MC. As MC is updated, SC dynamically refreshes its snapshots. Additionally, the updates to the chaintail and snapshot ledger are integrated into the verifier states in preparation for the next epoch.

4.2 Dual-Chain Structure

We introduce a novel sharding blockchain architecture that comprises two distinct chains: the MC and the SC. The dual-chain structure of LSBSP enhances storage efficiency and data sharing across the network. MC serves as the source of the blockchain’s complete state, while SC acts as a reduced ledger containing snapshots of the full state. This structure allows nodes in each shard to choose between loading data from MC or the more compact SC. The state of SC is periodically synchronized with MC, ensuring that data in SC reflects the latest state without redundancy. Each snapshot in SC condenses the state of θ blocks, defined as:

SCi=F(MCiθ),(5)

where F represents a snapshot function that encapsulates the state from MC. This design ensures efficient storage by removing redundant data from SC while maintaining blockchain integrity and accessibility across nodes.

Definition 1 (Main Chain, MC). The Main Chain can be represented as a sequence of blocks, MC={Gblock1,B12,⋯,B1θ,⋯,Gblockn,Bn1,⋯,Bnθ}, where containing n∗θ blocks, Gblock1 is the genesis block, Gblocki is a block whose height differs by multiples of θ from Gblock1, the number i in block Bij denotes the snapshot number, and j represents the position of the block relative to Gblock1.

Definition 2 (Snapshot Chain, SC). The Snapshot Chain SC can be represented as a sequence of snapshots derived from the Main Chain MC, SC={SC1,⋯,SCi,⋯,SCn}. Here SCi indicates the i-th snapshot in the chain, where SCi⊇Gblocki,Bi2,⋯,Biθ. In this context, Gblocki represents the initial block of the i-th snapshot, while Biθ marks the termination of snapshot i.

Definition 3 (Full Shard, Fshard). A Full Shard, denoted as Fshard, consists of nodes that fully replicate the ledger from the main chain MC. Each node within the Fshard retains a complete copy of the ledger, referred to as LFshard, which encompasses the entire transaction record TX of the MC. For any transaction tx∈TX, it follows that Ltx∈LFshard for all nodes n∈NFshard. The ledger LFshard can be expressed as follows:

LFshard←{Gblock1,B12,⋯,B1θ,⋯,Gblockn,Bn1,⋯,Bnθ}.(6)

Definition 4 (Snapshot Shard, Sshard). Snapshot shards, denoted as Sshard, consist of nodes that retrieve their ledgers from the SC. Each node within a snapshot shard is responsible for storing both the latest snapshot Bnθ and the chaintail Lct. Lct contains the most recent blockchain transaction records following the latest snapshot. The ledger for the snapshot shard is represented as:

LSshard←{Gblockn,Bn2,⋯,Bnθ∪Lct},(7)

where n represents the number of the latest snapshot.

The concept of a “chaintail” is derived from Coinprune [24] and refers to the collection of all blocks that appear on the MC subsequent to the creation of the latest snapshot. In LSBSP, the snapshot synchronization processes continuously monitor and compare the state of the SC with that of the MC. Whenever a block is detected on the MC with a height exceeding the height of the final block in the latest snapshot, it is promptly appended to the chaintail list Lct, where Lct←{Bo1,⋯,Boi}, n<o∧i<θ. This ensures that the chaintail remains up-to-date, reflecting the latest changes on the blockchain.

Definition 5 (Bootstrapping). For each node ni∈N, perform the synchronization operation L0→Ln, where L0 represents the original state and Ln denotes a new state achieved by validating transactions to qualify as a validator.

Definition 6 (Epoch). An epoch e is defined by the interval [t0,t1]. Within epoch e, transactions TXs that occur are packaged into a candidate block Bij according to their timestamps. The transactions within Bij are then executed Exec(Bij), and undergoes a consensus ensures that all participating nodes agree on the final state of Bij, allowing it to be added to the blockchain.

4.3 Snapshot Chain Model

The state of the MC at time t denote as MC(t) is transformed into a snapshot SCt, SCt=F(MC(t)), where F is the function capturing the process of deriving the snapshot. A new verification node ni is initialized using SCt from the SC instead of the complete MC.

1) Snapshot data structure

The structure of the snapshot is illustrated in Fig. 3, it consists of a header and a body. The header includes the snapshot number SCi, the hash of the previous snapshot Hash(SCi−1), the hash of the current snapshot Hash(SCi), and T(SCi), which denote the timestamp of the snapshot SCi. Moreover, it provides information regarding the number of blocks θ contained. The header of the i-th snapshot SCiH can be expressed as Eq. (9):

Figure 3: The graph of snapshot data structure

SCi represent the snapshot number, serving as a unique identifier for each snapshot within the chain. A smaller snapshot number corresponds to an older block record. Snapshots are generated automatically at fixed intervals. Formally, the ledger of snapshot SCi is defined as follows:

LSCi←{Bi1,Bi2,⋯,Bin},(8)

where LSCi is the set of blocks included in the snapshot SCi, the sequence of snapshots SCi can be ordered by their snapshot numbers.

SCiH←{SCi,Hash(SCi−1),Hash(SCi),T(SCi),θ}.(9)

Definition 7 (Snapshot start timestamp). The start timestamp of the snapshot SCm, denoted as SstartSCm, is defined as the moment when the initial snapshot block m is created.

Definition 8 (Snapshot end timestamp). The end timestamp of the snapshot, denoted as SendSCm, is defined as the time when the initial snapshot block m is submitted.

The snapshot timestamp comprises both a start timestamp and an end timestamp, denoted as T(SCm)=(SstartSCm,SendSCm). The snapshot encompasses a series of θ consecutive blocks, commencing with the initial block and culminating with the end block. Together, these blocks form the core of the snapshot. The hash value of the snapshot is computed independently for both its header and body, and this hash is represented as shown in Eq. (10):

Hash(SCm)=H(hash(Bm1)||hash(Bm2)||⋯||hash(Bmθ)||SCmH).(10)

2) Create a snapshot.

The generation of the snapshot is triggered when the count of blocks between the current block and the initial block of the snapshot, denoted as Gblocki, reaches the threshold value of θ. The miner generates the snapshot concurrently with the creation of the candidate block and stores the hash of the snapshot in the snapshot header.

As shown in Fig. 2, the initial block of the n-th snapshot in c is denoted as Gblockn. The condition h(Bnx−Gblockn)<θ indicates that the number of blocks between the current block and the initial block of the snapshot is below the threshold θ; consequently, the block is appended to the chaintail Lct. Whileh(Bnx−Gblockn)=θ, a snapshot SCn is instantiated, Bnθ representing the culminating block of snapshot SCn, where n is a positive integer.

3) Snapshot synchronization.

The synchronization process for snapshots ensures alignment between the most recent state of the SC and the state of the MC. Algorithm 1 provides a detailed outline of the snapshot generation and synchronization algorithm utilized within the LSBSP framework.

In Algorithm 1, the process begins by searching for the block with the maximum height h(Bmx) in MC starting from B(m−1)θ (line 2). The block is then appended to the chaintail: Lct←Lct∪Bmx (line 3). If the number of blocks in the chaintail reaches the threshold θ, i.e., |Lct|=θ (line 4), the process proceed to create a new snapshot SCi, defined as SCi=Bm1,Bm2,⋯,Bmθ (line 5). This snapshot is then appended to SC, SC←SC∪SCi (line 6).

Next, the timestamps for the snapshot are updated, setting SstartSCm←Timestamp(Bm1) and SendSCm←Timestamp(Bmθ) (lines 7–8). The snapshot time interval is then defined as TSCm←(SstartSCm,SendSCm) (line 9). After this, the chaintail is reset, Lct←∅ (line 10).

If the number of blocks in the chaintail is less than θ, i.e., |Lct|<θ, the process continues by adding blocks to Lct and updating SC, SC←SC∪Lct (line 11). The process resumes if there exists a block Bmx in MC that is not yet in SC, i.e., ∃Bmx∈MC∧Bmx∉SC (line 12), ensuring that SC remains synchronized with the latest state of the blockchain. Since each search operation necessitates traversing only the newly added blocks, the time complexity for each incremental search is O(θ), resulting in a constant level time complexity for each snapshot generation.

4) Snapshot Chain Maintenance.

In the LSBSP framework, maintaining the snapshot chain is essential for ensuring the integrity and consistency of the blockchain. Once a snapshot SCn is created, nodes are tasked with verifying its validity and ensuring that it accurately reflects the current state of the MC. Nodes initiate the verification process by checking the header information of the snapshot. This verification is crucial for ensuring the completeness and integrity of the SC:

Check(SCi,Hash(SCm−1),Hash(SCm),T(SCm)).(11)

Next, nodes compute the hash value of the snapshot using the following formula:

Hash(SCm)=H(hash(Bm1)||hash(Bm2)||⋯||hash(Bmθ)||SCmH).(12)

Additionally, nodes must verify that all blocks included in the snapshot SCm exist in the current state of the MC:

∀Bmi∈SCm,Bmi∈MCandBmi<Bmjfori<j.(13)

This step ensures that the blocks are not only present but also in the correct order, thereby maintaining the integrity of the snapshot in relation to the MC.

4.4 State Pruning Bootstrapping

Operating in an untrusted environment presents security challenges, especially from potentially malicious nodes. To counter these, the blockchain network employs a distributed random mapping function A, which randomly allocates nodes across shards, thus reducing the likelihood that a single shard falls under malicious control. The function A maps nodes to shards with randomness:

A:N→S.(14)

State pruning in the blockchain system aims to reduce storage and computational demands by retaining only the essential states for ongoing operations. To balance the workload between the Sshard and the Fshard, we define a load balancing function f(α), where TPSshard represents the throughput of the Sshard, TPFshard represents the throughput of the Fshard, and α is a load distribution parameter with 0<α≤1. The load balancing function is defined as follows:

f(α)=TPFshardTPSshard≤α.(15)

Our objective is to achieve f(α)≈α, which means the load ratio between transactions handled by the snapshot shard and the full shard aligns with the target distribution parameter. This balance enables efficient transaction processing between the two shard types, optimizing storage efficiency and maintaining a balanced load across both shards.

Node states are bootstrapped to ensure consistent, accurate data across the network. Let B represent the bootstrapping process and V represent the verification process. These processes are specifically defined for each shard type F or snapshot σ.

B:N×F→State,V:N×F→Bool.(16)

The model incorporates a continuous alignment mechanism with the MC. For any node in shard Si, a discrepancy measure function ensures consistency between the state Ln and LFshard. This alignment detects discrepancies or malicious attempts to alter state data. In addition, the isolation of each shard acts as a defense against potential DoS attacks, allowing unaffected shards to maintain normal operations.

1) State data flow.

In Fig. 4, the dashed line delineates the state data flow among the various shards. The SC synchronizes seamlessly with the MC in real-time, ensuring constant alignment of data. Nodes within the Sshard initiate their state bootstrapping process by retrieving data from the SC, while nodes in the Fshard directly load their state from the MC.

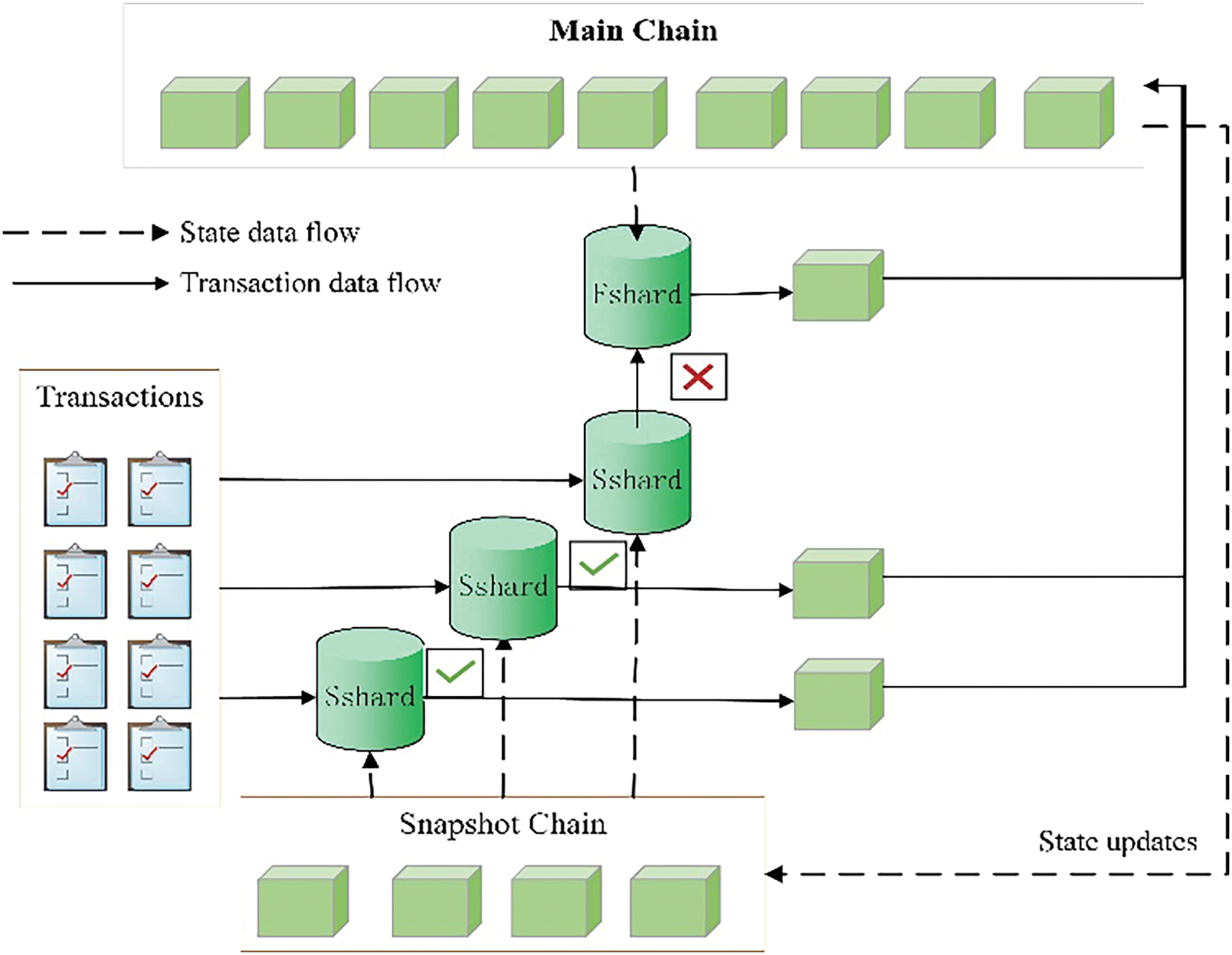
Figure 4: The state bootstrapping process of Fshard and Sshard

Here’s a comprehensive breakdown of the process: Initially, the verifier in Sshard performs a thorough search in the SC for the most recent snapshot. If the search yields SC=∅, it signifies that no snapshot has been generated as of yet. Consequently, the verifier retrieves the complete historical block states directly from the MC. Conversely, if SC≠∅, the verifier identifies the snapshot with the highest number and proceeds to verify if any subsequent blocks have been appended to the chaintail. This ensures that transactions initiated by various clients within the shard can be smoothly executed. The current and updated state of a snapshot, denoted as SCm, is represented by an indicator function as in Eq. (17).

I(SCm)={0misnotthelatestsnapshot1misthelatestsnapshot.(17)

2) Transaction data flow.

The transaction initially undergoes processing in the Sshard. If it fails to pass validation, it is forwarded to the Fshard for further execution. The Fshard maintains a comprehensive ledger of the blockchain, ensuring robust verification of transactions. This strategy efficiently resolves challenges related to transaction verification failures. Within a shard, nodes dynamically bootstrap their state ledgers, keeping them up-to-date as new blocks are appended to MC.

In LSBSP, the state block pruning method is adopted to dynamically maintain the state ledger, thereby enhancing its efficiency and scalability. The Snapshot-based State Bootstrapping Algorithm (SBA), outlined in Algorithm 2, facilitates the loading of distinct state ledger data based on the shard type of each node, optimizing the process and ensuring seamless integration across the network.

In Algorithm 2, the process begins by initializing the snapshot chain SC and the chaintail ledger Lct to empty sets: SC←∅,Lct←∅ (line 1). If Nodem∈Sshard and SC=∅, then the chaintail ledger Lct is set to the main chain MC, Lct←MC and Staten←Lct (lines 2–5). If SC≠∅, the maximum timestamp Tsn is searched for, and a snapshot ledger LSCn is downloaded by intersecting SCn with its index I(SCn) and unioning it with the next snapshot ledger SCn+1, LSCn←(SCn⋅I(SCn))∪SCn+1 (lines 6–8), if Lct=∅, then the node’s state Staten is set to LSCn, Staten←LSCn (lines 9–10), otherwise, Lct is updated by subtracting SC from MC, Lct←(MC−SC) and Staten is set to the union of LSCn and Lct, Staten←LSCn∪Lct (lines 11–15). For nodes not in the Sshard, if Nodem∉Sshard, their state Staten is directly set to the MC, Staten←MC (lines 16–18). Finally, the algorithm returns the node’s state Staten, ensuring that it reflects the current state of the blockchain (line 19).

5  Mathematical Analysis and Discussion

This section presents a comprehensive performance analysis of the LSBSP scheme, focusing on consistency, bootstrap time overhead, scalability and security.

5.1 Consistency Analysis

Theorem 1: The LSBSP scheme guarantees that for all transactions t processed across shards {S1,S2,⋯,Sk}, the probability of consistency is given by Pr[tisconsistent]≥1−ε, where ε converges to 0 as the number of nodes n approaches infinity.

Proof: After pruning, SC retains the most recent relevant states, allowing for efficient access to the current blockchain state. When a node i joins a shard, it synchronizes by downloading the latest snapshot and the current chain tail:

Li=LSCn+Lct.(18)

Transactions are initially validated against the SC. If the SC lacks sufficient information, validation is referred to the complete state maintained in the Fshard:

Li={LSshardLFshardif insufficient data inSC.(19)

Let Y be the random variable indicating the number of conflicting transactions during synchronization. For any transaction tx, it can be asserted that:

Pr[txisinconsistent]≤Pr[Y>0].(20)

If a transaction is inconsistent, it implies that the MC and SC are out of sync. To quantify the probability of conflicting transactions, the following expression can be used:

Pr[Y=0]=1−Pr[Y>0].(21)

Assuming nodes sample from a uniform distribution, the expected number of conflicts can be defined as:

E[Y]=n⋅p.(22)

where p is the probability of selecting a conflicting transaction. The probability of no conflicts occurring can be further bounded as:

Pr[Y>0]≤E[Y]=n⋅p.(23)

As n increases, with nodes synchronizing with the most recent state, it is expected that the probability of conflicts will decrease:

Pr[Y>0]→0asn→∞.(24)

This means that as the number of nodes grows, the likelihood of inconsistent transactions approaches zero.

5.2 Bootstrap Overhead Analysis

Generally, when considering the “Gen_shard” protocols and provided that SC≠∅ (signifying that the SC is non-empty), the mathematical expression for the time a verifier needs to fully load the blockchain’s ledger for transaction verification can be delineated as Eq. (25):

TGen_shard=∑s=0n∑i=0θTsi+∑j=0cT(n+1)j.(25)

Tsi represents the time required to bootstrap the i-th block of the s-th snapshot, while T(n+1)j denotes the bootstrap time cost of the j-th block in the chaintail, and c signifies the total number of blocks present in the chaintail.

The LSBSP protocol incorporates a SC to store historical blocks, wherein the snapshot blockchain comprises multiple snapshot blocks. Snapshots are generated based on a predetermined number of blocks on the MC. The time cost associated with snapshot bootstrapping in LSBSP is calculated as (26):

Tsnapshot=∑i=0θTni,(26)

where n symbolizes the latest snapshot number, the overall time required for the Sshard node to bootstrap its ledger is computed as Eq. (27):

TLSBSP=∑i=0θTni+∑j=0cT(n+1)j.(27)

Upon comparing Eqs. (25) and (27), it becomes evident that the time required for bootstrapping in the LSBSP protocol is substantially less than that needed in the Gen_shard protocol.

5.3 Scalability Analysis

The LSBSP approach demonstrates superior scalability compared to the No_shard scheme due to its ability to concurrently process transactions across multiple shards.

No_shard Method. In the No_shard framework, let Tb denote the block generation interval. The throughput TPSLSBSP can be calculated as:

TPSNo_shard=(Bp(t)Bp(u)−Bp(h))/Bp(t)Tb.(28)

The LSBSP utilizes k shards, facilitating simultaneous transaction processing within each shard. The throughput TPSLSBSP can be expressed as:

TPSLSBSP=k((Bp(t)Bp(u)−Bp(h))/Bp(t))Tb.(29)

To demonstrate scalability, the analysis focuses on how the throughput of the LSBSP scheme scales with the number of shards k. By comparing Eqs. (28) and (29), it is found that:

TPSLSBSP=k⋅TPSNo_shard.(30)

This relationship indicates that the throughput of the LSBSP scheme is directly proportional to the throughput of the No_shard scheme, scaled by a factor of k.

Assuming all shards operate independently and efficiently, the overall scalability of the LSBSP scheme can be expressed in terms of its throughput as:

TPSLSBSP∝k.(31)

This linear scaling persists as long as there are sufficient resources and transactions to keep all shards active. Let R be the total number of resources available, and T denote the total number of transactions that can be processed within a given time frame. The relationship can be expressed as:

TPSLSBSP=RT⋅k.(32)

This attribute is particularly important in environments such as IoMT data sharing, where high scalability is essential for timely data access and processing.

5.4 Safety Analysis

The assignment of nodes to shards in the LSBSP scheme is modeled as a random sampling problem, which can be simulated using a binomial distribution. Let f be the probability of selecting a malicious node, and F0 denote the threshold proportion of malicious nodes at which a shard is considered dishonest. The random variable X indicates the number of malicious nodes selected. The probability Pr of exactly nF0 malicious nodes being selected is given by the binomial distribution express in Eq. (33):

Pr[X=nF0]=(nnF0)fnF0(1−f)n(1−F0).(33)

A shard is considered dishonest if the proportion of malicious nodes X/n>F0. The probability of such a failure occurring is articulated as Eq. (34):

Pr[X≥⌈nF0⌉]=∑x=⌈nF0⌉n(nx)fx(1−f)n−x.(34)

Theorem 2: Given a shard of size n and a probability f of selecting a malicious node, the probability that a shard becomes dishonest (i.e., contains more than F0 fraction of malicious nodes) can be bounded by the Chernoff bound.

Proof: Using the Chernoff bound, it is possible to bound the probability that the number of malicious nodes X exceeds nF0:

Pr[X≥(1+δ)μ]≤(eδ/(1+δ)1+δ)μ,(35)

where μ=nf is the expected number of malicious nodes, and δ=nF0μ−1=nF0nf−1=F0f−1. Thus,

Pr[X≥nF0]≤(eF0f−1/(F0f)F0f)nf.(36)

As n grows, the probability of a shard becoming dishonest decreases exponentially. LSBSP scheme enhances security by reducing the probability of forming dishonest shards. By dynamically pruning and maintaining state ledgers, LSBSP ensures that even if a shard contains malicious nodes, their influence is minimized.

6  Experimental Evaluation

This section presents a comprehensive performance evaluation of the proposed scheme through simulation experiments on a payment system. The blockchain in this system securely records transfers and balance changes across all accounts. All simulations were performed on a Windows 11 operating system, leveraging an Intel(R) Core(TM) i9-12900 K processor and 64 GB of RAM.

In the simulation setup, a blockchain system was implemented to store transfer records, account balances, and verify blocks. Each shard proposing a block for parallel verification at each epoch t, with experiments replicated 20 times to ensure accuracy.

Simulations were run on a single computer with network nodes N ranging from 40 to 200, each performing sequential local computations. Nodes were evenly distributed across shards to model increasing network loads and measure throughput. The number of shards, k, was varied from 10 to 50 to evaluate performance impacts, while transactions were balanced across shards to simulate an even workload. Each simulation ran for t=2000 epochs to assess system stability and efficiency over time.

6.1 Baselines

To benchmark the performance of the proposed sharding scheme, three comparative schemes were employed:

1) No_shard. In this scheme, all nodes within the network maintain an complete replica of the blockchain and process transactions sequentially.

2) Gen_shard. This approach employs sharding to partition network nodes while maintaining a complete copy of the blockchain ledger without pruning. Each shard independently processes non-overlapping transactions.

3) PolyShard. The PolyShard protocol [14] employs polynomial coding computing technology to enhance the scalability of existing blockchains. It introduces computational redundancy in the form of unconventional coding to address failures.

6.2 Scalability Analysis of the Scheme

In the scalability experiment, the relationship between the number of network nodes, the number of epochs, and the system’s throughput is explored. Specifically, 2000 epochs are conducted, and the number of network nodes is gradually scaled up from 40 to 200 to assess the system’s scalability and observe changes in throughput. The number of nodes in each shard remains constant.

Fig. 5 provides a comprehensive comparison of the throughputs achieved by different schemes across varying epochs and node counts. The results are presented in four distinct subplots, each focusing on a specific strategy: (a) No_shard, (b) Gen_shard, (c) PolyShard, and (d) LSBSP.

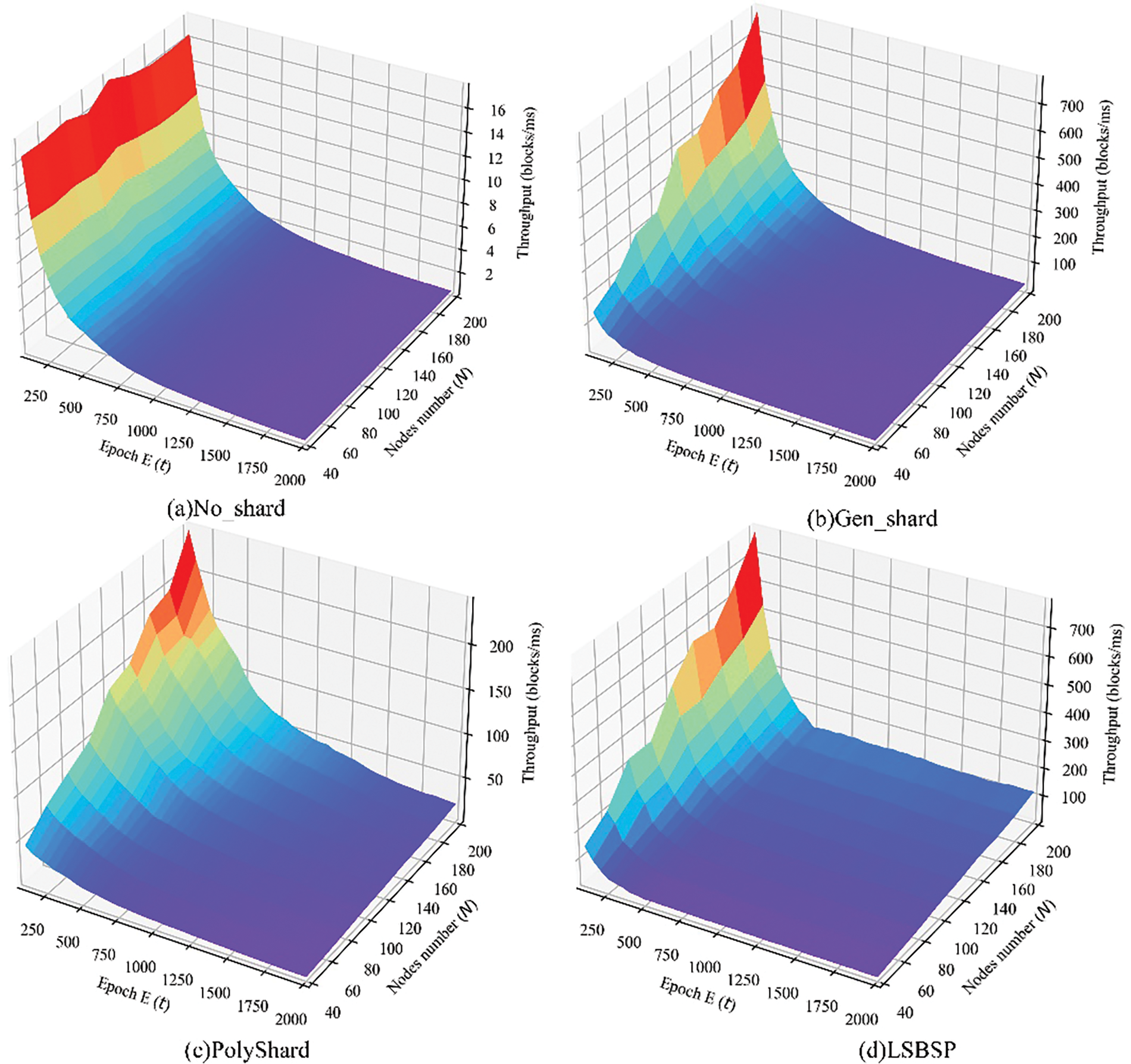
Figure 5: Comparison of throughput across different epochs and varying node counts

To improve observation and understanding, Fig. 6 illustrates the relationship between throughput and the number of epochs across different schemes, with the shard count set to (a) k=10, (b) k=20, (c) k=30, (d) k=40, respectively.

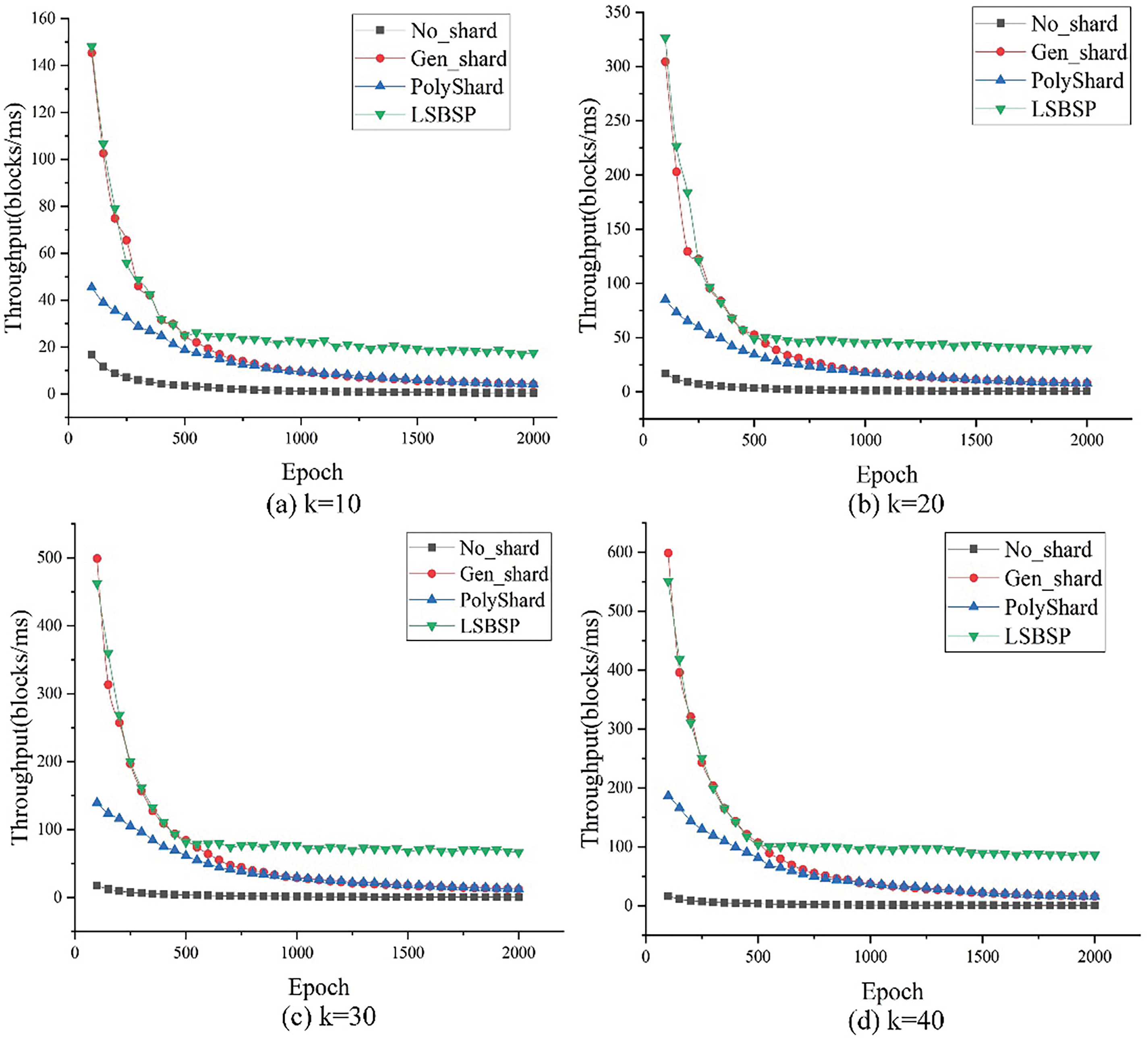
Figure 6: The correlation between throughput and various epochs across different schemes

The No_shard scheme shows limited scalability with stagnant throughput as node counts increase across all epochs. This is due to each node processing every transaction in the network, making the system prone to congestion and longer transaction delays as transaction volumes rise.

Both Gen_shard and PolyShard protocols increased achieve higher throughput as the network expands due to node partitioning and parallel processing of distinct transactions. However, as more blocks are added over successive epochs, the increased storage and computational demands lead to a throughput decline.

The LSBSP scheme demonstrates particularly evident superior scalability when the number of nodes increases and the epoch size is large, resulting in a rapid surge in throughput. This performance is driven by the implementation of pruning block technology, which periodically trims the MC, coupled with a lightweight blockchain shard approach. This strategy effectively mitigates issues such as significant state bootstrapping burdens and high time overhead, enabling LSBSP to consistently maintain high throughput as the epoch size increases. Specifically, in our experiments with k=40 and Epoch=2000, LSBSP achieved approximately 5.51 times higher throughput than PolyShard, 5.54 times higher than Gen_shard, and a remarkable 197 times higher than the No_shard scheme.

Fig. 7 clearly illustrates the relationship between throughput and the number of nodes across the four schemes when Epoch=850. As expected, the throughput in No_shard remains unaffected by the increasing number of nodes due to the sequential execution of all transactions. This suggests that, in the No_shard scenario, adding more nodes does not improve the overall efficiency of transaction processing in the blockchain. On the other hand, Gen_shard and PolyShard exhibit similar throughput patterns. As the number of nodes increases, the throughput increases slightly. This is attributed to the significant storage burden on network nodes. When N=200, the performance of LSBSP significantly surpasses that of the other schemes, achieving approximately 2.17 times higher throughput than Gen_shard, approximately 2.27 times higher than PolyShard, and an impressive 76.1 times higher than No_shard. As epochs increase, LSBSP is likely to achieve even better performance in terms of TPS.

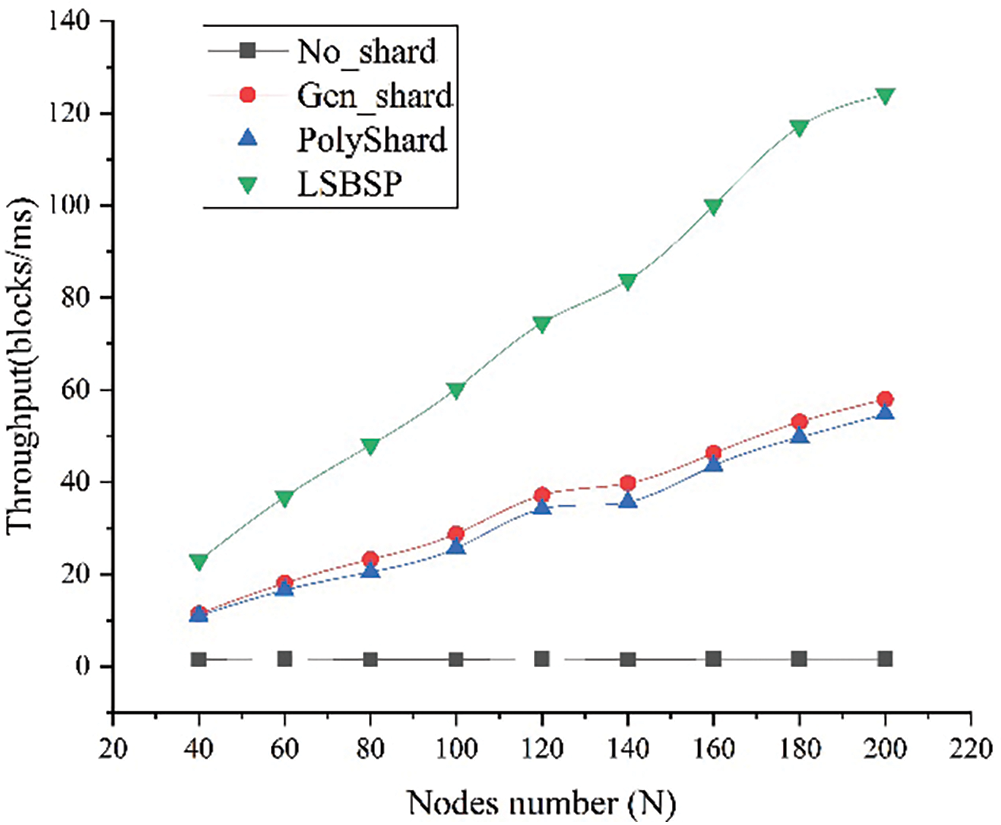
Figure 7: Throughput vs. the number of nodes for the four schemes

6.3 Latency Comparison of Different Shards

In this section, we conduct experiments to analyze latency across different shard counts within four distinct schemes. Tests were performed by varying the shard counts to precisely evaluate the impact on processing times. The results are displayed in Fig. 8, featuring subplots for (a) k=10, (b) k=20, (c) k=30, and (d) k=40.

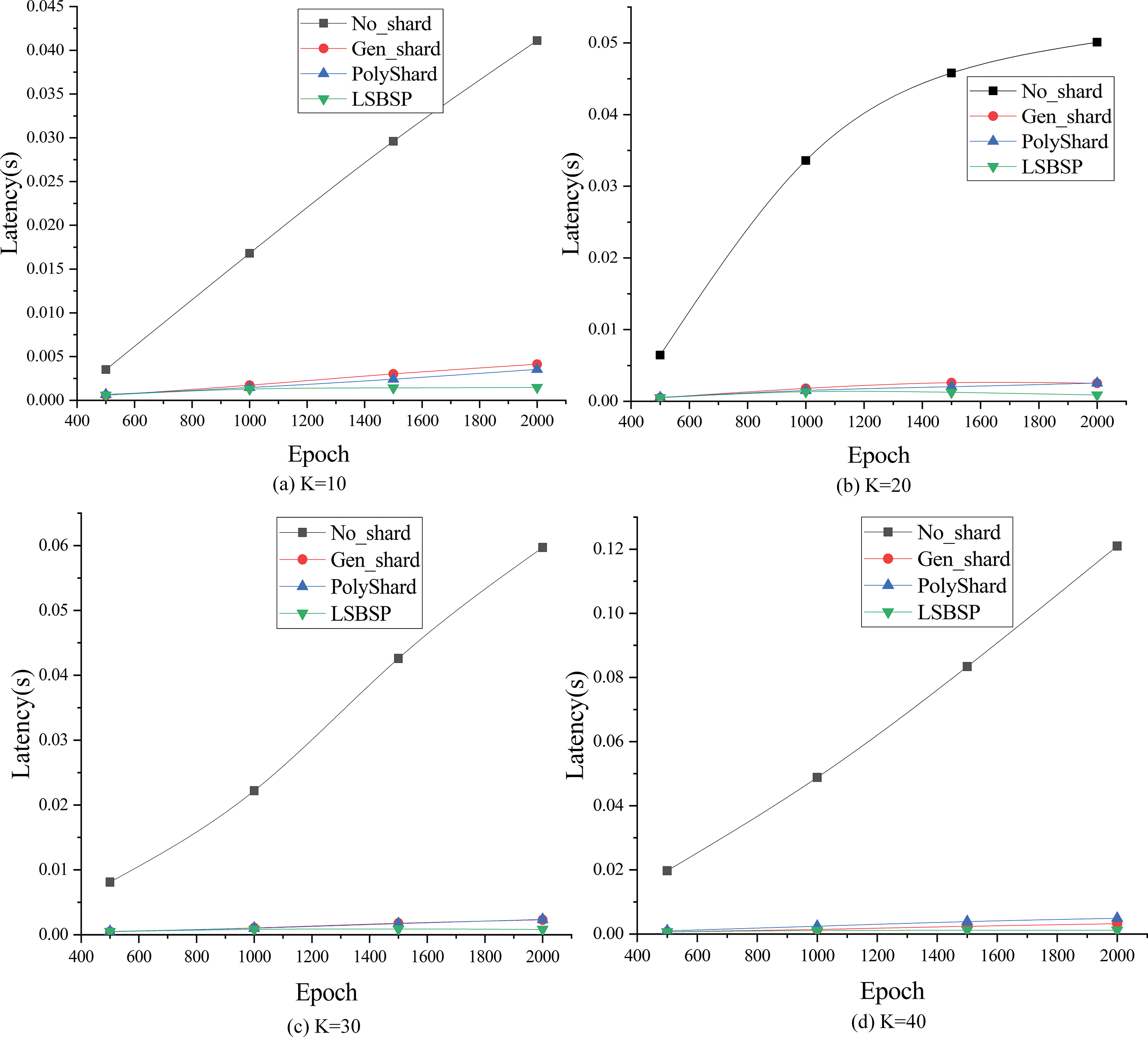
Figure 8: The latency under different number of shards

Notably, the latency of the No_shard scheme increases linearly with epoch size. The Gen_shard and PolyShard protocols perform well with smaller epochs but experience heightened latency as epoch sizes increase. This is due to more transactions being packed into each block, resulting in a larger number of blocks generated within each shard, which extends the time needed to validate historical blocks, thereby lengthening transaction processing times. In contrast, the LSBSP scheme exhibits strong performance as it prunes historical blocks, reducing the validation time and streamlining the process. When k=40 and Epoch=2000, the latency of the No_shard scheme is 101.68 times higher than that of LSBSP, Gen_shard’s latency is 2.69 times higher, and PolyShard’s latency is 4.1 times higher than that of LSBSP.

6.4 Bootstrap Overhead Analysis

This section explores the additional storage capacity costs incurred by a verification node when it joins and undergoes the state bootstrap process within the network. In the No_shard scheme, all nodes must store the entire ledger to facilitate transaction verification. However, in PolyShard, as the number of blocks appended to each shard grows, the computational complexity of block verification also increases. Verifiers create a comprehensive ledger copy by executing historical transactions within the blockchain, leading to a linear surge in state bootstrap overhead as the block height rises. To mitigate this storage consumption, LSBSP periodically generates snapshots and retrieves the latest state data from them. Assuming an average block size of 1.52 MB, Fig. 9 illustrates how the size of the node’s bootstrapping state varies as the number of blocks increases in both LSBSP and Polyshard schemes. Polyshard exhibits a linear growth in storage overhead, whereas LSBSP maintains a relatively stable storage overhead.

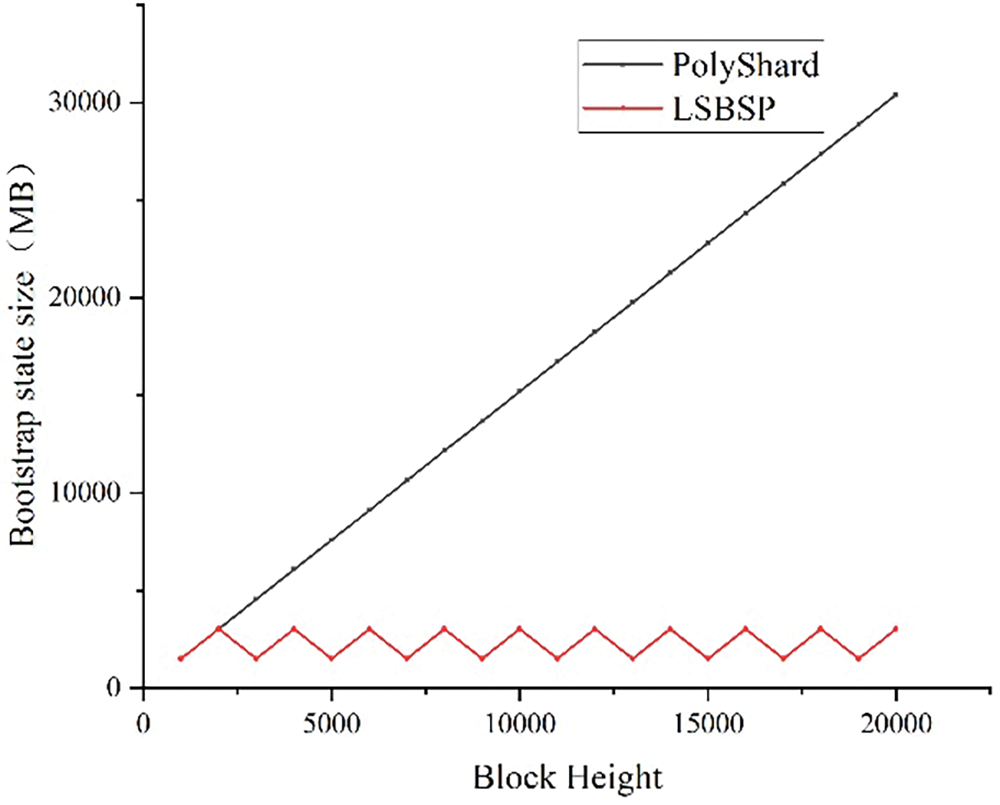
Figure 9: The overhead of state bootstrapping

6.5 Application in IoMT

Blockchain technology is playing a pivotal role in addressing various healthcare challenges, from safeguarding patient data to enhancing the efficient of EHR data sharing. However, in practical applications, blockchain for electronic medical records often functions as a generic data storage system, resulting in the accumulation of a vast amount of ledger data that includes numerous outdated and infrequently used entries [34]. Traditionally, validators are required to download and indefinitely store all ledger information, which not only imposes a significant burden on network nodes but also increases the risk of centralization [35]. To address the latency issues in real time IoT applications, the LSBSP model optimizes storage and reduces system latency, enhancing responsiveness. By selectively pruning outdated or infrequently accessed data from the blockchain, LSBSP minimizes the active ledger size, lowering retrieval times and overall processing delays.

As depicted in Fig. 10, data collectors upload electronic health records to the EHR blockchain. The LSBSP model enhances real-time performance by employing dual-chain structure that efficiently prune historical data. For example, medical records that have not been accessed or updated in over five years can be removed from the SC, ensuring that only relevant, recent data remains. This approach significantly reduces the storage and retrieval load on blockchain nodes, allowing the network to handle real-time IoMT transactions more effectively.

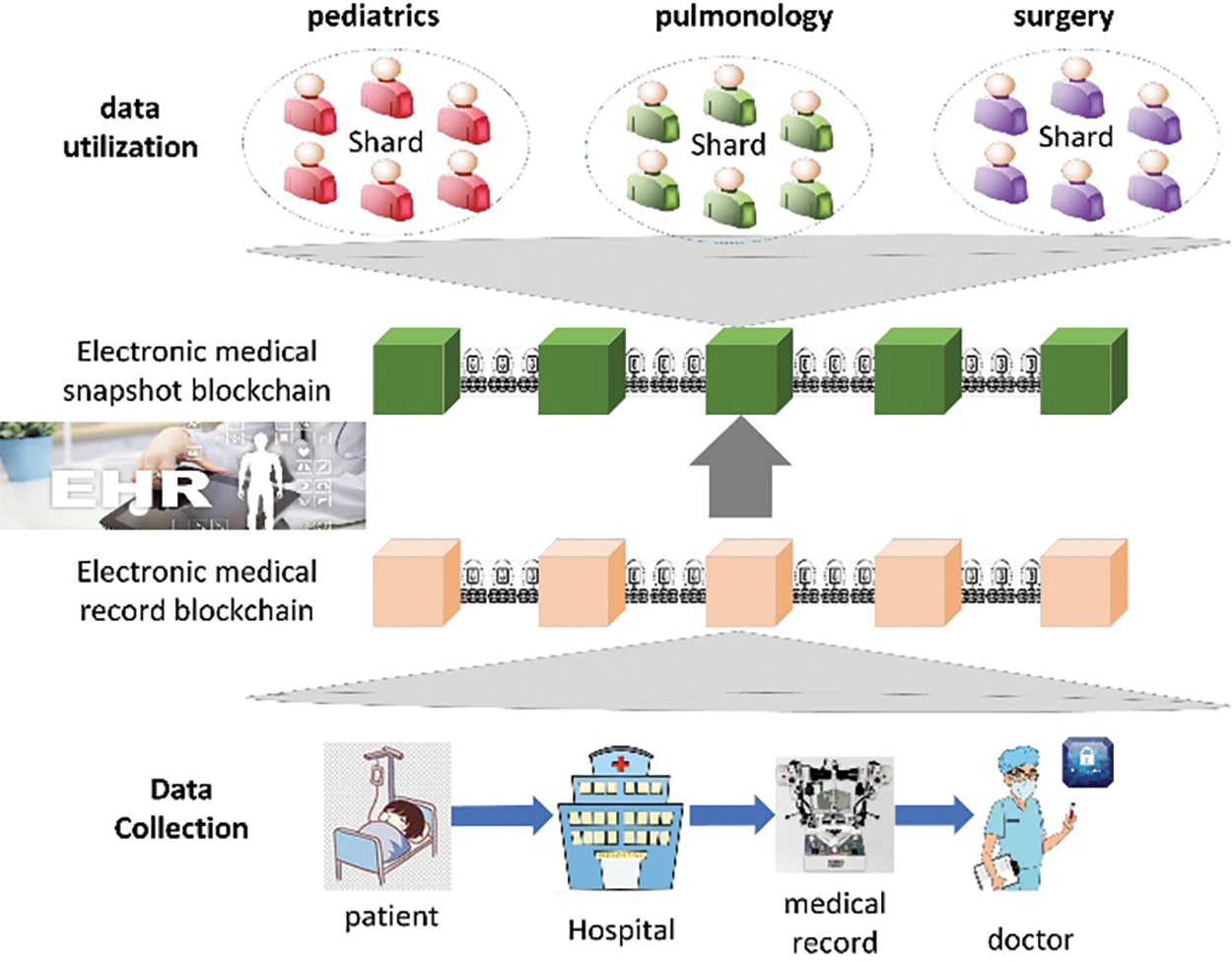
Figure 10: Application of LSBSP in the medical electronic health records blockchain

The LSBSP model addresses key security challenges in healthcare, including data confidentiality, integrity, and unauthorized access. By regularly pruning historical data, LSBSP limits access to recent records only, reducing exposure to older, sensitive information and mitigating risks of unauthorized access. Additionally, it can apply encryption to critical data blocks, ensuring access is restricted to authorized entities. To counter replay attacks, which may retransmit valid data to compromise records, LSBSP retains only recent validated snapshots, with hash-based verification maintaining data integrity and resistance to tampering. Against DoS threats, the model’s pruning mechanism reduces data load, easing validation demands and bolstering resilience under high request volumes.

7  Conclusions and Future Work

This article addresses data management and sharing challenges by introducing a lightweight blockchain sharding method that leverages snapshot technology. The LSBSP protocol combines state pruning with sharding to reduce storage demands on network nodes effectively. Through parallel transaction processing, this approach minimizes the typical overhead associated with sharding state bootstrapping, enhancing blockchain processing efficiency. Theoretical analysis and experimental results show that LSBSP outperforms existing sharding schemes in scalability and overhead reduction.

Currently, the solution lacks sufficient flexibility to dynamically adjust to fluctuating workloads, which may affect performance in high variable environments. To address this, future work will explore advanced optimization techniques, including AI-driven automated shard resizing and enhanced fault tolerance through redundancy protocols and recovery mechanisms, ensuring continuity during node failures. Furthermore, we plan to pursue real-world deployment within large scale IoMT ecosystems. This will involve pilot testing with healthcare providers to evaluate its practicality and identify areas for improvement. We also intend to strengthen security by incorporating advanced cryptographic methods to protect sensitive data, alongside machine learning techniques to predict transaction patterns and dynamically optimize shard management. Collectively, these efforts aim to create a more robust, secure, and effective data management and sharing framework, tailored to the rigorous demands of IoMT applications.

Acknowledgement: The authors express gratitude to the research group members for their support.

Funding Statement: This work is supported by the National Natural Science Foundation of China (62272207), the Key Project of Natural Science Foundation of Jiangxi Province (20224ACB202009), the Science and Technology Project of the Department of Education of Jiangxi Province (GJJ2200925) and the Jiangxi Provincial Health Commission Science and Technology Plan (202311147).

Author Contributions: The authors confirm contribution to the paper as follows: Methodology and design: Guoqiong Liao; Algorithm design and experimental analysis: Yinxiang Lei; Data analysis: Yufang Xie; Review and supervision: Neal N. Xiong. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data supporting this study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. A. Heidari, N. J. Navimipour, H. Dag, S. Talebi, and M. Unal, “A novel blockchain-based deepfake detection method using federated and deep learning models,” Cognit. Comput., vol. 16, no. 3, pp. 1073–1091, 2024. doi: 10.1007/s12559-024-10255-7. [Google Scholar] [CrossRef]

2. A. Qashlan, P. Nanda, and M. Mohanty, “Differential privacy model for blockchain based smart home architecture,” Future Gener. Comput. Syst., vol. 150, pp. 49–63, 2024. doi: 10.1016/j.future.2023.08.010. [Google Scholar] [CrossRef]

3. H. Xu, S. Qi, Y. Qi, W. Wei, and N. Xiong, “Secure and lightweight blockchain-based truthful data trading for real-time vehicular crowdsensing,” ACM Trans. Embed. Comput. Syst., vol. 23, no. 1, pp. 1–31, 2024. doi: 10.1145/3687309. [Google Scholar] [CrossRef]

4. S. Datta and S. Namasudra, “Blockchain-based smart contract model for securing healthcare transactions by using consumer electronics and mobile-edge computing,” IEEE Trans. Consum. Electron., vol. 70, no. 1, pp. 4026–4036, 2024. doi: 10.1109/TCE.2024.3357115. [Google Scholar] [CrossRef]

5. G. A. F. Rebello et al., “A survey on blockchain scalability: From hardware to layer-two protocols,” IEEE Commun. Surv. Tutor., vol. 26, no. 4, pp. 2411–2458, 2024. doi: 10.1109/COMST.2024.3376252. [Google Scholar] [CrossRef]

6. L. Luu, V. Narayanan, C. Zheng, K. Baweja, S. Gilbert and P. Saxena, “A secure sharding protocol for open blockchains,” in Proc. 2016 ACM SIGSAC Conf. Comput. Commun. Secur., New York, NY, USA, 2016, pp. 17–30. [Google Scholar]

7. E. Kokoris-Kogias, P. Jovanovic, L. Gasser, N. Gailly, E. Syta and B. Ford, “OmniLedger: A secure, scale-out, decentralized ledger via sharding,” in Proc. 2018 IEEE Symp. Secur. Priv. (SP), 2018, pp. 583–598. [Google Scholar]

8. M. Zamani, M. Movahedi, and M. Raykova, “RapidChain: Scaling blockchain via full sharding,” in Proc. 2018 ACM SIGSAC Conf. Comput. Commun. Secur., New York, NY, USA, 2018, pp. 931–948. [Google Scholar]

9. H. Luo, “ULS-PBFT: An ultra-low storage overhead PBFT consensus for blockchain,” Blockchain Res. Appl., vol. 4, no. 4, 2023, Art. no. 100155. doi: 10.1016/j.bcra.2023.100155. [Google Scholar] [CrossRef]

10. S. Yuan, B. Cao, Y. Sun, Z. Wan, and M. Peng, “Secure and efficient federated learning through layering and sharding blockchain,” IEEE Trans. Netw. Sci. Eng., vol. 11, no. 3, pp. 3120–3134, 2024. doi: 10.1109/TNSE.2024.3361458. [Google Scholar] [CrossRef]

11. F. Hu, S. Qiu, X. Yang, C. Wu, M. B. Nunes and H. Chen, “Privacy preserving healthcare and medical data collaboration service system based on blockchain and federated learning,” Comput. Mater. Contin., vol. 80, no. 2, pp. 1–10, 2024. doi: 10.32604/cmc.2024.052570. [Google Scholar] [CrossRef]

12. Z. Zhen, X. Wang, H. Lin, S. Garg, P. Kumar and M. S. Hossain, “A dynamic state sharding blockchain architecture for scalable and secure crowdsourcing systems,” J. Netw. Comput. Appl., vol. 222, 2024, Art. no. 103785. doi: 10.1016/j.jnca.2023.103785. [Google Scholar] [CrossRef]

13. R. Rana, S. Kannan, D. Tse, and P. Viswanath, “Free2Shard: Adversary-resistant distributed resource allocation for blockchains,” Proc. ACM Meas. Anal. Comput. Syst., vol. 6, no. 1, pp. 1–38, 2022. [Google Scholar]

14. S. Li, M. Yu, C. -S. Yang, A. S. Avestimehr, S. Kannan and P. Viswanath, “PolyShard: Coded sharding achieves linearly scaling efficiency and security simultaneously,” IEEE Trans. Inf. Forensics Secur., vol. 16, pp. 249–261, 2021. doi: 10.1109/TIFS.2020.3009610. [Google Scholar] [CrossRef]

15. M. Li, X. Luo, K. Xue, Y. Xue, W. Sun and J. Li, “A secure and efficient blockchain sharding scheme via hybrid consensus and dynamic management,” IEEE Trans. Inf. Forensics Secur., vol. 19, pp. 5911–5924, 2024. doi: 10.1109/TIFS.2024.3406145. [Google Scholar] [CrossRef]

16. Y. Xu, J. Zheng, B. Düdder, T. Slaats, and Y. Zhou, “A two-layer blockchain sharding protocol leveraging safety and liveness for enhanced performance,” in Proc. 2024 Netw. Distrib. Syst. Secur. (NDSS) Symp., San Diego, CA, USA, 2024. [Google Scholar]

17. A. Vakili, H. M. R. Al-Khafaji, M. Darbandi, A. Heidari, N. J. Navimipour and M. Unal, “A new service composition method in the cloud-based internet of things environment using a grey wolf optimization algorithm and mapReduce framework,” Concurr. Comput.: Pract. Exp., vol. 36, no. 16, 2024, Art. no. e8091. doi: 10.1002/cpe.8091. [Google Scholar] [CrossRef]

18. J. Zhang, W. Chen, S. Luo, T. Gong, Z. Hong and A. Kate, “Front-running attack in sharded blockchains and fair cross-shard consensus,” in Netw. Distrib. Syst. Secur. Symp. (NDSS), San Diego, CA, USA, 2024. [Google Scholar]

19. J. Xu, Y. Ming, Z. Wu, C. Wang, and X. Jia, “X-Shard: Optimistic cross-shard transaction processing for sharding-based blockchains,” IEEE Trans. Parallel Distrib. Syst., vol. 35, no. 4, pp. 548–559, 2024. doi: 10.1109/TPDS.2024.3361180. [Google Scholar] [CrossRef]

20. Y. Tao, B. Li, J. Jiang, H. C. Ng, C. Wang and B. Li, “On sharding open blockchains with smart contracts,” in Proc. 36th Int. Conf. Data Eng. (ICDE), 2020, pp. 1357–1368. [Google Scholar]

21. Z. Hong, S. Guo, E. Zhou, W. Chen, and H. Huang, “GriDB: Scaling blockchain database via sharding and off-chain cross-shard mechanism,” Proc. VLDB Endowment, vol. 16, no. 7, pp. 1685–1698, 2023. doi: 10.14778/3587136.3587143. [Google Scholar] [CrossRef]

22. L. Ren, W. -T. Chen, and P. A. S. Ward, “SnapshotSave: Fast and low storage demand blockchain bootstrapping,” in Proc. 36th Annu. ACM Symp. Appl. Comput., New York, NY, USA, 2021, pp. 291–300. [Google Scholar]

23. J. W. Heo, G. S. Ramachandran, A. Dorri, and R. Jurdak, “Blockchain data storage optimisations: A comprehensive survey,” ACM Comput. Surv., vol. 56, no. 7, pp. 1–27, Apr. 2024. doi: 10.1145/3645104. [Google Scholar] [CrossRef]

24. R. Matzutt, B. Kalde, J. Pennekamp, A. Drichel, M. Henze and K. Wehrle, “CoinPrune: Shrinking bitcoin’s blockchain retrospectively,” IEEE Trans. Netw. Serv. Manage., vol. 18, no. 3, pp. 3064–3078, 2021. doi: 10.1109/TNSM.2021.3073270. [Google Scholar] [CrossRef]

25. K. Suresh, K. Anand, G. Nagappan, and R. Pugalenthi, “A blockchain based cloud file storage system using fuzzy based hybrid flash butterfly optimization approach for storage weight reduction,” Int. J. Fuzzy Syst., vol. 26, no. 3, pp. 978–991, 2024. doi: 10.1007/s40815-023-01645-4. [Google Scholar] [CrossRef]

26. C. Wang, K. Wang, M. Li, F. Wei, and N. Xiong, “Chunk2vec: A novel resemblance detection scheme based on sentence bert for post deduplication delta compression in network transmission,” IET Commun., vol. 18, no. 2, pp. 145–159, 2024. doi: 10.1049/cmu2.12719. [Google Scholar] [CrossRef]

27. A. Heidari, N. J. Navimipour, H. Dag, and M. Unal, “Deepfake detection using deep learning methods: A systematic and comprehensive review,” WIREs Data Min. Knowl., vol. 14, no. 2, 2024, Art. no. e1520. doi: 10.1002/widm.1520. [Google Scholar] [CrossRef]

28. Y. Q. Fan, D. Sheng, and L. F. Wang, “Blockchain storage optimization based on erasure codes,” J. Comput., vol. 45, no. 4, pp. 858–876, 2022. [Google Scholar]

29. X. Qi, Z. Zhang, C. Jin, and A. Zhou, “A reliable storage partition for permissioned blockchain,” IEEE Trans. Knowl. Data Eng., vol. 33, no. 1, pp. 14–27, 2021. doi: 10.1109/TKDE.2020.3012668. [Google Scholar] [CrossRef]

30. P. Huang, X. Ren, T. Huang, A. S. Voundi Koe, D. S. Wong and H. Jiang, “SnapshotPrune: A novel bitcoin-based protocol toward efficient pruning and fast node bootstrapping,” Tsinghua Sci. Technol., vol. 29, no. 4, pp. 1037–1052, 2024. doi: 10.26599/TST.2023.9010014. [Google Scholar] [CrossRef]

31. R. Kumar, R. Tripathi, N. Marchang, G. Srivastava, T. R. Gadekallu and N. N. Xiong, “A secured distributed detection system based on IFPS and blockchain for industrial image and video data security,” J. Parallel Distr. Comput., vol. 152, pp. 128–143, 2021. doi: 10.1016/j.jpdc.2021.02.022. [Google Scholar] [CrossRef]

32. J. Wang, J. Chen, N. Xiong, O. Alfarraj, A. Tolba and Y. Ren, “S-BDS: An effective blockchain-based data storage scheme in zero-trust IoT,” ACM Trans. Internet Technol., vol. 23, no. 3, pp. 1–23, 2023. doi: 10.1145/3511902. [Google Scholar] [CrossRef]

33. F. Yang, Z. Ding, L. Jia, Y. Sun, and Q. Zhu, “Blockchain-based file replication for data availability of IPFS consumers,” IEEE Trans. Consum. Electron., vol. 70, no. 1, pp. 1191–1204, 2024. doi: 10.1109/TCE.2024.3364237. [Google Scholar] [CrossRef]

34. Z. Sun, D. Han, D. Li, T. -H. Weng, K. -C. Li and X. Mei, “MedRSS: A blockchain-based scheme for secure storage and sharing of medical records,” Comput. Ind. Eng., vol. 183, 2023, Art. no. 109521. doi: 10.1016/j.cie.2023.109521. [Google Scholar] [CrossRef]

35. T. Benil and J. Jasper, “Blockchain based secure medical data outsourcing with data deduplication in cloud environment,” Comput. Commun., vol. 209, pp. 1–13, 2023. doi: 10.1016/j.comcom.2023.06.013. [Google Scholar] [CrossRef]