Privacy-Preserving Fingerprint Recognition via Federated Adaptive Domain Generalization

1  Introduction

Biometric features, such as facial structure, fingerprints, and iris patterns, are critical physiological and behavioural attributes for verifying individual identity. Among them, due to their uniqueness and invariance, fingerprint features play a crucial role in various fields, such as public safety, criminal investigation, mobile device security, financial operations, and access control systems. Deep learning has demonstrated significant advantages in fingerprint recognition, particularly in handling low-quality and partially missing fingerprint data, with improved robustness and automated feature extraction capabilities. However, centralized training in traditional deep learning presents significant privacy risks, especially when handling sensitive information. Processing large datasets centrally further increases the likelihood of data leakage. Consequently, developing a framework that enables multiple clients to collaboratively train models without sharing raw data is essential. Federated Learning (FL) enables local training on clients and the subsequent upload of only the model parameters to a central aggregator, without disclosing any original data, achieving data decentralization and thereby effectively protecting privacy. In recent years, FL has been extended to various biometric systems, including facial [1–3] and finger vein recognition [4,5].

Despite the advantages of federated learning, it still faces challenges when applied to fingerprint recognition. Firstly, similar to facial data, the variations influenced by environmental, racial, sensor quality, image resolution, and other related factors lead to significant differences in fingerprint data. This heterogeneity causes biases in the local models’ representation vectors towards their data domains, which hampers their adaptability to other distributions and diminishes the overall representational capability of the global model [6]. Moreover, the local optimization objectives of different clients do not align with the global optimization goals, leading local models to converge in diverse directions and thereby impeding the global model’s ability to achieve consistent convergence [7]. Although federated learning ensures that original data remains on the client through data decentralization, reducing the risk of direct data leakage, it still cannot completely prevent data leakage caused by attacks on gradient information in model updates. Additionally, model updates may reveal sensitive information indirectly through membership inference attacks or model inversion attacks, where an attacker could infer if a particular data sample was used during training or even reconstruct parts of the data. For example, original data can be inferred through techniques such as gradient inversion. Furthermore, studies by Zhu et al. [8], Geiping et al. [9], and Wu et al. [10] have shown that attackers can reconstruct original training data through gradient inversion attacks. Therefore, FL still remains vulnerable to privacy attacks, and additional privacy protection measures, such as enhanced encryption or data obfuscation techniques, are necessary within the current federated learning framework.

We propose an Adaptive Federated Fingerprint Recognition (AFFR) method to address the issues above. In this method, an adaptive weighting mechanism is embedded to tackle the heterogeneity problem caused by the significant differences in fingerprint data resulting from various regional, racial, and environmental factors. Specifically, during the t-th round of global model generation θgt+1, the global model θgt from the t−1 round is first distributed to the clients i=1,2,…,C. On each client, a subset 𝒟i¯ of the local data is used to evaluate the performance of the distributed model, and the generalization gap G𝒟i¯(θgt) is calculated as the difference in performance between θgt and the previously updated local model θit−1′. After local training, both the generalization gap and the updated local model θit′are uploaded to the server. The server then uses the uploaded generalization gap to adjust the aggregation weights for generating θgt+1. This method effectively mitigates the degradation of model performance caused by data heterogeneity. Additionally, during local training on the client i, a differential privacy protection mechanism is embedded. By adding random noise to sensitive data, this reduces the risk of fingerprint privacy data leakage caused by gradient inversion attacks. Experiments have been conducted on three public datasets, demonstrating the method’s effectiveness in preserving data privacy, improving generalization in heterogeneous environments, and enhancing overall model performance.

2  Related Work

2.1 Fingerprint Recognition

Traditional methods rely heavily on manually extracted features, such as minutia and core points. However, in real-world applications, fingerprint data is often affected by factors such as sensor quality, acquisition conditions, and the condition of the finger, leading to inconsistent or partially missing data. These inconsistencies can make traditional feature extraction methods less effective. In contrast, deep learning methods are more capable of handling such complex data and can maintain high accuracy even in practical application scenarios.

Siamese networks have also been effectively employed in fingerprint recognition. Liu et al. [11] designed an embedded image processing algorithm based on a Siamese network to enable fingerprint recognition from any source without requiring a pre-built database. Zhu et al. [12] further compared the impact of different network structures on fingerprint recognition accuracy using three distinct Siamese networks.

Subsequently, techniques for fingerprint recognition have significantly improved through novel feature extraction and model structure optimization methods. Öztürk et al. [13] proposed a novel local descriptor generation model that generates embedding vectors for a fixed-size patch extracted around a minutia, using a local similarity assignment algorithm to produce a global similarity match score. Saeed et al. [14] aimed to determine the architecture of CNN models automatically adapted to fingerprint classification using FKT and the ratio of the traces of the between-class scatter matrix and the within-class scatter matrix to determine the number of layers and filters automatically. Zhang et al. [15] enhanced partial fingerprint recognition through occlusion-enhanced data augmentation and occlusion-aware modeling.

Moreover, attention mechanisms are widely employed in fingerprint recognition. Chen et al. [16] proposed a novel single-to-multiparty fingerprint recognition method based on the attention mechanism to solve the local fingerprint matching problem by adaptively extracting and fusing the features of a set of fingerprints. Grosz et al. [17] combined a conventional convolutional neural network (CNN) and a visual transformer (ViT) based on an attention mechanism to refine the global embedding representation by accurately comparing local features in two fingerprint images. Building on this, LFR-Net [18] introduces local enhancement and segmentation techniques to improve the quality of fingerprint images, a fusion of local features and global embeddings, and the introduction of a multi-stage matching process to improve the processing speed of latent fingerprint matching. Qiu et al. [19] first utilized ViT with a global attention mechanism to generate dense pixel-level correspondences of feature points on a given fingerprint pair.

However, the need for extensive training data and concerns over user privacy often limit the ability to adequately train and improve deep learning-based models. To address this issue, federated learning enables distributed model training without compromising data security.

2.2 Federated Learning

Constructing training datasets for biometric models in deep learning typically requires a large volume of private data. Federated Learning (FL), introduced by Google in 2016 [20], enables decentralized private data while maintaining privacy through the FedAvg method. Similar optimization challenges arise in cloud and IoT environments, particularly when handling large-scale, decentralized data [21]. Addressing statistical heterogeneity, FedCG [22] utilizes clustering and Graph Convolutional Networks (GCNs) for domain knowledge sharing and employs unsupervised teacher-student training for model adaptation. Similarly, FedSM [23] combats client drift in medical image segmentation by creating personalized models and introducing a novel model selector for effective test data alignment. FedDG [24] enhances fairness and generalization by dynamically adjusting aggregation weights through Generalization Adjustment. FedALA [25] improves personalization by adaptively aggregating global and local models, while FedPGP [26] balances personalization and generalization in federated prompt learning by combining CLIP generalization and low-rank personalization. Such methodologies are particularly valuable when integrated with federated learning to enhance the robustness and privacy of the distributed learning framework.

Face Recognition. Aggarwal et al. [1] used FL to train face recognition models collaboratively. Each client uploads the embedding layer vectors corresponding to its identity, while the server employs the Spreadout regularization technique to enhance the model’s generalization ability and robustness. Liu et al. [2] introduced a decoupled feature customization module (DFC) to better adapt a pre-trained face model to the individual needs of specific clients. In further research, Meng et al. [3] employed a differential privacy-based local clustering algorithm (DPLC) to achieve a uniform distribution of the global feature space through Consensus-Aware Face Recognition Loss, thus enhancing the model’s recognition capability while protecting privacy. Niu et al. [27] improved the discriminative power of cross-client class embeddings by introducing a softmax-based regularizer to correct the gradient of the class embeddings via the FedGC method. Deepfake detection techniques have also been explored to ensure the authenticity of facial data and prevent misuse in federated learning systems [28]. The FedForgery framework proposed by Liu et al. [29] combines federated and residual learning to learn robust discriminative residual feature mappings via the Variable Autoencoder (VAE) for detecting facial forgery.

Palmprint Recognition. Shao et al. [30] introduced FL into palmprint recognition using a public dataset, which differs from private data and may raise privacy concerns. FedML [31] detected facial forgeries by introducing Federated Metric Learning and constructing instance-level and relational-level communication loss, achieving improved palmprint recognition accuracy without sharing private data. Yang et al. [32] utilized different wavelength spectra’s physical properties to verify cross-spectrum palmprint.

Finger Vein Recognition. Lian et al. [4] proposed the FedFV framework, which addresses the heterogeneity problem of non-IID data through a personalized aggregation algorithm. Further, PAFedFV [5] designed a more complex personalized model aggregation method and employed a synchronized training module to utilize waiting time fully.

In our study, we introduce federated learning to fingerprint recognition, accounting for fingerprint heterogeneity, and adopt a generalized tuning strategy to enhance the model’s performance.

3  Method

We propose an adaptive weight adjustment federated learning method for fingerprint recognition. In this method, we address the performance issues caused by data heterogeneity while mitigating privacy and security risks associated with centralized training. First, we optimize the generalization gap during the global model aggregation process to mitigate the impact of client fingerprint differences, thereby enhancing the model’s generalization and robustness. Next, simple perturbation techniques are employed to protect data privacy further and counter security threats such as inference attacks. The overall framework of this method is illustrated in Fig. 1.

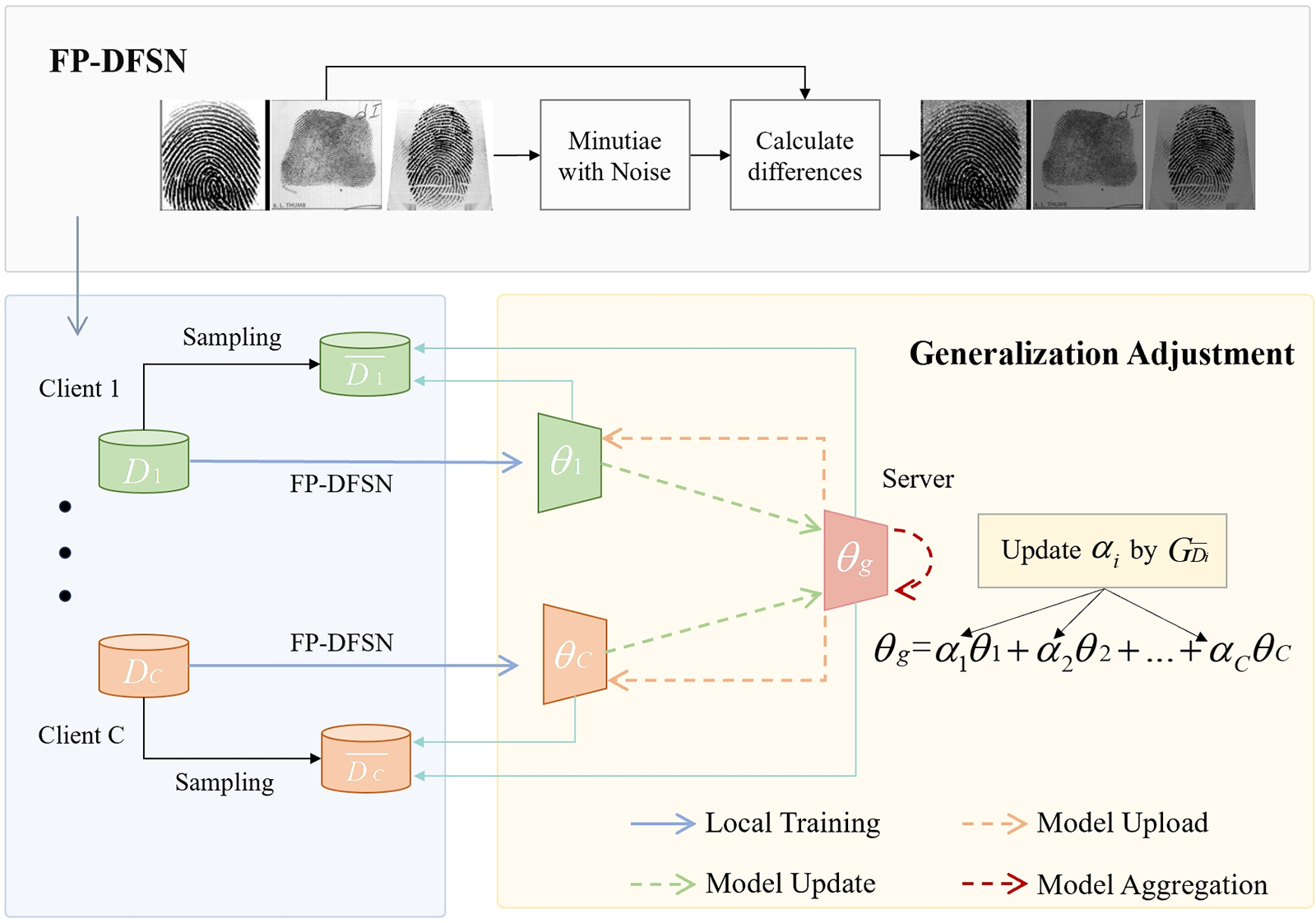
Figure 1: AFFR. Each client first processes the local data using FP-DFSN to protect the privacy of the datasource, then trains model θi and uploads the model to the server along with the accuracies of the selected validation set 𝒟i¯. The server uses the aggregated model θg to validate again. It dynamically adjusts the weights αi according to the generalization gap between the models to optimize recognition

3.1 Problem Description

Fingerprint verification systems use embedded classifiers to transform fingerprint images into discriminative feature vectors by mapping them into a multi-dimensional Euclidean space. A data sampler generates a pair of fingerprint images (x1,x2) and a label y, where x1 is the query image and x2 is the reference image with a known identity. The feature extractor fθ maps each image to a d-dimensional feature space and extracts features as fθ(x)∈Rd.

The training process involves optimizing the model parameters to minimize the loss function L:

L(x1,x2,y)=y⋅d(fθ(x1),fθ(x2))2+(1−y)⋅max(0,m−d(fθ(x1),fθ(x2)))2(1)

In Eq. (1), y=1 if x1 and x2 belong to the same identity, and y=0 otherwise. The distance function d(⋅) measures the Euclidean distance between the feature vectors, and m represents the margin. This adjustable hyperparameter specifies the minimum distance between pairs of different identities.

In the evaluation phase, the system generates feature vectors and calculates distances between test pairs to verify identity matches. As shown in Fig. 2, according to the mapped features fx1 and fx2, the model determines whether the two fingerprints belong to the same identity by calculating the feature similarity of the pair of fingerprint images. We get the matching result y by:

y(x1,x2)={1,if∥fx1−fx2∥2≤m0,otherwise(2)

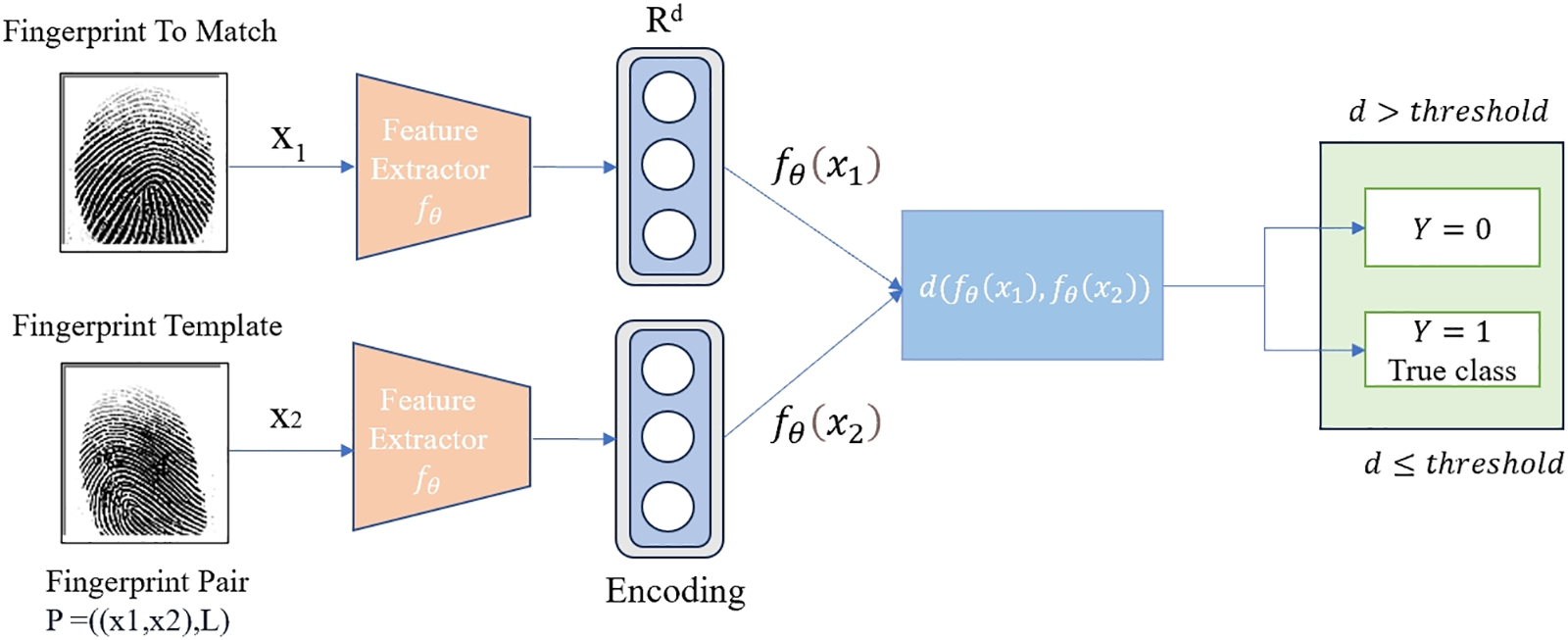
Figure 2: An overview of the training framework for fingerprint recognition. The training aims to optimize the network by minimizing the feature distance of positive samples and maximizing the feature distance of negative samples. In the evaluation stage, the distance between test pairs is calculated to verify the identity matching

In addition, deep learning models require a large amount of data for training. In traditional centralized learning methods, fingerprint data must be stored centrally on a server, which poses significant privacy risks due to the sensitive nature of such data. To address this issue, we adopt a FL approach. In this approach, user data remains on local devices; all model training is conducted locally, and only the resulting model parameters are uploaded to the central server. The server then aggregates these parameters to update the global model, which is redistributed to the clients. In this way, we use the distributed data for model training while avoiding the centralized storage and transmission of sensitive data, thus achieving reliable fingerprinting while preserving privacy. The global model θg is created by aggregating local client models, using a weighting mechanism based on the volume of data each client contributes:

minθgε(θg)=∑i=1Cαiε𝒟i(θi),αi=Ni∑j=1CNj(3)

In Eq. (3), ε𝒟i(θi)=1Ni∑j=1NiL(θi;aji,bji,yji) represents the prediction loss of the model θi on client i’s dataset 𝒟i. Here, Ni denotes the number of sample pairs (both positive and negative) on client i, and C represents the totalnumber of clients in the federated framework.

3.2 Model Aggregation with Adaptive Generalization Adjustment

In the context of fingerprint recognition within FL, given the significant differences and heterogeneity in fingerprint information across various countries and regions, as shown in Table 1, the distribution of fingerprint patterns (circular, spiral, and arched) varies among individuals of different ethnicities and geographical locations, influenced by genetic, environmental, and developmental factors.

Our primary optimization objective is to minimize the total loss function across all clients, according to Eq. (3), the optimization objective can be further described as:

minθg,α1,α2,…,αC⁡ε(θg)=α1ε𝒟1¯(θ1)+α2ε𝒟2¯(θ2)+…+αCε𝒟C¯(θC)(4)

However, minimizing the loss alone does not guarantee that the global model will generalize well on the data of each client. To evaluate the generalization performance of the global model on different clients, we can compute the difference in accuracy between the global model and the local model of client i during the i–th training round, which serves as the generalization gap:

G𝒟i¯(θgt)=Acc𝒟i¯(θgt)−Acc𝒟i¯(θit−1′)(5)

In Eq. (5), a larger generalization gap indicates a greater difference in accuracy between the global and local models for client i, suggesting that the global model generalizes less effectively on client i’s data. We can translate the analysis of the generalization gap into an analysis of the relationship between the global and local models, as expressed by Δθt in Eq. (6).

Δθt=θgt−θit−1′=θit−1′+(αi−1)θit−1′+∑j≠iαjθjt−1′−θit−1′=(1−αi)θit−1′+∑j≠iαjθjt−1′,s.t.αi+∑j≠iαj=1.(6)

According to Eq. (6), it’s easy to see that increasing αi brings the global model θgt closer to the local model θit−1′. This is beneficial as it reduces the accuracy difference G𝒟¯i(θgt) on client i’s data, thereby enhancing the global model’s performance for that client. Therefore, we integrate the following weight update scheme, as shown in Eq. (7).

αit′=(G𝒟i¯(θgt)−μ)⋅dt+αit−1maxj(G𝒟j¯(θgt)−μ),αit=αit′∑j=1Nαjt′(7)

In Eq. (7), μ=1C∑i=1CG𝒟i¯(θgt) represents the average generalization gap across all clients, and dt=(1−tT)⋅d is a hyperparameter that linearly decays with the number of communication rounds T, used to control the magnitude of weight adjustments, with larger adjustments allowed early in training and more stable updates as training progresses.

This dynamic weight adjustment mechanism is especially effective when clients’ data distributions differ significantly. For clients with more diverse data, the generalization errors tend to be larger. By increasing the weight αi of these clients, the global model can better adapt to their specific data features, thus enhancing the model’s generalization capabilities across different datasets. By increasing the weight for clients with larger generalization errors, the gap between them and other clients is reduced enabling the global model to balance the influence of different client data adaptively, thereby improving its overall performance in heterogeneous environments. The detailed procedure is outlined in Algorithm 1.

3.3 FP-DFSN: Fingerprint Privacy Protection by Introducing Noise and Computing Image Differentials

Although federated learning does not directly exchange data, security challenges exist, such as inference attacks, where participants can infer training data from other participants based on uploaded parameters. To address this, the study introduces noise and performs differential processing for fingerprint images in the client, the privacy protection process involves the following steps:

1. First, to enhance the clarity and detail of fingerprint images for superior feature extraction, we apply a frequency-domain-based sharpening technique:

g(x,y)=ℱ−1{ℱ[f(x,y)⋅(−1)x+y]⋅(1−exp⁡(−D22D02))}⋅(−1)x+y(8)

Initially, the input grayscale image f(x,y) is prepared for the Fast Fourier Transform (FFT) by multiplying it by (−1)x+y, which centers and resizes the image for optimal FFT performance. A Gaussian high-pass flter, defined by 1−exp⁡(−D22D02), is then applied In this expression, D represents the distance from any point to the center of the frequency domain, and D0 is the normalized cutof frequency. After filtering in the frequency domain, the processed data is converted back to the spatial domain using the inverse FFT. Finally, the image is re-centered by multiplying it again by (−1)x+y, resulting in a sharpened image. This process enhances high-frequency details by suppressing low-frequency components, thereby sharpening the image.

2. After sharpening the image, we extract minutia M={P∣ CN (P)=1\, or CN(P)=3} from the fingerprint image g(x,y) by calculating the Crossing Number (CN) of pixel points. For a binarized pixel point P its CN value is determined by the number of changes in pixel values in its 8-neighborhood as given by:

CN(P)=12∑i=07|xi+1−xi|(9)

In Eq. (9), xi and xi+1 represent 8 consecutive pixel values in the domain of P, and x8=x0. When CN(P)=1, P is considered an end point; when CN(P)=3, P is identified as a divergence point.

Next, we improve feature extraction accuracy by filtering out minutia too close to the image edge, using a distance threshold. In other words, for each minutia, if its distance D(p,M) to the nearest boundary is less than a given threshold Td, the detail point is discarded to eliminate noise and false detections.

3. Finally, we add random Gaussian noise in the local neighborhood of the minutia M extracted in the previous step. According to Eq. (10), the image data is further processed by computing the weighted difference between the noise-added and original images. The parameter β controls the influence of noise in the differential image processing. This weighted processing helps enhance privacy protection while maintaining data usability. The features extracted from the weighted difference processed fingerprint image are subsequently used to train models locally on the client side.

Idiff=I−β⋅Inoisy,

Inoisy(x,y)={f(x,y)+N(0,σ2),if(x,y)∈Mf(x,y),otherwise(10)

In Eq. (10), β is an adjustment parameter that controls the strength of the noise influence. A more significant value of β indicates that more noise is subtracted from the original image, resulting in a final differential image that visually differs more from the original image.

In this study, parameters such as the Gaussian filter’s cutoff frequency (D0), distance thresholds, and neighborhood sizes are optimized based on experimental results to achieve an ideal balance between image clarity, feature extraction accuracy, and privacy protection across various conditions. These steps significantly enhance the security of sensitive data in the client’s local environment when uploading model parameters. Fig. 3 compares the images before and after processing. The processed images show increased noise and reduced clarity, demonstrating the introduced perturbations’ effectiveness.

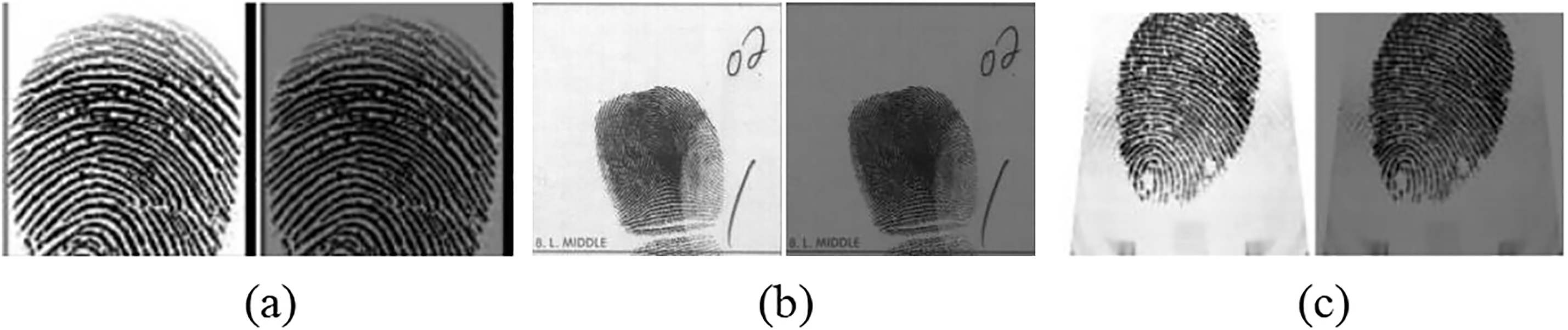
Figure 3: Panels (a), (b), and (c) represent the similarity comparison before and after processing for three datasets, respectively. The image on the right in each panel is the processed data, and the similarity between the two images is evaluated using the AlexNet model selected by LPIPS to evaluate the similarity between the two images

4  Theoretical Analysis

In this section, we analyze the convergence of the global loss function under the adaptive weighting mechanism.

Theorem: Suppose the loss function L is L-smooth, meaning there exists a constant LL>0 such that for any model parameters θ and θ′,

|∇L(θ)−∇L(θ′)|≤LL∥θ−θ′∥(11)

Additionally, let the weights αit in each round be adaptively adjusted based on the generalization gap of each client, ensuring that ∑i=1Cαit=1. If the learning rate η is chosen such that η≤2LL, then the global loss function Lgt will converge to a minimum L∗.

Proof:

1.   Stability of the Weight Adjustment Mechanism

Under the adaptive weighting mechanism, the weight update rule follows the scheme defined in Eq (7). In the early stages of training, dynamic adjustment of αit allows the model to better adapt to the data characteristics of different clients. As training progresses and the generalization gap dt diminishes, the weights stabilize, minimizing their interference with the global model updates. This approach enables models from clients that differ significantly from the global model to exert greater influence, thereby enhancing robustness in learning.

2.   Monotonic Decrease of the Global Loss

The global model update is achieved by aggregating local updates from each client. Suppose each client’s local update follows:

θit+1=θit−η∇Li(θit)(12)

then the global model update can be written as:

θgt+1=∑i=1Cαitθit+1=θgt−η∑i=1Cαit∇Li(θit)(13)

Using the Lipschitz continuity of ∇L, we can bound the change in the global loss as follows:

L(θgt+1)≤L(θgt)−η∥∇L(θgt)∥2+LL2η2∑i=1C⁡αit∇Li(θit)2(14)

Choosing the learning rate η such that η≤2LL ensures that the term −η∥∇L(θgt)∥2 dominates. This is crucial because it guarantees a net decrease in the global loss L(θg) with each iteration, leading to convergence.

3.   Accumulated Convergence of the Global Loss

By accumulating theinequality for each round, we obtain:

∑t=0T−1(Lgt−Lgt+1)≥η∑t=0T−1∥∇Lgt∥2−LL2η2∑t=0T−1∥∑i=1Cαit∇Li(θit)∥2(15)

Since the loss function is bounded, it follows that:

∑t=0T−1∥∇Lgt∥2<∞(16)

implying that as T→∞, ∥∇Lgt∥→0. Under the conditions established in the first point, the weights αit stabilize, minimizing interference with the descent of the global loss. Thus, we conclude that:

limt→∞Lgt=L∗(17)

where L∗ represents a minimum of the global loss.

In summary, this analysis proves that under the adaptive weighting mechanism, the global loss function Lg in federated learning will converge to a minimum value L∗. The stability of the weight adjustment and the choice of learning rate play pivotal roles in ensuring effective convergence. ◻

5  Experiment

5.1 Datasets

The NIST Supplemental Fingerprint Card Data Database (NIST SD10) [34] consists of 5520 fingerprint images from 522 individuals, each with a resolution of 832 × 768 pixels. These images are divided across three CD-ROMs and are classified into NCIC classes provided by the FBI.

The SOCOFing dataset [35] includes 6000 images from 600 subjects, captured using Hamster Plus and SecuGen SDU03PTM scanners. It offers three levels of difficulty (easy, medium, and hard) for synthetic modifications: deletion, center rotation, and z-cut modifications.

CASIA-FingerprintV5 [36] contains 20,000 fingerprint images from 500 volunteers, captured with the URU4000 sensor. Each subject contributed 40 images across eight fingers, stored as 8-bit gray-level BMP files with a resolution of 328 × 356 pixels.

As shown in Table 2, the NIST SD10, SOCOFing, and CASIA datasets exhibit significant differences in terms of image quality (NFIQ2.0 scores), image resolution, and regional sources. The Earth Mover’s Distance (EMD) heatmap and the t-SNE visualization in Fig. 4 quantify these distributional differences based on feature characteristics, illustrating the degrees of similarity and divergence between the datasets. Higher EMD values, or darker regions, indicate greater distributional differences between datasets. Each of the three datasets is assigned to a separate client, where data is processed for feature extraction and comparison. In the t-SNE plot, the features of each client dataset are represented by different colored dots, with minimal overlap between clusters, reflecting significant feature heterogeneity. This shows that each dataset has substantial differences at the feature level, and these differences will affect the overall accuracy and generalization ability of the model.

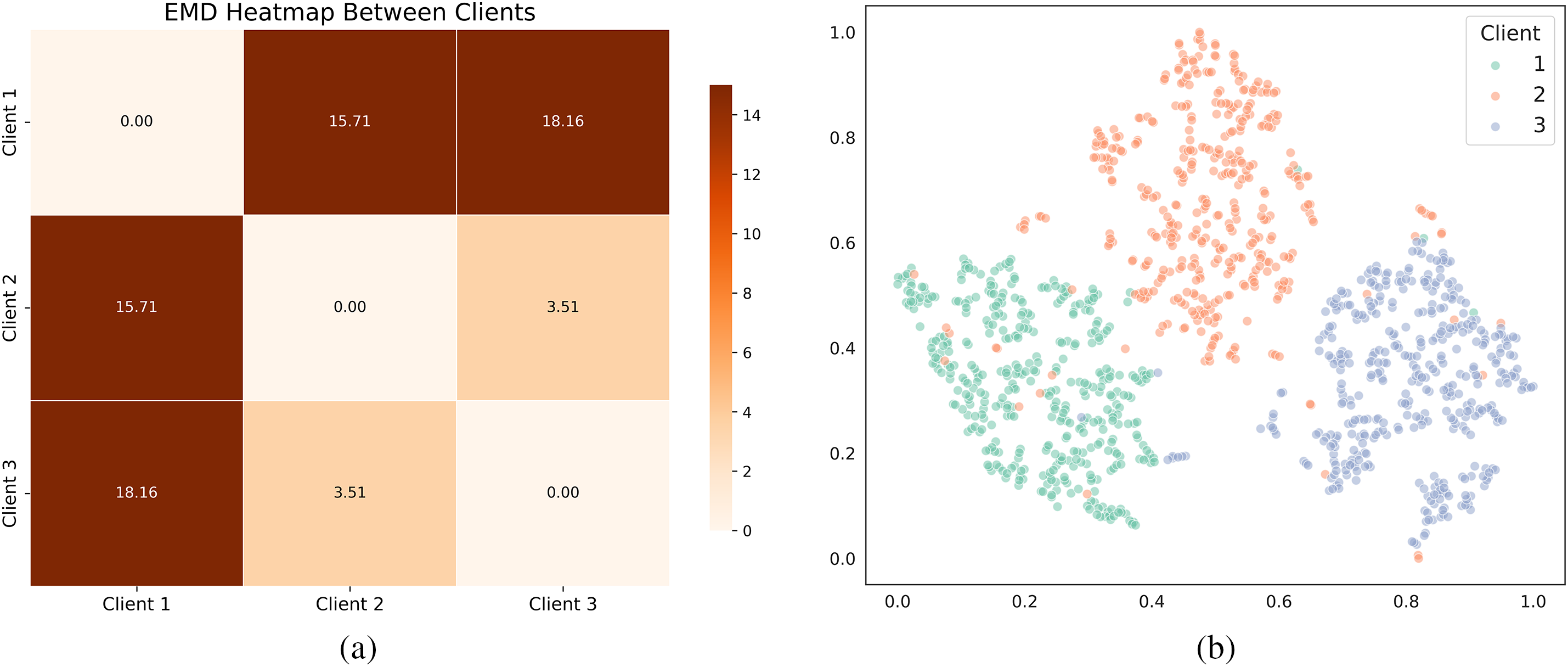
Figure 4: Illustration of feature heterogeneity: (a) EMD Distance Heatmap quantifies distributional differences, and (b) t-SNE Map visually shows the feature clusters for each dataset

5.2 Experiment Details

In our research, we consider each finger as a separate classification class. We utilize the SOCOFing and NIST SD10 datasets, which provide one fingerprint per finger per subject, and the CASIA dataset, which provides multiple fingerprints per finger. We choose one fingerprint per finger for our experiments to simplify data processing and ensure equitable fingerprint selection. This approach facilitates consistent experimental analysis.

We divide each client’s data into training and testing sets at a 4:1 ratio, with one-fifth of the training set randomly chosen as a validation set to tune model weights during global updates. We label fingerprint pairs (x1,x2) as 1 if they belong to the same finger (true pair) and 0 if not (false pair). We generate numerous fingerprint pairs and their corresponding labels using the training dataset. For testing, we create two types of fingerprint test sample pairs for each client. Each test sample pair consists of a fingerprint from the template library, a reference fingerprint, and a query fingerprint, which matches the fingerprint in the template library for verification. To comprehensively evaluate system performance, we generate all possible matching pairs. capping the generation of incorrect match pairs at 10,000 to maintain computational efficiency. The system is designed to detect correct and incorrect matches accurately.

Our model employs a Siamese network with two CNNs that share weights, trained using a contrastive loss function. We use a learning rate of 0.0003 and the Adam Optimizer. We set the batch size at 32. We conduct 1000 training epochs, 20 communication rounds, and 5 local epochs for single dataset experiments. For cross-dataset generalization, we extend training to 2000 epochs and 40 communication rounds, with a coefficient of 0.5 applied to process the difference image.

5.3 Experiment Results

5.3.1 Comparative Analysis of Training Strategies on a Single Dataset

In this section, we construct experiments to compare the performance of local training, centralized training, FedAvg [20], and our proposed AFFR framework, which incorporates FedDG [24] for adaptive weight updates, within a fingerprint recognition system to evaluate the specific impacts of federated learning on model performance. Each client independently trains a model with its own local training set in local training. We evaluate the performance of each model with the local test set and calculate the average accuracy For centralized training, we aggregate the training data from all clients onto a central server, and after training evaluate the performance of the global model using the combined test set.

The experimental results shown in Fig. 5 indicate that the models trained using the AFFR method significantly improve accuracy compared to the models trained only on local datasets. For example, on the NIST SD10 dataset, the locally trained model has an accuracy of 99.41%. The accuracy increased to 99.97% using the FedAvg training method, and further increased to 99.98% using the AFFR method, which is on par with the accuracy of the central training method. This shows that Federated Learning enhances the performance and robustness of its localmodels by integrating private data frommultiple clients without directly accessing them while maintaining data privacy.

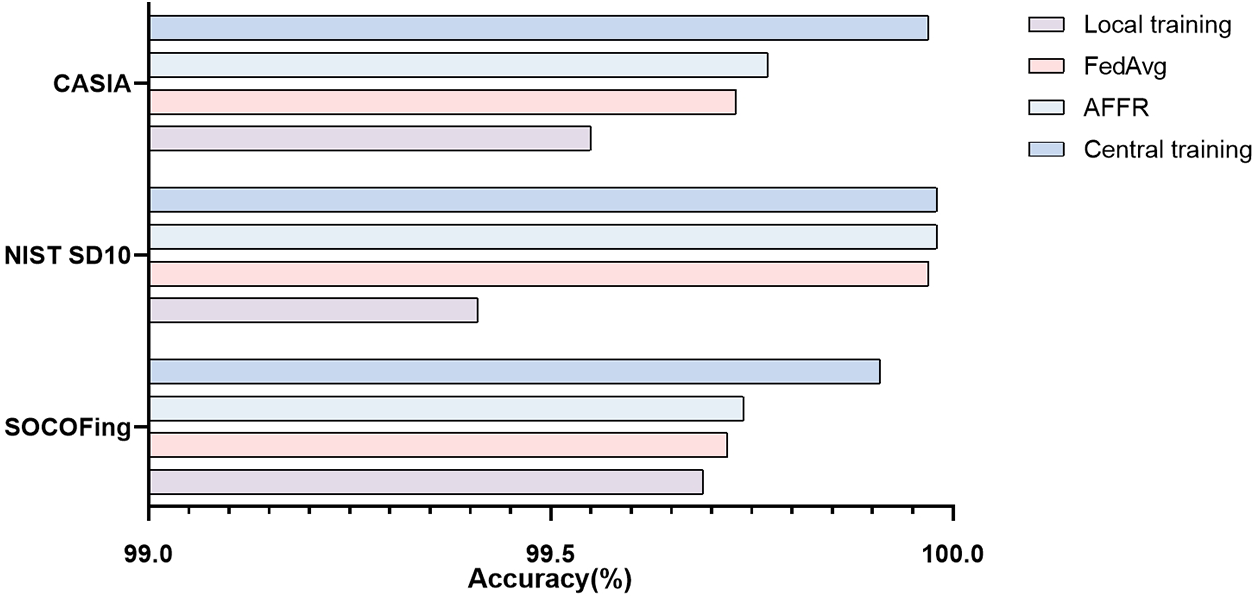
Figure 5: Comparison of local training, FedAvg, AFFR, and centralized training methods on three fingerprint datasets

5.3.2 Generalization Performance Analysis in Heterogeneous Data Settings

In this section, we evaluate the model’s generalization ability using our proposed method. We conduct experiments under various environmental conditions to determine the optimal global update strategy.

Analysis of Model Generalization Ability under Different Data Quality Conditions We introduce noise in the details of fingerprint images and compute differential images to improve security and protect user privacy. To evaluate the model’s robustness across various data quality conditions, we divided a single dataset into ten parts and distributed each to one of ten clients in our federated learning (FL) setup. Each client was assigned a distinct difference coefficient, β, ranging from 0 to 0.9. This range allowed us to simulate data environments of varying quality and analyze the impact of these differences on the model’s performance.

As shown in Fig. 6, the fingerprint image quality of different datasets under different β values is tested using the fingerprint image quality assessment algorithm NFIQ2.0. It can be observed that despite some fluctuations, the overall trend indicates a decline in image quality scores as the β increases, particularly in the SOCOFing dataset. Additionally, the effective region in the fingerprint image may become too small for the algorithm to extract sufficient features for evaluation.

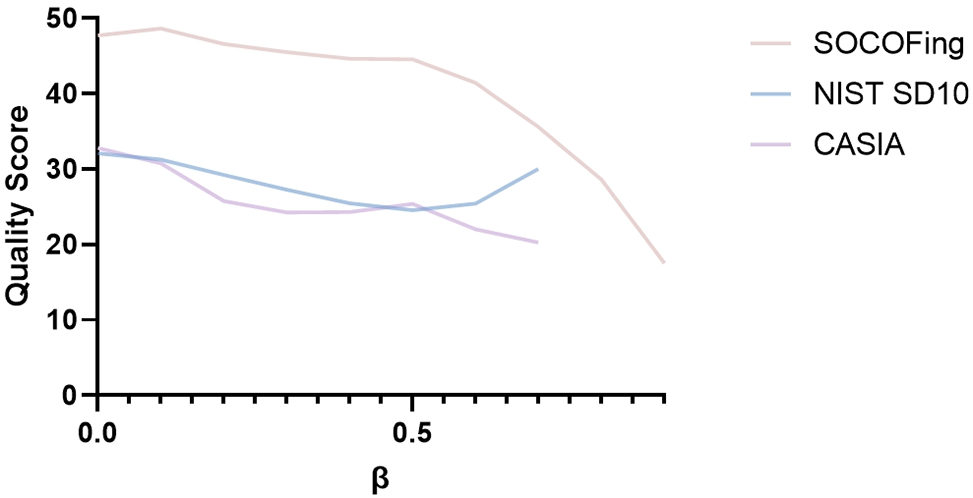
Figure 6: Comparison of fingerprint image quality at different β values using NFIQ2.0 evaluation on three datasets

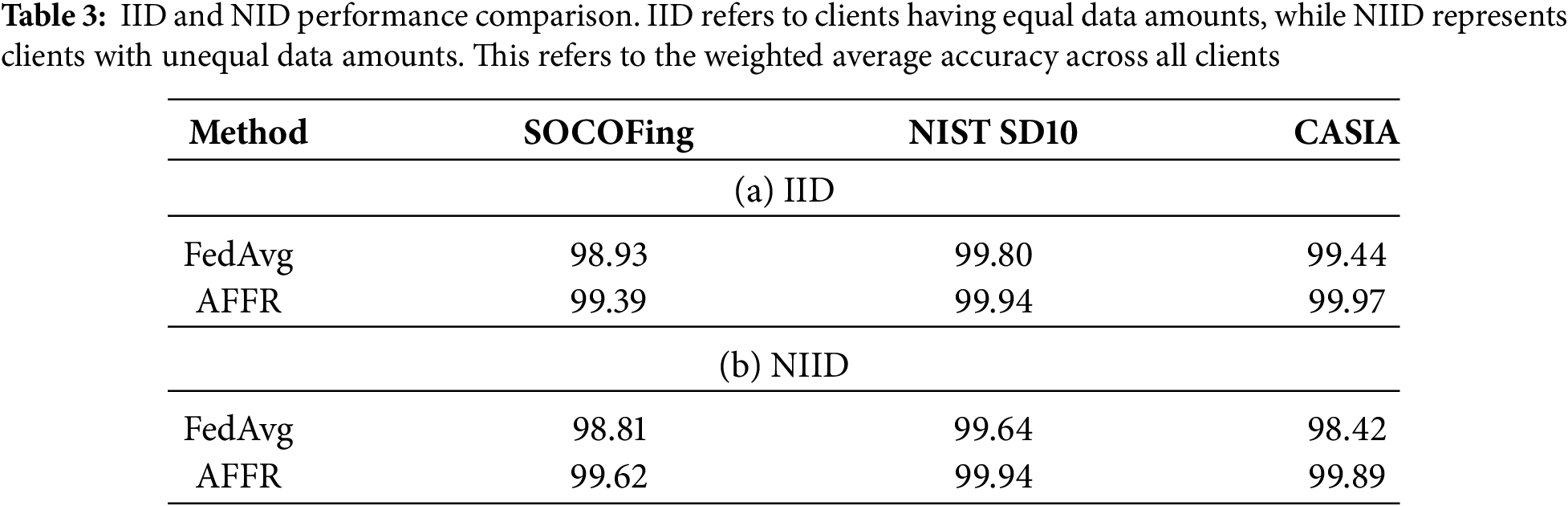
Table 3 demonstrates the effectiveness of our adaptive global model aggregation approach compared to FedAvg. Specifically, AFFR improves accuracy across all datasets. For example, AFFR improves accuracy on the CASIA dataset by 1.47% in the NIID condition. These results highlight the effectiveness of AFFR in improving model accuracy and generalization performance in different data quality environments, especially in environments with non-homogeneous data distributions.

Analysis of Model Generalization Performance under Diverse Dataset Features In our FL setup we conduct experiments on three clients, each using a distinct dataset. Fig. 7 presents the training loss and accuracy over communication rounds for the experiments with AFFR. As seen in the figure, the loss value decreases rapidly in the initial stages of training, indicating that the model effectively learns feature representations. As the training progresses, the loss stabilizes near zero. At the same time, accuracy rapidly increases and remains stable at near 1.0, demonstrating that the model has converged with high accuracy.

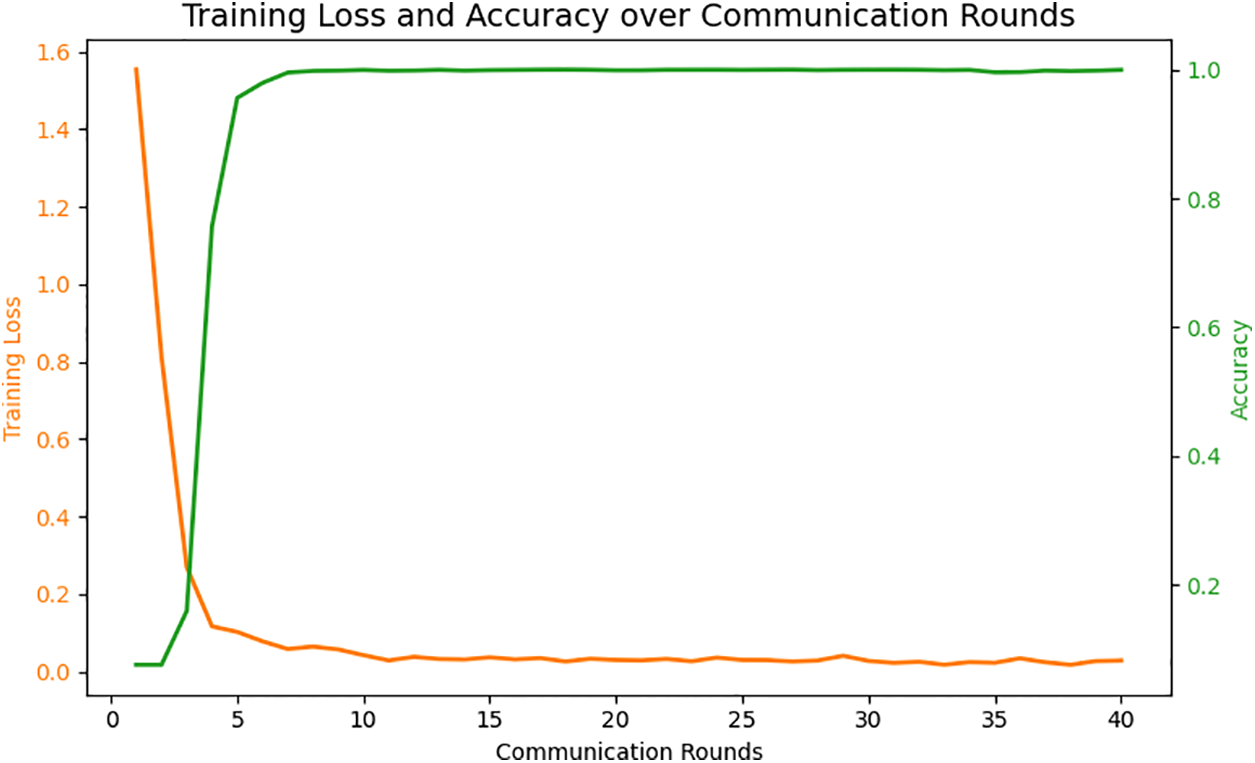
Figure 7: Training loss and accuracy over communication rounds with adaptive generalization mechanism

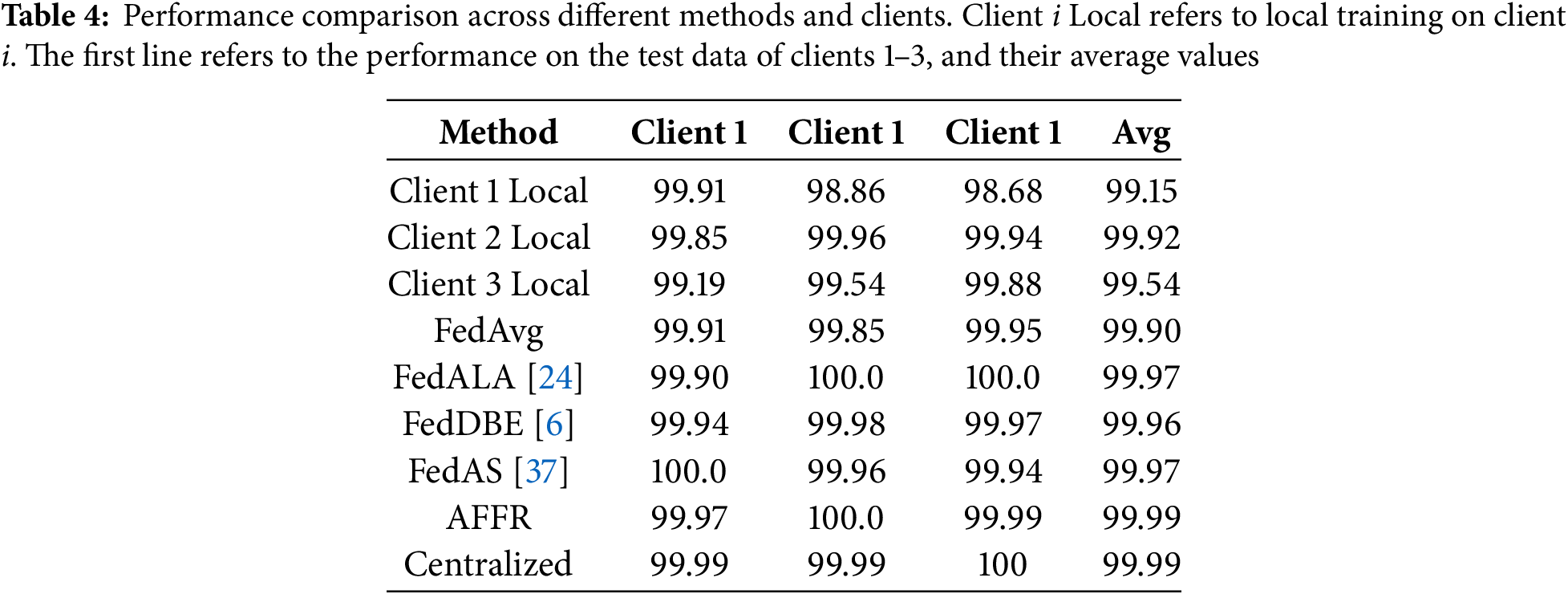
Table 4 shows that while locally trained models perform well on their data, they generalize poorly to data from other clients. FedAvg improves performance across all clients but is still impacted by data heterogeneity. In contrast, FedALA achieves an average accuracy of 99.97% but shows some fluctuation, with a slightly lower accuracy of 99.90% on Client 1. FedDBE achieves a balanced performance across clients with an average accuracy of 99.96%. FedAS also reaches an average accuracy of 99.97%, though it shows minor drops on some clients. AFFR further increases accuracy to 99.99% matching the performance of centralized training. This demonstrates that by incorporating an adaptive threshold generalization strategy, AFFR achieves optimal performance and generalization, highlighting the effectiveness of this approach.

5.3.3 Ablation Studies

Ablation Study: Evaluating the Privacy Protection Effectiveness of FP-DFSN in Federated Learning: In the federated learning environment, since users are required to upload model parameters for model aggregation, there is a potential risk that private data could be recovered using the uploaded gradient information. To explore this issue, we assume the attacker is a malicious server, which not only observes the gradient updates uploaded by users but also makes minimal modifications to the shared model architecture to directly recover private user data from the gradient updates. Specifically, the attacker employs a minimally modified model architecture by introducing additional linear layers and ReLU activation functions, creating structured gradients that can leak user input information. In this study, we integrate a new network layer, the Imprint Module, into the model architecture [38], aiming to evaluate whether gradients from this layer can be used to infer users’ original data. We conducted experiments using two methods: training with FP-DFSN (w.) and training directly on the original data (wo.). We used three datasets: SOCOFing, NIST SD10, and CASIA.

Fig. 8 shows that the fingerprint image processed using the FP-DFSN method suffers from severe loss of detail and blurred images compared to the original image, whereas the fingerprint image without the FP-DFSN method retains more detail and clarity, and is closer to the original real image.

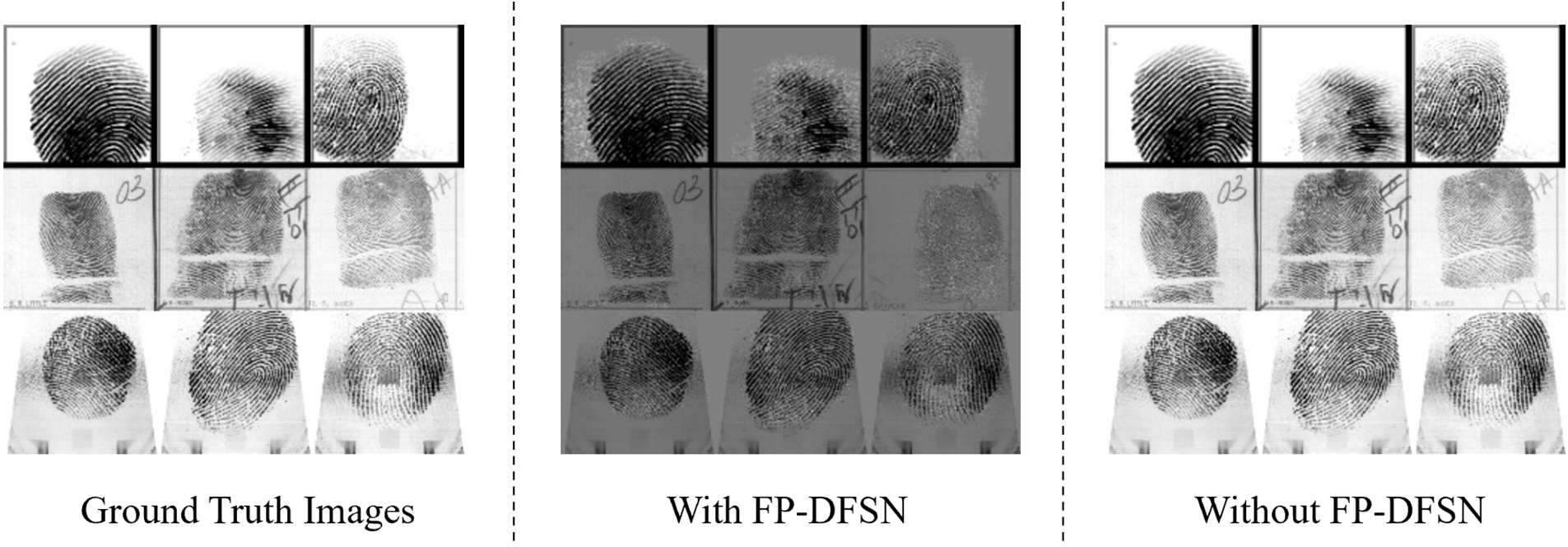
Figure 8: Comparison of fingerprint reconstruction quality across three scenarios: ground truth images images reconstructed with FP-DFSN, and images reconstructed without FP-DFSN

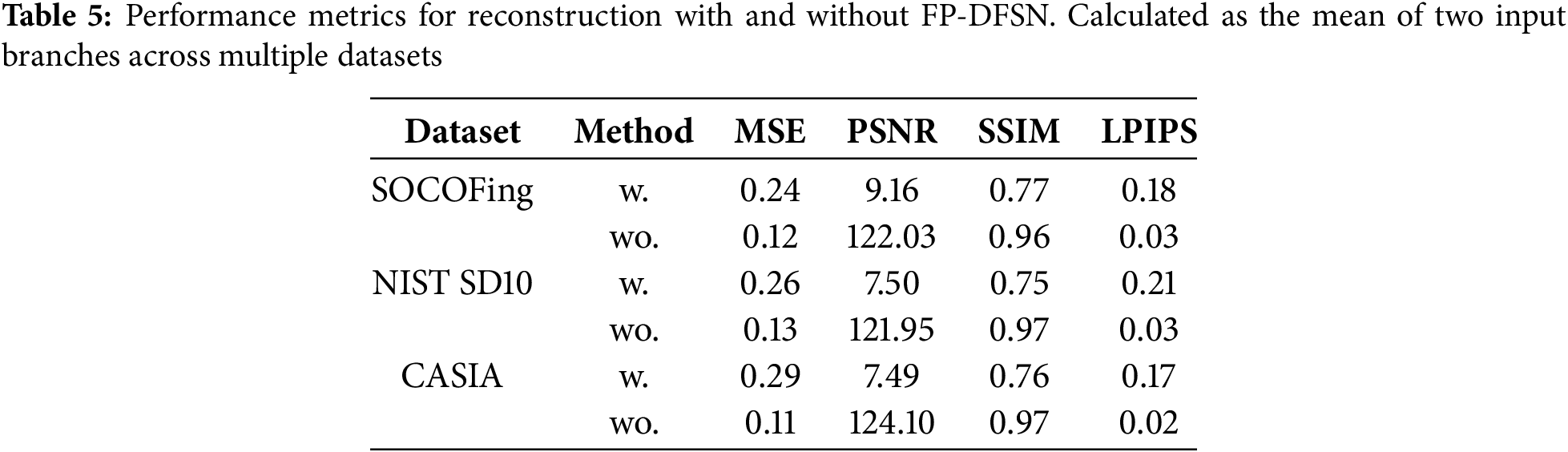
Table 5 shows the performance comparison of these methods on different datasets. The results indicate that while the proposed method degrades in terms of preserving image details and structural quality, it may enhance privacy protection by making it more difficult to recover the original data from the processed images.

To evaluate the privacy protection of fingerprint data in a federated learning environment, we use training data as member data and testing data as non-member data. The evaluation is conducted using the following metrics:

Membership Inference Attack Accuracy (MIA Accuracy): Measures the attacker’s success rate in correctly identifying whether a data sample belongs to the training set.

AUC Value (Area Under the ROC Curve): Reflects the model’s ability to distinguish between member and non-member data in a membership inference attack.

Mutual Information: Ouantifies the amount of shared information between the input data and the model outputs. Lower mutual information means the model outputs leakless information about the input data, reducing privacy risk.

Entropy: Measures the randomness or unpredictability in the model outputs. Lower entropy values indicate that the model outputs contain less information that could be exploited by an attacker, enhancing privacy protection.

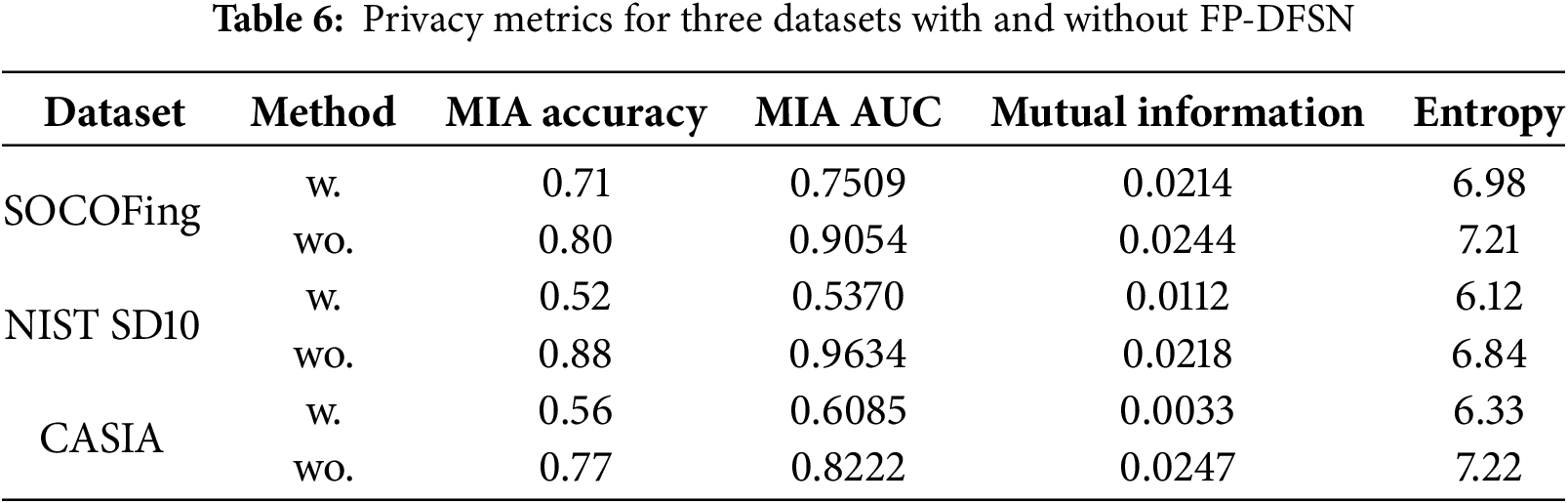
As shown in Table 6, when FP-DFSN is not applied (wo.), the values of MIA Accuracy, AUC Value Mutual Information, and Entropy are all higher. This indicates that the model is more susceptible to exploitation by attackers, with a higher risk of information leakage and weaker privacy protection effectiveness. In contrast, after applying FP-DFSN (w.), these metric values decrease, demonstrating stronger privacy protection performance. Lower MIA Accuracy and AUC values mean that the attacker’s success rate in membership inference attacks decreases. The reductions in Mutual Information and Entropy indicate that the amount of information about the input data contained in the model outputs decreases, reducing potential information leakage risks.

By calculating the difference between the original image and the noise-added image, we generate a differential image to enhance privacy protection. The coefficient parameter β is used to adjust the influence of this differential image on the final processed image, allowing us to blur certain details while retaining the main features of the fingerprint image. This effectively reduces the risk of reconstruction attacks.

Fig. 9 shows the variation in recognition accuracy across the SOCOFing, NIST SD10, and CASIA datasets under different β values. The experimental results indicate that an appropriate β value not only maintains recognition performance but also emphasizes the fine-grained details in the fingerprint images by adding noise to these details, similar to a regularization effect, thereby improving the model’s ability to capture these key features.

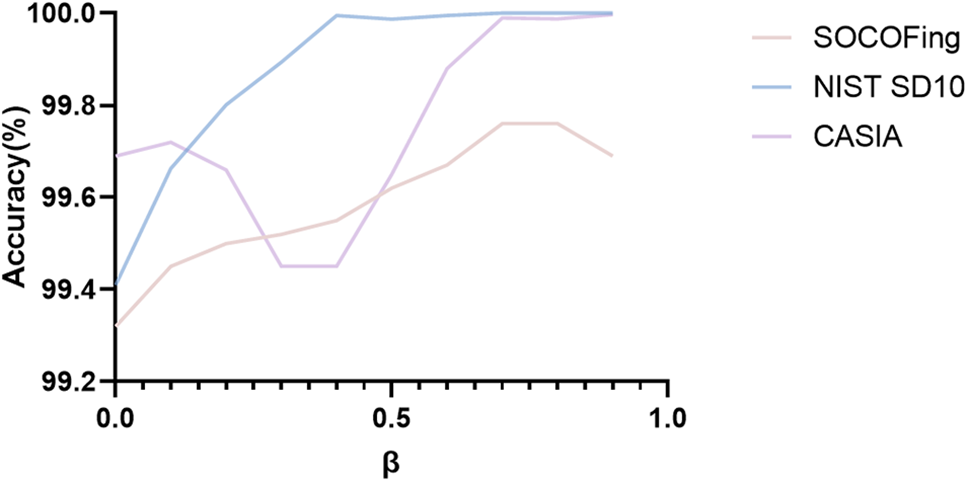
Figure 9: Comparison of recognition accuracy at different β values on three datasets

Further analysis shows that as β increases, the quality of the reconstructed images decreases significantly making it harder for attackers to reconstruct the original image using gradient information, thereby enhancing privacy protection. Specifically, the recognition accuracy for the SOCOFing and NIST SD10 datasets peaks when β approaches a certain optimal value. In contrast, while the recognition accuracy for the CASIA dataset also improves as β increases, it slightly declines after reaching its peak, suggesting that excessive blurring might have a minor negative impact on the recognition performance for certain datasets.

Furthermore, Fig. 10 illustrates the effect of noise variance (Var) on recognition performance. In this context, Var controls the amount of noise directly added to the images. It can be observed that as the noise variance increases, recognition accuracy first increases and then decreases. A moderate level of noise helps. the model focus on key features, thereby enhancing recognition performance; however, excessive noise variance leads to blurred details, which can negatively impact recognition.

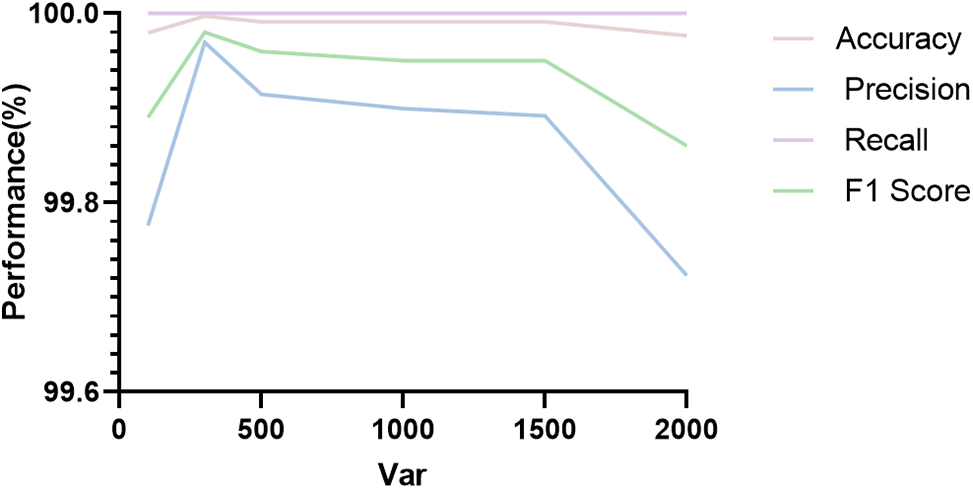
Figure 10: Impact of different noise variances on recognition accuracy across three datasets independently distributed on clients

In summary, the experimental results demonstrate that by carefully selecting and optimizing the differen tial image coefficient β and the noise variance Var, a balance between privacy protection and recognition performance can be effectively achieved. With moderate noise addition and appropriate blurring, the model can accurately recognize important features while reducing the quality of the reconstructed images, thus achieving a balance between privacy protection and recognition performance.

Ablation Studies of the Step Size and Linear Decay Strategy: Table 7 illustrates the trend in model performance across different step size settings. As the step size increases, the model’s recognition accuracy precision, and F1 Score all improve, rising from 99.91% accuracy and an Fl Score of 99.51% at a step size of 0% to 99.99% and 99.94% at a step size of 0.8. This indicates that a moderate increase in step size enhances the model’s generalization capability, allowing it to better adapt to the features of different datasets. However, when the step size reaches 1, the performance shows slight fluctuations, as an excessively large step size weakens the model’s ability to capture subtle features.

Fig. 11 presents the unified confusion matrix analysis across all datasets under different algorithms (FedAvg and AFFR). Specifically, Fig. 11a shows the overall confusion matrix for FedAvg, reflecting its classification performance under this algorithm. Fig. 11b displays the confusion matrix for the AFFR algorithm with a step size of 0.8. It can be observed that the performance improves at a step size of 0.8.

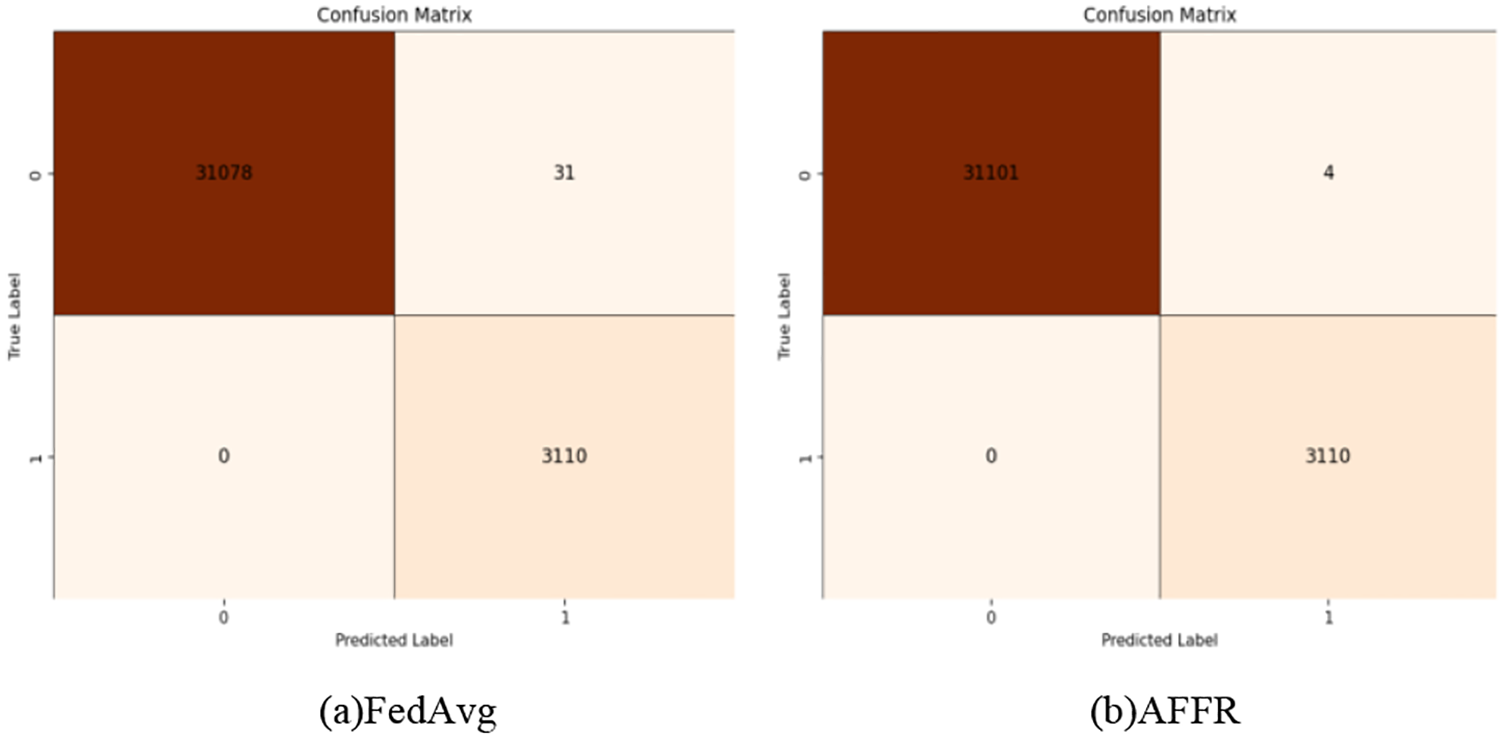
Figure 11: Illustration of the unified confusion matrix across all datasets

6  Conclusions

In this study, we present the Adaptive Weighted Global Aggregate Joint Learning framework (AFFR) for fingerprint recognition. The framework dynamically adjusts the weights during the model aggregation process, thus effectively narrowing the generalization gap between global and local models and addressing the performance degradation due to data heterogeneity. In addition, we implement a simple data preprocessing module that enhances security by blurring the raw data, thus effectively preventing potential inference attacks. This paper also reports experiments conducted on three datasets. The experimental results show that the proposed approach can effectively share data and improve the generalization and robustness of the model while preserving privacy. Future work may improve the framework by integrating more sophisticated cryptographic techniques to enhance security measures in joint learning environments.

Acknowledgement: The authors would like to express their appreciation to the National Natural Science Foundation of China and the Key Research and Promotion Projects of Henan Province for their financial support. The authors would like to thank the editor-in-chief, editor, and reviewers for their valuable comments and suggestions.

Funding Statement: This research was supported by the National Natural Science Foundation of China (Nos. 62002100, 61902237) and Key Research and Promotion Projects of Henan Province (Nos. 232102240023, 232102210063, 222102210040).

Author Contributions: Study conception, design, and supervision: Yonghang Yan, Ying Cao; data collection: Hongwei Chang; analysis and interpretation of results: Xin Xie, Yonghang Yan; draft manuscript preparation: Hengyi Ren, Ying Cao, Xin Xie. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Aggarwal D, Zhou J, Jain AK. FedFace: collaborative learning of face recognition model. In: 2021 IEEE International Joint Conference on Biometrics (IJCB); 2021; Piscataway, NJ, USA: IEEE. p. 1–8. doi:10.1109/ijcb52358.2021.9484386. [Google Scholar] [CrossRef]

2. Liu C-T, Wang C-Y, Chien S-Y, Lai S-H. FedFR: joint optimization federated framework for generic and personalized face recognition. Proc AAAI Conf Artif Intell. 2022;36(2):1656–64. doi:10.1609/aaai.v36i2.20057. [Google Scholar] [CrossRef]

3. Meng Q, Zhou F, Ren H, Feng T, Liu G, Lin Y. Improving federated learning face recognition via privacy-agnostic clusters. arXiv:2201.12467. 2022. [Google Scholar]

4. Lian F-Z, Huang J-D, Liu J-X, Chen G, Zhao J-H, Kang W-X. FedFV: a personalized federated learning framework for finger vein authentication. Mach Intell Res. 2023;20(5):683–96. doi:10.1007/s11633-022-1341-4. [Google Scholar] [CrossRef]

5. Mu H, Guo J, Han C, Sun L. PAFedFV: personalized and asynchronous federated learning for finger vein recognition. arXiv:2404.13237. 2024. [Google Scholar]

6. Zhang J, Hua Y, Cao J, Wang H, Song T, Xue Z, et al. Eliminating domain bias for federated learning in representation space. Adv Neural Inf Process Syst. 2024;36:14204–27. [Google Scholar]

7. Chen C, Liao T, Deng X, Wu Z, Huang S, Zheng Z. Advances in robust federated learning: heterogeneity considerations. arXiv:2405.09839. 2024. [Google Scholar]

8. Zhu L, Liu Z, Han S. Deep leakage from gradients. In: Advances in neural information processing systems. RedHook, NY, USA: Curran Associates, Inc.; 2019. Vol. 32. [Google Scholar]

9. Geiping J, Bauermeister H, Dröge H, Moeller M. Inverting gradients—how easy is it to break privacy in federated learning? Adv Neural Inform Process Syst. 2020;33:16937–47. doi:10.48550/arXiv.2003.14053. [Google Scholar] [CrossRef]

10. Wu R, Chen X, Guo C, Weinberger KQ. Learning to invert: simple adaptive attacks for gradient inversion in federated learning. In: Uncertainty in artificial intelligence. Cambridge, MA: PMLR; 2023. p. 2293–303. doi:10.48550/arXiv.2210.10880. [Google Scholar] [CrossRef]

11. Liu Y, Zhou B, Han C, Guo T, Qin J. A novel method based on deep learning for aligned fingerprints matching. Appl Intell. 2020;50:397–416. doi:10.1007/s10489-019-01530-4. [Google Scholar] [CrossRef]

12. Zhu L, Xu P, Zhong C. Siamese network based on CNN for fingerprint recognition. In: 2021 IEEE International Conference on Computer Science, Electronic Information Engineering and Intelligent Control Technology (CEI); 2021; Piscataway, NJ, USA: IEEE. p. 303–6. doi:10.1109/cei52496.2021.9574487. [Google Scholar] [CrossRef]

13. Öztürk Hİ, Selbes B, Artan Y. MinNet: Minutia patch embedding network for automated latentfingerprint recognition. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2022; Piscataway, NJ, USA: IEEE. p. 1627–35. doi:10.1109/cvprw56347.2022.00169. [Google Scholar] [CrossRef]

14. Saeed F, Hussain M, Aboalsamh HA. Automatic fingerprint classification using deep learning technology (DeepFKTNet). Mathematics. 2022;10(8):1285. doi:10.3390/math10081285. [Google Scholar] [CrossRef]

15. Zhang Y, Zhao R, Zhao Z, Ramakrishnan N, Aggarwal M, Medioni G, et al. Robust partial fingerprint recognition. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2023; Piscataway, NJ, USA: IEEE. p. 1011–20. doi:10.1109/cvprw59228.2023.00108. [Google Scholar] [CrossRef]

16. Chen S, Guo Z, Li X, Yang D. Query2Set: single-to-multiple partial fingerprint recognition based on attention mechanism. IEEE Trans Inf Forensics Secur. 2022;17:1243–53. doi:10.1109/tifs.2022.3159151. [Google Scholar] [CrossRef]

17. Grosz SA, Jain AK. AFR-Net: attention-driven fingerprint recognition network. IEEE Trans Biom, Behav, Identity Sci. 2023;6(1):30–42. doi:10.1109/TBIOM.2023.3317303. [Google Scholar] [CrossRef]

18. Grosz SA, Jain AK. Latent fingerprint recognition: fusion of local and global embeddings. IEEE Trans Inf Forensics Secur. 2023;18:5691–705. doi:10.1109/tifs.2023.3314207. [Google Scholar] [CrossRef]

19. Qiu Y, Chen H, Dong X, Lin Z, Liao IY, Tistarelli M, et al. IFViT: interpretable fixed-length representation for fingerprint matching via vision transformer. arXiv:2404.08237. 2024. [Google Scholar]

20. McMahan B, Moore E, Ramage D, Hampson S, y Arcas BA. Communication-efficient learning of deep networks from decentralized data. In: Artificial intelligence and statistics. Cambridge, MA: PMLR; 2017. p. 1273–82. doi:10.48550/arXiv.1602.05629. [Google Scholar] [CrossRef]

21. Vakili A, Al-Khafaji HMR, Darbandi M, Heidari A, Jafari Navimipour N, Unal M. A new service composition method in the cloud-based internet of things environment using a grey wolf optimization algorithm and mapreduce framework. Concurr Comput. 2024;36(16):e8091. doi:10.1002/cpe.8091. [Google Scholar] [CrossRef]

22. Caldarola D, Mancini M, Galasso F, Ciccone M, Rodolà E, Caputo B. Cluster-driven graph federated learning over multiple domains. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2021; Piscataway, NJ, USA: IEEE. p. 2749–58. doi:10.1109/cvprw53098.2021.00309. [Google Scholar] [CrossRef]

23. Xu A, Li W, Guo P, Yang D, Roth HR, Hatamizadeh A, et al. Closing the generalization gap of cross-silo federated medical image segmentation. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2022; Piscataway, NJ, USA: IEEE. p. 20866–75. doi:10.1109/cvpr52688.2022.02020. [Google Scholar] [CrossRef]

24. Zhang R, Xu Q, Yao J, Zhang Y, Tian Q, Wang Y. Federated domain generalization with generalization adjustment. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2023; Piscataway, NJ, USA: IEEE. p. 3954–63. doi:10.1109/cvpr52729.2023.00385. [Google Scholar] [CrossRef]

25. Zhang J, Hua Y, Wang H, Song T, Xue Z, Ma R, et al. FedALA: adaptive local aggregation for personalized federated learning. Proc AAAI Conf Artif Intell. 2023;37(9):11237–44. doi:10.1609/aaai.v37i9.26330. [Google Scholar] [CrossRef]

26. Cui T, Li H, Wang J, Shi Y. Harmonizing generalization and personalization in federated prompt learning. arXiv:2405.09771. 2024. [Google Scholar]

27. Niu Y, Deng W. Federated learning for face recognition with gradient correction. Proc AAAI Conf Artif Intell. 2022;36(2):1999–2007. doi:10.1609/aaai.v36i2.20095. [Google Scholar] [CrossRef]

28. Heidari A, Navimipour NJ, Dag H, Unal M. Deepfake detection using deep learning methods: a systematic and comprehensive review. Wiley Interdiscip Rev: Data Min Knowl Discov. 2024;14(2):e1520. doi:10.1002/widm.1520. [Google Scholar] [CrossRef]

29. Liu D, Dang Z, Peng C, Zheng Y, Li S, Wang N, et al. FedForgery: generalized face forgery detection with residual federated learning. IEEE Trans Inf Forensics Secur. 2023;18:4272–84. doi:10.1109/tifs.2023.3293951. [Google Scholar] [CrossRef]

30. Shao H, Zhong D. Towards privacy palmprint recognition via federated hash learning. Electron Lett. 2020;56(25):1418–20. doi:10.1049/el.2020.2076. [Google Scholar] [CrossRef]

31. Shao H, Liu C, Li X, Zhong D. Privacy preserving palmprint recognition via federated metric learning. IEEE Trans Inf Forensics Secur. 2023;19:878–91. doi:10.1109/TIFS.2023.3327667. [Google Scholar] [CrossRef]

32. Yang Z, Teoh ABJ, Zhang B, Leng L, Zhang Y. Physics-driven spectrum-consistent federated learning for palmprint verification. Int J Comput Vis. 2024;132:4253–68. doi:10.1007/s11263-024-02077-9. [Google Scholar] [CrossRef]

33. Swofford HJ. Fingerprint patterns: a study on the finger and ethnicity prioritized order of occurrence. J Forensic Identif. 2005;55(4):480. [Google Scholar]

34. Watson CI. NIST special database 10. NIST supplemental fingerprint card data (SFCD) (for special database 9-8-bit gray scale images). World Wide Web-Internet and Web Information Systems. Gaithersburg, MD: NIST; 2008. [Google Scholar]

35. Shehu YI, Ruiz-Garcia A, Palade V, James A. Sokoto coventry fingerprint dataset. arXiv:1807.10609. 2018. [Google Scholar]

36. Chinese Academy of Sciences’ Institute of Automation.CASIA-FingerprintV5. 2024 [cited 2024 Oct 11]. Available from: http://biometrics.idealtest.org/. [Google Scholar]

37. Yang X, Huang W, Ye M. FedAS: bridging inconsistency in personalized federated learning. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2024; Piscataway, NJ, USA: IEEE. p. 11986–95. doi:10.1109/cvpr52733.2024.01139. [Google Scholar] [CrossRef]

38. Fowl L, Geiping J, Czaja W, Goldblum M, Goldstein T. Robbing the fed: directly obtaining private data in federated learning with modified models. arXiv:2110.13057. 2021. [Google Scholar]