Rolling Bearing Fault Diagnosis Based on MTF Encoding and CBAM-LCNN Mechanism

1  Introduction

Rolling bearings are vital components of mechanical equipment, and their condition directly affects machinery’s production safety. Thus, effective fault diagnosis is essential.

Traditional methods for rolling bearing fault diagnosis primarily rely on signal processing techniques. Classic approaches include counterfactual augmentation for few-shot contrastive learning [1] and sequence attention-based data augmentation with adversarial variational autoencoders [2]. These methods depend on manual feature extraction and expert knowledge, representing shallow learning and lacking the capacity to handle large-scale data [3]. With the development of artificial intelligence technology, deep learning algorithms have gradually been applied to rolling bearing fault diagnosis, with classic convolutional neural network (CNN) receiving significant attention [4]. However, most traditional deep learning-based fault diagnosis methods for rolling bearings are based on one-dimensional (1D) vibration signals, which present challenges in feature extraction [5]. In contrast, two-dimensional (2D) image feature extraction is generally easier than that of 1D fault vibration signals. Therefore, converting 1D vibration signals into 2D images through various encoding methods has become a new trend in data preprocessing for rolling bearing fault diagnosis [6].

Zhang et al. [7] introduced a method based on deep convolutional neural network to diagnose one-dimensional fault vibration signals, achieving good classification results; however, traditional convolutional neural networks suffer from slow convergence. Huang et al. [8] utilized a multi-scale cascading convolutional neural network for bearing fault diagnosis, which significantly improved diagnostic accuracy compared to standard convolutional neural network (CNN). Nevertheless, multi-scale cascading networks present challenges in training difficulty and are prone to overfitting. Chen et al. [9] developed a fault diagnosis algorithm based on deep attention mechanisms and dual-path mixed-domain residual networks, achieving high fault diagnosis accuracy on a three-phase asynchronous motor experimental platform. Hou et al. [10] extracted frequency domain features of raw data using fast Fourier transform (FFT) and employed a designed multi-feature parallel fusion encoder to capture both local and global features of bearing data, which were then sent to a cross-flip decoder for fault classification. Tao et al. [11] proposed a rolling bearing fault diagnosis method based on wavelet transform and generalized Gaussian density modeling, where statistical parameters estimated via the maximum likelihood method were concatenated to form feature descriptors for classifying bearing faults. However, this method consumes significant computational resources when processing large-scale data. Guo et al. [12] combined wavelet transform with deformable convolutional neural network (D-CNN) to propose a fault diagnosis method for rolling bearings, noting that parameter selection during data preprocessing significantly impacts diagnostic results. In practical applications, careful consideration of data preprocessing steps and parameter choices is essential to ensure the reliability of diagnostic outcomes. Che et al. [13] proposed a domain-adaptive deep belief network (DBN) model, pre-trained with labeled samples generated from raw vibration signals and their time-domain and frequency-domain indicators for rolling bearing fault diagnosis. During domain adaptation, the model fine-tuned parameters by calculating the loss functions of multi-kernel maximum mean discrepancies (MK-MMD) and classification errors. Gu et al. [14] proposed a bearing fault diagnosis method based on complementary ensemble empirical mode decomposition (CEEMD). This method first detected abnormal components of CEEMD using permutation entropy, then decomposed the remaining signals with CEEMD. They selected intrinsic mode function components with high correlation coefficients for Hilbert envelope spectrum analysis, extracting fault features from the envelope plot. Despite employing the complementary CEEMD method and adding white noise with opposite signs to reduce reconstruction errors, the modal aliasing phenomenon could not be completely eliminated. During the signal decomposition process, a degree of modal confusion might occur, affecting the accurate extraction of fault features. Tang et al. [15] introduced a bidirectional deep belief network (Bi-DBN) to address the issues of low-quality training data and insufficient generalization ability. This model learns fault features from original vibration signals through forward training and backward sample generation, while reducing the similarity between generated and original samples. Additionally, quantum genetic algorithms were applied to optimize the parameters of Bi-DBN, enhancing feature learning efficiency.

Zheng et al. [16] converted raw vibration data into two-dimensional images, combining them with convolutional neural network (CNN) for rolling bearing fault diagnosis. However, traditional CNN suffer from low computational efficiency and high memory usage. Zheng et al. [17] transformed raw vibration signals into two-dimensional images and employed two-dimensional convolutional networks for fault diagnosis, yet standard two-dimensional CNN exhibited low diagnostic accuracy. Han et al. [18] used Gramian Angular Fields (GAF) to encode raw vibration signals and then employed random forest methods for fault diagnosis, achieving good results. Although GAF implicitly encodes temporal information, it cannot directly preserve timestamps and order, leading to suboptimal performance in tasks dependent on temporal sequences [19]. For noisy or non-stationary time series, GAF may not perform as well as other methods. In contrast, Markov Transition Field (MTF) demonstrates advantages in capturing the dynamic behavior, sequential dependencies, and noise resistance of time series, especially when handling non-stationary and noisy data [20]. Therefore, this paper adopts MTF for image encoding of raw vibration data from rolling bearings.

This paper proposes a rolling bearing fault diagnosis method integrating Markov Transition Field (MTF) and a lightweight convolutional neural network with a convolutional block attention module (CBAM-LCNN). Specifically, we first use MTF to convert the rolling bearing fault signal from a one-dimensional vibration signal to a two-dimensional image. Then, we construct a lightweight convolutional fault diagnosis neural network integrated with the convolutional block attention module (CBAM-LCNN). Finally, the two-dimensional images obtained from the MTF conversion are input into the CBAM-LCNN network for feature extraction and fault signal classification. We conducted experiments to validate the effectiveness of the proposed method on the Guangdong University of Petrochemical Technology multi-stage centrifugal fan dataset and the Case Western Reserve University dataset. The results indicate that, compared to other baseline methods, the proposed rolling bearing fault diagnosis method demonstrates high diagnostic accuracy and fast diagnostic speed. Meanwhile, we conducted experiments on the Xi’an Jiaotong University rolling bearing dataset, achieving excellent results in bearing fault diagnosis. These results validate the strong generalization performance of the proposed method. The method proposed in this paper not only effectively diagnoses faults in rolling bearings but also provides a reference for intelligent fault diagnosis of other equipment.

2  Fundamental Theories of Rolling Bearing Fault Diagnosis

2.1 Markov Transition Field (MTF)

Markov Transition Field (MTF) is a coding method that converts one-dimensional data into two-dimensional signals [21]. Suppose there exists a one-dimensional time series X={x1,x2,…,xt,…,xn}, t=1,2,…,n, where xt represents the observation of the signal at time t. Define a matrix P, which represents the probability of one subdomain signal being followed by another subdomain signal across all subdomains. The probability calculation formula in P is as follows:

ri,j=P(xi∈li|xi−1∈lj)(x)(1)

∑j=1Lri,j=1,ri,j≥0(2)

In the formula, r(i,j) represents the probability value of point i being followed by point j in the probability follow matrix, and the sum of the probabilities of point i being followed by other points equals 1.

By calculating the follow probability values for each element, we can obtain the L×L domain-weighted transition matrix π, expressed as follows:

R=[r11r12⋯r1Lr21r22⋯r2L⋮⋮⋱⋮rL1rL2⋯rLL](3)

To address the limitation of the Markov transition matrix, which neglects the dependency between the distribution of the time series X(t) and the time step t, time information is introduced to associate with the amplitude information of the vibration signal, generating the MTF matrix M. The matrix M encompasses the temporal correlation between each fractional position and the time intervals, expressed as follows:

M=[m11m12⋯m1Lm21m22⋯m2L⋮⋮⋱⋮mL1mL2⋯mLL](4)

mij=P{rij∥xi∈li,xj∈lj}(5)

In the formula, mij represents the probability of a state transition from li to lj.

Compared to other image encoding methods, the MTF encoding method has the following advantages:

(1) Long-Range Dependency Capture. Through the transition matrix, MTF encoding can capture dependencies over long time ranges in the time series, rather than being limited to relationships between adjacent time points. This is especially important for data with complex temporal dependency structures.

(2) Robustness to Noise and Outliers. MTF encoding exhibits a certain robustness to noise and outliers, as it primarily focuses on state transition patterns rather than specific values. This allows it to extract useful features more stably when dealing with noisy time series data.

(3) Global and Local Feature Capture. MTF encoding can capture both global features (transition patterns of the entire time series) and local features (transition patterns of specific time intervals). This combination provides richer information, enhancing the model’s prediction capability and recognition accuracy.

2.2 Convolutional Block Attention Module (CBAM)

The Convolutional Block Attention Module (CBAM) integrates channel attention and spatial attention mechanisms [22]. Compared to standard self-attention mechanisms, CBAM can be easily inserted into various convolutional neural network. The channel attention mechanism identifies important feature dimensions, enhancing useful information while suppressing irrelevant noise. The structure of CBAM is shown in Fig. 1.

Figure 1: Structure of convolutional block attention module

As shown in Fig. 1, the feature map is first enhanced by the channel attention module to produce an augmented map, then further refined by the spatial attention module. Finally, a feature map with a dual attention mechanism is output. CBAM can be embedded into various convolutional neural networks to enhance the model’s representational capacity, thereby improving its performance in rolling bearing fault diagnosis tasks.

2.3 Depthwise Separable Convolution Neural Network (DWCNN)

The Depthwise Separable Convolutional Neural Network (DWCNN), an improved version of the CNN model, can be divided into depthwise and pointwise convolutions [23]. The structure of the DWCNN module is illustrated in Fig. 2.

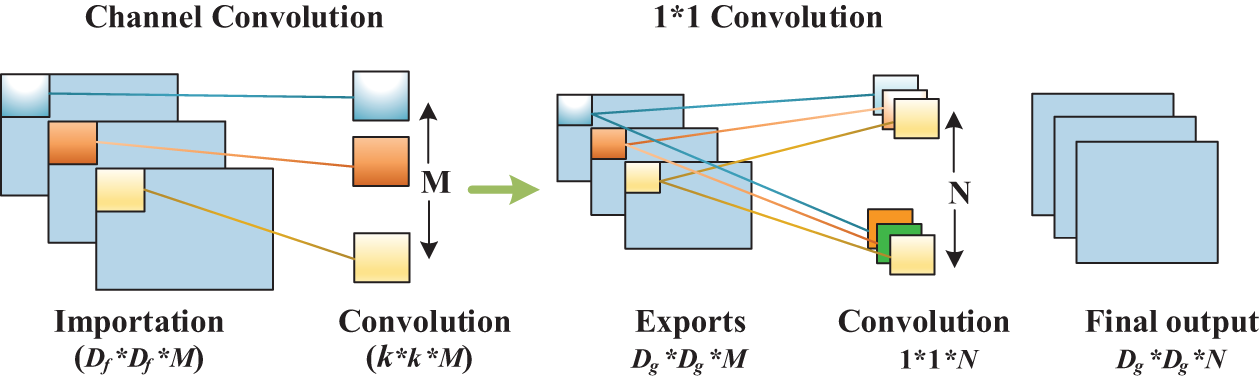
Figure 2: Depthwise separable convolutional neural network structure

As illustrated in Fig. 2, for the depthwise convolution, if the input image size is Df×Df×M and the convolution kernel size during the depthwise convolution process is k×k, the size of the output feature map will be Dg×Dg×M, where Df is the height and width of the input image, Dg is the height and width of the output image, and M is the number of channels. For pointwise convolution, the kernel size is 1×1, and each kernel has the same number of channels as the input feature map. If the number of convolution kernels is N, the size of the output feature map will be Dg×Dg×N. The output of the DWCNN model will serve as the input to the ShuffleNet V2 model.

2.4 ShuffleNet V2

ShuffleNet V2, introduced by Ma et al. in 2018 [24], is a lightweight convolutional neural network architecture that improves upon ShuffleNet V1, which was designed for high efficiency on mobile devices. The structure of the ShuffleNet V2 network is depicted in Fig. 3.

Figure 3: Structure of ShuffleNet V2: (a) Step length = 1; (b) Step length = 2

As shown in Fig. 3, ShuffleNet V2 aims to achieve efficient inference by reducing computational load and memory usage while maintaining high accuracy. Its key design features include channel balance, minimizing element-wise operations, parallel branch design, and channel shuffling. Channel balance ensures that the number of input and output channels in convolution operations is equal. Element-wise operations are minimized to improve efficiency. Parallel branches enhance computational efficiency, and channel shuffling promotes cross-channel information exchange by rearranging the feature channels. Compared to ShuffleNet V1, ShuffleNet V2 significantly enhances the network’s efficiency while maintaining a lightweight structure. The main improvements can be summarized as follows:

Channel Grouping and Feature Shuffling. ShuffleNet V2 uses grouped convolutions to divide features into multiple groups for separate convolution operations, reducing computational load. Additionally, by introducing a “channel shuffle” operation, it rearranges the channels across groups, allowing effective cross-group information exchange. This boosts the network’s representational power while maintaining a lightweight design.

Layer-Wise Computational Efficiency Optimization. ShuffleNet V2 optimizes the operators and parameter sizes of each layer, ensuring fewer floating-point operations (FLOPs) at the same accuracy level. This helps control the computational cost and model size.

Channel Splitting Mechanism. The network adopts a strategy to split part of the input channels, reducing the number of feature maps requiring computation. This channel splitting mechanism further reduces parameters and computational costs, allowing the model to operate efficiently even on resource-constrained environments like mobile devices.

3  The Bearing Fault Diagnosis Method Proposed in This Paper

3.1 The Lightweight Convolutional Neural Network Constructed in This Paper

This paper introduces a lightweight convolutional neural network (LCNN) by integrating the depthwise separable convolutional neural network (DWCNN) with ShuffleNet V2 [25]. The structure of the LCNN is shown in Fig. 4.

Figure 4: LCNN model structure diagram

As shown in Fig. 4, after image feature extraction, depthwise separable convolutions are used to process the spatial dimensions of the input features. This approach enhances feature extraction while effectively reducing computational complexity. ShuffleNet V2 is a lightweight convolutional neural network that uses pointwise convolutions to significantly reduce parameters and computations, enhancing computational efficiency and supporting fault signal classification. The combination of depthwise separable convolution networks and ShuffleNet V2 forms a lightweight convolutional neural network, which improves the speed of both network training and diagnosis.

3.2 The Bearing Fault Diagnosis Method Proposed in This Paper

The rolling bearing fault diagnosis method proposed in this paper is shown in Fig. 5.

Figure 5: Flowchart of the bearing fault diagnosis method

As shown in Fig. 5, the rolling bearing fault diagnosis method proposed in this paper is divided into four parts. Data preprocessing, feature extraction, CBAM-LCNN model construction, and fault signal classification.

Data Preprocessing. Initially, the original vibration signals for different rolling bearing faults are collected on the experimental platform. These one-dimensional signals are then transformed into two-dimensional images using the MTF. Finally, the dataset is split into training, validation, and testing sets with a ratio of 6:2:2.

Feature Extraction. We employed a convolutional neural network with integrated batch normalization layers for image feature extraction, incorporating the CBAM module between two convolutional layers to enhance the network’s perceptual range and representation capability.

LCNN Model Construction. The combination of the DWCNN and ShuffleNet V2 models enhances feature extraction while reducing parameter and computational complexity, thereby improving the computational efficiency of the bearing fault diagnosis model. The LCNN network is formed by integrating the DWCNN and ShuffleNet V2 networks.

Bearing Fault Classification. Fault classification of rolling bearings is performed using the SoftMax function following two Dense layers.

4  Experimental Verification and Result Analysis

4.1 Experimental Setup

4.1.1 Experiment 1

In Experiment 1, we used the bearing fault dataset of multi-stage centrifugal fans from Guangdong University of Petrochemical Technology (GDUPT dataset). During the data collection process for this dataset, the rolling bearing speed was 1200r/min, the vibration sensor used was EMT390, the sampling frequency of the sampler was 1024Hz, and the sampling duration was 8 s. The bearing model used in the experiment was HRB-1310ATN, with an inner diameter of 50mm, an outer diameter of 110mm, a height of 27mm, and 13 rolling elements. The dataset contains 4,096,000 data samples for each of the four fault types. Normal bearing, inner race worn, outer race worn, and rolling element missed. The data collection platform for the GDUPT dataset is shown in Fig. 6.

Figure 6: GDUPT dataset collection test platform

As shown in Fig. 6, it can be seen that the bearing fault signal acquisition platform for the multi-stage centrifugal fan mainly consists of five components. A variable frequency motor, transmission, load controller, multi-stage centrifugal fan, bearing seat and control panel. The vibration signals of the four types of bearing states included in the GDUPT dataset are shown in Fig. 7.

Figure 7: Four types of bearing states included in the GDUPT dataset: (a) Inner race worn (b) Normal bearing (c) Outer race worn (d) Rolling element missed

As shown in Fig. 7, the vibration signals of the four types of bearings included in the GDUPT dataset are different when rotating, and there is an issue of sample data imbalance in the vibration signal graph of the rolling element missed. To address this issue and to reduce the computational load of the model, we performed segmented truncation of the vibration data while ensuring that the fault diagnosis accuracy was not affected. We retained the first 1,024,000 sample data for each fault type for image encoding. The label values for the vibration data of the four types of bearings are shown in Table 1.

Table 1 shows that the vibration data for the four types of bearings were labeled as normal, ou, ro, and in, which aided in the subsequent classification of rolling bearing faults.

4.1.2 Experiment 2

To assess the generalization capability of the rolling bearing fault diagnosis method proposed in this study, we utilized the Case Western Reserve University (CWRU) bearing fault dataset (referred to as the CWRU dataset) for validation. This dataset includes fault signal acquisition experiments conducted using SKF6203 and SKF6205 rolling bearings manufactured by Svenska Kullager-Fabriken [26]. The data collection platform for the CWRU dataset is illustrated in Fig. 8.

Figure 8: CWRU dataset collection test platform

To assess the generalization capability of the rolling bearing fault diagnosis method proposed in this study, we utilized the Case Western Reserve University (CWRU) bearing fault dataset (referred to as the CWRU dataset) for validation. This dataset includes fault signal acquisition experiments conducted using SKF6203 and SKF6205 rolling bearings manufactured by Svenska Kullager-Fabriken [26]. The data collection platform for the CWRU dataset is illustrated in Fig. 8.

As shown in Fig. 8, the CWRU dataset collection platform consists of a fan-side bearing, drive-end bearing, motor, encoded torque sensor, and power meter. In the generalization experiment, we selected the drive-end bearing fault data collected at a sampling frequency of 12 kHz. The experiment introduced rolling element fault, inner race fault, and outer race fault data with defect diameters of 0.1778, 0.3556, and 0.5334 mm, respectively. Along with the data for bearings in a normal state, there are a total of 10 different bearing state types. The 12k fan-side bearing state categories and label values are set is shown in Table 2.

As shown in Table 2, we assigned label values ranging from 0 to 9 to the normal bearing and the nine fault state bearings, facilitating the subsequent classification of rolling bearing faults in the CWRU dataset.

4.2 Image Encoding Parameter Settings

During MTF encoding, we sampled the raw signal using a sliding window. The number of generated mapping images varies with different sliding window steps, and both the number of mapping images and the pixel size of the encoded images affect the accuracy of bearing fault diagnosis. To determine the optimal sliding window step and pixel size for MTF encoding, we conducted experiments with various sliding window steps and encoding pixel sizes, validated using the proposed method. The results are shown in Table 3.

As shown in Table 3, in selecting the sliding window step size, we primarily considered the impact of commonly used step ranges on accuracy and computational efficiency. While a smaller step size can capture finer-grained features, it significantly increases computational load and storage requirements, making it unsuitable for lightweight models. Conversely, a step size exceeding 512 loses considerable detail, reducing the accuracy of fault feature extraction. Therefore, we selected 128, 256, and 512 as experimental step sizes to balance computational load and feature completeness. These values are commonly found in the literature and provide stable performance support for our study.

The pixel size of the encoded image directly impacts feature clarity and computational resource requirements. Smaller pixel sizes may lead to feature loss, making fault patterns harder to distinguish, while excessively large pixel sizes substantially increase storage demands. In our experiments, we found that dimensions of 256 × 256 and above effectively capture fault features, with 512 × 512 yielding optimal performance in both diagnostic efficiency and accuracy. Thus, we experimented with the common pixel sizes of 32 × 32, 64 × 64, 128 × 128, 256 × 256, and 512 × 512 to ensure a balance between feature fidelity and processing efficiency. Based on this analysis, we selected an MTF encoding sliding step size of 256 and a pixel size of 512.

The two-dimensional mapping images obtained from the GDUPT dataset and the CWRU dataset using the MTF image encoding method are shown in Fig. 9.

Figure 9: MTF mapping diagrams of two datasets: (a) GDUPT (b) CWRU

As shown in Fig. 9, the two-dimensional mapping images obtained from the GDUPT dataset and the CWRU dataset after MTF encoding exhibit clear textures and distinct features, facilitating the subsequent diagnosis of rolling bearing faults.

4.3 Experimental Parameter Settings

In all experiments in this study, we used a server with an i9-12900KF CPU, an NVIDIA GeForce RTX 3090 GPU, 32 GB of memory, and the Windows 10 Professional operating system for training. The MTF-CBAM-LCNN model and other benchmark models were trained and tested on two bearing fault datasets. The hyperparameter settings for the MTF-CBAM-LCNN model and all benchmark models are shown in Table 4.

As shown in Table 4, to verify the advantage of faster diagnostic speed of the proposed CBAM-LCNN method compared to other rolling bearing fault diagnosis methods, we set up three benchmark methods. MTF-CNN [27], Mel-EfficientNetV2 [28], and VMD-FK-MobileNet V2 [29].

To compare the performance of the CBAM-LCNN model with other models in rolling bearing fault diagnosis, we set up four advanced benchmark models. DS-GAF-ResNet [30], GNN-Film [31], LAFICNN [32], and MMSI-SR-KNN [33].

4.4 Experimental Results and Analysis

We set the encoding sliding step size for the MTF encoding method to 256 and the encoding pixel size to 512 to perform image encoding on the GDUPT dataset. Comparative experiments were conducted using the proposed MTF-CNN, Mel-EfficientNet V2, and VMD-FK-MobileNet V2 methods. The curves of training accuracy and testing accuracy over iterations for the four methods are shown in Fig. 10.

Figure 10: Execution process of the four control methods: (a) Training set execution process (b) Value set execution process

As shown in Fig. 10, compared to the three benchmark methods—MTF-CNN, Mel-EfficientNet V2, and VMD-FK-MobileNet V2—the proposed MTF-CBAM-LCNN model achieves high fault diagnosis accuracy with fewer iterations, confirming the advantage of faster diagnostic speed for the MTF-CBAM-LCNN method.

To further confirm the advantages of the MTF-CBAM-LCNN approach, we documented the test accuracy, test loss, training time, and testing time for all benchmark methods. The results are presented in Table 5.

As shown in Table 5, compared to the three benchmark models, MTF-CNN, Mel-EfficientNet V2, and VMD-FK-MobileNet V2, the proposed method attains the highest test accuracy, the lowest test loss, and the shortest network training and testing times, verifying the advantage of the MTF-CBAM-LCNN method in terms of high fault diagnosis accuracy.

To further confirm the advantages of the MTF-CBAM-LCNN model in achieving higher accuracy and faster diagnosis speed for bearing fault diagnosis, we performed experiments using the GDUPT dataset. We recorded the test set accuracy, loss values, and memory usage of five methods: DS-GAF-ResNet [30], GNN-Film [31], LAFICNN [32], MMSI-SR-KNN [33], and the proposed MTF-CBAM-LCNN. The results are shown in Table 6.

As shown in Table 6, the proposed MTF-CBAM-LCNN model outperformed several advanced benchmark models in terms of test set accuracy, loss values, and memory usage during runtime. This further validates the superiority of the MTF-CBAM-LCNN model in rolling bearing fault diagnosis.

We conducted a rigorous training and validation process to prevent overfitting. First, we used multiple dataset validation methods to ensure consistent model performance across different training and validation sets, thus evaluating its generalization ability. Second, we also reduced the risk of overfitting by controlling the network’s complexity, such as reducing the number of parameters and using the lightweight ShuffleNet V2 architecture.

To ensure data independence and prevent data leakage, we strictly followed standard data splitting methods to separate the training and testing sets, ensuring that samples from the test set do not appear during the training process. Specifically, in the data preprocessing phase, we carefully checked the data segmentation and sliding window usage to ensure that each data sample was only involved in the training process once. To further validate data independence, we used different datasets in the model validation experiments and performed cross-validation, ensuring that the model performed well across multiple datasets without result inaccuracies caused by bias in any specific dataset.

To more intuitively visualize the results of rolling bearing fault diagnosis, we plotted the classification confusion matrices for the two datasets. The confusion matrices for the GDUPT and CWRU datasets are shown in Fig. 11.

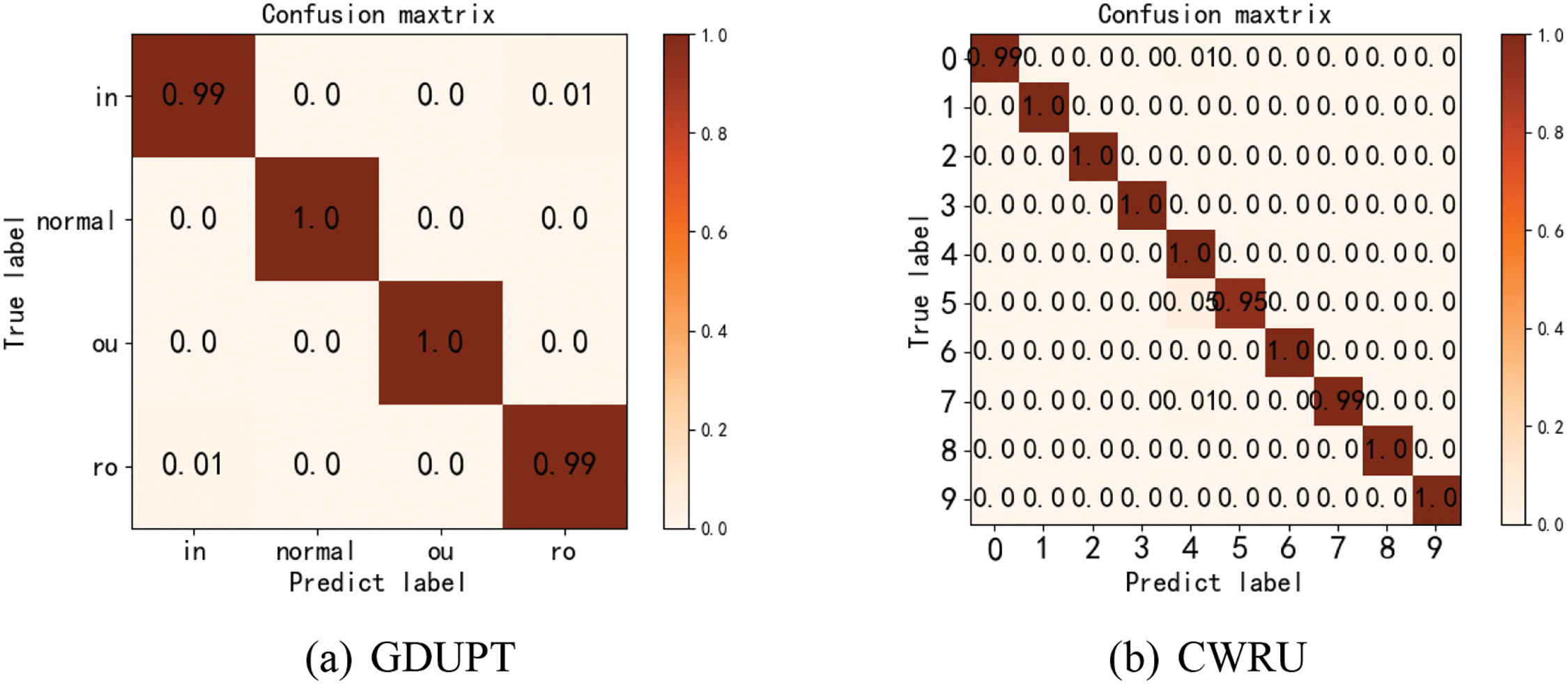
Figure 11: Classification confusion matrices of two datasets (a) GDUPT (b) CWRU

Fig. 11 shows the classification confusion matrix, where the horizontal axis represents the predicted labels of the image-encoded dataset, and the vertical axis shows the true labels of the four types of bearings in the dataset. Ideally, the diagonal elements should be close to 100%. In the GDUPT dataset, the classification accuracy for outer race wear and normal state bearings reached 100%, while the classification accuracy for the other two fault states was 99%, resulting in an overall test set accuracy of 99.4%. In the CWRU dataset, among the ten fault signal categories, all fault types achieved 100% classification accuracy except for Normal Condition, Inner Race Fault 2, and Outer Race Fault 1. The overall test set accuracy was 99.3%. The MTF-CBAM-LCNN model demonstrated high accuracy in rolling bearing fault diagnosis across both datasets, verifying its effectiveness in rolling bearing fault diagnosis.

Misclassifications occurred between inner race faults and ball faults in the GDUPT dataset, while in the CWRU dataset, misclassifications were observed in Normal Condition, Inner Race Fault 2, and Outer Race Fault 1. These misclassifications may result from the feature similarities among these fault types and the influence of minor signal fluctuations under specific operating conditions on feature extraction. Additionally, noise and variations in operating conditions could contribute to a small number of misclassifications.

To verify the impact of integrating CBAM into LCNN on the accuracy of rolling bearing fault diagnosis, we conducted experiments comparing LCNN with CBAM-LCNN. The fault diagnosis accuracy of the LCNN method was 98.31%, which is nearly 1% lower than that of the CBAM-LCNN method. This result confirms the effectiveness of incorporating CBAM into LCNN.

Additionally, to further validate the generalization performance of the MTF-CBAM-LCNN model, additional experiments were conducted on the XJTU-SY dataset. The classification accuracy achieved was 99.47%, with a training time of 77 s per iteration for the diagnostic network. Compared with the baseline models in this study, the MTF-CBAM-LCNN model demonstrated higher fault diagnosis accuracy and faster diagnostic speed. These results further confirm the characteristics of the MTF-CBAM-LCNN model, including high diagnostic accuracy, fast processing speed, and strong generalization capability. Additionally, they highlight the potential of the MTF-CBAM-LCNN model for real-world rolling bearing fault diagnosis scenarios.

5  Conclusion

This study investigates the challenges of slow diagnostic speed, low accuracy, and limited generalization associated with existing rolling bearing fault diagnosis methods. To address these issues, a novel rolling bearing fault diagnosis approach is proposed, integrating Markov Transition Field (MTF) image encoding with a CBAM-LCNN mechanism. Specifically, the raw vibration signals of bearing faults are first encoded into two-dimensional images using MTF. Then, a lightweight convolutional neural network (CBAM-LCNN) integrated with convolutional attention modules is constructed. Finally, the two-dimensional images obtained through MTF encoding are used as input to the CBAM-LCNN network for feature extraction and fault diagnosis.

We adopted ShuffleNet V2 as the foundation for constructing the lightweight convolutional neural network (LCNN) and further optimized the model’s computational requirements through operations such as channel grouping and feature shuffling, while maintaining accuracy. This approach enables the model to achieve efficient feature extraction capabilities for fault diagnosis tasks while reducing computational resource demands.

During the experiments, we monitored the model’s memory usage to evaluate its performance in practical application scenarios. The experimental results showed that the model meets real-time requirements across various devices and achieves a good balance between accuracy and efficiency. Furthermore, to reduce complexity, we explored different stride and pixel parameters during the experiments, ultimately selecting the optimal combination for accuracy and computational efficiency.

To demonstrate the effectiveness and superiority of the proposed method, experiments were conducted using the rolling bearing fault dataset of a multi-stage centrifugal fan from Guangdong University of Petrochemical Technology and the rolling bearing fault dataset from Case Western Reserve University. The study yielded the following findings. First, the MTF was employed to encode one-dimensional vibration signals into two-dimensional images, effectively transforming the vibration signal-based fault diagnosis problem into an image processing task. This approach mitigated the challenges posed by noise and poor smoothness in one-dimensional signals. Second, convolutional attention modules were incorporated into two convolutional layers, enhancing the model’s perceptual range and representational capacity, which significantly improved the accuracy of rolling bearing fault diagnosis. Third, DWCNN and ShuffleNet V2 were utilized to construct a lightweight convolutional neural network, reducing the model’s parameter count and computational complexity, as well as shortening the training time. Finally, compared with three baseline methods—MTF-CNN, Mel-EfficientNet V2, and VMD-FK-MobileNet V2—the CBAM-LCNN network demonstrated the shortest training time per iteration and the highest diagnostic accuracy. Additionally, compared with four advanced methods—DS-GAF-ResNet, GNN-Film, LAFICNN, and MMSI-SR-KNN—the proposed MTF-CBAM-LCNN model achieved higher diagnostic accuracy, lower loss values, and smaller memory consumption, effectively validating the efficiency of its lightweight design.

We conducted experiments on the CWRU, GDUPT, and XJTU-SY datasets using encoding parameters of a sliding window step size of 256 and an encoding pixel size of 512 × 512. The diagnostic accuracies of the MTF-CBAM-LCNN method on rolling bearing faults were 99.4%, 99.3%, and 99.47%, respectively, demonstrating the model’s strong generalization capability in fault diagnosis methods. The MTF-CBAM-LCNN model not only effectively diagnosed rolling bearing faults but also provides an important reference for intelligent fault diagnosis of other equipment.

Acknowledgment: The authors would like to express sincere gratitude to all the anonymous reviewers and the editorial team for their valuable comments and suggestions.

Funding Statement: This work was supported by the National Natural Science Foundation of China (52001340), the Henan Province Science and Technology Key Research Project (242102110332), and the Henan Province Teaching Reform Project (2022SYJXLX087).

Author Contributions: Wei Liu, as the first author, was responsible for the conception and design of image encoding and the CBAM-LCNN model and was the primary contributor to manuscript writing. Sen Liu was responsible for the collection and processing of the bearing fault dataset, validation of the CBAM-LCNN model’s effectiveness, and analysis of the experimental results. Yinchao He reviewed the manuscript and provided suggestions for control experiments. Jiaojiao Wang and Yu Gu assisted in collecting and organizing relevant literature, participated in the discussion of experimental results, and revised the paper. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, S. L., upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Liu Y, Jiang H, Yao R, Zeng T. Counterfactual-augmented few-shot contrastive learning for machinery intelligent fault diagnosis with limited samples. Mech Syst Sig Process. 2024;216:111507. doi:10.1016/j.ymssp.2024.111507. [Google Scholar] [CrossRef]

2. Liu Y, Jiang H, Yao R, Zhu H. Interpretable data-augmented adversarial variational autoencoder with sequential attention for imbalanced fault diagnosis. J Manuf Syst. 2023;71:342–59. doi:10.1016/j.jmsy.2023.09.019. [Google Scholar] [CrossRef]

3. Tang H, Tang Y, Su Y, Feng W, Wang B, Chen P, et al. Feature extraction of multi-sensors for early bearing fault diagnosis using deep learning based on minimum unscented kalman filter. Eng Appl Artif Intell. 2024;127(5):107138. doi:10.1016/j.engappai.2023.107138. [Google Scholar] [CrossRef]

4. Liu Y, Jiang H, Liu C, Yang W, Sun W. Data-augmented wavelet capsule generative adversarial network for rolling bearing fault diagnosis. Knowl Based Syst. 2022;252:109439. doi:10.1016/j.knosys.2022.109439. [Google Scholar] [CrossRef]

5. Tong A, Zhang J, Xie L. Intelligent fault diagnosis of rolling bearing based on gramian angular difference field and improved dual attention residual network. Sensors. 2024;24(7):2156. doi:10.3390/s24072156. [Google Scholar] [PubMed] [CrossRef]

6. Mishra RK, Choudhary A, Fatima S, Mohanty AR, Panigrahi BK. A fault diagnosis approach based on 2D-vibration imaging for bearing faults. J Vib Eng Technol. 2023;11(7):3121–34. doi:10.1007/S42417-022-00735-1. [Google Scholar] [CrossRef]

7. Zhang W, Peng G, Li C, Chen Y, Zhang Z. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals. Sensors. 2017;17(2):425. doi:10.3390/s17020425. [Google Scholar] [PubMed] [CrossRef]

8. Huang W, Cheng J, Yang Y, Guo G. An improved deep convolutional neural network with multi-scale information for bearing fault diagnosis. Neurocomputing. 2019;359(3):77–92. doi:10.1016/j.neucom.2019.05.052. [Google Scholar] [CrossRef]

9. Chen Y, Zhang D, Zhang H, Wang Q. Dual-path mixed-domain residual threshold networks for bearing fault diagnosis. IEEE Trans Ind Electron. 2022;69(12):13462–72. doi:10.1109/TIE.2022.3144572. [Google Scholar] [CrossRef]

10. Hou Y, Wang J, Chen Z, Ma J, Li T. Diagnosisformer: an efficient rolling bearing fault diagnosis method based on improved Transformer. Eng Appl Artif Intell. 2023;124(7):106507. doi:10.1016/J.ENGAPPAI.2023.106507. [Google Scholar] [CrossRef]

11. Tao X, Ren C, Wu Y, Li Q, Guo W, Liu R, et al. Bearings fault detection using wavelet transform and generalized Gaussian density modeling. Measurement. 2020;155(7):107557. doi:10.1016/j.measurement.2020.107557. [Google Scholar] [CrossRef]

12. Guo J, Liu X, Li S, Wang Z. Bearing intelligent fault diagnosis based on wavelet transform and convolutional neural network. Shock Vib. 2020;2020(1):6380486. doi:10.1155/2020/6380486. [Google Scholar] [CrossRef]

13. Che C, Wang H, Ni X, Fu Q. Domain adaptive deep belief network for rolling bearing fault diagnosis. Comput Indus Eng. 2020;143(1–4):106427. doi:10.1016/j.cie.2020.106427. [Google Scholar] [CrossRef]

14. Gu J, Peng Y. An improved complementary ensemble empirical mode decomposition method and its application in rolling bearing fault diagnosis. Digit Sig Process. 2021;113(2):103050. doi:10.1016/j.dsp.2021.103050. [Google Scholar] [CrossRef]

15. Tang J, Wu J, Hu B, Liu J. Towards a fault diagnosis method for rolling bearing with bi-directional deep belief network. Appl Acoust. 2022;192(7):108727. doi:10.1016/j.apacoust.2022.108727. [Google Scholar] [CrossRef]

16. Zheng Y, Mu L, Zhao J. Investigation of rolling bearing weak fault diagnosis based on CNN with two-dimensional image. Russ J Nondestruct Test. 2023;59(1):82–93. doi:10.1134/S1061830922600575. [Google Scholar] [CrossRef]

17. Zheng J, Wang J, Wang H, Ding J, Yi C. Diagnosis and classification of gear composite faults based on S-transform and improved 2D convolutional neural network. Int J Dyn Control. 2024;12(6):1659–70. doi:10.1007/s40435-023-01324-0. [Google Scholar] [CrossRef]

18. Han Y, Li B, Huang Y, Li L. Bearing fault diagnosis method based on Gramian angular field and ensemble deep learning. J Vibroeng. 2023;25(1):42–52. doi:10.21595/JVE.2022.22796. [Google Scholar] [CrossRef]

19. Gu X, Xie Y, Tian Y, Liu T. A lightweight neural network based on GAF and ECA for bearing fault diagnosis. Metals. 2023;13(4):822. doi:10.3390/met13040822. [Google Scholar] [CrossRef]

20. Lei C, Miao C, Wan H, Zhou J, Hao D, Feng R. Rolling bearing fault diagnosis method based on MTF-MFACNN. Meas Sci Technol. 2023;35(3):35007. doi:10.1088/1361-6501/ad11c7. [Google Scholar] [CrossRef]

21. Ding S, Rui Z, Lei C, Zhuo J, Shi J, Lv X. A rolling bearing fault diagnosis method based on Markov transition field and multi-scale Runge-Kutta residual network. Meas Sci Technol. 2023;34(12):125150. doi:10.1088/1361-6501/acf8e7. [Google Scholar] [CrossRef]

22. Xu S, Yuan R, Lv Y, Hu H, Shen T, Zhu W. A novel fault diagnosis approach of rolling bearing using intrinsic feature extraction and CBAM-enhanced InceptionNet. Meas Sci Technol. 2023;34(10):105111. doi:10.1088/1361-6501/ace19c. [Google Scholar] [CrossRef]

23. Dang L, Pang P, Lee J. Depth-wise separable convolution neural network with residual connection for hyperspectral image classification. Remote Sens. 2020;12(20):3408. doi:10.3390/rs12203408. [Google Scholar] [CrossRef]

24. Luo Z, Tan H, Dong X, Zhu G, Li J. A fault diagnosis method for rotating machinery with variable speed based on multi-feature fusion and improved ShuffleNet V2. Meas Sci Technol. 2022;34(3):35110. doi:10.1088/1361-6501/aca5a9. [Google Scholar] [CrossRef]

25. Cui K, Liu M, Meng Y. A new fault diagnosis of rolling bearing on FFT image coding and L-CNN. Meas Sci Technol. 2024;35(7):76108. doi:10.1088/1361-6501/ad3295. [Google Scholar] [CrossRef]

26. Chaleshtori AE, Aghaie A. A novel bearing fault diagnosis approach using the Gaussian mixture model and the weighted principal component analysis. Reliab Eng Syst Saf. 2024;242(5):109720. doi:10.1016/j.ress.2023.109720. [Google Scholar] [CrossRef]

27. Wang M, Wang W, Zhang X, Lu HH. A new fault diagnosis of rolling bearing based on Markov transition field and CNN. Entropy. 2022;24(6):751. doi:10.3390/e24060751. [Google Scholar] [PubMed] [CrossRef]

28. Shan S, Liu J, Wu S, Shao Y, Li H. A motor bearing fault voiceprint recognition method based on Mel-CNN model. Measurement. 2023;207(22):112408. doi:10.1016/j.measurement.2022.112408. [Google Scholar] [CrossRef]

29. Jiang W, Qi Z, Jiang A, Chang C, Xia X. Lightweight network bearing intelligent fault diagnosis based on VMD-FK-ShuffleNetV2. Machines. 2024;12(9):608. doi:10.3390/machines12090608. [Google Scholar] [CrossRef]

30. Li G, Ao J, Hu J, Hu D, Liu Y, Huang Z. Dual-source Gramian angular field method and its application on fault diagnosis of drilling pump fluid end. Expert Syst Appl. 2024;237(16):121521. doi:10.1016/j.eswa.2023.121521. [Google Scholar] [CrossRef]

31. Li Y, Yang H, Wu K, Zhang T, Xiong Q. A Gramian angular field for constructing graph-based GNNs and its applications in rolling bearing defect detection. IEEE Sens J. 2024;24(21):35141–55. doi:10.1109/JSEN.2024.3458409. [Google Scholar] [CrossRef]

32. Yu T, Ren Z, Zhang Y, Zhou S, Jiang Z, Zhou X. LAFICNN: a novel convolutional adaptive fusion framework for fault diagnosis of rotating machinery. IEEE Trans Instrum Meas. 2024;73:1–9. doi:10.1109/TIM.2024.3379402. [Google Scholar] [CrossRef]

33. Yang J, Bai Y, Tan X, Cheng R, Hu H, Wang P, et al. A new model for bearing fault diagnosis based on mutual mapping of signals and images and sparse representation. Meas Sci Technol. 2024;35(4):46122. doi:10.1088/1361-6501/AD1D4A. [Google Scholar] [CrossRef]