Coupling Magneto-Electro-Elastic Multiscale Finite Element Method for Transient Responses of Heterogeneous MEE Structures

Abbreviations

1  Introduction

Magneto-electro-elastic (MEE) materials are smart composites of piezoelectric and piezomagnetic phases, exhibiting three types of coupling effects: piezoelectric, piezomagnetic, and magneto-electric. Due to their exceptional mechanical, electrical, and magnetic coupling properties, MEE structures have become a research hotspot for developing new intelligent components for engineering applications in sensors, energy harvesters, magnetic field detectors, and electromagnetic transducers [1,2]. These intelligent components find widespread use in aerospace, machinery manufacturing, automobiles, medical equipment, and other advanced technological fields [3–5]. MEE materials are characterized by heterogeneity and multiscale properties, such as functionally graded MEE (FGMEE) materials [6] and fiber-reinforced MEE materials [7] with more complex microstructure than single-phase materials. MEE materials often experience dynamic loads (e.g., vibration) during operation. Consequently, investigating the transient response characteristics of heterogeneous MEE structures is crucial for advancing their application aspects, holding significant potential for smart devices performance enhancement.

MEE structural dynamics are primarily investigated through experimental, analytical, and numerical methods. While experiments can be time-consuming, costly, and susceptible to various factors affecting result stability, analytical methods often have limited applicability to complex real-world problems [8]. These limitations have been addressed via various numerical methods that have demonstrated efficiency in analyzing MEE structural dynamics due to their broad applicability and cost-effectiveness. Among these, the finite element method (FEM) stands out as a well-developed and widely used technique. Kiran et al. [9] employed FEM to study the impact of different porosity distributions in a FGMEE plate on its structural properties and the influence of material gradient index and pore volume on static behavior and free vibrations. Bhangale et al. [10–12] utilized FEM to analyze free vibration and static responses of MEE plates and cylindrical shells. Annigeri et al. [13] explored the free vibrations of a multiphase and layered MEE beam using FEM, calculating natural frequencies under three boundary conditions (BCs) and validating them against theoretical solutions. Zhao et al. [6] applied FEM to analyze static and dynamic properties of FGMEE shell structures, including output and magnetic potential characteristics under different stacking sequences. However, the FEM exhibits certain limitations, for which, several numerical methods have been suggested. Zhou et al. [14] adopted the enriched FEM to solve the transient dynamics of MEE intelligent structures. Jiang et al. [15] developed a coupling MEE edge-based smoothed finite element method (ES-FEM) model to evaluate the dynamic performance of the MEE solids, solving problems of the too-large constructed matrix when FEM solves the structures. Zhou et al. [16] combined FEM and gradient smoothing, proposing a coupled multi-physical cell-based smoothed FEM (CPCS-FEM) to solve the static behavior of FGMEE structures in a thermal environment. Compared to the FEM, this method generates a softer stiffness matrix with a higher calculation accuracy.

The aforementioned studies demonstrate that the microstructures of MEE composites exhibit greater complexity compared to single-phase materials, displaying notable heterogeneity. Consequently, when employing the FEM to obtain microscopic heterogeneity information of materials, refined mesh techniques must be utilized to ensure computational accuracy. This approach, however, results in a significant increase in modeling workload and computational demands, requiring longer run times and more resources. For structures with intricate microstructures and pronounced heterogeneity, obtaining accurate results may thus prove challenging. Therefore, to precisely and efficiently address the heterogeneous MEE structural dynamics problems, it is imperative to develop a multiscale numerical method that accounts for both heterogeneity and multi-field coupling.

The multiscale finite element method (MsFEM) proposed by Babuska et al. [17] has been extensively applied to address scalar field problems, particularly in the solution of seepage flows in porous media [18,19]. Zhang et al. [20] extended MsFEM to solid mechanics, a vector field problem, and developed the extended MsFEM(EMsFEM). Subsequently, a series of MsFEM-based studies were published to address several challenges including elasticity, elastic-plastic, thermo-elastic, crack propagation, and optimization analyses. Liu et al. [21] elucidated the fundamental principles of EMsFEM, applying them to analyze and compute elastic problems in heterogeneous materials and structures. Building upon EMsFEM, Zhang et al. [22] formulated a two-scale, collaborative iterative algorithm centered on the displacement decomposition approach. This algorithm is specifically designed to address the elastic-plastic analysis of periodic truss structures. Zhang et al. [23] introduced a coupled MsFEM (CEMsFEM) to simulate thermoelastic problems in heterogeneous multiphase materials by constructing multiscale basis functions for temperature and displacement fields. Zhang et al. [24] proposed a coupling method based on EMsFEM and evaluated its accuracy and effectiveness in quasi-static analysis of large structures exhibiting crack growth. Lv et al. [25] employed the EMsFEM methodology to investigate the mechanical characteristics of heterogeneous materials with randomly positioned polygonal microstructures. They further demonstrated the utility of this method through numerical simulations in two domains: analyzing heterogeneous wood structures and modeling enclosed liquid-filled cellular materials. Liu et al. [26] used the EMsFEM to realize the fast calculation of bandgap optimization of large-scale truss structures. Yan et al. [27] constructed a mathematical model for multi-material and multiscale optimization, leveraging the EMsFEM to enhance structural performance through topology optimization. Yan et al. [28] refined the MsFEM and proposed a parallel computing framework to facilitate multiscale analysis of three-dimensional (3D) network structures. Ammosov et al. [29] developed a multiscale algorithm based on the generalized MsFEM to address the piezo-magneto-electric problem and validated it through 2D and 3D model problems. These studies demonstrate that MsFEM, compared to traditional FEM, can significantly reduce computational requirements and enhance efficiency when solving heterogeneous material mechanics problems, leading to its widespread adoption. However, there remains a notable absence of research on heterogeneous MEE material dynamic problems utilizing the MsFEM approach.

In this study, we introduce the coupling MEE MsFEM (CM-MsFEM) for solving the dynamic problems of heterogeneous MEE structures. The method captures the microscopic heterogeneous information of the material by constructing multiscale basis functions for displacement, electric, and magnetic potentials. Consequently, the equivalent stiffness matrix of the macroscopic unit is derived, which reflects the heterogeneous mechanical-electro-magneto information of the material at the microscale. The article is organized as follows: Section 2 presents the fundamental equations of the transient problems of MEE structures; Section 3 introduces the basic concepts of the CM-MsFEM, which is developed from microscopic, macroscopic, and downscaling perspectives; Section 4 introduces the coupling MEE Newmark method; the accuracy and efficiency of the algorithm are validated using various examples in Section 5; and finally, Section 6 presents our primary conclusions.

2  Basic Equations and BCs

The fundamental equations governing dynamic problems in MEE materials encompass generalized equilibrium, geometric, and constitutive equations.

The generalized equilibrium equations for MEE material dynamics, neglecting damping, body force, volume charge, and volume current density, can be expressed as follows [30]:

σij,j(x,t)=ρu¨i(x,t),(1)

Di,i(x,t)=0,(2)

Bi,i(x,t)=0,(3)

where t is the time; σij, Di, and Bi are the components of stress, electric displacement, and magnetic induction, respectively; ρ and u¨i are the mass density and displacement acceleration, respectively; i, j = 1, 2, 3.

The generalized geometric equations can be expressed as follows [30]:

εij(x,t)=12(ui,j(x,t)+uj,i(x,t)),(4)

Ei(x,t)=−ϕ,i(x,t),(5)

Hi(x,t)=−ψ,i(x,t),(6)

where εij, Ei, and Hi are the components of strain, electric field, and magnetic field, respectively; and ui, ϕ, and ψ are the components of displacement, electric potential, and magnetic potential, respectively.

The constitutive equations can be expressed as follows:

σij(x,t)=Cijklεkl(x,t)−elijEl(x,t)−hlijHl(x,t),(7)

Di(x,t)=eiklεkl(x,t)+κilEl(x,t)+αilHl(x,t),(8)

Bi(x,t)=hiklεkl(x,t)+αilEl(x,t)+μilHl(x,t),(9)

where Cijkl is the elastic modulus coefficient under constant electric and magnetic fields; κil and μil are the coefficients of dielectric and magnetic permeability, respectively; elij and hlij are the piezoelectric and piezomagnetic stress coefficients under constant strain, respectively; αil is the magneto-electric coupling coefficient.

The natural and essential BCs are enumerated as follows [31]:

(i)   For mechanical fields:

ui(x,t)=u¯i(x,t), on ∂Γu(10)

σij(x,t)ni=t¯j(x,t),on∂Γσ(11)

(ii)   For electric fields:

ϕ(x,t)=ϕ¯(x,t),on∂Γϕ(12)

Di(x,t)ni=−Q¯(x,t),on∂ΓD(13)

(iii)   For magnetic fields:

ψ(x,t)=ψ¯(x,t),on∂Γψ(14)

Bi(x,t)ni=−ϑ¯(x,t),on∂ΓB(15)

where u¯i and t¯j are the given displacement and prescribed surface loads, respectively; ϕ¯ and Q¯ are the given electrical potential and prescribed surface density of free charge, respectively; ψ¯ and ϑ¯ are the given magnetic potential and prescribed magnetic flux, respectively; ni is the component of the outer unit normal vector; ∂Γu, ∂Γσ, ∂Γϕ, ∂ΓD, ∂Γψ, and ∂ΓB are the boundaries of the prescribed displacement, traction vector, electrical potential, electrical displacement vector, magnetic potential, and magnetic flux, respectively.

3  CM-MsFEM for Transient Analysis of MEE Structures

The CM-MsFEM is a numerical computation method that addresses large-scale problems while capturing small-scale heterogeneous information. The fundamental distinction between CM-MsFEM and traditional FEM lies in their basis functions. In FEM, these functions are given as analytical expressions that are independent of material properties. In contrast, CM-MsFEM constructs numerical multiscale basis functions for each element, reflecting the material heterogeneity within. These functions are then incorporated into the coarse-scale mesh to obtain appropriate results.

This study focuses on the problem of heterogeneous MEE structures in the plane (Fig. 1a). A two-grid system was employed for the solution using the CM-MsFEM. Initially, the entire structure was discretized into coarse grids (Fig. 1b), which were further subdivided into fine grids (Fig. 1d). The dimensional scale of the coarse grids can exceed that of the material’s characteristic dimensions, necessitating the fine grids to be sufficiently detailed to analyze the material heterogeneity within the selected region.

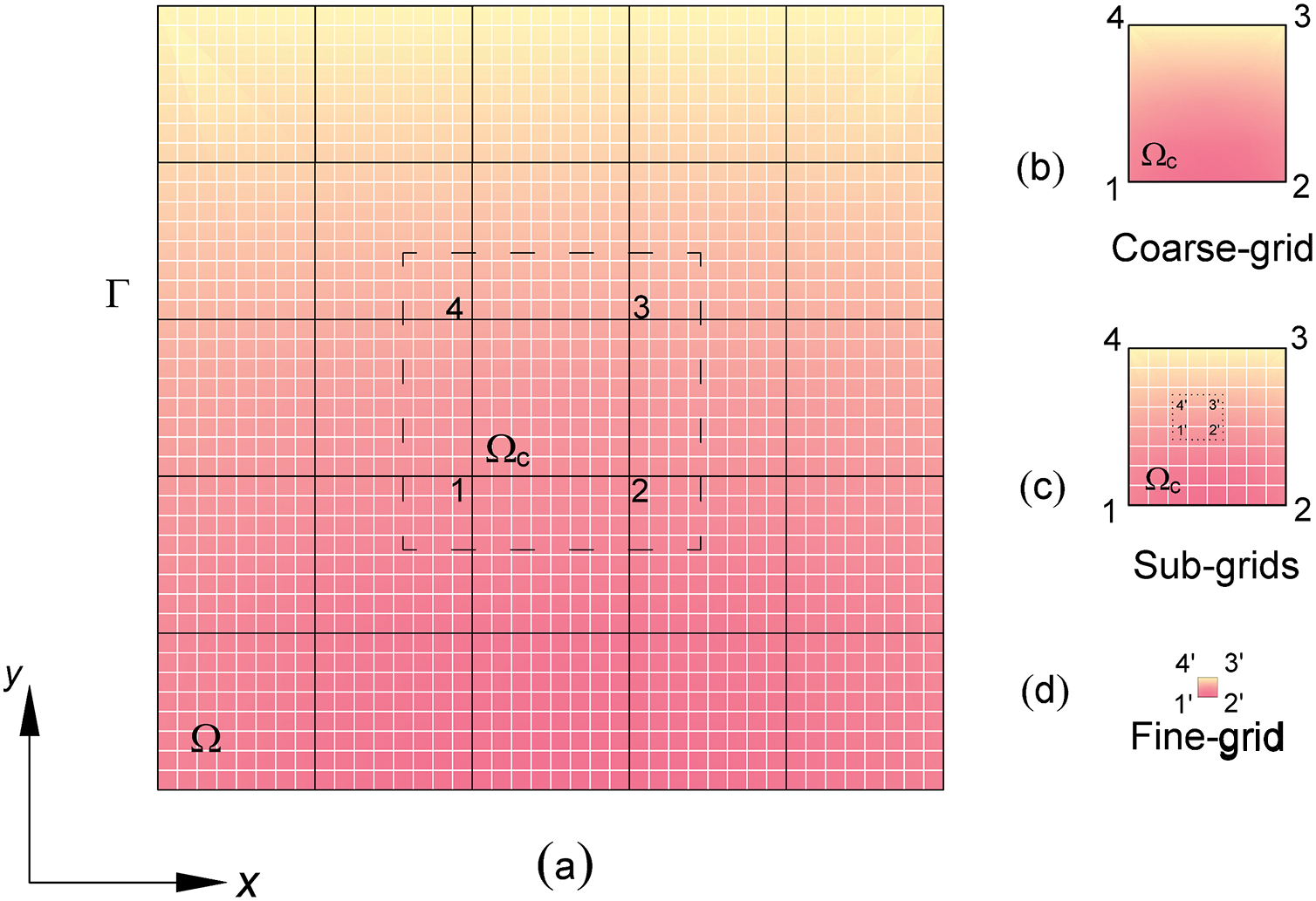
Figure 1: Heterogeneous MEE structure: (a) coarse and fine mesh, (b) coarse-grid, (c) sub-grid mesh of coarse element, (d) fine-grid

The CM-MsFEM calculation process for transient analysis of MEE structures comprises three main steps: microscopic, macroscopic, and downscaling computations. The microscopic calculation involved imposing BCs on the coarse grids, solving the generalized equilibrium equations within these grids using FEM, and numerically generating multiscale basis functions to effectively capture the microscopic heterogeneous information. For the macroscopic computation, these multiscale basis functions were employed to construct the macroscopic equivalent stiffness matrices of the coarse grids. Subsequently, the equivalent stiffness matrices, mass matrices, and loading arrays of the structure were integrated to solve the problem at the coarse scale, yielding relevant information about the displacement, electric, and magnetic fields of the macroscopic nodes. Subsequently, the downscaling computation utilized the multiscale basis functions to retrieve the fine-scale physical quantities of the displacement, electric, and magnetic fields via downscaling.

3.1 Microscopic Computation

To accurately represent the heterogeneity of displacement, electric, and magnetic field parameters, it is essential to simultaneously construct the corresponding multiscale basis functions (the following section describes the construction process under different BCs). The construction method of the multiscale basis functions is similar for (i) displacement in both y- and x-directions, and (ii) electric and magnetic potentials Therefore, this section focuses on the construction of the x-direction displacement and magnetic potential multiscale basis function.

3.1.1 Displacement Multiscale Basis Functions

Drawing from the fundamental principles of the EMsFEM, additional coupling terms were integrated into the multiscale basis functions. This integration is necessitated by the Poisson effect, which results in the interaction of displacements in each direction within the coarse grids. The expressions for displacement at the fine-grid nodes within the coarse-grid domains can be expressed as follows:

u=N¯uu¯,(16)

N¯u=[R1uTR2uT⋅⋅⋅Rn~uT]T,(17)

Riu=[N¯111u(i′)N¯121u(i′)⋅⋅⋅N¯11Mu(i′)N¯12Mu(i′)N¯211u(i′)N¯221u(i′)⋅⋅⋅N¯21Mu(i′)N¯22Mu(i′)],(18)

u=[u11u21⋯u1n~u2n~]T,(19)

u¯=[u¯11u¯21⋯u¯1Mu¯2M]T,(20)

where u is the matrix of displacement values for fine-grid nodes within coarse elements; u¯ is the matrix of displacement values for coarse-grid nodes; N¯u is the displacement multiscale basis function; N¯ijku is the displacement in the j direction resulting from a unit displacement applied in the i direction to coarse-grid node k, affecting all other coarse-grid nodes; M is the total number of coarse-grid nodes; n~ is the number of fine-grid nodes within one coarse-grid; and i′ = 1, 2, …, n~.

The displacement multiscale basis functions are constructed by solving specific boundary value problems (BVPs) using the FEM on the coarse-grid element domain, Ωc, which must satisfy the following equilibrium equations and BCs:

{LN¯k˙u=0,onΩcN¯k˙u=N~k˙u,on∂Ωc,(21)

where Ωc is the coarse-grid element domain; ∂Ωc is the coarse-grid element boundary; N¯k˙u is the displacement multiscale basis function for k˙ on the coarse-grid; N~k˙u is the basis functions BC; k˙ = 1, 2, …, M; and L is the differential operator which satisfies:

Lu=div(c:12(∇u+(∇u)T)).(22)

The selection of BCs significantly influences the accuracy of multiscale solutions. Consequently, for MEE materials exhibiting diverse heterogeneous microstructural characteristics, various BCs may be employed to construct multiscale basis functions. This study primarily focuses on the introduction and evaluation of commonly used linear and periodic BCs.

The displacement multiscale basis functions were constructed by applying linear BCs (Fig. 2a). A unit displacement is imposed in the x-direction of node 1, which at the boundaries, Γ12 and Γ14, decreased linearly from 1 to 0 along directions 12 and 14, respectively. The x-direction displacements of coarse-grid boundaries Γ23 and Γ34, and the y-direction displacements of all coarse-grid boundaries were fixed. Based on these conditions, the FEM was employed to solve Eq. (21) in Ωc. The displacement values of the microscopic nodes in the calculation results were extracted as N¯111u and N¯121u in the x- and y-directions, respectively. Other basis functions can be obtained similarly.

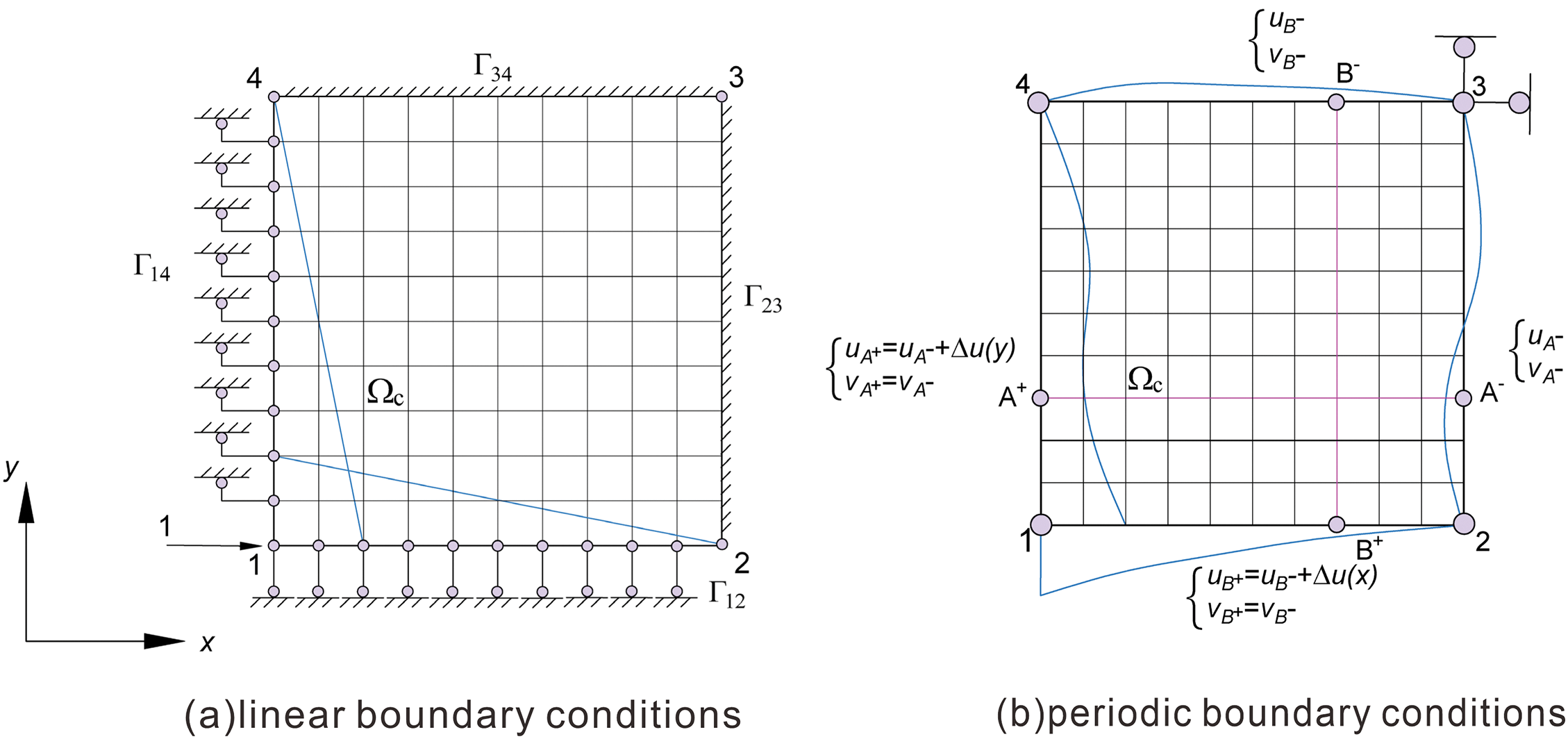
Figure 2: Constructing the displacement basis functions

Materials with periodic microstructures can be assumed to be composed of a repetitive arrangement of single cells, where the boundaries of adjacent cells must maintain continuity of displacements and forces. The periodicity of boundary deformation in single cells can be ensured by applying multi-point kinematic constraints [32]. In contrast to both fixed and forced displacement constraints, kinematic constraints do not have a given fixed displacement value. When constructing displacement multiscale basis functions using periodic BCs (Fig. 2b), two sets of kinematic constraints were imposed on opposite boundaries of the coarse grids to ensure the periodicity of mechanical characteristics between adjacent coarse grid elements. These constraints can be expressed as follows [33]:

{uA+=uA−+Δu(y)vA+=vA−{uB+=uB−+Δu(x)vB+=vB−.(23)

The change in displacement, Δu, in the x-direction decreases from 1 to 0 along the x- and y-directions of boundaries 12 and 14, respectively. To prevent rigid body motion, degrees of freedom in the two directions at the macroscopic node 3 were constrained. Eq. (21) was solved using the FEM within Ωc under these BCs. Subsequently, the x- and y-direction displacements of the microscopic nodes in the computational results were extracted as N¯111u and N¯121u, respectively.

3.1.2 Magnetic Potential Multiscale Basis Functions

In contrast to displacement, magnetic potential is a scalar quantity. Consequently, adhering to the fundamental principles of the MsFEM, the expressions for the magnetic potentials at the fine-grid nodes within the coarse-grid domains can be formulated as:

ψ=N¯ψψ¯,(24)

ψ=[ψ1ψ2⋯ψn~]T,(25)

ψ¯=[ψ¯1ψ¯2⋯ψ¯M]T,(26)

N¯ψ=[R1ψTR2ψT⋯Rn~ψT]T,(27)

Ri~ψ=[N¯1ψ(i~)N¯2ψ(i~)⋯N¯Mψ(i~)],i~=1,2,…,n~(28)

where ψ is the magnetic potential matrix of the fine-grid nodes within the coarse grids; ψ¯ is the magnetic potential matrix of the coarse-grid nodes; and N¯ψ is the magnetic potential multiscale basis function of the coarse-grid elements.

The magnetic potential multiscale basis functions were constructed by solving for specific BCs and equilibrium equations using the FEM within Ωc, expressed as:

{L¯N¯k~ψ=0,onΩcN¯k~ψ=N~k~ψ,on∂Ωc,(29)

where N¯k~ψ is the magnetic potential multiscale basis function of k~ within the coarse grids; N~k~ψ is the multiscale basis function BC; k~=1,2,⋯,M; and L¯ is the differential operator that satisfies

L¯ψ=−∇T(μ∇ψ).(30)

The magnetic potential basis functions were constructed using linear BCs (Fig. 3a). A single unit of magnetic potential was applied to macroscopic node 1 within the coarse grid. The magnetic potential of the microscopic nodes on boundaries, Γ14 and Γ12, decreased linearly from along directions 14 and 12, respectively. The magnetic potentials at the boundaries, Γ23 and Γ34, were set to zero. Under these BCs, Eq. (29) was solved using the FEM within Ωc. The magnetic potential at the microscopic nodes was then extracted from the results as N¯1ψ.

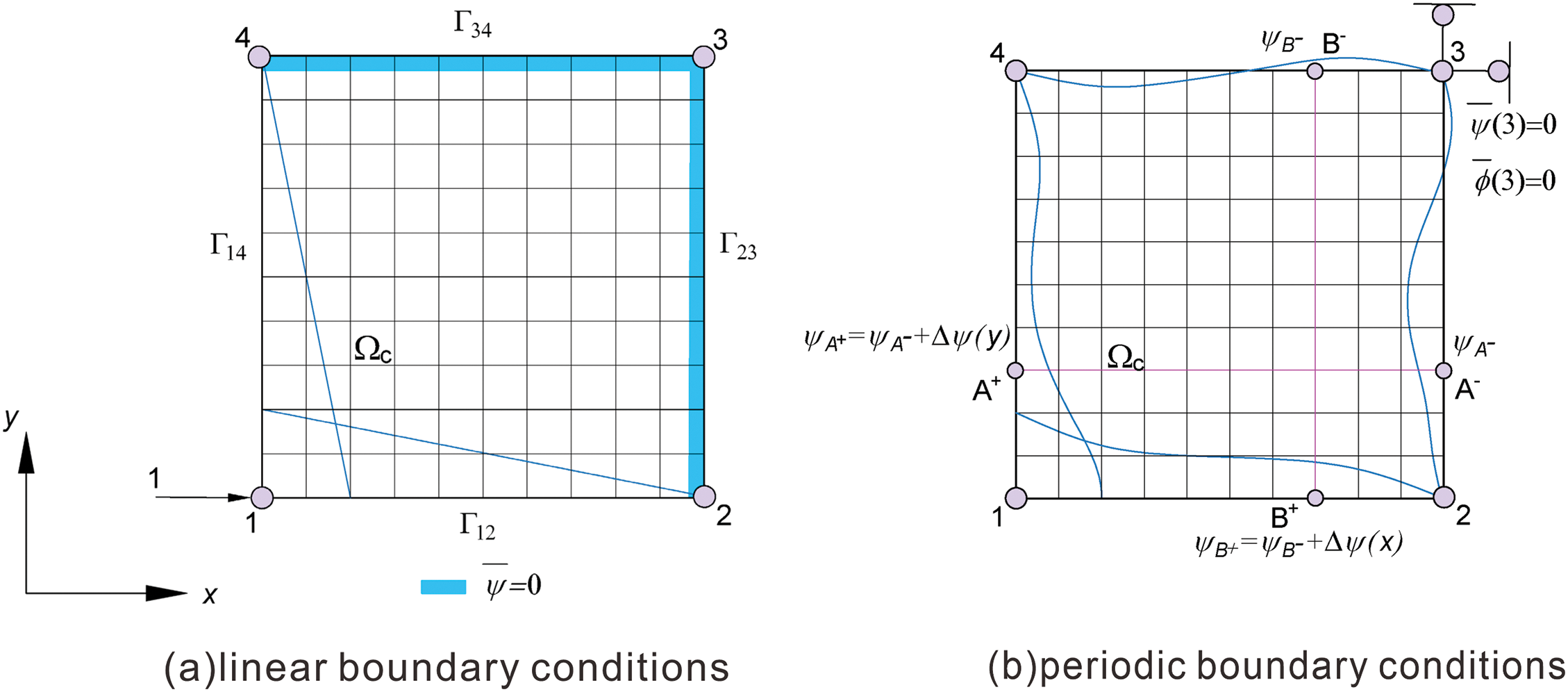
Figure 3: Constructing the magnetic potential basis functions

When constructing magnetic potential basis functions under periodic BCs (Fig. 3b), it is necessary to apply kinematic constraints to the nodes of two opposing sets of boundaries that define the coarse-grid elements. This ensures the periodicity of magnetic characteristics in adjacent coarse-grid elements as follows [33]:

{ψA+=ψA−+Δψ(y)ψB+=ψB−+Δψ(x),(31)

where the change in the magnetic potential of the microscopic node, Δψ, reduces along the x- and y-directions along boundaries 12 and 14, respectively. Eq. (29) was then solved using FEM in Ωc under these BCs. Subsequently, the magnetic potential of the microscopic nodes was extracted as N¯1ψ.

3.2 Macroscopic Computation

The potential energy of each coarse grid equals the sum of all the contained fine-grid potentials. Consequently, after establishing the multiscale basis functions for displacement, electric potential, and magnetic potential, it becomes feasible to derive the equivalent stiffness matrix and load vector for the coarse grids. Subsequently, the macroscale multiscale finite element formulation of CM-MsFEM for the transient responses can be deduced from Green’s formula and the Galerkin method using Eqs. (16) and (24) as

M¯u¨+K¯u=F¯(t),(32)

where M¯ is the generalized mass matrix; u¨ is the generalized acceleration; K¯ is the generalized stiffness matrix; u is the generalized displacement; and F¯(t) is the generalized force matrix, each expressed as follows:

M¯=[Muu00000000],(33)

K¯=[KuuKuϕKuψKϕuKϕϕKϕψKψuKψϕKψψ]=[GeuTKuueGeuGeuTKuϕeGeϕGeuTKuψeGeψGeϕTKϕueGeuvGeϕTKϕϕeGeϕGeϕTKϕψeGeψGeψTKψueGeuGeψTKψϕeGeϕGeψTKψψeGeψ],(34)

u(t)=[u¯ϕ¯ψ¯],(35)

F¯(t)=[fqp]=[GeuTfeGeϕTqeGeψTpe],(36)

where Kuu, Kuϕ, Kϕu, Kϕϕ, Kuψ, Kψu, Kψϕ, and Kψψ are the coarse-grid element stiffness matrices; f, q, and p are the coarse-grid element load arrays; Kuue, Kuϕe, Kϕue, Kϕϕe, Kuψe, Kψue, Kϕψe, Kψϕe, and Kψψe are the fine-grid element stiffness matrices; fe, qe, and pe are the fine-grid element load arrays; Geu, Geϕ, and Geψ are the transformation matrices that connect the displacements, and electric and magnetic potentials at the nodes of the coarse- and fine-grid elements; and the superscript e indicates a fine-grid element. The fine-grid elements include

Kuue=∫ΩeBuTCBudΩ,(37)

Kuϕe=∫ΩeBuTeBϕdΩ,(38)

Kϕue=∫ΩeBϕTeBudΩ,(39)

Kϕϕe=−∫ΩeBϕTκBϕdΩ,(40)

Kuψe=∫ΩeBuThBψdΩ,(41)

Kψue=∫ΩeBψThBudΩ,(42)

Kϕψe=−∫ΩeBϕTαBψdΩ,(43)

Kψϕe=−∫ΩeBψTαBϕdΩ,(44)

Kψψe=−∫ΩeBψTμBψdΩ,(45)

fe=∫ΩeNuTfdΩ+∫ΓσNuTt¯dΓ,(46)

qe=−∫ΩeNϕTqdΩ−∫ΓDNϕTQ¯dΓ,(47)

pe=−∫ΩeNψTpdΩ−∫ΓBNψTϑ¯dΓ,(48)

Geu=[Re1uTRe2uT⋯Ren¯uT]T,(49)

Geϕ=[Re1ϕTRe2ϕT⋯Ren¯ϕT]T,(50)

Geψ=[Re1ψTRe2ψT⋯Ren¯ψT]T,(51)

where Bu, Bϕ, and Bψ are the strain matrices; n¯ is the number of nodes in the fine-grid; and Ωe is the corresponding cell area.

3.3 Downscaling Computation

The CM-MsFEM establishes explicit connections between macroscopic and microscopic displacement, electric and magnetic fields by constructing multiscale basis functions. The coarse-scale solutions (displacement, electric, and magnetic potentials) of the structure were obtained through macroscopic calculation. These solutions were subsequently interpolated using the multiscale basis functions, which accounted for the small-scale information within the coarse-grid elements, for downscaling calculation. Subsequently, the microscopic fine-scale displacement, electric, and magnetic field responses were determined as

{ue=Geuu¯ϕe=Geϕϕ¯ψe=Geψψ¯,(52)

where ue, ϕe, and ψe are the displacement, electric potential, and magnetic potential matrices at the fine-grid element nodes, respectively.

4  Coupling MEE Newmark Method

This study employed the traditional Newmark method to address the magneto-electro-elastic coupling, generalizing it to an easily implementable coupling MEE Newmark method. This implicit integration method directly solves MEE coupling dynamics problems without transforming the dynamic equation. By integrating at each step, it yields the generalized displacement, velocity, and acceleration under load. This method is often used to analyze the transient responses of multi-physical systems. When parameters α and δ meet the conditions α ≥ 0.25 (0.5 + δ)2 and δ ≥ 0.5, any time step Δt is unconditionally stable, that is, the size of the time step does not affect the stability of the solution. In this study, considering that the average acceleration over each time step is constant, we select parameters α = 0.25 and δ = 0.5 [34]. The steps of the coupling MEE Newmark method are outlined as follows:

a.   Initial calculation:

(i)   Constructing the equivalent stiffness matrix, K¯ and generalized mass matrix, M¯;

(ii)   Initializing the ut,u˙t, and u¨t values;

(iii)   Determining Δt and specifying the integral constants as follows:

c1=1/(αΔt2),c2=δ/(αt),c3=1/(αt),c4=1/(2α)−1,c5=δ/α−1(53)

c6=Δt/2(δ/α−2),c7=Δt/(1−δ),c8=δΔt;(54)

(iv)   Constructing an effective stiffness matrix, K^,

K^=K¯+c1M¯,(55)

b.   For each time step (t=0,Δt,2Δt…):

(i)   Calculating the effective load, F^ at t+Δt as

F^t+Δt=F¯t+Δt+M¯(c1ut+c3u˙t+c4u¨t);(56)

(ii)   Solving for the displacement at t+Δt as

K^ut+Δt=F^t+Δt;(57)

(iii)   Calculating the generalized displacement, velocity, and acceleration at t+Δt as

u˙t+Δt=u˙t+c7u¨t+c8u¨t+Δt,u¨t+Δt=c1(ut+Δt−ut)−c3u˙t−c4u¨t,respectively.(58)

5  Numerical Case Studies

5.1 MEE Plate

This case study examines the plane strain problem for a BaTio3-CoFe2O4 MEE plate (2 m × 2 m; Fig. 4; Table 1), which consists of both piezoelectric (BaTiO3) and piezomagnetic (CoFe2O4) materials. The BCs of the plate were as follows:

y=b:qy=100N/my=0:uy=0,ϕ=0,ψ=0x=0:ux=0

Figure 4: MEE plate configuration

The model was discretized using 10 × 10 coarse grids, with each grid further discretized into 10 × 10 fine grids. The generalized displacement (ux, uy), electric potential (ϕ), and magnetic potential (ψ) of the MEE plate were computed using the FEM (100 × 100) and CM-MsFEM (10 × 10) simulations independently, and the results at point A were then compared with the analytical solutions [35] (Table 2) for validation. The results of FEM on a fine grid, CM-MsFEM for linear BCs (CM-MsFEM-L), and CM-MsFEM-for periodic BCs (CM-MsFEM-P) demonstrated excellent agreement with the analytical solutions, with the maximum error not exceeding 0.00024%. This confirmed the accuracy of the three methods for solving static problems in MEE structural systems.

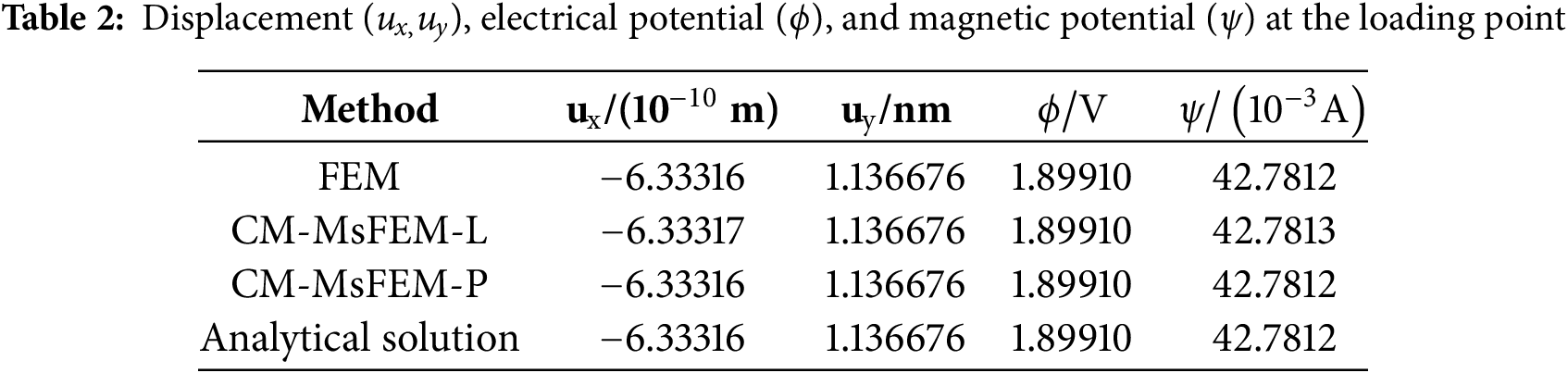
The computation time of FEM (100 × 100), CM-MsFEM-L (10 × 10), and CM-MsFEM-P (10 × 10) under the same hardware environment (Intel(R) Core(TM) i5-8265U @ 1.60 GHz 1.80 GHz) were found to be 28.45, 12.34, and 14.27 s, respectively. The total operating time of CM-MsFEM-L and CM-MsFEM-P was only 43.37% and 50.16% of that of FEM, respectively, verifying the substantially enhanced computational efficiencies.

5.2 FGMEE Clamped-Clamped Beam

A geometrical model of an FGMEE clamped-clamped (C-C) beam (30 mm × 2 mm; Table 1) was then analyzed for the plane stress problem (Fig. 5a). The model was discretized using 60 × 4 coarse grids, each with 5 × 5 fine grids (Fig. 5b). The distribution of material properties across the beam’s thickness was governed by the index f(y)=eξ(y/h). A sine-wave load was applied at point A along the beam’s span (Fig. 5c). The structural constraints were ux=uy=ϕ=ψ=0 at both clamped ends. Initial conditions were set as u = 0, u˙ = 0, u¨ = 0 at t = 0 s. The transient response of the FGMEE C-C beam was analyzed using FEM (240 × 25), FEM (60 × 4), CM-MsFEM-L (60 × 4), and CM-MsFEM-P (60 × 4) for exponential factor values of ξ = 0.1, 0.2, and 0.4 (Fig. 6). Subsequently, the accuracy, computational efficiency, and the impact of the exponential factor ξ on the transient responses were examined.

Figure 5: (a) 3D geometry, (b) 2D geometry, and (c) waveform of the sine-wave load applied at point A of the FGMEE C-C beam

Figure 6: Variation of the generalized displacement at point A with respect to time for ξ = 0.10, 0.20, and 0.40 [37]

The results from FEM (240 × 25) closely aligned with those in [37], validating the accuracy of these fine-scale results to act as a reference solution. The maximum errors of the CM-MsFEM-L solution at ξ = 0.1%, 0.2%, and 0.4% were 1.30% for uy, 2.97% for ϕ, and 0.66% for ψ. Whereas, CM-MsFEM-P yielded maximum errors of 0.30%, 2.20%, and 0.60% for uy, ϕ, and ψ, respectively. As ξ increased, the displacement, electric and magnetic potentials decreased. The generalized displacement cloud images obtained by FEM (240 × 25), CM-MsFEM-L (60 × 4), and CM-MsFEM-P (60 × 4) for the entire structure for varying ξ values at t = 0.026 s obtained (Fig. 7). Both CM-MsFEM-L and CM-MsFEM-P accurately captured the transient displacement, electric, and magnetic field responses of the FGMEE structures, thus verifying their accuracy in addressing such problems.

Figure 7: Contours of the generalized displacement at t = 0.026 s (ξ = 0.10, 0.20, 0.40)

Evaluating the computational accuracy of the methods in resolving the transient response problems of the FGMEE structures using the energy errors of the structures [30] (Table 3), computed as

Energy Error=|Eexact−ECM-MsFEM|=12limNe→∞∑i=1Ne∫Ωi(εTCε+ETκE+HTμH)dΩ−12(uTKuuu+ϕTKϕϕϕ+ψTKψψψ),(59)

where Eexact and ECM-MsFEM are the energy errors of CM-MsFEM and FEM, respectively; Ne is the number of nodes.

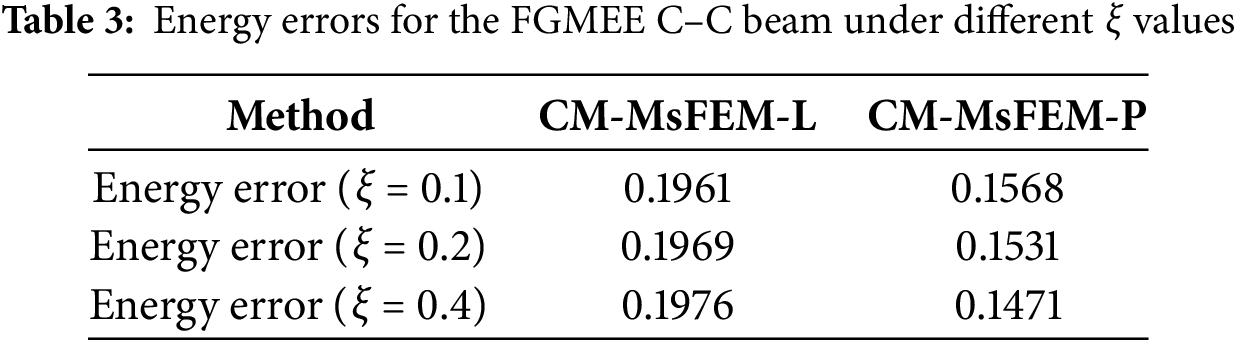
The calculation results in Table 3 demonstrated that CM-MsFEM-P to be superior compared to CM-MsFEM-L. This enhanced accuracy can be attributed to the fact that imposing linear BCs effectively establishes a more stringent constraint at the coarse-grid boundary, which inadequately reflects the influence of heterogeneous characteristics at the boundary. Consequently, the calculations employing periodic BCs yield more accurate results, aligning with previously reported findings [32]. In light of these observations, periodic BCs were utilized for constructing the multiscale basis functions in the subsequent examples.

Furthermore, under identical coarse-grid division density, the CM-MsFEM exhibited greater proximity to the reference solution and achieved higher solving accuracy compared to the traditional FEM. The multiscale basis functions effectively captured the heterogeneous information within the coarse grids, thus enhancing solution accuracy compared to the FEM polynomial basis function.

The computation time of FEM (240 × 25), CM-MsFEM-L (60 × 4), and CM-MsFEM-P (60 × 4) under the same hardware environment Intel(R) Core(TM) i5-8265U @ 1.60 GHz 1.80 GHz) were 29,347, 113, and 119 s, respectively. The total computation times for CM-MsFEM-L and CM-MsFEM-P were approximately 0.39% and 0.41% of that of the FEM, respectively. When applied to solve the transient response problems of the FGMEE structures, the CM-MsFEM significantly enhanced the solution efficiency and reduced the solving time. The CMSFEM-L and CMSFEM-P constructed the multiscale basis functions in 4.67 and 9.59 s, respectively. This represented only a small fraction of the total solution time, with the majority of computational resources allocated to the macroscopic calculation of the transient response of the MEE structure. The substantial difference in the computational times of CM-MsFEM and FEM primarily stemmed from the disparity in the total number of degrees of freedom.

5.3 Hybrid MEE Cantilever Beam with Voids

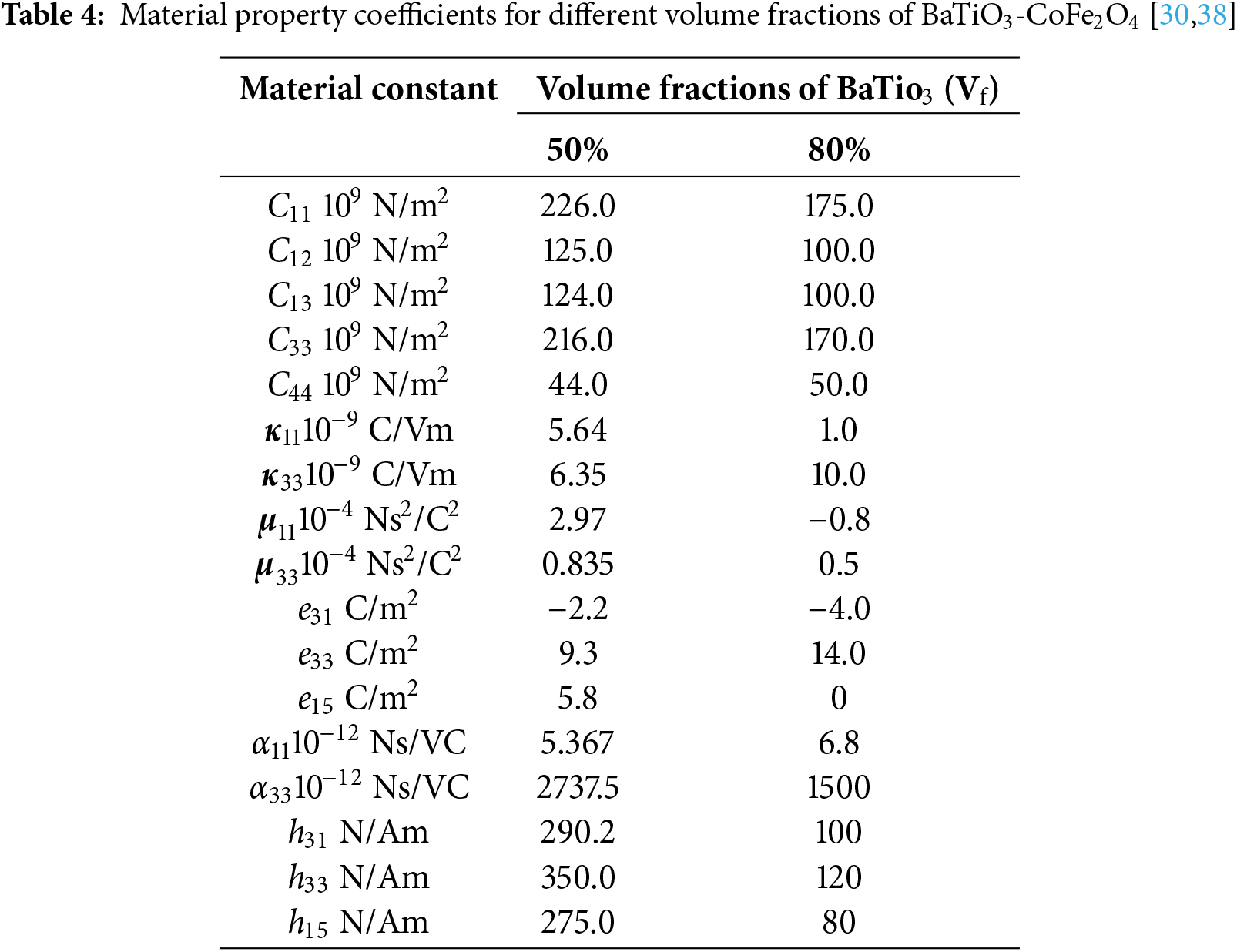
A hybrid MEE cantilever beam (4.5 mm × 0.3 mm) with voids (radius = 0.1 mm) was then considered for the plane stress problem (Fig. 8a). The entire model was discretized into 45 × 3 coarse grids, each with 120 fine grids (Fig. 8b). Two types of MEE materials were selected and combined: one composed of 50 vol.% BaTiO3 and 50 vol.% CoFe2O4, and another composed of 80 vol.% BaTiO3 and 20 vol.% CoFe2O4 (blue and yellow sections in Fig. 8, respectively; Table 4). The cantilever beam was subjected to a sine-wave load at point A in the upper right corner (Fig. 8c). The structural constraints were ux=uy=ϕ=ψ=0 at the left clamped end. The initial conditions were set as u = 0, u˙ = 0, and u¨ = 0 at t = 0 s. The transient response of the hybrid MEE cantilever beam with voids was analyzed using both FEM (135 × 120) and CM-MsFEM-P (45 × 3), and their accuracy and efficiency were evaluated.

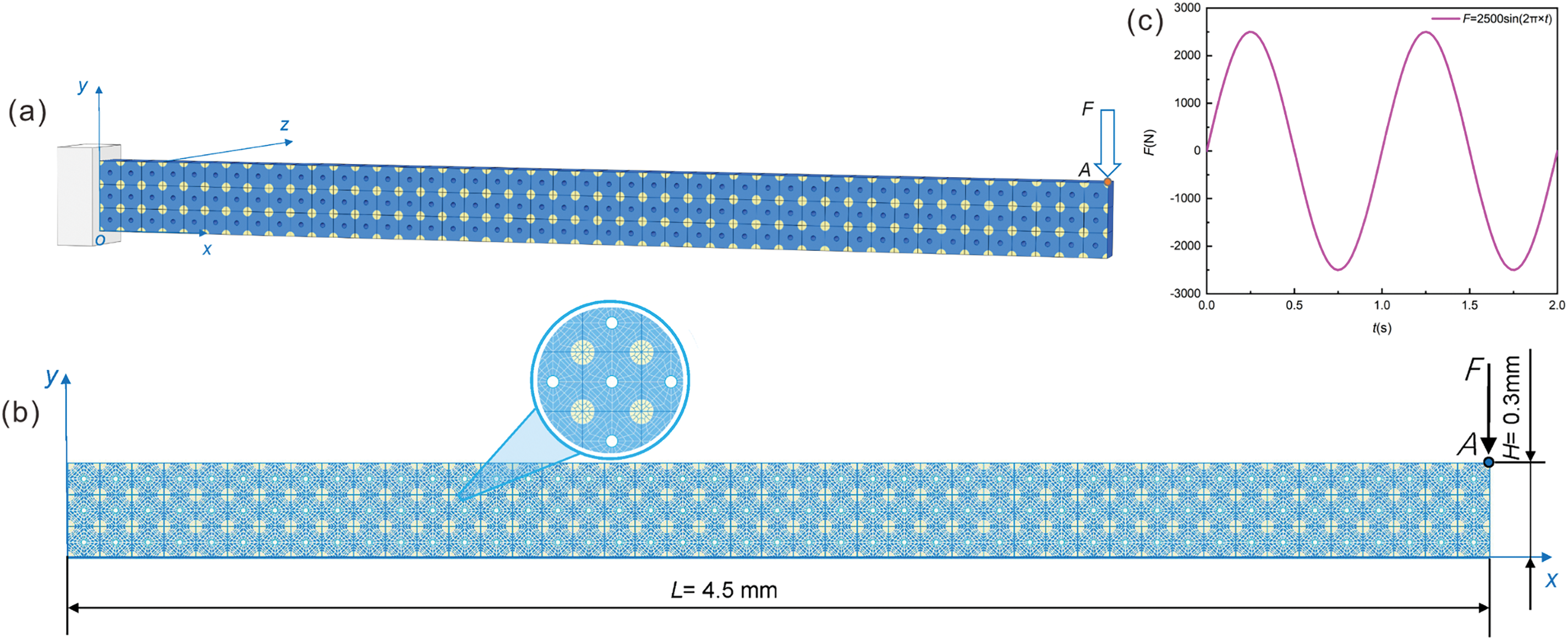
Figure 8: (a) 3D geometry, (b) 2D geometry, and (c) waveform of the sine-wave load applied at point of the hybrid MEE cantilever beam with holes

The temporal curves of generalized uy, ϕ, and ψ of the hybrid MEE cantilever beam with voids at point A obtained using FEM and CM-MsFEM-P were obtained (Fig. 9). The results of CM-MsFEM-P closely aligned with the FEM reference solution, with maximum errors of 0.28%, 0.95%, and 3.83% for uy, ϕ, and ψ, respectively. Fig. 10 presents the generalized displacement clouds of the entire structure obtained by FEM and CM-MsFEM-P at t = 0.2625 s. A comparative analysis of the results confirmed that CM-MsFEM-P accurately captured the transient displacement, electric, and magnetic field responses of the hybrid MEE cantilever beam with voids. This verification demonstrates both the accuracy of CM-MsFEM-P in addressing such problems and its applicability to various MEE structural dynamics problems.

Figure 9: Variation of the generalized displacement at the loading point with respect to time

Figure 10: Contours of the generalized displacement at t = 0.2625 s

The computation time of FEM (135 × 120) and CM-MsFEM-P (45 × 3) is compared under the same hardware environment (Intel(R) Core(TM) i5-8265U @ 1.60 GHz 1.80 GHz). The operating time is 13920 and 98 s, respectively. The computation time of CM-MsFEM-P is only 0.70% of that of FEM, suggesting CM-MsFEM has high computational efficiency and largely saves the computation time.

5.4 Hybrid MEE C-C Beam

Finally, the geometrical model of a hybrid MEE C-C beam (21 mm × 1 mm) was considered for the plane stress problem (Fig. 11a). The entire model is discretized using 84 × 4 coarse grids, each with 5 × 5 fine grids. Two MEE materials with different volume fractions were selected and combined for this model (green and red sections in Fig. 11b, respectively; Table 4). Point A along the span of the structure was subjected to a sine-wave load (Fig. 11c). The structural BCs were ux=uy=ϕ=ψ=0 at both clamped ends. The initial conditions were set as u = 0, u˙ = 0, u¨ = 0 at t = 0 s. FEM (336 × 25) and CM-MsFEM-P (84 × 4) were employed to compute the transient response of the fixed-end hybrid MEE C-C beam.

Figure 11: (a) 3D geometry, (b) 2D geometry, and (c) waveform of the sine-wave load applied to point A of the hybrid MEE C-C beam

The generalized uy, ϕ, and ψ vs. time curves of the hybrid MEE C-C beam at point A obtained using FEM and CM-MsFEM-P are presented in Fig. 12. The results from CM-MsFEM-P demonstrate strong agreement with the FEM reference solution, with maximum errors of 0.24%, 4.14%, and 4.18% for uy, ϕ, and ψ, respectively. Fig. 13 illustrates the generalized displacement clouds of the entire structure obtained by FEM and CM-MsFEM-P at t = 0.2625 s, demonstrating that CM-MsFEM-P applied to periodic BCs effectively solved the transient response problem of the hybrid MEE structure. Under given hardware conditions (Intel(R) Core(TM) i5-8265U @ 1.60 GHz 1.80 GHz), FEM (336 × 25) and CM-MsFEM-P (84 × 4) required 14,688 and 225 s for computing, the latter representing merely 1.50% of the former. Despite the complex heterogeneity of MEE materials, CM-MsFEM-P analysis of the dynamics ensured high accuracy and computational efficiency. This further validates the applicability of CM-MsFEM-P in solving dynamic problems of various heterogeneous MEE structures.

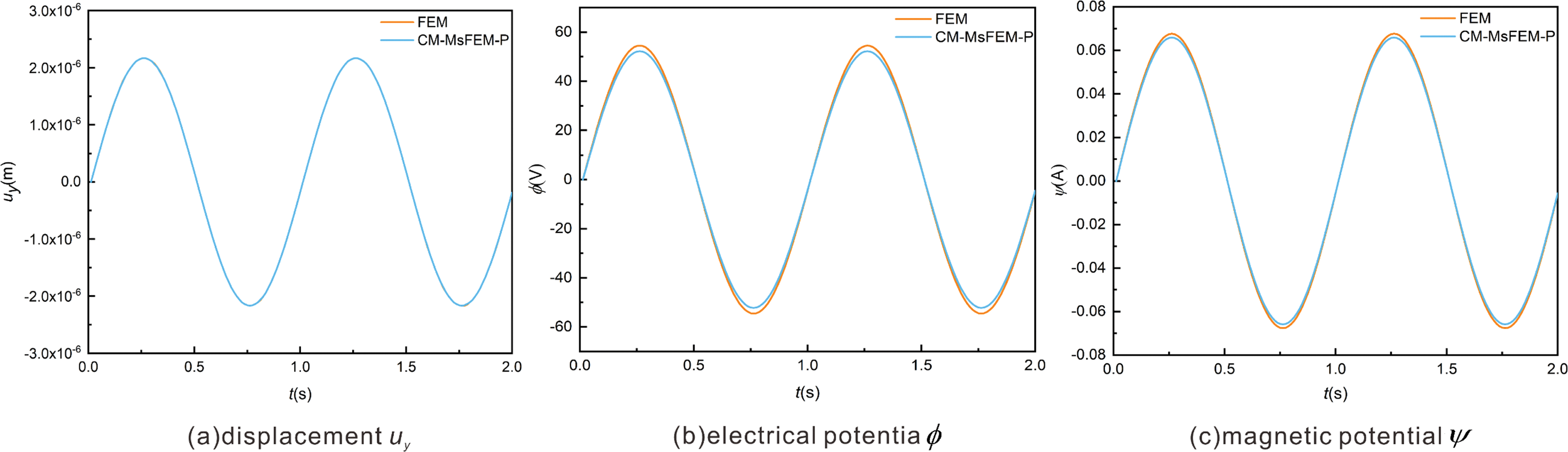
Figure 12: Variation of the generalized displacement at the loading point with respect to time

Figure 13: Contours of the generalized displacement at t = 0.2625 s

6  Conclusions

In this study, we introduce CM-MsFEM for analyzing transient response problems in heterogeneous MEE structures. This method constructs multiscale basis functions for displacement, electric potential, and magnetic potential, effectively capturing material heterogeneity. The macro-matrix on the coarse grid was assembled to reflect microscopic information at the macroscopic scale. Additionally, the macroscale multiscale finite element formulation of CM-MsFEM was derived, enabling problem-solving on coarse grids. This approach addresses the challenges of dense meshing and low computational efficiency associated with traditional FEM in analyzing mechanical problems of heterogeneous materials. The primary conclusions of the study are as follows:

     i)  In the analysis of heterogeneous MEE structural dynamics, the CM-MsFEM demonstrates superior computational efficiency compared to the FEM while maintaining comparable accuracy.

    ii)  Compared to FEM, CM-MsFEM offers superior accuracy in solving the dynamic problems of FGMEE structures using identical coarse meshes.

   iii)  The establishment of BCs in the construction of basic functions is closely linked to the microscopic properties of the materials. For materials exhibiting significant heterogeneity near the boundary, the periodic BC demonstrates superior accuracy.

Acknowledgment: The authors are grateful to the reviewers and editors for their valuable comments and suggestions.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Grant Nos. 42102346, 42172301).

Author Contributions: Xiaolin Li: Methodology, Software, Funding acquisition, Writing—original draft, Writing—review, Editing; Xinyue Li: Validation, Writing—original draft, Writing—review, Editing; Liming Zhou: Conceptualization, Methodology; Hangran Yang: Writing—original draft; Xiaoqing Yuan: Formal analysis. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Shirbani MM, Shishesaz M, Sedighi HM, Hajnayeb A. Parametric modeling of a novel longitudinal vibration-based energy harvester using magneto-electro-elastic materials. Microsyst Technol. 2017;23(12):5989–6004. doi:10.1007/s00542-017-3402-0. [Google Scholar] [CrossRef]

2. Zhou LM, Li M, Chen BK, Li F, Li Xl. An inhomogeneous cell-based smoothed finite element method for the nonlinear transient response of functionally graded magneto-electro-elastic structures with damping factors. J Intel Mat Syst Str. 2019;30(3):416–37. doi:10.1177/1045389X18812712. [Google Scholar] [CrossRef]

3. Zhang SQ, Zhao YF, Wang X, Chen M, Schmidt R. Static and dynamic analysis of functionally graded magneto-electro-elastic plates and shells. Compos Struct. 2022;281:114950. doi:10.1016/j.compstruct.2021.114950. [Google Scholar] [CrossRef]

4. Fetisov LY, Serov VN, Chashin DV, Makovkin SA, Srinivasan G, Viehland D, et al. A magnetoelectric sensor of threshold DC magnetic fields. J Appl Phys. 2017;121(15):154503. doi:10.1063/1.4981533. [Google Scholar] [CrossRef]

5. Wang J, Zhou L, Chai Y. The adaptive hygrothermo-magneto–electro-elastic coupling improved enriched finite element method for functionally graded magneto-electro–elastic structures. Thin-Walled Struct. 2024;200:111970. doi:10.1016/j.tws.2024.111970. [Google Scholar] [CrossRef]

6. Zhao YF, Zhao ZM, Zhang SQ, Wang X. Analysis of sensing performance for a fully clamped functionally graded magneto-electro-elastic shell. In: 2022 16th Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA); 2022 Oct 11–14; Nanjing, China: Nanjing University of Aeronautics and Astronautics. p. 386–90. [Google Scholar]

7. Li B, Zhong Y, Luo D, Mei B. Variational asymptotic micromechanics model of coating-fiber reinforced magneto-electro-elastic materials. Fuhe Cailiao Xuebao/Acta Materiae Compositae Sinica. 2018;35(10):2823–31. [Google Scholar]

8. Lei BX, You ZX, Zhang ZD, Shi Y. Analytical solutions for full-field radiations of magnetoelectric antennas with nonlinear magnetoelastic coupling. Acta Mech Sin. 2024;40:423514. [Google Scholar]

9. Kiran MC, Kattimani SC. Assessment of porosity influence on vibration and static behaviour of functionally graded magneto-electro-elastic plate: a finite element study. Eur J Mech A-Solid. 2018;71:258–77. [Google Scholar]

10. Bhangale RK, Ganesan N. Static analysis of simply supported functionally graded and layered magneto-electro-elastic plates. Int J Solids Struct. 2006;43(10):3230–53. [Google Scholar]

11. Bhangale RK, Ganesan N. Free vibration of simply supported functionally graded and layered magneto-electro-elastic plates by finite element method. J Sound Vib. 2006;294(4–5):1016–38. doi:10.1016/j.jsv.2005.12.030. [Google Scholar] [CrossRef]

12. Bhangale RK, Ganesan N. Free vibration of functionally graded non-homogeneous magneto-electro-elastic cylindrical shell. Int J Comput Meth En. 2006;7(3):191–200. doi:10.1080/15502280500388102. [Google Scholar] [CrossRef]

13. Annigeri AR, Ganesan N, Swarnamani S. Free vibration behaviour of multiphase and layered magneto-electro-elastic beam. J Sound Vib. 2007;299(1–2):44–63. doi:10.1016/j.jsv.2006.06.044. [Google Scholar] [CrossRef]

14. Zhou LM, Wang JY, Liu MR, Li M, Chai YB. Evaluation of the transient performance of magneto-electro-elastic based structures with the enriched finite element method. Compos Struct. 2022;280:114888. doi:10.1016/j.compstruct.2021.114888. [Google Scholar] [CrossRef]

15. Jiang Z, Gui Q, Li W, Chai Y. Assessment of the edge-based smoothed finite element method for dynamic analysis of the multi-phase magneto-electro-elastic structures. Eng Anal Boundary Elem. 2024;163:94–107. doi:10.1016/j.enganabound.2024.02.021. [Google Scholar] [CrossRef]

16. Zhou LM, Li M, Tian WJ, Liu P. Coupled multi-physical cell-based smoothed finite element method for static analysis of functionally grade magneto-electro-elastic structures at uniform temperature. Compos Struct. 2019;226:111238. doi:10.1016/j.compstruct.2019.111238. [Google Scholar] [CrossRef]

17. Babuška I, Osborn JE. Generalized finite element methods: their performance and their relation to mixed methods. Siam J Numer Anal. 1983;20(3):510–36. doi:10.2307/2157269. [Google Scholar] [CrossRef]

18. Dostert P, Efendiev Y, Hou TY. Multiscale finite element methods for stochastic porous media flow equations and application to uncertainty quantification. Comput Method Appl M. 2008;197(43–44):3445–55. doi:10.1016/j.cma.2008.02.030. [Google Scholar] [CrossRef]

19. Ye SJ, Xue YQ, Xie CH. Application of the multiscale finite element method to flow in heterogeneous porous media. Water Resour Res. 2004;40(9):W09202. doi:10.1016/S0167-5648(04)80062-5. [Google Scholar] [CrossRef]

20. Zhang HW, Wu JK, Lü J, Fu ZD. Extended multiscale finite element method for mechanical analysis of heterogeneous materials. Acta Mech Sinica. 2010a;26(6):899–920. doi:10.1007/s10409-010-0393-9. [Google Scholar] [CrossRef]

21. Liu H, Yang DS, Wu JK. An open-source matlab implementation for elastic analyses of heterogeneous materials using the extended multiscale finite element method. Int J Multiscale Com. 2022;20(1):19–43. doi:10.1615/IntJMultCompEng.2021039777. [Google Scholar] [CrossRef]

22. Zhang HW, Wu JK, Fu ZD. Extended multiscale finite element method for elasto-plastic analysis of 2D periodic lattice truss materials. Comput Mech. 2010b;45(6):623–35. doi:10.1007/s00466-010-0475-3. [Google Scholar] [CrossRef]

23. Zhang S, Yang DS, Zhang HW, Zheng YG. Coupling extended multiscale finite element method for thermoelastic analysis of heterogeneous multiphase materials. Comput Struct. 2013;121:32–49. doi:10.1016/j.compstruc.2013.03.001. [Google Scholar] [CrossRef]

24. Zhang H, Li H, Ye H, Zheng Y, Zhang Y. A coupling extended multiscale finite element and peridynamic method for modeling of crack propagation in solids. Acta Mech. 2019;230(10):3667–92. doi:10.1007/s00707-019-02471-2. [Google Scholar] [CrossRef]

25. Lv J, Zhang HW, Yang DS. Multiscale method for mechanical analysis of heterogeneous materials with polygonal microstructures. Mech Mater. 2013;56:38–52. doi:10.1016/j.mechmat.2012.09.002. [Google Scholar] [CrossRef]

26. Liu J, Li S. Efficient phononic band gap optimization in two-dimensional lattice structures using extended multiscale finite element method. Struct Multidiscipl Optim. 2024;67:166. doi:10.1007/s00158-024-03885-w. [Google Scholar] [CrossRef]

27. Yan J, Sui Q, Fan Z, Duan Z. Multi-material and multiscale topology design optimization of thermoelastic lattice structures. Comput Model Eng Sci. 2022;130(2):967–86. doi:10.32604/cmes.2022.017708. [Google Scholar] [CrossRef]

28. Yan J, Huo SX, Yu T, Zhang CG, Chai XH, Hu DP, et al. Multiscale analysis for 3D lattice structures based on parallel computing. Int J Numer Methods Eng. 2021;122(22):6756–76. doi:10.1002/nme.v122.22. [Google Scholar] [CrossRef]

29. Ammosov D, Nasedkin A, Muratova G. A computational macroscopic model of piezomagnetoelectric materials using generalized multiscale finite element method. J Comput Appl Math. 2024;437:115420. doi:10.1016/j.cam.2023.115420. [Google Scholar] [CrossRef]

30. Rojas-Díaz R, Sukumar N, Sáez A, García-Sánchez F. Fracture in magnetoelectroelastic materials using the extended finite element method. Int J Numer Meth Eng. 2011;88(12):1238–59. doi:10.1002/nme.3219. [Google Scholar] [CrossRef]

31. Feng WJ, Han X, Li YS. Fracture analysis for two-dimensional plane problems of nonhomogeneous magneto-electro-thermo-elastic plates subjected to thermal shock by using the meshless local Petrov-Galerkin method. Comput Model Eng Sci. 2009;48(1):1–26. doi:10.3970/cmes.2009.048.001. [Google Scholar] [CrossRef]

32. Lv J, Zhang HW, Gao XW, Huang Y. A new multiscale computational method for electromechanically coupled analysis of heterogeneous piezoelectric composites. J Intell Mater Syst Struct. 2015;26(4):434–49. doi:10.1177/1045389X14529030. [Google Scholar] [CrossRef]

33. Fu P, Liu H, Chu XH, Qu WZ. Multiscale finite element method for a highly efficient coupling analysis of heterogeneous magneto-electro-elastic media. Int J Multiscale Com. 2018;16(1):77–100. doi:10.1615/IntJMultCompEng.2018021237. [Google Scholar] [CrossRef]

34. Latifi M, Kharazi M, Ovesy HR. Nonlinear dynamic response of symmetric laminated composite beams under combined in-plane and lateral loadings using full layerwise theory. Thin-Walled Struct. 2016;104:62–70. doi:10.1016/j.tws.2016.03.006. [Google Scholar] [CrossRef]

35. Zhu XY, Huang ZY, Jiang AM, Chen WQ, Nishimura N. Fast multipole boundary element analysis for 2D problems of magneto-electro-elastic media. Eng Anal Bound Elem. 2010;34(11):927–33. doi:10.1016/j.enganabound.2010.06.006. [Google Scholar] [CrossRef]

36. Zhou L, Yang H, Ma L, Zhang S, Li X, Ren S, et al. On the static analysis of inhomogeneous magneto-electro-elastic plates in thermal environment via element-free Galerkin method. Eng Anal Boundary Elem. 2022;134:539–52. doi:10.1016/j.enganabound.2021.11.002. [Google Scholar] [CrossRef]

37. Zhou LM, Ren SH, Nie B, Guo GK, Cui XY. Coupling magneto-electro-elastic node-based smoothed radial point interpolation method for free vibration and transient analysis of functionally graded magneto-electro-elastic structures. Chin J Aeronaut. 2020;33(1):227–43. doi:10.1016/j.cja.2019.07.024. [Google Scholar] [CrossRef]

38. Jiang AM, Ding HJ. Analytical solutions to magneto-electro-elastic beams. Struct Eng Mech. 2004;18(2):195–209. doi:10.12989/sem.2004.18.2.195. [Google Scholar] [CrossRef]