Employing a Diversity Control Approach to Optimize Self-Organizing Particle Swarm Optimization Algorithms

Abbreviations

1  Introduction

The particle swarm algorithm simulates the emergence of wisdom manifested by simple biological groups, emphasizing collaboration, information interaction, and perception among simple individuals. Therefore, in the optimization algorithm model derived from this metaphor, the collaboration between simple individuals, the information dialog mode, and the effectiveness of the information perceived by the individuals directly affect the optimization performance of the algorithm. In the particle swarm algorithm, the best position experienced by the group is used as the only shared group information. This information is sensed by all the particles and guides them to fly quickly in the direction of this position. This unidirectional particle aggregation behavior directly leads to the rapid loss of population diversity. If the global optimal solution or suboptimal solution exists near the best position of the group, the algorithm may quickly converge to the global optimal solution or suboptimal solution. Otherwise, the algorithm is very likely to fall into a nonglobal optimal point and be difficult to escape. These phenomena are problems that make it difficult for the particle swarm algorithm to ensure global convergence [1,2].

The search dynamics of stochastic optimization algorithms based on group searches are difficult to predict. Suppose that the purpose of the search dynamics is to overcome the problem of premature convergence as much as possible. In that case, the system needs to be able to gain insight into and monitor the group dynamics during the search process. The system can also determine the time and scope of premature convergence of the group. Usually, the premature convergence of the PSO algorithm is caused by the premature loss of diversity in the group. Therefore, whether the optimal level of group diversity can be maintained under different search conditions fundamentally affects the global convergence of the algorithm. Fig. 1 is a typical PSO algorithm calculation and solution flow chart. Research scholar Zhenyu Zhang and others mentioned that the improved PSO algorithm is used to optimize the size of the tram battery supercapacitor energy storage system [3]. They proposed an innovative method, which is “An improved PSO algorithm with competition mechanism is developed for obtaining optimal energy storage elements”.

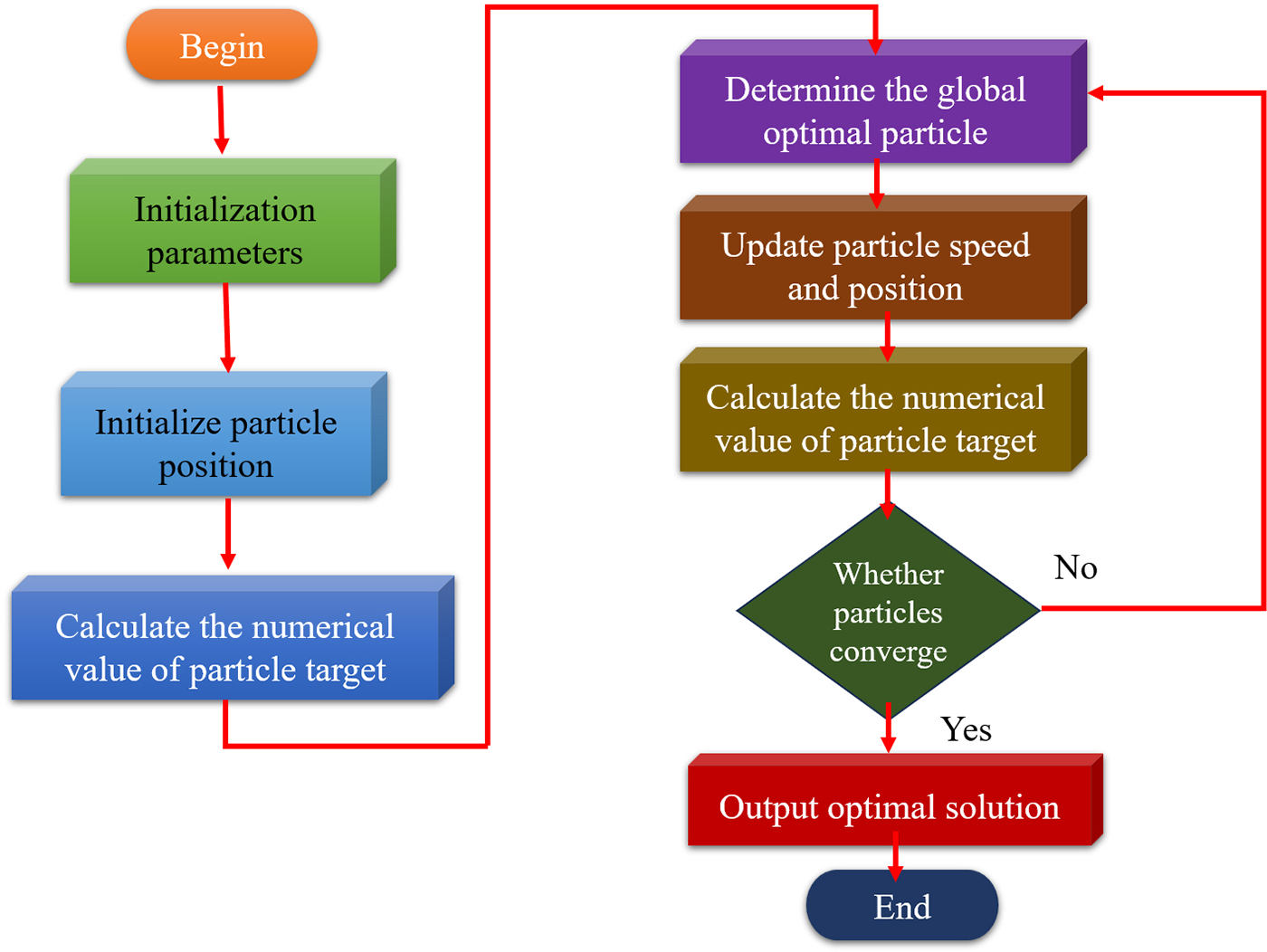
Figure 1: PSO calculation flow chart

In addition, researcher Zhenyu Zhang and others also mentioned that the competitive PSO algorithm is used to optimize the energy management strategy of the tram hybrid energy storage system [4]. These scholars proposed the contribution of “using an improved PSO algorithm based on a competition mechanism to obtain the optimal energy management strategy”. At the same time, they also constructed energy management strategy optimization models based on single threshold and multiple thresholds.

2  Self-Organizing Particle Swarm Algorithm

In the self-organized particle swarm algorithm self-organized PSO (SOPSO), the particle swarm behaves as a self-organizing system. Group diversity is a key factor affecting the behavior of individual particles and is an important group performance indicator. The interaction among individual particles and the group environment is simulated through the feedback mechanism existing in the self-organizing system. Moreover, this self-organizing system designs different control strategies. This strategy achieves the aggregation and dispersion of individuals and dynamically adjusts the balance between the global detection and local mining functions of the group. These conditions enable the group to maintain appropriate diversity and then converge globally with a greater probability [5,6].

In the above model, Di represents the reference input of group diversity, Do represents the actual diversity output of the group, and Pgo represents the best position experienced by the group. The final stable output of the system is the global solution to the target problem, as shown in Fig. 2. The self-organizing control particle swarm algorithm model uses a feedback mechanism to analogize the information perception and interactions in a particle swarm; this model is a typical negative feedback control system. The system includes three main parts: a diversity controller, a particle swarm optimizer, and a particle swarm. The particle group consists of particles of a certain group size, and its diversity information is directly fed back to the diversity controller. The diversity controller determines the strategy for increasing or decreasing the diversity of the group based on the real-time diversity information of the group and the deviation of the reference input. The optimizer changes the group diversity by adjusting the flight behavior of individual particles according to the rules or instructions output by the diversity controller. This situation makes the population more evolvable and ultimately yields better system output [7,8].

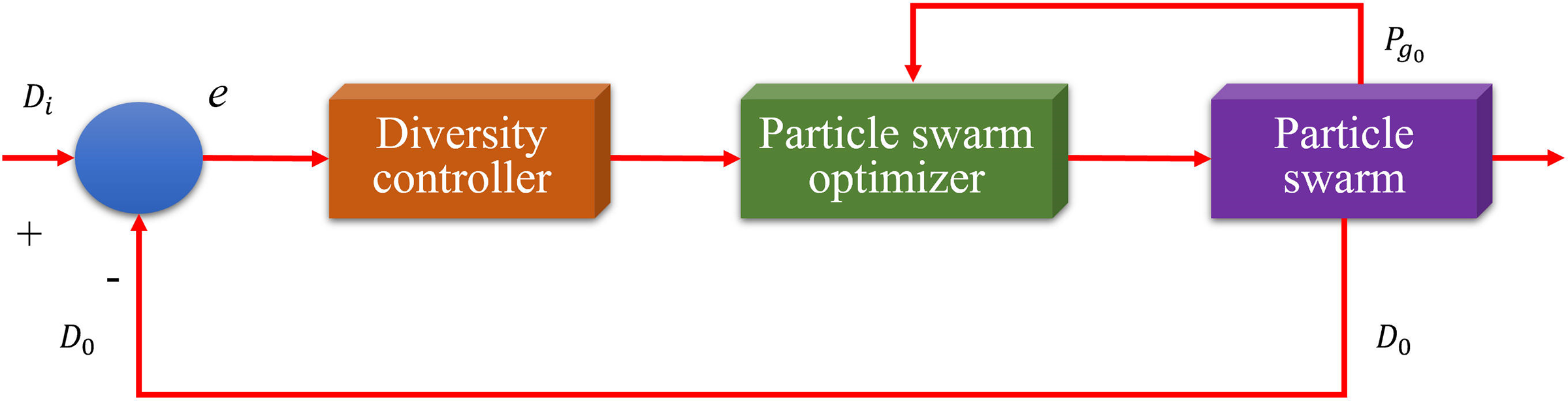
Figure 2: Self-organizing particle swarm algorithm model

There are three key issues that must be addressed when designing a model.

(a)   How to effectively calculate and measure group diversity.

(b)   How to determine the ideal diversity reference input to facilitate a global search.

(c)   How to design the control strategy of the diversity controller so that the behavior of individual particles can be correctly adjusted according to the dynamics of the group.

2.1 Group Diversity Measure

In the bionic algorithm based on the group search method, although group diversity is not the research purpose of the algorithm, it is closely related to the global optimization performance of the algorithm. Therefore, this situation has attracted the attention of many researchers. Different from many previous studies, the self-organizing particle swarm algorithm not only focuses on group diversity but also uses group diversity as an explicit indicator to quantitatively reflect the evolutionary dynamics of the group. A self-organizing particle swarm algorithm is also used to guide the evolutionary behavior of particles. Therefore, to achieve this goal, we must first find reasonable methods for measuring group diversity [9,10].

Group diversity is used to characterize the differences in characteristics of individuals within a group. It is generally believed that the more dispersed the individuals are in the solution space, the better the group diversity; the more concentrated the distribution of individuals is, the worse the diversity of the population. At present, the main measures of population diversity include population distribution variance, population entropy, and average point distance [11,12].

Assume that individual xit in the t-th generation population is composed of L components, that is, xit=(xi1t,xi2t,⋯,xijt,⋯,xiLt), where ∈1,2,⋯,N,j∈1,2,⋯,L,N is the group size; then, the average individual of the t-th generation population is defined as Eq. (1)

X ¯t=(X¯1t,X¯2t,…,X¯jt,…,X¯Lt)(1)

among X¯jt=1N∑i=1Nxijt.

From this definition, the variance of the t-th generation group is

Dt=(D1t,D2t,…,Djt,…,DLt)(2)

among Dt=1N∑i=1N(xijt−X¯jt)2,j∈1,2,⋯,L.

According to Eq. (2), in this study, the variance Dt is an L-dimensional row vector. Each component represents the spatial distribution deviation of the population in this dimensional coordinate system.

If the solution space Rn of the t-th generation population distribution is divided into Q subsets S1t,S2t,⋯,SQt, the number of individuals contained in each subset is recorded as |S1t|,|S2t|,⋯,|SQt|, and for any i,j∈1,2,⋯,Q,Sit∩Sjt=∅,⋃j=1QSit=At, where At is the set of the t-th generation group. Therefore, the entropy of the t-th generation population can be defined as Eq. (3)

Et=−∑j=1Qpilgpi(3)

where pi=|Sjt|N,j=1,2,⋯,Q,N is the group size.

As seen from the above definition, when all individuals in the group are the same. That is, when Q=1, the entropy takes the minimum value Et=0. When all individuals are different, that is, Q=N, the entropy takes the maximum value Et=lgN. The more individual types there are in the group and the more evenly they are distributed, the greater the entropy.

Let the group size be N and the length of the longest diagonal in its search space be S. If the t-th generation individual Xit consists of L components, that is, X it=(Xi1t,Xi2t,⋯,Xijt,⋯,XiLt,),i=1,2,⋯,N,j=1,2,⋯,L, the average center of the population is recorded as Eq. (4)

X ¯t=(X¯1t,X¯2t,…,X¯jt,…,X¯Lt)(4)

where X¯jt=1N∑i=1Nxijt; then, the average point distance from an individual to the population center can be defined as Eq. (5)

Dist=1N⋅S∑i=1N∑j=1L(xijt−X¯jt)2(5)

The three abovementioned measurement methods reflect the distribution of individuals in the group to varying degrees. However, as a measure of group diversity, each has its own advantages and disadvantages. The distribution variance of a group reflects only the degree of spatial deviation of the distribution of individuals in the group and cannot fully describe the degree of individual dispersion. For example, the population {1, 2, 3, 4, 5} consists of 5 individuals, and their variance is 2. The variance of population {1, 1, 1, 1, 5} is 2.56. Although the variance in the latter is greater than that in the former, the former has more evolutionary ability than does the latter. The population reflects the distribution of different types of individuals in the population but does not reflect the degree of dispersion of each individual in the population. In particular, it is difficult to predict the classification of individuals within the population during the actual calculation process. The calculation of group entropy depends on the correct cluster analysis of the group, so the calculation cost is relatively high. Therefore, groups are not practical [13,14].

In contrast, the average point distance defined by Eq. (5) reflects the distribution of individuals in the unit search space. This situation has nothing to do with the size of the population or the size of the search space. The above situation can better describe the density of individuals distributed in the solution space and is an ideal diversity measure. Therefore, for this paper, we choose the average point distance of the group as the measure of group diversity [15,16].

2.2 Determination of Diversity Reference Inputs

For the self-organizing particle swarm algorithm model in Fig. 2, the expectation is to utilize a negative feedback mechanism. By controlling the diversity reference input, the diversity of the particle population is maintained throughout the search period. Therefore, the diversity reference input Di must represent an ideal population diversity level that can ensure that the algorithm converges globally with a greater probability. Considering that the optimization process usually occurs early in the search process, it is desirable to maintain as much diversity of the population as possible. This situation is conducive to coarse-grained global detection and avoids prematurely falling into local extremes. As the search proceeds, the diversity gradually decreases, allowing detection and mining to proceed in tandem. In the later stages of the search, fine-grained local mining should be emphasized, and the diversity rapidly decreases until the population converges. In view of this, the system constructs the following linear function as the reference input for diversity as Eq. (6)

Di(t)={a(1−tb⋅Tmax),t<b⋅Tmax0,b⋅Tmax≤t<Tmax(6)

where Tmax represents the maximum number of iterative operations; a and b represent the control coefficients of the reference input; and a and b ∈ (0, 1]. Obviously, this reference input can linearly decrease from the initial value α to 0 within the limited search time. This situation is a reasonably simple choice.

Under the control of the reference input Di, the population diversity D0 changes as the reference input changes. When D0 is lower than Di, the particle behavior needs to be adjusted to make it diverge, expand the detection range, and increase the diversity of the population. When D0 is higher than Di, the particles are needed to gather toward the best position and conduct a fine search. Such a situation will reduce group diversity.

2.3 Design of Diversity Controllers

In the self-organizing particle swarm algorithm, the diversity controller adjusts the diversity of the group through the diversity increase operator and the diversity decrease operator. The method of this paper starts from the perspective of control parameters to seek adaptive control strategies to design diverse control rules [17,18].

For self-organizing particle groups, changes in group diversity are caused by changes in the behavior of individual particles. The system considers that the algorithm’s inertia weights and acceleration coefficients affect individual particle behavior differently. Therefore, in this study, we select parameters from two perspectives and adjust the divergence and aggregation of individual particles to achieve an increase or decrease in group diversity. This paper presents the diversity-controlled inertia weight (DCIW) and diversity-controlled acceleration coefficient (DCAC) methods.

2.3.1 Diversity Control Strategy Based on Inertia Weight

In the standard particle swarm algorithm, the inertia weight determines how much momentum the particles have to maintain inertial motion. To fundamentally overcome the premature birthtime problem in this study, individual particles must be able to fly over or escape with a larger momentum when they are in danger of falling into a local extreme. In the literature related to particle swarm optimization, the current selection of inertia weights relies mainly on experiments and experience. Most related studies refer to the work of Shi and Eberhard. Let ω∈(0,1) or linearly decrease from 0.9 to 0.4, and the acceleration coefficient is c1=c2=2.0. Bergh once noted that the standard particle swarm algorithm can cause individual particles to gradually converge to the weighted center of their own best history and the best group history. However, the convergence behavior described above depends on the parameter settings. When the algorithm parameters satisfy the following relationships, the movement trajectories of individual particles may converge [19,20].

1>ω>12(c1+c2)−1,  2.0≤c1+c2≤4.0(7)

Although the system condition |ω|<1 can ensure that the particles move in a converged trajectory, it is difficult to provide enough momentum for the particles to escape from the local extreme. Therefore, parameter combinations that violate the above conditions are introduced in the self-organizing particle swarm algorithm. When the system needs to increase the diversity of the population, the system condition is |ω|>1, which allows individual particles to obtain greater momentum dispersion or escape. When the system must reduce the diversity of the population, a parameter combination is selected according to the above formula so that individual particles gather in a convergent trajectory. Based on the above analysis, in this study, we designed the following diversity control rules based on inertia weighting.

(a) Diversity Adding Rules

When e(t)=Di(t)−D0(t)>0, the population diversity is lower than that of the reference input. Then, the system controller outputs a set of divergence parameters ω(t)>1,c1(t)=c2(t)=2.0. This will cause individual particles to diverge, increasing population diversity.

(b) Diversity Reduction Rules

When e(t)=Di(t)−D0(t)<0, the population diversity is greater than that of the reference input. Then, the system controller outputs a set of convergence parameters 1>ω(t)>12(c1(t)+c2(t))−1,2.0≤c1(t)+c2(t)≤4.0. This causes individual particles to clump together, reducing population diversity.

2.3.2 Diversity Control Strategy Based on the Acceleration Coefficient

Ozcan and Mohan performed a mathematical analysis of individual particle trajectories without inertial constraints. They found that individual particles fly in the solution space with sinusoidal trajectories, whose amplitude and frequency depend on the initial position, velocity, and acceleration coefficient. Kennedy carefully studied the impact of c1 and c2 on algorithm performance [21]. He found that when c1=0, the algorithm easily falls into local points. He also found that when c2=0, it is difficult for the algorithm to search for the global optimal solution. In the algorithm model, c1 determines the individual’s affirmation and persistence of his or her own experience and beliefs. Additionally, c2 determines the individual’s recognition of socially shared information and group goals. A larger c1 emphasizes the individualization of particles and is beneficial for maintaining the diversity of the population. A larger c2 emphasizes the social nature of particles, which leads to the convergence of particles and reduces group diversity. Therefore, the proposed method utilizes different acceleration coefficients to increase and decrease the diversity, and the specific rules are as follows:

(a) Diversity Increase Rules

When (t)=Di(t)−D0(t)>0, the population diversity is lower than that of the reference input. Then, the controller output parameters are ω∈(0,1),c1(t)=c1max,c2(t)=c2min. This approach will facilitate particle personalization to increase population diversity.

(b) Diversity Reduction Rules

When e(t)=Di(t)−D0(t)<0, the population diversity is greater than that of the reference input. Then, the controller output parameters are ∈(0,1),c1(t)=c1min,c2(t)=c2max. This will encourage individual particles to converge to reduce population diversity.

2.4 Simulation Experiments and Results Analysis

To verify the effectiveness of the algorithm in this paper, the performances of several algorithms proposed in this study were compared. These algorithms include the standard particle swarm optimization algorithm (SPSO), SOPSO-DCIW, SOPSO-DCAC, the SPSO algorithm with linear decreasing inertia weight (SPSO-LDIW), and the modified PSO algorithm with the time-varying acceleration constant method (MPSO-TVAC) [22,23].

Compared with that of the other algorithms, the population diversity of the SOPSO-DCIW algorithm changes slowly in the early stage and remains at the highest level; this shows that the algorithm performs the most complete global detection in the early stage. Although the algorithm slows down the early search speed, it prevents the algorithm from prematurely falling into local extremes. This approach is beneficial for subsequent global research. In the middle of the search process, the population diversity decreases at a relatively fast rate. Entering the later stage of the search, although the group diversity is already very small, an improvement in the optimal solution can still be observed; this shows that the diversity self-adjusting control inertia weight strategy can increase the effectiveness of the algorithm in controlling local mining and global detection. This method thereby improves its global convergence, which is why the SOPSO-DCIW algorithm has better average optimization performance.

Fig. 3 shows the impact of diverse reference inputs on algorithm performance, where the abscissa represents the evolutionary algebra. The ordinate represents the diversity, the dimension is 10, and the test function is the F21 function. Fig. 4 is a performance comparison chart of the F21 function when the dimension is 50. This experiment showed that SOPSO-DCAC seemed to have the most ideal group diversity. In the early stage of the search, its diversity level is slightly lower than that of SOPSO-DCIW and SPSO-LDIW. Similarly, in the early stage of the search, the diversity water criterion is higher than that of SPSO-TVAC and SPSO. In addition, in the middle stage of the search, the diversity reduction rate gradually increases. In the later stages of the search, when the diversity changes in the other algorithms almost stagnate, the diversity in the SOPSO-DCAC algorithm continues to decrease at a relatively rapid rate. A higher population diversity in the early stages prevents the algorithm from premature convergence.

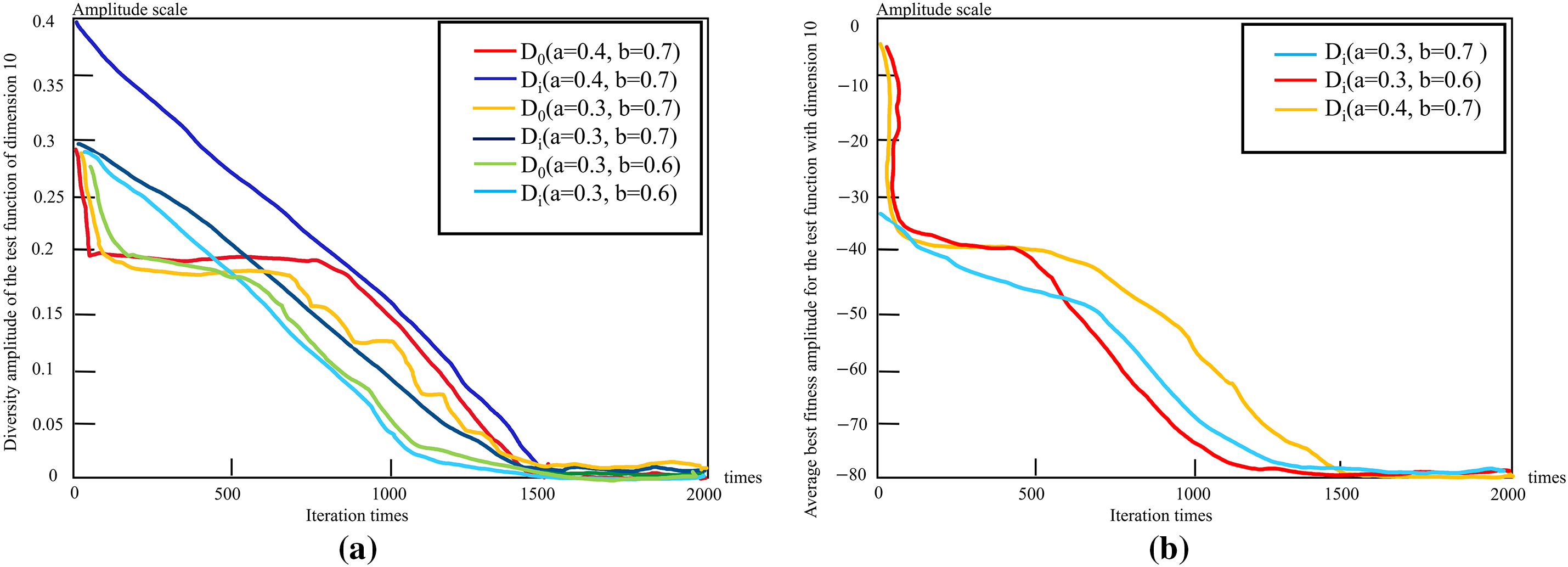
Figure 3: The impact of diverse reference inputs on the dynamic performance of the algorithm. (a) Group diversity; (b) Average optimal fitness value

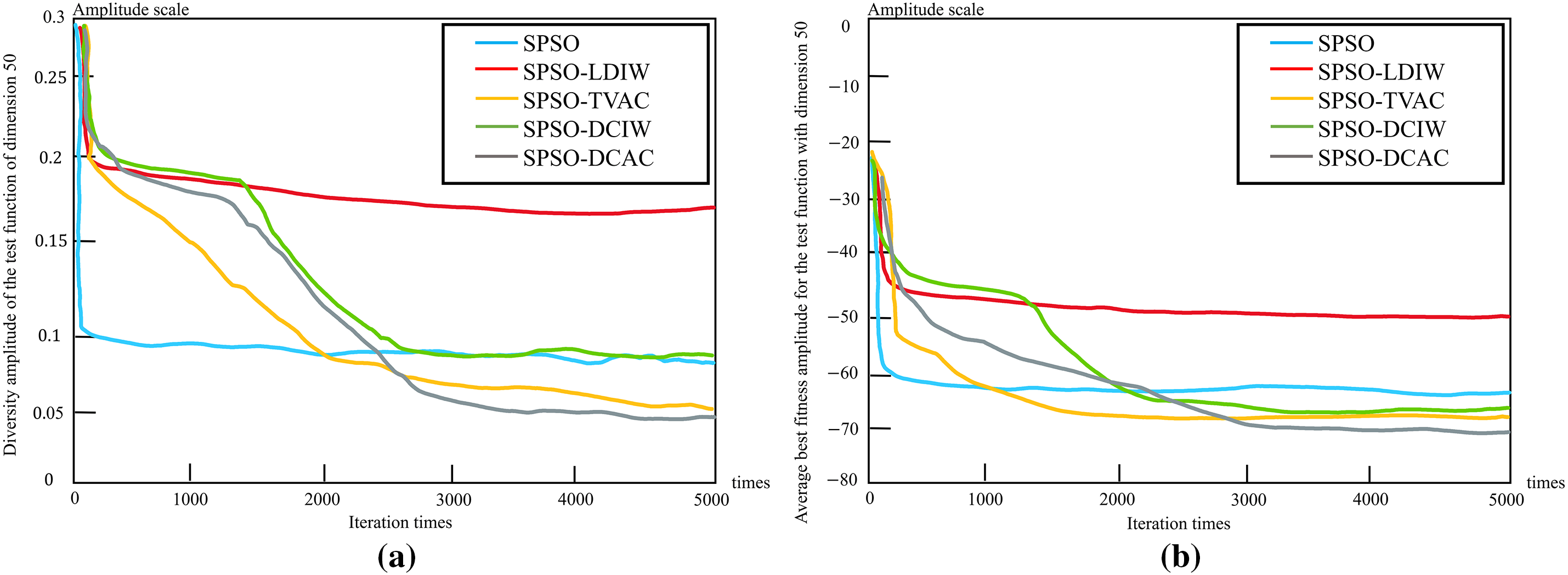
Figure 4: Different algorithms for optimizing the dynamic performance of the F21 function. (a) Group diversity; (b) Average optimal fitness value

Fig. 3a shows the performance of population diversity when the test function dimension is 10, and Fig. 3b shows the average best fitness value when the test function dimension is 10. Fig. 4a shows the performance of the population diversity when the test function dimension is 50, and Fig. 4b shows the average best fitness value when the test function dimension is 50. The strong fine search capability in the later stage continuously reduces the diversity of the group and accelerates the convergence of the algorithm. This approach significantly improves the quality of the solutions. These situations illustrate the effectiveness of the diversity control acceleration coefficient strategy and are also the fundamental reasons why SOPSO-DCAC has a good average optimization performance [23,24].

3  Application of the Self-Organizing Particle Algorithm in Constrained Layout Optimization

Layout optimization is a typical NP-hard problem and has a strong application background. Many practical engineering applications involve layout optimization problems, such as satellite cabin layout, mechanical assembly layout, and large-scale integrated circuit layout. Therefore, this topic has attracted widespread attention from researchers.

3.1 Constrained Layout Optimization Problem

Layout optimization involves optimally placing certain objects in a specific space according to certain requirements. During the layout process, the objects must usually be clothed, and the containers should not interfere with each other. In addition, space utilization should be improved as much as possible during the layout process. This type of problem has a layout without performance constraints. In addition, other performance constraints must be considered in some layout optimization problems, such as inertia, balance, and stability. These situations involve performance-constrained layouts, referred to as constrained layout optimization. Since layout optimization involves a variety of practical constraints, the solution space of this type of problem is usually nonconvex and discontinuous. Therefore, the above layout optimization is difficult to solve. In recent years, the use of smart computing has increased. People have begun to use different intelligent computing methods to solve this type of problem, such as analog annealing, genetic algorithms, and multiagent technology. As an emerging swarm intelligence computing method, the particle swarm algorithm is also suitable for solving NP-hard problems similar to constrained layout optimization problems.

In our research, artificial satellite cabin layout design was used as the background. This work also studied the layout optimization problem with performance constraints, as shown in Fig. 5. In a rotating satellite cabin, a circular partition is provided perpendicular to the central axis of the cabin. An artificial satellite cabin requires the needed system functional components, such as instruments and equipment. These elements are called objects. The items to be clothed are optimally arranged on these circular partitions. The objects to be clothed on each rotating partition should be gathered toward the center of the container as much as possible while meeting the series of constraint requirements. When the system is stationary, the static imbalance on the diaphragm is less than the allowable value. At a given angular velocity, the dynamic imbalance of each object to be clothed is less than the allowable value. If it is assumed that the objects to be clothed are all cylinders, the problem can be reduced to a balancing layout problem involving a rotating round table [25].

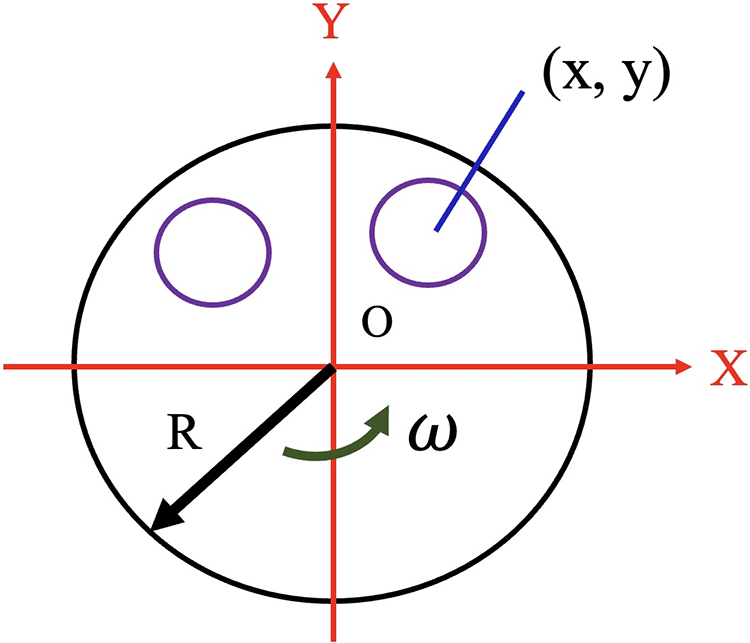
Figure 5: Schematic diagram of the layout of circular items to be clothed on the rotating partition

Assume that the radius of the round table is R, the table rotates at an angular speed ω, and n disks {Oi|i∈I={1,2,…,n}} are to be arranged on it. Taking the geometric center O of the round table as the origin, establish a plane rectangular coordinate system XOY. Assuming that the geometric center of the i-th disk is Xi=(xi,yi) and that its radius and mass are ri and mi, respectively, the object to be laid out is Oi=(Xi,ri,mi); then, let X=(X1,X2,…,Xn) represent the layout variable. Assume that the center of mass of each disk coincides with the geometric center and that the disk is fixed to the table. Obviously, the key to this issue lies in what follows. First, static layout optimization needs to be achieved within the two-dimensional plane of the round table. Ignoring the dynamic imbalance constraint of the problem, the mathematical model of the two-dimensional constrained layout optimization problem can be described as Eq. (8).

minf(x)=max{xi2+yi2+ri|i∈I,xi,yi∈[−R,R]}(8)

Moreover, the following constraints are satisfied, as Eqs. (9)–(11).

f1(Xi)=xi2+yi2+ri−R≪0,i∈I(9)

f2(Xi)=ri+rj−(xi−xj)2+(yi−yj)2≤0,i≠j,i,j∈I(10)

f3(X)=(∑i=1nmi⋅xi)2+(∑i=1nmi⋅yi)2−[δJ]≤0(11)

here, f(X) is the radius of the enveloping circle, and f1(Xi) is the noninterference constraint between the object to be clothed and the round table container. f2(Xi) is the noninterference constraint between objects to be distributed, f2(Xi) is the static imbalance constraint, and [δJ] is the allowable static imbalance value.

3.2 The SOPSO Algorithm for Solving Constrained Layout Optimization Problems

This paper will use SOPSO to solve the two-dimensional constrained layout problem described by Eqs. (8)–(11). For this reason, the common penalty function method is used to address the constraints of the problem. First, construct the penalty function as an Eq. (12).

Φ(X)=λ1∑i=1n[μ(f1)⋅f1(Xi)]+λ2∑i=1n−1∑j=i+1n[μ(f2)⋅f2(Xi)]+λ3⋅μ(f3)⋅f3(X)(12)

where λm is the penalty factor of constraint fm, λm>0,m∈{1,2,3}, as Eq. (13).

μ(fm)={0,fm(⋅)≤01,fm(⋅)>0(13)

For convenience, the polar coordinate encoding method is used, and the centroid O of the round table is used as the pole to establish the polar coordinate system. Then, the polar coordinates of the centroid Xi of any circle Oi to be distributed are (li,θi), and the corresponding rectangular coordinates are (xi,yi)=(licosθi,lisinθi), where li∈[0,R−ri],θi∈[−π,π]. At this time, the first constraint, that is, the noninterference between the cloth object and the round table container, can always be satisfied. Therefore, the penalty function in Eq. (12) can be simplified to Eq. (14).

Φ′(X)=λ2∑i=1n−1∑j=i+1n[μ(f2)⋅f2(Xi)]+λ3⋅μ(f3)⋅f3(X)(14)

This can transform the constrained layout optimization problem into the following unconstrained optimization problem, as Eq. (15).

minF(X)=f(X)+Φ′(X)(15)

In the above problem, if there are n objects to be distributed, the search space of the algorithm is 2n-dimensional, in which any particle represents a candidate solution of the objective function. This candidate solution can be expressed as a 2n-dimensional polar coordinate vector (l1,θ1,l2,θ2,…,ln,θn), where li∈[0,R−ri],θi∈[−π,π],1≤i≤n. Obviously, the smaller the objective function value is, the better the particles.

SOPSO is used to solve the performance-constrained layout problem described by Eq. (8). In our research, the problem is essentially transformed into an unconstrained optimization problem that solves Eq. (15), and its algorithm flow can be described as follows:

(1)   Letting t = 0, initialize the diversity input and diversity output of the system.

(2)   Randomly initialize the particle population (particle size is N) in the feasible solution space, including the position, speed, and best position of each particle; the best position of the group; and the control parameters of the particles.

(3)   Calculate the function value of each particle and update the historical best position of each particle and the best position of the group.

(4)   The diversity input and output of the system are updated, and the control parameters are adjusted according to the control rules.

(5)   If the termination condition is met, the algorithm ends. Otherwise, let t = t + 1 and continue Step (6).

(6)   Update the particle group, including the position and speed of each particle, and return to Step (3).

3.3 Example Application and Result Analysis

For this research, our proposed method selected a more complex 40-circle constrained layout optimization problem to observe the optimization performance of the SOPSO algorithm. The results were compared and analyzed with those of the human-computer interaction genetic algorithm (HCIGA) and the particle swarm optimization algorithm with a mutation operator (MPSO). The radius of the circular container is R = 880 mm, and 40 circular objects are laid out on it. Given that the allowable value of the static unbalanced J is δJ, the relevant information of the material to be clothed is shown in Table 1. The layout results are shown in Fig. 6 and Table 2. In the experiment, the population size of the HCIGA was 60. MPSO and SOPSO are 100: SOPSO adopts the DCIW control strategy, and the maximum number of iterations is 5000.

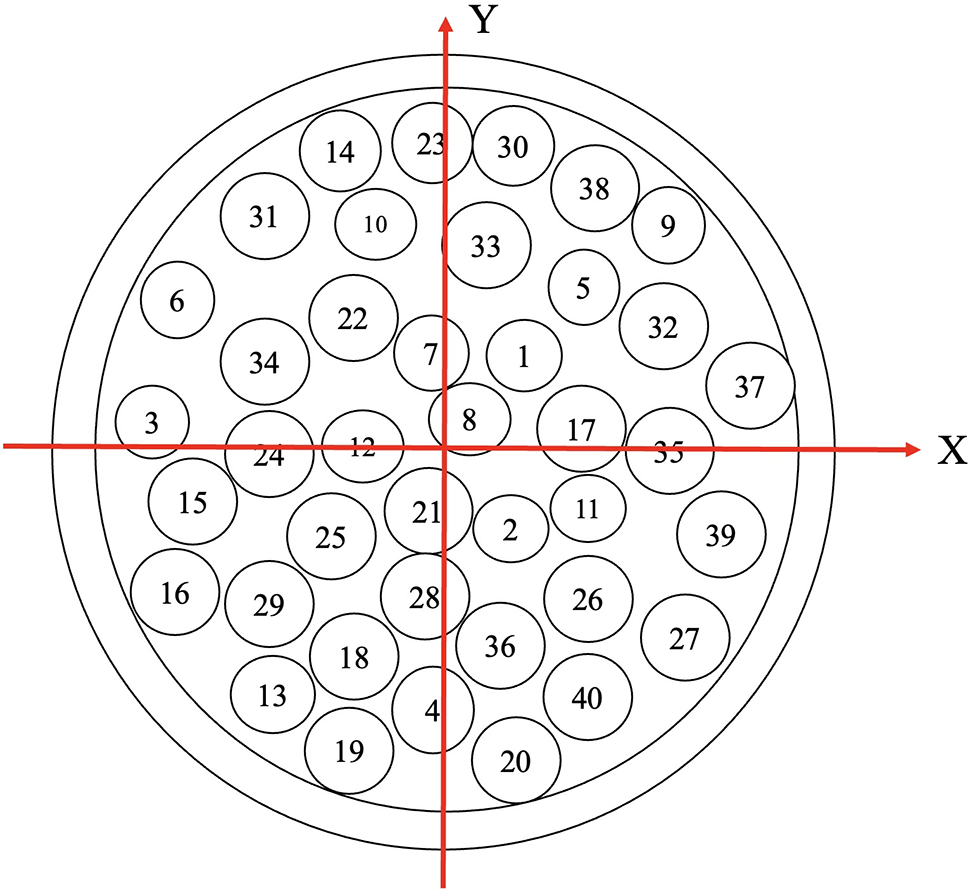
Figure 6: Schematic chart of the SOPSO algorithm layout results

Fig. 6 shows the optimal layout obtained by SOPSO when all the performance constraints are met. The figure shows that the outer large circle is the circular container, and the inner large circle is the outer enveloping circle in the optimal layout. There are 40 circles within the outer circle that do not interfere with each other. Table 2 records the constraint performance corresponding to the optimal layout. In addition, the system includes the best results obtained by the HCIGA and MPSO when solving this problem. Obviously, the optimal layouts obtained by these three algorithms all achieve noninterference between each waiting cloth and between containers. Therefore, the interference amount of each algorithm in this table is zero. Under this premise, the operator observes that the outer envelope circle radius HCIGA in each layout is 870.331 mm. The MPSO is 843.940 mm long, while the SOPSO is 816.650 mm long. Obviously, the envelope circle radius obtained by SOPSO is much smaller than that obtained by MPSO and the HCIGA. This shows that the layout results of SOPSO can better achieve the goal of gathering the items to be clothed toward the center as much as possible. At this time, although the static imbalance in the SOPSO layout is slightly greater than that in the other two algorithms, the static imbalance is also far less than the needed given value. The above results illustrate the effectiveness of SOPSO in complex constrained layout optimization problems.

4  Conclusion

The method proposed in this work starts from the nature of crowd intelligence and treats the particle group as a self-organizing system, which uses group diversity as a key factor affecting the behavior of individual particles and an important indicator of group dynamics. This method introduces a diversity feedback mechanism to control the evolutionary dynamics of the group, and this method also proposes a self-organizing particle swarm algorithm (SOPSO) model. By analyzing the different effects of algorithm parameters on the behavior of individual particles, the above method proposes two strategies for controlling the inertia weight and acceleration coefficient to increase and decrease the diversity of particle groups, respectively. By controlling the linear reference input of the system, the SOPSO algorithm can effectively improve the diversity level of the group during the entire search period, and the SOPSO algorithm can also appropriately adjust the evolvability of the group according to the search dynamics. The system thus effectively overcomes the premature convergence of the algorithm. The relevant experimental results show that if the SOPSO algorithm is compared with other typical improved particle swarming algorithms, SOPSO-DCIW and SOPSO-DCAC have better average optimization performances. In the experiment, it was found that when the system searches for global detection via the early adjustment algorithm, it is more effective to control the inertia weight than to control the acceleration coefficient. When the system searches for the local search of the later adjustment algorithm, it is more effective to adjust the acceleration coefficient than to adjust the inertia weight. With the successful application of the system in the two-dimensional constrained layout problem based on the satellite cabin layout, the above examples illustrate that the method model proposed in this paper has certain practical value.

Acknowledgement: This research was supported by the Department of Information Technology, Takming University of Science and Technology and Department of Electrical Engineering at the National Chin-Yi University of Technology. The authors would like to thank the National Chin-Yi University of Technology, Takming University of Science and Technology, Taiwan, for supporting this research.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Conceptualization, Wen-Tsai Sung; methodology, Sung-Jung Hsiao; formal analysis, Wen-Tsai Sung; writing—original draft preparation, review and editing, Sung-Jung Hsiao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data sharing does not apply to this article as no datasets were generated or analyzed during the current study.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Murala P, Nayak K, Kumar KV, Vishwakarma S. Bio-inspired algorithms for self-healing and adaptation in sensor networks. In: 2024 IEEE 13th International Conference on Communication Systems and Network Technologies (CSNT); 2024 Apr 6–7; Jabalpur, India. [Google Scholar]

2. Xu B. Research on the application of PSO algorithm in aviation control flight plan path search. In: 2024 IEEE 2nd International Conference on Sensors, Electronics and Computer Engineering (ICSECE); 2024 Aug 29–31; Jinzhou, China. [Google Scholar]

3. Zhang Z, Cheng X, Xing Z, Wang Z, Qin Y. Optimal sizing of battery-supercapacitor energy storage systems for trams using improved PSO algorithm. J Energy Storage. 2023;73(3):108962. doi:10.1016/j.est.2023.108962. [Google Scholar] [CrossRef]

4. Zhang Z, Cheng X, Xing Z, Wang Z. Energy management strategy optimization for hybrid energy storage system of tram based on competitive particle swarm algorithms. J Energy Storage. 2024;75(1):109698. doi:10.1016/j.est.2023.109698. [Google Scholar] [CrossRef]

5. Mammeri E, Necaibia A, Ahriche A, Bouraiou A, Hassani I. A hybrid GWO-PSO algorithm for global MPP tracking in PV systems under PSCs. In: 2023 Second International Conference on Energy Transition and Security (ICETS); 2023 Dec 12–14; Adrar, Algeria. [Google Scholar]

6. Zhao C, Guo D. Particle swarm optimization algorithm with self-organizing mapping for Nash equilibrium strategy in application of multiobjective optimization. IEEE Trans Neural Netw Learn Syst. 2021;32(11):5179–93. doi:10.1109/TNNLS.2020.3027293. [Google Scholar] [PubMed] [CrossRef]

7. Zhou L, Cui Y. Parameter optimization and its application of support vector machines based on improved particle swarm optimization algorithm. In: 2022 4th International Conference on Intelligent Information Processing (IIP); 2022 Oct 14–16; Guangzhou, China. [Google Scholar]

8. Wu H, Wang L, Li X, Huang Y, Zhou H. User-adjustable capability mining technology based on improved PSO and LSTM model. In: 2022 4th International Conference on Electrical Engineering and Control Technologies (CEECT); 2022 Dec 16–18; Shanghai, China. [Google Scholar]

9. Song Z, Xia Z. Carbon emission reduction of tunnel construction machinery system based on self-organizing map-global particle swarm optimization with multiple weight varying models. IEEE Access. 2022;10(10):50195–217. doi:10.1109/ACCESS.2022.3173735. [Google Scholar] [CrossRef]

10. Mujawar S, Gupta J. A statistical perspective for empirical analysis of bio-inspired algorithms for medical disease detection. In: 2022 International Conference on Emerging Smart Computing and Informatics (ESCI); 2022 Mar 9–11; Pune, India. [Google Scholar]

11. Sun J, Yang Y, Wang Y, Wang L, Song X, Zhao X. Survival risk prediction of esophageal cancer based on self-organizing maps clustering and support vector machine ensembles. IEEE Access. 2020;8:131449–60. doi:10.1109/ACCESS.2020.3007785. [Google Scholar] [CrossRef]

12. Dong J, Chen X, Zhang J, Li Z. Global path planning algorithm for USV based on IPSO-SA. In: 2019 Chinese Control and Decision Conference (CCDC); 2019 Jun 3–5; Nanchang, China. [Google Scholar]

13. Wang Z, Fu Y, Song C, Zeng P, Qiao L. Power system anomaly detection based on OCSVM optimized by improved particle swarm optimization. IEEE Access. 2019;7:181580–8. doi:10.1109/ACCESS.2019.2959699. [Google Scholar] [CrossRef]

14. Ma R, Xia C, Xu Z, Zhou H, Shi L, Zhang Q. Improved PSO-based parameters optimization of ESS’s active and reactive controllers. In: 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC); 2020 Sep 20–23; Nanjing, China. [Google Scholar]

15. Deng Y. Sliding mode variable structure controller for PSO-RBF hypersonic vehicle. In: 2018 International Computers, Signals and Systems Conference (ICOMSSC); 2018 Sep 28-30; Dalian, China. [Google Scholar]

16. Atiah FD, Helbig M. Dynamic particle swarm optimization for financial markets. In: 2018 IEEE Symposium Series on Computational Intelligence (SSCI); 2018 Nov 18–21; Bangalore, India. [Google Scholar]

17. Idoko GO. Drive path optimization for electric vehicles using particle swarm optimization. In: 2023 13th International Symposium on Advanced Topics in Electrical Engineering (ATEE); 2023 Mar 23–25; Bucharest, Romania. [Google Scholar]

18. Tian W, Zhu J, Cheng W, Bao J. PSO algorithm with decreasing inertia weights based on sigmoid function. In: 2024 2nd International Conference on Algorithm, Image Processing and Machine Vision (AIPMV); 2024 Jul 12–14; Zhenjiang, China. [Google Scholar]

19. Dayal N, Srivastava S. An RBF-PSO based approach for early detection of DDoS attacks in SDN. In: 2018 10th International Conference on Communication Systems & Networks (COMSNETS); 2018 Jan 3–7; Bengaluru, India. [Google Scholar]

20. Li J, Su J. Robot global path planning based on improved second-order PSO algorithm. In: 2022 IEEE International Conference on Mechatronics and Automation (ICMA); 2022 Aug 7–10; Guilin, China. [Google Scholar]

21. Han HG, Lu W, Hou Y, Qiao JF. An adaptive-PSO-based self-organizing RBF neural network. IEEE Trans Neural Netw Learn Syst. 2018;29(1):104–17. doi:10.1109/TNNLS.2016.2616413. [Google Scholar] [PubMed] [CrossRef]

22. Abbas G, Gu J, Farooq U, Raza A, Asad MU, El-Hawary ME. Solution of an economic dispatch problem through particle swarm optimization: a detailed survey—part II. IEEE Access. 2017;5:24426–45. doi:10.1109/ACCESS.2017.2768522. [Google Scholar] [CrossRef]

23. Hu H, Feng J, Zhai X, Guan X. The method for single well operational cost prediction combining RBF neural network and improved PSO algorithm. In: 2018 IEEE 4th International Conference on Computer and Communications (ICCC); 2018 Dec 7–10; Chengdu, China. [Google Scholar]

24. Makhloufi S, Mekhilef S. Logarithmic PSO-based global/local maximum power point tracker for partially shaded photovoltaic systems. IEEE J Emerg Sel Top Power Electron. 2022;10(1):375–86. doi:10.1109/JESTPE.2021.3073058. [Google Scholar] [CrossRef]

25. Tehsin S, Rehman S, Saeed MOB, Riaz F, Hassan A, Abbas M, et al. Self-organizing hierarchical particle swarm optimization of correlation filters for object recognition. IEEE Access. 2017;5:24495–502. doi:10.1109/ACCESS.2017.2762354. [Google Scholar] [CrossRef]