Multi-Order Neighborhood Fusion Based Multi-View Deep Subspace Clustering

1  Introduction

Clustering is the cornerstone in the domains of data mining and machine learning, which focuses on unsupervised classifying unlabeled data into the appropriate clusters based on the similarity between samples. Over the years, many advanced clustering methods (e.g., K-means clustering [1], spectral clustering [2], and subspace clustering [3]) have been proposed and widely used in many practical applications.

Nowadays, with the quick development of cameras, digital sensors, and social networks, massive data can be easily obtained from various perspectives and numerous sources, so-called multi-view data. In short, an object can be collected from different views, and each angle is regarded as a specific view that is independently used for analysis. Such as, an image can be described by various features like HOG [4], SIFT [5], and GIST [6]; videos usually contain visual frames, audio signals, and text messages; different languages can report the news; and cameras can capture an object from many angles.

Different from the single-view data, multi-view data exists the consistent redundant and supplementary information between distinct views. Therefore, how to efficiently handle the consistency and the supplementary information of each view to learn a unified expression is a critical problem.

Lately, many multi-view clustering algorithms have been researched intensively, including Multi-view graph clustering [7–10], Multi-kernel learning [11–15], and Multi-view subspace clustering [16–19]. Among them, multi-view graph clustering aims to learn a shared graph structure from different views for clustering, e.g., Wang et al. [20] proposed multi-view and multi-order structured graph learning, which introduced multiple different-order graphs into graph learning. Wang et al. [21] presented a local high-order graph learning for multi-view clustering, which uses the rotation tensor nuclear norm to exploit high-order relationships between views; Multi-kernel learning utilizes different predefined kernels to process the data of each view, then fuses these kernels in a linear or nonlinear way to form a unified kernel for clustering. Multi-view subspace clustering aims to obtain a unified latent representation reflecting the consistency across different views, which has attracted widespread research. Multi-view subspace clustering methods usually presume that a sample can be linearly represented by other samples in the same cluster, while they cannot handle the samples with non-linear structures. So, some researchers introduce kernel methods to map samples into one high-dimensional space to handle the nonlinear structure [19,22,23].

Recently, benefiting from the powerful non-linear representation and data-driven capabilities of neural networks, several multi-view deep subspace clustering algorithms have been explored [23–25] to extract the global proximity structure among latent non-linear features of samples, which receives much success for clustering tasks. Yu et al. [26] introduced contrastive learning and Cauchy-Schwarz (CS) divergence into multi-view subspace clustering. Cui et al. [27] introduced anchor graphs into deep subspace clustering networks. Wang et al. [28] proposed an attributed graph subspace clustering mode. However, there still exist two obvious drawbacks:

•   The only feature reconstruction constrain in the multi-view auto-encoder framework is not sufficient to accurately reveal the intrinsic structure hidden in the original multi-view data.

•   The above methods mostly exploit the first-order Laplacian matrix to guide the self-representation learning of samples while they ignore the hidden multi-order structural information of samples. High-order structures reflect the long-range neighbor relationship, which is important for mining the potential connected structure between intra-cluster samples.

Therefore, how to use the multi-order structural of the original sample for the multi-view subspace clustering task has important research significance.

In this article, we creatively present a multi-order neighborhood fusion based multi-view deep subspace clustering model to solve the above issues, which integrates the first-order and high-order Laplacian matrix of the original multi-view data into the self-expressive layer between multi-view auto-encoder framework to improve the self-expressive property. By this way, the model introduces the multi-order neighborhood relations of different views into the global consistent affinity structure learning, effectively adding some potential connections between samples in the same cluster and also reducing the connections between samples in the different clusters. Besides, the discriminative constraint is simultaneously imposed to restrict the samples belonging to different clusters.

We summarize the main contributions of this article:

•   We creatively propose a multi-view deep subspace clustering network that makes full use of the multi-order proximity structures of different views, which is obviously different from the commonly used first-order Laplacian matrix based multi-view deep clustering methods [29,30];

•   We design the multi-order neighborhood fusion module to construct an optimal multi-order Laplacian matrix, which constrains and maintains the inherent structure-property in the learned self-representation matrix;

•   We build the discriminative regularization to constrain the samples belonging to different clusters in different views far away from each other;

•   We analyze the parameter sensitivity and the convergence of the model through a series of experiments in detail, and conduct extensive experiments on six public datasets to demonstrate the superiority of the model.

The paper mainly consists of the following parts: Section 2 reviews related works. Section 3 constructs the multi-order proximity matrix. Section 4 presents the proposed multi-order neighborhood fusion based multi-view clustering model in detail. Section 5 conducts the experiments and reviews relevant analysis. Section 6 summarizes the work and looks forward to future work.

2  Related Work

This section briefly reviews the research related to multi-view subspace clustering.

2.1 Multi-View Subspace Clustering (MVSC)

The MVSC targets to study a self-representation matrix crossing latent spaces of different views, then conduct the clustering algorithm on it. Gao et al. [16] initially extended the single-view subspace clustering to MVSC, which conducts the subspace clustering on each view and unifies them into an indicator matrix. Cao et al. [17] further considered diversity to get the supplementary information of multi-view data, where the Hilbert Schmidt Independence Criterion (HSIC) was used as a diversity term. Zhang et al. [31] considered the latent representation from all views.

To solve the nonlinear features of multi-view data, a few researchers conduct the kernel model to multi-view subspace clustering [19,22,32]. Recently, Zhang et al. [33] designed a one-step clustering model to learn the unified representation. Kang et al. [34] presented the novel multi-view subspace clustering method, which uses the bipartite graph to handle large-scale data.

2.2 Multi-View Deep Subspace Clustering (MVDSC)

The MVDSC targets to study a self-representation matrix of multi-view data through neural networks. Andrew et al. [35] initially presented the deep canonical correlation analysis method (DCCA) that utilizes the neural network to learn the nonlinear mapping between two views. On this basis, Wang et al. [36] introduced the auto-encoder into above DCCA, which jointly optimizes the representation learning and the reconstruction loss.

However, such methods are limited to the two-view case and cannot handle data with three or more views. In response to this, Xu et al. [37] presented the deep multi-view concept learning method, which distinguishes the consistent and supplementary information in the multi-view data by performing the non-negative matrix factorization for each view. Inspired by deep subspace clustering and multi-modal data analysis, Abavisani et al. [38] proposed a deep multi-modal subspace clustering network to investigate various fusion methods and the corresponding network architectures. Zhu et al. [24] integrated the universality and diversity networks into a unified framework that learns the self-representation matrices in an end-to-end manner. Gao et al. [39] proposed a cross-modal subspace network architecture for DCCA, which introduces a self-expression layer in above the DCCA network to make full use of the correlation information between different modalities. Wang et al. [30] combined the global and local structure of all views with the self-representation layers to learn a unified representation matrix. Zheng et al. [40] embedded first-order neighbor matrices of different views into the multi-view representation learning. Guo et al. [41] collected the multi-view images of each action and designed the proper multi-view subspace clustering analysis method.

In the above, existing MVDSC methods seldom consider the structure information of each view or only exploit the first-order neighbor relationship, which results in poor representation capability.

3  Multi-Order Proximity Matrix

The first-order graph structure of origin data reflects the physical connection relationship between samples. As shown in Fig. 1a, sample A has three neighbors B, C, and D. The second-order proximity matrix describes the potential and deeper connection relationship, that is, samples with more shared neighbors are more likely to be the same cluster. Fig. 1b indicates that samples B, C and D have the same neighbor A, so they are more likely to belong to the same cluster. Based on the same assumptions, we explore the high-order proximity matrix to get more comprehensive and potential connection information between samples in complex scenes.

Figure 1: We briefly describe the multi-order structure information. First-order structure reflects the feature similarity between samples, and second-order structure displays the neighbor similarity between samples

Given the multi-view data X=[x1,x2,⋯,xN]T∈RN×D, where the N and D represent the amount of samples and the feature dimensionality, respectively. The adjacency matrix A∈RN×N constructed by the mKNN fashion describes the relationship between samples, and mKNN selects the K-nearest neighbors of each sample by,

Aij={κ(xi,xj)if xi and xj are mKNN,0otherwise,(1)

where κ(⋅,⋅) can be any kernel function or any distance measure method.

In general, the first-order proximity matrix reflects the feature similarity between nodes in the graph, while nodes with more shared neighbors should tend to be similar. So, the second-order proximity reflects the neighbor similarity between nodes, which is defined in the following.

Definition 1. [42] The similarity between the neighborhood structures of two vertices (u, v) is defined as their second-order proximity.

Therefore, the second-order proximity matrix A(2) can be written as,

A(2)=AA(2)

Then, the second-order Laplacian matrix can be easily constructed by,

L(2)=D(2)−A(2)(3)

where the diagonal element Dii(2)=∑j=1NAij(2).

Similarly, we extend the above second-order proximity matrix to the high-order proximity matrix to the high-order proximity matrix A(o) via,

A(o)=A(o−1)A(o−1)(4)

which is exploited in the following.

4  Methodology

Our method can be introduced from the following three parts, including multi-view encoder and decoder networks, multi-order neighborhood fusion, and discriminative learning between views. Fig. 2 shows the framework of our model.

Figure 2: A brief illustration of the model. Our model mainly includes three parts: multi-view encoder and decoder module, multi-order neighborhood fusion module, and discriminative learning between each view. Moreover, XV denotes the V-th view samples, ZV denotes the V-th view latent representation extracted by the V-th encoder network, and C represents the shared self-representation affinity matrix. The multi-view encoder and decoder networks aim to learn the ZV and C, the multi-order neighborhood fusion module aims to integrate the structure information of different orders of each view to learn a Laplacian matrix L∗, which supervises the learning of the self-representation affinity matrix C. Finally, discriminative learning aims to learn the important discriminative and complementary information between different views, which is imposed on ZV. Finally, spectral clustering is performed on C to obtain the clustering results

4.1 Motivation

Existing multi-view deep subspace clustering methods are sensitive to the quality of the latent space representation learned by the multi-view auto-encoder due to the deficiency of supervised information. To deal with this problem, some researches introduce the Laplacian regularization into the self-representation affinity matrix learning, while the performance may be limited by the predefined first-order Laplacian matrix. We owe to the first-order Laplacian matrix only reflects the local pair-wise relationship between samples, and is easily influenced by noise. To solve such issues, we propose to embed the multi-order Laplacian matrices of different views into the self-expressive layer to supervise the model learning. We briefly introduce its two main motivations:

•   We design a multi-order neighborhood fusion module to obtain an ideal multi-order Laplacian matrix that guides the global unified affinity matrix learning, which mines more potential connections between samples and effectively eliminates the negative impacts caused by wrong connections in the first-order Laplacian matrix.

•   We additionally introduce the discriminative constraints to capture the supplementary information from multi-view data.

4.2 Network Architecture

Given the multi-view data of V views 𝒳={X1,X2,⋯,XV}, the v-th view data is denoted as,

Xv={x1v,x2v,⋯,xNv}T∈RN×Dv, where N and Dv represent the amount of samples and the feature dimension, respectively. The network architecture mainly contains three components: the Encoder layer, Decoder layer and Self-representation layer.

4.2.1 Encoder Layer

Each view has its own encoder network. With the v-th view input Xv∈RN×Dv, the v-th encoder network fv(Xv;θev)→Zv linearly maps the original data Xv to the v-th latent space Zv∈RN×Mv, Mv<Dv where the parameter θev refers to the v-th encoder network fv.

4.2.2 Self-Representation Layer

The self-representation layer is shared by all encoder and decoder networks, which learns the unified self-representation matrix C by constraining the linear self-representation Zv=ZvC and other conditions.

4.2.3 Decoder Layer

Each view has its decoder network that is the opposite architecture to the previous encoder network. The v-th decoder network can be denoted as Xv~=gv(ZvC;θdv) inputs ZvC to reconstruct the v-th view data Xv~, where θdv is the network parameter of the v-th decoder network gv.

The objective function is shown as follows:

L=LR+λ1LSE+λ2LG+λ3LFL+LD(5)

where the reconstruction loss LR, the self-representaion loss LSE, the graph embedding regularization LG, the multi-order fusion LFL and the discrimination constraint LD are introduced in detail in the following subsections. λ1, λ2 and λ3 balance the importance of the corresponding loss.

4.3 Multi-View Encoder and Decoder Networks

For the reconstruction loss LR and the self-representation loss LSE, we respectively utilize one encoder to learn the latent feature representation Zv from each view data Xv, and reconstruct them Xv~ by the v-th decoder. Meanwhile we learn the shared coefficient matrix C crossing all views in the self-representation layer, which reflects the connection relationship between samples. So, we have,

LR=∑v=1V‖Xv−Xv~‖F2(6)

and

LSE=∑v=1V‖Zv−ZvC‖F2s.t.diag(C)=0.(7)

Generally speaking, LR ensures the latent representation Zv preserve as more as possible original information through the reconstruction loss between the original data and the reconstructed data. LSE fuses the latent representations {Z1,⋯,ZV} to learn the shared coefficient matrix C for the clustering task.

4.4 Multi-Order Neighborhood Fusion and Decoder Networks

The MVDSC methods rarely learn the latent structure information in the multi-view data, especially the hidden high-order neighbor relationship between samples, which results in poor structure capture capability. We believe the high-order proximity matrices can better mine the deeper connected relationship between samples. Motivated by the multi-order proximity strategy, we design a multi-order neighborhood fusion module as shown in Fig. 3, which fuses the structure of different orders of each view data.

Figure 3: The brief illustration of the multi-order neighborhood fusion. For the multi-view data 𝒳={X1,X2,⋯,XV}. We construct the first-order proximity matrix {A1(O),A2(O),⋯,AV(O)} and the high-order proximity matrix {A1(O),A2(O),⋯,AV(O)} for each view, then we separately get the A1(O),⋯,AV(O) by fusing the first-order adjacency matrix and high-order adjacency matrix of different views. So, the corresponding Laplacian matrix is L(1),…,L(O). Finally, we learn an optimal and unified Laplacian matrix L∗ from above first-order to high-order Laplacian matrix

For the original multi-view data 𝒳={X1,X2,⋯,XV}, Firstly, we construct the first-order proximity matrices, {A1(1),A2(1),⋯,AV(1)} and the high-order proximity matrices, {A1(O),A2(O),⋯,AV(O)} for each view according to Formulas (1), (2) and (4). Then, the o-order structural of different views is fused to obtain the unified o-order proximity matrix by,

A(o)=∑ijVAi(o)⊙Aj(o),o=1,⋯,O,(8)

where ⊙ represents the Hadamard product and Aj(o) denotes the o-order proximity matrix of the j-th view.

In cross-view fusion, the strong connections in one graph can be transferred to other corresponding graphs. With the help of complementary information, the similarity between samples in the same cluster should be enhanced, while the wrong connections in one graph may be disconnected or weakened. Besides, the corresponding high-order Laplacian matrix is defined as,

L(o)=D(o)−A(o),o=1,⋯,O,(9)

where the diagonal element Dii(o)=∑j=1NAij(o).

To fuse the advantages of different order data structures, we learn an optimal and unified Laplacian matrix from the above first-order to high-order Laplacian matrix, so-called multi-order neighborhood relationship. So, the multi-order fusion loss LFL is defined below:

LFL=∑o=1O‖L(o)−L∗‖1,(10)

where L∗ is the optimal Laplacian matrix, and L(o) is the Laplacian matrix corresponding to the o-order proximity matrix A(o). The ℓ1-norm ‖⋅‖1 constrains the sparsity of one matrix.

Through the multi-order neighborhood fusion loss LFL the optimized Laplacian matrix L∗ integrates a variety of neighborhood relationships of different orders, and collaboratively interacts with the edge information in the multi-order neighborhood.

To obtain an optimal self-representation affinity matrix, we integrate the multi-order graph structure information into the self-expressive layer. The learned optimal multi-order Laplacian matrix guides the learning procedure of the self-representation matrix C. So, the learned unified affinity matrix can better reflect the deeper and more comprehensive neighborhood relationships hidden in multi-view data. We formulate the multi-order Laplacian regularization as,

LG=Tr(CTL∗C),(11)

where the L∗ is the optimal Laplacian matrix learned from the Formula (10).

4.5 Discriminative Learning between Views

To study the supplementary and discriminative information between different views, the discriminative constraint LD is imposed on different views,

LD=∑ijV‖Zi⊙Zj‖1.(12)

Overall, after substituting above losses into Formula (5), it can be defined as follows:

L=∑v=1V(‖Xv−Xv~‖F2+λ1‖Zv−ZvC‖1)+λ2Tr(CTL∗C)+λ3∑o=1O‖Lo−L∗‖F2+∑ijV‖Zi⊙Zj‖1,(13)

which jointly optimizes the variables, Xv~, Zv, C and L∗. Algorithm 1 briefly shows the pseudo-code of the proposed model.

4.6 Training Procedure

The training procedure mainly consists of the following two steps.

4.6.1 First Step

Pre-training the multi-view auto-encoder network. Given the multi-view data 𝒳={X1,X2,⋯,XV}, we send it to the encoder layer to obtain the unified self-representation matrix C, then reconstruct the multi-view data 𝒳~={X1~,X2~,⋯,XV~} through the decoder layer. The parameters of encoder and decoder θev and θdv are optimized through the feature reconstruction loss LR. In addition, the learning rate is 0.001; the number of epochs is 2000; and the batch size is set to the number of samples.

4.6.2 Second Step

Updating the whole network parameters using the Formula (13). Specifically, the parameters of encoder and decoder learned in the first step are used to initialize the network. Then, the parameters θev, θdv, L∗ and C are updated by minimizing the overall objective function L.

Then, we obtain the unified self-representation matrix C and calculate the corresponding affinity matrix by,

Q=(|C|+|CT|)2.(14)

Finally, the spectral clustering is performed on the matrix Q.

4.7 Computational Complexity

Before we analyze the network complexity, we first present the necessary symbols below. For the multi-view data 𝒳={X1,X2,⋯,XV}, we denote the amount of samples and views as N and V, respectively. To streamline the calculation, the input feature dimensions of all views are consistent d. And {d1,d2,⋯,dL} represents the dimension of each view in the encoder and decoder networks, and denotes the dimension of the latent feature representation.

According to Algorithm 1, the computational complexity primarily consists of Steps 1, 3 and 5. In Step 1, the complexity is 𝒪(N3+VN2), which is related to the matrix multiplication and matrix element-wise product. In Step 3, the main operation is the matrix multiplication of each encoder-decoder layer, thus its complexity is 𝒪(VN(dd1+d1d2+⋯+dL−1dL)). In Step 5, the time complexity is 𝒪(VN2dz+N3+VNdz) due to the matrix multiplication and matrix element-wise product. Overall, the computational complexity of the model is 𝒪(VN2dz+N3).

5  Experiments

We implement a range of experiments to validate the efficiency of our method.

5.1 Experimental Settings

5.1.1 Dataset Descriptions

We choose six public and commonly used datasets from various applications, including face recognition, sensor network, gene lineage and natural language processing. The brief statistics information of the six datasets is outlined in Table 1, where V, C and N represent the amount of views, clusters, and samples, respectively. Dv denotes the number of feature dimension of the v-th view.

•   BUAA dataset [43] is composed of N=1350 images from C=150 subjects, which are collected from the near-infrared and visible light, respectively.

•   MSRCV dataset [44] is composed of N=210 images from C=7 objects, including airplanes, buildings, cows, cars, trees, bicycles, and clothes. Six type of features are extracted, i.e., CENT, CMT, GIST, HOG, LBP and SIFT.

•   CMU-PIE dataset [45] has a total of 41,386 facial images of C=68 persons captured under various illuminations, postures and expressions. We choose 21 images of each person and extract their LBP, GIST, and Gabor features form the multi-view dataset.

•   Yale Face dataset [46] is composed of N=165 grayscale images captured from C=5 persons, where each person has 11 images collected under different illuminations, postures and facial expressions. Three type of features are collected, i.e., GIST, LBP and Garbor.

•   SensIT Vehicle dataset [47] collects from the Wireless Distributed Sensor Network. It utilizes seismic sensors and acoustic to record different signals, which contains N=300 samples of C=3 clusters.

•   Prokaryotic Phyla dataset [48] is from the prokaryotic species, describing by protein composition, textual data, genetic information. It contains N=551 samples of C=4 categories.

5.1.2 Comparison Methods

To fairly consider the clustering efficiency of the model, we choose one single-view clustering baseline and nine advanced multi-view clustering baselines as comparison methods.

•   K-means [1] is applied to each view of multi-view data separately, and we report the best clustering results here.

•   Auto-Weighted Multiple Graph Learning (AMGL) [7] is a multi-graph learning framework with parameter-free, that assigns appropriate weights to each graph during learning.

•   Multi-View Learning with Adaptive Neighbors (MLAN) [49] constructs one initial graph for different view, and then fuses it to develop a unified graph for clustering.

•   Latent Multi-View Subspace Clustering (LMSC) [50] utilizes the latent representation of each view to cluster data points.

•   Deep Multi-Modal Subspace Clustering Networks (DMSCN) [38] contain three parts, i.e., multi-modal encoder, multi-modal decoder and self-expression layer. It is an important baseline.

•   Graph-based Multi-View Clustering (GMC) [51] is a multi-view fusion strategy, in which the learned unified graph optimizes the initial graph of each view.

•   Large-scale Multi-View Subspace Clustering in Linear Time (LMVSC) [34] aims to obtain a shared binary graph for spectral clustering tasks.

•   Deep Multi-View Subspace Clustering with Unified and Discriminative Learning (DMSC-UDL) [30] combines the global structure with the local structure of multi-view data to learn a better-unified connection matrix.

•   Multi-View Subspace Clustering Networks with Local and Global Graph Information (MSCNLG) [29] ingrates the local and global graph structure of multi-view data to learn a unified representation. It is an important baseline.

5.1.3 Evalution Metric

Three common metrics are chosen [52], including NMI, ACC, and ARI, to evaluate the performance of our model. NMI is an information theoretic metric based on ground-truth class labels and cluster labels, and normalizes the entropy of each class. ACC represents the proportion of correctly clustered samples to the total number of samples. ARI reflects the degree of overlap between the cluster labels and the true labels of samples. In all metrics, higher scores represent better performance.

5.1.4 Implementation Details

We use the deep learning toolbox Tensorflow 1.15 to implement the model, and conduct all experiments on the Ubuntun 18.04 platform, with NVIDIA RTX 2080s and 128 GB memory size.

The encoder and decoder networks of the model respectively contain 3 layers, and the nonlinear activation function is RELU. The Adam optimizer is selected to train the network, and the learning rate is set to 0.001. Three important parameters, i.e., λ1, λ2 and λ3 in our proposed model need to be tuned according to the specific applications, and the ideal parameters are chosen in the range {0.001, 0.01, 0.1, 1, 10, 100}.

For the BUAA dataset, the dimensions of encoder and decoder networks are set to 100 − 128 − 128 − 128 − 100 and 100−128−128 − 128 − 100, respectively, where λ1 = 0.001, λ2 = 0.01 and λ3 = 1. For the MSRCV dataset, the dimensions of encoder and decoder networks are set to 1302 − 512 − 128 −512 − 1302, 48 − 64 − 128 − 64 − 48, 512 − 256 − 128 − 256 − 512, 100 − 128 − 128 − 128 − 100, 256 − 128 − 128 − 128 − 256 and 210 − 128 − 128 − 128 − 210, respectively, where λ1 = 0.01, λ2 = 10 and λ3 = 0.001. For the CMU-PIE dataset, the dimensions of encoder and decoder networks are set to 900 − 1024 − 128 − 1024 − 900, 512 − 1024 − 128 − 1024 − 512 and 2560 − 1024 − 128 − 1024 − 2560, respectively, where λ1 = 0.001, λ2 = 1 and λ3 = 1. For the Yale Face database, the dimensions of encoder and decoder networks are set to 4096 − 1024 − 128 − 1024 − 4096, 3304 − 1024 − 128 − 1024–3304 and 6750 − 1024 − 128 − 1024 − 6750, respectively, where λ1 = 0.001, λ2 = 1 and λ3 = 0.01. For the SenIT Vehicle dataset, the dimensions of encoder and decoder networks are set to 50 − 128 − 128 − 128 − 50 and 50 − 128 − 128 − 128 − 50, respectively, where λ1 = 0.01, λ2 = 0.1 and λ3 = 1. For the Prokaryotic Phyla dataset, the dimensions of encoder and decoder networks are set to 393 − 512 − 128 − 512 − 393, 3 − 512 − 128 − 512 − 3 and 438 − 512 − 128 − 512 − 438, respectively, where λ1 = 0.001, λ2 = 1 and λ3 = 1.

We still adhere to the parameter settings in the original manuscripts for all comparison methods while using the original codes provided on the authors’ homepages. For LMSC, we set the latent representation dimension to 100, and search the optimal λ in the range {0.001, 0.01, 0.1, 1, 10, 100}. For DMSCN, we tune the optimal parameters λ1 and λ2 in the range {0.0001, 0.001, 0.01, 0.1, 1, 10, 100}. For LMVSC, we choose the ideal α in the range {0.001, 0.01, 0.1, 1, 10} and the number of anchors in the range {K, 50, 100, 200}, where K is the number of clusters. For DMSC-UDL, we set the parameter to λ1 = 0.01, and choose the optimal parameters λ2 and λ3 in the range {0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1}, respectively. As for MSCNG, we select the optimal parameters α and β in the range {0.001, 0.01, 0.1, 1, 10, 100, 10,000}.

All experiments are conducted 20 times to confirm the generality and equity, and the average values and square differences are calculated as the final results.

5.2 Experiment Results

Tables 2–4 summarize the performance of NMI, ACC and ARI on six public datasets, respectively. Besides, we use bold and underline to show the best and second-best results.

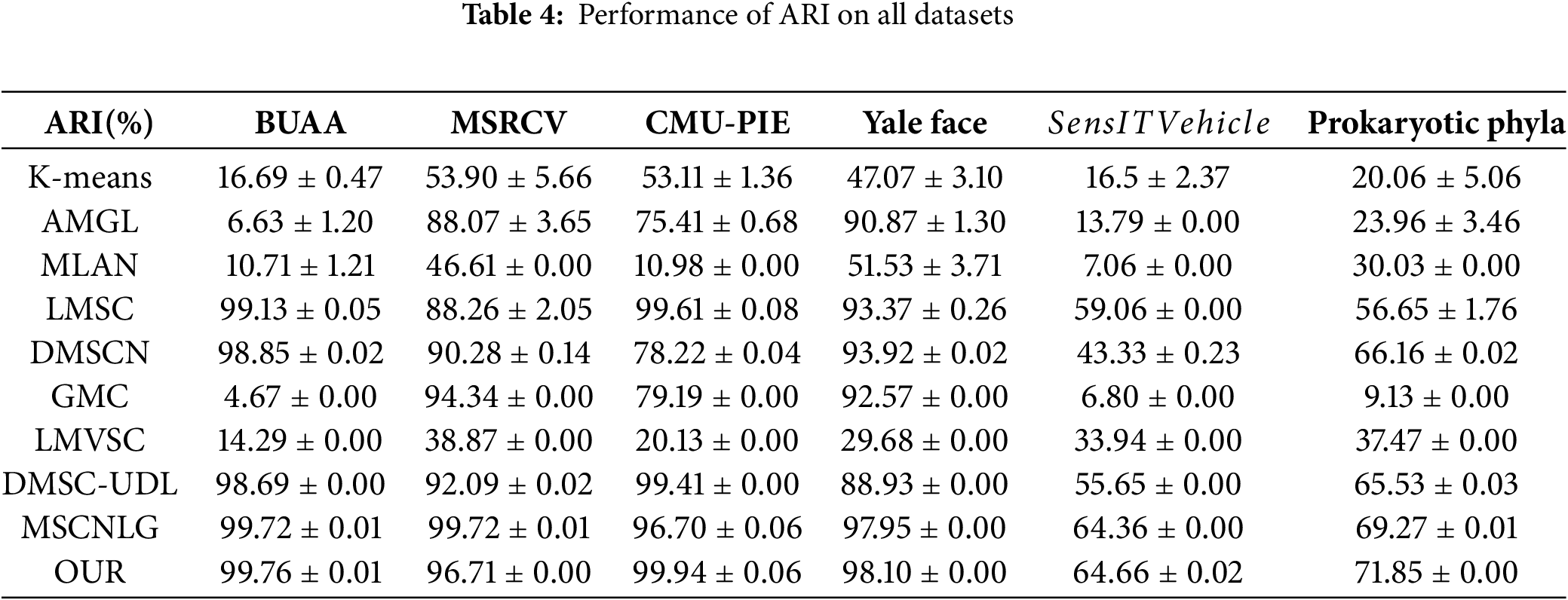
Obviously, in most cases, the proposed model provides the best results on all datasets. In particular, the clustering results on CMU-PIE and Yale Face datasets are close to 100%. The following conclusions are drawn from such tables:

1.    From a holistic perspective, deep multi-view methods consistently outperform traditional multi-view methods. The neural network adaptively learns the nonlinear and deeper feature information from the original data, so that the neural network improves the clustering results.

2.    Our model notably outperforms the K-means clustering results on all datasets, which demonstrates that the model extracts more heterogeneous information from different views and properly fuses it.

3.    Compared with several multi-view deep clustering methods learning the unified self-representation matrix from multi-view data, i.e., DMSCN and DMSC-UDL, our proposed model achieves the obvious promotions on BUAA, MSRCV, CMU-PIE and Yale Face datasets, demonstrating the effectiveness of the fused multi-order graph structure information.

4.    In certain aspects, the K-means clustering is even marginally superior to the multi-view methods, illustrating that several views contain the obvious discrimination information and how to explore the complementary information between views effectively is also a critical problem.

In general, the experiment results provide a complete verification of the excellence of the model. Unlike other multi-view deep subspace clustering methods, our model incorporates both the first-order and the hidden high-order neighborhood connection information in the unified self-representation affinity matrix learning, which notably improves the clustering results.

5.3 Convergence Analysis

In this section, we analyze the convergence of the model and visualize the objective function value of each iteration on six public datasets in Fig. 4, where the x-axis represents the amount of iterations and the y-axis represents the objective function value. We can see that for the entire dataset, our model converges quickly in less than 100 epochs.

Figure 4: The convergence curves of the model for all datasets

5.4 Parameter Analysis

As we mentioned before, three hyper-parameters, i.e., λ1, λ2 and λ3 require sensitivity analysis in our model. We plot the clustering results of our model with different parameters on Yale Face and MSRCV datasets in Fig. 5 to choose the optimal parameters, where we tune parameters λ1 = {0.001, 0.1, 10}, λ2 = {0.001, 0.01, 0.1, 1, 10, 100} and λ3 = {0.001, 0.01, 0.1, 1, 10, 100}. Obviously, our proposed model is robust to these parameters.

Figure 5: The parameter analysis of the model on Yale Face and MSRCV datasets

5.5 The Optimal Order-Number

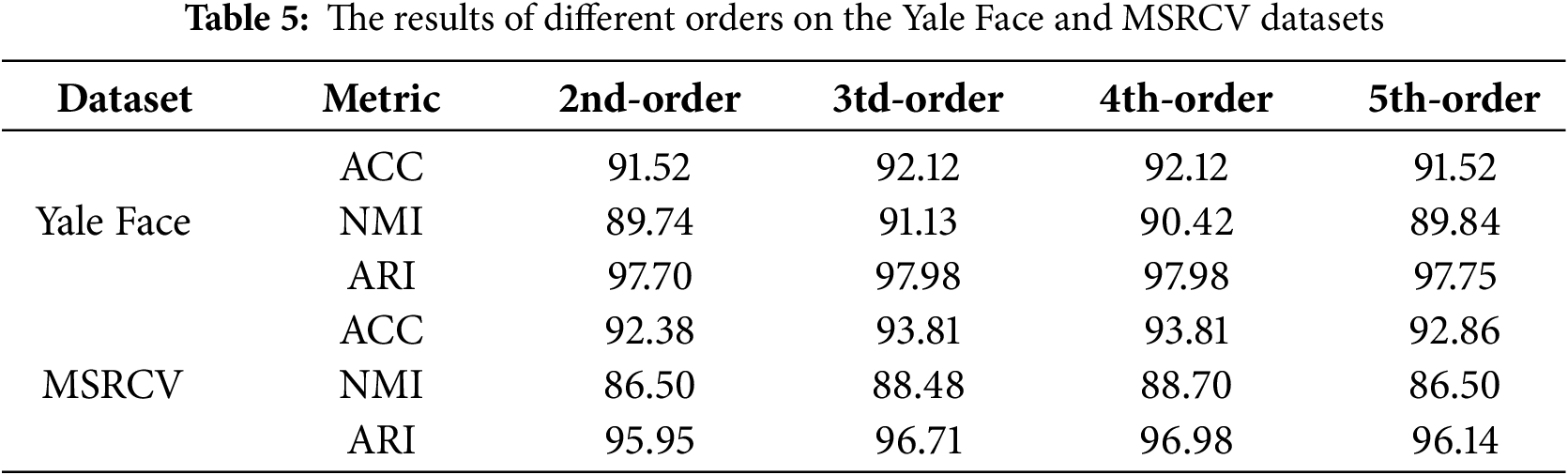
To explore the effects of different-order neighborhood information, we conduct experiments on 2nd-order, 3rd-order, 4th-order and 5th-order proximity matrices on Yale Face and MSRCV datasets, respectively. From Table 5 we can see, when the order of the proximity matrix increases, the range of the neighborhood becomes large and the clustering performance of the corresponding model begins to decline. Finally, we set the order number to 3 in all experiments.

5.6 Ablation Experiment

To further test the efficiency of the multi-order neighborhood information and the discriminative constraint, we implement ablation experiments on Yale Face and MSRCV datasets. The ablation experiment results as shown in Table 6.

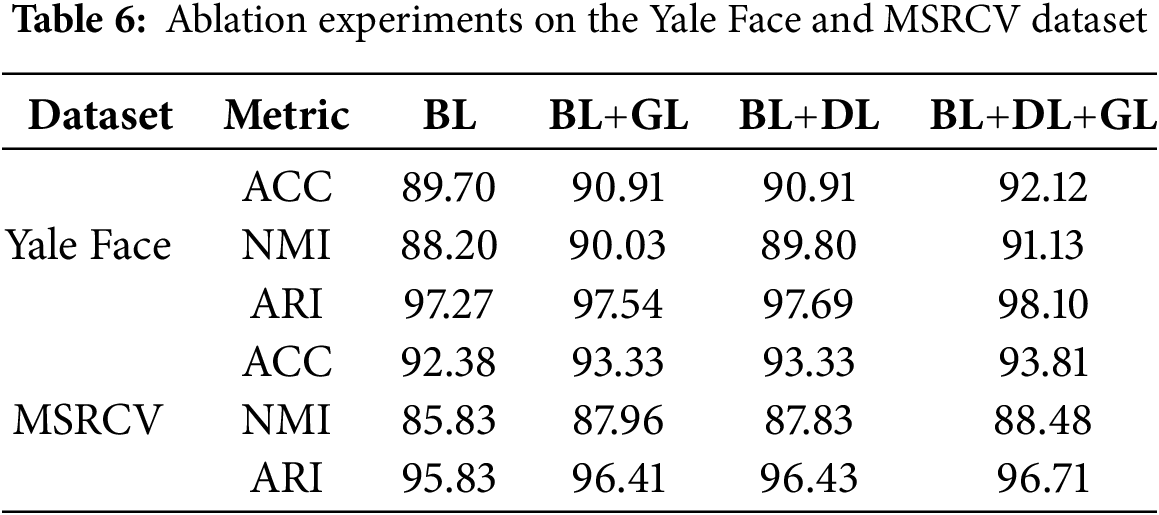
•   BL means the baseline, i.e., the multi-view encoder and decoder networks (LR+LSE).

•   GL denotes the multi-order neighborhood fusion mechanism (LG+LFL).

•   DL represents the discriminative constraint (LD).

From Table 6, we can see that both multi-order neighborhood fusion mechanism and discriminative constraint obviously improve the clustering performance of the proposed model. Besides, by combining two designs, the proposed model improves NMI by about 3% compared to the baselines.

6  Conclusion

In this article, we creatively design a multi-order neighborhoods fusion based multi-view deep subspace clustering model. By integrating the deep connection relationship of different order neighborhoods to guide the learning of one ‘‘good” unified self-representation for clustering tasks. An additional discrimination constraint is introduced to consider the supplementary information between views. It is worth noting that we showed that fusing the multi-order proximity matrix of different views can not only maintain the underlying structure but also improve the clustering performance, and creatively proposed a multi-order neighborhoods fusion method. A set of ablation experiments is designed to demonstrate the stability and efficiency of the model. A range of experiments verify that our method performs better than the advanced multi-view clustering methods. The weakness of our method is that the complexity is still a bit high, and future directions include reducing the computational overhead and adapting to incomplete multi-view clustering.

Acknowledgement: We sincerely appreciate every anonymous reviewer who generously invested their valuable time and energy. Their profound professional insights and constructive suggestions played a vital role in improving the academic level and research quality of the manuscript.

Funding Statement: The research project is partially supported by the National Key R&D Program of China (2023YFC3304600).

Author Contributions: The authors affirm their respective contributions to the manuscript as detailed below: study conception and design: Kai Zhou and Boyue Wang; code and experiment: Kai Zhou and Yanan Bai; draft manuscript preparation: Kai Zhou, Yanan Bai, Boyue Wang and Yongli Hu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used within this article are accessible to interested parties by contacting the corresponding authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Macqueen J. Some methods for classification and analysis of multivariate observations. In: Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability; 1967; Oakland, CA, USA: University of California Press. [Google Scholar]

2. A Ng, M Jordan, Y Weiss. On spectral clustering: analysis and an algorithm In: Advances in Neural Information Processing Systems 14; Phoenix, Arizona, USA; 2001. [Google Scholar]

3. Elhamifar E, Vidal R. Sparse subspace clustering: algorithm, theory, and applications. IEEE Trans Pattern Anal Mach Intell. 2013;35(11):2765–81. doi:10.1109/TPAMI.2013.57. [Google Scholar] [PubMed] [CrossRef]

4. Dalal N, Triggs B. Histograms of oriented gradients for human detection. In: 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05); 2005; San Diego, CA, USA. p. 886–93. [Google Scholar]

5. Lowe DG. Distinctive image features from scale-invariant keypoints. Int J Comput Vis. 2004;60:91–110. doi:10.1023/B:VISI.0000029664.99615.94. [Google Scholar] [CrossRef]

6. Oliva A, Torralba A. Modeling the shape of the scene: a holistic representation of the spatial envelope. Int J Comput Vis. 2001;42:145–75. doi:10.1023/A:1011139631724. [Google Scholar] [CrossRef]

7. Wang R, Nie F, Wang Z, Hu H, Li X. Parameter-free weighted multi-view projected clustering with structured graph learning. IEEE Trans Knowl Data Eng. 2019;32(10):2014–25. doi:10.1109/TKDE.2019.2913377. [Google Scholar] [CrossRef]

8. Huang S, Xu Z, Tsang IW, Kang Z. Auto-weighted multi-view co-clustering with bipartite graphs. Inf Sci. 2020;512:18–30. doi:10.1016/j.ins.2019.09.079. [Google Scholar] [CrossRef]

9. Zhan K, Nie F, Wang J, Yang Y. Multiview consensus graph clustering. IEEE Trans Image Process. 2019;28(3):1261–70. doi:10.1109/TIP.2018.2877335. [Google Scholar] [PubMed] [CrossRef]

10. Hu Y, Song Z, Wang B, Gao J, Sun Y, et al. AKM3C: adaptive k-multiple-means for multi-view clustering. IEEE Trans Circuits Syst Video Technol. 2021;31(11):4214–26. doi:10.1109/TCSVT.2020.3049005. [Google Scholar] [CrossRef]

11. Lu Y, Wang L, Lu J, Yang J, Shen C. Multiple kernel clustering based on centered kernel alignment. Pattern Recognit. 2014;47(11):3656–64. doi:10.1109/TCSVT.2021.3119956. [Google Scholar] [CrossRef]

12. Tzortzis G, Likas A. Kernel-based weighted multi-view clustering. In: 2012 IEEE 12th International Conference on Data Mining; 2012; Brussels, Belgium. p. 675–84. [Google Scholar]

13. Liu J, Cao F, Gao X, Yu L, Liang J. A cluster-weighted kernel k-means method for multi-view clustering. In: Proceedings of the AAAI Conference on Artificial Intelligence; 2020; New York City, New York, NY, USA. p. 4860–7. [Google Scholar]

14. Zhang P, Yang Y, Peng B, He M. Multi-view clustering algorithm based on variable weight. In: International Joint Conference on Rough Sets; 2017; Springer; Olsztyn, Poland; p. 599–610. [Google Scholar]

15. Lan M, Meng M, Yu J, Wu J. Generalized multi-view collaborative subspace clustering. IEEE Trans Circuits Syst Video Technol. 2021;32(6):3561–74. doi:10.1109/TCSVT.2021.3119956. [Google Scholar] [CrossRef]

16. Gao H, Nie F, Li X, Huang H. Multi-view subspace clustering. In: Proceedings of the IEEE International Conference on Computer Vision; 2015; Santiago, Chile; p. 4238–46. [Google Scholar]

17. Cao X, Zhang C, Fu H, Liu S, Zhang H. Diversity induced multi-view subspace clustering. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2015; Boston, MA, USA; p. 586–94. [Google Scholar]

18. Luo S, Zhang C, Zhang W, Cao X. Consistent and specific multi-view subspace clustering. In: Proceedings of the AAAI Conference on Artificial Intelligence; 2018; New Orleans, LA, USA. Vol. 32. [Google Scholar]

19. Zhang G-Y, Chen X-W, Zhou Y-R, Wang C-D, Huang D, He X-Y. Kernelized multi-view subspace clustering via auto-weighted graph learning. Appl Intell. 2022;52(1):716–31. [Google Scholar]

20. Wang R, Wang P, Wu D, Sun Z, Nie F, Li X. Multi-view and multi-order structured graph learning. IEEE Trans Neural Netw Learn Syst. 2024;35(10):14437–48. doi:10.1109/TNNLS.2023.3279133. [Google Scholar] [PubMed] [CrossRef]

21. Wang Z, Lin Q, Ma Y, Ma X. Local high-order graph learning for multi-view clustering. IEEE Trans Big Data. 2024 Jan;PP:1–14. doi:10.1109/TBDATA.2024.3433525. [Google Scholar] [CrossRef]

22. Sun M, Wang S, Zhang P, Liu X, Guo X, Zhou S, et al. Projective multiple kernel subspace clustering. IEEE Trans Multimed. 2021;24(4):2567–79. doi:10.1109/TMM.2021.3086727. [Google Scholar] [CrossRef]

23. Ji P, Zhang T, Li H, Salzmann M, Reid I. Deep subspace clustering networks. In: 31st Conference on Neural Information Processing Systems (NIPS 20172017; Long Beach, CA, USA. [Google Scholar]

24. Zhu P, Yao X, Wang Y, Hui B, Du D, Hu Q. Multi-view deep subspace clustering networks. arXiv:1908.01978. 2019. [Google Scholar]

25. Chen Z, Ding S, Hou H. A novel self-attention deep subspace clustering. Int J Mach Learn Cybern. 2021;12(8):2377–87. doi:10.1007/s13042-021-01318-4. [Google Scholar] [CrossRef]

26. Yu X, Yi J, Chao G, Chu D. Deep contrastive multi-view subspace clustering with representation and cluster interactive learning. IEEE Trans Knowl Data Eng. 2024;37(1):1–12. doi:10.1109/TKDE.2024.3484161. [Google Scholar] [CrossRef]

27. Cui C, Ren Y, Pu J, Pu X, He L. Deep multi-view subspace clustering with anchor graph. arXiv:2305.06939, 2023. [Google Scholar]

28. Wang L, En Z, Wang S, Guo X. Attributed graph subspace clustering with graph-boosting. In: Asian Conference on Machine Learning; 2023; Istanbul, Turkey: PMLR. p. 723–38. [Google Scholar]

29. Zheng Q, Zhu J, Ma Y, Li Z, Tian Z. Multi-view subspace clustering networks with local and global graph information. Neurocomputing. 2021;449(4):15–23. doi:10.1016/j.neucom.2021.03.115. [Google Scholar] [CrossRef]

30. Wang Q, Cheng J, Gao Q, Zhao G, Jiao L. Deep multi-view subspace clustering with unified and discriminative learning. IEEE Trans Multimed. 2020;23:3483–93. doi:10.1109/TMM.2020.3025666. [Google Scholar] [CrossRef]

31. Zhang C, Fu H, Hu Q, Cao X, Xie Y, Tao D, et al. Generalized latent multi-view subspace clustering. IEEE Trans Pattern Anal Mach Intell. 2018;42(1):86–9. doi:10.1109/TPAMI.2018.2877660. [Google Scholar] [PubMed] [CrossRef]

32. Zhang G, Zhou Y, He X, Wang C, Huang D. One-step kernel multi-view subspace clustering. Knowl Based Syst. 2020;189(1):105–26. doi:10.1016/j.knosys.2019.105126. [Google Scholar] [CrossRef]

33. Zhang P, Liu X, Xiong J, Zhou S, Zhao W, Zhu E, et al. Consensus one-step multi-view subspace clustering. IEEE Trans Knowl Data Eng. 2020;34(10):4676–89. [Google Scholar]

34. Kang Z, Zhou W, Zhao Z, Shao J, Han M, Xu Z. Large-scale multi-view subspace clustering in linear time. In: Proceedings of the AAAI Conference on Artificial Intelligence; 2020; New York City, New York, NY, USA. p. 4412–9. [Google Scholar]

35. Andrew G, Arora R, Bilmes J, Livescu K. Deep canonical correlation analysis. In: International Conferenceon Machine Learning; 2013; Atlanta, GA, USA: PMLR. p. 1247–55. [Google Scholar]

36. Wang W, Arora R, Livescu K, Bilmes J. On deep multi-view representation learning. In: International Conference on Machine Learning; 2015; Lille, France: PMLR. p. 1083–92. [Google Scholar]

37. Xu C, Guan Z, Zhao W, Niu Y, Wang Q, Wang Z. Deep multi-view concept learning. In: Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence (IJCAI-18); 2018; Stockholm, Sweden. p. 2898–904. [Google Scholar]

38. Abavisani M, Patel V. Deep multimodal subspace clustering networks. IEEE J Sel Top Signal Process. 2018;12(6):1601–14. doi:10.1109/JSTSP.2018.2875385. [Google Scholar] [CrossRef]

39. Gao Q, Lian H, Wang Q, Sun G. Cross-modal subspace clustering via deep canonical correlation analysis. In: Proceedings of the AAAI Conference on Artificial Intelligence; 2020. p. 3938–45. doi:10.1609/aaai.v34i04.5808. [Google Scholar] [CrossRef]

40. Zheng Q, Zhu J, Li Z, Tang H. Graph-guided unsupervised multiview representation learning. IEEE Trans Circuits Syst Video Technol. 2022;33(1):146–59. doi:10.1109/TCSVT.2022.3200451. [Google Scholar] [CrossRef]

41. Guo D, Li K, Hu B, Zhang Y, Wang M. Benchmarking micro-action recognition: dataset, method, and application. IEEE Trans Circuits Syst Video Technol. 2024;PP(99):1. doi:10.1109/TCSVT.2024.3358415. [Google Scholar] [CrossRef]

42. Zhou S, Liu X, Liu J, Guo X, Zhao Y, Zhu E, et al. Multi-view spectral clustering with optimal neighborhood laplacian matrix. In: Proceedings of the AAAI Conference on Artificial Intelligence; 2020; New York City, New York, NY, USA. p. 6965–72. [Google Scholar]

43. Shao M, Fu Y. Hierarchical hyper lingual-words for multi-modality face classification. In: 2013 10th IEEE International Conference and Workshops on Automatic Face and Gesture Recognition (FG); 2013; Shanghai, China. p. 1–6. [Google Scholar]

44. Xu J, Han J, Nie F. Discriminatively embedded k-means for multi-view clustering. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2016; Las Vegas, NV, USA. p. 5356–64. [Google Scholar]

45. Sim T, Baker S, Bsat M. The CMU pose, illumination and expression database of human faces. Carnegie Mellon University. Technical Report CMU-RI-TR-OI-02, 2001. [Google Scholar]

46. Cai D, He X, Hu Y, Han J, Huang T. Learning a spatially smooth subspace for face recognition. In: 2007 IEEE Conference on Computer Vision and Pattern Recognition; 2007; Minneapolis, MN, USA. p. 1–7. [Google Scholar]

47. Chang C-C. A library for support vector machines. 2001 [cited 2024 Nov 28]. Available from: http://www.csie.ntu.edu.tw/. [Google Scholar]

48. Brbi’c M, Piškorec M, Vidulin V, Kriško A, Šmuc T, Supek F. The landscape of microbial phenotypic traits and associated genes. Nucleic Acids Res. 2016;44(21):gkw964. doi:10.1093/nar/gkw964. [Google Scholar] [PubMed] [CrossRef]

49. Nie F, Cai G, Li X. Multi-view clustering and semi-supervised classification with adaptive neighbours. In: Proceedings of the AAAI Conference on Artificial Intelligence; 2017; San Francisco, CA, USA. Vol. 31. [Google Scholar]

50. Zhang C, Hu Q, Fu H, Zhu P, Cao X. Latent multi-view subspace clustering. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2017; Honolulu, HI, USA. p. 4279–87. [Google Scholar]

51. Wang H, Yang Y, Liu B. GMC: graph-based multi-view clustering. IEEE Trans Knowl Data Eng. 2019;32(6):1116–29. [Google Scholar]

52. Jia Y, Liu H, Hou J, Kwong S, Zhang Q. Multi-view spectral clustering tailored tensor low-rank representation. IEEE Trans Circuits Syst Video Technol. 2021;31(12):4784–97. [Google Scholar]