Optimizing AES S-Box Implementation: A SAT-Based Approach with Tower Field Representations

1  Introduction

Information security is crucial in the Internet of Things (IoT) [1,2], particularly in healthcare, transportation, and smart cities. Cryptography plays a key role in protecting the security of IoT data. However, IoT devices have limitations in computational, storage, and energy. Improving the efficiency of cryptographic implementations in terms of area, delay, and power consumption has become a critical challenge. As a dominant encryption, the performance requirements (such as low area and low delay) for AES [3] implementation have become increasingly urgent. The AES consists of four subfunctions: SubBytes (S-box), ShiftRows, MixColumns, and AddRoundKey. As a core component, the implementation of the S-box directly affects the circuit area and delay of the AES implementations [4–6]. Therefore, the goal of this paper is to improve the area and delay of the S-box implementation, thereby enhancing the performance of the AES implementation.

The AES S-box involves the inversion over and an affine transformation over . Since 2001, many approaches have been proposed to reduce the area and delay of the inversion circuit over . These approaches typically use tower field algorithms, which decompose as or . Tower field algorithms also include the selection of basis, e.g., polynomial basis (PB), normal basis (NB), Polynomial Ring Representation (PRR), or redundantly represented basis (RRB). In 2001, Rudra et al. [7] proposed an S-box implementation based on and Satoh et al. [8] optimized isomorphic mappings using a greedy algorithm and proposed an S-box implementation based on and PB. In 2005, Canright [9] proposed a tree search algorithm to eliminate the redundancy of the method in [8], and demonstrated -type S-box implementations based on different PB and NB. To get more isomorphic matrices, mixed bases was first used in [10,11]. Nogami et al. [10] proposed a -type S-box implementation based on NB and PB. Nekado et al. [11] proposed a -type S-box implementation with NB and RRB. However, these optimizations had non-cancellable property. Boyar et al. proposed two -type S-box implementations using cancellable heuristic methods. One minimizes area [12] and the other minimizes depth [13]. Ueno et al. introduced a mixed bases (NB, PRR and RRB) representation [14], and used multiplication offsets [15] to optimize the area and depth of -type S-box. Reyhani et al. proposed a small depth implementation of the NB-based -type S-box using cancellable Focused-Search heuristics [16]. Subsequently, they proposed an area-minimized implementation of -type S-box by extending logic gates [17]. Recently, multiplicative and exponential offsets were applied to optimize and -type S-boxes [18,19]. For -type S-box, Maximov et al. [18] proposed three implementations (small area, fast, and trade-off) based on NB. For -type S-box, Nakashima et al. [19] introduced two implementation variants (small area and fast) with NB, PRR and RRB. Additionally, several implementations [20,21] for resisting side-channel attacks have been proposed to improve security. Analysis of the above implementations, [18] and [19] are the most efficient implementations for and -type AES S-boxes, respectively.

Nowadays, the methods for optimizing combinational logic mainly include heuristic [22,23] and SAT-based methods [24,25]. The above AES S-box implementations are mainly based on heuristics. Heuristics provide satisfactory results, but they may not necessarily achieve the optimal results. Specifically, these heuristics primarily rely on 2-input logic gates. In fact, 3-input and 4-input logic gates (such as NOR3, OA21, MOAI) can also be used to optimize AES S-box. SAT-based methods includes more logic gate types than heuristics. Using more logic gate types can improve the performance of AES S-box. Although SAT-based methods cannot directly optimize the entire circuit of AES S-box, they can provide better optimization results in certain criticals (e.g., the inversion over , and the transformation matrix) for AES S-box.

Therefore, to enhance the performance of AES S-box, we combine SAT-based methods with field-tower approachs using a greater variety of logic gate types. This combination optimizes the implementations of -type S-box with NB and -type S-box with PB, PRB and RRB, as proposed in [18,19]. We first decompose the field-tower structures into smaller functions, such as the top/bottom matrix multiplications TL/BL, multiplication and addition Mul-(Sum), and inversion over . Then, SAT models for each component are designed to search for their optimized implementations. Finally, novel S-box implementations are proposed based on these implementations. The main contributions are as follows.

(1)   A novel SAT-based method (GEC model with more logic gate types) is proposed to optimize the inversion over for the above two types S-boxes. For the -type AES S-box, our small area implementation of the inversion over requires 15.33 GE, which is 31.35% smaller than [18]. For -type S-box, our small area implementation of the inversion over requires 23.00 GE, which corresponds to a reduction by 36.02% compared to [19].

(2)   Novel SAT-based methods using local solutions (LocalBGC and LocalGEC models) are introduced to optimize the implementations of TL/BL and Mul(-Sum). For -type AES S-box, a smaller area implementation of TL0 has been found that requires one XOR gate less and has the same depth compared to [18]. For -type, our minimum area implementations of TL1 and BL1 require 42.00 and 52.00 GE, respectively, which is 22.22% and 7.14% less than [19]. Moreover, our minimized area implementation of Mul(-Sum) requires 35.00 GE, which is 24.81% less than [19].

(3)   A comprehensive strategy (i.e., creating modules of different logic gate types using Verilog or setting comprehensive constraints) is proposed to avoid the automatic optimization of Synopsys Design Compiler. This automatic optimization may alter the logic gate types and structures of the original AES S-box designs. Additionally, the implementations and evaluations of -type and -type S-boxes with two variants (a small area variant and a high speed variant) are presented.

The performed synthesized experiments demonstrate that, when the area is considered, the area of the proposed -type small area variant is 171.00 GE, which is 18.57% smaller than the minimum area implementation in [19]. When the delay or AET is considered, The delay and AET of the proposed -type fast variant are 0.69 ns and 148.58 GE ns, respectively. Compared to the implementations with the best delay or AET in [19], it has been optimized by 41.03% and 43.36%, respectively. Considering the impact of automatic optimization of Synopsys Design Compile on the implementation results presented in [19], the works of [15–19] were also implemented and synthesized under the above comprehensive strategy. The implementation results of the proposed circuit structures were also compared with these implementation results of [15–19]. When considering implementation area, the small area variant of -type S-box achieves a smallest area, which is 3.93% smaller than the current minimum area implementation [18]. And the AET and energy of the small area variant reduced by 4.65% and 5.28% respectively compared to [18]. When delay, AET or energy is considered, the proposed -type fast variant has a better performance. For instance, the AET is reduced 2.71% compared to the best implementations in [15–19].

Summarizing the above experimental results, compared to the most efficient implementations [18,19], the proposed -type S-box, with two variants (small area and fast), has better implementation performance. To our knowledge, the small area variant of -type S-box sets new area records, and the fast variant of -type S-box sets new AET and energy consumption records. The source codes of our implementations are available online1, whereas the results are summarized in Section 4.

2  Theoretical Background and SAT-based Optimization Methods

2.1 A Tower Field Representation of AES S-Box

Fig. 1 shows the implementation process of the AES S-box based on a tower field representation. The main idea is that an element U in is first transformed, using the so-called isomorphic mapping matrix, so that it can be represented as an element of . Then, the inversion over (alternatively of ) is calculated. This inversion involves four 4-bit multiplications, two 4-bit XO Rings, one 4-bit Square, and the inversion over operations, as shown in Fig. 1b. As the last step, the computed result over is transformed so that it belongs to , and the output R of the AES S-box is obtained through the affine transformation .

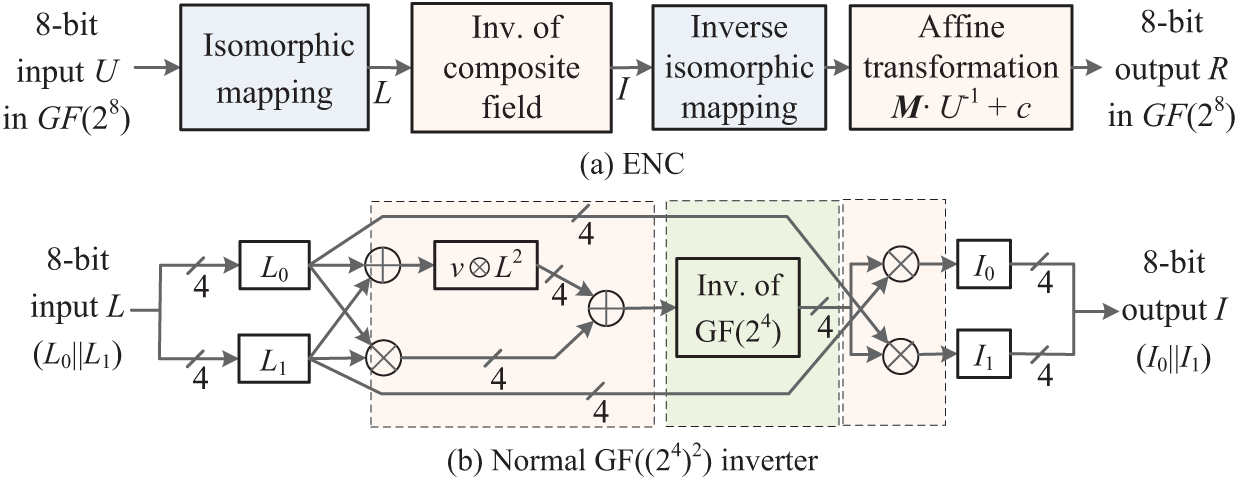
Figure 1: The computing process of the S-box using a tower of fields

Fig. 1 depicts quite a standard implementation. In recent works, the isomorphic mapping matrix representations of the S-boxes of -type and -type are extended using multiplicative and exponential offsets, respectively [18,19]. The multiplicative offset method calculates the inversion using , where () is a constant on . On the other hand, the method using exponential offset computes the inversion as , where is an integer, . The combination of multiplicative and exponential offsets can increase the cardinality of matrix representations by a factor 2040 (). The ultimate goal of these methods is to find a minimal implementation of the linear transformation matrix.

2.2 Boolean Satisfiability (SAT)

The main idea behind SAT-based methods is to establish a series of Boolean expressions between the inputs/outputs of the logic circuits, and use SAT solvers to search for optimal implementations. To optimize the implementation of logic circuits, Feng et al. [25] proposed three models: Bit-Slice Gate Complexity (BGC), Gate Equivalent Complexity (GEC), and local solutions models (LocalBGC and LocalGEC), for different design goals in moderately complex circuits. For instance, the GEC model is employed when searching for those implementations that use K logic gates, G gate equivalents (GE) or/and depth level D, for a circuit with inputs and outputs. The encoding process of this model is as follows:

First, define the inputs as , the outputs as , and assign their values based on the circuit.

Then, the encoding between the inputs and outputs of the circuit is established through the inputs and outputs, denoted by Q and T respectively of K logic gates.

Encoding gate inputs Q: For the -th gate , the input is one of the inputs and the gates’ outputs , as shown in Eq. (1).

(1)

Encoding outputs T and Y: The GEC model includes NOT and 2-, 3-, 4-input logic gates, and the encoding of the -th logic gate is given as in Eq. (2), where if then else endif, and is the -th bit of . is used to choice the logic gates. 15 logic gates are introduced, e.g., when then the logic gate is a 2-input XOR, i.e., . The encoding is given below:

(2)

The outputs is constrained as one of the K gates outputs , as shown in Eq. (3).

(3)

Finally, the area (the areas of K logic gates) of the circuit is constrained to be less than G using

(4)

where represents GE required for logic gate in library, see [25] for details.

Take a circuit with 2 inputs ( 0 × 6088, 0 × 9544) and 1 output ( 0 × 0A33) as an example, when searching for the implementations of this circuit that require logic gates and G GE, the GEC model described in CVC language2 is shown in Example 1. This encoding is saved as a CVC file, and solved using “stp./*.CVC – cryptominisat” command. In this command, STP (Satisfiability Theory Prover) solvers convert the CVC file into the corresponding logical formula and CryptoMiniSat solvers are used to solve this SAT problem. Finally, if the model has a solution, each variable will be listed. Otherwise, return Invalid.

The encoding of BGC is similar to that of GEC. The only difference lies in the encoding of the inputs/outputs of logic gates. BGC only includes XOR, OR, AND, and NOT, imposing constraints on the number of logic gate types. The encoding of a search model based on local solutions (LocalBGC/LocalGEC) is similar to the encoding of BGC/GEC models, except that it first finds a solution of partial outputs and then searches for a solution of the remaining outputs based on the found partial solution.

3  SAT-Based Optimization of AES S-Box Implementations

The implementation method of -type S-box was studied. And an area/speed-optimized method for -type AES S-box using SAT solvers was proposed, as shown in Fig. 2. From Fig. 1, it can be seen that only multiplication and inversion are nonlinear operations. Moreover, some linear operations are also included in multiplication operation. Therefore, the optimized method decomposes the implementation of AES S-box into some functions using the method [18]. All linear operations before/after the multiplication are defined as top/bottom linear matrices TL0/BL0 (as shown in Eq. (5)). The inversion over is a function with a 4-bit input and a 4-bit output, and its lookup table representation is shown in Table 1. Mul-Sum is a function with a 18-bit input and a 4-bit output, while 2Mul is a function with a 22-bit input and a 18-bit output. The detail of Mul-Sum and 2Mul can be found in [18]. The SAT-based methods are used to search for (sub)optimal solutions of each function. A GEC model is first used to search for a smaller area (or low depth) implementation of the inversion over . Afterwards, the LocalBGC and LocalGEC models are used to search for smaller area/depth implementations for TL0/BL0 and Mul(-Sum), respectively, as these functions involve more inputs and outputs.

(5)

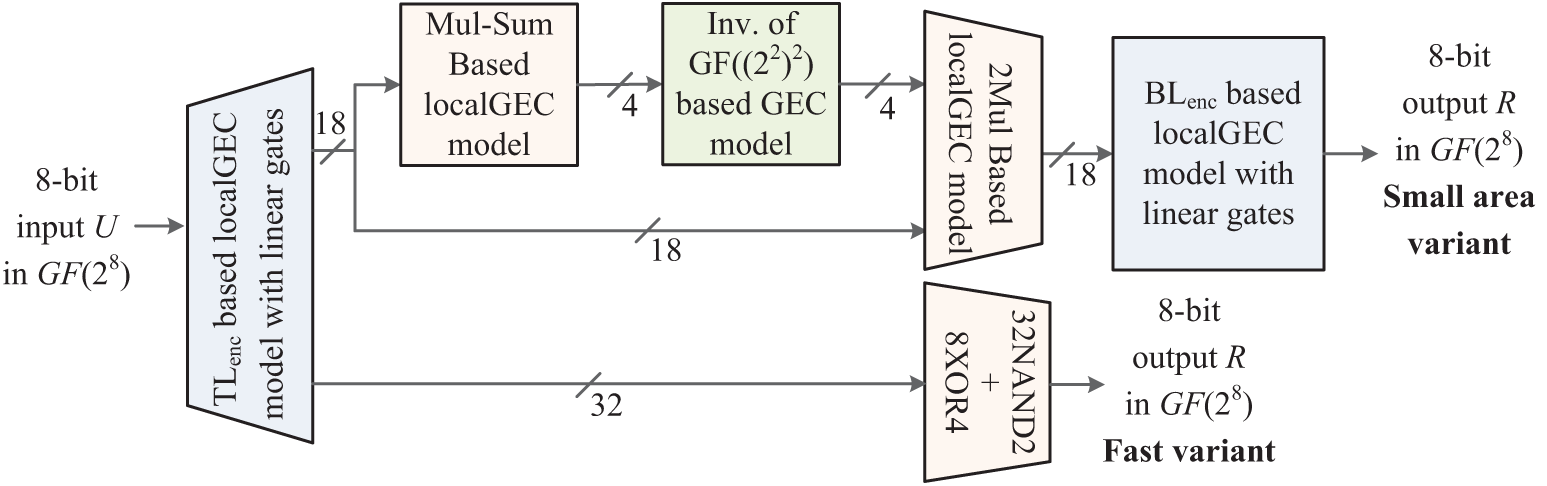
Figure 2: Optimized method for -type AES S-box using SAT

Meanwhile, the SAT-based method was also applied on the circuit structure of -type S-box in [15]. And an area/speed-optimized method of -type S-box was proposed, as shown in Fig. 3. All linear operations (e.g., isomorphic mapping matrix, exponential offset, multiplicative offset and H/L/F functions, see [15] for details) before/after the multiplication are also defined as top/bottom linear matrices TL1/BL1 (as shown in Eq. (6)). The inversion over based on RRB is a function with a 5-bit input and a 5-bit output, and its lookup table representation is shown in Table 2. The GEC, LocalBGC and LocalGEC models are used to search for smaller area/depth implementations of the inversion over based RRB, TL1/BL1 and Mul(-Sum), respectively.

(6)

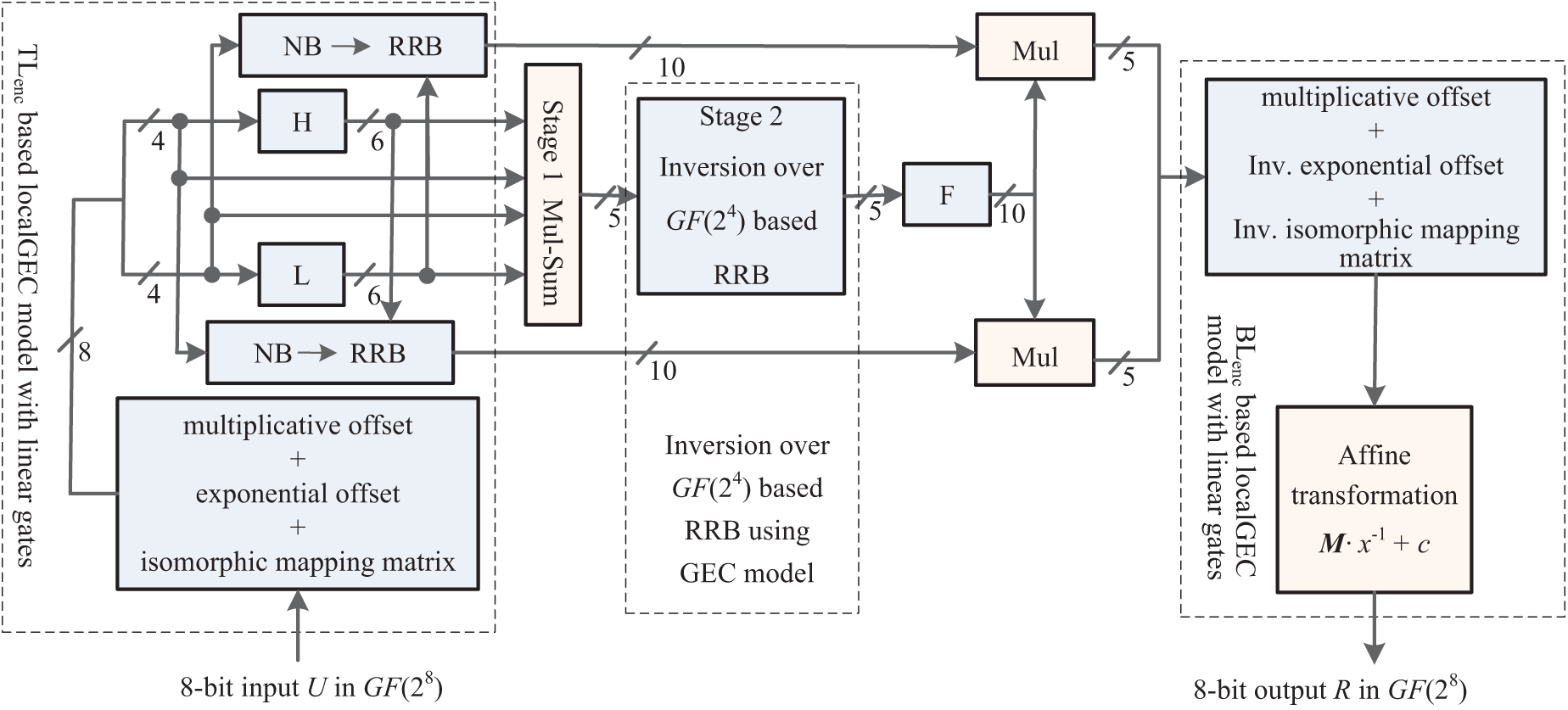
Figure 3: Optimized method for -type AES S-box using SAT

Furthermore, to optimize the implementation of the above functions based on more logic gates, the logic gate types used in the GEC/LocalGEC model have been further extended, as shown in Table 3. And for a fair comparison, the (sub) optimal solutions of each function have been searched based on Nangate 45 nm Open Cell Library. Moreover, to ensure the optimization implementation adopts the logic gate types in Table 3, a constraint has been added to the new GEC/LocalGEC model, as shown in Eq. (7). The specific search processes for different operations are described as below:

(7)

3.1 Inversion over GF(24)

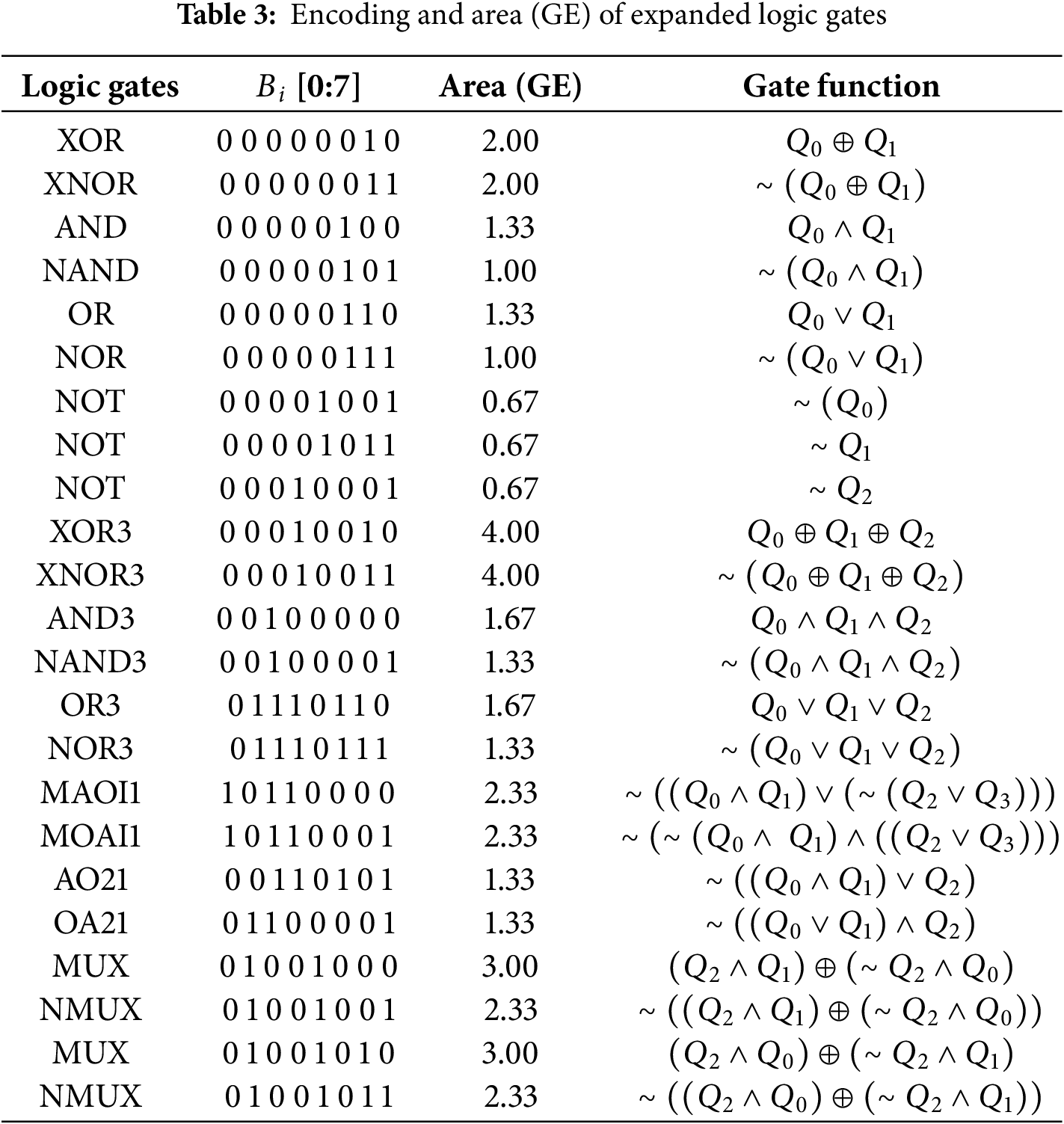
For instance, minimizing the implementation area, the specific process of using the GEC model to search for (sub)optimal implementations of the inversion is described as follows:

(1)   Defining inputs/outputs: The inversion over (using the tower-field with a normal basis) in [18] is shown as Table 1. Using bit-slicing, its inputs and outputs are defined as 0 × 00FF, 0 × 0F0F, 0 × 3333, = 0 × 5555, and = 0 × 6457, = 0 × 5371, = 0 × 0F93, = 0 × 0A6F.

(2)   Design goal: The inverse circuit (minimizing the area) with a depth of 3 and an area G of 22 GE was proposed by Maximov et al. [18]. So our goal is to search for solutions of the inversion that have an area smaller than G, according to Eq. (4).

(3)   Encoding inputs and outputs of logic gates: Constrain the number of logic gates as , and then encode the inputs and outputs of K logic gates using Eqs. (1), (2) and (7). In addition, encode the outputs using Eq. (3).

(4)   Using SAT to search for solutions: If the solution exists, obtain the area of the current solution and assign it to G. Go to step 2) and continue searching for a smaller area implementation. Otherwise, the minimum area of the inversion over is G.

Employing our method, for -type S-box with a normal basis, a smaller area implementation (with 15.33 GE) of the inversion over has been found compared to the implementation in [18]. Also, a lower depth implementation (with depth and 19.33 GE) for the inversion over could be specified. More precisely, compared to the implementation of the inversion over in [18], our approach that optimizes the area gives a reduction by 7 GE (from 22 to c.a. 15 GE), whereas targetting a lower depth we obtain a depth reduction by one and the area is reduced by 2.67 GE. The specific implementations of the inversion over are given in Table 4.

Furthermore, the inversion over based on RRB for the -type S-box in [15,19] are also optimized, as shown in Table 2. Similar improvements are obtained for the implementations of this inversion. A smaller area and depth implementation (23.00 GE and 2 depth) has been found. The specific implementation is given in Table 5. Compared with the small area implementations of the inversion over in [15,19], the area is reduced by 12.95 GE, and the depth is reduced by 1.

3.2 Optimizing TL/BL/Mul(-Sum) Using Local Solutions

Although the GEC and BGC models can search for optimized implementations for some logic circuits, including the TL/BL/Mul(-Sum) in our approach, their efficiency still depends on the complexity of the considered circuits. However, finding optimized/improved implementations for circuits with high computational complexity may become infeasible. Therefore, a method for optimizing the implementation of (complex) circuits using local solutions is proposed, as shown in Fig. 4. For a circuit with inputs and outputs , a BGC/GEC model with logic gates is first applied to search for the optimized implementations of ( outputs of Y, called local outputs, ). In the BGC model, logic gates only consists of two inputs (thus ). While in the GEC model, logic gates include four inputs, so . To find an optimal implementation of LY, the outputs are recorded as , and the solutions of LY are defined as . Finally, whether LY is equal to Y needs to be determined. If LY is equal to Y, an optimized implementation of this circuit has been found. Otherwise, the search for an optimized implementation of other local outputs using BGC/GEC models (based on X and T) is continued, until LY is equal to Y.

Figure 4: Optimized implementation of circuit based on local solution

For the -type S-box with a small area in [18], TL0/BL0 are and matrices, respectively. For the -type S-box in [15,19], TL1/BL1 are and matrices, respectively. At present, the optimization of TL/BL mainly relies on heuristics. Therefore, SAT solvers are used to search for better implementations of TL/BL. The main idea is to decompose the outputs of a matrix into parts, namely , where . Then, a BGC model is used to find the solutions for outputs. After obtaining the (sub)optimal implementation for outputs, the BGC model is used again to search for the implementation of outputs. This process continues iteratively until a solution for outputs is found. To provide a more detailed explanation of this method, the matrix M0 in [15] is used as an example, as shown in Eq. (8). Matrix M0 has 8 inputs and 8 outputs , where 0 × 80, …, 0 × 01, and 0 × CA, …, 0 × A4.

(8)

(1)   (Obtaining local outputs): Obtain a local output set based on the Hamming weight of the outputs Y. For instance specifying of M0, where the Hamming weight of is less than 4. Notice that other choices of Hamming weights of the output are possible.

(Partial encoding): Encode outputs, to obtain a minimal number/depth of XORs, and check whether there is an implementation of with XORs using BGC models, where is encoded as . The minimized implementations that use 9 XORs (with depth ) for have been found. One of the solutions is shown as follows:

Obtain other local outputs , alternatively the remaining subset . Based on the above solutions and X, the implementation of with / XORs has been searched, where ( specifies the number of XORs for the best-known implementation). Using the solution of , the optimal area implementations of have been found, which require 4 XORs and has depth 3. An optimal solution with minimized number of XORs is

Therefore, the minimum area and fast implementations of the matrix M0 require 13 (with depth 3) and 14 XORs (with depth 2), respectively. Compared to the implementations in [15], a reduction by 2 and 1 XORs has been achieved, respectively.

Based on the above method, for the -type S-box with the small area, the same implementations of TL0/BL0 as in [18] have been found. Moreover, for the fast variant, a smaller area implementation, requiring one XOR gate less (with the same depth of TL0 compared to [18]) could be specified. For the -type S-box, the smaller area implementations of the TL1/BL1 matrices have been identified. Our implementations require 21 and 26 XORs, for TL1/BL1, respectively, which is 6 and 2 XORs less than [19]. The specific implementations can be seen online 1.

Furthermore, LocalGEC models are employed in the search for efficient implementations of Mul(-Sum). In difference to the results in [18,19], our implementations replace some AND/OR gates with smaller area NAND/NOR gates. As a consequence, the implementation of Mul(-Sum) in [19] requires 25 ANDs and 10 ORs, while our approach, utilizing 25 NANDs and 10 NORs, achieves an area reduction of 11.55 GE.

4  Eexperimental Results

The implementations of -type and -type S-boxes are searched, primarily with respect to two optimization goals (small area and fast execution). Table 6 shows the number of logic gates, logic gate types, circuit path depth (CPD) and circuit path (CP) of the proposed hardware implementations for AES S-box, where XO3, XO, XN3, XN, AD, ND, NR, NT, MU, NM, MA, MO, OA, OA3 and OA4 represent XOR3, XOR, XNOR3, XNOR, AND, NAND, NOR, NOT, MUX, NMUX, MAOI1, MOAI1, OA21, OA32 and OA222, respectively. OA32 and OA222 are 5/6-input logic gates, where OA32 and OA222 . “Fields” denotes the representations of and . For S-box, compared to the works in [9,12,13,17,18], our small area variant has the smallest gate count of 93. Our fast variant has the lowest CPD of 11. For S-box, Compared to the works in [14–16,19], our small area variant has the smallest gate count of 120. For our fast variant, while its depth is not the lowest, its gate count is smaller than [15,19]. Based on the comparison, the two variants of the proposed -type S-box demonstrate certain advantages. The small area variant requires the fewest logic gates, while the fast variant has the lowest circuit depth.

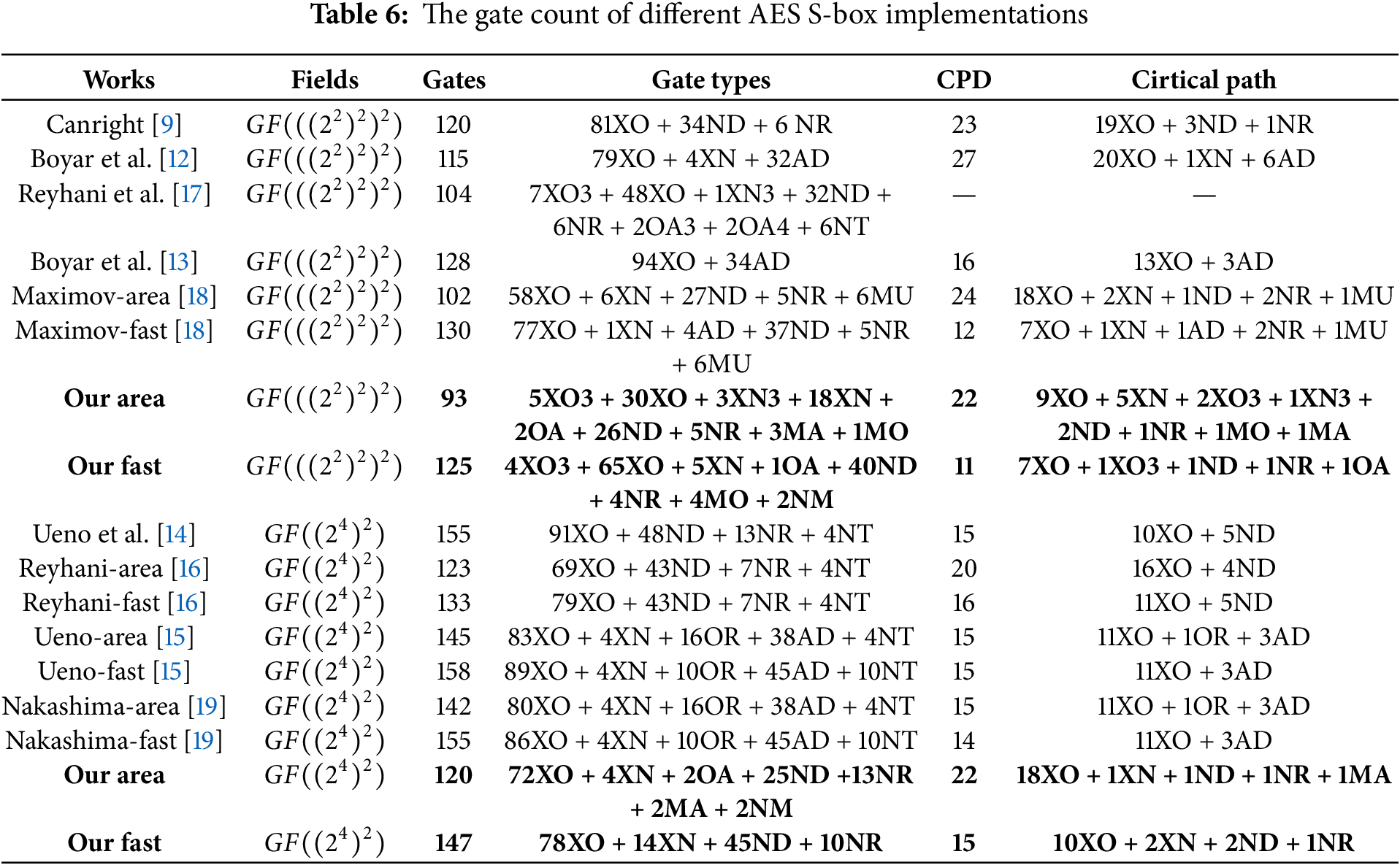
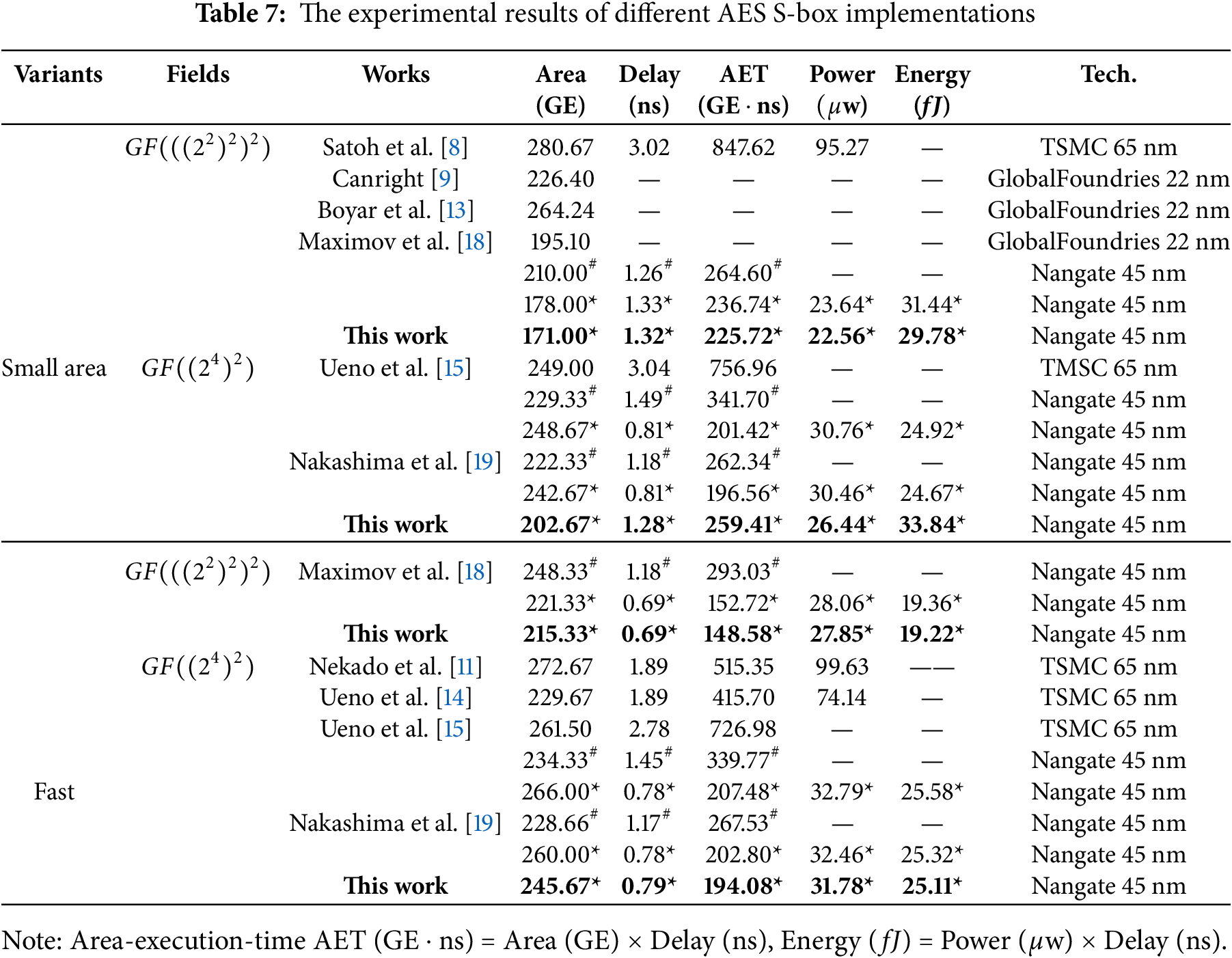
To verify the efficiency and performance of the above approach, the new AES S-box circuit structures are implemented using Verilog language and synthesized using Synopsys Design Compiler software with Nangate 45 nm Open Cell Library. The implementation performance have been evaluated, more precisely specifying the number of 2-input NAND gate equivalents (Area), the circuit delay for the critical path (Delay), the area-execution-time product (AET), power and energy. Table 7 presents the implementation results of different AES S-box structures on different standard cell libraries, where ‘#’ indicates the results from [19], and ‘*’ indicates the results implemented by the comprehensive strategy proposed by us.

The synthesis strategy covers the encapsulation technology of modules and logic gates. Its specific implementation includes using Verilog language to build modules with certain functions or specific logic gates. An example of a module using encapsulation techniques is presented, as shown in Eq. (9). It shows that an implementation module of the inverse over is encapsulated using Verilog. The logic gates used in this model are also encapsulated in this method. The specific implementations can be seen online 1. This prevents unnecessary optimization of AES S-box circuits by the Synopsys Design Compiler, as its automatic optimization could alter the logic gate types and structures of the original design.

(9)

Meanwhile, some strategies and constraints have been set up to prevent automatic optimization from changing the logic gate types and structure of the proposed S-box circuits. For example, the “set_dont_touch” command is used to protect specific modules, logic units, and signals, preventing their structures from being modified by the Synopsys Design Compiler. Furthermore, the timing, area, and power consumption evaluations provided by Design Compiler are based on actual comprehensive results. However, it is worth noting that it performs a logical synthesis rather than a physical implementation. Therefore, if the design constraints, tool settings, and verification process are consistent during logic synthesis, the performance indicators of the same circuit implementation will remain consistent. To ensure the stability of the circuit implementation, the specific comprehensive commands are described as Command 1.

Fig. 5 shows the comparison between the implementation results of the proposed structure and the implementation results in [19]. “M”, “U”, “N”, and “T” represent the works of [15,18,19] and this work, respectively. “A” and “F” represent the small area variant and the fast variant, respectively. “0” and “1” represent and S-box, respectively. In four proposed AES S-box implementation schemes, the implementation performance for the proposed two variants (TA0 and TF0) of -type S-box is better than that of the proposed two variants (TA1 and TF1) of -type S-box. For example, the area, AET, and power consumption of TA0 are 171.00 GE, 225.72 GE ns, and 22.56 w, respectively, which are 31.67 GE, 33.69 ns, and 3.58 w less than the implementation area, delay, and power consumption of TA1. Similar advantages have also been achieved by TF0, compared to TF1. While in existing AES S-box implementations, the small area implementation MA0 proposed by Maximov et al. [18] outperforms others in terms of area. On GlobalFoundries 22 nm library, it requires only 195.10 GE, significantly better than implementations in [9,13]. Similarly, on the Nangate 45 nm process library, MA0 also occupies the smallest area, according to existing experimental results in [19]. In addition, the MF0 proposed by Maximov et al. [18], and NA1 and NF1 proposed by Nakashima et al. [19], exhibit better delay performance. Specifically, the delay of these variants is 1.17–1.18 ns on Nangate 45 nm library. Their delay is significantly lower than other fast variant implementations in [11,14,15]. Therefore, the proposed implementations of AES S-box are also mainly compared with the current best works [18,19] on Nangate 45 nm library. When the area is considered, the area of TA0 is 18.57% smaller than [18]. When the delay or AET is considered, the delay and AET of TF0 are 0.69 ns and 148.58 GE ns, respectively. Compared to state-of-the-art implementations [19], TF0 achieves a 41.03% reduction in area and a 43.36% improvement in delay.

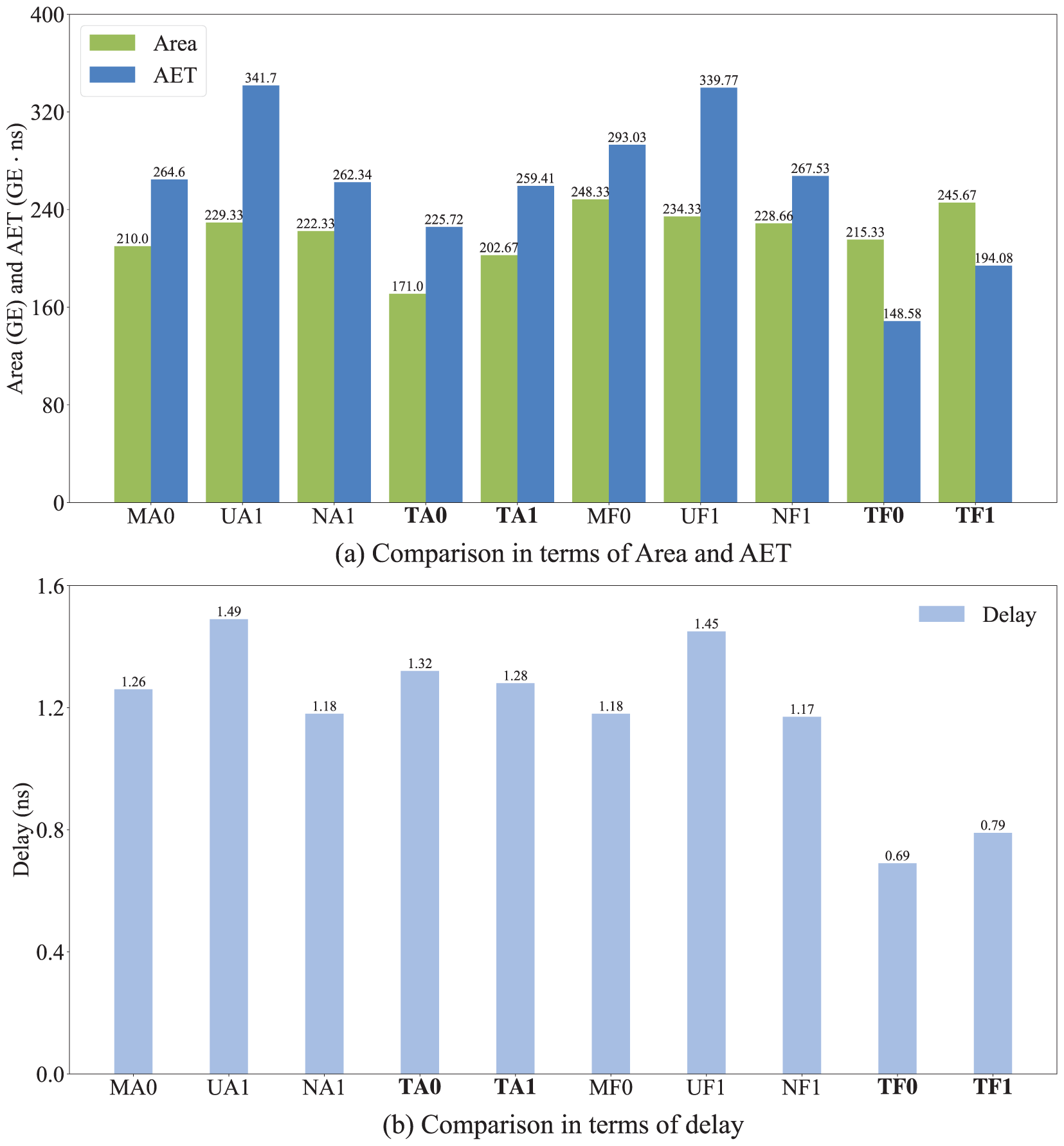
Figure 5: Comparison of implementation results between our structures (TA0, TA1, TF0 and TF1) and the structures in [19]

It is worth noting that Table 7 shows that MA0 in [18] requires 210.00 GE (reported in [19]). In contrast, MA0 requires 58 XORs, 6 XNORs, 27 NANDs, 5 NORs, and 6 MUXs, with an estimated area of GE. The significant difference in area arises because the implementation results of [15,18,19] from [19] do not fully account for the impact of the automatic optimization technology in Synopsys Design Compiler software on circuits. Therefore, the works of [15,18,19] were implemented on the NanGate 45nm standard cell library using the same conditions as the proposed structures. The implementation results show that, when considering the implementation area, the proposed -type small area variant achieves a 3.93% smaller area than the current minimum implementation [18]. Additionally, the AET and energy of this variant are reduced by 4.65% and 5.28%, respectively, compared to [18]. When the delay, AET or energy is considered, the proposed -type fast variant has a improved implementation performance. For instance, the AET of this fast variant is reduced 2.71% compared to the best implementations in [15,18,19].

From the above comparison, it can be concluded that the proposed -type S-box with a small area variant has the smallest area and power, and the proposed -type S-box with a fast variant has the smallest delay, AET and energy.

5  Conlusion

This paper presented a novel hardware implementation strategy for AES S-boxes. It combines composite field arithmetic with SAT solvers. We decomposed the AES S-box implementation into five optimization tasks. These tasks include inversion over , top and bottom linear transformations (TL/BL), multiplication (Mul), and multiplication-sum (Mul-Sum). Using the GEC model, we optimized the inversion over for -type S-boxes. This resulted in a small area implementation of 15.33 GE and a low-depth implementation of 19.33 GE with depth 2. We further improved TL/BL and Mul(-Sum) implementations using LocalBGC and LocalGEC models. These improvements surpass the current best-known implementations. Our key contribution is the implementations of two -type S-box variants. The first is a small area variant that sets new area records. The second is a fast variant that establishes new benchmarks for Area-Execute-Time (AET) efficiency and energy consumption. Evaluation results confirm that our proposed S-boxes achieve the smallest area and lowest delay, AET, and energy consumption compared to existing implementations. These optimizations contribute to more efficient and secure AES implementations, enhancing cryptographic applications in network security. Future research will extend this SAT-based method to other block cipher components. Furthermore, efficient implementation structures for diverse application requirements will be explored.

Acknowledgement: The authors also gratefully acknowledge the helpful comments and suggestions of the reviewers and editors, which have improved the presentation.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China (No. 62162016), and in part by the Innovation Project of Guangxi Graduate Education (Nos. YCBZ2023132 and YCSW2023304).

Author Contributions: Study conception and design: Jingya Feng, Ying Zhao; data collection: Jingya Feng, Tao Ye; analysis and interpretation of results: Jingya Feng, Ying Zhao, Wei Feng; draft manuscript preparation: Jingya Feng; supervision: Ying Zhao, Wei Feng. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

1https://github.com/fjyxzm/AESSbox (accessed on 01 February 2025).

2One of the file based input formats that STP reads, https://stp.readthedocs.io/en/stable/cvc-input-language.html (accessed on 01 February 2025).

References

1. Tangade S, Manvi SS, Lorenz P. Trust management scheme based on hybrid cryptography for secure communications in VANETs. IEEE Trans Vehicular Technol. 2020;69(5):5232–43. doi:10.1109/TVT.2020.2981127. [Google Scholar] [CrossRef]

2. Aydın H, Aydın GZG, Sertbaş A, Aydın MA. Internet of things security: a multi-agent-based defense system design. Comput Electr Eng. 2023;111(3):108961. doi:10.1016/j.compeleceng.2023.108961. [Google Scholar] [CrossRef]

3. National Institute of Standards and Technology. Advanced Encryption Standard (AES). Federal Information Processing Standards Publication (FIPS PUB 197). U.S. Department of Commerce; 2021 [cited 2024 Dec 10]. Available from: https://csrc.nist.gov/files/pubs/fips/197/final/docs/fips-197.pdf. [Google Scholar]

4. Cheng PY, Su YC, Chao PCP. Novel high throughput-to-area efficiency and strong-resilience datapath of AES for lightweight implementation in IoT devices. IEEE Internet Things J. 2024;11(10):17678–87. doi:10.1109/JIOT.2024.3359714. [Google Scholar] [CrossRef]

5. Lin MB, Chuang JH. The design of a high-throughput hardware architecture for the AES-GCM algorithm. IEEE Trans Consum Electron. 2024;70(1):425–32. doi:10.1109/TCE.2023.3332872. [Google Scholar] [CrossRef]

6. Zhang M, Shi T, Wu W, Sui H. Optimized quantum circuit of AES with interlacing-uncompute structure. IEEE Trans Comput. 2024;73(11):2563–75. doi:10.1109/TC.2024.3449094. [Google Scholar] [CrossRef]

7. Rudra A, Dubey PK, Jutla CS, amd Josyula Rao VK, Rohatgi P, et al. Efficient Rijndael encryption implementation with composite field arithmetic. In:Cryptographic Hardware and Embedded Systems–CHES 2001; 2001; Berlin/ Heidelberg: Springer. p. 171–84. [Google Scholar]

8. Satoh A, Morioka S, Takano K, Munetoh S. A compact Rijndael hardware architecture with S-box optimization. In: Advances in Cryptology–ASIACRYPT 2001; 2001; Berlin/Heidelberg: Springer. p. 239–54. [Google Scholar]

9. Canright D. A very compact S-box for AES. In: Cryptographic Hardware and Embedded Systems–CHES 2005; 2005; Berlin/Heidelberg: Springer. p. 441–55. [Google Scholar]

10. Nogami Y, Nekado K, Toyota T, Hongo N, Morikawa Y. Mixed bases for efficient inversion in F((22)2)2 and conversion matrices of subbytes of AES. In: Cryptographic Hardware and Embedded Systems–CHES 2010; 2010; Berlin/Heidelberg: Springer. p. 234–47. [Google Scholar]

11. Nekado K, Nogami Y, Iokibe K. Very short critical path implementation of AES with direct logic gates. In: Advances in information and computer security. Berlin/Heidelberg: Springer; 2012; p. 51–68. [Google Scholar]

12. Boyar J, Peralta R. A new combinational logic minimization technique with applications to cryptology. In: Experimental Algorithms, 9th International Symposium, SEA 2010; 2010; Berlin/Heidelberg: Springer. p. 178–89. [Google Scholar]

13. Boyar J, Peralta R. A small depth-16 circuit for the AES S-box. In: Information security and privacy research. Berlin/Heidelberg: Springer; 2012; p. 287–98. [Google Scholar]

14. Ueno R, Homma N, Sugawara Y, Nogami Y, Aoki T. Highly efficient GF(28) inversion circuit based on redundant GF arithmetic and its application to AES design. In: Cryptographic Hardware and Embedded Systems–CHES 2015. Berlin/Heidelberg: Springer; 2015; p. 63–80. [Google Scholar]

15. Ueno R, Homma N, Nogami Y, Aoki T. Highly efficient GF(28) inversion circuit based on hybrid GF representations. J Cryptographic Eng. 2019;9:101–13. doi:10.1007/s13389-018-0187-8. [Google Scholar] [CrossRef]

16. Reyhani-Masoleh A, Taha M, Ashmawy D. Smashing the implementation records of AES S-box. IACR Trans Cryptograp Hardw Embedded Syst. 2018;2018(2):298–336. doi:10.13154/tches.v2018.i2.298-336. [Google Scholar] [CrossRef]

17. Reyhani-Masoleh A, Taha M, Ashmawy D. New low-area designs for the AES forward, inverse and combined S-boxes. IEEE Trans Comput. 2020;69(12):1757–73. doi:10.1109/TC.2019.2922601. [Google Scholar] [CrossRef]

18. Maximov A, Ekdahl P. New circuit minimization techniques for smaller and faster AES S-boxes. IACR Trans Cryptograp Hardw Embedded Syst. 2019;2019(4):91–125. doi:10.13154/tches.v2019.i4.91-125. [Google Scholar] [CrossRef]

19. Nakashima A, Ueno R, Homma N. AES S-box hardware with efficiency improvement based on linear mapping optimization. IEEE Transact Circ Syst II: Express Briefs. 2022;69:3978–82. doi:10.1109/TCSII.2022.3185632. [Google Scholar] [CrossRef]

20. Song J, Lee K, Park J. Low area and low power threshold implementation design technique for AES S-box. IEEE Transact Circ Syst II: Express Briefs. 2023;70(3):1169–73. doi:10.1109/TCSII.2022.3217150. [Google Scholar] [CrossRef]

21. Singha TB, Palathinkal RP, Ahamed SR. Analysis of S-box hardware resources to improve AES intrinsic security against power attacks. IEEE Embed Syst Letters. 2024;16(4):525–8. doi:10.1109/LES.2024.3478070. [Google Scholar] [CrossRef]

22. Bao Z, Guo J, Ling S, Sasaki Y. PEIGEN-A platform for evaluation, implementation, and generation of S-boxes. IACR Transact Symmet Cryptol. 2019;2019:330–94. doi:10.46586/tosc.v2019.i1.330-394. [Google Scholar] [CrossRef]

23. Liu Q, Wang W, Fan Y, Wu L, Sun L, Wang M. Towards low-latency implementation of linear layers. IACR Transact Symmet Cryptol. 2022;2022:158–82. doi:10.46586/tosc.v2022.i1.158-182. [Google Scholar] [CrossRef]

24. Lu Z, Wang W, Hu K, Fan Y, Wu L, Wang M. Pushing the limits: searching for implementations with the smallest area for lightweight S-boxes. In: International Conference on Cryptology in India-INDOCRYPT; 2021; Cham: Springer. p. 159–78. [Google Scholar]

25. Feng J, Wei Y, Zhang F, Pasalic E, Zhou Y. Novel optimized implementations of lightweight cryptographic S-boxes via SAT solvers. IEEE Transact Circ Syst I: Regular Papers. 2024;71(1):334–47. doi:10.1109/TCSI.2023.3325559. [Google Scholar] [CrossRef]