Cyclical Training Framework with Graph Feature Optimization for Knowledge Graph Reasoning

1  Introduction

A knowledge graph (KG) organizes real-life knowledge by storing information in triples, each comprising two entities connected by a relation. KGs are crucial for various applications, including general recommender systems [1], news recommendation [2], information retrieval [3] and language model training [4]. However, owing to the large scale and complexity of constructing KGs, they often exhibit some degree of incompleteness, i.e., certain triples in the KGs are missing. To address this issue, researchers have proposed the task of KG completion, which aims to infer missing triples from existing triples. This task enhances the completeness of the KG and facilitates the discovery of new knowledge.

In order to tackle the task of KG completion, some researchers employ KG embedding methods [5] or similar approaches [6] to predict facts by assigning scores to given triples, with higher scores indicating a greater likelihood of the triple being valid. However, these methods lack interpretability because they do not provide an evidential reasoning chain. Another study such as MINERVA [7] focuses on interpretable KG completion via multi-hop knowledge graph reasoning (KGR). As shown in Fig. 1, given a query “(Tony Romo, athlete_plays _sport, ?)”, the model infers the missing tail entity “American football” via a reasoning path (<Leads_team, Team Dallas cowboys>,<plays_against, Team Seahawks>,<team_plays_sport, American football>). Multi-hop KGR models not only identify correct missing entities but also provide reasoning paths that justify their predictions.

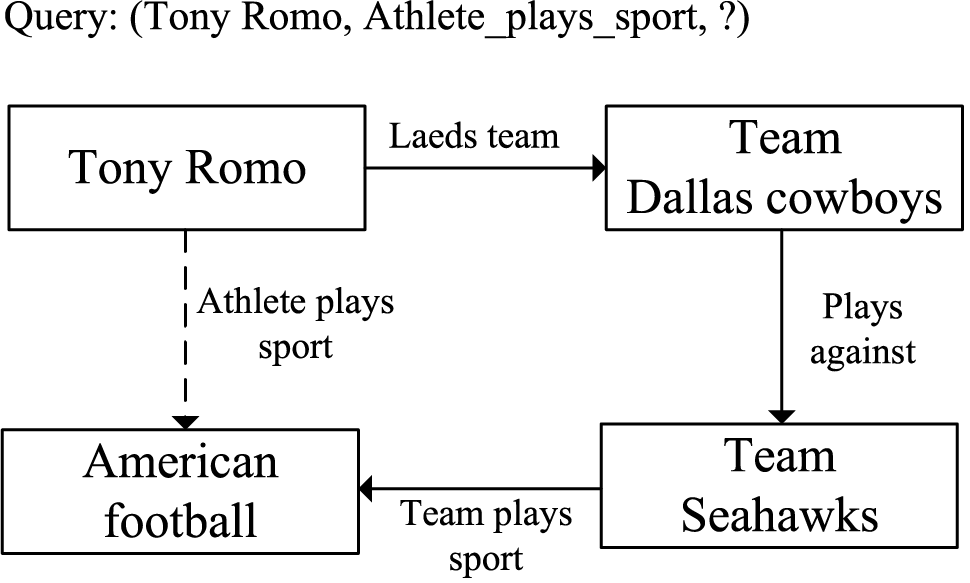
Figure 1: Multi-hop reasoning and completion example within a subset of a knowledge graph (KG). Each rectangle represents an entity, each solid arrow represents an existing relation in the KG, and the dashed arrow represents a missing link between entities

In particular, multi-hop knowledge graph reasoning (KGR) approaches can be categorized into two types: sequence-to-sequence (seq2seq) based methods and reinforcement learning (RL) based methods. Seq2seq-based methods, such as SQUIRE [8], treat the multi-hop reasoning as a sequence-to-sequence process. These models are designed to generate reasoning chains that connect the head entity to the missing tail entity, using a training set containing entity-relation trajectories. A key advantage of these methods is their ability to quickly learn from a large set of positive samples, resulting in faster learning compared to reinforcement learning (RL) methods. Additionally, the output space in this approach encompasses all entities and relations across the entire graph as potential targets. This enables the model to efficiently share and transfer knowledge across different graph patterns, thereby developing an optimal reasoning strategy for multiple patterns. However, these models are limited to learning from the positive samples in the training set and cannot explore unannotated reasoning chains, making them dependent on the availability of high-quality training datasets. On the other hand, RL-based methods use a neural network as an agent to walk and explore within the knowledge graph, including MINERVA [7], Multi-HopKG [9], CURL [10], PS-Agent [11], etc. For a query triple (eh,rq,?) with a missing entity, starting from the head entity, the agent moves to another entity through one of its relations and gradually reaches the final entity. During training, the rewards are assigned based on whether the final entity matches the correct answer, which guides parameter updates. As a result, RL-based methods excel at exploring unlabeled data and can function without being constrained by pre-retrieved reasoning chains in the training set. Another advantage of RL-based methods is that it demonstrates a strong specialization potential within specific graph patterns. However, RL methods struggle to transfer knowledge across diverse graph patterns, which results in low learning efficiency compared to seq2seq models. In addition, both methods share a common challenge: insufficient encoding of entities and relations. Previous KGR models either overly rely on encoding only entity features as inputs to the reasoning network, ignoring linear causal information and semantic correlations between relations in the reasoning chain, or use shallow observation vectors derived from raw graph features with simplistic network architecture, overlooking the structural information of the graph.

To address the above issues, we propose a novel multi-hop reasoning framework called CycDE, which includes a cyclical training method that alternates between the seq2seq phase and the policy-based RL phase during model training, as well as a multimodal data encoding module for optimizing and integrating entity and relation features. Specifically, the main contributions of the proposed CycDE framework are as follows:

(1) A multimodal data encoding (MDE) module is introduced to optimize graph features. The proposed module treats entities and relations as two distinct data modalities during representation. The MDE uses a gated recurrent unit (GRU) [12] aided by text-based relation attention mechanism obtained via BERT [13] to capture the linear temporal interactions among relations in the reasoning chain, and uses a graph attention network (GAT) [14] to capture the graph structural connections between entities in the KG. A gating mechanism is then introduced to dynamically fuse the entity and relation, minimizing conflicts between different modalities of information and integrating more useful data, thereby resulting in a more informative representation of entity-relation pairs.

(2) The CycDE framework provides a cyclical training strategy that alternates between the seq2seq and RL training phases across multiple cycles. In the seq2seq phase, the model uses the retrieved trajectories as supervised sequences for training, which enhances its adaptability to different graph patterns and accelerates the overall training process compared to RL-only methods. In the RL phase, policy-based RL is employed, which strengthens the model’s learning capabilities for specific graph patterns. Additionally, the RL phase enables the model to explore unannotated reasoning chains, overcoming limitations in example path retrieval and enhancing robustness, particularly when the training data is insufficient or of low quality. Moreover, the cyclical alternation between the two phases over several cycles prevents the model from getting stuck in local minima due to prolonged training in a single phase, ensuring that both approaches are fully leveraged.

(3) We validate the effectiveness of the proposed method by comparing CycDE against seq2seq-based and RL-based baselines across five benchmark KG datasets. The experimental results demonstrate that CycDE outperforms its counterparts. Furthermore, ablation studies and other analytical experiments confirm the impact of the proposed components of the CycDE framework.

2  Related Works

2.1 Knowledge Graph Embedding

Standard knowledge graph embedding (KGE) methods, such as TransE [5], ConvE [15], Complex [16] and CausE [17] embed high-dimensional, one-hot representations of entities and relations into a low-dimensional space. These approaches typically use a scoring function to evaluate triples and determine their likelihood of validity in the KG. Given the importance of online documents and text corpora as critical data sources for KGs, and the success of pretrained language models (PLMs) like BERT [13], T5 [18], and GPT2 [19] in processing such data, previous studies, such as KG-BERT [6], SimKGC [20], and KGT5 [21], leverage PLMs to generate text-based embeddings for both entities and relations. These embeddings are then used in downstream KG completion tasks with scoring functions similar to those in standard KGE methods. In addition, some KGE methods, such as RotateQVS [22], PTBox [23], and TCompoundE [24] are applied on temporal KGs to handle the completion of temporal KGs.

Despite KGE methods’ success in fact prediction, both standard and PLM-based embedding methods have limitations. Specifically, they struggle to capture symbolic rules among entities and relations, which undermines interpretability. Additionally, these methods involve scoring all candidate triples and selecting the highest-ranked triple, which makes inference time consuming.

2.2 Multi-Hop KG Reasoning

Multi-hop KGR aims to complete the KG in an interpretable manner by inferring reasoning paths. Xiong et al. introduce the first framework that applies RL to KGR across entire triples [25]. Building upon Xiong et al.’s work, Wang et al. focus on refining entity representations but do not employ a dedicated network for relation refinement [26]. Both of these frameworks face scalability issues with large KGs, as their models require training a separate classifier for each relation type. In contrast, MINERVA [7] redesigns the model to directly search for missing entities, eliminating the need to rank vast candidate triples repeatedly. Following MINERVA, MultiHopKG [9] uses a KGE model to shape the reward and address reward sparsity. CURL [10] clusters entities using the K-means algorithm and applies entity-cluster-level reasoning to guide entity-level reasoning. PS-Agent [11] reduces the negative influence of spurious paths during policy learning. AInvR [27] introduces adaptive learning rewards to optimize the policy network, while RKLE [28] uses logical embedding to obtain logical rewards.

Inspired by previous study [29] that transforms RL problems into sequence modeling tasks via supervised sequence-to-sequence training on pre-obtained offline supervision data, SQUIRE [8] uses retrieved entity-relation paths as supervision signals to train the KGR model. Although SQUIRE performs well on datasets with high-quality reasoning paths, its performance is significantly reduced on graphs lacking high quality reasoning paths for path training set construction.

2.3 Reinforcement Learning

RL methods can broadly be categorized into value-based and policy-based approaches. Value-based methods, such as double-Q-learning [30], Deep Q-Networks (DQN) [31], and Rainbow [32], focus on learning a value function that estimates the expected future rewards for each state-action pair. These methods derive an optimal policy by selecting actions that maximize the estimated value. Policy-based methods, on the other hand, directly optimize the policy by adjusting its parameters via gradient ascent on the expected reward. Popular algorithms include REINFORCE [33], TRPO [34], and proximal policy optimization (PPO) [35]. Unlike value-based methods, policy-based approaches are better suited for handling continuous action spaces and stochastic policies. In KGR tasks, rewards are typically sparse, making it challenging to learn an effective value function. Consequently, most RL-based KGR approaches favor policy-based RL methods.

3  Method

To achieve more informative entity and relation encodings while effectively integrating the strengths of seq2seq and RL-based models, we propose CycDE, which comprises three modules: the MDE, path reasoning, and cyclical training modules. First, the MDE module encodes the first k segments of reasoning paths, encompassing both the entities and relations. Next, the path reasoning module predicts the (k+1)-th segment of the reasoning path based on the previous k segments. Finally, these two modules are optimized through the cyclical training module, where the model alternates between seq2seq training phases and policy-based RL training phases over multiple cycles. The architecture and training pipeline of the model are illustrated in Fig. 2.

Figure 2: Overview of the proposed CycDE framework. The left panel illustrates the model architecture, marked as Fig. 2 (I), and the right panel depicts the training pipeline, marked as Fig. 2 (II)

3.1 Preliminaries

Let a KG be denoted as 𝒢={ℰ,ℛ,𝒯}, where ℰ, ℛ and 𝒯 represent the set of entities, relations, and triples, respectively. Given a triple query (eh,rq,?), our objective is to develop and optimize a model that performs multi-hop reasoning in the KG to infer the missing tail entity et. At the k-th step, the model predicts a relation-entity pair <rk,ek> based on its reasoning. The complete reasoning path is then represented as {eh,r1,e1,r2,e2,…,rK,eK}, where the missing tail entity et=eK.

3.2 Multimodal Data Encoding Module

The MDE module treats relations and entities in the reasoning chain as data of different modalities. In the reasoning chain, relations primarily follow a linear structure, with subsequent relations being inferred based on previous ones. Conversely, entities in the KG typically follow a graph structure. Therefore, we treat them as data of different modalities and use a GRU for relations and a GNN for entities to capture their representations.

Given the reasoning chain {e0,r1,e1,r2,e2,…,rk,ek} at step k, the rp is prefixed to the reasoning chain to form an extended sequence {r0,e0,r1,e1,…,rk,ek}, where r0=rp and e0=eh. The attention mechanism is then used to capture semantic interactions between different relations:

ariattn=∑j=0iαij⋅arjraw(1)

where arjraw is the raw embedding of relation rj; and αij is the text-based semantic attention score between ri and rj, which is calculated as follows:

αij=queryrj⋅keyri(2)

queryrj=zrj⋅Wquery(3)

keyri=Wkey⋅(zri)T(4)

where Wquery and Wkey are trainable weights; and zrk represents the embedding of the text description of the relation rk. Given the text description of the relation rk as textrk, zrk is obtained by BERT as follows:

zri=BERT(textri)(5)

The BERT model employs a Transformer encoder architecture [36], leveraging bidirectional attention to encode contextual dependencies effectively. This enables it to encode relation descriptions from a holistic perspective, thereby capturing connections between concepts effectively from a semantic standpoint.

Next, the GRU is selected to encode the relation embeddings in the reasoning chain by modeling the temporal interactions from earlier to later relations as follows:

ar0,ar1…ark=GRU(ar0attn,ar1attn,...arkattn)(6)

The GRU is chosen because its use of update and reset gates helps mitigate overfitting during the enhancement of relationship representation encoding. Moreover, its relatively low parameter count and model complexity contribute to improve training and inference efficiency.

Entities are treated as modality distinct from relations. While relation encoding focuses on linear temporal interactions, entity encoding emphasizes graph-based connections among entities in the KG. The MDE module utilizes a Graph Attention Network (GAT) to enhance entity representation. GAT encodes entities based on attention computation between entities and their neighbors, which helps capture the local states of target entities. Additionally, GAT does not require a predefined graph structure, making it more adaptable to incomplete knowledge graphs with missing edges. Given the set of original representations Beraw for all entities in 𝒢, the GAT computes optimized entities representations Begat:

Begat=GAT(Beraw,𝒢)(7)

From Begat, the representations of the entities within the reasoning chain are extracted and defined as be0gat,be1gat,…,bekgat. The MDE module then fuses the original entity representations with the entity representations learned by GAT to obtain the final entity representations as follows:

bei=λbeiraw+(1−λ)beigat(8)

The hyperparameter λ is set to zero when the average degree of the nodes in the KG is no less than three; otherwise, it is set to a value greater than zero.

After encoding both relations and entities, MDE module applies a gating mechanism to fuse their information to obtain a representation of the relation-entity pair in the reasoning chain:

pi=β⋅pifusion+(1−β)⋅[ari||bei](9)

pkfusion=Wfusion⋅[ari||bei](10)

β=σ(Wgate⋅[ari||bei])(11)

where Wfusion and Wgate are trainable parameters; σ denotes the sigmoid function; and [⋅||⋅] represents the concatenation operation over two elements. Due to the distinct characteristics of relations and entities, placing greater emphasis on simple concatenation helps prevent interference between entity and relation features, while a higher proportion of mixed features more effectively captures interactions. The gating mechanism dynamically adjusts the ratio between simple concatenation and mixed features at a fine-grained level, determining which features should be fused and which should remain independent.

3.3 Path Reasoning Module

The path reasoning module takes the relation-entity pair embedding sequences p0,p1,…,pk from step 0 to step k as input to calculate the prediction representation p^k+1, which is then used to predict the entity-relation pair for the next step in the subsequent process. The module is built on the decoder architecture of the Transformer [36]:

p^1,p^2,…,p^k+1=Transformer(p0,…pk)(12)

As observed by Dai et al. [37] and Geva et al. [38], the feed-forward layers of the Transformer act as a key-value memory structure that stores factual knowledge, effectively capturing structured information similar to triples in a KG. The residual connections and self-attention mechanisms of the Transformer further mitigate gradient vanishing, enabling deeper layer stacking and larger-scale parameterization. These properties of the Transformer enable us to construct a more extensive model architecture with additional knowledge neurons, thereby enhancing the ability to store more triple knowledge from KGs and improve reasoning task.

In the cyclical training of CycDE, during the seq2seq training phase, the input relation-entity pairs given to the reasoning module correspond to those in the ground truth paths from the training trajectory set. In contrast, during the policy-based RL training phase, each pair in the input sequence corresponds to the actual entity-relation pair decoded by the model in the previous reasoning step.

3.4 Cyclical Training Module

To leverage the strengths of both RL and seq2seq methods while mitigating their weaknesses, we propose a cyclical training approach that alternates between the seq2seq and policy-based RL phases for several loops. In the seq2seq phase, the training process features a set of pre-retrieved example paths that accelerate model training, as well as a global candidate output space encompassing all entities and relations in the graph for flexible knowledge transfer. In the policy-based RL phase, the model benefits from the advantages of RL to enhance its specialization within graph patterns and strengthen its robustness against low-quality seq2seq training data. During cyclical training, the model alternates between these two phases over several cycles, gaining the benefits of both approaches. The continuous alternation between the two phases helps prevent the model from training too long on a single phase and getting stuck in a local minima. To ensure stability during phase transitions and prevent catastrophic forgetting, a Kullback-Leibler (KL) divergence regularization term is introduced for both phases. The following sections first discuss the seq2seq and policy-based RL phases separately, then explain how these phases are organized in cyclical training. Finally, the KL divergence regularization term is described in detail. The cyclical training process is illustrated in Fig. 2 (II).

3.4.1 Seq2seq Training Phase

During the seq2seq training phase, for each triple in the knowledge graph, we adopt an approach inspired by previous seq2seq methods [8] to retrieve several multi-hop entity-relation trajectories that connect the head and tail entities, forming the example reasoning trajectory training set. Each trajectory in the training set is provided to the model with a causal mask. Unlike previous methods that assign separate input positions to each entity and relation, each relation-entity pair is encoded into a single embedding using the MDE module, effectively reducing the input sequence length by half. Subsequently, the output representations of the reasoning module are decomposed into relation-entity prediction representations. Let the relation-entity prediction representations for a complete reasoning path be defined as {a^r1,b^e1,a^r2,b^e2,…,a^rK,b^eK}. An output prediction representation pi^ of the reasoning transformer is decomposed into a^ri and b^ei via computing:

a^ri=p^i[de:de+dr](13)

b^ei=p^i[0:de](14)

where de and dr are the dimensions of entity and relation features in the output representation p^, respectively. The loss function for seq2seq training is defined as follows:

ℒseq=−∑1N∑k=0K−1(∑e∈ℰyelog⁡p(e∣p≤k)+∑r∈ℛyrlog⁡p(r∣p≤k))(15)

p(e∣p≤k)=b^ek+1⋅(beraw)T∑e′∈ℰb^ek+1⋅(be′raw)T(16)

p(r∣p≤k)=a^rk+1⋅(arraw)T∑r′∈ℛa^rk+1⋅(ar′raw)T(17)

where N is the batch size; if e is the ground-truth entity at the step k, then ye=1; otherwise, ye=0. Similarly, if r is the ground-truth relation in the step k, then yr=1; otherwise, yr=0.

As demonstrated by Eqs. (16) and (17), during the seq2seq phase, the model defines a global output candidate space that includes all the relations and entities in the graph. In contrast, during the RL phase, the action space is restricted to the local neighbors of the current node. This global target space in the seq2seq phase enables the model to learn reasoning strategies that consider the structure and information of the entire graph. Consequently, the model becomes less influenced by the connectivity or sparsity of the current graph when learning and transferring knowledge, thereby facilitating efficient knowledge transfer across diverse graph patterns. In summary, the seq2seq phase employs a universal target space containing all graph elements, rather than a unique target space determined by the graph’s connectivity. This design allows the model to transfer knowledge with greater flexibility across different graph structures. Furthermore, the availability of sufficient positive examples accelerates training, particularly during the early training epochs.

3.4.2 Policy-Based RL Phase

In the policy-based RL phase, the proposed model is optimized using a policy-based reinforcement learning approach. Starting from the head entity, the model selects an entity-relation pair at each reasoning step and moves to the next entity via the selected relation edge. This process is repeated until the model reaches the final tail entity or exhausts the maximum number of reasoning steps. The reward is calculated based on the validity of the tail entity, guiding parameter updates. Unlike the seq2seq phase, this approach does not require reasoning trajectories from the training set, enabling the model to learn positive examples that are not present in the trajectory training data. This feature addresses the robustness issue arising from the seq2seq phase. Furthermore, by assigning negative rewards to incorrect reasoning results, the RL phase functions as a mechanism for negative sampling and error correction, thereby enhancing the model’s ability to specialize in specific graph patterns. This improvement is particularly significant when the model has gained experience with a specific graph pattern. The following section outlines the construction and pipeline of the RL phase.

State definition: Given a query (eh,rq,?), the state sk∈𝒮 at reasoning step k in the RL phase consists of the relation-entity pair embeddings generated by the MDE module. It is defined as follows:

sk=p0,p1,…,pk(18)

Action definition: At reasoning step k, the candidate relation-entity pairs for the (k+1)-th step constitute the potential action space Actionsk+1. These candidate pairs can be categorized into two types: positive pairs {pairk+1=(rk+1,ek+1)|(ek,rk+1,ek+1)∈𝒢}, which form valid triples in the knowledge graph, and negative pairs {pairk+1=(rk+1neg,ek+1)|(ek,rk+1neg,ek+1)∉𝒢}, which are artificially generated and form invalid triples with the current entity. These negative pairs are used as negative samples to augment the training data. Furthermore, a self-loop is added to Actionsk+1, allowing the model to remain at the current target entity until the maximum reasoning step is reached.

Policy network definition: In this study, the policy network is the reasoning transformer module, which is defined in Section 3.3.

Reward setting and reward shaping: Following previous study [9], for each query (eh,rq,?), the reward is 1 if the final reasoning result et of the model is correct, i.e., (eh,rq,et)∈𝒢; otherwise, the reward is a decimal number between 0 and 1, which is calculated based on the ConvE [15] scoring function score(eh,rq,et) that evaluates the likelihood of the existence of a triple. However, we observe that even valid triples in the KG exhibit variations in their KGE scores. Therefore, instead of applying a sigmoid function directly to the raw KGE score as in previous studies, we first compute the average score of (eh,rq) with all possible tail entities in the KG, denoted as scoremean. Subsequently, the average score of all tail entities that forms valid triples with (eh,rq) is computed, denoted as scorevalid. Finally, the reward for the given query (eh,rq,?) is defined as:

RK=clip(score(eh,rq,et)−scoremeanscorevalid−scoremean,0,1)(19)

where clip(⋅,0,1) confines the value to the range (0,1).

Policy based RL optimization: The path reasoning module serves as the policy network, calculating the action distribution as follows:

actsk+1=softmax(Actk+1⋅p^k+1)(20)

πθ(pairk+1|sk)∼Categorical(actsk+1)(21)

where p^k+1 is the prediction representation used for candidate pair prediction, calculated by the path reasoning module for a given sk; and Actk+1 is a matrix in which each row represents the embedding of a candidate action from Actionsk+1. The softmax operation generates a normalized probability distribution over the set of actions from which an action is selected. After reaching the maximum reasoning step, policy gradient-based RL optimization is performed using the following loss function:

ℒRL=−∑1N∑k=0K−1(Rk+1sum−Rmean)log⁡πθ(pairk+1∣sk)(22)

where N represents the batch size; Rmean denotes the average reward within a training batch; Rksum is the accumulated reward from step k to the final step K which is defined as follows:

Rksum=∑i=kKRi(23)

3.4.3 Process of Cyclical Training

In cyclical training, the model’s training process alternates between the RL phase and the seq2seq phase for several cycles. In the early training epochs, the seq2seq method holds a relatively high proportion, as it demonstrates higher learning efficiency. Additionally, the seq2seq method applies softmax over all entities and relations in the entire graph. This expansive and universal output space enables the model to more easily transfer learned knowledge across different graph patterns, while also improving the robustness of the model’s parameters across diverse graph structures. Meanwhile, the RL method serves as a negative sample mechanism to identify and penalize inference errors. We use an online, on-policy RL algorithm, so the negative samples found during RL training are always relative to the current model parameters, enhancing the immediacy and effectiveness of error correction. As training progresses, the number of RL steps increases. Although RL exhibits less adaptability to various graph patterns compared to the seq2seq method, it shows stronger learning potential for individual graph patterns. Therefore, after several RL training epochs, the seq2seq phase is reintroduced to improve the model’s ability to adapt to a broader range of graph patterns. The model is then switched back to the RL training phase to leverage its superior error correction capabilities, thus enhancing the model’s learning potential within the graph patterns it has already mastered. If the model fails to improve its performance on certain graph patterns during the RL phase, the subsequent seq2seq phase helps prevent the model from forgetting knowledge of less dominant but learned graph patterns, enabling continued improvement in the next RL phase. Moreover, periodically alternating between the RL and seq2seq phases introduces variability in the model’s convergence goals, as the two phases differ in their input-output spaces and training objectives. This prevents the model from getting trapped in a local optimum specific to one phase due to prolonged training. In general, by cyclically switching between the two phases, our training approach leverages the strengths of both methods while mitigating the risk of local minima caused by extended training.

3.4.4 KL Divergence Regularization Term

The RL and seq2seq training phases differ in their input training trajectories and output target spaces, which can lead to instability and catastrophic forgetting of previously learned knowledge when switching between these phases. To address these issues, inspired by the PPO algorithm, which uses KL divergence [39] to regulate parameter updates, we introduce a KL divergence regularization term that incorporates only the correctly learned knowledge from both the seq2seq and RL phases.

To improve consistency between the RL and seq2seq training phases and mitigate catastrophic forgetting during phase transitions, the KL divergence regularization term is incorporated into both the RL and seq2seq loss functions. At each phase transition, a backup of the model parameters is created. As the model continues to update its parameters, the backup and current models generate different output distributions for the same input trajectory. Let dold denote the output distribution of the model parameters preserved at the training phase transition, and dcur represent the output distribution of the current model parameters. The KL divergence regularization term is then calculated using the following equation:

𝒦ℒ(dold∥dcur)=∑idioldlog⁡diolddicur(24)

where diold is the i-th element of dold. When computing the KL divergence, only the correct reasoning trajectories (those with the correct tail entities) are sampled for the KL divergence term, rather than using all input trajectories from the training set. When transitioning from the RL to the seq2seq training phase, the correct reasoning trajectories identified by the model during the final RL epoch are first collected to form the KL divergence input set. From this set, a batch of trajectories is sampled to compute the KL divergence regularization term during the seq2seq training phase. When switching from the seq2seq to the RL phase, the correct reasoning trajectories are also sampled for KL divergence computation of the RL training process. The KL divergence regularization term is incorporated into the loss function with a regularization coefficient as follows:

ℒRL′=ℒRL+γ𝒦ℒ(dold∥dcur)(25)

ℒseq′=ℒseq+γ(𝒦ℒent(dold∥dcur)+𝒦ℒrel(dold∥dcur))(26)

where γ is the regularization coefficient. The 𝒦ℒent and 𝒦ℒrel are the KL divergence terms corresponding to the entity and relation output distributions during the seq2seq training phase, respectively. In practice, this regularization term is applied throughout the entire seq2seq phase, whereas in the RL phase, it is only activated during the initial epochs, making the RL loss function similar to that used in the PPO algorithm [35].

4  Experiments

4.1 Datasets

We evaluated the proposed CycDE on five KGs, each with a distinct structure: (1) FB15K-237 [40], (2) WN18RR [15] (dataset based on wordnet [41]), (3) DBP-5L-English [42] (DBP_EN for short), (4) YAGO39K [43] and (5) NELL-995 [25]. The statistical information about these KGs is provided in Table 1.

4.2 Baseline Methods

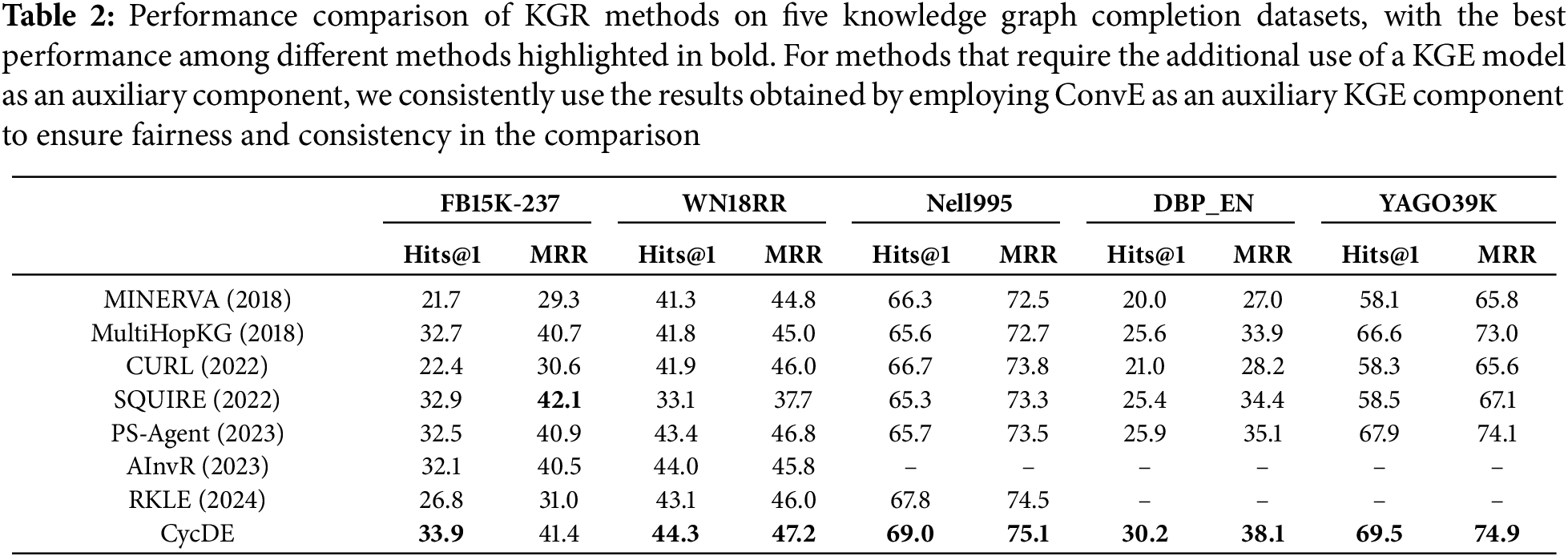
We compared the proposed CycDE with seven baselines, all of which perform multi-hop KGR: MINERVA [7], CURL [10], MultiHopKG [9], Ps-agent [11], AInvR [27] and RKLE [28] are based on policy-based RL methods; whereas SQUIRE [8] is based on sequence to sequence paradigm. In the aforementioned methods, for those that require the additional use of a KGE model as an auxiliary component, we consistently use the results obtained by employing ConvE as an auxiliary KGE component to ensure fairness and consistency in the comparison.

4.3 Evaluation Metrics

We use the Mean Reciprocal Rank (MRR) and Hits at One (Hits@1) metrics for evaluation. Following previous multi-hop reasoning studies, for a given triple query (eh,rq,?) with the tail entity et missing, the proposed model generates several candidate answer entities via beam search. The rank of the ground-truth tail entity among the candidate entities is calculated after filtering out the other correct entities. Based on this rank, two evaluation metrics are calculated: (1) MRR, which calculates the average reciprocals of the ranks for the ground-truth tail entities, and (2) Hits@1, which measures the proportion of test cases where the ground-truth tail entities are ranked first.

4.4 Main Results

Table 2 presents the results of knowledge graph reasoning across five datasets. The proposed CycDE framework outperforms all baseline methods in Hits@1 metric on every dataset. Specifically, CycDE achieves an average improvement of 1.7% in this metric compared to the best baseline methods for each dataset. Notably, on the DBP_EN dataset, the model demonstrates the largest improvement, reaching 4.3%. These Hits@1 results highlight CycDE’s effectiveness in accurately identifying the target missing entity, rather than providing a vague range of candidates. In terms of the MRR metric, CycDE outperforms all baseline models on four datasets and ranks second on the FB15K-237 dataset. On average, the improvement in MRR across all benchmarks is 0.8%, with the largest improvement observed on the DBP_EN dataset, reaching 3.0%. These results indicate that the proposed model is effective across a range of KGs due to the MDE and cyclical training. In addition, the seq2seq method SQUIRE is more sensitive to the quality and quantity of training data. For example, the performance of SQUIRE on the WN18RR dataset is significantly below average. By comparing the list of valid rules generated by SQUIRE on the WN18RR dataset, we find that the valid rules in this dataset are smaller in scale compared to those in other datasets. In SQUIRE, a path is considered to meet quality requirements only when its rule is in the valid rules list, meaning that most paths in this dataset are deemed low quality. This demonstrates that SQUIRE struggles to perform well on knowledge graphs containing a large number of low-quality paths. In contrast, RL-based methods, including the proposed CycDE model, demonstrate greater robustness on the WN18RR dataset.

4.5 Ablation Studies

The ablation studies are conducted by removing three key components: MDE (without MDE), seq2seq training phase (without seq2seq), and policy-based RL training phase (without RL). The results presented in Table 3 demonstrate that each component contributes significantly to the overall performance. For MDE module, the results indicate that the original CycDE with the MDE module outperforms the CycDE without it, achieving an average improvement of 4.05% in Hits@1 and 3.05% in MRR. Regarding the cyclical training module, the ablation study shows that the CycDE framework with cyclical training outperforms the training methods using only RL or seq2seq, with an average improvement of 7.0% in Hit@1 and 6.1% in MRR. At the same time, the ablation study results reveal that in the cyclical training, the policy-based RL phase plays a pivotal role.

4.6 Long Reasoning Path Performance

To assess whether our multimodal data encoding module effectively captures complex entity and relation features, we selected example triples from the NELL-995 test set where the answer entity is located at least two or three hops away from the head entity. Triples with a greater distance between the head and tail entities involve complex reasoning paths with multiple entities and relations, making the accurate understanding of graph structures and relational properties more challenging for the model. This requires the model to effectively model and extract information about entities, relationships, and their interactions, rather than merely memorizing the reasoning process. Table 4 presents the Hits@1 and MRR results for both the two-hop and three-hop conditions on the NELL-995 dataset, comparing the performance of the proposed CycDE method with MDE and the PS-agent method without MDE.

Overall, the proposed model with MDE achieves superior performance compared to the PS-agent model under both multi-hop conditions involving multiple entities and relations during inference. This indicates that the MDE module successfully encodes more expressive representations of entities and relations. As a result, the proposed model gains a deeper understanding of the graph structure and the correlations among relations and entities, enabling it to make decisions based on this advanced understanding rather than relying on memorized reasoning paths. In contrast, the PS-agent model, lacking an equivalent representation of graph components like the MDE module, tends to rely more on guesswork rather than making informed decisions. This tendency becomes more pronounced as the length of the reasoning paths increases.

4.7 Case Study

Fig. 3 shows several reasoning paths generated by the proposed CycDE model and the PS-agent model. In all cases, CycDE successfully infers the correct tail entities, and the corresponding reasoning paths exhibit good interpretability. For example, in the query (Team Seattle Mariners, Team plays sports, ?), CycDE correctly infers the tail entity “Baseball” and provides an evidential path. Through the triple (Team Seattle Mariners, Plays against, Team Chicago Cubs) in the evidential path, it establishes that the team Seattle Mariners has competed against the Chicago Cubs. Subsequently, the triple (Team Chicago Cubs, Team plays sports, Baseball) in the path demonstrates that the team Chicago Cubs plays the sport of baseball. Based on this reasoning, the conclusion that the sports team Seattle Mariners plays baseball can be drawn. The reasoning path outlined above effectively explains why the CycDE model provides “Baseball” as the answer entity. In contrast, the reasoning paths of the PS-agent model contain numerous invalid self-loops, leading to suboptimal interpretability and answer accuracy. This disparity can be attributed to the MDE module in the CycDE model, which produces more effective representations of entities and relations. Consequently, the CycDE quickly identifies relevant entities and relations, even when handling unfamiliar examples in the test set. For instance, in the query (Crosby, Athlete plays for team, Team Pittsburgh Penguins), the CycDE selects relations directly relevant to the query using BERT’s contextual relevance and the GRU structure, whereas the PS-agent selects unrelated relations. Unlike the CycDE model, the PS-agent model lacks an effective encoding module, resulting in frequent trial and error. Additionally, the frequent occurrence of the self-loop relation during training causes the PS-agent model to favor this operation, negatively impacting its output when faced with new queries from the test set.

Figure 3: Cases of reasoning paths. Prefix “Inv:” refers to the inverse of the relation

4.8 Convergence Analysis

In this section, the proposed cyclical training strategy is compared with RL training and seq2seq training on the DBP_EN dataset, focusing on the Hits@1 convergence curves of the validation set. To ensure a fair comparison, we use the same model architecture and train it using three different strategies: cyclical, seq2seq, and RL training.

As shown in Fig. 4, the cyclical training strategy demonstrates a faster convergence rate than the RL-only training strategy, highlighting the effectiveness of integrating the seq2seq phase into the proposed cyclical training of CycDE. The seq2seq phase enables the model to quickly learn from a sufficient number of positive examples, whereas the RL-only strategy has a lower likelihood of encountering positive examples, which reduces learning efficiency.

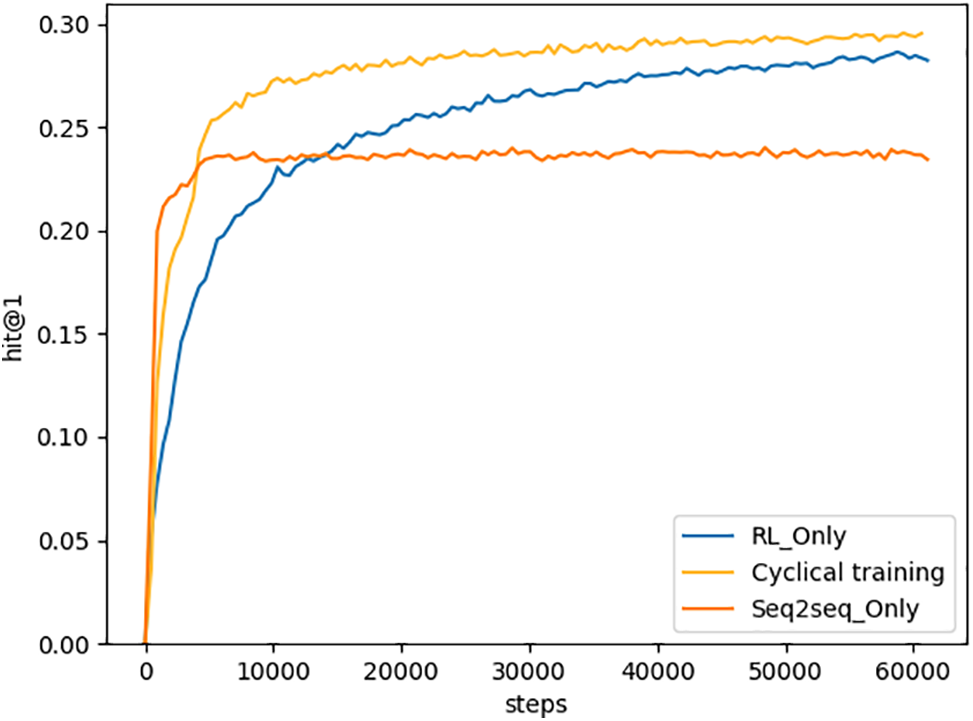
Figure 4: Convergence comparison between cyclical training (ours), RL training, and seq2seq training

Furthermore, the proposed cyclical training method achieves a higher Hits@1 convergence point than the other two methods, indicating a stronger ability to escape local minima. One possible explanation for this phenomenon is that by cyclically alternating between the seq2seq and RL phases over multiple loops, the model switches between two different input-output spaces and two distinct yet complementary training objectives. Specifically, when the model is trained in phase A for an extended period and is at risk of falling into a local minimum, switching to phase B adjusts the model parameters, positioning them differently in the parameter space and providing a fresh gradient direction. When the model returns to phase A in the next loop, it continues to converge from this new parameter state, thus avoiding being trapped in a local minimum caused by limited gradient directions during prolonged training in a single phase.

Additionally, the training curve of the proposed cyclical approach does not exhibit significant fluctuations, indicating that the method effectively enhances stability during phase transitions and reduces the likelihood of the model forgetting previous knowledge when switching to new training objectives, thus enabling continuous improvement in overall performance.

4.9 Analysis of Graph Pattern Clusters

In this section, the proposed CycDE framework based on cyclical training is compared with two baseline methods: (1) the PS-agent trained using the RL-only training strategy and (2) SQUIRE trained using the seq2seq-only training strategy. We evaluate their ability to adapt to different graph patterns and their level of specialization for individual graph patterns using the DBP_EN test set. To categorize each triple in the test set, K-means clustering with 200 clusters is applied, with each cluster representing a specific graph pattern. For this purpose, the KGE model ConvE [15] is trained to obtain the head entity and relation embeddings for each triple. The K-means algorithm clusters the triples based on their head entity and relation embeddings, ensuring that triples with the same head entity and relation are grouped under the same graph pattern. The subsequent experiments are conducted using the 200 graph patterns derived from this clustering process.

4.9.1 Hit Rate on Graph Pattern Clusters

To evaluate the effectiveness of each training strategy, for the model of each method, the Hits@1 value is calculated across all graph pattern clusters in the DBP_EN test set. If a model achieves a Hits@1 score greater than 20% among the triples within a specific graph pattern, it is considered to have acquired some knowledge about that pattern. For each model, the number of graph patterns with a Hits@1 score greater than 20% is counted, and this number is then divided by the total number of graph pattern clusters (200) to obtain the proportion of graph patterns that meet the Hits@1 threshold. Table 5 presents the results for the PS-agent (RL-based), SQUIRE (seq2seq-based), and CycDE (proposed framework), showing the proportion of graph pattern clusters with a Hits@1 score greater than 20% among the total 200 graph pattern clusters for each method. As shown in the table, the proposed CycDE framework with the cyclical training strategy adapts to more graph patterns than the others. Both CycDE and the seq2seq-based SQUIRE outperform the RL-based PS-agent, indicating that the seq2seq objective provides better adaptability across diverse graph patterns than the RL-only strategy. The reason behind this phenomenon is that, under the seq2seq process, the output space spans all the entities and relations of the graph, helping the model transfer knowledge more easily across various graph patterns without being limited by the connectivity of the knowledge graph (KG). In contrast, the action space of RL is determined by the connectivity of the graph, which includes entities and relations only a few hops away from the head entity. Furthermore, the superior performance of CycDE over the seq2seq-only strategy indicates that the proposed cyclical training not only inherits the good adaptation ability of the seq2seq trajectory but also extends its effectiveness to a broader range of graph patterns. This improvement can be attributed to cyclical training and the KL divergence term, which mitigate catastrophic forgetting during strategy transitions and enable the model to steadily expand its knowledge across more graph patterns.

4.9.2 Comparative Analysis of Specialization Abilities within Individual Graph Patterns

To evaluate the specialization ability of the three methods, the Hits@1 values of their corresponding models are compared. The comparison is made on the graph patterns where all three methods achieve a Hits@1 greater than 20%. Since most graph pattern clusters in the DBP_EN test set contain fewer than 30 triples, we focus only on those with more than 100 triples to minimize the impact of testing variance. Fig. 5 presents a pairwise comparison of the Hits@1 scores of the three methods based on the selected graph patterns. “RL” represents the PS-Agent method, “seq2seq” represents the SQUIRE method, and “CycDE” represents the proposed method. For example, the number 9 on the blue bar under the label “CycDE vs. seq2seq” in Fig. 5 indicates that CycDE achieves higher Hits@1 compared to SQUIRE in 9 graph patterns.

Figure 5: Pair-wise comparison among three training strategies w.r.t. Hits@1 of graph patterns that are mutually covered by three strategies and contained more than 100 triples. The number above each bar is the number of graph patterns

Fig. 5 confirms that the proposed CycDE exhibits the best overall performance, followed by the RL-only method, PS-agent, with the seq2seq-only method, SQUIRE, ranking last. As shown in Fig. 5, among the selected graph patterns, the RL-only method outperforms the seq2seq-only method, indicating that although the RL-only strategy adapts to fewer graph patterns compared to the seq2seq-only strategy, it explores certain graph patterns in greater depth, highlighting the specialization ability of the RL method. These advantages arise because the reasoning trajectories sampled during the training process using RL are highly correlated with the current model parameters. Therefore, in contrast to seq2seq, which uses fixed training trajectories, RL allows for more targeted error correction of the model. As a result, when the model has a foundational understanding of a pattern, RL achieves a higher learning capacity via better error correction. Furthermore, the comparison between CycDE and the RL-only method reveals that the proposed cyclical training-based CycDE not only covers a broader range of graph patterns but also performs better than the RL-only method in terms of Hits@1 across most graph patterns. This finding demonstrates that the proposed strategy effectively leverages the specialization ability to achieve a thorough understanding of the learned patterns, and the incorporation of the seq2seq phase into CycDE does not compromise its specialization ability in favor of adaptation capability.

5  Conclusion

In this paper, we present the CycDE framework, which incorporates a cyclical training method that alternates periodically between the reinforcement learning phase and the sequence-to-sequence training phase for several cycles, as well as a knowledge graph reasoning model that includes a multimodal data encoding module and a transformer-based reasoning module. Through experiment on five knowledge graph completion benchmarks of varying scales and content, our framework demonstrates more stable and superior performance compared to other baseline models. Additionally, through ablation studies, case studies, and other specific experiments, the roles and performance of each sub-module are validated from different perspectives.

Acknowledgement: We would like to express our sincere gratitude to all the teachers and students involved for their support and collaboration, and to our families for their unwavering encouragement.

Funding Statement: This work is supported by the National Key Research and Development Program of China (No. 2023YFF0905400) and the National Natural Science Foundation of China (No. U2341229).

Author Contributions: Xiaotong Han: Methodology, Software, Conceptualization, Investigation, Validation, Writing—original draft. Yunqi Jiang: Visualization, Investigation. Haitao Wang: Data curation. Yuan Tian: Supervision, Project administration, Resources, Writing—review and editing. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The sources of all datasets are cited in the paper, and can be accessed through the links or GitHub repositories provided in their corresponding papers. Other data content can be obtained by contacting the authors. Access links for datasets: (1) FB15K-237: https://www.microsoft.com/en-us/download/details.aspx?id=52312 (accessed on 07 January 2025); (2) WN18RR: https://github.com/TimDettmers/ConvE (accessed on 07 January 2025); (3) Nell-995: https://github.com/xwhan/DeepPath (accessed on 07 January 2025); (4) YAGO39K: https://github.com/davidlvxin/TransC (accessed on 07 January 2025); (5) DBP-5L (English): https://github.com/stasl0217/KEnS (accessed on 07 January 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Wang H, Zhou B, Zhang L, Ma H. Recommendation method for contrastive enhancement of neighborhood information. Comput Mat Cont. 2024;78(1):453–72. doi:10.32604/cmc.2023.046560. [Google Scholar] [CrossRef]

2. Chen H, Xie R, Cui X, Yan Z, Wang X, Xuan Z, et al. LKPNR: large language models and knowledge graph for personalized news recommendation framework. Comput Mater Contin. 2024;79(3):4283–96. doi:10.32604/cmc.2024.049129. [Google Scholar] [CrossRef]

3. Liu Z, Xiong C, Sun M, Liu Z. Entity-duet neural ranking: understanding the role of knowledge graph semantics in neural information retrieval. In: Gurevych I, Miyao Y, editors. Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics, ACL 2018; 2018 Jul 15–20; Melbourne, Australia: Association for Computational Linguistics; 2018. Vol. 1, p. 2395–405. [Google Scholar]

4. Moiseev F, Dong Z, Alfonseca E, Jaggi M. SKILL: structured knowledge infusion for large language models. In: Carpuat M, de Marneffe MC, Meza Ruiz MCIV, editors. Proceedings of the 2022 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies; 2022; Seattle, WA, USA. p. 1581–8. [Google Scholar]

5. Bordes A, Usunier N, García-Durán A, Weston J, Yakhnenko O. Translating embeddings for modeling multi-relational data. In: Burges CJC, Bottou L, Ghahramani Z, Weinberger KQ, editors. Advances in Neural Information Processing Systems 26: 27th Annual Conference on Neural Information Processing Systems 2013; 2013 Dec 5–8 Lake Tahoe, NV, USA; 2013. p. 2787–95. [Google Scholar]

6. Yao L, Mao C, Luo Y. KG-BERT: BERT for knowledge graph completion. arXiv:1909.03193. 2019. [Google Scholar]

7. Das R, Dhuliawala S, Zaheer M, Vilnis L, Durugkar I, Krishnamurthy A, et al. Go for a walk and arrive at the answer: reasoning over paths in knowledge bases using reinforcement learning. In: 6th International Conference on Learning Representations, ICLR 2018; 2018 Apr 30–May 3; Vancouver, BC, Canada. [Google Scholar]

8. Bai Y, Lv X, Li J, Hou L, Qu Y, Dai Z, et al. SQUIRE: a sequence-to-sequence framework for multi-hop knowledge graph reasoning. In: Goldberg Y, Kozareva Z, Zhang Y, editors. Proceedings of the 2022 Conference on Empirical Methods in Natural Language Processing. Abu Dhabi, United Arab Emirates; 2022. p. 1649–62. [Google Scholar]

9. Lin XV, Socher R, Xiong C. Multi-hop knowledge graph reasoning with reward shaping. In: Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing; 2018; Brussels, Belgium: Association for Computational Linguistics. p. 3243–53. [Google Scholar]

10. Zhang D, Yuan Z, Liu H, lin X, Xiong H. Learning to walk with dual agents for knowledge graph reasoning. Proce AAAI Conf Artif Intell. 2022;36(5):5932–41. doi:10.1609/aaai.v36i5.20538. [Google Scholar] [CrossRef]

11. Jiang C, Zhu T, Zhou H, Liu C, Deng T, Hu C, et al. Path spuriousness-aware reinforcement learning for multi-hop knowledge graph reasoning. In: Proceedings of the 17th Conference of the European Chapter of the Association for Computational Linguistics; 2023; Dubrovnik, Croatia. p. 3181–92. [Google Scholar]

12. Chung J, Gülçehre Ç, Cho K, Bengio Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv:1412.3555. 2014. [Google Scholar]

13. Devlin J, Chang M, Lee K, Toutanova K. BERT: pre-training of deep bidirectional transformers for language understanding. In: Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2019; 2019 Jun 2–7; Minneapolis, MN, USA; 2019. p. 4171–86. [Google Scholar]

14. Velickovic P, Cucurull G, Casanova A, Romero A, Liò P, Bengio Y. Graph attention networks. arXiv:1710.10903. 2017. [Google Scholar]

15. Dettmers T, Minervini P, Stenetorp P, Riedel S. Convolutional 2D knowledge graph embeddings. In: Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence and Thirtieth Innovative Applications of Artificial Intelligence Conference and Eighth AAAI Symposium on Educational Advances in Artificial Intelligence; 2018; New Orleans, LA, USA. [Google Scholar]

16. Trouillon T, Welbl J, Riedel S, Gaussier É., Bouchard G. Complex embeddings for simple link prediction. In: Knowledge graph and semantic computing: knowledge graph empowers artificial general intelligence; 2016 Jun 19–24; New York City, NY, USA; 2018. Vol. 48, p. 2071–80. [Google Scholar]

17. Yichi Z, Wen Z. CausE: towards causal knowledge graph embedding. In: Wang H, Han X, Liu M, Cheng G, Liu Y, Zhang N, editor. Knowledge Graph and Semantic Computing: Knowledge Graph Empowers Artificial General Intelligence; 2023; Singapore: Springer Nature Singapore. p. 17–28. [Google Scholar]

18. Raffel C, Shazeer N, Roberts A, Lee K, Narang S, Matena M, et al. Exploring the limits of transfer learning with a unified text-to-text transformer. J Mach Learn Res. 2020;21:140:1–67. [Google Scholar]

19. Radford A, Wu J, Child R, Luan D, Amodei D, Sutskever I, et al. Language models are unsupervised multitask learners. OpenAI Blog. 2019;1(8):9. [Google Scholar]

20. Wang L, Zhao W, Wei Z, Liu J. SimKGC: simple contrastive knowledge graph completion with pre-trained language models. In: Muresan S, Nakov P, Villavicencio A, editors. Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers); 2022; Dublin, Ireland. p. 4281–94. [Google Scholar]

21. Saxena A, Kochsiek A, Gemulla R. Sequence-to-sequence knowledge graph completion and question answering. In: Muresan S, Nakov P, Villavicencio A, editor. Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers); 2022; Dublin, Ireland. p. 2814–28. [Google Scholar]

22. Chen K, Wang Y, Li Y, Li A. RotateQVS: representing temporal information as rotations in quaternion vector space for temporal knowledge graph completion. In: Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long PapersACL 2022; 2022 May 22–27; Dublin, Ireland; 2022. p. 5843–57. [Google Scholar]

23. Fang Z, Qin J, Zhu X, Yang C, Yin X. Arbitrary time information modeling via polynomial approximation for temporal knowledge graph embedding. In: Proceedings of the 2024 Joint International Conference on Computational Linguistics, Language Resources and Evaluation, LREC/COLING 2024; 2024 May 20–25; Torino, Italy; 2024. p. 1455–65. [Google Scholar]

24. Ying R, Hu M, Wu J, Xie Y, Liu X, Wang Z, et al. Simple but effective compound geometric operations for temporal knowledge graph completion. In: Proceedings of the 62nd Annual Meeting of the Association for Computational Linguistics (Volume 1: Long PapersACL 2024; 2024 Aug 11–16; Bangkok, Thailand; 2024. p. 11074–86. [Google Scholar]

25. Xiong W, Hoang T, Wang WY. DeepPath: a reinforcement learning method for knowledge graph reasoning. In: Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, EMNLP 2017; 2017 Sep 9–11; Copenhagen, Denmark; 2017. p. 564–73. [Google Scholar]

26. Wang H, Li S, Pan R, Mao M. Incorporating graph attention mechanism into knowledge graph reasoning based on deep reinforcement learning. In: Inui K, Jiang J, Ng V, Wan X, editors. Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing, EMNLP-IJCNLP 2019; 2019 Nov 3–7; Hong Kong, China; 2019. p. 2623–31. [Google Scholar]

27. Zhang H, Lu G, Qin K, Du K. AInvR: adaptive learning rewards for knowledge graph reasoning using agent trajectories. Tsinghua Sci Technol. 2023;28(6):1101–14. doi:10.26599/TST.2022.9010063. [Google Scholar] [CrossRef]

28. Liu R, Yin G, Liu Z. Learning to walk with logical embedding for knowledge reasoning. Inf Sci. 2024;667:120471. doi:10.1016/j.ins.2024.120471. [Google Scholar] [CrossRef]

29. Chen L, Lu K, Rajeswaran A, Lee K, Grover A, Laskin M, et al. Decision transformer: reinforcement learning via sequence modeling. In: Advances in Neural Information Processing Systems 34: Annual Conference on Neural Information Processing Systems 2021, NeurIPS 2021; 2021 Dec 6–14; Virtual; Red Hook, NY, USA; 2021. p. 15084–97. [Google Scholar]

30. van Hasselt H. Double Q-learning. In: Advances in Neural Information Processing Systems 23: 24th Annual Conference on Neural Information Processing Systems 2010; 2010 Dec 6–9; Vancouver, BC, Canada; 2010. p. 2613–21. [Google Scholar]

31. Mnih V, Kavukcuoglu K, Silver D, Rusu AA, Veness J, Bellemare MG, et al. Human-level control through deep reinforcement learning. Nature. 2015;518(7540):529–33. doi:10.1038/nature14236. [Google Scholar] [PubMed] [CrossRef]

32. Hessel M, Modayil J, van Hasselt H, Schaul T, Ostrovski G, Dabney W, et al. Rainbow: combining improvements in deep reinforcement learning. In: Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, (AAAI-18the 30th Innovative Applications of Artificial Intelligence (IAAI-18and the 8th AAAI Symposium on Educational Advances in Artificial Intelligence (EAAI-18); 2018 Feb 2–7; New Orleans, LA, USA; 2018. p. 3215–22. [Google Scholar]

33. Williams RJ. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach Learn. 1992;8(3–4):229–56. doi:10.1007/BF00992696. [Google Scholar] [CrossRef]

34. Schulman J, Levine S, Abbeel P, Jordan MI, Moritz P. Trust region policy optimization. In: Bach FR, Blei DM, editors. Proceedings of the 32nd International Conference on Machine Learning, ICML 2015; 2015 Jul 6–11; Lille, France; 2015. Vol. 37, p. 1889–97. [Google Scholar]

35. Schulman J, Wolski F, Dhariwal P, Radford A, Klimov O. Proximal policy optimization algorithms. arXiv:1707.06347. 2017. [Google Scholar]

36. Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, et al. Attention is all you need. In: Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017; 2017 Dec 4–9; Long Beach, CA, USA; 2017. p. 5998–6008. [Google Scholar]

37. Dai D, Dong L, Hao Y, Sui Z, Chang B, Wei F. Knowledge neurons in pretrained transformers. In: Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long PapersACL 2022; 2022 May 22–27; Dublin, Ireland; 2022. p. 8493–502. [Google Scholar]

38. Geva M, Schuster R, Berant J, Levy O. Transformer feed-forward layers are key-value memories. In: Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing, EMNLP 2021; 2021 Nov 7–11; Punta Cana, Dominican Republic; 2021. p. 5484–95. [Google Scholar]

39. Kullback S, Leibler RA. On Information and Sufficiency. Ann Math Stat. 1951;22(1):79–86. doi:10.1214/aoms/1177729694. [Google Scholar] [CrossRef]

40. Toutanova K, Chen D. Observed versus latent features for knowledge base and text inference. In: Proceedings of the 3rd Workshop on Continuous Vector Space Models and their Compositionality, CVSC 2015; 2015 Jul 26–31; Beijing, China; 2015. p. 57–66. [Google Scholar]

41. Miller GA. WordNet: a lexical database for english. In: Human Language Technology: Proceedings of a Workshop held at Plainsboro, New Jersey; 1992 Feb 23–26; Harriman, TN, USA: Morgan Kaufmann. [Google Scholar]

42. Chen X, Chen M, Fan C, Uppunda A, Sun Y, Zaniolo C. Multilingual knowledge graph completion via ensemble knowledge transfer. In: Cohn T, He Y, Liu Y, editors. Findings of the Association for Computational Linguistics: EMNLP 2020; 2020 Nov 16–20; Stroudsburg, PA, USA; 2020. p. 3227–38. [Google Scholar]

43. Lv X, Hou L, Li J, Liu Z. Differentiating concepts and instances for knowledge graph embedding. In: Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing; 2018; Brussels, Belgium: Association for Computational Linguistics. p. 1971–9. [Google Scholar]