 Open Access
Open Access
ARTICLE
Frequency-Quantized Variational Autoencoder Based on 2D-FFT for Enhanced Image Reconstruction and Generation
1 School of Information Engineering, Dalian University, Dalian, 116622, China
2 Key Laboratory of Communication and Networks, Dalian University, Dalian, 116622, China
* Corresponding Author: Jianxin Feng. Email:
Computers, Materials & Continua 2025, 83(2), 2087-2107. https://doi.org/10.32604/cmc.2025.060252
Received 28 October 2024; Accepted 08 February 2025; Issue published 16 April 2025
Abstract
As a form of discrete representation learning, Vector Quantized Variational Autoencoders (VQ-VAE) have increasingly been applied to generative and multimodal tasks due to their ease of embedding and representative capacity. However, existing VQ-VAEs often perform quantization in the spatial domain, ignoring global structural information and potentially suffering from codebook collapse and information coupling issues. This paper proposes a frequency quantized variational autoencoder (FQ-VAE) to address these issues. The proposed method transforms image features into linear combinations in the frequency domain using a 2D fast Fourier transform (2D-FFT) and performs adaptive quantization on these frequency components to preserve image’s global relationships. The codebook is dynamically optimized to avoid collapse and information coupling issue by considering the usage frequency and dependency of code vectors. Furthermore, we introduce a post-processing module based on graph convolutional networks to further improve reconstruction quality. Experimental results on four public datasets demonstrate that the proposed method outperforms state-of-the-art approaches in terms of Structural Similarity Index (SSIM), Learned Perceptual Image Patch Similarity (LPIPS), and Reconstruction Fréchet Inception Distance (rFID). In the experiments on the CIFAR-10 dataset, compared to the baseline method VQ-VAE, the proposed method improves the above metrics by 4.9%, 36.4%, and 52.8%, respectively.Keywords
In recent years, the rapid development of deep learning technologies has brought increasing attention to discrete representation learning. Variational Autoencoders (VAE) [1] introduced a probabilistic approach to learning compressed latent representations, laying the foundation for discrete representation learning. The advent of Generative Adversarial Networks (GANs) [2] and Transformers [3] further enriched the downstream tasks of discrete representation learning, achieving stunning results. For instance, the Vector Quantized Generative Adversarial Network (VQGAN) [4] architecture, which combines the strengths of VAEs and GANs, has demonstrated remarkable performance in high-resolution image synthesis. More recently, the popularity of diffusion models has led to significant advancements in generative modeling. By incorporating discrete representation learning, such as in the Vector Quantized Diffusion [5] model, these techniques have not only enhanced the quality of generated samples but also greatly improved model efficiency. The success of these approaches underscores the importance and potential of discrete representation learning in the field of deep learning.
Among the various discrete representation learning methods, Vector Quantized Variational Autoencoders (VQ-VAE) [6] have gained prominence due to their advantages in representative capacity and ease of embedding. VQ-VAE maps continuous feature vectors into discrete spaces through vector quantization and employs a nearest-neighbor algorithm to select the most appropriate discrete vector, simplifying the optimization problem. This approach enables the model to more efficiently capture the fundamental structure and features of the data, leading to its widespread application across multiple domains [7].
Although VQ-VAE has been integrated into various deep learning models as a mature machine learning method, challenges remain regarding the efficiency and accuracy of quantization. In VQ-VAE, the encoder divides the input image into a regular fixed grid, segmented into multiple units, considered “tokens,” to represent the image’s features. During the quantization process, these tokens interact with a set of vectors known as a codebook, optimized such that the codebook captures as much of the image’s representational information as possible, thereby improving the expressive power of the quantized encoding. However, this process introduces a significant issue: disrupting the global relationships within the image.
Unlike the independence of words in natural language processing, image features are typically interrelated holistically. Processing individual image patches not only smooths out high-frequency information, causing blurring during reconstruction but also increases the difficulty of training for downstream tasks such as image generation. To address these issues, Tian et al. [8] designed a multi-scale VQ-VAE model, which quantizes data at different scales into latent vectors and shares a single codebook. On the other hand, Huang et al. [9] proposed a progressive quantization autoencoder from the perspective of maximizing information in limited discrete codes, aligning the codebook dimensions with the latent feature dimensions generated by the encoder. To some extent, these methods have preserved the global correlation of features, but progressive quantization increases the training complexity, undermining the advantages of parallel training in neural networks. Moreover, since code vectors are directly mapped from globally unseparated features, this leads to an information coupling issue—similar code vectors tend to capture redundant information. This reduces the amount of practical information in the codebook and limits the diversity in downstream tasks such as generation.
The efficiency of the codebook is one of the critical factors influencing the quality of representation learning in models. Several studies have explored the codebook collapse issue [10] to improve the reconstruction quality of models. Codebook collapse refers to a scenario where only a small subset of codevectors are co-optimized with latent features, leaving most of the entries in the codebook unused. The literature [10–12] has proposed various approaches to mitigate this problem, including random initialization, random quantization, and latent clustering. While these methods have improved codebook utilization to some extent, they are still based on spatial domain partitioning quantization, which neglects the global correlation of image features, thus limiting the model’s expressiveness and increasing the difficulty of training for downstream tasks such as image generation.
This paper proposes a Frequency-Quantized Autoencoder (FQ-VAE) to preserve images’ global relationships through frequency domain feature extraction while achieving high-quality image reconstruction. The core of this method lies in utilizing the 2D Fast Fourier Transform (2D-FFT) to encode the original data as a linear combination of different feature components in the frequency domain, with these components subsequently quantized. To further optimize the codebook, this paper dynamically updates it by considering both the usage frequency and dependency of codevectors. Moving codevectors with low usage frequency ensures that all codevectors are updated, effectively preventing codebook collapse. Codevectors with high dependency are significantly updated to avoid information coupling within the codebook. Additionally, this paper introduces graph convolution theory to design and solve correction weights for the quantized features, which helps refine the quantized features and further reduces quantization loss.
By performing quantization and encoding in the frequency domain, the proposed method effectively avoids the loss of global relationships caused by spatial domain partitioning, significantly enhancing the model’s expressive power and reconstruction quality while improving its applicability to downstream tasks.
The main contributions of this paper are as follows:
1. Proposed a novel frequency-quantized variational autoencoder (FQ-VAE) method: This method quantizes image features by transforming them from the spatial domain to the frequency domain, effectively preserving the global relationships among image features.
2. Designed an adaptive quantization encoder based on 2D-FFT: The encoder uses 2D-FFT to convert spatial domain feature maps into a combination of essential features in the frequency domain, enabling the adaptive extraction of more effective feature information.
3. Optimized the structure of the codebook: During the dynamic update of the codebook, both the usage frequency and dependency of code vectors were considered, preventing issues such as codebook collapse and information coupling.
4. Introduced graph convolution theory to refine quantized features: Using a Graph Convolutional Model (GCM), the method obtains correction weights for different frequency features, further reducing the information loss caused by quantization.
5. Validated the method’s effectiveness: In image reconstruction tasks, the proposed method was compared with state-of-the-art methods on four benchmark datasets, demonstrating superior performance. Additionally, it proved capable of generating high-quality images in generative tasks.
The remainder of this paper is structured as follows: Section 2 provides an overview of related work, focusing on VQ-VAE and its variants, as well as recent advances in 2D-FFT-based neural networks and graph convolutional networks. Section 3 presents the proposed FQ-VAE in detail, including the adaptive quantization encoder based on 2D-FFT, the codebook optimization strategy, and the graph convolution-based feature refinement module. Section 4 reports the experimental results on image reconstruction and generation tasks, along with relevant ablation studies. Finally, Section 5 summarizes the entire paper and discusses the limitations of the method and potential future research directions.
2.1 Vector Quantised Variational Autoencoder
VQ-VAE is a generative model combining Variational Autoencoders principles with vector quantization techniques. By quantizing continuous feature vectors into discrete representations, it learns and generates using a codebook composed of a finite set of codevectors. This approach not only enables the model to learn compact representations of data but is also widely applied across various downstream tasks, such as image generation [13], video generation [14], audio generation [15], communication systems [16], and recognition [17].
The reconstruction quality of VQ-VAE directly reflects the model’s ability to learn from the original data and, at the same time, sets an upper bound for performance in downstream tasks. To improve image reconstruction quality, several research works have proposed different enhancements. Razavi et al. [18] improved the VQ-VAE model by designing a multi-scale hierarchical structure, separating global information at the top layers from local information at the bottom layers, which enabled the generation of globally coherent and locally high-resolution images. Additionally, VQGAN and Vision-Transformer-based VQGAN (ViT-VQGAN) [19] introduced Generative Adversarial Networks and Transformer architectures into the training process, further enhancing reconstruction quality. Residual-Quantized VAE (RQ-VAE) and Modulating Quantized Vectors (MoVQ) [20] improved reconstruction by utilizing multi-channel representations, though at the cost of increasing the dimensionality of latent features, which reduces the model’s compression efficiency.
Recently, several methods have been proposed to address the codebook collapse issue. Williams et al. proposed Hierarchical Quantized Autoencoders (HQ-VAE), while Dhariwal et al. [21] introduced Jukebox. Both methods implement a codebook resetting mechanism, randomly reinitializing unused or infrequently used codebook entries. Takida et al. introduced the Stochastically Quantized Variational Autoencoder (SQ-VAE), which incorporates a self-annealing process to learn an effective codebook from the initial stochastic quantization. Vuong et al. [22] proposed the Vector Quantized Wasserstein Autoencoder (VQ-WAE), which replaces the KL divergence with the Wasserstein distance as a regularization term to ensure a uniform distribution of discrete representations. The most relevant work is the Clustering VQ-VAE (CVQ-VAE) proposed by Zheng et al., which takes into account the variability of features in deep networks by employing running mean updates within training batches to capture the dynamic changes throughout the training process. In contrast, CVQ-VAE achieves better reconstruction results while ensuring 100% codebook utilization. Despite the improvements these methods offer in terms of encoding-decoding and codebook utilization, they still suffer from issues affecting images’ global coherence. This paper maps latent features into multi-frequency combinations in the frequency domain, ensuring global information preservation in the images, thereby enhancing the codebook’s information capacity and the model’s representative capabilities.
Fourier transform has been widely applied in neural networks to enhance feature extraction capabilities in recent years. For instance, Lee-Thorp et al. [23] proposed the Filter Networks (FNet), which replaces the self-attention sublayer in the Transformer encoder with a standard, unparameterized Fourier transform, achieving competitive performance while accelerating the training process. Building on this, Sevim et al. [24] further improved the approach by introducing Fast-FNet, significantly enhancing model efficiency. These methods have been extensively applied in the field of natural language processing (NLP), and research on Fourier transforms in the vision domain has also been gradually increasing.
Rao et al. [25] proposed Global Filter Networks (GFNet), which utilize the 2D Discrete Fourier Transform (2D-DFT) to transform features into the frequency domain and multiply them with a global filter, achieving a reasonable balance between accuracy and complexity in image classification tasks. Subsequently, Rao et al. [26] applied this method to visual recognition tasks, improving efficiency while maintaining accuracy. However, the global filters in GFNet are shared parameters used by all samples, which somewhat weakens the model’s generalization ability. Wang et al. [27] designed an attention network based on multi-scale fast Fourier transform, extracting global information from images using FFT and combining it with spatial local information, further enhancing network performance. Building on this, Tatsunami et al. [28] developed dynamic global filters, narrowing the gap between Fourier transform-based global filters and the multi-head self-attention mechanism. These studies aim to enhance the feature extraction capability by acquiring a global receptive field through Fourier transform, with the final output in the frequency domain being a singular frequency domain feature map.
In contrast, the method proposed in this paper adaptively extracts multi-dimensional frequency domain features based on dynamic filtering and maps image features as linear combinations of these features. This provides new possibilities for feature quantization and better preserve information from the source data, reducing information loss.
2.3 Graph Convolution Networks
Graph convolution has emerged as a powerful tool for processing non-Euclidean data. By leveraging graph structures, Graph Convolutional Networks (GCNs) can effectively capture the complex relationships and dependencies among nodes in a graph, and have been widely applied in the field of computer vision. In recent years, graph convolution techniques have been increasingly employed in various tasks, including image classification [29], deep image clustering [30], feature fusion [31], and more.
In the context of feature optimization, graph convolution has shown great potential in enhancing learned features. Cai et al. [32] generated directional relationships between features by combining the Cross-Attention Mechanism and graph convolution techniques, thereby preserving image feature information to a higher degree. Yang et al. [33] introduced Spatial Graph Attention (SGA) to encode feature correlations in the spatial dimension, enriching feature representations and achieving significant performance improvements in the single image super-resolution (SISR) task. While these studies primarily apply graph convolution techniques in the spatial dimension, some research has also demonstrated promising results when applying them in the channel dimension. Li et al. [34] proposed a dynamic-channel graph convolutional network to map image channels to the topological space and synthesize the features of each channel on the topological map, addressing the limitation of insufficient channel information utilization and further enhancing image edge information. In the latest research, Xiang’s Adaptive Graph Channel Attention (AGCA) [35] introduces graph convolution theory into channel attention, treating each channel as a feature vertex and performing non-local operations on the features, significantly improving feature representation capabilities.
The proposed FQ-VAE method in this paper also leverages graph convolution to refine quantized features. By constructing a graph convolutional module, FQ-VAE learns the correction weights of different frequency components, which helps mitigate the information loss caused by quantization. The graph convolution operation enables the model to capture the relationships among frequency components and adaptively adjust their weights, resulting in more accurate and informative quantized features.
Given an image
VQ-VAE is trained by optimizing the following loss:
where
Our method is based on the VQ-VAE architecture, where the process from the original image input to the reconstructed image output passes through the encoder, quantizer, and decoder. As shown in Fig. 1, the encoder utilizes a 2D-FFT to transform image features into a representation in the frequency domain, forming a linear combination of frequency components. These components are then quantized in the quantizer. To avoid codebook collapse and mitigate potential information redundancy, we dynamically optimize the codebook by considering the usage frequency and dependencies among codevectors. In the decoder, we apply graph convolution theory to refine the quantized features and minimize quantization loss. The specific implementation details are provided in the subsequent sections.
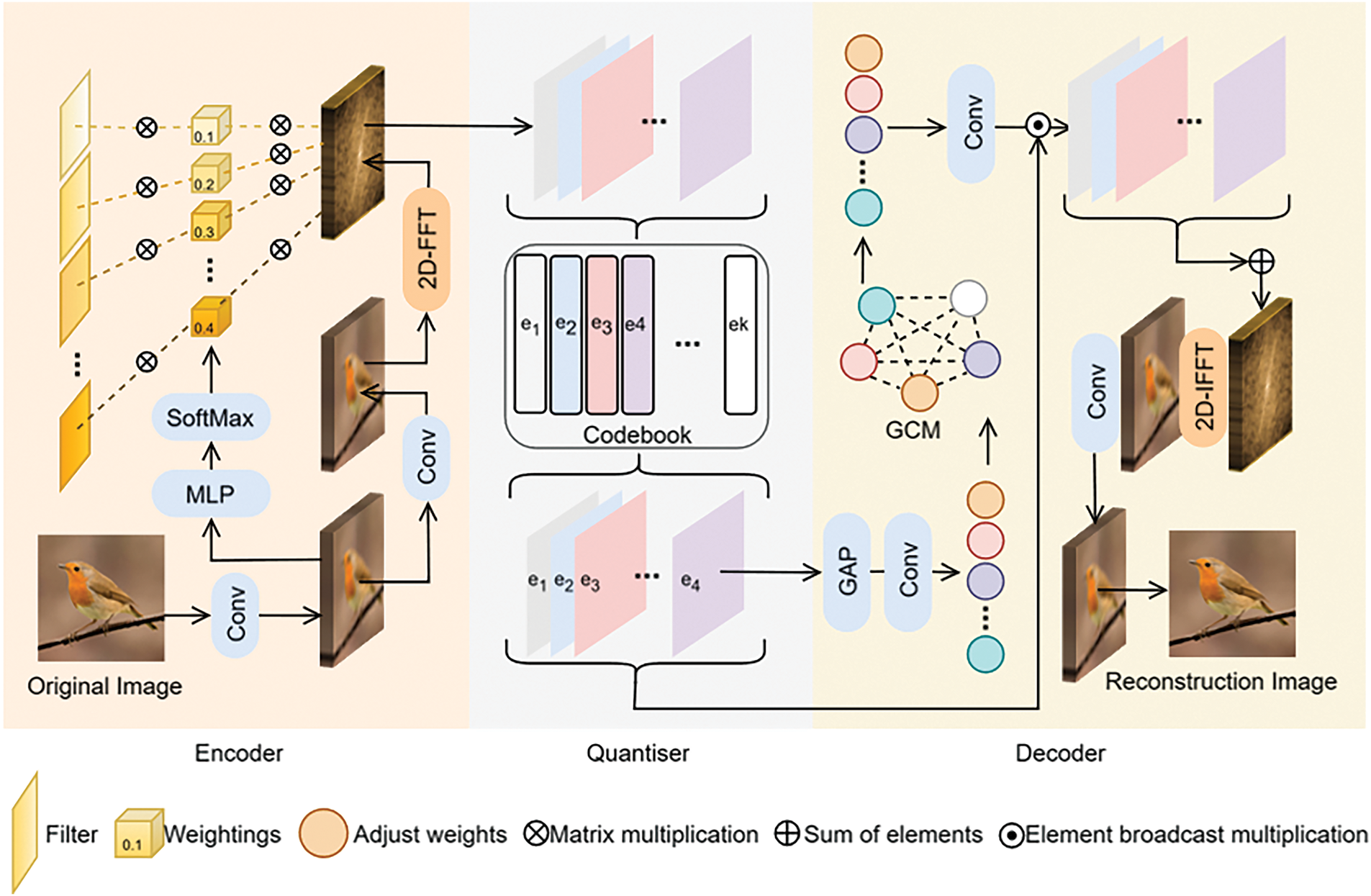
Figure 1: Architecture of the frequency quantized variational autoencoder (FQ-VAE)
We utilize 2D-FFT to transfer image features into the frequency domain and extract their components, quantizing these frequency domain features. During decoding, we use 2D-IFFT to return the image features back to the spatial domain, followed by convolution to complete the reconstruction. Additionally, we optimize the codebook and apply a Graph Convolutional Module (GCM) to generate corrective weights, reducing quantization loss. Compared to other VQ-VAE architectures, our method preserves the global relationships within the image, resulting in improved reconstruction performance.
Compared to traditional methods, which typically map raw data into a set of regular image blocks in the high-dimensional spatial domain and then quantize these blocks, such grid-based partitioning often disrupts the global relationships within the image, leading to information loss. In contrast, the method proposed in this paper preserves the image’s global characteristics throughout the encoding process. The encoder encodes the raw data as a linear combination of various frequency components in the frequency domain. Our method is based on the 2D-FFT, but a thorough understanding of the 2D-DFT is essential before implementing the 2D-FFT effectively.
For a given 2D signal
where
The 2D-DFT maps the data from the spatial domain to the frequency domain, where
As illustrated in the encoder module in Fig. 1, our method initially adheres to the conventional process of downsampling through convolution to map raw data into latent space, where the channel dimension is emphasized, resulting in latent features
where
In this paper, we utilize a multilayer perceptron (MLP) to generate a set of
Finally, the combination of learnable filters is:
The encoder extracts frequency-domain features from the channel dimension of the latent feature
To optimize inactive codevectors in the codebook, this paper proposes an improved dynamic codebook updating method. This approach updates the codebook dynamically based on the usage frequency of code vectors and their dependencies. The updated code vector
where
where
where
In addition, to reduce the dependency between codevectors in the codebook and better represent the quantized data with linear combinations, while avoiding excessive information coupling, the approach introduces the Pearson correlation coefficient
where
where
In traditional quantization methods, information loss is inevitable, primarily due to the distance discrepancy between the codevectors and latent vectors. In our method, the decoder’s input is a linear combination of various frequency-domain features. Additionally, through the optimization of correlation strength during codebook training, the codebook entries tend to form a linearly independent set. According to a theorem in linear algebra, if a set of
Inspired by recent work of Xiang et al. [35], which models inter-channel relationships using a graph structure, we introduce graph convolution theory to solve for the frequency feature coefficients
Specifically, we first apply global average pooling (GAP) to the feature map, reducing its dimension to
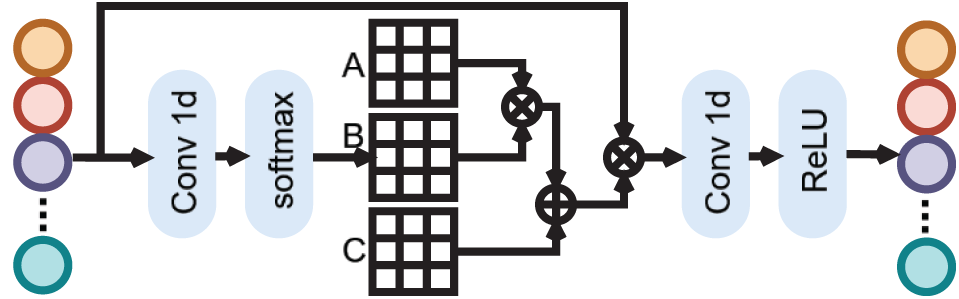
Figure 2: Architecture of the Graph Convolutional Module (GCM). After passing the input feature maps through the GCM, the corresponding weights for the quantized feature components are learned, which are used to further minimize the information loss caused by quantization
here,
The feature weights obtained via the graph convolution operation are used to recalibrate the frequency-level response. The weighted frequency features are then transformed back from the frequency domain to the spatial domain using the 2D inverse Fourier transform.
Subsequent operations are similar to those in traditional VQ-VAE. Through convolution operations, the latent features in the spatial domain are restored to their original space, achieving high-quality image reconstruction.
In the experimental evaluation, this paper conducts experiments on both image reconstruction and image generation tasks. To ensure fairness, all experiments utilize the same downsampling rates and hyperparameter settings. In the image reconstruction experiments, the superiority of the proposed method is validated by comparing the image reconstruction quality, codebook utilization rate, and codebook information capacity. Ablation studies further confirm the significance and practicality of all components on model performance, while determining the optimal combination of the number of channels and filters. In the image generation task, the proposed method demonstrates advantages in preserving global relationships for downstream tasks. Experimental results show that the proposed method outperforms current state-of-the-art methods in codebook construction, reconstruction performance, and generation quality, achieving significant improvements.
Datasets and Performance Measures. The models in this paper are trained on four publicly available datasets: MNIST [36], CIFAR10 [37], CelebA [38], and LSUN Church [39].
The following metrics are utilized as performance evaluation indicators: Structural Similarity Index (SSIM) at the image patch level, Learned Perceptual Image Patch Similarity (LPIPS) [40] at the feature level, and Reconstruction Fréchet Inception Distance (rFID) [41] at the dataset level.
Implementation Details. For VQ-VAE, HQ-VAE, SQ-VAE, and CVQ-VAE, this paper utilizes the official code and constructs models for all datasets except LSUN Church. LSUN Church was only applied to the image generation task in the CVQ-VAE paper, however, to demonstrate the model’s generalization capability, this paper includes this dataset in the image reconstruction task, using the same configuration parameters as those for CelebA.
The proposed method first maps features through convolutional layers. For the MNIST, CIFAR10, and CelebA datasets, the method modifies only the channel dimensions after resizing the images, without altering their resolution. for the LSUN Church dataset, the h and w are adjusted to H/2 and W/2, respectively.
Regarding learning rates, a rate of 2 × 10−3 is set for MNIST, while a rate of 3 × 10−3 is set for the reconstruction tasks on the other datasets. According to the study referenced in [12], the weight hyperparameter
This paper conducts image reconstruction tasks on four datasets. For the MNIST and CIFAR10 datasets, the experiments utilize their original resolutions of 28 × 28 pixels and 32 × 32 pixels, respectively. The CelebA dataset is first center-cropped to 140 × 140 pixels and then resized to 64 × 64 pixels. The LSUN Church dataset employs the official version and is split into training, validation, and test sets in an 8:1:1 ratio, with the image size adjusted to 128 × 128 pixels. The training process continues until the model converges completely. All data in the experiments undergo uniform standardization, with a mean of 0.5 and a variance of 0.5. To ensure fairness, the number of encoded features in the proposed method is consistent with the number of latent vectors in the compared methods, which is one-quarter of the original resolution, corresponding to a downsampling rate of
Codebook Utilization. The codebook utilization rates are calculated and visualized on the MNIST and CIFAR10 validation sets to verify the proposed method’s effective improvement of the codebook. Specifically, the total number of times all entries in the codebook are utilized to reconstruct the validation set is counted. As shown in Fig. 3, the orange curve represents the fitted curve of the codebook entries sorted by usage rate, demonstrating that the codebook utilization rate of the proposed method is higher than both the baseline VQ-VAE and the state-of-the-art CVQ-VAE. In the codebook of VQ-VAE, a large portion of the entries remain unused or infrequently used, while a small number of entries are used very frequently, which is a result of the codebook collapse problem. Compared to VQ-VAE, CVQ-VAE addresses this issue by introducing anchor points to update unused or less frequently used codevectors, ensuring that all codevectors are utilized. However, there still exists a subset of codevectors that are used with high frequency. The proposed method demonstrates a more balanced usage of codebook entries compared to CVQ-VAE, indicating a more effective utilization of the codebook.
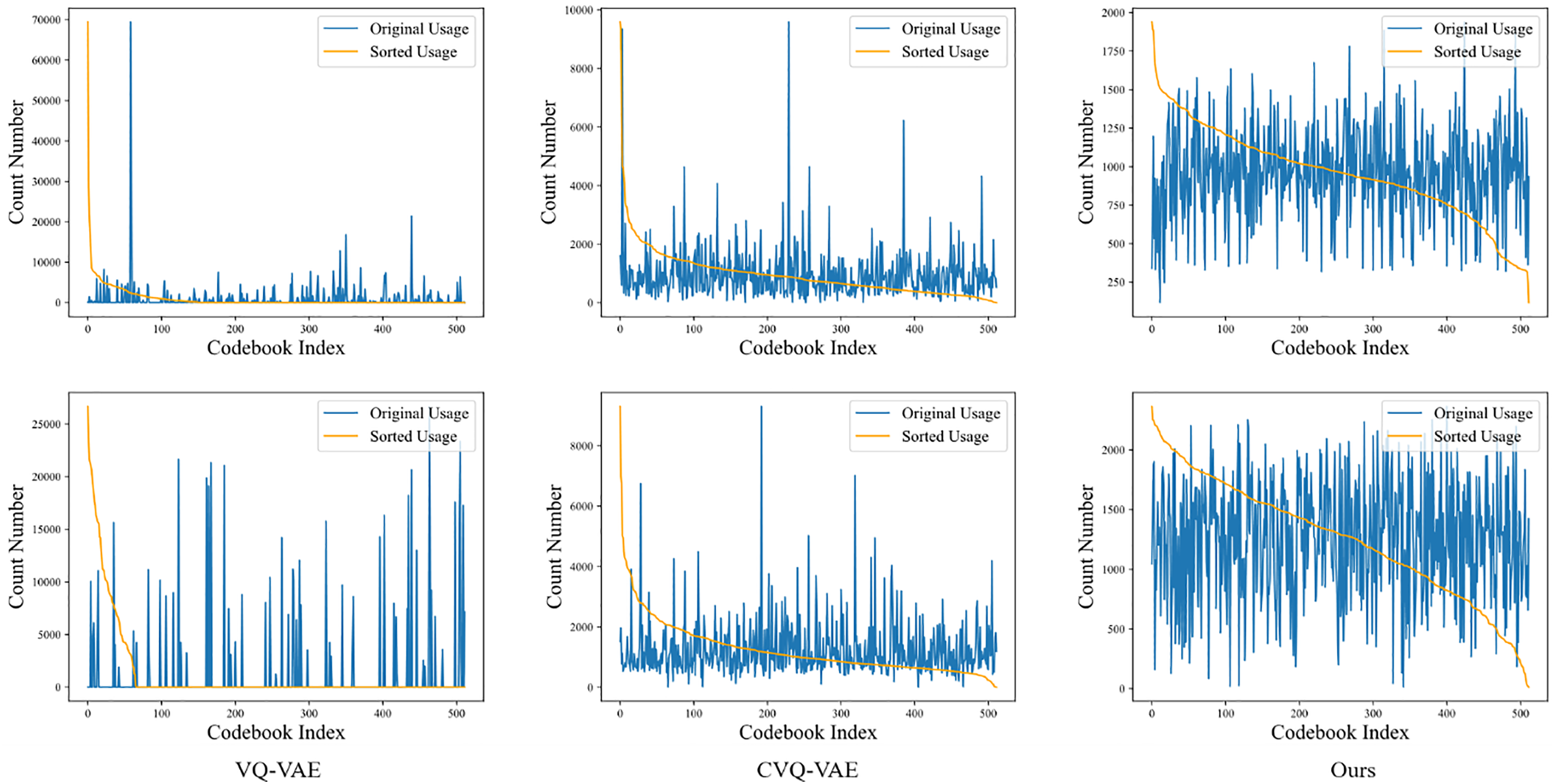
Figure 3: Visualization of Codebook Utilization on MNIST (top) and CIFAR-10 (bottom) validation sets. The blue line indicates the usage quantity of different code vectors in the codebook. The orange curve represents the fitted curve of the codebook entries sorted by usage frequency. In VQ-VAE, a large portion of the codebook entries remain unused due to codebook collapse. CVQ-VAE improves this issue by increasing codebook utilization. Our method further ensures a more balanced usage of codebook entries, making the codebook more efficient
The more uniform distribution of codevector usage in the proposed method suggests that it effectively captures a wider range of essential features and structures from the input data. This is achieved through the frequency-domain quantization, which preserves global relationships and extracts more informative features, as well as the dynamic codebook optimization, which prevents the dominance of a small subset of codevectors. As a result, the codebook in the proposed method is more efficient and better equipped to represent the complex characteristics of the data, leading to improved reconstruction and generation performance.
Unit Information Capacity of Codebook. Previous studies did not include calculations of the information capacity of individual codebook entries. Referring to the study in [9], this paper calculates the information capacity of codebook vectors by single codevector and measuring the change in mean squared error (MSE) loss between the generated image and the original image before and after the removal. By evaluating the MSE loss difference at the dataset level, the information capacity of individual code vectors is quantified. This metric reflects the effectiveness and compactness of the codebook’s information. The measurement results on the CelebA and LSUN Church datasets are presented in Fig. 4, showing that the average information capacity per codebook entry generated by the proposed method is higher than that of prior methods. This demonstrates that the frequency domain features introduced in this paper carry more effective information than traditional image features obtained via spatial domain partitioning, resulting in a more compact and efficient codebook.
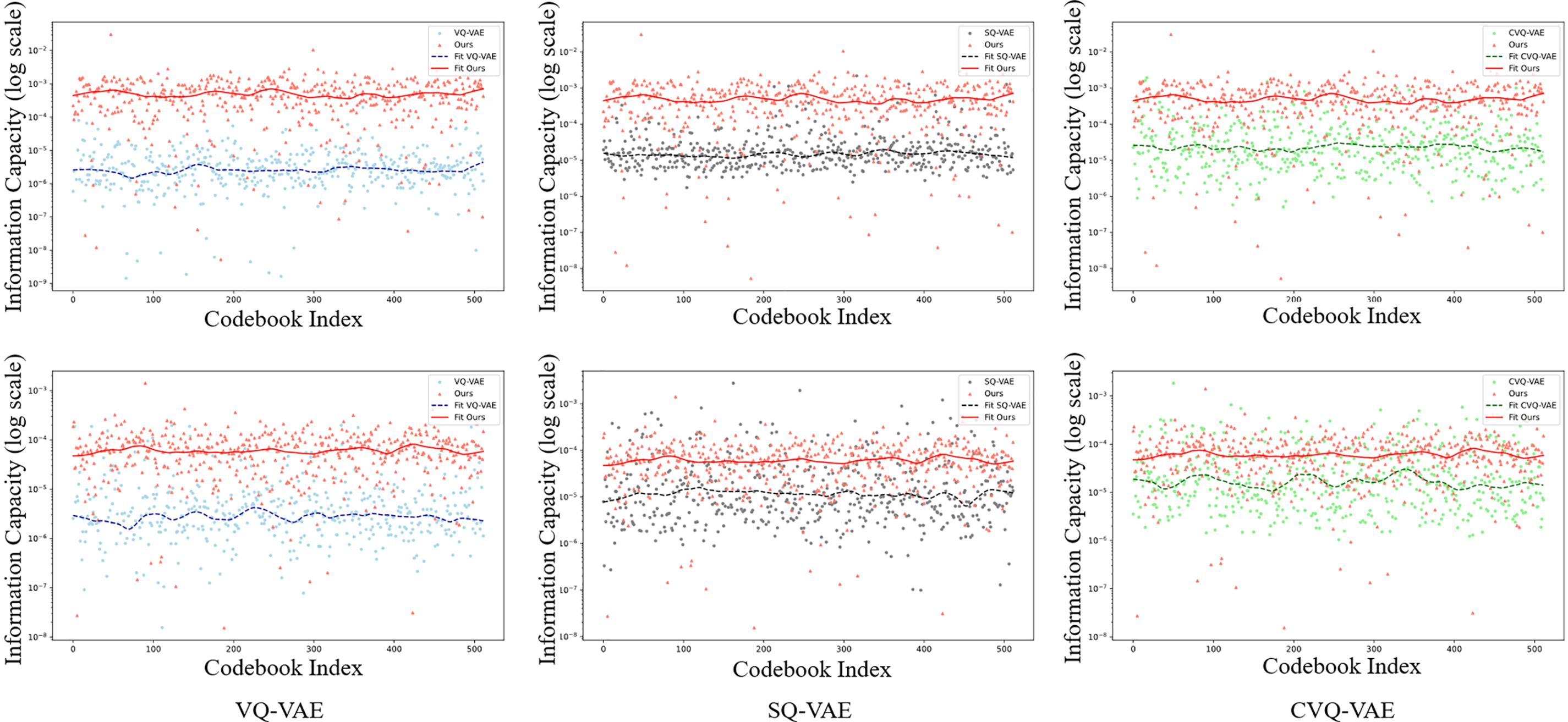
Figure 4: Visualization of Codebook Unit Information Comparison on CelebA (top) and LSUN Church (bottom) validation sets. The red dots and curve represent the information content of codebook entries and their fitting curve in the proposed method, respectively. Blue, gray, and green indicate the measurement results of VQ-VAE, SQ-VAE, and CVQ-VAE, respectively. Compared to other methods, the codebook generated by our approach exhibits a higher average information per entry, indicating less information coupling within the codebook. This suggests that our method captures richer and more compact data features in the codebook
Quantitative Evaluation. Table 1 presents the quantitative comparison results of image reconstruction across four publicly available datasets: MNIST, CIFAR10, CelebA, and LSUN Church. The results are compared with state-of-the-art quantized autoencoder models, including VQ-VAE, HVQ-VAE, SQ-VAE, and CVQ-VAE. By quantizing frequency domain features, optimizing the codebook structure, and refining the quantization of features, the proposed method significantly enhances image reconstruction quality, outperforms the four baseline models across all performance metrics on all datasets (with the exception of SSIM on MNIST and CelebA). Using the CIFAR-10 dataset as an example, the proposed method surpasses all baselines across all metrics. Its SSIM (0.9012), LPIPS (0.1597), and rFID (18.88) scores are 0.0034, 0.0376, and 6.01 points better than the best-performing baseline, CVQ-VAE, respectively. It is worth noting that in experiments on the CelebA and LSUN Church datasets, the rFID scores of CVQ-VAE increased by 0.43 and 1.00 compared to the baseline VQ-VAE. This can be attributed to the increased information coupling as the dataset resolution increases, which affects the strategy of updating the codebook solely through anchor points in CVQ-VAE. The proposed method avoids the issue of information coupling through its codebook optimization strategy that reduces dependencies, gaining a significant advantage. It outperforms the second-best method, SQ-VAE, by 15.1% and 18.8% on the rFID metric for the CelebA and LSUN Church datasets, respectively. This demonstrates that the model effectively captures more valuable information from the original images.
Qualitative Evaluation. Fig. 5 presents some example reconstruction results trained on the LSUN Church dataset. We report reconstruction examples for VQ-VAE, HVQ-VAE, SQ-VAE, CVQ-VAE, and the proposed method, FQ-VAE. It can be observed that the proposed method achieves better visual quality and performs well even in challenging detailed areas.


Figure 5: Qualitative comparison examples from LSUN Church validation set. The red box highlights areas in the image containing fine details that are difficult to reconstruct. The results demonstrate that our method achieves superior reconstruction performance compared to the baseline model in these regions
Core Factors. The core components of the proposed method are evaluated in Table 2, demonstrating that each designed components contributes significantly to the improvement of reconstruction quality. We begin with the baseline configuration (A) implementing VQ-VAE. In configuration (B), spatial vector quantization is replaced by frequency domain feature quantization, resulting in a notable performance boost, indicating that frequency domain quantization is the key driver behind the method’s performance enhancement. Configurations (C) and (D) evaluate the codebook optimization methods. Configuration (C) reinitializes rarely used codevectors by selecting anchor points, yielding significant gains on small datasets such as MNIST and CIFAR-10, with rFID reductions of 29.21% and 33.50%, respectively. However, on larger datasets like CelebA and LSUN Church, the performance across all metrics slightly declines due to more severe information coupling. Configuration (D) considers codebook dependencies on top of (C), further reducing codebook information coupling and outperforming configuration (C) on various datasets. For example, on LSUN Church, configuration (D) improves SSIM, LPIPS, and rFID by 1.01%, 9.67%, and 25.05%, respectively, compared to configuration (C), highlighting the importance of addressing the information coupling issue in the codebook. Configuration (E) employs a Graph Convolutional Module to refine the quantized features and reduce information loss. Compared to the baseline configuration (A), on the MNIST dataset, SSIM improves by 0.17%, while LPIPS and rFID decrease by 9.97% and 12.82%, respectively, demonstrating the effectiveness of the Graph Convolutional Module. Similar improvements are observed on other datasets.
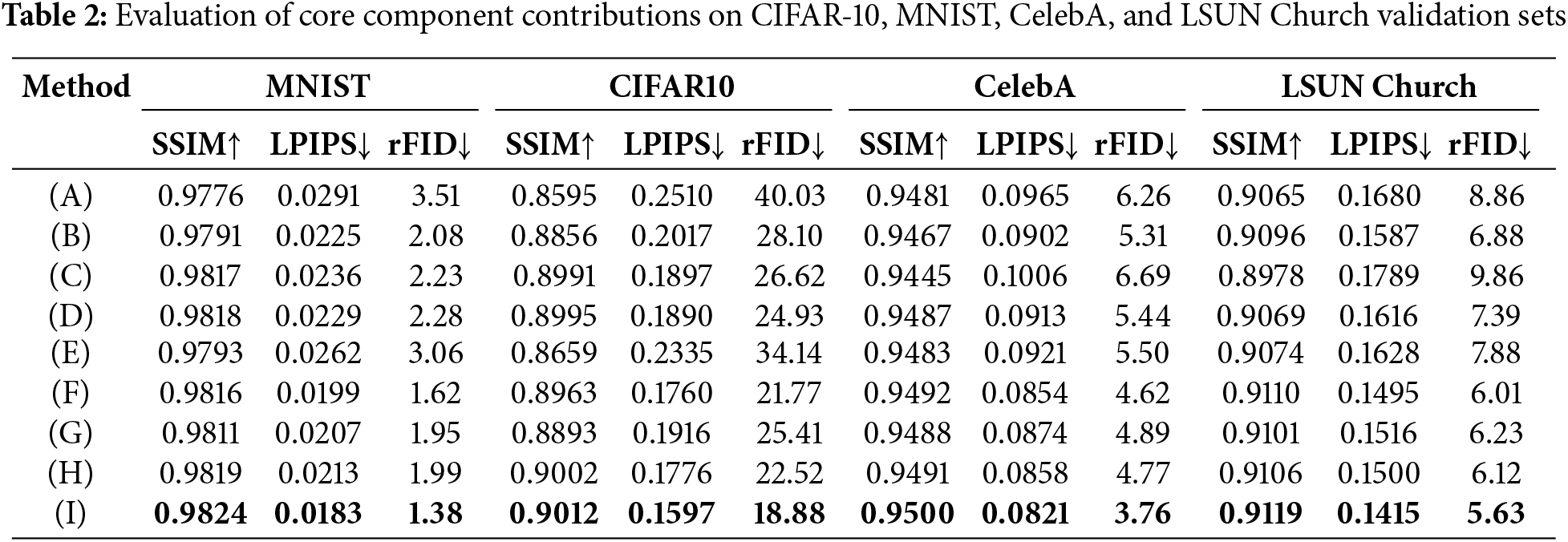
Configuration (F) combines the frequency-domain quantization method with the codebook optimization method, achieving better results than individual components. Taking the CelebA dataset as an example, configuration (F) achieves an SSIM of 0.9492, LPIPS of 0.0854, and rFID of 4.62, improving by 0.25%, 5.32%, and 13.00% compared to configuration (B), and by 0.05%, 6.46%, and 15.07% compared to configuration (D), respectively. This indicates that codebook collapse and information coupling problems remain major influencing factors under frequency-domain quantization. Moreover, configuration (G) combines the codebook optimization method with the Graph Convolutional Module, while configuration (H) combines the frequency-domain quantization method with the Graph Convolutional Module. Both configurations outperform their respective individual components, suggesting that the interaction among these components can generate positive gains.
Configuration (I) integrates all the proposed components and, as expected, achieves the best performance across all metrics on all datasets. For instance, on the CIFAR-10 dataset, compared to the second-best configuration (F), configuration (I) improves SSIM, LPIPS, and rFID by 0.55%, 9.26%, and 13.28%, respectively. This fully demonstrates the effectiveness of the proposed components and the advantages of their synergistic collaboration.
Balance between the Number of Channels and Filters. The proposed method quantizes raw image data into a linear combination of frequency features across different channels, where the number of latent features
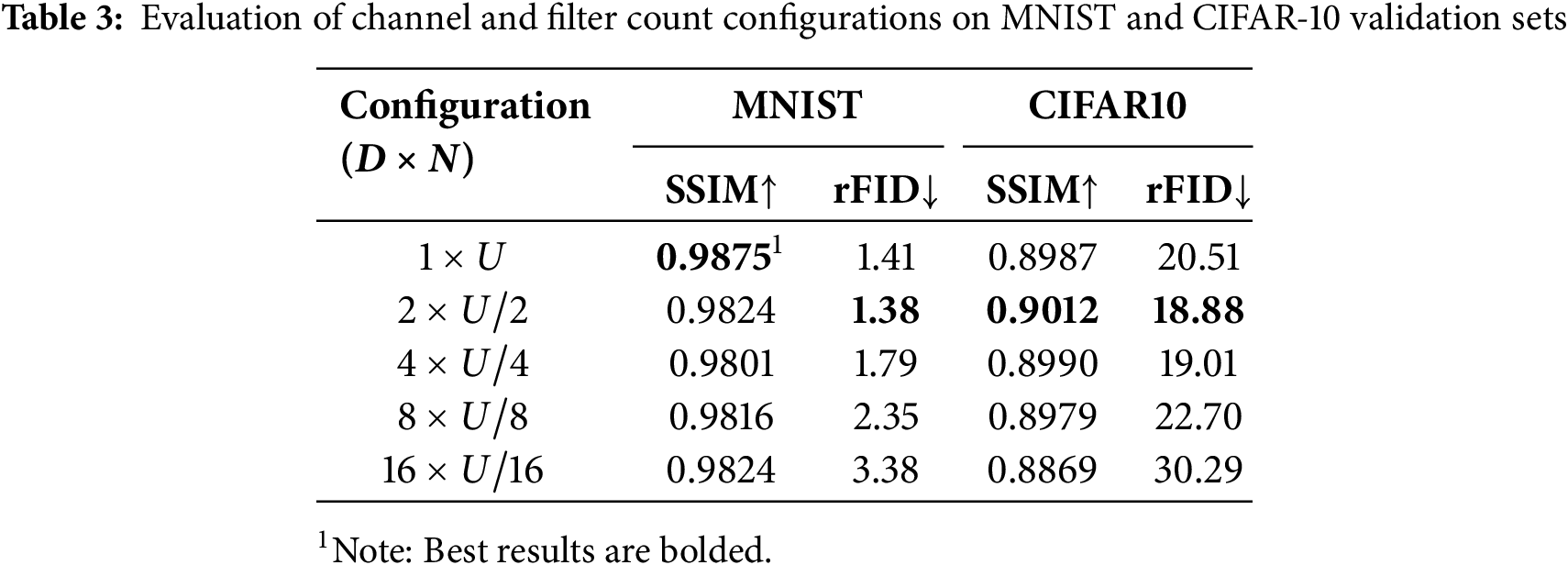
It is worth noting that increasing the number of channels beyond a certain point does not always lead to performance improvements. For example, in the CIFAR-10 experiments, the configurations with D = 4 and D = 8 result in lower SSIM scores and higher rFID scores compared to the optimal configuration with D = 2. This suggests that an excessive number of channels may introduce redundancy and hinder the model’s ability to learn compact and informative representations. The proposed method achieves its best overall performance when D = 2, demonstrating its effectiveness in learning expressive and efficient discrete representations.
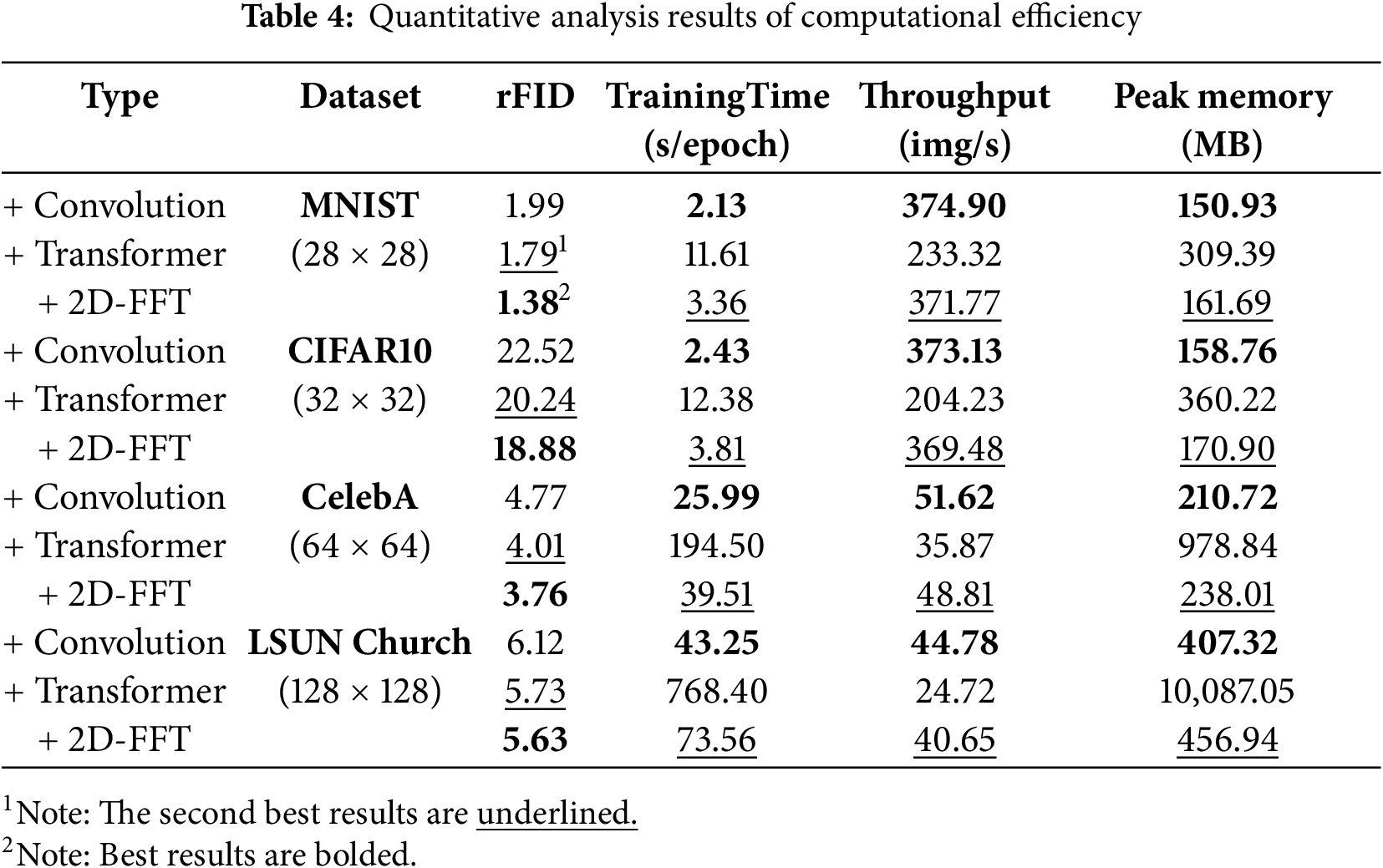
Computational Efficiency Analysis. Theoretically, for a feature map of size H × W with D channels, the time complexity of a 2D-FFT-based feature extractor is
Table 4 shows the quantitative results of different feature extractors on the four datasets. From the perspective of reconstruction quality, the 2D-FFT-based feature extractor achieves the best rFID scores on all datasets, followed by the transformer, with the convolutional operation performing the worst. This indicates that by performing global modeling in the frequency domain, FQ-VAE can better capture the global structure and details of images, thus generating higher-quality reconstructed images. Taking the CIFAR-10 dataset as an example, the training time of 2D-FFT is 3.81 s per epoch, which is only 30.8% of the transformer’s, while the throughput reaches 369.48 images per second, which is 1.81 times that of the transformer. This advantage is even more pronounced on the higher-resolution CelebA and LSUN Church datasets. It is worth noting that 2D-FFT does not introduce additional memory overhead while significantly reducing training time. Compared to the transformer, 2D-FFT has lower peak memory usage on all datasets. For example, on LSUN Church, the peak memory usage of 2D-FFT is only 456.94 MB, while that of the transformer is as high as 10,087.05 MB, with the former being only 4.5% of the latter. Overall, the 2D-FFT-based frequency-domain quantization method significantly improves reconstruction quality while avoiding the complexity issues introduced by global feature extractors such as transformers, exhibiting significant computational efficiency advantages.
The model is trained on the CelebA dataset and applied to downstream generation tasks using the latent diffusion model (LDM) [42]. Since the proposed method is largely consistent with the traditional VQ-VAE architecture, it can replace the VQ-VAE component in LDM directly. Specifically, following the settings in LDM, a cosine learning rate scheduler is used in the generation tasks, with a warm-up period set to 500 steps, and the weight decay for the Adam optimizer is set to 1 × 10−6. Additionally, the number of sampling steps is set to 1000, and mixed-precision training with fp16 is employed to enhance computational efficiency. The batch size is set to 64, and the model is trained for 100 epochs in total.
Fig. 6 presents several examples generated by the baseline CVQ-VAE and the proposed method. As expected, the images generated by the proposed method are sharper and more realistic compared to those generated through spatial vector quantization. Benefiting from frequency feature quantization, which preserves the global relationships within the image, the proposed method produces images with stronger overall coherence and avoids the distortions commonly seen in other methods, such as misaligned facial features, local ghosting, and facial warping.

Figure 6: Qualitative comparison examples of generation experiments between CVQ-VAE and the proposed method. The results indicate that the images generated by our method are more likely to preserve global relationships within the image, resulting in a more realistic overall appearance
This paper introduces a frequency-quantized variational autoencoder, which utilizes 2D-FFT to transform image features into the frequency domain for quantization, effectively preserving global image relationships. The method also dynamically optimizes the codebook by considering the frequency and dependency of code vector usage, preventing codebook collapse and reducing information coupling. Moreover, the quantized features are refined using graph convolutional theory to minimize quantization loss. Ablation experiments validate the effectiveness of each component, further confirming the key roles of frequency feature quantization, codebook optimization strategies, and corrected quantized features in enhancing model performance. Reconstruction and generation experiments show that the proposed method excels in image reconstruction and generation tasks, surpassing existing state-of-the-art approaches.
However, since each codebook entry in the proposed method maintains global information, the dimensionality of the codebook vectors increases dramatically as the image resolution rises. Unfortunately, downstream tasks often prefer lower-dimensional codevectors. This may hinder the scalability of the method on high-resolution datasets. Future work will explore more effective codebook compression techniques to reduce the codebook dimensionality while maintaining reconstruction quality, adapting to larger-scale data requirements and more downstream tasks.
Furthermore, maintaining global relationships within data has been a long-standing challenge in video and audio generation tasks. By addressing the above issues and adapting the method to capture temporal information for video data or 1D signals for audio data, the FQ-VAE could be extended to these modalities. Successful application of the proposed method to video and audio generation could lead to more coherent and globally consistent outputs, advancing the state-of-the-art in these domains.
Acknowledgement: The authors would like to express their gratitude for the valuable feedback and suggestions provided by all the anonymous reviewers and the editorial team.
Funding Statement: This work was supported by the Interdisciplinary project of Dalian University DLUXK-2023-ZD-001.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jianxin Feng, Xiaoyao Liu; data collection: Jianxin Feng, Xiaoyao Liu; analysis and interpretation of results: Jianxin Feng, Xiaoyao Liu; draft manuscript preparation: Xiaoyao Liu. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data used in the study are all available on the OpenDataLab official website (https://opendatalab.com/) (accessed on 07 February 2025).
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Kingma DP, Welling M. Auto-encoding variational bayes. arXiv:1312.6114. 2013. [Google Scholar]
2. Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. Generative adversarial networks. Commun ACM. 2020;63(11):139–44. doi:10.1145/3422622. [Google Scholar] [CrossRef]
3. Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, et al. Attention is all you need. In: NIPS’17: Proceedings of the 31st International Conference on Neural Information Processing Systems; 2017 Dec 4–9; Long Beach, CA, USA; 2017. Vol. 30, p. 3–19. [Google Scholar]
4. Esser P, Rombach R, Ommer B. Taming transformers for high-resolution image synthesis. In: 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2021 Jun 20–25; Nashville, TN, USA. p. 12868–78. doi:10.1109/cvpr46437.2021.01268. [Google Scholar] [CrossRef]
5. Gu S, Chen D, Bao J, Wen F, Zhan B, Chen D, et al. Vector quantized diffusion model for text-to-image synthesis. In: 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2022 Jun 18–24; New Orleans, LA, USA. p. 10696–706. [Google Scholar]
6. Oord A, Vinyals O, Kavukcuoglu K. Neural discrete representation learning. In: NIPS’17: Proceedings of the 31st International Conference on Neural Information Processing Systems; 2017 Dec 4–9; Long Beach, CA, USA. p. 6309–18. [Google Scholar]
7. Chen S, Guo W. Auto-encoders in deep learning—a review with new perspectives. Mathematics. 2023;11(8):1777. doi:10.3390/math11081777. [Google Scholar] [CrossRef]
8. Tian K, Jiang Y, Yuan Z, Peng B, Wang L. Visual autoregressive modeling: scalable image generation via next-scale prediction. arXiv:2404.02905. 2024. [Google Scholar]
9. Huang L, Qiu Q, Sapiro G. PQ-VAE: learning hierarchical discrete representations with progressive quantization. In: 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW); 2024 Jun 17–18; Seattle, WA, USA. p. 7550–8. doi:10.1109/CVPRW63382.2024.00750. [Google Scholar] [CrossRef]
10. Takida Y, Shibuya T, Liao W, Lai CH, Ohmura J, Uesaka T, et al. SQ-VAE: variational bayes on discrete representation with self-annealed stochastic quantization. arXiv:2205.07547. 2022. [Google Scholar]
11. Williams W, Ringer S, Ash T, MacLeod D, Dougherty J, Hughes J. Hierarchical quantized autoencoders. In: NIPS’20: Proceedings of the 34th International Conference on Neural Information Processing Systems; 2020 Dec 6–12; Vancouver, BC, Canada. p. 4524–35. [Google Scholar]
12. Zheng C, Vedaldi A. Online clustered codebook. In: 2023 IEEE/CVF International Conference on Computer Vision (ICCV); 2023 Oct 1–6; Paris, France. p. 22741–50. doi:10.1109/ICCV51070.2023.02084. [Google Scholar] [CrossRef]
13. Lee D, Kim C, Kim S, Cho M, Han WS. Autoregressive image generation using residual quantization. In: 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2022 Jun 18–24; New Orleans, LA, USA. p. 11513–22. doi:10.1109/CVPR52688.2022.01123. [Google Scholar] [CrossRef]
14. Yan W, Zhang Y, Abbeel P, Srinivas A. VideoGPT: video generation using VQ-VAE and transformers. arXiv:2104.10157. 2021. [Google Scholar]
15. Xie Z, Li B, Xu X, Wu M, Yu K. Enhancing audio generation diversity with visual information. In: ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2024 Apr 14–19; Seoul, Republic of Korea. p. 866–70. doi:10.1109/ICASSP48485.2024.10447384. [Google Scholar] [CrossRef]
16. Grassucci E, Mitsufuji Y, Zhang P, Comminiello D. Enhancing semantic communication with deep generative models: an overview. In: ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2024 Apr 14–19; Seoul, Republic of Korea. p. 13021–5. doi:10.1109/ICASSP48485.2024.10448235. [Google Scholar] [CrossRef]
17. Mao C, Jiang L, Dehghani M, Vondrick C, Sukthankar R, Essa I. Discrete representations strengthen vision transformer robustness. arXiv:2111.10493. 2021. [Google Scholar]
18. Razavi A, Oord AVD, Vinyals O. Generating diverse high-fidelity images with VQ-VAE-2. In: Proceedings of the 33rd International Conference on Neural Information Processing Systems; 2019 Dec 8–14; Vancouver, BC, Canada. p. 14866–76. [Google Scholar]
19. Yu J, Li X, Koh JY, Zhang H, Pang R, Qin J, et al. Vector-quantized image modeling with improved VQGAN. arXiv:2110.04627. 2021. [Google Scholar]
20. Zheng C, Vuong TL, Cai J, Phung D. Movq: modulating quantized vectors for high-fidelity image generation. In: NIPS’22: Proceedings of the 36th International Conference on Neural Information Processing Systems; 2022 Nov 28–Dec 9; New Orleans, LA, USA. p. 23412–225. [Google Scholar]
21. Dhariwal P, Jun H, Payne C, Kim JW, Radford A, Sutskever I. Jukebox: a generative model for music. arXiv:2005.00341. 2020. [Google Scholar]
22. Vuong TL, Le T, Zhao H, Zheng C, Harandi M, Cai J, et al. Vector quantized Wasserstein auto-encoder. arXiv:2302.05917. 2023. [Google Scholar]
23. Lee-Thorp J, Ainslie J, Eckstein I, Ontanon S. FNet: mixing tokens with Fourier transforms. arXiv:2105.03824. 2021. [Google Scholar]
24. Sevim N, Özyedek EO, Şahinuç F, Koç A. Fast-FNet: accelerating transformer encoder models via efficient Fourier layers. arXiv:2209.12816. 2022. [Google Scholar]
25. Rao Y, Zhao W, Zhu Z, Lu J, Zhou J. Global filter networks for image classification. In: NIPS’21: Proceedings of the 35th International Conference on Neural Information Processing Systems; 2021 Dec 6–14; Online. p. 980–93. [Google Scholar]
26. Rao Y, Zhao W, Zhu Z, Zhou J, Lu J. GFNet: global filter networks for visual recognition. IEEE Trans Pattern Anal Mach Intell. 2023;45(9):10960–73. doi:10.1109/TPAMI.2023.3263824. [Google Scholar] [PubMed] [CrossRef]
27. Wang Z, Zhao Y, Chen J. Multi-scale fast Fourier transform based attention network for remote-sensing image super-resolution. IEEE J Sel Top Appl Earth Obs Remote Sens. 2023;16:2728–40. doi:10.1109/JSTARS.2023.3246564. [Google Scholar] [CrossRef]
28. Tatsunami Y, Taki M. FFT-based dynamic token mixer for vision. Proc AAAI Conf Artif Intell. 2024;38(14):15328–36. doi:10.1609/aaai.v38i14.29457. [Google Scholar] [CrossRef]
29. Hong D, Gao L, Yao J, Zhang B, Plaza A, Chanussot J. Graph convolutional networks for hyperspectral image classification. IEEE Trans Geosci Remote Sens. 2020;59(7):5966–78. doi:10.1109/TGRS.2020.3015157. [Google Scholar] [CrossRef]
30. Xu Y, Huang D, Wang CD, Lai JH. Deep image clustering with contrastive learning and multi-scale graph convolutional networks. Pattern Recognit. 2024;146(2):110065. doi:10.1016/j.patcog.2023.110065. [Google Scholar] [CrossRef]
31. Chen Z, Fu L, Yao J, Guo W, Plant C, Wang S. Learnable graph convolutional network and feature fusion for multi-view learning. Inf Fusio. 2023;95(7):109–19. doi:10.1016/j.inffus.2023.02.013. [Google Scholar] [CrossRef]
32. Cai W, Wei Z. Remote sensing image classification based on a cross-attention mechanism and graph convolution. IEEE Geosci Remote Sens Lett. 2020;19:1–5. [Google Scholar]
33. Yang Y, Qi Y, Qi S. Relation-consistency graph convolutional network for image super-resolution. Vis Comput. 2024;40(2):619–35. doi:10.1007/s00371-023-02805-1. [Google Scholar] [CrossRef]
34. Li Y, Zhang Y, Cui W, Lei B, Kuang X, Zhang T. Dual encoder-based dynamic-channel graph convolutional network with edge enhancement for retinal vessel segmentation. IEEE Trans Med Imaging. 2022;41(8):1975–89. doi:10.1109/TMI.2022.3151666. [Google Scholar] [PubMed] [CrossRef]
35. Xiang X, Wang Z, Zhang J, Xia Y, Chen P, Wang B. AGCA: an adaptive graph channel attention module for steel surface defect detection. IEEE Trans Instrum Meas. 2023;72:5008812. doi:10.1109/TIM.2023.3248111. [Google Scholar] [CrossRef]
36. LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proc IEEE. 2002;86(11):2278–324. doi:10.1109/5.726791. [Google Scholar] [CrossRef]
37. Krizhevsky A, Hinton G. Learning multiple layers of features from tiny images. In: Technical report. Toronto, ON, Canada: University of Toronto; 2009. [Google Scholar]
38. Liu Z, Luo P, Wang X, Tang X. Deep learning face attributes in the wild. In: 2015 IEEE International Conference on Computer Vision (ICCV); 2015 Dec 7–13; Santiago, Chile. p. 3730–8. doi:10.1109/ICCV.2015.425. [Google Scholar] [CrossRef]
39. Yu F, Seff A, Zhang Y, Song S, Funkhouser T, Xiao J. LSUN: construction of a large-scale image dataset using deep learning with humans in the loop. arXiv:1506.03365. 2015. [Google Scholar]
40. Zhang R, Isola P, Efros AA, Shechtman E, Wang O. The unreasonable effectiveness of deep features as a perceptual metric. In: IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2018 Jun 18–23; Salt Lake City, UT, USA. p. 586–95. doi:10.1109/CVPR.2018.00068. [Google Scholar] [CrossRef]
41. Heusel M, Ramsauer H, Unterthiner T, Nessler B, Hochreiter S. Gans trained by a two time-scale update rule converge to a local nash equilibrium. In: NIPS’17: Proceedings of the 31st International Conference on Neural Information Processing Systems; 2017 Dec 4–9; Long Beach, CA, USA. p. 6629–40. [Google Scholar]
42. Rombach R, Blattmann A, Lorenz D, Esser P, Ommer B. High-resolution image synthesis with latent diffusion models. In: 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2022 Jun 18–24; New Orleans, LA, USA. p. 10674–85. doi:10.1109/CVPR52688.2022.01042. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF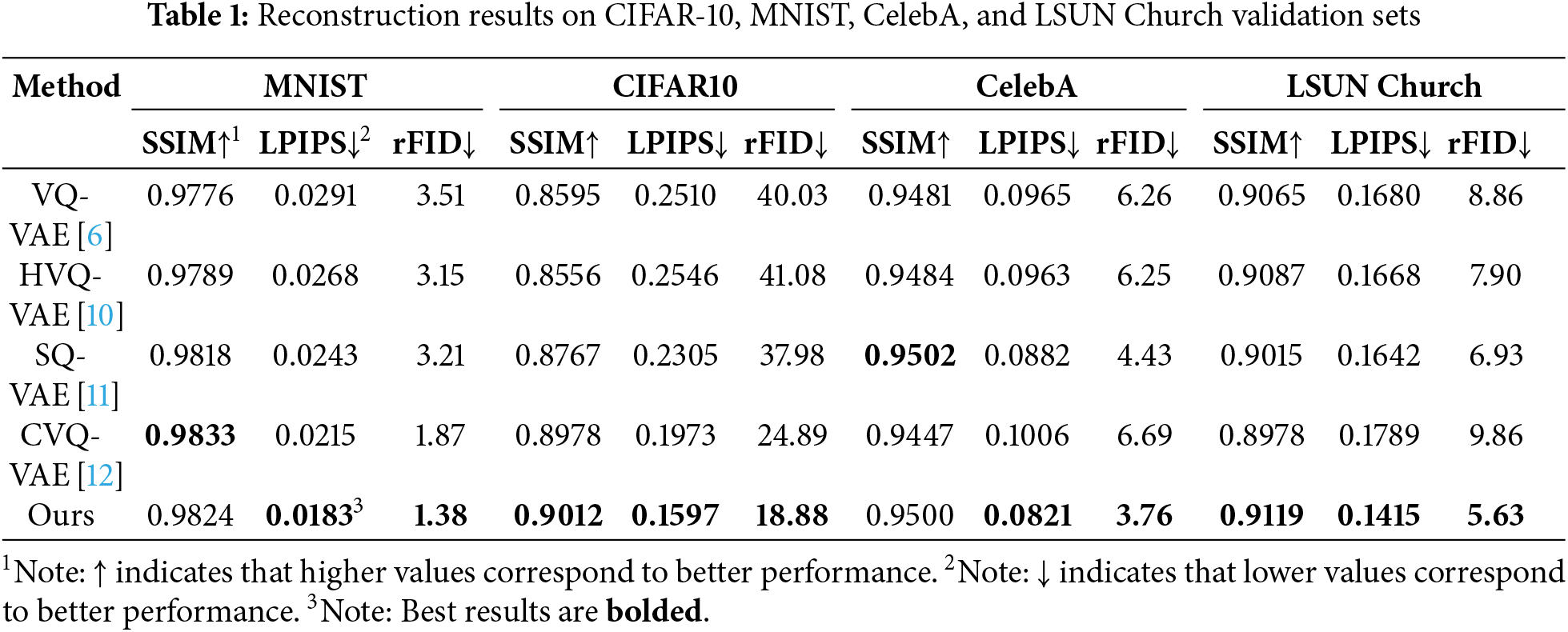
 Downloads
Downloads
 Citation Tools
Citation Tools