A Deep Learning-Based Salient Feature-Preserving Algorithm for Mesh Simplification

Abbreviations

1  Introduction

With the rapid advancement of 3D reconstruction technologies, the complexity and level of detail in generated mesh models have significantly increased. These enhancements, however, lead to challenges related to large data volumes, elevated computational costs, and reduced rendering performance. For example, complex 3D models used in cultural heritage preservation, such as the Zigong Lantern, may contain millions of triangular faces, making efficient processing and rendering essential. Mesh simplification algorithms are commonly employed to reduce polygon counts, thereby improving computational efficiency while maintaining acceptable visual fidelity. Among these methods, the Quadric Error Metrics (QEM) algorithm [1] has been a widely adopted traditional approach due to its balanced performance between simplification quality and computational efficiency.

Nevertheless, a major limitation of QEM lies in its inadequate preservation of critical geometric features, such as high-curvature regions and sharp edges. This shortcoming can cause a noticeable loss of visual fidelity, particularly detrimental in applications requiring high-precision models, including cultural heritage preservation and industrial design. Although existing methods such as Farthest Point Sampling (FPS) [2] and curvature-aware simplification techniques [3,4] partially address this issue, they often struggle to capture intricate local geometric complexities, especially in non-uniform or noisy models.

As a result, fine details in regions with high-frequency features may still be lost.

To overcome these limitations, we propose an enhanced version of QEM, named SFSP-QEM, which integrates a Salient Feature-Preserving Point Sampler (SFSP) module. This module improves the identification of critical geometric features by jointly considering curvature and normal variation. The identified feature points are then incorporated as constraints during the vertex merging phase of QEM. By dynamically adjusting merging costs based on proximity to these feature points, SFSP-QEM achieves superior feature preservation compared to existing methods. Our approach is particularly effective in scenarios where retaining critical geometric details is essential, such as cultural heritage digitization, industrial design, and high-fidelity model rendering.

The main contributions of this paper are as follows:

•   We introduce the SFSP module, which effectively detects and preserves key geometric features in complex mesh models.

•   We integrate this module into the QEM algorithm, adjusting vertex merging costs according to the distance to salient feature points, thereby ensuring improved feature retention during simplification.

•   We validate the proposed method through extensive experiments, demonstrating significant improve-ments in geometric detail preservation and notable reductions in Hausdorff distance, particularly in cultural heritage models and other high-precision applications.

The remainder of this paper is organized as follows. Section 2 reviews mesh generation, the QEM algorithm, and its extensions, along with recent advances in deep learning for point cloud processing. Section 3 describes the proposed SFSP-QEM algorithm in detail and explains its feature-preserving mechanism. Section 4 presents experimental results, comparing our method to state-of-the-art techniques on various types of models. Finally, Section 5 concludes the paper and discusses potential future directions.

2  Related Work

2.1 Mesh Generation

Mesh generation is a foundational step in numerous applications, including computational fluid dynamics (CFD), finite element analysis, and engineering simulations. Traditional mesh generation methods typically rely on manual parameter adjustments, geometric heuristics, and expert knowledge to produce structured or unstructured meshes tailored to specific domains [5]. While these approaches can achieve high-quality results for well-characterized geometries, they often lack scalability and adaptability, making it challenging to efficiently handle complex or dynamically changing shapes.

To mitigate these limitations, optimization-based mesh generation techniques have been developed. These methods utilize genetic algorithms, gradient-based optimizations, and heuristic-driven refinement strategies to systematically enhance mesh quality metrics such as element aspect ratio, orthogonality, and skewness [6,7]. Although optimization-driven approaches reduce the need for manual intervention and improve mesh quality, they are computationally intensive and require re-optimization when faced with new geometries or simulation conditions, limiting their applicability in dynamic or large-scale scenarios.

In recent years, the field has witnessed a shift towards Intelligent Mesh Generation (IMG), which leverages Deep learning (DL) and reinforcement learning (RL) to create adaptive and data-driven mesh refinement strategies. IMG frameworks enable meshes to dynamically adjust based on simulation feedback or geometric complexity, thereby enhancing flexibility and scalability [8]. For instance, Pan et al. and Foucart et al. applied deep reinforcement learning (DRL) to adaptively refine mesh resolution in fluid dynamics simulations, allowing the mesh to evolve in response to changing flow features. Similarly, frameworks such as MGNet and FreeMesh-RL treat mesh generation as a decision-making process, utilizing neural networks and RL policies to learn optimal meshing strategies from data [8–11].

Moreover, in the context of discrete element methods (DEM) and particle-based simulations, Feng [12] integrated traditional mesh simplification techniques with an energy-conserving contact model to effectively simulate interactions of arbitrarily shaped particles. Although Feng’s approach focuses on mesh simplification rather than DL-driven generation, it exemplifies the trend toward combining robust mesh representations with adaptive simplification strategies to manage complex and irregular particle shapes. This integration highlights the necessity for mesh generation techniques that can seamlessly handle diverse geometric complexities, thereby providing a solid foundation for subsequent mesh simplification and feature preservation efforts.

2.2 QEM Algorithm

As the complexity of mesh models increases, mesh simplification becomes essential to reduce computa-tional overhead while maintaining critical geometric details. The Quadric Error Metrics (QEM) algorithm, introduced by Garland et al. [1], is a widely adopted method due to its efficiency and balanced performance in simplifying mesh models. However, traditional QEM and its variants often struggle to preserve high-frequency geometric details and salient features, such as sharp edges and high-curvature regions, leading to a loss of visual fidelity and accuracy in critical applications.

To address these limitations, numerous enhancements to the QEM framework have been proposed. Some methods incorporate additional constraints based on color and texture [13,14], while others integrate curvature-aware metrics to identify and retain high-curvature regions [15,16]. Furthermore, boundary protection mechanisms are introduced to maintain the integrity of feature lines and edges [17,18]. Although these improvements can better preserve local geometric features, many constraint-based methods remain geometry-specific or rely on robust feature detection, which becomes challenging for highly irregular or noisy models. More recent efforts utilize Centroidal Voronoi Tessellation (CVT) energy terms and normal anisotropy terms to achieve an improved balance between precision and mesh quality [19]. Nevertheless, these methods may still encounter difficulties in simplifying local regions within complex models. Therefore, we guide the QEM algorithm by sampling significant feature points from mesh vertices, aiming to preserve salient features more effectively.

2.3 Deep Learning on Point Clouds

Point clouds are a versatile and direct representation of 3D geometry, playing a crucial role in mesh generation and simplification processes. However, their unordered and irregular nature poses significant chal-lenges for traditional Convolutional Neural Networks (CNNs). PointNet [20] addressed this by introducing a permutation-invariant architecture, enabling the application of deep learning techniques to point cloud data. Building on this, PointNet++ [21], PointCNN [22], and Dynamic Graph CNN (DGCNN) [23] have further advanced the field by enhancing local feature extraction through hierarchical processing and dynamic graph constructions.

Although these methods attempt to address the problem of local geometric structure extraction in point cloud data, some limitations remain. To better describe the local geometric characteristics of vertices, we use DevConv proposed by Potamias et al. [24], which employs max pooling to aggregate information from neighboring nodes and captures geometric features by comparing the relative coordinates of adjacent nodes. This method not only captures local geometric features more effectively but also improves the model’s performance in handling complex shapes and detailed features.

2.4 Point Cloud Sampling

Point cloud sampling is a critical preprocessing step aimed at reducing data redundancy while preserving essential geometric features for downstream applications such as mesh simplification and feature preservation. Traditional sampling methods, including Farthest Point Sampling (FPS) [2], random sampling, and uniform downsampling, are widely used due to their simplicity and computational efficiency. However, these methods often fail to retain important geometric details in regions with high complexity, leading to significant loss of critical features when applied at low sampling ratios.

To overcome these limitations, learning-based sampling strategies have been developed. Methods such as S-Net, SampleNet, APES, and APSNet leverage deep learning to learn data-driven sampling patterns that prioritize salient points based on geometric significance [25–28]. These approaches utilize attention mechanisms, differentiable sampling layers, and learned importance scores to ensure that key features are preserved while redundant points are discarded. Despite their improved performance in retaining important features, learning-based sampling methods can suffer from reduced generalization capabilities when faced with point cloud data distributions that differ significantly from those seen during training.

In this study, we extend the traditional Farthest Point Sampling (FPS) method to a trainable module, integrating it with a salient feature point sampler. This hybrid approach maintains the robustness and global coverage benefits of FPS while incorporating learned prioritization of significant feature points. By doing so, our method ensures high-quality sampling that effectively preserves critical geometric features, thereby enhancing the performance of the subsequent QEM mesh simplification process. This combination of traditional and learning-based sampling strategies offers a balanced solution that leverages the strengths of both approaches, ensuring both robustness and feature preservation across diverse and complex point cloud datasets.

3  Methods

Our method architecture consists of three main components: a high-dimensional embedding network, a salient feature point sampler, and the SFSP-QEM algorithm. The architecture of the proposed method is illustrated in Fig. 1.

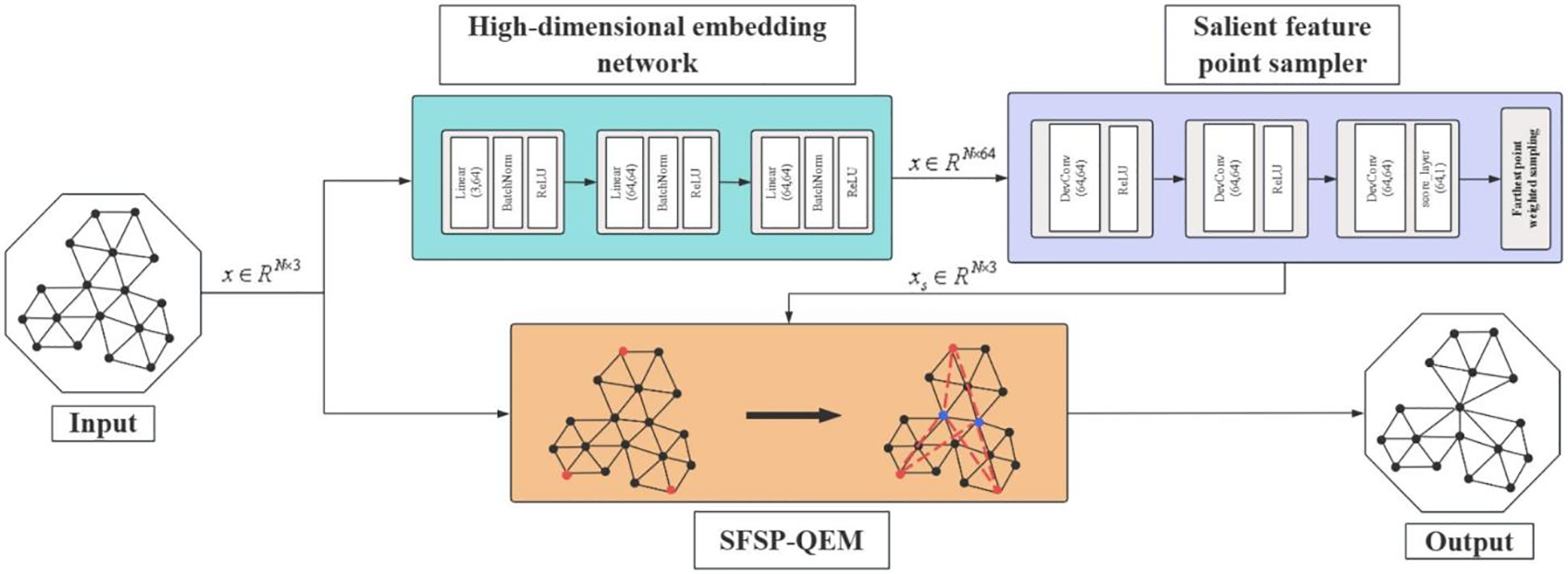
Figure 1: Overall architecture diagram of the deep learning-based salient feature-preserving algorithm for mesh simplification. First, the input mesh vertex data is processed by the high-dimensional embedding network (blue) to generate embedded features. Then, the sampling points (red) are selected using the salient feature point sampler (purple). Finally, the SFSP-QEM algorithm (orange) is applied for mesh simplification, adjusting the merging cost of vertex pairs during simplification based on the distance between effective vertices (blue) and key vertices (red), resulting in the simplified mesh model as the output

3.1 High-Dimensional Embedding Network

In the study of point cloud data, three-dimensional coordinates provide fundamental information about the shape and position of objects. However, directly inputting these raw coordinates into a neural network often limits the network’s ability to capture deep geometric features. This limitation arises because relying solely on the original three-dimensional coordinates does not fully represent the underlying geometric relationships between points. To address this constraint, we introduce a High-Dimensional Embedding Network (HDEN), which transforms each point into a high-dimensional feature space, enabling more effective extraction of rich geometric features.

The core component of this network is a Multi-Layer Perceptron (MLP), structured as follows:

hi=MLP(pi)=σ(W3⋅σ(W2⋅σ(W1⋅pi+b1)+b2)+b3).(1)

Here, pi=R3 represents the three-dimensional coordinate vector of the i-th point in the point cloud, specifically (xi,yi,zi). The output hi=R64 is the 64-dimensional feature vector of thei-th point in the high-dimensional feature space. The weight matrices W1=R64×3, W2=R64×64, and W3=R64×64 correspond to the first, second, and third layers of the MLP, respectively. Additionally, the bias vectors b1,b2,b3∈R64×3 are associated with each respective layer. The activation function σ denotes the ReLU activation function, defined as σ(x)=max(0,x), which introduces non-linearity into the network.

The MLP transforms each three-dimensional point pi into a high-dimensional feature vector hi through a series of fully connected layers. Specifically, the input point pi first undergoes a linear transformation using W1 and b1, followed by the ReLU activation function σ, resulting in the first layer’s activation a1:

a1=σ(W1⋅pi+b1).(2)

Next, a1 is passed through the second fully connected layer with weights W2 and bias b2, followed by another ReLU activation, yielding the second layer’s activation a2:

a2=σ(W2⋅a1+b2).(3)

Finally, a2 is fed into the third fully connected layer with weights W3 and bias b3, and another ReLU activation is applied to produce the high-dimensional feature vector hi:

hi=σ(W3⋅a2+b3).(4)

The introduction of the high-dimensional feature vector hi allows the network to capture not only local geometric structures but also more abstract and non-local relationships between points. This high-dimensional representation enhances the network’s ability to perceive complex geometric features, thereby enabling more effective utilization of these features in subsequent processing steps.

Our High-Dimensional Embedding Network extends previous methods such as PointNet [20]. While PointNet introduced symmetric functions to handle the unordered nature of point clouds, primarily focusing on global features, our HDEN emphasizes local geometric structures. By capturing point-level features and neighborhood information, and incorporating curvature and normal variations, our approach enhances the granularity of feature extraction. Specifically, our method retains local geometric information and effectively encodes complex relationships between points through high-dimensional embedding, providing richer feature representations for subsequent feature fusion and classification tasks.

3.2 Salient Feature Preservation Point Sampler

Traditional sampling methods, such as Farthest Point Sampling (FPS), perform poorly in regions containing complex local details because they focus on maximizing the overall coverage of the point cloud rather than prioritizing important geometric features. To overcome this limitation, we propose a Salient Feature Preservation Point Sampler (SFSP Point Sampler), a learnable sampling method that selects points based on curvature, normal vector variation, and high-dimensional feature scores.

Curvature is a key indicator of local geometric properties in a point cloud, capturing changes in surface shape and helping to identify prominent features like edges and corners. In our method, the curvature of each point pi is calculated using the covariance matrix method described by Potamias et al. [29]. Specifically, for each neighbor pj of point pi, we first compute the centroid p of the neighborhood:

p=1k∑j=1kpj,(5)

where pj is the j-th neighbor of pi and k is the number of neighbors in the neighborhood. The covariance matrix C is then computed as:

C=∑j=1k(pj−p)(pj−p)T.(6)

By performing eigenvalue decomposition on the covariance matrix C, we obtain the local surface normal vectors and curvature for each point. Specifically, the curvature ki is calculated as the ratio of the smallest eigenvalue λ0 to the sum of all eigenvalues λj:

ki=λ0∑j=0kλj,(7)

where λ0 is the smallest eigenvalue of C, representing the direction of minimal curvature.

Normal vector variation is another important factor for identifying sharp features. It measures the difference between the normal vectors of a point and its neighbors, detecting sudden changes in surface direction. The normal vector variation Δni for point pi is defined as:

Δni=‖ni−nj‖,(8)

where ni and nj are the normal vectors of point pi and its neighbor pj, respectively. Regions with significant normal vector variations typically correspond to edges or corners, which should be preserved during sampling.

After computing curvature and normal vector variation for all points, we combine these metrics with the high-dimensional features generated by the embedding network to calculate a score si for each point:

si=σ(W4⋅hi)(1+Δnimax(Δn)+9⋅(ki−μk)2σk2+1×10−8).(9)

In this equation, σ is the Sigmoid activation function, normalizing scores to the range [0,1]. The weight matrix W4 transforms the high-dimensional feature vector hi into a score. Here, hi is the 64-dimensional feature vector of point pi generated by the HDEN. The term Δni represents the normal vector variation of point pi, while ki is its curvature. The mean μk and standard deviation σk of the curvature across all points are used to standardize the curvature contribution. The constant 1×10−8 prevents numerical instability during computation. This scoring mechanism integrates normal vector variation and curvature information, weighted by high-dimensional feature embeddings, to prioritize points with significant geometric features.

To ensure that regions with prominent geometric features are adequately sampled, we enhance the FPS algorithm by incorporating the score si to guide the sampling process:

Ps=FPS(P,s,M).(10)

In this formulation, P is the input point cloud, s is the score vector containing the geometric saliency scores of each point, and M is the number of points to be sampled. The resulting Ps is the sampled point cloud. The enhanced FPS algorithm considers both the spatial distribution of points and their geometric feature scores, ensuring that important geometric features are preserved. The specific steps are:

1.    Select an initial point randomly from the point cloud as the first sampled point.

2.    Iteratively select points that are the farthest from the current set of sampled points and have higher scores si until M points are sampled.

By combining high-dimensional features, curvature information, and normal vector variation, our Salient Feature Preservation Point Sampler ensures that geometrically significant points are retained, achieving more accurate and feature-preserving mesh simplification.

3.3 SFSP-QEM Algorithm

The SFSP-QEM algorithm builds upon the traditional Quadric Error Metrics (QEM) algorithm by integrating the Salient Feature Sampling Point (SFSP) module. This integration prioritizes the preservation of key geometric features, such as sharp edges and high-curvature areas, during mesh simplification. While maintaining the fundamental structure of QEM, SFSP-QEM introduces additional steps to ensure the retention of significant features throughout the simplification process. The algorithm proceeds as follows.

3.3.1 Initialization of Quadric Error Metrics

Similar to the traditional QEM algorithm, we begin by initializing the quadric error matrices for all vertices in the mesh. The quadric error matrix Qv for a vertex v is a symmetric matrix that encodes the distance of the vertex to its adjacent triangular faces. For each vertex v, the initialization formula is:

Qv=∑f∈N(v)nfnfT.(11)

Here, Qv is the quadric error matrix of vertex v, with dimensions 4×4. The set N(v) represents the neighboring triangular faces of vertex v. The normal vector nf of face f, defined as (nfx,nfy,nfz), is used to define a plane with the equation nfx⋅x+df=0. The quadric error matrix Qv is the sum of the outer products of the normal vectors of all adjacent faces, reflecting the distance of vertex v to these planes. This initialization step provides the foundation for measuring geometric distortion in subsequent steps.

3.3.2 Salient Feature Sampling

Next, we apply the Salient Feature Preservation Point Sampler (SFSP) module described in Section 3.2 to select a set of salient feature points from the mesh. These feature points are crucial for maintaining important geometric details during simplification. The selection is based on curvature, normal vector variation, and high-dimensional feature scores, resulting in a set Ps of salient feature points. The salient feature points Ps include points with high curvature and significant normal vector variations, typically corresponding to sharp edges and corners. During the simplification process, these points are prioritized to minimize the loss of important geometric details.

3.3.3 Quadric Error Adjustment with Penalty Terms

For each pair of vertices (vi,vj) considered for edge contraction, we calculate the quadric error Q(vi,vj), which measures the geometric distortion caused by merging these two vertices. In SFSP-QEM, we modify the traditional quadric error by introducing a penalty term based on the distance between vertex pairs and the set of salient feature points Ps. The modified quadric error is defined as:

Q′(vi,vj)=Q(vi,vj)⋅(1+α⋅d(vi,Ps)).(12)

In this equation, Q′(vi,vj) is the penalized quadric error matrix, Q(vi,vj) is the traditional quadric error matrix for the vertex pair (vi,vj), d(vi,Ps) is the minimum Euclidean distance from vertex vi to the set Ps of salient feature points, and α is a constant controlling the strength of the penalty term. This modification increases the quadric error for vertex pairs close to salient feature points, thereby reducing the likelihood of contracting edges in these regions and preserving critical geometric features.

3.3.4 Edge Collapse and Mesh Simplification

After adjusting the quadric error matrices, the SFSP-QEM algorithm proceeds with edge contraction based on the modified quadric errors. The process involves iteratively collapsing the edges with the smallest quadric error until the desired level of simplification is achieved. The steps are as follows:

1.    Select Edge: Identify the edge with the smallest modified quadric error Q′(vi,vj) for contraction.

2.    Collapse Edge: Merge the selected edge (vi,vj) into a new vertex v′ and update the quadric error matrix for v′ as:

Qv′=Qvi+Qvj.

3.    Update Quadric Matrices: Recompute the quadric error matrices for vertices affected by the collapse.

4.    Repeat: Continue the process until the mesh is simplified to the desired level.

By incorporating the SFSP module and feature-based penalty terms, the SFSP-QEM algorithm effectively preserves key geometric features, such as sharp edges and high-curvature regions, better than the Quadric Error Metrics (QEM) algorithm (Algorithm 1).

3.4 Loss Function

To optimize the point cloud sampling process, we introduce multiple loss functions to train the point sampler. These loss functions draw inspiration from the methods proposed by Potamias et al. [29] and Potamias et al. [24]. Additionally, we design a Feature Preservation Loss to ensure the effectiveness of the sampled points. These loss functions collectively consider geometric features, curvature, probabilistic information, and normal vector variations to prioritize the retention of salient feature points.

3.4.1 Adaptive Chamfer Distance

The traditional Chamfer distance does not account for curvature information, leading to the loss of significant geometric features during simplification. By incorporating curvature as a weighting factor, the Adaptive Chamfer Distance prioritizes high-curvature regions, better preserving the geometric details of the point cloud. The formula for the Adaptive Chamfer Distance is:

dAdapt(P1,P2)2=1N1∑i=1N1[Ki⋅miny∈P2‖xi−y‖2]+1N2∑i=1N2[Kj⋅minx∈P1‖xj−y‖2].(13)

In this equation, dAdapt(P1,P2) is the Adaptive Chamfer Distance between point clouds P1 and P2. N1 and N2 are the number of points in P1 and P2, respectively. The curvature values Ki and Kj of points xi in P1 and xj in P2 serve as weights, adjusting the contribution of each point pair based on their curvature. Here, xi and y represent points in P1 and P2, respectively. This distance metric adjusts the contribution of each point pair by their respective curvature values, ensuring that points in high-curvature regions have a greater influence on the loss function.

3.4.2 Probabilistic Weighted Chamfer Distance

In point cloud data, different points hold varying levels of importance. By introducing probabilistic information, each point can be assigned a distinct weight, allowing the loss function to more accurately reflect the geometric features and probability distribution of the point cloud. The Probabilistic Weighted Chamfer Distance is defined as:

dp(P,Ps)=1N1∑i=1N1[pi⋅miny∈Ps‖xi−y‖2]+1N2∑i=1N2[qj⋅minx∈P‖xj−y‖2].(14)

Here, dp(P,Ps) is the Probabilistic Weighted Chamfer Distance between the original point cloud P and the sampled point cloud Ps. N1 and N2 are the number of points in P and Ps, respectively. The probability weights pi and qj assigned to points xi in P and xj in Ps adjust the contribution of each point pair based on their importance. In this context, xi and y represent points in P and Ps, respectively. This distance metric adjusts the contribution of each point pair based on their assigned probability weights, enhancing the influence of important points in the loss calculation.

3.4.3 Curvature Difference Loss

Curvature is a critical indicator of local geometric features in a point cloud. By measuring the difference in curvature, we can effectively evaluate the similarity of salient features between two point clouds, ensuring the retention of these features during simplification. The Curvature Difference Loss is defined as:

Ec=1N1∑i=1N1(K1(xi)−K2(NN(xi,P2)))2.(15)

In this equation, Ec is the Curvature Difference Loss, quantifying the discrepancy in curvature between the original and sampled point clouds. N1 is the number of points in the original point cloud P1. The curvature K1(xi) of point xi in P1 is compared to the curvature K2(NN(xi,P2)) of its nearest neighbor in the sampled point cloud P2. Here, NN(xi,P2) denotes the nearest neighbor of xi in P2. This loss function ensures geometric consistency by minimizing the curvature differences between corresponding points in the original and sampled point clouds.

3.4.4 Feature Preservation Loss

The Feature Preservation Loss ensures that sampled points effectively represent the geometric features of the original point cloud by comparing their enhanced scores and normalized normal vector variations. The loss is defined as:

Lp=1N∑i=1N(si−ni~)2.(16)

Here, Lp is the Feature Preservation Loss, measuring the discrepancy between the sampled points’ scores si and their normalized normal vector variations ni~. N is the total number of points in the point cloud. By minimizing this loss, we ensure that sampled points with higher scores, indicative of significant geometric features, are preserved accurately. This comparison promotes the accurate retention of important geometric features, enhancing the fidelity of the mesh simplification model.

3.4.5 Total Loss Function

Combining all the aforementioned loss functions, we define the Total Loss Function to comprehensively optimize the selection of sampled points, ensuring both efficiency and precision in the simplification process. The Total Loss Function is expressed as:

L=dAdapt(P1,P2)+dp(P,Ps)+Ec+Lp.(17)

In this formulation, L integrates the Adaptive Chamfer Distance dAdapt(P1,P2), Probabilistic Weighted Chamfer Distance dp(P,Ps), Curvature Difference Loss Ec, and Feature Preservation Loss Lp. This comprehensive loss function ensures that:

1)   Adaptive Chamfer Distance prioritizes high-curvature regions, preserving geometric details.

2)   Probabilistic Weighted Chamfer Distance adjusts the contribution of each point based on probability weights, enhancing the influence of important points.

3)   Curvature Difference Loss maintains geometric consistency by minimizing curvature discrepancies between original and sampled point clouds.

4)   Feature Preservation Loss ensures that sampled points accurately represent significant geometric features through their enhanced scores and normal vector variations.

By integrating these loss components, the Total Loss Function L ensures that the sampled points are not only well-distributed spatially but also highly faithful to the geometric features of the original point cloud, achieving efficient and precise mesh simplification.

4  Experiments

In this section, we evaluate our proposed method through quantitative and qualitative experiments. First, we compare our point sampling method with the following baseline methods: random sampling, uniform sampling, and farthest point sampling. Then, we compare the simplification effects of the traditional QEM algorithm with the SFSP-QEM algorithm on general models as well as on a personalized model (e.g., Zigong Lantern model).

4.1 Dataset

This study utilizes the TOSCA dataset to train our Salient Feature Preservation Point Sampler (SFSP). The TOSCA dataset is of medium size and consists of 80 high-resolution mesh models, representing 9 different categories of deformable objects, including humans, animals, and artificial objects. This dataset is characterized by the geometric complexity and rich deformation features of its models, providing a solid foundation for training the subsequent SFSP-QEM algorithm under various deformations and poses.

We split the TOSCA dataset into 80% for training and 20% for testing. The choice of this split ratio is based on the moderate size of the TOSCA dataset, which provides enough examples for training the model while ensuring that the testing set is large enough to accurately assess generalization performance. However, to assess the impact of different dataset splits, we also experimented with alternative ratios, such as 90% for training and 10% for testing, as well as 70% for training and 30% for testing.

When we increased the training data percentage to 90%, the model was trained on a larger portion of the dataset, improving training performance. However, the smaller testing set (10%) led to slightly reduced reliability of the testing metrics, as it provided fewer examples for evaluating the model’s generalization ability. Although training accuracy improved, we observed that the model tended to overfit the training set. On the other hand, when we reduced the training set to 70% and increased the testing set to 30%, the model’s generalization ability improved, as the larger testing set allowed for better evaluation of its performance on unseen data. However, with fewer examples available for training, the model’s performance during training slightly decreased. This configuration also resulted in higher variance in the model’s performance, indicating greater sensitivity to the specific data samples used during training. Ultimately, we chose the 80% training and 20% testing split, as it strikes a good balance between training performance and reliable model testing.

Ultimately, we chose the 80%/20% split, as it strikes a good balance between training performance and reliable model testing. In addition to the TOSCA dataset, we also used general models from the Stanford 3D Scanning Repository and personalized models as the validation set. These models were not part of the training or testing sets, ensuring that the point sampler was evaluated on unseen mesh topologies, thus providing valuable insights into its generalization capability.

4.2 Experimental Process

Our salient feature point sampler model uses a Multi-Layer Perceptron (MLP) to process the input points, outputting high-dimensional embedded features that are further processed by multiple graph convolution layers. A scoring layer assigns a score to each point for subsequent farthest point sampling. We use the AdamW optimizer for training, running the model for 150 epochs with a learning rate set to 1e − 3 and a weight decay of 0.99 per epoch. Additionally, the learning rate scheduler, Reduce Learning Rate on Plateau, adjusts the learning rate based on validation loss, with a reduction factor of 0.8 and a patience period of 20 epochs. The training process also employs Automatic Mixed Precision (AMP) and Gradient Scaling, along with Early Stopping, which halts training if the validation loss does not improve within 10 epochs. The sampled points are introduced as key vertices into the Quadric Error Metrics algorithm. The contraction cost is adjusted based on the minimum distance between valid vertex pairs and all key vertices. After merging each vertex pair, the minimum distance between the vertex pairs and all key vertices are updated until the simplification threshold is reached, resulting in the output of the simplified model.

4.3 Evaluation of Point Sampling Methods

To evaluate the performance of the salient feature preservation point sampler, we visualized the sampling results of our point sampler and three baseline methods on the general models and lantern model provided by the Stanford 3D Scanning Repository. Figs. 2–4 illustrate the differences between various methods on the general models.

Figure 2: Qualitative evaluation of point sampling on the buddha model at different sampling levels

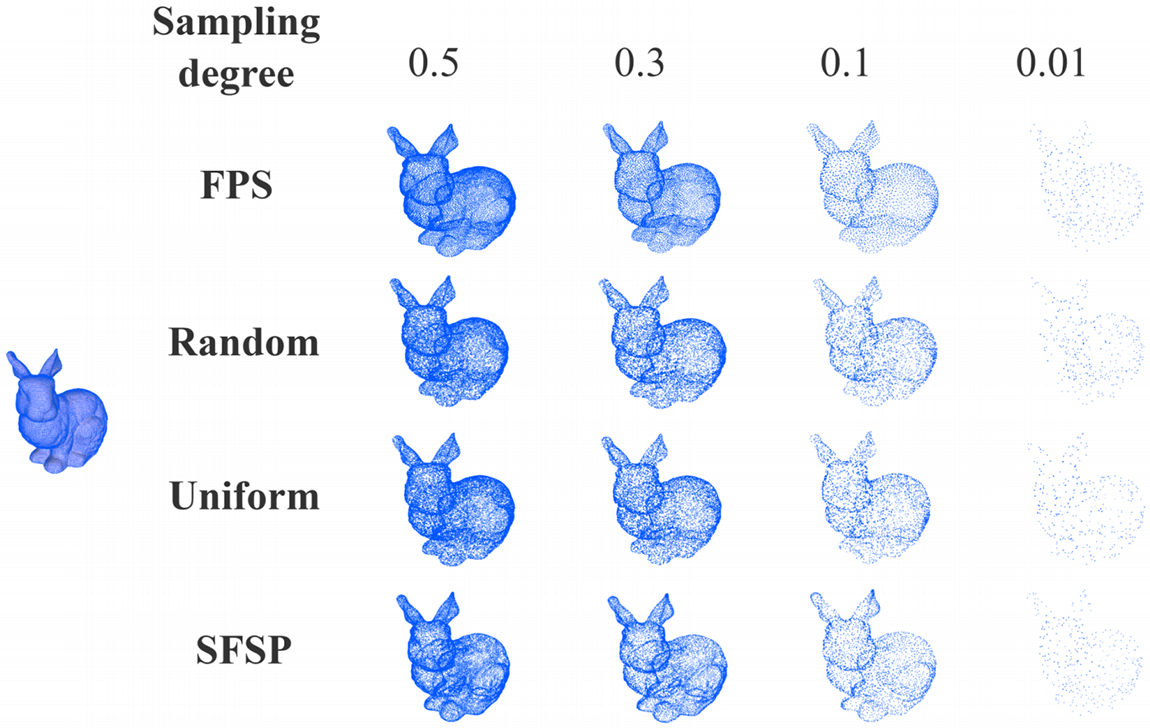
Figure 3: Qualitative evaluation of point sampling on the bunny model at different sampling levels

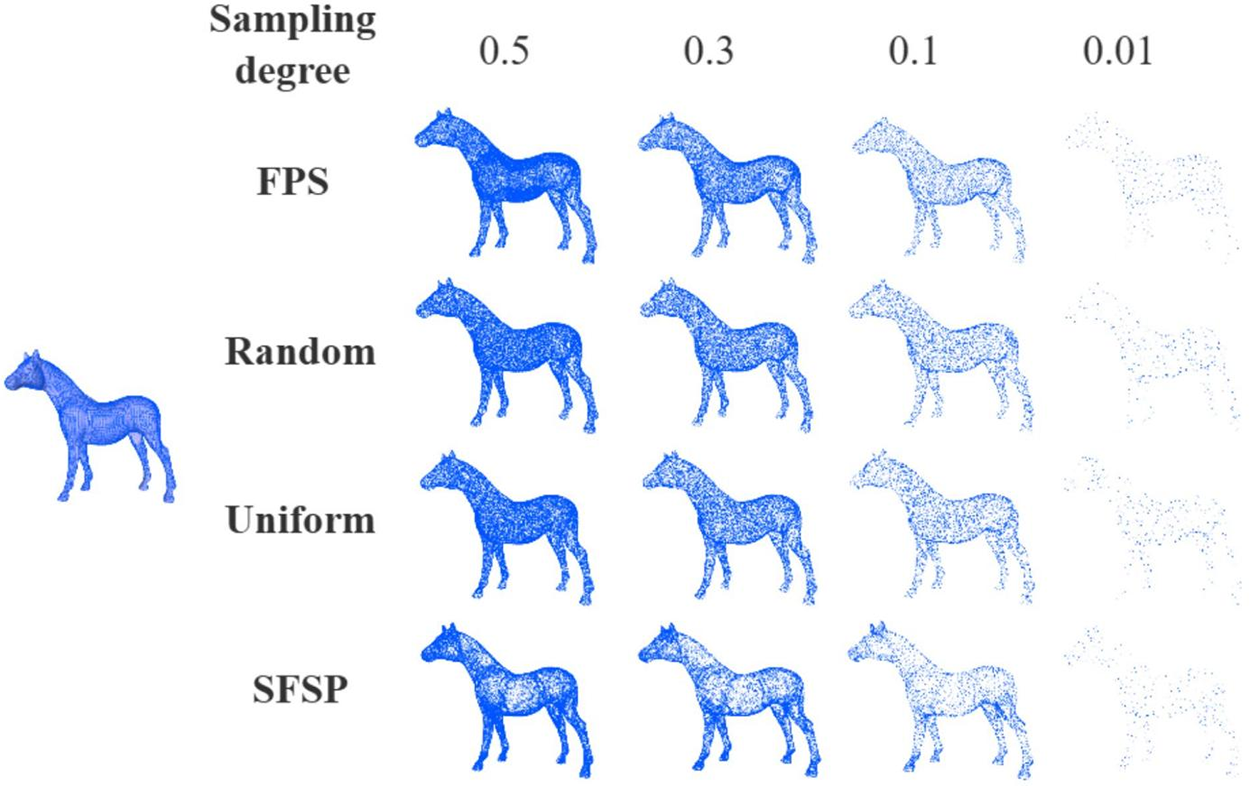
Figure 4: Qualitative evaluation of point sampling on the horse model at different sampling levels

The farthest point sampling method preserves the overall structure and details of the original model well at various simplification ratios, especially at higher ratios. However, at lower ratios, the sampled points are more sparsely distributed, resulting in significant detail loss. The random sampling method performs poorly, with uneven point distribution at all ratios, making it difficult to retain the overall structure and details of the model. At simplification ratios of 0.1 and 0.01, the model’s shape becomes blurred and inaccurate. The uniform sampling method performs well at high ratios, retaining some model structure and details. However, at lower ratios, it is less effective than farthest point sampling, with considerable detail loss. The SFSP method performs excellently across all simplification ratios, particularly at higher ratios, where it preserves model details and salient features effectively. Even at lower ratios, it significantly outperforms random and uniform sampling in retaining details.

As shown in Fig. 5, for the lantern gate model, the salient feature preservation sampling maintains its main structure and salient features at all sampling rates. Even at low sampling rates (e.g., 0.005 and 0.001), the salient feature preservation sampling method still clearly presents important parts of the model (e.g., the top decorations and central part). In comparison, farthest point sampling performs well at high sampling rates but loses many details at low sampling rates. At high sampling rates (e.g., 0.1 and 0.01), both SFSP and farthest point sampling retain details well. Uniform sampling also performs well in detail retention, but at low sampling rates (e.g., 0.005 and 0.001), its detail retention significantly decreases. Random sampling performs the worst in detail retention across all sampling rates, with substantial detail loss. Visually, salient feature preservation sampling offers the best visual effect at different sampling rates, preserving the model’s important features and overall aesthetics to the greatest extent. Farthest point sampling performs well at high sampling rates but blurs salient features at low sampling rates. Uniform sampling provides consistent visual effects but performs poorly in areas with complex details. Random sampling shows the worst visual effects across all sampling rates.

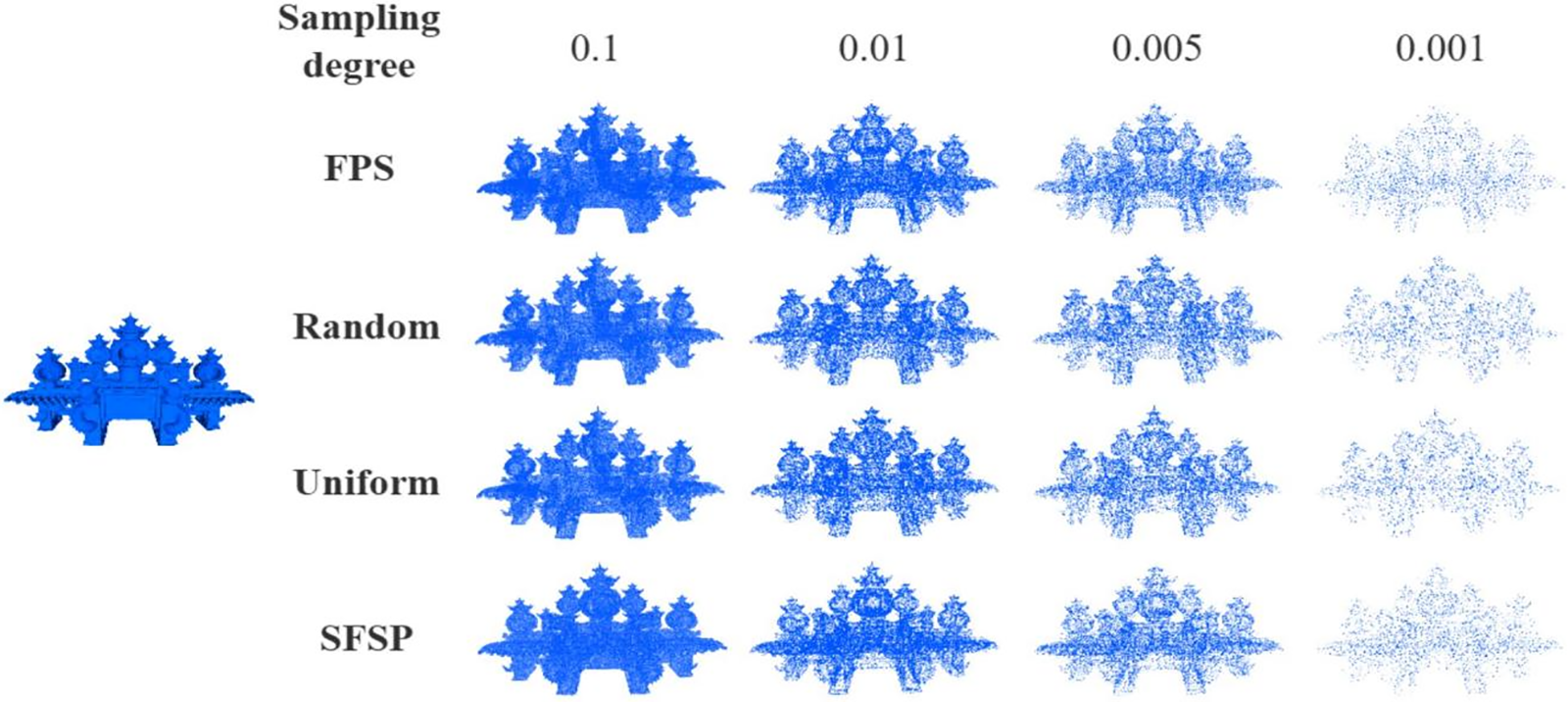
Figure 5: Qualitative evaluation of point sampling on the lantern gate model at different sampling levels

To quantify the differences in point sampling effectiveness among various methods, we used the evaluation methods proposed by Potamias et al. [29] and Potamias et al. [24]. As shown in Tables 1–4, the best results are highlighted in bold. We measured the sampling results at different levels using Chamfer Distance (CD), Curvature Error (CE), Normal Consistency (NC), and Roughness Error (RE). Fig. 6 demonstrates the superiority of our salient feature preservation point sampler.

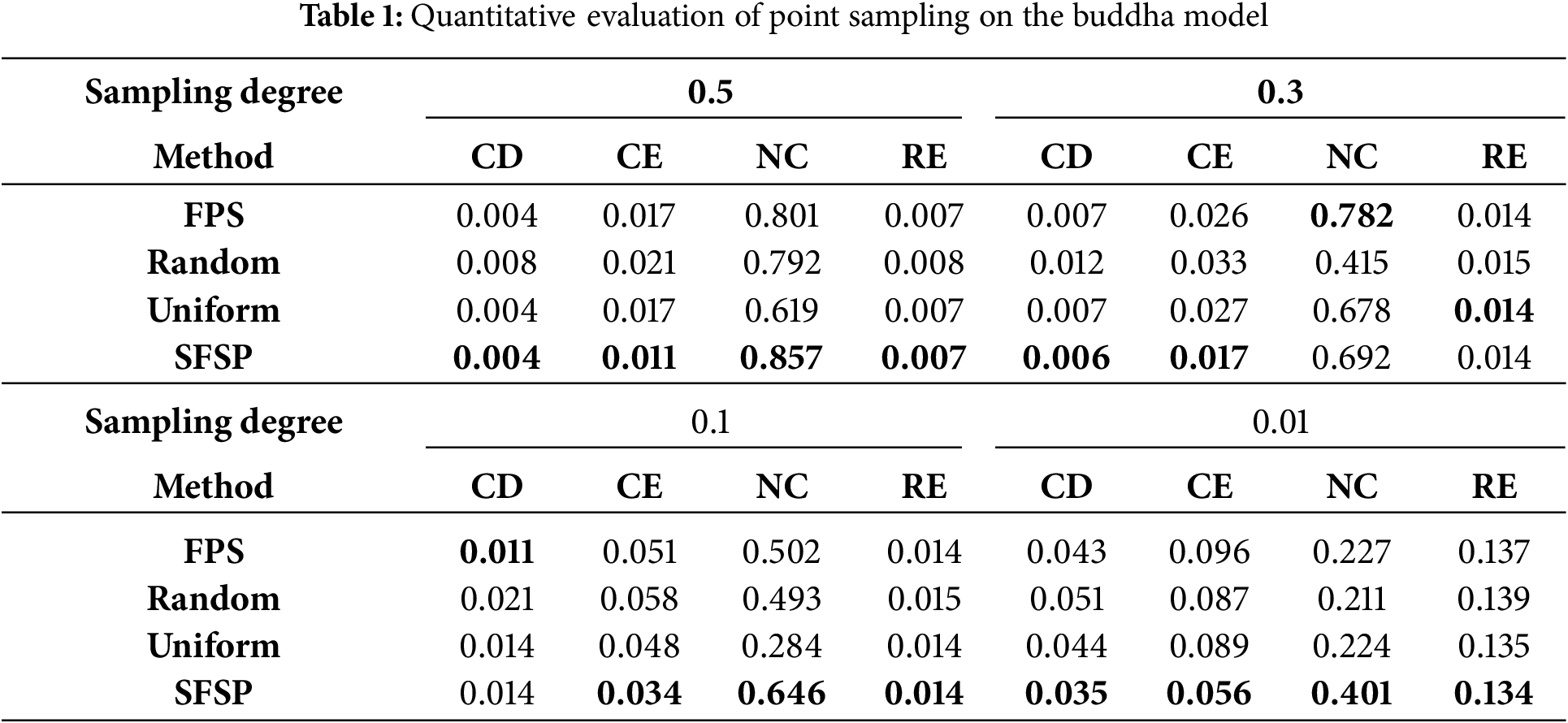
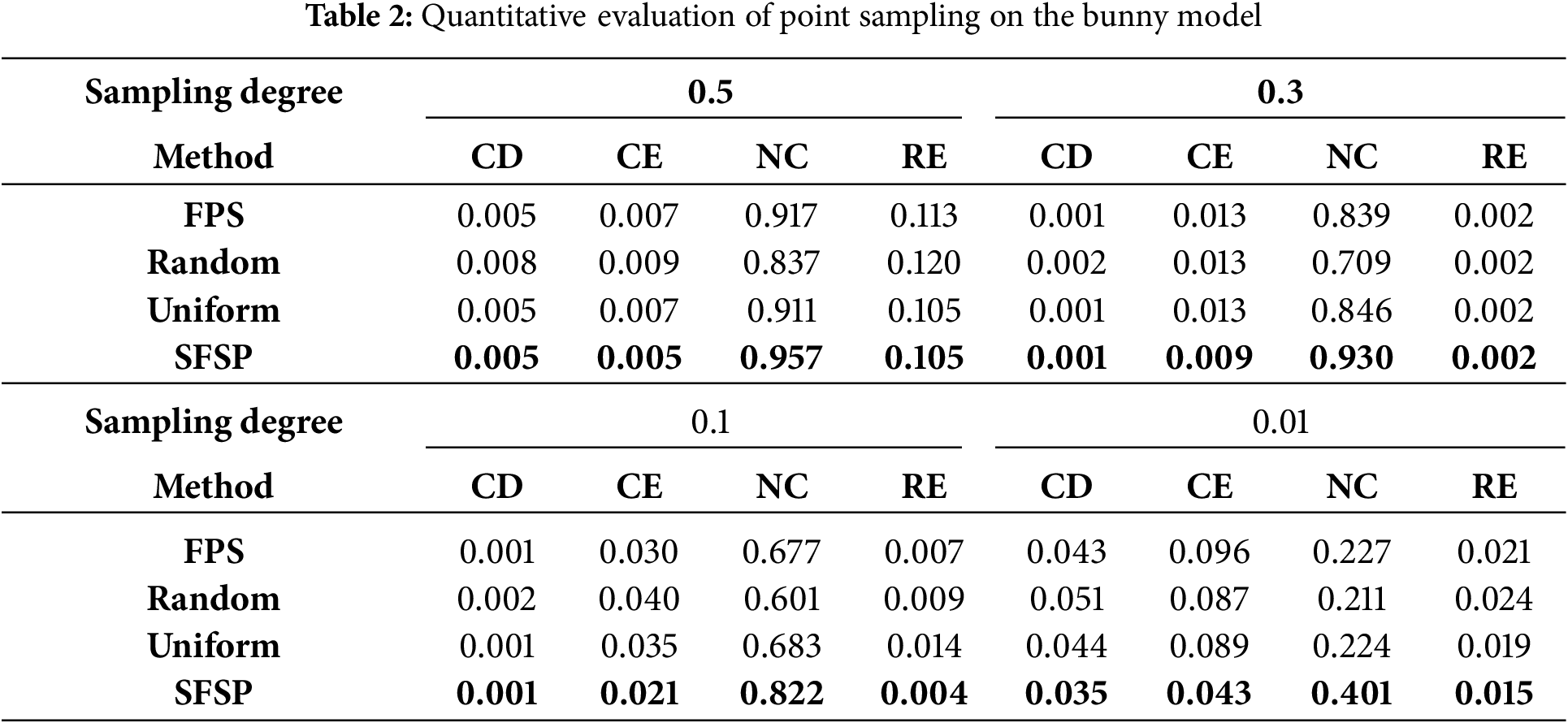
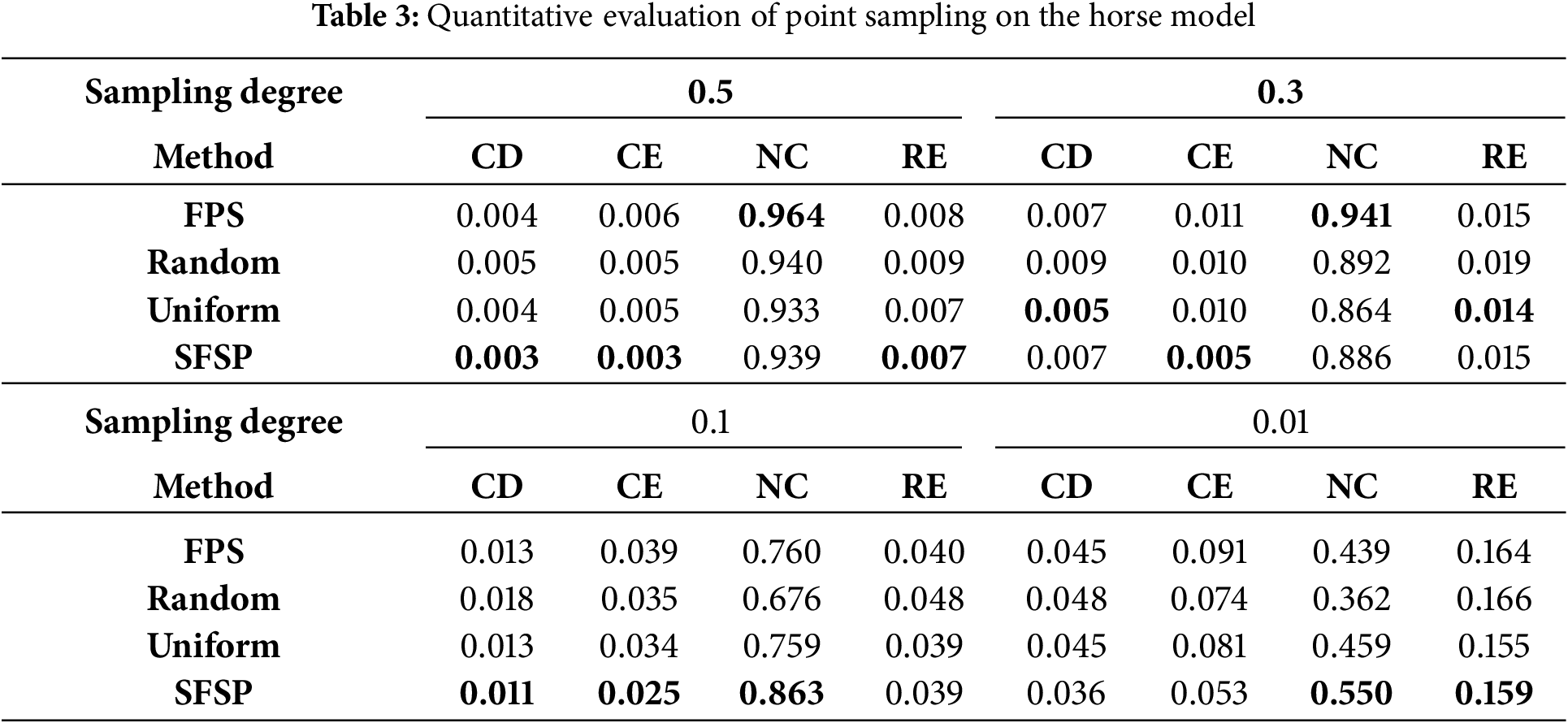
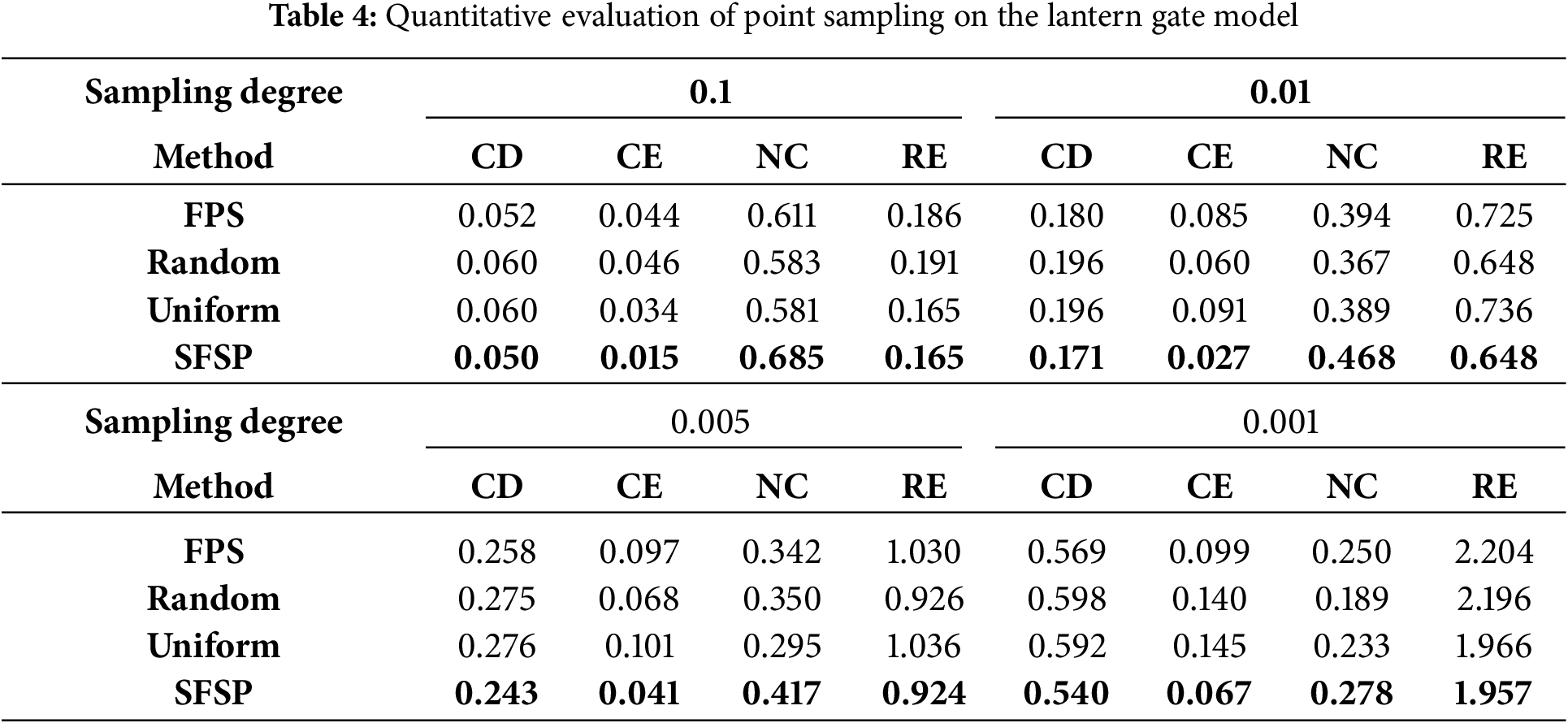
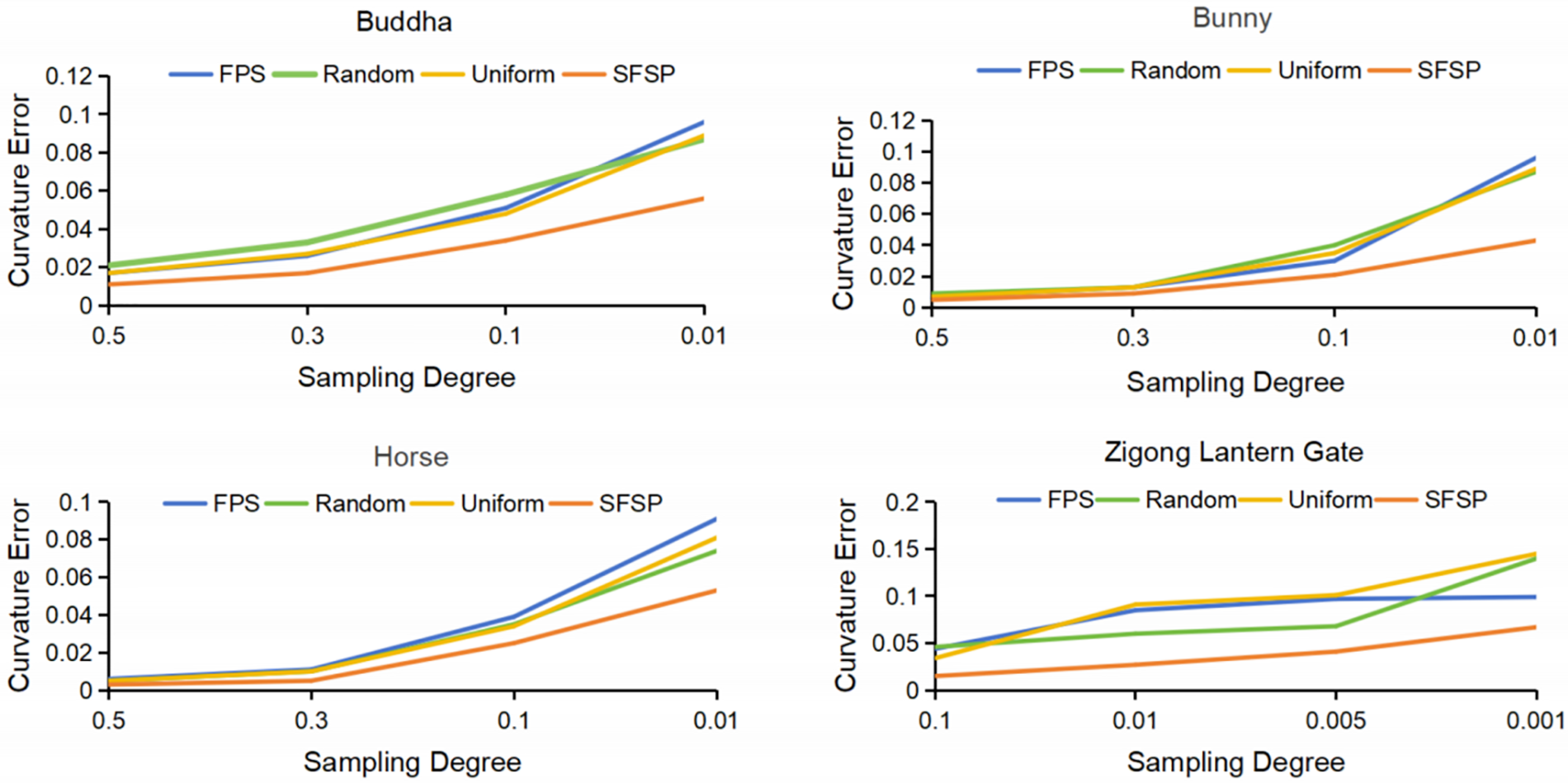
Figure 6: Comparison of curvature errors between SFSP and baseline methods at different simplification degrees

4.4 Evaluation of Mesh Simplification Methods

In this study, we selected multiple mesh models from the Stanford 3D Scanning Repository and personalized models as test subjects to compare with the traditional QEM algorithm. The objective was to thoroughly evaluate the performance of our proposed SFSP-QEM algorithm in simplification tasks. The five most representative models Dinosaur model, Fandisk model, Armadillo model, Dragon model, and Galloping Horse Treading on a Flying Swallow model are illustrated in Figs. 7–11, clearly demonstrating the effectiveness of different methods across various levels of simplification.

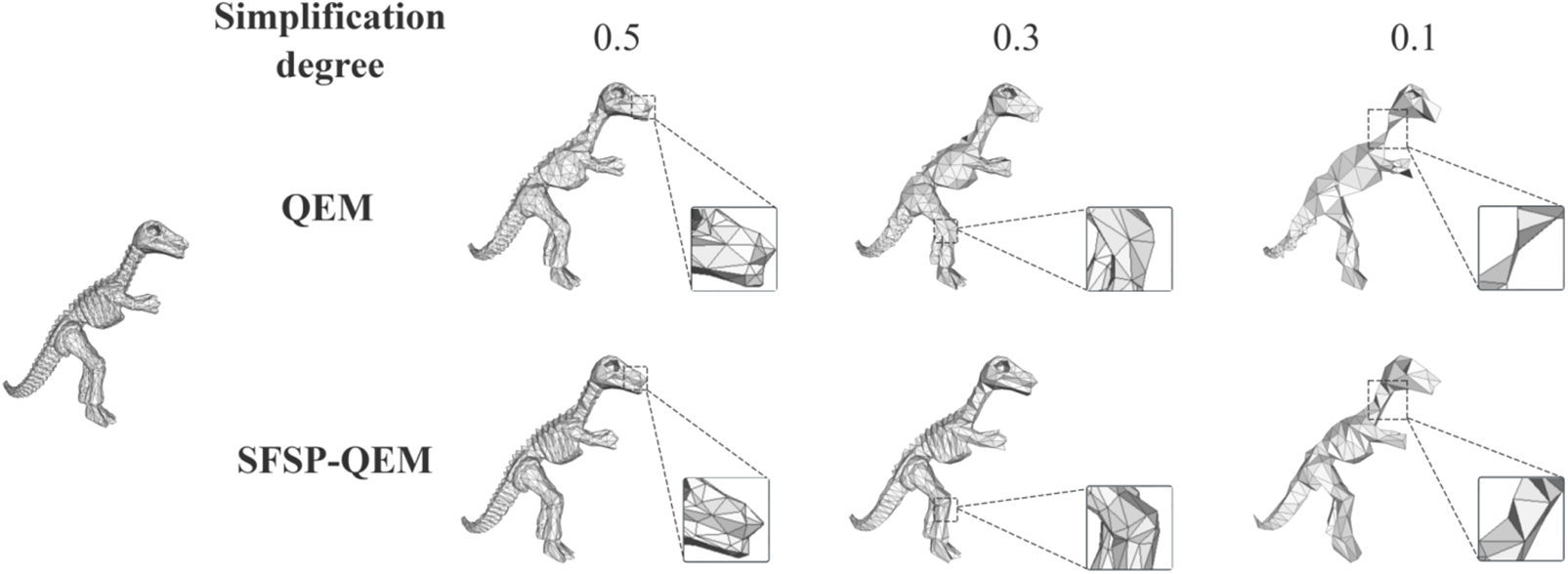
Figure 7: Qualitative evaluation of point sampling on the dinosaur model at different sampling levels

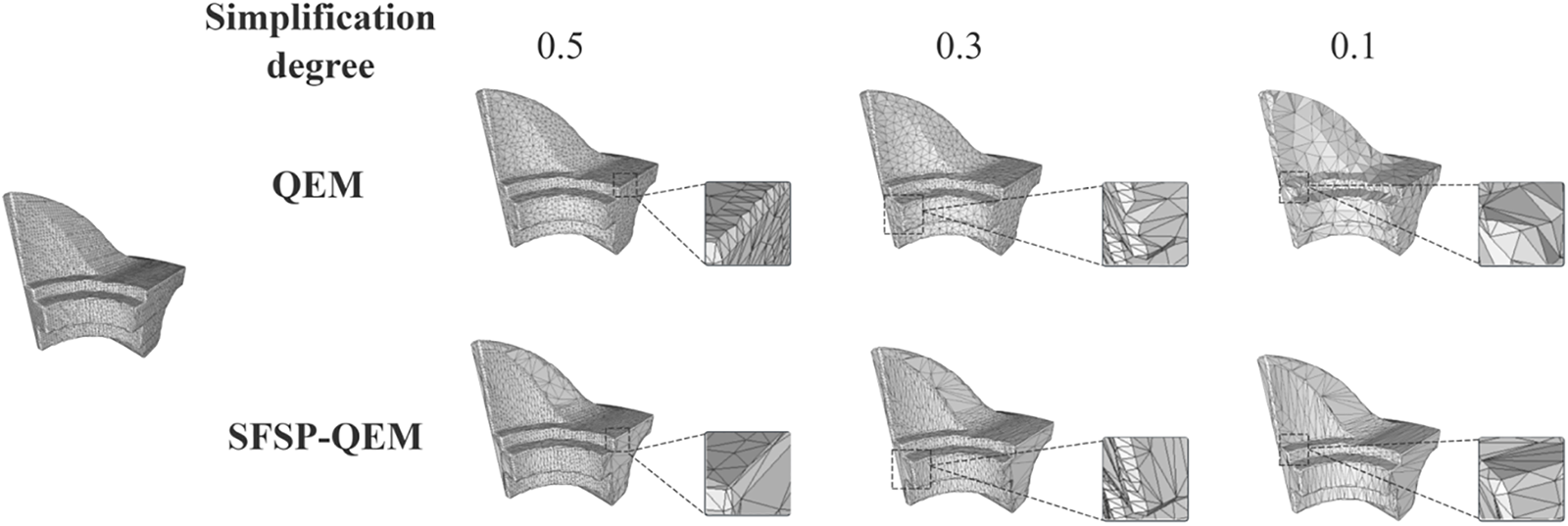
Figure 8: Qualitative evaluation of point sampling on the fandisk model at different sampling levels

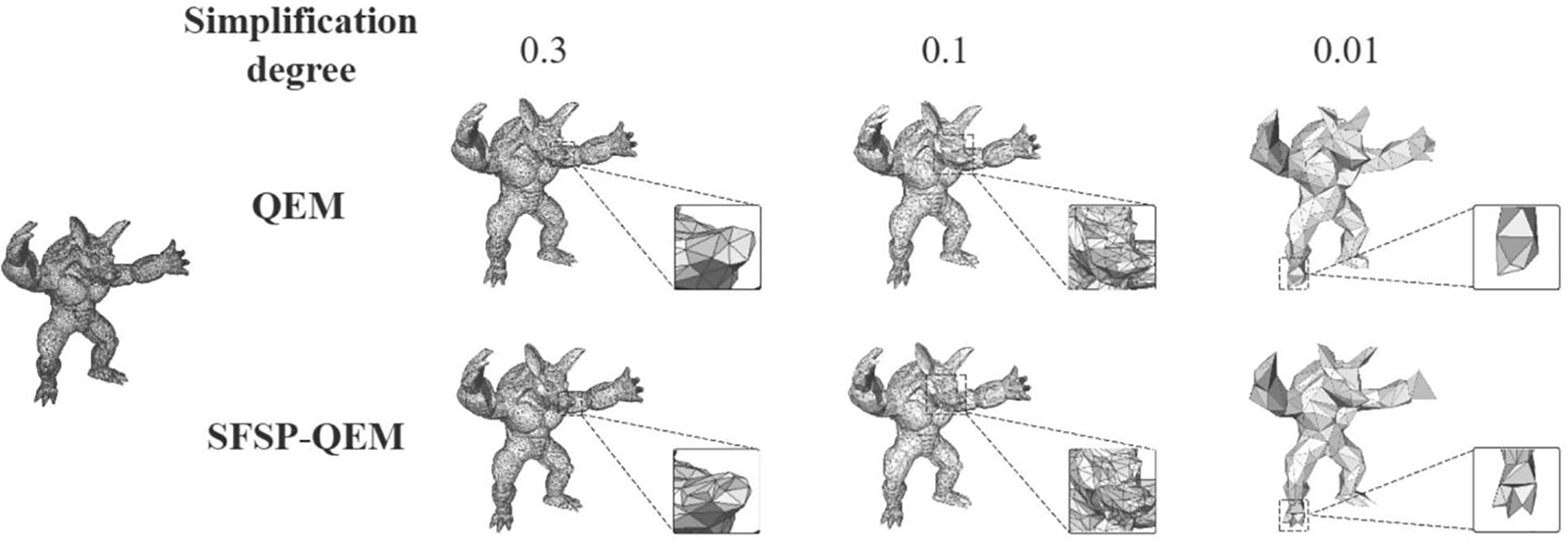
Figure 9: Qualitative evaluation of point sampling on the armadillo model at different sampling levels

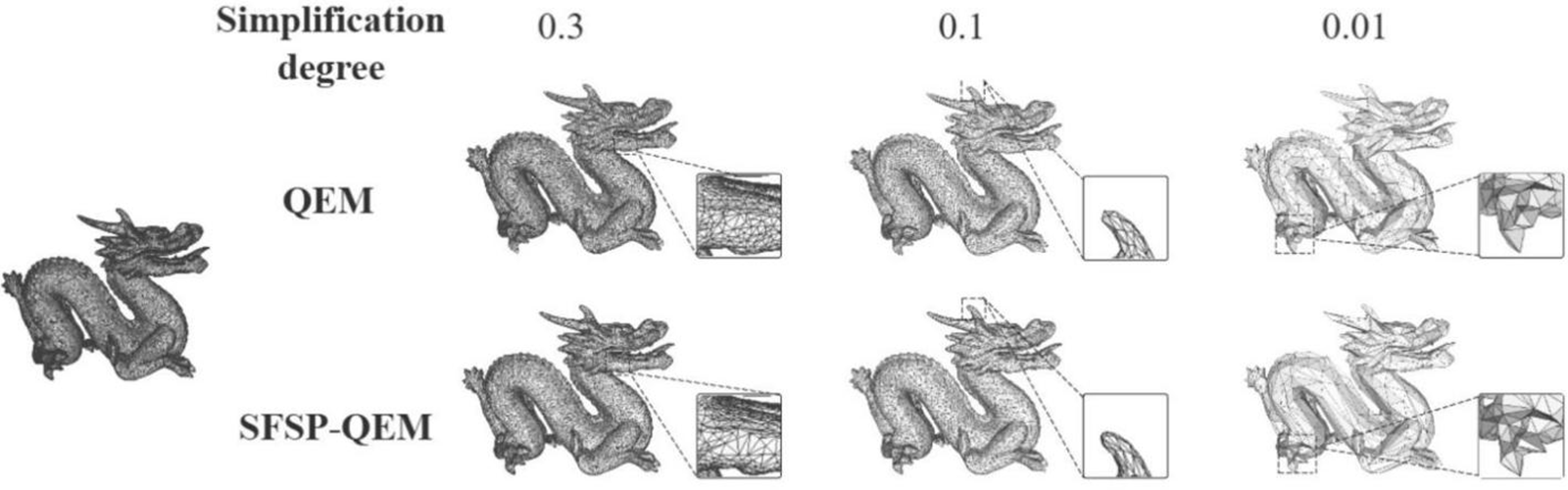
Figure 10: Qualitative evaluation of point sampling on the dragon model at different sampling levels

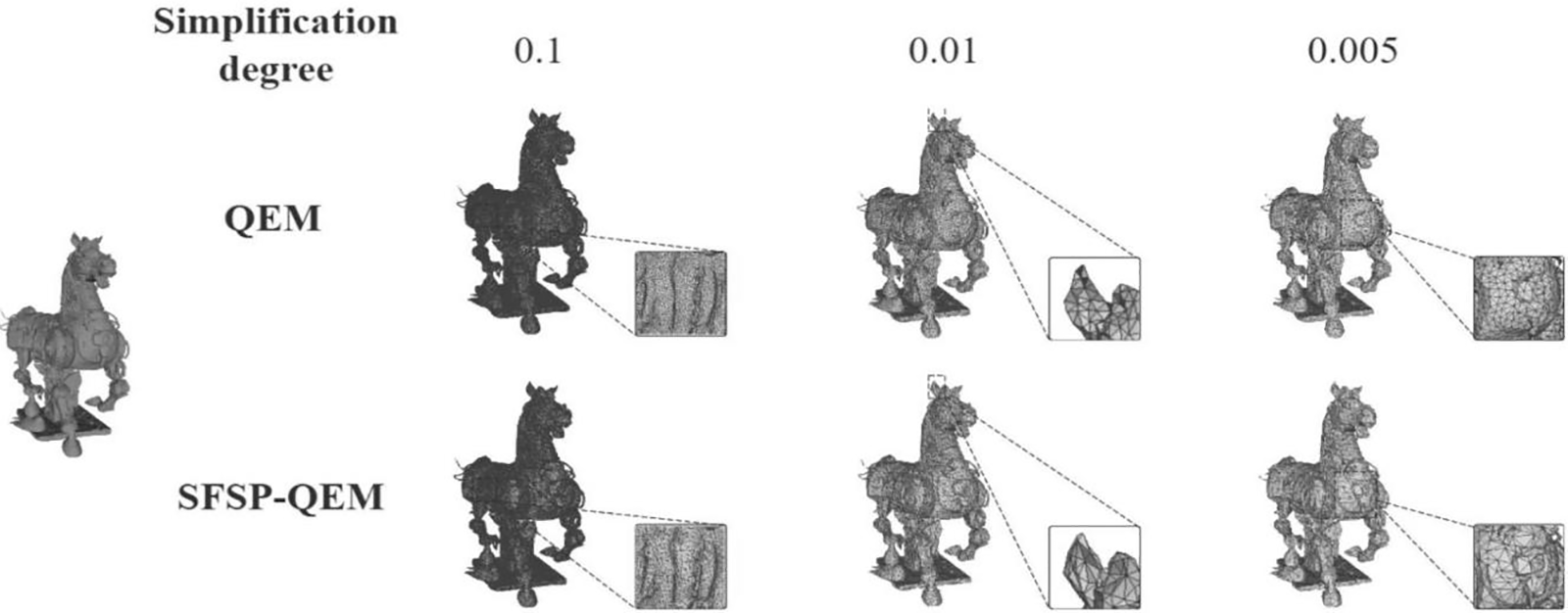
Figure 11: Qualitative evaluation of point sampling on the galloping horse treading on a flying swallow model at different sampling levels

As shown in Figs. 9 and 10, at a 0.3 sampling level, the QEM algorithm can retain much of the Armadillo model’s details, but the presence of polygonal mesh remains noticeable. Although this method can preserve the overall shape of the model, there is some loss of precision in local details (such as the nose). In contrast, the SFSP-QEM algorithm provides a more complete retention of the Armadillo model’s details at the same sampling level. Especially in detail-rich areas like the ears and hands, the SFSP-QEM algorithm better preserves the original geometric details and shapes. For the Dragon model, the QEM algorithm retains most details at a 0.3 sampling level, but the local mesh structure becomes more evident. For example, the dragon’s scales and other details are still clear, but the sparsity of the mesh increases. However, the SFSP-QEM algorithm retains more details, making the dragon’s scales and overall structure more complete, especially in detail-rich areas like the dragon’s head and scales.

As the sampling level is reduced to 0.1, the QEM algorithm’s simplified Armadillo model shows significant detail reduction, with the mesh structure becoming more apparent, particularly in the head and torso regions, making the shape rougher. The SFSP-QEM algorithm, at a 0.1 sampling level, still retains much of the Armadillo model’s details, with complex structures (such as the face) maintaining high fidelity even after simplification. For the Dragon model, the QEM algorithm results in significant detail loss at a 0.1 sampling level, especially in the dragon’s horns, where the mesh becomes sparser. While the overall shape remains clear, the detail loss is notable. In contrast, the SFSP-QEM algorithm maintains better detail retention at this sampling level, particularly in complex areas like the dragon’s horns and head, demonstrating higher fidelity.

At the lowest sampling level of 0.01, the QEM algorithm’s simplified Armadillo model becomes extremely simplified, with a significant reduction in the number of polygons, resulting in a blurry overall shape and severe detail loss. Although the SFSP-QEM algorithm undergoes the same level of simplification, it retains more details and structure of the Armadillo model compared to the traditional QEM algorithm, making the overall shape clearer. At the lowest sampling level of 0.01 for the Dragon model, the QEM algorithm’s simplified model shows obvious detail loss, with a significant reduction in details, especially in the dragon’s head and body, making the details almost indiscernible. Conversely, despite the high level of simplification, the SFSP-QEM algorithm retains certain details and structure, keeping the dragon’s overall shape clearer, particularly in local areas such as the dragon’s claws and mouth.

Fig. 11 shows enlarged detail images of the Galloping Horse Treading on a Flying Swallow model at different simplification levels. The results indicate that the SFSP-QEM algorithm has a clear advantage in retaining the smoothness and details of the mesh, with more uniform mesh structures and more regular triangle shapes, especially in retaining the details of the horse’s abdomen and legs. At a higher simplification level (0.01), the SFSP-QEM algorithm can better preserve the main shape and details of the horse, whereas the traditional QEM algorithm starts to show some shape distortion. At an extremely high simplification level (0.005), the SFSP-QEM algorithm shows significant advantages, still retaining the basic shape of the horse, while the traditional QEM algorithm results in severe shape distortion.

Based on the analysis and comparison of the above images, the SFSP-QEM algorithm outperforms the traditional QEM method at all simplification levels. The improved QEM algorithm not only retains the significant features of the model better at low simplification levels but also effectively preserves the overall shape and structure of the model at high simplification levels. Therefore, the SFSP-QEM algorithm demonstrates superior simplification performance, particularly advantageous in applications requiring high levels of simplification.

To quantitatively assess model similarity, we calculated the mean error (Mean), root mean square error (RMS), and Hausdorff distance (Max) between models at various simplification levels, considering overall, fluctuating, and worst-case scenarios, as presented in Tables 5 through 9, the best results are highlighted in bold. By conducting multi-level simplification tests on mesh models not included in the training set, the SFSP-QEM algorithm demonstrated significant advantages across different conditions, as illustrated in Fig. 12, thereby confirming its broad applicability and stability. In evaluating the Hausdorff distance for general models, the SFSP-QEM algorithm demonstrated a significant performance improvement, reducing the distance by an average of 46.58%. Similarly, when assessing the lantern gate model, SFSP-QEM achieved an average reduction of 28.99% in Hausdorff distance. Furthermore, compared to the QEM method, the proposed SFSP-QEM algorithm incurs a slight increase in computational cost, with an average rise of approximately 6%. Despite the marginally higher computation time, the significant advantages of SFSP-QEM in simplification performance render it superior in preserving model details and accuracy, thus offering greater practical value in real-world applications.

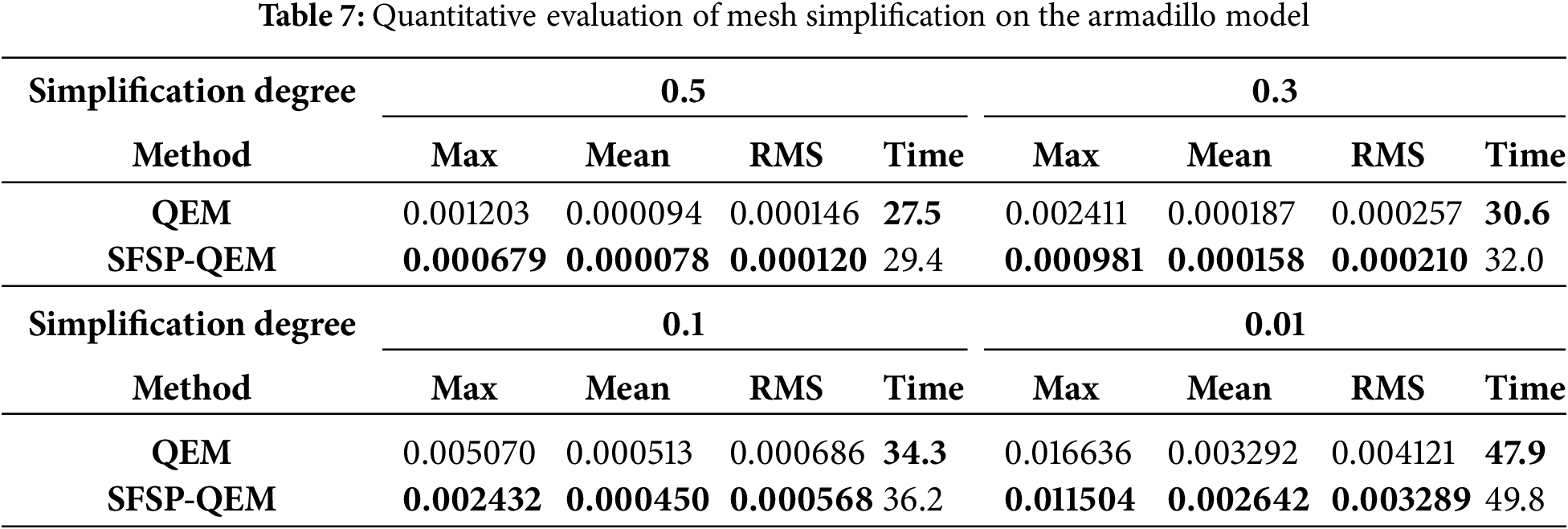
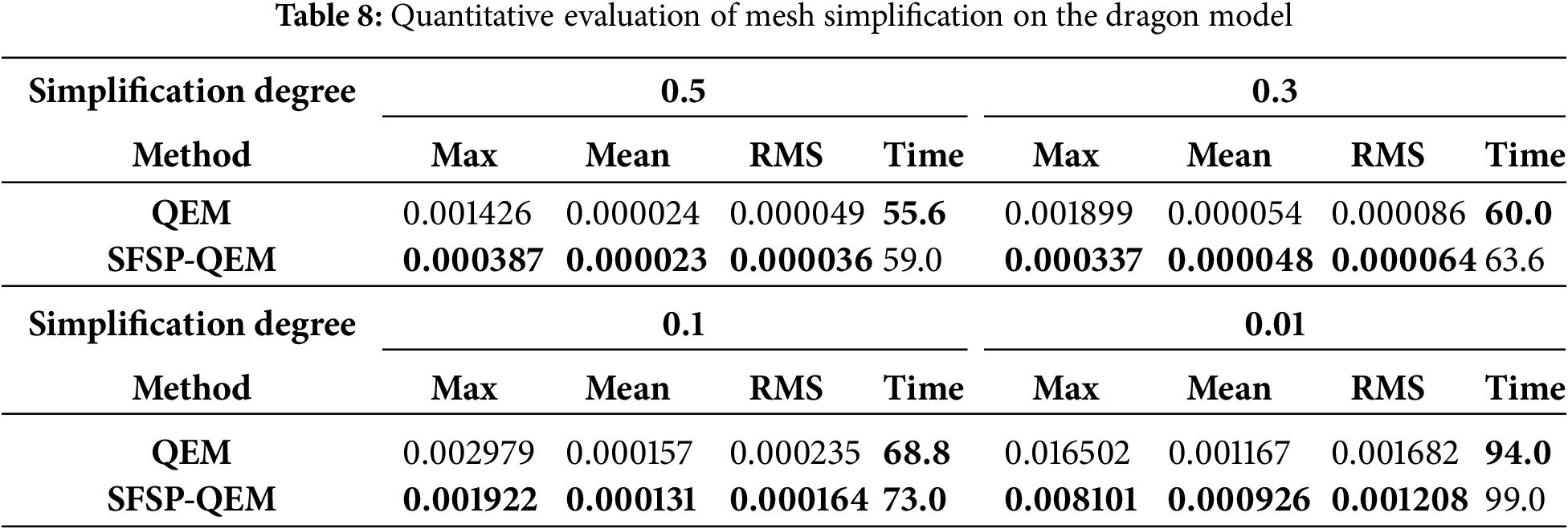
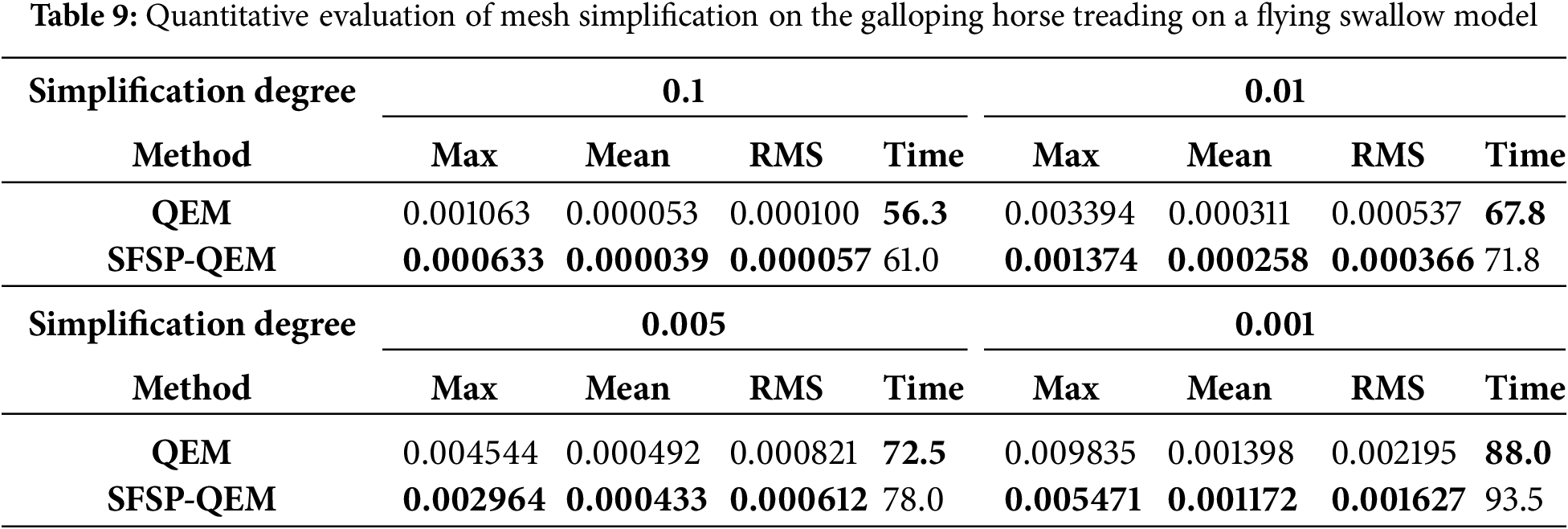
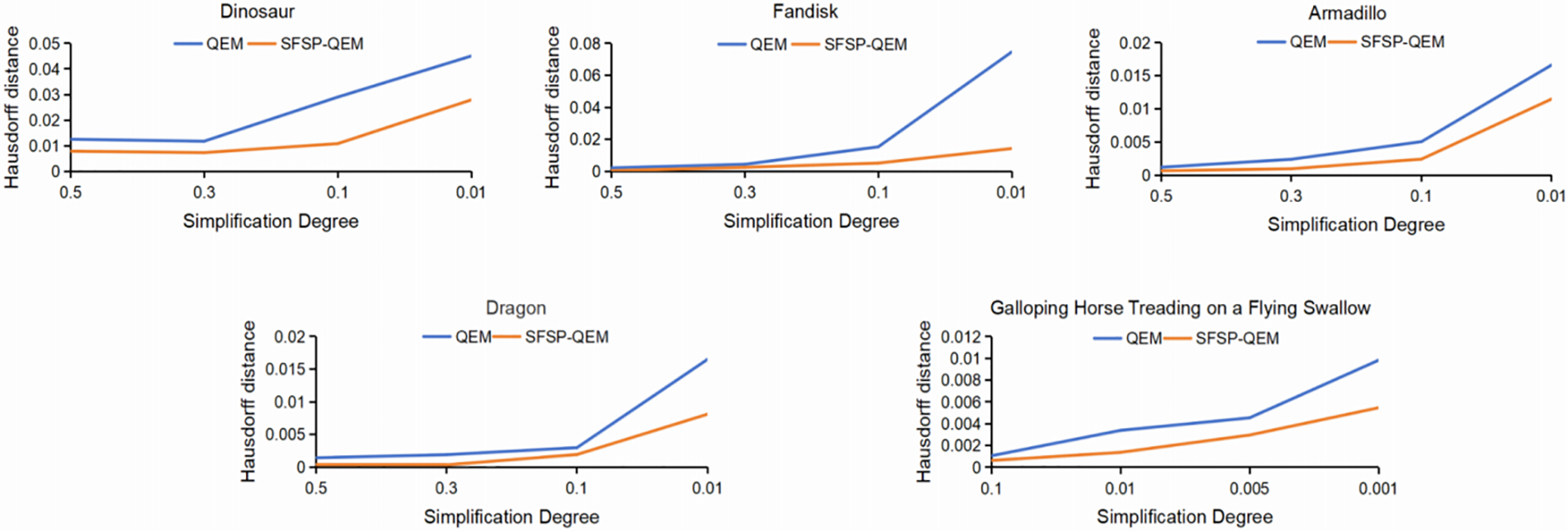
Figure 12: Comparison of Hausdorff distances between SFSP-QEM and QEM at different levels of simplification

5  Conclusions

Our research aims to enhance visual quality in the model simplification process using Quadric Error Metrics (QEM) by preserving salient features through point cloud sampling. We utilize a high-dimensional embedding network for feature extraction of mesh vertices, combined with a salient feature preservation point sampler to select representative sampling points. These sampling points serve as additional constraints in the QEM algorithm, adjusting the merging cost of valid vertex pairs to prioritize the retention of salient feature areas. This effectively addresses the issue of the QEM algorithm neglecting salient features.

As demonstrated by a series of qualitative and quantitative experiments, the proposed method better preserves geometric details and salient features of models across various sampling ratios compared to the traditional QEM algorithm, thereby improving the visual quality of simplified models. However, the SFSP-QEM algorithm may experience error accumulation effects during multiple simplification iterations, particularly in complex models requiring multi-level simplification. This limitation highlights the need for future research to control error accumulation and maintain geometric consistency throughout the simplification process.

Future work aims to package the improved techniques from this study into a tool or module, facilitating their easy extension to other traditional simplification algorithms for further enhancement. Additionally, we plan to integrate these sampling points with advanced 3D reconstruction techniques to directly generate simplified mesh models, thereby increasing the efficiency and applicability of model simplification in diverse real-world scenarios.

Acknowledgement: We sincerely thank Professor Yadong Wu for his invaluable guidance and support throughout our research. We also acknowledge the facilities and resources provided by the School of Computer Science and Engineering, Sichuan University of Science and Engineering, which greatly facilitated our work.

Funding Statement: Our research was funded by the Sichuan Key Provincial Research Base of Intelligent Tourism (No. ZHZJ23-02) and supported by the Scientific Research and Innovation Team Program of Sichuan University of Science and Engineering (No. SUSE652A006). Additional support was provided by the National Cultural and Tourism Science and Technology Innovation Research and Development Project (No. 202417) and the Lantern Culture and Crafts Innovation Key Laboratory Project of the Sichuan Provincial Department of Culture and Tourism (No. SCWLCD-A02).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jiming Lan, Bo Zeng; data collection: Bo Zeng; analysis and interpretation of results: Jiming Lan, Bo Zeng, Suiqun Li, Weihan Zhang; draft manuscript preparation: Jiming Lan, Bo Zeng, Suiqun Li, Weihan Zhang, Xinyi Shi. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The code and dataset are available at Zenodo, DOI: 10.5281/zenodo.13338210. Access URL: https://doi.org/10.5281/zenodo.13338210. The original source of the third-party data (TOSCA dataset) can be accessed at: https://github.com/dvirginz/DPC (accessed on 15 January 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Garland M, Heckbert PS. Surface simplification using quadric error metrics. In: Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques; 1997; New York, NY, USA: ACM Press/Addison-Wesley Publishing Co. p. 209–16. [Google Scholar]

2. Eldar Y, Lindenbaum M, Porat M, Zeevi YY. The farthest point strategy for progressive image sampling. IEEE Trans Image Process. 1997;6(9):1305–15. doi:10.1109/83.623193. [Google Scholar] [PubMed] [CrossRef]

3. Cignoni P, Montani C, Rocchini C, Scopigno R. A general method for preserving attribute values on simplified meshes. In: Proceedings Visualization’98 (Cat. No. 98CB36276); 1998; Piscataway, NJ, USA: IEEE. p. 59–66. doi:10.1109/VISUAL.1998.745285. [Google Scholar] [CrossRef]

4. Lee CH, Varshney A, Jacobs DW. Mesh saliency. In: ACM SIGGRAPH 2005 Papers; 2005; New York, NY, USA: ACM Press. p. 659–66. doi:10.1145/1186822.1073244. [Google Scholar] [CrossRef]

5. Bern MW, Plassmann PE. Mesh generation. In: Sack JR, Urrutia J, editors. Handbook of computational geometry. Amsterdam, Netherlands: Elsevier; 2000. [Google Scholar]

6. Persson PO. Mesh generation for implicit geometries [Ph.D. dissertation]. Cambridge, MA, USA: Massachusetts Institute of Technology; 2005. [Google Scholar]

7. Dittmer JP, Jensen CG, Gottschalk M, Almy T. Mesh optimization using a genetic algorithm to control mesh creation parameters. Comput Aided Des Appl. 2006;3(6):731–40. doi:10.1080/16864360.2006.10738426. [Google Scholar] [CrossRef]

8. Lei N, Li Z, Xu Z, Li Y, Gu X. What’s the situation with intelligent mesh generation: a survey and perspectives. IEEE Trans Vis Comput Graph. 2024;30(8):4997–5017. doi:10.1109/TVCG.2023.3281781. [Google Scholar] [PubMed] [CrossRef]

9. Chen X, Li T, Wan Q, He X, Gong C, Pang Y, et al. MGNet: a novel differential mesh generation method based on unsupervised neural networks. Eng Comput. 2022;38(5):4409–21. doi:10.1007/s00366-022-01632-7. [Google Scholar] [CrossRef]

10. Pan J, Huang J, Cheng G, Zeng Y. Reinforcement learning for automatic quadrilateral mesh generation: a soft actor-critic approach. Neural Netw. 2023;157(4):288–304. doi:10.1016/j.neunet.2022.10.022. [Google Scholar] [PubMed] [CrossRef]

11. Foucart C, Charous A, Lermusiaux PF. Deep reinforcement learning for adaptive mesh refinement. J Comput Phys. 2023;491:112381. doi:10.1016/j.jcp.2023.112381. [Google Scholar] [CrossRef]

12. Feng Y. An effective energy-conserving contact modelling strategy for spherical harmonic particles represented by surface triangular meshes with automatic simplification. Comput Methods Appl Mech Eng. 2021;379(1):113750. doi:10.1016/j.cma.2021.113750. [Google Scholar] [CrossRef]

13. Garland M, Heckbert PS. Simplifying surfaces with color and texture using quadric error metrics. In: Proceedings Visualization’98 (Cat. No. 98CB36276); 1998; IEEE. p. 263–9. [Google Scholar]

14. Cohen J, Olano M, Manocha D. Appearance-preserving simplification. In: Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques; 1998; New York, NY, USA: ACM Press. p. 115–22. doi:10.1145/280814.280832. [Google Scholar] [CrossRef]

15. Li Y, Zhu Q. A new mesh simplification algorithm based on quadric error metrics. In: 2008 International Conference on Advanced Computer Theory and Engineering (ICACTE); 2008; Piscataway, NJ, USA: IEEE. p. 528–32. [Google Scholar]

16. Chen Z, Zheng X, Guan T. Structure-preserving mesh simplification. KSII Trans Internet Inf Syst. 2020;14(11):4463–82. doi:10.3837/tiis.2020.11.012. [Google Scholar] [CrossRef]

17. Pan H, Xiao X, Huang Z, Peng S. Improved QEM simplification algorithm based on local area feature information constraint. In: 2022 China Automation Congress (CAC); 2022; Piscataway, NJ, USA: IEEE. p. 6137–42. doi:10.1109/CAC55689.2022.10054862. [Google Scholar] [CrossRef]

18. Xiang H, Huang X, Lan F, Yang C, Gao Y, Wu W, et al. A shape-preserving simplification method for urban building models. ISPRS Int J Geo Inf. 2022;11(11):562. doi:10.3390/ijgi11110562. [Google Scholar] [CrossRef]

19. Xu R, Liu L, Wang N, Chen S, Xin S, Guo X, et al. CWF: consolidating weak features in high-quality mesh simplification. arXiv:240415661. 2024. [Google Scholar]

20. Qi CR, Su H, Mo K, Guibas LJ. Pointnet: deep learning on point sets for 3D classification and segmentation. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR); 2017; Piscataway, NJ, USA: IEEE Computer Society. p. 652–60. doi:10.1109/CVPR.2017.16. [Google Scholar] [CrossRef]

21. Qi CR, Yi L, Su H, Guibas LJ. PointNet++: deep hierarchical feature learning on point sets in a metric space. Adv Neural Inf Process Syst. 2017;30:5099–108. [Google Scholar]

22. Li Y, Bu R, Sun M, Wu W, Di X, Chen B. PointCNN: convolution on X-transformed points. Adv Neural Inf Process Syst. 2018;31:828–38. [Google Scholar]

23. Wang Y, Sun Y, Liu Z, Sarma SE, Bronstein MM, Solomon JM. Dynamic graph CNN for learning on point clouds. ACM Trans Graph. 2019;38(5):1–12. doi:10.1145/3326362. [Google Scholar] [CrossRef]

24. Potamias RA, Ploumpis S, Zafeiriou S. Neural mesh simplification. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2022; Piscataway, NJ, USA: IEEE. p. 18583–92. [Google Scholar]

25. Dovrat O, Lang I, Avidan S. Learning to sample. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2019; Piscataway, NJ, USA: IEEE. p. 2760–9. [Google Scholar]

26. Lang I, Manor A, Avidan S. SampleNet: differentiable point cloud sampling. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2020; Piscataway, NJ, USA: IEEE. p. 7578–88. [Google Scholar]

27. Wu C, Zheng J, Pfrommer J, Beyerer J. Attention-based point cloud edge sampling. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2023; Piscataway, NJ, USA: IEEE. p. 5333–43. [Google Scholar]

28. Ye Y, Yang X, Ji S. APSNet: attention based point cloud sampling. arXiv:221005638. 2022. [Google Scholar]

29. Potamias RA, Bouritsas G, Zafeiriou S. Revisiting point cloud simplification: a learnable feature preserving approach. In: European Conference on Computer Vision (ECCV); 2022; Cham, Switzerland: Springer. p. 586–603. [Google Scholar]