Collaborative Decomposition Multi-Objective Improved Elephant Clan Optimization Based on Penalty-Based and Normal Boundary Intersection

1  Introduction

Multi-objective Optimization Problems (MOP) refer to optimization problems involving more than two conflicting objective functions. Assuming the optimization problem is a minimization problem, MOP is typically represented as:

minmizeF(x)=(f1(x),…,fM(x))Tsubjecttox∈Ω(1)

where M represents the objective variables, D is the number of decision variables, F = (f1,…, fM)T is the objective vector, x = (x1,…, xD) is the decision vector, and Ω is the D-dimensional decision space. Multi-objective algorithms can generally be divided into three main categories based on the techniques they use to handle multiple objectives: dominance-based multi-objective optimization algorithms, performance indicator-based multi-objective algorithms, and decomposition-based multi-objective optimization algorithms. A brief overview of representative methods for each category is provided below.

Dominance-based multi-objective algorithms utilize Pareto-based fitness allocation strategies to identify all non-dominated individuals from the current evolutionary population. Murata et al. [1] introduced a new Multi-objective Genetic Algorithm (MOGA). During the execution of the MOGA algorithm, a Pareto optimal solution set is maintained, where a certain number of individuals are preserved as elites and passed to the next generation. Zitzler et al. [2] introduced SPEA2, which includes fine-grained fitness assignment, density estimation, and a novel archive truncation method to enhance the balance and diversity of the non-dominated solution set, achieving a more optimal Pareto front. Deb et al. [3] proposed NSGA-II, which reduces computational complexity through fast non-dominated sorting and us-es crowding distance and elitism to maintain population diversity. It optimizes the population by using non-dominated rank and crowding distance, ensuring the generation of Pareto optimal solutions. Erickson et al. [4] proposed NPGA, which explores global information about the Pareto optimal front through population diversity and continuously improves individual fitness through evolutionary operators, thereby obtaining a set of well-balanced optimal solutions. Yicun Hua et al. [5] introduced a clustering-based adaptive MOEA (CAMOEA) aimed at solving multi-objective problems (MOPs) with irregular Pareto fronts. The core concept of CAMOEA is to adaptively generate a set of cluster centers that guide the selection process in each generation, promoting diversity while accelerating convergence. Gao et al. [6] proposed an algorithm for adaptively adjusting the balancing tendency, which is based on efficient non-dominated sorting to improve the distribution of the population. However, this type of approach generally lacks a robust diversity maintenance mechanism, often leading to poor distribution of the non-dominated solution set. Additionally, as the dimensionality continues to increase, the dominance relationship becomes unclear, selection pressure decreases, and the problem of insufficient selection pressure reappears, meaning this issue has not been fundamentally resolved.

Performance indicator-based multi-objective algorithms generally rely on performance metrics to guide the search process and select optimal solutions. Representative algorithm developments are as follows: Wang et al. proposed the hypervolume Newton method for solving unconstrained bi-objective optimization problems with objective functions [7]. For a given MOP, a deterministic numerical optimization is carried out by the Newton-Raphson method to maximize the hypervolume index. Phan et al. [8] proposed and evaluated an indicator-based EMOA (R2-IBEA), which uses a binary R2 indicator. This indicator adaptively adjusts the positions of reference points according to the distribution of individuals in the current generation within the objective space, helping to determine the dominant relationship between any two given individuals. Li et al. [9] proposed a multi-indicator algorithm based on stochastic ranking (SRA), which employs stochastic ranking techniques to balance the search biases of different indicators. Zhengping Liang et al. proposed a new MaOEA based on a boundary protection indicator (MaOEA-IBP) [10], developing a worst-case elimination mechanism grounded in the indicator and boundary protection strategy to improve the equilibrium of population convergence, diversity, and coverage. Peng et al. proposed a MaOEA (A Many-Objective Evolutionary Algorithm Based on Dual Selection Strategy, MaOEA/DS) [11]. A new distance function is designed as a diversity index, and a point congestion strategy based on the distance function is proposed to further enhance the ability of the algorithm to distinguish the optimal solutions overall.

The strength of performance indicator-based multi-objective evolutionary algorithms lies in their independence from Pareto dominance for exploring the objective space. However, their drawback is the high computational cost, which severely limits the application of these algorithms in high-dimensional objective spaces. Zhang et al. [12] introduced a decomposition-based multi-objective evolutionary algorithm (MOEA/D), which converts multi-objective problems into a set of single-objective subproblems using weight vectors. This approach significantly reduced the computational complexity of existing multi-objective algorithms and demonstrated good convergence, attracting considerable attention from scholars. Hui Li et al. [13] proposed a new implementation of MOEA/D based on DE operators and polynomial mutation (MOEA/D-DE), introducing two additional strategies to maintain population diversity. Ke et al. [14] combined MOEA/D with ant colony optimization (MOEA/D-ACO), using the positive feedback mechanism of pheromones to gradually converge toward high-quality solutions. In 2017, Xiang et al. [15] proposed a new MaOEA algorithm based on vector angles, VaEA, which achieves a balance between convergence and diversity. De Farias et al. [16] introduced MOEA/D-UR, a MOEA/D variant that updates as needed. This method employs an improvement detection metric to decide when to adjust the weight vectors while partitioning the objective space to enhance diversity. Wang et al. proposed a metric-based reference vector-adjusted MOEAs for the inconsistency between the reference vector distribution and the PF shape in MOEA/D [17]. It can be seen that decomposition-based MOEAs generally achieve better convergence when solving multi-objective problems. However, the weight vector setting makes these algorithms sensitive to the shape of the Pareto front, and their alignment with the true front can still be improved. Compared to the other two approaches, decomposition-based methods are currently the most widely utilized technique for solving multi-objective problems.

With the advancement of science and technology, various multi-objective problems are encountered in real life, such as robot path planning, industrial scheduling, and knapsack problems. Through mathematical analysis, these can be viewed as multi-objective optimization problems. Multi-objective optimization algorithms are currently an effective approach to solving these types of problems, comprising two aspects: first, the core evolutionary algorithm, and second, the multi-objective handling techniques. The former iteratively evolves to obtain optimal solutions, while the latter preserves these optimal solutions. In light of this, to further enhance the problem-solving capability of multi-objective optimization algorithms in engineering problems, this study focuses on two aspects: the core evolutionary strategy and the multi-objective framework, as outlined below: (1) Algorithmic evolution strategies can effectively solve multi-objective problems, so the merits of algorithmic evolution strategies are crucial to the optimization effect of multi-objective problems. Extensive experimental research has shown that compared to various evolutionary methods such as Genetic Algorithm and Differential Algorithm, the Elephant Clan Optimization Algorithm [18] exhibits certain advantages. Therefore, it will serve as the core evolutionary strategy for the multi-objective optimization algorithm. (2) Currently, multi-objective algorithms generally adopt decomposition-based multi-objective handling techniques. Experimental research indicates that in 2022, Wu et al. [19] proposed a Collaborative Decomposition (CoD) environmental selection method, which combines the advantages of the penalty-based boundary intersection (PBI) and normal boundary intersection (NBI) methods. This allows the multi-objective algorithms formed by CoD to achieve good convergence and distribution. Therefore, this paper selects CoD-based environmental selection and aims to improve it based on the characteristics of multi-objective optimization, constructing a Collaborative Decomposition Multi-objective Elephant Clan Optimization Algorithm with the Elephant Clan Optimization Algorithm as the core evolutionary strategy.

2  Elephant Clan Optimization Algorithm

In nature, elephant populations are organized into male herds and family groups led by matriarchs, who use their learning and memory abilities to find suitable survival resources and undertake long-distance migrations. Inspired by these behaviors, Jafari et al. proposed the Elephant Clan Optimization (ECO) algorithm in 2021. In the ECO algorithm, each individual represents the position of an elephant within the clan, and the fitness value of the algorithm represents the survival resources available at that position. The algorithm is divided into three stages: initialization and population division, individual updating of the population, and individual replacement within the population. The pseudocode for the ECO algorithm is shown in Algorithm 1.

3  Multi-Objective Elephant Clan Optimization Algorithm

To enhance the convergence and distribution of multi-objective algorithms, this section proposes the Collaborative Decomposition Multi-objective Improved Elephant Clan Optimization Algorithm (CoDMOIECO) by using the ECO algorithm introduced in Section 2 as the core evolutionary strategy and employing the Collaborative De-composition (CoD) environmental selection method [19]. This approach integrates the benefits of both the penalty-based boundary intersection (PBI) and normal boundary intersection (NBI) methods as a technique for handling multi-objective optimization. The pseudocode for CoDMOIECO is shown in Algorithm 2.

Algorithm 3 offers a comprehensive description of the process for constructing the rotation coefficient r based on the weight vector. In step 5 of Algorithm 3, αi represents the boundary-aware rotation factor of Wi, while βi denotes the vertex-aware rotation factor at position Wi. Here, m is the number of objectives.

3.1 New Individual Selection Strategy

To enable the CoDMOIECO algorithm to adapt to solving multi-objective optimization problems, an individual selection method has been designed that includes subpopulation construction and a ranking method for individuals based on NBI and angles. The specific details are as follows.

3.1.1 Subpopulation Construction

Typically, multi-objective optimization problems are solved using a decomposition approach. In this process, related individuals from single-objective problems form a cohesive solution through mutual learning and communication. Since the optimal solutions of each subproblem differ, the individuals guided by them naturally carry evolutionary information in different directions. It is noteworthy that due to the stability of the non-dominated Pareto front, subproblems corresponding to neighboring weights exhibit some similarities in their optimal solutions, leading to significant overlap in the evolutionary information contained in the related individuals. Compared to individuals with distinct evolutionary tendencies or information, learning among these similar individuals can more effectively obtain optimized solutions for the corresponding single-objective problems.

In light of this, this section no longer adopts the population-based evolutionary strategy from the ECO algorithm. Instead, specific subpopulations are created for each weight vector to promote the collaborative evolution of related individuals. Specifically, we first determine the neighborhood range of the weight vector using Eq. (8). Then, by computing the Euclidean distances between the weight vectors, we select the T weight vectors that are closest to the current weight vector to form its neighborhood. Finally, each weight vector selects individuals associated with its neighboring weight vectors to form a subpopulation.

T=max(N×(0.5−it/itmax),5)(8)

Here, N represents the number of individuals, while it and itmax denote the current iteration number and the maximum iteration number, respectively.

The Eq. (8) presented in this section modifies the conventional approach of using a constant neighborhood size, allowing it to adaptively change with the iteration count. In the initial stages of the algorithm’s evolution, the evolutionary levels among individuals differ significantly, and all are relatively distant from the optimal Pareto front. A larger number of neighboring individuals provide optimal individuals with more options, facilitating the use of evolutionary information from superior individuals in adjacent subproblems. This helps to rapidly narrow the evolutionary gap between themselves and other subproblems, thus accelerating convergence toward the optimal Pareto front. In the later stages of the algorithm, as all individuals are closer to the optimal Pareto front, reducing the number of neighboring individuals allows for a more precise selection of optimal individuals. This more accurately guides the evolution within the neighborhood, fostering a good distribution of solutions and effectively conserving computational resources.

3.1.2 Individual Ranking Based on NBI and Angles

To enhance the performance of the CoDMOIECO algorithm, which uses the ECO algorithm as its core evolutionary strategy, it is necessary to select the leader individual, male individuals, and juvenile individuals from the constructed subpopulations according to the individual update mechanism of the ECO algorithm.

Since the subpopulation construction is based on the weight vectors, the aggregation function values of the individuals within the subpopulation are utilized to assess their quality. The Chebyshev function of the NBI type can better measure the convergence of individuals, while the VaEA algorithm utilizes angles to assess the distribution of individuals. Therefore, this section proposes an individual evaluation method based on NBI and angles: first, calculate gNBI, then compute the angle using Eq. (9); next, calculate the aggregation function value using Eq. (10); finally, rank the individuals in each subpopulation based on the aggregation function values, with smaller aggregation function values indicating superior individuals.

The following formula calculates the angle between each individual X in the subpopulation and each weight vector Wi. Here, F(X) = f(X) − Z* represents the specific angle measurement.

angle(F(X),Wi,Z∗)=arccos⁡|∑m=1M(fm(X)−Zm∗)×Wi/‖f(X)−Z∗‖×‖Wi‖|(9)

sort(X)=gNBI(X|Wi)+δ×angle(F(X),Wi,Z∗)(10)

Here, gNBI(X|Wi)=maxj=1m{fj(x|wi)−wji}, δ represents the weighting factor, as shown in Eq. (11).

δ=2+(6×it/itmax)(11)

The individual ranking method based on NBI and angles introduced in this section offers several advantages. On one hand, a smaller gNBI value for individuals on the same weight vector indicates that the individuals are closer to the Pareto front, suggesting better convergence; conversely, the larger the angle between individuals and the same weight vector, the more dispersed the individuals are, indicating better distribution. Thus, the aggregation function, as shown in Eq. (9), comprehensively reflects both convergence and distribution. On the other hand, the weighting factor δ increases with iterations, enhancing the effect of the angle. In the initial stages of evolution, since individuals are typically far from the ideal point, the algorithm should focus more on convergence. In the later stages of evolution, as individuals gradually approach the ideal point, the algorithm needs to emphasize distribution more. In the early stages of evolution, since the value of angle(F(X),Wi,Z∗) ranges from [0, π/2], gNBI is likely to be much greater than angle(F(X),Wi,Z∗). The initial setting of δ balances gNBI and angle(F(X),Wi,Z∗). This section improves overall performance by reasonably adjusting the relationship between δ, gNBI, and angle(F(X),Wi,Z∗) to satisfy the algorithm’s requirements for convergence and distribution at various stages.

3.2 New Update Methods for Leaders, Male Elephants, and Juvenile Elephants

As mentioned in Section 2, the population individual updates in the ECO algorithm are divided into three methods: updating the matriarch leader individuals, updating the male elephant individuals, and updating the juvenile elephant individuals. In the CoDMOIECO algorithm, as introduced in Section 3.1, each individual to be updated will find its corresponding subpopulation. Within this subpopulation, individuals will be ranked based on their performance, and the updates will be categorized into three types: updating the leader individual at the optimal position, updating the male elephant individual at the worst position, and updating the juvenile elephant individuals at other positions. The specific update methods are as follows.

3.2.1 Leader Individual Update

According to the description in Section 3.1, in the CoDMOIECO algorithm, each weight vector selects a leader individual from the corresponding subpopulation. Generally, in the early stages of evolution, even though the leader individual possesses the best evolutionary information in the subpopulation, the information is not optimal because the individual is far from the theoretical Pareto front. In the later stages of evolution, as individuals gradually approach the theoretical Pareto front, the evolutionary information of the leader individual also approaches the theoretical optimal value. Although the evolutionary information of other individuals may be inferior to that of the leader individual, it is still similar. The exchange of information between these individuals can potentially generate superior evolutionary information; however, excessive communication may divert the leader individual from its original evolutionary direction, thereby reducing the algorithm’s convergence speed. As the optimal individual within the subpopulation, the lead individual needs to enhance its coverage of the search space while improving the effectiveness of the evolutionary information. Based on this analysis, the new update method for the leader individual is shown in Algorithm 4.

In the initial stages of evolution, it is advisable to retain a few characteristics of the leader individual while exchanging the majority of characteristics with another randomly selected individual from the population. Conversely, in the later stages of evolution, more characteristics of the leader individual should be preserved, as shown in Eq. (14). During the evolutionary process, a certain probability should be applied to introduce simulated binary crossover to enhance the leader individual’s coverage of the search space. This enables the leader individual to guide other members in exploring the potential solution space more thoroughly. As a guide for the individuals in the subpopulation, the leader individual must preserve the effectiveness of its evolutionary information to ensure the successful evolution of the population. The opposition learning strategy typically validates the solutions generated by checking for any significant opposition between two solutions. This helps filter out unreasonable solutions while retaining those that are valid.

3.2.2 Leader Individual Update

In the ECO algorithm, the primary goal of the male elephant individuals is to generate superior evolutionary information while maintaining population diversity. In the realm of multi-objective optimization, each individual typically corresponds to a solution for a problem, necessitating the acceleration of evolution for the male elephant individuals within the subpopulation. As noted, the male elephant individuals occupy the last position in the current subpopulation. Similar to the leader individual updates, in the initial stages of evolution, a few characteristics of the male elephant individuals should be replaced while the majority of characteristics are exchanged with the leader center individual. Conversely, in the later stages of evolution, more characteristics of the male elephant individuals should be preserved. When performing characteristic exchanges, as shown in Eq. (15), this significantly enhances the effectiveness of the male elephant individuals’ learning from superior individuals, accelerating the algorithm’s convergence speed while maintaining diversity. For other characteristics of the male elephants, they can be randomly replaced by the leader in-dividual of their subpopulation with a certain probability, as indicated in Eqs. (16) and (17). Random replacement helps maintain the diversity of the male elephant individuals, while direct replacement can improve their convergence. The new update method for the male elephant individuals is detailed in Algorithm 5.

3.2.3 Update of the Juvenile Elephant Individuals

The new update method for the juvenile elephant individuals is detailed in Algorithm 6.

In CoDMOIECO, the juvenile elephant individuals need to accelerate the convergence speed while maintaining a certain level of diversity, providing more evolutionary information for communication with the leader individuals. Therefore, the individual features that require communication, as shown in Eq. (18), evolve toward the optimal individual in the subpopulation to enhance their convergence speed while also learning from a randomly selected individual in the entire population to preserve diversity. For the individual features that do not require communication, they are replaced by the leader individual in the subpopulation with a certain probability, thereby speeding up convergence and increasing the diversity of the evolutionary information.

As mentioned above, with the evolution of individuals, the updating strategies introduced in this section gradually reduce the features updated for each individual. This aligns with the evolutionary requirement of individuals approaching the optimal front and conducting a more refined search. At the same time, different updating methods are designed for various individuals, ensuring that different information between individuals can be fully communicated. This, to some extent, accelerates the algorithm’s convergence speed toward the front. Additionally, through methods such as SBX, oppositional learning, random individual learning, and communication, as well as replacement strategies, new excellent evolutionary information is provided for each subpopulation, minimizing the likelihood of the algorithm becoming trapped in local optima during the evolutionary process.

3.3 New CoD-Based Environmental Selection Method

The PBI type of Chebyshev function is better able to maintain population diversity, and the specific aggregation function is shown in Eq. (19).

gPBI(x|wi)=d1(f(x),wi)+θ×d2(f(x),wi)(19)

where d1(f(x),wi) denotes the projection length of the target vector f (x) under the reference vector wi, the constant θ is used to balance convergence and distribution, and d2(f(x),wi) denotes the perpendicular distance from the target vector f (x) to the reference vector wi.

While PBI can maintain population diversity, it is unable to obtain uniform boundaries due to the radial spatial distribution of its reference lines, and while NBI can maintain population convergence, its parallel reference lines may result in poorer diversity due to undersampling near the boundaries. The CoD environment selection method, a synergistic decomposition method of PBI and NBI, inherits the advantages of the two methods in an integrated way. Therefore, this paper addresses the improvement of the CoD environment selection method. The aggregation function is specifically shown in Eq. (20).

minimizegCoD(X|Wi)=gNBI(X|Wi)+ri×d2(f(X),Wi)(20)

where ri denotes the rotation factor.

Upon further analysis, the NBI-type Tchebycheff function and vertical distance d2 can only evaluate the convergence and distribution of individuals to a certain extent, and they do not effectively assess these aspects in a coordinated manner. It is well recognized that in multi-objective evolutionary algorithms, the emphasis shifts between convergence in the early stages and distribution in the later stages of evolution. However, the current methods do not adequately address the differing emphasis on convergence and distribution across these evolutionary phases.

In light of this, to effectively enhance the evaluation of convergence and distribution by the gCoD aggregation function, a new CoD aggregation function is proposed, as shown in Eq. (21). This function combines the NBI-type Tchebycheff function with the angle of the individual’s objective vector relative to the corresponding weight vector and the vertical distance.

minimizegNCoD(X|Wi)=gNBI(X|Wi)+ε×angle(F(X),Wi,Z∗)+ri×d2(f(X),Wi)(21)

The coefficient ε of the angle ranges from 1 to 1.5 and increases with the number of iterations.

As seen from the above formula, this paper introduces the angle of the individual’s objective vector relative to the corresponding weight vector into the original CoD aggregation function. A smaller angle not only guides individuals to search toward the Pareto front along the associated weight vectors but also directs individuals’ distribution on the Pareto front as they converge near it. The dynamic adjustment of the angle coefficient allows the algorithm to focus more on exploration or distribution at different stages. In the initial iterations, the coefficient is relatively small, emphasizing exploration and helping to discover new solution spaces. In the later iterations, the coefficient gradually increases, leading to a greater distribution of individuals near the Pareto front, thereby enhancing the algorithm’s diversity and distribution and facilitating a more comprehensive exploration of the Pareto solution set. Therefore, the aggregation function proposed in this section, which combines the NBI-style Tchebycheff function, dynamic updates of the angle, and vertical distance, considers all three factors to offer a more accurate evaluation of an individual’s convergence and distribution. This approach improves the performance and effectiveness of multi-objective optimization algorithms.

CoDMOIECO represents the optimization algorithm when the aggregation function proposed in this paper is gNcoD, and CoDMOIECO1 represents the algorithm when the aggregation function is gcoD, and to ensure the fairness of the experiments, all parameters are set as shown in Section 4.1.

As can be seen from Fig. 1, the distribution of individuals in CoDMOIECO is significantly more dispersed than in ITLCO under the same conditions. This suggests that the CoDMOIECO proposed in this section can better balance the convergence speed and population diversity.

Figure 1: Scatter plot of different algorithms on DTLZ1

4  Experiments

To verify the performance of CoDMOIECO, it is compared with four currently outstanding algorithms on the DTLZ [20], WFG [21], and ZDT [22] test suites. In the DTLZ problems, the decision variable D = M + k – 1, where M represents the number of objectives, k is 5 for DTLZ1 and 10 for the others. In WFG, the decision variable D = k + l, where k = 2(M − 1) and l = 20. In ZDT, the decision variable is fixed at 30. The comparison algorithms include MOEA/D [12], CAMOEA [5], VaEA [16], and MOEA/D-UR [17].

4.1 Basic Parameter Settings

To ensure the fairness of the comparison experiments, for the ZDT problem with 2 objective functions, the population size N is set to 100, and the maximum number of function evaluations is 25,000. For the DTLZ and WFG problems with 3 objectives, the population size N is set to 91, and the maximum number of function evaluations is 45,500. Other parameter settings for each algorithm are shown in Table 1.

4.2 Experimental Results and Analysis

The values of HV and IGD for the CoDMOIECO algorithm and the comparison algorithms on three test sets are shown in Tables 2 and 3. The mean and standard deviation of HV and IGD are indicated by “±,” with the best results for each function highlighted in bold. Table 4 presents the Wilcoxon rank-sum test results between the CoDMOIECO algorithm and the comparison algorithms.

From Tables 2 and 4, it can be observed that in terms of the HV metric, the CoDMOIECO algorithm achieves the best performance compared to the comparison algorithms on ZDT1, ZDT2, ZDT4, ZDT6, DTLZ1–4, WFG2–4, WFG7, and WFG8. The VaEA algorithm demonstrates optimal performance on DTLZ5, DTLZ6, and WFG5. The MOEA/D algorithm and CAMOEA algorithm achieve the best results only on ZDT3 and DTLZ7, respectively. The MOEA/D-UR algorithm excels on WFG1, WFG6, and WFG9. In general evaluation, compared to the CoDMOIECO algorithm, the VaEA algorithm has an advantage on 8 functions but falls short on 13 functions. The CAMOEA algorithm performs better on 5 functions but is inferior to 15 functions. The MOEA/D-UR algorithm shows strong performance on 6 functions but is less effective on 11 functions. The MOEA/D algorithm exhibits a clear advantage on 3 functions but is outperformed on 14 functions.

According to Tables 3 and 4, in terms of the IGD metric, the CoDMOIECO algorithm achieves optimal results on ZDT1, ZDT2, ZDT4, ZDT6, DTLZ1–4, WFG2–5, and WFG8. The VaEA algorithm excels on DTLZ5–7 and WFG9. The CAMOEA algorithm performs best on ZDT3, DTLZ6, and DTLZ7. The MOEA/D-UR algorithm only achieves the best results on WFG1. The MOEA/D algorithm does not achieve the best results on any of the functions. Overall, compared to the CoDMOIECO algorithm, the MOEA/D algorithm performs better on 4 functions but is inferior on 17 functions. The VaEA algorithm has superior performance on 8 functions but is outperformed on 13 functions. The CAMOEA algorithm performs better on 8 functions but is less effective on 11 functions. The MOEA/D-UR algorithm excels on 7 functions but falls short on 12 functions.

As shown in Table 5, from the Friedman’s test results for IGD and HV, it is clear that CoDMOIECO performs best on both IGD and HV compared to other algorithms.

To clearly illustrate the overall performance of the CoDMOIECO algorithm, Figs. 2–4 show the Pareto front graphs of all algorithms for three representative functions in the ZDT, DTLZ, and WFG test sets. By observation, it can be noted that in terms of convergence, the CoDMOIECO algorithm converges to the true front on ZDT1, DTLZ3, and WFG2. Regarding distribution, although there is still a certain gap between the Pareto front obtained by CoDMOIECO and the true front for the WFG2 test function, it still demonstrates significant advantages in distribution compared to other comparative algorithms.

Figure 2: Pareto front graph of various algorithms on ZDT1

Figure 3: Pareto front graph of various algorithms on ZDTZ3

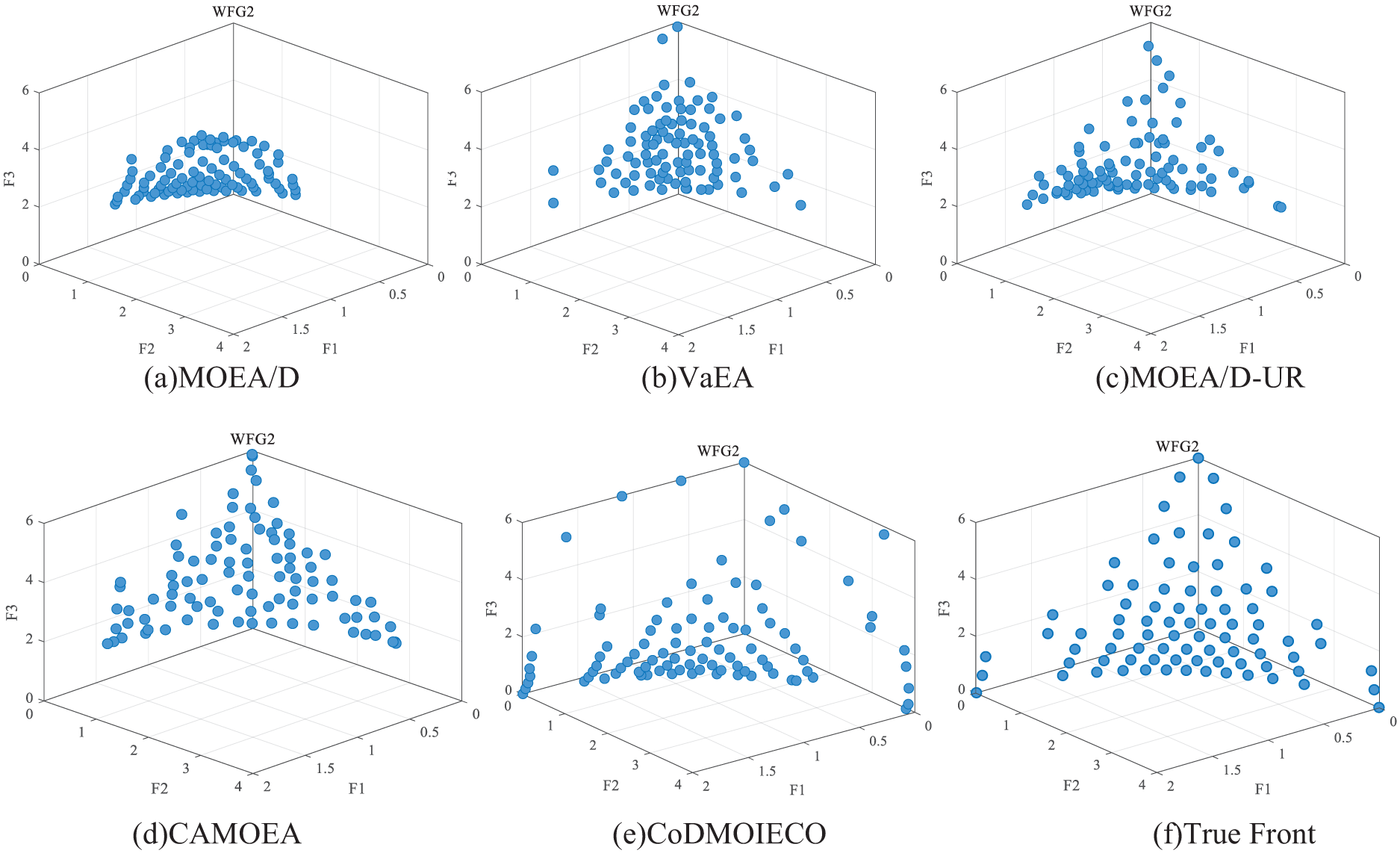
Figure 4: Pareto front graph of various algorithms on WFG2

In summary, the CoDMOIECO algorithm exhibits greater advantages in both convergence and distribution compared to the benchmark algorithms. This advantage allows the CoDMOIECO algorithm to more effectively identify high-quality solutions that are near the true Pareto front when addressing multi-objective optimization problems, thereby improving the quality of the optimization outcomes.

5  Conclusions

To tackle more complex and practical optimization challenges and improve the performance of multi-objective optimization algorithms in addressing these issues, this paper integrates the elephant clan optimization algorithm with multi-objective processing techniques, proposing the CoDMOIECO algorithm. Based on the characteristics of multi-objective optimization problems, new individual selection methods, updated strategies for the leader, male, and juvenile elephants, and a new CoD-based environmental selection method are introduced. Experiments on the ZDT, DTLZ, and WFG benchmark function sets demonstrate that CoDMOIECO exhibits superior convergence and distribution compared to benchmark algorithms. However, as the number of optimization objectives increases, the time complexity increases, and the performance of the algorithm decreases. Therefore, reducing the complexity and improving the performance of algorithms in large-scale multi-objective optimization is an important part of the research. CoDMOIECO can be further extended and applied to the engineering field to solve optimization problems in real engineering and maximize the benefits. For example, fuzzy overlapping community detection problem, and optimization problem of edge computing.

Acknowledgement: The authors would like to thank the anonymous reviewers and the editor for their valuable suggestions, which greatly contributed to the improved quality of this article.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Mengjiao Wei, Wenyu Liu; data collection: Mengjiao Wei; analysis and interpretation of results: Mengjiao Wei, Wenyu Liu; draft manuscript preparation: Mengjiao Wei, Wenyu Liu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available at https://gitcode.com/open-source-toolkit/4265b (accessed on 05 September 2024).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Murata T, Ishibuchi H. MOGA: multi-objective genetic algorithms. In: Proceedings of 1995 IEEE International Conference on Evolutionary Computation; 1995 Nov; Perth, Australia; p. 289–94. [Google Scholar]

2. Zitzler E, Laumanns M, Thiele L. SPEA2: improving the strength pareto evolutionary algorithm for multiobjective optimization. In: Proceedings of the EUROGEN; 2001 Sep; Athens, Greece; p. 95–100. [Google Scholar]

3. Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transact Evolu Comput. 2002 Apr;6(2):182–97. doi:10.1109/4235.996017. [Google Scholar] [CrossRef]

4. Erickson M, Mayer A, Horn J. Multi-objective optimal design of groundwater remediation systems: application of the niched Pareto genetic algorithm (NPGA). Adv Water Resour. 2002 Jan;25(1):51–65. doi:10.1016/S0309-1708(01)00020-3. [Google Scholar] [CrossRef]

5. Hua Y, Jin Y, Hao K. A clustering-based adaptive evolutionary algorithm for multiobjective optimization with irregular Pareto fronts. IEEE Trans Cybern. 2018 Jul;49(7):2758–70. doi:10.1109/TCYB.2018.2834466. [Google Scholar] [PubMed] [CrossRef]

6. Gao X, He F, Zhang S, Luo J, Fan B. A fast nondominated sorting-based MOEA with convergence and diversity adjusted adaptively. J Supercomput. 2024 Jan;80(2):1426–63. doi:10.1007/s11227-023-05516-5. [Google Scholar] [CrossRef]

7. Wang H, Emmerich M, Deutz A, Hernández VAS, Schütze O. The hypervolume newton method for constrained multi-objective optimization problems. Math Comput Appl. 2023 Jan;28(1):10. doi:10.3390/mca28010010. [Google Scholar] [CrossRef]

8. Phan DH, Suzuki J. R2-IBEA: R2 indicator based evolutionary algorithm for multiobjective optimization. In: Proceedings of 2013 IEEE Congress on Evolutionary Computation; 2013 Jun 20–23; Cancun, Mexico; p. 1836–45. [Google Scholar]

9. Li B, Tang K, Li J, Yao X. Stochastic ranking algorithm for many-objective optimization based on multiple indicators. IEEE Trans Evol Comput. 2016 Mar;20(6):924–38. doi:10.1109/TEVC.2016.2549267. [Google Scholar] [CrossRef]

10. Liang Z, Luo T, Hu K, Ma X, Zhu Z. An indicator-based many-objective evolutionary algorithm with boundary protection. IEEE Trans Cybern. 2020 Jan;51(9):4553–66. doi:10.1109/TCYB.2019.2960302. [Google Scholar] [PubMed] [CrossRef]

11. Peng C, Dai C, Xue X. A many-objective evolutionary algorithm based on dual selection strategy. Entropy. 2023 Jul;25(7):1015. doi:10.3390/e25071015. [Google Scholar] [PubMed] [CrossRef]

12. Zhang Q, Li H. MOEA/D: a multiobjective evolutionary algorithm based on decomposition. IEEE Trans Evol Comput. 2007 Dec;11(6):712–31. doi:10.1109/TEVC.2007.892759. [Google Scholar] [CrossRef]

13. Li H, Zhang Q. Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-I I. IEEE Trans Evol Comput. 2008 Apr;13(2):284–302. doi:10.1109/TEVC.2008.925798. [Google Scholar] [CrossRef]

14. Ke L, Zhang Q, Battiti R. MOEA/D-ACO: a multiobjective evolutionary algorithm using decomposition and antcolony. IEEE Trans Cybern. 2013 Dec;43(6):1845–59. doi:10.1109/TSMCB.2012.2231860. [Google Scholar] [PubMed] [CrossRef]

15. Xiang Y, Zhou Y, Li M, Chen Z. A vector angle-based evolutionary algorithm for unconstrained many-objective optimization. IEEE Trans Evol Comput. 2016 Feb;21(1):131–52. doi:10.1109/TEVC.2016.2587808. [Google Scholar] [CrossRef]

16. De Farias LRC, Araújo AFR. A decomposition-based many-objective evolutionary algorithm updating weights when required. Swarm Evol Comput. 2022 Feb;68:100980. doi:10.1016/j.swevo.2021.100980. [Google Scholar] [CrossRef]

17. Wang X, Zhang F, Yao M. A many-objective evolutionary algorithm with metric-based reference vector adjustment. Comp Intell Syst. 2024 Feb;10(1):207–31. doi:10.1007/s40747-023-01161-w. [Google Scholar] [CrossRef]

18. Malihe J, Eysa S, Javad S. Elephant clan optimization: a nature-inspired metaheuristic algorithm for the optimal design of structures. Appl Soft Comput. 2021 Dec;113:107892. doi:10.1016/j.asoc.2021.107892. [Google Scholar] [CrossRef]

19. Wu Y, Wei J, Ying W, Lan Y, Cui Z, Wang Z. A collaborative decomposition-based evolutionary algorithm integrating normal and penal-ty-based boundary intersection methods for many-objective optimization. Inf Sci. 2022 Nov;616:505–25. doi:10.1016/j.ins.2022.10.136. [Google Scholar] [CrossRef]

20. Liu HL, Gu F, Zhang Q. Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems. IEEE Trans Evol Comput. 2014 Sep;18(3):450–5. doi:10.1109/TEVC.2013.2281533. [Google Scholar] [CrossRef]

21. Huband S, Hingston P, Barone L, While L. A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans Evol Comput. 2006 Oct;10(5):477–506. doi:10.1109/TEVC.2005.861417. [Google Scholar] [CrossRef]

22. Zitzler E, Deb K, Thiele L. Comparison of multi-objective evolutionary algorithms: empirical results. Evol Comput. 2000 Jun;8(2):173–95. doi:10.1162/106365600568202. [Google Scholar] [PubMed] [CrossRef]