Machine Learning Model for Wind Power Forecasting Using Enhanced Multilayer Perceptron

1  Introduction

Wind energy is recognized as a renewable and sustainable source of energy that is both endless and efficient in electricity production [1]. It has gained considerable attention globally, with the Global Wind Energy Council reporting an installed capacity exceeding 600 gigawatts, including over 86.9 gigawatts installed in 2020 alone [2,3]. The accuracy of wind power forecasting is crucial for optimizing wind power generation, as a 1% improvement in forecasting accuracy can enhance wind energy production by approximately 3% [2]. However, the unpredictable nature of wind speed makes forecasting challenging, necessitating advancements in wind speed forecasting techniques [4,5].

Research in the field has categorized wind speed forecasting and prediction methodologies into three main types: physical, statistical, and machine-learning approaches. Physical models, such as the Numerical Wind Prediction [6], are prominent for their simulation of wind speed formation and are typically used for long-term forecasting. On the other hand, statistical methods like Autoregressive Moving Average (ARMA) [7], seasonal autoregressive integrated moving average (SARIMA) [8] and others are favored for short-term forecasts due to their immediacy but might not address the non-linear aspects of wind speeds adequately. Machine learning techniques have seen a surge in application for time-series forecasting due to their superior pattern recognition capabilities [9]. Models such as the Support Vector Machine (SVM) [10], and Random Forest (RF) [11] have been particularly noted for their efficacy.

The advent of neural network-based methods has further advanced the field, especially in wind power forecasting, through mechanisms allowing for previous data influences [12,13]. Various neural network models have been used, such as ANFIS [14], dendritic neural regression [15], recurrent Neural Network (RNN) [16,17], Multilayer perceptron [18], and many other deep learning models.

Recently, researchers have developed hybrid forecasting approaches that merge various machine learning and statistical models to enhance overall predictive power, often surpassing the capabilities of individual models. For example, Ge et al. [19] presented a new wind power forecasting approach to address the increasing volatility of renewable energy. The approach combines a Static-Dynamic Spatio-Temporal Mixture Network (SDSTMN) for numerical weather prediction correction and a Multi-Info-Feature Fusion Network (MIFFN) for long-term data feature extraction. This combined approach improves forecasting accuracy by considering both mesoscale and microscale data, and it was evaluated using a real wind farm in China. Moreover, metaheuristic optimization algorithms frequently play a crucial role in these combined strategies, optimizing the integration for improved accuracy and reliability. Various nature-inspired metaheuristic optimization methods have been adopted in the literature to optimize machine learning methods and boost prediction performance. For example, Dai et al. [20] presented a short-term wind speed prediction method that combines a nonlinear autoregressive model with exogenous inputs (NARX) and a hybrid chaos-cloud salp swarm algorithm (CC-SSA). A mixed modal decomposition approach using variational modal decomposition (VMD) and generalized S-transform (GST) reduces data complexity. The CC-SSA algorithm was employed to optimize the NARX weights, enhancing prediction accuracy. Sulaiman et al. [21] suggested a wind power forecasting method using multiple metaheuristics Neural Networks. Metaheuristics were applied for feature selection to improve prediction performance. Five metaheuristics were used, namely Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), Teaching-Learning-Based Optimization (TLBO), and Evolutionary Mating Algorithm (EMA). The evaluation showed that GA achieved the best performance. Sulaiman et al. [22] presented a wind power forecasting method by integrating deep learning (DL) with TLBO. The TLBO-DL model demonstrated superior accuracy compared to PSO-DL, BMO-DL, BBO-DL, and FA-DL. Wang et al. [2] presented a multivariate selection-combination short-term wind speed forecasting model based on convolutional and recurrent neural networks, along with a multi-objective chameleon swarm optimization algorithm (Mocsa). The evaluation showed that Mocsa had Pareto optimal solutions and demonstrated better performance compared to several multi-objective swarm optimization algorithms.

In [23], the authors used two optimization methods integrated with the ANFIS model to forecast wind speed: PSO and GA. They found that GA-ANFIS and PSO-ANFIS performed better than the original ANFIS. PSO was also employed with the ANFIS model in [24]. The marine predator algorithm was used to optimize the ANFIS in [25]. An enhanced dragonfly algorithm was used to optimize the SVM for wind power forecasting in [26], and the optimized SVM showed better performance compared to traditional SVM and other machine learning methods. In [27], an improved snake algorithm (SA) was utilized for hyperparameter optimization of long short-term memory (LSTM), with the evaluation showing that the improved SA increased prediction accuracy by 7.27%. The research outlined in [28] enhanced PSO through the integration of orthogonal learning, fostering efficient exploration and exploitation in wind integrated optimal power flow scenarios, thereby yielding more accurate and feasible solutions for complex optimization problems. In [29], PSO was employed to optimize the multi-layer extreme learning machine to boost wind power forecasting. Additionally, the quantum PSO (QPSO) was used by [30] to optimize a combined Convolutional Neural Network-Long Short-Term Memory Network (CNN-LSTM) model. A multi-objective salp swarm optimizer (SSO) was applied by [31] to optimize artificial neural networks for wind power forecasting. The multi-objective mechanism was employed to overcome the limitations of the traditional SSA. In [32], an efficient wind power forecasting model was presented by integrating deep belief networks, Elman neural networks, and the Hilbert-Huang transform, modified using an improved PSO. In [33], an optimized random vector functional link network based on the Capuchin search algorithm (CapSA) was proposed. In [34], a multi-objective mayfly optimization algorithm was employed to optimize deep learning methods and boost wind power forecasting accuracy. Finally, in [35], a new model was proposed based on a modified multi-objective tunicate algorithm and quantile regression.

Motivation and Contribution

Inspired by the successful integration of metaheuristics with machine learning methods, this paper proposes a new forecasting model that optimizes the MLP using a modified version of the Fire Hawk Optimizer (FHO) enhanced by the Non-Monopolize Search (NO). The FHO [36] was recently introduced to solve complex optimization problems. Its concept is inspired by the feeding habits of whistling kites, black kites, and brown falcons. The FHO has shown good performance in solving various problems, including feature selection [37,38], image processing [39], and function optimization [40], among others. The NO algorithm was proposed by [41] and operates as a unique, metaphor-independent algorithm that utilizes single-solution strategies. Its mechanisms are designed to navigate and exploit the search space effectively throughout each iteration. By using just one candidate solution, the NO adjusts dimensions and transitions the current solution across the search spectrum. This makes the NO an efficient local search (LS) technique that integrates both search exploration and exploitation. Unlike typical LS techniques, the NO avoids suboptimal solutions due to the stochastic elements integrated into its operational functions. In this paper, we utilize the advantages of the NO to enhance the search performance of the FHO, addressing shortcomings such as premature convergence and limited exploration. The perturbation introduced by the NO diversifies the search trajectory, preventing the algorithm from getting stuck in suboptimal regions and encouraging the exploration of a broader range of potential solutions. The developed FHONO is then applied to optimize the hyperparameters of the MLP, improving its configuration process and enhancing its prediction performance. The proposed model, FHONO-MLP, is evaluated using real-world wind power datasets from four wind turbines and compared to other forecasting models.

The main contributions of this paper can be summarized as follows:

•   Presenting a refined version of the Fire Hawk Optimizer (FHO), called FHONO, which incorporates the Non-Monopolize Search (NO) to optimize the Multilayer Perceptron (MLP) for wind power forecasting. The addition of NO enhances FHONO’s ability to explore solutions more effectively, preventing it from getting stuck in suboptimal solutions and improving both the quality and stability of the results.

•   Enriching the conventional MLP network architecture with FHONO to address prevalent obstacles, such as overfitting and prolonged training duration, while refining the parameter adjustment process to achieve superior solutions in wind power forecasting applications.

•   Conducting a comprehensive assessment of the FHONO-MLP model’s predictive efficacy using real-world wind power datasets and performing comparative evaluations against a range of optimization techniques to confirm its effectiveness through various performance metrics.

The rest of the sections of this paper are presented as follows. Section 2 introduces the fundamentals of the applied methods, including neural networks, the NO algorithm, and the FHO algorithm. Section 3 provides the details of the proposed method. Section 4 presents the evaluation experiments using real-world wind power datasets. Finally, Section 5 concludes the paper.

2  Background

2.1 Neural Network Model

The effectiveness of Artificial Neural Networks (ANNs) is significantly influenced by their training and learning mechanisms. Among these, Feedforward Neural Networks (FNNs) stand out for their efficacy and are recognized as a specialized form of neural architectures. FNNs are structured with multiple layers of elements termed “neurons”. These layers are sequentially aligned, allowing for a structured flow of information where neurons are arranged across them. Specifically, the Multilayer Perceptron (MLP), a renowned model of FNN, is adopted in this study for the purpose of predicting oil production. The architecture of the MLP is layered, starting with an input layer to introduce data into the network, and culminating with an output layer to deliver the end results. Encapsulated between these extremities are several hidden layers, which contribute to the model’s processing capability [42].

In MLPs, neurons link in a unidirectional and one-dimensional manner, with the connections among them quantified through weights, which are values within the range of [−1,1]. Mathematically, the operation of each layer in an MLP is encapsulated as follows:

Oi(l)=ϕ(ui(l))=ϕ(∑j=1nlOj(l−1)wj,i(l)+w0,i(l)),1≤l≤L(1)

Here, ϕ() denotes the activation function of the layer, often adopting non-linear forms such as the tangent hyperbolic function for hidden layers and a linear form for initializing the output layers’ results. The term l designates the current layer among the total L non-input layers, and nl denotes the count of neurons in the layer l. The output Oi(l) represents the output from the ith neuron in the current layer l. The weights wj,i(l), for 1≤l≤nl−1, illustrate the connection strength from the ith neuron of layer l to the preceding layer l−1. Meanwhile, w0,i(l) represents the bias for the ith neuron of the current layer.

Importantly, the initial layer’s output vector (l=0) with dimension n0 aligns with the input features (O(0)=x), while the final layer’s output vector (l=L), dimension nL, corresponds to the network’s final output (O(L)=y).

2.2 Fire Hawk Optimizer (FHO)

In this section, the foundational steps of the Fire Hawk Optimizer (FHO) are outlined. Like many other Metaheuristic (MH) strategies, FHO begins by initializing a population of N individuals, as represented by the equation below:

Xij=rand⋅(Uj−Lj)+Lj,j=1,2,…,D(2)

Here, Xij denotes the position of the ith individual in the jth dimension, with Uj and Lj serving as the upper and lower limits, respectively. The term rand∈[0,1] represents a uniformly distributed random number, and D signifies the dimensionality of each individual Xi.

Subsequently, the quality of each individual Xi is assessed using a designated fitness function. Following this evaluation, the leading solutions, termed Fire Hawks (FHl,l=1,2,…,n), and the remaining solutions, referred to as prey (PRk,k=1,2,…,m), are distinguished. The metric for measuring the separation between FH and PR is depicted by the equation:

Dlk=(x2−x1)2+(y2−y1)2,l=1,2,…,n,k=1,2,…,m(3)

In this scenario, m and n represent the quantities of FH and PR, respectively. The ensuing phase involves delineating the dominion of each FH by scattering PR. Updates to the position of each FH are made according to:

FHl(t+1)=FHl(t)+(r1⋅Xb−r2⋅FHn(t)),l=1,2,…,n(4)

In this formula, Xb denotes the optimal solution found thus far, while r1 and r2 are random numbers between 0 and 1.

Following, a sanctuary location (SPl) for the prey to regroup and avoid hazards is determined through:

SPl=∑q=1rPRqr,q=1,2,…,r,l=1,2,…,n(5)

Subsequently, the dynamics within the Fire Hawks’ domain aim to mimic actual animal movements, permitting the prey to adapt their positions accordingly:

PRq(t+1)=PRq(t)+(r3⋅FHl−r4⋅SPl(t)),l=1,2,…,n,q=1,2,…,r(6)

Here, SPl denotes the sanctuary spot under the lth Fire Hawk’s control. The external safe area for the lth Fire Hawk is defined as:

SP=∑k=1mPRkr,k=1,2,…,m(7)

The modification of the prey’s position is then formalized as:

PRq(t+1)=PRq(t)+(r5⋅FHa−r6⋅SP(t)),l=1,2,…,n,q=1,2,…,r(8)

This iterative refinement of solutions continues until predetermined termination criteria are met, concluding with the best found solution Xb.

2.3 Non-Monopolize Search (NO) Algorithm

This section introduces the NO algorithm and outlines its core mathematical concepts.

The NO approach is designed based on a straightforward mechanism that aims to identify the optimal solution efficiently. By employing a singular solution approach, it minimizes computational efforts while striving for the most effective outcome. Thus, NO iteratively explores the optimal solution by maintaining a sole candidate solution. The mathematical formulation of the NO approach is as follows:

Xnew(j)=rand×X(1,RP)(9)

Here, Xnew(j) represents the jth position in the new solution vector, while rand is a random coefficient ranging from 0 to 1. X denotes the current solution, and X(RP) refers to a randomly chosen position within the current solution, where RP stands for a random position, selected from 1 to the number of dimensions.

Xnew(j)=X(j)−(X(SRP)×rand)×eps−(X(j)−NO)(10)

In this equation, Xnew(j) is the jth position in the newly created solution, rand is again a random value between 0 and 1, and X(j) is the jth position of the existing solution. X(SRP) signifies a position randomly chosen from the current solution’s positions, and eps is a negligible constant to ensure numerical stability. SRP is a selected random position within the solution’s dimensions, and NO is an adjustable parameter influencing the search dynamics of the proposed algorithm. The principal steps of the NO method are summarized in Algorithm 1.

3  Proposed FHONO-MLP Wind Power Forecasting Model

In this section, we introduce the FHONO-MLP algorithm, a new approach designed to enhance wind forecasting capabilities through the synergistic integration of Multilayer Perceptrons (MLP) and the Fire Hawk Optimizer with Non-Monopolize Search (FHONO) algorithm. At its core, FHONO-MLP leverages the computational power of MLP while utilizing the optimization strengths of FHONO to refine the MLP’s parameters, thereby improving its performance in wind forecasting tasks.

The algorithm begins by establishing the essential parameters required for experimentation. This step involves defining key factors such as population size, maximum iterations, and parameter boundaries, which lay a solid foundation for the optimization process. Furthermore, the dataset is carefully partitioned into distinct training and testing subsets, ensuring a comprehensive evaluation. To foster diversity and prevent premature convergence, the Non-Monopolize Search (NO) algorithm is seamlessly integrated into the FHONO framework. This integration enhances the search process by infusing additional diversity, which is crucial for avoiding local optima and enabling thorough exploration of the solution space. By introducing localized perturbations to solutions, NO increases the algorithm’s maneuverability, helping it escape suboptimal solutions and find better ones. Specifically, the NO algorithm’s equations are applied after the execution of Eq. (4) in the FHONO framework. Eq. (4) governs the update of the Fire Hawks’ positions, marking an essential step in the optimization process. Once this update is performed, the NO equations are integrated into the process. Eq. (9) is applied in the first half of the optimization phase, while Eq. (10) is used in the latter half. The NO introduces localized perturbations to the solutions, diversifying the search process and preventing premature convergence. This diversification is vital for exploring the solution space effectively, allowing the algorithm to move beyond local optima. As a result, NO significantly enhances the algorithm’s ability to discover superior solutions and improve overall optimization performance.

After the update process, the optimization stage begins. Each potential solution, representing a unique set of MLP parameters, is thoroughly evaluated. The MLP is then trained using the dataset, and its performance is assessed using the Mean Squared Error (MSE) as defined in Eq. (11). This metric quantifies the difference between the MLP’s predicted outputs and the actual target values.

MSE=1N∑t=1N(yt−y^t)2(11)

Here, yt represents the actual wind speed at time t, y^t denotes the corresponding predicted wind speed by the MLP, and N denotes the total number of data points.

A lower MSE indicates better performance. With this feedback, the FHONO algorithm iteratively refines the population, steering it toward solutions that minimize MSE and enhance forecasting accuracy. By balancing exploration and exploitation, FHONO navigates the search space effectively. It explores new regions to uncover potentially superior solutions while refining promising candidates based on their fitness scores.

The optimization process continues until a specified termination criterion is met, such as reaching the maximum number of fitness function evaluations. Once this point is reached, the algorithm outputs the best solution found, which is the individual in the population with the lowest MSE. This optimal solution represents the finely-tuned MLP parameters, ready to be applied to wind forecasting tasks with new data. Fig. 1 provides a schematic representation of the proposed FHONO-MLP methodology.

Figure 1: Workflow of the proposed FHONO-MLP

4  Experiments and Results

The proposed model FHONO-MLP was compared to other models used to optimize MLP, including the traditional FHO, Differential evolution (DE) [43], Aquila optimizer [44], Educational competition optimizer (ECO) [45], Newton-Raphson-based optimizer (NRO) [46], Draco lizard optimizer (DLO) [47], and the classic MLP. Table 1 shows the parameters setting for the optimization algorithms.

4.1 Dataset Overview

In this study, the method is evaluated using four distinct wind power datasets from the La Haute Borne wind turbines in France, specifically turbines R80711 (Dataset 1), R80721 (Dataset 2), R80736 (Dataset 3), and R80790 (Dataset 4) (https://opendata-renewables.engie.com/explore/) (accessed on 31 January 2022). These datasets contain wind-related measurements, specifically wind speed and absolute wind direction, recorded over time. The wind speed data were collected from two anemometers mounted on the nacelle, along with the overall average wind speed. Each parameter is characterized using statistical metrics, including the average, minimum, maximum, and standard deviation. The data were collected at 10-min intervals throughout the year 2017.

In the experiments, the datasets were preprocessed using Min-Max normalization, scaling the data to the range of [−1, 1]. This step ensures consistent scaling and prevents features with larger magnitudes from dominating the training process.

4.2 Evaluation Metrics

To evaluate the performance of the proposed FHONO-MLP model and its comparison methods, four standard metrics are employed:

Root Mean Square Error (RMSE):

RMSE=1N∑t=1N(yt−y^t)2(12)

Mean Absolute Relative Error (MARE):

MARE=1N∑t=1N|yt−y^tyt|(13)

Mean Absolute Error (MAE):

MAE=1N∑t=1N|yt−y^t|(14)

Coefficient of Determination (R2):

R2=1−∑t=1N(yt−y^t)2∑t=1N(yt−y¯)2(15)

where yt represents the actual observed value, y^t denotes the predicted value, y¯ is the mean of the actual observed values, and N is the total number of data samples.

4.3 Results

This section evaluates the performance of the proposed model in comparison to the other algorithms across four datasets. For simplicity, the optimized MLP models-FHO-MLP, DE-MLP, AO-MLP, ECO-MLP, NRO-MLP, DLO-MLP, and FHONO-MLP-will be referred to by the name of the applied optimization algorithm (FHO, DE, AO, ECO, NRO, DLO, and FHONO).

4.3.1 Dataset 1

Table 2 presents the results of all compared models. FHONO showed strong performance, achieving the best MARE and R2 values. ECO emerged as a competitive model, achieving the lowest MAE (0.0858) and an RMSE (0.1144) nearly identical to FHO (0.1142). Although FHONO retained its strong position, these results suggest that ECO provides a viable alternative under certain conditions. For the MARE measure, FHONO outperformed all other models with a value of 1.1110, underscoring its ability to manage varying scales effectively. NRO demonstrated a strong performance with a MARE of 1.2015, outperforming several other models, including ECO (1.3319) and FHO (1.3577). These findings emphasize FHONO’s superior scale management capabilities while also positioning NRO as a competitive option for scenarios involving diverse data scales. DE and AO showed moderate performance, while MLP lagged significantly with the highest MARE. In terms of R2, FHONO achieved the highest value (0.9624). NRO followed closely with an R2 of 0.9612. FHO (0.9584) and ECO (0.9519) also exhibited strong R2 values, further highlighting their potential for reliable predictive performance in the dataset. In contrast, MLP recorded the lowest R2 (0.9041), consistent with its underperformance in other metrics.

4.3.2 Dataset 2

The results of Dataset 2 are listed in Table 3. FHONO demonstrated strong performance across several metrics, achieving the lowest RMSE (0.0941) and R2 (0.9710). However, DE outperformed FHONO in MAE (0.0705) and MARE (0.3391), highlighting its superior performance in minimizing error and handling scale variations. FHO also shows strong results, particularly in RMSE (0.0944), reinforcing its position as a reliable model, though slightly behind FHONO. For MARE, FHONO achieved a competitive value of 0.3857, showcasing its ability to manage varying scales effectively. DE exhibited the best performance in MAE with a value of 0.0705, reflecting its superior ability to minimize error and outperform the other models in this metric. DE also achieved the best MARE score (0.3391), positioning it as the top performer in this measure. FHO demonstrated a MARE of 0.3638, continuing to perform reliably in this metric. AO, while maintaining a moderate performance, recorded a higher MARE (0.4848), indicating its relative sensitivity to scale variations when compared to other models.

In terms of R2, FHONO again showed superior explanatory power with a value of 0.9710, slightly outperforming FHO (0.9702). NRO and ECO followed closely behind, with R2 values of 0.9657 and 0.9640, respectively. DLO also performed well in this metric (0.9652), contributing to its overall robust performance. MLP continued to underperform with the lowest R2 value (0.9100), indicating its limitations in capturing data patterns effectively. While FHONO continues to deliver strong overall performance, the inclusion of other models, such as ECO, NRO, and DLO demonstrates the diversity of effective models for this dataset. ECO performed strongly in both RMSE and MAE, while NRO demonstrated excellent generalization with a high R2. DE’s leading performance in MAE and MARE positions it as a solid choice for minimizing error and handling scale-sensitive datasets.

4.3.3 Dataset 3

The results of Dataset 3 are listed in Table 4. For RMSE, FHONO achieved the lowest value (0.0966), indicating the most accurate predictions with the least deviation from the actual values. DLO followed closely with an RMSE of 0.1026, while NRO performed similarly with an RMSE of 0.0968. AO recorded an RMSE of 0.1072, outperforming DE, which had an RMSE of 0.1194. MLP showed the highest RMSE of 0.1180, indicating the least accuracy among the models. For MAE, FHONO again performed the best with a value of 0.0742, closely followed by NRO with an MAE of 0.0758. FHO ranked second with an MAE of 0.0976, while AO recorded an MAE of 0.0850. ECO exhibited an MAE of 0.0873, and DLO had an MAE of 0.0782. MLP had the highest MAE of 0.0962.

For MARE, NRO exhibited the best performance with a value of 0.6429, followed by FHONO with 0.6662. FHO achieved a MARE of 0.7723, demonstrating a competitive performance. DE recorded a MARE of 0.7847, and DLO had a MARE of 0.7283, showing slightly better handling of scale variations than DE. AO’s MARE of 0.9628 indicates it struggled with scale sensitivity, and MLP showed the highest MARE of 0.9655. Regarding R2, FHONO outperformed all models with the highest value of 0.9730, demonstrating its superior ability to explain the variance in the dataset. FHO achieved an R2 of 0.9647, while AO followed with 0.9690. NRO (0.9717) and DLO (0.9672) also performed well in this metric. ECO recorded an R2 of 0.9651. MLP, with the lowest R2 value of 0.9426.

Overall, FHONO demonstrated the best performance across most metrics, achieving the lowest RMSE (0.0966), MAE (0.0742), and the highest R2 (0.9730). FHO followed closely, excelling in RMSE (0.1187) and MAE (0.0976), with a strong R2 of 0.9647. NRO showed strong performance, excelling in R2 (0.9717) and MARE (0.6429), while ECO performed well across the metrics, with a MARE of 0.7267. AO demonstrated solid middle-range performance, particularly in R2 (0.9690), though it did not match the top-tier results of FHONO or FHO. DE and DLO exhibited moderate performance, with DE struggling regarding scale variations (MARE of 0.7847). MLP lagged behind in all metrics, particularly with the highest MARE (0.9655).

4.3.4 Dataset 4

The evaluation results of Dataset 4 are listed in Table 5. FHONO demonstrated the best overall performance across all measures, achieving the lowest RMSE (0.1138) and MAE (0.0899), reflecting its superior accuracy and minimal error. FHO followed closely, with an RMSE of 0.1395 and an MAE of 0.1130, showing strong performance, though slightly behind FHONO. DE performed well with an RMSE of 0.1184 and an MAE of 0.0924, positioning it as a solid middle performer. ECO, with an RMSE of 0.1314 and an MAE of 0.1016, also displayed moderate accuracy, while AO (RMSE = 0.1236, MAE = 0.1090) showed a more moderate performance. MLP, with the highest RMSE (0.1412) and MAE (0.1169), exhibited higher errors compared to the other models.

In terms of MARE, FHONO again led with the lowest MARE (0.4875), reflecting its robust ability to handle varying scales in the data. NRO and ECO followed with MARE values of 0.5310 and 0.5327, respectively, also performing well in this area. DE (0.5558) and FHO (0.6170) showed somewhat weaker performance, indicating that they were less effective at managing scale variations compared to FHONO, ECO, and NRO. AO (1.3193) and MLP (1.5446) displayed the highest MARE values.

When considering R2, FHONO achieved the highest value (0.9648), indicating the best ability to explain the variance in the dataset. FHO also performed well with an R2 of 0.9526, reflecting its strong explanatory power. NRO (0.9639) and DE (0.9604) showed comparable results, highlighting their capacity for effective generalization. AO (0.9537) and DLO (0.9508) also performed decently but did not reach the top-tier results of FHONO, FHO, or NRO. MLP lagged behind with the lowest R2 value (0.9079).

Overall, FHONO stands out as the best-performing model across all metrics in this dataset, consistently achieving the lowest errors and highest explanatory power. FHO and DE provide solid alternatives, showing strong performance, particularly in error minimization and R2. ECO and NRO also offer reliable results, with ECO excelling in handling scale variations. While AO and DLO deliver middle-range performances, they do not reach the level of FHONO, FHO, or NRO. MLP’s performance indicates room for improvement through optimization.

Moreover, Fig. 2 shows the average of RMSE, MAE, and R2 measures for all datasets.

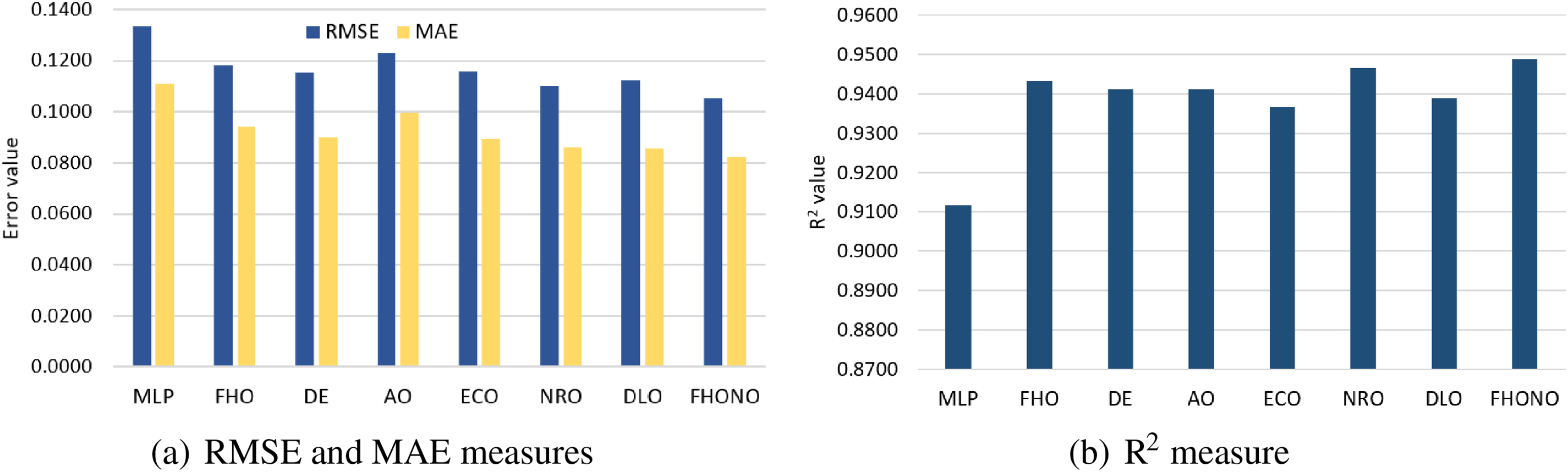
Figure 2: Average of RMSE, MAE, and R2 measures

For more analysis, Fig. 3 shows the Taylor diagram for all compared methods across all employed datasets (i.e., testing data). This figure also confirmed the superior performance of the proposed method against the compared methods, as it obtained the nearest position to the target.

Figure 3: Taylor diagram comparing model performance across four datasets, illustrating correlation, standard deviation, and RMSE. The distance from the reference point indicates a prediction error

4.3.5 Statistical Test

For further analysis, Table 6 presents the results of the Friedman statistical tests. The Friedman test is a non-parametric statistical method used to detect differences in treatments across multiple test attempts. The p-value measures the strength of the evidence against the null hypothesis: a low p-value (typically below 0.05) suggests that the observed results are unlikely to have occurred by chance, providing evidence that one model is significantly better than the others.

Table 6 confirms that FHONO outperforms all other models, achieving the best rankings in RMSE, MAE, MARE, and R2, with a p-value of 0.0042 indicating statistical significance. FHO follows closely behind, with competitive rankings in MAE (4.750) and RMSE (4.250), and a strong R2 ranking of 5.250. It performs well but does not surpass FHONO in error minimization or variance explanation. NRO and ECO perform similarly, with NRO ranking best in R2 (3.750) and ECO excelling in MARE (3.750). DE and DLO show moderate performance, with DE ranking 4.250 in both MAE and RMSE, while DLO ranks 4.250 in RMSE. MLP ranks the lowest in almost all metrics, with the highest rankings in MAE (7.750) and MARE (8.000). Overall, the results validate the superiority of FHONO, with FHO as a strong alternative. ECO and NRO demonstrate strengths in specific areas but are outperformed by FHONO.

Overall, FHONO stands out as the most robust model in the experiments, excelling in RMSE, MAE, and R2, although it exhibits slight inconsistencies in explaining variance. FHO closely follows, showing competitive performance, especially in R2. ECO and NRO each perform well in specific areas-ECO excels in MARE, while NRO performs well in R2-but both are ultimately outperformed by FHONO. DE and DLO show moderate performance, although they lack the consistency observed in FHONO and FHO.

5  Conclusion

In this study, we presented an efficient approach for forecasting wind power using an optimized Multilayer Perceptron (MLP). This advancement stems from integrating a new modified metaheuristic called FHONO, a modified version of the Fire Hawk Optimizer (FHO) based on the Non-Monopolize Search (NO) algorithm. The enhancement focuses on enhancing the traditional FHO’s exploratory capabilities to address its inherent search constraints. The core innovation of the FHONO-MLP methodology lies in employing the FHONO to refine the MLP parameters, thereby elevating its predictive precision. To assess the efficacy of the FHONO-MLP, we conducted comparative analyses against a spectrum of optimization algorithms, including the original FHO, DE, AO, ECO, NRO, DLO, and the conventional MLP. The results demonstrate that the MLP model, when optimized by the FHNO, surpasses its counterparts in performance metrics. The findings underscored the FHONO role as a potent optimization tool that enhances the forecasting performance of the MLP. Given its demonstrated efficacy, future work could investigate the potential of FHONO to optimize a broader range of complex problems, including deep learning model training, feature selection, machine scheduling, image processing, and other advanced applications. Additionally, future work could investigate the integration of additional optimization techniques to enhance the performance of MMLPs and other neural network models, particularly for time series analysis and forecasting.

Acknowledgement: The authors extend their appreciation to the Deanship of Graduate Studies and Scientific Research at University of Bisha, Saudi Arabia for funding this research work through the Promising Program under Grant Number (UB-Promising-42-1445).

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Conceptualization: Ahmed A. Ewees, Mohammed A. A. Al-qaness; Methodology: Ahmed A. Ewees, Mohammed A. A. Al-qaness; Investigation: Ahmed A. Ewees, Mohamed Abd Elaziz; Data Curation: Mohammed A. A. Al-qaness; Writing—Original Draft: Ahmed A. Ewees, Mohammed A. A. Al-qaness, Mohamed Abd Elaziz, Ali Alshahrani; Writing—Review & Editing: Ahmed A. Ewees, Mohamed Abd Elaziz, Mohammed A. A. Al-qaness, Ali Alshahrani. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Abdel-Aty AH, Nisar KS, Alharbi WR, Owyed S, Alsharif MH. Boosting wind turbine performance with advanced smart power prediction: employing a hybrid ARMA-LSTM technique. Alexandria Eng J. 2024;96:58–71. doi:10.1016/j.aej.2024.03.078. [Google Scholar] [CrossRef]

2. Wang J, Lv M, Li Z, Zeng B. Multivariate selection-combination short-term wind speed forecasting system based on convolution-recurrent network and multi-objective chameleon swarm algorithm. Expert Syst Appl. 2023;214:119129. doi:10.1016/j.eswa.2022.119129. [Google Scholar] [CrossRef]

3. Wang S, Wang J, Lu H, Zhao W. A novel combined model for wind speed prediction _ n dash combination of linear model, shallow neural networks, and deep learning approaches. Energy. 2021;234:121275. doi:10.1016/j.energy.2021.121275. [Google Scholar] [CrossRef]

4. Aljeddani SM, Mohammed M. An extensive mathematical approach for wind speed evaluation using inverse Weibull distribution. Alexandria Eng J. 2023;76:775–86. doi:10.1016/j.aej.2023.06.076. [Google Scholar] [CrossRef]

5. Yang W, Hao M, Hao Y. Innovative ensemble system based on mixed frequency modeling for wind speed point and interval forecasting. Inform Sci. 2023;622:560–86. doi:10.1016/j.ins.2022.11.145. [Google Scholar] [CrossRef]

6. Wu YK, Wu YC, Hong JS, Phan LH, Quoc DP. Probabilistic forecast of wind power generation with data processing and numerical weather predictions. In: 2020 IEEE/IAS 56th Industrial and Commercial Power Systems Technical Conference (I&CPS); 2020; Las Vegas, NV, USA: IEEE. p. 1–11. [Google Scholar]

7. Rigby A, Baker U, Lindley B, Wagner M. Generation and validation of comprehensive synthetic weather histories using auto-regressive moving-average models. Renew Energy. 2024;224:120157. doi:10.1016/j.renene.2024.120157. [Google Scholar] [CrossRef]

8. Zhang W, Lin Z, Liu X. Short-term offshore wind power forecasting—a hybrid model based on Discrete Wavelet Transform (DWTSeasonal Autoregressive Integrated Moving Average (SARIMAand deep-learning-based Long Short-Term Memory (LSTM). Renew Energy. 2022;185:611–28. doi:10.1016/j.renene.2021.12.100. [Google Scholar] [CrossRef]

9. Jørgensen KL, Shaker HR. Wind power forecasting using machine learning: state of the art, trends and challenges. In: 2020 IEEE 8th International Conference on Smart Energy Grid Engineering (SEGE); 2020; Oshawa, ON, Canada: IEEE. p. 44–50. [Google Scholar]

10. Ding M, Zhou H, Xie H, Wu M, Liu KZ, Nakanishi Y, et al. A time series model based on hybrid-kernel least-squares support vector machine for short-term wind power forecasting. ISA Trans. 2021;108:58–68. doi:10.1016/j.isatra.2020.09.002. [Google Scholar] [PubMed] [CrossRef]

11. Hao J, Zhu C, Guo X. Wind power short-term forecasting model based on the hierarchical output power and poisson re-sampling random forest algorithm. IEEE Access. 2020;9:6478–87. doi:10.1109/ACCESS.2020.3048382. [Google Scholar] [CrossRef]

12. Wang Y, Zou R, Liu F, Zhang L, Liu Q. A review of wind speed and wind power forecasting with deep neural networks. Appl Energy. 2021;304:117766. doi:10.1016/j.apenergy.2021.117766. [Google Scholar] [CrossRef]

13. Liu X, Zhou J. Short-term wind power forecasting based on multivariate/multi-step LSTM with temporal feature attention mechanism. Appl Soft Comput. 2024;150:111050. doi:10.1016/j.asoc.2023.111050. [Google Scholar] [CrossRef]

14. Aly HH. A hybrid optimized model of adaptive neuro-fuzzy inference system, recurrent Kalman filter and neuro-wavelet for wind power forecasting driven by DFIG. Energy. 2022;239:122367. doi:10.1016/j.energy.2021.122367. [Google Scholar] [CrossRef]

15. Ji J, Dong M, Lin Q, Tan KC. Forecasting wind speed time series via dendritic neural regression. IEEE Comput Intell Mag. 2021;16(3):50–66. doi:10.1109/MCI.2021.3084416. [Google Scholar] [CrossRef]

16. Kisvari A, Lin Z, Liu X. Wind power forecasting—a data-driven method along with gated recurrent neural network. Renew Energy. 2021;163:1895–909. doi:10.1016/j.renene.2020.10.119. [Google Scholar] [CrossRef]

17. Arora P, Jalali SMJ, Ahmadian S, Panigrahi BK, Suganthan PN, Khosravi A. Probabilistic wind power forecasting using optimized deep auto-regressive recurrent neural networks. IEEE Trans Ind Inform. 2022;19(3):2814–25. doi:10.1109/TII.2022.3160696. [Google Scholar] [CrossRef]

18. Zhang S, Liu M, Xie M, Lin S. Two-stage short-term wind power probabilistic prediction using natural gradient boosting combined with neural network. Appl Soft Comput. 2024;159:111669. doi:10.1016/j.asoc.2024.111669. [Google Scholar] [CrossRef]

19. Ge C, Yan J, Song W, Zhang H, Wang H, Li Y, et al. Middle-term wind power forecasting method based on long-span NWP and microscale terrain fusion correction. Renew Energy. 2025;240:122123. doi:10.1016/j.renene.2024.122123. [Google Scholar] [CrossRef]

20. Dai J, Lh Fu. A wind speed forecasting model using nonlinear auto-regressive model optimized by the hybrid chaos-cloud salp swarm algorithm. Energy. 2024;298:131332. doi:10.1016/j.energy.2024.131332. [Google Scholar] [CrossRef]

21. Sulaiman MH, Mustaffa Z, Saari MM, Abas MF. Wind power forecasting with metaheuristic-based feature selection and neural networks. Cleaner Energy Syst. 2024;9:100149. doi:10.1016/j.cles.2024.100149. [Google Scholar] [CrossRef]

22. Sulaiman MH, Mustaffa Z. Enhancing wind power forecasting accuracy with hybrid deep learning and teaching-learning-based optimization. Cleaner Energy Syst. 2024;9:100139. doi:10.1016/j.cles.2024.100139. [Google Scholar] [CrossRef]

23. Kumar N, Sudha K, Tharani K. Wind power prediction analysis by ANFIS, GA-ANFIS and PSO-ANFIS. J Inform Optim Sci. 2022;43(3):481–6. doi:10.1080/02522667.2022.2054997. [Google Scholar] [CrossRef]

24. Adedeji PA, Akinlabi S, Madushele N, Olatunji OO. Wind turbine power output very short-term forecast: a comparative study of data clustering techniques in a PSO-ANFIS model. J Clean Prod. 2020;254:120135. doi:10.1016/j.jclepro.2020.120135. [Google Scholar] [CrossRef]

25. Al-qaness MA, Ewees AA, Fan H, Abualigah L, Abd Elaziz M. Boosted ANFIS model using augmented marine predator algorithm with mutation operators for wind power forecasting. Appl Energy. 2022;314:118851. doi:10.1016/j.apenergy.2022.118851. [Google Scholar] [CrossRef]

26. Li LL, Zhao X, Tseng ML, Tan RR. Short-term wind power forecasting based on support vector machine with improved dragonfly algorithm. J Clean Prod. 2020;242:118447. doi:10.1016/j.jclepro.2019.118447. [Google Scholar] [CrossRef]

27. Zhou Y, Huang R, Lin Q, Chai Q, Wang W. Probabilistic optimization based adaptive neural network for short-term wind power forecasting with climate uncertainty. Int J Electr Power Energy Syst. 2024;157:109897. doi:10.1016/j.ijepes.2024.109897. [Google Scholar] [CrossRef]

28. Bai W, Meng F, Sun M, Qin H, Allmendinger R, Lee KY. Differential evolutionary particle swarm optimization with orthogonal learning for wind integrated optimal power flow. Appl Soft Comput. 2024;160:111662. doi:10.1016/j.asoc.2024.111662. [Google Scholar] [CrossRef]

29. Liu Y, Wang J. Transfer learning based multi-layer extreme learning machine for probabilistic wind power forecasting. Appl Energy. 2022;312:118729. doi:10.1016/j.apenergy.2022.118729. [Google Scholar] [CrossRef]

30. Hong YY, Rioflorido CLPP, Zhang W. Hybrid deep learning and quantum-inspired neural network for day-ahead spatiotemporal wind speed forecasting. Expert Syst Appl. 2024;241:122645. doi:10.1016/j.eswa.2023.122645. [Google Scholar] [CrossRef]

31. Cheng Z, Wang J. A new combined model based on multi-objective salp swarm optimization for wind speed forecasting. Appl Soft Comput. 2020;92:106294. doi:10.1016/j.asoc.2020.106294. [Google Scholar] [CrossRef]

32. Liu W, Xue F, Gao Y, Tuerxun W, Sun J, Hu Y, et al. Wind-speed forecasting model based on DBN-Elman combined with improved PSO-HHT. Glob Energy Interconnect. 2023;6(5):530–41. doi:10.1016/j.gloei.2023.10.002. [Google Scholar] [CrossRef]

33. Al-qaness MA, Ewees AA, Fan H, Abualigah L, Elsheikh AH, Abd Elaziz M. Wind power prediction using random vector functional link network with capuchin search algorithm. Ain Shams Eng J. 2023;14(9):102095. doi:10.1016/j.asej.2022.102095. [Google Scholar] [CrossRef]

34. Huang X, Wang C, Zhang S. Research and application of a model selection forecasting system for wind speed and theoretical power generation in wind farms based on classification and wind conversion. Energy. 2024;293:130606. doi:10.1016/j.energy.2024.130606. [Google Scholar] [CrossRef]

35. Wang J, Wang S, Li Z. Wind speed deterministic forecasting and probabilistic interval forecasting approach based on deep learning, modified tunicate swarm algorithm, and quantile regression. Renew Energy. 2021;179:1246–61. doi:10.1016/j.renene.2021.07.113. [Google Scholar] [CrossRef]

36. Azizi M, Talatahari S, Gandomi AH. Fire Hawk optimizer: a novel metaheuristic algorithm. Artif Intell Rev. 2023;56(1):287–363. doi:10.1007/s10462-022-10173-w. [Google Scholar] [CrossRef]

37. Moosavi SKR, Saadat A, Abaid Z, Ni W, Li K, Guizani M. Feature selection based on dataset variance optimization using hybrid sine cosine-firehawk algorithm (HSCFHA). Future Gener Comput Syst. 2024;155:272–86. doi:10.1016/j.future.2024.02.017. [Google Scholar] [CrossRef]

38. Rani BS, Vairamuthu S, Subramanian S. Archimedes fire Hawk optimization enabled feature selection with deep maxout for network intrusion detection. Comput Secur. 2024;140:103751. doi:10.1016/j.cose.2024.103751. [Google Scholar] [CrossRef]

39. Prabu S, Gnanasekar J. Robust object detection using fire Hawks optimizer with deep learning model for video surveillance. J Circ Syst Comput. 2024;33(13):2450226. doi:10.1142/S0218126624502268. [Google Scholar] [CrossRef]

40. Ashraf A, Anwaar A, Haider Bangyal W, Shakir R, Ur Rehman N, Zhao QJ. An improved fire hawks optimizer for function optimization. In: International Conference on Swarm Intelligence; 2023; Shenzhen, China: Springer. p. 68–79. [Google Scholar]

41. Abualigah L, Al-Qaness MA, Abd Elaziz M, Ewees AA, Oliva D, Cuong-Le T. The non-monopolize search (NOa novel single-based local search optimization algorithm. Neural Comput Appl. 2024;36(10):5305–32. doi:10.1007/s00521-023-09120-9. [Google Scholar] [CrossRef]

42. Basheer IA, Hajmeer M. Artificial neural networks: fundamentals, computing, design, and application. J Microbiol Methods. 2000;43(1):3–31. doi:10.1016/S0167-7012(00)00201-3. [Google Scholar] [PubMed] [CrossRef]

43. Storn R, Price K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optimiz. 1997;11(4):341–59. doi:10.1023/A:1008202821328. [Google Scholar] [CrossRef]

44. Abualigah L, Yousri D, Abd Elaziz M, Ewees AA, Al-Qaness MA, Gandomi AH. Aquila optimizer: a novel meta-heuristic optimization algorithm. Comput Ind Eng. 2021;157:107250. doi:10.1016/j.cie.2021.107250. [Google Scholar] [CrossRef]

45. Lian J, Zhu T, Ma L, Wu X, Heidari AA, Chen Y, et al. The educational competition optimizer. Int J Syst Sci. 2024;55(15):3185–222. doi:10.1080/00207721.2024.2367079. [Google Scholar] [CrossRef]

46. Sowmya R, Premkumar M, Jangir P. Newton-Raphson-based optimizer: a new population-based metaheuristic algorithm for continuous optimization problems. Eng Appl Artif Intell. 2024;128:107532. doi:10.1016/j.engappai.2023.107532. [Google Scholar] [CrossRef]

47. Wang X. Draco lizard optimizer: a novel metaheuristic algorithm for global optimization problems. Evol Intell. 2025;18(1):1–20. doi:10.1007/s12065-024-00998-5. [Google Scholar] [CrossRef]