A Fuzzy Multi-Objective Framework for Energy Optimization and Reliable Routing in Wireless Sensor Networks via Particle Swarm Optimization

Abbreviations

1  Introduction

A wireless sensor network (WSN) is a critical tool for studying and interacting with the physical world. As illustrated in Fig. 1, a sensor network typically comprises numerous small sensor nodes. Each sensor node contains one or more sensing components to sense environmental factors such as temperature, humidity, and pressure. It also contains a processing component to perform simple basic operations on the data and communicate with its neighboring nodes. Sensor nodes are distributed over a large area and communicate with each other via wireless links [1]. Control nodes called base stations process the data collected from sensor nodes, collect control commands for sensor nodes, and connect this network to other networks such as the Internet. The base station forms the core of WSN. It implements various programs ranging from critical signal processing and routing protocol configuration to application programs. Sensor nodes are typically deployed randomly and then form a sensor network in an ad hoc manner to perform specific tasks. There is usually no infrastructure support for WSNs [2].

Figure 1: The architecture of WSN communication

A large number of applications based on WSNs have emerged and been deployed in different geographical areas such as scientific exploration, military surveillance, traffic monitoring, marine surveillance, environmental protection, object tracking, and other valuable applications. So it is natural to talk about special cases in WSN, which usually include sensor node failure or communication failure due to power outages [3]. Besides, there are many other problems that they suffer from such as low reliability of wireless communication systems, how to balance the loads on the available nodes, limited available power, and instability of nodes. These limitations are mainly caused by the limited resources of sensor nodes and the variability of network scenarios. Solving such problems requires the development of new routing protocols that improve energy utilization, network lifetime, load balancing, and reliability [4,5]. Numerous research studies have been conducted to explore various optimization algorithms aimed at addressing the challenges associated with WSNs. Routing strategies can be classified into two categories, namely the traditional approach and the swarm intelligence-based approach. Previously implemented techniques such as Low Energy Adaptive Clustering Hierarchy (LEACH) work on the hierarchical clustering algorithm to improve the network lifetime problem by using balanced power distribution [6]. These techniques have been useful in static, small, and less tangled environments. However, they suffer from obvious drawbacks when applied to dynamic or large networks. Swarm intelligence techniques are known to enhance flexibility and increase throughput in wireless sensor networks, which will be reviewed here. These techniques have been useful in small, less tangled, and static environments, but they have obvious drawbacks when applied to dynamic or large networks. Swarm intelligence techniques are known to enhance flexibility and increase throughput in wireless sensor networks, which will be reviewed here. In 2015, Umadevi et al. applied ACO to optimize the placement of sensor nodes in an attempt to achieve the best possible stability of the overall network and reduce path failures [7]. Similarly, in 2016, Mohajerani et al. also used ACO in wireless sensor networks to extend the network lifetime by prioritizing paths with the highest remaining energy [8]. A fault-tolerant routing based on PSO has been proposed to increase the reliability of the network architecture, showing great compatibility with WSNs [9]. An improved genetic algorithm is used to select an energy-efficient multi-hop path, showing significant improvements in network lifetime and energy utilization [10]. Similarly, a chaotic genetic algorithm is introduced for clustering and routing, which effectively balances the energy consumption across nodes while enhancing load balancing [11]. An improved ABC algorithm has been used to improve data transmission in power-constrained WSN environments [12]. The multipath adaptive routing techniques discussed in [13] use genetic algorithms to find reliable multiple paths with higher data throughput and fault tolerance. A new DRL routing protocol for WSNs has been proposed in [14]. This approach improves the traditional decision-making approach because it adapts to changes in network conditions. A PSO-based routing protocol was proposed in [15] to achieve better energy efficiency and load balancing by dynamically adjusting routing decisions. A dynamic routing algorithm based on distributed neural networks has been developed to increase the flexibility and energy saving in different WSNs [16]. To alleviate the packet reordering problem in lossless data centers, an innovative load balancing method that encapsulates intra-network recirculation has been proposed to improve network performance and availability [17]. Thus, the development of new efficient heuristic techniques, including techniques based on combining swarm intelligence, machine learning, and adaptive techniques that mimic natural processes, has been shown to improve both the convergence rate and solution quality of more complex optimization problems in recent years [18]. A self-healing path approach was proposed in [19] to enhance fault tolerance in WSNs. This approach is based on a path selection method that changes its path in case of a node or some links that pose a hindrance to communication processes. A new ACO-based routing protocol specifically designed for WSNs in the IoT environment is presented in [20].

Based on these works, the proposed study presents a PSO-fuzzy algorithm specifically designed for WSNs. Unlike ACO, genetics and DRL deal with one or two objectives and face problems such as slow convergence or high resource consumption. For example, adaptive DRL protocols exhibit some slow convergence in the training process, which is time-consuming. Also, using a different number of nodes or changing the spatial configuration also requires retraining the DRL model, which is computationally expensive. Although ACO is effective at optimizing a single objective, it has difficulty managing multiple conflicting objectives. It requires separate heuristics for different objectives, which can lead to inefficiency. The combination of PSO and fuzzy in the proposed PSO-fuzzy directly addresses these issues. PSO can converge faster without the need for prolonged training. Fuzzy logic is incorporated to guide particle updates, dynamic weight adjustment, and multiple fitness evaluations to optimize routing. These improvements address multiple conflicting objectives together in a single protocol, which were missing in previous studies. The proposed routing method is designed to achieve operational gains in case of minor failure of some of its components, especially in hard-to-reach environments.

The rest of this paper is organized as follows: Section 2 outlines the mathematical modeling of the problem, including the formulation of all objectives and the fuzzy system along with its membership functions. Section 3 provides the methodology in detail. Section 4 describes the experimental setup, simulation environment, and parameter settings, followed by an analytical study of the results. Finally, the conclusions of this study and future trends are stated in Section 5.

2  The Problem Formulation

This section presents the mathematical model for routing optimization in WSNs based on multiple objectives, including minimizing the path length, reducing energy consumption, maximizing routing reliability, and achieving load balancing. Together, these objectives aim to reduce node failure and connectivity loss. Consider a WSN comprising a certain number of sensor nodes (NoS). Each node X ∈ {1,2,…,NoS} has a status STi which is defined by Eq. (1).

STi={1ifsensorworks0ifsensorfail(1)

Network connections (C) represented by Eq. (2) are defined as a measure of the number of active sensors that can communicate within the network. In fully connected networks, it is necessary to achieve at least one path between sensors to ensure data flow between them.

C=∑i=1NoS∑j=iNoSAijSiSj∀i≠j(2)

where C represents the WSN connections, S is the sensor node, NoS contains the number of sensor nodes and Aij denotes the connectivity matrix, which represents the relationship between sensors Si and Sj. The contents of Aij are determined using Eq. (3).

Aij={1ifsensorsiandjareconnected0ifsensorsiandjareDisconnected(3)

where 1 indicates connections between two sensors, while 0 indicates no connection between them.

2.1 Formulating the Main Objectives Mathematically

Reducing power consumption remains a critical concern in WSNs, as the majority of sensor nodes rely on limited battery power. It has been observed that edge nodes, which forward or broadcast messages, as well as those positioned within efficient network architectures, tend to consume more energy. Consequently, these nodes experience significant battery degradation, increasing the likelihood of network failures and reducing duty cycles. The energy consumption of a sensor node i is denoted as Ei, and its mathematical representation is provided in Eqs. (4) and (5).

ETotal=∑i=1NoSEi(4)

Ei=Eitx+Eirx+Eiex(5)

where ETotal is the total energy consumption, Ei is the energy consumption of sensor i. Eitx, Eirx, and Eiex are the transmission, reception, and computing energy of sensor node i, respectively.

From Eqs. (4) and (5), which quantify energy consumption, we establish a foundation for evaluating the energy efficiency of WSNs, as well as for designing and comparing more energy-efficient network configurations. To achieve efficient energy utilization, equal energy consumption should be achieved by all nodes. Therefore, the next goal is to reduce the variation in energy demand across sensor nodes to promote equal energy utilization across the network using Eq. (6).

σE=1NoS∑i=1NoS(Ei−μE)2(6)

where σE is the variance of energy consumption, μE represents the average energy consumption across all sensor nodes, which is calculated by Eq. (7).

μE=1NoS∑i=1NoSEi(7)

To improve routing efficiency, choosing the shortest path to use for data transmission is always vital. This effectively addresses the issues of power drain and latency. Eq. (8) calculates the total path distance.

D=∑i=1Nosdij(8)

where dij represents the distance between sensor i and sensor j in the path.

The performance related to routing reliability is essential for the ability of data packets to pass through the network from source nodes to the base station or sink. The quality of service in WSN applications is directly determined by this metric which is measured by Eqs. (9) and (10).

R=∏i=1Nosrij(9)

rij=ω1.SNR+ω2.LQI+ω3.BER+ω4.PDR+ω5.REN(10)

where R is the total path reliability, rij the reliability of the link between i and j.

The product Π represents the probability of a path’s reliability based on the reliability of each link within it. The reliability of a link depends on sundry factors. Key factors include a signal-to-noise ratio (SNR), Link Quality Indicator (LQI), Bit Error Rate (BER), Packet Delivery Ratio (PDR), and Residual Energy of Nodes (REN). REN represents the remaining energy of the transmitting and receiving sensors in the link. The link constructed from node to node has more reliability if the sensor node has high residual energy [21].

2.2 Fuzzy Multi-Objective Model Formulation

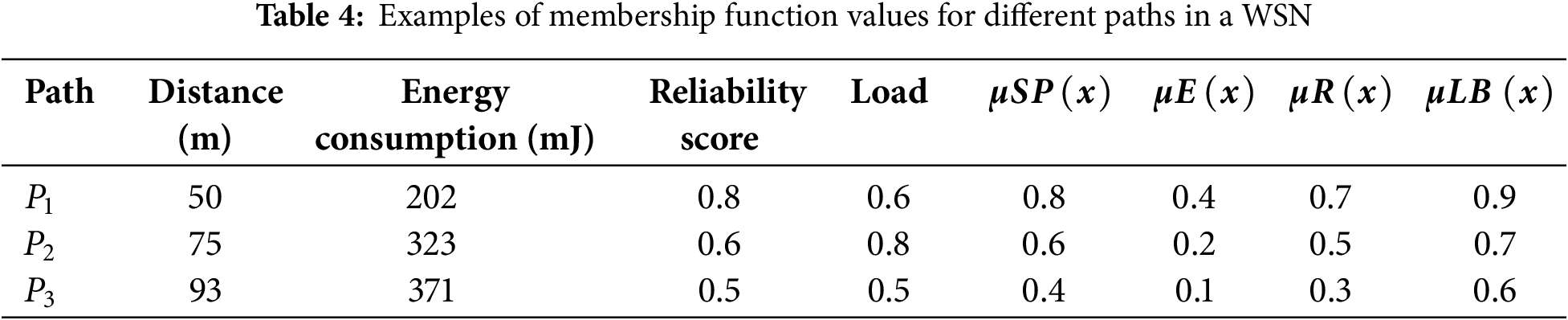
Fuzzy multi-objective models have attracted increasing attention in the recent past due to their suitability for dealing with the complexities of uncertain and multi-objective problems. These models use the concept of fuzzy logic to address the ambiguity and imprecision present in a real-world system. In contrast to classical optimization techniques, multi-objective models under fuzzy theory are exceptionally efficient because they allow for degrees of membership in the criteria at hand [22]. Fig. 2 illustrates an example of three membership functions related to the “height” level. They indicate the level of activity of each input within a given fuzzy set. In particular, it places weights on the inputs, measures the degree of intersection between them, and determines the influence provided to generate the output response [23]. In this paper, multi-objective fuzzy models are used for a WSN routing protocol. When fuzzy logic and PSO are combined, several trade-offs can be analyzed and suitable solutions can be provided. The multi-objective fuzzy routing scheme aims to minimize energy consumption, balance load, maximize data transmission reliability, and find the shortest path. We employ fuzzy membership functions for each objective.

Figure 2: Three membership functions for “height” level

These functions enable the transition between different levels of the performance metrics, which provides flexibility together with stability in decision-making processes. Below, we present the mathematical model for each membership function, justify their selection, define their bounds, and explain how they are combined to guide optimization. The membership for the shortest path (μSP) is defined by a piecewise linear decreasing function as in Eq. (11). It defines a high level of satisfaction for short distances and a decreasing level of satisfaction as the distances increase. It also ensures that moderate deviations can be tolerated easily, especially when the increase is not too sharp before punishing long paths.

μSP(x)={1,x≤SPminSPmax−xSPmax−SPmin,SPmin<x<SPmax0,x≥SPmax(11)

where μSP(x) is the membership of the shortest path for solution x, SPmin and SPmax are the minimum acceptable path length and maximum tolerable path length, respectively.

The membership for energy minimization (μE) is defined by a linear decreasing function as in Eq. (12) which specifies a high level of satisfaction with decreased energy consumption and a decreasing level of satisfaction with increased consumption.

μE(x)=1−x−EminEmax−Emin,Emin≤x≤Emax(12)

where Emin and Emax are the minimum acceptable power consumption and maximum allowed power consumption levels, respectively.

The proposed PSO-fuzzy scheme enhances energy consumption in WSNs by prioritizing energy-efficient nodes and distributing energy consumption equitably among all nodes, particularly those with the least remaining energy. This is done using a fuzzy logic scheme that evaluates other parameters such as the potential remaining energy of any node, the distance to be traveled to make the connection, or the size of the data packet to be sent. Since energy-intensive nodes get a higher order in terms of paths, the overloading problem of low-energy nodes is solved, thus prolonging their life cycle. Therefore, providing energy in this more stable way means that they are ready to adapt to different conditions in the long run. Furthermore, the PSO mechanism continuously optimizes the path selection in energy aspects to ensure a reliable and sustainable selection of energy-efficient paths. The routing reliability membership function is given by Eq. (13). It is represented by a piecewise linear increasing function. This membership function would represent the logical progress toward the routing paths that have greater reliability. It prioritizes routes with higher reliability but without degrading the performance.

μR(x)={0,x≤Rminx−RminRmax−Rmin,Rmin<x<Rmax1,x≥Rmax(13)

where Rmin and Rmax are the minimum reliability threshold and desired reliability level, respectively.

The load balancing membership function is given by Eq. (14). It is represented as a routing reliability membership function. In this way, we can ensure that the load distribution across the nodes is essential and should not allow the formation of heterogeneous loads, which would cause premature failure within the system.

μLB(x)={0,x≤Bminx−BminBmax−Bmin,Bmin<x<Bmax1,x≥Bmax(14)

where Bmin and Bmax are the minimum acceptable load and ideal load, respectively.

Table 1 summarizes the fuzzy membership functions in this study. Each membership function is designed to address a specific routing objective, allowing the proposed model to prioritize the optimal solutions to the WSN routing problem.

The proposed PSO-fuzzy uses fuzzy membership functions to improve routing by addressing four main objectives. Based on pre-defined thresholds, these functions determine satisfaction levels to optimize path selection and energy consumption to extend the network lifetime. The shortest path function ensures that the shortest paths are prioritized. The energy minimization function takes care of the energy-efficient nodes. The reliability membership function ensures reliable communication paths to eliminate the possibilities so that performance and data delivery are guaranteed. Finally, the load balancing function prevents traffic inequality that leads to network node failure and premature node failure. The overall fuzzy score µtotal is computed by combining all the above individual membership functions by Eq. (15).

µtotal(x)=λ1.μSP(x)+λ2.μE(x)+λ3.μR(x)+λ4.μLB(x)(15)

where λi represents the weight of the corresponding objective such that the sum of λi equals one.

These weights should be chosen based on considerations of the level of importance of each objective. This would add more flexibility due to the difference in application needs to create suitable solutions. The above overall fuzzy score that integrates the contribution of all objectives follows the following fuzzy logic rule.

IF path length is Low, path energy consumption is Low AND routing reliability  is High AND Load balancing degree is High, THEN the solution is considered perfect.

Consequently, the defuzzification process identifies the best solution from the aggregated results. The solution that achieves the highest overall satisfaction in terms of power, reliability, shortest path, and load distribution with the fewest faults is selected. This fuzzy score leads to a more flexible and dynamic decision-making process that is appropriate in the many different WSN settings.

3  The Methodology

This section introduces the process of using the PSO algorithm in conjunction with a fuzzy multi-objective system. It includes a description and modification of the PSO algorithm, the inclusion of fuzzy logic control, and a general analysis of the computational requirements. Fig. 3 depicts the velocities and positions of the PSO algorithm. Each particle in the PSO algorithm consists of a position and a velocity coming from the decision space that determines the direction of the particle’s flight. At each iteration, the particle moves from one position to another within the space in its search for the best solution. The two parameters used in PSO are the global best solution (gBest) and the stopping criterion that indicates the exit point of the PSO. gBest is the global best solution obtained at any time during the PSO run. It is useful in guiding the particles toward the target.

Figure 3: Velocities and positions of the PSO algorithm

The velocity of a particle in the flock is scaled concerning the distance to the destination point. This velocity is supported using the relationship shown in Eq. (16).

Vi(t+1)=Vi(t)+U1C1.(pBesti−Xi(t))+U2C2.(gBesti−Xi(t))(16)

where Vi(t+1) represents the new velocity, Vi(t) is the current speed, U1 and U2 are two random variables, while C1 and C1 are learning factors representing self-attraction and social attraction, respectively.

After that, each particle jumps to a new position in the search space depending on the calculated velocity as shown in Eq. (17). Such repeated exploration and exploitation occurrence allows particles to obtain better solutions.

Xi(t+1)=Xi(t)+Vi(t+1)(17)

where Xi(t+1) and Xi(t) represent the new position and the current position, respectively.

Fig. 4 shows the pseudo-code of the proposed multi-objective PSO-fuzzy to improve routing for WSNs that rely on several routing objectives.

Figure 4: Pseudo-code of the proposed multi-objective PSO-fuzzy model

First, the WSN is initialized with NoS sensor nodes where each node possesses an initial energy level and the connectivity between the nodes is represented by a matrix A[i][j]. Parameters such as the number of particles, the maximum number of iterations, and the maximum speed are also specified. Then the weights of the optimization objectives are specified. The best paths are determined by the routing module possessed by the algorithm. Similarly, when there are any changes in the size of the WSN such as failed nodes or additional sensors, they are identified and then the routing paths are recalculated by calling the same function with new parameters. It also provides dynamic integration of the optimization criterion by continuously re-adjusting the paths under the current network configurations. The proposed system includes a robust fault detection technique where the energy level is the primary measure of node health. Each node monitors its energy level, and the nodes with the fastest energy decline are selected for further analysis including packet delivery success rates and response time at specified threshold values. Each node also sends periodic “heartbeat” signals to its neighbors. If a node fails to send such a signal in the mentioned time frame, it is suspected to have developed a fault. After a node fails, it is considered to be out of the active communication topology network. This elimination process aims to restore routing across the remaining nodes. To address scalability considerations, let new nodes integrated into the network be represented by NoSnew. Routing paths must be changed and adapted at runtime to accommodate the new topology without depriving the network of its efficiency and performance. Thus, by invoking the proposed algorithm, the number of particles will be directly proportional to the number of sensor nodes. The Pseudo-code of the routing module is modulated in Fig. 5. It searches for the best routing paths in WSN by leveraging Particle PSO integrated with fuzzy score. First, it eliminates the failed nodes from WSN and includes newly added sensor nodes. A vector of paths is initialized empty to store best-obtained paths and their fitness values. The routing problem is modeled in a PSO network by treating each possible path as a particle in the solution space. The position of the particle represents a specific routing path. Initially, a random solution is generated for each particle that reflects the path from any randomly chosen source sensor node to the base station. Over Tmax, the algorithms compute the fitness of each particle’s path using fuzzy score by Eq. (15). This obtained path is normally added to a vector of paths if it improves performance. The velocity as well as the position is changed in each iteration to obtain new routing paths. The equations of velocity and position are based on the overall fuzzy score µtotal in Eq. (15). The velocity is adjusted using Eq. (16). When computing the velocity, pBesti will be μtotal(particleBest), Xi(t) will be μtotal(particleSol) and gBesti will be μtotal(GBSol). So, it primarily depends on the aggregated membership functions of the global best solution, the current best particle solution, and the current solution. The key here is that we use fuzziness as a decision-making layer that produces adaptive methodology I in the PSO framework. Thus, membership functions are defined to determine concrete fuzzy sets in quantitative values. The calculated velocity adjusts the particle’s motion towards GBSol. By associating the velocities with the combined membership functions, the particles are directed according to the nature of the multi-objective problem being addressed. Then the position update rule is applied by Eq. (17) after updating the relevant velocities. Also, to adapt the proposed routing module to enhance the WSN, some changes have been made. The first alteration concerns the expansion of the particle encoding type to include multiple scales as subtypes of particle position. Fuzzy sore is utilized to make sure that particles look for the routing solutions that fulfill the conflicted objectives at once and make compensation between them.

Figure 5: Pseudo-code of the proposed routing module

The complexity analysis of the proposed routing module, shown in Fig. 5, can be explained by studying the pseudo-code. The complexity can be divided into two phases: initialization and iterative optimization. In the initialization phase, in order to exclude a failed node, (Nf) operations are required, where F is the total failed nodes, and in order to add an expanded node, it needs (NoSnew) where NoSnew is the count of expanded nodes. Random selection of source nodes has a complexity of (Ns), where Ns is the number of source nodes. In the iterative optimization, the amount of computation work in general varies only by the number of particles (NoP), the iterations (Tmax), and the dimension of the problem space which is the numbers nodes in WSN (NoS). The algorithm executes for a maximum of Tmax iterations, where each iteration involves updating NoP particles. For each particle, the fitness calculation by the proposed fuzzy score of a routing path depends on traversing edges of the wireless sensor network graph, resulting in a complexity of O (F). In addition, path additions or updates, as well as velocity and position updates, are constant-time operations, (1). Therefore, the overall complexity of the algorithm can be expressed as O(Tmax×NoP×F) with the initialization cost O(Nf++NoSnew+Ns) which is relatively small compared to the iterations which can be neglected.

Some of the limitations when using the fuzzy PSO model in real-time include: computational time delay and environmental variability. The delays are inherent in the computation of the underlying PSO algorithm which often requires multiple iterations. This can be compensated for either by using concurrent computing or simply running the model on a boosted computing device. Fuzzy contributes to overcoming the challenge of unpredictability. There are inherent physical limitations of sensor nodes including limited memory capacity and computing power. Hence, relatively low-complexity and energy-efficient algorithms should be used which are addressed by the proposed fuzzy PSO model.

4  Experimental Results

The simulation environment of NS-3 in [24,25] was designed to evaluate the performance of the proposed PSO-fuzzy model in various WSN scenarios. Tables 2 and 3 summarize the environmental settings of the NS-3 simulation and PSO parameters. The network topology used in the simulation of this model is a grid where nodes are placed at equal distances and in equal numbers to achieve connectivity across the area of interest. Node densities are set as medium and high as a way to create variation in scalability and performance. In the traffic scenario, both constant bit rate and variable bit rate sources are used to simulate a wide range of traffic characteristics for connectivity requirements.

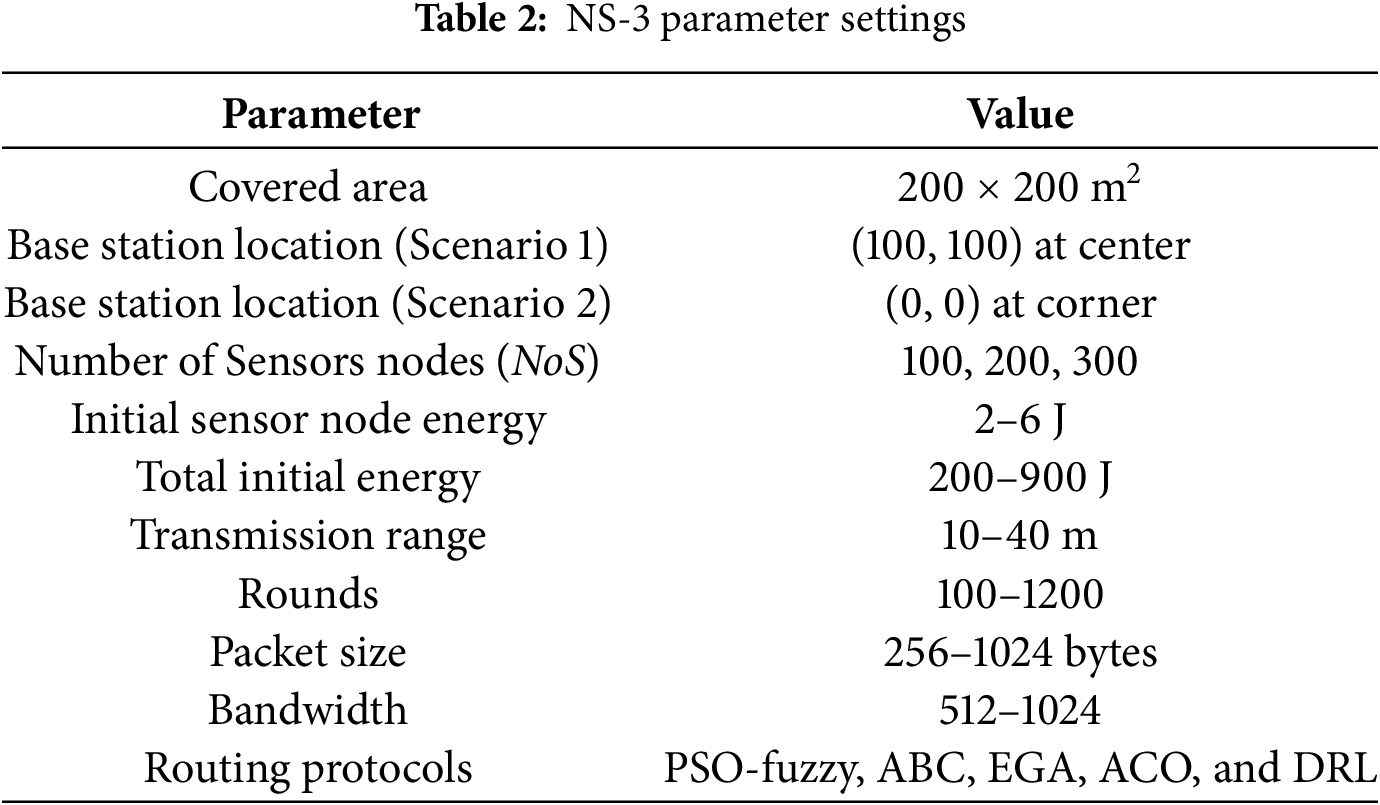
The simulation settings in Table 2, include a covered area of 200 × 200 m2, with two base station placement scenarios: centrally located at (100, 100) and at the corner in (0, 0). The central base station is particularly suitable in the agricultural sector where many sectors use sensor nodes to measure variables such as humidity, temperature, and moisture. In particular, a central base station allows the data received from all nodes to be collected and reduces the timing delay and energy consumption of the entire network. Essentially, this format allows for precision agriculture by ensuring that the large distance for data transmission to the base station is optimized. In urban environments, the central base station may operate nodes that will track various parameters including traffic flow. The distribution of nodes will be uniform and the reduction in energy consumption makes the system more sustainable and responsive. Sometimes, it may be necessary to place a base station in the corner to reduce exposure to hazardous areas due to physical security needs during natural disasters. Although this design is physically reasonable, it makes the power consumption of the remote nodes high.

The proposed PSO-fuzzy model will be demonstrated to work successfully on these two different network topologies. The network contains 100 to 300 sensor nodes with an initial energy of 2 to 6 J per node and a total initial energy of 200 to 900 J. The transmission range ranges between 10 and 40 m with the rounds between 100 and 1200. Various routing protocols such as PSO-fuzzy, ABC, EGA, ACO, and DRL are tested and evaluated. The selected parameters for the proposed PSO-fuzzy in Table 3 are as follows. The swarm size is therefore between 50 and 150 with the maximum iteration count of Tmax is 100. Random weights (U1 and U2) are 0.3 whereas C1 and C2 coefficients are 1.5 and 2, respectively. Influence factors (λ1,λ2,λ3,andλ4) are set to equal to 0.25 this is because multiple objectives are valued equally in the optimization process. The parameters λ1,λ2,λ3andλ4 represent the weights assigned to the four main objectives. A sensitivity analysis was performed to evaluate the impact of changing these weights. The weights were changed individually while keeping the other weights constant. The performance metrics analyzed included measurements of the four objectives. Increasing λ1 gave more preference to the shortest paths while occasionally leading to lower energy utilization and path reliability. With the increase of λ2, the energy efficiency was enhanced, but the path distance became longer, and the reliability was low. Higher λ3 improved reliability but resulted in longer paths and higher power consumption. The network stability is improved when λ4 is increased, but the path length and the power consumption are also affected. The choice of these weights is influenced by the specific requirements of the application and the main considerations are as follows:

•   Real-time applications should have a higher λ3 weight to ensure network reliability.

•   Energy-Constrained Networks should have a higher λ2 weight to prioritize energy conservation.

•   Long-lifetime networks increase the weights of λ2 and λ4 to ensure that the network does not suffer from premature node failure or energy drain.

•   General Purpose Networks assign equal weights to λ1,λ2,λ3andλ4 to provide a balanced trade-off between all objectives.

So, we assume that λ1,λ2,λ3andλ4 are all equal. This approach was chosen to balance the optimization of the objectives without favoring any particular objective. The performance of the proposed PSO-fuzzy is tested for WSNs with four common algorithms namely Enhanced Genetic Algorithm [10], Improved Artificial Bee Colony (ABC) Algorithm [12], Deep Reinforcement Learning (DRL) [14], and Ant Colony Optimization (ACO) [20]. The evaluation depends on various metrics such as network lifetime, stability duration, residual energy, energy consumption, and load balancing. These metrics quantify the energy consumption, communication, reliability, and fairness of routing load in WSNs [10,12,26]. The network lifetime metric for two scenarios of the proposed PSO-fuzzy vs. four other methods is shown in Figs. 6 and 7. Network lifetime as used in this context refers to the time that elapses between the time the network has commenced operation and a particular performance level is attained. These results prove that the proposed PSO-fuzzy provides the longest network lifetime than other algorithms in the two scenarios concerning all the sensor densities.

Figure 6: Network Lifetime metric of the proposed PSO-fuzzy vs. four other methods in scenario 1

Figure 7: Network lifetime metric of the proposed PSO-fuzzy vs. four other methods in scenario 2

Table 4 summarizes the computed values of μSP(x),μE(x),μR(x)andμLB(x) for various paths sample in a WSN. It provides a better visual understanding of how membership is changed. For Path P1, the µtotal is computed as follows. µtotal(P1)=0.25(0.8)+0.25(0.4)+0.25(0.7)+0.25(0.9)=0.7. This table helps in understanding membership functions and their role in the fuzzy logic model.

The stabilization time for the two scenarios is illustrated in Figs. 8 and 9 shows how long all nodes of the network will perform without energy exhaust. The proposed PSO-fuzzy algorithm significantly outperforms the other methods in terms of maximum stability time where up to 1000 cycles are realized with 100 sensors and also high efficiency when network size is increased.

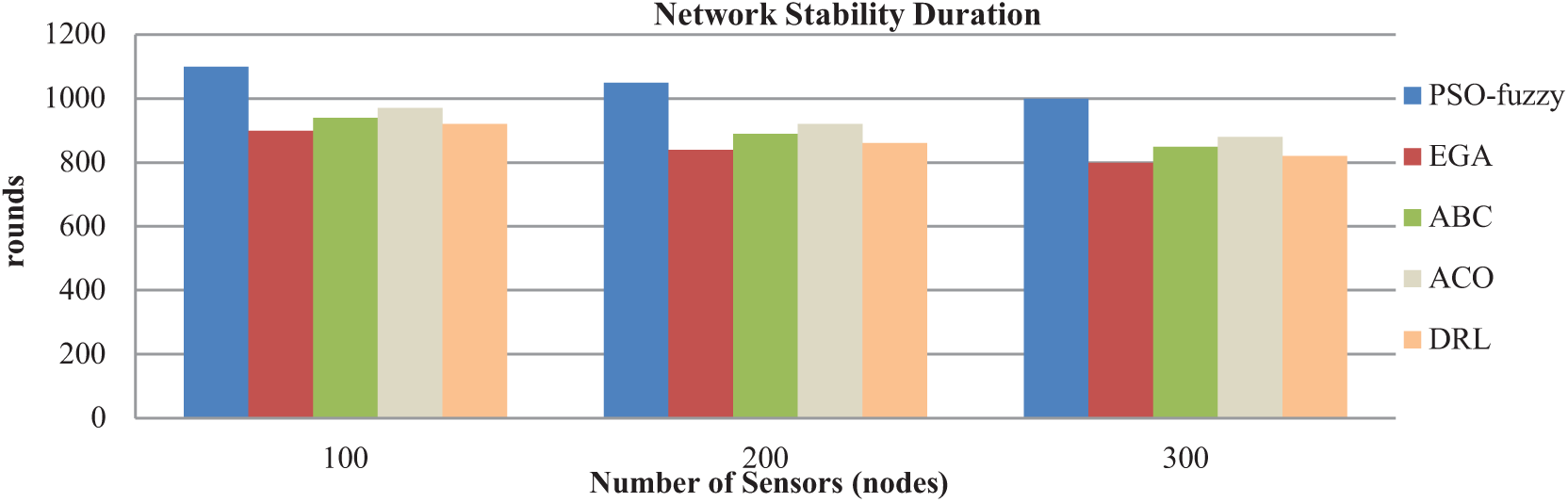
Figure 8: Stabilization time measurement of scenario 1

Figure 9: Stabilization time measurement of scenario 2

Figs. 10 and 11 summarize the total remaining energy for the two scenarios. Each figure contains three charts clarifying the remaining energy levels for networks with 100, 200, and 300 nodes, respectively.

Figure 10: The total residual energy measurement for scenario 1. (A) WSN with 100 sensors. (B) WSN with 200 sensors. (C) WSN with 300 sensors

Figure 11: The total residual energy measurement for scenario 2. (A) WSN with 100 sensors. (B) WSN with 200 sensors. (C) WSN with 300 sensors

This metric can be used to gain an understanding of the energy consumption patterns of network protocols and to estimate the remaining lifespan of the network. In the initial round, each algorithm begins with the same total available energy for a specified number of sensors reducing the impact of energy differences between algorithms in the evaluation of the energy consumption patterns during the construction of the network. In terms of energy consumption, the PSO-fuzzy algorithm shows better performance than other algorithms.

Figs. 12 and 13 illustrate the standard deviation of load for the two scenarios. It is possible to observe an increase in standard deviations as the rounds continue in two scenarios, due to the decreasing balance in energy levels and workload distribution between nodes over time. The proposed PSO-fuzzy model demonstrates significant advantages over the four compared methods (ABC, EGA, ABC, and DRL). Although ABC and ACO are widely used optimization algorithms for path finding and energy utilization in wireless sensor networks, their effectiveness decreases while working with multiple conflicting objectives.

Figure 12: The standard deviation of the load for scenario 1

Figure 13: The standard deviation of the load for scenario 2

ABC and ACO often select one or two objectives. They only deal with energy efficiency in routing without any decision-making capability for reliability and load balancing in a dynamic environment. Similarly, EGA enhances multi-hop routing but lacks the multi-objective adaptability that the proposed method relies on. Conversely, Deep Reinforcement Learning (DRL) for policy-based methods is a moderate method for learning the best approaches and choices to make regarding decision-making problems, but it entails a large number of samples and computational costs. On the other hand, the routing method applies a framework of PSO, which is in fact, more efficient in terms of offering a more straightforward approach to achieve the real-time balance of multiple goals. In general, the proposed routing method demonstrates the best performance in terms of various measurements compared to other algorithms.

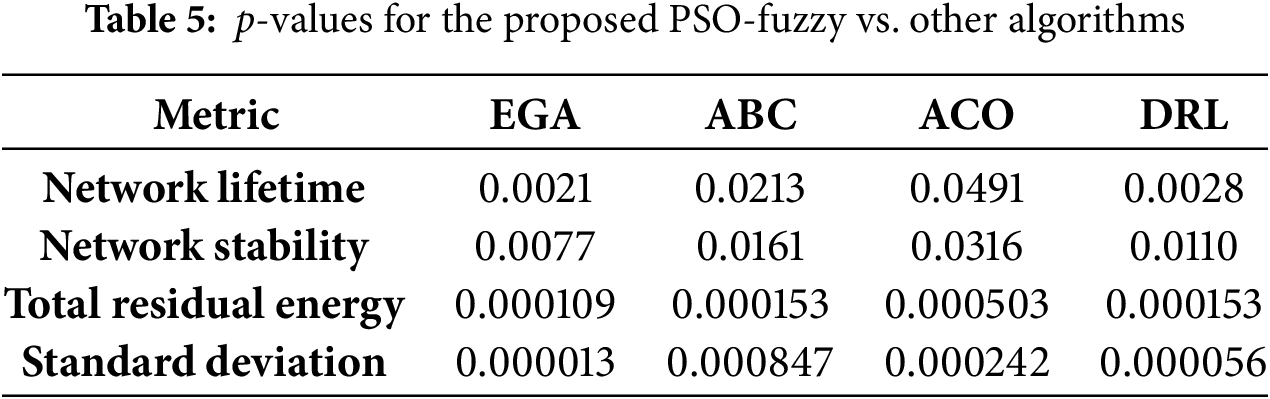
Table 5 presents the p-values for the comparative performance of the proposed PSO-fuzzy vs. the EGA, ABC, ACO, and DRL algorithms across four key metrics. Lower p-values (typically less than 0.05) indicate significant differences between the proposed PSO-fuzzy and the respective algorithms in the given metrics. Table 5 demonstrates that the proposed PSO-fuzzy algorithm exhibits statistically significant improvements in most of the evaluated metrics compared to the other algorithms. This suggests that PSO-fuzzy is a promising approach for optimizing WSN performance in terms of lifetime, stability, energy efficiency, and load balancing.

It is pertinent to mention that based on all the comparisons, the decision-making process in the proposed PSO-fuzzy model involves and benefits from the adaptive integration of multiple objectives in WSN to monitor the environment. For example, when sensor nodes need to send data to a central node with certain objectives, the model uses fuzzy logic to summarize several fuzzy variables and calculate their membership values. These values are then combined until a distinct path that addresses the desired objectives is chosen. For example, there may be two paths that are equally energy efficient but have different degrees of reliability. In this case, the model will prioritize reliability. This decision is then optimized by PSO which runs along the selected path and provides the best solution through an iterative system. The proposed fuzzy PSO framework shows great real-world relevance in extreme potential situations, e.g., disaster relief, and environmental conservation. It is best suited where there is dynamism and where the solution must include variables within the emergency environment. In disaster recovery, it determines the resource efficiency of environmental monitoring and how to manage the energy required to support a long-term wireless sensor network. The fuzzy logic component allows for handling changing priorities or unexpected conditions. These capabilities have proven effective in a range of simulation tests such as lifetime, stability, etc. These results qualify the model to respond to various real-time applications such as fire monitoring, autonomous driving systems, etc.

5  Conclusions and Future Work

This paper proposes a comprehensive solution for routing optimization in WSNs by combining PSO and a multi-objective fuzzy framework. A mathematical model of multi-objective and fuzzy systems in WSNS is presented. The proposed model successfully addresses critical challenges, including minimizing energy consumption, shortest path, maximizing routing reliability, and achieving load balancing to ensure reduced node failure and communication loss. Simulation results show that the proposed PSO-fuzzy model can outperform other techniques using different criteria in energy efficiency metrics, load standard deviation, network lifetime, and routing stability.

For future work, the proposed multi-objective PSO-fuzzy model will be tested using more advanced algorithms and other metrics. Case studies simulating real-world environments such as flood response operations and urban pollution tracking can be validated to verify the model’s adaptability to complex and evolving conditions. This helps to demonstrate the potential of the proposed model to enhance operational efficiency and decision-making in these real-world domains. IoT-enabled WSN technologies can also be used to demonstrate their applicability. Other optimization methods can be combined with PSO to enhance the scalability and convergence factors of the result.

Acknowledgement: This work was funded by Deanship of Graduate studies and Scientific Research at Jouf University.

Funding Statement: This work was funded by Deanship of Graduate studies and Scientific Research at Jouf University under grant No. (DGSSR-2023-2-02038).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Medhat A. Tawfeek; analysis and interpretation of results: Madallah Alruwaili; manuscript preparation and writing: Ibrahim Alrashdi; programming: Fatma M. Talaat. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Kingston Roberts M, Ramasamy P, Dahan F. An innovative approach for cluster head selection and Energy Optimization in wireless sensor networks using Zebra Fish and Sea Horse Optimization techniques. J Ind Inf Integr. 2024;41(4):100642. doi:10.1016/j.jii.2024.100642. [Google Scholar] [CrossRef]

2. Savithri G, Sai NR. Dynamic deep learning for enhanced reliability in wireless sensor networks: the DTLR-net approach. Comput Mater Contin. 2024;81(2):2547–69. doi:10.32604/cmc.2024.055827. [Google Scholar] [CrossRef]

3. Roberts MK, Thangavel J, Aldawsari H. An improved dual-phased meta-heuristic optimization-based framework for energy efficient cluster-based routing in wireless sensor networks. Alex Eng J. 2024;101(1):306–17. doi:10.1016/j.aej.2024.05.078. [Google Scholar] [CrossRef]

4. Nanthini S, Nithya Kalyani S, Sengan S. Energy efficient clustering protocol to enhance network lifetime in wireless sensor networks. Comput Mater Contin. 2021;68(3):3595–614. doi:10.32604/cmc.2021.015038. [Google Scholar] [CrossRef]

5. Zhang Z, Zhao H, Yao X, Xing Z, Liu X. Metro timetable optimization for improving regenerative braking energy utilization efficiency. J Clean Prod. 2024;450(1):141970. doi:10.1016/j.jclepro.2024.141970. [Google Scholar] [CrossRef]

6. Palan NG, Barbadekar BV, Patil S. Low energy adaptive clustering hierarchy (LEACH) protocol: a retrospective analysis. In: 2017 International Conference on Inventive Systems and Control (ICISC); 2017 Jan 19–20; Coimbatore, India. p. 1–12. doi:10.1109/ICISC.2017.8068715. [Google Scholar] [CrossRef]

7. Umadevi M, Devapriya M. An enhanced ant colony-based approach to optimize the usage of critical node in Wireless Sensor Networks. Procedia Comput Sci. 2015;47(2):452–9. doi:10.1016/j.procs.2015.03.229. [Google Scholar] [CrossRef]

8. Mohajerani A, Gharavian D. An ant colony optimization based routing algorithm for extending network lifetime in wireless sensor networks. Wirel Netw. 2016;22(8):2637–47. doi:10.1007/s11276-015-1061-6. [Google Scholar] [CrossRef]

9. Abba S, Lee JA. Bio-inspired self-aware fault-tolerant routing protocol for network-on-chip architectures using Particle Swarm Optimization. Microprocess Microsyst. 2017;51(6):18–38. doi:10.1016/j.micpro.2017.04.003. [Google Scholar] [CrossRef]

10. Al-Shalabi M, Anbar M, Wan TC, Alqattan Z. Energy efficient multi-hop path in wireless sensor networks using an enhanced genetic algorithm. Inf Sci. 2019;500(3):259–73. doi:10.1016/j.ins.2019.05.094. [Google Scholar] [CrossRef]

11. Wang C, Liu X, Hu H, Han Y, Yao M. Energy-efficient and load-balanced clustering routing protocol for wireless sensor networks using a chaotic genetic algorithm. IEEE Access. 2020;8:158082–96. doi:10.1109/ACCESS.2020.3020158. [Google Scholar] [CrossRef]

12. Wang Z, Ding H, Li B, Bao L, Yang Z. An energy efficient routing protocol based on improved artificial bee colony algorithm for wireless sensor networks. IEEE Access. 2020;8:133577–96. doi:10.1109/ACCESS.2020.3010313. [Google Scholar] [CrossRef]

13. Wang S. Multipath routing based on genetic algorithm in wireless sensor networks. Math Probl Eng. 2021;2021(2):4815711. doi:10.1155/2021/4815711. [Google Scholar] [CrossRef]

14. Zhang A, Sun M, Wang J, Li Z, Cheng Y, Wang C. Deep reinforcement learning-based multi-hop state-aware routing strategy for wireless sensor networks. Appl Sci. 2021;11(10):4436. doi:10.3390/app11104436. [Google Scholar] [CrossRef]

15. Ghawy MZ, Amran GA, AlSalman H, Ghaleb E, Khan J, AL-Bakhrani AA, et al. An effective wireless sensor network routing protocol based on particle swarm optimization algorithm. Wirel Commun Mob Comput. 2022;2022(17):8455065. doi:10.1155/2022/8455065. [Google Scholar] [CrossRef]

16. Hu J, He Y, Luo W, Huang J, Wang J. Enhancing load balancing with in-network recirculation to prevent packet reordering in lossless data centers. IEEE/ACM Trans Netw. 2024;32(5):4114–27. doi:10.1109/TNET.2024.3403671. [Google Scholar] [CrossRef]

17. Liu Z, Liu Y, Wang X. Intelligent routing algorithm for wireless sensor networks dynamically guided by distributed neural networks. Comput Commun. 2023;207(6):100–12. doi:10.1016/j.comcom.2023.05.018. [Google Scholar] [CrossRef]

18. Taheri A, RahimiZadeh K, Beheshti A, Baumbach J, Rao RV, Mirjalili S, et al. Partial reinforcement optimizer: an evolutionary optimization algorithm. Expert Syst Appl. 2024;238(3):122070. doi:10.1016/j.eswa.2023.122070. [Google Scholar] [CrossRef]

19. Guo C, Su M, Cui F. A route self-repair method for wireless sensor networks. In: Proceedings of the 2024 International Conference on Computer and Multimedia Technology; 2024 May 24–26; Sanming, China. p. 129–34. doi:10.1145/3675249.3675273. [Google Scholar] [CrossRef]

20. Han H, Tang J, Jing Z. Wireless sensor network routing optimization based on improved ant colony algorithm in the Internet of Things. Heliyon. 2024;10(1):e23577. doi:10.1016/j.heliyon.2023.e23577. [Google Scholar] [PubMed] [CrossRef]

21. Harinisree R, Nagaraj R. LQI-per-based range adaptation for enhanced communication range in wireless networks. J Namib Stud Hist Politics Cult. 2023;33:5127–46. [Google Scholar]

22. Lodwick AW, Elizabeth AAU. Fuzzy optimization. In: Granular, fuzzy, and soft computing. New York, NY, USA: Springer US; 2023. p. 755–91. [Google Scholar]

23. Alsini RA, Tawfeek MA. Power consumption and temperature minimization in cloud computing. IOSR J Eng. 2017;7(3):49–62. doi:10.9790/30210-0703014960. [Google Scholar] [CrossRef]

24. Lavacca FG, Salvo P, Costantini L, Mammi E, Pompei S, Rea L, et al. Studying and simulation of a NS3 framework towards a 5G complete network platform. In: 2019 International Workshop on Fiber Optics in Access Networks (FOAN); 2019 Sep 2–4; Sarajevo, Bosnia and Herzegovina. p. 62–7. doi:10.1109/foan.2019.8933704. [Google Scholar] [CrossRef]

25. NS-3 simulation, [cited 2022 May 1]. Available from: https://www.nsnam.org/releases/ns-3-40/. [Google Scholar]

26. Rahmati V. Near optimum random routing of uniformly load balanced nodes in wireless sensor networks using connectivity matrix. Wirel Pers Commun. 2021;116(4):2963–79. doi:10.1007/s11277-020-07829-7. [Google Scholar] [CrossRef]