Two-Hop Delay-Aware Energy Efficiency Resource Allocation in Space-Air-Ground Integrated Smart Grid Network

1  Introduction

The Internet of Things (IoT) and communication technologies are essential components in modern power grids, enhancing the intelligence and efficiency of electrical systems. IoT connects sensors, devices, and meters to communication networks, enabling real-time monitoring, analysis, and control of power networks, which can achieve local load fluctuation suppression, and provide ancillary services to maintain grid stability and efficiency [1]. Firstly, the local load fluctuations, arising from factors such as varying consumer demand, time-of-day effects, and weather conditions, can disrupt the grid’s stability and efficiency. Suppressing these fluctuations helps stabilize power flow, reduce system stress, and improve the overall reliability of the distribution system. Meanwhile, this suppression interacts with the distribution system by influencing power flow management, voltage stability, and load balancing. In this context, real-time monitoring and control systems, such as IoT devices play a key role in detecting and mitigating these fluctuations, ensuring that the grid can adapt dynamically to changing conditions. Secondly, IoT devices can provide ancillary services to maintain grid stability and efficiency. These services, including frequency regulation, voltage control, and reserve power, are necessary to support the grid during periods of fluctuation or abnormal conditions. Frequency regulation, for instance, ensures that any imbalances between electricity supply and demand are quickly corrected, thus preventing system overloads or frequency deviations that can lead to blackouts.

Communication technologies, particularly 5G and low power wide area networks (LPWAN), provide efficient, low-latency data transmission for IoT devices. In power networks, these technologies support functions such as remote control and fault diagnosis, improving system responsiveness and operational efficiency. With high-speed and reliable communication networks, power companies can access real-time data regarding equipment status, load changes, and environmental factors, allowing for more precise dispatch decisions. Additionally, the integration of IoT and communication technologies supports the intelligent upgrading of power networks, including demand response management, distributed energy integration, and electric vehicle charging management, thereby fostering the green transformation of energy. As smart grids advance, IoT and communication technologies will continue to be critical in optimizing power resource allocation, improving supply reliability, and supporting sustainable development [1]. However, the lack of communication infrastructure in remote areas presents significant challenges for smart power sensors (SPSs) in transmitting data to the grid control center. To address this issue, the space-air-ground integrated network has been proposed as a viable solution. In this framework, low Earth orbit (LEO) satellites function as intermediaries, collecting and transmitting data from ground-based SPSs [2]. Furthermore, unmanned aerial vehicles (UAVs) in the aerial network offer advantages such as high mobility, low cost, flexible deployment, and reliable line-of-sight communication. By integrating terrestrial, aerial, and satellite networks, the space-air-ground integrated network facilitates efficient data transmission and collection from SPSs in smart grid systems [3].

The mobility of UAVs introduces time-varying channel conditions, which result in a dynamic network topology and pose challenges in maintaining consistent data transmission delays [4,5]. To mitigate this issue, this paper incorporates a statistical delay analysis approach.

Statistical delay, defined by delay bounds and violation probabilities, is a crucial metric for real-time data transmission. Significant research has been conducted to explore its complexities in various systems. For example, an energy-efficient power allocation algorithm was developed to maximize energy efficiency under statistical delay constraints in multiple-input multiple-output (MIMO) networks [6]. Another study [7] focused on reliable transmission for industrial delay-sensitive applications over stochastic wireless channels, utilizing an automatic repeat request scheme within the Industrial Internet of Things (IIoT). In a system with intelligent reflecting surfaces (IRS) for energy harvesting, a joint algorithm for transmission power allocation and IRS phase-shift adjustment was proposed to optimize transmission rates while satisfying statistical delay constraints [8]. Furthermore, a joint resource allocation algorithm for multi-user secure cognitive radio networks was designed to minimize the β-fair cost function, while ensuring statistical delay requirements through a time-division multiple-access scheme [9]. Despite these advances, statistical delay has not been adequately addressed in the context of the space-air-ground integrated smart grid network. In this system, time-varying wireless channels and UAV mobility present substantial challenges in meeting data transmission delay requirements. Therefore, incorporating statistical delay considerations is critical for the effective operation of such networks.

This study aims to maximize data transmission energy efficiency within the space-air-ground integrated smart grid network while considering constraints related to effective capacity and fronthaul link capacity. Due to the non-convex nature of the formulated problem, the objective function is first reformulated. To tackle this challenge, a delay-aware energy efficiency power allocation and UAV trajectory design (DEPATD) algorithm is proposed. The DEPATD algorithm is structured as a two-loop framework to address the complexity of the non-convex inner loop problem. The inner loop problem is decomposed into three subproblems, each solved using a specific solution method. Simulation results validate the effectiveness of the DEPATD algorithm in enhancing energy efficiency. The main contributions of this study are as follows:

•   A data transmission energy efficiency maximization problem is formulated for the space-air-ground integrated smart grid network, incorporating effective capacity and fronthaul link capacity constraints.

•   The non-convex optimization problem is addressed by reformulating the fractional objective function and developing a two-loop iterative algorithm. The inner loop problem is tackled using the block coordinate descent (BCD) method, decomposing it into three subproblems, which are solved using the Lagrangian dual method and CVX optimization tool, offering a comprehensive solution to the challenge.

•   Simulation results demonstrate the accuracy and effectiveness of the proposed DEPATD algorithm in significantly enhancing data transmission energy efficiency.

The remainder of this paper is organized as follows. Section 2 reviews relevant literature. Section 3 presents the system model for the problem under consideration. In Section 4, the data transmission energy efficiency maximization problem is formulated, and the objective function is reformulated. Section 5 introduces the proposed DEPATD algorithm, utilizing the BCD method. Section 6 provides simulation results, and Section 7 concludes the paper.

2  Related Works

The space-air-ground integrated network has recently garnered significant attention. Improving system energy efficiency and reducing transmission delay are two key research areas within this domain.

In the space-air-ground integrated mobile edge computing network, a study in [10] explored the joint optimization of UAV 3D trajectories and resource allocation to enhance system energy efficiency. The authors developed an effective iterative algorithm based on the BCD method. To improve energy efficiency in space-air-ground networks for IoT applications, a study in [11] proposed a combined greedy base station sleeping strategy alongside a Lagrangian-dual-based power allocation algorithm. In [12], a comprehensive strategy was introduced to minimize energy consumption by jointly optimizing terminal power allocation, computation allocation, and task offloading in the space-air-ground network. This approach decomposed the problem into two subproblems and applied an iterative optimization method. Considering the terrestrial ground 5G is no longer able to fulfill the communication requirement of industrial power IoT, the NOMA-enabled space-air-ground integrated IoT network was proposed. A joint subchannel and terminal power algorithm was proposed to maximize the system’s energy efficiency [13].

To minimize task offloading delay in space-air-ground integrated networks, a novel deep risk-sensitive reinforcement learning algorithm was proposed in [14]. To reduce transmission delay in cognitive satellite-UAV networks, a multi-agent deep deterministic policy gradient-based algorithm with a centralized training framework was introduced in [15]. Considering the delay constraints of multimedia services, a joint caching and resource allocation strategy for multimedia services in space-air-ground integrated networks was formulated. Using convex optimization and two many-to-many swap matching algorithms, an alternating iteration optimization approach was proposed [16]. To achieve efficient resource management in the LEO multi-satellite beam hopping network, Guo et al. introduced a multi-dimensional resource collaborative allocation strategy aimed at minimizing total transmission delay [17]. Addressing the need for tasks to be processed either by satellite onboard systems or a remote cloud computing center, a freshness-aware task offloading and resource scheduling algorithm was proposed to minimize information freshness [18].

However, previous research does not address the time-varying wireless channels induced by UAV mobility, which may hinder meeting data transmission delay requirements. In such cases, it is essential to consider statistical delay within the space-air-ground integrated smart grid network. As a result, previous works should be revisited to tackle this challenge effectively.

3  System Model

We present the system model of the space-air-ground integrated smart grid network, encompassing both the network model and the transmission model.

3.1 Network Model

In this paper, we examine uplink data transmission within the space-air-ground integrated smart grid network, as shown in Fig. 1. The network consists of K SPSs, M UAVs, and one low LEO satellite. The SPSs collect and transmit information over a wireless channel to the UAVs, which then relay the data to the LEO satellite. We denote the sets of SPSs and UAVs as 𝒦={1,…,K} and ℳ={1,…,M}, respectively. UAV m is associated with a subset of km SPSs, which we denote as 𝒦m={1,…,Km}, where ∑m∈MKm=K. The total time period is denoted as T, divided into N time slots, each with duration τ. The set of time slots is denoted as 𝒩={1,…,n,…,N}. The heights of the UAVs and the LEO satellite are Huav and Hleo, respectively. The horizontal position of the SPS km is denoted as Pkm=(xkm,ykm), and the horizontal position of UAV m at time slot n is expressed as qm(n)=(xm(n),ym(n)) [3]. Let v represent the speed of the UAVs, and the distance each UAV can travel in one-time slot is vτ. Therefore, the trajectory of UAV m must satisfy the following condition.

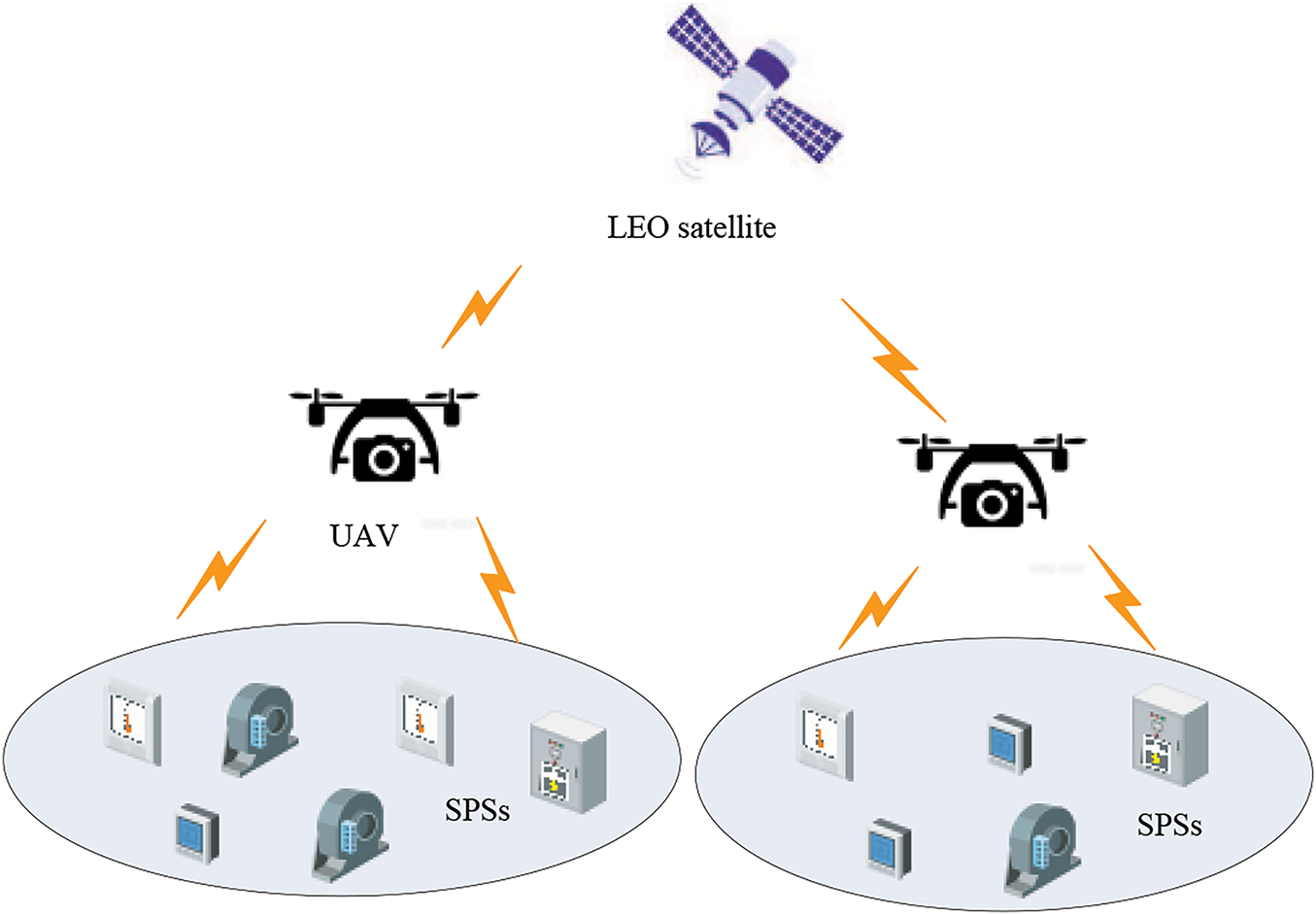
Figure 1: System model

‖qm(n+1)−qm(n)‖2≤(vτ)2(1)

To ensure that each UAV can serve the SPSs in subsequent time periods, the UAVs must return to their starting points. Therefore, the following constraint must be satisfied.

qm=qm[N](2)

Additionally, to maintain a safe distance between the UAVs, the following constraint must be satisfied.

‖qm(n)−qt(n)‖2≥dmin2,∀m,t∈ℳ,m≠t(3)

where dmin represents the minimum safe distance between any two UAVs.

3.2 Transmission Model

In this paper, the SPSs collect data and transmit it to the LEO satellite via the UAVs, thus the data transmission process is modeled as a two-hop transmission. The first hop consists of data transmission from the SPSs to the UAVs. Given that the wireless link between the SPSs and the UAVs is line-of-sight, the channel gain between SPS km and UAV m at time slot n is expressed as

hkm(n)=hH2+‖qm(n)−Pkm‖2(4)

where h represents the channel gain at a reference distance of 1 m.

In this system, the total bandwidth available to each UAV is Bm. Each UAV operates on a distinct spectrum, and its bandwidth is allocated orthogonally to the associated SPSs, ensuring there is no interference during the first hop. Let pkm(n) represent the transmission power of SPS km at time slot n. The corresponding transmission rate from SPS km to UAV m at time slot n can be expressed as

rkm(n)=bkmlog⁡(1+hkm(n)pkm(n))(5)

where bkm is the bandwidth allocated to the SPS km.

The time-varying nature of wireless channels presents significant challenges in meeting strict delay constraints for SPSs. As noted in the literature [19,20], effective capacity offers a practical solution to address statistical delay requirements. Effective capacity is defined as the maximum constant rate that a wireless channel can support while adhering to statistical delay constraints.

Let R(i),i=0,1,2,... represent the ergodic stochastic service process, and the effective capacity of this process is given by

EC(θ)=−1θlog⁡(E(e−θR(i)))(6)

where θ is a positive constant that governs the statistical delay constraints. It represents the steady-state delay violation probability and can be expressed as

Pr(D>Dmax)≈e−θμDmax(7)

where D denotes the delay of the SPSs, Dmax is their delay tolerance, and µ is a parameter influenced by the data arrival and service processes. Given a specified θ, the delay violation probability is determined by the QoS exponent. A smaller θ indicates a more relaxed delay requirement, whereas a larger θ represents a stricter delay constraint.

When θ is provided, the effective capacity of the SPSs can be expressed as

ECkm(θkm)=−1θkmlog⁡(E(e−θkmrkm(n)))(8)

The second hop involves data transmission from the UAVs to the LEO satellite. Given the considerable distance between the UAVs and the LEO satellite, variations in distance and angle between them can be considered negligible [13,14]. As a result, the channel gain between UAV m and the LEO satellite can be expressed as

huav=h(Hleo−Huav)2(9)

Let B represent the total bandwidth of the LEO satellite, which is allocated orthogonally to each UAV. This ensures that there is no interference during the second hop. Let pm(n) represent the transmission power of UAV m at time slot n. The corresponding transmission rate from UAV m to the LEO satellite at time slot n can be expressed as

rm(n)=bmlog⁡(1+huavpm(n))(10)

where bm is the bandwidth allocated to the UAV m.

4  Problem Formulation and Reformulation

Initially, we define a problem focused on optimizing the energy efficiency of data transmission from the SPSs to the LEO satellite, taking into account the limitations of effective capacity and fronthaul link capacity. Next, we adjust the objective function of the problem to simplify its resolution.

4.1 Problem Formulation

This paper aims to optimize the energy efficiency of data transmission from the SPSs to the LEO satellite, a goal that can be mathematically represented as shown in [21,22].

EE=R(pm,pkm,Q)P(pm,pkm)=∑m=1M∑km=1Km∑n=1N(rkm(n)+rm(n))∑m=1M∑km=1Km∑n=1N(pkm(n)+pm(n))(11)

where pm={pm(n),∀m∈ℳ}, pkm={pkm(n),∀km∈𝒦m}, Q={qkm(n),∀km∈𝒦m}.

Taking into account the effective capacity of the SPSs, the problem of power allocation for delay-aware energy efficiency can be expressed as follows:

(P1)maxpm,pkm,QEE(12a)

s.t.ECkm(θkm)≥ECkmmin(12b)

0≤pkm(n)≤Pkmmax(12c)

∑km=1Kmrkm(n)≤Cmmax(12d)

0≤pm(n)≤Pmmax(12e)

∑m=1Mrm(n)≤Cleomax(12f)

s.t.(1),(2),(3)(12g)

where Pkmmax and Pmmax represent the maximal transmission power of SPS km and UAV m, respectively, and ECkmmin denotes the minimal effective capacity of SPS km. Cmmax and Cleomax represent the maximal fronthaul link capacity of UAV m and the LEO satellite, respectively. Constraint (12b) represents the effective capacity constraint for the SPSs, while constraint (12c) imposes the transmission power constraint for the SPSs. Constraint (12d) limits the fronthaul link capacity of the UAV, and constraint (12e) restricts the transmission power of the UAV. Finally, constraint (12f) defines the fronthaul link capacity constraint for the LEO satellite. In problem (P1), the objective function is fractional, and the optimization variables are interdependent. Consequently, problem (P1) is non-convex, presenting challenges for direct resolution through traditional convex optimization techniques.

4.2 Problem Reformulation

Given the nonlinear fractional programming nature of the objective function in problem (P1), the main objective is to reformulate this function.

We denote a nonnegative variable γ∗, which represents the optimal value of energy efficiency, where γ∗=R∗(pm∗,pkm∗,Q∗)P∗(pm∗,pkm∗), P∗(pm∗,pkm∗) is the optimal power allocation, and R∗(pm∗,pkm∗,Q∗) is the corresponding data transmission rate.

Proposition 1: We can obtain γ∗ if and only if

maxpm,pkm,QR(pm,pkm,Q)−γ∗P(pm,pkm)=R∗(pm∗,pkm∗),Q∗)−γ∗P∗(pm∗,pkm∗)=0(13)

Proof: The proof of Proposition 1 is presented in Appendix A.

Building upon Proposition 1, problem (P1) can be reformulated as shown below:

(P2)maxpm,pkm,QR(pm,pkm,Q)−γ∗P(pm,pkm)(14a)

s.t. (12b),(12c),(12d),(12e),(12f),(1),(2),(3)(14b)

Proposition 1 demonstrates the conversion of the objective function from a fractional form into a subtractive form. To solve problem (P2), we can use the following proposition to define an equivalent function as follows: G(γ)=maxpm,pkm,QR(pm,pkm,Q)−γP(pm,pkm)

Proposition 2: For all feasible P(pm,pkm), R(pm,pkm,Q), and γ, G(γ)≥0, and G(γ) is monotonic decreasing with γ.

Proof: The proof of Proposition 2 is presented in Appendix B.

5  The Proposed Delay-Aware Energy Efficiency Power Allocation and UAV Trajectory Design Algorithm

In this section, we introduce the DEPATD algorithm to tackle the energy efficiency maximization problem. The DEPATD algorithm is designed as a two-loop process. Within the inner loop, the problem is decomposed into three subproblems using the BCD method. By solving these subproblems sequentially, the inner loop problem is efficiently addressed.

5.1 Problem Reformulation

Building on Propositions 1 and 2 from the previous section, we propose the DEPATD algorithm to iteratively update γ and obtain γ∗as follows.

The proposed Algorithm 1 employs two iterative loops to maximize energy efficiency. In the outer loop, γ(i+1) is updated in each iteration using P(i)(pm(i),pkm(i)) and R(i)(pm(i),pkm(i),Q(i)) obtained from the previous iteration. In the inner loop, the optimal power allocation P(i)(pm(i),pkm(i)) and the corresponding data transmission rate R(i)(pm(i),pkm(i),Q(i)), given a fixed γ(i), are determined by solving the following inner loop problem.

(P3)maxpm,pkm,QR(pm,pkm,Q)−γ(i)P(pm,pkm)(15a)

s.t.(12b),(12c),(12d),(12e),(12f),(1),(2),(3)(15b)

where γ(i) is the value of energy efficiency in the i-th iteration.

Proposition 3: The proposed DAEEPA algorithm converges to the global optimal solution of problem (P3).

Proof: The proof of Proposition 3 is presented in Appendix C.

For problem (P3), although the objective function is not fractional, the optimization variables are coupled, making it a non-convex problem. This complexity presents challenges in obtaining an optimal solution.

5.2 SPSs Power Allocation Subproblem

Problem (P3) is non-convex, and we can utilize the fundamental principle of BCD to solve it. With the given power allocation of the UAVs pm and their trajectory Q, the problem is formulated as follows:

(P4)maxpkmR(pkm)−γ(i)P(pkm)(16a)

s.t. (12b),(12c),(12d)(16b)

As problem (P4) is convex, we can use the Lagrangian dual method to solve it. In accordance with [23], the Lagrangian function is expressed as follows:

ℒ({pkm(n)},{λkm},{μ(n)},{νkm(n)})

=∑m=1M∑km=1K∑n=1Nrkm(n)−γ(i)(∑m=1M∑km=1K∑n=1Npkm(n))−∑m=1M∑km=1Kλkm(ECkm(θkm)−ECkmmin)(17)

−∑m=1M∑n=1Nμ(n)(∑km=1Krkm(n)−Cmmax)−∑m=1M∑km=1K∑n=1Nνkm(n)(pkm(n)−Pkmmax)

where λkm, μ(n), and νkm(n) are the Lagrangian multipliers.

To maximize the Lagrangian function, we aim to maximize the power allocation pointwise. By applying the Lagrangian dual method, we differentiate with respect to pkm and set the derivative equal to zero. This yields the following result:

∂ℒ({pkm(n)},{λkm},{μ(n)},{νkm(n)})∂pkm(n)=0(18)

By solving Eq. (18), we can determine the optimal power allocation pkm(n).

The Lagrangian multipliers in Eq. (18) can be updated using the method described in [24,25].

λkml+1=[λkml+ξλ(E[e−θkmrkml(n)]−e−θkmECkmmin)]+(19)

μl+1(n)=[μl(n)+ξμ(∑km=1Kmrkml(n)−Cmmax)]+(20)

νkml+1(n)=[νkml(n)+ξν(pkml(n)−Pkmmax)]+(21)

where ξλ, ξμ, and ξν are the positive step size, and l is the iteration index.

For Eq. (19), we need to compute the expectation. However, obtaining the expected value in an actual communication system is challenging. To address this issue, we rewrite Eq. (19) following the approach in [26].

λkml+1=[λkml+ξλl(e−θkmrkml(n)−e−θkmECkmmin)]+(22)

where ξλl is a positive scalar, which satisfies the following condition:

∑l=1∞ξλl=∞,∑l=1∞(ξλl)2<∞(23)

5.3 UAVs Power Allocation Subproblem

Given the power allocation of the SPSs pkm and the UAV trajectory Q, the problem is formulated as follows:

(P5)maxpmR(pm)−γ(i)P(pm)(24a)

s.t. (12e),(12f)(24b)

Since problem (P5) is convex, the Lagrangian dual method can be applied to its solution. As outlined in [23], the Lagrangian function is expressed as follows:

ℒ({pm(n)},{μ(n)},{νm(n)})=∑m=1M∑n=1Nrm(n)−γ(i)(∑m=1M∑n=1Npm(n))−∑n=1Nμ(n)(∑m=1Krm(n)−Cleomax)−∑m=1M∑n=1Nνm(n)(pm(n)−Pmmax)(25)

where μ(n), and νm(n) are the Lagrangian multipliers.

To maximize the Lagrangian function, we concentrate on maximizing the power allocation pointwise. By applying the Lagrangian dual method, we differentiate ℒ({pm(n)},{μ(n)},{νm(n)}) with respect to pm(n) and set the result equal to zero. This leads to the following:

∂ℒ({pm(n)},{μ(n)},{νm(n)})∂pm(n)=0(26)

The optimal power allocation pm(n) can be obtained by solving Eq. (26).

The Lagrangian multipliers in Eq. (26) can be updated using the following method.

μl+1(n)=[μl(n)+ξμ(∑m=1Mrml(n)−Cleomax)]+(27)

νml+1(n)=[νml(n)+ξν(pml(n)−Pmmax)]+(28)

where ξμ, and ξν are the positive step size, and l is the iteration index. For the expectation in Eq. (22), we can apply the same method as in the previous subsection to solve it.

5.4 UAVs Trajectory Design Subproblem

Given the power allocation of the SPSs pkm and the power allocation of the UAVs pm, the problem is formulated as follows:

(P6)maxQR(Q)(29a)

s.t. (12b),(12d),(1),(2),(3)(29b)

Problem (P6) is non-convex with respect to Q, but it can be noted that rkm(n) is convex in relation to ‖qm(n)−Pkm‖2. Since a convex function possesses a globally lower bound defined by its first-order Taylor expansion at a given point, the SCA method can be utilized to solve this problem [27]. We define Dkml(n)=‖qml(n)−Pkm‖ as the distance between the SPS km and UAV m at time slot n in the l-th iteration. When qkml(n) is fixed, the lower bound of rkm(n) can be obtained as follows:

r~km(n)=rkml(n)+∇rkml(n)(‖qm(n)−Pkm‖−Dkml(n)),(30)

where rkml(n) is the transmission rate between the SPS km and UAV m at time slot n of l-th iteration. ∇rkml(n) is the first-order derivative of rkml(n).

For constraint (3), given that ‖qm(n)−qt(n)‖2 is convex in relation to the UAV trajectory, the SCA method can be employed to relax this constraint. By applying the first-order Taylor expansion at the specified points and qtl(n), constraint (3) can be approximated as follows:

‖qm(n)−qt(n)‖2≥−‖qml(n)−qtl(n)‖2+2(qml(n)−qtl(n))T(qm(n)−qt(n)).(31)

Based on the above analysis, problem (P6) can be reformulated as follows:

(P7)maxQ∑m=1M∑km=1Km∑n=1Nr~km(n)(32a)

s.t. (1),(2),(32b)

−‖qml(n)−qtl(n)‖2+2(qml(n)−qtl(n))T(qm(n)−qt(n))≥dmin,(32c)

−1θmlog⁡(E(e−θmr~km(n)))≥ECkmmin,(32d)

∑km=1Kmr~km(n)≤Cmmax.(32e)

Since problem (P7) is convex, we can apply the Lagrangian dual method, as discussed in the previous two subsections, to solve it.

5.5 Inner Loop Problem Solution Algorithm

By setting the initial system parameters, we present Algorithm 2 to solve the inner loop problem.

5.6 Complexity of Proposed DEPATD Algorithm

The proposed DEPATD algorithm follows a two-loop structure. In the inner loop, both problems (P4) and (P5) are convex. By employing the interior point method, the complexities of problems (P4) and (P5) are 𝒪(K3.5M3.5) and 𝒪(M3.5), respectively [23]. For problem (P6), the SCA method is applied to convert it into a convex problem, with a complexity of 𝒪(K3.5M3.5). As a result, the overall complexity of the inner loop is 𝒪(K3.5M3.5). In the outer loop, the algorithm’s complexity is mainly influenced by the maximum number of iterations. Therefore, the total complexity of the proposed DEPATD algorithm is 𝒪(K3.5M3.5).

6  Simulation Results

We demonstrate the effectiveness of the proposed DEPATD algorithm through numerical simulations. There are 1 LEO satellite, 3 UAVs, and 5 SPSs in the coverage area of each UAV. The total bandwidth allocated to SPS in each UAV coverage area is 3 MHz, and the total bandwidth allocated to each UAV is 6 MHz. The bandwidth is allocated to each UAV and SPS on average. The maximal transmission power of SPSs and UAVs are 0.1 and 1 W, respectively. The QoS exponent θ of SPSs is 0.01. The maximal fronthaul link capacity of each UAV and LEO satellite are 5, and 20 Mbps, respectively.

To evaluate the performance of the proposed DEPATD algorithm, we compare it with the following three benchmark algorithms:

•   Average Power Allocation (APA) Algorithm: In this algorithm, both the power allocation of SPSs and UAVs follows an average power allocation scheme, while the UAV trajectory design scheme remains consistent with that used in this paper.

•   Water Filling Power Allocation (WFPA) Algorithm: In this algorithm, the power allocation of SPSs and UAVs follows a water-filling power allocation scheme, and the UAV trajectory design scheme is the same as in this paper.

•   Improved Traveling Salesman Problem (ITSP) Algorithm: In this algorithm, the power allocation of SPSs and UAVs is identical to that in this paper, but the UAV trajectory design utilizes the ITSP method outlined in [28].

Fig. 2 illustrates the energy efficiency performance as a function of the QoS exponent for four different algorithms. It is observed that as the QoS exponent increases, the energy efficiency also improves for all four algorithms. This is because higher QoS exponents correspond to more stringent delay requirements, which typically demand a more efficient use of energy to satisfy these constraints. Among the algorithms, the proposed DEPATD algorithm exhibits superior performance in terms of energy efficiency, particularly at higher QoS exponents. The ITSP and WFPA algorithms show moderate improvements, while the APA algorithm consistently demonstrates the lowest energy efficiency across the entire range of QoS exponents.

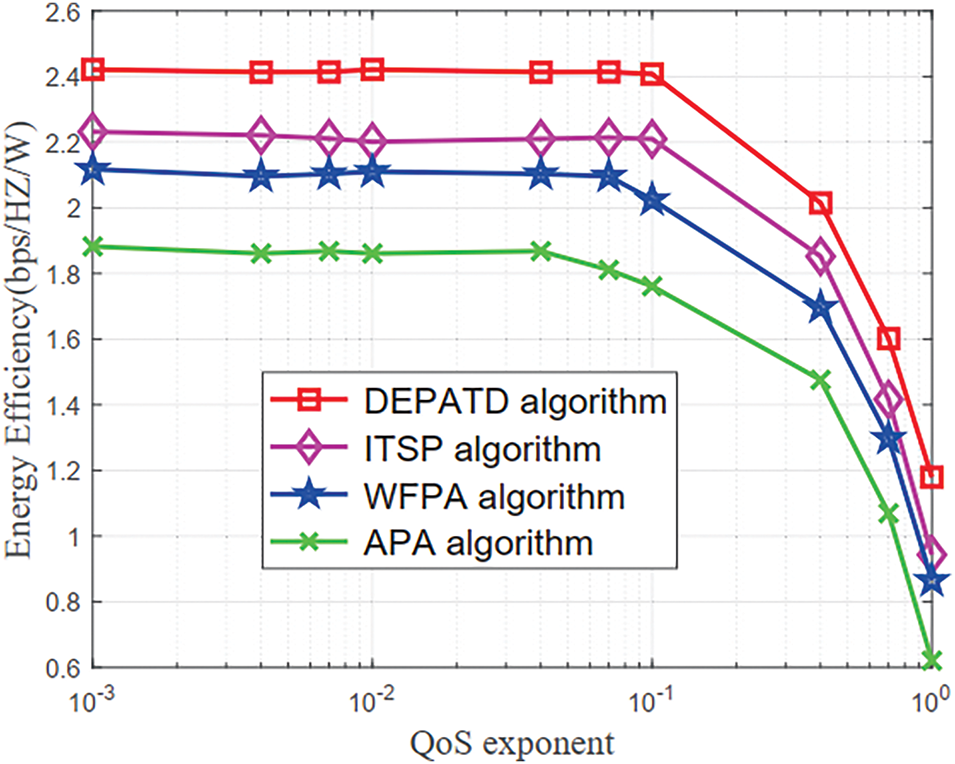
Figure 2: Energy efficiency vs. QoS exponent θ under different algorithms

Moreover, the results indicate that the proposed DEPATD algorithm achieves the highest energy efficiency, closely followed by the ITSP algorithm. Compared to the ITSP algorithm, the energy efficiency of the DEPATD algorithm increases by approximately 11.05% as θ increases from 10−3 to 100. The WFPA algorithm performs moderately well but does not reach the efficiency levels of either the DEPATD or ITSP algorithms. In contrast, the APA algorithm shows consistently lower energy efficiency, suggesting it may not be the optimal choice for applications requiring high energy efficiency under varying QoS requirements.

Fig. 3 shows the energy efficiency performance as a function of the maximum transmission power of the SPSs for four different algorithms. It is evident that energy efficiency increases with the maximum transmission power, though the rate of improvement gradually diminishes. Initially, an increase in transmission power leads to a significant boost in channel capacity, but as the power continues to rise, the incremental gain in capacity becomes smaller. Among all the algorithms, the proposed DEPATD algorithm consistently achieves the highest energy efficiency across all levels of transmission power. Specifically, when the maximum transmission power of the SPSs rises from 0.1 to 0.45 W, the DEPATD algorithm enhances energy efficiency by 10% compared to the ITSP algorithm, demonstrating its effectiveness in optimizing energy efficiency.

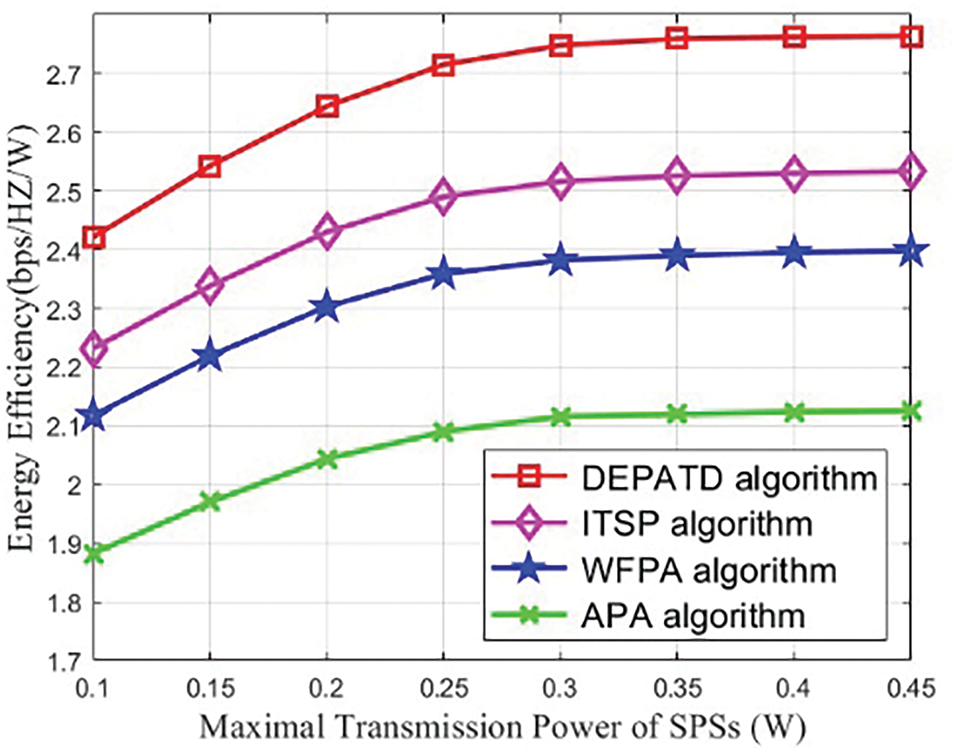
Figure 3: Energy efficiency against the maximal transmission power of SPSs under different algorithms

Fig. 4 presents the energy efficiency performance as a function of the maximum transmission power of the UAVs for four different algorithms. As observed in Fig. 3, energy efficiency increases with the UAVs’ maximum transmission power, though the rate of increase gradually diminishes. This trend can be attributed to the same reasoning as in Fig. 3. Additionally, the proposed DEPATD algorithm outperforms the benchmark algorithms. Specifically, at a maximum transmission power of 2 W, the DEPATD algorithm achieves an energy efficiency of approximately 3.1 bps/Hz/W, while the ITSP algorithm reaches around 2.9 bps/Hz/W. In comparison, the WFPA and APA algorithms exhibit lower energy efficiencies, with the WFPA algorithm yielding about 2.5 bps/Hz/W and the APA algorithm approximately 2.3 bps/Hz/W at the same transmission power.

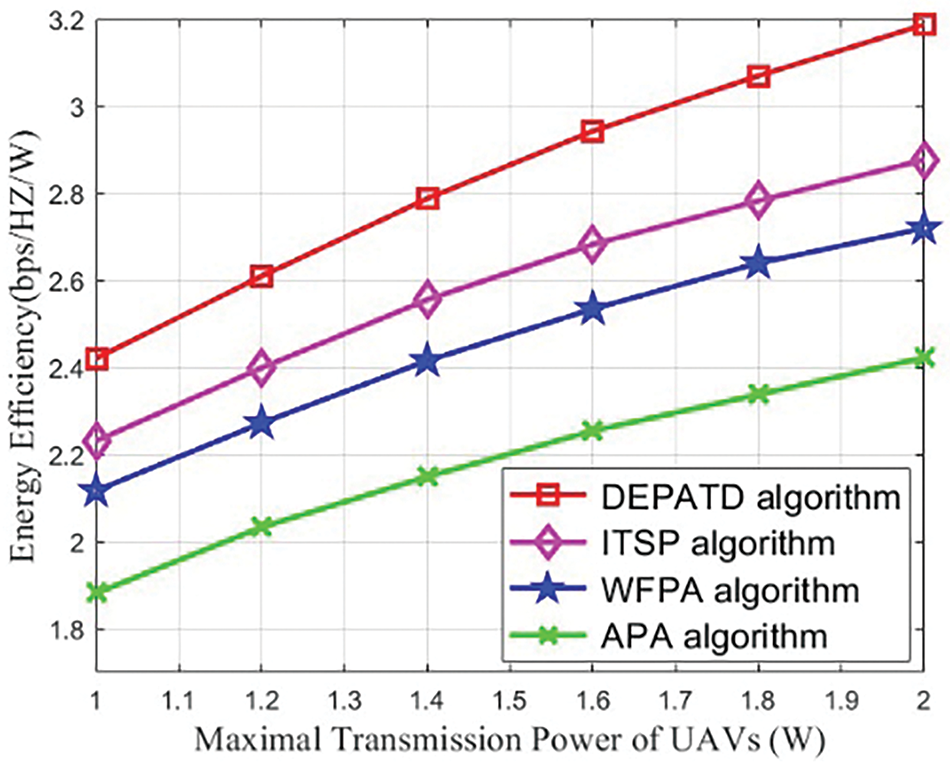
Figure 4: Energy efficiency against the maximal transmission power of UAVs under different algorithms

Fig. 5 illustrates the total energy efficiency as a function of the number of SPSs for four different algorithms. It is evident that total energy efficiency declines as the number of SPSs increases. This occurs because, as the number of SPSs rises, the competition for limited resources intensifies, resulting in a reduction in energy efficiency for each individual SPS. Specifically, as the number of SPSs grows, the energy efficiency of all four algorithms shows a downward trend. However, the proposed DEPATD algorithm consistently outperforms the other algorithms in terms of energy efficiency across all SPS configurations. When the number of SPSs increases from 3 to 7, the DEPATD algorithm improves energy efficiency by 9.52%, 15.25%, and 30.08% compared to the ITSP, WFPA, and APA algorithms, respectively.

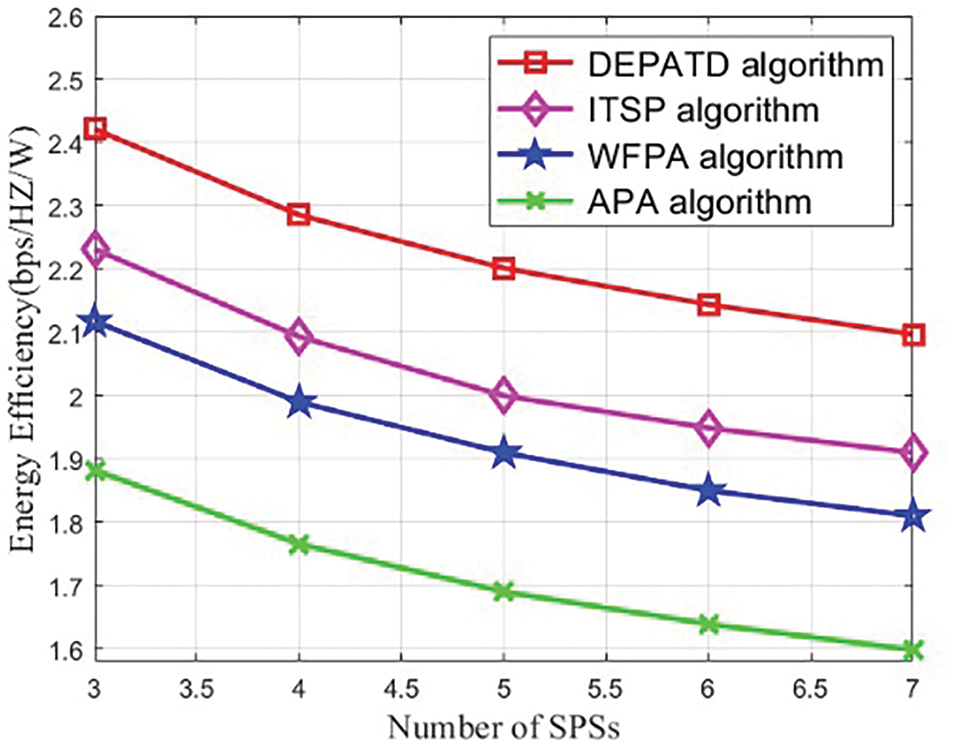
Figure 5: Energy efficiency against the number of SPSs under different algorithms

Fig. 6 illustrates the total energy efficiency as a function of the number of UAVs for four different algorithms. From this figure, it is evident that as the number of UAVs increases, the total energy efficiency tends to decrease. This is attributed to the fact that with more UAVs, the resources allocated to each individual UAV decrease. Additionally, the figure shows a general decline in the total energy efficiency of all four algorithms as the number of UAVs rises. Among these, the performance of the proposed DEPATD algorithm outperforms the other algorithms, demonstrating superior energy efficiency.

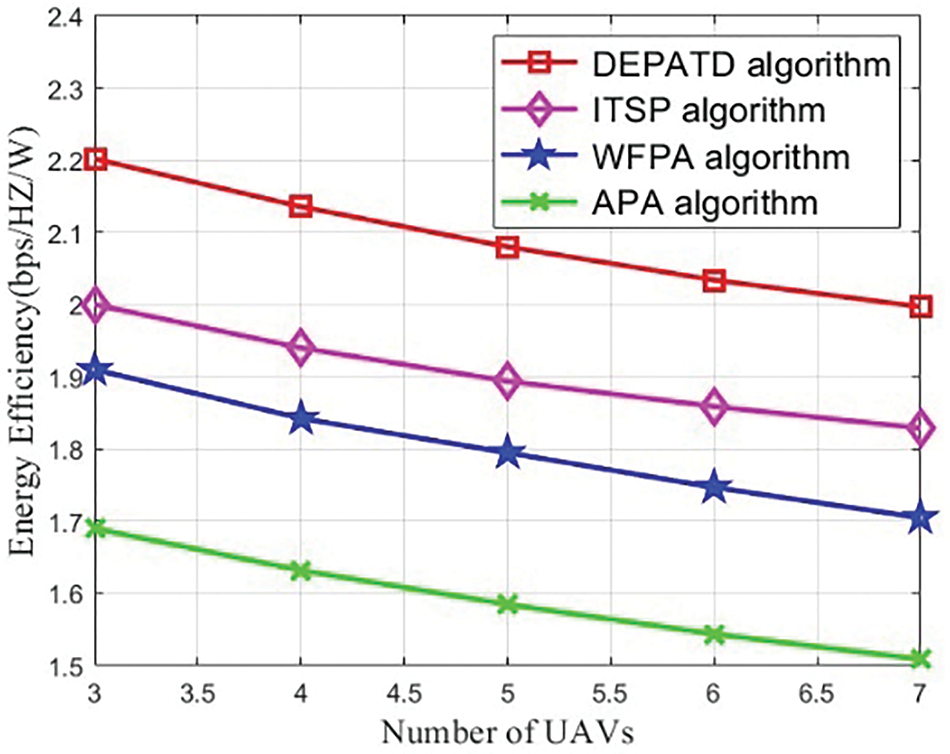
Figure 6: Energy efficiency against the number of UAVs under different algorithms

Fig. 7 shows the UAV trajectory as a function of the time period. The figure clearly illustrates that the UAV trajectory follows a pattern corresponding to the UAVs’ movement within a 200 m × 200 m area. When the time period T is small (T = 10 s), the UAV trajectory forms a relatively small loop, which may not effectively cover all the SPSs. As T increases to 15 s, the UAVs’ trajectories extend further, covering a larger portion of the area and approaching the SPSs more closely. This is because a longer time period provides the UAVs with more flight time, allowing them to optimize their paths and improve coverage and data collection from the SPSs. From Fig. 6, it is evident that increasing the time period enhances the UAVs’ ability to approach and collect data from the SPSs more efficiently.

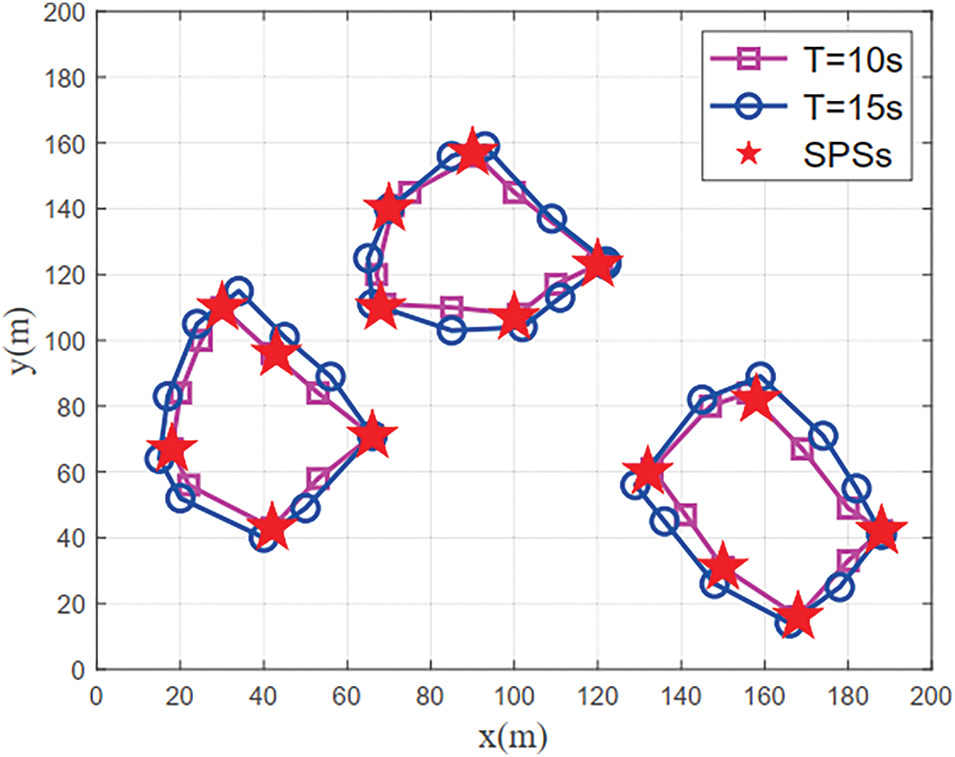
Figure 7: UAV trajectory vs. the time period

7  Conclusion

In this paper, we tackled the problem of maximizing data transmission energy efficiency while considering constraints on effective capacity and fronthaul link capacity in a space-air-ground integrated smart grid network. Due to the non-convex nature of the problem, we first reformulated the objective function and then introduced the DEPATD algorithm, a two-loop approach. Given the non-convexity of the inner loop problem, we decomposed it into three subproblems. By applying the Lagrangian dual method and the SCA method, we successfully solved these subproblems. Using the solutions obtained, the inner loop problem was effectively resolved. Simulation results validated the effectiveness of the proposed DEPATD algorithm.

In this paper, we considered two-hop uplink data transmission to maximize the energy efficiency of the system. In future work, we can investigate the next two aspects. Firstly, when the software or system of the SPSs devices needs to be updated, the downlink transmission of data needs to be considered. Second, in this paper, the traditional method of convex optimization is used for solving the problem. The method of deep reinforcement learning has more versatility and adaptability than the convex optimization algorithm, especially in dealing with complex, high-dimensional, dynamically changing non-convex problems with significant advantages. Therefore, deep reinforcement learning methods can be used for problem-solving in future work.

Acknowledgement: The authors thank the editor and reviewers for handling the manuscript.

Funding Statement: This work is Supported by the Self-funded Research Project of Beijing FibrLink Communications Co. Ltd. “Research on Key Technologies for Unified Management of Air-to-Earth Integrated Communication Networks (546826230034).”

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Qinghai Ou; data collection: Min Yang; analysis and interpretation of results: Jingcai Kong and Yang Yang; draft manuscript preparation: Qinghai Ou. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Appendix A

Proof of Proposition 1: To prove Lemma 1, we present the proofs for both the sufficient and necessary conditions, respectively.

For the proof of the sufficient condition, let the optimal value of energy efficiency be denoted as γ∗=R∗(pm∗,pkm∗,Q∗)P∗(pm∗,pkm∗), with P∗(pm∗,pkm∗)representing the optimal power allocation and R∗(pm∗,pkm∗,Q∗) the corresponding data transmission rate. Clearly, the following holds

γ∗=R∗(pm∗,pkm∗,Q∗)P∗(pm∗,pkm∗)≥R(pm,pkm,Q)P(pm,pkm)(A1)

where P(pm,pkm) denotes a feasible power allocation and R(pm,pkm,Q) represents the corresponding data transmission rate. Based on Eq. (A1), we obtain

R(pm,pkm,Q)−γ∗P(pm,pkm)≤0(A2)

R∗(pm∗,pkm∗,Q∗)−γ∗P∗(pm∗,pkm∗)=0(A3)

From the above equations, it follows that if the optimal power allocation P∗(pm∗,pkm∗) is obtained, then R(pm,pkm,Q)−γ∗P(pm,pkm)=0 is achieved. Therefore, the sufficient condition is proven.

For the proof of the necessary condition, suppose that P^∗(P^m∗,P^km∗) and R^(P^m∗,P^km∗,Q^∗) represent the optimal power allocation and corresponding data transmission rate, respectively. We have R^(P^m∗,P^km∗,Q^∗)−γ∗P^∗(P^m∗,P^km∗)=0 satisfying the conditions. For any feasible power allocation P(pm,pkm) and corresponding data transmission rate R(pm,pkm,Q), we can derive

R(pm,pkm,Q)−γ∗P(pm,pkm)≤R^(P^m∗,P^km∗,Q^∗)−γ∗P^∗(P^m∗,P^km∗)=0,(A4)

The above equation can be expressed as

R(pm,pkm,Q)P(pm,pkm)≤γ∗(A5)

R^(P^m∗,P^km∗,Q^∗)P^∗(P^m∗,P^km∗)=γ∗(A6)

□

Appendix B

Proof of Proposition 2: We define G(γ)=maxP(pm,pkm)R(pm,pkm,Q)−γP(pm,pkm)=0, and γ1, γ2 are the corresponding optimal energy efficiency value for (R1(pm1,pkm1,Q1),P1(pm1,pkm1)) and (R2(pm2,pkm2,Q2),P2(pm2,pkm2)), respectively. Meanwhile, γ1>γ2. We have

G(γ2)=R2(pm2,pkm2,Q2)−γ2P2(pm2,pkm2)>R1(pm1,pkm1,Q1)−γ2P1(pm1,pkm1)>R1(pm1,pkm1,Q1)−γ1P1(pm1,pkm1)=G(γ1)(A7)

Therefore, G(γ) is a monotonic decreasing function with γ.

We denote P′(pm′,pkm′) as the feasible power allocation and R′(pm′,pkm′,Q′) as the corresponding data transmission rate. We set γ′=R′(pm′,pkm′,Q′)P′(pm′,pkm′).

G(γ′)=maxP(pm,pkm)R(pm,pkm,Q)−γ′P(pm,pkm)≥R′(pm′,pkm′,Q′)−γ′P′(pm′,pkm′)=0(A8)

Therefore, we have G(γ)≥0.

□

Appendix C

Proof of Proposition 3: We denote γ(i) and γ(i+1) as the energy efficiencies in the ith and i + 1th iterations of the outer loop, respectively. Note that γ(i) and γ(i+1) are not the optimal energy efficiencies γ∗. The value of γ(i+1) can be obtained by γ(i+1)=R(i+1)(pm(i+1),pkm(i+1),Q(i+1))P(i+1)(pm(i+1),pkm(i+1)). Since γ∗ represents the optimal energy efficiency, it follows that γ(i+1) cannot exceed γ∗. We have already established that G(γ)≥0 when γ is not the optimal value, it cannot achieve the optimal energy efficiency.

G(γ(i))=R(i)(pm(i),pkm(i),Q(i))P(i)(pm(i),pkm(i))=P(i)(pm(i),pkm(i))(γ(i+1)−γ(i))>0(A9)

Considering P(i)(pm(i),pkm(i))>0, we can obtainγ(i+1)>γ(i). This implies that γ increases with each iteration of the outer loop in Algorithm 1. According to Proposition 2, we can deduce that the value of G(γ) decreases as the number of iterations increases.

Furthermore, Proposition 2 establishes that the optimal solution is G(γ∗)=0. Algorithm 1 ensures a monotonically increasing γ. When γ reaches its maximum value γ∗, problem (P2) can be solved with γ∗, yielding G(γ∗)=0 and providing the optimal power allocation P(∗)(pm(∗),pkm(∗)) and the corresponding data transmission rate R(∗)(pm(∗),pkm(∗),Q(∗)). It can be shown that G(γ) converges to zero as the number of iterations increases sufficiently, leading to the attainment of the optimal solution, as established in Proposition 1. Therefore, Proposition 3 is proven.

□

References

1. Kumar P, Lin Y, Bai G, Paverd A, Dong JS, Martin A. Smart grid metering networks: a survey on security, privacy and open research issues. IEEE Commun Surv Tutor. 2019;21(3):2886–927. doi:10.1109/COMST.2019.2899354. [Google Scholar] [CrossRef]

2. Qin X, Ma T, Zhang X, Wang Y, Zhou H, Zhao L. Ultra-dense LEO-MEO constellation integrated 6G: a distributed hierarchical mobility management approach. IEEE Trans Wirel Commun. 2025;24(1):323–39. doi:10.1109/TWC.2024.3491794. [Google Scholar] [CrossRef]

3. Li S, Yu Z, Dong M, Ota K, Chen H, Zhang N, et al. Two-hop packet scheduling, resource allocation, and UAV trajectory design for Internet of remote things in air-ground integrated network. IEEE Internet Things J. 2024;11(15):26160–72. doi:10.1109/JIOT.2024.3393444. [Google Scholar] [CrossRef]

4. Mary Anthony S, Pradeep Kumar TS. Three-dimensional mobility management of unmanned aerial vehicles in flying ad-hoc networks. IEEE Access. 2024;12:190102–19. doi:10.1109/ACCESS.2024.3515799. [Google Scholar] [CrossRef]

5. Li S, Lin S, Cai L, Li W, Zhu G. Joint resource allocation and computation offloading with time-varying fading channel in vehicular edge computing. IEEE Trans Veh Technol. 2020;69(3):3384–98. doi:10.1109/TVT.2020.2967882. [Google Scholar] [CrossRef]

6. Kwon JH, Ko YC, Shin J. Energy efficient power allocation for multi-user MIMO downlink systems with statistical delay constraints. In: IEEE Conference on Standards for Communications and Networking (CSCN); 2019 Oct 28–30; GRANADA, Spain: IEEE; 2019. p. 1–6. doi:10.1109/cscn.2019.8931355. [Google Scholar] [CrossRef]

7. Hong X, Wang X, Gao Y, He J, Yang H. Statistical delay guarantee of wireless channel with automatic repeat request in industrial IoT. IEEE Commun Lett. 2023;27(9):2511–5. doi:10.1109/LCOMM.2023.3293168. [Google Scholar] [CrossRef]

8. Ahmed I, Yan S, Rawat DB, Pu C. Dynamic resource allocation for IRS assisted energy harvesting systems with statistical delay constraint. IEEE Trans Veh Technol. 2022;71(2):2158–63. doi:10.1109/TVT.2021.3133825. [Google Scholar] [CrossRef]

9. Bai Z, Ma L, Dong Y, Ma P, Ma Y. Energy-efficient resource allocation for secure cognitive radio network with delay QoS guarantee. IEEE Syst J. 2019;13(3):2795–805. doi:10.1109/JSYST.2018.2875835. [Google Scholar] [CrossRef]

10. Hu Z, Zeng F, Xiao Z, Fu B, Jiang H, Xiong H, et al. Joint resources allocation and 3D trajectory optimization for UAV-enabled space-air-ground integrated networks. IEEE Trans Veh Technol. 2023;72(11):14214–29. doi:10.1109/TVT.2023.3280482. [Google Scholar] [CrossRef]

11. Yu P, Li Y, Zhang M, Xiong A, Li W, Qiu X, et al. Self-organized and distributed green resource allocation for space-air–ground IoT networks. IEEE Internet Things J. 2023;10(11):9385–97. doi:10.1109/JIOT.2022.3222238. [Google Scholar] [CrossRef]

12. Qin P, Wang S, Lu Z, Xie Y, Zhao X. Deep reinforcement learning-based energy minimization task offloading and resource allocation for air ground integrated heterogeneous networks. IEEE Syst J. 2023;17(3):4958–68. doi:10.1109/JSYST.2023.3266769. [Google Scholar] [CrossRef]

13. Qin P, Zhao H, Fu Y, Geng S, Chen Z, Zhou H, et al. Energy-efficient resource allocation for space-air–ground integrated industrial power Internet of Things network. IEEE Trans Ind Inform. 2024;20(4):5274–84. doi:10.1109/TII.2023.3331127. [Google Scholar] [CrossRef]

14. Zhou C, Wu W, He H, Yang P, Lyu F, Cheng N, et al. Deep reinforcement learning for delay-oriented IoT task scheduling in SAGIN. IEEE Trans Wirel Commun. 2021;20(2):911–25. doi:10.1109/TWC.2020.3029143. [Google Scholar] [CrossRef]

15. Guo S, Zhao X. Multi-agent deep reinforcement learning based transmission latency minimization for delay-sensitive cognitive satellite-UAV networks. IEEE Trans Commun. 2023;71(1):131–44. doi:10.1109/TCOMM.2022.3222460. [Google Scholar] [CrossRef]

16. Yin F, Liu Q, Liu D, Zhang Y, Jin L, Li S. Joint coded caching and resource allocation for multimedia service in space-air-ground integrated networks. IEEE Trans Commun. 2024;72(11):6839–53. doi:10.1109/TCOMM.2024.3405308. [Google Scholar] [CrossRef]

17. Guo Q, Cui G, He M, Wang W. Multi-dimensional resource allocation strategy for LEO multi-satellite beam hopping systems. In: 2023 9th International Conference on Computer and Communications (ICCC); 2023 Dec 8–11; Chengdu, China: IEEE; 2023. p. 301–5. doi:10.1109/ICCC59590.2023.10507281. [Google Scholar] [CrossRef]

18. Cai H, Yang X, Wu H, Bu Z. Freshness-aware task offloading and resource scheduling for satellite edge computing. In: 2024 IEEE Wireless Communications and Networking Conference (WCNC); 2024 Apr 21–24; Dubai, United Arab Emirates: IEEE; 2024. p. 1–6. doi:10.1109/WCNC57260.2024.10570547. [Google Scholar] [CrossRef]

19. Moosavi N, Sinaie M, Azmi P, Huusko J. Delay aware resource allocation with radio remote head cooperation in user-centric C-RAN. IEEE Commun Lett. 2021;25(7):2343–7. doi:10.1109/LCOMM.2021.3069235. [Google Scholar] [CrossRef]

20. Qasmi F, Shehab M, Alves H, Latva-Aho M. Effective energy efficiency and statistical QoS provisioning under Markovian arrivals and finite blocklength regime. IEEE Internet Things J. 2022;9(18):17741–55. doi:10.1109/JIOT.2022.3157956. [Google Scholar] [CrossRef]

21. Pathak V, Chethan R, Pandya RJ, Iyer S, Bhatia V. Deep learning based energy, spectrum, and SINR-margin tradeoff enabled resource allocation strategies for 6G. IEEE Access. 2024;12:74024–44. doi:10.1109/ACCESS.2024.3404473. [Google Scholar] [CrossRef]

22. El Hassani H, Savard A, Belmega EV, de Lamare RC. Multi-user downlink NOMA systems aided by ambient backscattering: achievable rate regions and energy-efficiency maximization. IEEE Trans Green Commun Netw. 2023;7(3):1135–48. doi:10.1109/TGCN.2023.3261499. [Google Scholar] [CrossRef]

23. Boyd SP, Vandenberghe L. Convex Optimization. 1st ed. Cambridge, IL, USA: Cambridge University Press; 2004. [Google Scholar]

24. Xu D, Duan L, Zhao H, Zhu H. Effective computation throughput maximization for MEC-enabled WP-IoT networks with short packet communications. IEEE Trans Veh Technol. 2025;74(1):1137–52. doi:10.1109/TVT.2024.3465036. [Google Scholar] [CrossRef]

25. Grant M, Boyd S. CVX: matlab software for disciplined convex programming, version 2.1; 2014 [cited 2025 Feb 5]. Available from: http://cvxr.com/cvx. [Google Scholar]

26. Phan KT, Tho LN. Online QoS-based dynamic scheduling in multi-channel wireless networks. In: 2013 IEEE Wireless Communications and Networking Conference (WCNC); 2013 Apr 7–10; Shanghai, China: IEEE; 2013. p. 586–90. doi:10.1109/WCNC.2013.6554629. [Google Scholar] [CrossRef]

27. Li S, Ale L, Chen H, Tan F, Quek TQS, Zhang N, et al. Joint computation offloading and multidimensional resource allocation in air-ground integrated vehicular edge computing network. IEEE Internet Things J. 2024;11(20):32687–700. doi:10.1109/JIOT.2024.3441236. [Google Scholar] [CrossRef]

28. Zhang S, Shi S, Wang W, Xu Z, Gu X. An energy-efficient UAV deployment scheme for emergency communications in air-ground networks with joint trajectory and power optimization. China Commun. 2022;19(7):67–78. doi:10.23919/JCC.2022.07.006. [Google Scholar] [CrossRef]