Cat Swarm Algorithm Generated Based on Genetic Programming Framework Applied in Digital Watermarking

1  Introduction

With the widespread application of artificial intelligence (AI) technologies in real-world domains, the solutions to numerous problems in various fields have become increasingly diverse [1,2]. As researchers gradually delve deeper into problem models, they have recognized that the majority of practical problem models are nonlinear and exhibit non-differentiable characteristics [3]. Evolutionary Algorithms (EAs), a robust stochastic approach, iteratively refine a population until an optimal solution to the problem is found [4]. In recent years, EAs have garnered significant attention and application. They have been implemented in various fields, such as medical imaging [5,6], unmanned aerial vehicle (UAV) path planning [7,8], information hiding and encryption [9,10], industrial production [11], and many others.

Due to the exceptional feasibility of EAs in addressing real-world issues, a growing contingent of scholars has embarked on research endeavors focusing on EAs. Consequently, novel forms of EAs have been continually developed. Furthermore, EAs are classified as meta-heuristic algorithms, drawing inspiration from natural phenomena [12]. Classical EAs include Genetic Algorithm (GA) [13], which are inspired by the evolutionary processes observed in nature. Particle Swarm Optimization (PSO) draws its inspiration from the social behavior of bird flocks [14]. Furthermore, numerous EAs have been inspired by certain behaviors of insects or animals, such as reproduction, predation, and others. Examples of these include the Grey Wolf Optimizer (GWO) [15], Cat Swarm Optimization (CSO) [16], Ant Colony Optimization (ACO) [17], Northern Goshawk Optimization (NGO) [18], and Whale Optimization Algorithm (WOA) [19]. Additionally, many algorithms are derived from human society, such as the Teaching-Learning-Based Optimization (TLBO) [20], Love Evolution Algorithm (LEA) [21], and Tabu Search (TS) [22]. Besides, Genetic Programming (GP) [23], which represents problem solutions as trees, such as binary trees, is widely applied to symbolic regression problems [24].

Currently, most evolutionary frameworks of EAs are inspired by certain laws in nature or human behaviors. The artificial construction of an evolutionary framework is a feasible undertaking. Researchers have established such frameworks through repeated studies, in-depth contemplation, and proficiency in understanding the relevant phenomena. This aspect is challenging for machines to achieve. The particular evolutionary formulations, or update schemes, incorporated into these frameworks are typically devised manually by scholars. By studying previous EAs update schemes and gaining an understanding of the chosen evolutionary framework, scholars combine and map specific characteristics of the population using mathematical methods, thereby designing appropriate update schemes. However, the No Free Lunch Theorem states that no single EAs can solve all practical problems [25]. Researchers are prone to neglecting specific characteristics of the designed evolutionary framework due to the influence of the forms of evolutionary formulas in previous EAs. This leads to the underutilization of certain population traits within specific evolutionary frameworks, and consequently, the comprehensive performance of the designed algorithms has not been fully explored.

To address the issues above within the field of computer technology, this paper proposes a viable framework, which has been named GP-EAs. Given the black-box nature of GP and its extensive application in symbolic regression. This paper aims to optimize GP to enhance its suitability for EAs. GP-EAs maintain GP’s evolutionary framework and solution paradigm, thereby enabling it to derive more comprehensive and superior evolutionary formulations for specific EAs based on a given set of terminals and functions. When utilizing GP-EAs to design or improve evolutionary formulas for EAs, it is necessary to devise the objective function, terminal set, and function set. The objective function is contingent upon the problem that the algorithm seeks to resolve. With the initial objective of enhancing the algorithm’s overall performance, the objective function designed in this paper is intended to test the comprehensive performance of the newly evolved formula. The variables within the terminal set and function set can originate from certain variables that have been widely used in EAs, as well as from newly introduced variables manually added by researchers based on a profound understanding of the characteristics of the selected algorithm.

The main contributions of the GP-EAs are as follows:

(1)   Reducing human intervention in the design process of evolutionary formulas. The GP-EAs framework continuously generates new evolutionary formulas by combining and ordering the variables in the set.

(2)   Reducing the time expenditure for designing evolutionary formulas for EAs. GP-EAs substitute for the researchers’ manual and iterative process of designing, testing, and eliminating evolutionary formulas. The training process using GP-EAs belongs to the offline design state, wherein researchers are only required to select the more appropriate evolutionary formula from the results presented after the program termination.

To validate the effectiveness of the proposed GP-based framework, this paper selects the CSO algorithm as a case study. The CSO algorithm was first introduced in 2006 and draws inspiration from the natural behavior of cats. Since its inception, numerous variants of CSO have emerged. Sharafi et al. proposed an extension of CSO to a binary form, namely Binary Cat Swarm Optimization (BCSO) [26]. Pradhan et al. enhanced CSO to address multi-objective problems (MOCSO) [27]. Zhao et al. enhanced CSO using a compact strategy, designated as CCSO [28]. In contrast to CCSO, Pan et al. employed a parallel strategy, whereby sub-populations were divided to optimize CSO (PCSO) [29]. Building on PCSO, Tsai et al. combined it with the Artificial Bee Colony (ABC) algorithm, resulting in a hybrid CSO algorithm (PCSOABC) [30]. Furthermore, hybrid versions of CSO have been proposed, including CSO-CS [31]. This paper employs GP-EAs and CEC2017 as a foundation for regenerating a velocity update formula for CSO, designated GP-CSO. The comprehensive performance of GP-CSO was evaluated using CEC2017, and its performance was compared with that of several competitive algorithms with dimensions of 30D and 50D.

Furthermore, GP-CSO was applied to digital watermarking to assess the real-world application capability of the GP-EAs framework. In the context of the information age, as people’s awareness of copyright protection gradually intensifies, digital watermarking technology has been widely applied to copyright protection [32]. The essential processes of digital watermarking can be broadly classified into two categories: watermark embedding and watermark extraction. A successful digital watermark should not impair the regular usage of the original image [33]. This implies that it must be embedded in an appropriate location and possess the requisite level of invisibility. Consequently, for the watermark to serve its purpose of verifying the authenticity of the image, it is essential that it can be successfully extracted from the watermarked image. The most commonly utilized methodologies include the Discrete Wavelet Transform (DWT) [34], Least Significant Bit (LSB) replacement [35], Discrete Cosine Transform [36], and Fourier Transform (DFT) [37]. The embedding and extraction operations are typically inverse processes of each other. To date, there have been many studies on the application of EAs to digital watermarking. The process of watermark embedding and extraction is influenced by an embedding factor, which must, therefore, be identified to ensure the robustness of the watermark. Dey et al. designed a medical image verification system using the cuckoo search algorithm (CS) and DWT technique to embed hospital logos in the form of watermarks into ECG images [38]. The CS algorithm searched for suitable embedding factors in the solution space. Cui et al. used the DWT-SVD algorithm to embed watermarks into the four sub-bands of the bright component of a color image [39]. An embedding factor with four dimensions corresponding to the four sub-bands was solved using the DE algorithm. Sharma et al. proposed an adaptive color image watermarking method based on the artificial bee colony (ABC) algorithm and RDWT-SVD, embedding the watermark into the low-frequency sub-bands of the host image [40]. Zhang et al. proposed a dual-embedded watermarking algorithm using the PSO algorithm to solve the watermark embedding factor [41]. The watermark is embedded into the low-frequency sub-bands and high-frequency sub-bands of the image using the DWT-DCT-SVD [42,43]. Pan et al. improved the states of matter search algorithm (SMS) using adaptive parameters and co-evolutionary strategies [10]. After solving the embedding factor, the watermark is embedded into the color QR code image using the DWT-SVD algorithm. Most of the above studies solve for single-scale embedding factors, i.e., each image sub-band corresponds to a single-dimension embedding factor. This paper employs GP-CSO to search for the multi-scale embedding factor with 64 dimensions, corresponding to each dimension of the image sub-bands, and selects DWT-DCT-SVD for watermark embedding and extraction.

The principal contributions of this paper are outlined below:

(1)   A novel framework, designated GP-EAs, is proposed to autonomously generate evolutionary formulas for EAs.

(2)   The GP-EAs is applied to the CSO algorithm, which has been designated as GP-CSO. The velocity update formula of the tracking mode in GP-CSO is autonomously trained using this framework. The objective is to validate the effectiveness of the GP-EAs framework for generating update formulas for EAs.

(3)   The performance of GP-CSO was evaluated in comparison with several classical EAs, as well as a selection of popular EAs, on the CEC2017 test set.

(4)   Applying the improved GP-CSO to digital watermarking.

The following paragraphs set out the key points concerning the content of other sections in this paper. Section 2 comprehensively explains the essential technologies, including CSO, GP, and digital watermarking. Section 3 provides a comprehensive introduction to the GP-based framework (GP-EAs) proposed in this paper, along with the newly derived velocity update formula. Section 4 presents a comparative analysis of GP-CSO with other algorithms and applies GP-CSO to digital watermarking, with the presentation and analysis of the experimental results. Section 5 provides a summary of the content of this paper and an analysis of potential avenues for future research.

2  Related Technologies

The primary work of this research is to modify tree-based GP. Autonomous training of evolutionary formulas in EAs using improved GP. A framework is a structure encompassing predefined modules and methods to simplify the training and evaluation processes. The enhanced GP presented in this study is named the Genetic Programming-based Framework for Evolutionary Algorithms (GP-EAs). GP-EAs aim to minimize human intervention in the design process of evolutionary formulas, thereby enabling programs to train evolutionary formulas offline autonomously. The subsequent sections of this paper discuss the relevant techniques and applications.

2.1 Cat Swarm Optimization

The evolutionary process of the CSO algorithm is based on the emulation of the search and observation behaviors observed in cat colonies. Before the commencement of the evolutionary process, the population must be initialized. This is typically achieved through random initialization within the problem’s search space. Once the initialization process is complete, the cat colony is comprised of N individuals, which are denoted as Xi. The dimensions of Xi vary depending on the specific problem under consideration. The CSO algorithm can be classified into two distinct modes: tracking mode and seeking mode. The algorithm comprises a total of five parameters, with the following descriptions of their specific meanings:

•   Proportion of the two modes (MR): The proportion of individuals engaged in the seeking mode within the entire population is represented by the value of MR, while the remaining individuals perform the tracking mode.

•   Size of the search pool (SMP): It is necessary for each Xi executing the search mode to replicate SMP copies, thereby forming a search pool corresponding to the Xi. Each individual within the search pool is represented by the symbol xi.

•   Whether the current position is stored (SPC): SPC is employed to ascertain whether the present Xi will be incorporated directly into the search pool without any modification. In particular, SPC is a random boolean value.

•   Dimensional change quantity (CDC): In the seeking mode, the proportion of dimensions that undergo changes among the xi in the search pool of Xi is represented by the CDC.

•   Seeking range of the selected dimension (SRD): The range of variation for each dimension of xi in the search pool is [(1−SRD)xi,j,(1+SRD)xi,j], where xi,j represents the specific value of the j-th dimension.

2.1.1 Seeking Mode

When individuals in the population engage in this mode of behavior, they emulate the actions of cats in a state of repose in the natural environment. Cats will determine their subsequent actions based on the circumstances of the moment. The precise methodology is as follows:

(1)   By the magnitude of the SMP values, Xi is replicated to form a search pool. It is worthy of note that if SPC is indicated as true, Xi is retained as an individual within the search pool without any modification.

(2)   The following operations should be performed on the samples in the search pool (with the exception of the Xi, which should be retained): a random selection of certain dimensions should be made for mutation, with the proportion of these dimensions to the total being CDC, and the mutation range should conform to SRD.

(3)   Evaluate the mutated samples using the fitness function: fi.

(4)   Calculate the probability using Eq. (1): pi.

(5)   Based on pi, randomly select a sample to replace Xi in the population.

pi=|fi−fpool|fb−fw(1)

In cases where a minimum value is sought, fpool represents the minimum fitness value observed among the samples within the search pool. In contrast, for problems seeking a maximum value, the situation is reversed. The values fb and fw represent the highest and lowest fitness values, respectively, among the samples in the pool.

2.1.2 Tracing Mode

This mode has been developed with the objective of enhancing the developmental performance of CSO. The approach is inspired by the tracking behavior of cats and can be mathematically represented as a process of convergence towards the current optimal solution, as demonstrated in Eqs. (2) and (3).

ViT+1=ViT+R⋅C⋅(XgbestT−XiT)(2)

XiT+1=XiT+ViT+1(3)

In this context, the variable T represents the current iteration number. Xgbest represents the best individual within the population. In this context, the symbols R and C represent, respectively, a random number and a learning constant (R∈[0,1],C=2.05). The term Vi is used to indicate the velocity of movement for a given sample. Eq. (2) is employed to update an individual’s future movement speed and direction. With Vi as the guiding factor, the individual moves towards Xgbest based on the disparity between Xi and Xgbest, while being regulated by parameters R and C. Subsequently, Eq. (3) is used to determine the individual’s new position.

2.2 Genetic Programming

The GP algorithm was first proposed by researchers in 1998. The advantage of GP lies in its minimal requirement for manual intervention, enabling it to autonomously address target problems. It has been extensively applied in areas such as optimizing algorithm parameters, symbolic regression, and optimizing parameters for target problems. Since its inception, GP has evolved into various types of variants. For instance, there are tree-based GP, stack-based GP, and linear-structure-based GP, among others.

Among the numerous types, the most classic is the tree-based GP. The GP-EAs framework proposed in this paper utilizes a binary tree structure. In this type of GP, each individual in the population, i.e., each solution, is represented by a tree. Initialization in GP is conducted under the given conditions of a function set and a terminal set. Following the attributes of the tree structure, a hybrid initialization approach is typically employed, whereby half of the individuals in the population are initialized using a depth-first method and the remaining half are initialized using a breadth-first method. Moreover, each tree in the population must satisfy the specified depth requirement. After the initialization phase, the genetic programming process is conducted sequentially, comprising three distinct steps: selection, crossover, and mutation.

Selection: The specific process entails the selection of distinct individuals from the extant population for modification to facilitate their evolution into the subsequent generation. This process can be classified into three distinct categories. The initial method entails the selection of a subset of superior individuals, who are then retained in the subsequent generation without undergoing any modifications. The second type comprises the selection of parent individuals for crossover operations. The third method entails the selection of individuals that require mutation. The most commonly employed selection methods are random selection, roulette wheel selection, and tournament selection [44].

Crossover: In this process, a node is randomly selected from among the two parent individuals, and the subtree of that node is then exchanged. As illustrated in Fig. 1.

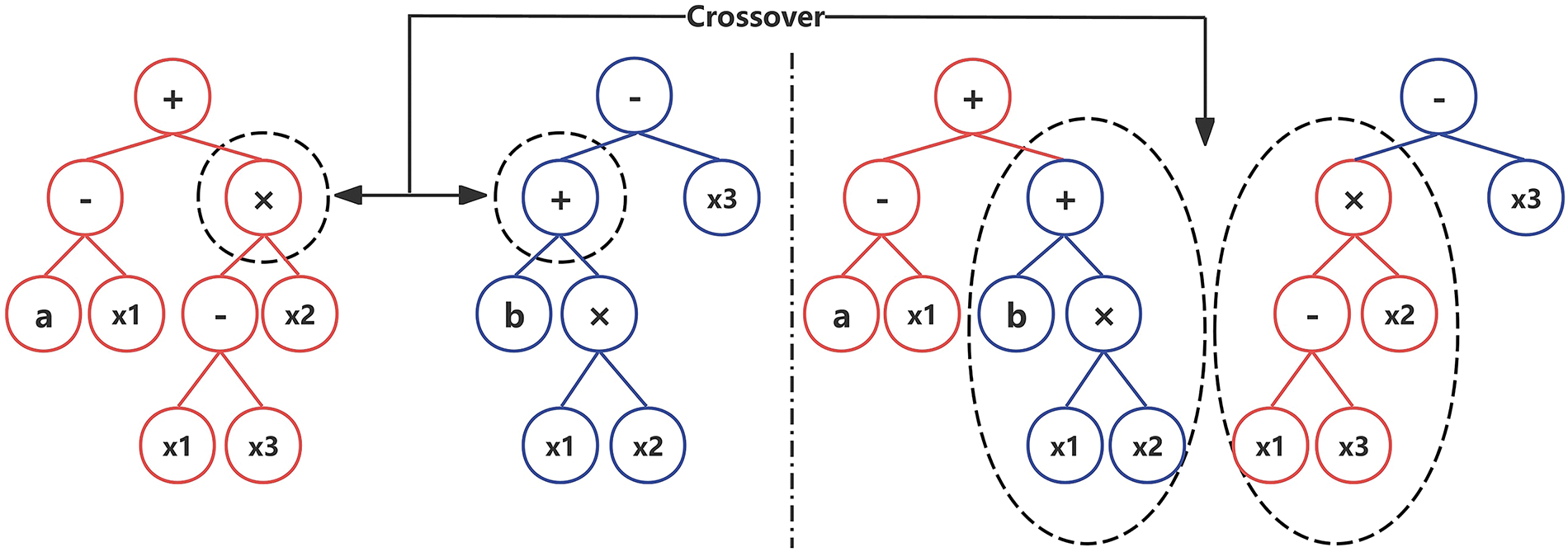
Figure 1: Sample diagram of crossover operation

Mutation: Mutation can be classified into two principal categories: single-point mutation and growth mutation. Single-point mutation involves the random selection of either a terminal node or a non-terminal node for mutation. The specific process is illustrated in the left half of Fig. 2. In this process, a randomly chosen element from the function set replaces a non-terminal node, or a randomly selected element from the terminal set replaces a terminal node. Growth mutation, on the other hand, involves the replacement of a node with a new subtree, as shown in the right half of Fig. 2.

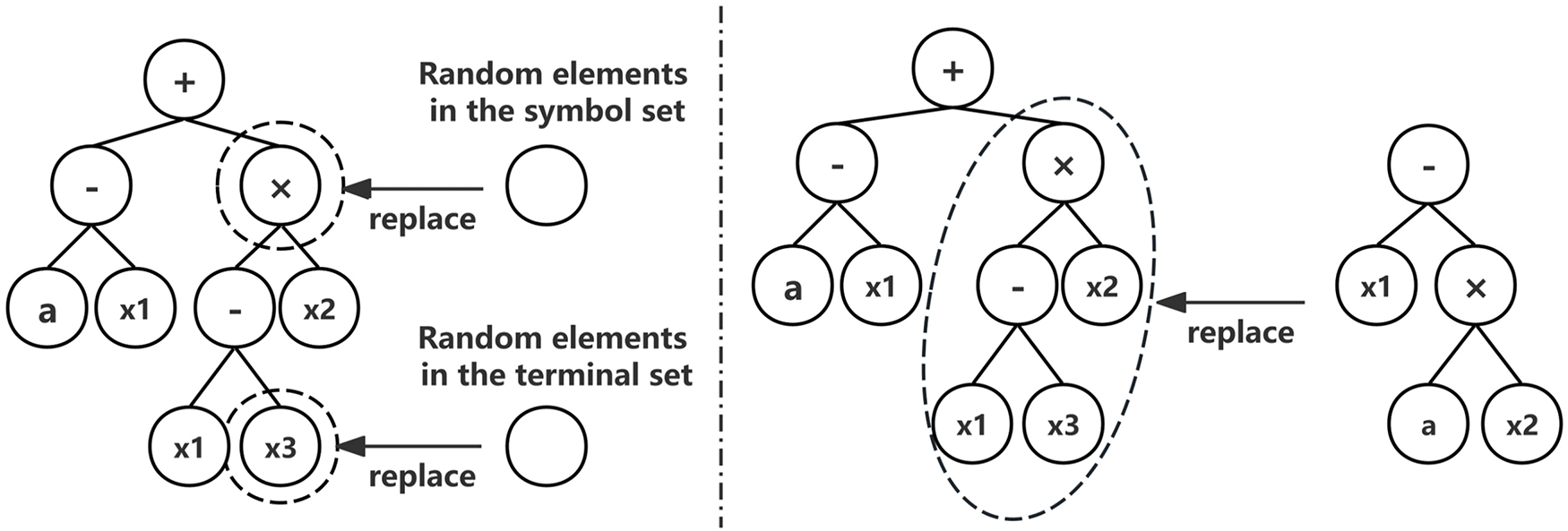
Figure 2: Sample diagram of mutation operation

2.3 Digital Watermarking

This section introduces the brief process of digital watermarking and how DWT-DCT-SVD is applied to watermarking.

Before the insertion of the watermark into the designated host image, the watermark image must undergo a series of processing steps. This step is analogous to the further encryption of the watermark, which serves to enhance the invisibility of the secret information and improve its security performance. The Arnold transform [45] is a frequently employed technique for such a transformation, which essentially entails stretching, compressing, and reordering pixel values to encrypt the image information. However, this method exhibits a distinctive characteristic, namely periodicity. This implies that after a certain number of consecutive transformations, the encrypted information can be cracked. The encryption method employed in this paper is based on the generation of a chaotic sequence through the use of Logistic mapping [46], binarizing it according to the pixel values, and performing a bitwise AND or OR with the watermarked image to achieve encryption.

DWT facilitates multi-scale image decomposition, allowing for the insertion of watermark information across various scales. Post-DWT processing, an image is segmented into multiple sub-bands, each characterized by unique frequency properties. Notably, the LL sub-band comprises low-frequency content, encapsulating the primary image information, whereas the LH, HL, and HH sub-bands encompass high-frequency details [47]. The DCT shifts an image from the spatial domain to the frequency domain, thereby facilitating the extraction of features conducive to watermark embedding within the frequency spectrum. The SVD, a matrix decomposition technique, breaks down a matrix into a product of three distinctive matrices (L, S, R), thereby aiding in the extraction of crucial image information for watermark embedding. This process is illustrated in Eq. (4). L and R are orthogonal matrices, and t denotes the transpose operation. Notably, the singular value matrix S demonstrates robustness, implying that minor image disturbances do not significantly alter its singular values.

G=L×S×Rt(4)

Among the various watermarking techniques, DWT-DCT-SVD stands out as a commonly utilized method. The method combines three key technologies related to digital watermarking, which are divided broadly into three phases. In the initial phase, the target image is subjected to a DWT, which may be applied either once or on multiple occasions. The primary objective of this algorithm is to insert the watermark into the designated sub-band, which can be either a single sub-band or multiple sub-bands. The second phase comprises the further refinement of the selected sub-band through the application of DCT, with the objective of extracting its image characteristics. The third phase entails the utilization of SVD for the processing of the matrix derived from the preceding phase, in conjunction with the watermark image. Subsequently, an embedding coefficient (Q) is employed for the integration of the singular value matrix Sw of the watermark image with the singular value matrix Si of the selected sub-band, thereby embedding the watermark into the image. This process is depicted in Eq. (5). Ultimately, by applying the inverse processes to all aforementioned operations, an image with the embedded watermark can be derived.

Siw=Si+Q×Sw(5)

The present research employs the DWT-DCT-SVD algorithm for the embedding of watermarks, with the DWT stage being applied consecutively on three occasions to obtain three-level sub-bands. The CSO algorithm, augmented by GP-EAs, is utilized to identify suitable embedding factors. A bespoke objective function is employed to achieve a balance between invisibility and robustness. In contradistinction to the watermarking embedding factors of previous studies, the embedding factors in this study possess multiple dimensions. The performance scalability of the algorithm improved by GP-EAs in practical high-dimensional problems can be indirectly verified.

3  CSO Algorithm Based on the GP-EAs Framework

This chapter presents the GP-EAs framework. It covers the framework’s structure and the design of its associated parameters. Additionally, it introduces the application of GP-EAs to CSO and analyses the update formulas developed explicitly for CSO.

3.1 Overall Structure

Fig. 3 illustrates the overall structure of this study, with red lines indicating the data flow. Before commencing, it is necessary to determine which evolutionary algorithm will be improved using the GP-EAs framework; here, the CSO is taken as an example. The initial phase involves researchers manually designing the function set, terminal set, and objective function. Step ① represents the input of these designed parameters into the GP-EAs. Subsequently, GP-EAs perform iterative selection, where formulas with better performance are gradually retained while those with poorer performance are eliminated during the iterations. The iterative training process is an offline operation, and after a new formula has been designed for the EAs, the new evolutionary formula can be used directly in different real-world applications without re-training it separately. The evaluation process for individuals within the GP population is as follows: the individual, representing a newly evolved formula, replaces the original formula in CSO. Then, the algorithm’s performance, assessed using the objective function, is taken as a proxy for the performance of the new formula. Step ② signifies the replacement of the optimal formula trained by GP-EAs into CSO, and the CSO algorithm using this new formula is named GP-CSO. When validating the practical application capabilities of GP-CSO, the algorithm is applied to digital watermarking to solve for the embedding factor. The performance of GP-CSO in practical applications is verified by evaluating the invisibility and robustness of the watermark.

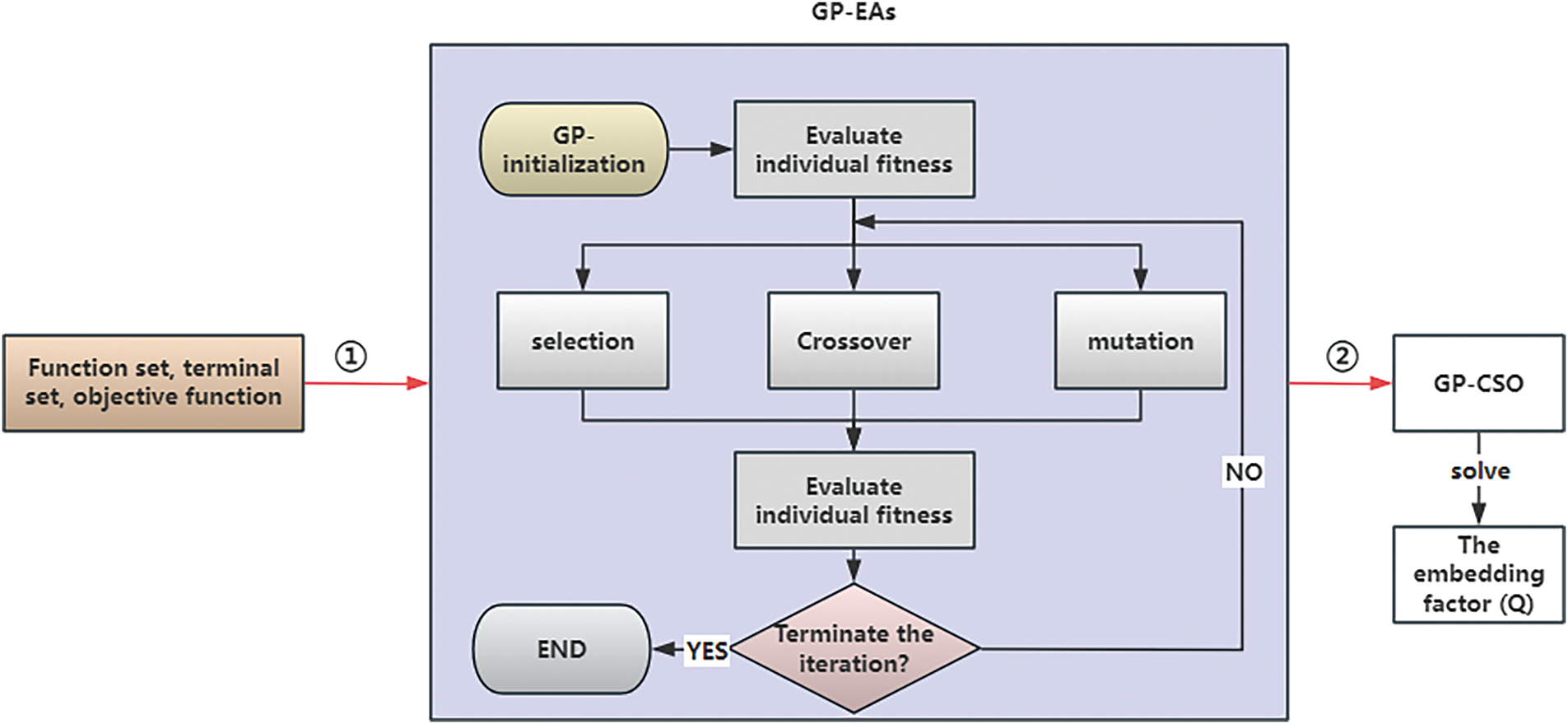
Figure 3: Overall structure diagram

The time complexity volatility of the manual design of evolutionary formulas is high and different to evaluate. Researchers often need to debug parameters and pair variables multiple times, followed by performance testing. The GP-EAs framework replaces manual design patterns and reduces human intervention, with variable matching and performance testing continuously performed by the program. During the operation of the GP-EAs framework, each individual can be considered a variant of the CSO algorithm when combined with the CSO. It means that the variants with poor performance are eliminated, while the variants with superior performance are retained and continuously learned. Compared with manual design, the time cost and complexity of GP-EAs will be relatively low because they do not have too much human intervention.

3.2 The GP-EAs Framework

This paper aims to enhance the capabilities of tree-based GP and enable its utilization in the autonomous generation of specific evolutionary formulas for EAs. Table 1 provides a comprehensive overview of the specific parameters associated with GP-EAs.

The specific process of GP-EAs is as follows:

(1)   The population is randomly initialized based on the set of functions and the set of terminals, and half of the individuals in the population are generated using a depth-first strategy. In contrast, the other half is generated using a breadth-first strategy.

(2)   Individuals in the population are used to generate new evolutionary formulas using mid-order traversal, and fitness is assessed (using the new evolutionary formulas to replace the old evolutionary formulas in the goal evolutionary algorithm and subsequently evaluating the algorithm’s performance using the objective function).

(3)   Select a portion of the top individuals for direct deposit into the next generation.

(4)   Use a roulette wheel to select individuals for the cross-mutation operation.

(5)   Evaluate the fitness of individuals in the new population.

(6)   Cycle through the above steps until the algorithm termination condition is met.

Algorithm 1 presents the pseudo-code for GP-EAs. Based on previous research on evolutionary formulas in EAs, it has been observed that most of these formulas can be represented by binary trees with depths ranging from 3 to 5. Accordingly, in GP-EAs, the depth of individuals is set within this range of 3 to 5. At the outset of the process, a depth is randomly selected for each individual within the specified limits. To efficiently find suitable formulas in a shorter period and accelerate convergence, the top 20% of individuals from the previous generation are directly carried over to the next generation. In the next generation, 80% of the individuals are generated through crossover and mutation operations. To enhance population diversity, one of the methods is randomly chosen for individuals selected to undergo mutation: terminal node mutation, non-terminal node mutation, or growth mutation.

This paper specifically designs an evaluation function (F) for the GP-EAs framework to evaluate the newly generated formulas within a population. The CEC2017 introduced four categories of test functions, ranging from simple to complex in their difficulty. Similar to these functions, various practical problems or applications also exhibit differing levels of complexity. Therefore, to enhance the overall performance of the formulas produced by GP-EAs, this paper decides to randomly select one function from each of the four categories in CEC2017, collectively forming the final evaluation function. The detailed evaluation process involves substituting the newly evolved formula (individuals within the GP-EAs population) into the algorithm that necessitates enhancement, followed by the algorithm’s execution. For the sake of simplicity, the algorithm under improvement that employs the newly evolved formula during the evaluation process is referred to as new-EAs in the following text. Eq. (6) defines an individual’s fitness. In this context, fitj∗ represents the theoretical optimal value of the jth test function, whereas fitj denotes the mean result obtained from five independent runs of new-EAs on the jth test function. By combining four objective functions of varying complexities through a product operation, the objective is to evaluate the comprehensive ability of new-EAs to handle different problems, thereby indirectly proving the effectiveness of the newly evolved formula.

F(treei)=∏j=14fitjfitj∗(6)

3.3 The GP-CSO Algorithm

The objective of this paper is to optimize the CSO algorithm using GP-EAs, resulting in the creation of a new algorithm, GP-CSO. The GP-EAs is used to autonomously generate the velocity update formula, which is Eq. (2) introduced above. The problem dimension for F is set to 10. As previously stated, F1, F10, F18, and F28 are selected to constitute the evaluation functions. Furthermore, the terminal set and function set’s design is paramount for GP. Based on the research on CSO variants and EAs, the terminal set and function set designed for CSO are presented as follows:

{Terminal:{ω,Xc,Xi,Vc,Vi,Xgbest,R,C}Function:{+,−,×,÷}

The value of ω represents a rational number that decreases with the number of iterations, from 0.8 to 0.2. The value of Xc represents the centroid of individuals within a cat population, while Vc represents the velocity centroid. The four classes of operators in the function set are widely used in numerous evolutionary formulas. Since EAs are stochastic methods, the random numbers denoted by R are necessary to be added to the terminal set. Xgbest and Xi typically involve the process of learning from the current best individual, which is closely related to the core characteristics of EAs and has the effect of accelerating convergence. In addition to this, ω and C are inspired by PSO and DE and their variant algorithms, and have the effect of preventing too fast convergence leading to a fall into a local optimum, as well as controlling the degree of learning between individuals, respectively. Under the influence of these two types of parameters, EAs usually have a certain balance between convergence and exploitation. The rationale for adding Xc and Vc to the terminal set is that the centroid of the relevant data in the population is theoretically smoother and less prone to extremes compared to single data. Also, the terminal set can be further enriched. The resulting equations from the GP-EAs are presented in Eq. (7).

ViT+1=RXiT⋅VcT+ω⋅C⋅(XgbestT−XiT)(7)

In comparison to Eq. (2), in Eq. (7) autonomously generated by GP-EAs, an individual’s velocity is primarily determined by Vc. After performance testing and screening of various formulas using GP-EAs, it was ultimately determined that during the process of updating the velocity, a coefficient is required to scale Vc. This coefficient is jointly determined by R and Xi. Similar to the evolutionary formulas of most EAs, Eq. (7) also contains a component that reflects the gradual approximation of Xi towards Xgbest during the evolutionary process, specifically manifested through using C to learn from Xgbest. Unlike previous EAs, which use R to control the learning degree, Eq. (7) employs ω to regulate this learning extent. As ω gradually decreases with the number of iterations, this implies that as the iterations increase, the degree of learning towards Xgbest diminishes. This helps to prevent the algorithm from becoming trapped in a local optimum. When dealing with complex problems, ω is more reasonable and exhibits superior performance compared to R.

The pseudo-code of GP-CSO is presented in Algorithm 2.

4  Results

This chapter analyzes the comprehensive performance of GP-CSO through simulation experiments. GP-CSO is a CSO algorithm that employs evolutionary formulas autonomously generated by GP-EAs. The practical effects of optimizing EAs using GP-EAs are verified. Furthermore, it indirectly validates the practical application effects of GP-EAs by applying GP-CSO to digital watermarking.

4.1 Experimental Settings for Benchmark Function Testing

The simulation experiments were conducted using the MATLAB 2018b software environment. To assess the overall performance of the GP-CSO, the CEC2017 benchmark suite was selected, with problem dimensions of 30D and 50D employed. CEC2017 contains a total of 30 functions, divided into four categories. F1 to F3 are unimodal functions, used to test the convergence speed and accuracy of algorithms. F4 to F10 are simple multimodal functions, designed to evaluate the search capability of algorithms in scenarios where multiple local optima exist. F11 to F20 are hybrid functions, which are combinations of different types of functions that simulate more complex optimization problems and are used to test the performance of optimization algorithms on complex problems. F21 to F30 are composition functions, formed by combining different types of functions through weighted sums, products, and other forms, aimed at assessing the balance between the global search capability and local exploitation ability of optimization algorithms.

Uniformly setting the basic parameters for each optimization algorithm to ensure the fairness of the experiment. The population size is configured to be 50, the number of iterations is set to 500, and the search range from −100 to 100. To ensure the validity of the experimental data, each algorithm was run independently 20 times. This paper employs three distinct metrics to evaluate the performance discrepancies between algorithms: the best value (B) among the 20 runs, the mean (M) of all final results, and the standard deviation (Z) of the final results. The aim is to provide a comprehensive assessment of both the stability and the true performance of the algorithms. Different optimization algorithms possess unique parameters, with specific settings detailed in Table 2. Cp1 and Cp2 represent the two learning constants in the PSO algorithm, while wp denotes the weight factor. Fp and CR stand for the scaling factor and crossover rate, respectively. a and a1 linearly decrease from 2 to 0 during the iteration process, while a2 decreases from −1 to −2.

4.2 Analysis of Experimental Results of Each Algorithm on CEC2017 (30-Dimensions)

This paper employs the CEC2017 test suite for 30-dimensional (30D) problems to assess the comprehensive capability of the GP-CSO in addressing low- to mid-dimensional issues. As GP-EAs are typically trained with 10D problems as the foundation for evolving iterative update formulas, this paper does not assess the performance of GP-CSO on 10D problems. To more effectively assess the scalability of the self-trained formulas, 30D is selected as the representative of low- to mid-dimensional problems. Under the same operational environment, GP-CSO and its competing algorithms were independently run 20 times, yielding results as presented in Tables 3–5. Data in black and bold represent the best value in the same data. The definition and purpose of the symbols (+, −, =) in the tables are explained in Section 4.4.

Table 3 presents the operational results for both simple problems and simple multimodal problems. GP-CSO demonstrates a more pronounced advantage compared to the original CSO algorithm, with GP-CSO only performing inferior to CSO on F6 and F9. However, GP-CSO exhibits a lower standard deviation on these two problems, indicating superior robustness. This result suggests that GP-CSO possesses stronger convergence performance than CSO, which is attributed to the fact that the velocity update process of GP-CSO is influenced by the velocity of the entire population rather than being dependent on individual velocities. Additionally, when compared to novel algorithms such as GWO and classical algorithms like PSO, GP-CSO demonstrates superior convergence when dealing with simple problems. Table 4 presents the operational results of hybrid functions, which typically exhibit complex modalities and have the potential to trap algorithms into local optima. Across the ten hybrid functions from F11 to F20, GP-CSO outperforms all competing algorithms, indicating that GP-CSO is more capable of avoiding the influence of local optimal solutions. This advantage stems from the fact that, as the number of iterations increases, the movement velocity of individuals in the GP-CSO population becomes increasingly less influenced by the current optimal solution. GP-CSO demonstrates higher solution accuracy. After 20 independent runs, GP-CSO exhibits a smaller standard deviation, with notably higher values only on F17 and F20 compared to the CSO algorithm. This implies that GP-CSO possesses better stability when solving complex problems. Table 5 displays the performance metrics of different algorithms on composite functions, which pose greater complexity than hybrid functions. Analysis of the data in Table 5 reveals that GP-CSO surpasses CSO on most composite functions, with the underlying reasons aligning with prior explanations. In comparison to PSO and WOA, GP-CSO shows superiority based on both average and standard deviation metrics. Only in a few instances does GP-CSO lag behind GWO and DE, where GWO excels in convergence and DE instability.

Fig. 4 exhibits the convergence curves of various algorithms on 30-dimensional benchmark functions. Owing to space limitations, only a portion of the convergence plots are displayed, with the sub-figure titles representing the identification numbers of the benchmark functions. Upon comprehensive analysis of these plots, it is apparent that GP-CSO exhibits outstanding performance on most benchmark functions, surpassing nearly all competing algorithms in terms of final results. The performance on F6 is relatively poor, which is related to the characteristics of the benchmark function. There are also functions similar to F6, such as F9. In the F6 and F9 functions, the peaks and troughs are unevenly and not densely distributed. Populations using the velocity update dominated by Vc tend to explore the search space more gradually and stably, maintaining a degree of exploration while retaining the exploitation of the surrounding landscape around individuals. In contrast, populations using the velocity update dominated by Vi exhibit a broader search range but lack detailed exploitation of the surrounding function landscape. They have a higher potential to discover superior values in unevenly distributed function spaces. Therefore, the original CSO algorithm using Vi is more likely to solve better solutions on such functions but is less stable. Additionally, GP-CSO demonstrates a substantial improvement in early-stage convergence speed compared to CSO, indicating its ability to derive superior solutions with limited computational resources. In later iterations, its capacity to escape local optima has also been significantly enhanced. The convergence ability of the algorithm is most evident when solving problems of low to medium dimensions. In EAs, the convergence phenomenon is shown as the individuals in the population move closer to Xgbest. When Xgbest is in the local optimum, too much reliance on learning Xgbest will easily cause the population to fall into the wrong zone. In GP-CSO, the degree of learning is controlled by the parameter ω. As the number of iterations continues to increase, the degree of learning from Xgbest by individuals in the population gradually decreases. This allows GP-CSO to remain somewhat exploratory in the later stages of the algorithm. As shown in Fig. 4a,d,g, GP-CSO is still able to further explore the function space when other algorithms stagnate.

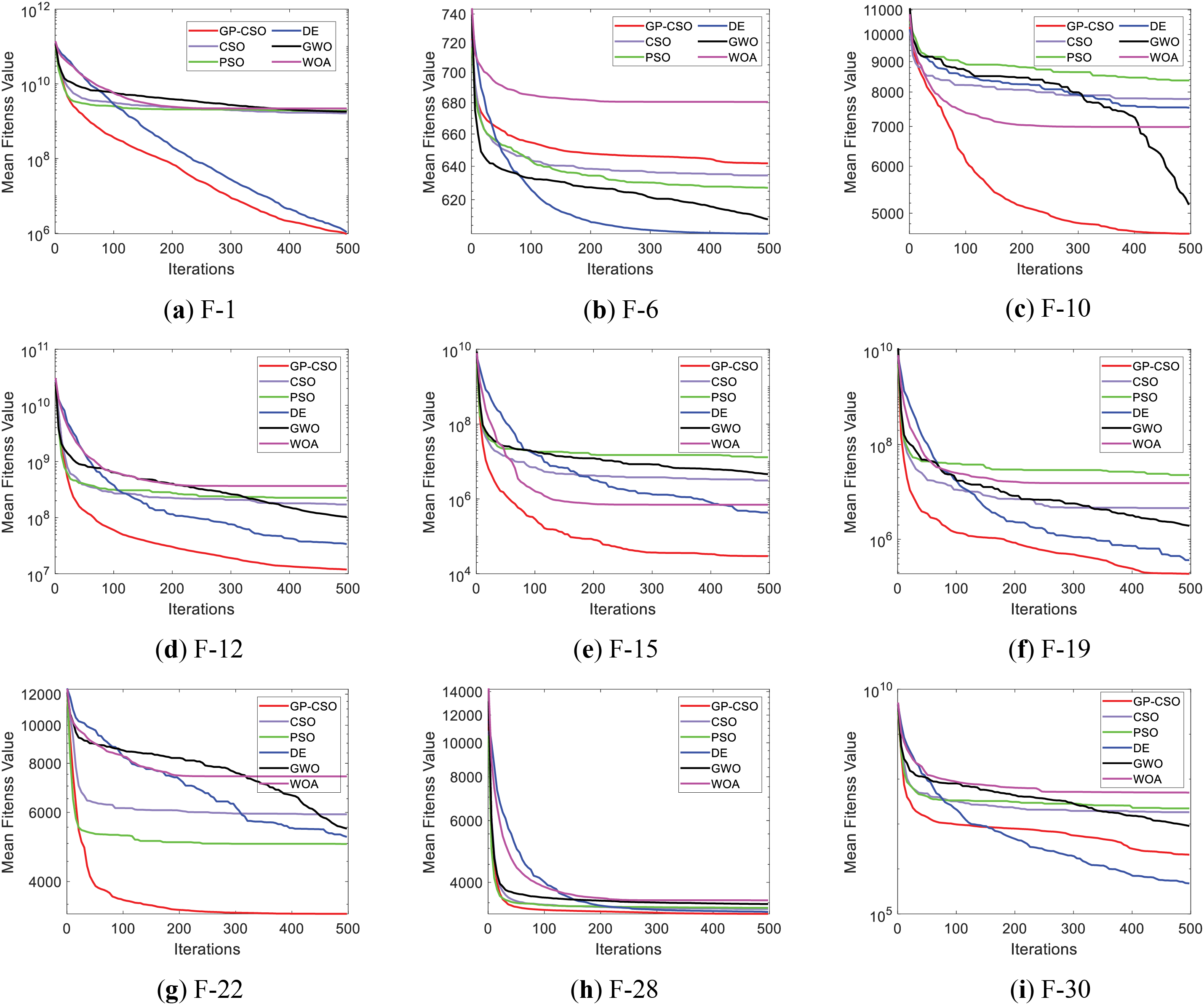
Figure 4: Convergence plot of each competing algorithm on 30-dimensions

4.3 Analysis of Experimental Results of Each Algorithm on CEC2017 (50-Dimensions)

In order to evaluate the comprehensive capability of the GP-CSO algorithm in addressing complex problems, this paper conducts tests on the algorithm using a 50D benchmark function. The statistical results after 20 independent runs are presented in Tables 6–8. In order to minimize redundancy, the definitions of the relevant data labels in these tables are consistent with those used when the dimension was 30.

The data presented in Table 6 are derived from the results of the testing of the selected algorithms on unimodal and multimodal functions with 50 dimensions. A comparative analysis with the CSO reveals that as the dimensionality increases to 50, the advantage of the update formulas autonomously generated by GP-EAs becomes more pronounced. Although GP-CSO demonstrated inferior performance relative to CSO on the F6 and F9 functions at 30 dimensions, as the dimensionality increased, its mean performance leveled off with CSO, while exhibiting a lower standard deviation, indicating superior stability for GP-CSO. A comparison of GP-CSO with other competing algorithms revealed that it demonstrated enhanced performance in addressing simpler problems of higher dimensionality, essentially surpassing all rival approaches. This underscores the conclusion that utilizing the population velocity centroid as the dominant force for updates aligns more closely with the update logic of CSO than relying on the velocity of individual particles themselves. Table 7 summarizes the final data for all algorithms that address the 50D hybrid function. Similarly to the 30D condition, GP-CSO outperforms the majority of competing algorithms, with only a slight difference from DE on F19. Notably, GP-CSO is able to solve better solutions within a fixed limit on the number of iterations, which is demonstrated by the data results in the table, where GP-CSO’s optimal results after 20 independent runs are the best of all the algorithms on the vast majority of problem functions. Table 8 presents the final data for various algorithms processing composite functions under 50D conditions. GP-CSO is only underperformed by CSO on F27, indicating its stronger ability to escape from local optima. When compared with PSO, DE, and WOA, GP-CSO achieves superior results in the majority of cases. Although it outperforms GWO on only half of the composite functions, GP-CSO demonstrates higher stability.

Fig. 5 illustrates a portion of the convergence graphs for the 50D benchmark functions. GP-CSO demonstrates a high level of convergence speed in the initial stages. The results displayed in the chart indicate that GP-CSO exhibits significant advantages compared to other competing algorithms. In complex high-dimensional problems, GP-CSO retains robust exploration capabilities throughout the entire iteration process. This is closely related to the utilization of ω to control the degree of learning from the optimal individual. In hybrid and composite functions, where the function space has many similar numerical troughs, the use of Vi to dominate the velocity update is prone to excessive speed, leading to insufficient exploitation of the landscape around the individual. Using a velocity update formula that is jointly dominated by Vc and ω is more able to balance the exploitation of the local area as well as the exploratory nature of the global area. Therefore, the performance advantage of GP-CSO in dealing with complex problems becomes more obvious as the dimensionality rises.

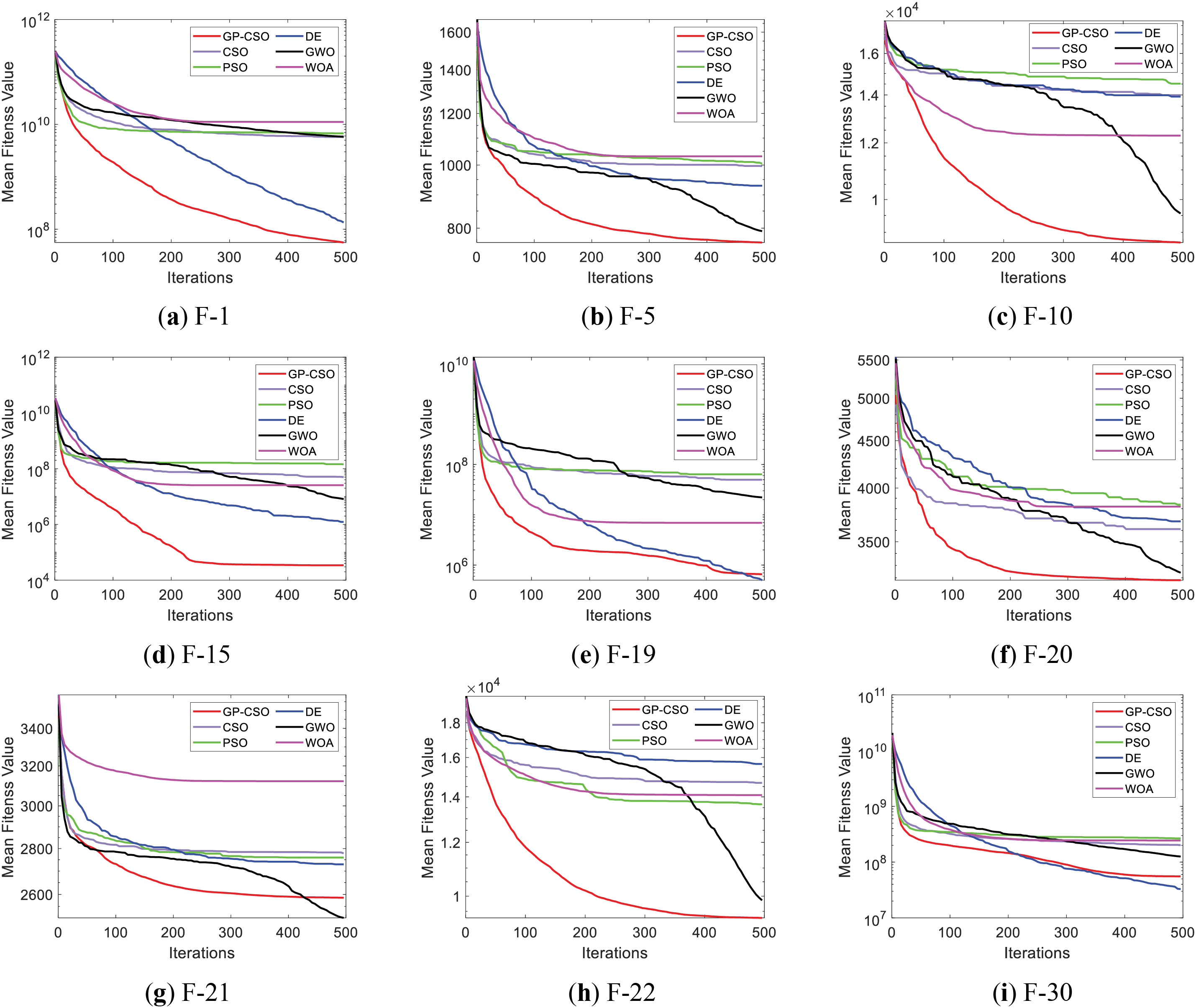
Figure 5: Convergence plot of each competing algorithm on 50-dimensions

4.4 Mathematical and Statistical Analyses

This chapter conducts a statistical analysis on the data results introduced in the previous chapter, aiming to visually compare the performance of GP-CSO with competitive algorithms. The analysis results are presented in Table 9. The first statistical test employed is the Friedman test, which calculates the average ranking of each algorithm across all functions. The parameter p, in this context, signifies that a smaller p-value indicates a higher reliability of the statistical results. Following computation, the p-values under two distinct dimensionality conditions were found to be 3.3821E−16 and 3.3938E−14, respectively. Both values are sufficiently small, approaching zero, thereby rendering the statistical results credible. GP-CSO achieved an average ranking of 1.6 and ranked first under both dimensionality conditions, indicating that GP-CSO possesses superior comprehensive capabilities when dealing with unknown problems.

Additionally, this paper conducted a Wilcoxon rank-sum test with a significance level set at 0.05. The symbol ‘+’ indicates that GP-CSO significantly outperforms the competitive algorithm, ‘=’ suggests no significant difference between GP-CSO and the competitive algorithm, and ‘−’ implies that GP-CSO’s performance is significantly inferior to that of the competitive algorithm. According to the data from this statistical test method presented in the table, when the dimensionality is 30D, the GP-CSO algorithm improved by GP-EAs demonstrates superior performance compared to the original algorithm. The fact that it won on 26 functions and lost on only 2 functions demonstrates this point. In comparison to other competitive algorithms, GP-CSO also demonstrates superior performance on the majority of functions. In the case of 50D, GP-CSO’s performance is only inferior to the original CSO algorithm on one benchmark function. Nevertheless, in comparison to GWO, the advantage of the algorithm is diminished as the dimensionality increases.

Fig. 6 is a radar chart plotted by taking the mean data for each algorithm and ranking them. The representation provides an intuitive understanding of the ranking order of the competing algorithms across different functions. The concentric circles, commencing at the center and extending in an outward direction, represent the ranking levels. The proximity of a given circle to the center indicates a higher ranking. Each vector emanating from the center represents a benchmark function. Observing the phenomena presented in Fig. 6, regardless of whether it is for 30D or 50D, the red data points are concentrated heavily towards the central part, implying that GP-CSO has a higher ranking and exhibits superior overall performance. Following GP-CSO are DE and GWO, which are ranked second. In third place is the CSO algorithm. The PSO algorithm ranks fourth, while WOA performs the worst.

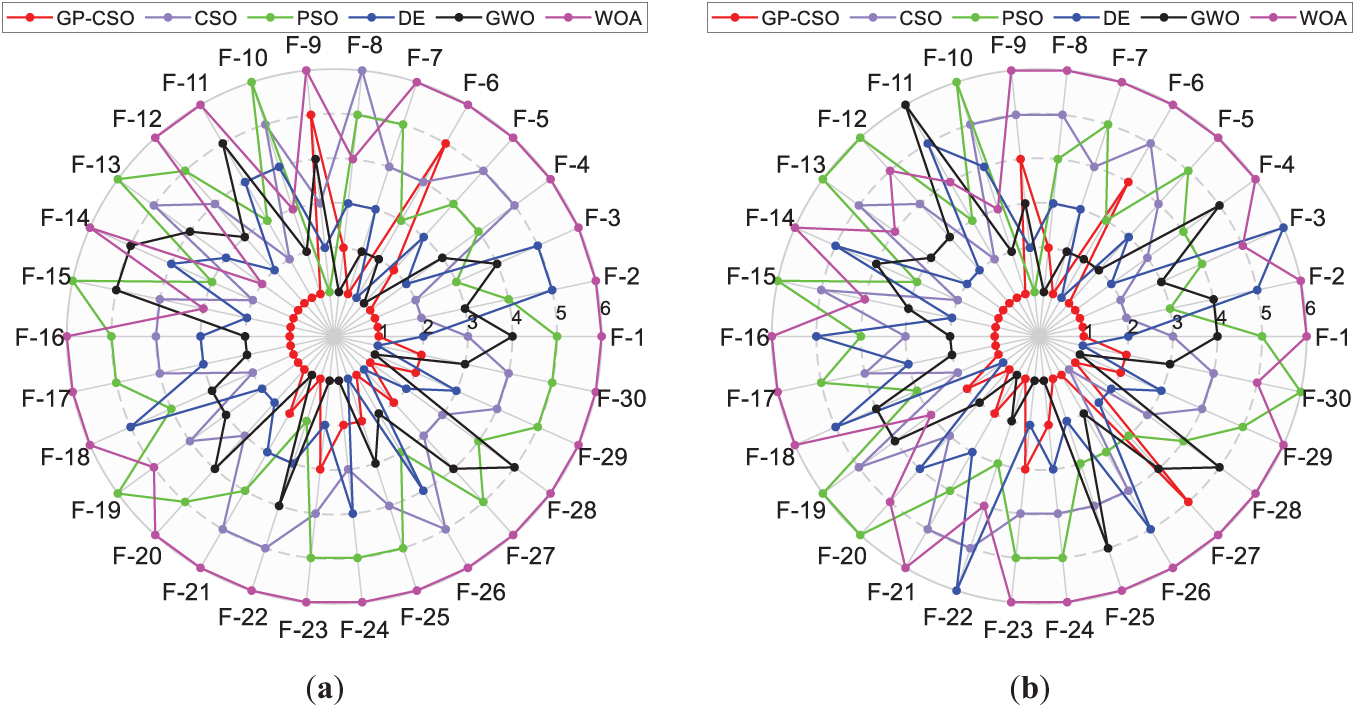
Figure 6: Radar charts for algorithmic ranking (a) Ranking in the 30D situation; (b) Ranking in the 50D situation

The time complexity of the velocity update formula grows from O(1) to O(n) for GP-CSO compared to CSO. This is because the calculation of Vc necessitates the involvement of the entire population. With identical population parameter settings, the average computation times for GP-CSO and CSO in solving 30 benchmark functions with a dimension of 50 were recorded as 7.2853 and 7.3353, respectively. The data results indicate that the difference in runtime is insignificant, yet there is a notable improvement in performance. Therefore, it can be concluded that the increase in computational cost is substantially smaller than the magnitude of performance enhancement.

4.5 Simulation Experiments of GP-CSO in Digital Watermarking

Two-dimensional code is extensively utilized in commerce and people’s daily lives. They possess a unique encoding format that stores information through the arrangement of geometric patterns in black and white colors. QR codes represent a specific type of two-dimensional barcode, featuring an overall square shape composed of alternating black and white squares [48]. These codes are capable of storing substantial amounts of information and responding rapidly, which has led to their widespread adoption in practical domains such as mobile payments, information verification, and commercial promotion.

In this paper, a beautified color QR code image is selected as the carrier image (Ci) for embedding the watermark, as illustrated in Fig. 7a, with dimensions of 512×512. The information stored within the QR code is the title of this paper, which can be extracted by scanning with a QR code scanning device. The original watermark image (Wi∗), presented in Fig. 7b, is a 128×128 black-and-white image. To further enhance the secrecy of the watermark image, Logistic chaotic mapping is utilized to encrypt Wi∗, thereby reducing the correlation between adjacent pixels. The resulting encrypted watermark image (Wi) is shown in Fig. 7c. Despite the error correction capability of QR codes, improper watermark embedding processes can still result in failure to decode the correct information when reading. Accordingly, this paper utilizes EAs to ascertain suitable embedding factors (Q) for the watermark, with a common Q utilized across the embedding processes in four distinct frequency sub-bands. Due to the size of the singular value matrix being 64×64, Q thus has 64 dimensions. To enhance fairness in solving for Q among diverse algorithms, the population size of each algorithm is uniformly set to 20, the number of iterations is uniformly set to 20, the search range for each dimension is constrained to the interval [0.01,20]. The hyperparameter settings for GP-CSO, CSO, PSO, GWO, and DE are consistent with those described in Section 4.1. The parameter settings for other competing algorithms are shown in Table 10.

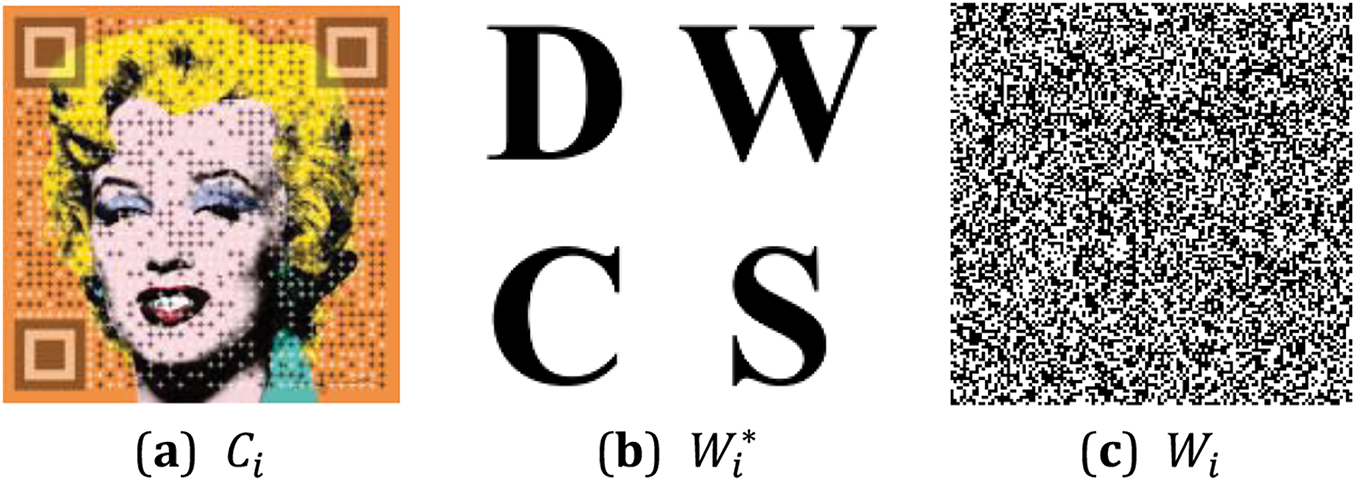
Figure 7: Images involved in the experiment

(5)   The singular value matrices of the corresponding frequency sub-bands from Ci and Wi are combined using Eq. (5), thereby embedding the watermark information into the respective sub-bands of Ci.

(6)   By sequentially performing inverse SVD, inverse DCT, and three levels of inverse DWT, the watermarked image Ciw is obtained.

The extraction process of the watermark is as follows: after performing the inverse operation of step 6 on Ciw, the singular value matrix of each sub-band of the watermark is extracted by Sw′=Siw−SiQ. The watermark information is obtained after the inverse operation of each operation, and finally, the extracted watermark image is obtained by using chaotic sequence decryption. The objective function used in solving the appropriate embedding factor Q using EAs is shown in Eq. (8).

f(Q)=1PSNR(Ci,Ciw)×∑t=1n(NC(Wi,Wi′)+1)n(8)

In this context, the variable “Wi′” represents the watermark that has been extracted from the image in which it has been embedded. PSNR can be employed to evaluate the discrepancy between images prior to and following watermark embedding. The unit of PSNR is decibel (dB), with a higher PSNR value indicating reduced image distortion. Evaluating the PSNR between Ci and Ciw serves as an indicator of the invisibility of the embedded watermark, with higher values indicating a higher level of invisibility. The NC is an index that measures the similarity between two images, with a value range of [−1,1]. The closer the NC value between Wi and Wi′ is to 1, the higher the similarity between them. In this experiment, six of the nine common image attacks (n = 6) were randomly selected for analysis. The nine attacks are: histogram equalization attack, image rotation attack, Gaussian noise, multiplicative noise, contrast reduction, contrast increase, image brightening, image darkening, and image cropping. Following the attacks, the watermarks were extracted individually, and the NC values between the watermarked images after the attacks were calculated. These NC values were then normalized and averaged. A smaller f(Q) value indicates a higher fitness level of Q.

This paper utilizes GP-CSO, alongside several competitive algorithms, to search for embedding factors for watermark images. The objective is to assess the viability of utilizing EAs enhanced by the GP-EAs framework in practical applications. The embedding and extraction methods outlined above are employed, with Eq. (8) serving as the objective function. During the execution of each algorithm, a population comprising 20 individuals is utilized. Fig. 8 exhibits the results of watermark embedding using the values of Q obtained through various algorithms. Fig. 9 shows the extraction of the watermarks in the absence of any attacks, with each corresponding to a respective sub-figure in Fig. 8. It is evident that the watermarks embedded using DWT-DCT-SVD do not impair the normal usage of the original images, and that valid watermarks can be successfully extracted from all of Ciw. Scanning each of the result images in Fig. 8 to retrieve the information stored in the QR codes yields correct information consistently.

Figure 8: Resulting graph of watermark embedding using different algorithms

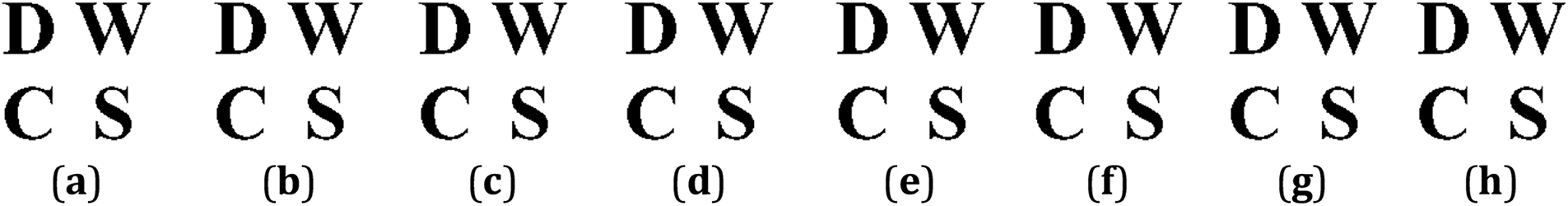
Figure 9: Watermark extracted from Ciw

Table 11 presents the data results obtained under different algorithm conditions, which were acquired through image-based comparisons between the final embedded result images and the original images. Bolded data represents the best value in the same category. When Q solved using different algorithms is used for watermarking algorithm, the final NC value obtained was 1.0000. This outcome indicates that the extracted watermarked image is highly analogous to the original watermarked image. Moreover, the embedding watermarking process guided by Q, which is solved using GP-CSO, results in the highest PSNR value, indicating the smallest degree of difference from Ci and thus achieving the lowest distortion rate. A comprehensive analysis demonstrates that the embedded digital watermark utilizing GP-CSO exhibits enhanced imperceptibility and superior stability. Therefore, the practical performance of the CSO algorithm improved by GP-EAs in the field of digital watermarking is relatively good. Moreover, Q has 64 dimensions, which belong to the middle and high dimensions. Therefore, compared with CSOs, the GP-CSOs generated by training with the 10D benchmark function also show a good performance improvement in real-world problems with medium and high dimensions. This validates the performance scalability of GP-CSO for real-world problems.

5  Conclusions and Outlook

Based on the GP algorithm, this paper proposes a framework for autonomously generating evolutionary update patterns for EAs. GP-EAs autonomously generate evolutionary formulas without much human intervention, which belongs to the category of offline training. Researchers only need to design the terminal set, function set, and evaluation function. The computer program continuously matches the variables and evaluates the performance of the evolutionary formulas. GP-EAs replace the iterative process of researchers continuously designing formulas, testing them, retaining those with superior performance, and discarding those with inferior performance. Reduce the time overhead of designing evolutionary formulas for EAs. Evolutionary formulas generated using GP-EAs exhibit excellent performance scalability, meaning that formulas trained on low-dimensional problems can still maintain efficient performance when applied to solve high-dimensional problems. Utilizing GP-EAs to generate more reasonable velocity update formulas for CSO, the improved algorithm is named GP-CSO. The scalability of GP-CSO performance is then tested using medium-to-high-dimensional problem functions. GP-CSO is employed in the field of digital watermarking to validate the effectiveness of the algorithm improved by GP-EAs in practical applications. Specifically, GP-CSO is used to solve for the embedding factors of the watermark, which are then embedded into different frequency sub-bands of the image in combination with the DWT-DCT-SVD algorithm, further enhancing the robustness of the watermarking process.

However, GP-EAs are still partially flawed. Dependent on the researcher-designed terminal set and function set, it cannot be completely free from human intervention. It cannot continuously generate many different types of evolutionary formulas. The efficiency of generating formulas still has room for improvement. Attention should be paid to the protection of division operation in the initialization and mutation stages to avoid the situation where the divisor is zero. Therefore, the main directions for future research are as follows: firstly, a library of operation symbols for EAs can be constructed. In the subsequent use of GP-EAs, it is not necessary to design terminal sets and function sets for specific EAs, and it is possible to selectively and directly extract them from the operation symbol library. Secondly, the concept of multi-tree GP can be introduced, so that GP-EAs can generate different stages of evolutionary formulas for EAs at the same time. Reverse learning theory is introduced to accelerate the training process. Furthermore, the objective function within the algorithm for digital watermarking will be optimized, enabling EAs to determine more reasonable embedding factors.

Acknowledgement: The authors would like to thank the anonymous reviewers and the editor for their valuable suggestions, which greatly contributed to the improved quality of this article.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Shu-Chuan Chu, Libin Fu, Jeng-Shyang Pan, Xingsi Xue, Min Liu; data collection: Libin Fu, Jeng-Shyang Pan; analysis and interpretation of results: Shu-Chuan Chu, Libin Fu, Xingsi Xue; draft manuscript preparation: Shu-Chuan Chu, Libin Fu, Jeng-Shyang Pan, Min Liu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Zhang C, Lu Y. Study on artificial intelligence: the state of the art and future prospects. J Ind Inf Integr. 2021;23(1):100224. doi:10.1016/j.jii.2021.100224. [Google Scholar] [CrossRef]

2. Chaka C. Fourth industrial revolution—a review of applications, prospects, and challenges for artificial intelligence, robotics and blockchain in higher education. Res Pract Technol Enhanc Learn. 2022;18:2. doi:10.58459/rptel.2023.18002. [Google Scholar] [CrossRef]

3. Deng W, Shang S, Cai X, Zhao H, Song Y, Xu J. An improved differential evolution algorithm and its application in optimization problem. Soft Comput. 2021;25(7):5277–98. doi:10.1007/s00500-020-05527-x. [Google Scholar] [CrossRef]

4. Liu Z, Yang D, Wang Y, Lu M, Li R. EGNN: graph structure learning based on evolutionary computation helps more in graph neural networks. Appl Soft Comput. 2023;135(1):110040. doi:10.1016/j.asoc.2023.110040. [Google Scholar] [CrossRef]

5. Abualigah L, Habash M, Hanandeh ES, Hussein AM, Shinwan MA, Zitar RA, et al. Improved reptile search algorithm by salp swarm algorithm for medical image segmentation. J Bionic Eng. 2023;20(4):1766–90. doi:10.1007/s42235-023-00332-2. [Google Scholar] [PubMed] [CrossRef]

6. Ren L, Zhao D, Zhao X, Chen W, Li L, Wu T, et al. Multi-level thresholding segmentation for pathological images: optimal performance design of a new modified differential evolution. Comput Biol Med. 2022;148(11):105910. doi:10.1016/j.compbiomed.2022.105910. [Google Scholar] [PubMed] [CrossRef]

7. Jiang Y, Xu XX, Zheng MY, Zhan ZH. Evolutionary computation for unmanned aerial vehicle path planning: a survey. Artif Intell Rev. 2024;57(10):267. doi:10.1007/s10462-024-10913-0. [Google Scholar] [CrossRef]

8. Zhang M, Han Y, Chen S, Liu M, He Z, Pan N. A Multi-strategy improved differential evolution algorithm for UAV 3D trajectory planning in complex mountainous environments. Eng Appl Artif Intell. 2023;125(6568):106672. doi:10.1016/j.engappai.2023.106672. [Google Scholar] [CrossRef]

9. Rezaei B, Ghanbari H, Enayatifar R. An image encryption approach using tuned Henon chaotic map and evolutionary algorithm. Nonlinear Dyn. 2023;111(10):9629–47. doi:10.1007/s11071-023-08331-y. [Google Scholar] [CrossRef]

10. Pan JS, Sun XX, Chu SC, Abraham A, Yan B. Digital watermarking with improved SMS applied for QR code. Eng Appl Artif Intell. 2021;97(5):104049. doi:10.1016/j.engappai.2020.104049. [Google Scholar] [CrossRef]

11. Ji Y, Liu S, Zhou M, Zhao Z, Guo X, Qi L. A machine learning and genetic algorithm-based method for predicting width deviation of hot-rolled strip in steel production systems. Inf Sci. 2022;589(2):360–75. doi:10.1016/j.ins.2021.12.063. [Google Scholar] [CrossRef]

12. Darvishpoor S, Darvishpour A, Escarcega M, Hassanalian M. Nature-inspired algorithms from oceans to space: a comprehensive review of heuristic and meta-heuristic optimization algorithms and their potential applications in drones. Drones. 2023;7(7):427. doi:10.3390/drones7070427. [Google Scholar] [CrossRef]

13. Katoch S, Chauhan SS, Kumar V. A review on genetic algorithm: past, present, and future. Multimed Tools Appl. 2021;80(5):8091–126. doi:10.1007/s11042-020-10139-6. [Google Scholar] [PubMed] [CrossRef]

14. Gad AG. Particle swarm optimization algorithm and its applications: a systematic review. Arch Comput Meth Eng. 2022;29(5):2531–61. doi:10.1007/s11831-021-09694-4. [Google Scholar] [CrossRef]

15. Makhadmeh SN, Al-Betar MA, Doush IA, Awadallah MA, Kassaymeh S, Mirjalili S, et al. Recent advances in grey wolf optimizer, its versions and applications. IEEE Access. 2023;12(3):22991–3028. doi:10.1109/ACCESS.2023.3304889. [Google Scholar] [CrossRef]

16. Chu SC, Tsai PW, Pan JS. Cat swarm optimization. In: PRICAI 2006: Trends in Artificial Intelligence: 9th Pacific Rim International Conference on Artificial Intelligence; 2006 Aug 7–11; Guilin, China. Berlin/Heidelberg, Germany: Springer. p. 854–8. doi:10.1007/978-3-540-36668-3_94. [Google Scholar] [CrossRef]

17. Morin M, Abi-Zeid I, Quimper CG. Ant colony optimization for path planning in search and rescue operations. Eur J Oper Res. 2023;305(1):53–63. doi:10.1016/j.ejor.2022.06.019. [Google Scholar] [CrossRef]

18. Dehghani M, Hubálovský Š, Trojovský P. Northern goshawk optimization: a new swarm-based algorithm for solving optimization problems. IEEE Access. 2021;9:162059–80. doi:10.1109/ACCESS.2021.3133286. [Google Scholar] [CrossRef]

19. Mirjalili S, Lewis A. The whale optimization algorithm. Adv Eng Softw. 2016;95(12):51–67. doi:10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

20. Zou F, Chen D, Xu Q. A survey of teaching-learning-based optimization. Neurocomputing. 2019;335(7-9):366–83. doi:10.1016/j.neucom.2018.06.076. [Google Scholar] [CrossRef]

21. Gao Y, Zhang J, Wang Y, Wang J, Qin L. Love evolution algorithm: a stimulus-value–role theory-inspired evolutionary algorithm for global optimization. J Supercomput. 2024;80(9):12346–407. doi:10.1007/s11227-024-05905-4. [Google Scholar] [CrossRef]

22. Xie J, Li X, Gao L, Gui L. A hybrid genetic tabu search algorithm for distributed flexible job shop scheduling problems. J Manuf Syst. 2023;71(5):82–94. doi:10.1016/j.jmsy.2023.09.002. [Google Scholar] [CrossRef]

23. Mei Y, Chen Q, Lensen A, Xue B, Zhang M. Explainable artificial intelligence by genetic programming: a survey. IEEE Trans Evol Comput. 2023;27(3):621–41. doi:10.1109/TEVC.2022.3225509. [Google Scholar] [CrossRef]

24. Huang Z, Mei Y, Zhong J. Semantic linear genetic programming for symbolic regression. IEEE Trans Cybern. 2024;54(2):1321–34. doi:10.1109/TCYB.2022.3181461. [Google Scholar] [PubMed] [CrossRef]

25. Joyce T, Herrmann JM. A review of no free lunch theorems, and their implications for metaheuristic optimization. In: Nature-inspired algorithms and applied optimization. Berlin/Heidelberg, Germany: Springer; 2018. p. 27–51. doi:10.1007/978-3-319-67669-2_2. [Google Scholar] [CrossRef]

26. Sharafi Y, Khanesar MA, Teshnehlab M. Discrete binary cat swarm optimization algorithm. In: 2013 3rd IEEE International Conference on Computer, Control and Communication (IC4); 2013 Sep 25–26; Karachi, Pakistan. p. 1–6. doi:10.1109/IC4.2013.6653754. [Google Scholar] [CrossRef]

27. Pradhan PM, Panda G. Solving multiobjective problems using cat swarm optimization. Expert Syst Appl. 2012;39(3):2956–64. doi:10.1016/j.eswa.2011.08.157. [Google Scholar] [CrossRef]

28. Zhao M, Pan JS, Chen ST. Compact cat swarm optimization algorithm. In: Security with intelligent computing and big-data services. Berlin/Heidelberg, Germany: Springer; 2018. p. 33–43. doi:10.1007/978-3-319-76451-1_4. [Google Scholar] [CrossRef]

29. Tsai PW, Pan JS, Chen SM, Liao BY, Hao SP. Parallel cat swarm optimization. In: 2008 International Conference on Machine Learning and Cybernetics; 2008 Jul 12–15; Kunming, China. p. 3328–33. doi:10.1109/ICMLC.2008.4620980. [Google Scholar] [CrossRef]

30. Tsai PW, Pan JS, Shi P, Liao BY. A new framework for optimization based-on hybrid swarm intelligence. In: Handbook of swarm intelligence: concepts, principles and applications. Berlin/Heidelberg, Germany: Springer; 2011. p. 421–49. doi:10.1007/978-3-642-17390-5_18. [Google Scholar] [CrossRef]

31. Pratiwi AB. A hybrid cat swarm optimization-crow search algorithm for vehicle routing problem with time windows. In: 2017 2nd International conferences on Information Technology, Information Systems and Electrical Engineering (ICITISEE); 2017 Nov 1–2; Yogyakarta, Indonesia. p. 364–8. doi:10.1109/ICITISEE.2017.8285529. [Google Scholar] [CrossRef]

32. Kadian P, Arora SM, Arora N. Robust digital watermarking techniques for copyright protection of digital data: a survey. Wirel Pers Commun. 2021;118(4):3225–49. doi:10.1007/s11277-021-08177-w. [Google Scholar] [CrossRef]

33. Wan W, Wang J, Zhang Y, Li J, Yu H, Sun J. A comprehensive survey on robust image watermarking. Neurocomputing. 2022;488:226–47. doi:10.1016/j.neucom.2022.02.083. [Google Scholar] [CrossRef]

34. Muslim MA, Dasril Y, Khusniati M, Subhan S. Analysis of image watermarking with a discrete wavelet transform for digital data security. J Phys: Conf Ser. 2021;1918(4):042014. doi:10.1088/1742-6596/1918/4/042014. [Google Scholar] [CrossRef]

35. Singh RK, Dube AP, Singh R. Least significant bit-based image watermarking mechanism. Int J Soc Ecol Sustain Dev. 2022;13(1):1–9. doi:10.4018/IJSESD. [Google Scholar] [CrossRef]

36. Alomoush W, Khashan OA, Alrosan A, Attar HH, Almomani A, Alhosban F, et al. Digital image watermarking using discrete cosine transformation based linear modulation. J Cloud Comput. 2023;12(1):96. doi:10.1186/s13677-023-00468-w. [Google Scholar] [CrossRef]

37. Ma Y, Sun W, Zhang P, Wang S. Frequency domain digital watermarking algorithm based on arnold transform and quaternion fourier transform. Autom Mach Learn. 2022;3(1):58–64. doi:10.23977/autml.2022.030109. [Google Scholar] [CrossRef]

38. Dey N, Samanta S, Yang XS, Das A, Chaudhuri SS. Optimisation of scaling factors in electrocardiogram signal watermarking using cuckoo search. Int J Bio Inspired Comput. 2013;5(5):315. doi:10.1504/IJBIC.2013.057193. [Google Scholar] [CrossRef]

39. Cui X, Niu Y, Zheng X, Han Y. An optimized digital watermarking algorithm in wavelet domain based on differential evolution for color image. PLoS One. 2018;13(5):e0196306. doi:10.1371/journal.pone.0196306. [Google Scholar] [PubMed] [CrossRef]

40. Sharma S, Sharma H, Sharma JB. An adaptive color image watermarking using RDWT-SVD and artificial bee colony based quality metric strength factor optimization. Appl Soft Comput. 2019;84(17):105696. doi:10.1016/j.asoc.2019.105696. [Google Scholar] [CrossRef]

41. Zhang L, Wei D. Dual DCT-DWT-SVD digital watermarking algorithm based on particle swarm optimization. Multimed Tools Appl. 2019;78(19):28003–23. doi:10.1007/s11042-019-07902-9. [Google Scholar] [CrossRef]

42. Devi HS, Mohapatra H. A novel robust blind medical image watermarking using GWO optimized DWT-DCT-SVD. Multimed Tools Appl. 2023;82(26):41267–86. doi:10.1007/s11042-023-15158-7. [Google Scholar] [CrossRef]

43. Sun XX, Pan JS, Weng S, Hu CC, Chu SC. Optimization of MSFs for watermarking using DWT-DCT-SVD and fish migration optimization with QUATRE. Multimed Tools Appl. 2023;82(2):2255–76. doi:10.1007/s11042-022-13173-8. [Google Scholar] [CrossRef]

44. Hussain A, Riaz S, Amjad MS, Haq EU. Genetic algorithm with a new round-robin based tournament selection: statistical properties analysis. PLoS One. 2022;17(9):e0274456. doi:10.1371/journal.pone.0274456. [Google Scholar] [PubMed] [CrossRef]

45. Liu X, Xiao D, Liu C. Three-level quantum image encryption based on Arnold transform and logistic map. Quantum Inf Process. 2021;20(1):23. doi:10.1007/s11128-020-02952-7. [Google Scholar] [CrossRef]

46. Rohith S, Hari Bhat KN, Sharma AN. Image encryption and decryption using chaotic key sequence generated by sequence of logistic map and sequence of states of Linear Feedback Shift Register. In: 2014 International Conference on Advances in Electronics Computers and Communications; 2014 Oct 10–11; Bangalore, India. p. 1–6. doi:10.1109/ICAECC.2014.7002404. [Google Scholar] [CrossRef]

47. Hosseini SA, Farahmand P. An attack resistant hybrid blind image watermarking scheme based on combination of DWT, DCT and PCA. Multimed Tools Appl. 2024;83(7):18829–52. doi:10.1007/s11042-023-16202-2. [Google Scholar] [CrossRef]

48. Tsai MJ, Peng SL. QR code beautification by instance segmentation (IS-QR). Digit Signal Process. 2023;133(9):103887. doi:10.1016/j.dsp.2022.103887. [Google Scholar] [CrossRef]

49. Meng Z, Pan JS, Xu H. QUasi-affine TRansformation evolutionary (QUATRE) algorithm: a cooperative swarm based algorithm for global optimization. Knowl Based Syst. 2016;109(2):104–21. doi:10.1016/j.knosys.2016.06.029. [Google Scholar] [CrossRef]