Machine Learning for Smart Soil Monitoring

1  Introduction

Ensuring a healthy environment, access to green spaces, and a nutritious diet are among the key necessities for well-being. To maintain control over our living conditions, it is critical to protect our environment from harmful chemicals and the negative effects predominantly found in the soil [1]. Therefore, the objective of this study was to control soil quality, focusing on the parameters that significantly impact plant nutrition [2]. Machine learning applications in agriculture can be divided into four primary areas: soil, water, crop, and livestock management. In [3], the authors used an optimized extreme learning machine to predict and classify soil attributes. Various machine learning techniques, such as random forests, extreme learning machines, and support vector machines, have been utilized in the study of water management [4]. Crop management, which is crucial for farmers, has benefited from numerous machine-learning techniques aimed at enhancing crop quality and productivity. Additionally, machine learning techniques have been extensively applied to support livestock production and improve animal welfare.

The presence of plants in our environment is an essential component of human well-being. Proper care of plants ensures the provision of healthy nutrition and air quality. The quantities of products added to and found in the soil must be carefully controlled. If the quantity of elements in the soil is insufficient, the plants will be of low quality. Conversely, if the quantity is excessive, which is the focus of this study, it presents several challenges. To properly manage agricultural processes and maintain an optimal environment for plants, the condition of the soil must be adequately controlled. The objective of this study is to monitor and control the levels of soil parameters. By employing the proposed method and analyzing measured soil data, we aim to diagnose these observations and maintain an optimal agricultural environment.

The issues of very high or even low quantities generate challenges for producers, impacting yields and crop rotation options. For the majority of crops, controlling and monitoring the quantities of soil parameters optimizes plant growth and improves crop competitiveness. Thus, monitoring the quantities of soil parameters ensures that a product that complies with standards and preserves the environment and safety of trees is obtained. In this case, soil that receives or contains a large quantity of chemical products could represent a danger to human health. Therefore, the objective of this study was to control soil quality and monitor the quantities of critical parameters in the soil [5]. The study area was located in the regional unit of Grevena in northern Greece. This dataset can be applied to assess soil conditions for various tasks.

To effectively monitor soil quality and ensure an outstanding agricultural season, it is imperative to properly control and identify all quantities that exceed the established standards. Several methods for detection and control can be found in the literature [6–8]. The kernel method plays an interesting role in fault detection and system monitoring. In fact, multivariate statistical process methods have had great success owing to their efficiency and simplification of monitoring systems. The general purpose of these techniques is based on the analysis of historical system data from a database to model and study relationships between variables. Kernel Partial Least Squares (KPLS) is an extension approach that has been suggested for nonlinear processes [9,10].

The KPLS approach addresses the challenge of eigenvalues by leveraging its kernel matrix. Consequently, this method finds widespread application in the domain of fault detection for nonlinear, large-scale, and complex industrial systems. However, owing to the large amount of data studied, the KPLS method presents some limitations in the fault detection and monitoring procedure of this type of system. Precisely, the number of selected latent variables was large in the KPLS method, which resulted in a progressive increase in computation time throughout the identification step of the KPLS monitoring model.

The KPLS method demonstrates elegance and efficiency in developing nonlinear systems compared to other nonlinear techniques. However, these properties render the KPLS method a highly appealing approach for monitoring nonlinear systems. Nevertheless, two significant challenges have been identified concerning the application of conventional KPLS for monitoring nonlinear processes:

•   Determine the optimal parameter for the detection index.

•   Size of memory and computation time, which gradually increases with the amount of training data for large-scale systems.

The first step is to use the reduced RKPLS method, which involves reducing the number of training data. This approach processes only the observations containing essential information, resulting in a smaller kernel matrix. In this way, we address one of the major challenges presented by the KPLS method. The KPLS method allows us to select a reduced model that presents only the important data regarding system behavior. As a second step, to obtain the optimal version, we propose an optimal method that combines the RKPLS approach with the Tabu search algorithm. Consequently, an Optimized Reduced Kernel Partial Least Squares (ORKPLS) approach is proposed, which involves identifying the set of measurement observations that capture the most informative components of the system. To achieve the objectives of monitoring and control, the ORKPLS approach is proposed to predict soil parameter concentrations and help understand changes in soil quality networks. In this study, a comparative analysis of the detection performance of static methods was conducted.

The proposed ORKPLS method presents a very important principle. Thus, the ORKPLS method is valid and updates the reduced model if and only if:

•   A measurement without faults.

•   A measurement that is important and rich in information on the system operation using mainly optimal detection indices.

To increase the detection performance of the KPLS and ORKPLS approaches, we use the index Squared Prediction Error (SPE) to detect any anomalies and faults in the systems [11]. To effectively select the kernel parameter, we propose an optimized RKPLS model using a tabu search algorithm. This study presents a comparative analysis of the detection performance of the proposed techniques. We evaluated the detection methods using performance metrics including the False Alarm Rate, Good Detection Rate, and Computation Time [12,13].

The remainder of this paper is structured as follows. Section 2 outlines the principles of KPLS and the proposed ORKPLS approach. Sections 3 and 4 evaluate the performance of the proposed ORKPLS approach and other kernel-based techniques. Finally, Section 5 concludes the study.

2  Detection Methods

Monitoring algorithms are crucial for ensuring the safety of both systems and nature. Several detection methods have been suggested in the literature [14,15]. Currently, these methods are primarily used to protect nature and maintain human health. This section describes the fault detection functions using the KPLS method [16] and the proposed ORKPLS method.

2.1 KPLS Method for Fault Detection

The PLS (Partial Least Squares) approach presents a vector set extension called the latent components of the input and output measurement space to finally construct a linear multivariate regression model. In this case, the input and output measurements are as follows:

Xin=[x1..xN]∈RN×m,Yout=[y1..yN]∈RN×J(1)

Indeed, given an input matrix Xin∈RN×m containing N measurements with m process variables and an output matrix Yout∈RN×J including N measurements with J quality variables. Thus, the main PLS approach projects and processes the input and output matrices into a low-dimensional space with L of latent variables. The PLS approach presents the Xin and Yout (input/output) matrices by:

{Xin=TST+EYout=UHT+F(2)

where S=[s1s2…sl] and H=[h1h2…hl] are the loadings for Xin and Yout, respectively. Then, matrices E and F are the PLS residuals corresponding to the input matrix Xin and output matrix Yout.

However, the PLS method has a linear structure, whereas real processes have a nonlinear structure. Therefore, the PLS method is limited to nonlinear systems. Several techniques have been proposed for this purpose. In fact, among the trends and popular approaches, the KPLS method has been found.

The KPLS approach is known as a kernel matrix named mainly by the Gram matrix which consists of constructing and presenting nonlinear latent components or variables with an approximately linear calculation cost. Thus, the basic concept is to determine and transform the observations, characterized by inputs/outputs, into feature space F, as shown in the following equation:

Γ:xi∈RN→Γ(xi)∈F(3)

Therefore, the KPLS technique is determined in the traditional PLS feature space in its nonlinear kernel form. In this case, we could not compute the nonlinear transformation of each measurement from the batch system. To surpass this issue, the Mercer kernel k(.,.) is used:

k(xi,xj)=⟨Γ(xi),Γ(xj)⟩=Γ(xi)Γ(xj)T(4)

In this case, Γ(xi)∈R1×Z, i = 1, …, N and Z is the dimension of feature space. The exigency of the kernel function verifies Mercer’ s theorem. Based to Eq. (4), the Gram matrix K∈RN×N can be computed by:

K=Γ(Xin)Γ(Xin)T(5)

where Γ(Xin)=[Γ(x1)T,…,Γ(xN)T]

Most kernel functions that regularly used have been are presented in the literature [17]. Thus, different kernel functions are presented and determined in the following forms:

•   Polynomial kernel: k(x,t)=⟨x,t⟩p

•   Sigmoid kernel: k(x,t)=tanh⁡(θ0⟨x,t⟩+θ1)

•   Radial Basis Function (RBF): k(x,t)=exp⁡(−‖x−t‖2μ22) where p,θ0,θ1 and μ are determined using metaheuristic method.

The Gram matrix K is centered using equation Eq. (6):

K=(In−1n1n1nT)K(In−1n1n1nT)(6)

denoted by 1n=(1…1N−11N)T and In=(10..0010.0....0.....0...1)∈RN×N

The deflation step was computed using the rank-one reduction of K and Yout. Using a new T score vector, the K and Yout matrices were deflated as follows:

K=(In−ttT)K(In−ttT)=K−ttT−KttT+ttTKttTYout=Yout−ttTYout(7)

Finally, the KPLS model was determined, after computation the loadings and scores, as:

Y^=KU(TTKU)−1TTYout(8)

The concerning prediction outputs of validation samples can be computed by:

Y^=KtU(TTKU)−1TTYout(9)

where Kt is the kernel matrix of the validation observations.

Algorithm of Fault Detection

A KPLS algorithm, for nonlinear systems, is presented by Algorithm 1:

2.2 Proposed Optimized RKPLS Using Tabu Search Approach

Indeed, significant drawbacks of the KPLS approach emerge as the number of measurements increases. In such cases, computer memory usage and training time become substantial. Although the KPLS method addresses the issue of nonlinearity, the training and computation times present significant challenges when the number of measurements grows.

Therefore, the Optimized Reduced KPLS (ORKPLS) technique is proposed to reduce the maximum number of measurements and select the most informative observations. The primary objective of the ORKPLS method is to retain only the essential data that provide rich information about the system’s functioning. This methodology avoids the need to study missing data. Using the data projection principle, out of 781 survey points, approximately 10.49% of the data are retained specifically, the most important and effective data.

2.2.1 Mathematical Formulation

A kernel approach is a class of algorithms used for pattern analysis, where the core concept involves implicitly mapping input measurements into a high-dimensional feature Hilbert space (see Fig. 1). This enables the linear separation of measurements that are not linearly separable in the original space. In the proposed technique, we determine a reduced number of measurements from the N available variables in the observation matrix. The best-retained observations represent the L latent components.

Figure 1: Principle of kernel methods

The ORKPLS technique approaches each latent component {wj}j=1…P using a transformed input measurement Γ(xLatent(j))∈ψ{xi}j=1…M which has the maximum projection value in the direction of wj.

The projection of the vector Γ(xLatent(j)) can be computed using Eq. (10):

Γ(xLatent(j))=αjkj(x),j=1,…,L(10)

Then, we project, in this case, all vectors of the transformed measurement Γ{xi}j=1…M on the latent component wj and we retain xLatent(j)∈{xi}j=1…M that satisfies Eq. (11):

{Γ(xLatent(j))j=maxi=1,…,MΓ{xi}jandΓ(xLatent(j))i≠j⟨ς(11)

where ς is the threshold determined.

When the reduced data set {xLatent(j)}j=1…L is presented, a downsized measurement matrix is expressed by:

Xr=[xLatent(1)xLatent(2)…xLatent(L)]T(12)

Meanwhile, we obtain a reduced matrix Kr related to the function K (kernel function), as expressed by the Eq. (13):

Kr=[k(x1,x1)…k(x1,xL)...k(x1,x1)…k(x1,xL)]∈RL×L(13)

In our case, the proposed ORKPLS detection method uses a basic radial kernel and is expressed by:

k(x,t)=exp⁡(−‖x−‖22μ2)(14)

where σ is the width of the Gaussian function.

To choose the kernel parameter accurately, it is necessary to choose the optimization method. Thus, the Tabu Search approach is an optimization algorithm for controlling an integrated heuristic technique. This method has been widely used in several fields [18]. The optimal kernel parameter is almost computed as one that can improve FD (Fault Detection) performance. Therefore, the selection of the μ parameter must be treated according to the given application. To minimize the search space by referring to previous literature using the ORKPLS model, it is advised to introduce the constraints of the parameter μ which are respectively attributes to the range μ∈[2−8,28].

2.2.2 Algorithm of Fault Detection

Indeed, the main algorithm of the ORKPLS approach is given by Algorithm 2:

2.3 Fault Detection Indices

Several indices have been developed for the fault detection stage [13]. In general, statistical methods use Hotelling’s T2 and the SPE or Q statistic, which are developed and presented in terms of Mahalanobis and Euclidean distances, respectively [19]. T2 is given by Eq. (15), whose principle is based on the projections of the measurements in the feature space to different temporal samples.

T2=XTW^Λ^−1W^TX(15)

where Λ^=diag(λ1,…,λL): diagonal matrix of the eigenvalues and W^: the weights matrix.

The SPE is a fault detection index based on the residual subspace. This index identifies new events for new measurements. For both the KPLS and ORKPLS methods, the SPE index is calculated as the sum of the squares of the residuals. The SPE index is characterized by its sensitivity to model errors and, on the other hand, its dependence on the number of retained components. Therefore, in this paper, we focus on the SPE index, which can be expressed as follows:

SPE=‖X−X^‖2=‖(I−W^W^T)X‖(16)

However, the confidence threshold is presented using χ2 the distribution.

SPE(k)⟩gχh,α2(17)

where g=2ba and h=2a2b

a is the estimated mean of the SPE and b is the variance of the SPE.

To explain the principle of the above kernel methods. The flowcharts of the KPLS and the proposed OKPLS approaches are presented in Figs. 2 and 3.

Figure 2: The flowchart of the KPLS approach based SPE chart

Figure 3: The flowchart of the proposed OKPLS approaches based SPE chart

3  Soil Analysis

In this paper, we aimed to secure and control soil quality in northern Greece [5]. This study was conducted to verify the impact of soil quality characteristics such as pH (Pondus Hydrogenii), Organic Matter (OM), Electric Conductivity (EC), major elements (N, P, K, Mg), and microelements (Fe, Zn, Mn, Cu, B) on plant nutrition. To ensure high-quality agriculture and promote plant health, 781 survey points were analyzed across the study area, as illustrated in the following figure.

3.1 Data Description

The soil data consisted of a set of soil information collected between 2015 and 2019. From each survey point, as shown in Fig. 4, 16 soil parameters were measured, resulting in a total of 12,480 data points. The altitude of the study area ranges from 500 m above sea level to 900 m further north, covering approximately 270 km2. Finally, the raw data was compiled and stored in an XLSX file. All these results were carried out by the Soil and Water Research Institute (SWRI) by the administrative authorities of the region of West Macedonia, Greece.

Figure 4: The main study area and survey points in Greece

3.2 Value of the Data

The soil quality monitoring network was operational in Thessaloniki, Greece. It is composed of 16 parameters to be monitored and distributed over several sites: pH, OM, EC, CaCO3, N-NO3, P, K, Mg, Fe, Mn, Zn, Cu, B. The observation vector x(k) contains 16 monitored variables named v1 to v16, which corresponds to pH, OM, EC, CaCO3, N-NO3, P, K, Mg, Fe, Mn, Zn, Cu, B, ad are represented as follows:

x(k)=[v1(k)v2(k)v3(k)…v10(k)v11(k)v12(k)…v14(k)v15(k)v16(k)]T(18)

3.3 Simulation Results

In this section, the proposed fault detection and monitoring strategy is applied to the diagnosis of a soil analysis monitoring network.

The detection performances used in this paper are:

•   False Alarm Rate (FAR)

FAR=Violated samplesFaultess data%(19)

•   Good Detection Rate (GDR):

GDR=Detected faultFaulty region%(20)

•   Computation Time (CT)

In this study, fault detection utilizes the RBF (radial basis function) kernel. Consequently, kernel parameters must be determined based on the reduced dataset size and false alarm rate (FAR) values under normal operating conditions. The optimal values for these parameters are identified using the Tabu search algorithm. In our case, optimality corresponds to a lower FAR and a smaller reduced data matrix size. A total of 781 observations were analyzed: 181 observations served as training data to develop the reduced ORKPLS model, while 600 observations were processed as test data to evaluate the fault detection algorithms. The number of reduced observations is 19, representing 10.49% of the training dataset.

3.3.1 Fault Detection Based on the KPLS Method

In this section, fault detection performance using the KPLS method is presented. To demonstrate its application, simulated faults are introduced across multiple variables, as depicted in the figures below. The FD results for the KPLS-based SPE method are illustrated in Fig. 5. This figure illustrates the temporal progression of SPE indices during a simulated bias fault in the parameter ‘ Zn’ , injected between time steps 250 and 350.

Figure 5: Monitoring faults in the parameter Zn using KPLS method in sample intervals of [250, 350]

Fig. 6 presents the temporal evolution of different SPE indices using the KPLS method. In this case, the bias fault was between times 300 and 500 for the ‘pH’ parameter.

Figure 6: Monitoring faults in the parameter pH using KPLS method in sample intervals of [300, 500]

3.3.2 Fault Detection Based on the Proposed ORKPLS Method

This section presents the fault detection phase using the developed ORKPLS method. The following figures present show the detection performance using the SPE index for the ORKPLS method. The FD results of the ORKPLS-based SPE method are illustrated in Fig. 7. This figure presents the temporal evolution of different SPE indices when injecting a bias fault between times 250 and 350 for the parameter ‘Zn’.

Figure 7: Monitoring faults in the parameter Zn using ORKPLS method in sample interval of [250, 350]

Fig. 8 presents the temporal evolution of the different SPE indices using the RKPLS method. In this case, the bias fault was between times 300 and 500 for the ‘pH’ parameter.

Figure 8: Monitoring faults in the parameter pH using ORKPLS method in sample interval of [300, 500]

From the results obtained using the KPLS and proposed ORKPLS methods, we observe that the defects were well detected with a high good detection rate (GDR), nearly 100%. Regarding the rate of false alarms, the KPLS method produced a FAR of 6.4 for the defect related to the Zn parameter and a FAR of 7.5 for the pH parameter. In contrast, the ORKPLS method demonstrated minimal FAR compared to the other methods, with FARs of 2.8 and 3.25 for the Zn and pH parameters, respectively.

Figs. 9–11 show the experimental results of the proposed ORKPLS, KPLS, Reduced Kernel Principal Component Analysis (RKPCA) and KPCA techniques. We note that the proposed OKPLS presents a higher performance compared to other techniques.

Figure 9: FAR performance for proposed ORKPLS, KPLS, RKPCA and KPCA methods

Figure 10: GDR performance for proposed ORKPLS, KPLS, RKPCA and KPCA methods

Figure 11: CT performance for proposed ORKPLS, KPLS, RKPCA and KPCA methods

Table 1 summarizes the detection performance of several soil parameters, using the proposed ORKPLS, KPLS, RKPCA, and KPCA detection methods.

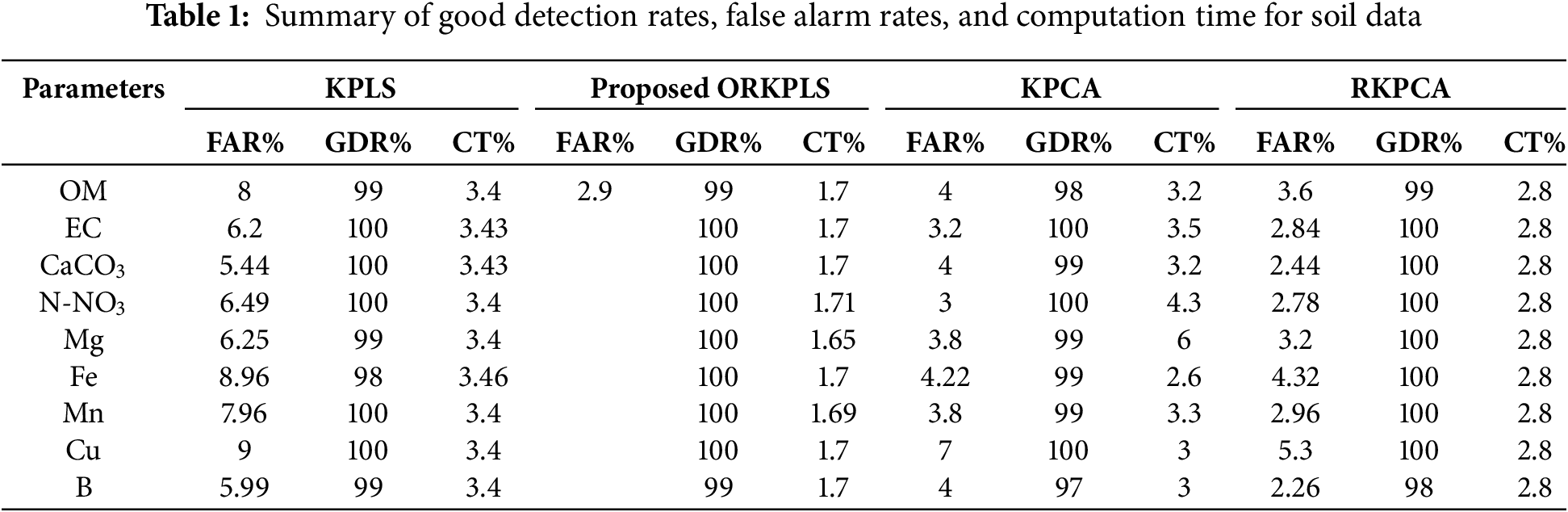
As can be seen in Table 1, all four methods can detect defects well with high detection rates. On the other hand, we notice that the proposed ORKPLS method has a minimal false alarm rate compared to the other techniques.

According to Table 1, the ORKPLS method presents good results compared to other methods thanks firstly to the Tabu search method which allows to determine the parameters and the optimal indices of the kernel matrix which presents the most important axis for the detection of defects. On the other hand, the ORKPLS method allows treating just the important data and is rich in information. Thanks to this step, we obtain good performances in terms of FAR and calculation time. Thus, according to several researchers, the KPLS method presents by nature good performances in the detection of defects. Thus, by using the principles of reduction and optimization, the proposed method ORKPLS shows its effectiveness compared to other methods. This proposed method is essentially to monitor the state and environmental impact on the soil. As soon as the soil parameter rate increases through the proposed ORKPLS method, any environmental change that influences the soil parameters is easily detected.

4  The Air Quality Monitoring Network (AIRLOR)

To further demonstrate the effectiveness of the proposed ORKPLS method, we will use another database that consists of determining air quality. The air quality monitoring network (AIRLOR) installed in Lorraine, (France) consists of 20 stations located essentially and mainly in rural, peri-urban, and urban sites [20]. The input data matrix contains 18 variables, which contain the ozone concentration O3, NO, and NO2, respectively, named scv1 to scv18 of each station.

x(k)=[scv1(k)scv2(k)scv3(k)⏟Station1…scv10(k)scv11(k)scv12(k)⏟Station2…scv16(k)scv17(k)scv18(k)⏟Station6]T(21)

The RBF kernel values are used, and the optimal parameter of the kernel function is computed using the TS (Tabu Search) algorithm. Then, 500 samples were collected from the AIRLOR system to prove the performance of the ORKPLS method. One bias fault is introduced. The Fault is an additive fault by adding 30% of the standard O3 variation from station v4, between observations 250 and 350. To evaluate the obtained results, Figs. 12 and 13 depict the fault detection results of the KPLS method and the ORKPLS-based SPE technique.

Figure 12: Monitoring faults in the parameter ozone O3 using KPLS method

Figure 13: Monitoring faults in the parameter ozone O3 using ORKPLS method

The following Table 2 summarizes the detection performance for several soil parameters, using proposed ORKPLS, KPLS, RKPCA, and KPCA detection methods for the AIRLOR process to verify the effectiveness of the proposed method.

From these results, we notice that the proposed ORKPLS method presents good capabilities for fault detection. The proposed method proves its effectiveness with another database. In this case, using real data, the ORKPLS method presents good results in terms of false alarm rate, as well as the computation time thanks to the observation reduction principle and the choice of optimal parameter. The proposed method can be applied firstly for several types of databases and, secondly a large number of observations. Their profitability is dedicated firstly to the principle of observation reduction and keeping only useful and relevant information. Thus, the choice of optimal kernel parameters with taboo search improves the detection quality. From the results obtained, it is noted that the proposed ORKPLS method essentially presents a minimal false alarm rate compared to the RKPCA, KPCA method, and even compared to the classical KPLS method, which are methods developed in the literature. It is also noted that the proposed method has a minimal calculation time, thanks to the principle of parameter reduction and optimization, compared to the methods developed in the literature (KPLS, KPCA, RKPCA). Thus, the proposed method has an acceptable detection rate compared to the method developed in the literature.

5  Conclusion

Soil safety and agriculture are critical for ensuring good health. This study presents four kernel methods for fault detection aimed at controlling soil parameters, with faults being detected as soon as values exceed their normal range. We note that the proposed ORKPLS method demonstrates strong fault detection performance. Specifically, the developed ORKPLS approach shows a minimal false alarm rate compared to the other methods. To properly manage the environment and ensure the quality of agricultural soil, we used the ORKPLS method to monitor soil parameters and intervene as necessary. Based on real data collected from the soil, it can be concluded that the ORKPLS approach is effective in detecting faults when parameter quantities exceed their normal range. This method is capable of detecting potential excesses of necessary products for any soil type at any time. Currently, the proposed ORKPLS method is designed for offline scenarios. However, to monitor soil parameters in real-time, the algorithm must be adapted to detect anomalies affecting the soil’s chemical characteristics. For future work, a dynamic version of the ORKPLS method could be explored to enable online detection of soil parameters and facilitate timely decision-making.

Acknowledgement: The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number (0226-1443-S).

Funding Statement: This work was supported by the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number (0226-1443-S).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Khaoula Ben Abdellafou, Kamel Zidi; draft manuscript preparation: Khaoula Ben Abdellafou, Kamel Zidi; funding acquisition and supervision: Ahamed Aljuhani, Okba Taouali, Mohamed Faouzi Harkat. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors. The data that support the findings of this study are available from the Corresponding Author, Okba Taouali, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Pozza L, Field D. The science of soil security and food security. Soil Secur. 2020;1(3):100002. doi:10.1016/j.soisec.2020.100002. [Google Scholar] [CrossRef]

2. Amundson R, Berhe A, Asefaw H, Jan W, Olson C, Sztein A, et al. Soil and human security in the 21st century. Science. 2015;348(6235):1–8. doi:10.1126/science.1261071. [Google Scholar] [PubMed] [CrossRef]

3. Suchithra MS, Pai ML. Improving the prediction accuracy of soil nutrient classification by optimizing extreme learning machine parameters. Inf Process Agric. 2020;7(1):72–82. doi:10.1016/j.inpa.2019.05.003. [Google Scholar] [CrossRef]

4. Zhu M, Wang J, Yang X, Zhang Y, Zhang L, Ren H, et al. A review of the application of machine learning in water quality evaluation. Eco-Environ Health. 2022;1(2):107–16. doi:10.1016/j.eehl.2022.06.001. [Google Scholar] [CrossRef]

5. Tziachris P, Aschonitis V, Metaxa E, Bountla A. A soil parameter dataset collected by agricultural farms in northern Greece. Data Brief. 2022;43(1):108408. doi:10.1016/j.dib.2022.108408. [Google Scholar] [PubMed] [CrossRef]

6. Hamrouni I, Lahdhiri H, Abdellafou K, Taouali O. Fault detection of uncertain nonlinear process using reduced interval kernel principal component analysis (RIKPCA). Int J Adv Manuf Technol. 2022;106(9–10):4567–76. doi:10.1007/s00170-019-04889-3. [Google Scholar] [CrossRef]

7. Guo F, Xu Z, Ma H, Liu X, Gao L. On optimizing hyperspectral inversion of soil copper content by kernel principal component analysis. Remote Sens. 2024;16(16):2914. doi:10.3390/rs16162914. [Google Scholar] [CrossRef]

8. Zhang Y, Ma C. Fault diagnosis of nonlinear processes using multiscale KPCA and multiscale KPLS. Chem Eng Sci. 2011;66(1):64–72. doi:10.1016/j.ces.2010.10.008. [Google Scholar] [CrossRef]

9. Jia Q, Zhang Q. Quality-related fault detection approach based on dynamic kernel partial least squares. Chem Eng Res Des. 2016;106(1):242–52. doi:10.1016/j.cherd.2015.12.015. [Google Scholar] [CrossRef]

10. Liu X, Zhou S. Quality-related fault detection based on approximate kernel partial least squares method. J Grid Comput. 2023;21(2):29. doi:10.1007/s10723-023-09670-1. [Google Scholar] [CrossRef]

11. Choi SW, Lee C, Lee J, Park J, Lee I. Fault detection and identification of nonlinear processes based on kernel PCA. Chemom Intell Lab Syst. 2005;75(1):55–67. doi:10.1016/j.chemolab.2004.05.001. [Google Scholar] [CrossRef]

12. Lahdhiri H, Said M, Abdellafou K, Taouali O, Harkat MF. Supervised process monitoring and fault diagnosis based on machine learning methods. Int J Adv Manuf Technol. 2019;102(5–8):2321–37. doi:10.1007/s00170-019-03306-z. [Google Scholar] [CrossRef]

13. Li G, Alcala CF, Qin SJ, Zhou D. Generalized reconstruction-based contributions for output-relevant fault diagnosis with application to the Tennessee Eastman process. IEEE Trans Control Syst Technol. 2011;19(5):1114–27. doi:10.1109/TCST.2010.2071415. [Google Scholar] [CrossRef]

14. Chine W, Mellit A, Pavan AM, Kalogirou SA. Fault detection method for grid-connected photovoltaic plants. Renew Energy. 2014;66:99–110. doi:10.1016/j.renene.2013.11.073. [Google Scholar] [CrossRef]

15. Schein J, Bushby S, Castro N, House JM. A rule-based fault detection method for air handling units. Energy Build. 2006;38(12):1485–92. doi:10.1016/j.enbuild.2006.04.014. [Google Scholar] [CrossRef]

16. Zina D, Jouni S, Otto L, Tuomas S, Satu R, Heikki H. KF-PLS: optimizing kernel partial least-squares (K-PLS) with kernel flows. Chemom Intell Lab Syst. 2024;254(1):105238. doi:10.1016/j.chemolab.2024.105238. [Google Scholar] [CrossRef]

17. Nguyen V, Golinval J. Fault detection based on kernel principal component analysis. Eng Struct. 2010;32(11):3683–91. doi:10.1016/j.engstruct.2010.08.012. [Google Scholar] [CrossRef]

18. Ben AK, Hadda H, Korbaa O. An improved tabu search meta-heuristic approach for solving scheduling problem with non-availability constraints. Arab J Sci Eng. 2019;44(4):3369–79. doi:10.1007/s13369-018-3525-3. [Google Scholar] [CrossRef]

19. Yue H, Qin J. Reconstruction-based fault identification using a combined index. Ind Eng Chem Res. 2001;40(20):4403–14. doi:10.1021/ie000141. [Google Scholar] [CrossRef]

20. Harkat MF, Mourot G, Ragot J. Sensor failure detection of air quality monitoring network. IFAC Proc. 2000;33(11):529–34. doi:10.1016/S1474-6670(17)37413-X. [Google Scholar] [CrossRef]