An Enhanced VIKOR and Its Revisit for the Manufacturing Process Application

1  Introduction

Decision-making (DM) problems can be found everywhere in our daily lives. Most problems encountered are relatively simple, with a single criterion for decision-making that is easy to evaluate and solve. As a decision problem escalates into a project or a plan, the number of criteria and dimensions that must be considered increases, as do the decision-making constraints. Therefore, a complicated problem of multi-criteria decision-making (MCDM) is formed. MCDM is a mathematical method of determining the optimal alternative to a decision-making problem by considering several criteria. It is widely used by scholars in the fields of operational research and management science [1]. Since conflicting criteria often occur when evaluating options, multi-criteria decision-making techniques are required to analyze and find the optimal solution. Consequently, MCDM has been a rapidly developing decision-making technique in recent years.

VlseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) is a MCDM method proposed by Opricovic [2]. In decision-making process, conflicting criteria often exist, resulting in the fact that every alternative can only meet some criteria simultaneously. VIKOR is a method of ranking alternatives that uses the concept of compromise to deal with conflicting criteria. It uses the evaluation of the decision-maker on each criterion and alternative to define the positive-ideal and negative-ideal solutions of each criterion. The distance between each alternative and the positive and negative ideal solutions is determined. Finally, the index values are calculated to obtain the priority relationship between the alternatives. The greatest advantage of the VIKOR method is its ability to identify a compromise solution acceptable to the decision-maker. It achieves this by providing the maximum group utility for the majority while ensuring the minimum individual regret for the opponent.

Herein, the relevant literature on VIKOR will be classified into four main types of research, as explained below.

(1) Application

This type of literature primarily applies VIKOR as a single method to solve problems encountered in various fields. The relevant literature, applied cases, and main contributions are summarized in Table 1. Moreover, those studies demonstrate that VIKOR is a highly effective decision-making tool across multiple industries, from renewable energy planning to financial performance evaluation. The research highlights its ability to solve complex, multi-criteria problems by offering balanced trade-offs among competing factors. As industries continue to embrace digital transformation and sustainability, VIKOR is poised to become even more relevant in data-driven and AI-assisted decision-making frameworks.

The VIKOR method has been suggested for use in this category among various MCDM comparisons. The relevant literature on VIKOR with other methods of comparison is shown in Table 2. Those studies reinforce VIKOR’s growing role in environmental sustainability, disaster risk management, and healthcare decision-making. Its superior performance over other MCDM methods highlights its potential for more complex, uncertain, and high-stakes decision scenarios. As global challenges in climate change, waste management, and natural disasters intensify, VIKOR is a valuable decision-support tool for policy-makers, researchers, and industry leaders.

This category mainly combines VIKOR with other decision-making technologies. The literature on the integrated approach and its main contribution is summarized in Table 3. Those researches showcase the evolution of VIKOR as a powerful MCDM tool that can be customized for complex decision-making problems by integrating subjective and objective weighting methods, fuzzy logic, and hybrid decision frameworks.

In this category, many scholars have modified the VIKOR method and improved its shortcomings. The literature is summarized in Table 4. The research literature demonstrates the continued evolution of VIKOR as an MCDM tool by integrating advanced mathematical models, fuzzy logic, regret theory, and ranking stability enhancements. The developments have made VIKOR more accurate, flexible, and applicable across industrial, environmental, financial, and behavioral decision-making domains. As decision-making problems grow more complex and data-driven, these enhanced VIKOR methodologies provide valuable frameworks for making balanced, data-driven, and human-centered decisions.

This study explores the spirit and meaning of the VIKOR and consequently focuses on the revised VIKOR. It found that the spirit of VIKOR, which simultaneously aims to maximize group benefits and minimize individual regret, amplified the portion of individual regret in the actual calculation. In addition, the index value has a problem, which magnifies individual regrets. The drawbacks of VIKOR that we observed are explained in detail in Section 2.3 (Observations of VIKOR and Its Variants), which includes several figures to illustrate and highlight these weaknesses. It echoes what previous scholars have mentioned, that VIKOR suffers from rank reversal issues similar to other MCDM methods [25,26]. Therefore, this paper modifies the disadvantages of VIKOR and proposes an enhanced VIKOR to make the decision-making process more objective and rational. The proposed enhanced VIKOR is explained in detail in Section 3 (Proposed Enhanced VIKOR). The specific improvements and their effectiveness are thoroughly discussed in Section 5 (Sensitivity Analysis) and Section 6 (Discussions). This paper verifies that the proposed enhanced VIKOR can be applied to various versions of VIKOR through an example of a manufacturing selection problem.

The remainder of this paper is organized as follows. Section 2 introduces VIKOR, its variants, and its disadvantages. Section 3 describes the improvements contributed by this paper. Section 4 presents an illustrative example. Section 5 conducts a sensitivity analysis to evaluate the robustness and stability of the proposed method under varying criteria weights. Section 6 provides a discussion, comparing the proposed enhanced VIKOR with traditional VIKOR, its variants, and other MCDM methods. Finally, the research draws conclusions in Section 7.

2  VIKOR Method and Its Variants

The following describes the original VIKOR method and the improvement concept of VIKOR that previous scholars have improved. The method of VIKOR is discussed in Section 2.1. Section 2.2 compares the different variants of VIKOR. The disadvantages of VIKOR and its variants are discussed in Section 2.3.

2.1 VIKOR Method

The following is the evaluation analysis process using the VIKOR method.

Step 1. Establishing a decision matrix

The most fundamental part of the MCDM process is the decision matrix, which consists of (1) alternatives, which are all options considered by the decision-maker; (2) criteria, which are the items used to evaluate the options, i.e., the factors that affect the choice of decision-maker; and (3) weight, which is the importance that the decision-maker places on each criterion. The decision matrix of the general type is shown in Table 5, where xmn is the evaluation of the criteria Cn of the alternative Am.

Step 2. Normalize the evaluation

Since some criteria are benefits criteria and some are cost criteria, the units of measurement are different between them and cannot be directly compared. To eliminate the problem of incomparability between criteria, it is necessary to normalize the evaluation. Normalization converts the evaluation between 0 and 1, and into the same direction of polarity to compare the criteria. The normalization of benefits criteria is shown in Eq. (1). The normalization of cost criteria is shown in Eq. (2).

rij=xij−mjMj−mj(1)

rij=Mj−xijMj−mj(2)

where rij is the normalized evaluation of the criteria Cj of alternative Ai; xij is the original evaluation of the criteria Cj of the alternative Ai (i=1,…,m;j=1,…,n); Mj=max(xij) is the best normalized evaluation of criteria Cn; mj=min(xij) is the worst normalized evaluation of criteria Cn.

Step 3. Definition of positive and negative ideal solutions

The best solution under each criterion is defined as the positive ideal solution, as in Eq. (3). The worst solution under each criterion is defined as the negative ideal solution, as in Eq. (4).

rj∗=[maxi(rij)](3)

rj−=[mini(rij)](4)

where rj∗ is the positive solution of criteria Cj; rj− is the negative solution of criteria Cj.

Step 4. Calculate the group utility and individual regret of each alternative

Calculate the distance between the evaluated value of each alternative Ai and the positive ideal solution, multiply it by its respective weight, and sum it up to define the distance between the alternative Ai and the positive ideal solution, that is, the group utility of the alternative Ai, as in Eq. (5); and taking its maximum value as the criterion for the farthest distance from the positive ideal solution, defining it as the individual regret of the alternative Ai, as in Eq. (6).

Si=∑j=1n(Cjweight×(rj∗−rijrj∗−rj−))(5)

Ri=maxj[Cjweight×(rj∗−rijrj∗−rj−)](6)

where Si is the group utility of the alternative Ai; Ri is the individual regret of the alternative Ai; Cjweight is the weight of criteria Cj.

Step 5. Calculate the index value

The advantage of the VIKOR method is that it can consider group utility and individual regret. The evaluated group utility is defined as the proportion of the distance of each alternative Ai from the minimum group utility alternative to the overall group utility distance, which should be as small as possible. The equaiton is shown as Eq. (7).

SiΔ=Si−S∗S−−S∗(7)

where SiΔ is the evaluated group utility of alternative Ai; S∗=min(Si) is the alternative with the minimum group utility of all alternatives; S−=max(Si) is the alternative with the maximum group utility of all alternatives.

The evaluated individual regret is defined as the proportion of the distance of each alternative Ai from the minimum individual regret alternative to the overall individual regret distance, which should be as small as possible. The equation is shown as Eq. (8).

RiΔ=Ri−R∗R−−R∗(8)

where RiΔ is the evaluated individual regret of alternative Ai; R∗=min(Ri) is the alternative with the minimum individual regret of all alternatives; R−=max(Ri) is the alternative with the maximum individual regret of all alternatives.

The index value is the indicator for considering maximum group utility and minimum individual regret of each alternative, as in Eq. (9). The smaller index value is the better alternative.

Qi=Dweight×SiΔ+(1−Dweight)×RiΔ=Dweight×Si−S∗S−−S∗+(1−Dweight)×Ri−R∗R−−R∗(9)

where Qi is the index value of the alternative Ai is the decision mechanism coefficient, which represents the weight of maximizing the group utility; 1−Dweight is the weight of minimizing the individual regret. Decision-makers usually set Dweight to 0.5, while seeking to maximize group utility and minimize individual regret.

Step 6. Rank the alternative

The ranking of the alternatives according to Si, Ri and Qi. The final ranking of the solutions according to the size of Qi when the following two conditions hold, and a smaller Qi means a better solution.

Condition 1: Threshold conditions for acceptable benefits

The difference between the index value Qi of the two neighboring alternatives after ranking must exceed the threshold (1/(M−1)) to determine that the first ranked alternative is better than the second ranked alternative. If there are several alternatives, we should compare the first alternative with the second, third, and last alternative in order to confirm whether the conditions are met between the alternatives, as in Eq. (10).

QA(2)−QA(1) ≥ 1M−1(10)

where QA(2) is the index value of the second ranked alternative; QA(1) is the index value of the first ranked alternative; M is the number of alternatives evaluated.

Condition 2: Acceptable reliability of decision-making

After ranking the alternatives according to the index value Q1, the S of the first ranked alternative (SA(1)) must perform better than the S of the second ranked alternative (SA(2)). On the other hand, the R of the first ranked alternative (RA(1)) must also perform better than the R of the second ranked alternative (RA(2)). If there are several alternatives, then compare the first alternative with the second, third and last alternative in order of compliance. Rules of Judgment:

a.   If the first ranked alternative and the second ranked alternative meet both conditions 1 and 2, then the first ranked alternative is accepted as the best solution.

b.   If the first and the second ranked alternative meet only condition 2, then both the first ranked alternative and the second ranked alternative are accepted as the best solution.

2.2 VIKOR Method’s Variants

The VIKOR method has been developed for more than twenty-five years. Many scholars have improved the flaws of VIKOR. These improved VIKOR methods still retain the spirit of VIKOR that is emphasized, i.e., maximizing group utility and minimizing individual regrets. The following will illustrate where scholars have improved VIKOR, as shown in Table 6.

From Table 6, it can be seen that the improvements and deformations proposed by previous scholars for the VIKOR method can be divided into two main types: (1) improvements Si of Ri: Opricovic [17], Huang et al. [18], Sayadi et al. [19], Vahdani et al. [20], Jahan et al. [21], Liou et al. [22], Devi [24], and Yang et al. [25]. (2) improvement of decision mechanism coefficient Dweight of index value: Opricovic [23].

2.3 Observations of VIKOR and Its Variants

From the previous mentions, two problems have been observed from VIKOR method. This study uses the graphical representation to describe the problems of VIKOR original conception. Assume there are five criteria of the decision problem, and C4 is the worst criteria of alternative Ai, as shown in Fig. 1. Two problems are shown as follows.

Figure 1: Graphical representation of VIKOR original conception

(1) Problem 1: Double counting the worst criterion

The VIKOR method calculates the distance between the positive ideal solution and alternative Ai by using Eq. (5) to sum the difference between the evaluation of all criteria in each alternative and the evaluation of the best criterion, i.e., the group utility of alternative Ai. As shown on the left side of Fig. 1a, there are five blocks stacked on top of each other, which are C1 to C5. In calculating the distance between the negative ideal solution and alternative Ai, Eq. (6) is used to calculate which criterion has the most significant difference between the evaluation and the evaluation of the best criterion in each alternative, i.e., the worst criterion in each alternative or the individual regret of alternative Ai. As shown on the right side of Fig. 1a, there is only the criterion C4 block, which is labeled with a blue background color in this study. Therefore, the evaluation of Ri is already included in the calculation of Si. However, in Eq. (9), Ri is calculated independently in the Qi of each alternative as the basis for ranking each alternative, which is considered unreasonable in this study. When the index value does not consider the decision mechanism coefficient, the graphical representation of the sum of group utility and individual regret is shown in Fig. 1b. The calculation of Qi, not only is Ri double-counted, but it is also equivalent to magnifying the value of Ri and calculating the worst criterion in each alternative Ai twice. In Table 6, although many scholars have improved many kinds of calculations of Si and Ri, they have not taken into account the unreasonable aspects mentioned in this study and still recalculated Ri.

(2) Problem 2: Overestimating the evaluated individual regret

Furthermore, in calculating the index value Qi for each alternative Ai, it can be seen from Eq. (9) that Dweight is the decision mechanism coefficient indicating the weight of evaluated group utility, and 1−Dweight is the weight of evaluated individual regret. When the Dweight setting is greater than 0.5, it means that the decision is made based on the majority decision; when the Dweight setting is less than 0.5, it means that the decision is made based on rejection; and when the Dweight setting is 0.5, it means that both group utility maximization and individual regret minimization are pursued. This part of the study is considered unreasonable because the Si is the sum of all individual criteria evaluations multiplied by their weights, while the Ri is only the result of multiplying one of the criteria evaluations by its weight. If 1−Dweight is set to 0.5, it will aggravate the scoring of Ri, as shown in Fig. 1c. That is, amplify the opposing views, which will easily result in the ranking result of the alternative if one of the criteria is evaluated poorly when evaluating the alternative. Although Opricovic [23] mentioned the unreasonable parts mentioned in this study by changing the equation to Dweight=(n+1)/2n, taking into account the number of criteria included in the Si and Ri values, this paper argues that it does not take into account the importance of the criteria in the Si and Ri, so the improvement by Opricovic [23] is still unreasonable.

3  Proposed Enhanced VIKOR

In Section 2.3, it has been described that the VIKOR method of calculating the index value Qi under Eqs. (5)–(9) will result in duplicated scoring of Ri as well as aggravate the scoring of objections. Therefore, this study proposes an enhanced VIKOR with a reasonable improvement equation for this problem. The graphical representation to describe the enhanced VIKOR conception proposed in this study is shown in Fig. 2. The problem of double counting the worst criterion is improved shown in Fig. 2a,b. The modified concept of overestimating the evaluated individual regret problem is shown in Fig. 2c.

Figure 2: Graphical representation of enhanced VIKOR conception in this study

To solve the problem of double counting the worst criterion, this study redefines the group utility Si. The detail is described in Section 3.1. to solve the problem of overestimating the evaluated individual regret, this study improves the weight of evaluated group utility SiΔ and evaluated individual regret RiΔ. The detail is described in Section 3.2. The flowchart of the proposed assessment framework of VIKOR is presented in Fig. 3.

Figure 3: The flowchart of proposed framework of the enhanced VIKOR

From Fig. 3, the process is divided into two stages. The first phase primarily involves data input before the alternative evaluation, including the selection of various criteria, confirmation of the total number of alternatives, and the corresponding weight distribution for the relevant criteria. The second phase serves as the core of alternative selection, mainly focusing on the execution steps of the proposed method. A detailed explanation of these steps will be presented in Section 4.2. Herein, only a brief overview of the procedure is provided.

Step 1. Establish the decision matrix

Step 2. Normalize the evaluation

Step 3. Definition of positive and negative ideal solutions

Step 4. Calculate the group utility and individual regret of each alternative

Step 5. Calculate the index value

Step 6. Rank the alternatives

3.1 The Improved Definition of Group Utility Si

Si represents the total value of the distance between all criteria and the positive ideal solution for each alternative Ai, and Ri is the difference between the evaluation of the criterion and the evaluation of the best criterion among all criteria for each alternative Ai. Therefore, the value of Si already includes the value of Ri. In order not to allow double counting of Ri, this study considers that the worst evaluation of Ri should not be summed up in the calculation of Si, as shown in Fig. 2a. When the index value does not consider the decision mechanism coefficient, the graphical representation of the sum of group utility and individual regret is shown in Fig. 2b. The index value of each alternative takes into account all the criteria and none of them are double-counted. Assuming that there are j criteria (j=1,2,…,λ,…,n) and the worst evaluation is Rλ, the calculation of Si should be corrected as in Eq. (9) by excluding the Rλ when summing up the evaluation of the criteria. The Eq. (11) replaces the Eq. (5).

Si=∑j=1,j≠λnCjweight(rj∗−rijrj∗−rj−)=∑j=1nCjweight(rj∗−rijrj∗−rj−)−Ri(11)

3.2 Improving Weight of Evaluated Group Utility SiΔ and Evaluated Individual Regret RiΔ

Since Si is the sum of the evaluation scores, Ri is only the evaluation score for one of the criteria. If Dweight is assigned to 0.5, it will increase the score of Ri and does not consider the importance of the worst criteria affecting the alternative. The decision mechanism coefficient Dweight should take into account the effect of influence of the weights contained in Si and Ri. Assuming there are ten criteria, the traditional VIKOR sets Dweight to 0.5, then 1−Dweight is 0.5. Using the calculation of Opricovic [23], then Dweight is 0.55 and 1−Dweight is 0.45. If the weight of the criterion in Ri is only 0.01, i.e., the effect of this criterion in Ri on the alternative Ai is only 0.01, then the value of Ri is scaled up by using the traditional VIKOR and Opricovic [23] algorithms. On the contrary, if the criterion weight in Ri is 0.7, i.e., the criterion in Ri has a significant of 0.7 on alternative Ai, the impact of Ri on alternative Ai is not well taken into account through the algorithm of VIKOR and Opricovic [23]. As shown in Fig. 2c, when group utility and individual regret consider the criteria weights, individual regret will not be magnified. As can be seen from Fig. 1c, individual regret C4 is magnified significantly. However, adding the weight of the consideration criterion itself returns C4 to the original type, as shown in Fig. 2c. This paper believes that the evaluated individual regret RiΔ should not influence the overall decision score, and the weight of each criterion should be taken into consideration to reduce the impact of RiΔ and further decrease the interference. Therefore, this paper suggests that the criterion weight should be considered for evaluated group utility SiΔ and evaluated individual regret RiΔ without affecting the decision-maker’s preferences. Assuming there are j=1,2,…,λ,…n criteria, the worst evaluation value Ri is criterion Cλ. The index value is as in Eq. (12), which replaces the Eq. (9).

Qi′=Dweight×((1−Cλweight)×Si−S∗S−−S∗)+(1−Dweight)×(Cλweight×Ri−R∗R−−R∗)(12)

4  Illustrative Example

4.1 Background Description

There are many problems in the manufacturing industry that can be solved with the MCDM approach, including process selection, risk management, material selection, supplier selection, and performance evaluation. In addition, the issue of manufacturing process selection problems has been a concern for numerous scholars [27]. For example, process selection for water pump [28,29], process selection for additive manufacturing [30–32], and selection of lean production methods [33]. This study refers to the case study of Nabeeh et al. [29] evaluating the process of manufacture water pump. The water pump manufacturing process serves as an excellent case study for the proposed methods because it involves complex trade-offs, real-world industrial challenges, and sustainability considerations. Applying the enhanced VIKOR approach of this study can effectively balance factors such as material selection, manufacturing cost, energy efficiency, production efficiency and product quality. It’s bringing substantial cost benefits and competitive advantages to the company.

4.2 Calculation for Alternative Selection

This paper selects the best manufacturing process according to the steps in Section 2.1, but the steps 4–5 are based on the enhanced VIKOR proposed in the paper in Section 3.

Phase 1: Preparatory work

There are five manufacturing process selection, including gravity die casting, investment casting, pressure die casting, sand casting, and additive manufacturing. The seven criteria are presented in Table 7.

Step 1. Establish the decision matrix

This problem is prioritizing the manufacturing process of five alternatives and considering seven criteria. The decision matrix is presented in Table 8. In the case study by Nabeeh et al. [29], the criteria weights were determined using the AHP method.

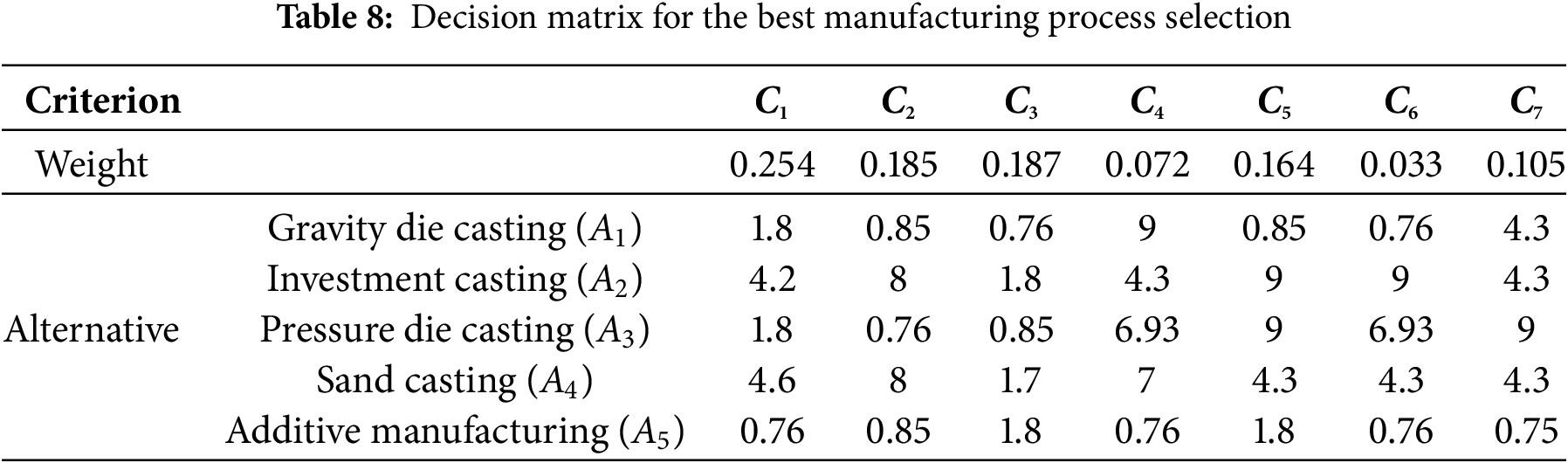
Step 2. Normalize the evaluation

This paper uses Eqs. (1) and (2) to normalize and convert the evaluation of each criterion into a number 0 and 1, shown in Table 9.

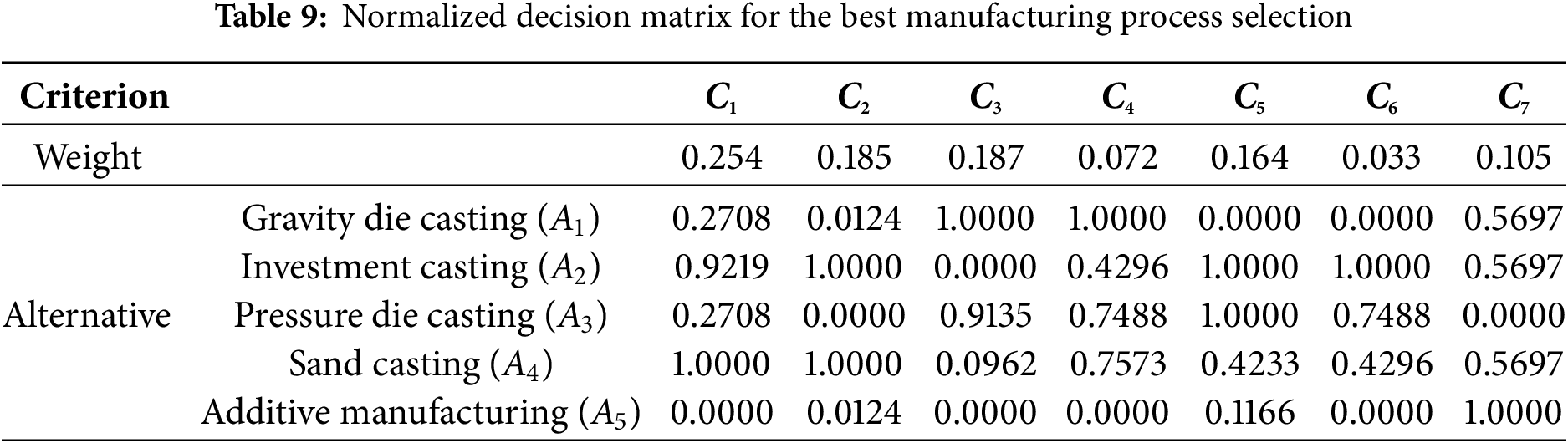
Phase 2: Decision supporting- enhanced VIKOR

This paper follows the steps of the proposed enhanced VIKOR in Section 3 to select the best manufacturing process.

Step 3. Definition of positive and negative ideal solutions

Using Eqs. (3) and (4) to define the positive as well as the negative ideal solution for each criterion, and the positive ideal solution is the highest evaluation value, as shown in Table 10.

Step 4. Calculate the group utility and individual regret of each alternative

This steps follow Eqs. (11) and (6) to calculate the group utility and individual regret, as shown in Table 11.

Step 5. Calculate the index value

This step follows Eqs. (7), (8) and (12) to calculate index value. The decision mechanism coefficient Dweight is setting to 0.5, while seeking to maximize group utility and minimize individual regret. The results are shown in Table 12.

Step 6. Rank the alternatives

This paper uses a total number of twenty-two MCDM methods to solve this problem. The selection includes ten VIKOR variants, all exhibiting the two issues identified in this study, including the traditional VIKOR [2], fuzzy VIKOR [17], revised VIKOR [18], interval VIKOR [19], interval fuzzy VIKOR [20], comprehensive VIKOR [21], modified VIKOR [22], modified VIKOR [23], intuitionistic fuzzy VIKOR [24], R-VIKOR [25]. This allows us to assess whether the proposed improvements effectively address these problems. Additionally, we included widely used MCDM methods with different decision-making philosophies to examine whether the ranking results remain consistent across various approaches, ensuring robustness, including simple average weight (SAW) [34], TOPSIS [35], multi-objective optimization on the basis of ratio analysis (MOORA) [36], WASPAS [37], multi-attributive border approximation area comparison (MABAC) [38], EDAS [39], multiattributive ideal-real comparative analysis (MAIRCA) [40], combined compromise solution (CoCoSo) [41]. Finally, we incorporated newly developed MCDM methods to compare the competitiveness and effectiveness of the enhanced VIKOR against the latest decision-making techniques, including MARCOS [42], ranking of alternatives through functional mapping of criterion sub-intervals into a single interval (RAFSI) [43], and alternative ranking order method accounting for two-step normalization (AROMAN) [44].

The results show that investment casting (A2) is chosen as the best manufacturing process for water pump of the proposed enhanced VIKOR and Nabeeh et al. [29]. The traditional VIKOR and nine VIKOR variants think sand casting (A4) is the best manufacturing process. The results of the ranking of the twenty-three techniques are shown in Table 13.

As shown clearly in Table 13, the evaluation of the water pump manufacturing process using the enhanced VIKOR method identified investment casting (A2) as the optimal choice among the five manufacturing processes. This selection is attributed to its superior performance in high productivity (C1), high accuracy (C2), high material utilization (C5), and high quality (C6). These advantages contribute to the company’s cost efficiency and competitive advantage as detailed below:

(1)   Cost efficiency:

Investment casting (A2) achieved the highest score of 1.0 in high material utilization (C5), indicating near-zero material waste. This significantly reduces raw material consumption and scrap costs. Moreover, as investment casting is a precision molding process, it minimizes the need for secondary machining, effectively shortening the production cycle and further reducing labor and equipment costs.

These factors collectively lead to substantial cost savings and enhanced cost efficiency for the company.

(2)   Competitive advantage:

Investment casting demonstrates exceptional performance in accuracy (C2) and quality (C6), both scoring 1.0, ensuring high dimensional accuracy and superior surface finish. This reduces the need for post-processing and inspection, thereby lowering associated costs. Additionally, the high-quality output leads to fewer after-sales issues and lower return rates, which enhances customer satisfaction, brand reputation, and brand loyalty.

Furthermore, investment casting (A2) shows a score of 0.92 in productivity (C1), reflecting its efficient production cycles and high output capacity, enabling the company to respond swiftly to market demands.

The high material utilization (C5) not only reduces raw material and energy consumption but also lowers production costs and carbon emissions, supporting the company’s green branding strategy and competitive positioning.

Through the above analysis, it is evident that the selection of investment casting (A2) significantly enhances the company’s competitive advantage in the industry, ensuring a cost-effective, high-quality, and environmentally friendly manufacturing process.

5  Sensitivity Analysis

Sensitivity analysis was conducted to examine the robustness of the decision-making results under varying conditions by systematically adjusting the weights of the evaluation criteria. This section investigates how changes in the relative importance of criteria affect the ranking. The preferences of decision-makers were represented using ordered weighted averaging (OWA) weights, with the calculation formula shown in Eq. (13). Preference intensities ranged from 0.1 to 0.9, covering nine distinct levels. Based on these intensities, nine sets of weights were generated for the seven criteria to evaluate the sensitivity of the rankings.

Cjweight=(jn)1−αα−(j−1n)1−αα(13)

where α is the attitude preferences of decision-makers. The weight distribution results of the OWA method are shown in Table 14 and Fig. 4.

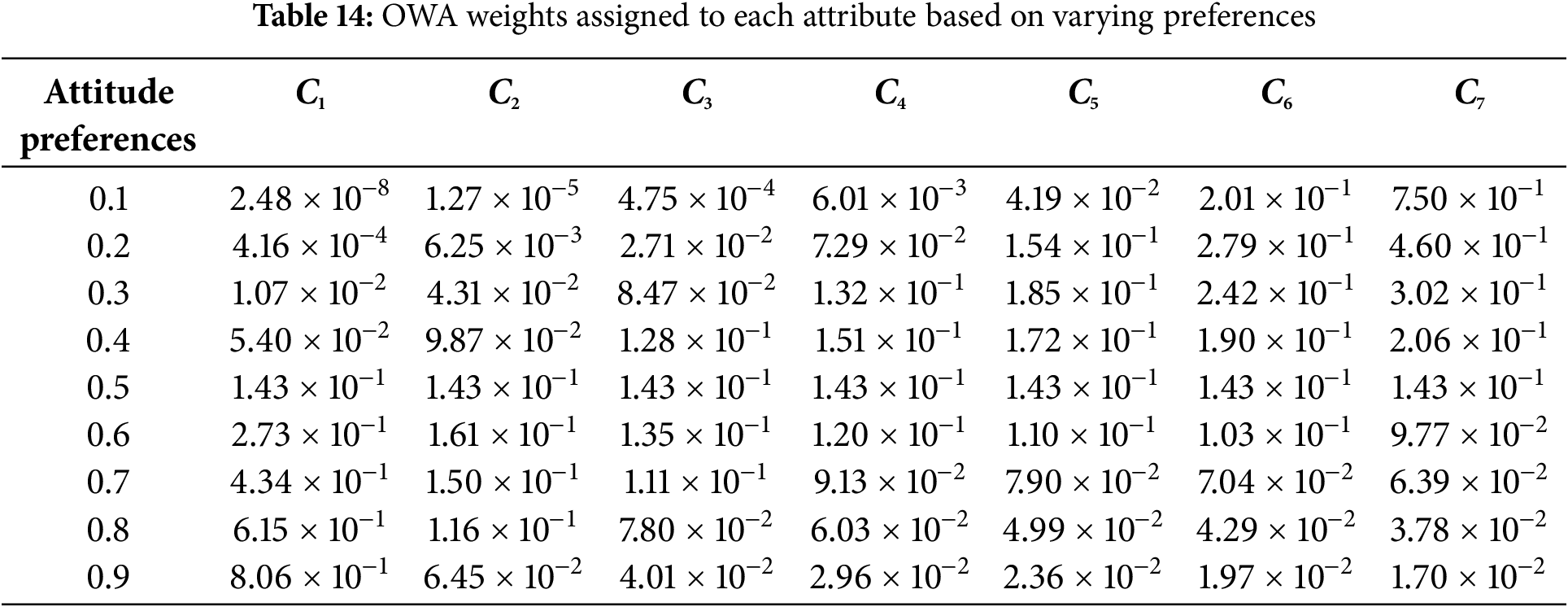
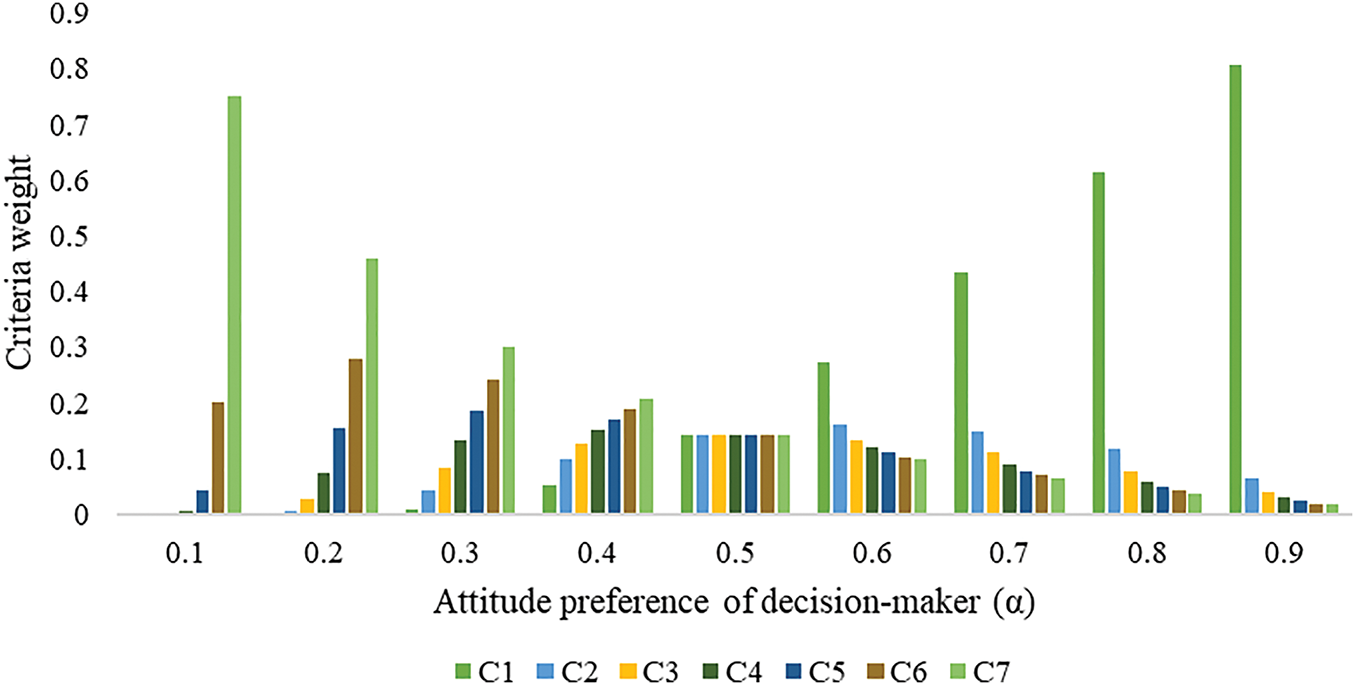
Figure 4: OWA weights with different attitude preferences of decision-makers

Table 15 displays the ranking results with OWA wights under different attitude preferences of decision-makers. Due to the large amount of data, this section presents the ranking results for preference attitudes at 0.3, 0.5, and 0.7 as representative examples.

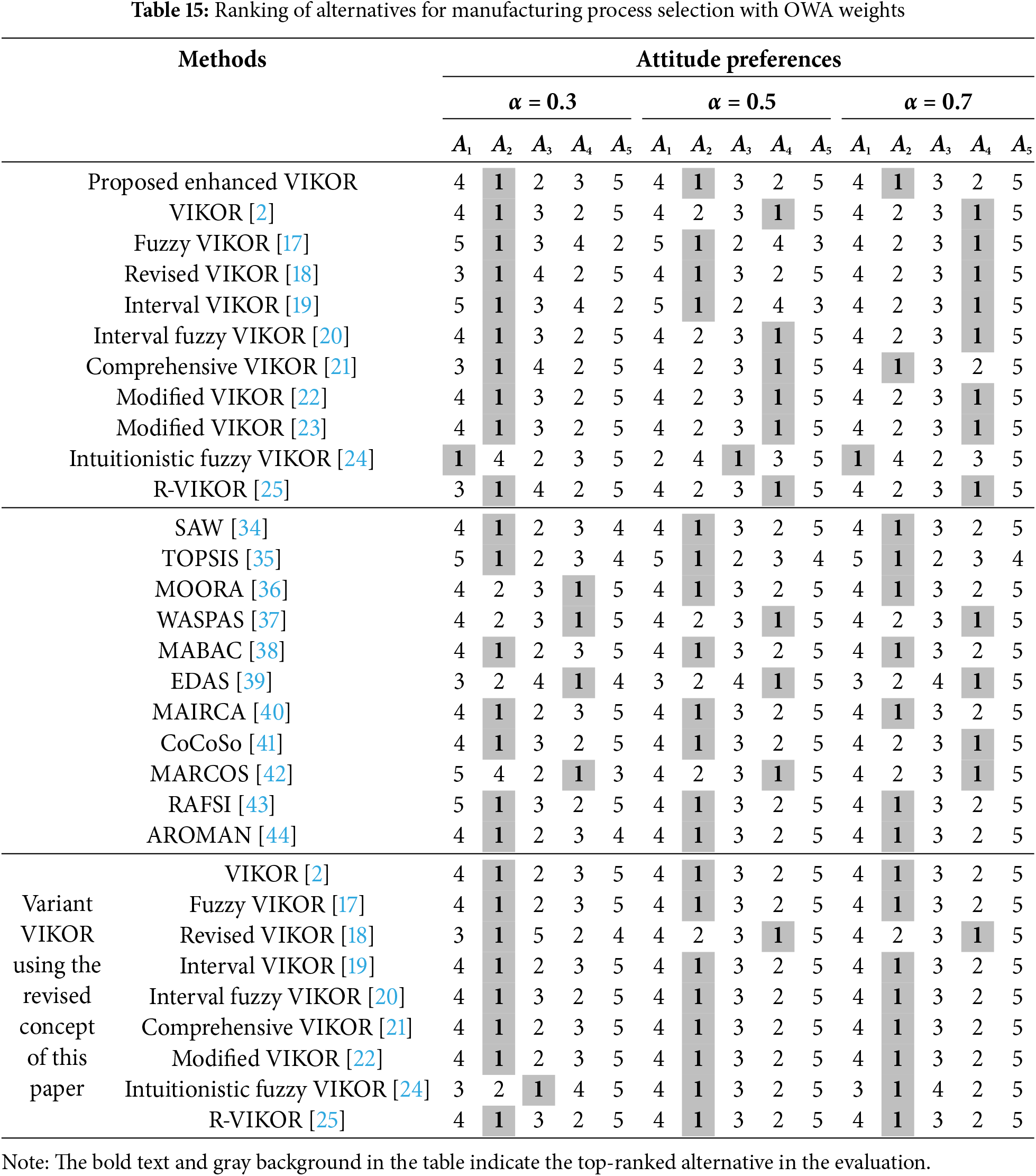
(1)   Table 15 shows that regardless of the attitude preference being 0.3, 0.5, or 0.7, the enhanced VIKOR proposed in this paper consistently selects A2 as the best process method. Additionally, most other MCDM methods also identify A2 as the optimal choice, reinforcing the robustness and reliability of the proposed method.

(2)   When α = 0.3, among the variant VIKOR methods, only Intuitionistic Fuzzy VIKOR does not select A2 as the best alternative, ranking it 4th instead. In contrast, most other MCDM methods support A2 as the optimal process. When the improved concept proposed in this paper is applied to different VIKOR variants, it is observed that intuitionistic Fuzzy VIKOR is still the only method that does not rank A2 as the top choice. However, a significant improvement can be seen, with A2 rising from 4th to 2nd position, demonstrating an explicit correction in the ranking.

(3)   When α = 0.5, the proposed enhanced VIKOR and most MCDM methods select A2 as the best process. Only three of the ten VIKOR versions identify A2 as the top alternative. However, after applying the proposed correction concept to different VIKOR versions, it is observed that only Revised VIKOR still ranks A4 as the best option. All other VIKOR versions successfully achieve the correction, recognizing A2 as the optimal process method. This demonstrates the effectiveness of the proposed improvements in enhancing consistency across different VIKOR variants.

(4)   When α = 0.7, the proposed enhanced VIKOR and most MCDM methods consistently select A2 as the best process method. Only four of the ten VIKOR versions identify A2 as the top choice. Incorporating the proposed correction concept into different VIKOR versions shows that Revised VIKOR is the only method still ranking A4 as the best option. The remaining VIKOR variants successfully adopt the correction, ranking A2 as the best process, highlighting the correction’s effectiveness in improving the ranking consistency and decision accuracy.

(5)   Fig. 5a presents the ranking results of different VIKOR versions when the attitude preference is 0.5. It is evident from the radar chart that the rankings for A2 vary significantly across the original VIKOR versions. While some versions identify A2 as the top choice, others rank it much lower. This inconsistency indicates a lack of stability and reliability in the original VIKOR versions. Fig. 5b shows the ranking results after applying the proposed correction concept. The radar chart clearly illustrates the improved consistency and stability of the rankings, with nearly all VIKOR versions now identifying A2 as the top alternative. This significant improvement demonstrates the effectiveness of the proposed enhancement in reducing ranking bias and increasing reliability across different VIKOR versions.

(6)   The enhanced VIKOR proposed in this paper demonstrates exceptional stability, proving its robustness under varying decision-maker preference intensities. In contrast, the traditional VIKOR and its variants exhibit noticeable ranking fluctuations across different α values, indicating a higher sensitivity to weight changes for some alternatives. The sensitivity analysis highlights the importance of method selection in ensuring stability and reliability in decision-making.

Figure 5: Sensitivity analysis of variant VIKOR when α = 0.5

6  Discussions

The VIKOR method uses the performance for each criterion and the alternative of decision-makers to define the positive and negative ideal solutions for each criterion. The distance between each solution and the positive and negative ideal solutions was calculated. In the last step, the index value is obtained to obtain the relationship between the advantages and disadvantages of the alternatives. However, there are some unreasonable points in calculating the distance between the positive ideal solution and the solution and in deciding the decision mechanism Dweight. Therefore, this paper corrects these two points and verifies them by an example of manufacturing process selection referenced by Nabeeh et al. [29]. According tof Nabeeh et al. [29], investment casting (A2) is the best manufacturing process. Therefore, this paper uses investment casting (A2) as the standard answer for this illustrative example of industrial engineering to compare and analyze the results. Table 13 shows that the enhanced VIKOR proposed in this study select the investment casting (A2) as the best manufacturing process. Among the ten versions of the VIKOR variant, nine VIKOR select the sand casting (A4) as the best manufacturing process. In the other eleven MCDM methods, most of the methods select the investment casting (A2) as the best manufacturing process.

The comparison of the proposed enhanced VIKOR with traditional VIKOR is discussed in Section 6.1. The comparison of the proposed enhanced VIKOR with the variant VIKOR proposed by previous scholars is discussed in Section 6.2. The comparison of adding the revised concept of this paper to the VIKOR proposed by previous scholars is discussed in Section 6.3. Section 6.4 discuss the comparison between VIKOR and other MCDM methods.

6.1 Proposed Enhanced VIKOR vs. Traditional VIKOR

The enhanced VIKOR method proposed in this paper is compared with the traditional VIKOR method for alternative ranking. The traditional VIKOR method considers the sand casting (A4) as the best process. The VIKOR method enhanced in this paper considers the investment casting (A2) as the most outstanding student, and the analysis and discussion are as follows.

(1)   From the index value point of view, the smaller the evaluated individual regret is, the better. In the traditional VIKOR, the evaluated individual regret of A2 is 0.2116, and the evaluated individual regret of A4 is 0.0000. When the decision mechanism is set to 0.5 under the decision preference of the decision maker, the evaluated group utility and the evaluated individual regret will be multiplied by 0.5 and then summed up as the basis for the ranking. However, this study believes this is irrational because the individual regret of A2 is C1. The weight of C1 is 0.1870, which means that C1 is only 18.70% of the importance in the overall decision-making. However, the traditional VIKOR considers the evaluated individual regret to be 100% important. If the significance (weight) of the criterion itself is not taken into account, the score of the evaluated individual regret is 0.2116. Otherwise, if the significance (weight) of the criterion itself is taken into account, the score of the evaluated individual regret is 0.0346, i.e., the traditional VIKOR magnifies the evaluated individual regret by a magnitude of 5.3476 times, which results in the overestimation of the individual regret. Therefore, the enhanced VIKOR proposed in this study considers that both the evaluated group utility and the evacuated individual regret should consider the criterion weight not to overestimate individual regret.

(2)   In the traditional VIKOR method, decision mechanism Dweight is usually set to 0.5, which simultaneously maximizes group utility and minimizes individual regret. If the criterion of individual regret is less important in influencing the decision result, the weight of this criterion is less than 0.5. However, the decision mechanism Dweight set at 0.5 (1−Dweight=0.5) will magnify individual regret. That is, although the criterion has the worst evaluation value, it does not significantly affect on the decision-making result. If individual regret is magnified, it will result in a distorted decision-making result. Therefore, adding the weight of each criterion to the evaluated group utility SiΔ and evaluated individual regret RiΔ can take into account the importance of the criterion itself and the decision-making preferences.

(3)   To summarize the two points above, the traditional VIKOR method double-counts R and magnifies the calculation of individual regrets as a basis for decision-making. The distance between the positive ideal solution and the alternative (S), the evaluated group utility, and the evaluated individual regret are modified in this study. R is subtracted from the calculation of S. The evaluated group utility and the evaluated individual regret consider the criterion weight of each alternative. Therefore, sand casting (A4) was recognized as the best manufacturing process by calculating the traditional VIKOR and VIKOR variants. However, investment casting (A2) was recognized as the best manufacturing process after the enhanced VIKOR method in this study. Therefore, finding the optimal solution through the improved VIKOR proposed in this study makes the results of decision-making more reasonable.

6.2 Proposed Enhanced VIKOR vs. Variant VIKOR

This section compares the VIKOR proposed in this paper with the eight variants of VIKOR improved by previous scholars, including fuzzy VIKOR [17], revised VIKOR [18], interval VIKOR [19], interval fuzzy VIKOR [20], comprehensive VIKOR [21], modified VIKOR [22], modified VIKOR [23], intuitionistic fuzzy VIKOR [24], R-VIKOR [25]. The results showed that the intuitionistic fuzzy VIKOR considered the pressure die casting (A3) the best manufacturing process; all other methods considered the sand casting (A4) the best manufacturing process. The results are analyzed and discussed as follows.

(1)   Among the nine variations of VIKOR proposed by previous scholars, eight selected the sand casting (A4) as the best manufacturing process. Among them, fuzzy VIKOR, interval VIKOR, and interval Fuzzy VIKOR, only change the types of evaluations to fuzzy, interval, and interval fuzzy. Huang et al. [18] used the regret theory to calculate the distance between each alternative and the optimal solution. Comprehensive VIKOR [21] improved the definition of a positive ideal solution. The modified VIKOR [22] only changes the calculation of R. The modified VIKOR [23] modified the decision-making mechanism to consider the number of criteria. Yang and Wu [25] considered the absolute distance between the positive and negative ideal solutions and each solution. None of these variants consider what has been mentioned in this study. Namely, the S calculation includes R, magnifying individual regrets. None of the above eight methods consider the two VIKOR drawbacks mentioned in this study. Therefore, the result of this decision is the same as that of the traditional VIKOR, which selects the sand casting (A4) as the best manufacturing process.

(2)   Revised VIKOR and Modified VIKOR select A2 as the best student. The scholars integrated the regret theory into the traditional VIKOR so that the alternative is only affected by the best solution and not the worst one. Although the revised methods are the same as the first-ranked solution of the enhanced method in this paper, this method still double-counts R, magnifying individual regrets.

(3)   Modified VIKOR [23] has revised the decision mechanism Dweight, but the modification concept is still unreasonable and does not take into account the disadvantages mentioned in this paper. The decision-making mechanism Dweight of the other seven variant VIKOR methods is usually set at 0.5, the same as in the traditional VIKOR method. If the importance of the criterion of individual regret is greater than 0.5, it will decrease individual regret; conversely, it will increase individual regret. Therefore, the evaluated group utility SiΔ should consider and multiply the sum of the group utility criterion weights, while the evaluated individual regret RiΔ should consider and multiply the weight of the individual regret criterion.

6.3 Proposed Enhanced VIKOR vs. Variant VIKOR Using the Revised Concept of This Paper

This section incorporates the modified concepts of distance between the positive ideal solution and the alternative (S), the evaluated group utility (SiΔ), and the evaluated individual regret (RiΔ) proposed in this paper into various VIKOR methods. Since Modified VIKOR proposed by Opricovic [23] has modified the decision mechanism, it is not possible to add the concepts proposed in this paper to this method. The results showed that A2 was considered the best student in eight variants of the VIKOR method, as shown in Table 16. The results of the analysis and discussion are as follows.

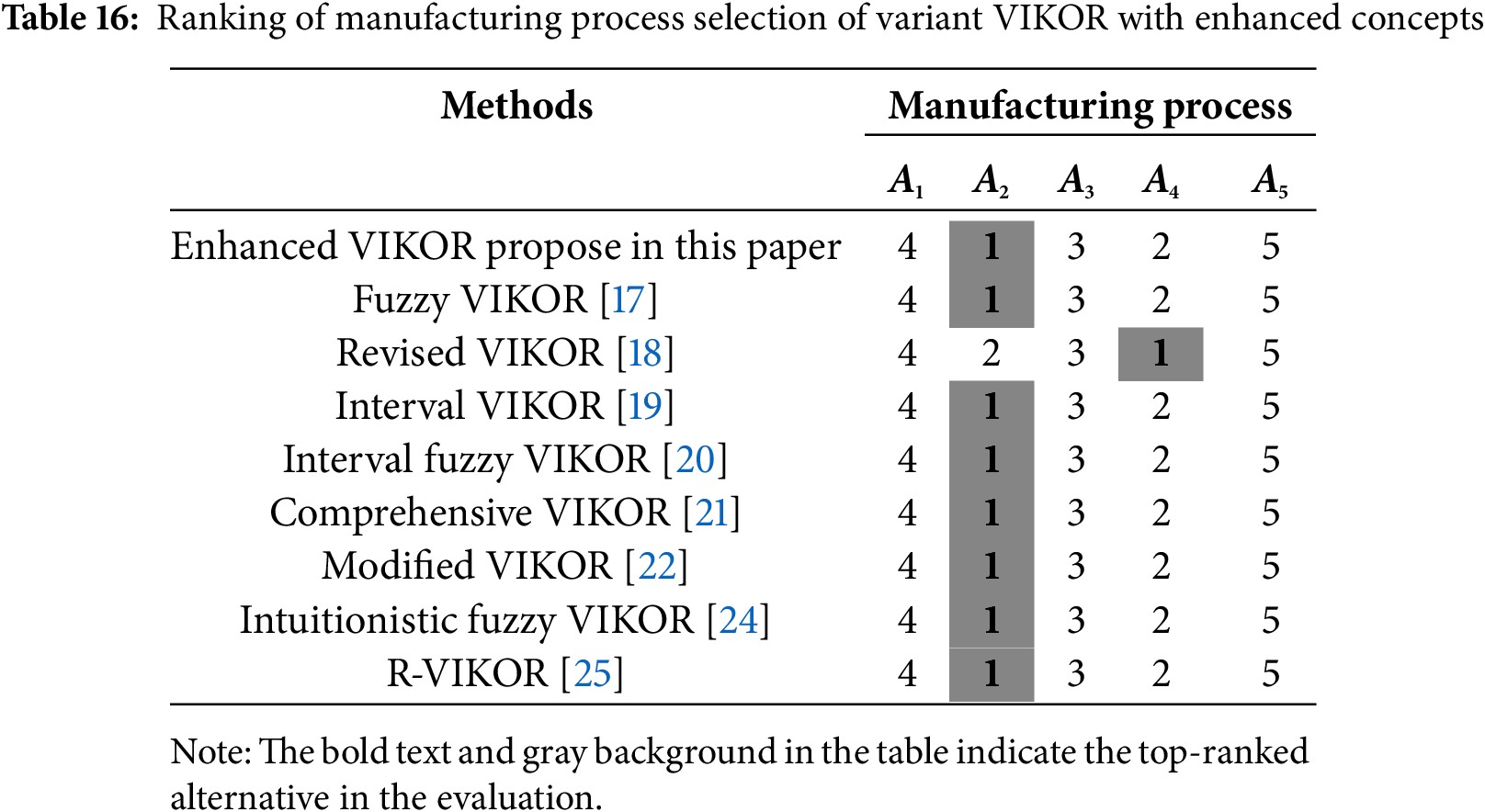
(1)   With the modification of the distance between the positive solution and the alternatives, the above seven methods do not duplicate the calculation of R, nor do they magnify individual regrets. Moreover, by modifying the index value, the evaluated group utility, and the evaluated individual regret have taken into account the significance of individual regrets to the decision-making problem so that individual regrets will not be magnified or reduced. The impact caused by individual regrets can be considered in a comprehensive manner.

(2)   The results of the enhanced VIKOR proposed in this paper and the seven variant VIKOR with the modified concept show that most chose investment casting (A2) as the first-ranked alternative. In addition to validating the methodology of this paper, it makes the ranking of the alternatives more reasonable and makes the ranking of all the methods more consistent.

6.4 Proposed Enhanced VIKOR vs. Other MCDM Methods

This section discusses the comparison between VIKOR and other MCDM methods, highlighting the strengths of VIKOR over existing methods, including SAW, TOPSIS, MOORA, WASPAS, MABAC, EDAS, MAIRCA, CoCoSo, MARCOS, RAFSI, and AROMAN. The discussion focuses on several key aspects:

(1)   Unlike many other methods that prioritize either maximum utility or minimum loss, VIKOR emphasizes a compromise solution by balancing group utility and individual regret. This makes it more suitable for resolving conflicts in MCDM.

(2)   SAW uses a linear weighted sum, which has limited capacity to balance conflicting criteria. TOPSIS ranks alternatives based on their distance from the ideal and anti-ideal solutions but is prone to rank reversal issues. MOORA is simple to compute but lacks discrimination power when alternatives have small differences. WASPAS combines additive and multiplicative aggregation, which may cause bias toward highly weighted criteria. MABAC is sensitive to weight changes and can be difficult for decision-makers to interpret. EDAS focuses on the average solution but may overlook extreme values, causing ranking bias. MAIRCA is less commonly used and lacks the concept of a compromise solution. CoCoSo has complex formulas and limited interpretability of results. MARCOS is sensitive to data normalization and scale changes. RAFSI lacks a compromise solution perspective and can be biased toward a single criterion. AROMAN is still in the early stages of development and has fewer real-world applications and case studies compared to more established methods like VIKOR.

(3)   VIKOR demonstrates higher stability across different preference intensities (as shown in the sensitivity analysis), while methods like MOORA, WASPAS, EDAS, CoCoSo, and MARCOS are more sensitive to weight changes, leading to ranking fluctuations.

(4)   As shown in previous sensitivity analyses, the proposed enhanced VIKOR demonstrates high stability across different preference intensities, unlike some other methods that are more sensitive to criteria weight changes. Table 13 supports this discussion, showing that most methods agree on A2 as the best alternative, aligning with the proposed enhanced VIKOR. The comparison highlights that VIKOR’s unique approach ensures reliable and balanced decision-making, particularly in multi-criteria environments with conflicting objectives.

7  Conclusions

This study improves the VIKOR method by addressing ranking biases, refining distance calculations, and adjusting parameter settings, leading to more accurate, objective, and applicable decision-making solutions. The enhanced VIKOR model provides a significant theoretical advancement while also offering practical benefits for complex multiple-criteria decision-making problems in various industries. Besides, an enhanced VIKOR model is validated through an illustrative case study on manufacturing process selection. This case not only enhances the scientific rigor of decision-making but also promotes the modernization of the manufacturing industry.

7.1 Limitations of This Research and Possible Solution

Despite its advancements, the proposed approach has certain limitations, along with potential solutions to address them.

(1)   Ranking instability (Rank reversal problem): The instability of VIKOR rankings can make it unreliable in dynamic decision-making environments. The causes of this phenomenon can be summarized into two main points: (i) The choice of reference points and normalization methods can significantly affect the relative distances between alternatives, leading to ranking changes. (ii) Variations in criteria weights can lead to substantial changes in ranking results, revealing the sensitivity of VIKOR to weight adjustments. However, these issues can be effectively alleviated through two approaches: (i) By applying robustness analysis and adopting more stable normalization techniques, the impact of reference point changes on rankings can be minimized. (ii) Applying sensitivity analysis to evaluate how rankings fluctuate under different conditions can enhance decision robustness and consistency. In this study, to mitigate the issue of rank reversal, a weight sensitivity analysis approach has been employed, allowing us to observe and assess the impact of weight variations on ranking stability, thereby enhancing the reliability of the decision-making process.

(2)   Difficulty handling uncertain and fuzzy data: Many real-world decision-making scenarios involve linguistic or fuzzy variables (e.g., “moderate cost,” “high efficiency”), making it challenging for standard VIKOR to process such imprecise data. Incorporating fuzzy techniques within VIKOR can effectively address this limitation, improving its ability to handle uncertainty and vagueness in decision-making.

(3)   Limited applicability to multi-objective optimization: VIKOR is not directly applicable to problems that require continuous trade-offs, such as engineering design or supply chain logistics optimization. This limitation can be addressed by developing a hybrid VIKOR model that integrates metaheuristic algorithms (e.g., Genetic algorithms; GA, Particle swarm optimization; PSO) to enhance its multi-objective optimization capabilities.

(4)   Computational complexity in large-scale problems: When handling a large number of alternatives, VIKOR’s ranking calculations and pairwise comparisons can become computationally intensive, slowing down the decision-making process. To mitigate this issue, parallel computing techniques or clustering algorithms can be employed to preprocess data and optimize computational efficiency, ensuring VIKOR remains scalable for large-scale problems.

7.2 Future Research Directions

To ensure that VIKOR remains a powerful and reliable MCDM tool capable of enhancing decision quality in complex multi-criteria environments, several future research directions are proposed:

(1)   Enhancing data preprocessing: Implementing outlier detection methods or modifying normalization techniques (e.g., robust statistical normalization) as preprocessing steps can effectively mitigate the impact of extreme outliers, improving the stability and accuracy of decision-making.

(2)   Developing hybrid VIKOR models: Integrating metaheuristic algorithms (e.g., GA, PSO) with VIKOR can enhance its ability to handle multi-objective optimization problems, leading to more efficient and precise decision outcomes.

(3)   Addressing uncertainty in decision-making: Extending VIKOR with fuzzy logic, interval analysis, or Z-number theory can significantly improve its ability to model semantic uncertainty, making it more suitable for real-world applications where data may be imprecise or ambiguous.

(4)   Advancing real-time decision-making: Integrating AI-driven analytics with VIKOR can enhance its capability for real-time decision-making, enabling dynamic and adaptive decision processes in rapidly changing environments.

By exploring these research directions, VIKOR can be further refined to enhance its adaptability, robustness, and efficiency in complex decision-making scenarios, ensuring its continued relevance and effectiveness in MCDM applications.

Acknowledgement: The authors extend their heartfelt gratitude to the editors, anonymous reviewers, and all contributors for their invaluable feedback, suggestions, and support, which have significantly enhanced the quality of this work and its underlying concepts. This work was supported by the National Science and Technology Council (NSTC), Taiwan (Grant No. NSTC 113-2222-E-029-005), with additional computational resources provided by the project. The work of Josef Jablonsky was supprted by the Faculty of Informatics and Statistics, Prague University of Economics and Business.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Ting-Yu Lin and Kuo-Chen Hung; methodology, Ting-Yu Lin and Kuo-Chen Hung; software, Ting-Yu Lin; validation, Ting-Yu Lin, Kuo-Chen Hung, Josef Jablonsky and Kuo-Ping Lin; formal analysis, Ting-Yu Lin and Kuo-Chen Hung; investigation, Ting-Yu Lin, Josef Jablonsky and Kuo-Ping Lin; resources, Ting-Yu Lin; data curation, Ting-Yu Lin; writing—original draft preparation, Ting-Yu Lin; writing—review and editing, Ting-Yu Lin, Kuo-Chen Hung, Josef Jablonsky and Kuo-Ping Lin; visualization, Ting-Yu Lin and Kuo-Chen Hung; supervision, Kuo-Chen Hung; project administration, Kuo-Chen Hung. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Dodevska Z, Petrović A, Radovanović S, Delibašić B. Changing criteria weights to achieve fair VIKOR ranking: a postprocessing reranking approach. Auton Agent Multi Agent Syst. 2002;37(1):9. doi:10.1007/s10458-022-09591-5. [Google Scholar] [CrossRef]

2. Opricovic S. Multicriteria optimization of civil engineering systems [dissertation]. Belgrade, Serbia: University of Belgrade; 1998. 302 p. [Google Scholar]

3. Zheng G, Wang X. The comprehensive evaluation of renewable energy system schemes in tourist resorts based on VIKOR method. Energy. 2020;193(1):116676. doi:10.1016/j.energy.2019.116676. [Google Scholar] [CrossRef]

4. Koppiahraj K, Bathrinath S, Saravanasankar S. A fuzzy VIKOR approach for selection of ergonomic assessment method. Mater Today: Proc. 2021;45(2):640–5. doi:10.1016/j.matpr.2020.02.725. [Google Scholar] [CrossRef]

5. Kaya A, Basham V, Ust Y. Selection of marine type air compressor by using fuzzy VIKOR methodology. Proc Inst Mech Eng, Part M: J Eng Marit Environ. 2021;236(1):103–12. doi:10.1177/14750902211028791. [Google Scholar] [CrossRef]

6. Abdel-Basset M, Mohamed R, Elhoseny M, Abouhawash M, Nam Y, AbdelAziz NM. Efficient MCDM model for evaluating the performance of commercial banks: a case study. Comput Mater Contin. 2021;67(3):2729–46. doi:10.32604/cmc.2021.015316. [Google Scholar] [CrossRef]

7. Vadivel SM, Pranamya B, Arivazhagan P, Sequeira AH, Chandana V. Application of VIKOR Method for green postal sustainable service design. Intell Syst Des Appl. 2023;2022:342–50. doi:10.1007/978-3-031-27440-4. [Google Scholar] [CrossRef]

8. Bera B, Shit PK, Sengupta N, Saha S, Bhattacharjee S. Susceptibility of deforestation hotspots in Terai-dooars belt of himalayan foothills: a comparative analysis of VIKOR and TOPSIS models. J King Saud Univ-Comput Inform Sci. 2022;34(10) Part A:8794–806. doi:10.1016/j.jksuci.2021.10.005. [Google Scholar] [CrossRef]

9. Malakar S, Rai AK. Estimating seismic vulnerability in West Bengal by AHP-WSM and AHP-VIKOR. Nat Hazards Res. 2023;3(3):464–73. doi:10.1016/j.nhres.2023.06.001. [Google Scholar] [CrossRef]

10. Gao F, Han M, Wang S, Gao J. A novel Fermatean fuzzy BWM-VIKOR based multi-criteria decision-making approach for selecting health care waste treatment technology. Eng Appl Artif Intell. 2024;127(Part B):107451. doi:10.1016/j.engappai.2023.107451. [Google Scholar] [CrossRef]

11. Shah AI, Pan ND. Flood susceptibility assessment of Jhelum River Basin: a comparative study of TOPSIS, VIKOR and EDAS methods. Geosyst Geoenviron. 2024;3(4):100304. doi:10.1016/j.geogeo.2024.100304. [Google Scholar] [CrossRef]

12. Li H, Wang W, Fan L, Li Q, Chen X. A novel hybrid MCDM model for machine tool selection using fuzzy DEMATEL, entropy weighting and later defuzzification VIKOR. Appl Soft Comput. 2020;91(5–8):106207. doi:10.1016/j.asoc.2020.106207. [Google Scholar] [CrossRef]

13. Wang CN, Nguyen NAT, Dang TT, Lu CM. A compromised decision-making approach to third-party logistics selection in sustainable supply chain using fuzzy AHP and fuzzy VIKOR methods. Mathematics. 2021;9(8):886. doi:10.3390/math9080886. [Google Scholar] [CrossRef]

14. Paul TK, Jana C, Pal M, Simic V. Sustainable carbon-dioxide storage assessment in geological media using modified Pythagorean fuzzy VIKOR and DEMATEL approach. Int J Hydrogen Energy. 2023;48(25):9474–97. doi:10.1016/j.ijhydene.2022.12.024. [Google Scholar] [CrossRef]

15. Chaturvedi S, Bhatt N, Shah V, Jadhani KH, Patel D, Singh SK. Landfill site selection in hilly terrains: an integrated RS-GIS approach with AHP and VIKOR. Waste Management Bulletin. 2025;3(1):332–48. doi:10.1016/j.wmb.2025.01.010. [Google Scholar] [CrossRef]

16. Gul R. An extension of VIKOR approach for MCDM using bipolarfuzzy preferenceδ-covering based bipolar fuzzy roughset model. Spectrum Oper Res. 2025;2(1):72–91. doi:10.31181/sor21202511. [Google Scholar] [CrossRef]

17. Opricovic S. A fuzzy compromise solution for multicriteria problems. Int J Uncertain, Fuzziness Knowl-Based Syst. 2007;15(3):363–80. doi:10.1142/S0218488507004728. [Google Scholar] [CrossRef]

18. Huang JJ, Tzeng GH, Liu HH. A revised VIKOR model for multiple criteria decision making- The perspective of regret theory. Cutting-Edge Res Topics Mult Criteria Decis Mak. 2009;761–8. doi:10.1007/978-3-642-02298-2. [Google Scholar] [CrossRef]

19. Sayadi MK, Heydari M, Shahanaghi K. Extension of VIKOR method for decision making problem with interval numbers. Appl Math Model. 2009;33(5):2257–62. doi:10.1016/j.apm.2008.06.002. [Google Scholar] [CrossRef]

20. Vahdani B, Hadipour H, Sadaghiani JS, Amiri M. Extension of VIKOR method based on interval-valued fuzzy sets. Int J Adv Manuf Technol. 2010;47(9):1231–9. doi:10.1007/s00170-009-2241-2. [Google Scholar] [CrossRef]

21. Jahan A, Mustapha F, Ismail MY, Sapuan SM, Bahraminasab M. A comprehensive VIKOR method for material selection. Mater Des. 2011;32(3):1215–21. doi:10.1016/j.matdes.2010.10.015. [Google Scholar] [CrossRef]

22. Liou JJH, Tsai CY, Lin RH, Tzeng GH. A modified VIKOR multiple-criteria decision method for improving domestic airlines service quality. J Air Transp Manag. 2011;71(2):57–61. doi:10.1016/j.jairtraman.2010.03.004. [Google Scholar] [CrossRef]

23. Opricovic S. Fuzzy VIKOR with an application to water resources planning. Expert Syst Appl. 2011;38(10):12983–90. doi:10.1016/j.eswa.2011.04.097. [Google Scholar] [CrossRef]

24. Devi K. Extension of VIKOR method in intuitionistic fuzzy environment for robot selection. Expert Syst Appl. 2011;38(1):14163–8. doi:10.1016/j.eswa.2011.04.227. [Google Scholar] [CrossRef]

25. Yang Q, Wu Y. A new improvement method to avoid rank reversal in VIKOR. IEEE Access. 2020;8:21261–71. doi:10.1109/ACCESS.2020.2969681. [Google Scholar] [CrossRef]

26. Mousavi-Nasab SH, Sotoudeh-Anvari AS. A new multi-criteria decision making approach for sustainable material selection problem: a critical study on rank reversal problem. J Clean Prod. 2018;182(4):466–84. doi:10.1016/j.jclepro.2018.02.062. [Google Scholar] [CrossRef]

27. Xu S, Nupur R, Kannan D, Sharma R, Sharma P, Kumar S, et al. An integrated fuzzy MCDM approach for manufacturing process improvement in MSMEs. Ann Oper Res. 2023;322:10371073. [Google Scholar]

28. Ghaleb AM, Kaid H, Alsamhan A, Mian SH, Hidri L. Assessment and Comparison of Various MCDM Approaches in the Selection of Manufacturing Process. Adv Mater Sci Eng. 2020; 2020:4039253. [Google Scholar]

29. Nabeeh NA, Abdel-Monem A, Mohamed M, Sallam KM, Abdel-Basset M, El-Abd M, et al. A comparative analysis for a novel hybrid methodology using neutrosophic theory with MCDM for Manufacture selection. In: Paper presented at: 2022 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE); 2022 Jul 18–23; Padua, Italy. [Google Scholar]

30. Raigar J, Sharma VS, Srivastava S, Chand R, Singh J. A decision support system for the selection of an additive manufacturing process using a new hybrid MCDM technique. Sādhanā. 2020;45:101. [Google Scholar]

31. Chandra M, Shahab F, Vimal KEK, Rajak S. Selection for additive manufacturing using hybrid MCDM technique considering sustainable concepts. Rapid Prototyp J. 2022;28(7):1297–311. [Google Scholar]

32. Nath S, Sarkar B. Performance evaluation of advanced manufacturing technologies: a De novo approach. Comput Indust Eng. 2017;110:364–78. [Google Scholar]

33. Soltani M, Aouag H, Anass C, Mouss MD. Development of an advanced application process of Lean Manufacturing approach based on a new integrated MCDM method under Pythagorean fuzzy environment. J Clean Prod. 2023;386(2):135731. doi:10.1016/j.jclepro.2022.135731. [Google Scholar] [CrossRef]

34. Churchman CW, Ackoff RL. An approximate measure of value. J Oper Res Soc Am. 1954;2(2):172–87. doi:10.1287/opre.2.2.172. [Google Scholar] [CrossRef]

35. Hwang CL, Yoon K. Multiple attribute decision making-methods and applications. Lect Notes Econ Math Syst. 1981;186:115–27. [Google Scholar]

36. Brauers WK, Zavadskas EK. The MOORA method and its application to privatization in a transition economy. Control Cybern. 2006;35(2):445–69. [Google Scholar]

37. Zavadskas EK, Turskis Z, Antucheviciene J, Zakare-vicius A. Optimization of weighted aggregated sum product assessment. Elektron Elektrotech. 2012;122(6):3–6. doi:10.5755/j01.eee.122.6.1810. [Google Scholar] [CrossRef]

38. Pamucar D, Cirovic G. The selection of transport and handling resources in logistics centers using multi-attributive border approximation area comparison (MABAC). Expert Syst Appl. 2015;42(6):3016–28. doi:10.1016/j.eswa.2014.11.057. [Google Scholar] [CrossRef]

39. Ghorabaee MK, Zavadskas EK, Olfat L, Turskis Z. Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica. 2015;26(3):435–51. doi:10.15388/Informatica.2015.57. [Google Scholar] [CrossRef]

40. Gigovic L, Pamucar D, Bajic Z, Milicevic M. The combination of expert judgment and GIS-MAIRCA analysis for the selection of sites for ammunition depots. Sustainability. 2016;8(4):372. doi:10.3390/su8040372. [Google Scholar] [CrossRef]

41. Yazdani M, Zarate P, Zavadskas EK, Turskis Z. A com-bined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Manage Decis. 2019;57(9):2501–19. doi:10.1108/MD-05-2017-0458. [Google Scholar] [CrossRef]

42. Stevic Z, Pamucar D, Puska A, Chatterjee R. Sustainable supplier selection in healthcare industries using a new MCDM method: measurement of alternatives and ranking according to Compromise solution (MARCOS). Comput Indust Eng. 2020;140(1–4):10623. doi:10.1016/j.cie.2019.106231. [Google Scholar] [CrossRef]

43. Zizovic M, Pamucar D, Albijanic M, Chatterjee P, Pribicevic I. Eliminating rank reversal problem using a new multi-attribute model—the RAFSI method. Mathematics. 2020;8(6):1015. doi:10.3390/math8061015. [Google Scholar] [CrossRef]

44. Boskovic S, Svadlenka L, Jovcic S, Dobrodolac M, Simic V, Bacanin N. An alternative ranking order method accounting for two-step normalization (AROMAN)—a case study of the electric vehicle selection problem. IEEE Access. 2023;11(3):39496–507. doi:10.1109/ACCESS.2023.3265818. [Google Scholar] [CrossRef]