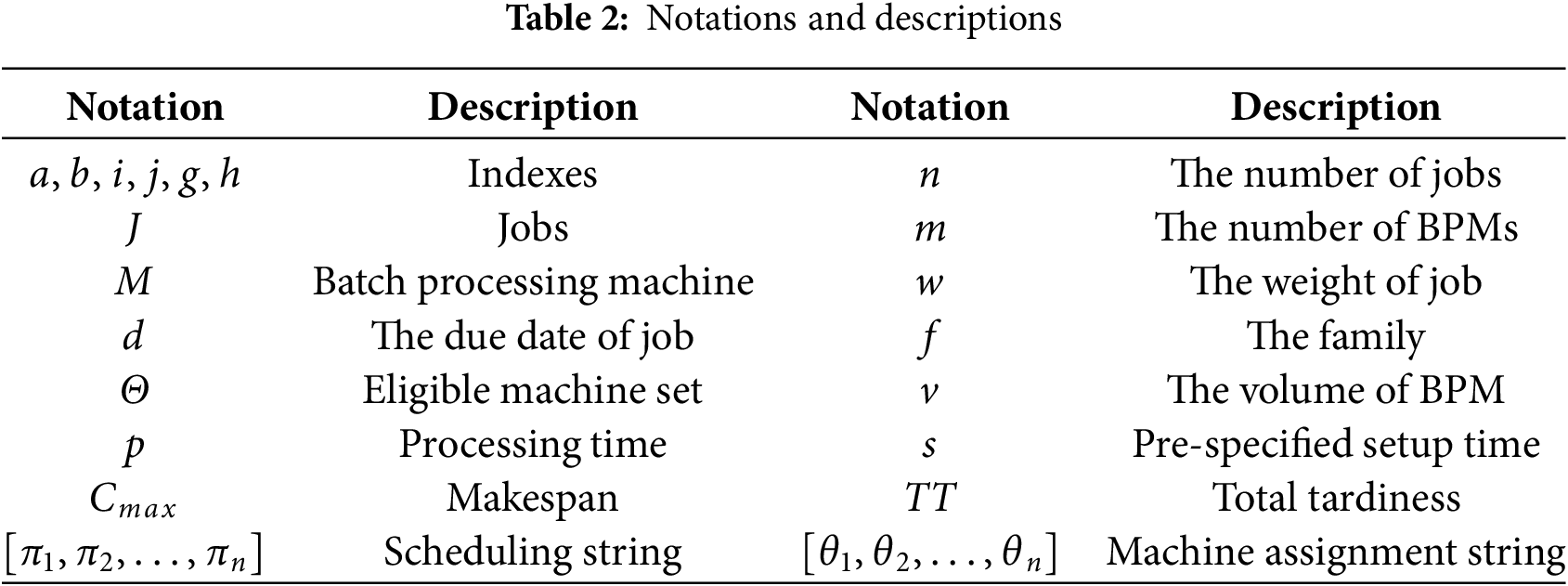
 Open Access
Open Access
ARTICLE
An Adaptive Cooperated Shuffled Frog-Leaping Algorithm for Parallel Batch Processing Machines Scheduling in Fabric Dyeing Processes
School of Automation, Wuhan University of Technology, Wuhan, 430070, China
* Corresponding Author: Deming Lei. Email:
(This article belongs to the Special Issue: Algorithms for Planning and Scheduling Problems)
Computers, Materials & Continua 2025, 83(2), 1771-1789. https://doi.org/10.32604/cmc.2025.063944
Received 29 January 2025; Accepted 10 March 2025; Issue published 16 April 2025
Abstract
Fabric dyeing is a critical production process in the clothing industry and heavily relies on batch processing machines (BPM). In this study, the parallel BPM scheduling problem with machine eligibility in fabric dyeing is considered, and an adaptive cooperated shuffled frog-leaping algorithm (ACSFLA) is proposed to minimize makespan and total tardiness simultaneously. ACSFLA determines the search times for each memeplex based on its quality, with more searches in high-quality memeplexes. An adaptive cooperated and diversified search mechanism is applied, dynamically adjusting search strategies for each memeplex based on their dominance relationships and quality. During the cooperated search, ACSFLA uses a segmented and dynamic targeted search approach, while in non-cooperated scenarios, the search focuses on local search around superior solutions to improve efficiency. Furthermore, ACSFLA employs adaptive population division and partial population shuffling strategies. Through these strategies, memeplexes with low evolutionary potential are selected for reconstruction in the next generation, while those with high evolutionary potential are retained to continue their evolution. To evaluate the performance of ACSFLA, comparative experiments were conducted using ACSFLA, SFLA, ASFLA, MOABC, and NSGA-CC in 90 instances. The computational results reveal that ACSFLA outperforms the other algorithms in 78 of the 90 test cases, highlighting its advantages in solving the parallel BPM scheduling problem with machine eligibility.Keywords
Batch processing machine (BPM) has been widely applied in many real applications such as fabric dyeing [1], chemical production [2], tire manufacturing [3], steel smelting [4], semiconductor manufacturing [5]. BPMs are capable of simultaneously processing multiple jobs within a single batch, where all jobs in the batch share the same start and end times. Scheduling problems involving BPM can be broadly divided into single BPM scheduling [6,7], parallel BPM scheduling, and other BPM problems [8,9]. Parallel BPM scheduling, as a representative type, is an extension of the parallel machine scheduling problem and has attracted extensive research attention in recent years.
Table 1 summarizes relevant research. In Scenario 1, researchers use different algorithms to solve BPM-related scheduling problems in various industries, aiming at different objectives. Scenario 2 focuses on the shuffled frog-leaping algorithm (SFLA) and its applications in scheduling problems. Scenario 3 covers other multi-objective scheduling problems solved by different algorithms. However, parallel BPM scheduling in fabric dyeing still has many unsolved problems.
The parallel BPM scheduling problem in fabric dyeing is crucial for real-world production. Efficient BPM scheduling in fabric dyeing can shorten production time, reduce costs, and improve resource utilization. However currently, this field faces several severe challenges. For example, job family compatibility is a major hurdle. In fabric dyeing, jobs with different color-dyeing needs, such as those from different job families, can’t be processed in the same batch. Also, machine eligibility matters. Each machine has its capabilities, so not all machines can handle every job. These constraints make the problem more complex than traditional models, and existing algorithms often can’t handle them well. Another challenge is the difficulty of multi-objective optimization. Simultaneously minimizing makespan and total tardiness in fabric dyeing parallel BPM scheduling is very hard. In actual production, achieving both objectives is crucial for efficient operations and customer satisfaction. However, most current research only focuses on one of these goals. For example, algorithms that prioritize reducing makespan often result in numerous jobs being tardy.
Because of the limitations of existing algorithms in dealing with the complex constraints and multi-objective requirements of parallel BPM scheduling in fabric dyeing, a new algorithm is urgently needed. A well-designed meta-heuristic can comprehensively explore the large solution space, considering both practical constraints and multi-objective optimization.
The shuffled frog-leaping algorithm (SFLA), inspired by the foraging behavior of frogs, is a good choice for developing a new algorithm. SFLA has unique advantages as it combines local search and global information exchange effectively. In scheduling problems, local search helps it explore the area around promising solutions to find better-optimized ones. Global information exchange enables sharing good solutions across different parts of the solution space, preventing the algorithm from getting stuck in local optima. SFLA has been applied to similar BPM-related scheduling problems and has achieved good results through techniques like reinforcement learning, cooperation, and memeplex grouping. These successful applications show its potential for the parallel BPM scheduling problem in fabric dyeing.
This study focuses on the parallel BPM scheduling problem in fabric dyeing and aims to develop an enhanced SFLA to minimize makespan and total tardiness at the same time. The main contributions are as follows.
(1) The parallel BPM scheduling problem with machine eligibility refinement from the fabric dyeing process is solved.
(2) An Adaptive Cooperated Shuffled Frog-Leaping Algorithm (ACSFLA) is proposed, featuring two key strategies: an adaptive population division strategy, which ensures the uninterrupted evolution of high-potential memeplexes, and a diversified search based on adaptive cooperation, which balances global exploration and local exploitation according to dominance relationships.
(3) The performance of ACSFLA is evaluated through experiments, which show that the new strategies are effective and that ACSFLA offers significant advantages in solving the considered problem.
The rest of the paper is organized as follows. Section 2 describes the parallel BPM scheduling problem defined by the fabric dyeing process. Section 3 introduces the SFLA. Section 4 presents the ACSFLA for the considered problem in the fabric dyeing process. The computational experiments are shown in Section 5. In the last section, conclusions are drawn, and potential topics for future research are discussed.
Zhang et al. [1] developed a Mixed-Integer Linear Programming (MILP) model for parallel BPM scheduling based on a real fabric dyeing process, which is described as follows. There are
All jobs are classified into F families according to the required dyeing color. Jobs within the same family share the same processing time, with
There are some constraints on jobs and machines:
Each BPM can only process one batch at a time.
No job can be processed in distinct batches across multiple BPMs.
The processing cannot be interrupted.
All BPMs and jobs are accessible at all times.
Solving the BPMs scheduling problem requires addressing three sub-problems: (1) batch formation determines which jobs are grouped to form each batch; (2) BPM assignment selects an
Suppose that batches
where
The goal of the problem is to simultaneously minimize the maximum completion time and total tardiness of all jobs, whilst satisfying all constraints. The makespan
The MILP model proposed by Zhang et al. [1] can be directly applied once the total finishing time of all machines is replaced by the maximum finishing time of all machines, which is equal to
For the problem with
The SFLA [24] is a meta-heuristic based on the behavior of frogs. In SFLA, each solution represents the position of a frog, and the population of possible solutions is modeled as a set of virtual frogs. After generating the initial population P, the algorithm iteratively performs population division, memeplex search, and population shuffling until the stopping criterion is satisfied.
Population division is shown below. All solutions are sorted in the descending order of fitness, suppose that
The search process in memeplex
where rand is a random real number following uniform distribution in
A new population P is constructed by shuffling all evolved memeplexes.
In ACSFLA, both the quality of the memeplex and its evolution quality are considered to determine the shuffling pool for partial population shuffling and the diverse search process of the memeplex. Meanwhile cooperated search is conducted within the diversified search processes, which is determined by the degree of dominance between the two memeplexes. The detailed steps of ACSFLA are shown below.
4.1 Population Initialization and Adaptive Division
The solution representation and decoding process follow the approach [25], which is described as follows. For the BPM scheduling problem with
The population initialization process generates an initial population P consists of N solutions, as follows:
ACSFLA introduces an adaptive population division strategy. This strategy can adjust the population division targets based on
(1) If
(2) Let
(3) If
(4)
The quality
After calculating the quality
4.2 Adaptive Cooperated and Diversified Search
Unlike existing SFLA [26,27] and MGFLA [19], which apply the same process to all memeplexes or uniformly conduct cooperated searches, ACSFLA dynamically determines whether memeplexes cooperate based on their dominance relationship and adjust search strategies accordingly. This method emphasizes the balance of exploration and exploitation, executing cooperation when there is a significant advantage, to enhance solution quality and maintain population diversity. The diversified search processes are listed as follows:
(1) For the best memeplex
If
Let
(ii) If
(iii) Perform
(iv) Perform
(v)
Else if
(i) Let
(ii) Randomly choose a solution
(iii) Perform
(iv) Perform
(v) Perform
(vi)
For the worst memeplex
If
(i) Let
(ii) If
(iii) Perform
(iv) Perform
(v)
Else if
(i) Let
(ii) Randomly choose a solution
(iii) Perform
(iv) Perform
(v)
For each memeplex
(i) Decide a non-dominated solution
(ii) Perform
(iii) Perform
(iv) Perform
Metric C [28] is employed to describe the dominance relationship between two solution sets. Specifically,
where
There are 3 global search operators and 6 local search operators used in the search process.
In the global search between
In the local search on
Initially,
4.3 Partial Population Shuffling
Partial Population Shuffling is a key step in ACSFLA, aimed at dynamically constructing the division pool
(1) Let
(2) Compute
(3) If
(4)
where
where
ACSFLA is described in Algorithm 1.

Unlike previous SFLA, ACSFLA incorporates several features that improve optimization performance. First, it determines the search times for each memeplex based on its quality, efficiently focusing on high-quality memeplexes and minimizing effort on low-quality ones. Second, it decides whether to perform a cooperated search by evaluating dominance relationships, maintaining population diversity, and avoiding premature convergence. Third, during the cooperated search, the algorithm uses a segmented and dynamic targeted search strategy, while in non-cooperated scenarios, it focuses on local search around higher-quality solutions to improve efficiency and explore promising regions more effectively. Finally, adaptive population division and partial shuffling select low-quality memeplexes for reconstruction in the next generation. These features balance exploration and exploitation, sustain diversity, and improve search efficiency. Fig. 1 shows the flowchart of ACSFLA.
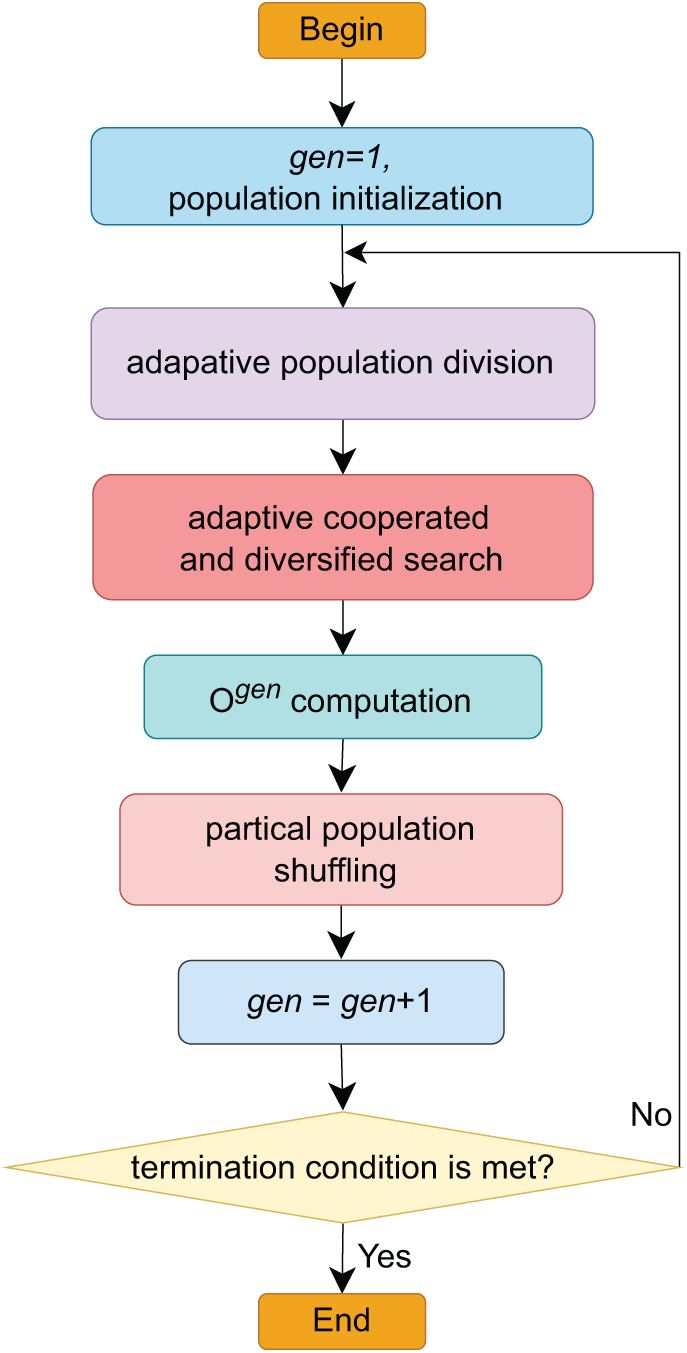
Figure 1: Flowchart of ACSFLA
Extensive experiments are conducted to test the performances of ACSFLA for the BPM scheduling problems in the fabric dyeing process. Experiments are implemented by using Matlab R2021a and run on 16 G RAM 3.1 GHz CPU PC.
5.1 Test Instances, Metrics and Comparative Algorithms
A total of 90 test instances are utilized, which is provided by Zhang et al. [1]. The related data are shown below.
Metric
The metric
IGD [30] is used to calculate the distance of the non-dominated set
where
Three comparative algorithms are chosen. Zhang et al. [1] presented MOABC for parallel BPM scheduling in the fabric dyeing process and MOABC is directly used in this study. Lei et al. [25] proposed ASFLA, an adaptive SFLA-based algorithm, that integrating dynamic population division and adaptive search processes. Li et al. [20] provided an NSGA-CC, which is formed by using NSGA-II [31] framework, incorporating a hierarchical clustering-based environmental selection strategy. An SFLA is also applied to show the effect of new strategies of ACSFLA, deleting the adaptive population and diversified cooperated search.
ACSFLA has following parameters: N,
Taguchi method [32] is used to decide the settings for other parameters by using instance 25, which belongs to combination
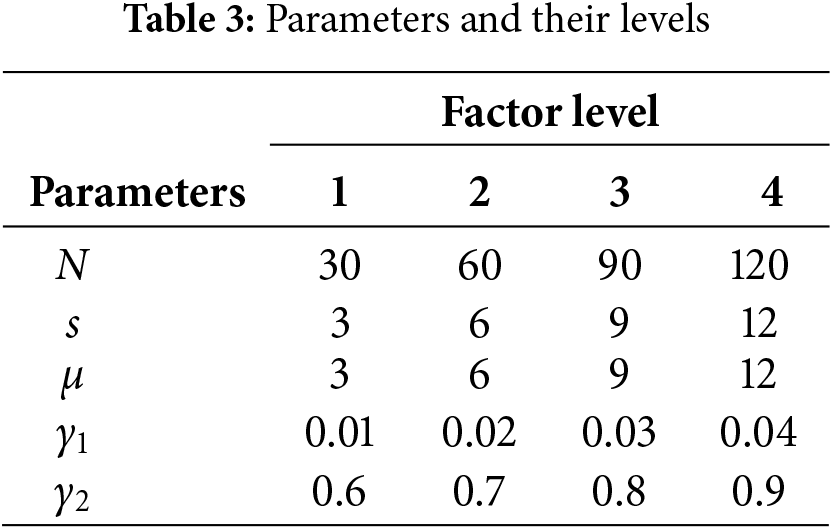
Fig. 2 shows the results of
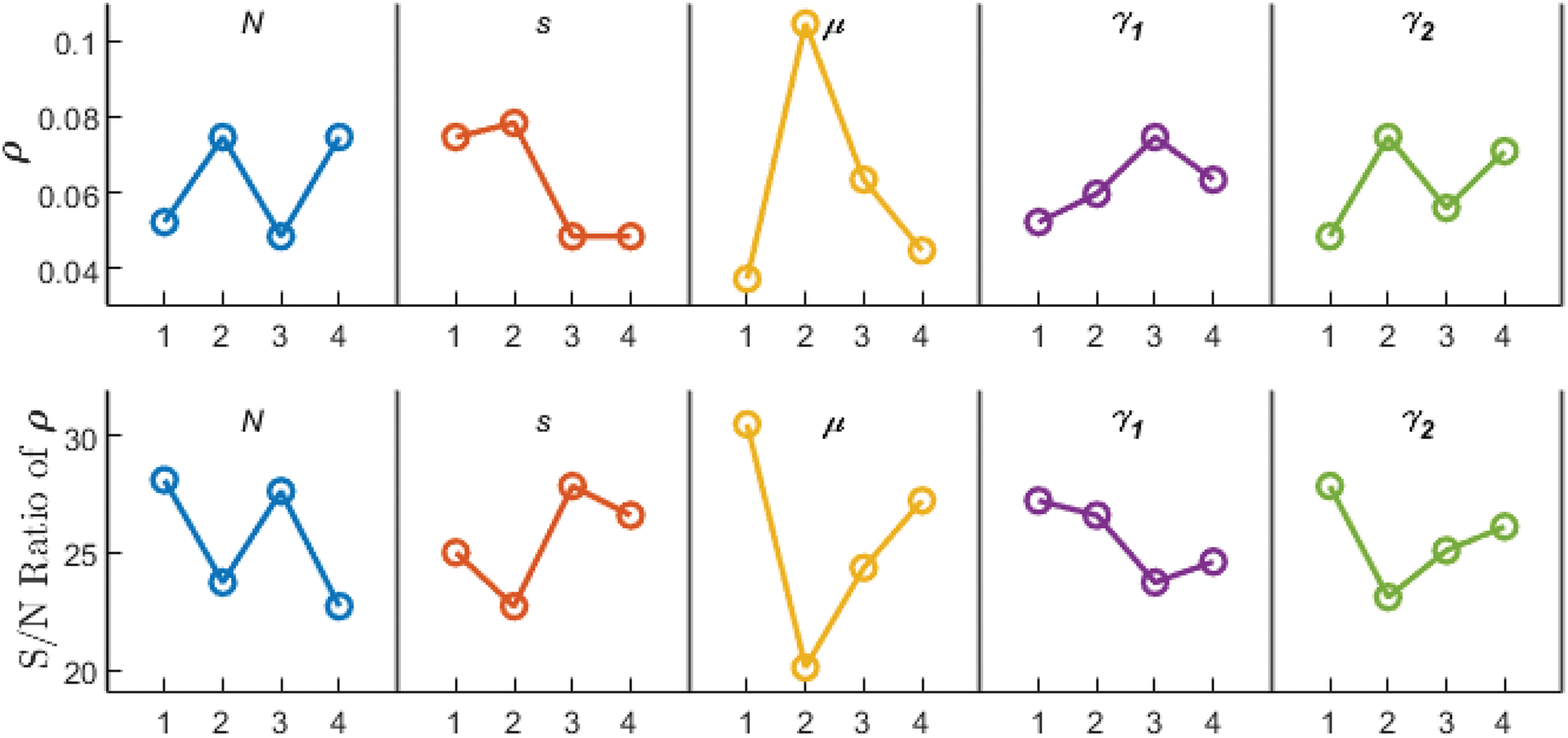
Figure 2: Main effect plot for means and S/N ratios
SFLA has
ACSFLA, ASFLA, and three comparative algorithms are used. Each algorithm randomly runs 10 times for each instance. Tables 4–7 describe the corresponding results of five algorithms, in which AC, S, A, M, N indicate ACSFLA, SFLA, ASFLA, MOABC, NSGA-CC. Fig. 3 gives a mean plot with 95% confidence interval. Fig. 4 shows distributions of non-dominated solutions produced by each algorithm.
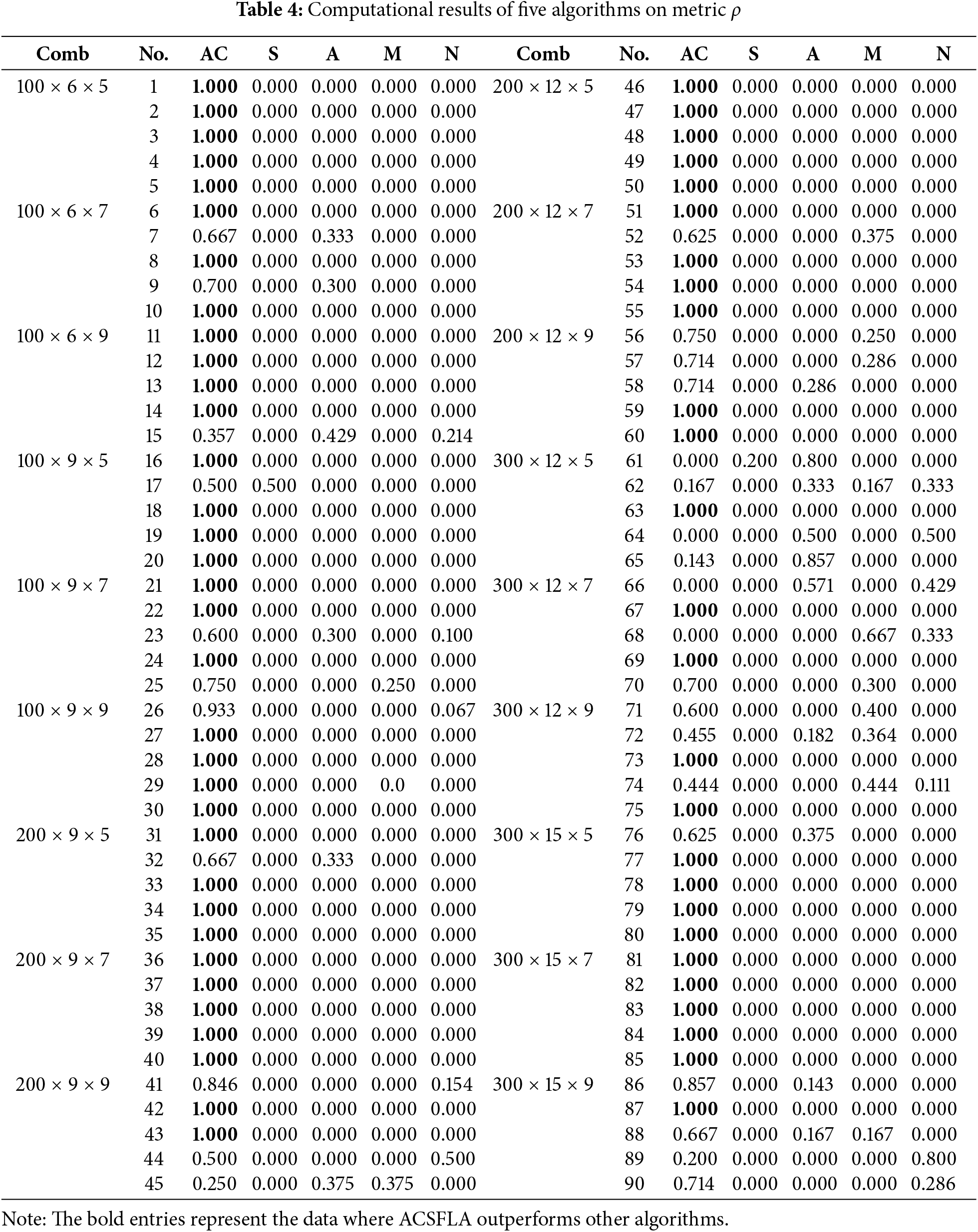
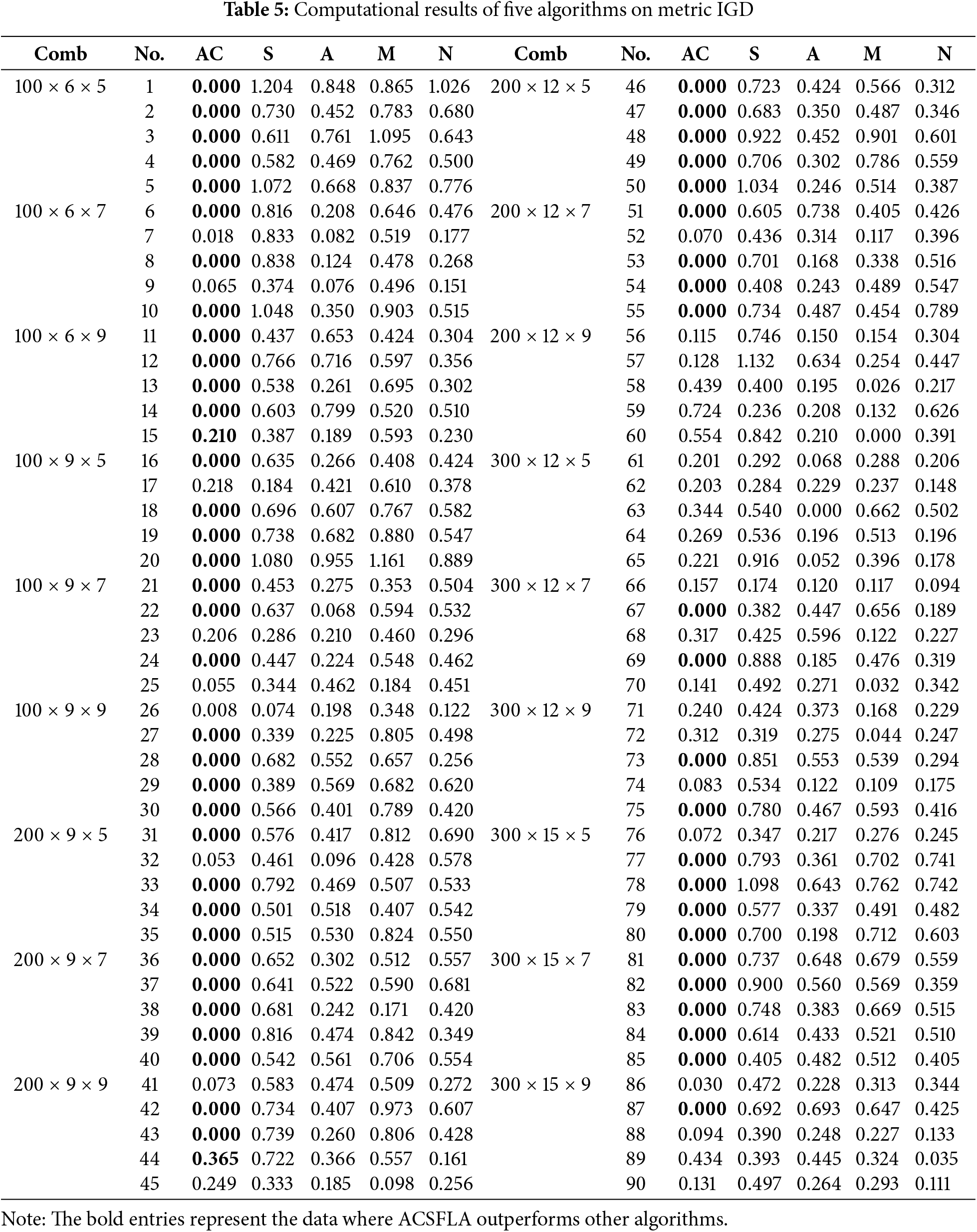
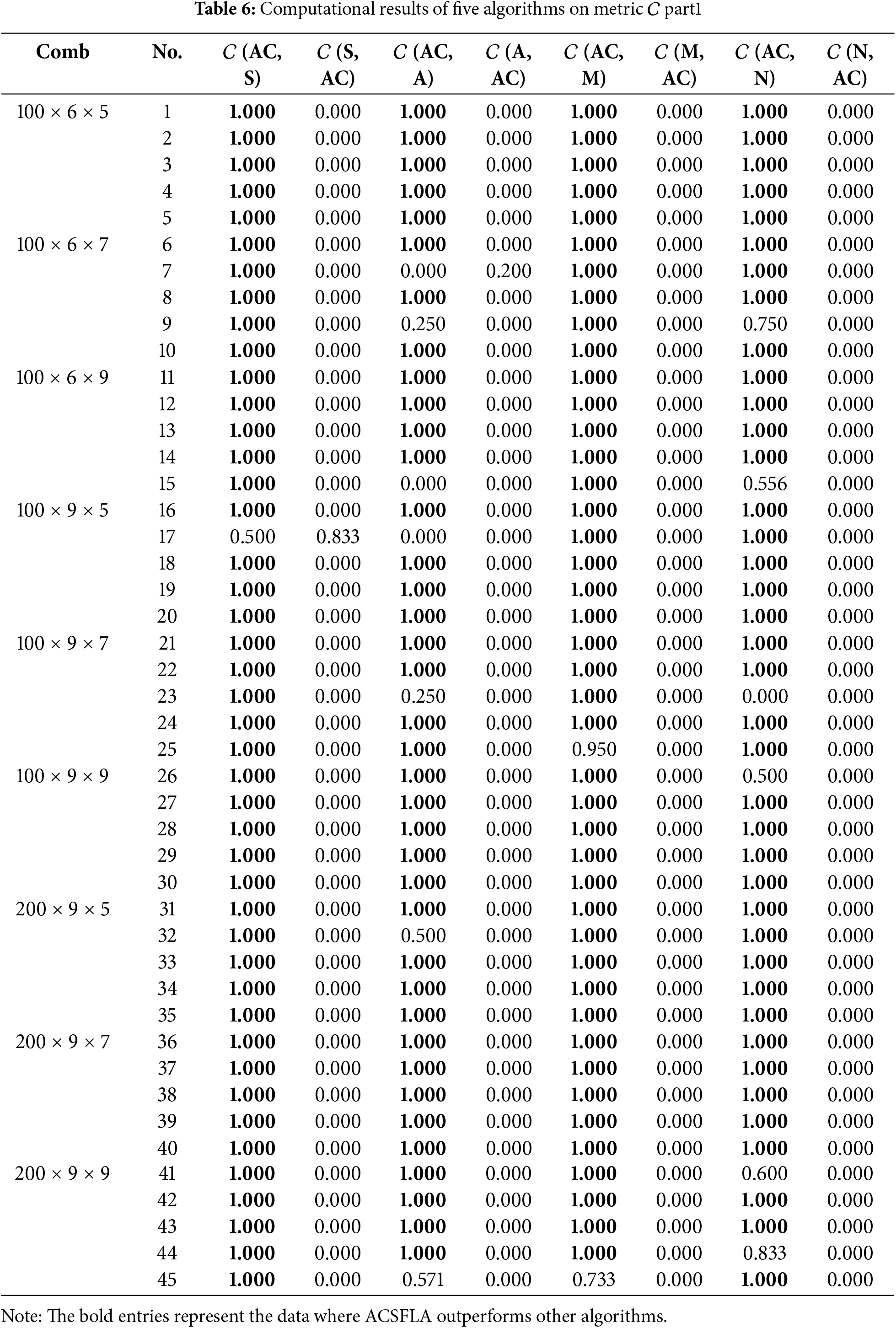
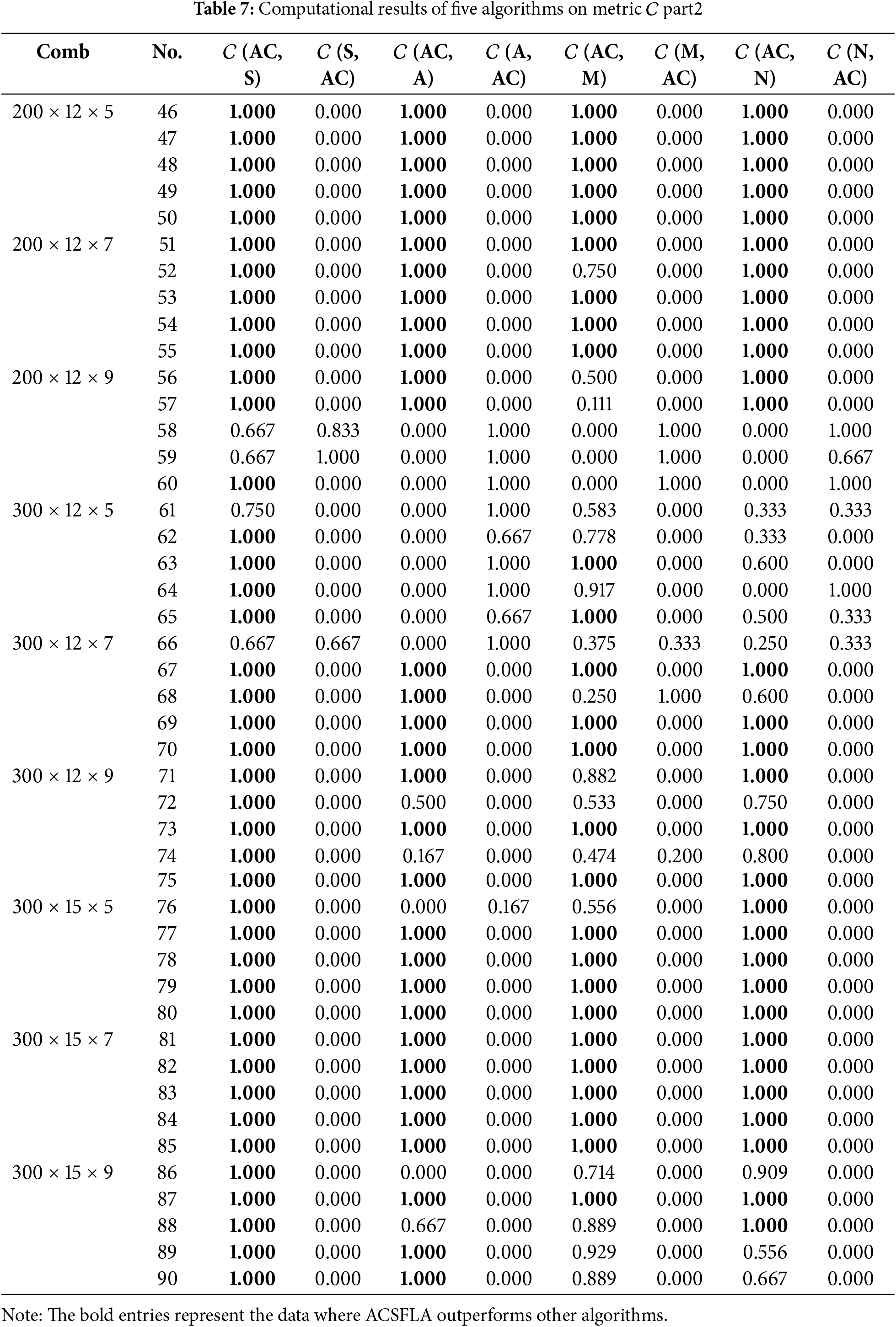
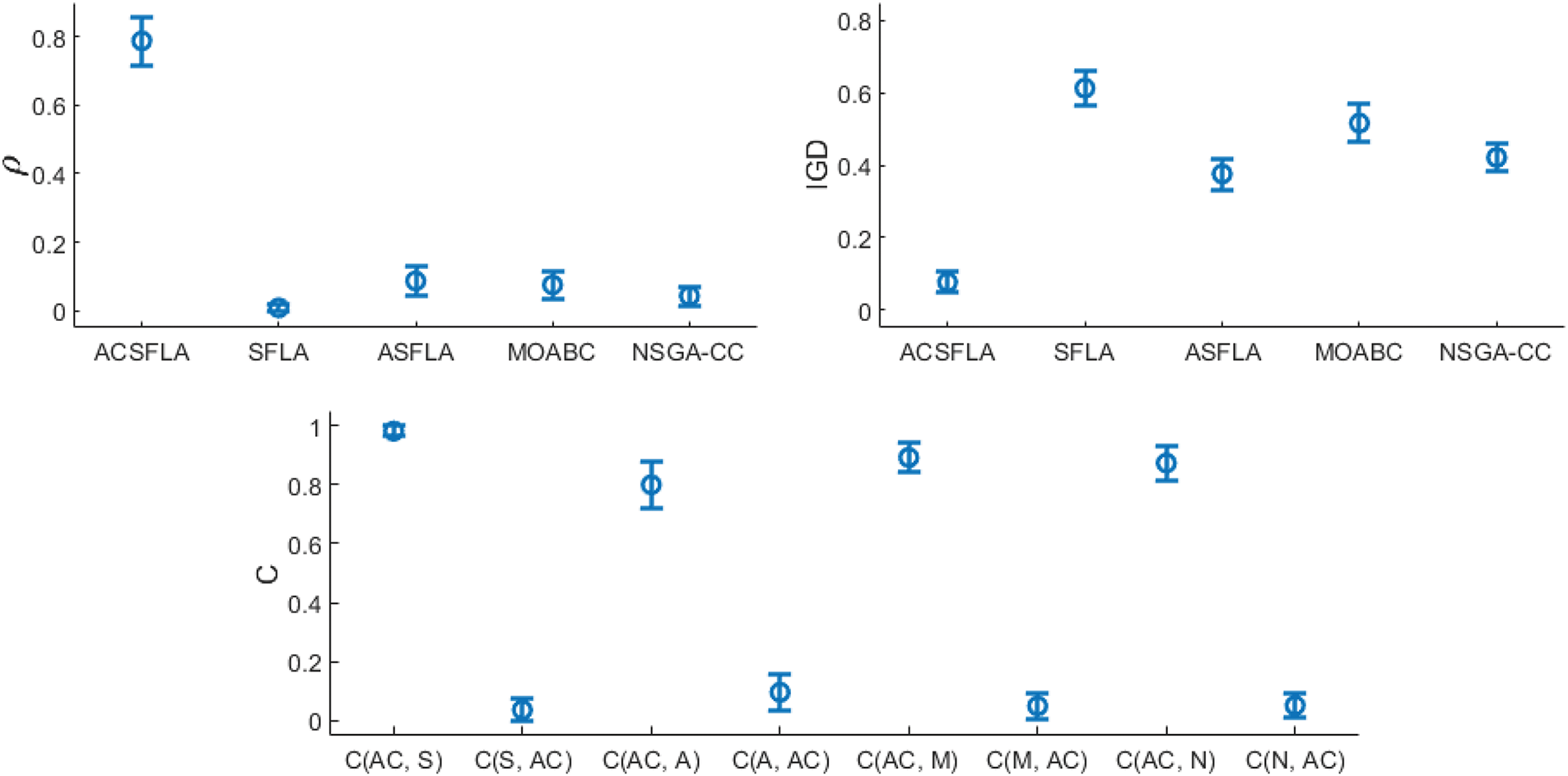
Figure 3: Mean plot with 95% confidence interval
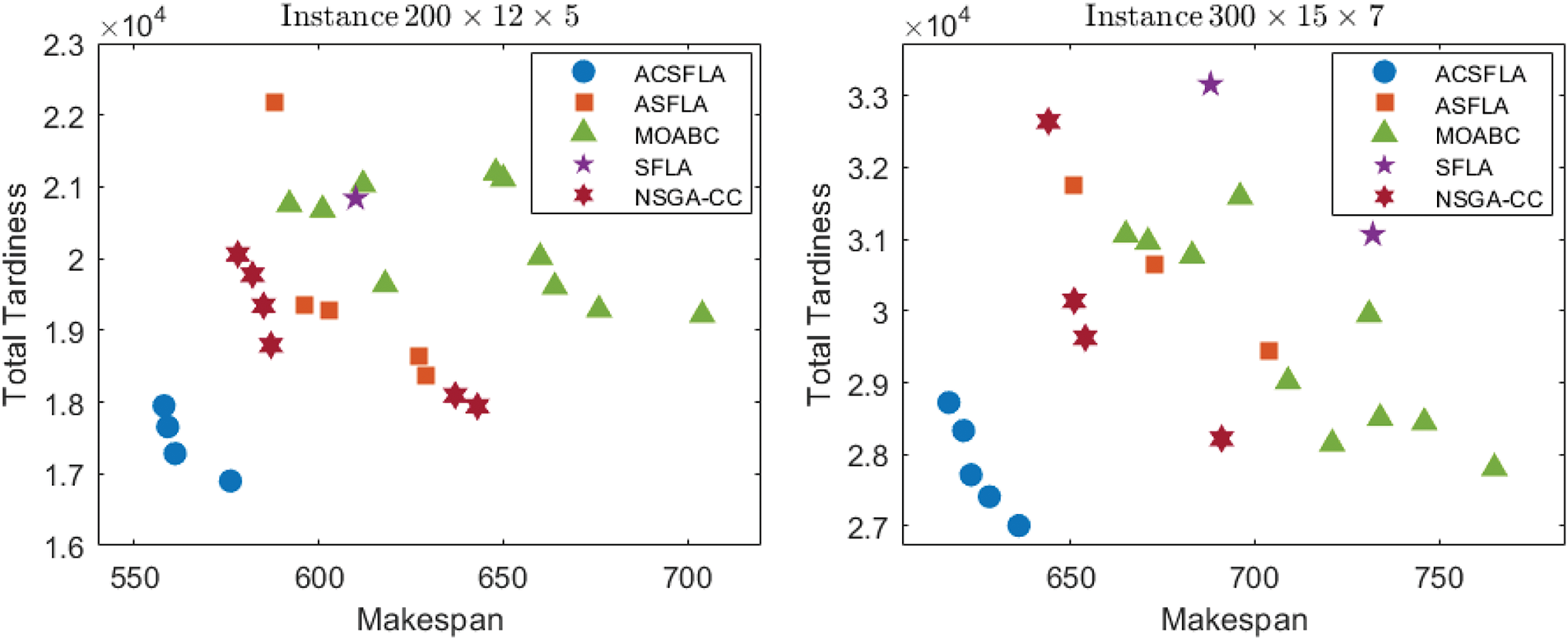
Figurer 4: Distribution of non-dominated solutions
ACSFLA demonstrates clear superiority in terms of the
ACSFLA also demonstrates superior performance in terms of the IGD metric. Table 5 shows that ACSFLA achieves smaller IGD values than SFLA in 88 instances, ASFLA in 78 instances, MOABC in 83 instances, and NSGA-CC in 82 instances. These results highlight ACSFLA’s superior ability to approximate the ideal reference set
In terms of the
The above result analyses show that ACSFLA obtains better results than its three comparative algorithms. Initialization is done by the heuristic method,
6 Conclusion and Future Topics
In this paper, we have effectively resolved the parallel BPM scheduling problem with machine eligibility in fabric dyeing processes using the newly developed adaptive cooperated shuffled frog-leaping algorithm (ACSFLA). ACSFLA incorporates innovative strategies based on the quality
For future research directions in parallel BPM scheduling for fabric dyeing, several promising paths could be explored. Incorporating energy consumption as an additional objective might be a key step toward achieving more energy-efficient processes. This could involve devising algorithms considering the power consumption patterns of machines and job sequences to minimize energy use during dyeing. Developing new neighborhood search methods could be an effective way to enhance search efficiency, enabling the algorithm to find better solutions in a shorter time. Applying reinforcement learning techniques may also hold great potential in making the scheduling more intelligent and adaptable to dynamic production situations. The key features of the algorithm include adaptive population division, as well as an adaptive cooperated and diversified search strategy.
Acknowledgement: We sincerely appreciate the perceptive feedback from the anonymous reviewers. It has substantially contributed to improving the overall quality of this paper.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: Study conception and design: Lianqiang Wu; analysis and interpretation of results: Yutong Cai; draft manuscript preparation: Lianqiang Wu; review and editing: Deming Lei. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data supporting this study are described in the first paragraph of Section 5.1.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Zhang R, Chang PC, Song S, Wu C. A multi-objective artificial bee colony algorithm for parallel batch-processing machine scheduling in fabric dyeing processes. Knowl-Based Syst. 2017;116(7):114–29. doi:10.1016/j.knosys.2016.10.026. [Google Scholar] [CrossRef]
2. Burkard RE, Hatzl J. A complex time based construction heuristic for batch scheduling problems in the chemical industry. Eur J Oper Res. 2006;174(2):1162–83. doi:10.1016/j.ejor.2005.03.011. [Google Scholar] [CrossRef]
3. Bellanger A, Oulamara A. Scheduling hybrid flowshop with parallel batching machines and compatibilities. Comput Oper Res. 2009;36(6):1982–92. doi:10.1016/j.cor.2008.06.011. [Google Scholar] [CrossRef]
4. Tang L, Wang G, Chen ZL. Integrated charge batching and casting width selection at Baosteel. Oper Res. 2014;62(4):772–87. doi:10.1287/opre.2014.1278. [Google Scholar] [CrossRef]
5. Hulett M, Damodaran P, Amouie M. Scheduling non-identical parallel batch processing machines to minimize total weighted tardiness using particle swarm optimization. Comput Ind Eng. 2017;113(8):425–36. doi:10.1016/j.cie.2017.09.037. [Google Scholar] [CrossRef]
6. Trindade RS, De Araujo OCB, Fampa MHC, Muller FM. Modelling and symmetry breaking in scheduling problems on batch processing machines. Int J Prod Res. 2018;56(22):7031–48. doi:10.1080/00207543.2018.1424371. [Google Scholar] [CrossRef]
7. Kong M, Wang W, Deveci M, Zhang Y, Wu X, Coffman D. A novel carbon reduction engineering method-based deep Q-learning algorithm for energy-efficient scheduling on a single batch-processing machine in semiconductor manufacturing. Int J Prod Res. 2024;62(18):6449–72. doi:10.1080/00207543.2023.2252932. [Google Scholar] [CrossRef]
8. Jia W, Jiang Z, Li Y. Combined scheduling algorithm for re-entrant batch-processing machines in semiconductor wafer manufacturing. Int J Prod Res. 2015;53(6):1866–79. doi:10.1080/00207543.2014.965355. [Google Scholar] [CrossRef]
9. Zhao A, Bard JF. Batch scheduling in a multi-purpose system with machine downtime and a multi-skilled workforce. Int J Prod Res. 2024;62(12):4470–93. doi:10.1080/00207543.2023.2265508. [Google Scholar] [CrossRef]
10. Jing Wang DL, Tang H. An adaptive artificial bee colony for hybrid flow shop scheduling with batch processing machines in casting process. Int J Prod Res. 2024;62(13):4793–808. doi:10.1080/00207543.2023.2279145. [Google Scholar] [CrossRef]
11. Abedi M, Seidgar H, Fazlollahtabar H, Bijani R. Bi-objective optimisation for scheduling the identical parallel batch-processing machines with arbitrary job sizes, unequal job release times and capacity limits. Int J Prod Res. 2015;53(6):1680–711. doi:10.1080/00207543.2014.952795. [Google Scholar] [CrossRef]
12. Zhang H, Li K, Chu C, Zh Jia. Parallel batch processing machines scheduling in cloud manufacturing for minimizing total service completion time. Comp Oper Res. 2022;146(2):105899. doi:10.1016/j.cor.2022.105899. [Google Scholar] [CrossRef]
13. Zhou S, Li X, Du N, Pang Y, Chen H. A multi-objective differential evolution algorithm for parallel batch processing machine scheduling considering electricity consumption cost. Comput Oper Res. 2018;96(1):55–68. doi:10.1016/j.cor.2018.04.009. [Google Scholar] [CrossRef]
14. Xue L, Zhao S, Mahmoudi A, Feylizadeh MR. Flexible job-shop scheduling problem with parallel batch machines based on an enhanced multi-population genetic algorithm. Complex Intell Syst. 2024;10(3):4083–101. doi:10.1007/s40747-024-01374-7. [Google Scholar] [CrossRef]
15. Arroyo JEC, Leung JYT. An effective iterated greedy algorithm for scheduling unrelated parallel batch machines with non-identical capacities and unequal ready times. Comput Ind Eng. 2017;105(6):84–100. doi:10.1016/j.cie.2016.12.038. [Google Scholar] [CrossRef]
16. Cai J, Lei D. A cooperated shuffled frog-leaping algorithm for distributed energy-efficient hybrid flow shop scheduling with fuzzy processing time. Complex Intell Syst. 2021;7(5):2235–53. doi:10.1007/s40747-021-00400-2. [Google Scholar] [CrossRef]
17. Kong M, Liu X, Pei J, Pardalos PM, Mladenovic N. Parallel-batching scheduling with nonlinear processing times on a single and unrelated parallel machines. J Global Optim. 2020;78(4):693–715. doi:10.1007/s10898-018-0705-3. [Google Scholar] [CrossRef]
18. Yang Y, Song Y, Guo W, Lei Q, Sun A, Fan L. Guided shuffled frog-leaping algorithm for flexible job shop scheduling problem with variable sublots and overlapping in operations. Comput Ind Eng. 2023;180(19):109209. doi:10.1016/j.cie.2023.109209. [Google Scholar] [CrossRef]
19. Lei D, Wang T. Solving distributed two-stage hybrid flowshop scheduling using a shuffled frog-leaping algorithm with memeplex grouping. Eng Optim. 2020;52(9):1461–74. doi:10.1080/0305215X.2019.1674295. [Google Scholar] [CrossRef]
20. Li K, Zhang H, Chu C, Zh Jia, Wang Y. A bi-objective evolutionary algorithm for minimizing maximum lateness and total pollution cost on non-identical parallel batch processing machines. Comput Ind Eng. 2022;172(3):108608. doi:10.1016/j.cie.2022.108608. [Google Scholar] [CrossRef]
21. Wang Y, Han Y, Wang Y, Pan QK, Wang L. Sustainable scheduling of distributed flow shop group: a collaborative multi-objective evolutionary algorithm driven by indicators. Trans Evol Comp. 2024;28(6):1794–808. doi:10.1109/TEVC.2023.3339558. [Google Scholar] [CrossRef]
22. Wang Y, Han Y, Wang Y, Wang X, Liu Y, Gao K. Reinforcement learning-assisted memetic algorithm for sustainability-oriented multiobjective distributed flow shop group scheduling. IEEE Trans Syst Man Cybern: Syst. 2025;1–15. doi:10.1109/TSMC.2025.3541795. [Google Scholar] [CrossRef]
23. Wu X, Cao Z. An improved multi-objective evolutionary algorithm based on decomposition for solving re-entrant hybrid flow shop scheduling problem with batch processing machines. Comput Ind Eng. 2022;169(1):108236. doi:10.1016/j.cie.2022.108236. [Google Scholar] [CrossRef]
24. Eusuff M, Lansey K, Pasha F. Shuffled frog-leaping algorithm: a memetic meta-heuristic for discrete optimization. Eng Optim. 2006;38(2):129–54. doi:10.1080/03052150500384759. [Google Scholar] [CrossRef]
25. Lei D, Dai T. An adaptive shuffled frog-leaping algorithm for parallel batch processing machines scheduling with machine eligibility in fabric dyeing process. Int J Prod Res. 2024;62(21):7704–21. doi:10.1080/00207543.2024.2324452. [Google Scholar] [CrossRef]
26. Cai J, Zhou R, Lei D. Dynamic shuffled frog-leaping algorithm for distributed hybrid flow shop scheduling with multiprocessor tasks. Eng Appl Artif Intell. 2020;90(1):103540. doi:10.1016/j.engappai.2020.103540. [Google Scholar] [CrossRef]
27. Xu Y, Wang L, Wang S, Liu M. An effective shuffled frog-leaping algorithm for solving the hybrid flow-shop scheduling problem with identical parallel machines. Eng Optim. 2013;45(12):1409–30. doi:10.1080/0305215X.2012.737784. [Google Scholar] [CrossRef]
28. Zitzler E, Thiele L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE Trans Evol Comput. 1999;3(4):257–71. doi:10.1109/4235.797969. [Google Scholar] [CrossRef]
29. Lei D. A pareto archive particle swarm optimization for multi-objective job shop scheduling. Comput Ind Eng. 2008;54(4):960–71. doi:10.1016/j.cie.2007.11.007. [Google Scholar] [CrossRef]
30. Bosman PAN, Thierens D. The balance between proximity and diversity in multiobjective evolutionary algorithms. IEEE Trans Evol Comput. 2003;7(2):174–88. doi:10.1109/TEVC.2003.810761. [Google Scholar] [CrossRef]
31. Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput. 2002;6(2):182–97. doi:10.1109/4235.996017. [Google Scholar] [CrossRef]
32. Taguchi G. Introduction to quality engineering. Tokyo, Japan: Asian Productivity Organization; 1986. [Google Scholar]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools