A Q-Learning-Assisted Co-Evolutionary Algorithm for Distributed Assembly Flexible Job Shop Scheduling Problems

1  Introduction

Currently, traditional manufacturing modes have been impacted and developed rapidly towards the direction of distributed production due to the advancement of intellectual technologies [1–3]. Many enterprises are applying the distributed production mode having multiple factories to actual industrial manufacturing environments, aiming to achieve the reduction of operation cost and the improvement of response speed [4]. At the same time, scheduling is widely adopted in distributed manufacturing systems to efficiently arrange production tasks with limited resources [5].

Nowadays, distributed production scheduling problems are broadly discussed and investigated by scholars and engineers [6]. Distributed flexible job scheduling problems (DFJSPs), classic distributed scheduling problems, refer to an extension of flexible job shop scheduling problems to distributed production environments. In a DFJSP, a collection of jobs necessitates allocation to flexible job shops for processing. Each flexible job shop contains a group of machines to process the assigned jobs. DFJSPs are widespread in actual industry applications, such as building materials equipment manufacturing [7] and food processing [8]. Hence, research on modeling and optimization of DFJSPs has become the key content for manufacturing enterprises.

Furthermore, the overall optimization of supply chains is gradually receiving more and more attention [9]. Managing various activities in supply chains from the integration perspective is becoming a core measure of reducing operation costs [10]. In these activities, production and assembly are crucial in the supply chain. The former involves processing jobs on machines, while the latter is about assembling these jobs into products. However, the existing studies on integrated scheduling of production and assembly activities mainly focus on single-factory manufacturing environments [11]. Research on distributed production scheduling problems considering assembly operations is lacking, especially in distributed flexible job shop scenarios.

Consequently, this research studies integrated scheduling problems of production and assembly operations within distributed flexible job shop environments. Since the NP-hard features of DFJSPs have been demonstrated [5], the investigated problems are also NP-hard. Therefore, we develop a meta-heuristic incorporating cooperative evolutionary strategies and Q-learning approaches to handle the investigated problem. The concrete contributions of this work are given as follows.

(1)   A DFJSP with assembly operations is proposed. To handle the problem, a mixed integer programming model is formulated to minimize maximum completion time (MCT).

(2)   A Q-learning-assisted co-evolutionary algorithm (QA-CEA) is devised to solve the model. Multi-population strategies, crossover approaches, and Q-learning-based local search methods are designed to improve the performance of QA-CEA. A Q-learning approach is employed to adaptively assist the best individuals in the population in selecting neighborhood structures for further enhancing exploitation abilities.

(3)   Numerical experiments regarding QA-CEA and three popular meta-heuristics are carried out on problem instances. Comparison outcomes validate the preeminent performance of QA-CEA in coping with the researched problem.

The remainder of this work is outlined below. Section 2 provides an overview of relevant studies. Section 3 gives the statement and model of the studied problem. The designed algorithm is given in Section 4. In addition, the results and analysis of the comparison experiments are reported in Section 5. The conclusion and future research are provided in Section 6.

2  Literature Review

Recently, studies regarding distributed production scheduling problems have emerged endlessly. Many scholars and practitioners in manufacturing and service fields have conducted in-depth discussions on such issues. Lei et al. [12] consider a distributed parallel machine scheduling problem to reach minimal tardiness and makespan. An artificial bee colony (ABC) approach is presented to deal with the problem. Bai et al. [13] study a distributed flow shop scheduling problem (DFSP) considering uniform machines and release dates. They propose an ABC method to minimize makespan. Pan et al. [14] solve a DFSP to realize minimal makespan. They design five meta-heuristics, namely genetic algorithm, harmony search, Jaya, ABC, and particle swarm optimization method. Xie et al. [15] cope with a DFJSP to minimize makespan. A hybrid approach combining genetic algorithm and tabu search is presented to handle it. Cao et al. [16] propose a DFJSP to achieve minimal energy consumption (EC) and makespan. A cooperative optimization method with the inverse model and neighborhood search is employed to solve this problem. Liu et al. [17] focus on handling a DFSP having blocking constraints. An iterated greedy method is adopted to reach a minimal makespan. Yan et al. [18] propose a memetic algorithm (MA) to solve a DFSP, aiming to achieve makespan and carbon emission minimization. Yu et al. [8] address a DFJSP to realize minimal makespan and EC. They devise a bi-population evolutionary strategy to handle the problem. Tang et al. [19] study a DFJSP with sequencing flexibility. An MA is presented to solve the problem. Zhu et al. [5] discuss a DFJSP with order cancellation. An MA is proposed to realize minimal makespan and EC.

Meanwhile, in the supply chain management field, the current hot topics lie in integrated scheduling problems of production and assembly. Existing research focuses on production models combined with assembly operations, such as flow shop [20,21] and job shop [11,22]. Many objectives are considered according to real problem indicators, including makespan [23,24], total tardiness [25], EC [26], and cost-related criteria [27]. To effectively handle the problems, various meta-heuristics have been used and improved, e.g., MA [28], ABC [26], and teaching-learning-based optimizer [11].

Due to the development of market globalization, research on distributed production processes that consider assembly operations is also increasing. Wang et al. [29] settle a distributed assembly flow shop scheduling problem (DAFSP). They use an MA to minimize EC and makespan. Zhao et al. [30] study a DAFSP considering no-wait constraints. They adopt an iterated greedy approach to minimize flow time. Luo et al. [31] investigate a DAFSP to minimize total tardiness and EC. An MA is improved to deal with it. Huang et al. [32] discuss a DAFSP considering an assembly machine. They employ an MA to minimize tardiness. Shao et al. [33] solve a DAFSP to minimize makespan by using a hyper-heuristic. Tian et al. [34] study a distributed assembly job shop scheduling problem. They adopt a genetic algorithm to address it.

In addition, reinforcement learning is combined with meta-heuristics to solve complex scheduling problems since its learning mechanisms contribute to improving the performance of meta-heuristics [35]. Wang et al. [36] propose an ABC based on Q-learning to solve a DAFSP considering factory eligibility, transport capacity, and setup time. The objectives of this research are to minimize makespan and total tardiness. Zhang et al. [37] present a Q-learning-based particle swarm optimizer to address a DFSP, aiming to reach minimal makespan and EC. Yu et al. [38] propose a DAFSP to minimize MCT, earliness, tardiness, and carbon emission. Five meta-heuristics combined with Q-learning are designed to deal with this problem. Zhao et al. [39] consider a DFSP with no-wait conditions. An iterative greedy method based on Q-learning is devised to achieve minimal makespan and total tardiness. Zhang et al. [40] adopt a Q-learning-driven ABC to handle a DFJSP considering maintenance and transportation operations, aiming to minimize MCT and factory workload. Chen et al. [41] investigate a dynamic flexible job shop problem having limited transportation resources. They design a Q-learning-based genetic algorithm to minimize makespan and total tardiness. Zhang et al. [7] consider a DFJSP to minimize the sum of makespan and EC. A hyper-heuristic incorporating Q-learning is presented to solve it.

Based on the above work, they share the following features: (1) Distributed scheduling problems have been widely investigated. Nevertheless, fewer studies consider subsequent assembly operations, especially the work on DFJSPs. (2) Research on integrated scheduling of production and assembly has attracted much attention. However, distributed manufacturing scenarios regarding flexible job shops are rarely considered. (3) Integration methods of meta-heuristics and reinforcement learning are widely adopted to solve optimization scheduling problems in many studies. A great many numerical experiments indicate that they have stronger abilities in addressing these problems. According to the analysis, the DFJSP with assembly operations is ignored in existing studies. Thus, we study such scheduling problems by designing a QA-CEA.

3  Presented Problem and Model

3.1 Problem Statement

This article investigates a DFJSP with assembly operations. In the first phase, multiple factories operate in parallel, with each one being regarded as a flexible job shop equipped with a versatile array of multi-functional machines. A group of jobs necessitates handling within shops, where each job comprises a series of operations having a given processing sequence. Each operation ought to be handled on one of the available machines, and all operations of a job are fabricated at the same shop. In the second phase, multiple assembly machines are utilized. A collection of products requires assembling by using the jobs finished in the production phase. The objective of solving the problem is to minimize the MCT, i.e., the latest time that all products are finished for assembly.

To acquire a feasible solution, the following requirements need to be met: (1) At time zero, all machines are available, and all jobs wait to be processed; (2) A machine is capable of executing at most one operation at a time; (3) An operation undergoes processing only once; (4) An assembly machine can fabricate at most one product at a time; (5) A product can be assembled only once; (6) Machine interruption is not allowed in the two phases.

The considered problem includes five key decisions: (1) Factory assignment of jobs; (2) Machine assignment of operations at factories; (3) Operation processing sequence; (4) Assembly machine assignment of products; (5) Product assembly sequence on assembly machines. To visualize the studied problem, a schematic is provided in Fig. 1, where three products with six jobs need to be handled on a production system with two factories, two jobs per factory, and two assembly machines.

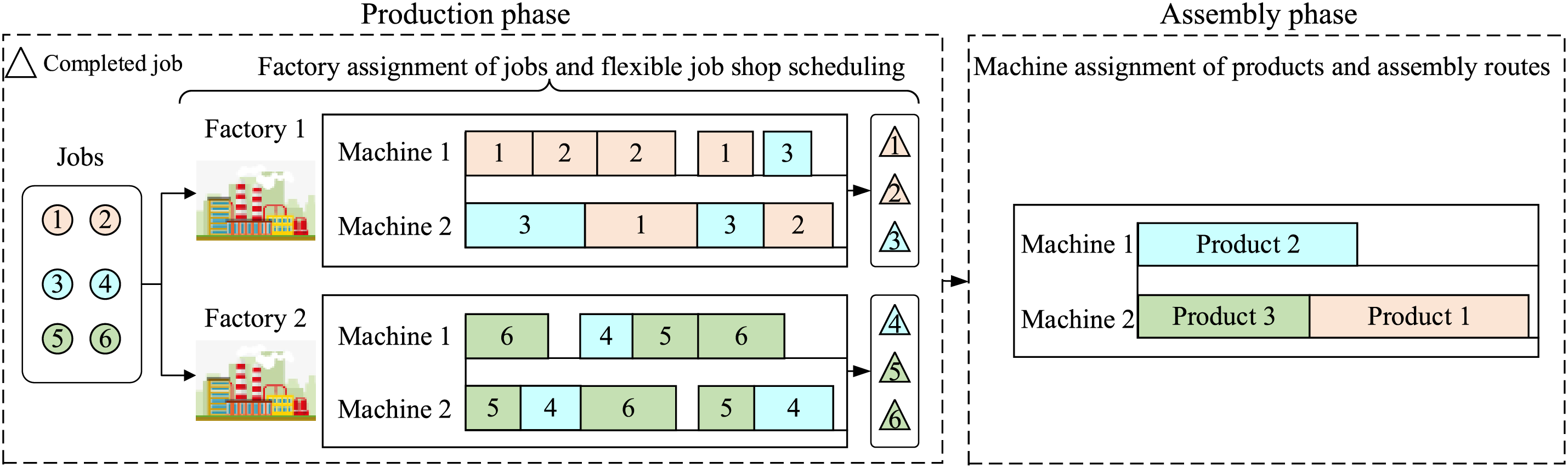
Figure 1: Illustration of the studied problem

3.2 Model Formulation

To build a mathematical programming model of the investigated problem, this work uses the following symbols.

Set and index

F: Set of factories, F={1,2,…,f}, f indicates the number of factories. g∈F, g is a factory index.

M: Set of machines at a factory, M={1,2,…,m}, m represents the quantity of machines at a factory. h∈M, h is a machine index.

N: Set of products, N={0,1,2,…,n}, where 0 indicates a dummy product without assembly time, and n represents the number of products. i∈N, i is a product index.

J: Set of jobs, J={0,1,2,…,j}, where 0 implies a dummy job without processing time, and j indicates the number of jobs. k∈J, k is a job index.

Qk: Set of operations regarding job k, Qk={1,2,…,qk}, qk signifies the number of operations about job k. l∈Qk, l is an operation index.

V: Set of assembly machines, V={1,2,…,v}, v represents the number of assembly machines. u∈V, u is an assembly machine index.

Parameter

Okl: l-th operation of job k.

ηklhg: If machine h at factory g is one of the available machines in processing Okl, ηklhg=1; Otherwise, ηklhg=0.

pklhg: Processing time of Okl on machine h at factory g.

ξik: If job k is a component of product i, ξik=1; Otherwise, ξik=0.

aiu: Assembly time of product i on assembly machine u.

G: A very large number.

Decision variable

Xkg: If job k is allocated to factory g for processing, Xkg=1; Otherwise, Xkg=0.

Yklk′l′hg: If machine h at factory g processes Ok′l′ immediately after Okl, Yklk′l′hg=1; Otherwise, Yklk′l′hg=0.

Zii′u: If assembly machine u fabricates product i′ immediately after i, Zii′u=1; Otherwise, Zii′u=0.

Sklα: Production start time of Okl.

Cklα: Production completion time of Okl.

Ekα: Production completion time of job k.

Siβ: Assembly start time of product i.

Ciβ: Assembly completion time of product i.

CM: MCT.

By using the above notations, this research establishes a mixed integer programming model for the considered problem below.

minCM(1)

s. t.

∑g∈FXkg=1,∀k∈J∖{0}(2)

Xkg=∑k′∈J∑l′∈Qk′∑h∈MYklk′l′hg,∀k∈J∖{0},∀l∈Qk,∀g∈F(3)

∑k′∈J∑l′∈Qk′∑h∈M∑g∈FYklk′l′hg=1,∀k∈J∖{0},∀l∈Qk(4)

Yklklhg=0,∀k∈J∖{0},∀l∈Qk,∀h∈M,∀g∈F(5)

∑k′∈J∑l′∈Qk′Yklk′l′hg≤ηklhg,∀k∈J∖{0},∀l∈Qk,∀h∈M,∀g∈F(6)

∑k′∈J∑l′∈Qk′Yklk′l′hg=∑k′∈J∑l′∈Qk′Yk′l′klhg,∀k∈J∖{0},∀l∈Qk,∀h∈M,∀g∈F(7)

∑k∈J∖{0}∑l∈QkY0l′klhg≤1,∀l′∈Q0,∀h∈M,l′=h,∀g∈F(8)

Sklα≥Ck,l−1α,∀k∈J∖{0},∀l∈Qk∖{1}(9)

Sklα≥Ck′l′α+G×(Yk′l′klhg−1),∀k∈J∖{0},∀k′∈J,∀l∈Qk,∀l′∈Qk′,∀h∈M,∀g∈F(10)

Cklα≥Sklα+pklhg×Yklk′l′hg,∀k∈J∖{0},∀k′∈J,∀l∈Qk,∀l′∈Qk′,∀h∈M,∀g∈F(11)

Ekα=Ckqkα,∀k∈J∖{0}(12)

∑i′∈N∑u∈VZii′u=1,∀i∈N∖{0},i≠i′(13)

∑i′∈NZii′u=∑i′∈NZi′iu,∀i∈N{0},∀u∈V(14)

Z0iu≤1,∀i∈N∖{0},∀u∈V(15)

Siβ≥Ekα×ξik,∀i∈N∖{0},∀k∈J∖{0}(16)

Siβ≥Ci′β+G×(Zi′iu−1).∀i∈N∖{0},∀i′∈N,∀u∈V(17)

Ciβ≥Siβ+aiu×Zii′u,∀i∈N∖{0},∀i′∈N,∀u∈V(18)

CM≥Ciβ,∀i∈N∖{0}(19)

Xkg∈{0,1},∀k∈J∖{0},∀g∈F(20)

Yklk′l′hg∈{0,1},∀k,k′∈J,∀l∈Qk,∀l′∈Qk′,∀h∈M,∀g∈F(21)

Zii′u∈{0,1},∀i,i′∈N,∀u∈V(22)

Sklα≥0,Cklα≥0,C0lα=0,Ekα≥0,Siβ≥0,Ciβ≥0,C0β=0,CM≥0,∀k∈J,∀l∈Qk,∀i∈N(23)

where Eq. (1) is to realize minimal MCT. Eq. (2) indicates that each job must be allocated to only one factory. Eq. (3) guarantees that all operations belonging to a job must be machined within the same factory. Eqs. (4) and (5) stipulate that an operation ought to be processed on machines only once. Eq. (6) indicates that each operation can be only handled by the machines that are available for the operation. Eq. (7) defines that an operation possesses a unique predecessor operation and a unique successor operation. Eq. (8) implies that each dummy operation possesses at most one successor operation. Eqs. (9) and (10) define the production start time of operations. Eqs. (11) and (12) give the production completion time of operations and jobs, respectively. Eq. (13) ensures that a product can be assembled only once. Eq. (14) indicates that a product has only one predecessor product and one successor product. Eq. (15) signifies that a dummy product has at most one successor product. Eqs. (16) and (17) define the assembly start time of products. Eq. (18) formulizes the assembly completion time of products. Eq. (19) defines the MCT. Eqs. (20)–(23) provide the values of decision variables.

4  Proposed Algorithm

Drawing inspiration from the co-evolutionary processes found in nature, numerous studies are devoted to designing various collaborative approaches to further enhance the performance of evolutionary algorithms when tackling intricate engineering optimization challenges [42,43]. The fundamental concept of co-evolutionary strategies revolves around partitioning a complex system into distinct subsystems, with each subsystem undergoing independent evolution. Then, the evolved subsystems are combined into a new system to achieve the goal of overall evolution [44]. By integrating co-evolutionary technologies, meta-heuristics are empowered to perform more efficient searches. This is because they can simultaneously explore the solution space for optimal solutions from multiple directions.

Meanwhile, local search methods are widely adopted to further improve the exploitation abilities [40]. Moreover, Q-learning, one of the most well-known reinforcement learning methods, is widely utilized to assist meta-heuristics in selecting search strategies and user parameters to enhance algorithms’ performance [41]. Thus, a Q-learning-based iterative local search method is designed to refine individuals. Then, a co-evolutionary algorithm combined with it (QA-CEA) is developed to deal with the problem under consideration. Among them, multiple populations are established according to production decisions. Each population independently evolves to search for better decisions. Finally, the optimal solution to the studied problem is derived by integrating individuals in multiple populations. The introduction of QA-CEA is provided as follows.

4.1 Encoding and Decoding Methods

This research employs an integer string π=(πF,πM,πO) with three substrings to represent a solution. πF=(π1F,π2F,…,πjF) denotes the factory allocation of jobs, and πkF indicates a factory index assigned to job k. πM=(π1M,π2M,…,πjM) implies the machine assignment of operations, πkM=(πk1M,πk1M,…,πkqkM) denotes the machine assignment as regards all operations belonging to job k, and πklM refers to a machine index to which operation Okl is arranged. πO=(π1O,π2O,…,πsO) represents the processing sequence of operations, and s indicates the total quantity of operations about all jobs. Each element represents a job index, and the number of occurrences of a job index signifies the corresponding operation respecting this job.

Fig. 2 showcases an illustrative example of the encoding method. πF represents that jobs 1, 2, and 3 are severally assigned to factories 1, 1, and 2 for processing. From πM, it is found that O11 and O12 are respectively arranged to be handled on machines 1 and 2. πO depicts that O31 is arranged to machine 2 in factory 2 for fabricating at first, and then O11 is arranged to machine 1 in factory 1 for performing. In this way, all production decisions can be obtained. Once the production decisions have been made, the decisions in the assembly phase are determined by a designed decoding approach as mentioned later. Thus, all the decisions regarding the problem under consideration are obtained.

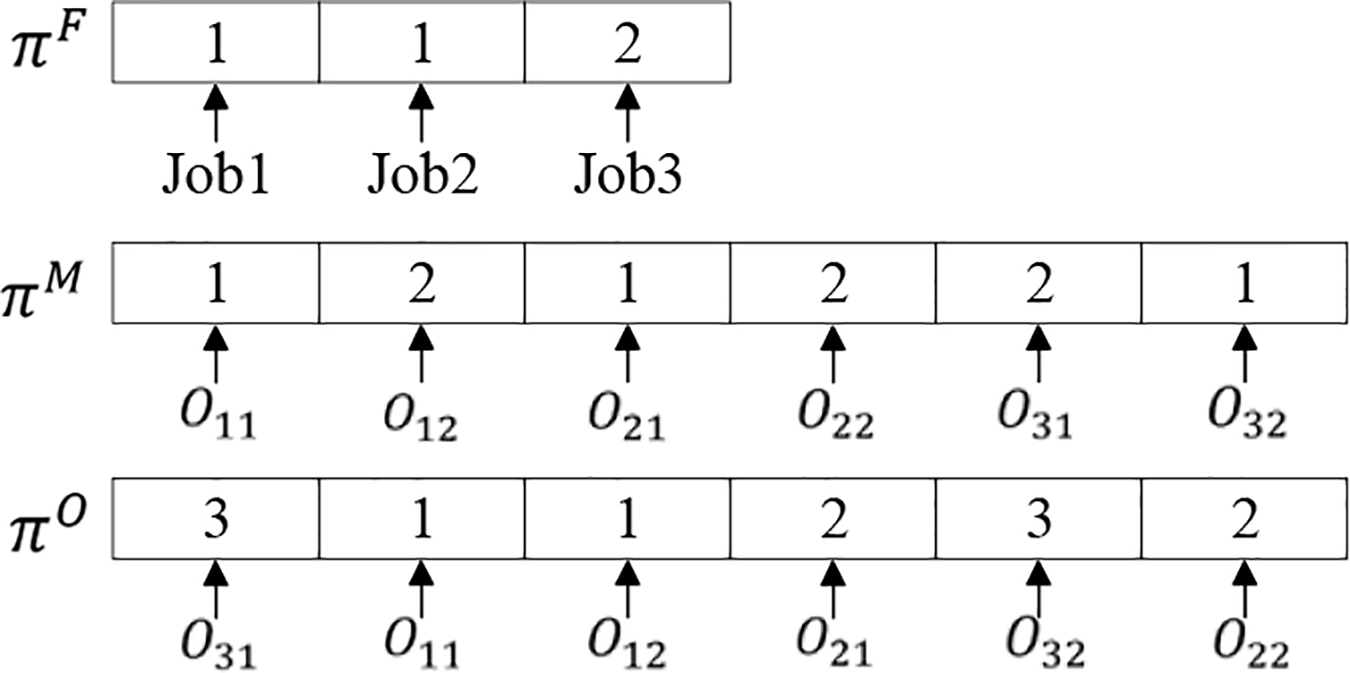
Figure 2: Illustration of the encoding method

It is noteworthy that the aforementioned encoding methodology solely encapsulates the decisions pertinent to the production phase, and the decisions about the assembly phase are not explicitly derived. Thus, this research meticulously crafts a decoding approach as follows: (1) When jobs are processed in production factories, a left shift method is adopted [45] to reduce idle time; (2) In the assembly phase, a product is assembled once its involved jobs finish being handled in the production phase, and the assembly start time for a given product is equal to the latest production completion time of all jobs that constitute the particular product. Based on the above method, a solution can be directly decoded into an executable program.

4.2 Population Initialization

The encoding scheme comprises three substrings, each one corresponds to a distinct decision. To tackle these decisions individually, this work introduces three populations: PF, PM, and PO. Each population is dedicated to exploring one of the decisions. PF aims to search for a better factory allocation of jobs, where each individual is linked to πF in π. PM focuses on obtaining a preferable machine arrangement of operations, where each individual corresponds to πM in π. PO focuses on finding a superior operation processing sequence, where each individual is related to πO in π.

To produce populations with diverse and high-quality characteristics, this research employs a blend of heuristic rules and stochastic methods to initialize populations with individuals. The combination method is offered below.

In PO, the first two individuals are generated using the most work remaining and most operation remaining [46] rules, respectively. The remaining individuals are created by using random methods. In PF, we adopt an NR1 rule [47] to produce the first two individuals, and randomly generate the rest individuals. In PM, the first two individuals are created by employing the minimum completion time and operation minimum processing time [46] rules, respectively. The remaining individuals are generated at random. Based on the above methods, we can generate N individuals for the three populations, respectively, where N denotes the population size.

It is noteworthy that a solution is made up of three components. Each component corresponds to an individual in each population. To assess the effectiveness of individuals across these three populations, we select individuals with the same indices from PF, PM, and PO to form a solution. Importantly, the objective value of this constructed solution is identical to the objective values achieved by the individuals themselves.

4.3 Evolutionary Strategies

In QA-CEA, genetic operations are used as evolutionary strategies to achieve independent evolution of populations. The specific process is described as follows.

(1)   Evolutionary strategies of PF: (a) A binary selection method [48] is adopted to select two individuals from PF as parent individuals. (b) A two-point crossover [49] method is employed to create new individuals. It randomly selects two positions on πF. The elements between two positions in the new individual come from one parent individual, and the remaining elements are from the other parent individual. (c) A mutation strategy with a probability of σ is applied, randomly chooses a job, and alters its factory index in πF. Notably, the best-performing individual is directly propagated to the next generation, and the aforementioned process is utilized to create the remaining N−1 individuals. In addition, an example is used to illustrate the crossover method and mutation strategy as shown in Fig. S1a in the Supplementary File.

(2)   Evolutionary strategies of PM: (a) The same parent individual selection approaches as evolutionary strategies of PF are used. (b) A uniform crossover method [50] is used to create new individuals. A binary string is produced. If the corresponding numbers of elements in new individuals are zero, they are derived from one parent individual; Conversely, they are derived from the other parent individual. (c) A mutation approach having probability σ is executed. It randomly chooses an operation and adjusts its machine index in πM. The generation method of the new population is the same as the evolutionary strategies of PF. To better explain the crossover method and mutation strategy, this work provides an example as reported in Fig. S1b in the Supplementary File.

(3)   Evolutionary strategies of PO: (a) The same parent individual selection approaches as evolutionary strategies of PF are adopted. (b) A precedence operation crossover [51] method is employed to create new individuals. It randomly generates a job set, and elements in new individuals in the set are inherited from one parent individual in the same position. The remaining elements come from the other parent individual in the corresponding order. (c) A mutation approach with probability σ is used. It randomly selects two operations and exchanges their positions on πO. The construction method of the new population adheres to the same evolutionary strategies employed in PF. This work offers an example to explain the evolutionary strategies, as given in Fig. S1c in the Supplementary File.

4.4 Q-Learning-Assisted Iterative Local Search

This work designs a Q-learning-assisted iterative local search method to improve the best solution identified during the historical search procedure, aiming to further enhance the exploitation capabilities of QA-CEA. The specific description is offered as follows.

4.4.1 Neighborhood Structures

Based on the characteristics of the problem under study, this research proposes a concept of critical products and jobs to further explore the problem’s knowledge. The critical product refers to the last product that has idle time before being assembled on the last completed machine in the assembly phase. The critical jobs are all the jobs that constitute the critical product. Fig. 3 gives an illustration of critical products and critical jobs. It is seen that the critical product is product 1, and the critical jobs are jobs 1 and 2. Adjusting the factory allocation, machine arrangement, and processing sequence of the critical jobs is likely to change the MCT of a solution.

Figure 3: Illustration of the critical product and critical jobs

Based on this, this work devises three neighborhood structures as follows:

L1: Select a critical job at random and change its factory index in πF.

L2: Choose an operation of a critical job randomly and change its machine index in πM.

L3: Select an operation of a critical job, and swap it with a randomly chosen operation in πO.

4.4.2 Q-Learning-Assisted Selection of Neighborhood Structures

To intelligently help the best solution to select neighborhood structures, a Q-learning method is adopted by utilizing historical search information at each iteration. Currently, the Q-learning methods are widely used in combination with meta-heuristics to improve their search abilities [39]. The Q-learning method mainly includes five parts: agents, states, actions, reward value, and Q-table. In QA-CEA, the introduction of the Q-learning method is given as follows.

(1) Agent and state

In this work, the best solution at each iteration is regarded as an agent since it can directly reflect the effectiveness of neighborhood structures. Based on the difference between the objective values of the best solution πb and a new solution πn obtained by using a selected neighborhood structure, we define three states: ΔO>0, ΔO=0, and ΔO<0, which are indexed as 1, 2, and 3, respectively. Thereinto, ΔO=O(πb)−O(πn), where O(πb) and O(πn) represent the objective values of πb and πn, respectively.

(2) Action

This work designs three actions in QA-CEA, which are named actions 1, 2, and 3, respectively. Each action corresponds to a neighborhood structure, i.e., actions 1, 2, and 3 are associated with L1, L2, and L3, respectively. In addition, an ε-greedy method [52] is adopted to help the agent select a promising action at each local search iteration. If a random number from an interval [0, 1] is less than ε, the agent randomly selects an action, and otherwise it selects an action having the maximal Q value in the current state from the Q table. In QA-CEA, ε is set to 0.1.

(3) Reward value

After performing an action, the agent will receive a reward value. According to the definition of states, we find that state 1 is the best since the new individual is better than the original individual. On the contrary, state 3 is the worst. Therefore, this research proposes a reward function based on state changes, which is defined as follows.

rt={st−1−st,st<st−1(S−st)/2,st=st−10,other(24)

where the symbols “S” and “st” indicate the number of states and the agent state at the t-th local search iteration, respectively. rt represents the reward value obtained by the agent after the chosen action is performed.

(4) Q-table update

The Q value in the Q-table is used to store the search information after reward values are acquired during the iteration process. In QA-CEA, the updated equation of the Q-table is provided as follows.

Q(st,at)←Q(st,at)+α×(rt+γ×max{Q(st+1,a)}−Q(st,at))(25)

where the symbol at indicates the chosen action of an agent at the t-th local search iteration. max{Q(st+1,a)} implies the maximum Q value in the Q-table at st+1. The symbols α and γ represent the learning rate and discount factor, respectively. It is noteworthy that all elements within the Q-table are initialized with a value of zero.

4.4.3 Local Search Methods

This work designs a Q-learning-assisted iterative local search (ILS) method to improve the best solution at each iteration. The pseudo-code of ILS is shown in Algorithm S1 in the Supplementary File, where μ is a given parameter.

4.5 Framework of the Proposed Algorithm

All the components of QA-CEA are described above. To illustrate their execution methods, we provide a flowchart of QA-CEA as shown in Fig. 4. The concrete procedure is as follows. First, all algorithm parameters and populations are initialized. Second, the following processes are looped: (1) The evolutionary strategies based on crossover and mutation operations are conducted to update populations; (2) The Q-learning-assisted ILS approach is performed to enhance the best individual. Finally, if a given stopping condition is satisfied, the best solution is output.

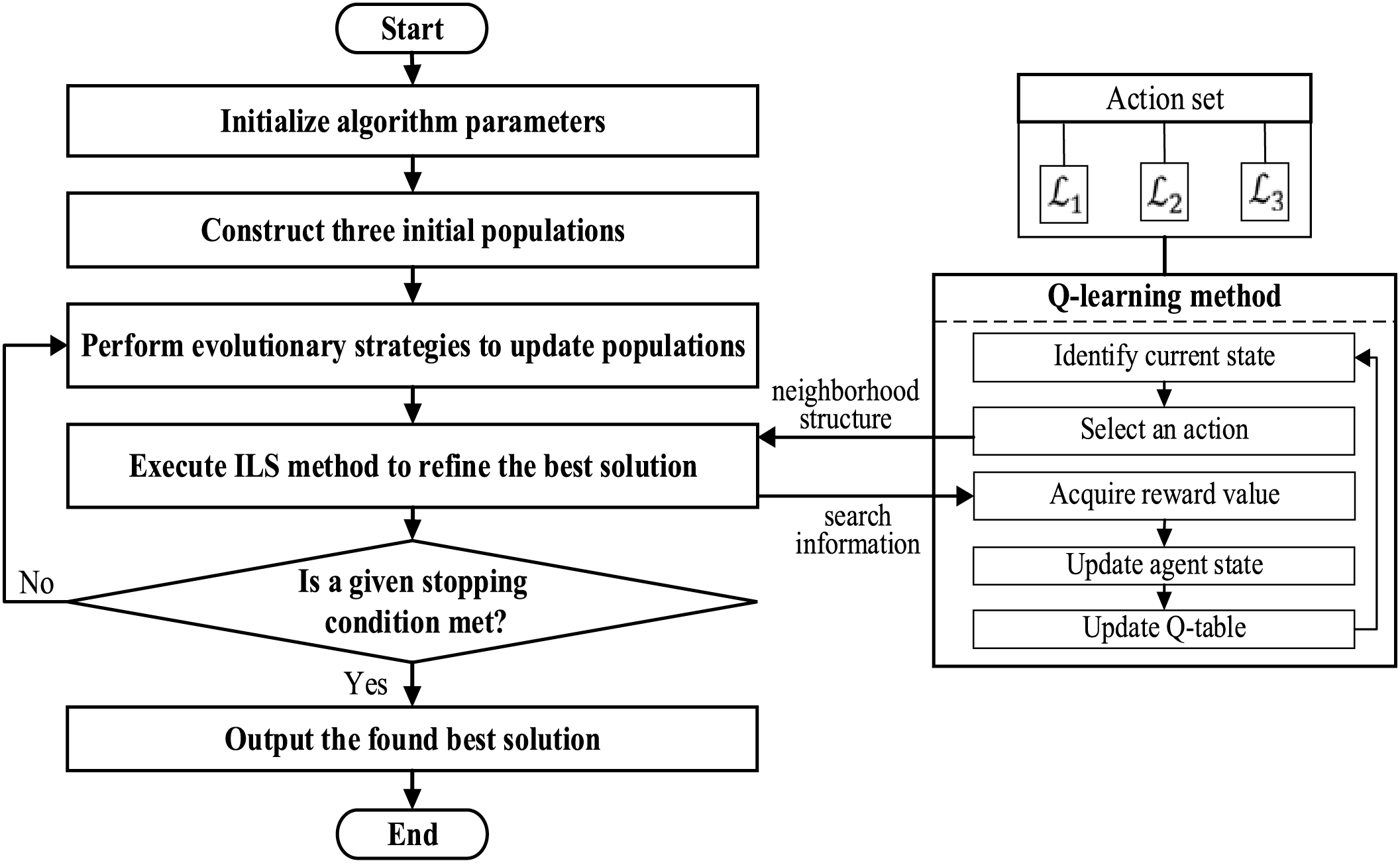
Figure 4: Flowchart of QA-CEA

5  Experiment Results and Discussions

To evaluate QA-CEA’s effectiveness in tackling the considered problem, comparison experiments are conducted on a set of instances. Three advanced metaheuristics are chosen from existing literature as competitive algorithms, namely, hybrid genetic algorithm (HGA) [53], hybrid teaching-learning-based optimization (HTLBO) [54], and improved gray wolf optimization (IGWO) [55], respectively. All the approaches are coded in C++ and executed on computers equipped with an Intel Core i5-8265U CPU @ 1.60 GHz processor and 8 GB of RAM.

5.1 Problem Instance Generation

To test the capacities of the QA-CEA in working out the studied problem, this work constructs a group of instances as shown in Table S1 in the Supplementary File. The number of jobs, job processing time, and the number of machines at factories come from flexible job shop scheduling problems of the Hurink, Jurisch & Thole benchmark [56]. The quantity of jobs, machines, and factories belong to {20,40,60,80,100}, {5,10}, {2,3,4}, respectively. Furthermore, the number of products is equal to 0.3∗j. The quantity of assembly machines is from roundup(0.2∗n), where roundup(X) is the largest integer close to X. The assembly time of products is uniformly generated from an interval [1, 99]. Through the above approaches, this work establishes 30 instances named “DPSAab”, where “ab” indicates an instance index.

5.2 Performance Metrics

In the following comparisons, this article uses the maximum running time of 1.5⋅m⋅j s as the termination criteria for all the used methods. Each instance is handled independently 20 times. We use the relative percentage deviation (RPD) to evaluate the results of QA-CEA and its peers, and the computation equation is given below.

RPD=CMλ−CM∗CM∗×100%(26)

The symbol CM∗ represents the best objective value received by QA-CEA and its rivals, and CMλ denotes the objective value obtained by the method at the λ-th run. Subsequently, the average RPD (aRPD), the best RPD (bRPD), and the standard deviation of RPD (sRPD) are computed across all instances. The smaller values of aRPD, bRPD, and sRPD indicate the superior abilities of the respective method.

5.3 Parameter Setting

To investigate the impact of parameters N, σ, μ, α, and γ on the performance of QA-CEA, Taguchi experiment methods [57] are conducted on the instance DPSA15. Each parameter encompasses four distinct levels: N∈{30,50,70,90}, σ∈{0.1,0.2,0.3,0.4}, μ∈{10,15,20,25}, α∈{0.2,0.4,0.6,0.8}, and γ∈{0.2,0.4,0.6,0.8}. Thus, we adopt an orthogonal array L16(45) with 16 parameter combinations. For every combination of parameters, QA-CEA is executed 20 times for solving this instance. The stopping condition for each run is set to 1.5⋅m⋅j s. The objective value functions as the response variable (RV), with the average of the 20 executions serving as the average RV (ARV). All the parameter combinations alongside their respective outcomes are reported in Table S2 in the Supplementary File.

Table S3 provides the significance level of parameter combinations. It is observed that N possesses the strongest impact on the solving abilities of QA-CEA, followed by σ, μ, γ, and α. The impact trends of each parameter are illustrated in Fig. S2 in the Supplementary File. It is found that a better parameter combination of QA-CEA is: N=30, σ=0.1, μ=15, α=0.6 and γ=0.8. This combination will be used in subsequent experiments.

Furthermore, to show the structure and direct result of DFJSP with assembly operations more clearly, a Gantt chart of results obtained by QA-CEA solving instance DPSA01 is provided as reported in Fig. 5. DPSA01 has two factories, five processing machines per factory, 20 jobs, five operations per job, two assembly machines, and six products. In Fig. 5, jobs with the same color markings at processing factories are assembled into products with the same color markings at an assembly factory. It is seen that the MCT of the schedule is 750.

Figure 5: Gantt chart of results regarding DFJSP with assembly operations

5.4 Effectiveness of Q-Learning Approaches

This research uses a Q-learning approach to enhance the performance of QA-CEA. To validate the efficacy of the Q-learning approach, this article devises a variant of QA-CEA (named CEA) which randomly selects a neighborhood structure for the best solution in the local search phase. The 15 instances having different sizes are employed to perform the comparison experiments between QA-CEA and CEA.

The comparison results of QA-CEA and CEA in metrics aRPD, bRPD, and sRPD are reported in Table S10 in the Supplementary File. QA-CEA achieves better results than CEA in solving the used instances. Meanwhile, the t-test method at a significance level of 0.05 with a freedom degree of 38 [40] is used to analyze comparison results. The symbols “+”, “~”, and “−” indicate that QA-CEA is significantly better than, statistically equal to, and significantly worse than CEA. It is seen that QA-CEA is significantly better than CEA in most instances. Thus, it is declared that the incorporation of the Q-learning approach significantly contributes to enhancing the performance of QA-CEA in handling the targeted problem.

5.5 Comparisons between QA-CEA and Its Rivals

This work selects three well-known meta-heuristics, i.e., HGA, HTLBO, and IGWO, as competitive methods to test the performance of QA-CEA for the studied problem. In their original work, the three methods are adopted to solve DFJSPs. Meanwhile, the same solution representation approaches with QA-CEA are used. Therefore, they can be straightforwardly extended to handle the considered problem. Consequently, this research chooses them as competitive methods. To ensure the fairness of comparison experiments, we perform the Taguchi experiments to meticulously adjust the user parameters of the rival methods. The exhaustive experimental outcomes are appended in the Supplementary File, while the finalized parameter configurations are clearly outlined in Table 1.

The comparison outcome of QA-CEA and its rivals is given in Table S11 in the Supplementary File. In terms of metrics aRPD, bRPD, and sRPD, we see that QA-CEA beats HGA, HTLBO, and IGWO in most instances. It is discovered that QA-CEA realizes better results than HGA, HTLBO, and IGWO in general. The average of aRPD, bRPD, and sRPD values in all the instances, we find that QA-CEA obtains smaller values than its comparison algorithms. Therefore, we deduce that QA-CEA is an excellent solver.

Subsequently, we provide the boxplot graphs of four instances with several scales as shown in Fig. 6. It is seen that QA-CEA has more stable and centralized results than its competitors. Therefore, we confirm that QA-CEA is more suitable to settle the studied problem.

Figure 6: Boxplot graphs of instances regarding QA-CEA and the peers

In addition, this work adopts the t-test, Friedman test [40], and Nemenyi posthoc test [44] approaches to analyze the statistical difference in results obtained by the four methods. The detailed analysis and discussion are given as follows.

(1) The t-test results are reported in Table S11 in the Supplementary File. We see that QA-CEA is significantly superior to HGA and HTLBO in all 30 instances, and significantly superior to IGWO in most instances. (2) The Friedman test at a significance level of 0.05 for aRPD values is adopted. The statistic outcomes are offered in Table S11 in the Supplementary File, and the average ranks are given in Fig. 7. We can find that the average ranks of QA-CEA, HGA, HTLBO, and IGWO are 1.0667, 3.9000, 3.1000, and 1.9333, respectively. The p-value is 0.0000, signifying that the outcomes acquired by the four algorithms are significantly different. (3) The Nemenyi posthoc test at a significance level of 0.05 is adopted to scrutinize the performance disparities between QA-CEA and its competitors. Based on Table S11 in the Supplementary File, we see that the average rank differences between QA-CEA and HGA, HTLBO, and IGWO are respectively 2.8333, 2.0333, and 0.8666, all exceeding the critical range value of 0.8563. It is manifested that QA-CEA is significantly better than its competitors.

Figure 7: Average ranks of four algorithms

6  Conclusions and Future Research

This article presents distributed flexible job scheduling problems with assembly operations to minimize the MCT. To address the problem, this article formulates a mixed integer programming model. Then, this article proposes a Q-learning-assisted co-evolutionary algorithm to deal with the model. The developed algorithm mainly consists of specific solution representation, population initialization methods, crossover approaches, and local search methods based on Q-learning. To evaluate the performance of the developed algorithm, comparison experiments are carried out, and three popular meta-heuristics are chosen for comparisons. The results obtained underscore the remarkable abilities of the designed algorithm in coping with the considered problem. This research not only enriches the theoretical framework of integrated scheduling of production and assembly but also provides assistance for producers in making production and assembly scheduling decisions.

The future research will focus on the following points: (1) Considering more practical operations in supply chains based on the developed model, such as inventory and distribution; (2) Designing more effective methods integrating meta-heuristics with reinforcement learning techniques to tackle the studied problems.

Acknowledgement: We thank all the members who have contributed to this work with us.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Song Gao; analysis and interpretation of results: Shixin Liu; draft manuscript preparation: Song Gao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All datasets generated during the study are available upon request from the primary author.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Supplementary Materials: The supplementary material is available online at https://doi.org/10.32604/cmc.2025.058334.

References

1. Perez-Gonzalez P, Framinan JM. A review and classification on distributed permutation flowshop scheduling problems. Eur J Oper Res. 2024;312(1):1–21. doi:10.1016/j.ejor.2023.02.001. [Google Scholar] [CrossRef]

2. Fu Y, Hou Y, Wang Z, Wu X, Gao K, Wang L. Distributed scheduling problems in intelligent manufacturing systems. Tsinghua Sci Technol. 2021;26(5):625–45. doi:10.26599/TST.2021.9010009. [Google Scholar] [CrossRef]

3. Tao XR, Pan QK, Gao L. An iterated greedy algorithm with reinforcement learning for distributed hybrid FlowShop problems with job merging. IEEE Trans Evol Comput. 2024;PP(99):1. doi:10.1109/TEVC.2024.3443874. [Google Scholar] [CrossRef]

4. Pan Z, Wang L, Wang J, Zhang Q. A bi-learning evolutionary algorithm for transportation-constrained and distributed energy-efficient flexible scheduling. IEEE Trans Evol Comput. 2025;29(1):232–46. doi:10.1109/TEVC.2024.3354850. [Google Scholar] [CrossRef]

5. Zhu N, Gong G, Lu D, Huang D, Peng N, Qi H. An effective reformative memetic algorithm for distributed flexible job-shop scheduling problem with order cancellation. Expert Syst Appl. 2024;237(3):121205. doi:10.1016/j.eswa.2023.121205. [Google Scholar] [CrossRef]

6. Fu Y, Gao K, Wang L, Huang M, Liang YC, Dong H. Scheduling stochastic distributed flexible job shops using an multi-objective evolutionary algorithm with simulation evaluation. Int J Prod Res. 2025;63(1):86–103. doi:10.1080/00207543.2024.2356628. [Google Scholar] [CrossRef]

7. Zhang ZQ, Wu FC, Qian B, Hu R, Wang L, Jin HP. A Q-learning-based hyper-heuristic evolutionary algorithm for the distributed flexible job-shop scheduling problem with crane transportation. Expert Syst Appl. 2023;234:121050. doi:10.1016/j.eswa.2023.121050. [Google Scholar] [CrossRef]

8. Yu F, Lu C, Zhou J, Yin L, Wang K. A knowledge-guided bi-population evolutionary algorithm for energy-efficient scheduling of distributed flexible job shop problem. Eng Appl Artif Intell. 2024;128(2):107458. doi:10.1016/j.engappai.2023.107458. [Google Scholar] [CrossRef]

9. Fu Y, Wang Y, Gao K, Suganthan PN, Huang M. Integrated scheduling of multi-constraint open shop and vehicle routing: mathematical model and learning-driven brain storm optimization algorithm. Appl Soft Comput. 2024;163(6):111943. doi:10.1016/j.asoc.2024.111943. [Google Scholar] [CrossRef]

10. Hou Y, Wang H, Fu Y, Gao K, Zhang H. Multi-Objective brain storm optimization for integrated scheduling of distributed flow shop and distribution with maximal processing quality and minimal total weighted earliness and tardiness. Comput Ind Eng. 2023;179(3):109217. doi:10.1016/j.cie.2023.109217. [Google Scholar] [CrossRef]

11. Sun J, Zhang Z, Zhang G, Huang Z. Multi-objective evolutionary algorithm based flexible assembly job-shop rescheduling with component sharing for order insertion. Comput Oper Res. 2024;169(5):106744. doi:10.1016/j.cor.2024.106744. [Google Scholar] [CrossRef]

12. Lei D, Yuan Y, Cai J. An improved artificial bee colony for multi-objective distributed unrelated parallel machine scheduling. Int J Prod Res. 2021;59(17):5259–71. doi:10.1080/00207543.2020.1775911. [Google Scholar] [CrossRef]

13. Bai D, Liu T, Zhang Y, Chu F, Qin H, Gao L, et al. Scheduling a distributed permutation flowshop with uniform machines and release dates. IEEE Trans Autom Sci Eng. 2024;22:215–27. doi:10.1109/TASE.2023.3349167. [Google Scholar] [CrossRef]

14. Pan Y, Gao K, Li Z, Wu N. Improved meta-heuristics for solving distributed lot-streaming permutation flow shop scheduling problems. IEEE Trans Autom Sci Eng. 2023;20(1):361–71. doi:10.1109/TASE.2022.3151648. [Google Scholar] [CrossRef]

15. Xie J, Li X, Gao L, Gui L. A hybrid genetic tabu search algorithm for distributed flexible job shop scheduling problems. J Manuf Syst. 2023;71(5):82–94. doi:10.1016/j.jmsy.2023.09.002. [Google Scholar] [CrossRef]

16. Cao S, Li R, Gong W, Lu C. Inverse model and adaptive neighborhood search based cooperative optimizer for energy-efficient distributed flexible job shop scheduling. Swarm Evol Comput. 2023;83(4):101419. doi:10.1016/j.swevo.2023.101419. [Google Scholar] [CrossRef]

17. Liu F, Li G, Lu C, Yin L, Zhou J. A tri-individual iterated greedy algorithm for the distributed hybrid flow shop with blocking. Expert Syst Appl. 2024;237:121667. doi:10.1016/j.eswa.2023.121667. [Google Scholar] [CrossRef]

18. Yan X, Zuo H, Hu C, Gong W, Gao L. Distributed heterogeneous flow shop scheduling method for dual-carbon goals. IEEE Trans Autom Sci Eng. 2024;22(3):7409–20. doi:10.1109/TASE.2024.3371940. [Google Scholar] [CrossRef]

19. Tang J, Gong G, Peng N, Zhu K, Huang D, Luo Q. An effective memetic algorithm for distributed flexible job shop scheduling problem considering integrated sequencing flexibility. Expert Syst Appl. 2024;242(2):122734. doi:10.1016/j.eswa.2023.122734. [Google Scholar] [CrossRef]

20. Zhang Z, Tang Q. Integrating flexible preventive maintenance activities into two-stage assembly flow shop scheduling with multiple assembly machines. Comput Ind Eng. 2021;159(2):107493. doi:10.1016/j.cie.2021.107493. [Google Scholar] [CrossRef]

21. Cao F, Feng Y, Wang S, Zhang G, Xing K. Deadlock control and hybrid social spider scheduling algorithm for two-stage assembly permutation flowshop with limited buffers. Expert Syst Appl. 2024;245(1):122744. doi:10.1016/j.eswa.2023.122744. [Google Scholar] [CrossRef]

22. Cheng L, Tang Q, Zhang L. Mathematical model and adaptive simulated annealing algorithm for mixed-model assembly job-shop scheduling with lot streaming. J Manuf Syst. 2023;70:484–500. doi:10.1016/j.jmsy.2023.08.008. [Google Scholar] [CrossRef]

23. Daneshamooz F, Fattahi P, Hosseini SMH. Scheduling in a flexible job shop followed by some parallel assembly stations considering lot streaming. Eng Optim. 2022;54(4):614–33. doi:10.1080/0305215X.2021.1887168. [Google Scholar] [CrossRef]

24. Sun M, Cai Z, Zhang H. A teaching-learning-based optimization with feedback for L-R fuzzy flexible assembly job shop scheduling problem with batch splitting. Expert Syst Appl. 2023;224(1):120043. doi:10.1016/j.eswa.2023.120043. [Google Scholar] [CrossRef]

25. Du B, Han S, Guo J, Li Y. A hybrid estimation of distribution algorithm for solving assembly flexible job shop scheduling in a distributed environment. Eng Appl Artif Intell. 2024;133(1):108491. doi:10.1016/j.engappai.2024.108491. [Google Scholar] [CrossRef]

26. Hu Y, Zhang L, Zhang Z, Li Z, Tang Q. Matheuristic and learning-oriented multi-objective artificial bee colony algorithm for energy-aware flexible assembly job shop scheduling problem. Eng Appl Artif Intell. 2024;133(9):108634. doi:10.1016/j.engappai.2024.108634. [Google Scholar] [CrossRef]

27. Wang H, Sarker BR, Li J, Li J. Adaptive scheduling for assembly job shop with uncertain assembly times based on dual Q-learning. Int J Prod Res. 2021;59(19):5867–83. doi:10.1080/00207543.2020.1794075. [Google Scholar] [CrossRef]

28. Ba Z, Yuan Y, Liu J. A modified memetic algorithm with multi-operation precise joint movement neighbourhood structure for the assembly job shop scheduling problem. Int J Prod Res. 2024;62(17):6292–324. doi:10.1080/00207543.2024.2313087. [Google Scholar] [CrossRef]

29. Wang JJ, Wang L. A cooperative memetic algorithm with feedback for the energy-aware distributed flow-shops with flexible assembly scheduling. Comput Ind Eng. 2022;168(4):108126. doi:10.1016/j.cie.2022.108126. [Google Scholar] [CrossRef]

30. Zhao F, Xu Z, Wang L, Zhu N, Xu T, Jonrinaldi J. A population-based iterated greedy algorithm for distributed assembly no-wait flow-shop scheduling problem. IEEE Trans Ind Inform. 2023;19(5):6692–705. doi:10.1109/TII.2022.3192881. [Google Scholar] [CrossRef]

31. Luo C, Gong W, Ming F, Lu C. A Q-learning memetic algorithm for energy-efficient heterogeneous distributed assembly permutation flowshop scheduling considering priorities. Swarm Evol Comput. 2024;85(12):101497. doi:10.1016/j.swevo.2024.101497. [Google Scholar] [CrossRef]

32. Huang YY, Pan QK, Gao L. An effective memetic algorithm for the distributed flowshop scheduling problem with an assemble machine. Int J Prod Res. 2023;61(6):1755–70. doi:10.1080/00207543.2022.2047238. [Google Scholar] [CrossRef]

33. Shao Z, Shao W, Chen J, Pi D. A feedback learning-based selection hyper-heuristic for distributed heterogeneous hybrid blocking flow-shop scheduling problem with flexible assembly and setup time. Eng Appl Artif Intell. 2024;131(4):107818. doi:10.1016/j.engappai.2023.107818. [Google Scholar] [CrossRef]

34. Tian S, Zhang C, Fan J, Li X, Gao L. A genetic algorithm with critical path-based variable neighborhood search for distributed assembly job shop scheduling problem. Swarm Evol Comput. 2024;85(7):101485. doi:10.1016/j.swevo.2024.101485. [Google Scholar] [CrossRef]

35. Fu Y, Wang Y, Gao K, Huang M. Review on ensemble meta-heuristics and reinforcement learning for manufacturing scheduling problems. Comput Electr Eng. 2024;120(3):109780. doi:10.1016/j.compeleceng.2024.109780. [Google Scholar] [CrossRef]

36. Wang J, Tang H, Lei D. A Q-learning artificial bee colony for distributed assembly flow shop scheduling with factory eligibility, transportation capacity and setup time. Eng Appl Artif Intell. 2023;123(1):106230. doi:10.1016/j.engappai.2023.106230. [Google Scholar] [CrossRef]

37. Zhang W, Geng H, Li C, Gen M, Zhang G, Deng M. Q-learning-based multi-objective particle swarm optimization with local search within factories for energy-efficient distributed flow-shop scheduling problem. J Intell Manuf. 2025;36(1):185–208. doi:10.1007/s10845-023-02227-9. [Google Scholar] [CrossRef]

38. Yu H, Gao K, Li Z, Suganthan PN. Energy-efficient multi-objective distributed assembly permutation flowshop scheduling by Q-learning based meta-heuristics. Appl Soft Comput. 2024;166(12):112247. doi:10.1016/j.asoc.2024.112247. [Google Scholar] [CrossRef]

39. Zhao F, Zhuang C, Wang L, Dong C. An iterative greedy algorithm with Q-learning mechanism for the multiobjective distributed no-idle permutation flowshop scheduling. IEEE Trans Syst Man Cybern Syst. 2024;54(5):3207–19. doi:10.1109/TSMC.2024.3358383. [Google Scholar] [CrossRef]

40. Zhang Z, Fu Y, Gao K, Pan Q, Huang M. A learning-driven multi-objective cooperative artificial bee colony algorithm for distributed flexible job shop scheduling problems with preventive maintenance and transportation operations. Comput Ind Eng. 2024;196(5):110484. doi:10.1016/j.cie.2024.110484. [Google Scholar] [CrossRef]

41. Chen R, Wu B, Wang H, Tong H, Yan F. A Q-Learning based NSGA-II for dynamic flexible job shop scheduling with limited transportation resources. Swarm Evol Comput. 2024;90(3):101658. doi:10.1016/j.swevo.2024.101658. [Google Scholar] [CrossRef]

42. Lei D. Co-evolutionary genetic algorithm for fuzzy flexible job shop scheduling. Appl Soft Comput. 2012;12(8):2237–45. doi:10.1016/j.asoc.2012.03.025. [Google Scholar] [CrossRef]

43. Ma X, Fu Y, Gao K, Sadollah A, Wang K. Integration routing and scheduling for multiple home health care centers using a multi-objective cooperation evolutionary algorithm with stochastic simulation. Swarm Evol Comput. 2022;75(1):101175. doi:10.1016/j.swevo.2022.101175. [Google Scholar] [CrossRef]

44. Zhang Z, Fu Y, Gao K, Zhang H, Wang L. A cooperative evolutionary algorithm with simulated annealing for integrated scheduling of distributed flexible job shops and distribution. Swarm Evol Comput. 2024;85(1):101467. doi:10.1016/j.swevo.2023.101467. [Google Scholar] [CrossRef]

45. Wang L, Zhou G, Xu Y, Wang S, Liu M. An effective artificial bee colony algorithm for the flexible job-shop scheduling problem. Int J Adv Manuf Technol. 2012;60(1):303–15. doi:10.1007/s00170-011-3610-1. [Google Scholar] [CrossRef]

46. Gao K, Cao Z, Zhang L, Chen Z, Han Y, Pan Q. A review on swarm intelligence and evolutionary algorithms for solving flexible job shop scheduling problems. IEEE/CAA J Autom Sin. 2019;6(4):904–16. doi:10.1109/JAS.2019.1911540. [Google Scholar] [CrossRef]

47. Naderi B, Ruiz R. The distributed permutation flowshop scheduling problem. Comput Oper Res. 2010;37(4):754–68. doi:10.1016/j.cor.2009.06.019. [Google Scholar] [CrossRef]

48. Fu Y, Tian G, Fathollahi-Fard AM, Ahmadi A, Zhang C. Stochastic multi-objective modelling and optimization of an energy-conscious distributed permutation flow shop scheduling problem with the total tardiness constraint. J Clean Prod. 2019;226(2):515–25. doi:10.1016/j.jclepro.2019.04.046. [Google Scholar] [CrossRef]

49. Fu Y, Tian G, Li Z, Wang Z. Parallel machine scheduling with dynamic resource allocation via a master-slave genetic algorithm. IEEJ Trans Electr Electron Eng. 2018;13(5):748–56. doi:10.1002/tee.22625. [Google Scholar] [CrossRef]

50. Li R, Gong W, Wang L, Lu C, Zhuang X. Surprisingly popular-based adaptive memetic algorithm for energy-efficient distributed flexible job shop scheduling. IEEE Trans Cybern. 2023;53(12):8013–23. doi:10.1109/TCYB.2023.3280175. [Google Scholar] [CrossRef]

51. Shi S, Xiong H, Li G. A no-tardiness job shop scheduling problem with overtime consideration and the solution approaches. Comput Ind Eng. 2023;178:109115. doi:10.1016/j.cie.2023.109115. [Google Scholar] [CrossRef]

52. Wang F, Fu Y, Gao K, Wu Y, Gao S. A Q-learning based hybrid meta-heuristic for integrated scheduling of disassembly and reprocessing processes considering product structures and stochasticity. Complex Syst Model Simul. 2024;4(2):184–209. doi:10.23919/CSMS.2024.0007. [Google Scholar] [CrossRef]

53. Chang HC, Liu TK. Optimisation of distributed manufacturing flexible job shop scheduling by using hybrid genetic algorithms. J Intell Manuf. 2017;28(8):1973–86. doi:10.1007/s10845-015-1084-y. [Google Scholar] [CrossRef]

54. Tang H, Fang B, Liu R, Li Y, Guo S. A hybrid teaching and learning-based optimization algorithm for distributed sand casting job-shop scheduling problem. Appl Soft Comput. 2022;120:108694. doi:10.1016/j.asoc.2022.108694. [Google Scholar] [CrossRef]

55. Li X, Xie J, Ma Q, Gao L, Li P. Improved gray wolf optimizer for distributed flexible job shop scheduling problem. Sci China Technol Sci. 2022;65(9):2105–15. doi:10.1007/s11431-022-2096-6. [Google Scholar] [CrossRef]

56. Hurink J, Jurisch B, Thole M. Tabu search for the job-shop scheduling problem with multi-purpose machines. Oper Res Spektrum. 1994;15(4):205–15. doi:10.1007/BF01719451. [Google Scholar] [CrossRef]

57. Fu Y, Zhou M, Guo X, Qi L, Gao K, Albeshri A. Multiobjective scheduling of energy-efficient stochastic hybrid open shop with brain storm optimization and simulation evaluation. IEEE Trans Syst Man Cybern Syst. 2024;54(7):4260–72. doi:10.1109/TSMC.2024.3376292. [Google Scholar] [CrossRef]