A Lightweight IoT Data Security Sharing Scheme Based on Attribute-Based Encryption and Blockchain

1  Introduction

The Internet of Things (IoT) has been advancing at a rapid pace in recent years, encompassing and deepening a variety of application areas, including smart healthcare [1], smart infrastructure [2], and smart transportation [3]. The number of IoT devices has also increased significantly, and by 2025, it will reach 38.6 billion connected to the Internet [4]. This vast number of IoT devices generates significant data, including sensitive and private data. Addressing the essential challenge of securely sharing this data is imperative, as any leakage will result in substantial losses [5].

Attribute-based encryption (ABE) [6] is a one-to-many encryption algorithm capable of securing data and attaining fine-grained access control, making it an essential data security method. ABE is divided into two categories: key policy attribute-based encryption (KP-ABE) [7] and ciphertext policy attribute-based encryption (CP-ABE) [8]. The user attributes are embedded in the ciphertext, and the key is associated with the access structure of the ciphertext in KP-ABE. The ciphertext can only be decrypted effectively if the user’s attributes align with the access structure. CP-ABE, in contrast to KP-ABE, embeds the user attributes in the key and associates the ciphertext with the access structure of the key. This renders it more suitable for IoT application scenarios requiring high scalability and many users. The computational capacity of lightweight IoT devices is insufficient to execute complex encryption and decryption operations, and current CP-ABE encryption schemes rely on complex bilinear pairing. Cloud servers process intricate operations and store encrypted data in related research [9]. Nevertheless, the cloud server is not entirely trustworthy, which will result in the breach of privacy data and the inability to ensure the integrity and accuracy of the data. Cloud servers cannot withstand the heavy computing and storage pressures resulting from the increasing number of IoT devices [10]. This has resulted in a single point of failure and high latency, and computational efficiency must be enhanced. The utilization of edge computing [11] in distributed networks, which entails the cooperative processing of data by multiple edge servers can improve system reliability and decrease system latency. This method is particularly well-suited for data sharing on lightweight IoT devices. However, edge nodes are semi-trusted, and malicious edge nodes may attempt to obtain shared data for commercial purposes.

Blockchain is considered a distributed database that is comprised of a series of sequentially connected blocks, forming an immutable chain structure. This structure is characterized by decentralization, security, and tamper resistance [12]. Its immutability is primarily derived from the chain structure and hash functions, which ensure that data is difficult to modify or delete once it has been recorded [13], thereby ensuring the credibility of the data. In terms of data security, blockchain employs encryption algorithms, consensus mechanisms, and smart contract technology to ensure data integrity and confidentiality, preventing unauthorized tampering and access [14]. Additionally, by leveraging decentralized storage and multi-party consensus [15], blockchain reduces the risks of single points of failure and malicious alterations, providing a secure, transparent, and trustworthy environment for data exchange.

Although blockchain has significant advantages in ensuring data security and credibility, it still faces numerous challenges in practical applications. For example, the current data sharing schemes, which integrate CP-ABE and blockchain, typically generate and manage keys through a completely trusted organization [16]. However, this approach is inevitably plagued by the key escrow problem, which poses a risk of key leakage and a single point of failure in the system. The key escrow problem is addressed by certain schemes [17] by utilizing multiple authorization agencies. Each authorization agency is responsible for managing distinct attribute keys. However, when the number of attributes is excessive, the ciphertext can still be decrypted by the attribute keys managed by a single authorization agency, which results in difficulties in distributing the keys and a high communication cost.

In order to resolve the aforementioned issues, this paper conducts additional research on the data sharing scheme. It suggests a lightweight IoT data security sharing scheme based on attribute-based encryption and blockchain. The primary contributions are as follows:

1) An elliptic curve cipher-based lightweight CP-ABE algorithm is proposed. Instead of bilinear pairing, which has a high computational overhead, elliptic curve scalar multiplication is employed to implement the encryption and decryption function of the CP-ABE algorithm. A portion of the decryption operation is transferred to the edge node, enabling the lightweight IoT devices to complete the data sharing process securely and efficiently.

2) Blockchain and edge nodes are combined to propose a distributed key management method. An edge blockchain is created by deploying a blockchain network on edge nodes. The edge blockchain solves the key escrow and single-point-of-failure issues of a single authorized organization in the traditional scheme by allowing multiple edge nodes to collaborate in storing and distributing attribute private keys. The blockchain is employed to ensure data security by recording the entire data sharing process, preventing tampering.

3) A distributed storage method that integrates off-chain and on-chain ciphertext storage methods is proposed. Rather than directly storing data on the blockchain, the data is stored in the interplanetary file system (IPFS) after symmetric encryption. The blockchain only stores the symmetric key and the ciphertext index returned by IPFS, avoiding storing a significant quantity of plaintext data directly. This storage method not only enhances the security of data sharing but also decreases the storage burden and overhead of the blockchain.

The subsequent sections of the paper are structured as follows: Section 2 discusses the relevant work, Section 3 provides the preparatory knowledge, Section 4 provides a detailed description of the system model, and Section 5 conducts the security and performance analyses. Lastly, Section 6 provides a comprehensive paper summary and outlines potential areas for future research.

2  Related Works

2.1 Data Security Sharing Scheme Based on Cloud Storage

Sahai and Waters [18] introduced attribute-based encryption in 2005. This method encrypts data by extracting the user’s feature information as attributes to enable flexible data sharing. Bethencourt et al. [19] proposed the CP-ABE algorithm in 2007, which is derived from this algorithm. It embeds the access structure into the ciphertext and associates the key with the user’s set of attributes. The ciphertext can only be effectively decrypted when the user’s set of attributes aligns with the access structure, thereby providing more fine-grained security and flexible privilege control. This algorithm is particularly applicable to data security sharing scenarios in cloud storage environments. Many scholars have conducted a lot of research on secure data sharing schemes based on CP-ABE and cloud storage, for example, Chen et al. [20] proposed a CP-ABE scheme for shared decryption. In this scheme, multiple standby users are delegated to collaborate rather than a single user to decrypt the ciphertext for security purposes. The authorized user can independently recover the message, while the standby users must collaborate to obtain the message. This solution resolves the issue of the authorized decryption user’s inability to decrypt the ciphertext in a timely manner. However, this approach fails to achieve attribute revocation and key update. Wei et al. [21] recommended a revocable storage hierarchical attribute-based encryption (RS-HABE) scheme that augments the original ABE with user revocation, key delegation, and ciphertext updating to create a framework for the secure sharing of EHRs (Electronic Health Records) in public clouds. The system relies on a single authorization authority to generate keys and manage system attributes. Therefore, this approach is susceptible to key escrow issues and a single point of failure. Zhao et al. [22] proposed an online/offline multi-privilege CP-ABE scheme that supports policy hiding functionality. This scheme utilizes a Central Authority (CA) and multiple Attribute Authorities (AAs), each controlling a distinct set of attributes and sending the attribute private key to the user. However, this approach exacerbates the complexity of attribute management and key generation. Yang et al. [23] have created a multi-privilege ciphertext policy attribute-based encryption (CP-ABE) scheme that applies to various application environments. The scheme utilizes a white-box monitoring mechanism, certificate-less public data integrity auditing techniques, and an access policy hiding mechanism to protect user privacy and cloud encryption to extend the scheme to multiple clouds and mitigate key misuse and escrow issues. However, the computational efficiency has not been significantly enhanced. To solve the problem of high computation of the CP-ABE algorithm, many scholars have introduced edge computing to improve the computational efficiency of the scheme. For example, Cai et al. [24] introduced an edge computing layer in 5G IoT systems to delegate decryption to edge servers and cloud servers, thereby reducing the computational burden of data users. They also proposed a group key management scheme based on the Chinese remainder theorem to achieve efficient dynamic group management in IoT. However, the edge computing environment is complex and diverse, and security management is difficult. To mitigate the influence of a single component and prevent authorized agencies from altering the user’s identity, Zhao et al. [25] employed two authorized parties to generate user keys collaboratively. Additionally, they deployed numerous fog nodes at the edge of the cloud servers to aid under-resourced users in encryption and decryption computations. However, the management and storage of the shared data at the fog nodes increased the risk of data leakage.

2.2 Data Security Sharing Scheme Based on Blockchain

In recent years, numerous scholars have employed the decentralized feature of blockchain in conjunction with the CP-ABE algorithm to enhance the security of data sharing, thereby resolving security issues such as data tampering and a single point of failure that are inherent in centralized cloud storage architectures. For example, Li et al. [26] established distinct VANET (Vehicular Ad Hoc Network) data access rights based on user attributes and employed blockchain technology instead of a third-party service provider for user identity administration and data storage, thereby eliminating the need for third-party service providers and minimizing the risk of a single point of failure caused by centralized services. Le et al. [27] developed a blockchain-based smart grid log management scheme that includes non-repudiation and introduced a hybrid blockchain system to generate a novel signature chain, the new signature chain safeguards the integrity of log records, prevents the tampering or deletion of logs, and can effectively safeguard private logs. Zhang et al. [28] utilized blockchain nodes serve as attribute authorization authority to construct the CP-ABE encryption system, a tracking encryption algorithm is employed to track malicious blockchain nodes and a smart contract is implemented to ensure fair retrieval of ciphertexts. Nevertheless, it is not a solution to the issue of the high computational complexity of CP-ABE and is not appropriate for lightweight devices with limited computing capacity. Guo et al. [29] proposed an efficient attribute revocation mechanism that assured the real-time and effective management of access rights and mitigated the latency problem in rights management. This mechanism combines IPFS and Roadside Unit (RSU) blockchain for distributed collaborative storage, thereby enhancing the reliability, availability, and scalability of data storage and effectively reducing the storage burden of blockchain. Fugkeaw et al. [30] implemented fog computing to execute computationally intensive encryption and decryption tasks for CP-ABE, and implemented an adaptive load-sharing algorithm to optimize workload distribution among fog nodes. Nevertheless, the security and privacy dangers that were introduced by fog nodes were not considered. Zhang et al. [31] introduced blockchain technology to verify the download privileges of data users that addresses the issue of malignant user revocation during an EDoS (Economic Denial of Sustainability) attack by modifying ciphertext and symmetric cryptography, thereby enhancing the security of the system. Nevertheless, the optimization effect of the encryption and decryption computational burden of the scheme is not immediately apparent, as the ciphertext update necessitates a significant number of encryption and decryption operations.

This paper suggests a novel data security sharing scheme based on blockchain and CP-ABE, taking into account the advantages and disadvantages of the aforementioned schemes. The scheme guarantees data security by administering the key and storing the ciphertext on the edge blockchain. In the interim, elliptic curve scalar multiplication is employed to optimize the encryption and decryption process and minimize the computational latency. Furthermore, this paper proposes a distributed key management scheme to mitigate the risk of key leakage.

3  Preliminaries

3.1 Blockchain

A decentralized distributed database technology, blockchain is characterized by high security, transparency, immutability, and decentralization. It documents transactions and data through an immutable public ledger. The relevant introduction is as follows:

1) Block structure. Fig. 1 illustrates the block structure of the blockchain. Blocks are the fundamental units of blockchain technology: a block header and a block body. The block header comprises information such as the Merkle Root, Nonce, and Time Stamp. However, the block body contains comprehensive transaction information that enables tracing and verifying the entire transaction history.

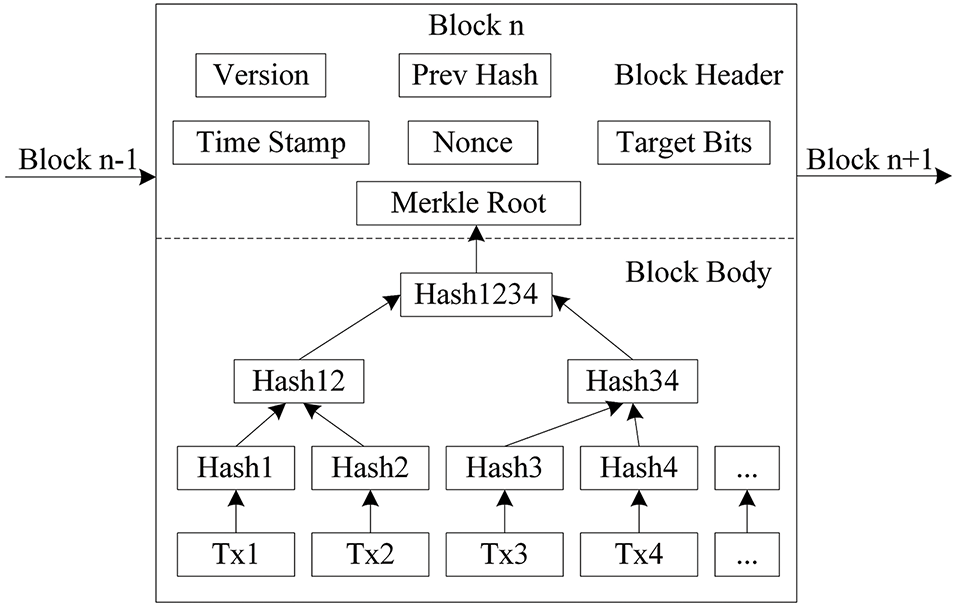
Figure 1: Block structure

2) Consensus mechanism. The principles and algorithms governing the agreement between the states of blockchain nodes in a blockchain network are called consensus mechanisms. These mechanisms guarantee the security, consistency, and reliability of the blockchain. Popular consensus mechanisms consist of Practical Byzantine Fault Tolerance (PBFT), Proof of Stake (PoS), and Proof of Work (PoW). In comparison to other consensus mechanisms, PBFT has a higher consensus speed and lower energy consumption, and it permits the presence of malicious nodes in the system. Consequently, this paper decides to employ the PBFT consensus mechanism.

3) Smart contract. The smart contract is a protocol that replaces manual arbitration with programmed algorithms and automates its execution through blockchain technology.

3.2 Elliptic Curve Encryption

Elliptic curve cryptography (ECC) is a public-key cryptography regime that provides advantages in terms of computational complexity and storage compared to other cryptographic algorithms in its category. An elliptic curve is a binary cubic equation with variables and coefficients in a finite domain Zp (p is the order of the finite domain), denoted as Ep(a,b):y2=x3+ax+b, and satisfying 4a3+27b2≠0. The computational regulations are as follows:

1) A point on an elliptic curve that satisfies Q+O=Q−O=Q.

2) A point U(x1,y1) on an elliptic curve with its symmetry V(x1,−y1), which satisfies U+V=O, V is referred to as a negative element of U.

3) Points U(x1,y1) and V(x2,y2) on an elliptic curve that satisfy U≠−V are described by R=U+V=(x3,y3).

x3=△2−x1−x2,y3=△(x1,x3)−y1(1)

△={y2−y1x2−x1(modp),x1≠x23x12+u2y1(modp),x1=x2(2)

3.3 Linear Secret Sharing Scheme

Define the secret sharing scheme Π of the set of participants as linear on the domain Zp, satisfying the following conditions:

1) A vector in domain Zp is composed of the secret share of each participant.

2) The secret sharing scheme Π has a shared generation matrix A with n rows and m columns. The function ρ maps the ith row of the matrix A to the participant ρ(i).

The construction of an access structure (A,ρ) based on linear secret sharing scheme (LSSS) can be accomplished in various ways, and this paper employs a more expedient method. A single-entry matrix AU=[ 1 ] is used to depict each attribute. Constructing a matrix AOR=Z(na+nb)×(ma+mb−1) is possible for any OR structure (Pa or Pb). The construction rule is as follows: Ca is the first column of the Pa access matrix, Ra represents the remaining columns, exclusive of the first column, Cb and Rb are identical.

AOR=[CaRa0Cb0Rb](3)

For any AND structure (Pa and Pb), a matrix can be AAND=Z(na+nb)×(ma+mb) constructed according to the following rules:

AAND=[CaCaRa00Cb0Rb](4)

A secret value s∈Zp is concealed in a randomly selected vector v=(s,r2,…,rm)T, and the access structure AS of the attribute set S is obtained from A. If the access structure is satisfied, the secret value s is eventually recovered from s=ωλ, λ is computed from ASv=λ, ω is computed from ωAS=ε. If the access structure is unmet, the secret value s cannot be recovered, and ω does not exist.

3.4 Threshold Secret Sharing Scheme

Threshold secret sharing scheme (TSSS) divides a secret value s into n parts and distributes them to n participants, each of whom possesses a sub-secret value. When t and more participants are cooperating to reconstruct the secret value s. Based on the Lagrange interpolation formula, Shamir suggests the following process for TSSS:

1) Initialization phase: the secret distributor constructs a polynomial g(x)=a0+a1x+⋯+an−1xn−1 of order (n − 1) over a finite field GF(p), with a1,a2,⋯an−1∈Zp, and a0=s denoting the secret value to be shared.

2) Secret distribution phase: n mutually distinct non-zero elements xi are randomly selected from a finite domain GF(p). The sub-secret value si=g(xi)modp(1≤i≤n) is determined, and the participants are assigned (xi,si).

3) Secret reconstruction phase: the following equation can be used to recover the secret value s when t or more participants share the sub-secret value si.

s=g(0)=∑i=1tsi∏i=1,i≠jt(x−xi)(xj−xi)(5)

4  System Model

4.1 System Architecture

The system architecture of the scheme is illustrated in Fig. 2, which comprises five entities: edge blockchain (EBC), central authority (CA), data owner (DO), data user (DU), and interplanetary file system (IPFS).

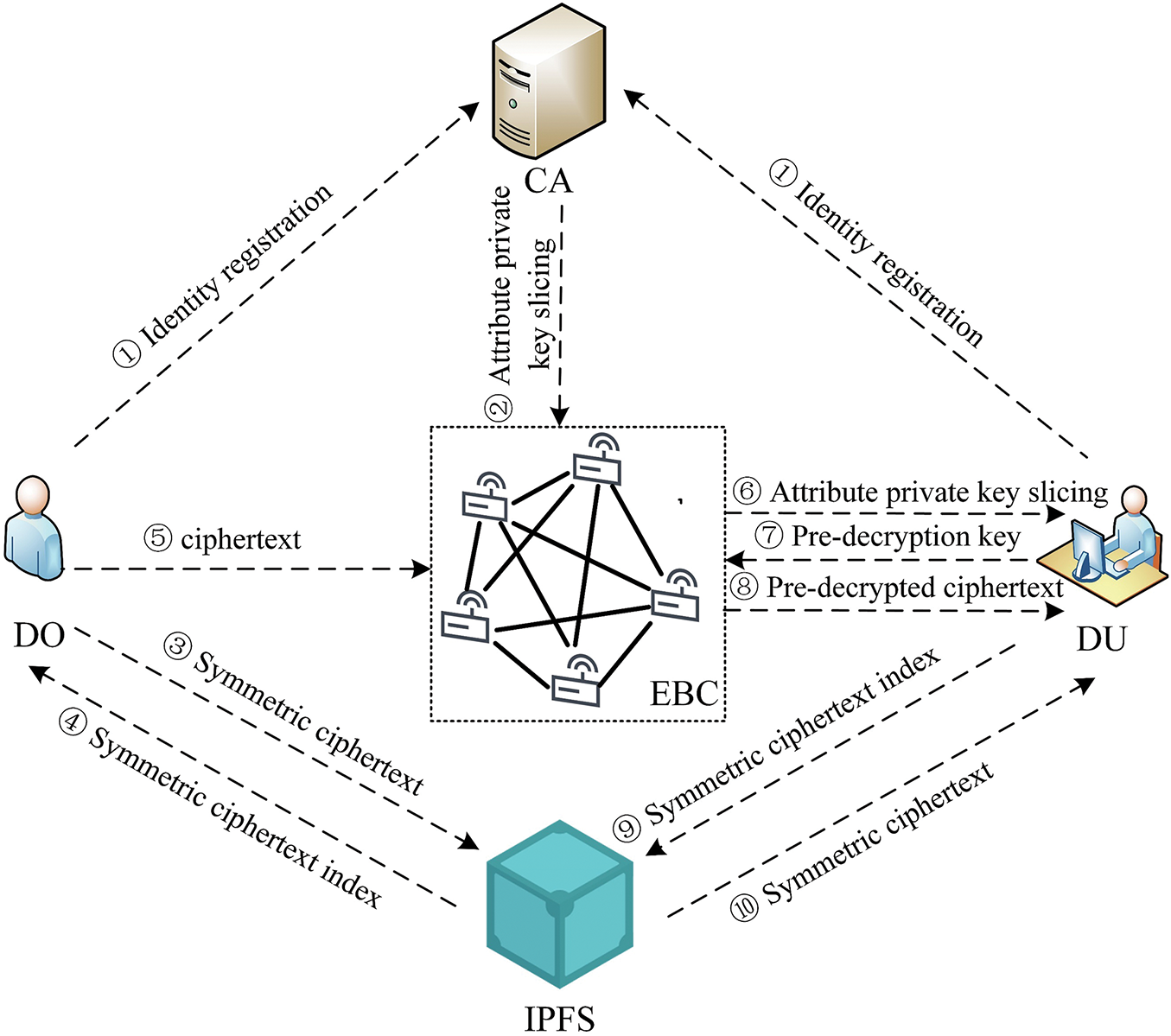
Figure 2: System architecture

EBC is a federated blockchain composed of numerous edge nodes (ENs). ENs are responsible for maintaining ciphertexts and pre-decryption keys. At the same time, EBC provides a trusted and secure environment for ENs, which provide low-latency computation and attribute private key storage and management services for the system. Furthermore, EBC is accountable for verifying the accuracy of the transactions and documenting the entire data sharing process to prevent tampering, thereby effectively safeguarding data security.

CA is the sole trusted entity inside the entire system, tasked with establishing public parameters and overseeing the management and maintenance of the attribute list. Upon a user’s entry into the system, it facilitates user registration, assigns a unique user identifier, and generates an attribute private key derived from the user’s attribute collection. Subsequently, CA slices the attribute private key and distributes it to ENs in the EBC via a secure channel. Each EN discreetly retains a copy of the attribute private key slice to facilitate distributed key management.

DO is an IoT device responsible for generating and publishing ciphertexts and providing shared data. At first, DO symmetrically encrypts the plaintext data and stores the symmetrically encrypted ciphertext in IPFS. This process returns the index of the symmetrically encrypted ciphertext, encrypts the returned index and symmetric key according to the specified access structure, and uploads the ciphertext to the EBC.

DU is an IoT device that necessitates data access. DU transmits a data access request to an EN, which broadcasts a key generation request in the EBC. When DU receives a sufficient number of slices of the attribute private key, it reconstructs the attribute private key at the user side, generates a user private key and a pre-decryption key using the attribute private key, and sends the pre-decryption key to the EBC to be saved. DU retains the user’s private key. EN decrypts the ciphertext using the pre-decryption key and transmits the decrypted pre-decrypted ciphertext to DU. DU completes the final decryption operation and decrypts the ciphertext to obtain the IPFS storage index and the symmetric key. DU employs this index to retrieve symmetrically encrypted ciphertext from IPFS and symmetrically decrypt it to recover plaintext data.

IPFS is a decentralized storage system that does not depend on a single central server. Rather, it stores and retrieves data through numerous nodes in the network, thereby avoiding the impact of a single point of failure. IPFS is primarily responsible for the distributed storage of symmetric ciphertexts following the symmetric encryption of plaintext data. This ensures that only a minimal quantity of critical information is stored in the blockchain, thereby reducing the storage pressure on the blockchain.

4.2 Algorithm Description

The system paradigm in this paper consists of four algorithmic components: System Initialization (Setup), Key Generation (KeyGen), Data Encryption (Encrypt), and Data Decryption (Decrypt).

1) System initialization algorithm.

Setup(λ,U)→(PP,UID,PK,MSK). CA establishes the security parameter λ during the initialization phase and utilizes it and the complete set of attributes U as inputs to obtain the public parameter PP, the user identifier UID, the system public key PK, and the master key MSK.

2) Key generation algorithms.

SK.KeyGen(PK,MSK,S,UID)→SK. The algorithm is executed by CA, which receives the system public key PK, the master key MSK, the user identifier UID, and the set of user attributes S as input. The algorithm then outputs the attribute private key SK associated with the UID.

ShamirS(SK,t,n)→(SK1,⋯,SKn). CA executes this algorithm to generate n attribute private key slices SKi from the generated attribute private key SK. These slices are distributed to the ENs in the EBC, and each EN saves an SKi. However, CA does not need to store SK, which enables the distributed storage and dissemination of SK. Among them, n denotes the total number of blockchain nodes (i.e., ENs) and t denotes the minimal number of SKi necessary to restore SK.

ShamirR(SK1,⋯,SKt)→SK. DU transmits the SK generation request to EN, which broadcasts the request to other ENs in EBC. ENs then send sliced SKi of its saved attribute private key to DU, and DU reconstructs the SK according to this algorithm when it receives t and more SKi. To mitigate the security issue resulting from malicious ENs collaborating to unlawfully reconstruct SK in EBC, EBC implements the PBFT consensus mechanism, which can accommodate up to f=(n−1)/3 malicious nodes (where f represents the number of malicious ENs). To prevent the security issues resulting from the collision of malicious ENs, t>(n−1)/3 is restricted in this context.

TK.KeyGen(SK)→(USK,TK). DU uses the algorithm to derive the user’s private key USK and the pre-decryption key TK from the reconstructed attribute private key SK. The generated pre-decryption key TK is then sent to EN. After successful verification, TK is saved to EBC, while DU retains USK and is responsible for the final decryption process. The algorithm guarantees that the final decryption cannot be completed to obtain plaintext m, even if malicious ENs collude to reconstruct SK. Consequently, the security of the scheme is enhanced.

3) Data encryption algorithms.

AES.Enc(ck,m)→M. DO randomly selects the symmetric key ck, acquires the symmetric ciphertext M using the AES symmetric encryption algorithm, and uploads M to IPFS storage. After successful storage, the symmetric ciphertext index is returned.

DO.Enc(PK,(A,ρ),W)→CT. DO utilizes the access structure (A,ρ) established by LSSS and denotes the symmetric ciphertext index and symmetric key ck returned by IPFS as W. DO executes this algorithm and generates the ciphertext CT using the system public key PK, the access structure (A,ρ), and W as inputs. It then uploads the ciphertext CT to the EBC for storage.

4) Data decryption algorithms.

EN.Dec(PK,TK,CT)→CT′. EN obtains the ciphertext CT from the EBC after the DU transmits an access request to the EN. EN executes the algorithm, inputs the system public key PK, the pre-decryption key TK, the ciphertext CT, and outputs the pre-decrypted ciphertext CT′.

DU.Dec(USK,CT′)→W. After the EBC verifies the veracity of the access transaction, the DU acquires the pre-decrypted ciphertext and decrypts CT′ to obtain W using the user’s private key USK.

AES.Dec(ck,M)→m. W obtained is the one that determines the symmetric ciphertext index. The index retrieves the symmetric ciphertext M from IPFS, and the plaintext m is obtained after symmetric decryption.

4.3 Schematic Design

This paper’s scheme explicitly comprises the subsequent phases: initialization phase, key generation phase, data encryption phase, EBC upload verification phase, pre-decryption phase, EBC access verification phase, and data decryption phase.

1) Initialization phase: CA initializes the entire system using Setup( ) algorithm. A finite field GF(q) of order q is generated using the security parameter λ as the input. The elliptic curve discrete logarithm problem (ECDLP) guarantees the system’s security, and an elliptic curve E with generator G is selected from the finite field GF(q). Create the hash function H:{0,1}→Zp, which converts the user identifier UID into an element in the Zp. Define the complete set of attributes as U={u1,u2,⋯,un}. At this juncture, the public parameter PP={GF(q),G,E,H,U} is obtained and made public. Each attribute ui in U is assigned a random number yi,ki∈Zp to generate the master key MSK={yi,ki|ui∈U} and the public key PK={yiG,kiG|ui∈U}. The public key PK is made public, while the master key MSK is kept confidential by CA.

2) Key generation phase: SK.KeyGen( ) algorithm is used by CA to construct an attribute private key SK={yi+kiH(UID)|ui∈S} with a user identifier UID and an attribute set S for DU. To circumvent the key escrow and leakage issues inherent in the conventional CP-ABE algorithm, which involves CA directly transmitting the SK to the DU, this paper proposes a distributed key management approach implemented in conjunction with EBC. CA divides the attribute private key SK into n attribute private key slices SKi using Lagrange interpolation following the threshold value (t,n) using ShamirS( ) algorithm. SKi is then transmitted to ENs in EBC via a secure channel to facilitate the distributed management of the private key. Following the transmission, CA deletes SK without storing it. When DU sends the SK generation request, EN broadcasts it to other ENs in EBC. After the request is verified, each EN transmits its own SKi to DU. DU receives one or more SKi and regenerates SK at the user’s side using ShamirR( ) algorithm. DU generates the user’s private key USK={z} by selecting a random number z∈Zp. It then obtains the pre-decryption key TK={yi+kiH(UID)−z|ui∈S} using TK.KeyGen( ) algorithm, Subsequently, DU transmits TK to EN, which generates the transaction Txstorage={ID,TK,TKcheck,sign} of TK and submits it to EBC for validation. TK can only be transferred to the data ledger for storage after successful validation. EN partially decrypts ciphertext CT using TK to generate semi-decrypted ciphertext CT′ when DU transmits a data request to EN. DU retains USK, which is utilized to decrypt the ciphertext that EN has converted. The transaction identifier is ID, and each transaction in the EBC has a unique identifier. The hash value of TK is TKcheck=H(TK), and sign is used to verify the identity of EN that generated transaction Txstorage. TK will not be tampered with during transmission, as it will be disseminated to other ENs for verification after transaction Txstorage is generated. The other ENs calculate Txstorage hash value MD′=H(ID,H(TK)) and signature value MD=ComputerBPKEN(sign). If MD=MD′, then TKcheck′=H(TK) is computed. If TKcheck′=TKcheck, Txstorage transaction passes the validation; otherwise, it returns the validation failure.

When a sufficient number of ENs verification transactions Txstorage are completed, TK can be submitted to EBC data book for storage. If an attribute of DU is revoked or exited from the system, the transaction Txupdate={ID,TK,TKcheckupdate,sign} is generated and uploaded to EBC for verification. Upon successful verification, TK is designated as a revocation state, and ENs no longer utilize the revoked TK to perform pre-decryption operations for DU. Consequently, real-time and flexible attribute revocation occurs.

3) Data encryption phase: CP-ABE is not suitable for lightweight IoT devices due to the substantial time and intricate operations required for the encryption and decryption of large volumes of data. This paper employs a hybrid encryption and outsourcing decryption scheme to address this issue. This scheme guarantees the high efficiency of data encryption and decryption while also considering the security of the key and data. The LSSS defines the access structure (A,ρ) to establish the conditions for the user to access the data. The attribute corresponding to each row in the access matrix A is denoted by ρ(x), and the xth row of the access matrix is denoted by Ax. The access matrix A has n rows and m columns. DO randomly selects the symmetric key ck, and the plaintext m is symmetrically encrypted to produce the symmetric ciphertext M, which is then uploaded to IPFS for storage. The symmetric ciphertext index and symmetric key ck are recorded as W as input and DO.Enc( ) algorithm is used to encrypt W. Map W to a point on the elliptic curve E, select a random secret value s∈Zp, calculate C0=W+sG, and select a random vector v,u∈Zpm, where the first element of v is the random secret value s and the first element of u is 0, and calculate λx=Axv and ωx=Axu, where x∈[1,n]. Next, choose a random number rx∈Zp, calculate C1,x=λxG+yρ(x)rxG, C2,x=ωxG+kρ(x)rxG and Rx=rxG, and ultimately obtain the ciphertext CT={(A,ρ),C0,C1,x,C2,x,Rx|x∈[1,n]}. In conclusion, Fig. 3 illustrates the process of uploading the shared data.

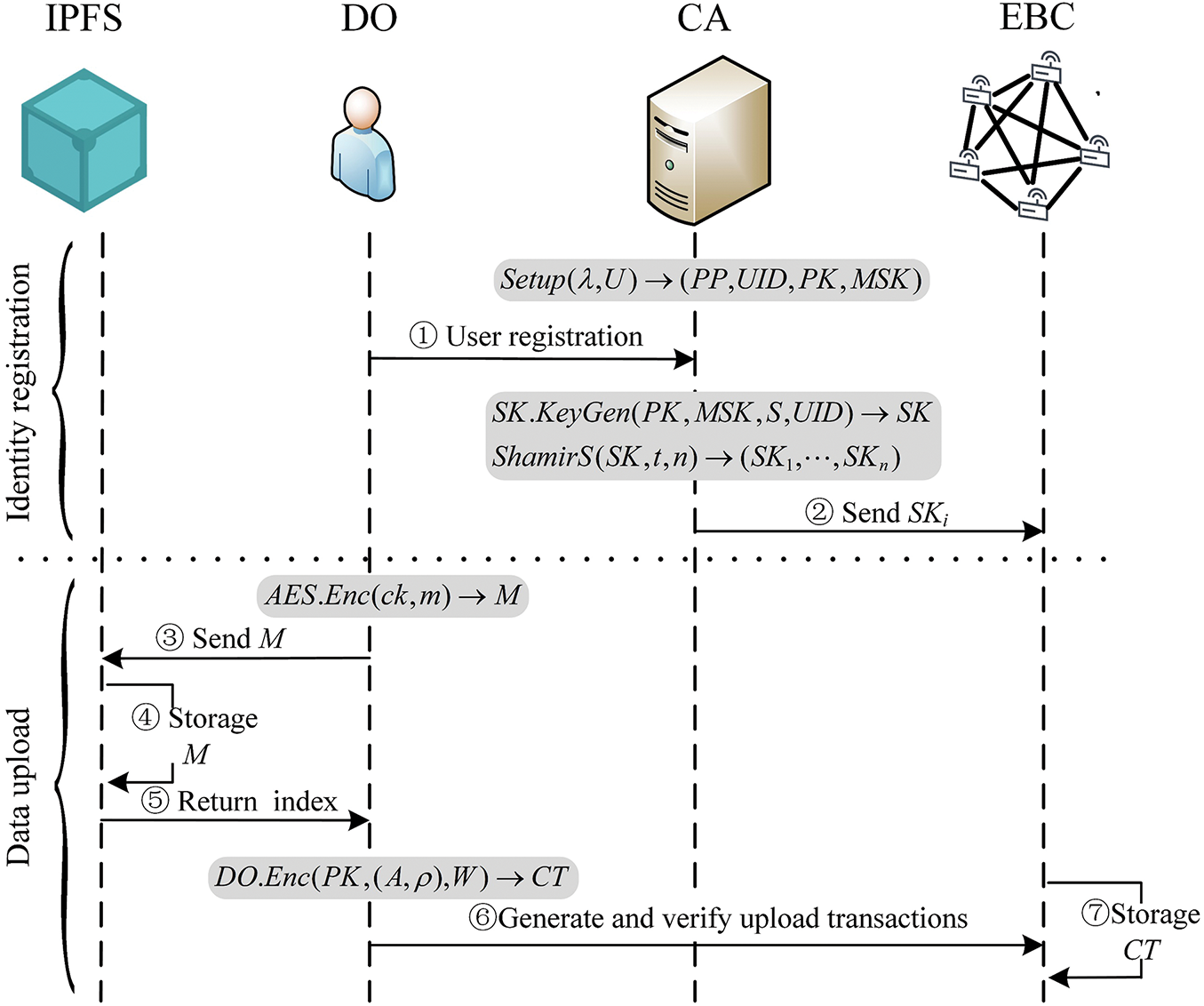
Figure 3: Shared data upload process

4) EBC upload verification phase: When the shared data is uploaded, DO generates a transaction proposal that is sent to endorsing nodes (ENs). The endorsing nodes receive the proposal, emulate the execution of the chain code, and return the endorsement result to DO. DO generates a complete upload transaction Txupload={ID,CTcheck,sign} after receiving sufficient endorsements. The upload transaction identifier is denoted by ID, and the ciphertext CT check code is generated by the hash-hash algorithm and is denoted by CTcheck=H(CT). Any node of the blockchain can verify the integrity of the ciphertext CT through CTcheck, and the signing private key of DO, the initiator of upload request, is denoted by sign.

DO sends the upload transaction Txupload to orderer node after generating it. Orderer node packages multiple transactions into a block and transmits the generated block to all peer nodes in the channel. To verify the validity of the upload transaction Txupload, peer nodes compare hash value MD′=H(ID,H(CT)) computed by the upload transaction Txupload to hash value MD=ComputerBPKDO(sign) generated using the public key BPKDO signature. MD=MD′ indicates that the upload transaction Txupload is valid; otherwise, it is considered invalid. Subsequently, the integrity of the ciphertext is ensured by comparing CTcheck′ generated by ciphertext CT calculation with CTcheck in Txupload to determine if they are equivalent. If CTcheck′=CTcheck, ciphertext has not been tampered with. The transaction is packaged into a block and ciphertext CT is successfully uploaded to EBC after a sufficient number of peer nodes (ENs) have verified and reached consensus according to PBFT.

5) Pre-decryption phase: When DU sends a data access request to EN, EN obtains the ciphertext CT from EBC and pre-decrypts it using the pre-decryption key TK and EN.Dnc( ) algorithm. This approach can simplify the DU decryption operation and is appropriate for lightweight IoT devices.

Assuming that the set X={x|ρ(x)∈S} satisfying the access structure is generated by the set S of attributes of DU, there is a constant set {cx∈Zp,x∈X} such that ∑x∈XcxAx=(1,0,⋯,0), ∑x∈Xcxλx=s, and ∑x∈Xcxωx=0

Ax=C1,x−TK⋅Rx+H(UID)C2,x=λxG+yρ(x)rxG−(yρ(x)+kρ(x)H(UID)−z)rxG+H(UID)(ωxG+kρ(x)rxG)=λxG+zrxG+H(UID)ωxG(6)

D=∑x∈XcxAx=∑x∈Xcx(λxG+zrxG+H(UID)ωxG)=sG+z∑x∈XcxrxG(7)

D′=∑x∈XcxRx=∑x∈XcxrxG(8)

The pre-decrypted ciphertext generated by EN is CT′={CT0,D,D′} in accordance with the aforementioned equation.

6) EBC access verification phase: EBC generates and verifies transaction proposal for accessing transaction Txaccess after receiving semi-decrypted ciphertext CT′. There is a constant set {cx∈Zp,x∈X}, such that ∑x∈Xcxωx=0, when the set of attributes of a DU satisfies the access structure. In the user rights verification algorithm V(x)=CxRx, the presence of ∑x∈XV(x)=0 indicates that DU has access rights to the data file. The hash value of the access transaction Txaccess is calculated using pre-decryption key TK, ciphertext CT, semi-decrypted ciphertext CT′, and signing public key BPKDU. Suppose the hash value of access transaction Txaccess can be matched during the verification process. In that case, it is indicative that the ENs have not modified the information in the access transaction Txaccess.

A valid access transaction Txaccess={ID,ACcheck,time,sign} is generated and sent to the orderer node after DU’s access rights are verified. Orderer node concatenates multiple transactions into a block and transmits the generated block to all peer nodes in the channel. The generated transaction identifier is denoted by ID, ACcheck represents the hash value of the access transaction, the generation time of the access transaction is represented by time, and sign indicates which node is responsible for pre-decryption operation. The validity of the transaction is confirmed by comparing the hash value MD′=H(ID,ACcheck,time) calculated by access transaction Txaccess to the hash value MD=ComputerBPKEN(sign) generated by the public key BPKEN signature. If MD=MD′, then compare the hash value ACcheck′=H(BPKDU,CT,CT′,TK) of the access transaction to ACcheck calculated by peer nodes. The verification is successful if the values are equal; otherwise, it is unsuccessful. The entire access process and associated data are recorded to ensure traceability and access transaction Txaccess verification is packaged and stored in EBC. Afterward, EN transmits the semi-decrypted ciphertext CT′ to DU.

7) Data decryption phase: When DU receives the CT′ decrypted by EN, it is decrypted by DU.Dec( ) algorithm to obtain W.

C0−D+USK⋅D′=W+sG−(sG+z∑x∈XcxrxG)+z∑x∈XcxrxG=W(9)

W is composed of a symmetric key ck and a symmetric ciphertext index. The symmetric ciphertext M is obtained from IPFS using the symmetric ciphertext index, and the plaintext m is subsequently obtained using the symmetric key ck. In conclusion, Fig. 4 illustrates the process of shared data access.

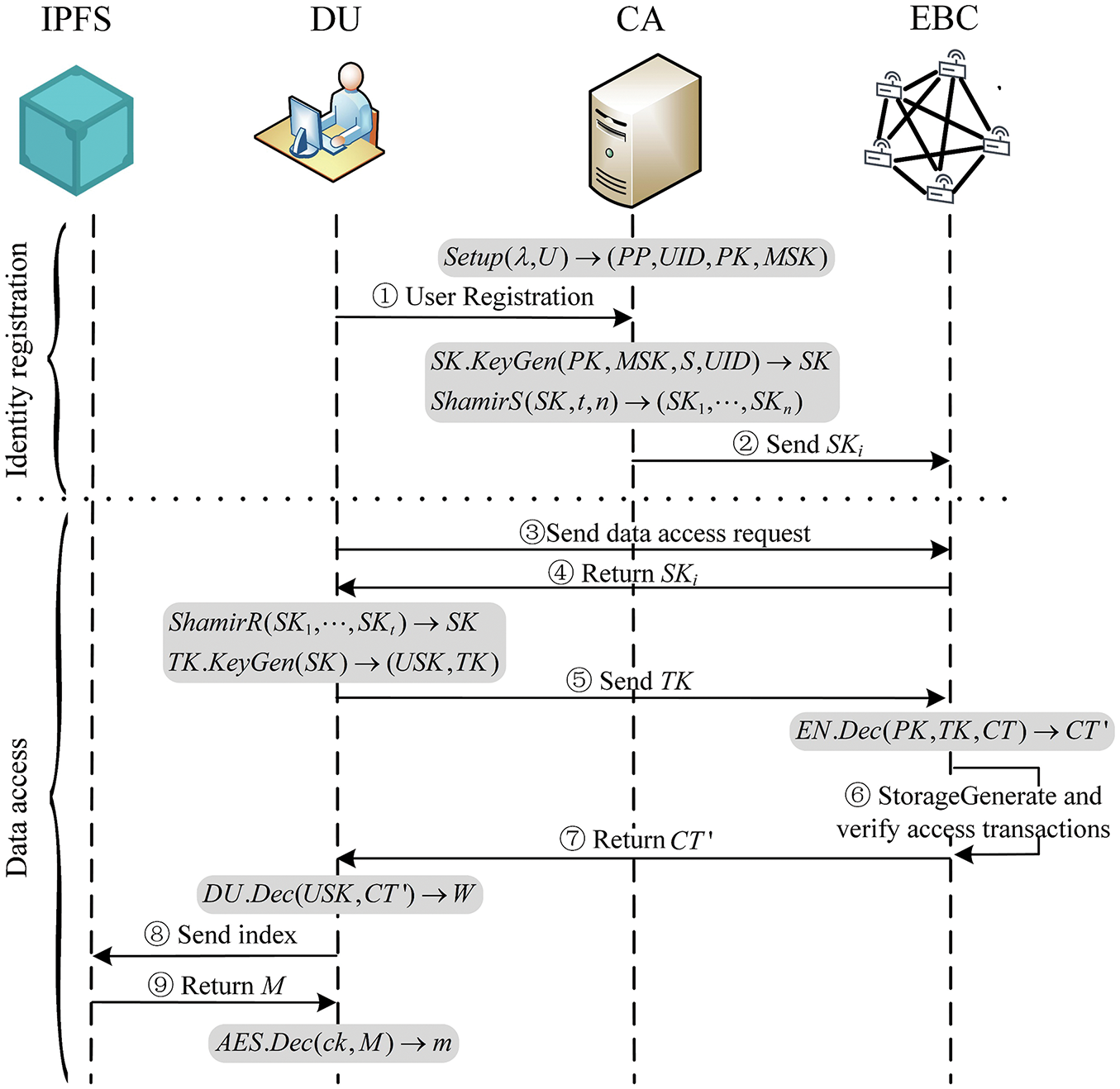
Figure 4: Shared data access process

5  Safety Analysis and Performance Analysis

5.1 Safety Analysis

This section is dedicated to the security analysis of the proposed scheme in this paper under the Decisional Diffie-Hellman assumption (DDH). To further demonstrate that the scheme in this paper is indistinguishable under a chosen plaintext attack (IND-CPA), it develops a security model by constructing an attack game. In addition, it is capable of guaranteeing data confidentiality, EBC security, and resistance to collusion attacks.

Theorem 1. If adversary A breaches the scheme proposed in this paper in polynomial time with a non-negligible advantage by ε>0, challenger B can also breach the DDH assumption in polynomial time.

Let G be a group with a large prime r as the order and P as the generator. The challenger B randomly selects x,y∈Zp, β∈{0,1} and R∈P. When β=0, Z=xyG, and when β=1, Z=RG. Adversary A receives tuple (G,xG,yG,Z) from challenger B. Presuming that adversary A has a non-negligible advantage ε>0 to win the security game, the procedure is as follows:

Initialization. The access structure (A,ρ) is selected by adversary A and transmitted to challenger B.

Setup. In order to generate the public key for each attribute ui in the system for adversary A, challenger B initializes the system, selects the random number yi,ki∈Zr, generates the public key PK={yiG,kiG}, and transmits the public key to adversary A.

Phase 1. To request the private key associated with the user’s attribute, adversary A submits the attribute (ui,UID) to challenger B, which corresponds to the user’s identity. A subset of entries in the access matrix A that adversary A intends to query for the attribute ui is denoted by As. The adversary cannot obtain a set of keys that can be decrypted, as the requested subset of rows cannot contain (1,⋯,0).

Challenge. m0 and m1 are two data plaintexts of equal length that are transmitted by adversary A to challenger B. Selecting random vectors v,u∈Zpm, calculates λx=Axv and ωx=Axu. Ax represents the xth row of access matrix A. In order to encrypt mβ, execute the encryption algorithm, select the parameter β∈{0,1}, compute C0=mβ+sG, and subsequently compute to generate the encrypted ciphertext C1,x=λxG+yρ(x)rxG, C2,x=ωxG+kρ(x)rxG and Rx=rxG. Ultimately, obtain the ciphertext CT={(A,ρ),C0,C1,x,C2,x,Rx|x∈[1,n]} send to adversary A.

Phase 2. In a manner similar to Phase 1, adversary A submits the attribute (ui,UID) corresponding to the user identification to challenger B and requests the private key of the attribute associated with ui from challenger B, all while adhering to the constraints of the attribute set.

Guess. In the game, if β′=β, challenger B outputs 0, which indicates that Z=xyG. Conversely, challenger B outputs 1, which indicates that Z=RG. When adversary A has the ability to win the game by a non-negligible margin ε>0, the likelihood that adversary A will prevail is:

|Pr[B(G,xG,yG,Z=xyG)=0]|=12+ε|Pr[B(G,xG,yG,Z=xyG)=0]|=12+ε(10)

The likelihood that adversary A fails is:

|Pr[B(G,xG,yG,Z=R)=0]|=12(11)

Consequently, Challenger B holds the following benefits:

12|Pr[B(G,xG,yG,Z=xyG)=0]|+|Pr[B(G,xG,yG,Z=R)=0]|−12=ε2(12)

In the procedure above, the scheme is secure under the DDH assumption if no attacker completes in polynomial time.

1) Anti-collusion attack.

Unauthorized DUs may illegally access data, resulting in the leakage of encrypted data due to the collusion of DUs with distinct sets of attributes. Consequently, it is crucial to prevent multiple DUs that cannot decrypt independently from collaborating to create attribute sets that satisfy the access structure and achieve the objective of decrypting the shared data. During the key generation phase, the scheme outlined in this paper generates the attribute private key SK={yi+kiH(UID)|ui∈S} that is linked to the user attribute set S and the user identifier UID. If the identities of the colluding DUs are UID1 and UID2, the decryption operation results in λxG+zrxG+H(UID1)ωxG and λxG+zrxG+H(UID2)ωxG, where H(UID1)ωxG≠H(UID2)ωxG. This prevents the introduction of sG, which in turn prevents the decryption of the ciphertext, and thus does not allow for ∑x∈Xcxλx=s. As a result, this strategy is designed to withstand collusion. In addition, ENs will authenticate upon joining EBC; however, malicious ENs may unlawfully join EBC by forging legitimate user identities and may reconstruct SK through collusion, resulting in security issues. EBC in this paper utilizes PBFT consensus mechanism, which is capable of accommodating up to f=(n−1)/3 malicious nodes. The system is capable of functioning correctly and achieving consensus when n≥3f+1. In order to prevent malevolent ENs from colluding, the number of SKi necessary to reconstruct SK in the distributed key management scheme must satisfy t>(n−1)/3. Through TK.KeyGen( ) algorithm, the scheme generates the user’s private key USK, which is responsible for the ultimate decryption. This ensures that malicious ENs are unable to decrypt the plaintext even if they only obtain SK.

2) Data confidentiality.

In the initialization phase, CA generates and covertly saves MSK={yi,ki}. CA is the only trustworthy entity that will not disclose MSK. The Elliptic Curve Discrete Logarithmic Problem (ECDLP) is a difficult problem, and an illegal user cannot derive MSK from the publicly available PK={yiG,kiG}. DO maps W, which is composed of a symmetric key ck and a symmetric ciphertext index, to any point on the elliptic curve E. Once more, the attacker cannot acquire any intelligence on W due to the complexity of ECDLP. Furthermore, the access matrix in this paper is constructed using LSSS. If the attribute set S of DU does not adhere to the access structure, the secret value s cannot be introduced into the random vector v, and the attribute private key SK cannot be obtained. Consequently, the illegal user is unable to decrypt the ciphertext CT. Consequently, this scheme ensures the confidentiality of data.

3) EBC security.

The integrity of ciphertext can be verified without the involvement of intermediate entities, the construction cost can be reduced, and a single point of failure can be avoided by utilizing the tamper-proof and traceability characteristics of blockchain to establish a trusted environment for the data sharing process. Concurrently, the user’s privileges are verified. CT′ cannot be obtained from EN by users who do not meet the access structure and cannot decrypt it. The information in EBC can be monitored and verified in this paper. Non-tamperable transactions are recorded for any data submission and user access. The entire data sharing procedure can be traced by determining which DO uploads the data and which DU interacts with EN to access the data. Consequently, this scheme is protected by EBC.

5.2 Performance Analysis

The performance of blockchain, the computing capacity of IoT devices, and the CP-ABE encryption and decryption algorithm are the primary factors that influence the efficiency of data sharing in this paper. The consensus algorithm is the primary factor influencing the blockchain’s efficacy. The scheme employs the more efficient PBFT consensus algorithm to expedite the ENs in EBC’s consensus process, and the computing capacity of the IoT device is contingent upon its configuration. Consequently, this paper emphasizes the utilization of basic scalar multiplication in elliptic curve encryption for the purpose of enhancing the encryption and decryption efficiency of CP-ABE, as opposed to bilinear pairing. The computational overhead of the proposed scheme is compared to that of the literature [16,32,33] scheme in DO encryption, DU decryption, and outsourcing decryption through simulation experiments. A server with the Ubantu22.04 operating system is constructed as ENs and CA using an Intel Xeon Silver 4110 @ 2.10 GHz processor and 16 GB RAM. The Hyperledger Fabric 2.4.4 alliance chain is deployed on ENs. The build environment for the Ubantu22.04 operating system is constructed as DO and DU using an Intel Core i5-8250U @ 1.60 to 1.80 GHz processor and 4 GB RAM, with a docker deployment IPFS cluster. The simulation experiment is based on the Java Pairing-based Cryptography (JPBC) library, which employs y2=x3+ax+b elliptic curves of order 160 over a 512-bit finite field. The values of a=1 and b=1. The computational overheads of the phases are evaluated for varying quantities of attributes, and the results of the tests are averaged over 20 experiments.

The proposed scheme in this paper is compared to references [16,32–34] in terms of system functionality, theoretical computational overhead, and actual computational overhead to assess its performance. Reference [32] introduces public and private clouds. The public cloud is responsible for storing the encrypted data of DO, sending the encrypted user request list to the private cloud, and providing the corresponding ciphertexts for the authorized users. The private cloud is responsible for maintaining the authorized user lists and authenticating the users. The scheme employs multiple authorized authorities for key management; however, key management becomes challenging when the number of attributes exceeds a certain threshold and there is still a key escrow issue. Reference [33] developed an online privacy-preserving decryption test algorithm to allow the third-party cloud server to access the attribute values in the access policy and the user’s attribute values. Nevertheless, this approach regards the cloud server as a wholly trusted entity, despite the fact that it still poses security risks. Reference [16] guarantees the integrity and traceability of the data by storing the submitted encrypted data in the blockchain as transaction records. Additionally, it optimizes computational efficiency through outsourcing decryption. Nevertheless, the computational efficiency must be further enhanced due to the difficulty of bilinear pairing calculation, and the issue of limited storage capacity in the blockchain is not considered. Reference [34] developed and implemented a distributed IoT environment access control and access detection model that was combined with zero-knowledge proofs to prevent the leakage of user secrets to the server. Nevertheless, the edge server in this scheme is not entirely trustworthy and poses certain security dangers. This paper proposes a distributed key management scheme that capitalizes on the distributed characteristics of the edge blockchain to address the security issue and key leakage of the edge nodes. In the interim, the elliptic curve scalar multiplication method is employed to develop and execute an efficient CP-ABE algorithm. To mitigate the computational overhead at the user’s end, most decryption computations are transmitted to ENs. Table 1 displays the functional comparison of the various schemes mentioned above.

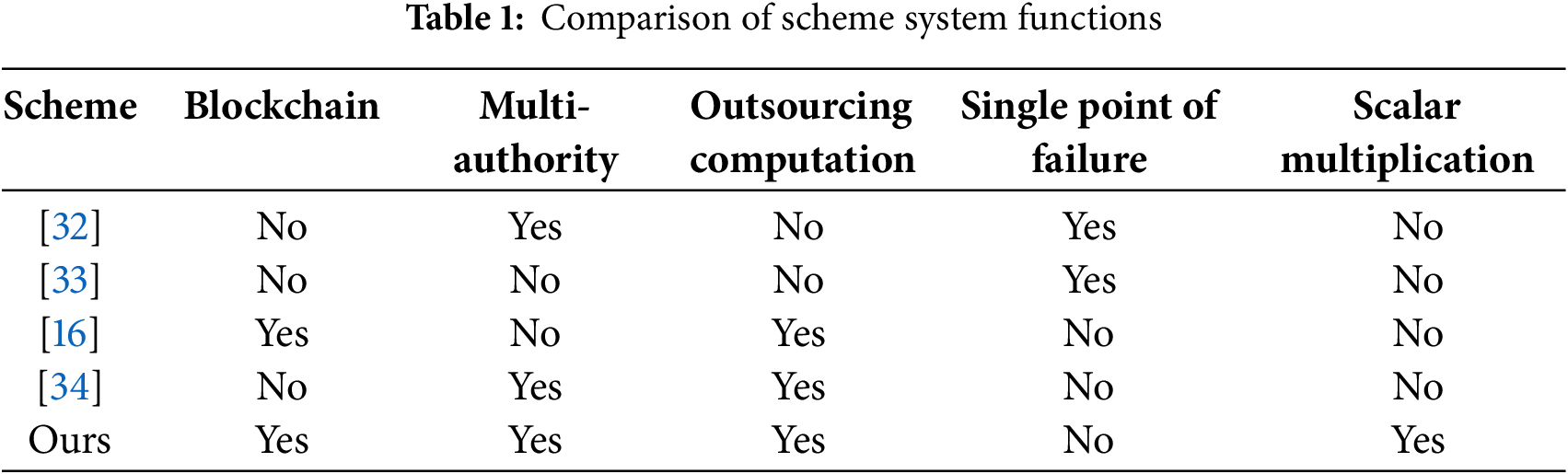
Table 2 illustrates the theoretical computational overhead of key generation, user encryption, user decryption, and outsourcing decryption in this scheme and References [16,32–34]. S denotes the number of attributes in the access matrix defined by DO, s denotes the minimum number of attributes satisfied by DU in the access matrix, Em denotes the multiplication operation in group G, Ee denotes the exponential operation in group G, P denotes the bilinear pairing operation, and E denotes the scalar multiplication operation of an elliptic curve.

Then, this paper’s experimental tests are conducted to compare the scheme with [16,32–34] in terms of actual computational overheads. The results are illustrated in Figs. 5–8, which correspond to the key generation time, DO encryption computation time, DU decryption computation time, and outsourcing decryption computation time, respectively. The key generation procedure in HCMACP-ABE is divided into two stages: the private cloud generates DO_key, and AAx_key generated by the AAs is aggregated on the CUA to generate AA_key. The keys generated in HP-CP-ABE consist of a decryption key and a test key. These keys are employed to decrypt the ciphertext and to confirm that the user is capable of decrypting it, respectively. Outsourced decryption is a component of the scheme in this paper and CEC-ABE and MA-CP-ABE, and pre-decryption keys must be generated during the key generation phase. This paper suggests a distributed key management method that is in conjunction with the distributed characteristics of edge blockchain. The key generation time of each scheme is illustrated in Fig. 5, and the results indicate that the key generation time of the scheme described in this paper is superior to that of the comparison scheme when the same number of attributes are used.

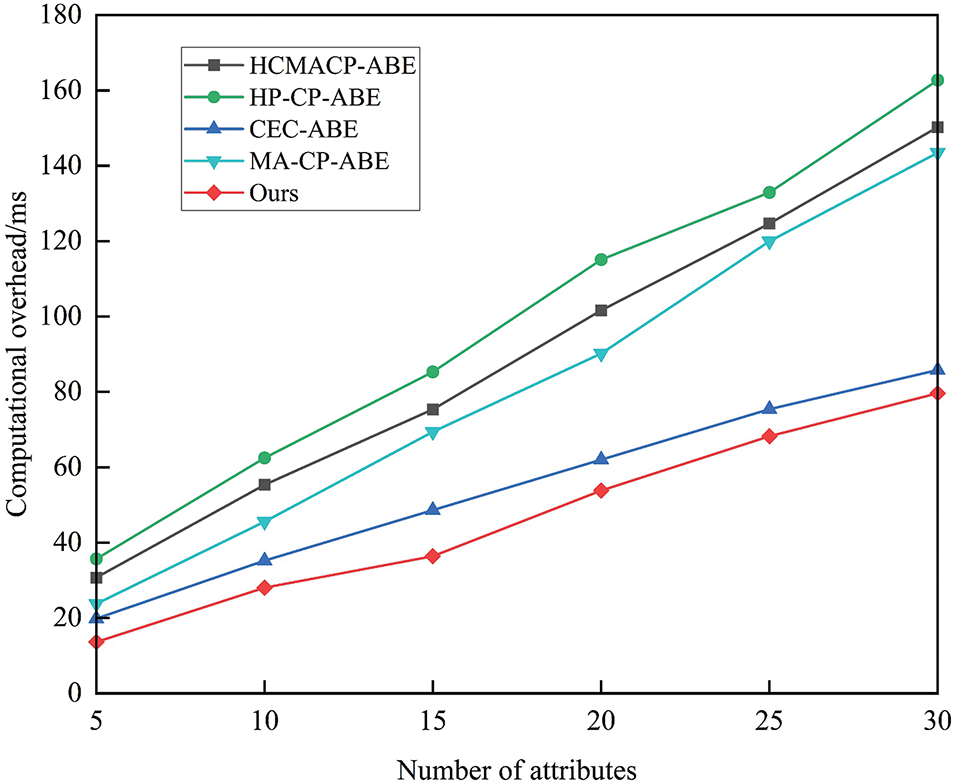
Figure 5: Key generation time

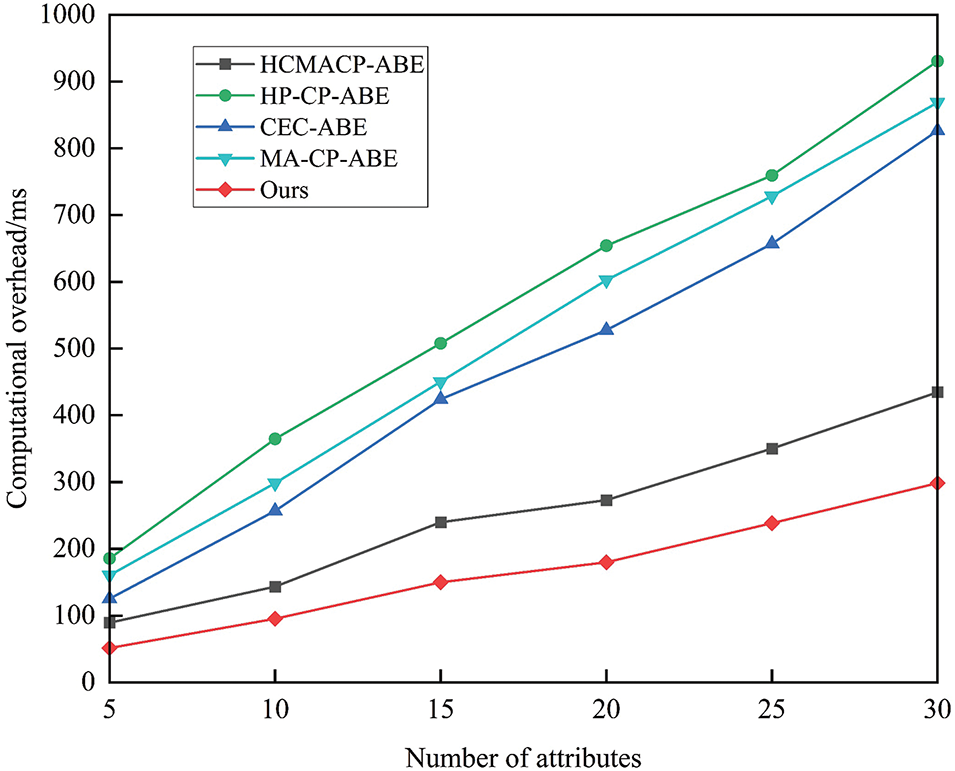
Figure 6: DO encryption calculation time

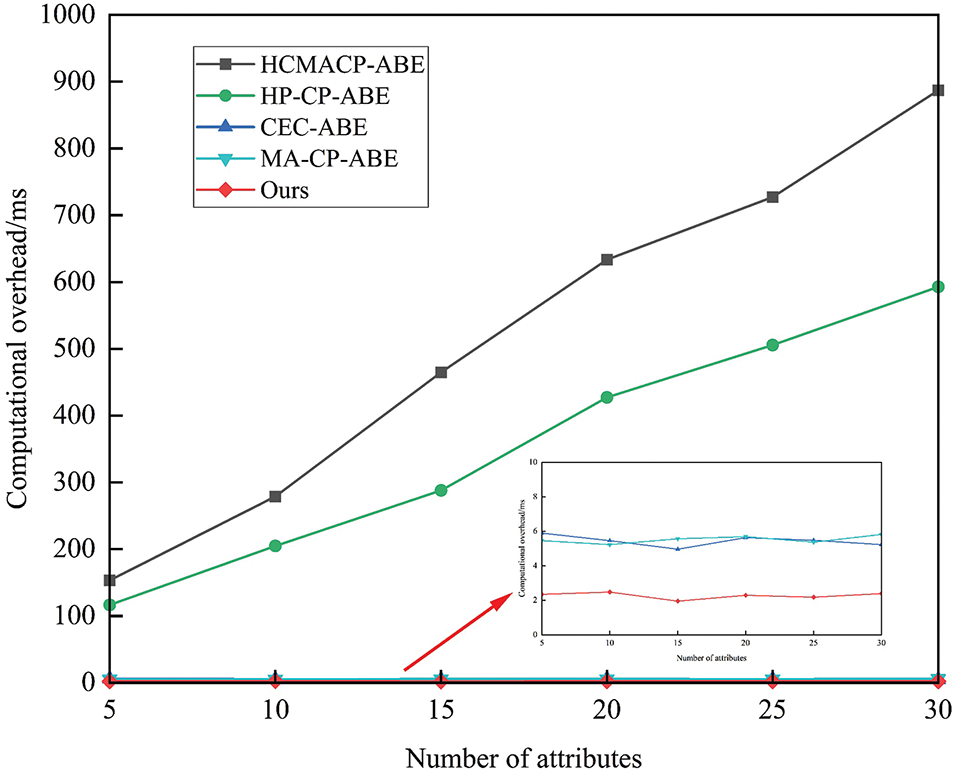
Figure 7: DU decryption calculation time

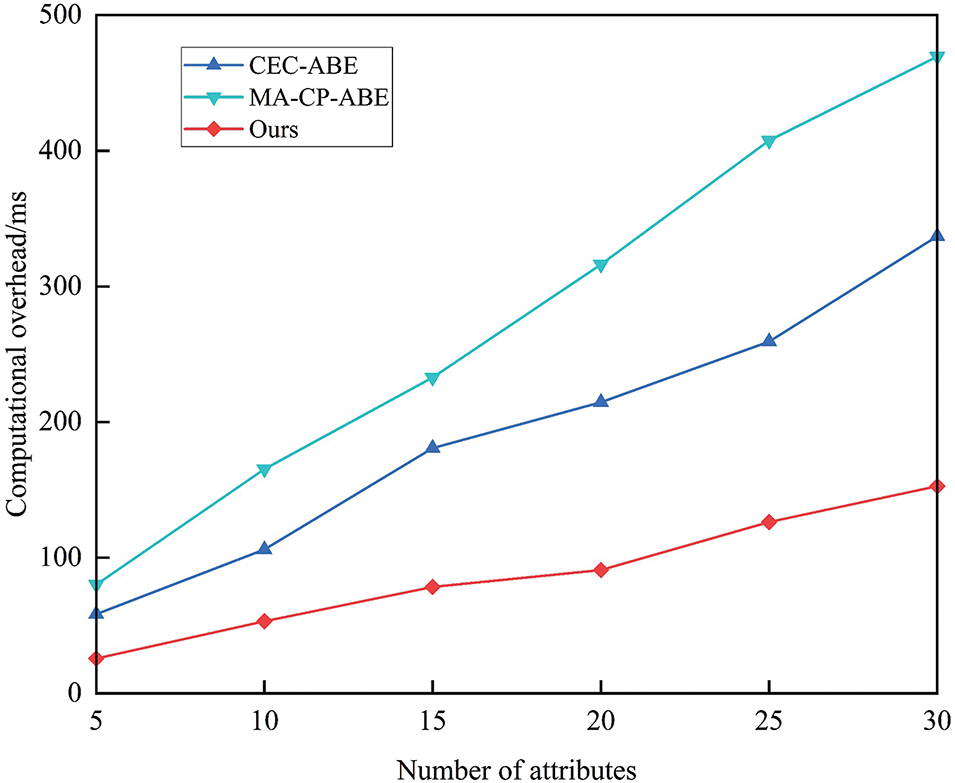
Figure 8: Outsourcing decryption calculation time

Fig. 6 illustrates the computation time for DO encryption. HCMACP-ABE suggested that data security could be achieved by storing and managing the ciphertext through a combination of public and private clouds. HP-CP-ABE developed an online privacy-preserving decryption test algorithm to prevent attribute value leakage. Furthermore, MA-CP-ABE integrates CP-ABE with zero-knowledge proofs to protect data privacy from cloud servers. Although these schemes improve data security to a certain extent, they invariably increase the computational overhead. In this paper’s scheme and CEC-ABE, the ciphertext is stored on the blockchain, which uses the blockchain’s features, including decentralization and tampering, to secure the data and reduce the computational overhead. It is evident from Fig. 6 that the time required for encrypted computation of DO in the scheme of this paper and comparison references increases as the number of attributes increases. Among them, HP-CP-ABE scheme has the maximum growth rate and consumes more time as the number of attributes increases compared to the other schemes. The elliptic curve scalar multiplication employed by DU of this paper scheme enhances the encryption efficiency of CP-ABE in comparison to the bilinear pairwise operation. The comparison reveals that the encryption time of DU of this paper scheme is shorter than that of the other schemes, and the growth rate is the smallest.

Fig. 7 illustrates the computation time for DU decryption. DU finalizes the decryption operations in HCMACP-ABE and HP-CP-ABE. However, this method has a substantial computational overhead and is not appropriate for lightweight IoT environments. The scheme described in this paper, in conjunction with CEC-ABE and MA-CP-ABE, transfers a portion of the decryption operations to ENs. DU is required to complete a minimal number of operations, and the computation time is not dependent on the number of attributes. In HCMACP-ABE and HP-CP-ABE, DU is required to perform an exponential operation, whereas the scheme in this paper only requires scalar multiplication, which has a more advantageous computational efficiency.

Fig. 8 illustrates the calculation time for outsourcing decryption. The schemes in HCMACP-ABE and HP-CP-ABE do not involve outsourcing decryption calculation; therefore, there is no data line segment in HCMACP-ABE and HP-CP-ABE in Fig. 8. The outsourcing function is introduced exclusively in CEC-ABE and MA-CP-ABE. Consequently, this paper’s scheme contrasts with schemes in CEC-ABE and MA-CP-ABE. It is evident from the figure that DU is more appropriate for lightweight IoT environments and does not require complex operations after transferring the majority of the decryption operations in the decryption phase to ENs. When contrasted with the completion of all decryption operations on DU, ENs possess superior computing capacity and significantly enhance computational efficiency. Simultaneously, the elliptic curve scalar multiplication employed in this scheme effectively reduces the calculation quantity.

6  Conclusion

This paper proposes a lightweight IoT data security sharing scheme based on attribute-based encryption and blockchain to address the issue of the current CP-ABE-based data security sharing scheme not satisfying the needs of lightweight IoT devices. A CP-ABE algorithm that is both efficient and lightweight is developed using elliptic curve cryptography. The encryption and decryption functions of the algorithm are implemented through elliptic curve scalar multiplication, as opposed to bilinear pairing. The pre-decryption stage is defined, and the pre-decryption key is employed to ensure the secure transmission of most decryption operations to ENs. Simultaneously, a distributed key management method is developed by integrating the EBC and CP-ABE algorithms. The issue of key escrow and leakage in existing CP-ABE schemes is resolved by the cooperative storage and distribution of attribute private keys by multiple ENs in EBC. The entire data sharing process is recorded and verified by EBC, which provides a trusted environment for ENs and incorporates tamper-proof and traceability features. Ultimately, the issue of insufficient storage capacity of EBC is resolved by combining IPFS with on-chain and off-chain storage. The application environment of IoT devices is intricate. Future research will concentrate on enhancing the efficiency of attribute revocation and key updates in lightweight IoT scenarios, resolving performance bottlenecks that may arise during the storage and retrieval of large amounts of data on the blockchain, and investigating optimization schemes to enhance the efficiency of data storage and retrieval. Moreover, the system’s flexibility and scalability will be further improved by the integration of cross-chain technology, which will facilitate the exchange of data between IoT devices across various chains.

Acknowledgement: The authors would like to express their gratitude to the members of the research group for their support.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Hongliang Tian; simulation, analysis, interpretation of results and draft manuscript preparation: Meiruo Li. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data is not available due to the nature of this research, participants of this study did not agree for their data to be shared publicly, so supporting data is not available.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Yang YL, Wang HC, Jiang RZ, Guo XN, Cheng J, Chen YY. A review of IoT-enabled mobile healthcare: technologies, challenges, and future trends. IEEE Internet Things J. 2022;9(12):9478–502. doi:10.1109/JIOT.2022.3144400. [Google Scholar] [CrossRef]

2. Esenogho E, Djouani K, Kurien AM. Integrating artificial intelligence internet of things and 5G for next-generation smartgrid: a survey of trends challenges and prospect. IEEE Access. 2022;10(4):4794–831. doi:10.1109/ACCESS.2022.3140595. [Google Scholar] [CrossRef]

3. Sun Y, Liu C, Li J, Liu Y. FADSF: a data sharing model for intelligent connected vehicles based on blockchain technology. Comput Mater Contin. 2024;80(2):2351–62. doi:10.32604/cmc.2024.048903. [Google Scholar] [CrossRef]

4. Karie NM, Sahri NM, Haskell-Dowland P. IoT threat detection advances, challenges and future directions. In: 2020 Workshop on Emerging Technologies for Security in IoT (ETSecIoT); 2020; Sydney, NSW, Australia. p. 22–9. [Google Scholar]

5. Nayak SK, Swain SK, Mohanta BK, Paikaray BK. Secure framework for data leakage detection and prevention in iot application. In: 2022 IEEE 2nd International Symposium on Sustainable Energy, Signal Processing and Cyber Security (iSSSC); 2022; Gunupur, India. p. 1–6. [Google Scholar]

6. Fu JS, Wang N. A practical attribute-based document collection hierarchical encryption scheme in cloud computing. IEEE Access. 2019;7:36218–32. doi:10.1109/ACCESS.2019.2905346. [Google Scholar] [CrossRef]

7. Yu Y, Shi JB, Li HL, Li YN, Du XJ, Guizani M. Key-policy attribute-based encryption with keyword search in virtualized environments. IEEE J Sel Areas Commun. 2020;38(6):1242–51. doi:10.1109/JSAC.2020.2986620. [Google Scholar] [CrossRef]

8. Han DZ, Pan NN, Li KC. A traceable and revocable ciphertext-policy attribute-based encryption scheme based on privacy protection. IEEE Trans Dependable Secure Comput. 2022;19(1):316–27. doi:10.1109/TDSC.2020.2977646. [Google Scholar] [CrossRef]

9. Xiong SM, Ni Q, Wang LM, Wang Q. SEM-ACSIT: secure and efficient multiauthority access control for IoT cloud storage. IEEE Internet Things J. 2020;7(4):2914–27. doi:10.1109/JIOT.2020.2963899. [Google Scholar] [CrossRef]

10. Xue KP, Gai N, Hong JN, Wei DSL, Hong PL, Yu NH. Efficient and secure attribute-based access control with identical sub-policies frequently used in cloud storage. IEEE Trans Dependable Secure Comput. 2022;19(1):635–46. doi:10.1109/TDSC.2020.2987903. [Google Scholar] [CrossRef]

11. Pu YW, Hu CQ, Deng SJ, Alrawais A. R2PEDS: a recoverable and revocable privacy-preserving edge data sharing scheme. IEEE Internet Things J. 2020;7(9):8077–89. doi:10.1109/JIOT.2020.2997389. [Google Scholar] [CrossRef]

12. Zheng WL, Zheng ZB, Chen XP, Dai KM, Li PS, Chen RF. NutBaaS: a Blockchain-as-a-service platform. IEEE Access. 2019;7:134422–33. doi:10.1109/ACCESS.2019.2941905. [Google Scholar] [CrossRef]

13. Lian J, Wang S, Xie Y. TDRB: an efficient tamper-proof detection middleware for relational database based on blockchain technology. IEEE Access. 2021;9:66707–22. doi:10.1109/ACCESS.2021.3076235. [Google Scholar] [CrossRef]

14. Maesa DDF, Mori P, Ricci L. A blockchain based approach for the definition of auditable access control systems. Comput Secur. 2019;84(7):93–119. doi:10.1016/j.cose.2019.03.016. [Google Scholar] [CrossRef]

15. Zhao C, Han D, Li C, Wang H. A blockchain consensus mechanism to optimize reputation-based distributed energy trading in urban energy system. IEEE Access. 2024;12:53698–712. doi:10.1109/ACCESS.2024.3387715. [Google Scholar] [CrossRef]

16. Jiang Y, Xu XL, Xiao F. Attribute-based encryption with blockchain protection scheme for electronic health records. IEEE Trans Netw Serv Manag. 2022;19(4):3884–95. doi:10.1109/TNSM.2022.3193707. [Google Scholar] [CrossRef]

17. Xu H, He Q, Li XC, Jiang BC, Qin KY. BDSS-FA: a blockchain-based data security sharing platform with fine-grained access control. IEEE Access. 2020;8:87552–61. doi:10.1109/ACCESS.2020.2992649. [Google Scholar] [CrossRef]

18. Sahai A, Waters B. Fuzzy identity-based encryption. In: Advances in Cryptology-EUROCRYPT 2005: 24th Annual International Conference on the Theory and Applications of Cryptographic Techniques; 2005 May 22–26; Aarhus, Denmark. p. 457–73. [Google Scholar]

19. Bethencourt J, Sahai A, Waters B. Ciphertext-policy attribute-based encryption. In: 2007 IEEE Symp Secur Privacy (SP’07); 2007; Berkeley, CA, USA. p. 321–34. [Google Scholar]

20. Chen NY, Li JG, Zhang YC, Guo YY. Efficient CP-ABE scheme with shared decryption in cloud storage. IEEE Trans Comput. 2022;71(1):175–84. doi:10.1109/TC.2020.3043950. [Google Scholar] [CrossRef]

21. Wei JH, Chen XF, Huang XY, Hu XX, Susilo W. RS-HABE: revocable-storage and hierarchical attribute-based access scheme for secure sharing of e-health records in public cloud. IEEE Trans Dependable Secure Comput. 2021;18(5):2301–15. [Google Scholar]

22. Zhao CB, Xu L, Li JG, Fang H, Zhang YH. Toward secure and privacy-preserving cloud data sharing: online/offline multiauthority CP-ABE with hidden policy. IEEE Syst J. 2022;16(3):4804–15. doi:10.1109/JSYST.2022.3169601. [Google Scholar] [CrossRef]

23. Yang YB, Zhang JW, Liu XM, Ma JF. A scalable and auditable secure data sharing scheme with traceability for fog-based smart logistics. IEEE Internet Things J. 2023;10(10):8603–17. doi:10.1109/JIOT.2022.3220850. [Google Scholar] [CrossRef]

24. Cai JY, Zhang HJ, Duo Z, Wang X, Zhao XW. A multi-group-supporting policy hidden fine-grained data sharing scheme in 5G-enabled IoT with edge computing. IEEE Access. 2024;12:46362–78. doi:10.1109/ACCESS.2024.3381509. [Google Scholar] [CrossRef]

25. Zhao CC, Zhang LY, Wu Q, Rezaeibagha F. Publicly accountable data-sharing scheme supporting privacy protection for fog-enabled VANETs. IEEE Trans Veh Technol. 2024;73(6):8487–502. doi:10.1109/TVT.2024.3360698. [Google Scholar] [CrossRef]

26. Li H, Pei LS, Liao D, Chen S, Zhang M, Xu D. FADB: a fine-grained access control scheme for VANET data based on blockchain. IEEE Access. 2020;8:85190–203. doi:10.1109/ACCESS.2020.2992203. [Google Scholar] [CrossRef]

27. Le TV, Hsu CL, Chen WX. A hybrid blockchain-based log management scheme with nonrepudiation for smart grids. IEEE Trans Ind Inform. 2022;18(9):5771–82. doi:10.1109/TII.2021.3136580. [Google Scholar] [CrossRef]

28. Zhang LY, Zhang TS, Wu Q, Mu Y, Rezaeibagha F. Secure decentralized attribute-based sharing of personal health records with blockchain. IEEE Internet Things J. 2021;9(14):12482–96. doi:10.1109/JIOT.2021.3137240. [Google Scholar] [CrossRef]

29. Guo ZZ, Wang GL, Zhang GY, Li YX, Ni JQ. A multifactor combined data sharing scheme for vehicular fog computing using blockchain. IEEE Internet Things J. 2023;10(22):20049–64. doi:10.1109/JIOT.2023.3282672. [Google Scholar] [CrossRef]

30. Fugkeaw S, Gupta RP, Worapaluk K. Secure and fine-grained access control with optimized revocation for outsourced IoT EHRs with adaptive load-sharing in fog-assisted cloud environment. IEEE Access. 2024;12:82753–68. doi:10.1109/ACCESS.2024.3412754. [Google Scholar] [CrossRef]

31. Zhang QY, Xu C, Zhong H, Gu CJ, Cui J. Revocable and efficient blockchain-based fine-grained access control against EDoS attacks in cloud storage. IEEE Trans Comput. 2024;73(8):2012–24. doi:10.1109/TC.2024.3398502. [Google Scholar] [CrossRef]

32. Xie MD, Ruan YY, Hong HB, Shao J. A CP-ABE scheme based on multi-authority in hybrid clouds for mobile devices. Fut Gener Comput Syst. 2021;121(5):114–22. doi:10.1016/j.future.2021.03.021. [Google Scholar] [CrossRef]

33. Zhang ZS, Zhang W, Qin ZG. A partially hidden policy CP-ABE scheme against attribute values guessing attacks with online privacy-protective decryption testing in IoT assisted cloud computing. Fut Gener Comput Syst. 2021;123(4):181–95. doi:10.1016/j.future.2021.04.022. [Google Scholar] [CrossRef]

34. Zhang Z, Zhou S. A decentralized strongly secure attribute-based encryption and authentication scheme for distributed Internet of Mobile Things. Comput Netw. 2021;201(1):108553. doi:10.1016/j.comnet.2021.108553. [Google Scholar] [CrossRef]